Novel Method of Fitting a Nonlinear Function to Data of Measurement Based on Linearization by Change Variables, Examples and Uncertainty
Abstract
1. Introduction
2. Main Idea of Proposed Method
- The simplest form with the determined dependent variable y, i.e., y = f (x).
- On each side of the equal sign are nonlinear functions of only y or x, .
- The implicit form of the nonlinear function H(x, y) = 0.
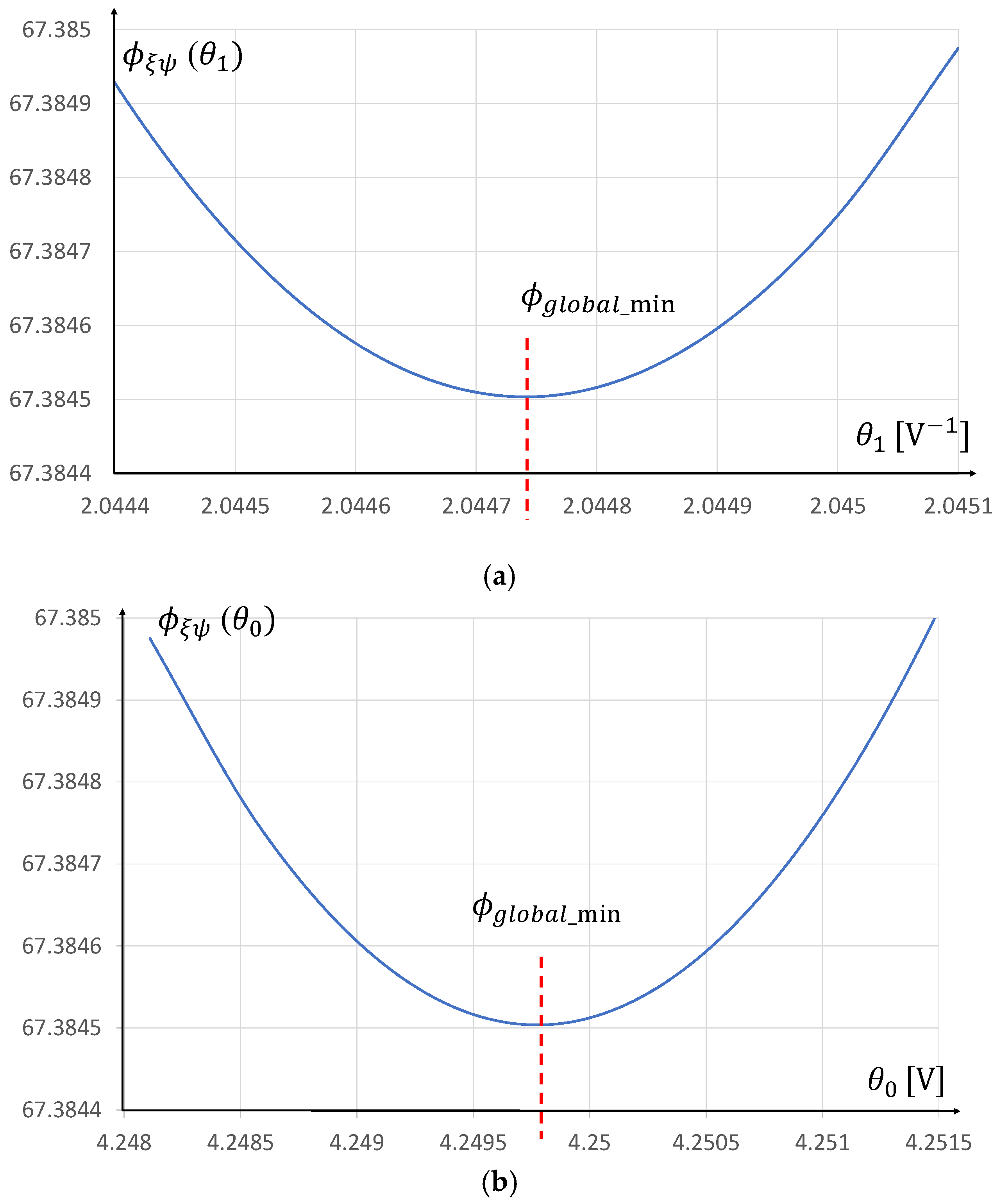
3. Examples of Nonlinear Functions Fitted by Change Variables for Linearization
3.1. Transformations of Single Coordinate x (Type I)
Parabola Fitting—Method I
3.2. Transformation of Both Separatable Coordinates (Type II)
3.3. Fitting the Implicit Dependence (Type III)
- standard uncertainties:
- expanded uncertainties:
4. Examples of Measurement Circuits with Nonlinear Functions
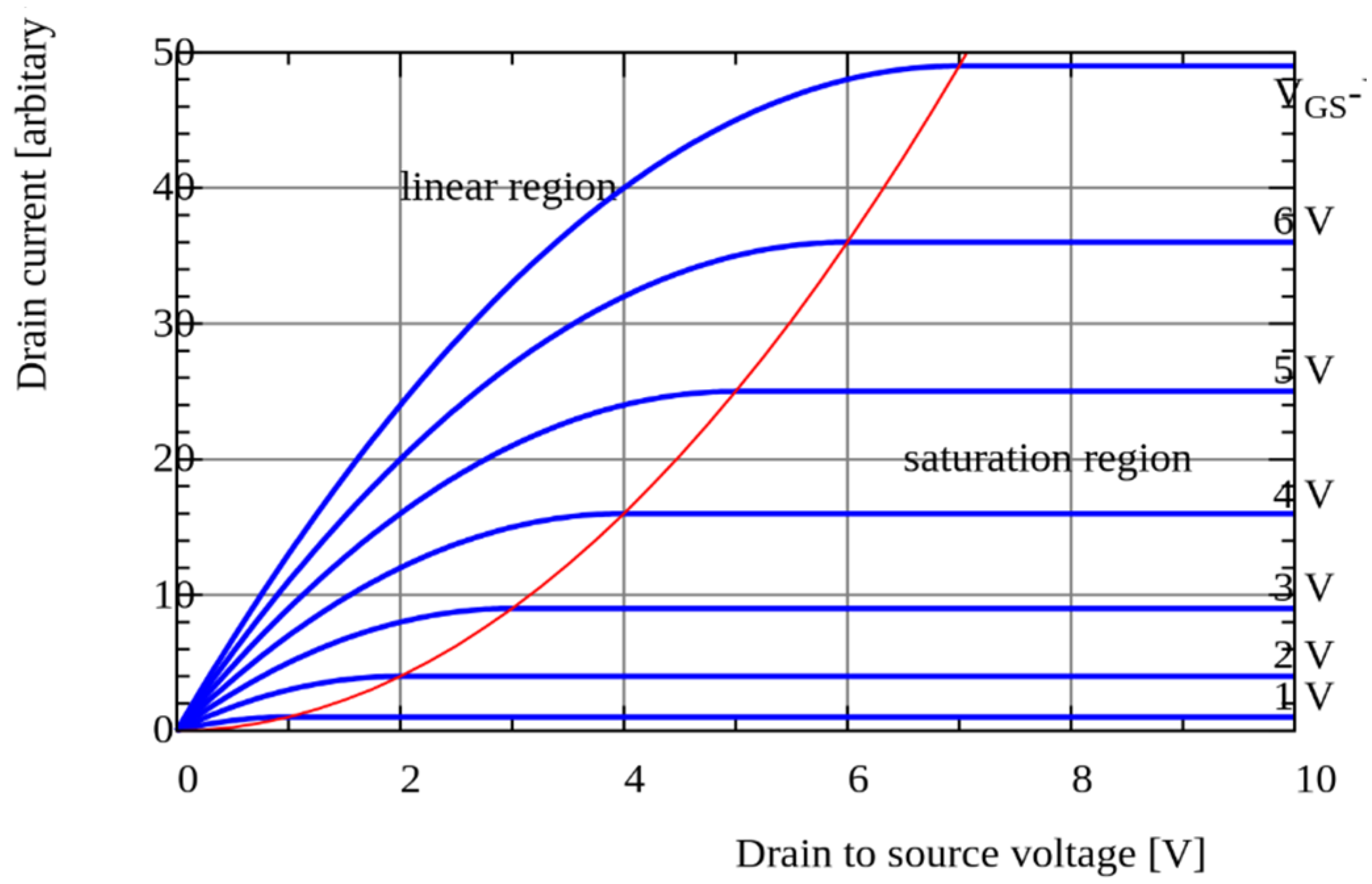
4.1. Matching the Characteristics of a MOSFET
4.2. Measurement of a Series Connection of a Diode D and Resistor r Representing Internal Resistance of This Circuit (Type III)
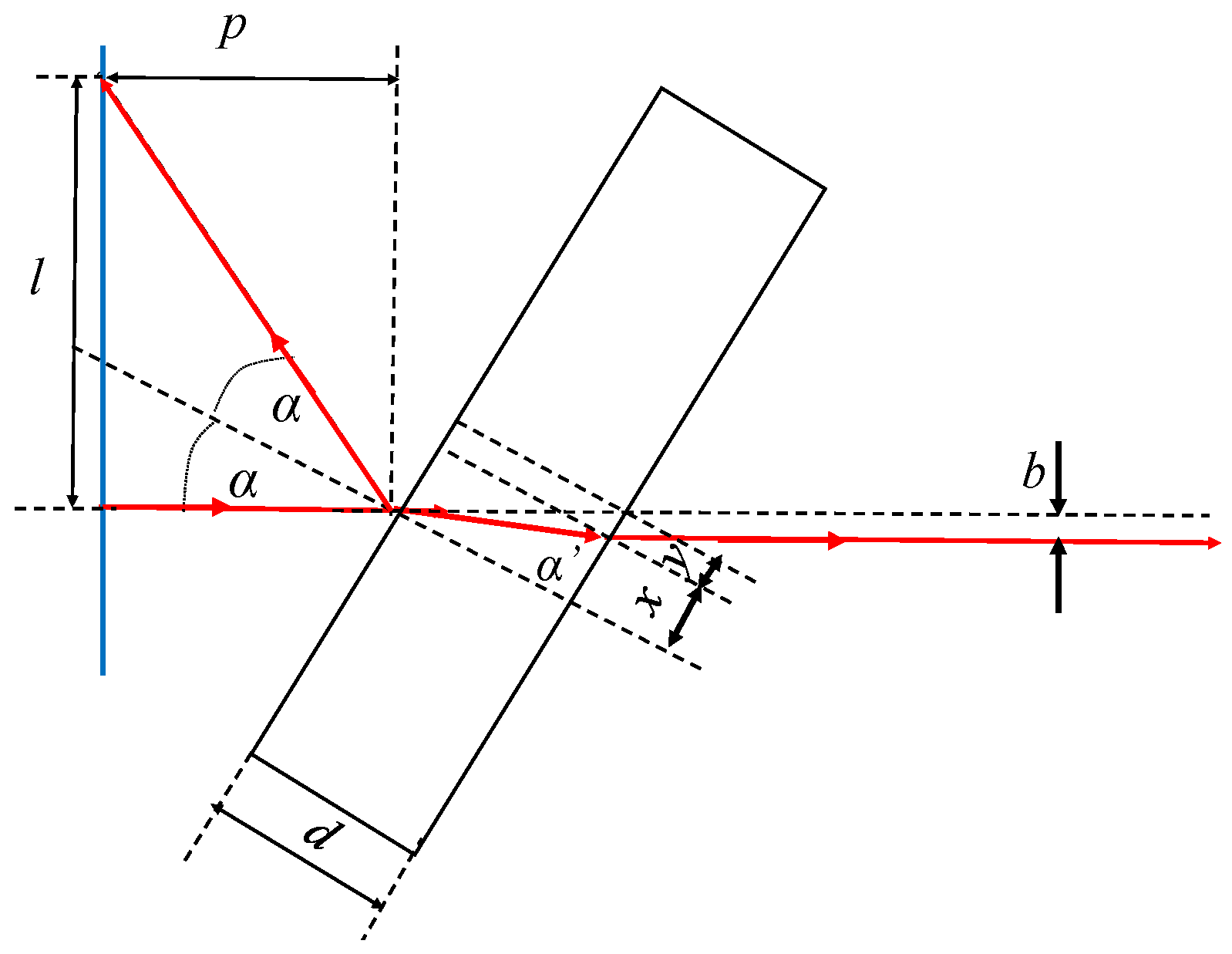
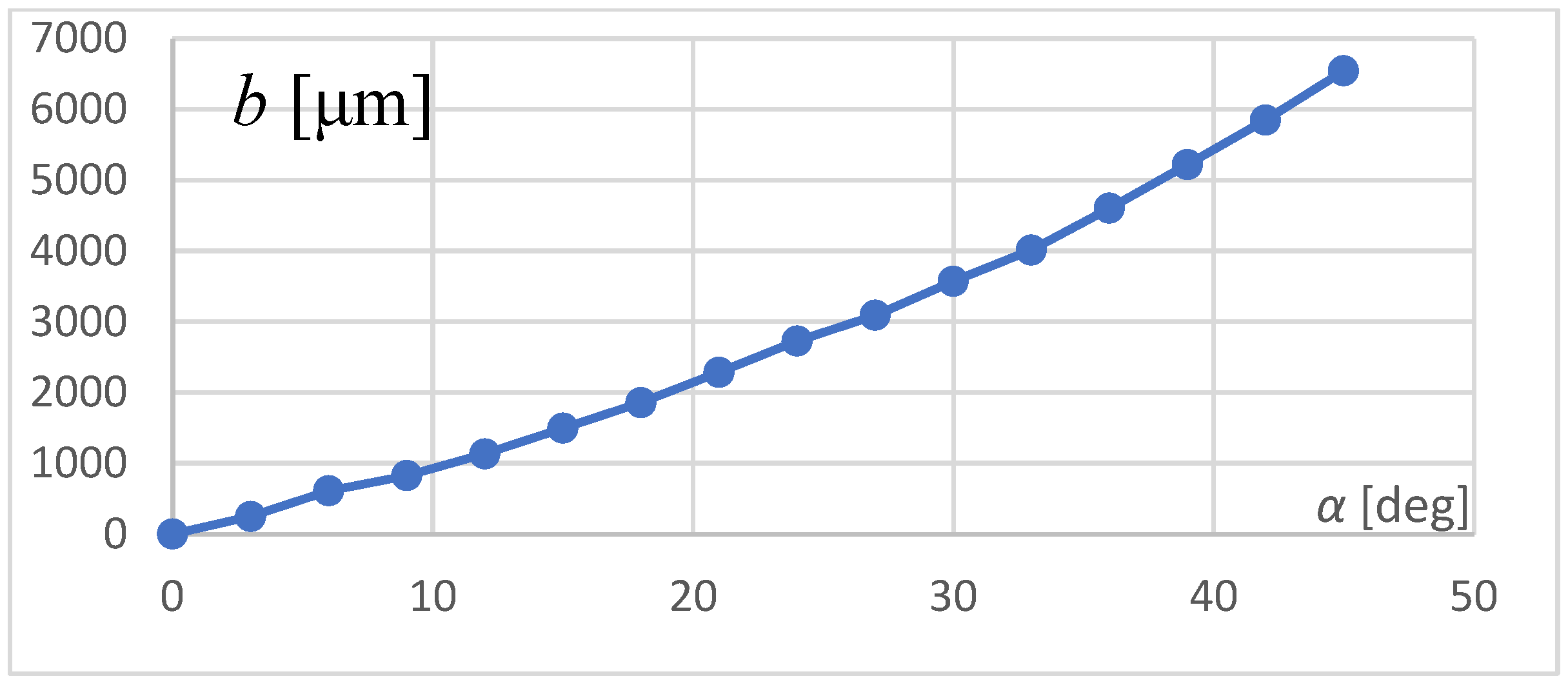
4.3. Measuring the Thickness of a Plane-Parallel Plate Using the Law of Refraction
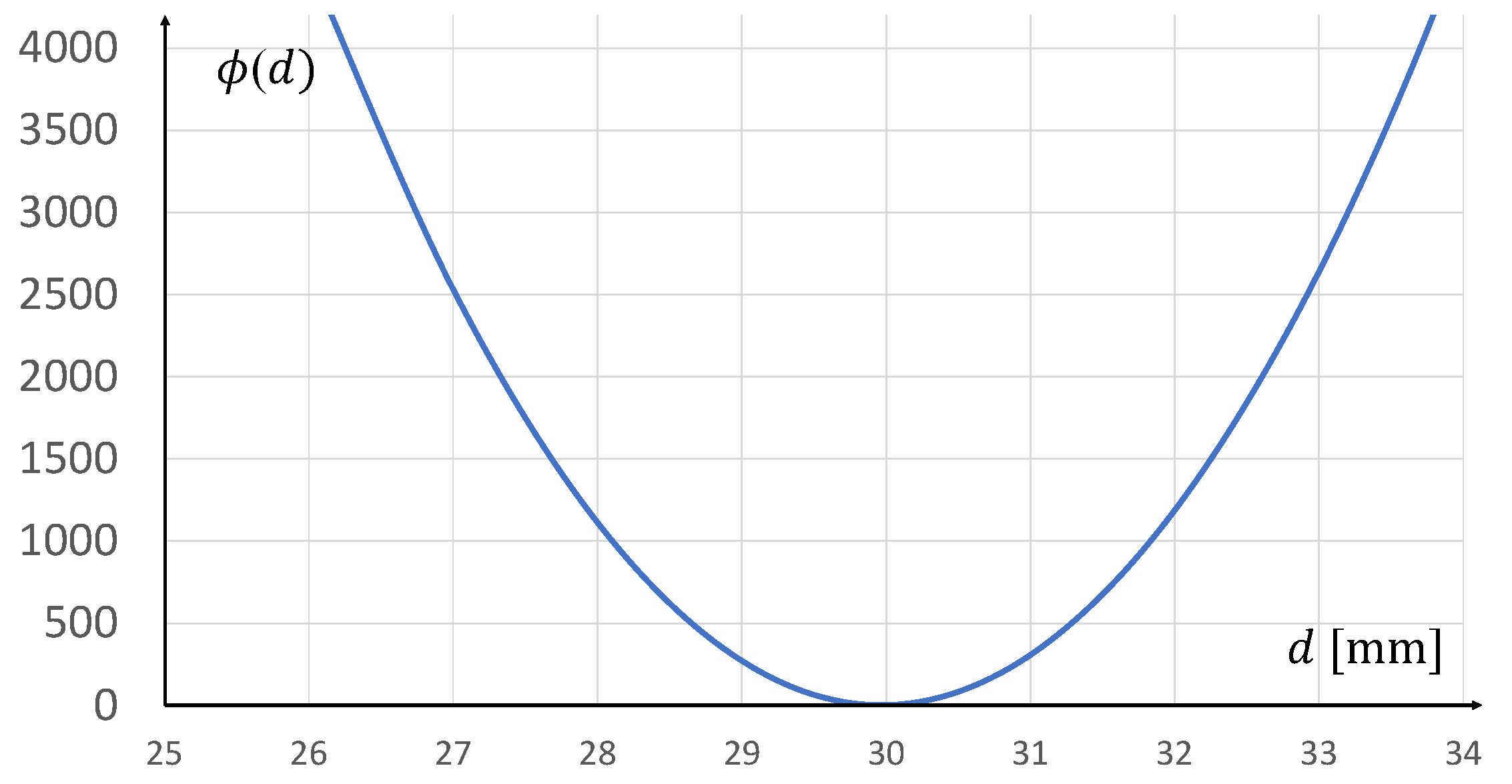
4.4. Calculation of the Measured Value d and Its Uncertainty
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Joint Committee for Guides in Metrology (BIPM, IEC, IFCC0, ILAC, ISO, IUPAC, IUPAP & OIML). JCGM 100:2008 Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, and its Supplements; International Bureau of Weights and Measures BIPM: Sevres, France, 2008. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Dennis, J.E., Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; SIAM 1996 Reproduction of Prentice-Hall: New York, NY, USA, 1983. [Google Scholar]
- Draper, R.D.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Kanzov, C.H.; Yamashita, N.; Fukushima, M. Levenberg–Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints. J. Comput. Appl. Math. 2004, 172, 375–391. [Google Scholar] [CrossRef]
- Madsen, K.; Nielsen, H.B. Tinglef. Method for Non-Linear Least Squares Problems, 2nd ed.; Informatics and Mathematical Modelling, Technical University of Denmark: Lyngby, Denmark, 2004. [Google Scholar]
- Krystek, M.; Mathias, A. A least-squares algorithm for fitting data points with mutually correlated coordinates to a straight line. Meas. Sci. Technol. 2011, 22, 035101. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Jazaeri, S. Weighted total least squares formulated by standard least squares theory. J. Geod. Sci. 2012, 2, 113–124. [Google Scholar] [CrossRef]
- Grafarend, E.W.; Awange, J.L. Applications of Linear and Nonlinear Models—Fixed Effects, Random Effects, and Total Least Squares. J. Geod. Sci. 2013, 3, 77–78. [Google Scholar] [CrossRef]
- Christodoulos, A.; Par Floudalos, M. Encyclopedia of Optimization; Springer: Berlin/Heidelberg, Germany, 2008; p. 1130. ISBN 978038774583. [Google Scholar]
- Mascarenha, S.W.F. The divergence of the BFGS and Gauss Newton Methods Math. Programming 2013, 147, 253–276. [Google Scholar] [CrossRef]
- Gulsen, M.; Smith, A.E.; Tate, D.M. A Genetic Algorithm Approach to Curve Fitting. Int. J. Prod. Res. 1995, 33, 911–933. [Google Scholar] [CrossRef]
- Denison, D.G.T.; Mallic, B.K.; Smith, A.F.M. Automatic Bayesian Curve Fitting. Journal of the Royal Statistical Society. Ser. B (Stat. Methodol.) 1998, 60, 333–350. [Google Scholar] [CrossRef]
- Karr, C.L.; Weck, B.; Massart, D.L.; Vankerbergh, P. Least Median Squares Curve Fitting Using a Genetic Algorithm. Eng. Appl. Artif. Intell. 1995, 8, 177–189. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Least Squares Methods for Treating Problems with Uncertainty in x and y. Anal. Chem. 2020, 92, 10863–10871. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Verma, B. Nonlinear Curve Fitting to Stopping Power Data Using RBF Neural Networks. Expert Syst. Appl. 2016, 45, 161–171. [Google Scholar] [CrossRef]
- Li, M.; Li, L.D. Novel Method of Curve Fitting Based on Optimized Extreme Learning Machine. Appled Artif. Intell. 2020, 34, 849–865. [Google Scholar] [CrossRef]
- Klauenberg, K.; Martens, S.; Bošnjaković, A.; Cox, M.G.; Van der Veen, A.M.H.; Elster, C. The GUM perspective on straight-line errors-in-variables regression. Measurement 2022, 187, 110340. [Google Scholar] [CrossRef]
- Puchalski, J.; Warsza, Z.L. Assessment of the uncertainty of selected nonlinear functions determined from measurements by the linear regression method. In Advanced Mathematical and Computational Tools in Metrology and Testing XIII; Series on Advances in Mathematics for Applied, Sciences; Pavese, F., Bošnjaković, A., Eichstädt, S., Forbes, A.B., Alves e Sousa, J., Eds.; World Scientific Publishing Co.: New York, NY, USA; London, UK; Singapore, 2024; Volume 94, pp. 288–307. [Google Scholar] [CrossRef]
- Puchalski, J.; Warsza, Z.L. The method of fitting a non-linear function to data of measured points and its uncertainty band. Pomiary Automatyka Robotyka PAR. n3_2023. pp. 45–55. Available online: https://par.pl/Archiwum/2023/3-2023/Metoda-dopasowania-funkcji-nieliniowej-do-danych-punktow-pomiarowych-i-jej-pasmo-niepewnosci (accessed on 12 November 2024). (In Polish).
- Puchalski, J.G. Nonlinear Curve Fitting to Measurement Points with WTLS Method Using Approximation of Linear Model. Int. J. Auto. AI Mach. Learn. 2024, 4, 36–60, ISSN 2593-7568. [Google Scholar] [CrossRef]
- MOSFET Physics. Available online: https://www.mks.com/n/mosfet-physics (accessed on 1 January 2020).

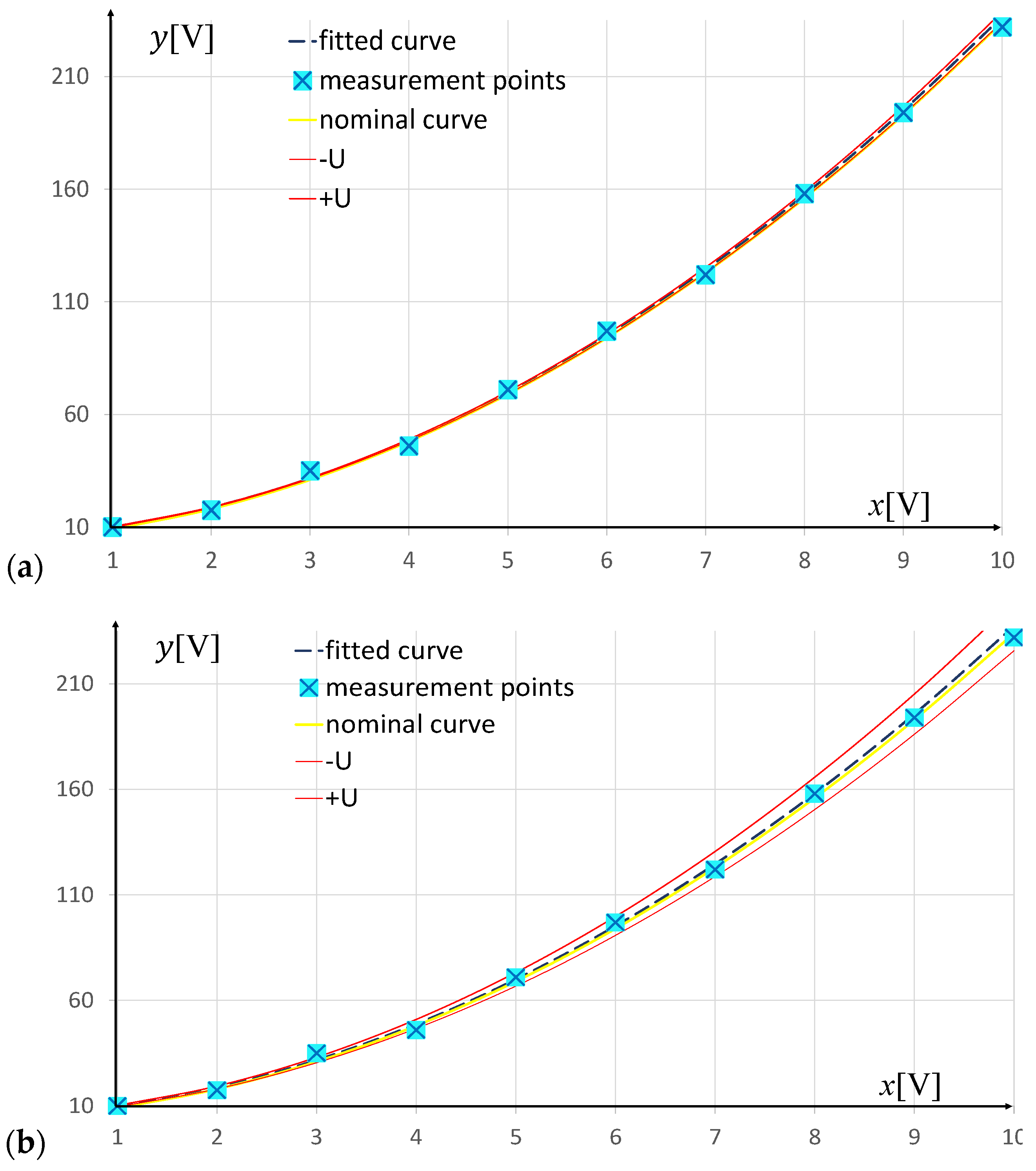

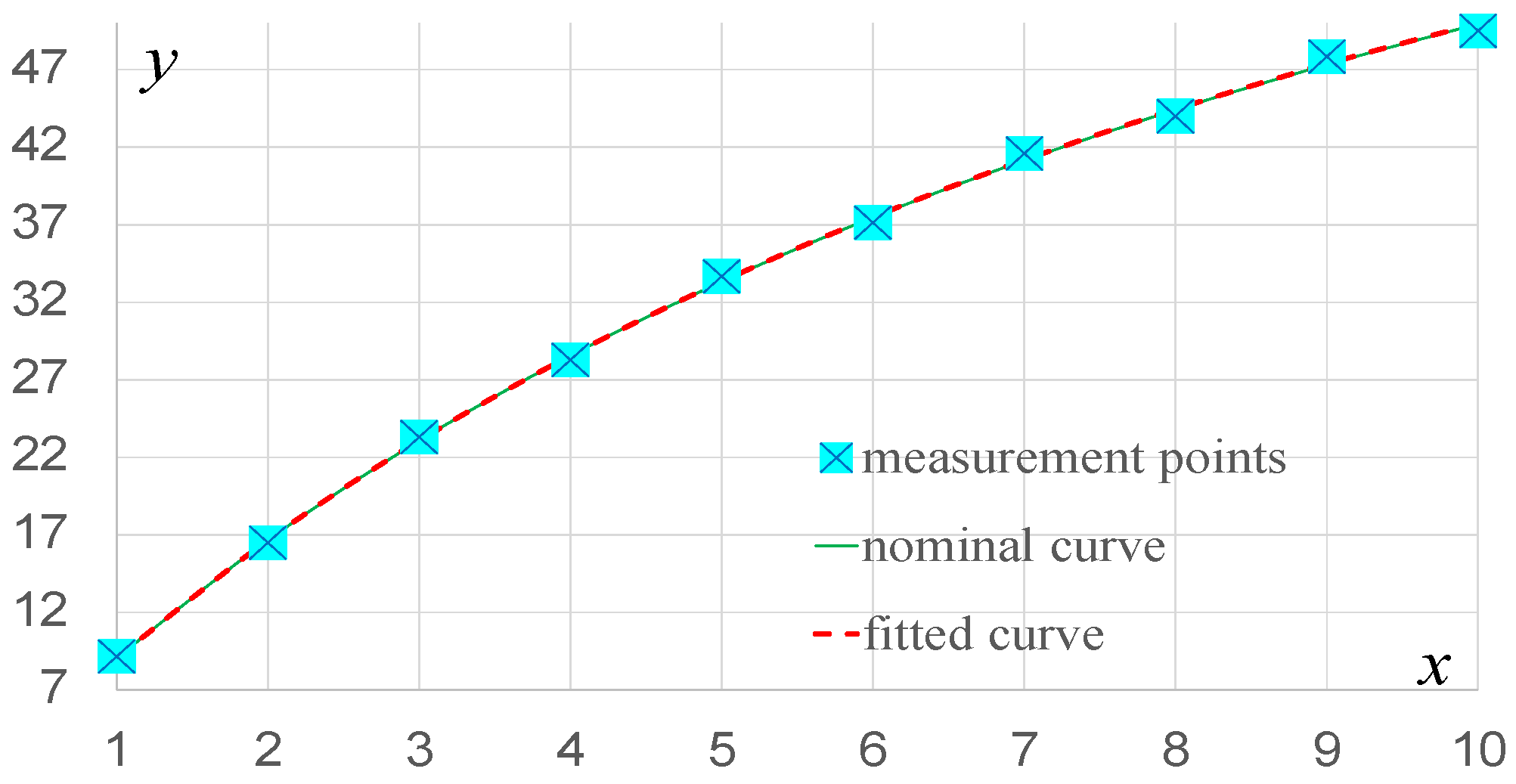

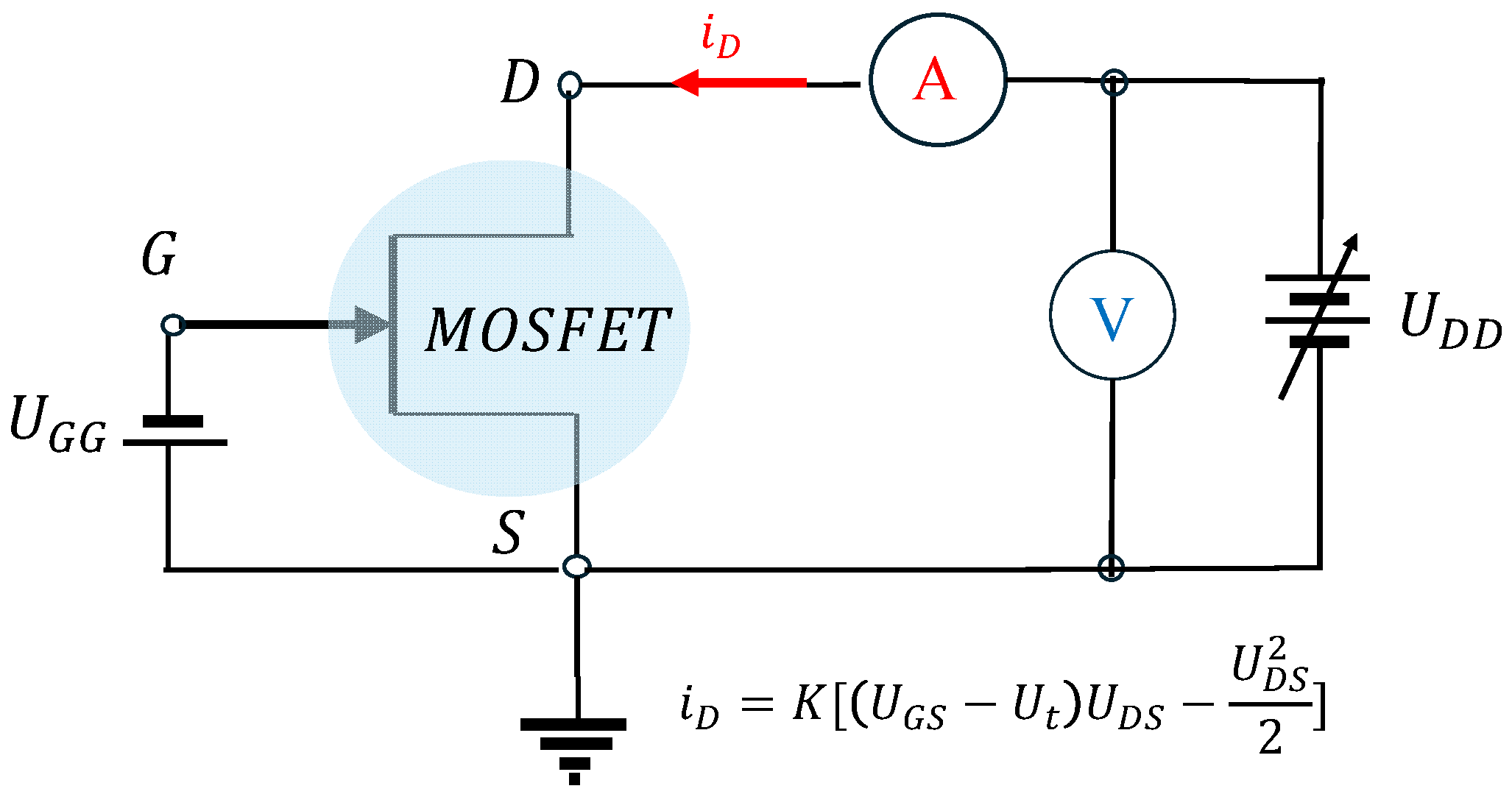
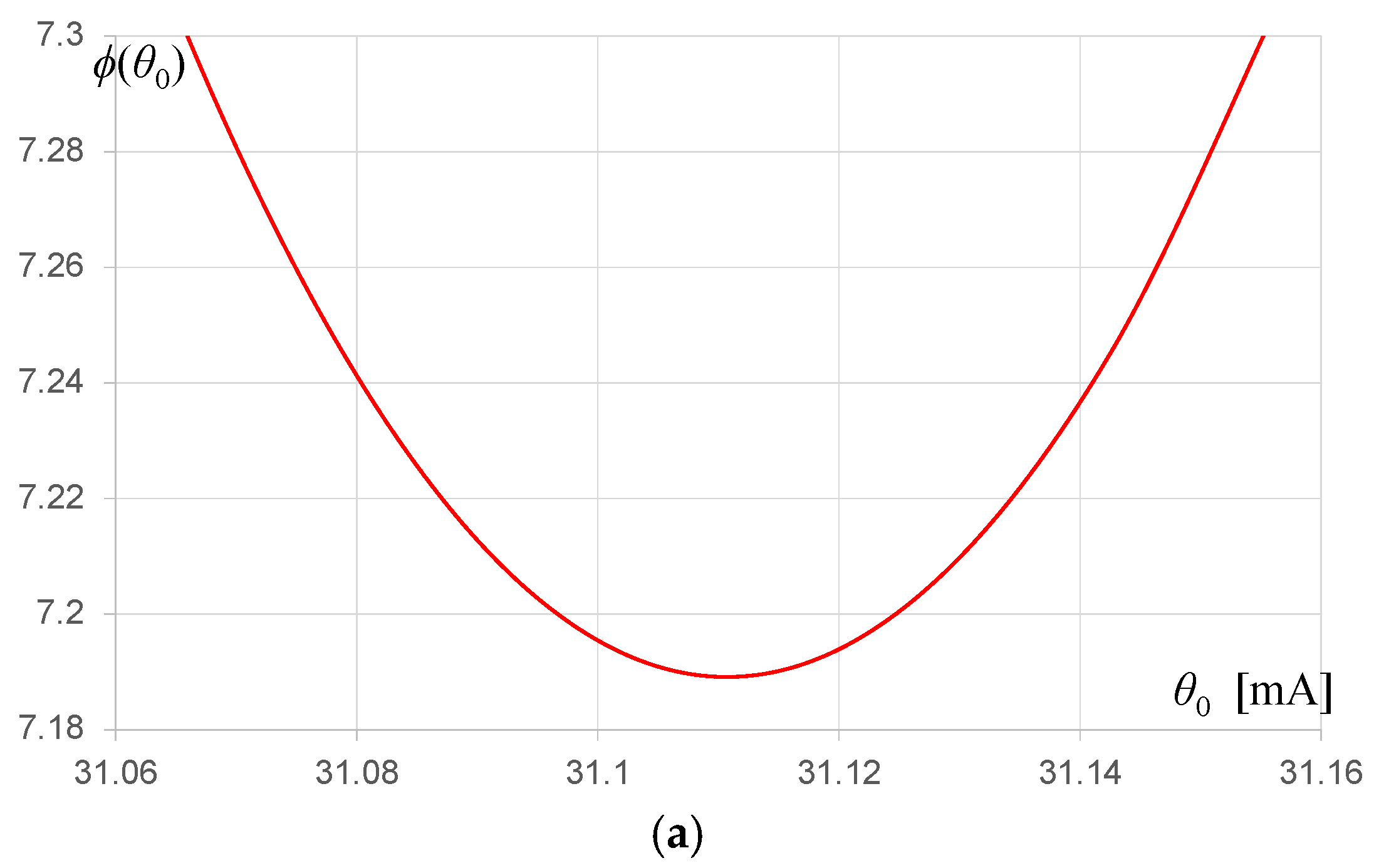

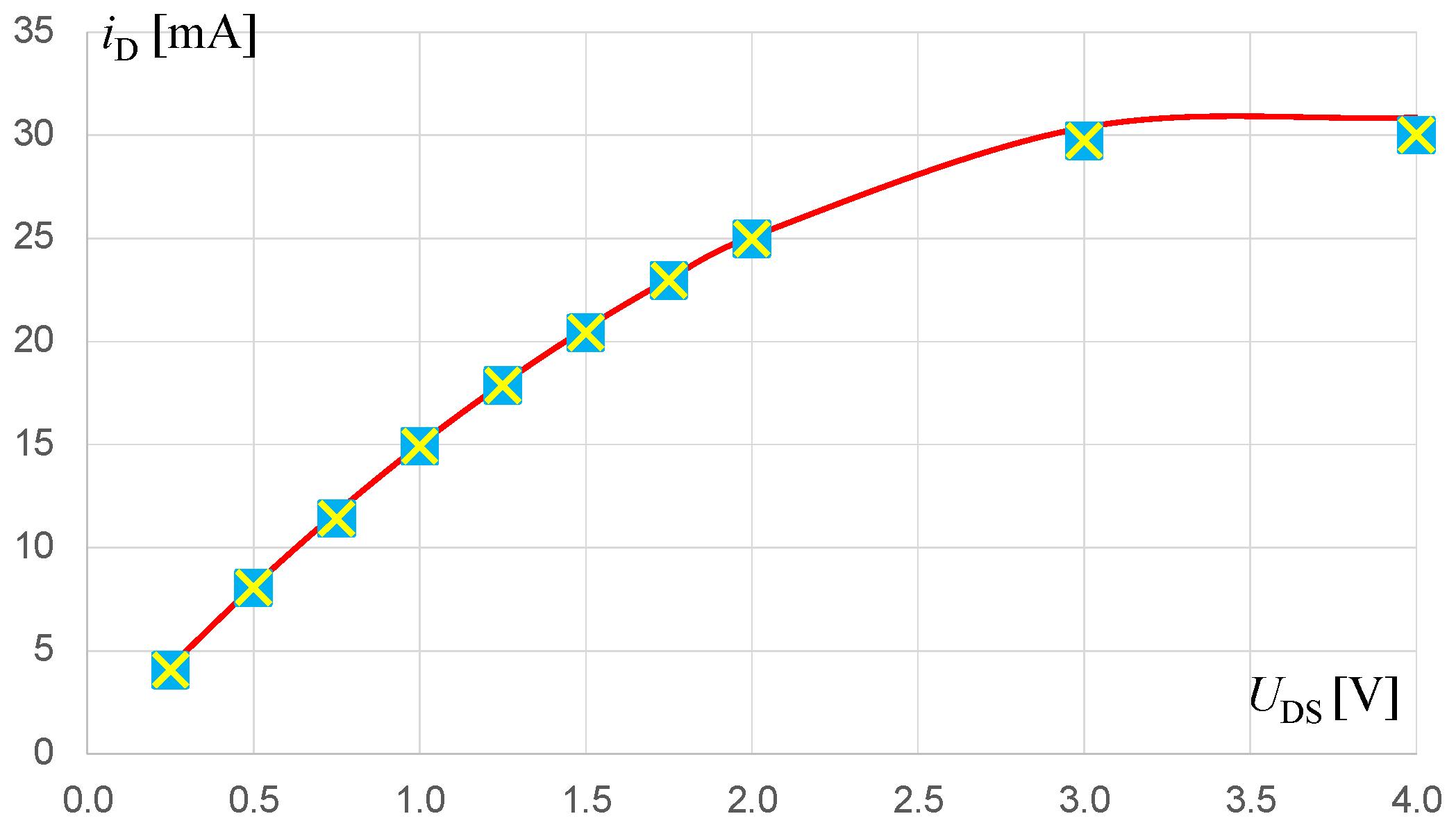
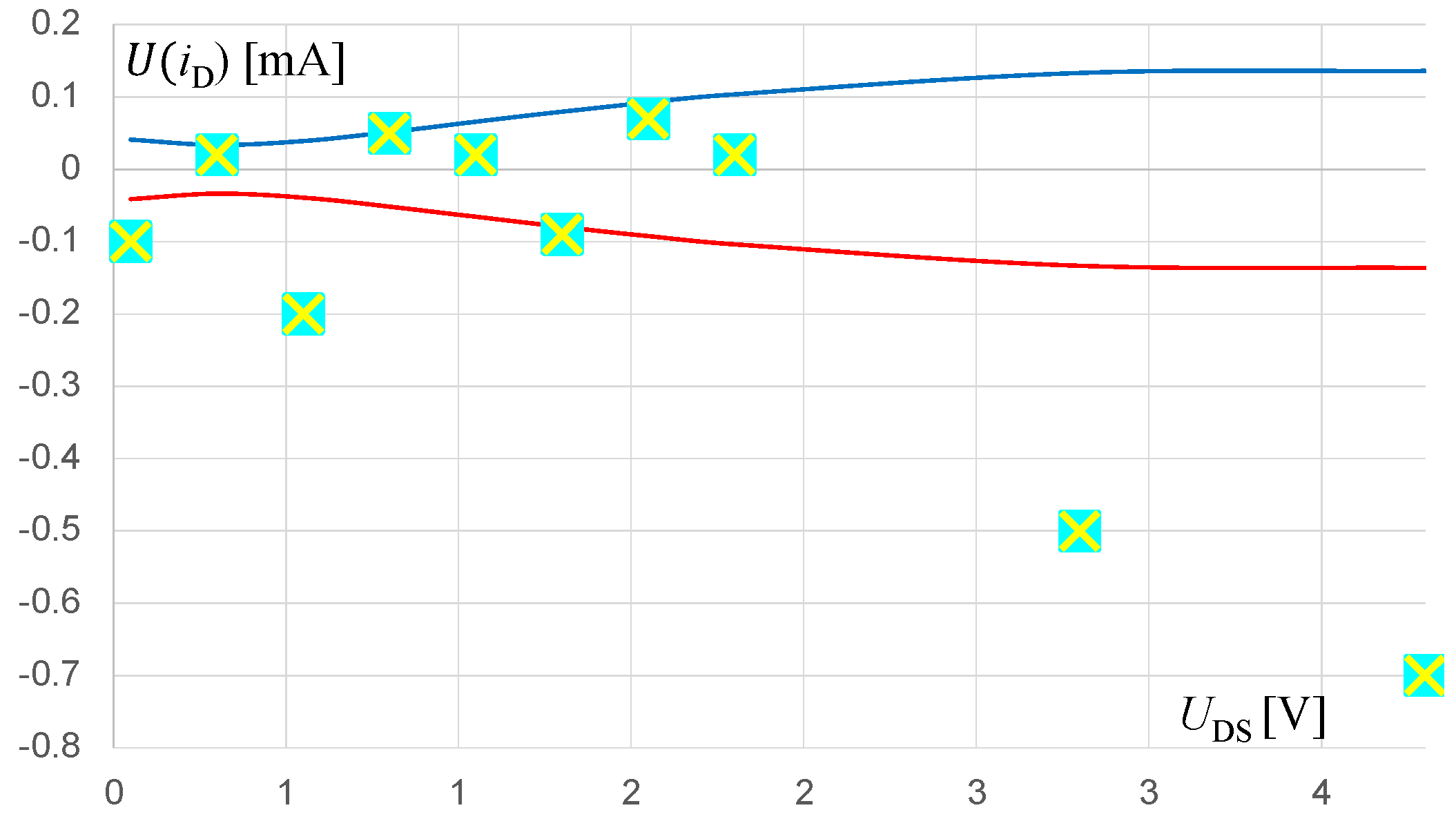



| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 9.18 | 16.50 | 23.31 | 28.29 | 33.67 | 37.13 | 41.59 | 44.00 | 47.84 | 49.50 |
| No. | Coordinates of Measurement Points | Matching Errors to Nominal Parabolic Characteristic Δy [V] | |
|---|---|---|---|
| xi [V] | [V] | ||
| 1 | 2.79 | 10.00 | −1.00 |
| 2 | 7.13 | 17.50 | 0.50 |
| 3 | 13.47 | 35.00 | −4.00 |
| 4 | 21.81 | 46.00 | 2.00 |
| 5 | 32.15 | 71.00 | −2.00 |
| 6 | 44.49 | 97.00 | −3.00 |
| 7 | 58.83 | 122.00 | 1.00 |
| 8 | 75.17 | 158.00 | −2.00 |
| 9 | 93.51 | 194.00 | −1.00 |
| 10 | 113.85 | 232.00 | 2.00 |
| (mA) | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 | 3 | 4 |
| 4.07 | 8.06 | 11.41 | 14.93 | 17.87 | 20.48 | 22.96 | 24.98 | 29.74 | 30.02 |
| I (mA) | 1.10 | 1.37 | 3.29 | 6.80 | 21.98 | 69.09 | 148.75 | 317.59 | 970.12 | 1975.35 |
| U (mV) | 120 | 130 | 150 | 170 | 200 | 230 | 250 | 270 | 300 | 320 |
| α [deg] | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 |
| b [μm] | 0 | 247.9 | 609.7 | 824.1 | 1132.3 | 1494.1 | 1855.9 | 2284.7 | 2726.9 | 3088.7 | 3571.1 | 4013.3 | 4602.9 | 5219.3 | 5849.1 | 6545.9 |
| α [rad] | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
| b (mm) | 0.51 | 1.02 | 1.53 | 2.06 | 2.59 | 3.15 | 3.72 | 4.31 | 4.92 | 5.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Warsza, Z.L.; Puchalski, J.; Więcek, T. Novel Method of Fitting a Nonlinear Function to Data of Measurement Based on Linearization by Change Variables, Examples and Uncertainty. Metrology 2024, 4, 718-735. https://doi.org/10.3390/metrology4040042
Warsza ZL, Puchalski J, Więcek T. Novel Method of Fitting a Nonlinear Function to Data of Measurement Based on Linearization by Change Variables, Examples and Uncertainty. Metrology. 2024; 4(4):718-735. https://doi.org/10.3390/metrology4040042
Chicago/Turabian StyleWarsza, Zygmunt L., Jacek Puchalski, and Tomasz Więcek. 2024. "Novel Method of Fitting a Nonlinear Function to Data of Measurement Based on Linearization by Change Variables, Examples and Uncertainty" Metrology 4, no. 4: 718-735. https://doi.org/10.3390/metrology4040042
APA StyleWarsza, Z. L., Puchalski, J., & Więcek, T. (2024). Novel Method of Fitting a Nonlinear Function to Data of Measurement Based on Linearization by Change Variables, Examples and Uncertainty. Metrology, 4(4), 718-735. https://doi.org/10.3390/metrology4040042





