Using a Multivariate Virtual Experiment for Uncertainty Evaluation with Unknown Variance
Abstract
1. Uncertainty Evaluation Using a Virtual Experiment
2. The Reference Monte Carlo Procedure According to the JCGM-102
| Algorithm 1 JCGM-102 Monte Carlo algorithm |
|
3. A Monte Carlo Sampling Procedure Using the Virtual Experiment
| Algorithm 2 Virtual experiment Monte Carlo algorithm. |
|
4. Examples
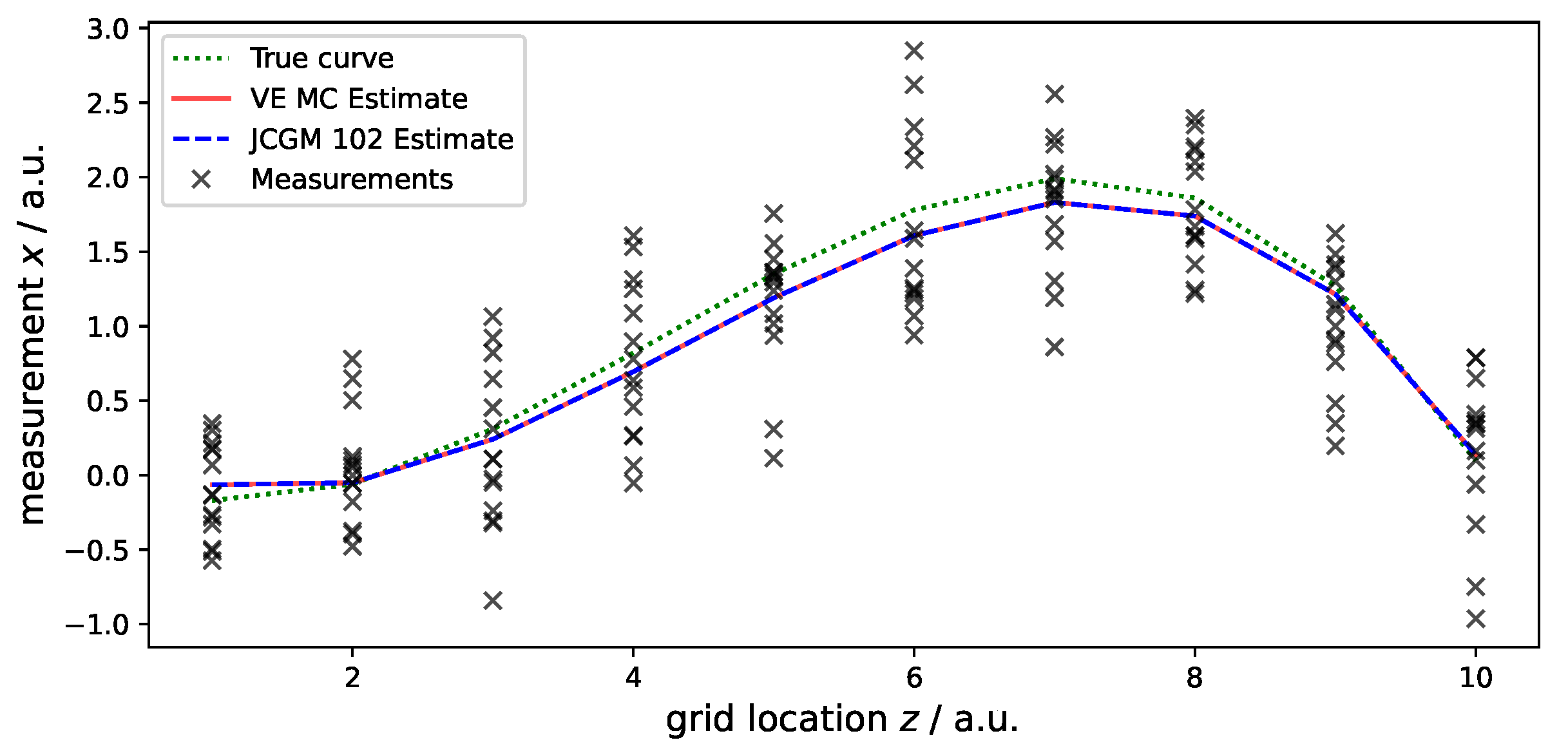
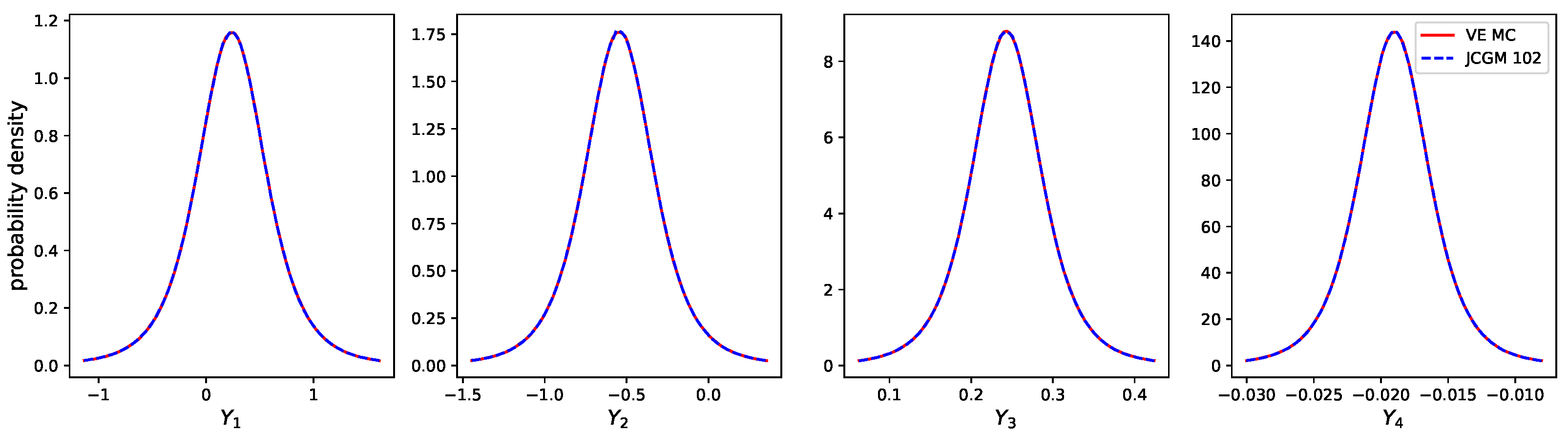
4.1. Generic Example Using Polynomial Regression
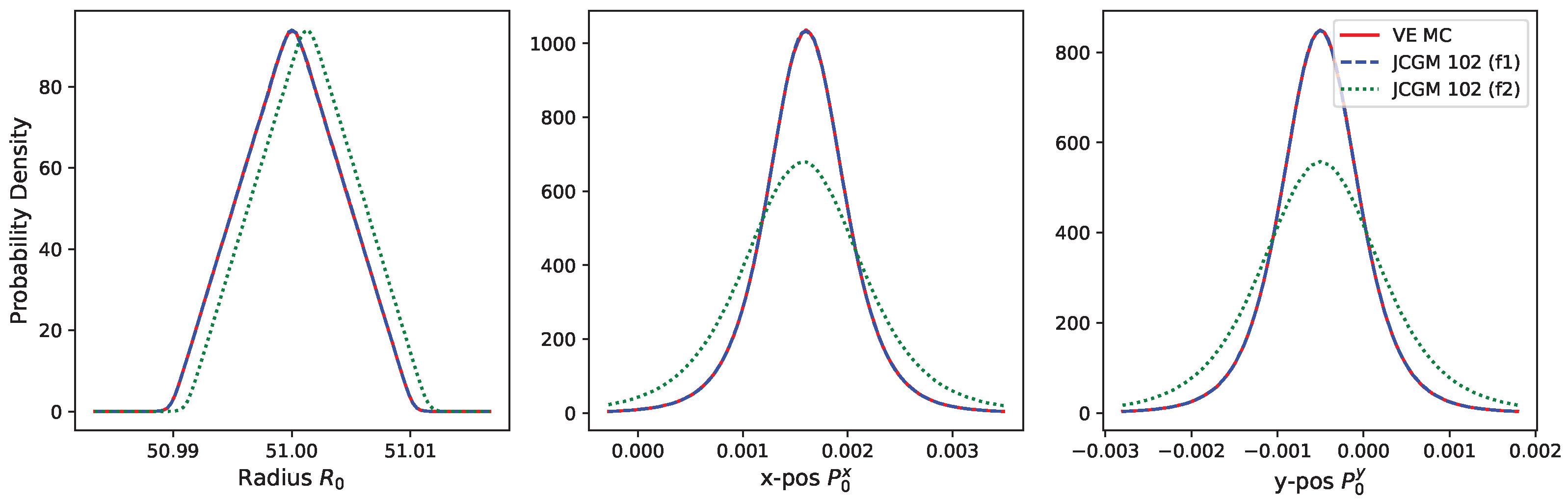
4.2. Coordinate Measuring Machine
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jing, X.; Wang, C.; Pu, G.; Xu, B.; Zhu, S.; Dong, S. Evaluation of measurement uncertainties of virtual instruments. Int. J. Adv. Manuf. Technol. 2006, 27, 1202–1210. [Google Scholar] [CrossRef]
- ISO-30173:2023; Digital Twin—Concepts and Terminology. International Standard; International Organization for Standardization: Geneva, Switzerland, 2023.
- Wright, L.; Davidson, S. Digital twins for metrology; metrology for digital twins. Meas. Sci. Technol. 2024, 35, 051001. [Google Scholar] [CrossRef]
- Irikura, K.K.; Johnson, R.D., III; Kacker, R.N. Uncertainty associated with virtual measurements from computational quantum chemistry models. Metrologia 2004, 41, 369. [Google Scholar] [CrossRef]
- Trenk, M.; Franke, M.; Schwenke, H. The “Virtual CMM” a software tool for uncertainty evaluation–practical application in an accredited calibration lab. Proc. ASPE Uncertain. Anal. Meas. Des. 2004, 9, 68–75. [Google Scholar]
- Liu, G.; Xu, Q.; Gao, F.; Guan, Q.; Fang, Q. Analysis of key technologies for virtual instruments metrology. In Fourth International Symposium on Precision Mechanical Measurements; SPIE: Bellingham, WA, USA, 2008; Volume 7130, pp. 1216–1221. [Google Scholar]
- Heiβelmann, D.; Franke, M.; Rost, K.; Wendt, K.; Kistner, T.; Schwehn, C. Determination of measurement uncertainty by Monte Carlo simulation. In Advanced Mathematical and Computational Tools in Metrology and Testing XI; World Scientific: Singapore, 2019; pp. 192–202. [Google Scholar]
- Straka, M.; Weissenbrunner, A.; Koglin, C.; Höhne, C.; Schmelter, S. Simulation uncertainty for a virtual ultrasonic flow meter. Metrology 2022, 2, 335–359. [Google Scholar] [CrossRef]
- Sun, H.; Yang, M.; Wang, H. A virtual experiment for measuring system resilience: A case of chemical process systems. Reliab. Eng. Syst. Saf. 2022, 228, 108829. [Google Scholar] [CrossRef]
- Balzani, D.; Brands, D.; Schröder, J.; Carstensen, C. Sensitivity analysis of statistical measures for the reconstruction of microstructures based on the minimization of generalized least-square functionals. Tech. Mech.-Eur. J. Eng. Mech. 2010, 30, 297–315. [Google Scholar]
- Wübbeler, G.; Marschall, M.; Kniel, K.; Heißelmann, D.; Härtig, F.; Elster, C. GUM-compliant uncertainty evaluation using virtual experiments. Metrology 2022, 2, 114–127. [Google Scholar] [CrossRef]
- Kok, G.; van Dijk, M.; Wübbeler, G.; Elster, C. Virtual experiments for the assessment of data analysis and uncertainty quantification methods in scatterometry. Metrologia 2023, 60, 044001. [Google Scholar] [CrossRef]
- Kok, G.; Wübbeler, G.; Elster, C. Impact of imperfect artefacts and the modus operandi on uncertainty quantification using virtual instruments. Metrology 2022, 2, 311–319. [Google Scholar] [CrossRef]
- Hughes, F.; Marschall, M.; Wübbeler, G.; Kok, G.; van Dijk, M.; Elster, C. JCGM 101-compliant uncertainty evaluation using virtual experiments. arXiv 2024, arXiv:2404.10530. In press for XXIV IMEKO World Congress. [Google Scholar]
- Lira, I.; Wöger, W. Comparison between the conventional and Bayesian approaches to evaluate measurement data. Metrologia 2006, 43, S249. [Google Scholar] [CrossRef]
- Watzenig, D.; Fox, C. A review of statistical modelling and inference for electrical capacitance tomography. Meas. Sci. Technol. 2009, 20, 052002. [Google Scholar] [CrossRef]
- Higdon, D.; Gattiker, J.; Williams, B.; Rightley, M. Computer model calibration using high-dimensional output. J. Am. Stat. Assoc. 2008, 103, 570–583. [Google Scholar] [CrossRef]
- Heidenreich, S.; Gross, H.; Bar, M. Bayesian approach to the statistical inverse problem of scatterometry: Comparison of three surrogate models. Int. J. Uncertain. Quantif. 2015, 5, 511–526. [Google Scholar] [CrossRef]
- Hammerschmidt, M.; Weiser, M.; Santiago, X.G.; Zschiedrich, L.; Bodermann, B.; Burger, S. Quantifying parameter uncertainties in optical scatterometry using Bayesian inversion. In Modeling Aspects in Optical Metrology VI; SPIE: Bellingham, WA, USA, 2017; Volume 10330, pp. 8–17. [Google Scholar]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Gadd, C.; Xing, W.; Nezhad, M.M.; Shah, A.A. A surrogate modelling approach based on nonlinear dimension reduction for uncertainty quantification in groundwater flow models. Transp. Porous Media 2019, 126, 39–77. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A. An introduction to the proper orthogonal decomposition. Curr. Sci. 2000, 78, 808–817. [Google Scholar]
- Schwab, C.; Todor, R.A. Karhunen–Loève approximation of random fields by generalized fast multipole methods. J. Comput. Phys. 2006, 217, 100–122. [Google Scholar] [CrossRef]
- Oseledets, I.V. Tensor-train decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Balsamo, A.; Di Ciommo, M.; Mugno, R.; Rebaglia, B.; Ricci, E.; Grella, R. Evaluation of CMM uncertainty through Monte Carlo simulations. CIRP Ann. 1999, 48, 425–428. [Google Scholar] [CrossRef]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; JCGM 101:2008; Joint Committee for Guides in Metrology: Sèvres, France, 2008. [Google Scholar]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Supplement 2 to the “Guide to the Expression of Uncertainty in Measurement”—Extension to Any Number of Output Quantities; JCGM 102:2011; Joint Committee for Guides in Metrology: Sèvres, France, 2011. [Google Scholar]
- Kotz, S.; Nadarajah, S. Multivariate t-Distributions and Their Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Robert, C.P.; Casella, G.; Casella, G. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 1999; Volume 2. [Google Scholar]
- Fuller, W.A. Measurement Error Models; John Wiley & Sons: Toronto, ON, Canada, 2009. [Google Scholar]
- Lira, I.; Grientschnig, D. Error-in-variables models in calibration. Metrologia 2017, 54, S133. [Google Scholar] [CrossRef]
- Marcel van Dijk, G.K. Comparison of uncertainty evaluation methods for virtual experiments with an application to a virtual CMM. In Proceedings of the XXIV IMEKO World Congress, Hamburg, Germany, 26–29 August 2024. [Google Scholar]
- Coope, I.D. Circle fitting by linear and nonlinear least squares. J. Optim. Theory Appl. 1993, 76, 381–388. [Google Scholar] [CrossRef]
| Symbol | Description | Comment |
|---|---|---|
| Quantity for the measurand having elements. | Quantity of interest for which an estimate and associated uncertainty is to be derived. | |
| Z | Parameter for which Type-B information is available in terms of a state-of-knowledge PDF . | Possibly multivariate and its value is considered to be unknown but fixed in the real experiment. |
| , | Observations in the real experiment. We assume independent observations, each of dimension . | To circumvent ill-posedness, we assume and to ensure the existence of the JCGM-102 input PDF, also . |
| Statistical error term. Here, we consider only the additive case. | Realizations of a normal distribution might not be known to the user of the virtual experiment. | |
| Covariance used in virtual experiment to model statistical variability in repeated measurements. | Variances are known to the user of the virtual experiment. |
| Quantity | Mean | Std. unc. | CI (95%) |
|---|---|---|---|
| Virtual Experiment approach | |||
| 0.24 | 0.462 | [−0.67, 1.15] | |
| −0.55 | 0.303 | [−1.14, 0.05] | |
| 0.24 | 0.061 | [0.12, 0.36] | |
| −0.02 | 0.004 | [−0.03, −0.01] | |
| JCGM-102 Monte Carlo approach | |||
| 0.24 | 0.462 | [−0.67, 1.15] | |
| −0.55 | 0.303 | [−1.14, 0.05] | |
| 0.24 | 0.061 | [0.12, 0.36] | |
| −0.02 | 0.004 | [−0.03, −0.01] | |
| Quantity | Mean | Std. Unc. | CI (95%) |
|---|---|---|---|
| Virtual Experiment approach | |||
| R | 51.0000 | 0.0042 | [50.9920, 51.0080] |
| 0.0016 | 0.0005 | [0.0007, 0.0026] | |
| −0.0005 | 0.0006 | [−0.0017, 0.0006] | |
| JCGM-102 Monte Carlo approach using (15) | |||
| R | 51.0000 | 0.0042 | [50.9920, 51.0080] |
| 0.0016 | 0.0005 | [0.0007, 0.0025] | |
| −0.0005 | 0.0006 | [−0.0017, 0.0006] | |
| Quantity | Mean | Std. Unc. | CI (95%) |
|---|---|---|---|
| JCGM-102 Monte Carlo approach using (19) | |||
| R | 51.0013 | 0.0042 | [50.9933, 51.0093] |
| 0.0016 | 0.0007 | [0.0001, 0.0030] | |
| −0.0005 | 0.0009 | [−0.0023, 0.0013] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marschall, M.; Hughes, F.; Wübbeler, G.; Kok, G.; van Dijk, M.; Elster, C. Using a Multivariate Virtual Experiment for Uncertainty Evaluation with Unknown Variance. Metrology 2024, 4, 534-546. https://doi.org/10.3390/metrology4040033
Marschall M, Hughes F, Wübbeler G, Kok G, van Dijk M, Elster C. Using a Multivariate Virtual Experiment for Uncertainty Evaluation with Unknown Variance. Metrology. 2024; 4(4):534-546. https://doi.org/10.3390/metrology4040033
Chicago/Turabian StyleMarschall, Manuel, Finn Hughes, Gerd Wübbeler, Gertjan Kok, Marcel van Dijk, and Clemens Elster. 2024. "Using a Multivariate Virtual Experiment for Uncertainty Evaluation with Unknown Variance" Metrology 4, no. 4: 534-546. https://doi.org/10.3390/metrology4040033
APA StyleMarschall, M., Hughes, F., Wübbeler, G., Kok, G., van Dijk, M., & Elster, C. (2024). Using a Multivariate Virtual Experiment for Uncertainty Evaluation with Unknown Variance. Metrology, 4(4), 534-546. https://doi.org/10.3390/metrology4040033





