Abstract
A virtual experiment simulates a real measurement process by means of a numerical model. The numerical model produces virtual data whose properties reflect those of the data observed in the real experiment. In this work, we explore how the results of a virtual experiment can be employed in the context of uncertainty evaluation for a corresponding real experiment. The uncertainty evaluation was based on the Guide to the Expression of Uncertainty in Measurement (GUM), which defines the de facto standard for uncertainty evaluation in metrology. We show that, under specific assumptions about model structure and variance of the data, virtual experiments in combination with a Monte Carlo method lead to an uncertainty evaluation for the real experiment that is in line with Supplement 1 to the GUM. In the general case, a GUM-compliant uncertainty evaluation in the context of a real experiment can no longer be based on a corresponding virtual experiment in a simple way. Nevertheless, virtual experiments are still useful in order to increase the reliability of an uncertainty analysis. Simple generic examples as well the case study of a virtual coordinate measuring machine are presented to illustrate the treatment.
1. Introduction
A virtual experiment is a numerical model of an experiment or a measurement process [1]. It produces virtual data whose properties reflect those of the data observed in the corresponding real experiment. Virtual experiments have become increasingly important in modern metrology and industrial applications [2,3,4,5,6,7]. They are utilized, for example, to explore the accuracy of a measurement device, or to specify machine tolerances needed to reach a required accuracy [8]. Virtual experiments in combination with a sensitivity analysis can be useful in identifying significant sources of uncertainty [9,10]. In the design and optimization of a measurement process, virtual experiments often play a vital role and allow one to easily explore many different experimental scenarios, which would be infeasible using real experiments. Combined with Monte Carlo methods, virtual experiments have been proposed for the evaluation of measurement uncertainties [6,11,12,13]. For this purpose, the virtual experiment is carried out on a computer many times by randomly varying its physical conditions, and the spread of the resulting distribution of virtual data is then used for uncertainty quantification [12].
However, the measurand (i.e., the quantity of interest) is often not observed directly in an experiment. Instead, the observed data will depend on the measurand and on other input quantities influencing the measurement process. For example, in the optical form measurement of aspheres by means of a tilted wave interferometer [14], the observed data will consist of interferograms, while the measurand is the topography of an asphere. Together with other input quantities, such as the parameters of the employed optical system, the measurand determines the interferogram that will be observed in the experiment. However, even when the experiment aims at a direct measurement of the measurand, proper inference of the measurand usually requires the application of an analysis model that contains additional correction terms. Hence, also in these cases, the analysis model plays a different role than the numerical model of the virtual experiment. Figure 1a illustrates a generic virtual experiment that takes known values of the measurand and input quantities as its inputs to produce simulated observations of the corresponding real measurement.
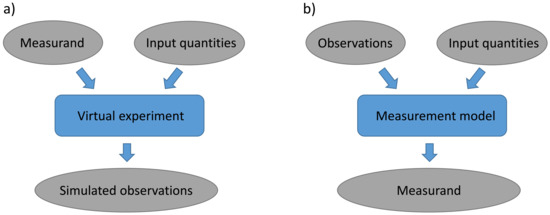
Figure 1.
Comparison of virtual experiment and GUM measurement model: (a) generic virtual experiment that produces simulated observations given known values of measurand and input quantities. (b) Generic GUM measurement model which relates the measurand with observations and input quantities.
The Guide to the Expression of Uncertainty in Measurement (GUM) [15], together with its supplements, defines the de facto standard for uncertainty evaluation in metrology. The GUM uncertainty framework is based on a measurement model that determines the measurand as a function of its input quantities, and the data observed in the real experiment typically represent one of these input quantities. The GUM measurement model thus can be viewed as a partial inversion of the forward model utilized in a virtual experiment, cf. Figure 1b. Supplements 1 (GUM-S1) [16] and 2 (GUM-S2) [17] recommend a Monte Carlo method for uncertainty evaluation that propagates probability density functions (PDFs) characterizing one’s state of knowledge about the input quantities through the GUM measurement model in order to determine the PDF for the measurand. While GUM-S1 treats the case of a scalar measurand, GUM-S2 extends the treatment to multivariate measurands.
Given the opposing nature of the forward model employed in a virtual experiment and the corresponding GUM measurement model, questions arise whether the results of a virtual experiment can be directly embedded in the GUM uncertainty evaluation associated with a real measurement, or how an implementation of the GUM uncertainty framework could benefit from a virtual experiment that represents a realistic model of the corresponding real experiment. The goal of this paper is to explore these questions. We consider different levels of complexity in the relationship between the data and the measurand. We show that, for a linear relationship that typically arises in direct measurements, the results of the virtual experiment can be immediately used for a GUM-compliant uncertainty evaluation, provided that the variance of the distribution of the real data is known with sufficient accuracy. In the general case, such a direct use of the results of a virtual experiment for a GUM uncertainty evaluation is no longer possible. Nevertheless, we argue that the virtual experiment can be vital for the construction of a reliable GUM measurement model, or for characterizing the model uncertainty of an approximate GUM measurement model. Our treatment is illustrated in terms of simple generic examples and the case study of a virtual coordinate measuring machine.
The paper is organized as follows. In Section 2, the basic concepts underlying GUM-S1 and virtual experiments are introduced. In Section 3, the application of virtual experiments in the context of a GUM-S1 Monte Carlo uncertainty evaluation is discussed for different types of models. The methodological treatment in this section is accompanied with simple, generic examples. Section 4 then presents the application to a virtual coordinate measuring machine. Finally, some conclusions are drawn in Section 5.
2. Concepts
In this section, the GUM-S1 Monte Carlo uncertainty evaluation is briefly reviewed and the basic concept of a virtual experiment is introduced. For the sake of simplicity, we concentrate on a single measurand and univariate observations. Generalization to the multivariate case is possible (see the application considered in Section 4).
2.1. GUM-S1 Monte Carlo Uncertainty Evaluation
The GUM framework assumes that a measurement model of the form
is available, which relates the measurand y to the input quantity x, which is estimated by the observed data, and to further input quantities . The measurement model (1) represents a partial inverse model to the deterministic part of the forward model in a virtual experiment as specified in (2) below. The GUM-S1 Monte Carlo method assumes that a PDF is available for x, together with a (joint) PDF for , which shall encode the state of knowledge about these input quantities. GUM-S1 provides guidance for the construction of these PDFs given type A information on x and type B information on . Specifically, in the presence of normally distributed observations for x, GUM-S1 assigns a t-distribution with degrees of freedom to , shifted and scaled by and , respectively, where and s denote the mean and standard deviation of the observations . The case when the variance of the Gaussian distribution of the observations on x is assumed to be known is addressed in the following by assigning a Gaussian distribution to x with mean equal to the mean of the observations and variance . Albeit not directly mentioned in GUM-S1, such an assignment can be seen as being in line with GUM-S1, see for example [18].
The GUM-S1 Monte Carlo method proceeds as follows:
MC GUM-S1
- (i)
- Select a at random from the PDF ;
- (ii)
- Select an x at random from the PDF ;
- (iii)
- Calculate .
Repeated application of MC GUM-S1 then produces independent samples from the target distribution for the measurand y, and using a large number of such samples allows to determine arbitrarily accurately. The PDF , or the random samples from it produced by the GUM-S1 Monte Carlo method, can be used to calculate an estimate for the measurand and its associated uncertainty, or a so-called coverage interval. As stated in Clause 5.4, Note 2 in GUM-S1 [16], the GUM-S1 Monte Carlo method is regarded as a numerical tool for the evaluation of the distribution for the measurand rather than representing a simulation of a measurement process. In GUM-S2 [17], a similar Monte Carlo method is proposed, which can be applied to multivariate measurands.
In many situations, the measurement model can be stated in analytical form. However, when the measurement process is more complex, or when the employed model needs to be accurate, using a realistic numerical model for the experiment can become mandatory for the development of an adequate measurement model. Since the GUM uncertainty framework requires a model for the measurand rather than a model for the data, the challenge emerges to determine a partial inversion of a model that is available only numerically. Moreover, the specification of a forward model for the data obtained from a complex measurement process is often easier to achieve compared to immediately establishing a corresponding GUM measurement model. Examples for such a scenario include forward models involving the numerical solution of partial differential equations (see, e.g., [19]).
2.2. Virtual Experiment
We assume a numerical model for the virtual experiment that produces virtual data x according to
For the sake of simplicity in notation, we do not distinguish between the quantity x and possible data on that quantity, and we also do not distinguish between real and virtual data or real and virtual measurands; in each case, the meaning should be clear from the context. The deterministic function has as its inputs chosen values for the measurand y and all input quantities that influence the mean outcome of the experiment. Random fluctuations observed in repeated measurements are represented by , which is modeled as a realization of a Gaussian distribution with zero mean and variance , i.e., . The calculation of a single simulated observation through the virtual experiment is carried out as follows:
Virt-Exp
- (i)
- Given y, , and ;
- (ii)
- Select an at random from the PDF ;
- (iii)
- Calculate a simulated observation .
The virtual experiment is assumed to represent the real experiment sufficiently well, i.e., for given y, , and , the data produced by the virtual experiment represent those observed in the real experiment. The realistic modeling underlying the virtual experiment allows one to analyze the sensitivity of the observed data in dependence on physically meaningful parameters such as the positioning of a lens in an optical experiment. Physical insight provides information about such parameters, and virtual experiments allow their consequences to be estimated; gaining corresponding information through real experiments is often infeasible.
The validation of a virtual experiment, i.e., the question whether a virtual experiment adequately models a real experiment, is an important issue that is not treated in this paper. Basically, statistical tools for model checking can be employed for this purpose. These techniques assess whether observed real data are consistent with the assumed model for the data given by the virtual experiment (2) [20,21,22].
Finally, we note that a forward model for the experimental data in the form (2) represents a statistical model which is the starting point for a statistical inference of the measurand given real data, e.g., by applying a maximum likelihood estimation [23] or a Bayesian inference [24]. The statistical model has also been referred to as observation equation [18,25]. However, the application of these approaches is not a topic a this paper.
3. GUM-Compliant Uncertainty Evaluation Using Virtual Experiments
In this section, we explore how the results of a virtual experiment can be used to support a GUM uncertainty evaluation. The treatment is illustrated using simple, generic examples.
First, we show that, for linear models and known variance of the distribution of observations in the real experiment, a Monte Carlo procedure applied to the virtual experiment produces samples that equal those of the GUM-S1 Monte Carlo uncertainty evaluation. Then, in a second step, the variance is considered as unknown and it is demonstrated that the results of the Monte Carlo procedure applied to the virtual experiment are no longer connected to those of a GUM-S1 Monte Carlo uncertainty evaluation. Finally, the potential benefit of virtual experiments to develop and assess evaluation procedures or models is considered for the general case of nonlinear models.
3.1. Linear Model and Known Variance
We consider a virtual experiment following a linear model of the form
Model (3) describes an almost direct measurement, i.e., the mean outcome of the experiment equals the measurand up to a systematic error . The physical parameters of the experiment determine the error . Examples of physical parameters causing systematic errors could be the tilt of a lens in an optical experiment or the misalignment of a laser. While the function generally depends nonlinearly on , we will nevertheless refer to (3) as a linear model, since it is linear in y and . Note that, while is a systematic error in the virtual experiment (3), serves as a correction term in a corresponding GUM measurement model.
We first assume that the variance of the distribution of the observations in the real experiment is known. Furthermore, a PDF shall be available which encodes our state of knowledge about the value of in the real experiment. Let denote the mean of m repeated observations of the real experiment. In order to apply GUM-S1 to the considered scenario, the measurement model corresponding to (3) is employed and the random samples from the PDF in MC GUM-S1 are drawn according to . Note that, if the function in the linear model (3) is available numerically only, the measurement model can be specified as a numerical model as well, e.g., by using the measurement model for some fixed value taken for .
The following Monte Carlo scheme utilizing the virtual experiment in combination with a fixed value for taken for the measurand can then be applied:
MC Virtual
- (i)
- Select a at random from the PDF ;
- (ii)
- Calculate simulated observations through m runs of Virt-Exp for model (3), while using the chosen virtual measurand (and generated in step(i));
- (iii)
- Calculate the mean of the simulated observations ;
- (iv)
- Calculate .
Steps (ii) and (iii) in MC Virtual can equivalently be carried out by calculating from a single run of Virt-Exp, while using the variance . Figure 2 shows a graphical illustration of the sampling procedure. We denote by the PDF defined by the Monte Carlo procedure MC Virtual. Step (iv) in the above algorithm can be equivalently stated as , where is distributed according to . It follows that, in the considered setting of the linear model (3) with known variance , the PDF is equivalent to obtained by the application of MC GUM-S1. Consequently, the samples obtained for y through the Monte Carlo procedure MC Virtual, which utilizes simulated observations from the virtual experiment, can directly be taken as samples from a GUM-S1 calculation. These samples can then be used to determine an estimate, a standard uncertainty, or a coverage interval for the measurand that is in line with the principles of the GUM.
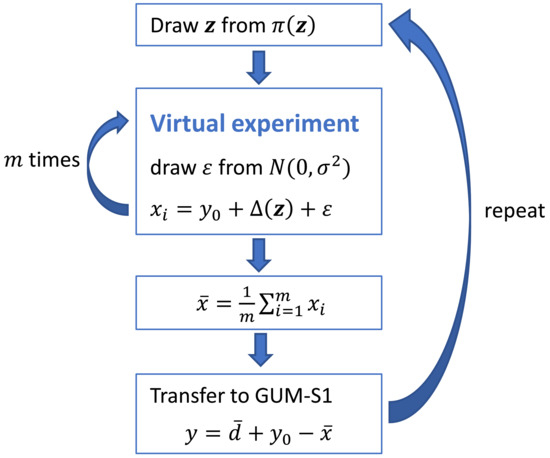
Figure 2.
Graphical illustration of the sampling procedure MC Virtual used for the linear model. The inputs of the procedure are the virtual experiment, the mean of m repeated observations of the real experiment, the variance of the distribution of the observations used in the virtual experiment, the (joint) PDF of the input quantities z, and the chosen virtual measurand .
Figure 3 shows an example for the particular model
where z is distributed according to a Gaussian distribution with mean 0 and variance , and where the variance is assumed for the distribution of the observations. Furthermore, the mean is taken, assuming observations, and is used for the measurand when generating the virtual data. For both Monte Carlo procedures MC GUM-S1 and MC Virtual, samples were generated and the PDFs and shown in Figure 3 were obtained using the histograms of these samples. The simple model (4) is selected for the purpose of illustration. In a real application, such a simple expression for depending only on a univariate z does usually not exist; instead, would be the result of the numerical model for the virtual experiment, and could consist of many different physical parameters.
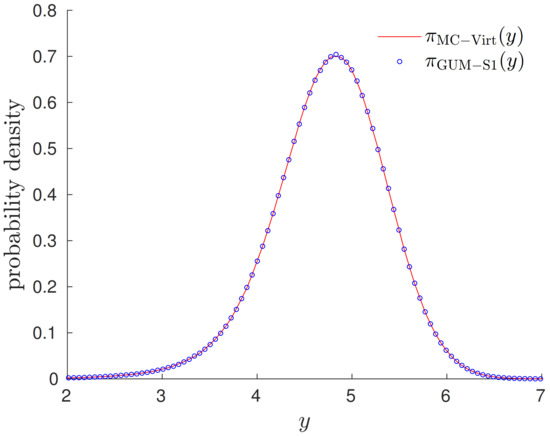
Figure 3.
Results obtained for the numerical example of a linear model. Comparison of the PDFs obtained by application of GUM-S1 and by a Monte Carlo calculation using the virtual experiment.
An important aspect in the above treatment for the linear model (3) is that is required to be independent of the measurand y. If there is a significant (nonlinear) dependence of on y, this would imply a model instead of (3), and the treatment would be incorrect (see also the subsequent subsection on nonlinear models). However, the proposed methodology may still be valid when can be ensured to be almost independent of y, e.g., in a region covering a range of values expected for the measurand. Note that this may possibly require to adapt with respect to this expected range for the measurand.
In cases in which one is not directly interested in y but in some (known) nonlinear function of y, independent samples from the corresponding PDF can be obtained simply by applying the function to the samples determined for y either by MC GUM-S1 or by MC Virtual. In Section 5, an example is presented for such a procedure using a virtual coordinate measuring machine.
In conclusion, when an additive correction model of the form (3) can be assumed along with a PDF that describes one’s state of knowledge about the input parameters , and when the variance of the distribution of the observations on x in the real experiment is known, the virtual data produced by virtual experiments can be employed in a GUM-S1 uncertainty evaluation as specified by MC Virtual above.
3.2. Linear Model and Unknown Variance
Consider next the case where can no longer be assumed to be known. In this case, the above proposed approach using the virtual experiment will not produce samples from the PDF produced by GUM-S1. The reason for this is that the virtual experiment needs to still use normally distributed random errors for some chosen value of the variance, since this is the mechanism assumed for the real experiment (Figure 2). The GUM-S1 Monte Carlo procedure, however, will sample from a t-distribution for x, which results in a different form of the PDFs. Furthermore, the choice of can no longer be assumed to match the variance of (infinitely many) repeated observations in the real experiment. The difference caused by the fact that the virtual experiment uses normally distributed random errors, while the GUM-S1 PDF uses a t-distribution for x, reflects the different roles of the two models, as well as the fact that the assignment of the t-distribution by GUM-S1 follows a Bayesian inference using a noninformative prior for the variance (and for the observation quantity x) [24]. We finally note that while only normally distributed random errors have been considered here, different distributions may arise depending on the measurement process. For example, for counting processes of particles or photons, the outcome usually follows a Poisson distribution.
Figure 4 shows results for the example from Figure 3, when the variance is treated as unknown in the GUM-S1 uncertainty evaluation. Note that the variance chosen for the virtual experiment was (unrealistically) set to the true variance used to produce the data . While being conceptually different generally, the (numerical) difference of the PDFs arising in the context of a not exactly known variance can be expected to be small, as long as the uncertainty about the input quantities dominates the uncertainty resulting for the measurand. For a given set of observed data with unknown variance, the difference of the PDFs can be expected to decrease when the uncertainty about increases. Whether or not the difference of the PDFs may be viewed as being relevant needs to be judged in the context of the intended application of the measurement results.
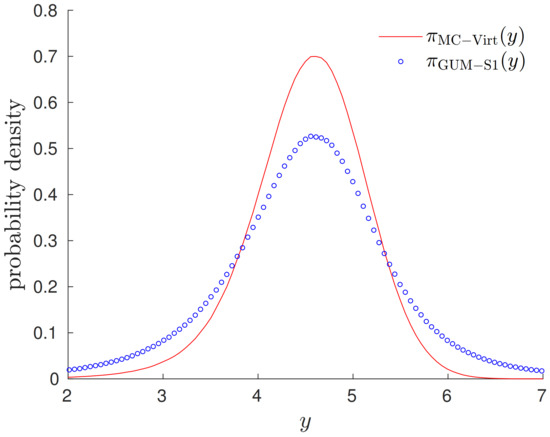
Figure 4.
Results obtained for the numerical example of a linear model when can no longer be assumed to be known. Comparison of the PDFs obtained by application of GUM-S1 and by a Monte Carlo calculation using the virtual experiment.
In conclusion, when the variance of the data in the real experiment is not known, and when the uncertainty about is not dominating, then a Monte Carlo procedure using the virtual experiment will not lead to a PDF that yields the result of a GUM-S1 uncertainty evaluation. Of course, the virtual experiment can still be used to produce samples from the PDF for , when omitting the addition of normally distributed random errors . By combining (the negative of) these samples with samples drawn from a scaled and shifted t-distribution, the GUM-S1 PDF is produced, and the benefit of the virtual experiment to calculate is granted. However, such procedure does no longer utilize the (complete) results of the virtual experiment.
3.3. Nonlinear Model
We consider the general case where the deterministic part
of model (2) for the experiment is nonlinear in y. In order to apply a GUM uncertainty evaluation, the deterministic part of (2) needs to be partially inverted, leading to the measurement model
In cases where the deterministic part of the forward model (2) is the result of a numerical model, the partially inverted model (6) is usually no longer available, or may not even exist. Instead, one will dispose of some approximate inverse model
The approximate model (7) could itself be the result of a numerical procedure, or an analytic expression taken as a proxy for the measurement model.
In general, the virtual experiment cannot be employed for an uncertainty evaluation about the measurand in a simple way, as it was possible for the linear model (3). The main benefit of the virtual experiment in the general case is, perhaps, its potential to assess evaluation procedures, or the validity of employed (approximate) measurement models. This can be done by producing virtual data and assessing the results achieved for them in view of the known ground truth, i.e., the known value of the measurand used to produce the virtual data. One could, for example, assess interval estimates for the measurand and explore whether they cover the true measurand or not; or a PDF constructed for the measurand on basis of the virtual data could be assessed in terms of its consistency with the ground truth. In order to get a comprehensive view, different ground truths should be considered. A modification of evaluation procedures, or evaluation models used by them, could be assessed in this way. Assessing a measurement model via virtual experiments and a related uncertainty evaluation furthermore allows to check whether a candidate model is fit for purpose in view of the required accuracy of its intended application. We also refer the reader to previous applications combining virtual experiments and uncertainty evaluation [6,11,12,13].
In the following, we present a simple nonlinear example, and as estimation procedure, we apply the GUM-S1 Monte Carlo procedure to produce a PDF for the measurand. The considered model for the virtual experiment reads
where for z a rectangular distribution with lower bound 5 and upper bound 10 is used, and where is distributed according to a zero mean Gaussian distribution with variance . We assume that for the virtual experiment (8), two different approximate measurement models are available and given by
and
where a value of was taken. The approximate measurement models (9) and (10) were obtained here from a Taylor approximation of the exact measurement model . The resulting PDFs obtained by GUM-S1 for the two approximate measurement models are shown in Figure 5 for the example of a single observation with known variance . In addition, Figure 5 also shows the GUM-S1 result for the exact measurement model , which, however, might be unavailable in the case of a complex virtual experiment. As can be seen, the measurement model in (10) provides a better approximation to the exact measurement model in terms of the distribution resulting for the measurand.
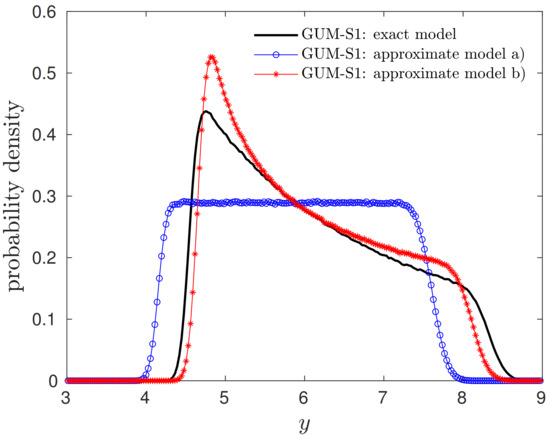
Figure 5.
GUM-S1 results for the numerical example of a nonlinear model when applying different approximations of the measurement model.
We conclude this section by stating that in a nonlinear model, the virtual experiment cannot be utilized for a GUM uncertainty evaluation about the measurand in a simple way. Moreover, in a nonlinear model such as (8), the observations x and the measurand y will typically have different physical dimensions, which would render a methodology similar to the one proposed for the linear model meaningless.
4. Application
In this section, data from a real coordinate measuring machine were used to demonstrate the application of the virtual experiment uncertainty evaluation approach described in Section 3.1. The task of determining the diameter of a cylindrical object was considered for which a set of n measured coordinate pairs was available. The measured points were assumed to be located in a plane perpendicularly oriented to the cylinder axis and the z coordinates are hence omitted in the following. In order to determine the diameter for a given set of measured or simulated coordinates, a circle fitting routine was applied. To this end, we employed the linear least squares approach proposed in [26], which has been shown to be robust with respect to outliers. We also note that alternative methods for fitting circles or ellipses are available which could be advantageous for certain applications (see, e.g., [27]).
The model for the virtual experiment simulating the recordings at the sensing points was taken as
where and denote independent random errors distributed according to and with known variance . The coordinates denote points on the surface of the cylinder that specify the virtual measurand used in the simulation. The error terms and model influences such as geometry deviations of the CMM, the probing behavior, thermal stability of the environment, influences of the workpiece, and others. The denote corresponding physical input parameters whose PDFs are known. Examples of these parameters include the mean temperature of the scales of the CMM, the surface roughness, and the temperature of the workpiece. A detailed description of the considered influences is provided in [6]. The summation over p different error terms in (11) and (12) was introduced to reflect influences due to different physical effects. Figure 6 illustrates the GUM-compliant Monte Carlo sampling procedure for the considered application following the methodology described in Section 3.1.
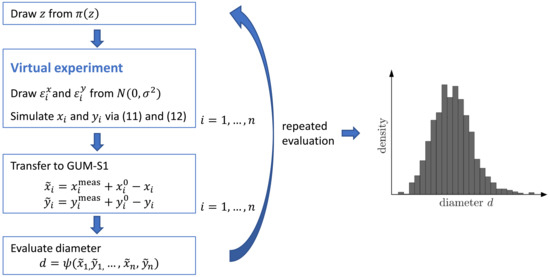
Figure 6.
Graphical illustration of the Monte Carlo procedure for the coordinate measurement task. The inputs of the procedure are the virtual experiment, the measured coordinates , the variance of the distribution of the observations used in the virtual experiment, the (joint) PDF of the input quantities z, and the chosen virtual measurand .
Note that the error terms and may depend on the sensing location as indicated by the index i and these functions may hence show some dependence with respect to the actual measurand. While such a dependence would violate the assumption of an almost direct observation underlying the proposed methodology, an uncertainty evaluation via virtual experiments may still be valid when the virtual measurand is close to the actual measurand, and when the error functions and can be assumed to be approximately correct in the vicinity of the measurand. For the bearing standard example presented below, we assumed that the corresponding virtual experiment was exact. Here, we did not address the validation of the virtual experiment and the results shown below are not intended to be used for such a validation. As discussed in Section 2.2, the validation of virtual experiments is an important task. This can be dealt with by the statistical analysis of the difference between real measurements, that are based on accurately known specimens such as calibrated standards, and corresponding virtual data.
In the following, we used the measured coordinates from a large bearing standard with a nominal diameter of 600 mm (see Figure 7) and utilized the above-described virtual experiment for a GUM compliant uncertainty evaluation. The measurement was carried out with a state-of-the-art 3D coordinate measuring machine and the precise calculation of its error terms, including the variability due to the variance , was carried out using the PTB VCMM kernel [6]. When applying the software program, the measured coordinates were used in the virtual experiment as . Figure 8 displays the measured coordinates as well as scatter plots of the simulated coordinates for four different positions and obtained by the proposed procedure. Figure 9a shows the PDF resulting for the diameter of the measured bearing standard when using the 36 points for circle fitting. The PDF for the diameter is almost Gaussian-shaped with mean 591.8339 mm and standard deviation 0.0005 mm which is taken as the standard uncertainty associated with the diameter of the bearing standard. The corresponding expanded uncertainty () is given by 0.001 mm. Figure 9b also shows the distribution of the center points of the fitted circles.

Figure 7.
Bearing standard with a nominal diameter of 600 mm.
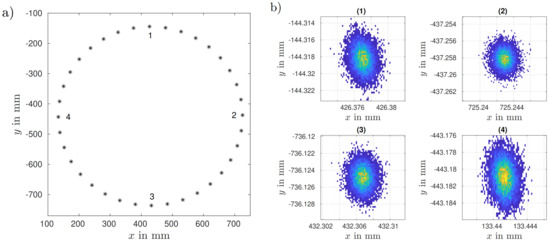
Figure 8.
(a) Coordinates from the measurement of a large bearing standard. (b) A total of simulated coordinates and at the locations 1, 2, 3 and 4 indicated in Figure 8(a). The colors indicate the density of the simulated coordinates from low (blue) to high (yellow).
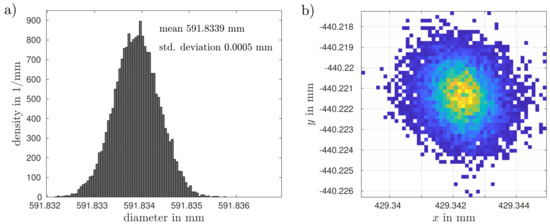
Figure 9.
(a) PDF resulting for the diameter of the bearing standard. (b) Distribution of the center points of the fitted circles. The colors indicate the density of the center points from low (blue) to high (yellow).
5. Conclusions
Virtual experiments are helpful to develop and assess uncertainty evaluation within the framework of the GUM. For almost direct measurements, i.e., when the quantity observed in the experiment differs from the quantity of interest only by an additive correction quantity, a Monte Carlo procedure using the virtual experiment was proposed, which yields a GUM-compliant uncertainty analysis. This holds exactly, as long as the variance of the measurements is accurately known, or the uncertainty is dominated by the uncertainty contribution of input quantities that are not observed. When the variance of the measurements is not known and when it leads to a significant contribution to the uncertainty, the proposed use of the virtual experiment does no longer provide a GUM-compliant uncertainty evaluation. An essential benefit of the virtual experiment in this context is that the uncertainty associated with the correction quantity can be reliably determined when the numerical model correctly reflects the relevant parts of the measurement process. As a case study, the example of a virtual coordinate measuring machine was presented. The case study also illustrated the application of a virtual experiment for a GUM-compliant uncertainty evaluation when the measurand is multivariate. When the observed quantity depends nonlinearly on the measurand, the distribution of randomly drawn virtual data cannot be easily transformed into a GUM-compliant uncertainty evaluation. The development of corresponding approaches will be the topic of future research. Nevertheless, virtual experiments already play a significant role in these cases, for example in the development and assessment of evaluation models needed for the application of the GUM framework.
Author Contributions
Conceptualization, G.W. and C.E.; methodology, G.W. and C.E.; validation, G.W., M.M. and C.E.; formal analysis, G.W. and C.E.; investigation, G.W., M.M. and C.E.; writing—original draft preparation, G.W. and C.E.; writing—review and editing, G.W., M.M., K.K., D.H., F.H. and C.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The simulation data that support the findings of this study are available upon reasonable request from the authors.
Acknowledgments
The authors thank Matthias Franke (PTB) for providing the numerical results with VCMM software.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jing, X.; Wang, C.; Pu, G.; Xu, B.; Zhu, S.; Dong, S. Evaluation of measurement uncertainties of virtual instruments. Int. J. Adv. Manuf. Technol. 2006, 27, 1202–1210. [Google Scholar] [CrossRef]
- Irikura, K.K.; Johnson, R.D., III; Kacker, R.N. Uncertainty associated with virtual measurements from computational quantum chemistry models. Metrologia 2004, 41, 369. [Google Scholar] [CrossRef]
- Trenk, M.; Franke, M.; Schwenke, H. The “Virtual CMM” a software tool for uncertainty evaluation—Practical application in an accredited calibration lab. Proc. ASPE Uncertain. Anal. Meas. Des. 2004, 9, 68–75. [Google Scholar]
- Liu, G.; Xu, Q.; Gao, F.; Guan, Q.; Fang, Q. Analysis of key technologies for virtual instruments metrology. In Fourth International Symposium on Precision Mechanical Measurements; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 7130, p. 71305B. [Google Scholar]
- Doytchinov, I.; Tonnellier, X.; Shore, P.; Nicquevert, B.; Modena, M.; Durand, H.M. Application of probabilistic modelling for the uncertainty evaluation of alignment measurements of large accelerator magnets assemblies. Meas. Sci. Technol. 2018, 29, 054001. [Google Scholar] [CrossRef]
- Heißelmann, D.; Franke, M.; Rost, K.; Wendt, K.; Kistner, T.; Schwehn, C. Determination of measurement uncertainty by Monte Carlo simulation. In Advanced Mathematical and Computational Tools in Metrology and Testing XI; World Scientific: Singapore, 2019; pp. 192–202. [Google Scholar]
- Sepahi-Boroujeni, S.; Mayer, J.; Khameneifar, F. Efficient uncertainty estimation of indirectly measured geometric errors of five-axis machine tools via Monte-Carlo validated GUM framework. Precis. Eng. 2021, 67, 160–171. [Google Scholar] [CrossRef]
- Wiegmann, A.; Stavridis, M.; Walzel, M.; Siewert, F.; Zeschke, T.; Schulz, M.; Elster, C. Accuracy evaluation for sub-aperture interferometry measurements of a synchrotron mirror using virtual experiments. Precis. Eng. 2011, 35, 183–190. [Google Scholar] [CrossRef]
- Balzani, D.; Brands, D.; Schröder, J.; Carstensen, C. Sensitivity analysis of statistical measures for the reconstruction of microstructures based on the minimization of generalized least-square functionals. Tech. Mech. 2010, 30, 297–315. [Google Scholar]
- Fortmeier, I.; Stavridis, M.; Wiegmann, A.; Schulz, M.; Baer, G.; Pruss, C.; Osten, W.; Elster, C. Sensitivity analysis of tilted-wave interferometer asphere measurements using virtual experiments. In Modeling Aspects in Optical Metrology IV; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8789, p. 878907. [Google Scholar]
- Trapet, E.; Wäldele, F. The Virtual CMM Concept. In Advanced Mathematical Tools in Metrology; World Scientific: Singapore, 1996; Volume 2, pp. 238–247. [Google Scholar]
- Balsamo, A.; Di Ciommo, M.; Mugno, R.; Rebaglia, B.; Ricci, E.; Grella, R. Evaluation of CMM uncertainty through Monte Carlo simulations. CIRP Ann. 1999, 48, 425–428. [Google Scholar] [CrossRef]
- Aggogeri, F.; Barbato, G.; Barini, E.M.; Genta, G.; Levi, R. Measurement uncertainty assessment of coordinate measuring machines by simulation and planned experimentation. CIRP J. Manuf. Sci. Technol. 2011, 4, 51–56. [Google Scholar] [CrossRef]
- Fortmeier, I.; Stavridis, M.; Wiegmann, A.; Schulz, M.; Osten, W.; Elster, C. Evaluation of absolute form measurements using a tilted-wave interferometer. Opt. Express 2016, 24, 3393–3404. [Google Scholar] [CrossRef] [PubMed]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008; BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML, JCGM 100:2008, GUM 1995 with minor corrections. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008; BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML, JCGM 101: 2008. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Supplement 2 to the ‘Guide to the Expression of Uncertainty in Measurement’—Extension to Any Number of Output Quantities; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2011; BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML, JCGM 102: 2011. [Google Scholar]
- Forbes, A.; Sousa, J. The GUM, Bayesian inference and the observation and measurement equations. Measurement 2011, 44, 1422–1435. [Google Scholar] [CrossRef]
- Model, R.; Stosch, R.; Hammerschmidt, U. Virtual experiment design for the transient hot-bridge sensor. Int. J. Thermophys. 2007, 28, 1447–1460. [Google Scholar] [CrossRef]
- Snee, R.D. Validation of regression models: Methods and examples. Technometrics 1977, 19, 415–428. [Google Scholar] [CrossRef]
- Gelman, A.; Meng, X.L.; Stern, H. Posterior predictive assessment of model fitness via realized discrepancies. Stat. Sin. 1996, 6, 733–760. [Google Scholar]
- Jiang, X.; Mahadevan, S. Bayesian risk-based decision method for model validation under uncertainty. Reliab. Eng. Syst. Saf. 2007, 92, 707–718. [Google Scholar] [CrossRef]
- Pawitan, Y. All Likelihood: Statistical Modelling and Inference Using Likelihood; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: London, UK, 2013. [Google Scholar]
- Possolo, A.; Toman, B. Assessment of measurement uncertainty via observation equations. Metrologia 2007, 44, 464. [Google Scholar] [CrossRef]
- Coope, I.D. Circle fitting by linear and nonlinear least squares. J. Optim. Theory. Appl. 1993, 76, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Gander, W.; Golub, G.H.; Strebel, R. Least-squares fitting of circles and ellipses. BIT Numer. Math. 1994, 34, 558–578. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).