Entropy-Based Solubility Parameter-Translated Peng–Robinson Equation of State (eSPT-PR EoS)
Abstract
1. Introduction
2. Materials and Methods
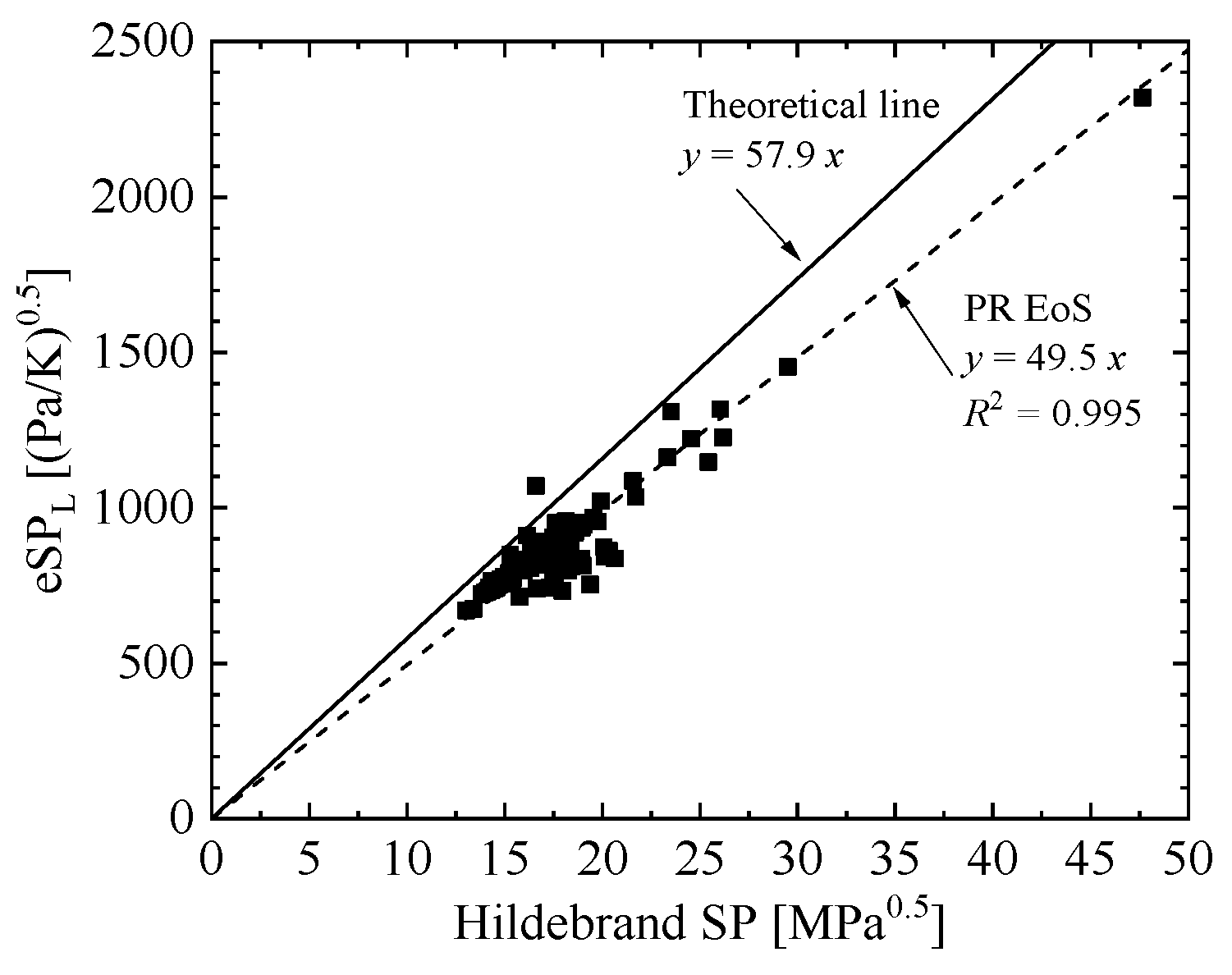
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Peng, D.-Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Mushrif, S.H.; Phoenix, A.V. Effect of Peng−Robinson Binary Interaction Parameters on the Predicted Multiphase Behavior of Selected Binary Systems. Ind. Eng. Chem. Res. 2008, 47, 6280–6288. Available online: https://pubs.acs.org/doi/10.1021/ie800599t (accessed on 23 August 2025). [CrossRef]
- Jaubert, J.-N.; Mutelet, F. VLE predictions with the Peng–Robinson equation of state and temperature dependent kij calculated through a group contribution method. Fluid Phase Equilib. 2004, 224, 285–304. [Google Scholar] [CrossRef]
- Maeta, Y.; Ota, M.; Sato, Y.; Smith, R.L.; Inomata, H. Measurements of vapor–liquid equilibrium in both binary carbon dioxide–ethanol and ternary carbon dioxide–ethanol–water systems with a newly developed flow-type apparatus. Fluid Phase Equilib. 2015, 405, 96–100. [Google Scholar] [CrossRef]
- Soma, S.; Ota, M.; Sato, Y.; Smith, R.L.; Inomata, H. Measurement and correlation of vapor-liquid distribution coefficients of flavonoids in high pressure carbon dioxide—Ethanol—Water systems. Fluid Phase Equilib. 2019, 489, 90–98. [Google Scholar] [CrossRef]
- Urabe, M.; Ota, M.; Smith, R.L.; Watanabe, M. High-pressure phase equilibria of liquid CO2 with ethanol—Water mixtures. Fluid Phase Equilib. 2025, 597, 114450. [Google Scholar] [CrossRef]
- Ueno, Y.; Hoshino, Y.; Ota, M.; Sato, Y.; Inomata, H. Experiments and simulation of counter-current extraction (subcritical fluid separation) by supercritical CO2 with hops-extract ethanol solution. Kagaku Kogaku Rombunshu 2021, 47, 23–27. [Google Scholar] [CrossRef]
- Hoshino, Y.; Ueno, Y.; Ota, M.; Sato, Y.; Inomata, H. Measurement and correlation of vapor–liquid distribution coefficients of compounds contained in hops-extract ethanol solution with supercritical CO2. Kagaku Kogaku Rombunshu 2021, 47, 17–22. [Google Scholar] [CrossRef]
- Péneloux, A.; Rauzy, E.; Fréze, R. A consistent correction for Redlich-Kwong-Soave volumes. Fluid Phase Equilib. 1982, 8, 7–23. [Google Scholar] [CrossRef]
- Ahlers, J.; Gmehling, J. Development of an universal group contribution equation of state. I. Prediction of liquid densities for pure compounds with a volume translated Peng-Robinson equation of state. Fluid Phase Equilib. 2001, 191, 177–188. [Google Scholar] [CrossRef]
- Tsai, J.-C.; Chen, Y.-P. Application of a volume-translated Peng-Robinson equation of state on vapor-liquid equilibrium calculations. Fluid Phase Equilib. 1998, 145, 193–215. [Google Scholar] [CrossRef]
- Schmid, B.; Gmehling, J. Present status of the group contribution equation of state VTPR and typical applications for process development. Fluid Phase Equilib. 2016, 425, 443–450. [Google Scholar] [CrossRef]
- Ota, M.; Hashimoto, Y.; Sato, M.; Sato, Y.; Smith, R.L.; Inomata, H. Solubility of flavone, 6-methoxyflavone and anthracene in supercritical CO2 with/without a co-solvent of ethanol correlated by using a newly proposed entropy-based solubility parameter. Fluid Phase Equilib. 2016, 425, 65–71. [Google Scholar] [CrossRef]
- Ota, M.; Sugahara, S.; Sato, Y.; Smith, R.L.; Inomata, H. Vapor-liquid distribution coefficients of hops extract in high pressure CO2 and ethanol mixtures and data correlation with entropy-based solubility parameters. Fluid Phase Equilib. 2017, 434, 44–48. [Google Scholar] [CrossRef]
- Hildebrand, J.H.; Scott, R.L. The Solubility of Nonelectrolytes, 3rd ed.; Reinhold Pub. Corporation: New York, NY, USA, 1950. [Google Scholar]
- Tomai, T.; Tajima, N.; Kimura, M.; Yoko, A.; Seong, G.; Adschiri, T. Solvent accommodation effect on dispersibility of metal oxide nanoparticle with chemisorbed organic shell. J. Colloid Interface Sci. 2021, 587, 574–580. [Google Scholar] [CrossRef] [PubMed]
- Elliott, J.R.; Diky, V.; Knotts, T.A., IV; Wilding, W.V. The Properties of Gases and Liquids, 6th ed.; Mc Graw Hill: New York, NY, USA, 2023; pp. 687–747. [Google Scholar]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- NIST Chemistry Webbook. Available online: https://webbook.nist.gov/chemistry/fluid (accessed on 23 August 2025).
- Levelt Sengers, J.M.H. From Van der Waals’ equation to the scaling laws. Physica 1974, 73, 73–106. [Google Scholar] [CrossRef]
| No. | Substance | Mw 1 [-] | TC 2 [K] | PC 3 [MPa] | ρC 4 [kg/m3] | ω 5 [-] | ρL at SATP [kg/m3] | Hildebrand SP [MPa0.5] |
|---|---|---|---|---|---|---|---|---|
| 1 | Water | 18.015 | 647.1 | 22.064 | 321.98 | 0.345 | 997.0 | 48.0 |
| 2 | Ethylene Glycol | 62.068 | 719 | 8.2 | 331.91 | 0.521 | 1110.1 | 34.5 |
| 3 | N-Methyl-2-pyrrolidone | 99.131 | 721.6 | 4.52 | 319.78 | 0.373 | 1026.1 | 30.3 |
| 4 | Methanol | 32.042 | 512.5 | 8.084 | 273.86 | 0.566 | 789.6 | 29.5 |
| 5 | Ethanol | 46.068 | 514 | 6.137 | 274.21 | 0.644 | 785.9 | 26.4 |
| 6 | Dimethyl Sulfide | 62.134 | 503.04 | 5.53 | 309.12 | 0.194 | 842.6 | 26.3 |
| 7 | 1-Propanol | 60.095 | 536.8 | 5.169 | 274.41 | 0.621 | 799.5 | 24.6 |
| 8 | N,N-Dimethylformamide | 73.094 | 649.6 | 4.42 | 279.00 | 0.318 | 944.5 | 24.0 |
| 9 | 1-Butanol | 74.122 | 563.1 | 4.414 | 271.51 | 0.588 | 804.0 | 23.3 |
| 10 | 2-Butanol | 74.122 | 535.9 | 4.188 | 274.53 | 0.581 | 802.3 | 22.6 |
| 11 | Pyridine | 79.1 | 619.95 | 5.63 | 311.42 | 0.239 | 978.0 | 21.8 |
| 12 | Cyclopentanone | 84.116 | 624.5 | 4.6 | 326.03 | 0.288 | 944.2 | 21.1 |
| 13 | Acetophenone | 120.149 | 709.6 | 4.01 | 311.27 | 0.383 | 1023.5 | 20.9 |
| 14 | Dichloromethane | 84.933 | 510 | 6.08 | 459.10 | 0.199 | 1318.2 | 20.4 |
| 15 | Dimethyl Carbonate | 90.078 | 548 | 4.5 | 358.88 | 0.385 | 1063.2 | 20.3 |
| 16 | Cyclohexanone | 98.143 | 653 | 4 | 315.57 | 0.299 | 942.7 | 20.1 |
| 17 | Acetone | 58.079 | 508.1 | 4.7 | 272.67 | 0.307 | 785.6 | 19.8 |
| 18 | Tetrahydrofuran | 72.106 | 540.15 | 5.19 | 321.90 | 0.225 | 880.0 | 19.1 |
| 19 | Benzene | 78.112 | 562.05 | 4.895 | 305.13 | 0.21 | 873.0 | 18.8 |
| 20 | Toluene | 92.138 | 591.75 | 4.108 | 291.58 | 0.264 | 863.9 | 18.3 |
| 21 | 1-Decanol | 158.281 | 688 | 2.308 | 245.40 | 0.607 | 821.0 | 17.8 |
| 22 | Trans-Decahydronaphthalene | 138.25 | 687 | 3.2 | 288.02 | 0.299 | 866.7 | 17.0 |
| 23 | Cyclohexane | 84.159 | 553.8 | 4.08 | 273.24 | 0.208 | 773.1 | 16.7 |
| 24 | Tetradecane | 198.388 | 693 | 1.57 | 221.17 | 0.643 | 759.3 | 15.9 |
| 25 | 1-Decene | 140.266 | 616.6 | 2.223 | 240.18 | 0.48 | 738.2 | 15.9 |
| 26 | Decane | 142.282 | 617.7 | 2.11 | 230.60 | 0.492 | 726.6 | 15.5 |
| 27 | Hexane | 86.175 | 507.6 | 3.025 | 232.28 | 0.301 | 656.0 | 15.0 |
| a0 | b0 | KC1 | KC2 | KC3 | C | |
|---|---|---|---|---|---|---|
| Original PR EoS [1] | 0.45724 | 0.07780 | 0.37464 | 1.54226 | −0.26990 | 0 |
| eSPT-PR EoS | 0.47024 | 0.08085 | 0.32183 | 1.84761 | −0.18613 | Substance-dependent |
| No. | Substance | Group | C [J·mol−1·K−1] | ARD () [%] | ARD () [%] | ||
|---|---|---|---|---|---|---|---|
| 1 | Water | Water | 1.7068 | 3.4 | (17.5) 1 | 3.8 | (28.6) 1 |
| 2 | Ethylene Glycol | Alcohol | 1.1163 | 1.4 | (10.1) 1 | 1.2 | (20.2) 1 |
| 3 | N-Methyl-2-pyrrolidone | Cyclic Compound | 1.6422 | 2.7 | (17.1) 1 | 3.0 | (27.3) 1 |
| 4 | Methanol | Alcohol | 1.7852 | 5.1 | (17.5) 1 | 5.8 | (30.9) 1 |
| 5 | Ethanol | Alcohol | 1.2025 | 6.4 | (6.7) 1 | 6.0 | (24.9) 1 |
| 6 | Dimethyl Sulfide | Sulfur compound | 0.5601 | 5.5 | (2.4) 1 | 5.0 | (17.3) 1 |
| 7 | 1-Propanol | Alcohol | 0.8655 | 6.2 | (2.0) 1 | 5.6 | (21.1) 1 |
| 8 | N,N-Dimethylformamide | Nitrogen compound | 2.3108 | 3.0 | (37.7) 1 | 1.0 | (33.3) 1 |
| 9 | 1-Butanol | Alcohol | 0.7835 | 5.8 | (1.2) 1 | 5.3 | (19.9) 1 |
| 10 | 2-Butanol | Alcohol | 0.8906 | 5.8 | (2.7) 1 | 5.3 | (21.0) 1 |
| 11 | Pyridine | Aromatic | 0.4891 | 1.7 | (0.5) 1 | 1.7 | (13.7) 1 |
| 12 | Cyclopentanone | Ketone | 1.5600 | 6.2 | (11.7) 1 | 6.2 | (28.9) 1 |
| 13 | Acetophenone | Ketone | 0.9394 | 1.7 | (7.0) 1 | 1.4 | (18.4) 1 |
| 14 | Dichloromethane | Halide | 0.7571 | 3.2 | (2.4) 1 | 2.7 | (17.5) 1 |
| 15 | Dimethyl Carbonate | Carbonate | 1.1720 | 4.3 | (7.8) 1 | 3.8 | (22.9) 1 |
| 16 | Cyclohexanone | Ketone | 1.6131 | 5.1 | (13.8) 1 | 5.2 | (28.7) 1 |
| 17 | Acetone | Ketone | 1.5010 | 3.8 | (13.4) 1 | 3.6 | (26.3) 1 |
| 18 | Tetrahydrofuran | Aromatic | 0.6463 | 6.9 | (2.5) 1 | 6.4 | (19.4) 1 |
| 19 | Benzene | Aromatic | 0.5147 | 5.1 | (2.5) 1 | 4.7 | (16.6) 1 |
| 20 | Toluene | Aromatic | 0.6947 | 4.5 | (0.5) 1 | 4.0 | (17.9) 1 |
| 21 | 1-Decanol | Alcohol | 1.0130 | 1.4 | (8.7) 1 | 1.2 | (19.0) 1 |
| 22 | Trans-Decahydronaphthalene | Aromatic | 0.4547 | 5.4 | (3.3) 1 | 5.2 | (16.3) 1 |
| 23 | Cyclohexane | Cyclic Compound | 0.3409 | 5.3 | (4.8) 1 | 5.1 | (15.1) 1 |
| 24 | Tetradecane | Alkane | 1.5126 | 0.0 | (18.4) 1 | 0.4 | (23.9) 1 |
| 25 | 1-Decene | Alkene | 1.0125 | 4.4 | (5.5) 1 | 3.9 | (21.2) 1 |
| 26 | Decane | Alkane | 1.0892 | 3.2 | (7.9) 1 | 2.8 | (21.1) 1 |
| 27 | Hexane | Alkane | 0.6060 | 4.8 | (0.8) 1 | 4.4 | (17.3) 1 |
| - | - | Average | 4.2 | (8.4) 1 | 3.9 | (21.8) 1 | |
| a0 | b0 | KC1 | KC2 | KC3 | D | E | ARD () [%] 1 | ARD () [%] 1 | |
|---|---|---|---|---|---|---|---|---|---|
| Original PR EoS [1] | 0.45724 | 0.07780 | 0.37464 | 1.54226 | −0.26990 | - | - | 8.4 | 21.8 |
| VT-PR EoS [10] (Predictive form) | 0.45724 | 0.07780 | - | - | - | - | - | 7.3 | 21.8 |
| eSPT-PR EoS (Predictive form) | 0.51119 | 0.09079 | 0.34687 | 1.93487 | −0.25698 | −27.6704 | 8.73306 | 4.1 | 2.0 |
| n-Hexane | eSPT-PR EoS ARD () [%] | eSPT-PR EoS ARD () [%] | pc-SAFT EoS ARD () [%] | pc-SAFT EoS ARD () [%] |
| (Tr = 0.8, Pr = 0.8) | 1.8 | - | 2.2 | - |
| (Tr = 1.15, Pr = 1.2) | - | 23.9 | - | 2.6 |
| CO2 | eSPT-PR EoS ARD () [%] | eSPT-PR EoS ARD () [%] | pc-SAFT EoS ARD () [%] | pc-SAFT EoS ARD () [%] |
| (Tr = 0.8, Pr = 0.8) | 1.1 | 6.0 | - | |
| (Tr = 1.2, Pr = 1.2) | - | 19.0 | - | 5.1 |
| Methanol | eSPT-PR EoS ARD () [%] | eSPT-PR EoS ARD () [%] | pc-SAFT EoS ARD () [%] | pc-SAFT EoS ARD () [%] |
| (Tr = 0.8, Pr = 0.8) | 3.5 | - | 0.53 | - |
| (Tr = 1.2, Pr = 1.2) | - | 43.7 | - | 1.7 |
| Water | eSPT-PR EoS ARD () [%] | eSPT-PR EoS ARD () [%] | pc-SAFT EoS * ARD () [%] | pc-SAFT EoS * ARD () [%] |
| (Tr = 0.8, Pr = 0.8) | 3.9 | - | 0.09 | - |
| (Tr = 1.2, Pr = 1.2) | - | 42.3 | - | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ota, M.; Yang, N.; Komatsu, H.; Inomata, H.; Smith, R.L., Jr. Entropy-Based Solubility Parameter-Translated Peng–Robinson Equation of State (eSPT-PR EoS). Liquids 2025, 5, 21. https://doi.org/10.3390/liquids5030021
Ota M, Yang N, Komatsu H, Inomata H, Smith RL Jr. Entropy-Based Solubility Parameter-Translated Peng–Robinson Equation of State (eSPT-PR EoS). Liquids. 2025; 5(3):21. https://doi.org/10.3390/liquids5030021
Chicago/Turabian StyleOta, Masaki, Naishu Yang, Hiroyuki Komatsu, Hiroshi Inomata, and Richard Lee Smith, Jr. 2025. "Entropy-Based Solubility Parameter-Translated Peng–Robinson Equation of State (eSPT-PR EoS)" Liquids 5, no. 3: 21. https://doi.org/10.3390/liquids5030021
APA StyleOta, M., Yang, N., Komatsu, H., Inomata, H., & Smith, R. L., Jr. (2025). Entropy-Based Solubility Parameter-Translated Peng–Robinson Equation of State (eSPT-PR EoS). Liquids, 5(3), 21. https://doi.org/10.3390/liquids5030021







