Abstract
Mole fraction of solubilities are reported for the: o-acetoacetanisidide, anthracene, benzoin, 4-tert-butylbenzoic acid, 3-chlorobenzoic acid, 3-chlorobenzoic acid, 2-chloro-5-nitrobenzoic acid, 4-chloro-3-nitrobenzoic acid, 3,4-dichlorobenzoic acid, 2,3-dimethoxybenzoic acid, 3,4-dimethoxybenzoic acid, 3,5-dimethoxybenzoic acid, 3,5-dinitrobenzoic acid, diphenyl sulfone, 2-ethylanthraquinone, 2-methoxybenzoic acid, 4-methoxybenzoic acid, 2-methylbenzoic acid, 3-methylbenzoic acid, 2-methyl-3-nitrobenzoic acid, 3-methyl-4-nitrobenzoic acid, 4-methyl-3-nitrobenzoic acid, 2-naphthoxyacetic acid, 3-nitrobenzoic acid, 4-nitrobenzoic acid, salicylamide, thioxanthene-9-one, 3,4,5-trimethoxybenzoic acid, and xanthene dissolved in isobutyl acetate at 298.15 K. The results of our experimental measurements, combined with the published literature data, were used to obtain Abraham model equations for isobutyl acetate. The mathematical correlations presented in the current study describe the observed molar solubility ratios of the solutes dissolved in isobutyl acetate to within an overall standard deviation of 0.12 log units or less.
1. Introduction
Several million tons of organic solvents are consumed annually by the chemical manufacturing sector. Organic solvents serve as the reaction media in the synthesis of new chemical products, as the mobile phase in high-performance liquid chromatographic separations, and as extractants in biphasic liquid–liquid partitioning systems. Considerable effort has been devoted to developing and revising guidelines to aid industrial workers in selecting the most appropriate organic solvent for a particular application. The guidelines are revised continually as compounds are added to or removed from the list of “acceptable” solvents for use in manufacturing processes. Workers are instructed to focus not only the safety and economic aspects, but to also consider the solvents’ polarity and hydrogen-bonding characteristics, as these are important items as well. Solute–solvent interactions that result from hydrogen-bond formation and from differences in dipole moments can not only increase a given solute’s solubility, but can also alter the thermodynamic states of chemical reactants, synthesized products, and reaction intermediates. Product yields and selectivity, as well as chemical reaction rates, can be controlled to some extent through the solvent selection process. Slight increases in product yield and reaction rates can make a manufacturing process significantly more profitable.
It is only natural that industrial researchers utilize all of the available resources at their disposal in designing synthetic processes. Design engineers ideally prefer to utilize actual experimental data whenever available, as this provides less uncertainty in the required input values/parameters. Experimental data are often unavailable for the many possible solute–solvent combinations currently encountered in the various manufacturing processes. This is particularly true in the case of more environmentally friendly organic mono-solvents and solvent mixtures that are now being suggested as possible solvent alternatives to replace the more toxic, hazardous compounds that have been traditionally used in industrial manufacturing processes. Increased environmental awareness and worker safety, combined with much larger disposal costs, have encouraged the manufacturing sector to reduce (and in certain cases to completely eliminate) the use of specific organic solvents. The disposal of toxic organic compounds in accordance with prevailing governmental regulations can represent a significant expenditure, which is then passed on to the consumer in the form of a higher product purchase price.
Over the last 50 years, a multitude of predictive methods have been developed to provide the scientific and manufacturing communities with the needed input values if measured data are unavailable. The expressions derived from such predictive methods can be used to prioritize potential organic solvent candidates for possible thermodynamic and solubility determinations. Predictive expressions must yield reasonably accurate estimates of the desired property to be of any real value. The more reliable of the proposed models have incorporated mathematical terms to account for the various molecular interactions believed to be present.
The objective of the current study is to develop Abraham model expressions [1,2,3], as follows:
for estimating the logarithm water-to-isobutyl acetate partition coefficients, log P, the logarithm of gas-to-isobutyl acetate partition coefficients, log K, and the logarithm of molar solubility ratios, log (CS,organic/CS,water) and log (CS,organic/CS,gas), for solid nonelectrolyte organic compounds and inorganic gases dissolved in the isobutyl acetate mono-solvent. The subscripts “organic,” “water,” and “gas” are used to define the two solubility ratios that denote the phase to which each molar solute concentration pertains.
log P or log (CS,organic/CS,water) = cp + ep × E + sp × S + ap × A + bp × B + vp × V
log K or log (CS,organic/CS,gas) = ck + ek × E + sk × S + ak × A + bk × B + lk × L
Each multiplicative term on the right-hand side of Equations (1) and (2) describes a different type of solute–solvent molecular interaction. Each interaction is quantified as the product of a solvent property (cp, ep, sp, ap, bp, vp, ck, ek, sk, ak, bk, and lk) times the complementary solute property (E, S, A, B, V, and L). The solvent properties are defined as follows: (ep and ek) give the tendency of the solvent to interact with solute molecules through polarizability-type interactions involving electron pairs; (sp and sk) are measures of the solvent phase’s dipolarity/polarity; (ap and ak) and (bp and bk) quantify the solvent’s ability to function as a hydrogen-bond acceptor and hydrogen-bond donor in its interactions with the surrounding solute molecules, respectively; and (vp and lk) represent the ease of breaking the solvent–solvent interaction in regards to the formation of a solvent cavity in which the dissolved solute will reside. The numerical values of the aforementioned properties are deduced by curve-fitting measured partition coefficient data and molar solubility ratios for a series of solutes with known solute descriptors (E, S, A, B, V, and L) in accordance with Equations (1) and (2). In the present study, we focus our attention on the lowercase solvent properties. A detailed discussion of the solute descriptors and their determination based on measured chromatographic retention times, partition coefficients, and molar solubilities is available in several published review articles [4,5,6,7,8] and research papers [2,3,9,10,11,12].
There are published experimental data for the following: hydrogen [13], nitrogen [13], carbon dioxide [13], carbon monoxide [13], naphthalene [14], fluorene [15], benzoic acid [16], acetylsalicylic acid [17], isophthalic acid [16], forchlorfenuron [18], metronidiazole benzoate [19], iminostilbene [20], isovanillin [21], lansoprazole [22], 2,2′-bis(2-hydroxyethoxy)-1,1′-binaphthalene [23], lovastatin [24], etodolac [25], simvastatin [26,27], 18β-glycyrrhetinic acid [28], and exo-5,6-dehydronorcantharidin [29] dissolved in isobutyl acetate. An experimental gas-to-liquid partition coefficient for isobutyl acetate dissolved in itself is also available from the vapor pressure measurements of Monton and coworkers [30]. Unfortunately, the number of experimental values is not sufficient for us to develop meaningful Abraham model expressions. To supplement the published literature values, we have determined the mole fraction of the solubilities of the following: o-acetoacetanisidide, anthracene, benzoin, 4-tert-butylbenzoic acid, 3-chlorobenzoic acid, 3-chlorobenzoic acid, 2-chloro-5-nitrobenzoic acid, 4-chloro-3-nitrobenzoic acid, 3,4-dichlorobenzoic acid, 2,3-dimethoxybenzoic acid, 3,4-dimethoxybenzoic acid, 3,5-dimethoxybenzoic acid, 3,5-dinitrobenzoic acid, diphenyl sulfone, 2-ethylanthraquinone, 2-methoxybenzoic acid, 4-methoxybenzoic acid, 2-methylbenzoic acid, 3-methylbenzoic acid, 2-methyl-3-nitrobenzoic acid, 3-methyl-4-nitrobenzoic acid, 4-methyl-3-nitrobenzoic acid, 2-naphthoxyacetic acid, 3-nitrobenzoic acid, 4-nitrobenzoic acid, salicylamide, thioxanthene-9-one, 3,4,5-trimethoxybenzoic acid, and xanthene dissolved in isobutyl acetate at 298.15 K based on UV/visible spectrophotometric measurements.
Our solute selection was based, in part, on the compounds’ availability within the laboratory from prior solubility studies, and the fact that their solute descriptor values were determined from large numbers of experimental measurements. Furthermore, our past studies have shown that these compounds are not prone to form solid solvates with alkyl acetates, and their solubilities can be readily determined by either UV/visible absorbance measurements or volumetric acid–base titrations. The senior author is also currently preparing a volume for the IUPAC-NIST Solubility Data Series (project number #2021-023-1-500) that will update his earlier volume on the solubility of benzoic acid and substituted benzoic acids dissolved in both neat organic solvents and organic solvent mixtures [31]. The solubility data from the current study will likely be part of the new volume. We further note that the carboxylic acid functional group is present in many medicinal compounds, such as nonsteroidal anti-inflammatory drugs (e.g., acetylsalicylic acid, salicylic acid, naproxen, ketoprofen, ibuprofen, etodolac, flurbiprofen, ketorolac, and tolfenamic acid), statins (e.g., atorvastatin, Lipitor®, fluvastatin, pitavastatin, pravastatin, and cerivastatin) and β-lactam antibiotics (e.g., amoxicillin, oxacillin, flucloxacillin, and benzylpenicillin). The results of our experimental measurements, combined with the published literature data, were used to obtain Abraham model equations for isobutyl acetate. The derived Abraham model correlations reported in the current study are based on 49 experimental data points.
2. Chemical Materials and Experimental Methodology
The crystalline organic solutes selected for the solubility measurements include 21 carboxylic acids, as well as 8 noncarboxylic acid solutes of varying polarity and molecular sizes. All chemicals used in the current study were purchased from commercial sources in the highest purity available. Several of the noncarboxylic acid solutes were further purified by recrystallization from either acetone or anhydrous methanol prior to performing the solubility measurements. All solid compounds were dried for at least two days at 333 K to remove trace moisture. The purification details and chemical suppliers are given in Table 1, along with the final purities, as determined by either gas–liquid chromatographic analysis (noncarboxylic acid solutes and flame ionization detector) or non-aqueous acid–base volumetric titration based on a modification of the published method used by Fritz and Lisicki [32]. Our modified titration procedure replaced benzene with toluene as a component in the titration solvent for health reasons.

Table 1.
Chemical sources and final mass fraction purities of chemicals used in the solubility studies.
The experimental mole fraction solubilities were determined using a spectrophotometric method of chemical analysis based on the Beer–Lambert law that establishes a mathematical relationship between the measured solution absorbance and the molar concentration of the dissolved solid solute. The saturated solutions were prepared by placing excess solid solute and approximately 20 mLs of isobutyl acetate into amber glass bottles. The resulting solutions were then equilibrated at 298.15 ± 0.05 in a constant-temperature water bath. The sealed solutions were periodically shaken to facilitate the mixing and dissolution of the solid solute. After a three-day equilibration period, weighed aliquots of the saturated solutions were transferred into tared volumetric flasks, and the transferred sample was diluted quantitatively with 2-propanol. The absorbances of the diluted solutions were recorded with a Milton Roy Spectronic 1000 Plus single-beam spectrophotometer (Milton Roy, Rochester, NY, USA). An additional dilution was sometimes required to ensure that the sample’s measured absorbance fell within the range of values determined for the standard solutions. Our earlier publications contain the analysis wavelength and concentration range for each solute considered in the current study. For the convenience of the reader, this information is summarized in Table 2.

Table 2.
Analysis wavelengths and concentration ranges of standard solutions used in the spectrophotometric determination of solubility.
We noted that isobutyl acetate is optically transparent at the analysis wavelengths listed in Table 2. We checked for possible interferences from the small amount of isobutyl acetate in the dilute samples that were subjected to absorbance measurements. We found that, to within experimental uncertainty, identical absorbances were obtained for standard solutions that contained no isobutyl acetate and for standard solutions that contained up to 5 percent isobutyl acetate by volume. We also checked for both solvate formation and solid-to-solid phase transitions by determining the melting point temperatures of the solid residue that remained in the amber glass bottles after the solubility measurements were complete. While there is no evidence for either phenomenon in the published literature for the organic solutes considered in the current study, we wanted to confirm that the solid phase remained the same during the initial equilibration period and during the additional equilibration time before the replicate follow-up set of solubility measurements. The attainment of equilibrium was verified by performing a second set of solubility measurements two (or three) days after the initial set of measurements. In all cases, the measured point temperature of the recovered solid material was within the experimental error of the melting point temperature of the purchased commercial sample or the recrystallized compound prior to being placed in contact with the isobutyl acetate mono-solvent. The measured melting point temperatures, given in Table 3, show no indication of solid–solvate formation or polymorphism.

Table 3.
Comparison of the melting point temperatures of the crystalline solutes prior to contact with isobutyl acetate, Tmp,initial a, and of the recovered crystalline solutes in equilibrium with the saturated solution, Tmp,equilibrated a at 101 kPa a.
3. Results and Discussion
The experimental mole fraction solubilities, XS,organic, of the 29 different crystalline organic solutes dissolved in isobutyl acetate are tabulated in the second and fourth columns of Table 4. The numerical values represent the average of 6 to 10 independent experimental determinations, including the follow-up measurements that were performed after the initial three-day equilibration time. The follow-up studies confirmed that, in all cases, equilibrium was achieved after three days. The tabulated XS,organic values were reproducible to within ±2.5% (relative error). We were not able to find in the published chemical and engineering literature solubility data for these organic solutes in isobutyl acetate that we could compare our experimental values against. This was not unexpected, in that it was only until recently that researchers started performing solubility measurements in isobutyl acetate.

Table 4.
Mole fraction solubilities, XS,organic, of select crystalline nonelectrolyte organic compounds dissolved in isobutyl acetate at a temperature of 298.15 K and an ambient atmospheric pressure of 101 kPa a.
The published experimental solubility data that we found were for the following: hydrogen [13], nitrogen [13], carbon dioxide [13], carbon monoxide [13], naphthalene [14], fluorene [15], benzoic acid [16], acetylsalicylic acid [17], isophthalic acid [16], forchlorfenuron [18], metronidiazole benzoate [19], iminostilbene [20], isovanillin [21], lansoprazole [22], 2,2′-bis(2-hydroxyethoxy)-1,1′-binaphthalene [23], lovastatin [24], etodolac [25], simvastatin [26,27], 18β-glycyrrhetinic acid [28], and exo-5,6-dehydronorcantharidin [29] dissolved in isobutyl acetate. Our Abraham model solute descriptor database contains solute descriptors for 13 of the 20 aforementioned solutes. As part of the current study, descriptor values were determined for forchlorfenuron, metronidiazole benzoate, iminostilbene, 2,2′-bis(2-hydroxyethoxy)-1,1′-binaphthalene, etodolac, and 18β-glycyrrhetinic acid using the published solubility data taken from the published chemical literature [18,19,20,23,25,28]. In calculating the solute descriptors of etodolac we eliminated the solubility data reported by Rathi and Deshpande [44] from our computations. The authors reported the solubility of etodolac in 1,4-dioxane and in water in terms of mole fraction and molar solubilities. The reported mole fraction solubilities are not internally consistent with the solubility data expressed in units of molarity [45].
As an informational note, we attempted to calculate the solute descriptors for the remaining two solutes without success. The database for exo-5,6-dehydronorcantharidin contained only a single solvent capable of acting as hydrogen-bond donors (no alcohol solvents), which prevented the calculation of a meaningful set of solute descriptor values. The two lone pairs of electrons on each of the four oxygen atoms on exo-5,6-dehydronorcantharidin can serve as H-bond acceptor sites. In calculating the molecule’s solute descriptors, it is imperative that the database contains solvent molecules capable of acting as H-bond donors. In Table 5, we have compiled our newly calculated solute descriptors, as well as the numerical values for all of the solutes that will be considered in the current study. Readers interested in learning about how the Abraham model solute descriptors are calculated from published solubility data can refer to earlier papers [12,46,47] that describe the computational method in detail.

Table 5.
Solute descriptors of the compounds used in the regression analysis for determining the Abraham model correlations for isobutyl acetate.
The Abraham model correlations that we have derived thus far for describing the solubilizing properties of organic mono-solvents have used the two molar solubility ratios, log (CS,organic/CS,water) and log (CS,organic/CS,gas), as the independent solute property that appears on the left-hand side of Equations (1) and (2), respectively. Published solubility data are often reported in the published literature as mole fraction solubilities, and this is how we have elected to report our measured solubility data in Table 3 for the 29 crystalline organic compounds for which solubility measurements were performed. The conversion of mole fraction solubilities to molar solubilities is relatively straightforward and involves dividing XS,organic by the ideal molar volume of the saturated solution, as follows:
CS,organic ≈ XS,organic/[XS,organic VSolute + (1 − XS,organic) VSolvent]
A numerical value of Vsolvent = 0.1341 liter mol−1 was used for the molar volume of the isobutyl acetate solvent. Mole fraction solubility data taken from the published chemical literature [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] were converted into molar solubilities in a similar fashion. The estimated values of Vsolute, taken from the Chemspider website [48], were used for the solid organic solutes. In Table 6, we have assembled the calculated molar solubility ratios for the 44 solid organic compounds that will be used in the regression analyses for obtaining Abraham model correlations for isobutyl acetate. Also included in Table 6 are the logarithms of the gas-to-isobutyl acetate partition coefficients, log K, and logarithms of the water-to-isobutyl acetate transfer coefficients, log P, for the four inorganic gases (hydrogen, nitrogen, carbon monoxide, and carbon dioxide) and for isobutyl acetate, as well as the log CS,gas and log CS,water values used in calculating the individual molar solubility ratios.

Table 6.
Experimental logarithms of molar solubility ratios, log (CS,organic/CS,gas) and log (CS,organic/CS,water), for solutes dissolved in isobutyl acetate at 298.15 K, as well as the logarithms of solute’s molar gas phase concentration, log CS,gas, and the solute’s molar solubility in water, log CS,water, at 298.15 K.
While most of the experimental data points compiled in Table 6 pertain to solid organic compounds, the range of values spanned by the individual solute descriptors are as follows: from E = 0.000 to E = 3.610; from S = 0.000 to S = 3.377; from A = 0.000 to A = 1.186; from B = 0.000 to B = 1.860; from V = 0.1086 to V = 3.4628; and L= −1.200 to L = 17.398, which is sufficiently large enough to allow for the development of meaningful Abraham model correlations for predicting the molar solubilities of many organic compounds commonly encountered in industrial manufacturing processes. The range of solute descriptors covered determines the area of predictive chemical space over which the correlation can be used. An analysis of the experimental data points in Table 6 yielded the following two Abraham model expressions:
where the numerical value enclosed within the parentheses following each coefficient represents the standard error in the respective coefficient. The statistical information associated with correlation includes the following: the number of experimental data points used in determining the equation coefficients, N; the standard deviation, SD; the squared correlation coefficient, R2; the standard error of the estimate, SEE; and the Fisher F-statistic, F. As an informational note, the b × B term was not included in the Equation (5) regression analysis because isobutyl acetate lacks acidic hydrogen, and thus cannot act as an H-bond donor. Both correlations were obtained using the IBM SPSS Statistical 22 commercial software.
log P or log (CS,organic/CS,water) = 0.234(0.055) + 0.351(0.053) E − 0.471(0.080) S − 1.050(0.060) A − 4.982(0.142) B + 4.212(0.081) V
(with N = 49, SD = 0.112, SEE = 0.119; R2 = 0.992, F = 1099)
(with N = 49, SD = 0.112, SEE = 0.119; R2 = 0.992, F = 1099)
log K or log (CS,organic/CS,gas) = 0.173(0.044) − 0.353(0.047) E + 1.183(0.073) S + 2.463(0.058) A
+ 0.936(0.015) L
(with N = 49, SD = 0.112, SEE = 0.117, R2 = 0.999, F = 15753)
+ 0.936(0.015) L
(with N = 49, SD = 0.112, SEE = 0.117, R2 = 0.999, F = 15753)
Careful examination of the statistical information reveals that both mathematical expressions provide a reasonably accurate description of the observed log (CS,organic/CS,water) and log (CS,organic/CS,gas) values, as documented by the small standard deviations (SD = 0.112 log units for both equations) and small standard errors of the estimate (SEE = 0.117 and SEE = 0.119 log units for Equations (4) and (5), respectively). The descriptive ability of both equations is depicted graphically in Figure 1 and Figure 2, which compare the logarithms of the observed molar solubility ratios to the back-calculated values based on our derived Abraham model correlations. As expected from the near-unity squared correlation coefficients, the back-calculated and observed values are in very good agreement.
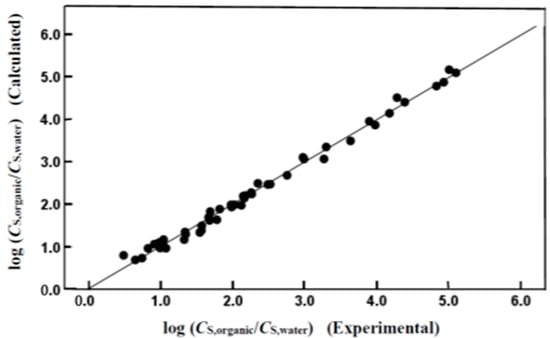
Figure 1.
Comparison of experimental log (CS,organic/CS,water) data versus back-calculated values based on Equation (4) for organic compounds and inorganic gases dissolved in isobutyl acetate.
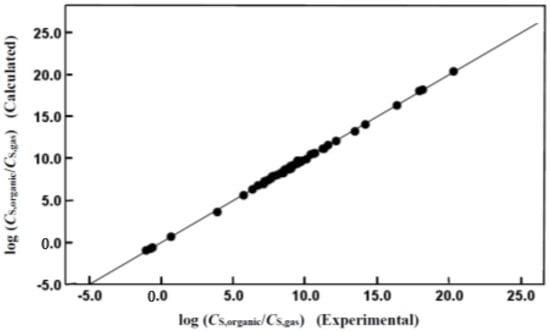
Figure 2.
Comparison of experimental log (CS,organic/CS,gas) data versus back-calculated values based on Equation (5) for organic compounds and inorganic gases dissolved in isobutyl acetate.
Abraham model correlations have now been determined for eleven alkyl alkanoate mono-solvents. In Table 7, we have summarized the equation coefficients for the following: methyl acetate, ethyl acetate, propyl acetate, isopropyl acetate, butyl acetate, isobutyl acetate, tert-butyl acetate, pentyl acetate, methyl butanoate, isopropyl myristate, and dimethyl adipate [49,50,51,52]. The tabulated equation coefficients pertain to the ‘dry, anhydrous’ organic solvents. The words ‘dry, anhydrous’ indicate that the organic solvent was not in direct contact with water, as would be the case for practical partitioning processes involving the removal of the solute from water with, for example, either ethyl acetate or butyl acetate as the extracting organic solvent. Abraham model correlations have been published for ‘wet’ ethyl acetate and ‘wet’ butyl acetate in an earlier paper [53]; however, there has not been sufficient practical partition coefficient data for the other biphasic aqueous-alkyl alkanoate extraction systems to develop meaningful Abraham model correlations.

Table 7.
Abraham model correlations for predicting log (CS,organic/CS,water) and log (CS,organic/CS,gas) molar solubility ratios into select alkyl alkanoate mono-solvents.
An examination of the numerical entries in Table 7 reveals that the equation coefficients for isobutyl acetate are very similar to those of butyl acetate. There should be very little difference in the solubilizing characteristics of these two alkyl acetate solvents. The sign and the magnitude of the cp, ep, sp, ap, bp, and vp coefficients determine whether or not a given solute–solvent interaction increases or decreases the solute’s solubility in the organic solvent relative to the solute’s solubility in water. For example, the negative ap and bp equation coefficients for isobutyl acetate, when substituted into Equation (1), would result in negative ap × A and bp × B terms, and thus decrease the calculated log (CS,organic/CS,water) value. In other words, a solute capable of hydrogen-bond formation is expected to be more soluble in water than in isobutyl acetate when all other solute–solvent interactions are ignored. Large solute molecules, on the other hand, would have a positive vp × V term, which would increase the calculated log (CS,organic/CS,water) value. Large solute molecules would tend to be more soluble in isobutyl acetate when all other solute–solvent interactions are ignored. It is the sum of the five interaction terms, however, that determines the molar solubility ratio.
4. Summary
Mathematical equations based on the Abraham solvation parameter model have been determined by performing multi-linear regression analyses on a chemically diverse set containing 49 organic solutes dissolved in isobutyl acetate. The derived Abraham model expressions were found to accurately predict the observed solubility data to within an overall standard deviation of 0.12 log units or less. Based on prior experience using the Abraham model, we expect that the derived correlations reported in the current study will provide accurate solubility predictions for additional organic compounds dissolved in isobutyl acetate, provided that one does not venture outside of the range of the predictive area of chemical space defined by the 49 solute data sets used in deriving Equations (4) and (5). Moreover, the derived Abraham model correlations will allow us to use experimental solubility data determined in isobutyl acetate in our future solute descriptor calculations. As noted previously in the manuscript, several research groups have started measuring the solubility of drug molecules dissolved in isobutyl acetate.
Author Contributions
Conceptualization and writing—original draft preparation, W.E.A.J.; data curation and analysis, R.M., T.K., J.F., J.C., E.Y., S.M., A.C., D.K. and N.S.; writing—review and editing, R.M., T.K., J.F., J.C., E.Y., S.M., A.C., D.K. and N.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abraham, M.H. Scales of solute hydrogen-bonding: Their construction and application to physicochemical and biochemical processes. Chem. Soc. Rev. 1993, 22, 73–83. [Google Scholar] [CrossRef]
- Abraham, M.H.; Ibrahim, A.; Zissimos, A.M. Determination of sets of solute descriptors from chromatographic measurements. J. Chromatogr. A 2004, 1037, 29–47. [Google Scholar] [CrossRef]
- Abraham, M.H.; Smith, R.E.; Luchtefeld, R.; Boorem, A.J.; Luo, R.; Acree, W.E., Jr. Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 2010, 99, 1500–1515. [Google Scholar] [CrossRef] [PubMed]
- Jalan, A.; Ashcraft, R.W.; West, R.H.; Green, W.H. Predicting solvation energies for kinetic modeling. Annu. Rep. Prog. Chem. Sec. C Phys. Chem. 2010, 106, 211–258. [Google Scholar] [CrossRef]
- Clarke, E.D. Beyond physical properties–application of Abraham descriptors and LFER analysis in agrochemical research. Bioorg. Med. Chem. 2009, 17, 4153–4159. [Google Scholar] [CrossRef] [PubMed]
- Poole, C.F.; Ariyasena, T.C.; Lenca, N. Estimation of the environmental properties of compounds from chromatographic properties and the solvation parameter method. J. Chromatogr. A 2013, 1317, 85–104. [Google Scholar] [CrossRef]
- Poole, C.F.; Atapattu, S.N. Recent advances for estimating environmental properties for small molecules from chromato-graphic measurements and the solvation parameter model. J. Chromatogr. A 2022, 1687, 463682. [Google Scholar] [CrossRef]
- Endo, S.; Goss, K.-U. Applications of polyparameter linear free energy relationships in environmental chemistry. Environ. Sci. Technol. 2014, 48, 12477–12491. [Google Scholar] [CrossRef]
- Poole, C.F. Assessment of liquid-liquid partition for the assignment of descriptors for the solvation parameter model. J. Chromatogr. A 2024, 1721, 464850. [Google Scholar] [CrossRef]
- Poole, C.F. Determination of solvation parameter model compound descriptors by gas chromatography. J. Chromatogr. A 2024, 1717, 464711. [Google Scholar] [CrossRef]
- Dayani, M.T.; Ambagaspitiya, A.W.T.D.; Atapattu, S.N.; Ariyasena, T.C. Determination of experimental solute descriptor values for safrole by liquid-liquid partitioning and gas chromatography. Phys. Chem. Liq. 2024, in press. [CrossRef]
- Liu, X.; Acree, W.E., Jr.; Abraham, M.H. Descriptors for some compounds with pharmacological activity; calculation of properties. Int. J. Pharm. 2022, 617, 121597. [Google Scholar] [CrossRef] [PubMed]
- Orlov, A.A.; Demenko, D.Y.; Bignaud, C.; Valtz, A.; Marcou, G.; Horvath, D.; Coquelet, C.; Varnek, A.; de Meyer, F. Chemoinformatics-driven design of new physical solvents for selective CO2 absorption. Environ. Sci. Technol. 2021, 55, 15542–15553. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.-S.; Yi, Z.-M.; Su, M.-G.; Sun, X.-F. Solubility of naphthalene in isobutyl acetate, n-butyric acid, ethyl acetate, N-methyl pyrrolidone, N,N-dimethylformamide, and tetrahydrofuran. J. Chem. Eng. Data 2008, 53, 2701–2703. [Google Scholar] [CrossRef]
- Sun, M.; Xiao, Y.; Zhou, Y.; Zhang, B.; Cui, P.; Zhou, L.; Yin, Q. Solubility measurement and thermodynamic properties of fluorene in 14 pure solvents at temperatures from 278.15 to 318.15 K. J. Chem. Eng. Data 2023, 68, 2491–2499. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, X.; Dai, Q.; Wang, L. Solubilities of benzene carboxylic acids in isobutyl acetate from (299.73 to 353.15) K. J. Chem. Eng. Data 2011, 56, 2399–2402. [Google Scholar] [CrossRef]
- Tully, G.; Hou, G.; Glennon, B. Solubility of benzoic acid and aspirin in pure solvents using focused beam reflective measurement. J. Chem. Eng. Data 2016, 61, 594–601. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y.; Li, H.; Li, Y.; Li, T.; Ren, B. Solubility measurement and Hansen solubility parameter of forchlorfenuron in 12 organic pure solvents at various temperatures. J. Chem. Eng. Data 2022, 67, 3278–3289. [Google Scholar] [CrossRef]
- Yu, F.; Wang, F.; Zhang, L.; Zhang, M.; Zhou, L.; Xie, C.; Bao, Y.; Chen, W.; Gong, J. Uncovering dissolution behavior and thermodynamic properties of metronidazole benzoate in twelve mono-solvents by experiments and molecular simulation. J. Mol. Liq. 2024, 393, 123539. [Google Scholar] [CrossRef]
- Wan, Y.; Gao, X.; Wang, R.; Li, F.; Li, Y.; He, H. Research on solubility behavior of iminostilbene in twelve mono-solvents: Measurement, modeling, molecular simulation and thermodynamic properties. J. Chem. Thermodyn. 2024, 188, 107182. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Dai, J.; Niu, Y.; Yin, Q.; Zhou, L. Solubility determination, model evaluation and solution thermodynamics of isovanillin in 15 pure solvents and 4 binary solvents. J. Mol. Liq. 2021, 340, 116847. [Google Scholar] [CrossRef]
- Hong, M.; Xu, L.; Ren, G.; Chen, J.; Qi, M. Solubility of lansoprazole in different solvents. Fluid Phase Equilib. 2012, 331, 18–25. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, P.; Zhou, L.; Yin, Q. Measurement and correlation of solubility and thermodynamic properties of 2,2′-bis(2-hydroxyethoxy)-1,1′-binaphthalene form B in twelve pure solvents. J. Chem. Eng. Data 2022, 67, 1541–1549. [Google Scholar] [CrossRef]
- Nti-Gyabaah, J.; Chiew, Y.C. Solubility of lovastatin in ethyl acetate, propyl acetate, isopropyl acetate, butyl acetate, sec-butyl acetate, isobutyl acetate, tert-butyl acetate, and 2-butanone, between (285 and 313) K. J. Chem. Eng. Data 2008, 53, 2060–2065. [Google Scholar] [CrossRef]
- Hu, X.; Gong, Y.; Cao, Z.; Huang, Z.; Sha, J.; Li, Y.; Li, T.; Ren, B. Solubility, Hansen solubility parameter and thermodynamic properties of etodolac in twelve organic pure solvents at different temperatures. J. Mol. Liq. 2020, 316, 113779. [Google Scholar] [CrossRef]
- Yan, J.; Yin, Q.; Jiang, C.; Gong, J.; Zhang, M.; Wang, Y.; Hou, B.; Hao, H. Solution thermodynamics of simvastatin in pure solvents and binary solvent mixtures. Fluid Phase Equilib. 2015, 406, 77–90. [Google Scholar] [CrossRef]
- Nti-Gyabaah, J.; Chan, V.; Chiew, Y.C. Solubility and limiting activity coefficient of simvastatin in different organic solvents. Fluid Phase Equilib. 2009, 280, 35–41. [Google Scholar] [CrossRef]
- Shen, Y.; Li, R.; Zhao, P.; Liu, W.; Yang, X.; Zhang, Z. Equilibrium solubility of 18β-glycyrrhetinic acid in 12 pure solvents: Determination, correlation, and Hansen solubility parameter. J. Chem. Eng. Data 2022, 67, 3243–3251. [Google Scholar] [CrossRef]
- He, H.; Wan, Y.; Sha, J.; Sun, R.; Jiang, G.; Li, Y.; Li, T.; Ren, B. Equilibrium solubility of exo-5,6-dehydronorcantharidin in thirteen pure solvents: Determination, correlation, Hansen solubility parameter and thermodynamic properties. J. Mol. Liq. 2020, 312, 113384. [Google Scholar] [CrossRef]
- Monton, J.B.; Munoz, R.; Burguet, M.C.; de la Torre, J. Isobaric vapor-liquid equilibria for the binary systems isobutyl alcohol + isobutyl acetate and tert-butyl alcohol + tert-butyl acetate at 20 and 101.3 kPa. Fluid Phase Equilib. 2005, 227, 19–25. [Google Scholar] [CrossRef]
- Acree, W.E., Jr. IUPAC-NIST Solubility Data Series. Volume 99. Solubility of Benzoic Acid and Substituted Benzoic Acids in Both Neat Organic Solvents and Organic Solvent Mixtures. J. Phys. Chem. Ref. Data 2013, 42, 033103/1–033103/525. [Google Scholar] [CrossRef]
- Fritz, J.S.; Lisicki, N.M. Titration of acids in nonaqueous solvents. Anal. Chem. 1951, 23, 589–591. [Google Scholar] [CrossRef]
- Maiti, A.; Reddy, P.V.N.; Sturdy, M.; Marler, L.; Pegan, S.D.; Mesecar, A.D.; Pezzuto, J.M.; Cushman, M. Synthesis of casimiroin and optimization of its quinone reductase 2 and aromatase inhibitory activities. J. Med. Chem. 2009, 52, 1873–1884. [Google Scholar] [CrossRef]
- Acree, W.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds and Ionic Liquids. Sublimation, Vaporization, and Fusion Enthalpies from 1880 to 2015. Part 2. C11-C192. J. Phys. Chem. Ref. Data 2017, 46, 013104/1–013104/532. [Google Scholar] [CrossRef]
- Bai, H.; Fang, X.; Peng, C.; Liu, Q.; Xie, W.; Jia, L.; Song, Z. Dissolution behavior of 2-ethylanthraquinone in various neat solvents: Solubility, correlation and thermodynamic analysis. J. Mol. Liq. 2019, 289, 111122. [Google Scholar] [CrossRef]
- Liu, C.X. Solubility Measurement and Intrinsic Kinetics Study on Hydrogenation of Alkylanthraquinone. Ph.D. Thesis, Tianjin University, Tianjin, China, 2005. [Google Scholar]
- Acree, W.; Chickos, J.S. Phase transition enthalpy measurements of organic and organometallic compounds. sublimation, vaporization and fusion enthalpies from 1880 to 2015. Part 1. C1–C10. J. Phys. Chem. Ref. Data 2016, 45, 033101/1–033101/565. [Google Scholar] [CrossRef]
- Dippy, J.F.J.; Hughes, S.R.C.; Laxton, J.W. Chemical constitution and the dissociation constants of monocarboxylic acids. XV. Steric effects in substituted nitrobenzoic acids. J. Chem. Soc. 1956, 2995–3000. [Google Scholar] [CrossRef]
- Le Fave, G.M. Some reactions of the trifluoromethyl group in the benzotrifluoride series. I. Hydrolysis. J. Am. Chem. Soc. 1949, 71, 4148–4149. Available online: https://pubs.acs.org/doi/epdf/10.1021/ja01180a507 (accessed on 10 May 2024). [CrossRef]
- Wan, Y.; He, H.; Gao, X.; Guo, X.; Li, F.; Li, Y. Solid-liquid equilibrium of 2,3-dimethoxybenzoic acid in fifteen mono-solvents: Determination, correlation, Hansen solubility parameter, molecular dynamic simulation and thermodynamic analysis. J. Mol. Liq. 2022, 348, 118029. [Google Scholar] [CrossRef]
- Monte, M.J.S.; Hillesheim, D.M. Thermodynamic study on the sublimation of six methylnitrobenzoic acids. J. Chem. Thermodyn. 2001, 33, 103–112. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Wu, Y.; Li, Y.; Li, T.; Ren, B. Solubility and thermodynamic properties of 2-naphthoxyacetic acid in twelve mono-solvents. J. Chem. Thermodyn. 2023, 177, 106934. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Tang, M.; Chen, Y.-P. Solid-liquid equilibria for 3-aminophenol + 2-aminophenol, 4-(acetylamino)toluene + 2-(acetylamino)toluene, and 3,4,5-trimethoxybenzoic acid + 2,4,5-trimethoxybenzoic acid. J. Chem. Eng. Data 2005, 50, 40–43. [Google Scholar] [CrossRef]
- Rathi, P.B.; Deshpande, K.V. Extended Hildebrand approach: An empirical model for solubility prediction of etodolac in 1,4-dioxane and water mixtures. J. Solut. Chem. 2014, 43, 1886–1903. [Google Scholar] [CrossRef]
- Acree, W.E., Jr. Commentary on Extended Hildebrand approach: An empirical model for solubility prediction of etodolac in 1,4-dioxane and water mixtures. J. Solut. Chem. 2017, 46, 2130–2133. [Google Scholar] [CrossRef]
- Charlton, A.K.; Daniels, C.R.; Acree, W.E., Jr.; Abraham, M.H. Solubility of crystalline nonelectrolyte solutes in organic solvents: Mathematical correlation of acetylsalicylic acid solubilities with the Abraham general solvation model. J. Solut. Chem. 2003, 32, 1087–1102. [Google Scholar] [CrossRef]
- Hart, E.; Lee, G.; Qian, E.; Jodray, M.; Barrera, M.; Fischer, R.; Che, M.; Liu, Y.; Zha, O.; Woods, D.; et al. Determination of Abraham model solute descriptors for 4-tert-butylbenzoic acid from experimental solubility data in organic mono-solvents. Phys. Chem. Liq. 2019, 57, 445–452. [Google Scholar] [CrossRef]
- ChemSpider Database, The Royal Society of Chemistry. Available online: http://www.chemspider.com/ (accessed on 14 May 2024).
- Sinha, S.; Yang, C.; Wu, E.; Acree, W.E., Jr. Abraham solvation parameter model: Examination of possible intramolecular hydrogen-bonding using calculated solute descriptors. Liquids 2022, 2, 131–146. [Google Scholar] [CrossRef]
- Shanmugam, N.; Zhou, A.; Motati, R.; Yao, E.; Kandi, T.; Longacre, L.; Benavides, D.; Motati, S.; Acree, W.E., Jr. Development of Abraham model correlations for dimethyl adipate from measured solubility data of nonelectrolyte organic compounds. Phys. Chem. Liq. 2023, 61, 328–339. [Google Scholar] [CrossRef]
- Longacre, L.; Wu, E.; Yang, C.; Zhang, M.; Sinha, S.; Varadharajan, A.; Acree, W.E., Jr. Development of Abraham model correlations for solute transfer into the tert-butyl acetate mono-solvent and updated equations for both ethyl acetate and butyl acetate. Liquids 2022, 2, 258–288. [Google Scholar] [CrossRef]
- Sedov, I.A.; Salikov, T.M.; Khaibrakhmanova, D.R.; Wadawadigi, A.; Zha, O.; Qian, E.; Hart, E.; Barrera, M.; Acree, W.E., Jr.; Abraham, M.H. Determination of Abraham model correlations for solute transfer into propyl acetate based on experimental activity coefficient and solubility data. J. Solut. Chem. 2018, 47, 634–653. [Google Scholar] [CrossRef]
- Sprunger, L.M.; Proctor, A.; Acree, W.E., Jr.; Abraham, M.H.; Benjelloun-Dakhama, N. Correlation and prediction of partition coefficient between the gas phase and water, and the solvents dry methyl acetate, dry and wet ethyl acetate, and dry and wet butyl acetate. Fluid Phase Equilib. 2008, 270, 30–44. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).