Next Article in Journal
Unprecedented High Probe-Reported Polarity of Deep Eutectic Solvents Composed of Lanthanide Salts and Urea
Previous Article in Journal
Abraham General Solvation Parameter Model: Predictive Expressions for Solute Transfer into Isobutyl Acetate
Previous Article in Special Issue
Revisiting the Total Hildebrand and Partial Hansen Solubility Parameters of Analgesic Drug Meloxicam
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Liquids
Volume 4
Issue 3
10.3390/liquids4030027
liquids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Benchmark Test of High-Throughput Atomistic Modeling for Octa-Acid Host–Guest Complexes

by
Xiaohui Wang
1,
Zhe Huai
2,
Lei Zheng
3,4,
Meili Liu
5 and
Zhaoxi Sun
6,*
1
Beijing Leto Laboratories Co., Ltd., Beijing 100083, China
2
Clickmab Biotechnology Research Center, Beijing 100094, China
3
NYU-ECNU Center for Computational Chemistry at NYU Shanghai, Shanghai 200062, China
4
Department of Chemistry, New York University, New York, NY 10003, USA
5
Civil and Architectural Engineering, University of Miami, Coral Gables, FL 33146, USA
6
Changping Laboratory, Beijing 102206, China
*
Author to whom correspondence should be addressed.
Liquids 2024, 4(3), 485-504; https://doi.org/10.3390/liquids4030027
Submission received: 15 April 2024 / Revised: 18 June 2024 / Accepted: 4 July 2024 / Published: 10 July 2024
(This article belongs to the Special Issue Solubility and Solubilization of Drugs: Modeling and Thermodynamic Analysis)
Browse Figures
Review Reports Versions Notes

Abstract

:
Years of massive applications of high-throughput atomistic modeling tools such as molecular docking and end-point free energy calculations in the drug industry and academic exploration have made them indispensable parts of hierarchical screening. While the similarities between host–guest and protein–ligand complexes lead to the direct extension of techniques for protein–ligand screening to host–guest systems, the practical performance of these hit identification tools remains unclear in host-–-guest binding. Recent reports on specific host–guest complexes suggest that the experience on the accuracy ladder accumulated from protein–ligand cases could be invalid in host–guest complexes, which makes it an urgent need to perform a systematic benchmark to secure solid numerical supports and guidance of practical setups. Concerning molecular docking, there still lacks a comprehensive benchmark considering popular docking programs. As for end-point reranking, quantitative and rigorous free energy estimation via end-point formulism requires establishing statistically meaningful measurements of uncertainties due to finite sampling, which is neglected or underestimated by a significant portion in almost all main-stream applications. Further, a face-to-face comparison between different screening tools is required for the design of a hierarchical workflow. To fill the above-mentioned critical gaps, in this work, using a dataset containing tens of host–guest complexes involving basket-like macromolecular hosts from the octa acid family, we extensively benchmark seven academic docking protocols and perform post-docking end-point rescoring with twenty protocols. The resulting comprehensive benchmark provides conclusive pictures of the practical value of docking and end-point screening in OA host–guest binding.

1. Introduction

Due to efficiency and accuracy considerations, modern virtual screening often follows a hierarchical procedure. Low-cost techniques are applied first to eliminate most of the non-promising molecules in an original dataset, and then it comes to the stage employing screening tools of higher costs and accuracy to distill hits from the pool of promising candidates. In the stages where both 3D chemical structures of individual compounds and atomic-detailed interaction patterns between them are incorporated, molecular docking and end-point free energy calculations are the most relevant and popular high-throughput tools for screening of protein–ligand complexes [1,2,3,4,5].
Similar to biomacromolecular assemblies, host–guest complexes are formed by two interacting components of different sizes packed in a shape-complementary manner. Macromolecular hosts are relatively small in size and simpler in composition compared with biomolecules. Commonly encountered species include cyclodextrins, cucurbiturils, and pillararenes, which are often applied as drug carriers and reservoirs [6,7,8,9,10,11]. Their central cavities are often hydrophobic to encapsulate external agents, and their rims are often hydrophilic to serve as hydrogen bond acceptors and/or donors that form directional polar interactions with solvents or guest molecules staying inside the cavity. As host–guest complexes are often considered prototypical analogues of protein–ligand complexes, computational techniques developed for virtual screening of protein–ligand complexes are directly extended to that in host–guest binding [12,13,14,15,16]. However, the validity of such direct extensions has not been systematically validated. Further, several recent application reports on specific host–guest datasets report the violation of existing experiences accumulated in protein–ligand situations [17,18], which makes the act of directly extending the computational ladder designed for protein–ligand complexes to host–guest cases questionable.
To fill this critical gap and provide direct numerical evidence and guidance of the design of the hierarchical screening workflow, we devote the current paper to a practical docking and end-point screening on a series of octa-acid (OA) host–guest complexes. A dataset containing 31 OA–guest pairs and 17 host–guest pairs involving the methylated form TEMOA are constructed from SAMPL challenges [19,20,21,22], and fourteen molecular docking protocols and twenty end-point protocols are employed to rank the binding strength. Compared with previous computational works (e.g., those focusing on docking protocols) [18], our work considers larger datasets and many mainstream docking protocols unexplored in the current literature. Further, the extensiveness of the exploration of end-point protocols is also unprecedented. Our benchmark test covers not only many mainstream implicit-solvent models but, more importantly, both the single- and three-trajectory sampling realizations.
The 2D chemical structures of the prototype OA basket, its methylated form, TEMOA, and the guest molecules are presented in Figure 1. Although, in some situations, multiple guest molecules could be encapsulated simultaneously in a single host cavity [23,24], we limit the current investigation to the 1:1 binding in both experimental reference and computational modeling.

2. Computational Setup

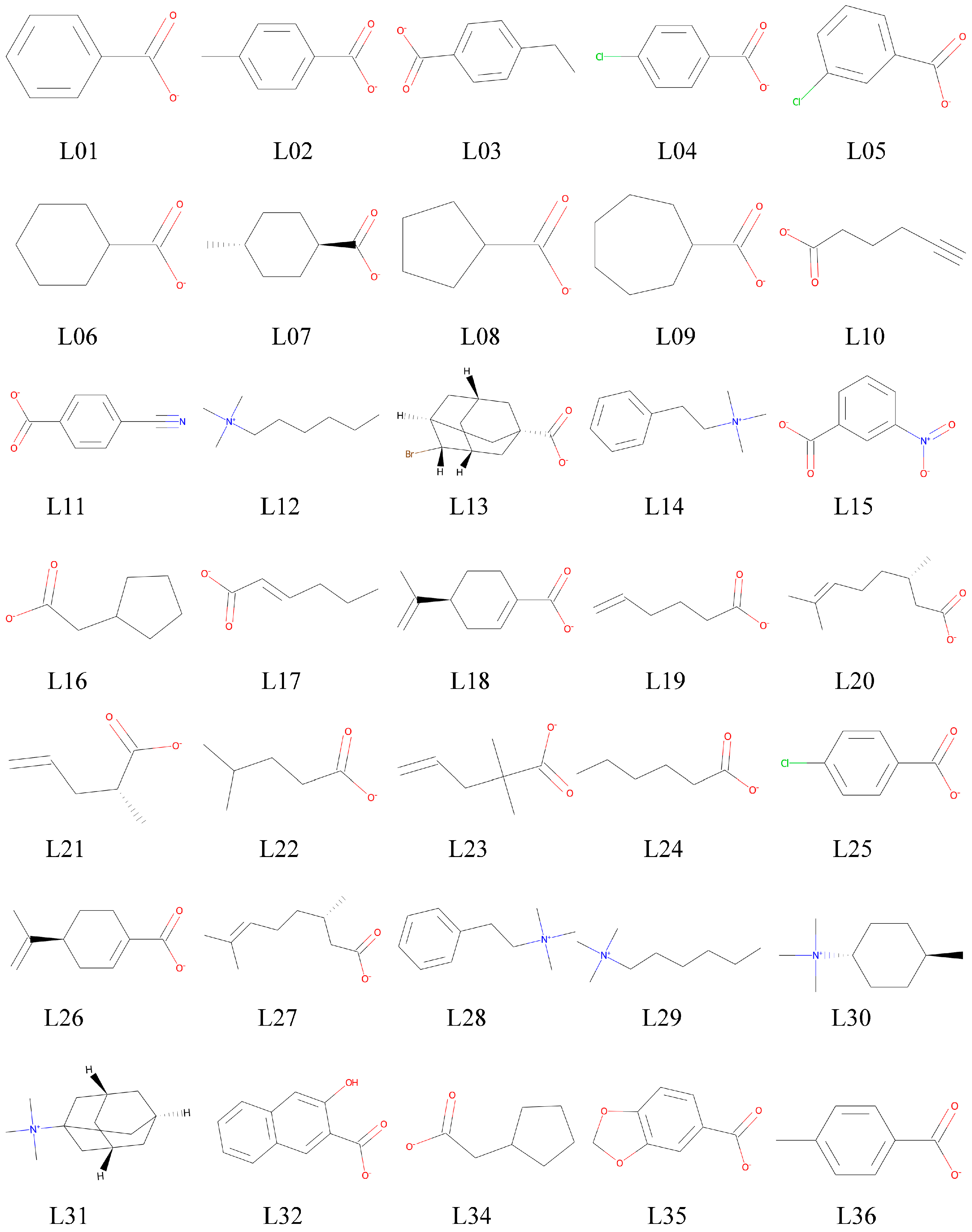
2.1. Docking Screening of Host–Guest Pairs

Molecular docking is a technique that packs two components (e.g., protein and ligand and, similarly, host and guest) into a single interacting complex with a certain level of conformational compatibility. The main components involved in this technique are conformational search and scoring functions. Conformational search techniques and scoring functions of varying features have been constructed up to now. For instance, scoring functions could be primarily derived from all-atom force fields (e.g., AMBER-like AutoDock) [25,26] and include empirical terms (e.g., plp and chemplp) [27,28,29,30,31]. Below, we briefly introduce the docking protocols considered in this work.
The well-known open-source AutoDock tool is presumably the most popular program in protein–ligand docking. The method achieves good performance in various benchmark calculations on protein–ligand docking [32,33]. The up-to-date implementation is Autodock Vina [25]. Our benchmark test with the Autodock Vina software involves two scoring functions (Vina and Vinardo) [25,26,34,35], the results of which would thus be abbreviated as AutoDock-Vina and AutoDock-Vinardo in lateral presentations.
Protein–ligand ANT System (PLANTS) docking calculations are performed with two scoring functions (plp and chemplp) [31,36]. The conformational search method features a hybrid ant colony optimization that imitates the foraging behavior of ants via artificial pheromones [37,38,39]. The scoring functions with PLANTS are constructed as a weighted combination of scoring terms of various origins, such as force-field energetics (e.g., torsional potential from Tripos) [40] and hydrogen bond terms from Chemscore [41,42]. While, from the names of scoring functions, it is straightforward to know that the plp and chemplp docking regimes with PLANTS differ in the scoring functions for ranking different structures, there are further differences in conformational search parameters. According to existing experiences published in the literature on protein–ligand complexes, the chemplp scoring function is generally slower in speed but higher in accuracy compared with the plp selection. The PLANTS results will be abbreviated as PLANTS-plp and PLANTS-chemplp in the following paragraphs.
The latest implementation of the DOCK program, DOCK6.10, is also considered. The recommended workflow in the newest implementation incorporates a sphere representation of the molecular surface, an anchor growth algorithm for flexible conformational search, and many selections for pose scoring [43,44,45]. Two scoring functions benchmarked in this work include the popular (grid-based) energy scoring and contact scoring with a cutoff of 4.5 Å, which will be abbreviated as DOCK6-energy and DOCK6-contact in this manuscript.
The rDock [46] protocol originally developed as RiboDock is designed for RNA–ligand docking [47]. Later, the method is refined and extended to protein-ligand binding [46]. The sampling procedure in rDock involves a genetic algorithm search, Monte Carlo and minimization. The rDock scoring function is estimated as the weighted sum of a series of physical and empirical terms, e.g., inter- and intra-molecular energetics, empirical solvation, torsional potential from Tripos, and pharmacophore restraints [48].
We summarize in Table 1 the seven docking protocols considered in this work, and the docking-packed bound structures of all host–guest pairs are shared at https://github.com/proszxppp/virtual_screening_OA (accessed on 7 January 2024). The center of the host pocket is selected as the center of the docking box, and a radius of 7 Å or a side length of 13 Å is used for the dimension of the search space. The unmentioned search algorithm parameters are set to their default values. For each docking protocol, we compute the binding strength of the host–guest complexes with two regimes. The first one follows the most straightforward and popular top-1 treatment that considers the docking score of the top-1 binding pose as the estimate, while the second one considers the multi-modal binding behavior by calculating the exponential sum of the top-10 binding modes [18], i.e.,
Δ G b i n d i n g = − β − 1 ln ⁡ ∑ i e − β ∗ s c o r e i
Consequently, there are fourteen estimates of the binding strengths from molecular docking.

2.2. Fixed-Charge Parametrization and End-Point Reranking

In end-point screening, the most popular workflow employs fixed-charge force fields to describe intra- and inter-molecular interactions, samples the end-point ensembles in the binding/unbinding reaction, and computes the binding strengths with force-field energetics.
To build the fixed-charge model, for both host and guest molecules, the restrained electrostatic potential (RESP) [49] scheme with the B3LYP [50,51,52]/6-31G* geometry optimization and electrostatic potential (ESP) scan at the traditional HF [53,54,55]/6-31G* level is employed to parametrize the atomic charges, considering its accurate reproduction of molecular ESP and robustness exhibited in our previous modeling of host–guest binding [14,56,57,58], biphasic partition of drug-like molecules [59,60,61], and extensive validation of host parameters [56,57,62,63]. For bonded parameters, we use the transferable GAFF2 parameter set [64] for all molecules, considering its success in reproducing the correct host dynamics observed in our recent work [62]. The RESP charge files (.mol2) are shared online at https://github.com/proszxppp/virtual_screening_OA (accessed on 7 January 2024) for reproduction usage.
We then proceed to the sampling procedure. The popular single-trajectory protocol in end-point calculations only requires the sampling in the host–guest bound state, while the three-trajectory realization also requires the simulations in the unbound state (i.e., solvated host and solvated guest). Thus, for each host–guest pair, three simulation boxes are needed. The unbound host and guest cells could be constructed via solvation and neutralization of individual molecules, while some initial guess of the bound conformation is needed for the bound state. As the computational cost of our sampling and free energy estimation protocol is high, we only pick the docked poses with one docking protocol as the starting configurations for the host–guest complexes. Normally, the docking protocol for generating the initial condition for atomistic simulations should be selected according to the performance of the docking screening. Therefore, the details of the selected docking protocol would be discussed later in the results section. The docking-produced initial conditions are also available in the online repository. The docked host–guest complex is then solvated in TIP3P water [65], with the 15 Å solute-edge distance and spherical monovalent counter ions of Na+ or Cl− [66,67] added for neutralization. Periodic boundary conditions are always employed in our simulations.
Molecular simulations are then initiated using the hybrid-precision GPU engine in AMBER [68]. We apply SHAKE constraints [69,70] on bonds involving hydrogen, a 2 fs time step [71], Langevin dynamics for temperature regulation at 300 K, isotropic scaling and Monte Carlo barostat for pressure regulation at 1 atm, the AMBER default 8 Å real-space cutoff for non-bonded interactions, and PME for long-range electrostatics. Starting from the packed initial conditions, we relax the system by performing energy minimization for 5000 cycles, constant-volume heating in 120 ps, and NPT equilibration for 1 ns, after which, 1000 ns unbiased sampling in the host–guest and unbound guest states and 10,000 ns for the unbound host state are spawned. The uneven distribution of sampling lengths in different ensembles arises from the difficult-to-sample behavior (higher energetic fluctuation) observed in a recent work [72]. The longer sampling time in the solvated host ensemble helps the minimization of the statistical uncertainty of the three-trajectory estimates. Such a time scale is extremely long in end-point sampling, reaching a practical limit in end-point screening. The sampling interval of successive configurations is set to 10 ps.
For free energy extraction, we utilize MM/PBSA and MM/GBSA with four popular GB models (GBHCT [73,74], GBOBC-I, GBOBC-II [75,76], and GBneck2 [77]). The two GBOBC models correspond to the two sets of parameters published in the original article [75]. The salt concentration of counter ions for Debye–Hückel screening is set to 0.1 M. The nonpolar solvation contribution (the SA part) is computed with the solvent-accessible surface area method [78]. The popular normal mode approximation [2] is applied on a subsampled configuration set (1/4 of all configurations) to compute the entropic contribution.
The above-mentioned energetics, accumulated and extracted from trajectories, are arranged to form the end-point estimate
Δ G b i n d i n g = G h o s t − g u e s t − G h o s t − G g u e s t
Each free-energy term includes enthalpic and entropic components, i.e.,
G i = E intra - molecular + E e l e c t r o s t a t i c s + E v d W + G s o l v − T S g a s
The difference between the single- and three-trajectory sampling protocols lies in the ensemble that the above terms are estimated. For the popular single-trajectory realization, all energetics are extracted from the host–guest bound state, while host- and guest-only terms are computed with configurations from solvated host and solvated guest ensembles in the three-trajectory realization.
Another consideration concerning the above end-point equation is the exclusion/inclusion of the entropic term (TSgas). There is a tendency to neglect this term in many applications of the end-point tool, the reasons for which are mostly the similarity of receptor–ligand pairs (and thus, the cancellation of the entropic contribution when computing the relative affinity) and the small improvements of including the entropic term. While the former cancellation statement could be valid under certain circumstances, in most virtual screening scenarios dealing with ligands/guests with diverse chemical features, such an approximation is obviously unsolid, introducing systematic biases of unknown magnitude. Further, such a treatment does not follow the rigorous derivation of the end-point protocol and, thus, could be harmful when the reproduction of absolute affinities is pursued. As for the small improvements observed in certain application reports, the end-point protocol has long been recognized as exhibiting a severe system-dependent behavior in its screening power. Thus, the magnitude of improvements by including the entropic contribution as an open question for newly encountered species requires extensive validation. Whether such a treatment is preferred remains to be revealed in host–guest complexes. We thus compute two estimates for each end-point protocol, i.e., with and without the entropic contribution. In Table 2, a summary of all end-point protocols considered in this work is presented.

3. Results and Discussion

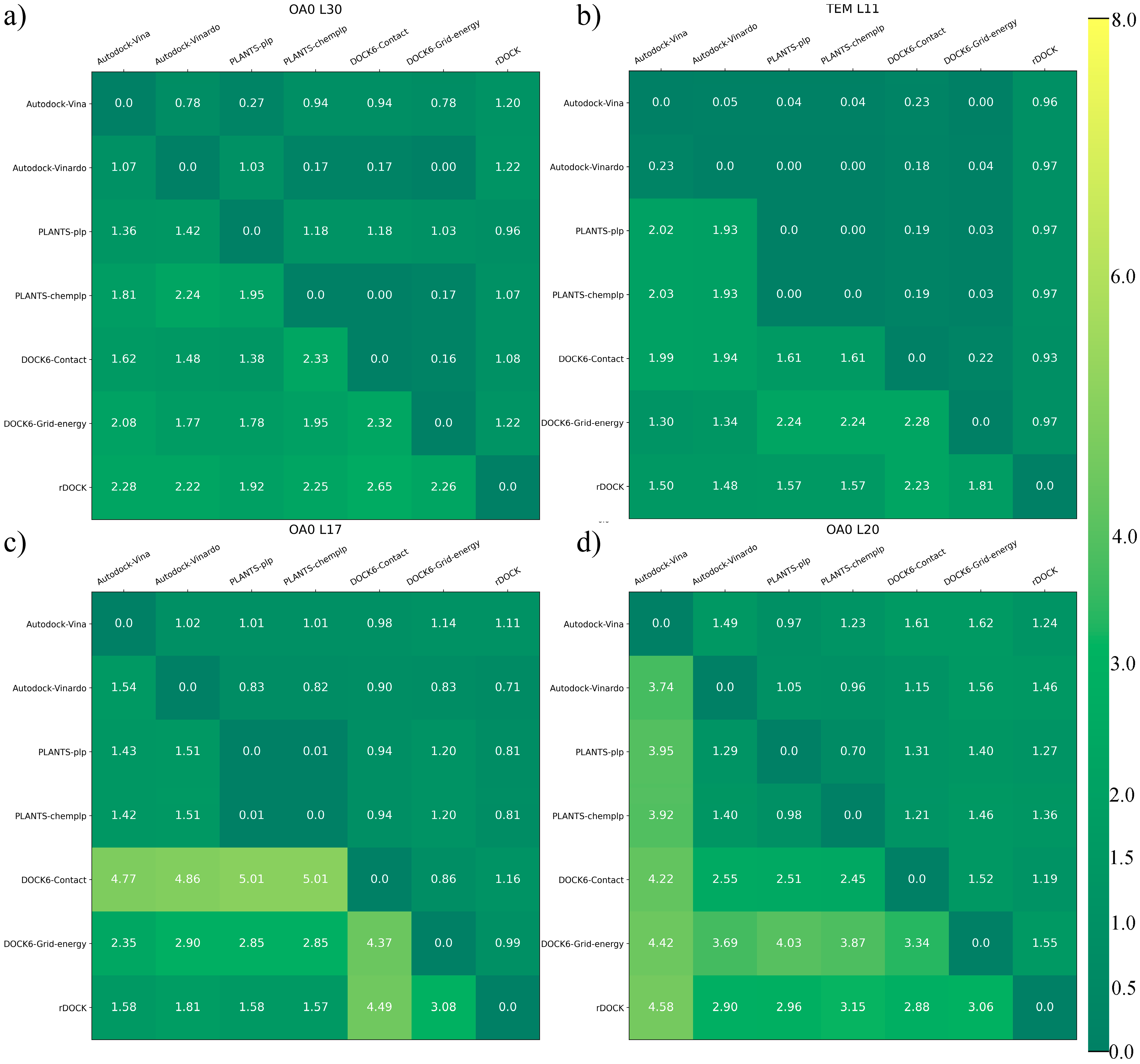
3.1. Performance of Docking Methods

3.1.1. Scoring Power

In virtual screening, the predictive power of a method is often evaluated by the scoring power and the ranking power. The former could be quantified with the root-mean-squared error (RMSE) and the Pearson correlation coefficient, while for the latter, we could compute ranking coefficients including Kendall τ [79] and the Pearlman’s predictive index (PI) [80]. RMSE quantifies the deviations of computed values from the reference, Pearson r measures the linear correlation between the calculated and experimental reference, Kendall τ assesses the correspondence of the computed affinity rank with the reference rank, and PI, as a metric similar to Kendall rank coefficient, also takes the difference between experimental values into consideration. While RMSE is larger than zero, the other three metrics range from −1 to 1. A close-to-unity Pearson correlation coefficient suggests perfect linear calculation–experiment correlation, and close-to-unity Kendall τ and PI indicate perfect predictions of the affinity rank. A fact worth noting here concerns the physical meaning of docking scores. As the reproduction of absolute values of binding affinities is often considered a critical goal, many scoring functions as a weighted combination of physics-based and empirical terms take on an energy-like form. In most situations, the unit of scoring functions is set as kcal/mol [27,28,29,30]. Thus, computing the absolute deviations of docking scores from experimental affinities is a reasonable analysis. In cases where the dimensionless behavior of the scoring function is explicitly claimed, e.g., the contact-based scoring (DOCK6-contact), we should instead focus only on the ranking power of the docking method.
All docking estimates and the associated quality metrics are summarized in Tables S1 and S2. We visualize the prediction performance in Figure 2 to facilitate enabling a straightforward comparison. When it comes to the scoring power, for all docking techniques, a certain level of host-dependent behavior is observed for the quality metrics. For Pearson r, the OA performance is much better than TEMOA, while the opposite is true for RMSE. The AutoDock family (AutoDock-Vina and AutoDock-Vinardo) are superior to all other docking tools, regardless of the use of the top-1 or exponential sum treatment. AutoDock-Vina is slightly better than AutoDock-Vinardo in both Pearson correlation and RMSE. The RMSE from AutoDock is as small as 1~2 kcal/mol, which deduces that the AutoDock family of docking are powerful tools in reproducing the absolute affinities of host–guest complexes. The next top-performing method varies with the quality metrics used as the criterion. When considering Pearson r, the next top-performing family is the PLANTS docking (PLANTS-chemplp and PLANTS-plp). By contrast, when using RMSE as the criterion, the rDock tool achieves better performance. Compared with the rDOCK RMSE ~5–8 kcal/mol, the PLANTS-plp and PLANTS-chemplp scores exhibit huge deviations from the experimental binding affinities, although the units of their scoring functions are claimed to be kcal/mol [27,28,29,30]. However, a major performance difference in Pearson r is observed between OA– and TEMOA–guest systems for rDOCK, indicating the poor robustness of the docking tool. Specifically, the Pearson correlation coefficients of PLANTS and rDock scores are similar (~0.5) for OA–guest complexes, but huge differences could be observed in the TEMOA–guest cases (PLANTS~0.2 but rDOCK~−0.2). Therefore, the rDOCK method lacks robustness in host–guest screening and is excluded in the current performance comparison. The DOCK6 results with both energy and contact scoring perform worst in Pearson correlation coefficient (~0–0.2), although the DOCK6-energy estimates are closer to experimental affinities when compared with PLANTS. Overall, using the Pearson correlation coefficient as the criterion, the performance rank is AutoDock-Vina > AutoDock-Vinardo > PLANTS-plp/PLANTS-chemplp > DOCK6-contact > DOCK6-energy, whereas under the RMSE criterion, the performance follows AutoDock-Vina > AutoDock-Vinardo > DOCK6-energy > PLANTS-plp/PLANTS-chemplp > DOCK6-contact.
In terms of the ranking power, interestingly, the disparities in performance among various docking methods do not appear to be as significant as those observed in the previous scoring scenario. While AutoDock-Vina remains the top performer for host–guest complexes involving both OA and TEMOA, AutoDock-Vinardo exhibits a major failure when applied to TEMOA-guest systems. Aside from AutoDock-Vinardo, rDOCK scores also demonstrate an obvious disparity in ranking performance for OA and TEMOA. As the unstableness of their ranking performance is an undesired behavior of robust screening tools, we omit the two docking methods from the performance comparison. The performance rank of the remaining docking methods is AutoDock-Vina > PLANTS-plp/PLANTS-chemplp > DOCK6-contact > DOCK6-energy.

3.1.2. Computational Cost

In addition to the predictive power, another property of great practical interest is the computational cost of a docking tool. We thus summarize the CPU times of finishing the docking calculations for all host–guest pairs using each docking protocol, as shown in Figure S1. Note that we always employ the embarrassingly parallel approach in distributed computing, in order to minimize the communication overhead and maximize the timing performance. A single trail is performed and the consumed CPU time could be influenced by various factors in the computing node, but the current timing data still enable a reasonable comparison. From the CPU time comparison, we know that the AutoDock family, rDOCK and DOCK6-energy docking protocols require similar computational resources, while the PLANTS family and DOCK6-contact protocols are much faster (almost 1/10 CPU time).

3.1.3. Structural Consideration

Apart from the screening power and timing information, another crucial aspect of a docking protocol is the quality of bound structures produced. Unfortunately, the absence of experimentally deposited bound structures makes it impossible to perform a face-to-face comparison of this docking power. However, valuable insights could still be obtained if we take a deeper analysis of the bound structures. To compare the binding modes produced by different docking protocols, we consider two calculation regimes. The quantitative estimator of the structural variation is the root-mean-squared deviation (RMSD) of non-hydrogen heavy atoms of the guest molecule. With the bound structures produced by different docking protocols, the first RMSD estimation regime aligns the guest molecules and computes the RMSD of the guest molecule, i.e., setting the weights of all host atoms to zero in both structural alignment and RMSD calculation. This is the most traditional method in RMSD analysis, and measures the intra-molecular conformational variation of the guest molecule in the bound state. The second RMSD estimation follows a slightly modified regime, which aligns the host molecule (i.e., setting weights of guest atoms to zero but those of host atoms to one) and computes the RMSD of the guest molecule (weights of host atoms to zero and guest weights to one). In contrast to the conventional approach used previously, the RMSD from this altered regime accounts for both translational and rotational contributions of the guest in the host cavity (e.g., change of the binding site) and the intra-molecular conformational variation of the guest molecule. As a result, the second strategy reflects the net structural difference in the binding modes.
As the structural comparison is performed between pairs of the docking protocols, 2D RMSD matrices are formulated. The RMSD matrices of the two estimation regimes are merged for a clearer presentation, with the upper-right triangle holding the first traditional estimates and the bottom-left triangle containing the values of the second altered regime. The heatmaps of several examples are presented in Figure 3, while those of all host–guest pairs are summarized in Figures S2 and S3. For the first two cases (i.e., Figure 3a,b), both the RMSD of intra-molecular conformational variations (upper-right triangle) and the net structural difference (bottom-left triangle) are small, which indicates that the bound structures produced by all docking protocols are similar. In the other cases (Figure 3c,d), various docking protocols yield bound structures with substantial disparities, which implies that the bound-structure similarity does not always hold and there are situations in which different docking protocols predict distinct bound structures.
From the 2D RMSD matrices for all systems shown in Figures S2 and S3, an interesting observation is the small RMSD of the PLANTS-chemplp and PLANTS-plp structures in both of the two RMSD estimation regimes, which indicates a certain level of similarity of bound structure predictions with the two protocols of similar origins (i.e., PLANTS). Thus, it seems indifferent, practically, to pick a scoring protocol with PLANTS docking. Such a behavior is generally absent for the AutoDock family (AutoDock-Vina and AutoDock-Vinardo) and DOCK6 (energy and contact scoring), which insinuates that these scoring protocols are truly independent by construction and serve as independent tools in structure ranking.
Another structural similarity is observed between the top-performing AutoDock-Vina and PLANTS protocols, where the net structural RMSD is below 2 Å for more than 60% host–guest pairs. This suggests that the PLANTS family of intermediate ranking power could reproduce the top-performing AutoDock-Vina structures with a high probability.

3.1.4. Take-Home Message

Overall, considering all the above analyses of scoring and ranking powers, we recommend the AutoDock-Vina protocol as the docking tool for screening host–guest complexes. If the practitioners are dealing with a huge dataset with relatively limited computational resources, the PLANTS family (PLANTS-plp or PLANTS-chemplp) serve as a much cheaper solution with intermediate accuracy in docking screening. The other techniques (DOCK6-contact, DOCK6-energy, rDOCK, and AutoDock-Vinardo) are not recommended due to unstable and/or low performance.
Regarding the bound structures produced by different algorithms, the closeness to reference cannot be evaluated due to the absence of experimentally deposited structures. However, the top-performing AutoDock-Vina, PLANTS-plp, and PLANTS-chemplp often produce similar structures (c.f., low RMSDs from both of the two computing regimes shown in Figure 3, Figures S2 and S3). Therefore, structurally, the bound structures and the guest conformations produced by the three recommended docking protocols would not be significantly different, and either of them could produce bound structures of a reasonable quality.

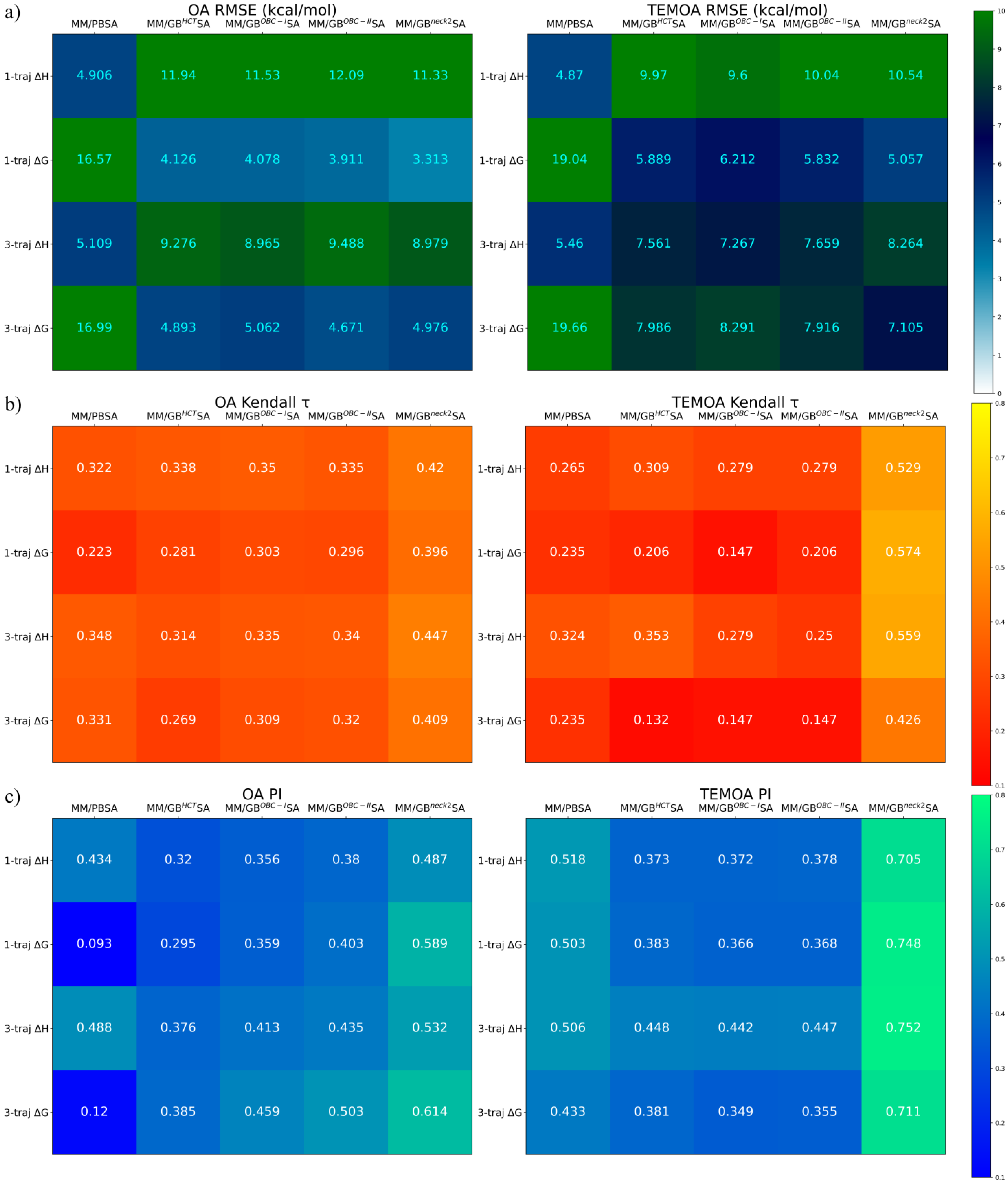
3.2. End-Point Free-Energy Calculations

3.2.1. How Long Do We Need to Converge the Statistics

With all the docking results summarized above, we then turn to the post-docking end-point screening in this section. Since AutoDock-Vina consistently outperforms other methods in both quality metrics and host-specific datasets, the most straightforward and reasonable treatment for post-docking end-point screening is extracting the AutoDock-Vina-generated docked poses as the starting configurations of the end-point simulation of the bound complex. Note that the docking-produced bound structures are also available in the online GitHub repository.
Before comparing the performance statistics of end-point screening, we conduct preliminary sanity checks to consolidate the simulation outcome. The convergence check is indispensable in the free-energy calculation. It supports the validity of approximating the ensemble averages with the time-series data. Therefore, instead of directly comparing the end-point results with experimental values, we first look into the time-series data. The time variations of the single-trajectory MM/GBneck2SA estimates for 31 OA and 17 TEMOA host–guest complexes are plotted in Figures S4 and S5, respectively, with the longest 1000 ns bound-state statistics as the reference value for the long-time limit. The plots clearly show that the end-point estimates of most host–guest pairs could be well-converged with deviations below kBT (~0.59 kcal/mol at room temperature) within tens of ns, but, in some situations (e.g., OA-L30 and OA-L31 pairs), the end-point results still exhibit noticeable fluctuations and/or systematic drifts with 1000 ns unbiased sampling. Based on these observed convergence behaviors of the absolute affinities, we believe that ~100 ns serves as a practically usable setup for converged end-point estimates for most host–guest complexes involving OA derivatives.
Despite the variations in end-point results in some systems, even with 1000 ns sampling, they may not significantly perturb the prediction quality or screening power. To check whether this not-so-well convergence behavior of specific systems would impact the quality metrics in a statistically significant manner, we computed the time series of the four quality metrics (RMSE, τ, PI, and Pearson r), as depicted in Figure 4. For both OA and TEMOA host–guest binding, all four of the quality metrics keep fluctuating in the first 40 ns, and only after 100 ns do the statistics seem stabilized, although minor fluctuations could still be observed in the last several blocks. This phenomenon illustrates that end-point free-energy calculations generally converge after ~100 ns sampling in host–guest complexes involving OA derivatives. Therefore, a practical recommendation for practitioners using end-point free-energy techniques is to extend the sampling time to at least ~100 ns in order to avoid systematic biases introduced by sampling insufficiency. Notably, end-point sampling of such length is generally much longer than commonly applied selections, e.g., several to 10 ns in existing reports [13,81,82], highlighting potential pitfalls in current practices.

3.2.2. Screening Power of End-Point Estimators

The long-time 1000 ns estimates of all end-point protocols (with or without normal mode entropy, implicit solvent model, and the single- or three-trajectory sampling protocol) are summarized in Tables S3–S10. The four quality metrics (RMSE, τ, PI, and Pearson r) and an additional error metric, named mean signed error (MSE), for each dataset are also provided. For easier comparison between performances of different end-point protocols, we plot the quality metrics in Figure 5.
We first focus on the most popular end-point regime based on the single-trajectory sampling protocol and investigate whether the inclusion/exclusion of the entropic contribution would incur noticeable variations. Comparing the statistical metrics of the ΔH and ΔG, intriguingly, the end-point performance, in most cases, is improved with the inclusion of the entropic term. For example, the RMSE measuring the reproduction of absolute affinities is too huge ~10 kcal/mol for the ΔH estimates, but is minimized to ~4 kcal/mol by the addition of the entropic contribution. Therefore, including the entropic contribution is not a treatment that merely increases the computational cost, but serves as a treatment that completes the theoretical rigor of the end-point workflow and deserves to be considered. Although this observation could be dependent on the system under investigation, for safety, the most reliable end-point estimation scheme for practitioners to follow is still the most rigorous workflow, i.e., including the entropic contribution.
We then include the three-trajectory results into the analysis set and compare the performance statistics of all end-point protocols. We start by picking the top-performing methods for the OA and TEMOA host–guest datasets. The top-2 end-point protocols based on various quality metrics are listed in Table 3, where different methods achieve top performance under different criteria. To extract some statistical insights into the top-performing selections, we perform two types of analyses. The first one aims at achieving the highest robustness across different hosts (receptors) in virtual screening, and thus picks the end-point protocol that exhibits the top performance for both OA and TEMOA hosts. The robust end-point selections based on individual quality metrics are then given in Table 4. Interestingly, for four quality metrics reflecting different aspects of the screening problem (i.e., ranking and scoring), only two unique end-point protocols appear in the table, i.e., single-trajectory MM/GBneck2SA ΔG and three-trajectory MM/GBneck2SA ΔH. These two options are robust screening protocols that perform consistently top for OA derivatives. The second analysis is based on the number of occurrences in the top-2 table (i.e., Table 3). Interestingly, this analysis identifies two end-point regimes that are exactly the same as the previous robustness analysis, as given in Table 5. According to the statistical insights observed from the two analyses, we recommend the two end-point protocol, single-trajectory MM/GBneck2SA ΔG and three-trajectory MM/GBneck2SA ΔH, in practical virtual screening of host–guest complexes.

3.3. The Value of Post-Docking End-Point Rescoring

With all the reliable docking and end-point statistics accumulated so far, it is finally possible to explore the most significative aspect of virtual screening and inspect the practical value of applying post-docking end-point rescreening. The recommended protocols of both molecular docking and end-point free energy calculations are compared in a face-to-face manner in Figure 6. While the recommended docking protocol AutoDock-Vina performs best in reproducing the absolute affinities (RMSE) for both hosts and achieves very high correlation coefficients for the OA host–guest pairs, its ranking power for the methylated form (TEMOA host–guest pairs) exhibits a severe performance drop. By contrast, both of the two recommended end-point protocols, single-trajectory MM/GBneck2SA ΔG and three-trajectory MM/GBneck2SA ΔH, perform reasonably well for both hosts. Such a stable performance confirms the robustness of the recommended end-point protocols, validating the value of post-docking end-point screening.

4. Concluding Remarks

Virtual screening often follows a hierarchical workflow design based on efficiency and accuracy considerations. In protein–ligand binding, high-throughput techniques based on atomistic modeling include molecular docking and end-point free-energy calculations, which are directly extended to host–guest complexes due to the similarity of these receptor–ligand assemblies. However, recent reports on specific systems suggest that the computational ladder based on protein–ligand experience could be no longer valid in the altered receptor–ligand/host–guest complexes. Therefore, there is an urgent need for a face-to-face comparison between the screening performance of molecular docking and end-point calculations in order to provide solid numerical data guiding the design of hierarchical virtual screening. To this end, based on a comprehensive dataset containing ~50 host–guest pairs formed by basket-like OA derivatives and drug-like guests, we perform a detailed and systematic benchmark on docking and end-point screening of OA host–guest systems.
Seven docking protocols with varying features are considered. While rDock, DOCK6-energy and DOCK6-contact and AutoDock-Vinardo are rejected due to low accuracy predictions or lack of robustness across different hosts/receptors, the AutoDock-Vina and PLANTS family (chemplp and plp) are considered usable options in host–guest docking. These three selections perform reasonably well in ranking different host–guest pairs with a given receptor/host, and the binding poses predicted by the three recommended docking protocols agree well, with more than 60% host–guest pairs having structural deviations < 2 Å. As for efficiency considerations, the AutoDock-Vina protocol achieves the highest performance statistics but is costlier compared with the PLANTS family.
Twenty protocols (implicit solvent models, single- and three-trajectory sampling, and the inclusion/exclusion of the entropic contribution) are considered for end-point screening. Under the popular single-trajectory realization, we observe that the inclusion of the entropic contribution could be pivotal in reproducing the absolute values of binding affinities, and it also improves the correlation statistics under most circumstances. As the theoretical rigor of the end-point workflow is achieved with the inclusion of this entropic term, we believe that it should not be casually neglected. Unless there is solid evidence supporting the elimination of the entropic term, it is undesirable to perform this approximation. As for the overall performance of all end-point protocols, while the prevailing protocol exhibits certain dependence on the binding target (receptors/hosts) and criterion (quality metrics), statistically, we identify two end-point protocols, single-trajectory MM/GBneck2SA ΔG and three-trajectory MM/GBneck2SA ΔH, that consistently deliver top-tier performance across different hosts/receptors. Face-to-face comparison between the recommended end-point and docking protocols reveals the higher robustness of the end-point tool, validating the value of post-docking end-point screening.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/liquids4030027/s1, Figure S1: The computational costs of different docking protocols; Figures S2 and S3: the 2D RMSD matrices with two computational regimes; Figures S4 and S5: the time-dependent behavior of single-trajectory MM/GBneck2SA estimates; Tables S1 and S2: the docking scores; Tables S3–S10: end-point estimates in single- and three-trajectory regimes under all parameter combinations; These are given in the supporting information.

Author Contributions

X.W.: data curation, formal analysis, funding acquisition, investigation, methodology, resources, software, validation, visualization, writing—review and editing. Z.H.: data curation, formal analysis, investigation, methodology, resources, software, validation, writing—review and editing. L.Z.: investigation, resources, software, visualization, writing—review and editing. M.L.: investigation, resources, software, writing—review and editing. Z.S.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft, writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Beijing Natural Science Foundation (Grant No. 7224357).

Data Availability Statement

The atomic charge files of all molecules and the docking-produced initial bound structures with Vina are shared online at https://github.com/proszxppp/virtual_screening_OA (accessed on 7 January 2024). All binding-strength estimates obtained in this work are given in the main article and the Supporting Information.

Acknowledgments

We thank the anonymous reviewers for valuable comments and critical reading.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Giordano, D.; Biancaniello, C.; Argenio, M.A.; Facchiano, A. Drug Design by Pharmacophore and Virtual Screening Approach. Pharmaceuticals 2022, 15, 646. [Google Scholar] [CrossRef] [PubMed]
  2. Wang, L.; Wang, Y.; Yu, Y.; Liu, D.; Zhao, J.; Zhang, L. Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhibitors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations. Molecules 2023, 28, 2583. [Google Scholar] [CrossRef] [PubMed]
  3. Xu, Y.; Fan, B.; Gao, Y.; Chen, Y.; Han, D.; Lu, J.; Liu, T.; Gao, Q.; Zhang, J.Z.; Wang, M. Design Two Novel Tetrahydroquinoline Derivatives against Anticancer Target LSD1 with 3D-QSAR Model and Molecular Simulation. Molecules 2022, 27, 8358. [Google Scholar] [CrossRef]
  4. Procacci, P. Reformulating the entropic contribution in molecular docking scoring functions. J. Comput. Chem. 2016, 37, 1819–1827. [Google Scholar] [CrossRef] [PubMed]
  5. Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.; Hou, T. End-point binding free energy calculation with MM/PBSA and MM/GBSA: Strategies and applications in drug design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef] [PubMed]
  6. Jansook, P.; Ogawa, N.; Loftsson, T. Cyclodextrins: Structure, physicochemical properties and pharmaceutical applications. Int. J. Pharm. 2018, 535, 272–284. [Google Scholar] [CrossRef]
  7. Ahmadian, N.; Mehrnejad, F.; Amininasab, M. Molecular Insight into the Interaction between Camptothecin and Acyclic Cucurbit [4] urils as Efficient Nanocontainers in Comparison with Cucurbit [7] uril: Molecular Docking and Molecular Dynamics Simulation. J. Chem. Inf. Model. 2020, 60, 1791–1803. [Google Scholar] [CrossRef] [PubMed]
  8. Duan, Q.; Xing, Y.; Guo, K. Carboxylato-Pillar [6] arene-Based Fluorescent Indicator Displacement Assays for Caffeine Sensing. Front. Chem. 2021, 9, 816069. [Google Scholar] [CrossRef] [PubMed]
  9. Cova, T.F.; Milne, B.F.; Pais, A.A.C.C. Host flexibility and space filling in supramolecular complexation of cyclodextrins: A free-energy-oriented approach. Carbohydr. Polym. 2019, 205, 42–54. [Google Scholar] [CrossRef]
  10. Otero-Espinar, F.; Torres-Labandeira, J.; Alvarez-Lorenzo, C.; Blanco-Méndez, J. Cyclodextrins in drug delivery systems. J. Drug Deliv. Sci. Technol. 2010, 20, 289–301. [Google Scholar] [CrossRef]
  11. Rasheed, A. Cyclodextrins as drug carrier molecule: A review. Sci. Pharm. 2008, 76, 567–598. [Google Scholar] [CrossRef]
  12. Aksu, H.; Paul, S.K.; Herbert, J.M.; Dunietz, B.D. How Well Does a Solvated Octa-acid Capsule Shield the Embedded Chromophore? A Computational Analysis Based on an Anisotropic Dielectric Continuum Model. J. Phys. Chem. B 2020, 124, 6998–7004. [Google Scholar] [CrossRef]
  13. Suárez, D.; Díaz, N. Affinity Calculations of Cyclodextrin Host–Guest Complexes: Assessment of Strengths and Weaknesses of End-Point Free Energy Methods. J. Chem. Inf. Model. 2019, 59, 421–440. [Google Scholar] [CrossRef] [PubMed]
  14. Huai, Z.; Yang, H.; Li, X.; Sun, Z. SAMPL7 TrimerTrip host-guest binding affinities from extensive alchemical and end-point free energy calculations. J. Comput. Aided Mol. Des. 2021, 35, 117–129. [Google Scholar] [CrossRef] [PubMed]
  15. Wang, X.; Wang, M.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar [6] arene Host-guest Binding: IV. The QM treatment, GB models and the Multi-Trajectory Extension. Liquids 2023, 3, 426–439. [Google Scholar] [CrossRef]
  16. Zhikol, O.A.; Miasnikova, D.Y.; Vashchenko, O.V.; Pinchukova, N.A.; Zbruyev, O.I.; Shishkina, S.V.; Kyrychenko, A.; Chebanov, V.A. Host-guest complexation of (pyridinyltriazolylthio) acetic acid with cucurbit [n] urils (n = 6, 7, 8): Molecular calculations and thermogravimetric analysis. J. Mol. Struct. 2023, 1294, 136532. [Google Scholar] [CrossRef]
  17. Liu, X.; Zheng, L.; Qin, C.; Zhang, J.Z.H.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar [6] arene Host-guest Binding: I. Standard Procedure. J. Comput. Aided Mol. Des. 2022, 36, 735–752. [Google Scholar] [CrossRef] [PubMed]
  18. Casbarra, L.; Procacci, P. Binding free energy predictions in host-guest systems using Autodock4. A retrospective analysis on SAMPL6, SAMPL7 and SAMPL8 challenges. J. Comput. Aided Mol. Des. 2021, 35, 712–729. [Google Scholar] [CrossRef] [PubMed]
  19. Gibb, C.L.D.; Gibb, B.C. Binding of cyclic carboxylates to octa-acid deep-cavity cavitand. J. Comput. Aided Mol. Des. 2014, 28, 319–325. [Google Scholar] [CrossRef]
  20. Sullivan, M.R.; Sokkalingam, P.; Nguyen, T.; Donahue, J.P.; Gibb, B.C. Binding of carboxylate and trimethylammonium salts to octa-acid and TEMOA deep-cavity cavitands. J. Comput. Aided Mol. Des. 2017, 31, 21–28. [Google Scholar] [CrossRef]
  21. Suating, P.; Nguyen, T.T.; Ernst, N.E.; Wang, Y.; Jordan, J.H.; Gibb, C.L.; Ashbaugh, H.S.; Gibb, B.C. Proximal charge effects on guest binding to a non-polar pocket. Chem. Sci. 2020, 11, 3656–3663. [Google Scholar] [CrossRef] [PubMed]
  22. Rizzi, A.; Murkli, S.; McNeill, J.N.; Yao, W.; Sullivan, M.; Gilson, M.K.; Chiu, M.W.; Isaacs, L.; Gibb, B.C.; Mobley, D.L. Overview of the SAMPL6 host–guest binding affinity prediction challenge. J. Comput.-Aided Mol. Des. 2018, 32, 937–963. [Google Scholar] [CrossRef] [PubMed]
  23. Zhang, X.; Wu, W.; Tao, Z.; Ni, X.-L. Host–guest interactions in nor-seco-cucurbit [10] uril: Novel guest-dependent molecular recognition and stereoisomerism. Beilstein J. Org. Chem. 2019, 15, 1705–1711. [Google Scholar] [CrossRef]
  24. Wu, X.; Meng, X.; Cheng, G. A novel 1: 2 cucurbit [8] uril inclusion complex with N-phenylpiperazine hydrochloride. J. Incl. Phenom. Macrocycl. Chem. 2009, 64, 325–329. [Google Scholar] [CrossRef]
  25. Eberhardt, J.; Santos-Martins, D.; Tillack, A.F.; Forli, S. AutoDock Vina 1.2.0: New Docking Methods, Expanded Force Field, and Python Bindings. J. Chem. Inf. Model. 2021, 61, 3891–3898. [Google Scholar] [CrossRef] [PubMed]
  26. Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef]
  27. Verkhivker, G.M. Computational analysis of ligand binding dynamics at the intermolecular hot spots with the aid of simulated tempering and binding free energy calculations. J. Mol. Graph. Model. 2004, 22, 335–348. [Google Scholar] [CrossRef] [PubMed]
  28. Verkhivker, G.M.; Bouzida, D.; Gehlhaar, D.K.; Rejto, P.A.; Freer, S.T.; Rose, P.W. Computational detection of the binding-site hot spot at the remodeled human growth hormone–receptor interface. Proteins Struct. Funct. Bioinform. 2003, 53, 201–219. [Google Scholar] [CrossRef]
  29. Verkhivker, G.M.; Bouzida, D.; Gehlhaar, D.K.; Rejto, P.A.; Freer, S.T.; Rose, P.W. Monte Carlo simulations of the peptide recognition at the consensus binding site of the constant fragment of human immunoglobulin G: The energy landscape analysis of a hot spot at the intermolecular interface. Proteins Struct. Funct. Bioinform. 2002, 48, 539–557. [Google Scholar] [CrossRef]
  30. Gehlhaar, D.K.; Verkhivker, G.M.; Rejto, P.A.; Sherman, C.J.; Fogel, D.R.; Fogel, L.J.; Freer, S.T. Molecular recognition of the inhibitor AG-1343 by HIV-1 protease: Conformationally flexible docking by evolutionary programming. Chem. Biol. 1995, 2, 317–324. [Google Scholar] [CrossRef]
  31. Korb, O.; Stutzle, T.; Exner, T.E. Empirical scoring functions for advanced protein—Ligand docking with PLANTS. J. Chem. Inf. Model. 2009, 49, 84–96. [Google Scholar] [CrossRef] [PubMed]
  32. Pagadala, N.S.; Syed, K.; Tuszynski, J. Software for molecular docking: A review. Biophys. Rev. 2017, 9, 91–102. [Google Scholar] [CrossRef] [PubMed]
  33. Gaillard, T. Evaluation of AutoDock and AutoDock Vina on the CASF-2013 Benchmark. J. Chem. Inf. Model. 2018, 58, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
  34. Nguyen, N.T.; Nguyen, T.H.; Pham, T.N.H.; Huy, N.T.; Bay, M.V.; Pham, M.Q.; Nam, P.C.; Vu, V.V.; Ngo, S.T. Autodock Vina Adopts More Accurate Binding Poses but Autodock4 Forms Better Binding Affinity. J. Chem. Inf. Model. 2020, 60, 204–211. [Google Scholar] [CrossRef] [PubMed]
  35. Quiroga, R.; Villarreal, M.A. Vinardo: A Scoring Function Based on Autodock Vina Improves Scoring, Docking, and Virtual Screening. PLoS ONE 2016, 11, e0155183. [Google Scholar] [CrossRef] [PubMed]
  36. Korb, O.; Stützle, T.; Exner, T.E. PLANTS: Application of ant colony optimization to structure-based drug design. In International Workshop on ant Colony Optimization and Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; pp. 247–258. [Google Scholar]
  37. Deneubourg, J.-L.; Aron, S.; Goss, S.; Pasteels, J.M. The self-organizing exploratory pattern of the argentine ant. J. Insect Behav. 1990, 3, 159–168. [Google Scholar] [CrossRef]
  38. Goss, S.; Aron, S.; Deneubourg, J.-L.; Pasteels, J.M. Self-organized shortcuts in the Argentine ant. Naturwissenschaften 1989, 76, 579–581. [Google Scholar] [CrossRef]
  39. Stützle, T.; Hoos, H.H. MAX–MIN ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
  40. Clark, M.; Cramer III, R.D.; Van Opdenbosch, N. Validation of the general purpose tripos 5.2 force field. J. Comput. Chem. 1989, 10, 982–1012. [Google Scholar] [CrossRef]
  41. Murray, C.W.; Auton, T.R.; Eldridge, M.D. Empirical scoring functions. II. The testing of an empirical scoring function for the prediction of ligand-receptor binding affinities and the use of Bayesian regression to improve the quality of the model. J. Comput.-Aided Mol. Des. 1998, 12, 503–519. [Google Scholar] [CrossRef]
  42. Eldridge, M.D.; Murray, C.W.; Auton, T.R.; Paolini, G.V.; Mee, R.P. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput.-Aided Mol. Des. 1997, 11, 425–445. [Google Scholar] [CrossRef] [PubMed]
  43. Allen, W.J.; Balius, T.E.; Mukherjee, S.; Brozell, S.R.; Moustakas, D.T.; Lang, P.T.; Case, D.A.; Kuntz, I.D.; Rizzo, R.C. DOCK 6: Impact of new features and current docking performance. J. Comput. Chem. 2015, 36, 1132–1156. [Google Scholar] [CrossRef] [PubMed]
  44. Shoichet, B.K.; Kuntz, I.D.; Bodian, D.L. Molecular docking using shape descriptors. J. Comput. Chem. 1992, 13, 380–397. [Google Scholar] [CrossRef]
  45. Kuntz, I.D.; Blaney, J.M.; Oatley, S.J.; Langridge, R.; Ferrin, T.E. A geometric approach to macromolecule-ligand interactions. J. Mol. Biol. 1982, 161, 269–288. [Google Scholar] [CrossRef] [PubMed]
  46. Ruiz-Carmona, S.; Alvarez-Garcia, D.; Foloppe, N.; Garmendia-Doval, A.B.; Juhos, S.; Schmidtke, P.; Barril, X.; Hubbard, R.E.; Morley, S.D. rDock: A Fast, Versatile and Open Source Program for Docking Ligands to Proteins and Nucleic Acids. PLoS Comp. Biol. 2014, 10, e1003571. [Google Scholar] [CrossRef] [PubMed]
  47. Morley, S.D.; Afshar, M. Validation of an empirical RNA-ligand scoring function for fast flexible docking using RiboDock®. J. Comput.-Aided Mol. Des. 2004, 18, 189–208. [Google Scholar] [CrossRef] [PubMed]
  48. Hasel, W.; Hendrickson, T.F.; Still, W.C. A rapid approximation to the solvent accessible surface areas of atoms. Tetrahedron Comput. Methodol. 1988, 1, 103–116. [Google Scholar] [CrossRef]
  49. Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1992, 97, 10269–10280. [Google Scholar] [CrossRef]
  50. Hertwig, R.H.; Koch, W. On the parameterization of the local correlation functional. What is Becke-3-LYP? Chem. Phys. Lett. 1997, 268, 345–351. [Google Scholar] [CrossRef]
  51. Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
  52. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  53. Mcweeny, R.; Diercksen, G. Self-Consistent Perturbation Theory. II. Extension to Open Shells. J. Chem. Phys. 1968, 49, 4852–4856. [Google Scholar] [CrossRef]
  54. Pople, J.A.; Nesbet, R.K. Self-Consistent Orbitals for Radicals. J. Chem. Phys. 1954, 22, 571–572. [Google Scholar] [CrossRef]
  55. Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
  56. Sun, Z.; Zheng, L.; Kai, W.; Huai, Z.; Liu, Z. Primary vs Secondary: Directionalized Guest Coordination in β-Cyclodextrin Derivatives. Carbohydr. Polym. 2022, 297, 120050. [Google Scholar] [CrossRef]
  57. Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit [8] uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef] [PubMed]
  58. Sun, Z.; He, Q.; Li, X.; Zhu, Z. SAMPL6 host–guest binding affinities and binding poses from spherical-coordinates-biased simulations. J. Comput.-Aided Mol. Des. 2020, 34, 589–600. [Google Scholar] [CrossRef] [PubMed]
  59. Sun, Z.; Zheng, L.; Zhang, Z.-y.; Cong, Y.; Yang, J.; Wang, X. Molecular Modelling of Ionic Liquids: Perfluorinated Anionic Species with Enlarged Halogen Substitutions. J. Mol. Liq. 2023, 378, 121599. [Google Scholar] [CrossRef]
  60. Sun, Z.; Zheng, L.; Zhang, Z.-Y.; Cong, Y.; Wang, M.; Wang, X.; Yang, J.; Liu, Z.; Huai, Z. Molecular Modelling of Ionic Liquids: Situations When Charge Scaling Seems Insufficient. Molecules 2023, 28, 800. [Google Scholar] [CrossRef]
  61. Sun, Z.; Wang, M.; He, Q.; Liu, Z. Molecular Modelling of Ionic Liquids: Force-Field Validation and Thermodynamic Perspective from Large-Scale Fast-Growth Solvation Free Energy Calculations. Adv. Theory Simul. 2022, 5, 2200274. [Google Scholar] [CrossRef]
  62. Wang, X.; Huai, Z.; Sun, Z. Host Dynamics under General-Purpose Force Fields. Molecules 2023, 28, 5940. [Google Scholar] [CrossRef] [PubMed]
  63. Sun, Z.; He, Q.; Gong, Z.; Kalhor, P.; Huai, Z.; Liu, Z. A General Picture of Cucurbit [8] uril Host-Guest Binding: Recalibrating Bonded Interactions. Molecules 2023, 28, 3124. [Google Scholar] [CrossRef] [PubMed]
  64. Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1173. [Google Scholar] [CrossRef]
  65. Price, D.J.; Brooks III, C.L. A Modified TIP3P Water Potential for Simulation with Ewald Summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
  66. Joung, I.S.; Cheatham III, T.E. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
  67. Joung, I.S.; Cheatham, T.E. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [PubMed]
  68. Case, D.A.; Cheatham, T.E.; Tom, D.; Holger, G.; Luo, R.; Merz, K.M.; Alexey, O.; Carlos, S.; Bing, W.; Woods, R.J. The Amber Biomolecular Simulation Programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
  69. Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical Integration of The Cartesian Equations of Motion of A System with Constraints: Molecular Dynamics of n -alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
  70. Miyamoto, S.; Kollman, P.A. Settle: An Analytical Version of The SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
  71. Case, D.A. Normal mode analysis of protein dynamics. Curr. Opin. Struct. Biol. 2010, 4, 285–290. [Google Scholar] [CrossRef]
  72. Liu, X.; Zheng, L.; Qin, C.; Yalong, C.; Zhang, J.Z.; Sun, Z. Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar [6] arene Host-Guest Binding: III. Force-Field Comparison, Three-Trajectory Realization and Further Dielectric Augmentation. Molecules 2023, 28, 2767. [Google Scholar] [CrossRef]
  73. Hawkins, G.D.; Cramer, C.J.; Truhlar, D.G. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 1996, 100, 19824–19839. [Google Scholar] [CrossRef]
  74. Hawkins, G.D.; Cramer, C.J.; Truhlar, D.G. Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett. 1995, 246, 122–129. [Google Scholar] [CrossRef]
  75. Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef]
  76. Feig, M.; Onufriev, A.; Lee, M.S.; Im, W.; Case, D.A. Performance comparison of generalized born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. J. Comput. Chem. 2004, 25, 265–284. [Google Scholar] [CrossRef] [PubMed]
  77. Hai, N.; Pérez, A.; Bermeo, S.; Simmerling, C. Refinement of Generalized Born Implicit Solvation Parameters for Nucleic Acids and their Complexes with Proteins. J. Chem. Theory Comput. 2015, 11, 3714. [Google Scholar]
  78. Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
  79. Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
  80. Pearlman, D.A.; Charifson, P.S. Are Free Energy Calculations Useful in Practice? A Comparison with Rapid Scoring Functions for the p38 MAP Kinase Protein System. J. Med. Chem. 2001, 44, 3417–3423. [Google Scholar] [CrossRef]
  81. Nutho, B.; Khuntawee, W.; Rungnim, C.; Pongsawasdi, P.; Wolschann, P.; Karpfen, A.; Kungwan, N.; Rungrotmongkol, T. Binding mode and free energy prediction of fisetin/β-cyclodextrin inclusion complexes. Beilstein J. Org. Chem. 2014, 10, 2789–2799. [Google Scholar] [CrossRef]
  82. Rungrotmongkol, T.; Chakcharoensap, T.; Pongsawasdi, P.; Kungwan, N.; Wolschann, P. The inclusion complexation of daidzein with β-cyclodextrin and 2,6-dimethyl-β-cyclodextrin: A theoretical and experimental study. Monatsh. Chem. 2018, 149, 1739–1747. [Google Scholar] [CrossRef]
Liquids 04 00027 g001aLiquids 04 00027 g001b
Figure 1. OA host–guest systems studied in this work.
Figure 1. OA host–guest systems studied in this work.
Liquids 04 00027 g001aLiquids 04 00027 g001b
Liquids 04 00027 g002
Figure 2. Performance comparison between docking protocols for four quality metrics: Pearson correlation coefficient, RMSE, PI, and Kendall τ. The exact values of docking scores are summarized in Tables S1 and S2.
Figure 2. Performance comparison between docking protocols for four quality metrics: Pearson correlation coefficient, RMSE, PI, and Kendall τ. The exact values of docking scores are summarized in Tables S1 and S2.
Liquids 04 00027 g002
Liquids 04 00027 g003
Figure 3. 2D RMSD of guest molecules for host–guest bound structures produced by various docking protocols. The upper-right triangle presents the intramolecular conformational variation estimated by the align-guest-compute-guest strategy, while the bottom-left triangle depicts the overall displacement (including both translational and rotational motions of the molecule and intra-molecular conformational change) evaluated with the align-host-compute-guest strategy. In (a,b) we present two examples that all docking protocols give similar models for the bound state, while subplots (c,d) are examples where some of the docking protocols produce bound structures significantly different from the other. The heatmaps of all host–guest pairs are given in Figures S2 and S3.
Figure 3. 2D RMSD of guest molecules for host–guest bound structures produced by various docking protocols. The upper-right triangle presents the intramolecular conformational variation estimated by the align-guest-compute-guest strategy, while the bottom-left triangle depicts the overall displacement (including both translational and rotational motions of the molecule and intra-molecular conformational change) evaluated with the align-host-compute-guest strategy. In (a,b) we present two examples that all docking protocols give similar models for the bound state, while subplots (c,d) are examples where some of the docking protocols produce bound structures significantly different from the other. The heatmaps of all host–guest pairs are given in Figures S2 and S3.
Liquids 04 00027 g003
Liquids 04 00027 g004
Figure 4. The quality metrics of the single-trajectory MM/GBneck2SA protocol as a function of the sampling time for both OA and TEMOA host–guest complexes: RMSE, Kendall τ, PI, and Pearson r. The time-dependent behaviors of free energy estimates of individual systems are provided in Figures S4 and S5.
Figure 4. The quality metrics of the single-trajectory MM/GBneck2SA protocol as a function of the sampling time for both OA and TEMOA host–guest complexes: RMSE, Kendall τ, PI, and Pearson r. The time-dependent behaviors of free energy estimates of individual systems are provided in Figures S4 and S5.
Liquids 04 00027 g004
Liquids 04 00027 g005aLiquids 04 00027 g005b
Figure 5. Screening power of end-point protocols: (a) RMSE, (b) Kendall τ, (c) PI, and (d) Pearson r. The exact values of end-point estimates are summarized in Tables S3–S10.
Figure 5. Screening power of end-point protocols: (a) RMSE, (b) Kendall τ, (c) PI, and (d) Pearson r. The exact values of end-point estimates are summarized in Tables S3–S10.
Liquids 04 00027 g005aLiquids 04 00027 g005b
Liquids 04 00027 g006
Figure 6. Performance comparison between recommended end-point and docking protocols for OA (bottom) and TEMOA (top).
Figure 6. Performance comparison between recommended end-point and docking protocols for OA (bottom) and TEMOA (top).
Liquids 04 00027 g006
Table 1. Docking protocols benchmarked in this work.
Table 1. Docking protocols benchmarked in this work.
Docking ProgramSampling/Scoring ProtocolDocking Protocol
AutoDock VinaVinaAutodock Vina
AutoDock VinaVinardoAutodock Vinardo
PLANTSplpPLANTS-plp
PLANTSchemplpPLANTS-chemplp
DOCK6ContactDOCK6-Contact
DOCK6Grid EnergyDOCK6-Grid-energy
rDockrDockrDOCK
Table 2. End-point protocols benchmarked in this work.
Table 2. End-point protocols benchmarked in this work.
Sampling ProtocolWith/Without Normal-Mode EntropyEnergy Evaluation
MM/PBSAMM/GBHCTSAMM/GBOBC-ISAMM/GBOBC-IISAMM/GBneck2SA
Single-trajectory samplingenthalpy-only ΔHsingle-trajectory MM/PBSA ΔHsingle-trajectory MM/GBHCTSA ΔHsingle-trajectory MM/GBOBC-ISA ΔHsingle-trajectory MM/GBOBC-IISA ΔHsingle-trajectory MM/GBneck2SA ΔH
with entropy ΔGsingle-trajectory MM/PBSA ΔGsingle-trajectory MM/GBHCTSA ΔGsingle-trajectory MM/GBOBC-ISA ΔGsingle-trajectory MM/GBOBC-IISA ΔGsingle-trajectory MM/GBneck2SA ΔG
Three-trajectory samplingenthalpy-only ΔHthree-trajectory MM/PBSA ΔHthree-trajectory MM/GBHCTSA ΔHthree-trajectory MM/GBOBC-ISA ΔHthree-trajectory MM/GBOBC-IISA ΔHthree-trajectory MM/GBneck2SA ΔH
with entropy ΔGthree-trajectory MM/PBSA ΔGthree-trajectory MM/GBHCTSA ΔGthree-trajectory MM/GBOBC-ISA ΔGthree-trajectory MM/GBOBC-IISA ΔGthree-trajectory MM/GBneck2SA ΔG
Table 3. Best-performing screening regimes for the two host–guest sets with different quality metrics.
Table 3. Best-performing screening regimes for the two host–guest sets with different quality metrics.
HostOA Top-1OA Top-2TEMOA Top-1TEMOA Top-2
Metrics
RMSESingle-trajectory MM/GBneck2SA ΔGSingle-trajectory MM/GBOBC-IISA ΔGSingle-trajectory MM/PBSA ΔHSingle-trajectory MM/GBneck2SA ΔG
Kendall τThree-trajectory MM/GBneck2SA ΔHSingle-trajectory MM/GBneck2SA ΔHSingle-trajectory MM/GBneck2SA ΔGThree-trajectory MM/GBneck2SA ΔH
PIThree-trajectory MM/GBneck2SA ΔGSingle-trajectory MM/GBneck2SA ΔGThree-trajectory MM/GBneck2SA ΔHSingle-trajectory MM/GBneck2SA ΔG
Pearson rThree-trajectory MM/GBneck2SA ΔHSingle-trajectory MM/GBneck2SA ΔHThree-trajectory MM/GBneck2SA ΔHSingle-trajectory MM/GBneck2SA ΔG
Table 4. Robust end-point protocols that achieve top performances for both OA and TEMOA host–guest pairs under individual criteria.
Table 4. Robust end-point protocols that achieve top performances for both OA and TEMOA host–guest pairs under individual criteria.
MetricsRobust Selection
RMSESingle-trajectory MM/GBneck2SA ΔG
Kendall τThree-trajectory MM/GBneck2SA ΔH
PISingle-trajectory MM/GBneck2SA ΔG
Pearson rThree-trajectory MM/GBneck2SA ΔH
Table 5. Number of observations for which end-point protocols perform at the top in the top-2 analysis.
Table 5. Number of observations for which end-point protocols perform at the top in the top-2 analysis.
End-Point ProtocolNumber of Observations
Single-trajectory MM/GBneck2SA ΔG6
Single-trajectory MM/GBneck2SA ΔH2
Single-trajectory MM/GBOBC-IISA ΔG1
Single-trajectory MM/PBSA ΔH1
Three-trajectory MM/GBneck2SA ΔH5
Three-trajectory MM/GBneck2SA ΔG1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, X.; Huai, Z.; Zheng, L.; Liu, M.; Sun, Z. A Benchmark Test of High-Throughput Atomistic Modeling for Octa-Acid Host–Guest Complexes. Liquids 2024, 4, 485-504. https://doi.org/10.3390/liquids4030027

AMA Style

Wang X, Huai Z, Zheng L, Liu M, Sun Z. A Benchmark Test of High-Throughput Atomistic Modeling for Octa-Acid Host–Guest Complexes. Liquids. 2024; 4(3):485-504. https://doi.org/10.3390/liquids4030027

Chicago/Turabian Style

Wang, Xiaohui, Zhe Huai, Lei Zheng, Meili Liu, and Zhaoxi Sun. 2024. "A Benchmark Test of High-Throughput Atomistic Modeling for Octa-Acid Host–Guest Complexes" Liquids 4, no. 3: 485-504. https://doi.org/10.3390/liquids4030027

APA Style

Wang, X., Huai, Z., Zheng, L., Liu, M., & Sun, Z. (2024). A Benchmark Test of High-Throughput Atomistic Modeling for Octa-Acid Host–Guest Complexes. Liquids, 4(3), 485-504. https://doi.org/10.3390/liquids4030027

Article Metrics

Back to TopTop