Polarity of Organic Solvent/Water Mixtures Measured with Reichardt’s B30 and Related Solvatochromic Probes—A Critical Review

Abstract

The UV/Vis absorption energies (ν_max) of different solvatochromic probes measured in co-solvent/water mixtures are re-analyzed as a function of the average molar concentration (N_av) of the solvent composition compared to the use of the mole fraction. The empirical E_T(30) parameter of Reichardt’s dye B30 is the focus of the analysis. The Marcus classification of aqueous solvent mixtures is a useful guide for co-solvent selection. Methanol, ethanol, 1,2-ethanediol, 2-propanol, 2-methyl-2-propanol, 2-butoxyethanol, formamide, N-methylformamide (NMF), N,N-dimethylformamide (DMF), N-formylmorpholine (NFM), 1,4-dioxane and DMSO were considered as co-solvents. The E_T(30) values of the binary solvent mixtures are discussed in relation to the physical properties of the co-solvent/water mixtures in terms of quantitative composition, refractive index, thermodynamics of the mixture and the non-uniformity of the mixture. Significant linear dependencies of E_T(30) as a function of N_av can be demonstrated for formamide/water, 1,2-ethanediol/water, NMF/water and DMSO/water mixtures over the entire compositional range. These mixtures belong to the group of solvents that do not enhance the water structure according to the Marcus classification. The influence of the solvent microstructure on the non-linearity E_T(30) as a function of N_av is particularly clear for alcohol/water mixtures with an enhanced water structure.

1. Introduction

The development of Reichardt’s dye 2,6-diphenyl-4-(2,4,6-triphenyl-1-pyridinium)-phenolate (B30) (see Scheme 1) was a milestone in the study of solvent properties [1]. Recall that the original empirical solvent parameter E_T(30) is defined as the molar absorption energy of B30 expressed in kcal/mol, measured in a given solvent [1]:

E_T(30) (kcal/mol) = 28,591/λ_max (nm)

(1)

There are numerous studies in the literature classifying the polarity of pure solvents and solvent mixtures according to their composition, measured with B30 and other solvatochromic probe molecules [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].

Explanatory concepts on solvatochromism can be found in the informative review of [34]. A preliminary summary of the solvent mixtures treated can be found in Table 3 of [35]. In this context, B30 and related solvatochromic probes have been used to establish so-called hydrogen bond strength (HBD) scales for organic solvents [36,37,38,39,40,41]. In addition to the HBD classification, there is a definition for the hydrogen-bond-accepting (HBA) strength of solvents [42]. The HBD and HBA classifications reflect the molecular properties of the solvent molecule in relation to hydrogen bonding in terms of the Kamlet–Taft approach and other similar concepts by Catalan and Laurence [36,37,38,39,40,41]. The interaction of the solvent HBD groups with the phenolate oxygen was considered to be critical in measuring the HBD strength of solvents and solvent mixtures. However, this approach is only partially justified, as we have recently shown [43]. The concept of determining HBD parameters works quite well for ionic liquids (ILs) and other salts due to the electrostatic interaction between the B30 phenolate anion and the constituent cation of the IL [41,44,45,46]. However, due to some contradictions between theory and experimental results, the phenomenon is still under investigation [46].

B30 in particular is routinely used as a polarity indicator for binary solvent mixtures [2,6,7,8,9,13,14,15,16,17,18,19,20,21]. One of the most difficult problems in interpreting the solvatochromism of B30 in solvent mixtures is the issue of preferential solvation and its influence on the E_T(30) value [10,15,16,17,18,19,20,21,24,34]. However, the concept of preferential solvation is interpreted differently in the literature [9,10,11,12,24]. The fundamental problem with the definition of preferential solvation was correctly recognized by Ghoneim [24]. Two basic scenarios must be distinguished in this question for B30:

i.

The solvent mixture (true micelles are a different situation) is inherently inhomogeneous and the solute B30 is therefore preferentially entrapped by a specific microdomain.

ii.

The solute probe such as B30 preferably forms a specific complex with one of the two solvent components.

A complementary good definition for preferential solvation is given by Morisue and Ueno regarding case ii. “Preferential solvation is a phenomenon, whereby solvent proportion of binary mixed solvent in the vicinity of a solute molecule differentiates from the statistic proportion in bulk” [29]. It is therefore necessary to clearly distinguish whether the probe molecule is specifically solvated by the solvent molecule or is present in a partial volume enriched with a component of the mixture. Scenario i. assumes that the physical structure of the solvent mixture is not affected by the solute B30. In the case of scenario ii., the type of probe itself determines the extent to which preferential solvation occurs. Thus, if scenario ii. is true, then different solvatochromic probes should each show different UV/Vis absorption energy dependencies on the quantitative solvent composition for the same mixture. Langhals had already shown in 1981 that different solvatochromic probes used for the same mixture measure the same qualitative dependencies as a function of solvent composition, e.g., for ethanol/water [5]. This crucial finding would rule out scenario ii. But the situation is not so simple.

Despite ambitious work on the subject, the problem of solvatochromism in solvent mixtures has not really been adequately addressed in the literature. It is therefore necessary to explain the chronological development of the concepts for interpreting UV/Vis spectroscopic absorption energy data of probe molecules in solvent mixtures. In the first papers on B30 [1,2], the E_T(30) values of various binary solvent mixtures, including ethanol/water and 1,4-dioxane/water, were determined. It was shown that E_T(30) depends in a complex way on the quantitative composition of the mixture. Langhals recognized that the solvatochromism of B30, the E_T(30) values, can be described empirically as a logarithmic function depending on the concentration of the solvent components [6]. As early as 1982, Langhals also showed that the E_T(30 values of the homologous primary n-alcohol series are a linear function of the total molar concentration of the respective alcohol (N) [7]. The core problem was that no theoretical justification for this link had been presented in the past. Perhaps as a result, this very important discovery was not properly understood by many scientists and its significance was not fully appreciated. These seemingly empirical findings [6,7] have an important physical background based on the Lorentz–Lorenz relation [47].

Later in 1986, Haak and Engberts presented a valuable paper on the influence of temperature (T) on the solvatochromic properties of B30 in aqueous solvent mixtures [8]. It is worth analyzing this study in detail, as the authors have correctly identified the effects of the hydrophobic alcoholic component such as 2-n-butoxyethanol (BE) in water on E_T(30). However, several interpretations need to be re-evaluated in the light of new physical research on specific solvent mixtures, as will be shown in the course of this study.

Since 1982, the general topic of preferential solvation in solvent–water mixtures has been studied in detail by Marcus in numerous papers based on thermodynamics using the Kirkwood–Buff theory for fully miscible aqueous solvent mixtures [48,49,50,51]. Even then, Marcus was aware of various discrepancies between thermodynamic results and solvatochromic measurements [12]. He stated: “A single probe, such as the betaine used for the E_T(30) polarity parameter, cannot provide an answer”. As early as 1988, Dorsey [9] concluded that B30 perceived the hydrogen bond network rather than direct hydrogen bonds: “Therefore, it could be that a change in the hydrogen-bonding network of the solution is being sensed by the ET-30 probe in the dilute alcohol concentration as well”. This is the thesis that reaches the heart of the matter.

Since 1992, O. Connor and Rosés have independently developed the preferential solvation model [11,15,16]. The preferential solvation model suggests the formation of stoichiometrically defined complexes between the solvatochromic probe (solute) and the two solvents, as well as between solvent molecules. It was assumed that the measured UV/Vis shift was caused by the formation of a complex between the B30 probe or similar probes and the solvent molecule [1,36,37]. This scenario belongs to case ii. These models assume that the strength of the H-bridge bond to B30 is linearly correlated with the magnitude of the UV/Vis shift.

In the important paper by Kipkemboi [13], which was not considered further, the solvatochromism of B30 in 2-methyl-2-propanol/water and 2-amino-2-methylpropane/water mixtures was studied in detail. The authors concluded that preferential solvation cannot be the main reason for the observed effects. Taking into account the refractive index and the partial molar concentration of the components in the qualitative interpretation, both the polarizability and the number of water dipoles have an influence on the solvatochromic shifts of B30.

In 2004, however, Bentley took up Langhals’ discovery [7] and showed the dependence of E_T(30) on the global polarity of alcohols with respect to N. In addition, the relationships between the E_T(30) values of alcohol/water mixtures were alternatively analyzed as a function of volume or molar fraction of the mixture composition [27]. Bentley concluded that preferential solvation may be overestimated.

An actual preferential solvation could be demonstrated for B30 in the phenol/acetone and phenol/acetonitrile systems [43,44]. A stoichiometric 1:1 complex of B30 with phenol can be clearly identified. In phenol/1,2-dichloroethane, depending on the quantitative composition, both effects i. and ii. can be observed simultaneously with different proportions depending on the phenol concentration [43,52,53,54]. Importantly, these UV/Vis studies have convincingly demonstrated that the effect of specific hydrogen bond formation on E_T(30) is much less than that of the bulk solvent phenol [43]. Recent studies show that preferential solvation can be detected, but the solute/solvent complexes must be unambiguously identified by independent spectroscopic measurements. [55,56].

As mentioned above, the preferential solvation models are based in particular on the assumption that the UV/Vis shift of B30 and related probes such as 1-ethyl-4-(methoxycarbonyl) pyridinium iodide (K), cis-dicyano-bis(1,10-phenanthroline) iron II (Fe), or Brookers Merocyanine (BM), is mainly caused by the formation of specific interactions (hydrogen bonds) between the solvent and the probe. This assumption is a fundamental misunderstanding. This fact can be clearly demonstrated, independently of each other, using three different derivatives of the Reichardt dye family found in the literature [57,58,59]. C. Reichardt himself ignored the results of the solvatochromism of the thiolate betaine derivative of B30, which did not show the desired difference from B30 when measured in HBD solvents [57]. It was an unpleasant experience for us to discover that the H-bridge bonding patterns at the barbiturate anion substituent of the B30 derivative caused only a negligible UV/Vis shift compared to the bulk HBD solvents [58]. However, at the time, we did not fully appreciate the implications of this finding for understanding the UV/Vis shift. Unfortunately, we had to abandon the concept of molecular recognition by UV/Vis shift of solvatochromic probes. Recently, the Sander group showed that the [2,6-di-tert.-butyl-4-(pyridinium-1-yl)] phenolate forms a defined 1:1 complex with water, leading to only small shifts in the π-π* transition compared to the influence of the global polarity of the bulk water [59]. Thus, B30 and other related probes do not fulfil this purported property as an indicator of the HBD strength of the solvent molecule when the bulk solvent is measured [36,37,40,41]. The overall UV/Vis shift of B30 in pure HBD solvents is mainly due to the effect of the global polarity of the hydrogen bonding network of the solvent and not to direct hydrogen bonding with the dissolved probe [7,9,28,43,60,61,62]. Sander and co-workers also showed that the stoichiometric B30/HBD solvent complex is the true solvatochromic species and not the original B30. This result was the missing link in understanding the discrepancies between the different interpretations of the derivatives of Reichardt’s dye, as it was known that steric shielding of the phenolate oxygen of the B30 derivatives leads to a change in the solvatochromic properties [1].

The misinterpretation that the total UV/Vis shift is primarily due to the direct formation of hydrogen bonds at B30 must be fundamentally corrected, even though many papers have taken this as a defined basis. Accepting this fact will be difficult for many scientists working in this field, as it overturns entrenched patterns of thought. Following Bentley [27], we question the classical preferential solvation approach of special solvatochromic probes for certain alcohol/water and related aqueous binary solvent systems with respect to scenario ii., as reported in [4,19,20,21,25,26,27,30,31,32].

Suppan also concluded that the process of hydrogen bonding between solute and solvent in water can be endergonic, using the preferential solvation index for interpretation [63]. Later, Rezende recognized that the concept of preferential solvation has some weaknesses, and the preferential solvation index was also recommended to overcome some problems in explaining difficult results [64,65].

However, the real scientific problem with the evaluation of UV/Vis absorption energy data of solvatochromic probes in solvent mixtures in the literature is much more serious. Most authors routinely use the mole fraction x of a component of the solvent mixture to define the quantitative composition in physical terms. It has been assumed that a strictly linear dependence of the UV/Vis absorption energy of the dissolved solvatochromic dye on x would indicate ideal mixing behavior [10,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. This thesis must be fundamentally questioned, since only the change in the Gibbs free energy (ΔG) of a solvent mixture can be linearly related to the mole fraction of the components involved [10,66]. The Gibbs free energy is a composite variable [66]. For the UV/Vis absorption energy of a dissolved probe molecule in a solvent mixture, however, the situation is somewhat different. The number of transition moments, i.e., the atoms and molecules that are affected by both the light and solvent in a given volume depends on the average molar concentration (N_av,x) of the solvent dipoles with respect to x, but not directly on x [47,67,68]. Therefore, the experimentally found curvilinear relationship E_T(30) as a function of x(water) may indicate a preferred solvation [10,14,15,16,17,18,19,20,21], since N_av,x is reciprocal to x(water). We assume that the real reason for the curved shape of the function E_T(30) or EP_HBD (see later Equation (2)) as a function of x(water) is not necessarily the preferred solvation, but the influence of inhomogeneity due to the difference in mass of the two different solvents. This aspect is particularly relevant for aqueous mixtures due to the low molar mass of water. EP_HBD is usually the UV/Vis absorption energy (ν_max in cm⁻¹) or in kcal/mol [E_T(30)] of the solvatochromic probe such as B30 measured at λ_max, Equations (1) and (2).

EP_HBD ≡ ν_max (cm⁻¹) ≈ aN (mol/cm³) + b.

(2)

N refers to the molar concentration, according to Equation (3), of the solvent dipoles or the polarized solvent molecules according to the Debye–Lorenz, Clausius–Mosotti–Lorenz or Lorentz–Lorenz relation [47]. σ is the physical density and M the molar mass of the pure solvent substance.

N (mol/cm³) = σ(g/cm³)/M (g/mol).

(3)

There are hardly any well-founded studies on the subject of the various quantities of mixture composition, as the mole fraction x seems to have become established as a routine basis for calculation. There are only a few papers that briefly mention the influence of the different composition variables on E_T(30) and qualitatively illustrate it with some examples [9,27,43,50]. Significantly, Marcus already suspected that this topic would raise a number of unanswered questions; he mentioned timidly “the different measures of composition of a binary solvent mixture should be borne in mind” [50].

In addition, it has been empirically found that the EP_HBD of pure solvents is linearly correlated with the N (total molar concentration) of the solvent under solvent variation for specific solvent families [7,27,43,61,62]. Furthermore, there is a fundamental relationship between N and the spectroscopic quantities ν_max and ε_max (Lmol/cm = 10³ cm²/mol) as the molar absorption coefficient as shown in Equation (4).

N (mol/cm³) = ν_max(cm⁻¹)/ε_max(cm²/mol),
ν_max (cm⁻¹⁾) = N (mol/cm³) ε_max (cm²/mol).

(4)

Equation (4) has been completely overlooked in the past. The relationship is not artificial. The physical relationship between the absorption energy ν_max, the molar absorption coefficient ε_max and N is theoretically determined through Beer’s approximation and the Lorentz–Lorenz relation [67,68]. The fundamental Lorentz–Lorenz relation is given by Equation (5).

$$\mathrm{f}\left(n_D^{20}\right)=N 4/3\pi R_{\mathrm{m}}.$$

(5)

With $n_D^{20}$ the refractive index measured at 589 nm; R_m molar refractivity and f($n_D^{20}$) = [($n_D^{20}$)² − 1]/[($n_D^{20}$)² + 2].

It is a matter of identifying the physically correct amount of N in the solvent system [69]. The general factor N in the original Lorentz–Lorenz relation, Equation (5), refers to the molar concentration of the total number of solvent molecules [47]. It has recently been shown that, within homologous series of n-alkane derivatives, the correlation of the refractive index as a function of N results in a negative slope [69], which theoretically does not agree with the original Lorentz–Lorenz relation [47]. Since N is empirically related to ν_max by Equation (2), many correlations of ν_max with $n_D^{20}$ from the literature are not meaningful. Only when the actual molar concentration of the “chromophore” of the solvent molecule, the C-H bond concentration N_CH, is taken into account, is the applicability of the Lorentz–Lorenz relationship for correlation analysis fulfilled. The reason for this is simple, because N ~ −N_CH. [69]. Therefore, instead of N, the respective concentration of the corresponding functional fractions of the solvent is actually required which is N_CH for special solvent families. Accordingly, N should be replaced by N_CH when investigating structure–property relationships with respect to refractive index. Then, Equation (6) is obtained:

$$\mathrm{f}\left(n_D^{20}\right)=N_{\mathrm{CH}} 4/3\pi R_{\mathrm{m}}.$$

(6)

For solvents containing hydroxyl- and/or -CO-NH-groups, the situation is straightforward, as the HBD groups are the dominant dipoles in the solvent volume. Thus, Equation (2) essentially holds when solvent families are treated individually, but is convincingly applicable to HBD solvents [6,27,61]. Indeed, many EP_HBD correlate linearly with the physically determined hydroxyl group density, which is proportional to the molar concentration N [Equation (2)], rather than with the acidity in terms of the pKa of the solvent [43]. For non-HBD solvents, linear relationships between EP and N are only found if one stays within the series of a particular solvent family [61].

The reason for the clear result of Equation (2) is that ε_max of negative solvatochromic probes, Equation (4), changes inversely linearly with ν_max as the solvent is varied [1,70,71]. Equation (2) works only moderately well for positive solvatochromic dyes as the preliminary evaluation of Nile Red shows; see Figure S1a in the supplementary materials; the UV/Vis-spectroscopic data are taken from [72]. In this context, the question is how the molar absorption coefficient ε_max of the solvatochromic probe changes systematically linearly with N, since ε_max also correlates with the refractive index due to the Kramer–Kronig relation [73]. For positive solvatochromic dyes, ε_max remains essentially unchanged within structurally similar solvent series [70,71]. This consideration is in line with older studies by Suppan [74,75]. Since the electromagnetic coupling of the solvent chromophore with the dye is theoretically understood for negative solvatochromic dyes [70,71], only the solvatochromism of such dyes with respect to N is analyzed in this review.

There are several reasons for the motivation of this review and re-evaluation of the E_T(30) parameters of organic co-solvent/water mixtures. Enormous progress has been made in the study of aqueous solvent mixtures, both experimentally and theoretically. Many new insights into their microstructure and dynamics, structure and properties have been gained in recent years for alcohol/water mixtures [76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96] and other co-solvent/water mixtures (see references in the main text). In particular, these new findings on the microstructure of alcohol/water mixtures require a re-evaluation of many older results on the solvatochromism of probes in these mixtures. A crucial argument for testing the solvatochromism of B30 in aqueous mixtures is that water is not a strongly acidic solvent in the sense of the HBD property, but is one of the most polar solvents due to its exceptionally high molar concentration N and the polarization of the volumetric OH bonds [60]. A very precise distinction must be made between volumetric water and smaller quantities of water as a solute in a mixture [75]. From x(water) < 0.2, the situation is different for aqueous mixtures than in the water-rich range, as water behaves more like a solute than a solvent [75,76,77].

Another key argument concerns the appropriate use of the various measures of mix composition [50]. Recently, we have shown that E_T(30) is an approximately linear function of the average molar concentration (N_av) of ethanol/water and methanol/chloroform mixtures [43]. This is true for certain concentration ranges, then the correlation coefficient for the linear relationship r (regression coefficient) is ~0.99 [43]. It is likely that linear dependencies E_T(30) as a function of N_av only arise if the thermal motion of the solvent molecules overcomes the structuring of the solvent mixture. Is the solvatochromic probe measuring an average number of different solvent dipoles as a snapshot in certain compositional ranges? To answer such questions, we need to take a closer look at the dynamics of the solvent mixture [84,85,86]. Pure alcoholic solvents and alcohol/water mixtures fit into a relationship when the dielectric relaxation time τ₁ and the number of OH dipoles are correlated on the basis of N (see Figure 4 in [86]). Relaxation time of ethanol/water mixtures increases with decreasing number of OH dipoles due to increasing alcohol content. Reminder, the dielectric relaxation time τ₁ is defined as the time it takes 63% of the molecules in the sample to return to disorder [87]. Thus, the degree of ordering of binary alcohol/water mixtures containing two different types of OH-dipoles probably increases with increasing structuring, i.e., concentration of C-C bonds originating from the alcohol molecules.

The following question arises: Can (binary) solvent mixtures can be treated in the same way as pure solvents with regard to the average molar concentration (N_av) of relevant solvent dipoles or polarizable solvent molecules? The situation regarding the appropriate measure to use is complicated. To correlate the results of UV/Vis spectroscopy or dielectric spectroscopy, different composition variables, such as the molar and volume fractions of the mixture, are sometimes used alternately [9,27,88,89]. For ternary mixtures or multicomponent systems, the determination of the composition in suitable parameters is even more complex. However, the work of F. Martin et al. shows that solvation models can in principle also be used to explain the solvatochromism of probes in ternary mixtures [97,98]. Measuring the physical properties of ternary solvent mixtures in terms of density, refractive index and heat of mixing requires careful and extensive studies. There is not as much data available in this area. Therefore, only binary mixtures will be considered in this review. The fundamental aspect of compositional quantities is covered in the methods chapter of this paper.

2. Methods

The average molar concentration N_av is a crucial physical property of all non-homogeneous substances. It must be clearly defined which atoms and molecules are being considered. This study deals with binary solvent mixtures. The N_av of any homogeneous binary solvent mixture can be easily calculated from the composition of the two components, their molar masses and the actual physical density of the solvent mixture according to Equation (7) [66].

N_av,Z = ρ_m/M_AV,z = ρ_m(1,2)/(Z₁M₁ + Z₂M₂)

(7)

ρ_m(1,2) is the actual density (after mixing) of the mixture at given Z.

M₁ and M₂ are the molar masses (g/mol) of solvent 1 and 2, respectively;

M_av,z is the average molar mass of the solvent components.

The factors Z₁ and Z₂ are either:

the molar fraction (Z = x; →N_av,x),

mass fraction (Z = w; →N_av,w), or

volume fraction (Z = φ; →N_av,v) of solvent 1 and solvent 2 before mixing.

The average molar concentrations N_av._z in terms of different M_av,z have not yet been fully considered as quantitative composition size in evaluating physical measurands of solvent mixtures. We had underestimated this point in a previous paper [62]. The linearity of a relationship between a measured quantity and a quantitative composition is not necessarily a criterion for physical correctness. It must be emphasized that the decisive quantity is the average molar mass M_av,z which can be calculated either by x, w or φ [99]; see Equation (8):

M_av,z = z₁(M₁ − M₂) + M₂

(8)

Therefore, the numerical differences between N_av,x, N_av,w and N_av,v are due to the differences in M₁ and M₂ as well as the quantitative ratio of the two solvents, rather than to the density changes, as shown for various alcohol/water mixtures when N_av,x is plotted as a function of x(water) (see Figure S1b in the Supplementary Materials).

The problem of average molecular weight is a central one in polymer chemistry. Different physical measurement methods, such as end-group analysis through NMR or acid-based titration, viscosity, osmotic pressure of the polymer solution, light scattering and ultracentrifugation, are used to measure different numerical values of the average molar mass for the same polymer sample [100]. The numerical value of the average molecular weight depends not only on the method of measurement but also on the shape of the molecular weight distribution curve [101]. Note that colligative physical methods measure the number average (M_n) of the polymer sample. This would correspond to the M_av,x of solvent mixtures. Non-colligative physical methods (preferably) measure data related to the weight average (M_w). The result of the non-colligative method depends on the nature of the solvent and polymer solute. For example, the refractive index is a non-colligative measurement. It is therefore not surprising that the determination of mixture composition through refractive index measurements is always controversial [102,103,104].

The non-uniformity of a polymer is defined by the ratio M_w/M_n [100,101]. Following the teachings of polymer chemistry [101], the ratio of M_av,w/M_av,x = DI has been defined in this work as the dispersion index of a binary solvent mixture. Accordingly, Equation (9) is used in practice as an indicator of the non-uniformity of the solvent mixture. DI is an artificially constructed variable, but the approach is borrowed from polymer chemistry.

M_av,w/M_av,x = DI

(9)

For a binary mixture, this approach is straightforward. Figure 1a shows the dependence of DI as a function of x(water) for methanol/water, 2-propanol/water and 2-methyl-2-propanol/water mixtures. M_av,x and M_av,w are calculated by Equations (10) and (11), respectively.

The 2-methyl-2-propanol/water mixtures show the greatest inhomogeneity at x(water) = 0.8 (strongest curvature of the graph in Figure 1b), since the quotient M_av,w/M_av,x as a function of x(water) has its maximum at this position. This x(water) = 0.8 corresponds to N_av,x = 0.25 mol/cm³ and N_av,w = 0.15 mol/cm³, respectively. As would be expected arithmetically, the greater the mass difference, the greater the DI for a given x. The smaller the mass difference, the wider the distribution of DI at DI_max. It cannot be overlooked that the position of DI_max with respect to x(water) corresponds to both the order of the excess molar volume of water and the excess thermodynamic properties for these alcohol/water mixtures [78,79,80,83,95]. This is remarkable because the DI only considers the masses and their proportions and does not include any other physical data. It can be assumed that this agreement is rather random for alcohol/water mixtures. Therefore, the suitability of the DI to support the interpretation of E_T(30) as a function of solvent composition in alcohol/water mixtures will be demonstrated in this work.

As explained in the introduction, for the evaluation of UV/Vis spectroscopic absorption data) [67,68], the mole fraction (x) is theoretically suitable for the determination of the average molar mass. Therefore, N_av,x, determined through Equation (10), is preferred in this paper for correlation with E_T(30).

N_av,x = ρ_m/M_AV,z = ρ_m(1,2)/(x₁M₁ + x₂M₂)

(10)

The weight fraction w₁ is calculated from the mass fractions m₁ and m₂ of the two components according to w₁ = m₁/(m₁ + m₂). N_av,w is obtained from Equation (11).

N_av,w = ρ_m/M_AV,w = ρ_m(1,2)/(w₁M₁ + w₂M₂)

(11)

Since M_av,w is inherently greater than M_av,x [100,101], N_av,x is always greater than N_av,w. For example, Figure 1b shows the relationships between the compositional quantities N_av,x and N_av,w with x(water) for the binary solvent mixture 2-methyl-2-propanol/water. Figure 1b clearly shows that N_av,w reflects the inhomogeneity of the mixture as a function of the quantitative composition more strongly than N_av,x, since the curve N_av,w versus x(water) shows a stronger deviation from linearity than N_av,x versus x(water) (see also Figure S1b in the Supplementary Materials section).

The volume fraction can also be used to determine N_av,v, Equation (12). However, there are still some open questions regarding the physical meaning of this quantity.

N_av,v = ρ_m/M_AVv,v = ρ_m(1,2)/(φ₁M₁+ φ₂M₂).

(12)

This consideration refers to the solvent volume of each solvent component before mixing according to the IUPAC definition of volume fraction: “Volume of a constituent of a mixture divided by the sum of volumes of all constituents prior to mixing” [105]. This definition assumes ideal mixing behavior, which is not the case for most aqueous and non-aqueous solvent mixtures [106]. When two liquids are mixed, neither the total number nor the total mass of molecules changes, but the sum of the volumes may change compared to the volumes before mixing. Therefore, the use of the volume fraction in the determination of N_av,v is controversial as to its true physical meaning. The use of N_av,v (average molar concentration related to volume fraction) can only serve as an empirical guide.

Because of these well-known problems with volume changes after mixing, the issue is treated thermodynamically in terms of excess molar volume (V_E) by Equation (13) and described semi-empirically by several sophisticated concepts and approaches [66,78,107]. Equation (13) is well established in the textbooks.

V_E = (x₁M₁+x₂M₂)/ρ_m(1,2) − (x₁M₁/ρ_m(1)) − (x₂M₂)/ρ_m(2))

(13)

where ρ_m(1) and ρ_m(2) are the densities of the pure solvent 1 and 2, respectively. x1 and x2 are the mole fractions of solvent 1 and solvent 2, respectively. Analyses of V_E as a function of x(solvent 1) and x(solvent 2) can provide valuable information on the partial excess partial molar volumes of solvents 1 and 2 as a function of composition.

If only the molar fraction of the OH groups of a component on N_av is considered, i.e., that of the HBD solvent fraction (M₁), then Equation (7) can be modified to Equation (14).

N_av (component1) = x₁.ρ_m/M_AV = x₁.ρ_m(1,2)/(x₁M₁ + x₂M₂)

(14)

The approach of Equation (14) is useful in determining whether the influence of the proportion of HBD solvents mixed with non-HBD solvents is due to the overall polarity or to the preference of the HBD component. This procedure has been demonstrated for the dependencies of E_T(30) as function of N_av,x compared to N_av,x(CH₃OH) for methanol/chloroform mixtures [43]. It has been shown that methanol is the dominant solvent according to scenario i of preferential solvation.

Equation (14) can also be used to consider the average number of OH groups (D_,av,xDHB) of a multifunctional OH component in the mixture, e.g., for dihydric alcohols such as 1,2-ethanediol [62]. For pure 1,2-ethanediol, then, 2N = D_HBD. See later the treatment of 1,2-ethanediol/water mixtures in relation to E_T(30).

The problem with the average molar concentration is that the sum of the two dipoles is considered, e.g., for methanol and water. This is correct if the sum of the dipoles of the solvent and their effects is proportional to the measured quantity. Recently, we have shown that the total molar concentration N of pure solvents is not suitable to describe the changes in refractive index $n_D^{20}$ as a function of structural variation within homologous series of n-alkane derivatives [69]. Instead, the molar concentration of the C-H bonds (or N-H) is crucial to adequately reflect the theoretically required linear relationship between $n_D^{20}$ and N according to the modified Lorentz–Lorenz Equation (6). Equation (15) is particularly suitable for co-solvent/water mixtures to calculate the average molar concentration of C-H and/or N-H bonds of the co-solvent [71].

N_av,x,CH = [m x(co-solvent)] N_av,x,

(15)

The factor m is the number of C-H and N-H bonds per co-solvent molecule; x is the mole fraction of the respective co-solvent. Since the atomic refraction of the C-H and N-H (amide) bonds are nearly equal [108], no additional correction is necessary for formamide (FA), N-methylformamide (NMF) and N,N-dimethylformamide (DMF). For mixtures of organic solvents, the situation is more complicated because additional chemical bonds contribute to the molar refraction of the individual solvent molecules. This is particularly important for halogenated and aromatic solvents. Therefore, only the co-solvent/water mixtures are straightforward, as water is a weak (negligible) chromophore.

Basically, the general statement of this chapter shows that the absorption energy (EP) of a dissolved dye in a mixture is inversely proportional to the mole fraction due to M_av ~ x(co-solvent) ~ 1/EP according to Equations (4) and (8). These basic relationships are independent of a physical law such as the Lorentz–Lorenz equation.

3. Results

3.1. Selection of the Solvent Mixtures

Because of the huge amount of data, we looked for a common thread to make statements that are as representative as possible and that also reveal fundamental correlations. Marcus distinguishes two groups of aqueous solvent mixtures in which the co-solvent either enhance or does not enhance the water structure. The evaluation is based on the excess partial molar volume or the excess partial molar heat capacity of the water [109,110]. Note that the Marcus classification only applies to the water-rich section of the mixture [x(water) > 0.7, x_co-solvent < 0.3] [109,110]. Marcus stated “Some solutes such as ethylene glycol, 1,4-dioxane, acetonitrile, NMF, FA, urea, ethanolamine, and dimethylsulfoxide, many of which hydrogen-bond very strongly with water, do not enhance the water structure” [110]. The selection was made according to this scientifically justified criterion. However, the Marcus evaluation can only be used as a rough guide because some co-solvents can be classified differently depending on whether the excess partial molar volume or the corresponding heat capacity is used. For some co-solvents, such as DMF, acetone, acetonitrile or THF, the classification is borderline [109,110], which shows how difficult the issue is. The binary mixtures acetonitrile/water, acetone/water and THF/water are each unique and will be discussed together in a separate publication. The situation regarding the non-enhancement of the water structure is quite clear for the FA/water, 1,2-ethanediol/water and glycerol/water mixtures [109,110]. Enhancement of the water structure is particularly relevant for the ethanol/water, 2-propanol/water and 2-methyl-2-propanol/water mixtures [109,110]. However, the term “water structure enhancement” sounds mysterious. [78,79]. The problem is that there are qualitatively different microdomains of water in alcohol/water mixtures in terms of structure and size [90,91,92,93,111]. Marcus [110] noted that the “Enhancement of the water structure then consists of the changing of some of the dense (water) domains to bulky ones”. This phenomenon would inevitably lead to an increase in the average alcohol concentration in the remaining mixed phase compared to the co-existing microdomain water phase or the hypothetical phase resulting from the initial mixing ratio for each composition. Therefore, the overall polarity of the actual ethanol/water mixed phase should be lower than the phase that would result if ethanol and water were statistically completely mixed at a given composition. This should be kept in mind.

The ethanol/water mixture seems to be one of the most difficult solvent mixtures to understand when considering simple systems; see [111] and the references cited. The temperature increase associated with volume shrinkage when ethanol and water are mixed is apparently a thermodynamic anomaly [79]. The strongly negative entropy of the mixing process suggests complex structure formation depending on the composition, as demonstrated through dielectric spectroscopy and a special microscopic technique [86,87,88,89,111].

The curves of the solvatochromic parameters as a function of x(water) in [18,19] agree remarkably well with those of the partial excess molar volume as a function of x(water) of methanol/water, ethanol/water, 2-propanol/water and 2-methyl-2-propanol/water [95,96]. Therefore, the physics of alcohol/water mixtures deserves special attention in this study. There has been little discussion of the effect of the microstructure of alcohol/water mixtures on a solvatochromic probe [33].

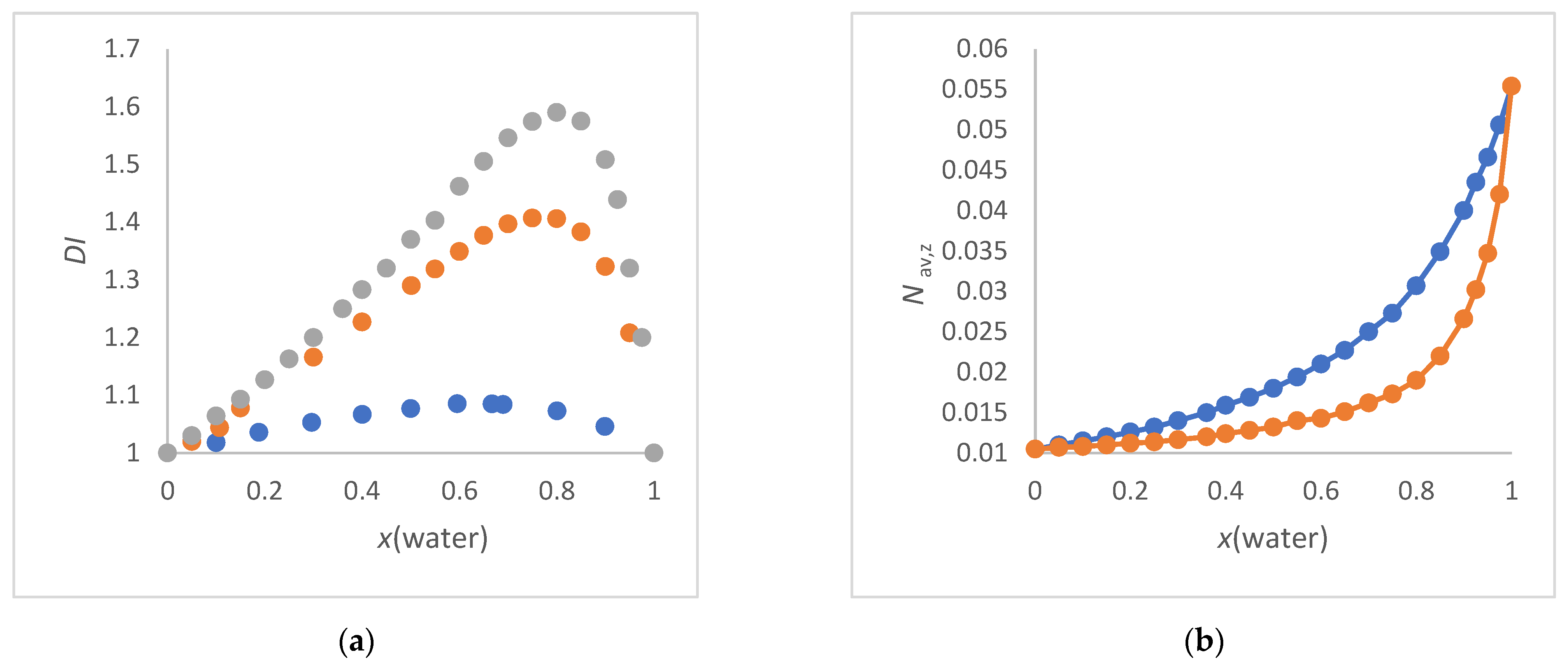
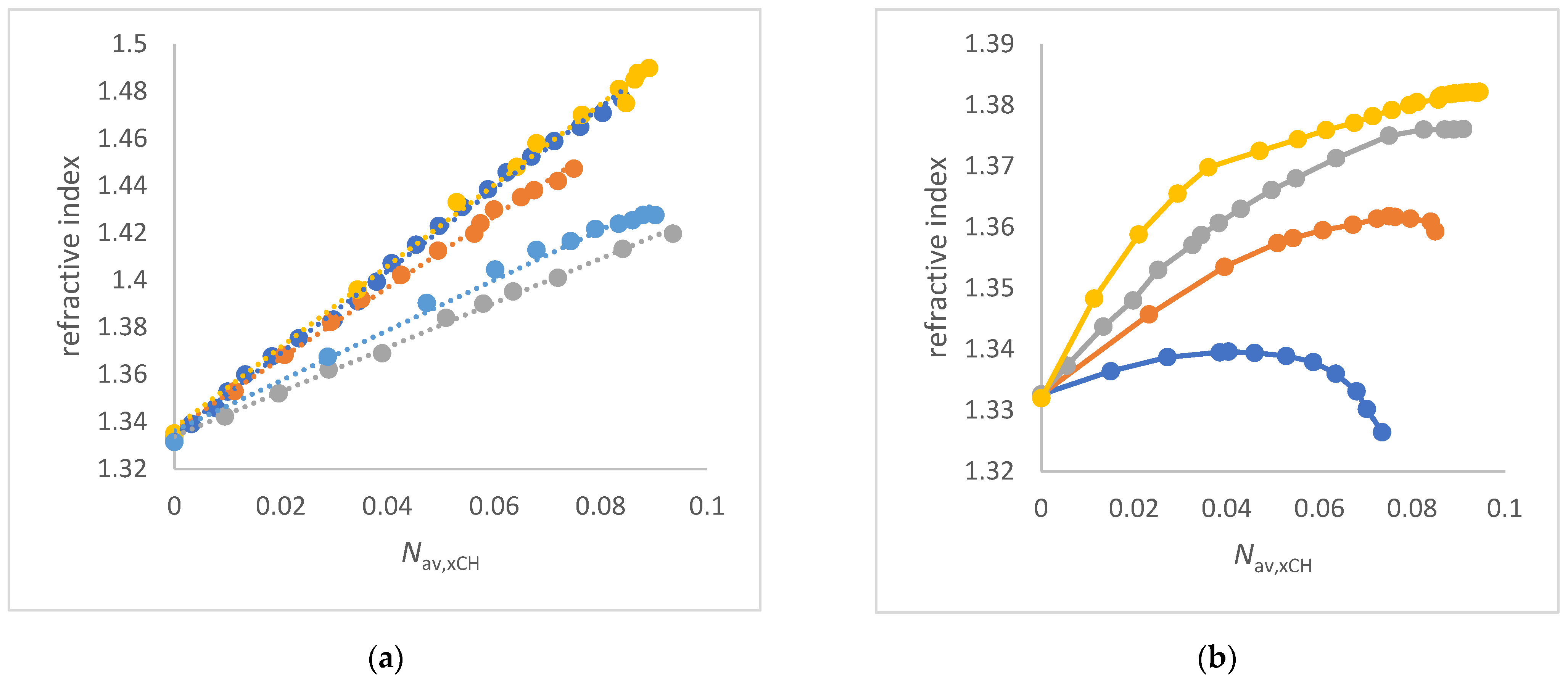
3.2. Refractive Index of Aqueous Solvent Mixtures

The suitability of Equation (6) in combination with Equation (15) is illustrated for several amide derivative/water, DMSO/water and 1,4-dioxane/water mixtures. These solvent mixtures belong to the class where no enhancement of the water structure is observed [109,110]. References for $n_D^{20}$ data are given in Tables in the Supplementary Materials section. No usable refractive index data could be found in the literature for NMF/water mixtures.

Plotting the refractive index ($n_D^{20}$) measured at a wavelength of 589 nm as a function of N_av,x,CH gives a straight line, as can be seen in Figure 2a and from Equation (16) to Equation (20). The 1,2-ethanediol/water and glycerol/water mixtures, both of which show excellent linearity of $n_D^{20}$ as a function of N_av,x,CH, are described in Section 3.4.6.

$$\begin{gathered} n_D^{20}=1.5 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.34, \\ \mathrm{n} = 12 (\mathrm{FA}/\mathrm{water}); \mathrm{r} = 0.9997. \end{gathered}$$

(16)

$$\begin{gathered} n_D^{20}=1.736 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.334, \\ \mathrm{n} = 8 (\mathrm{NFM}/\mathrm{water}); \mathrm{r} = 0.9977. \end{gathered}$$

(17)

$$\begin{gathered} n_D^{20}=1.065 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.34, \\ \mathrm{n} = 14 (\mathrm{DMF}/\mathrm{water}); \mathrm{r} = 0.988. \end{gathered}$$

(18)

$$\begin{gathered} n_D^{20}=1.5 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.34, \\ \mathrm{n} = 18 (\mathrm{DMSO}/\mathrm{water}); \mathrm{r} = 0.9952. \end{gathered}$$

(19)

$$\begin{gathered} n_D^{20}=1.5 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.34, \\ \mathrm{n} = 12 (1,4\text{-}\mathrm{dioxane}/\mathrm{water}); \mathrm{r} = 0.9977. \end{gathered}$$

(20)

The positive slopes Δ$n_D^{20}$/ΔN_av,x,CH and the excellent quality of the linear correlations$n_D^{20}$ as a function of N_av,x,CH for several co-solvent/water mixtures are a clear proof of the approach of Equations (6) and (15) for solvent mixtures. The quantity N_av,x,CH fulfils the theoretical requirements of Beer’s approximation and the Lorentz–Lorenz relation [47,67,69]. The E_T(30) parameters of these aqueous solvent mixtures decrease with increasing $n_D^{20}$ (see Figure S2 in Supplementary Materials). These results will be explained at the appropriate place in the following text where the particular mixture is discussed.

The conclusive linear relationships in Figure 2a clearly demonstrate the approach of Equations (6) and (15) when analyzing the refractive index of aqueous solvent mixtures. However, this is only true as long as alcohol/water mixtures are not considered.

Remarkably, the linearity $n_D^{20}$ as a function of N_av,x,CH does not apply to alcohol/water mixtures in which the water structure is enhanced [109,110]. In particular, the methanol/water and ethanol/water systems give a maximum curve of $n_D^{20}$ as a function of N_av,x,CH; see Figure 2b. For the other alcohol/water mixtures, an asymptotic curve is obtained, but with a positive slope along the curve; Figure 2b. In the past there were empirical concepts to get around the non-linearity $n_D^{20}$ as function of composition for methanol/water; i.e., by using the quotient $n_D^{20}$/density instead $n_D^{20}$ alone [112]. However, the physical background is more complicated and is still under investigation [113,114,115]. Recent studies have shown that at the mesoscale there are microdomains of water and ethanol/water consisting of different refractive indices [111]. Depending on the balance between segregation and aggregation of these regions [115], the non-linearity of $n_D^{20}$ as a function of composition is due to the coexistence of two different microdomains with different compositions and hence different refractive indices. The ratio of the two domains is a function of the original solvent proportions before mixing. The polarization effects and dipolar dispersion forces relevant to methanol/water mixtures may have an additional influence [60,93,94]. Figure 2b clearly supports the hypothesis of the coexistence of different microdomains of water/alcohol mixtures [90,91,111]. The following preliminary result can be stated: the alcohol/water mixtures that show an enhancement of the water structure according to Marcus do not show a linear dependence $n_D^{20}$ on N_av,x,CH.

Alcohol/water mixtures will be further discussed in this paper under the aspect of the co-existence of different microdomains.

3.3. Temperature Influence on E_T(30) in Terms of Density Impact

The E_T(30) data of ethanol measured at different temperatures are taken from the original work of Dimroth–Reichardt and Linert to his subject [1,116]. The used data are provided in Supplementary Materials, Table S1. With increasing temperature, E_T(30) decreases due to the decreasing density of the solvent and thus the decreasing number of dipoles per volume, which leads to perfect linear correlations of E_T(30) as a function of N(T); see Equations (21) and (22). The diagram is shown in Figure S3.

E_T(30) = 1834 N (T) + 20.9,
n = 8 (Reichardt), r = 0.9969.

(21)

E_T(30) = 2205 N (T) + 14.3,
n = 7 (Linert), r = 0.9978

(22)

The influence of temperature on the E_T(30) value of solutions of B30 in ethanol and methanol was also investigated by Zhao [117]. The authors hypothesized a de-defined B30/methanol complexation with decreasing temperature due to the appearance of an apparent isosbestic point in the UV/Vis spectrum series, in contrast to B30 in ethanol. This conclusion is not yet clear because the increase in the intensity of the UV/vis absorption band is probably due to volume shrinkage on cooling, for which correction is not included in the reference. It is therefore possible that the isosbestic point is caused by the contribution of two or more different species. The presence of alcohol/B30 complexes was also suggested by temperature-dependent UV/vis studies performed by El Soud [118]. However, complexation of B30 with ethanol has not been directly demonstrated through independent spectroscopic measurements. Sanders suggested that the B30/HBD solvent complex would be the actual solvatochromic species as derived from theoretical considerations [59]. However, the specific influence of the dye/solvent complex on E_T(30) is much smaller than the volume effect of the global hydrogen bonding network. For these reasons, these few results represent only a snapshot, as much remains to be done to understand the effect of temperature on E_T(30) in terms of density fluctuations associated with structural changes as a function of temperature [118,119]. However, this first inventory shows that the increase in E_T(30) with decreasing temperature is mainly due to an increase in density and thus in N.

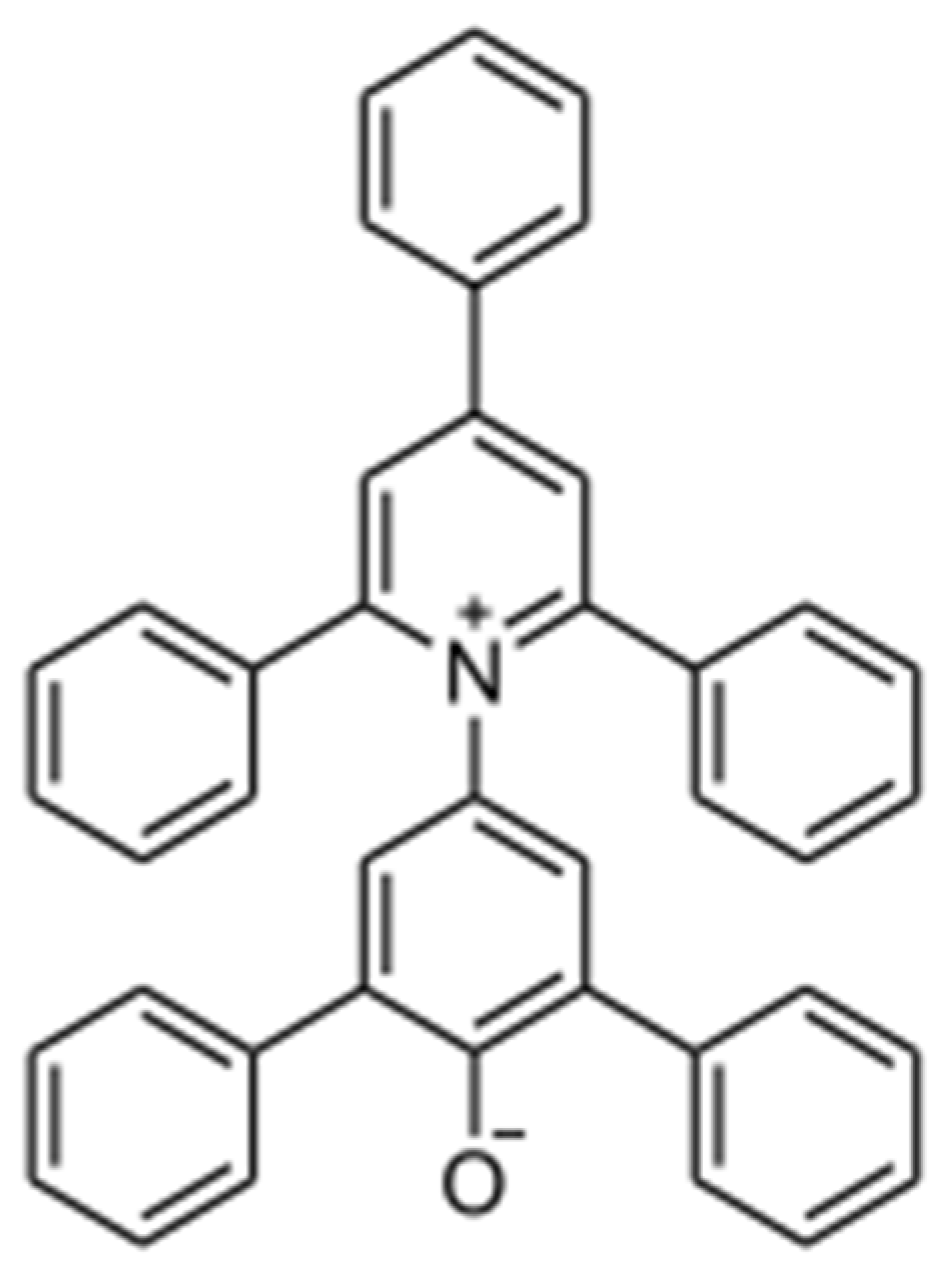
3.4. Solvatochromism of B30 in Aqueous Solvent Mixtures

This part of the manuscript is the central concern. It is about correcting many misinterpretations in the literature. Most of the E_T(30) data of the solvent mixtures to be evaluated were taken from [1,2,3,4,11,12,13,14,15,16,17,18,19,20] and others. Some specific comments on the datasets used are necessary, as several aspects have to be taken into account. It is necessary to check which E_T(30) value corresponds exactly to the given concentration, as mole fractions, weight fractions and volume fractions are used alternatively [1,2,8,11,12,13,14,15,16,17,18,19,20].

The densities of the mixtures for each specific composition and temperature are required for evaluation. This was the most difficult problem to solve. Fortunately, the densities of alcohol/water mixtures often correlate significantly with the mole fraction (x) in certain ranges of the composition. Thus, unknown densities for certain compositions can be calculated from correlation equations using accurate data from the literature. References are given in the headings of the figures and tables in the Supplementary Material section.

Fortunately, many of the measured E_T(30) values from the literature are in very good agreement between different authors for series of measurements. We have compared the data of Reichardt [2] and Rosés [18,19,20] and found that an almost perfect agreement of the measured E_T(30) values as a function of N_av,x is found. For an example, see Figure S4a for the ethanol/water mixture. For this task, it was necessary to convert the volume percentages from [1,2] to derive a mole fraction. Despite the very good agreement, a dataset from the same source was generally used for the analysis if sufficient measured values were available. For the FA/water mixture, data from two different references were mixed because the authors’ measurements covered different composition ranges [21,120]. The deviations are very small. When staying within one data series, the regression coefficient r approaches one for FA/water. For the NMF/water mixtures, there is no large variation above x(water) > 0.2, see Supplementary Materials of [21].

The high quality of the overall dataset from Rosés should be emphasized. Rosés also used the carboxylate substituted betaine dye of B30; the B30-COONa to study alcohol/water mixtures due to the low solubility of B30 in pure water and highly water concentrated mixtures [19]. There is an almost perfect agreement between E_T(30) and E_T(30-COONa) over the whole composition range. This aspect will be taken up again in the discussion section.

The perfect complementarity of the different E_T(30) values for DMSO/water from several references [7,12,14,121,122] should be noted (see Figure S4b). All datasets fit exactly in one relationship (see below). However, there are very small differences [ΔE_T(30) ~ 1 kcal) between the authors’ results.

Since the E_T(30) datasets for 1,2-ethanediol/water show some unacceptable differences in the low water concentration range between the data from [12,15], we used only the dataset from [12] which fits well (see Figure S5).

The perfect complementary agreement of the E_T(30) data from [13,19] for the 2-methyl-2-propanol/water mixture at high water concentration is also particularly noteworthy.

An unfortunate and common problem was that many measured UV/Vis data of various solvatochromic dyes were accurately reported neither in the tables nor in the Supplementary Materials [6,10]. Often only the coefficients of the applied solvation models or artificially modified parameters were given instead of the original spectroscopic data.

To support the correlations of E_T(30) as a function of N_av,x, Kosower’s Z-scale was considered appropriate [123,124,125] because of the linear correlation of Z with the E_T(30) parameter [1,34,35]. However, this proved not to be the case. It is important to clarify the situation of the different Z values for DMSO/water and ethanol/water mixtures in the literature, as only the Z values given by Kosower have been directly determined with K [123,124]. The Z values used by Marcus for correlations were calculated by himself indirectly using Brownstein’s S values [126] (see note in citation 23 of Marcus’ paper) [12]. The same applies to Gowland’s Z values, which were also determined indirectly from 4-pyridine-N-oxide via a correlation equation [127]. We are convinced that the main problem is the reproducible measurement of Z values with Kosower’s dye, because in [127] it was mentioned that the Z value depends on the concentration of K in ethanol/water. Sufficient dilution is necessary or, alternatively, extrapolation to infinite dilution if experimental problems may occur.

To test whether case ii. of preferential solvation is significant, the literature data of other negatively solvatochromic probes such as B1 [(2,4,6-triphenyl-1-pyridinium)-phenolate] [1], Brooker’s Merocyanine (BM) [128] or Fe [129] were considered, although fewer data points per individual correlation are available. For this purpose, EP of BM or the UV/Vis absorption energy at the peak maximum ν_max(Fe) are analyzed as a function of N_av,x.

3.4.1. 1,2-Ethanediol/Water, Methanol/Water and Ethanol/Water Mixtures

The reason for considering 1,2-ethanediol/water mixtures in comparison to methanol/water and ethanol/water mixtures is as follows. In all three binary solvent mixtures, the enthalpy of mixing is exothermic over the whole composition range [82,83,130]. While 1,2-ethanediol as a co-solvent does not enhance the water structure, methanol and ethanol do [109,110].

As mentioned above, the relationship E_T(30) as function of x(water) resulted in a curved line, regardless whether methanol/water, ethanol/water or 1,2-ethanediol/water mixtures were considered, as seen in Figure 3b. This was discussed in the introduction and is well described in the literature [2,8,10,11,12,13,14,15,16,17,18,19,20]. The greater the difference in molar mass, the more non-uniform the mixture will be. The order of DI_max is as follows: ethanediol/water mixtures (green) > ethanol/water mixtures (blue) > methanol/water mixtures (grey) (see Figure 3b). This in turn depends on the x(water) in the mixture. It can be clearly seen that the strongest curvature along a line of E_T(30) as a function of x(water) for each specific co-solvent/water mixture occurs when the DI is highest. This is a purely physical effect and has nothing to do with the specific solvation.

The situation is different when E_T(30) is theoretically correctly correlated with N_av,x (see Figure 3a). An excellent linear correlation of E_T(30) as a function of N_av,x is then obtained for the 1,2-ethanediol/water mixtures (Equations (23) and (24)). This overall result is very significant. This corresponds to the physical finding that the 1,2-ethanediol/water mixtures do not show abrupt structural changes over the entire composition range [77,110,130]. The interpretation of the E_T(30) curve as function of N_av,x for the 1,2-ethanediol/water mixtures requires an essential comment, because each 1,2-ethanediol molecule contains two OH groups. Therefore, the number of OH dipoles per 1,2-ethanediol is doubled. For the 1,2-ethanediol/water mixtures, the hydroxyl group concentration is calculated as a function of the number of the total OH dipoles using the D_HBD model [62]. The D_,av,xHBD quantities are calculated from Equation (14) using the partial OH concentration of the 1,2-ethanediol component in the mixture (see Table S2). The function E_T(30) versus D_HBD for 1,2-ethanediol/water mixtures determined according to Equation (14) is the orange dotted line in Figure 3a. This curve is completely congruent with the relationship E_T(30) versus N_av,x for methanol/water mixtures in the water-rich range (N_av,x > 0.04 mol/cm³) (grey dotted line of Figure 3a). However, it is noteworthy that the correlation E_T(30) versus N_av,x of methanol/water mixtures from N_av,x < 0.04 mol/cm³ runs parallel to the correlation E_T(30) versus N_av,x (dark blue) for 1,2-ethanediol/water mixtures. This agreement illustrates the significant influence of the concentration of OH dipoles on E_T(30). This result also shows the strong influence of the total number of OH groups of binary aqueous mixtures in terms of D_,av,xHBD or N_av,x on E_T(30) [62]. These clear results completely exclude a preferential solvation of B30 in methanol/water, ethanol/water and 1,2-ethanediol/water mixtures in the sense of scenario ii. The results for the methanol/water and ethanol/water mixtures do not really correspond to scenario i either. It is always the total number of dipoles per volume that determines the E_T(30) value within certain composition ranges, regardless of structural variations.

A kink can be seen in the correlation line E_T(30) as a function of N_av,x for both methanol/water and ethanol/water mixtures in Figure 3a. These noticeable kinks in the graphs of E_T(30) as a function of composition in alcohol/water mixtures have been recognized in several previous studies and attributed to structural changes in the solvent structure [5,6,131,132].

However, the linear correlations of E_T(30) as function of N_av,x for each section of the solvent mixture are of excellent quality as shown by Equations (23)–(28).

E_T(30) = 181.3 N_av,x + 53.02,
n = 12 (1,2-ethanediol/water); r = 0.999.

(23)

E_T(30) = 341.1 D_HBD + 44,
n = 12 (1,2-ethanediol/water); r = 0.999.

(24)

E_T(30) = 342 N_av,x + 44.02,
n = 7 (methanol/water; N_av,x >0.04); r = 0.9957.

(25)

E_T(30) = 162 N_av,x + 51.5
n = 6 (methanol/water; N_av,x < 0.04; r = 0.9985.

(26)

E_T(30) = 500.7 N_av,x + 35.6,
n = 8 (ethanol/water; N_av,x > 0.04; r = 0.995.

(27)

E_T(30) = 158.6 N_av,x + 49.27,
n = 10 (ethanol/water; N_av,x < 0.04); r = 0.998.

(28)

Various physical data on the properties of methanol-water mixtures indicate a structural variation in the range of x(water) = 0.5 to 0.6; corresponding to N_av,x = 0.035 and 0.04 mol/cm³ [86,87,88,89,90,91,92,93,94,95].

This wide distribution is also confirmed by the heat of interaction as a function of composition, with the largest measured heat of about −850 kJ/mol in a range from x(water) ~06 to 0.75 [81,82]. The refractive index of methanol/water mixtures reaches its maximum at x(water) = 0.6 [112,113,114]. The highest heat of the exothermic interaction is at x(water) = 0.6 [82,83] (N_av,x = 0.038 mol/cm³), which is fully reflected by the DI_max of the methanol/water mixtures, which is highest at x(water) = 0.6 (see Figure 1b).

However, the overall situation with these two monohydric alcohol/water mixtures is not entirely clear. For ethanol/water mixtures, the function E_T(30) versus N_av,x shows a clear kink at exactly N_av,x = 0.04 mol/cm³ corresponding to x(water) = 0.8. The excess molar volume for ethanol/water mixtures is at x(water) = 0.6, but the heat of interaction is highest at x(water) = 0.82 to 0.845 [82,83]. Therefore, the refractive index maximum of ethanol/water mixtures does not correspond to thermodynamics, as is apparently the case for methanol/water mixtures. The different behavior of the composition of methanol/water and ethanol/water mixtures with respect to the refractive index was also noted by Langhals [112]. For the ethanol/water mixtures, the plots E_T(30) as function of N_av,x or x(water) are clearly determined through thermodynamics. Exactly at this composition, where the largest heat of interaction is measured, the graphs show a kink in the line indicating the structural change [5,81,82,84,89]. This agreement between the curves in Figure 3a and the thermodynamics or refractive index clearly show the influence of the physical properties of the mixture on E_T(30), as suggested in previous studies [5,6,131,132].

However, there are a number of other aspects to consider. Bentley [27] has shown that the volume fraction correlates better linearly with the static dielectric constant (ε_r) or the E_T(30) values of alcohol/water mixtures than the mole fraction as a composition parameter of alcohol/water mixtures. The volume fraction has also been recommended in a recent publication to explain the E_T(30) as a function of solvent composition more accurately than using the mole fraction [133]. Accordingly, for ethanol/water and methanol/water mixtures, the N_av,w and N_av,v quantities have been calculated and empirically tested as variables for correlation with E_T(30) [62]. It seems surprising that the N_av,w and N_av,v quantities give a much better linear relationship with E_T(30) than the use of N_av,x when the whole range of composition is considered. The methanol/water and ethanol/water mixtures fit seamlessly into the primary alcohol series when the full dataset E_T(30) of primary alcohols is included; see Equations (29) and (30) and Figure S6a in the Supplementary Materials. The overall correlations with 42 data points are convincing.

E_T(30) = 313 N_av,v + 46.7,
n = 42 (methanol/water, ethanol/water and primary alcohol); r = 0.994.

(29)

E_T(30) = 304.8 N_av,w + 46.7,
n = 42 (methanol/water, ethanol/water and primary n-alcohol); r = 0.994.

(30)

We are therefore in full agreement with the conclusions of [133], that the volume fraction gives better results in terms of linear correlation. For the correlation with E_T(30), however, it makes no qualitative difference whether the mass or the volume fraction is used to determine N_av,z. Therefore, the motivation for using the volume fraction given in [133] should be reconsidered. Using the mass fraction would give similar results. Whichever alcohol/water mixture is considered, the actual curve E_T(30) versus N_av,w or N_av,v is not really strictly linear, although a very good regression coefficient for linearity can be calculated. The data points along the relationship lines show a significant pattern like a string of pearls, as can be seen in Figure S6 in the Supplementary Materials. This is an important detail. Thus, the subtleties observed in the correlation of E_T(30) with N_av,x do not disappear, but are merely reduced in the plots E_T(30) as a function of either N_av,w or N_av,v. The approximate linearity of E_T(30) as a function of N_av,w or N_av,v is due to the stronger algorithmic consideration of the inhomogeneity of the solvent components in N_av,w or N_av,v (see Figure 1b).

These results clearly show that the discussed preferential solvation of B30 by water is meaningless for methanol/water and ethanol/water mixtures. This is also an indication that the polarization forces and dipolar effects of the molecules in the solvated mixture act collectively on B30. In 1963, in the first paper on phenolate betaine dyes, Dimroth and Reichardt also studied the better water soluble B1 probe in ethanol/water mixtures [1]. For data, see Table S4. There is also a very good correlation of E_T(1) as function of N_av,v, as can be seen from Equation (31). The correlation of E_T(1) as versus N_av,x is equivalent to that of E_T(30) versus N_av,x.

E_T(1) = 216.7 N_av,v + 57.95,
n = 10 (B1 in ethanol/water and water), r = 0.988.

(31)

If pure water is omitted from Equation (31), then the correlation quality is significantly improved to r = 0.999. This is also a strong indication that B1 is preferentially enriched in ethanol/water-rich regions when the mixture is examined. The x_b values of BM (x_b is the shift of the UV/Vis peak of BM in methanol/water) [128]) correlate very well with N_av,x; see Equation (32).

x_b = 201.2 N_av,x + 57.8,
n = 11 (BM in methanol/water), r = 0.997.

(32)

Consequently, the preferential solvation of BM in methanol/water as assumed by Machado [26] or Tanaka [134] is not applicable when N_av,x is used instead of x(water) to evaluate solvatochromism. The methanol/water mixtures were also studied by Taha using the Fe probe [129]. There is also a linear correlation and no curved curve for ν_max(Fe) as function of N_av,x, Equation (33).

ν_max(Fe) [10³ cm⁻¹] = 36.66 N_av,x + 17.32,
n = 11 (Fe in methanol/water), r = 0.992.

(33)

For ethanol/water mixtures, the ν_max(Fe) as function of N_av,x shows a similar correlation with excellent quality as previously reported [43]. The correlation of ν_max(Fe) with x(water) in place with N_av,x is worse.

These results clearly show that several types of negatively solvatochromic dyes such as B30, B1, BM and Fe do not indicate preferential solvation in the methanol/water and ethanol/water mixtures. Thus, the linear correlations of EP parameters as function of N_av,x according to Equation (2) are clearly confirmed by other solvatochromic dyes despite the smaller dataset compared to E_T(30). Since the UV/Vis energies of the different solvatochromic probes show the same linear dependencies as a function of N_av,x, it is quite clear that the solvent structure determines the solvatochromism and not the preferred solvation according to scenario ii. This conclusion is in complete agreement with older results by Langhals [5].

3.4.2. Formamide/Water and other Amide/Water Mixtures

FA/water is the only binary aqueous mixing system considered in this study that fulfils the thermodynamics of ideal mixing [66,110,135,136]. The heat of mixing is endothermic, and the entropy is positive over the whole composition range. The mixing entropy is highest at x = 0.5 [135,136].

The best linear correlations (r about 1) of E_T(30) as a function of N_av,x over the whole composition range of the solvent mixture were found for FA/water, NMF/water and 1,2-ethanediol/water mixtures (see Figure 3a and Figure 4a).

For FA/water mixtures the linear correlations E_T(30) as function of N_av,x are of excellent quality; see Figure 4a as well as Equation (34).

E_T(30) = 229 N_av,x + 50.2,
n = 16 (FA/water); r = 0.999.

(34)

The perfect linearity of E_T(30) as a function of N_av,x can be explained by the excellent physical properties of the FA/water mixtures [109,110,135,136,137,138]. The water-like structure of FA is due to the fact that water and FA molecules can exchange positions without changing the solvent structure [139]. Only the V_E (Equation (13)) changes a little, as a function of composition [138]. There is no segregation within the FA/water mixtures and the average number of dipoles per volume perfectly determines the E_T(30) at room temperature. A very good linear relationship E_T(30) versus N_av,x is also obtained for NMF/water mixtures, see Equation (35).

E_T(30) = 212 N_av,x + 50.5,
n = 17 (NMF/water); r = 0.993.

(35)

Furthermore, for NFM/water and DMF/water mixtures, there are also excellent linear correlations of E_T(30) as function of N_av,x in the section of higher water content range; x_co-solvent < 0.35 [31,107,140,141,142].

The slight kinks in the curves at lower water contents are due to the non-linear change in density as a function of composition [140,141,142]. The physical data of the NMF/water, DMF/water and NFM/water mixtures are given in Tables S2–S5 in the Supplementary Materials. According to [76], water is considered to be a solute rather than a solvent when N_av,x < 0.035 mol/cm³. However, an excellent linear correlation of the refractive index as a function of N_av,x,CH is seen for all mixtures (see Figure 2a) over the entire composition range, including the range of low water concentrations.

Marcus also described the aqueous urea solution as a binary solvent mixture system in which no enhancement of the water structure occurs, although pure urea is a solid at room temperature [110]. Accordingly, we analyzed the E_T(30) values of the urea/water and N,N-dimethylpropylene urea/water binary mixtures from the literature [143,144,145]. There are very good linear correlations of E_T(30) as a function of N_av.x for both urea/water and N,N-dimethylpropylene urea/water mixtures with high correlation quality (see Figure S6a in Supplementary Materials). This result shows that solutions of solids in water can also be treated in the same way. If the co-solvent or co-component (urea, N,N-dimethylpropylene urea) can form a three-dimensional hydrogen bond structure with water, then a linear correlation of E_T(30) with N_av,x is found.

3.4.3. DMSO/Water Mixture

DMSO/water mixtures represent a physical challenge among binary aqueous solvent systems due to the unclear thermodynamics at higher DMSO contents [146,147,148,149,150,151,152,153,154]. This was therefore chosen for this fundamental work as an illustrative example. There are a large number of physical studies on these mixtures, so only those relevant to the explanation of solvatochromism in terms of N_av,x will be referred to. The following analysis shows where the problems lie. There results a very good linear correlation of E_T(30) as function of N_av,x including E_T(30) data from several references, Equation (36) and Figure 4b.

E_T(30) = 432 N_av,x + 39.7,
n = 22 (DMSO/water) r = 0.993.

(36)

Although the overall correlation E_T(30) with N_av,x seems convincing due to the clear linearity, there is a small kink in the linear plot at N_av,x ≈ 0.025 to 0.03 mol/cm³. The kink becomes more obvious when considering only the data from [15], see Equations (37) and (38).

E_T(30) = 414 N_av,x + 40.7,
n = 9 (DMSO/water-rich; N_av,x > 0.02); r = 0.998.

(37)

E_T(30) = 624 N_av,x + 36.2,
n = 5 (DMSO/water low; N_av,x < 0.02); r = 0.999.

(38)

This small effect has a significant physical background as the density of the binary solvent mixture changes significantly at this composition [146,148]. However, density measurements for DMSO/water mixtures in the DMSO-rich region are not consistent in the literature [146,148]. In the water-rich range from N_av,x < 0.05541 mol/cm³ (pure water) to N_av,x = 0.03 mol/cm³, the density of water/DMSO mixtures decreases linearly with increasing water content. The density is almost constant in the range from N_avx = 0.03 (60% weight DMSO) to 0.014 mol/cm³ (pure DMSO) (see Table S9). In [148], it was reported that the density even decreases slightly. It should be noted that exactly at this mixture composition N_av,x = 0.028 mol/cm³ the plot of E_T(30) as a function of N_av,x has a slight, imperceptible kink.

In the literature, there are several investigations on the DMSO/water mixtures using different solvatochromic probes [12,15,129,155,156,157]. Regardless of the type of solvatochromic probe used, it is clear that at N_av,x ≈ 0.03 mol/cm³ a slight change in the profile of the parameter values can be observed as a function of the composition. Thus, the physical structural change of the DMSO/water mixtures determines the empirical parameter and not the artificially constructed acid-base properties of the solvent system [155,157]. This result is fully consistent with the prediction in the introduction that no differences should occur in scenario ii. when different probes are used. For reasons of space, the analyses of the Kamlet–Taft (KAT) parameters of DMSO/water mixtures [157] are presented in Figure S9 in the Supplementary Materials. As a consequence of this result, the determination of individual empirical polarity parameters in terms of the KAT or Catalán scale is meaningless for DMSO/water mixtures. Furthermore, a curved function of the E_T(30) value of the solvatochromic probe on x(water) of DMSO/water mixtures is found (see (Figure 5) of [12]). If the x(water) is replaced by N_av,x, a linear correlation is obtained, as shown in Figure 4b. The correlation of the UV/Vis absorption energy of other probes such as Fe [ν_max10⁻³ cm⁻¹ (Fe)] [129] as function of N_av,x for DMSO/water mixtures clearly shows a linear dependence, see Equation (39).

ν_max10⁻³ cm⁻¹ (Fe) = 67.7 N_av,x + 15.8,
n = 12 (DMSO/water), r = 0.996.

(39)

The change in the curve of the solvatochromic parameter after at N_av,x about 0.03 mol/cm³ is clearly due to physical changes in the solvent structure. Furthermore, if the static dielectric constant (ε_r) of DMSO/water mixtures is plotted as a function of N_av,x, then the kink at N_av,x at 0.03 mol/cm³ becomes also evident (see Figure S7a). The ε_r data are taken from [151]. This property is also shown in the plots of E_T(30) as a function of $n_D^{20}$ (Figure S2). While the correlation of $n_D^{20}$ as a function of N_av,CH (Equation (10)) is nearly linear (Figure 2a), the correlation of E_T(30) as function of $n_D^{20}$ shows a slight kink at N_av,x = 0.03 mol/cm³.

To return to the DMSO/water mixtures, the concentration of all dipoles (water + DMSO) of the system determines the solvatochromic property and not the preferential solvation. This is a clear result. The only surprising thing is the rather good linearity of the function E_T(30) versus N_av,x when many data from the literature are used together. This shows that B30 is not very sensitive to physical changes in the DMSO/water mixture system at RT. Therefore, the solvatochromic method is not well suited to detecting the physical change in the liquid structure of DMSO/water at different compositions.

What is the reason for the good linearity of E_T(30) as a function of N_av,x although major structural changes of the mixture occur at N_av,x = 0.03 mol/cm³? The complexity of the water dynamics of DMSO/water mixtures has been thoroughly investigated through ultrafast IR experiments and dielectric spectroscopy [149,150,151]. These results are very important in partially explaining the results of the correlations in this study. The average lifetime of water-bound DMSO changes (decreases) almost linearly with the mole fraction of water. This result is consistent with E_T(30) increasing almost linearly with water content (see also Figure 5 in [149]). This explains why the barely noticeable kink in the correlation can be neglected, as the water dynamics overcome the local structuring around the dissolved dye. Thus, the lifetime of the water/water component is independent of the water concentration in the high DMSO region N_av,x < 0.03 mol/cm³. Obviously, neither water/DMSO nor B30/water complexes are relevant for the determination of E_T(30) since the solvent mixture has a high dynamic at 298 K [150,151]. Thus, even if DMSO/water or B30/water complexes are present, they cannot be detected using B30 due to the fast dynamics of the binary solvent system. The situation is similar to other solvatochromic dyes such as Fe. Therefore, other physical measurements such as dielectric spectroscopy are more suitable than solvatochromic probe molecules for analyzing the structure of DMSO/water mixtures. The outstanding behavior of the DMSO/water mixtures at higher DMSO contents N_av,x < 0.028 mol/cm³ has been the subject of numerous simulation experiments [152,153,154]. Apparently, the behavior at N_av,x < 0.03 mol/cm³ is due to the entropy increase in the system, which is still difficult to understand theoretically [154], since the experimentally determined heat of interaction is exothermic over the whole composition range.

3.4.4. 1,4-Dioxane/Water Mixtures

The 1,4-dioxane/water mixtures were subjected to numerous physical tests [158,159,160,161,162,163,164,165,166,167,168,169]. The dependence of the UV/Vis-absorption energy maxima of solvatochromic dyes such as B30, Fe, M540, various 7-N,N-diethylaminocoumarins or harmaline as function of dioxane/water composition has been extensively studied in the literature [2,5,70,129,165,166,167,168,169].

The thermodynamics of 1,4-dioxane/water mixtures is characterized by a transition from exothermic to endothermic heat of mixing with increasing 1,4-dioxane content [158]. This is the main difference to the DMSO/water system [147]. The heat of interaction ΔrH of 1,4-dioxane/water mixtures has its maximum exothermic heat at around x(water) = 0.8 (yellow dot in Figure 5b) corresponding to N_av,x = 0.032 mol/cm³ or N_av,v = 0.018 mol/cm³. The largest partial molar volume of water in 1,4-dioxane/water mixtures is x = 0.8 [167]. Δ_rH is zero at x(water) = 0.52 (N_av,x = 0.02 mol/cm³). With this composition, the 1,4-dioxane/water mixture has the highest density and the lowest −TΔS value. At x(water) < 0.52, the heat of interaction becomes endothermic. For the evaluation in this paper, the volume fractions of the 1,4-dioxane/water mixtures given in [2] were reconverted to the average molar concentration of the solvent dipoles. Fortunately, there is excellent agreement between the E_T(30) data from four different literature sources, as shown in Table S7. The E_T(30) data from these four different sources fit perfectly into a relationship. To evaluate the influence of the inhomogeneity of the mixture with respect to the composition, we plotted E_T(30) as function of N_av,x and N_av,v as well as x(water) (Figure 5a,b).

The correlation of E_T(30) as a function of N_av,x results in two consecutive linear lines with different slopes. The change in the function E_T(30) as function of N_av, is at Nav,x = 0.015 [x(water) = 0.3] mol/cm³; see Equations (40) and (41) and Figure 5a.

At this composition (at E_T(30) ~ 46 kcal/mol), there is also the strongest curvature in the curve E_T(30) as a function of x(water) in the 1,4-dioxane-rich section (see Figure 5b).

E_T(30) = 2997.5 N_av,x + 2.123
r = 0.944, n= 7 (N_av,x < 0.02 mol/cm³, 1,4-dioxane rich section)

(40)

E_T(30) = 398,8 N_av,x + 40.42
r = 0.997, n= 12 (N_av,x > 0.02 mol/cm³, water-rich section)

(41)

The correlation of E_T(30) as a function of N_av,v (blue dots in Figure 5a) gives an asymptotic curve without linearity of specific sections. This could be explained by the fact that the variable N_av,v better reflects the inhomogeneities of the composition.

The 1,4-dioxane/water mixtures are subject to fine structuring over the whole composition range, in which both types of molecules are always involved [161,162,163,164]. The volume structure of 1,4-dioxane/water mixtures changes significantly in the range of N_av,x < 0.02 mol/cm³. Accordingly, the strongest bend in the graph E_T(30) as function of N_av,x corresponds to the composition where the significant change in the volume structure of the 1,4-dioxane/water mixtures takes place. Exactly at E_T(30) = 47 kcal/mol (N_av,x = 0.018 mol/cm³), the dielectric relaxation time τ₁ passes through a maximum (τ₁ ≈ 25 ps) for 1,4-dioxane/water mixtures [162]. The use of N_av,X(water) according to Equation (14) as the mixture composition parameter gives a similar plot as when N_av,x is used (see Figure S8b), indicating that 1,4-dioxane and water are always involved together in the volumetric structure and thus in the dissolution of dissolved B30. Thus, 1,4-dioxane does not enhance the water structure in any way, which is in full agreement with the Marcus classification [110].

It is worth analyzing the correlations of E_T(30) as a function of x(water) from the point of view of thermodynamics and the structural change of the 1,4-dioxane/water mixtures as shown in Figure 5b. At x(water) = 0.52 (N_av,x = 0.02 mol/cm³), the curve E_T(30) as a function of x(water) shows an inflection point (not marked in Figure 5b). It is precisely at this composition that this binary solvent system behaves in an athermal manner, i.e., ΔrH mixture = 0 [158,159]. The strong curvature E_T(30) as a function of x(water) = 0.8 (marked in yellow) (N_av,v = 0.015 mol/cm³) is clearly due to the inherent mass inhomogeneity of the mixture, as shown in the simultaneous plot for the DI (Figure 5b). At this composition (N_av,x = 0.032 mol/cm³), mixing has the highest exotherm. This result is consistent with the results from the thermodynamics of methanol/water and ethanol/water mixtures, which are a good indication that x(water) reflects the thermodynamics of the mixture in relation to other quantities more comprehensively than the quantity N_av,x. Thus, the S-shaped function E_T(30) versus x(water) (Figure 5b, orange dots) is attributed to the change in interaction heat as function of composition. This feature is only partly recognized when N_av,x is used as the composition size, as seen in Figure 5a. There is no bend or kink in the plot E_T(30) as function of N_av,x for N_av,x ~ 0.032 mol/cm³ (largest exothermic heat), but at N_av,x = 0.02 mol/cm³ (zero heat).

The linear function of E_T(30) as a function of N_av,x in the water-rich region N_av,x > 0.02 mol/cm³ is due to the fact that the average concentration of both the water dipoles and 1,4-dioxane molecules determines the E_T(30) value. Both fractions are constantly mixed together and do not segregate [162,163]. The larger E_T(30) in the 1,4-dioxane rich fraction, compared to a hypothetical linear plot of E_T(30) versus N_av,x, can be easily explained by the results of Buchner: “This indicates a largely microheterogeneous structure for such mixtures, with the presence of water-rich domains of significant size in the dioxane-rich fraction” [163]. Thus, B30 preferentially measures the water enriched portions of the 1,4-dioxane/water domains within the compositional spectrum. Obviously, the water clusters are solvated by the 1,4-dioxane excess and the B30 is enriched in the 1,4-dioxane clusters below N_av,x < 0.015 mol/cm³.

The refractive index as a function of the composition N_av,xCH of the 1,4-dioxane mixture (see Figure 2a, red dots) and Equation (23) give a linear curve. This is consistent with the fact that the static permittivity ε_r of 1,4-dioxane/water mixtures is also a linear function of N_av,x including pure 1,4-dioxane (see Figure S7b). For this investigation, the composition data x(water) from [162] were converted to N_av,x. In contrast, the correlation of E_T(30) as a function of ε_r or $n_D^{20}$ is not linear over the whole composition range, because the values of the pure 1,4-dioxane or the 1,4-dioxane-rich fraction do not fit linearly; see Figure S8a.

As a consequence, the B30 probe reflects the volumetric structure of 1,4-dioxane/water differently compared to volumetric polarity-related physical measurements such as dielectric spectroscopy or refractive index. In summary, the 1,4-dioxane/water mixtures present a challenge in terms of the formation of solvent structures as a function of the quantitative composition, since different physical methods (UV/vis spectroscopy of B30, dielectric spectroscopy, refractive index, calorimetry) register different dependencies of the measurand on the different composition sizes.

Note that only x and N_av,x are physically based quantities, referring to thermodynamic and UV/Vis spectroscopic quantities, respectively. Despite this concern, in summary, the complex dependence of E_T(30) on the composition of 1,4-dioxane/water mixtures can be readily interpreted in terms of N_av,x, N_av,v or x(water). This is possible by analyzing the physical properties of this binary solvent system, where thermodynamics, dipole concentration and solvent dynamics play a role. Despite this caveat, it is clear that the specific solvation of B30 by HBD solvent molecules is not responsible for this UV/Vis shift. The E_T(30) of 1,4-dioxane/water mixtures is mainly determined through the concentration of water dipoles permanently mixed with 1,4-dioxane molecules.

3.4.5. 2-Propanol/Water and 2-methyl-2-propanol/Water Mixtures

The 2-propanol/water and 2-methyl-2-propanol/water mixtures are considered separately because they show a change in the heat of mixing with increasing alcohol content in the sense of a reversal from exothermic to endothermic heat [80,82], similar to the 1,4-dioxane/water mixtures [158]. In particular, the 2-methyl-2-propanol-water mixtures in particular have been the subject of research and speculative interpretations in recent decades [170,171,172,173,174,175,176,177,178,179]. A mystical character has been attributed to this particular mixture due to the method-dependent results of the mixture [178].

First, the correlations of E_T(30) as function of N_av,x and x(water) are discussed; Figure 6a,b.

The plot of E_T(30) as a function of mole fraction x(water) shows relatively similar curves for all mixtures (see Figure S10 in the Supplementary Materials).

If one compares the curves E_T(30) with the curve of the inhomogeneity (DI) of the solvent mixture, both as a function of x(water), see Figure 3b and Figure 6b, then the same result is obtained for 2-propanol/water and 2-methyl-2-propanol/water, methanol/water, ethanol/water and 1,4-dioxane/water mixtures. The strongest curvature of the plot E_T(30) versus x(water) always occurs immediately after the strongest inhomogeneity. This corresponds “immediately after” to a difference of about 1.5 kcal/mol with respect to E_T(30), which is illustrated by the horizontal lines (grey and green dots) between the two curves in Figure 6b. This scenario can be found in all plots of E_T(30) versus M_av,w/M_av,x, regardless of the type of alcohol/water mixture.

The curves E_T(30) as a function of N_av,x for methanol/water, ethanol/water, 2-propanol/water and 2-methyl-2-propanol/water mixtures differ qualitatively for both methanol/water and ethanol/water mixtures compared to both 2-propanol/water and 2-methyl-2-propanol/water mixtures in the low water content range. Therefore, the plots of E_T(30) as a function of N_av,x show an inflection points at about 0.031 mol/cm³ and 0.0273 mol/cm³ for 2-propanol/water and 2-methyl-2-propanol/water mixtures, respectively.

At lower water concentrations, the 2-propanol/water mixtures (x(water) < 0.5; N_av,x = 0.02 mol/cm³) and 2-methyl-2-propanol mixtures (x(water) < 0.55; N_avx = 0.018 mol/cm³) are endothermic in terms of the heat of mixture. At about x = 0.65 to x = 0.5 (water) (N_av,x ≈ 0.03, see Figure 6a), both systems behave athermally; i.e., ΔH_mixing = 0. Exactly at this composition, the curve E_T(30) as a function of N_av,x (see Figure 6a) shows an inflection point. The same result is found for the 1,4-dioxane/water mixtures (see Figure 5b). In the composition range with endothermic heat of mixing, both curves E_T(30) vs. N_avx show a higher E_T(30) than would be expected from linearity. In this region, the entropy of mixing is positive and the proportion of water in the mixture determines the E_T(30) proportionally, more than in the water-rich region does. The dielectric relaxation time decreases significantly from low to high water content, i.e., the structure in the water-poor region is more stable in time than in the water-rich region.

The Fe complex has also been studied in 2-propanol/water mixtures [129]. Consistent with the correlations of E_T(30) versus N_av,x,, the plot of ν_max (Fe) as a function of N_av,x (see Figure S11) shows a similar pattern to that of Figure 6a. This shows the influence of the physical structure of the solvent as a function of composition.

In addition, there are numerous studies with positive solvatochromic probes such as Nile Red [7], 4-nitroaniline [18,180,181,182], 4-nitroanisole [18], 4-(1-azetidinyl)-benzo-nitrile [177] or coumarin 343 and 480 [178] in various alcohol/water mixtures.

While E_T(30) as a function of N_av,x for 2-propanol/water and 2-methyl-2-propanol/water mixtures show similar curves, the situation is different for the 2-butoxyethanol/water mixtures.

3.4.6. 2-Butoxyethanol/Water Mixtures

As a final example, the solvatochromism of B30 in 2-butoxyethanol (BE)/water mixtures is reanalyzed. The E_T(30) data are taken from [8]. BE itself is partially hydrophobic, but it mixes completely with water at room temperature; separation occurs only at higher temperatures [8,183]. Due to their self-structuring properties, BE/water mixtures have been the subject of numerous physical investigations [184,185,186,187,188,189,190,191,192,193]. The self-propelled agglomeration of the BE molecules in water has been demonstrated through various scattering methods [184,185]. At x(BE) > 0.02 agglomeration begins to occur resulting in an inhomogeneous solvent mixture at the level of about 1 nm [184]. However, other studies have shown that 130 nm aggregates are present [185]. The inhomogeneity of the BE/water mixing system is complicated by the fact that this feature can be observed at different length and time scales [188,189,190,191,193].

The mixtures BE/water and 2-methyl-2-propanol/water are often compared for their similarity [193]. We will show that, despite the discussion in the literature, the two solvent mixtures are completely different. The microstructures of both solvent mixtures are very subtle and are strongly influenced by the composition in the water-rich part. However, the heat of mixing is exothermic over almost the whole composition range for BE/water mixtures, but weakly endothermic at high BE concentrations (about 95 wt%) [187,188]. In addition, photo-switchable spiro compounds have been measured in BE/water mixtures [192]. It has been suggested that the solvent structure of BE/water is affected by this type of photo-switching. Therefore, it cannot be excluded that the dissolved probe molecule co-determines the fine structure of BE/water mixtures, complicating the whole situation. Therefore, only the analysis of the E_T(30) values will be discussed here. Unfortunately, the interesting solvatochromic results of El Seoud on this solvent system were not given as original data [22]. Plotting E_T(30) as a function of N_av,x for BE/water mixtures gives an asymmetric profile, as shown in Figure 7a (grey dots).

The crucial region of low BE content (at N_av,x = 0.0497 mol/cm³) deserves special attention, since, at this composition, the agglomeration of BE molecules occurs [x(BE) ≈ 0.02; or N_av,xCH = 0.017 mol/cm³] [184]. B30 dye is apparently absorbed by these BE-rich agglomerates, leading to an abrupt decrease in E_T(30) at N_av,x ≈ 0.05 mol/cm³, as shown by the grey dotted line in Figure 7a. This is consistent with the fact that E_T(30) decreases abruptly with increasing C-H concentration due to the BE component at N_av,CH = 0.017 mol/cm³ (not plotted; for data, see Table S13). There is only a narrow transition.

This result exactly fulfils the preferential solvation scenario i., as explained in the Introduction. The agglomeration of BE is driven by hydrophobic interactions, as also suggested by the analysis of the fluorescence of coumarin and related probe molecules in BE/water mixtures [193,194]. Obviously, the trapping of probes is also determined through the solvent cage property of the BE/water mixtures. This is in contrast to 2-methyl-2-propanol/water mixtures, where strong thermal fluctuations in partial concentrations occur [195,196]. Thus, in 2-methyl-2-propanol/water mixtures there is no true hydrophobic solvation of B30, but the partial water structures are changed depending on the composition, as discussed in the previous chapter.

The two binary solvent mixtures glycerol/water and 1.2-ethanediol/water show a perfect mixing behavior according to the Marcus classification, so that there is no enhancement of the water structure in any way [110]. These two mixtures are documented in Figure 7b as references. For glycerol/water and 1,2-ethanediol/water mixtures, there are perfect linear correlations of $n_D^{20}$ as a function of N_avx,CH; see Equations (42) and (43) [89,197].

$$\begin{gathered} n_D^{20}=2.062 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.335, \\ \mathrm{n} = 12 (\mathrm{glycerol}/\mathrm{water}); \mathrm{r} = 0.9999. \end{gathered}$$

(42)

$$\begin{gathered} n_D^{20}=1.381 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.333, \\ \mathrm{n} = 14 (1,2\text{-}\mathrm{ethanediol}/\mathrm{water}); \mathrm{r} = 0.997. \end{gathered}$$

(43)

The larger slopes of Δ$n_D^{20}$/ΔN_avx,CH for glycerol/water and 1,2-ethanediol/water mixtures compared to BE/water mixtures are attributed to the influence of the polarizability of the hydrogen bond network and the higher refraction of the C-O bond compared to C-H [60,62,108].

The change in the overall bulk solvent structure of 2-methyl-2-propanol/water mixtures as a function of composition is also clearly visible in the plot of the refractive index as function of N_av,xCH (yellow dotted lines in Figure 2b and Figure 7b), which shows a kink at about 0.035 to 0.04 mol/cm³. Remarkably, the kink in the plot of E_T(30) as a function of N_av,x is also observed at this composition; see Figure 6a. In this concentration range, the thermodynamic changes from exothermic to endothermic with increasing N_av,xCH for 2-methy-2-propanol/water mixtures. This thermodynamic scenario does not apply to BE/water mixtures [187,188].

Remarkably, the correlation of $n_D^{20}$ as function of N_av,xCH for BE/water mixtures is approximately linear over the whole composition range; see Equation (44) and Figure 7b (grey dotted line).

$$\begin{gathered} n_D^{20}=0.876 N_{\mathrm{av},\mathrm{x},\mathrm{CH}}+1.353, \\ \mathrm{n} = 11 (\mathrm{BE}/\mathrm{water}); \mathrm{r} = 0.998. \end{gathered}$$

(44)

Obviously, BE as a co-solvent does not enhance the water structure, but water enhances the BE structure. That is the special thing. According to the Marcus classification, this is the reverse scenario of solvent structure enhancement. These considerations convincingly show the qualitative differences between BE/water and 2-methyl-2-propanol/water mixtures. The different solvation behavior of B30 in BE/water mixtures compared to 2-methyl-2-propanol/water mixtures can also be supported by considering the DI from Equation (9). The BE/water mixtures show the greatest inhomogeneity with respect to DI at x(water) = 0.85 (N_av,x = 0.029 mol/cm³), while the kink in the curve E_T(30) as a function of N_av,x occurs far away from this at ≈ 0.045 mol/cm³. This is the crucial difference between BE/water mixtures and all other (monohydric) alcohol/water mixtures studied in this work. Therefore, this result could be used as a criterion to define the preferential solvation scenario of case i. However, the results do not exclude that the B30 dye itself has an influence on the solvent cage of the BE/water mixture at low BE content, as mentioned in [192,193] for other solutes.

4. Discussion

The plot of E_T(30) as a function of N_av,x for co-solvent/water mixtures shows a different pattern depending on the co-solvent of the mixture. The scenario of each specific co-solvent/water mixture can be clearly assigned according to the Marcus classification. Four different scenarios can be identified:

A.

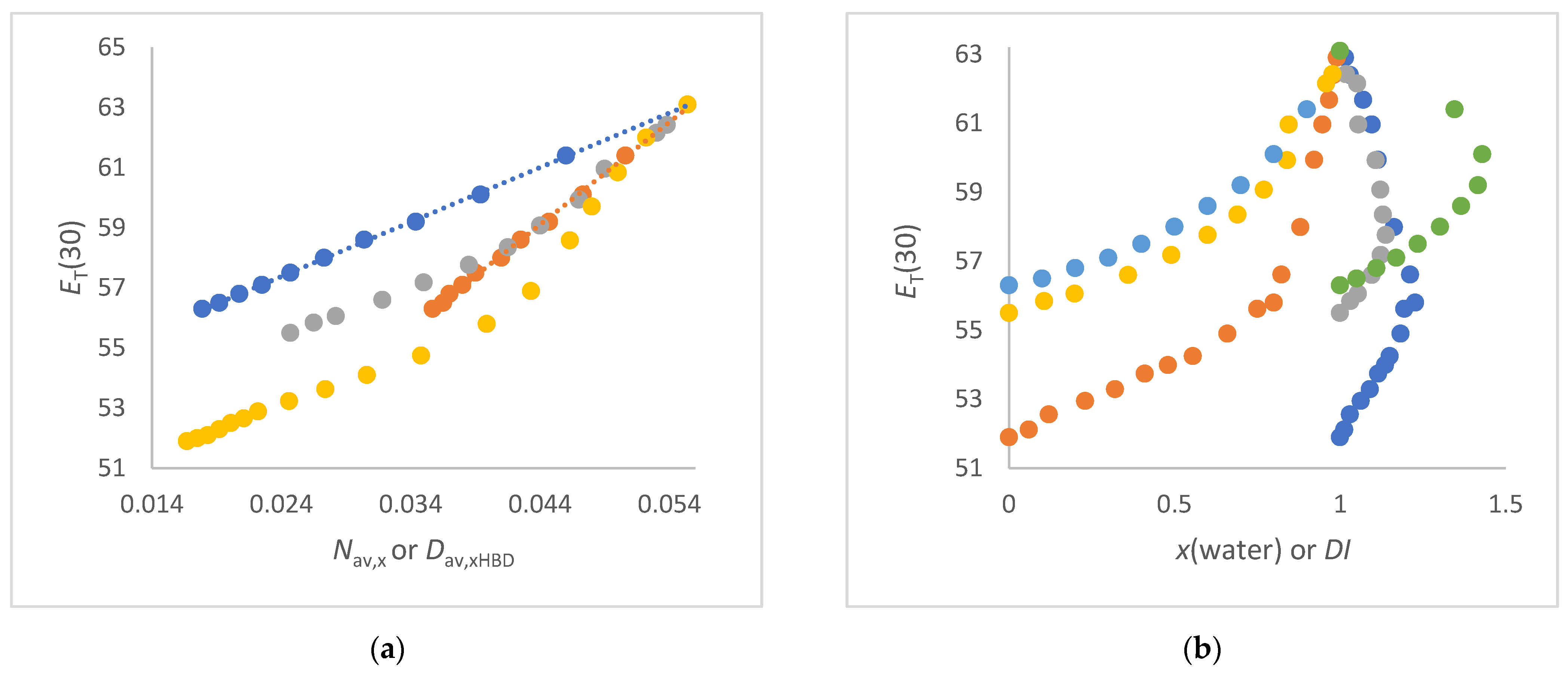
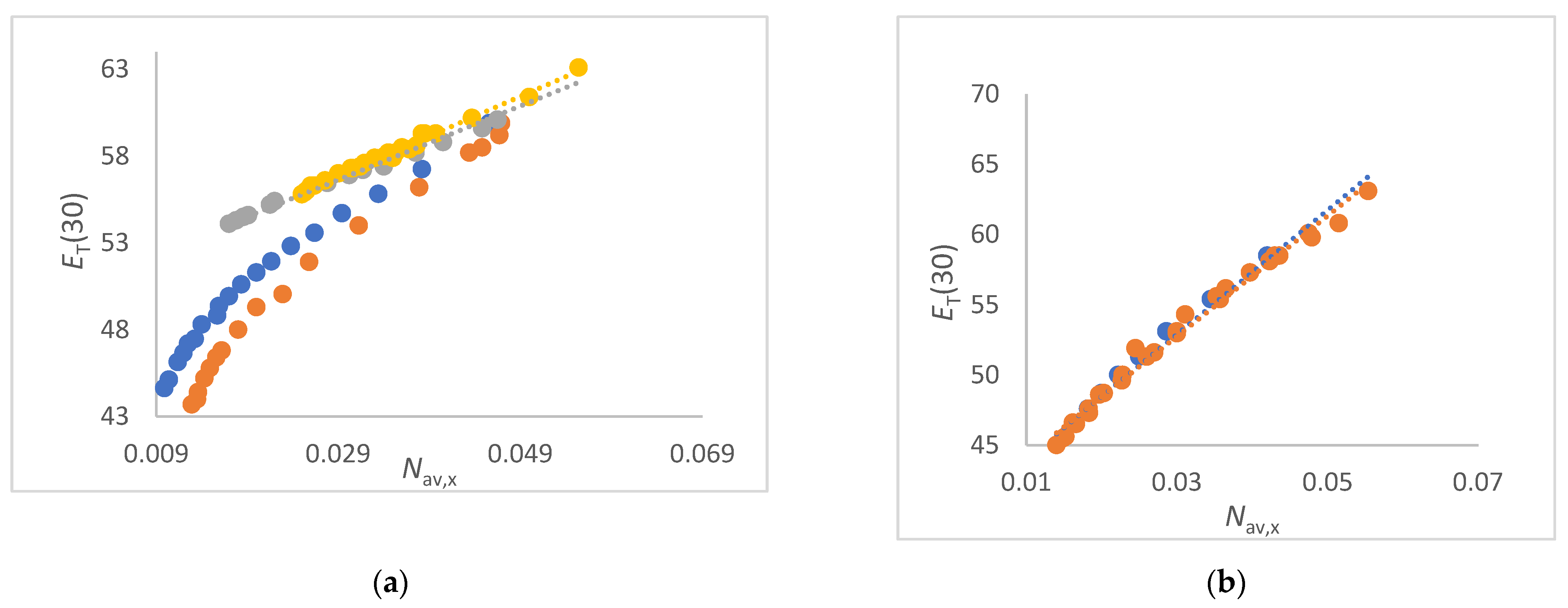
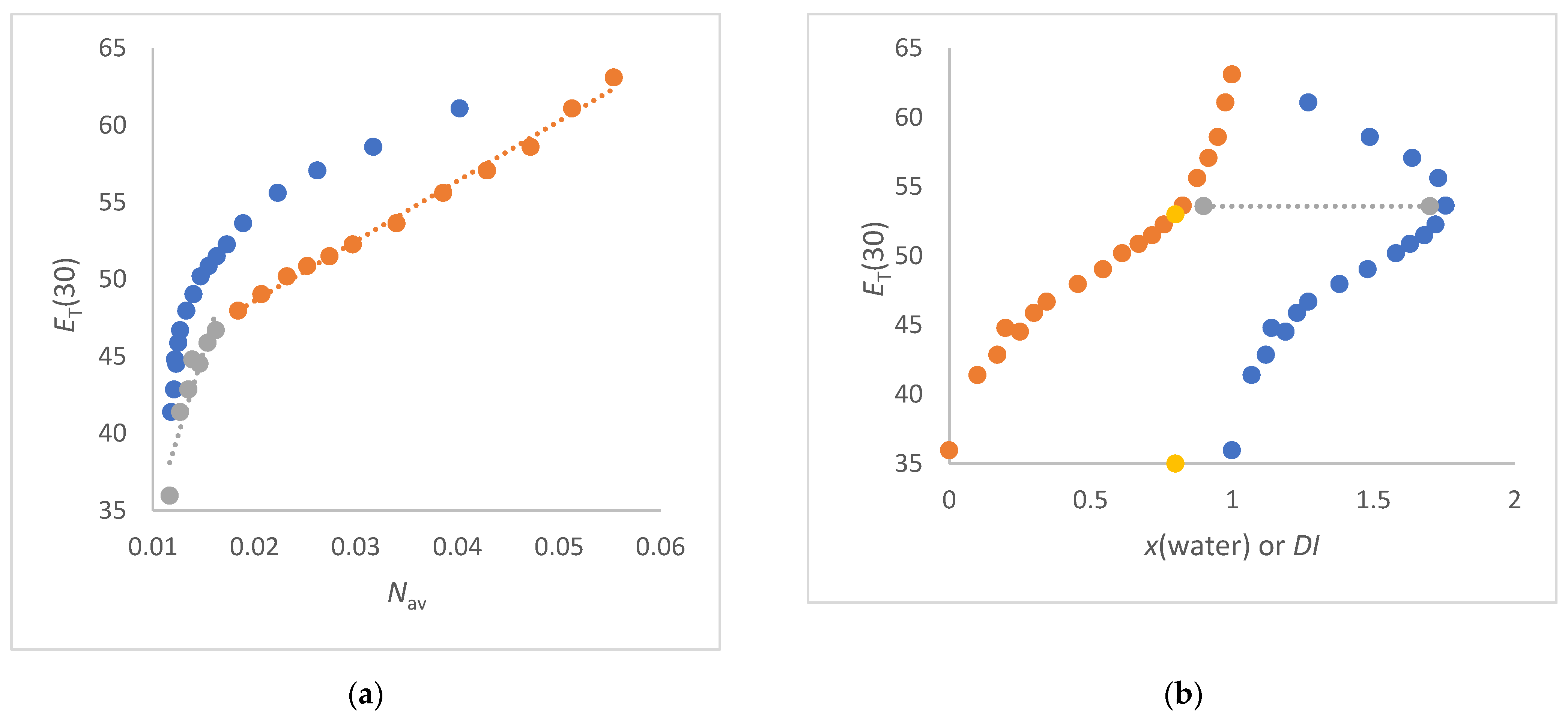
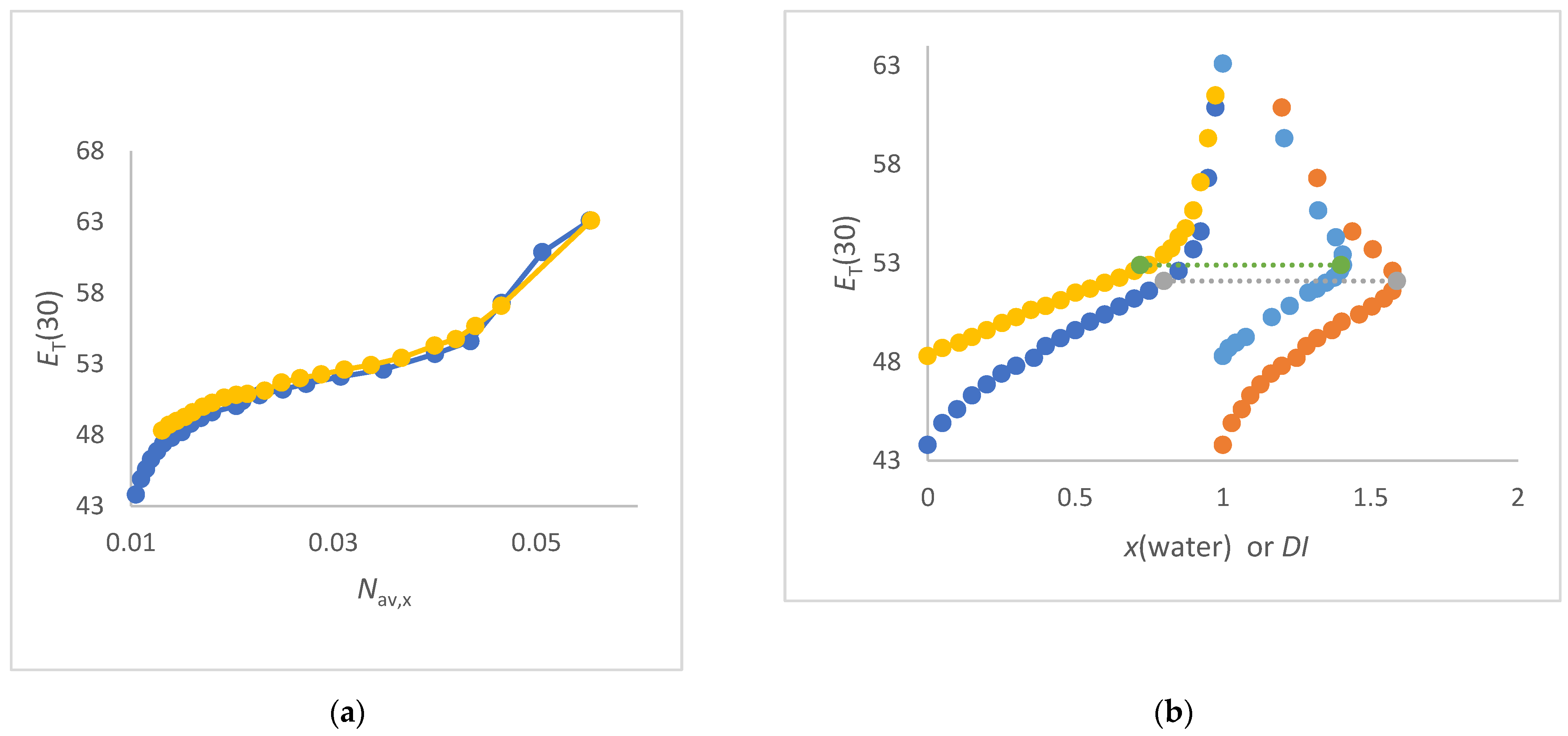
The E_T(30) increases significantly and linearly with N_av,x (1,2-ethanediol/water, FA/water, urea/water, NMF/ water and DMSO/water mixtures) (see Figure 3a and Figure 4a,b). These co-solvents belong to the group of solvents that do not enhance the water structure at all and form strong hydrogen bonds with water. In these cases, the E_T(30) of the pure co-solvent is fitted to the linear plot.

B.

The E_T(30) increases asymptotically with increasing N_av,x where the E_T(30) value is always higher than with a linear dependence (1,4-dioxane/water, DMF/water and NFM/water mixtures) (see Figure 4a and Figure 5a). In these cases, the co-solvent-rich fraction shows the non-linearity E_T(30) as function of N_av,x. These co-solvents do not enhance the water structure but form weaker hydrogen bonds with water than those belonging to scenario (A).

C.

The E_T(30) increases as N_av,x increases, with the E_T(30) value always being lower than expected for a linear dependence (see Figure 3a). This scenario applies to methanol/water and ethanol/water mixtures. These co-solvents enhance the water structure.

D.

E_T(30) shows an S-shaped curve as a function of N_av,x (see Figure 6a). With increasing N_av,x the E_T(30) value is always higher than expected with a linear dependence in the co-solvent-rich part. In the water-rich part, the E_T(30) is lower than with a linear dependence according to scenario (C). The mixtures 2-propanol/water, 2-methyl-2-propanol/water and 2-butoxyethanol/water belong to this group. This scenario applies to binary solvent mixtures that interact either on the structure of the water or on the structure of the co-solvent.

In particular, these binary co-solvent/water mixtures of scenario (A), which include glycerol/water mixtures, have been shown to be robust reference liquids for contact angle measurements, as no segregation occurs when in contact with different types of surfaces [198]. This is an important result in support of the Marcus theory for the classification of aqueous mixtures.

When rapid solvent dynamics occur in a particular solvent system, thermal motion overcomes local structuring effects. An almost perfect linear relationship of E_T(30) as a function of N_av,x is then observed. This scenario is shown to hold for FA/water, DMSO/water, 1,2-ethanediol/water, urea/water and NMF/water mixtures. This interpretation is strongly supported by the results of dielectric spectroscopy and ultrafast IR experiments.

The heat of mixing of the 1,2-ethanediol/water, DMSO/water and NMF/water mixtures is exothermic over the whole composition range, whereas the heat of interaction of the FA/water mixtures is always weakly endothermic. The best fits of E_T(30) as a function of N_av,x are for 1,2-ethanediol/water, NMF/water mixtures (exothermic over the whole composition range) and FA/water mixtures (weak endothermic over the whole composition range). For all co-solvent/water mixtures with respect to scenario (A), the qualitative heat of interaction does not change as a function of composition.

With regard to scenario (B), these co-solvents also belong to the Marcus classification, which do not enhance the water structure. There is a linear dependence of E_T(30) as a function of N_av,x up to N_av,x > 0.02 mol/cm³. However, the water fraction obviously has a greater effect on E_T(30) than the average number of dipoles over the whole composition range would suggest. A linear correlation of E_T(30) as a function of N_av,x is always found in the range of higher water contents. Thus, the average molar concentration of the dipoles (water and co-solvent) acting on the probe is the dominant factor in the higher water content range. Only from N_av,x > 0.0135 is there a bend in the curve, indicating that water as a co-component loses its influence on E_T(30). These co-solvents form weaker hydrogen bonds with water compared to scenario (A), indicating that the water structure changes non-linearly with composition [199,200,201]. These co-solvents can be classified differently depending on the criteria used by Marcus for evaluation.

For the 1,4-dioxane/water mixtures, the E_T(30) is always larger than expected from the sum of water and 1,4-dioxane dipoles. The curves for 1,4-dioxane/water and DMF/water mixtures are congruent up to N_av,x = 0.0135 mol/cm³. However, while the heat of mixing of DMF with water is exothermic over the whole composition range, the situation is different for 1,4-dioxane/water mixtures, as discussed above. Therefore, the thermodynamic changes in the DMF/water and dioxane/water mixtures are not always captured by the correlation of E_T(30) with N_av,x.

The correlation of E_T(30) with x(water) gives a better indication of the thermodynamic changes at different compositions of the 1,4-dioxane/water mixture.

This detailed result is very significant because it shows the linkage of x(water) with thermodynamics but not directly with the UV/Vis shift. In summary, scenario (B) requires more detailed studies using related binary solvent mixtures. Further studies will consider the complexity of THF/water, acetone/water and acetonitrile/water mixtures and other binary solvent mixtures such as pyridine/water or piperidine/water mixtures [2] with respect to solvatochromism. These evaluations are necessary to clarify or complement some of the conclusions regarding scenario (B) of this study. As shown by Marcus [200,201], each specific mixture actually requires special treatment in order to understand the many physical effects. Therefore, this review provides only a rough overview of the overall problem using selected examples.

In scenarios (C) and (D), the co-solvents belong to the Marcus classification, which enhance the water structure. But why is the E_T(30) value for methanol/water, ethanol/water, 2-propanol/water and 2-methyl-2-propanol/water mixtures lower at high water concentrations than would be expected from a linear dependence such as that observed for 1,2-ethanediol/water, as seen in Figure 3a? The answer is quite pragmatic: the hydrophobic dye B30 is difficult to dissolve in pure water [1]. It therefore dissolves much better in the alcohol/water domain, where the partial alcohol concentration is greater than the total alcohol concentration in the initial mixture. Accordingly, a lower E_T(30) is logically measured than would be expected from the total average molar concentration (N_av,x), since the average water concentration in the partial alcohol/water fraction must be lower outside the areas of enhanced water structure. The mole fraction x(water), as a measure of solvent composition in solvatochromism analysis, falsifies preferential solvation, since x is inversely proportional to N_av,x. The previously observed curved functions of E_T(30) as a function of x(water) determined so far are due to the inhomogeneity (DI) of the solvent mixture.

This result is a significant contribution to the identification of enhanced water structures in alcohol/water mixtures. The enhanced microdomain water structure ranges of alcohol/water mixtures are apparently not recognized by B30 for two reasons: firstly, B30 dissolves poorly in pure water; secondly, the molar absorption coefficient of B30 in water is rather low [1,70].

The first argument is supported by the fact that different solvatochromic dyes such as 4-nitroaniline, 4-nitrophenol, 4-nitroanisole or B30 show qualitatively different dependencies of the UV/Vis absorption energy as a function of alcohol/water composition, especially in the water-rich range x(water) > 0.8 [18,19]. This observation holds regardless of the methanol/water, ethanol/water, 2-propanol/water or 2-methyl-2-propanol/water mixtures is considered. Obviously, hydrophilic dyes are distributed in all these fractions and hydrophobic dyes are preferentially dissolved in the alcohol/water fraction. As B30 itself is a hydrophobic molecule, this scenario is likely.

This explanation is also consistent with the results of the BE/water mixtures. The BE/water domain captures the hydrophobic B30 particularly well, as there is an abrupt decrease in E_T(30) with increasing BE content occurs when agglomeration of n-butoxyethanol takes place.

However, it appears that B30 and B30-COONa measure the water-rich fraction in the same sense [19]. Note that the full width at half maximum of the UV/Vis absorption band of B30 measured in alcohol/water mixtures is quite broad. These very broad UV/Vis spectra with large half-widths are often measured in water/salt mixtures [202]. Unfortunately, the UV/Vis spectra are not given in [19]. Therefore, it is not possible to say whether there are superpositions of several UV/Vis bands originating from different solvation states. A definitive statement is therefore not yet possible.

The 2-propanol/water and 2-methyl-2-propanol/water mixtures belong to scenario (D). In the co-solvent rich range the B30 is preferentially influenced by the partial water concentration of the mixture due to the larger E_T(30) is measured as expected from the linearity. The situation is quite delicate because the thermodynamics of the mixture changes from exothermic to endothermic depending on the composition. Then, at Δ_rH_mixing = 0, the plot E_T(30) as function of N_av,x shows an inflection point, as is clearly seen for 2-propanol/water, 2-methyl-2-propanol/water and 1,4-dioxane/water mixtures. However, this is only a preliminary result that needs to be confirmed by further studies.

The conclusion from these considerations is that the thermodynamics of the interaction between the solvatochromic probe and the solvent mixture is crucial. Unfortunately, the dissolution thermodynamics of B30 in different solvents has not yet been systematically studied. There are only two papers with calorimetric results on the solvation thermodynamics of B30 [203,204]. The ambiguous results of the two references are not consistent with the theory of exothermic solvation of the probe leading to a lowering of the ground state energy [34,35]. The dissolution process of B30 in acetonitrile, ethyl acetate and higher alcohols is found to be endothermic, which is difficult to explain and may be due to entropic effects rather than re-association of B30 as discussed [204]. Thus, the thermodynamics of the B30/HBD solvent interaction is not trivially explainable in terms of specific hydrogen bond formation. This is consistent with the results of the present study that hydrogen bond formation has no significant effect on the E_T(30) value. As consequence, the influence of the thermodynamics of solvation of B30 in terms of the real ground state energy is difficult to assess because the calorimetric studies on several B30/solvent systems are difficult to interpret.

There are various approaches to correlating polarity data with calorimetric results, which are partly successful, but also give very strange results [180,205]. Therefore, this approach has often not been pursued further.

The complicated situation regarding solvation thermodynamics is similar for positive solvatochromic dyes such as 4-nitroaniline [206]. The dissolution process of 4-nitroaniline in co-solvent/water mixtures is endothermic in terms of the heat of mixing in the high-water content range [180,206]. Therefore, a reinterpretation of the solvatochromic results of 4-nitroaniline and related probes in co-solvent/water mixtures from the literature [18,19,181,182] is imperative. The effect of endothermic solvation and its impact on the UV/Vis absorption energy requires more detailed analysis in future work. The idea that solvation of an electronic state leads to an energetic decrease should be abandoned.

There is another aspect to consider. Dissolved B30 probes are statistically influenced by the dynamically moving solvent molecules. For this reason, the UV/visible spectrum only measures a snapshot of different solvation states. A superposition of many solvation states is recorded. Thus, the discrimination of domain formation in solvent mixtures by solvatochromic probes is only possible if the dynamics of the solvent is much lower than that of the optical excitation process of B30. This argument applies precisely to those mixtures where the co-solvent enhances the water structure. This can be explained by considering the relaxation time τ₁ measured by dielectric spectroscopy. The larger the τ₁ values, the more structural subtleties of the mixture are detected using the solvatochromic probe at ambient temperature, as shown for 2-propanol/water and 2-methyl-2-propanol/water mixtures [86,88,89]. Therefore, the results of dielectric spectroscopy in terms of relaxation time are a useful adjunct to explain the results of UV/Vis measurements.

The two groups of co-solvents, which either enhance or do not enhance the water structure, can probably be distinguished on the basis of the refractive index. When $n_D^{20}$ is correlated as function of N_av,x,CH as shown in Figure 2, different curves are obtained. If there is no linear correlation of $n_D^{20}$with N_av,x over the entire composition range, then microdomains of water have formed in the mixture in the form of enhanced water structures. This hypothesis should be tested in further studies. However, this proposed rule does not apply to the correlation of the dielectric constant as a function of N_av,x for DMSO/water mixtures, where a curved line is found instead of a straight line [207,208,209]. For this, ε_r correlates linearly with x(water), but not linearly with $n_D^{20}$ [208]. This particular behavior of DMSO/water mixtures is due to the recently recognized unusual microheterogeneity of these particular mixtures [209]. This important detail supports the thesis that the local mass inhomogeneity in terms of DI has an influence on the result of the physical measurement. Therefore, nothing is riskier than relying on routine evaluations of measurement results as a function of the composition of co-solvent/water mixtures.

Due to the complex structure of aqueous solvent mixtures, a growing body of knowledge is emerging based on conventional and modern measurement methods that take into account the density, refractive index, heat of interaction and other properties (dielectric relaxation) of the individual solvent mixture systems. The combination of UV/Vis spectroscopic data such as E_T(30) with physical properties of the solvent mixture (molar concentration of dipoles, dielectric dynamics, thermodynamics, domain size formation) has proved to be necessary but very complex.

New work on the structure of ethanol/water or 2-methyl-2-propanol/water mixtures continues to emerge, providing a refined picture of these unusual solvent systems [111,210,211]. However, the results of recent studies clearly confirm the presence of coexisting microdomains of water and alcohol/water. The considerations of this study also apply to organic solvent mixtures. As early as 1981, Langhals showed that the same relationships that apply to aqueous mixtures can also be used for binary organic solvent mixtures [212]. This motivates us to re-evaluate and classify binary organic solvent mixtures as well, in terms of the average molar concentration. This evaluation requires an extensive literature search for density data. However, the formation of hydrogen bonds on the probe can have a stronger effect in special systems [213], but the use of N_av,x instead of x is necessary for a correct evaluation of UV/Vis spectroscopic data [67,68]

Despite the correlations found between UV/Vis data and physical solvent properties of mixtures, it must be made clear that solvatochromism is of limited use for analyzing the chemical properties of solvent mixtures, unless one simply wants to measure the composition quickly using calibration curves [6]. To understand the complex dependence of the absorption energy of a solvatochromic probe on the solvent composition, the structure of the solvent mixture must be analyzed. However, solvatochromism cannot analyze structures, as Marcus correctly concluded for acetonitrile/water mixtures [214].

5. Conclusions

The Marcus classification of aqueous solvent mixtures has proved to be very useful and explains the qualitatively different correlations of E_T(30) with N_av,x for different co-solvent/water mixtures. This should easily solve many puzzles in the literature, as all previous evaluations of solvatochromic data using the molar fraction x(water or co-solvent) as the composition variable are physically incorrect. Various linear and curvilinear relationships of E_T(30) as a function of solvent composition in terms of N_av,x have been analyzed. With increasing both the OH dipole and co-solvent dipole concentration, E_T(30) increases linearly for those mixtures where the co-solvent does not enhance the water structure. This characteristic holds for FA/water, 1,2-ethandiol/water, NMF/water, urea/water and DMSO/water.

Co-solvents which enhance the water structure of aqueous mixtures (Marcus) show an S-shaped or curved curve of E_T(30) as function of N_av,x. Whether a curved or an S-shaped function is obtained depends on the thermodynamics of the mixing process and the solvent dynamics in terms of the relaxation time. Even if preferential solvation of a solute occurs, this may not always be observed with solvatochromic probes if the dynamics in the binary solvent mixture are too high. An average number of solvation states is then recorded. The complexity of the structure of alcohol/water mixtures is reflected in the correlation of the refractive index or E_T(30) as a function of various compositional quantities such as x(water), N_av,x, N_av,x,CH or N_av,v.

The N_av,x of the binary mixture is physically justified as a suitable measure of composition for the analysis of UV/Vis results of solvatochromic probes, because of its linear relationship with the UV/Vis absorption energy according to the Lorentz–Lorenz relation. The refined interpretations of E_T(30) as a function of solvent composition in this work were only possible on the basis of many new and modern insights into the physical structure of solvent mixtures and the true significance of optical measurements.

In general, the significance of the various measures of the average molar mass of solvent mixtures requires further research into their relationship with physical methods of investigation and their informative value. The use of the inhomogeneity of the solvent mixtures in terms of the M_av,w/M_av,x quantity should be considered for other solvent mixtures in order to support the conclusions of this study in future work.

Finally, it is incomprehensible why hardly anyone has used the average molar concentration N_av,z as a measure of the composition of solvent mixtures. The molar fraction x is needed for thermodynamics, but not for spectroscopy. However, both x and N_av,z are crucial in understanding the physics of mixing. Irrespective of the theoretically justified relationships of the Debye, Clausius–Mosotti or Lorentz–Lorenz equations, the use of the molar concentration is actually necessary for the evaluation of UV/vis spectroscopic data and the refractive index.