Development of Abraham Model Correlations for Solute Transfer into the tert-Butyl Acetate Mono-Solvent and Updated Equations for Both Ethyl Acetate and Butyl Acetate
Abstract
1. Introduction
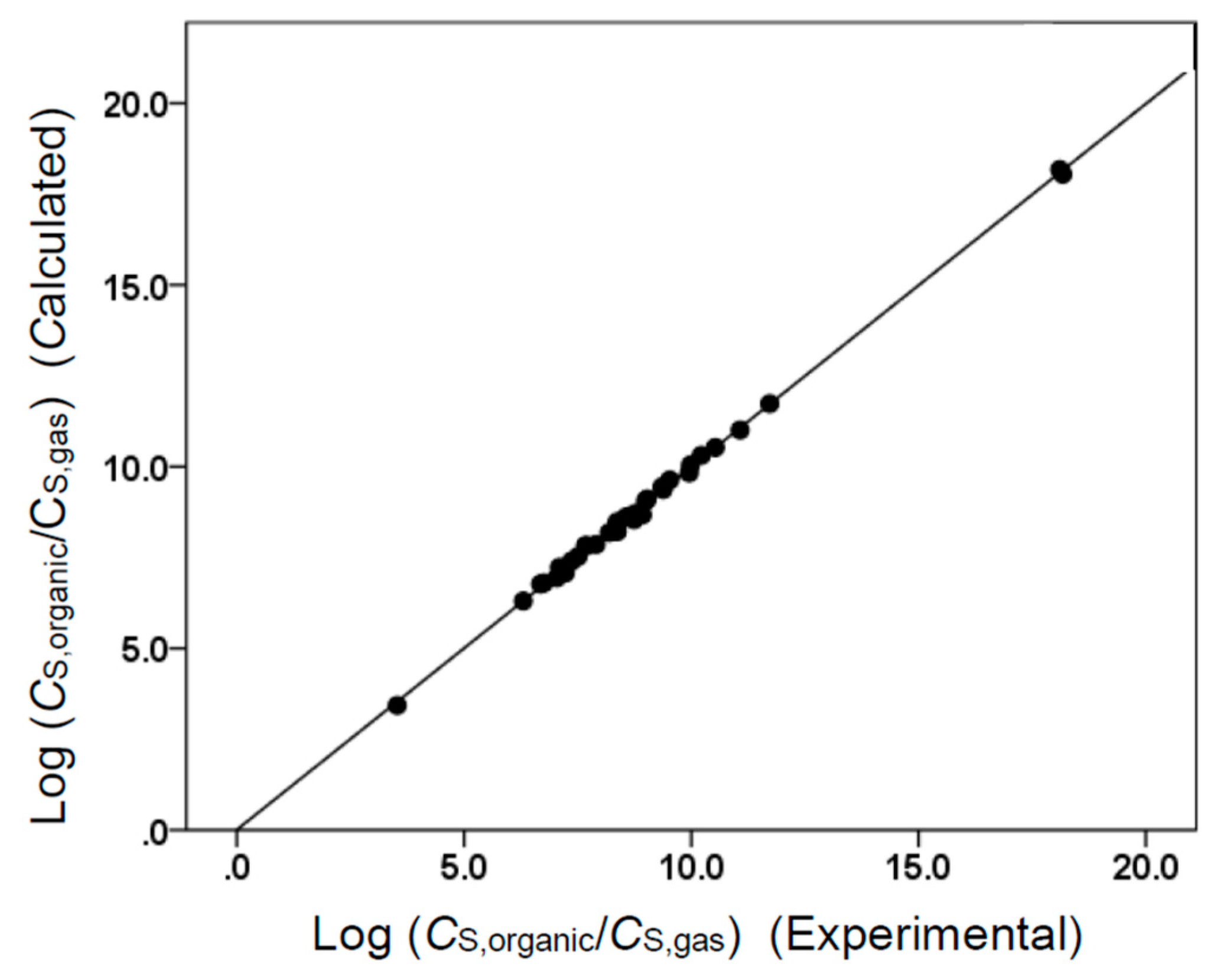
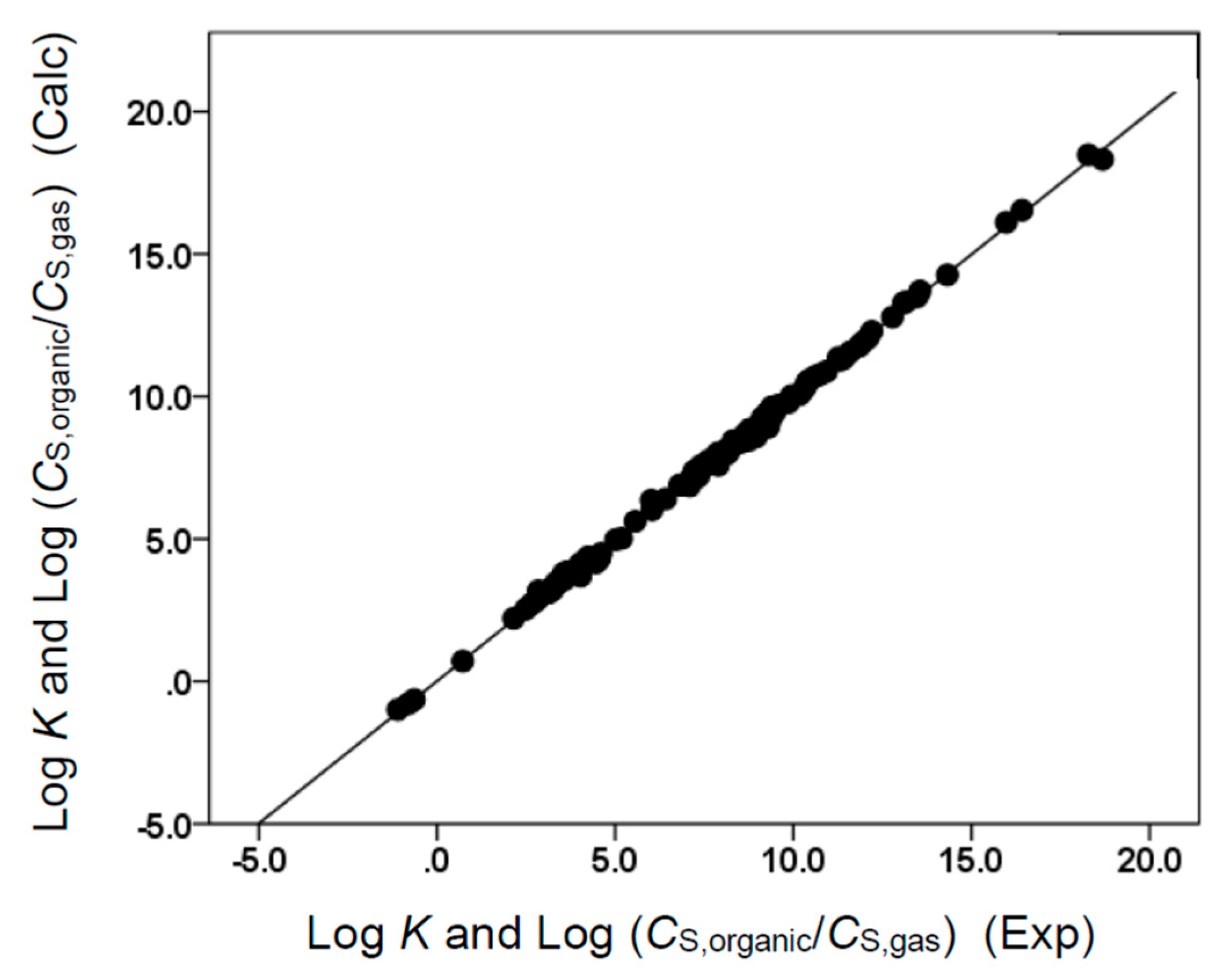
(N = 106, SD = 0.165, R2 = 0.996, F = 4475.1)
(N = 106, SD = 0.148, R2 = 0.998, F = 15,635.1)
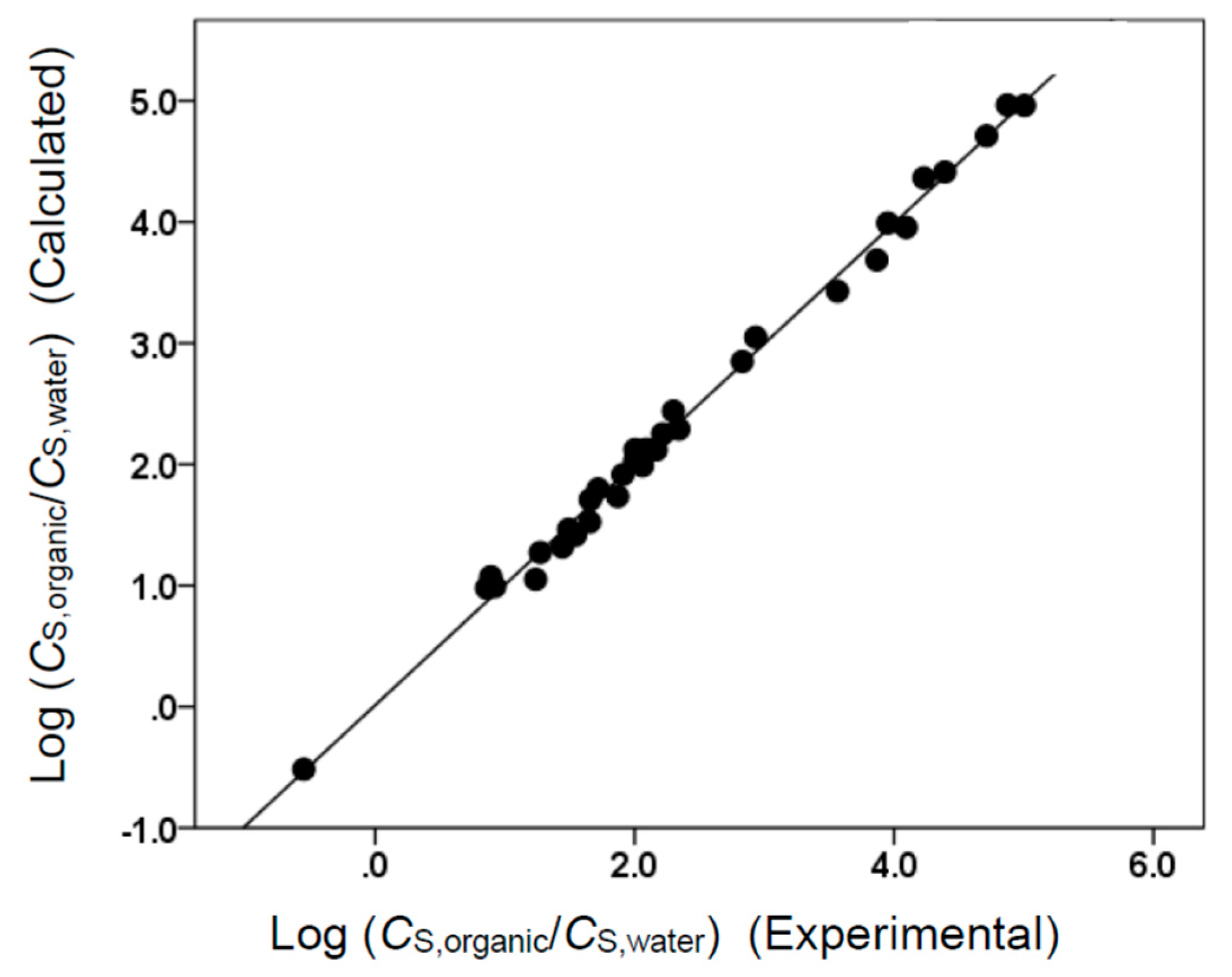
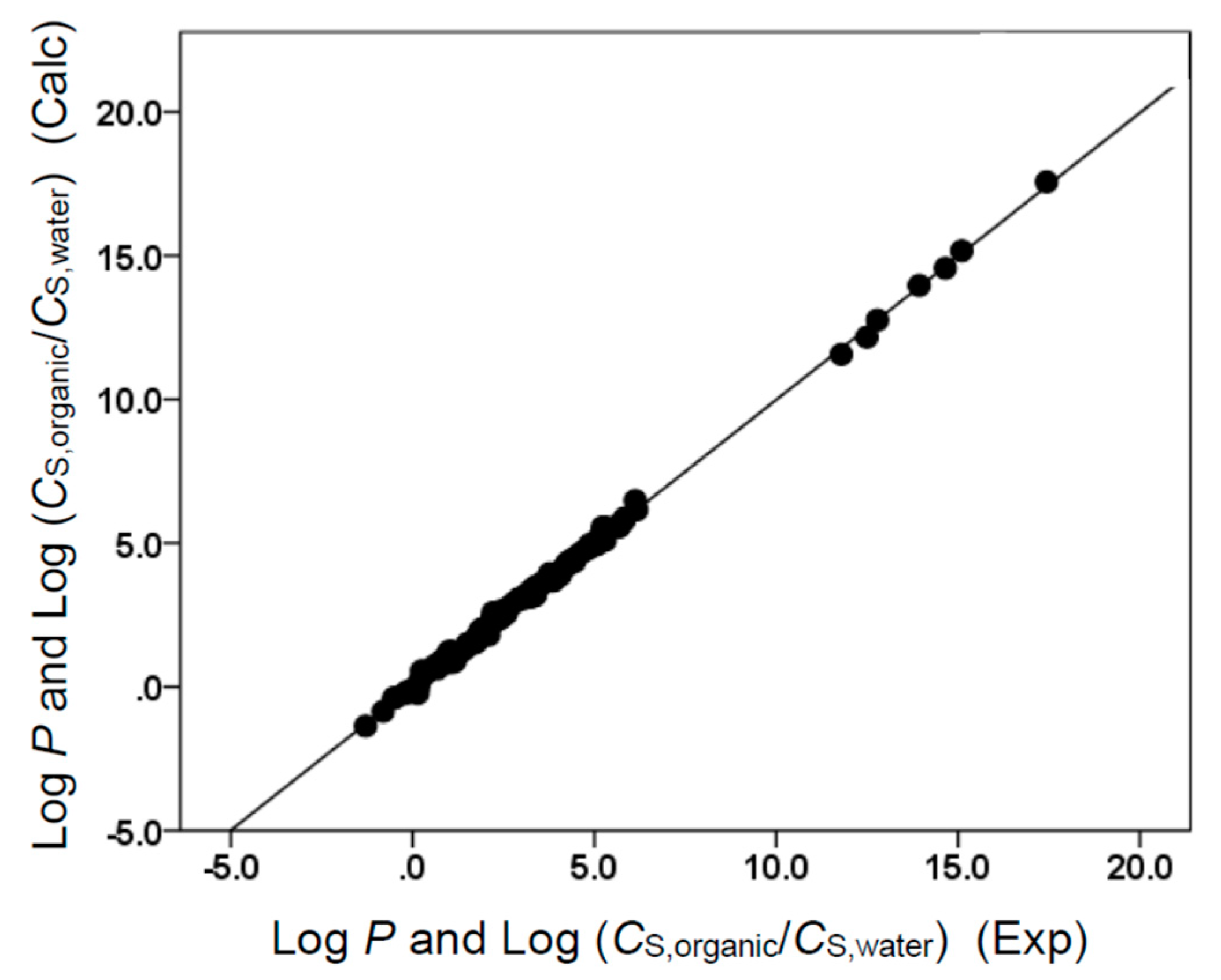
(N = 73, SD = 0.160, R2 = 0.998, F = 7380)
(N = 73, SD = 0.157, R2 = 0.998, F = 6174.7)
2. Experimental Methodology
3. Results and Discussion
(with N = 34, SD = 0.100, R2 = 0.994, F = 990.6)
(with N = 34, SD = 0.103, R2 = 0.999, F = 5319),
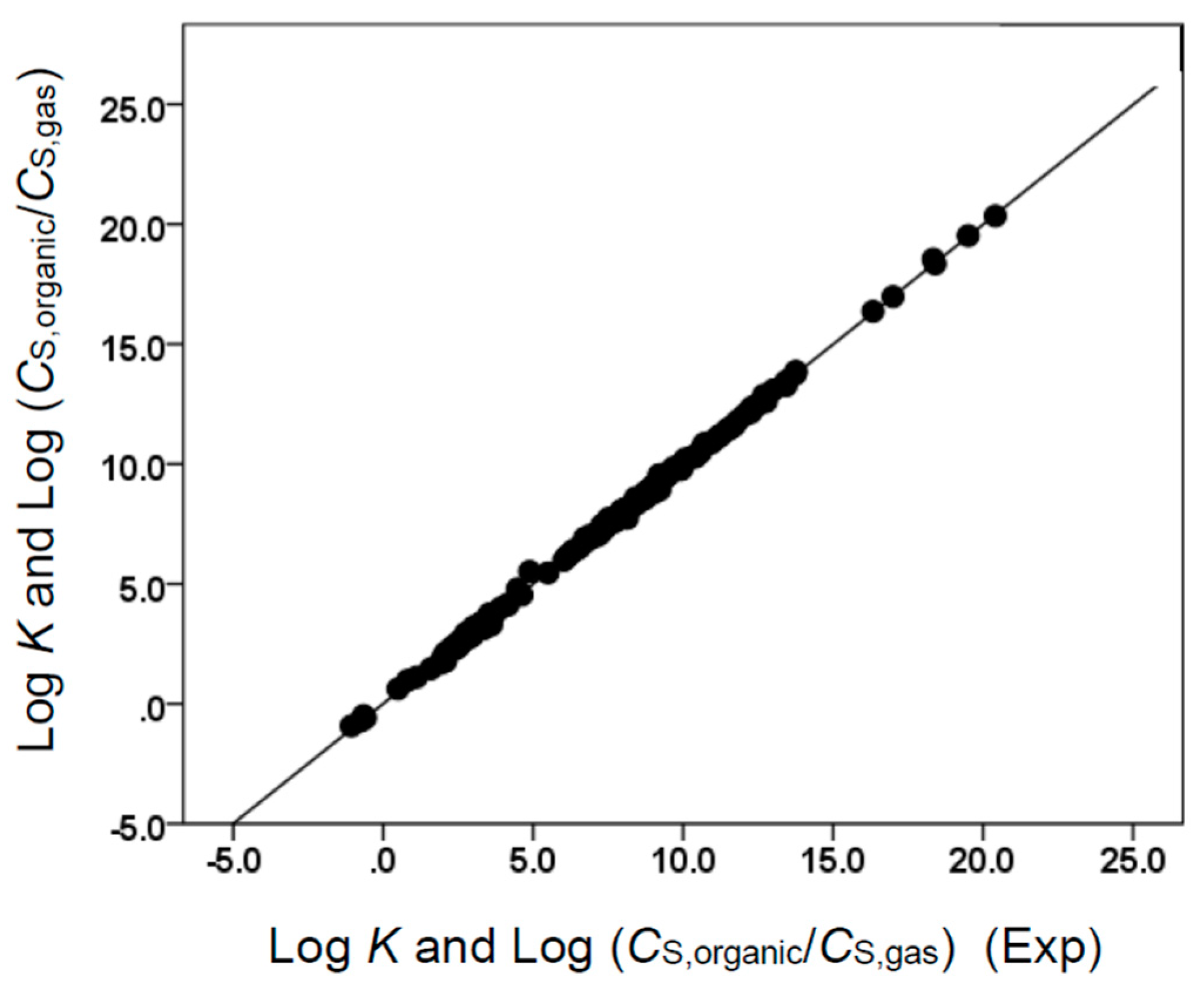
(with N = 170, SD = 0.144, R2 = 0.996, F = 7548)
(with N = 170, SD = 0.131, R2 = 0.999, F = 42942)
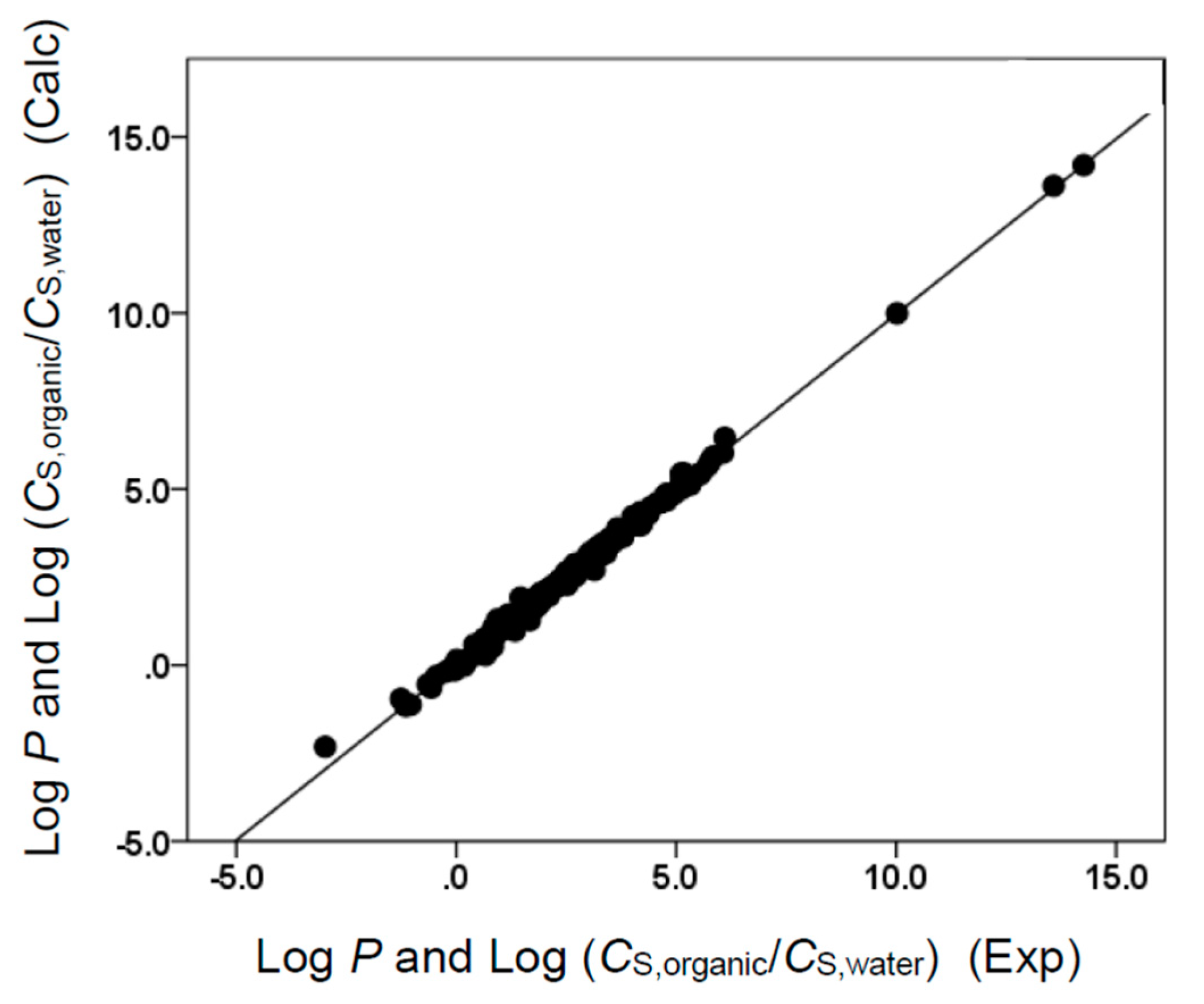
(with N = 108, SD = 0.140, R2 = 0.998, F = 11519)
(with N = 108, SD = 0.148, R2 = 0.999, F = 17169)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, A.; Varadharajan, A.; Shanmugam, N.; Kim, K.; Huang, E.; Cai, S.K.; Acree, W.E., Jr. Abraham model description of the solubilising properties of the isopropyl acetate organic mono-solvent. Phys. Chem. Liq. 2022, 60, 312–324. [Google Scholar] [CrossRef]
- Kim, K.; Shanmugam, N.; Xu, A.; Varadharajan, A.; Cai, S.K.; Huang, E.; Acree, W.E., Jr. Abraham model correlations for describing solute transfer into anisole based on measured activity coefficients and molar solubilities. Phys. Chem. Liq. 2022, 60, 452–462. [Google Scholar] [CrossRef]
- Cai, S.K.; Huang, E.; Kim, K.; Shanmugam, N.; Varadharajan, A.; Xu, A.; Acree, W.E., Jr. Development of Abraham model correlations for solute transfer into cyclopentanol from both water and the gas phase based on measured solubility ratios. Phys. Chem. Liq. 2022, 60, 287–296. [Google Scholar] [CrossRef]
- Strickland, S.; Ocon, L.; Zhang, A.; Wang, S.; Eddula, S.; Liu, G.; Tirumala, P.; Huang, J.; Dai, J.; Jiang, C.; et al. Abraham model correlations for describing dissolution of organic solutes and inorganic gases in dimethyl carbonate. Phys. Chem. Liq. 2021, 59, 181–195. [Google Scholar] [CrossRef]
- Ruddigkeit, L.; van Deursen, R.; Blum, L.C.; Reymond, J.-L. Enumeration of 166 billion organic small molecules in the Chemical Universe Database GDB-17. J. Chem. Inf. Model. 2012, 52, 2864–2875. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H. Scales of solute hydrogen-bonding: Their construction and application to physicochemical and biochemical processes. Chem. Soc. Rev. 1993, 22, 73–83. [Google Scholar] [CrossRef]
- Abraham, M.H.; Ibrahim, A.; Zissimos, A.M. Determination of sets of solute descriptors from chromatographic measurements. J. Chromatogr. A 2004, 1037, 29–47. [Google Scholar] [CrossRef]
- Abraham, M.H.; Smith, R.E.; Luchtefeld, R.; Boorem, A.J.; Luo, R.; Acree, W.E., Jr. Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 2010, 99, 1500–1515. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E., Jr. Descriptors for the prediction of partition coefficients of 8-hydroxyquinoline and its derivatives. Sep. Sci. Technol. 2014, 49, 2135–2141. [Google Scholar] [CrossRef]
- Sinha, S.; Yang, C.; Wu, E.; Acree, W.E., Jr. Abraham solvation parameter model: Examination of possible intramolecular hydrogen-bonding using calculated solute descriptors. Liquids. 2022, 2, 131–146. [Google Scholar] [CrossRef]
- Byrne, F.P.; Jin, S.; Paggiola, G.; Petchey, T.H.M.; Clark, J.H.; Farmer, T.J.; Hunt, A.J.; McElroy, C.R.; Sherwood, J. Tools and techniques for solvent selection: Green solvent selection guides. Sustain. Chem. Process. 2016, 4, 1–24. [Google Scholar] [CrossRef]
- Henderson, R.K.; Jimenez-Gonzalez, C.; Constable, D.J.C.; Alston, S.R.; Inglis, G.G.A.; Fisher, G.; Sherwood, J.; Binks, S.P.; Curzons, A.D. Expanding GSK’s solvent selection guide-embedding sustainability into solvent selection starting at medicinal chemistry. Green Chem. 2011, 13, 854–862. [Google Scholar] [CrossRef]
- Jimenez-Gonzalez, C.; Curzons, A.D.; Constable, D.J.C.; Cunningham, V.L. Expanding GSK’s solvent selection guide-application of life cycle assessment to enhance solvent selections. Clean Technol. Environ. Policy. 2005, 7, 42–50. [Google Scholar] [CrossRef]
- Welton, T. Solvents and sustainable chemistry. Proc. R. Soc. A. 2015, 471, 20150502. [Google Scholar] [CrossRef]
- Duereh, A.; Sato, Y.; Smith, R.L., Jr.; Inomata, H. Methodology for replacing dipolar aprotic solvents used in API processing with safe hydrogen-bond donor and acceptor solvent-pair mixtures. Org. Process Res. Dev. 2017, 21, 114–124. [Google Scholar] [CrossRef]
- Joshi, D.R.; Adhikari, N. An overview on common organic solvents and their toxicity. J. Pharm. Res. Int. 2019, 28, JPRI.49840. [Google Scholar] [CrossRef]
- Prat, D.; Hayler, J.; Wells, A. A survey of solvent selection guides. Green Chem. 2014, 16, 4546–4551. [Google Scholar] [CrossRef]
- Byrne, F.P.; Forier, B.; Bossaert, G.; Hoebers, C.; Farmer, T.J.; Hunt, A.J. A methodical selection process for the development of ketones and esters as bio-based replacements for traditional hydrocarbon solvents. Green Chem. 2018, 20, 4003–4011. [Google Scholar] [CrossRef]
- Sprunger, L.M.; Proctor, A.; Acree, W.E., Jr.; Abraham, M.H.; Benjelloun-Dakhama, N. Correlation and prediction of partition coefficient between the gas phase and water, and the solvents dry methyl acetate, dry and wet ethyl acetate, and dry and wet butyl acetate. Fluid Phase Equilib. 2008, 270, 30–44. [Google Scholar] [CrossRef]
- Xu, R.; Wang, J. Solubility measurement and thermodynamic model correlation and evaluation of 2-chloro-5-nitroaniline in 12 pure solvents. J. Chem. Eng. Data. 2019, 64, 1357–1365. [Google Scholar] [CrossRef]
- Ji, W.; Meng, Q.; Li, P.; Yang, B.; Wang, F.; Ding, L.; Wang, B. Measurement and correlation of the solubility of p-coumaric acid in nine pure and water + ethanol mixed solvents at temperatures from 293.15 to 333.15 K. J. Chem. Eng. Data. 2016, 61, 3457–3465. [Google Scholar] [CrossRef]
- Wu, H.; Dang, L.; Wei, H. Solid-liquid phase equilibrium of nicotinamide in different pure solvents: Measurements and thermodynamic modeling. Ind. Eng. Chem. Res. 2014, 53, 1707–1711. [Google Scholar] [CrossRef]
- Nti-Gyabaah, J.; Chiew, Y.C. Solubility of lovastatin in ethyl acetate, propyl acetate, isopropyl acetate, butyl acetate, sec-butyl acetate, isobutyl acetate, tert-butyl acetate, and 2-butanone, between (285 and 313) K. J. Chem. Eng. Data. 2008, 53, 2060–2065. [Google Scholar] [CrossRef]
- Holley, K.; Acree, W.E., Jr.; Abraham, M.H. Determination of Abraham model solute descriptors for 2-ethylanthraquinone based on measured solubility ratios. Phys. Chem. Liq. 2011, 49, 355–365. [Google Scholar] [CrossRef]
- Bao, Y.; Wu, J.; Zhao, X.; Zhao, H. 2-Methoxy-4-nitroaniline solubility in several monosolvents: Measurement, correlation, and solvent effect analysis. J. Chem. Eng. Data. 2020, 65, 757–765. [Google Scholar] [CrossRef]
- Ouyang, J.; Zhang, Y.; Na, B.; Liu, Z.; Zhou, L.; Hao, H. Solubility determination of nicotinamide and its application for the cocrystallization with benzoic acid. J. Chem. Eng. Data. 2018, 63, 4157–4165. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E., Jr. Descriptors for ferrocene and some substituted ferrocenes. J. Mol. Liq. 2017, 232, 325–331. [Google Scholar] [CrossRef]
- Wu, K.; Li, Y. Solubility Measurement and thermodynamic modeling for o-toluenesulfonamide in 16 solvents from T = 273.15 to 323.85 K. J. Chem. Eng. Data. 2019, 64, 5238–5247. [Google Scholar] [CrossRef]
- Zhang, Z.; Qu, Y.; Li, M.; Wang, S.; Wang, J. Solubility and thermodynamic modeling of dimethyl terephthalate in pure solvents and the evaluation of the mixing properties of the solutions. J. Chem. Eng. Data. 2019, 64, 4565–4579. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Qu, C.; Li, M.; Qu, Y. Solid-liquid equilibrium of chlorpropamide in 14 pure solvents at temperature of 283.15 to 323.15 K. J. Chem. Eng. Data. 2020, 65, 2859–2871. [Google Scholar] [CrossRef]
- Peng, H.; Liu, Y.; Yan, H.; Yu, C.; Feng, S.; Yin, H.; Chen, M. Solubility measurement and data correlation of salicylanilide in 12 pure solvents at temperatures ranging from 283.15 to 323.15 K. J. Chem. Eng. Data. 2021, 66, 1501–1507. [Google Scholar] [CrossRef]
- Hu, W.; Shang, Z.; Wei, N.; Hou, B.; Gong, J.; Wang, Y. Solubility of benorilate in twelve monosolvents: Determination, correlation and COSMO-RS analysis. J. Chem. Thermodyn. 2021, 152, 106272/1–106272/10. [Google Scholar] [CrossRef]
- Wu, K.; Li, Y. Solid-liquid phase equilibrium and solution thermodynamics of 2-chlorobenzenesulfonamide in 16 mono solvents at temperature ranging from 273.15 K to 324.65 K. J. Mol. Liq. 2020, 304, 112795/1–112795/11. [Google Scholar] [CrossRef]
- Li, Y.; Lu, C.; Chen, R.; Wu, K. Determination, correlation, and thermodynamic analysis of the solid-liquid phase equilibrium of 1,4-dicyanobenzene in pure solvents at various temperatures. J. Chem. Eng. Data. 2020, 65, 4991–5002. [Google Scholar] [CrossRef]
- Liu, J.-Q.; Zhang, Y.; Wang, W. Solubility measurement and correlation of 2-chlorothioxanthone (CTX) in twelve mono organic solvents. J. Mol. Liq. 2022, 360, 119503/1–119503/11. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, Q.; Bai, J.; Guo, C. Solubility determination, solute-solvent interactions, and model correlation of sorafenib in twelve pure organic solvents between T = 273.15 and 313.15 K. J. Chem. Eng. Data. 2021, 66, 4286–4292. [Google Scholar] [CrossRef]
- Gao, X.; Yu, S.; Wu, G.; Cheng, Y.; Xue, F. Solid-liquid phase equilibrium of 2-mercapto-1,3,4-thiadiazol in pure organic solvents. J. Chem. Eng. Data. 2021, 66, 4706–4713. [Google Scholar] [CrossRef]
- Li, T.; Zhu, L.; Li, J.; Cao, Z.; Sha, J.; Li, Y.; Ren, B. Solubility, thermodynamic properties and molecular simulation of tinidazole in fourteen mono-solvents at different temperatures. J. Chem. Thermodyn. 2022, 170, 106767/1–106767/14. [Google Scholar] [CrossRef]
- Wu, K.; Guan, Y.; Yang, Z.; Ji, H. Solid-liquid phase equilibrium of isophthalonitrile in 16 solvents from T = 273.15 to 324.75 K and mixing properties of solutions. J. Chem. Eng. Data. 2021, 66, 4442–4452. [Google Scholar] [CrossRef]
- Wilson, A.; Tian, A.; Chou, V.; Quay, A.N.; Acree, W.E., Jr.; Abraham, M.H. Experimental and predicted solubilities of 3,4-dichlorobenzoic acid in select organic solvents and in binary aqueous-ethanol mixtures. Phys. Chem. Liq. 2012, 50, 324–335. [Google Scholar] [CrossRef]
- Bowen, K.R.; Stephens, T.W.; Lu, H.; Satish, K.; Shan, D.; Acree, W.E., Jr.; Abraham, M.H. Experimental and predicted solubilities of 3,4-dimethoxybenzoic acid in select organic solvents of varying polarity and hydrogen-bonding character. Eur. Chem. Bull. 2013, 2, 577–583. [Google Scholar]
- Hart, E.; Klein, A.; Zha, O.; Wadawadigi, A.; Qian, E.; Dunn, S.; Herron, J.; Kankolongo, K.; Ryan, S.; Acree, W.E., Jr.; et al. Determination of Abraham model solute descriptors for monomeric 3,4,5-trimethoxybenzoic acid from experimental solubility data in organic solvents measured at 298.2 K. Phys. Chem. Liq. 2018, 56, 381–390. [Google Scholar] [CrossRef]
- Qian, E.; Lee, G.; Che, M.; Wang, L.; Yue, D.; Fischer, R.; Jodray, M.; Gupta, A.; Neal, R.; Liu, Y.; et al. Determination of Abraham model solute descriptors for xanthone based on experimental solubility measurements at 298.2 K. Phys. Chem. Liq. 2020, 58, 214–221. [Google Scholar] [CrossRef]
- Liu, J.-Q.; Chen, H.; An, S.-F.; Li, T.-T. Solubility measurement and correlation of 2-phenyl-1H-indole in fourteen mono organic solvents from 289.05 K to 338.55 K. J. Mol. Liq. 2020, 302, 112491/1–112491/11. [Google Scholar] [CrossRef]
- Xu, R.; Wang, J.; Du, C.; Han, S.; Meng, L.; Zhao, H. Solubility determination and thermodynamic dissolution functions of 1,3-diphenylguanidine in nine organic solvents at evaluated temperatures. J. Chem. Thermodyn. 2016, 99, 86–95. [Google Scholar] [CrossRef]
- Xu, K.; Zhu, J.; Li, T. Measurement and correlation of the dissolution equilibria of o-iodoaniline and p-iodoaniline in pure solvents. J. Chem. Eng. Data. 2018, 63, 217–224. [Google Scholar] [CrossRef]
- Song, T.; Xiao, Y.; Shi, K.; Bai, Y.; Li, J.; Qi, L.; Xie, C. Solubility measurement and data correlation of pyrimethamine in 13 pure solvents at temperatures from 278.15 to 318.15 K. J. Chem. Eng. Data. 2022, 67, 28–36. [Google Scholar] [CrossRef]
- Li, J.; Yao, M.; Kang, X.; Yu, C.; Liu, Y.; Yan, H.; Yin, H.; Chen, M. Equilibrium solubility determination and dissolution property analysis of 5,6-dimethoxy-1-indanone in 15 pure solvents from 283.15 to 323.15 K. J. Chem. Eng. Data. 2021, 66, 1813–1820. [Google Scholar] [CrossRef]
- Sinha, S.; Varadharajan, A.; Xu, A.; Wu, E.; Acree, W.E., Jr. Determination of Abraham model solute descriptors for hippuric acid from measured molar solubilities in several organic mono-solvents of varying polarity and hydrogen-bonding ability. Phys. Chem. Liq. 2022, 60, 563–571. [Google Scholar] [CrossRef]
- Xu, S.; Cao, T.; Ma, M.; Wang, Y. Uncover the effect of solvent and temperature on solid-liquid equilibrium behavior of 2-bromodibenzofuran. J. Chem. Thermodyn. 2022, 171, 106813. [Google Scholar] [CrossRef]
- Xu, R.; Xu, A.; Du, C.; Cong, Y.; Wang, J. Solubility determination and thermodynamic modeling of 2,4-dinitroaniline in nine organic solvents from T = (278.15 to 318.15) K and mixing properties of solutions. J. Chem. Thermodyn. 2016, 102, 178–187. [Google Scholar]
- Wang, J.; Xu, A.; Xu, R. Determination and correlation of terephthaldialdehyde solubility in (ethanol, isopropanol, ethyl acetate, isopentanol) + N,N-dimethylformamide mixed solvents at temperatures from 273.15 K to 318.15 K. J. Chem. Thermodyn. 2017, 105, 327–336. [Google Scholar] [CrossRef]
- Hart, E.; Lee, G.; Qian, E.; Jodray, M.; Barrera, M.; Fischer, R.; Che, M.; Liu, Y.; Zha, O.; Woods, D.; et al. Determination of Abraham model solute descriptors for 4-tert-butylbenzoic acid from experimental solubility data in organic mono-solvents. Phys. Chem. Liq. 2019, 57, 445–452. [Google Scholar] [CrossRef]
- Hart, E.; Ramirez, A.M.; Cheeran, S.; Barrera, M.; Horton, M.Y.; Wadawadigi, A.; Acree, W.E., Jr.; Abraham, M.H. Determination of Abraham model solute descriptors for 2-methyl-3-nitrobenzoic acid from measured solubility data in alcohol, alkyl ether, alkyl acetate and 2-alkoxyalcohol mono-solvents. Phys. Chem. Liq. 2017, 55, 796–804. [Google Scholar] [CrossRef]
- Acree, W.E., Jr.; Bowen, K.R.; Horton, M.Y.; Abraham, M.H. Computation of Abraham model solute descriptors for 3-methyl-4-nitrobenzoic acid from measured solubility data. Phys. Chem. Liq. 2017, 55, 482–491. [Google Scholar] [CrossRef]
- Wang, S.; Liu, K.; Zhang, A.; Dai, J.; Gupta, A.; Zhu, S.; Eddula, S.; Jiang, C.; Acree, W.E., Jr.; Abraham, M.H. Solubility of 4-methyl-3-nitrobenzoic acid in organic mono-solvents: Calculation of Abraham model solute descriptors. Phys. Chem. Liq. 2020, 58, 782–791. [Google Scholar] [CrossRef]
- Stephens, T.W.; Loera, M.; Calderas, M.; Diaz, R.; Montney, N.; Acree, W.E., Jr.; Abraham, M.H. Determination of Abraham model solute descriptors for benzoin based on measured solubility ratios. Phys. Chem. Liq. 2012, 50, 254–265. [Google Scholar] [CrossRef]
- Fletcher, K.A.; Coym, K.S.; Roy, L.E.; Hernandez, C.E.; McHale, M.E.R.; Acree, W.E., Jr. Solubility of thioxanthen-9-one in organic nonelectrolyte solvents. Comparison of observed versus predicted values based upon mobile order theory (MOT). Phys. Chem. Liq. 1998, 35, 243–252. [Google Scholar] [CrossRef]
- Ye, S.; Saifullah, M.; Grubbs, L.M.; McMillan-Wiggins, M.C.; Acosta, P.; Mejorado, D.; Flores, I.; Acree, W.E., Jr.; Abraham, M.H. Determination of the Abraham model solute descriptors for 3,5-dinitro-2-methylbenzoic acid from measured solubility data in organic solvents. Phys. Chem. Liq. 2011, 49, 821–829. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, M.; Zhu, P.; Ouyanga, J.; Gong, J.; Chen, W.; Xu, F. Solubility and solution thermodynamics of sorbic acid in eight pure organic solvents. J. Chem. Thermodyn. 2015, 85, 202–209. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, B.; Yang, Z.; Yao, G.; Zhao, H. Solubility of dichloronitrobenzene in eight organic solvents from T = (278.15 to 303.15) K: Measurement and thermodynamic modeling. J Chem. Eng, Data. 2014, 59, 1281–1287. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, H.; Yang, Z.; Li, R. Solubility of 3,4-dichloronitrobenzene in methanol, ethanol, and liquid mixtures (methanol + water, ethanol + water): Experimental measurement and thermodynamic modeling. J. Chem. Eng. Data. 2013, 58, 3061–3068. [Google Scholar] [CrossRef]
- Lee, G.; Che, M.; Qian, E.; Wang, L.; Gupta, A.; Neal, R.; Yue, D.; Downs, S.; Mayes, T.; Rose, O.; et al. Determination of Abraham model solute descriptors for o-acetoacetanisidide based on experimental solubility data in organic mono-solvents. Phys. Chem. Liq. 2019, 57, 528–535. [Google Scholar] [CrossRef]
- Sun, R.; He, H.; Wan, Y.; Li, L.; Sha, J.; Jiang, G.; Li, Y.; Li, T.; Ren, B. Kojic acid in fourteen mono-solvents: Solubility data, Hansen solubility parameter and thermodynamic properties. J. Chem. Thermodyn. 2021, 152, 106280/1–116280/13. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, H.; Xu, S.; Zhang, H.; Zhu, M.; Shi, P.; Fu, X.; Yang, Y.; Gong, J. Thermodynamic study of solubility for pyrazinamide in ten solvents from T = (283.15 to 323.15) K. J. Chem. Thermodyn. 2017, 112, 204–212. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, K.; Wan, X.; Gao, Z.; Gong, J.; Rohani, S. Effects of temperature and solvent properties on the liquid-solid phase equilibrium of γ-pyrazinamide. J. Chem. Eng. Data. 2020, 65, 3667–3678. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, Z.; Jiao, W.; Cheng, X.; Yang, J.; Hu, Y.; Mi, L. Determination and analysis of solubility of 2-bromo-9-fluorenone in 10 different organic solvents and three binary solvent mixtures at different temperatures (T = 278.15-323.15 K). J. Chem. Eng. Data 2022, in press. [Google Scholar] [CrossRef]
- Li, W.; Ma, Y.; Yang, Y.; Xu, S.; Shi, P.; Wu, S. Solubility measurement, correlation and mixing thermodynamics properties of dapsone in twelve mono solvents. J. Mol. Liq. 2019, 280, 175–181. [Google Scholar] [CrossRef]
- Long, B.; Yang, Z. Measurements of the solubilities of m-phthalic acid in acetone, ethanol and acetic ether. Fluid Phase Equilib. 2008, 266, 38–41. [Google Scholar] [CrossRef]
- Noubigh, A.; Abderrabba, M. Solid-liquid phase equilibrium and thermodynamic properties of vanillic acid in different pure solvents. J Mol Liq. 2016, 223, 261–266. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Siddiqui, N.A. Solubility and thermodynamic function of vanillin in ten different environmentally benign solvents. Food Chem. 2015, 180, 244–248. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, J.; Zhou, Y.; Guo, N.; Liu, Q.; Zong, S.; Bao, Y.; Hao, H. Solid-liquid phase equilibrium and dissolution properties of ethyl vanillin in pure solvents. J. Chem. Thermodyn. 2017, 105, 345–351. [Google Scholar] [CrossRef]
- Guo, Y.; Hao, Y.; Zhou, Y.; Han, Z.; Xie, C.; Su, W.; Hao, H. Solubility and thermodynamic properties of vanillyl alcohol in some pure solvents. J. Chem. Thermodyn. 2017, 106, 276–284. [Google Scholar] [CrossRef]
- Wu, K.; Li, Y. Solubility and solution thermodynamics of p-toluenesulfonamide in 16 solvents from T = 273.15 to 324.75 K. J. Mol. Liq. 2019, 293, 111577. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Guo, N.; Wang, N.; Hao, Y.; Luan, Y.; Chen, K.; Huang, X. Solubility and thermodynamic properties of maltol in different pure solvents. J. Mol. Liq. 2017, 243, 313–323. [Google Scholar] [CrossRef]
- Shi, J.; Liu, L.; Wang, L.; Ding, Z.; Wu, S. Solubility measurement and correlation of probenecid in 12 pure organic solvents and thermodynamic properties of mixing of solutions. J. Chem. Eng. Data. 2019, 64, 624–631. [Google Scholar] [CrossRef]
- Wu, K.; Han, R.; Xu, L.; Li, X.; Li, Y. Thermodynamic modelling for solubility of methyl 2-sulfamoylbenzoate in sixteen organic solvents from T (272.15-324.15 K) and dissolution properties. J. Mol. Liq. 2021, 337, 116618. [Google Scholar] [CrossRef]
- Li, Y.; Wu, K.; Liang, L. Solubility determination, modeling, and thermodynamic dissolution properties of benzenesulfonamide in 16 neat solvents from 273.15 to 324.45 K. J. Chem. Eng. Data. 2019, 64, 3606–3616. [Google Scholar] [CrossRef]
- Xu, J.; Han, S.; Cong, Y.; Du, C.; Cheng, C.; Wang, J.; Zhao, H. Thermodynamic functions of 1-methyl-4-(methylsulfonyl)benzene solubility in nine organic solvents from T = (278.15 to 318.15) K. J. Chem. Thermodyn. 2016, 103, 234–243. [Google Scholar] [CrossRef]
- Vilas-Boas, S.M.; Vieira, V.; Brandao, P.; Alves, R.S.; Coutinho, J.A.P.; Pinho, S.P.; Ferreira, O. Solvent and temperature effects on the solubility of syringic, vanillic or veratric acids: Experimental, modeling and solid phase studies. J. Mol. Liq. 2019, 289, 111089. [Google Scholar] [CrossRef]
- Buchowski, H.; Jodzewicz, W.; Milek, R.; Ufnalski, W.; Maczynski, A. Solubility and hydrogen bonding. I. Solubility of 4-nitro-5-methylphenol in one-component solvents. Roczniki Chemii. 1975, 49, 1879–1887. [Google Scholar] [CrossRef]
- Tong, Y.; Wang, Z.; Yang, E.; Pan, B.; Jiang, J.; Dang, L.; Wei, H. Determination and correlation of solubility and solution thermodynamics of ethenzamide in different pure solvents. Fluid Phase Equilib. 2016, 427, 549–556. [Google Scholar] [CrossRef]
- Wang, K.; Shang, Z.; Zhang, J.; Liu, Y.; Han, J.; Tang, W. Solubility determination and thermodynamic correlation of 2-ethoxybenzamide in 12 pure solvents from 288.15 to 328.15 K. J. Chem. Eng. Data. 2021, 66, 1508–1514. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, Y.; Cheng, X.; Yang, J.; Zhou, B.; Mi, L.; Hu, Y. Investigation on Hansen solubility parameter, solvent effect and thermodynamic properties of 3-methylflavone-8-carboxylic acid dissolved in different solvents. J. Mol. Liq. 2022, 356, 119017. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E., Jr. Gas-solvent and water-solvent partition of trans-stilbene at 298 K. J. Mol. Liq. 2017, 238, 58–61. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Dai, J.; Niu, Y.; Yin, Q.; Zhou, L. Solubility determination, model evaluation and solution thermodynamics of isovanillin in 15 pure solvents and 4 binary solvents. J. Mol. Liq. 2021, 340, 116847. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, C.; Zhao, C.; Qi, L.; Bao, Y.; Zhou, L.; Yin, Q. Analysis of solid-liquid equilibrium behavior of highly water-soluble beet herbicide metamitron in thirteen pure solvents using experiments and molecular simulations. J. Mol. Liq. 2022; in press. [Google Scholar] [CrossRef]
- Nti-Gyabaah, J.; Chan, V.; Chiew, Y.C. Solubility and limiting activity coefficient of simvastatin in different organic solvents. Fluid Phase Equilib. 2009, 280, 35–41. [Google Scholar] [CrossRef]
- Fritz, J.S.; Lisicki, N.M. Titration of acids in nonaqueous solvents. Anal Chem. 1951, 23, 589–591. [Google Scholar] [CrossRef]
- Knofczynski, G.T.; Daniel Mundfrom, D. Sample sizes when using multiple linear regression for prediction. Educ. Psychol. Meas. 2008, 68, 431–442. [Google Scholar] [CrossRef]
- Austin, P.C.; Steyerberg, E.W. The number of subjects per variable required in linear regression analyses. J. Clin. Epidemiol. 2015, 68, 627–636. [Google Scholar] [CrossRef] [PubMed]
- Charlton, A.K.; Daniels, C.R.; Acree, W.E., Jr.; Abraham, M.H. solubility of crystalline nonelectrolyte solutes in organic solvents: Mathematical correlation of acetylsalicylic acid solubilities with the Abraham general solvation model. J. Solution Chem. 2003, 32, 1087–1102. [Google Scholar] [CrossRef]
- Abraham, M.H.; Zissimos, A.M.; Acree, W.E., Jr. Partition of solutes into wet and dry ethers; an LFER analysis. New J. Chem. 2003, 27, 1041–1044. [Google Scholar] [CrossRef]
- Blake-Taylor, B.H.; Deleon, V.H.; Acree, W.E., Jr.; Abraham, M.H. Mathematical correlation of salicylamide solubilities in organic solvents with the Abraham solvation parameter model. Phys. Chem. Liq. 2007, 45, 389–398. [Google Scholar] [CrossRef]
- Flanagan, K.B.; Hoover, K.R.; Garza, O.; Hizon, A.; Soto, T.; Villegas, N.; Acree, W.E., Jr.; Abraham, M.H. Mathematical correlation of 1-chloroanthraquinone solubilities in organic solvents with the Abraham solvation parameter model. Phys. Chem. Liq. 2006, 44, 377–386. [Google Scholar] [CrossRef]
- Stovall, D.M.; Givens, C.; Keown, S.; Hoover, K.R.; Barnes, R.; Harris, C.; Lozano, J.; Nguyen, M.; Rodriguez, E.; Acree, W.E., Jr.; et al. Solubility of crystalline nonelectrolyte solutes in organic solvents: Mathematical correlation of 4-chloro-3-nitrobenzoic acid and 2-chloro-5-nitrobenzoic acid solubilities with the Abraham solvation parameter model. Phys. Chem. Liq. 2005, 43, 351–360. [Google Scholar] [CrossRef]
- Stovall, D.M.; Acree, W.E., Jr.; Abraham, M.H. Solubility of 9-fluorenone, thianthrene and xanthene in organic solvents. Fluid Phase Equilib. 2005, 232, 113–121. [Google Scholar] [CrossRef]
- Hoover, K.R.; Pop, K.; Acree, W.E., Jr.; Abraham, M.H. Solubility of crystalline nonelectrolyte solutes in organic solvents: Mathematical correlation of 3-chlorobenzoic acid solubilities with the Abraham solvation parameter model. S. Afr. J. Chem. 2005, 58, 25–29. [Google Scholar]
- Hoover, K.R.; Stovall, D.M.; Pustejovsky, E.; Coaxum, R.; Pop, K.; Acree, W.E., Jr.; Abraham, M.H. Solubility of crystalline nonelectrolyte solutes in organic solvents—Mathematical correlation of 2-methoxybenzoic acid and 4-methoxybenzoic acid solubilities with the Abraham solvation parameter model. Can. J. Chem. 2004, 82, 1353–1360. [Google Scholar] [CrossRef]
- Charlton, A.K.; Daniels, C.R.; Wold, R.M.; Pustejovsky, E.; Acree, W.E., Jr.; Abraham, M.H. Solubility of crystalline nonelectrolyte solutes in organic solvents: Mathematical correlation of 3-nitrobenzoic acid solubilities with the Abraham general solvation model. J. Mol. Liq. 2004, 116, 19–28. [Google Scholar] [CrossRef]
- Hoover, K.R.; Coaxum, R.; Pustejovsky, E.; Acree, W.E., Jr.; Abraham, M.H. Thermochemical behavior of dissolved carboxylic acid solutes: Part 5-mathematical correlation of 3,5-dinitrobenzoic acid solubilities with the Abraham solvation parameter model. Phys. Chem. Liq. 2004, 42, 457–466. [Google Scholar] [CrossRef]
- Hoover, K.R.; Coaxum, R.; Pustejovsky, E.; Stovall, D.M.; Acree, W.E., Jr.; Abraham, M.H. Thermochemical behavior of dissolved carboxylic acid solutes: Part 4—Mathematical correlation of 4-nitrobenzoic acid solubilities with the Abraham solvation parameter model. Phys. Chem. Liq. 2004, 42, 339–347. [Google Scholar] [CrossRef]
- Coaxum, R.; Hoover, K.R.; Pustejovsky, E.; Stovall, D.M.; Acree, W.E., Jr.; Abraham, M.H. Thermochemical behavior of dissolved carboxylic acid solutes: Part 3—MATHEMATICAL correlation of 2-methylbenzoic acid solubilities with the Abraham solvation parameter model. Phys. Chem. Liq. 2004, 42, 313–322. [Google Scholar] [CrossRef]
- Daniels, C.R.; Charlton, A.K.; Wold, R.M.; Acree, W.E., Jr.; Abraham, M.H. Thermochemical behavior of dissolved carboxylic acid solutes: Solubilities of 3-methylbenzoic acid and 4-chlorobenzoic acid in organic solvents. Can. J. Chem. 2003, 81, 1492–1501. [Google Scholar] [CrossRef]
- Acree, W.E., Jr.; Abraham, M.H. Solubility of crystalline nonelectrolyte solutes in organic solvents: Mathematical correlation of benzil solubilities with the Abraham general solvation model. J. Solution Chem. 2002, 31, 293–303. [Google Scholar] [CrossRef]
- Acree, W.E., Jr.; Abraham, M.H. Solubility predictions for crystalline nonelectrolyte solutes dissolved in organic solvents based upon the Abraham general solvation model. Can. J. Chem. 2001, 79, 1466–1476. [Google Scholar] [CrossRef]
- Acree, W.E., Jr.; Abraham, M.H. Solubility predictions for crystalline polycyclic aromatic hydrocarbons (PAHs) dissolved in organic solvents based upon the Abraham general solvation model. Fluid Phase Equilib. 2002, 201, 245–258. [Google Scholar] [CrossRef]
- Chung, Y.; Vermeire, F.H.; Wu, H.; Walker, P.J.; Abraham, M.H.; Green, W.H. Group contribution and machine learning approaches to predict Abraham solute parameters, solvation free energy, and solvation enthalpy. J. Chem. Inf. Model. 2022, 62, 433–446. [Google Scholar] [CrossRef]
- Brown, T.N. Empirical regressions between system parameters and solute descriptors of polyparameter linear free energy relationships (PPLFERs) for predicting solvent-air partitioning. Fluid Phase Equilib. 2021, 540, 113035. [Google Scholar] [CrossRef]
- Hille, C.; Ringe, S.; Deimel, M.; Kunkel, C.; Acree, W.E.; Reuter, K.; Oberhofer, H. Generalized molecular solvation in non-aqueous solutions by a single parameter implicit solvation scheme. J. Chem. Phys. 2019, 150, 041710. [Google Scholar] [CrossRef]
- Kashefolgheta, S.; Oliveira, M.P.; Rieder, S.R.; Horta, B.A.C.; Acree, W.E., Jr.; Hunenberger, P.H. Evaluating classical force fields against experimental cross-solvation free energies. J. Chem. Theory Comput. 2020, 16, 7556–7580. [Google Scholar] [CrossRef]
- Kashefolgheta, S.; Wang, S.; Acree, W.E.; Hunenberger, P.H. Evaluation of nine condensed-phase force fields of the GROMOS, CHARMM, OPLS, AMBER, and OpenFF families against experimental cross-solvation free energies. Phys. Chem. Chem. Phys. 2021, 23, 13055–13074. [Google Scholar] [CrossRef]
- Lee, S.; Cho, K.-H.; Acree, W.E., Jr.; No, K.T. Development of surface-SFED models for polar solvents. J. Chem. Inf. Model. 2012, 52, 440–448. [Google Scholar] [CrossRef]
- Ma, S.; Hwang, S.; Lee, S.; Acree, W.E.; No, K.T. Incorporation of hydrogen bond angle dependency into the generalized solvation free energy density model. J. Chem. Inf. Model. 2018, 58, 761–772. [Google Scholar] [CrossRef]
- Avdeef, A.; Kansy, M. Predicting solubility of newly-approved drugs (2016–2020) with a simple ABSOLV and GSE(flexible-acceptor) consensus model outperforming Random Forest regression. J. Solut. Chem. 2022, 51, 1020–1055. [Google Scholar] [CrossRef]
- Ulrich, N.; Endo, S.; Brown, T.N.; Watanabe, N.; Bronner, G.; Abraham, M.H.; Goss, K.-U. UFZ-LSER Database v 3.2.1 [Internet], Leipzig, Germany, Helmholtz Centre for Environmental Research-UFZ. 2017. Available online: http://www.ufz.de/lserd (accessed on 1 September 2022).
- Platts, J.A.; Butina, D.; Abraham, M.H.; Hersey, A. Estimation of molecular linear free energy relation descriptors using a group contribution approach. J. Chem. Inf. Comput. Sci. 1999, 39, 835–845. [Google Scholar] [CrossRef]
- Platts, J.A.; Abraham, M.H.; Butina, D.; Hersey, A. Estimation of molecular linear free energy relationship descriptors by a group contribution approach. 2. Prediction of partition coefficients. J. Chem. Inf. Comput. Sci. 2000, 40, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, N.; Ebert, A. Can deep learning algorithms enhance the prediction of solute descriptors for linear solvation energy relationship approaches? Fluid Phase Equilib. 2022, 555, 113349. [Google Scholar] [CrossRef]
| Chemical | Supplier | Purification Method | Purity (Mass Fraction) |
|---|---|---|---|
| tert-Butyl acetate | TCI America, Portland, OR, USA | Stored over activated molecular sieves and distilled | 0.997 |
| 1-Chloroanthraquinone | Aldrich Chemical Company, Milwaukee, WI, USA | Recrystallized from anhydrous methanol | 0.997 |
| 2-Ethylanthraquinone | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.996 |
| Acenaphthene | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.997 |
| Benzil | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.997 |
| Anthracene | Aldrich Chemical Company | Recrystallized from anhydrous acetone | 0.997 |
| Acetylsalicylic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| Diphenyl sulfone | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.996 |
| Salicylamide | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.997 |
| Benzoin | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.997 |
| Xanthene | Aldrich Chemical Company | Recrystallized from anhydrous methanol | 0.996 |
| Benzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 4-tert-Butylbenzoic acid | TCI America Chemical Company | Dried for two days at 333 K | 0.998 |
| 3-Chlorobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.997 |
| 4-Chlorobenzoic acid | Acros Organics, Morris Plains, NJ, USA | Dried for two days at 333 K | 0.996 |
| 2-Chloro-5-nitrobenzoic acid | Acros Organics | Dried for two days at 333 K | 0.998 |
| 4-Chloro-3-nitrobenzoic acid | Acros Organics | Dried for two days at 333 K | 0.998 |
| 3,4-Dichlorobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| Hippuric acid | TCI America | Dried for two days at 333 K | 0.997 |
| 2-Hydroxybenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.997 |
| 2-Methoxybenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 4-Methoxybenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 3,4-Dimethoxybenzoic acid | Acros Organics | Dried for two days at 333 K | 0.998 |
| 3,4,5-Trimethoxybenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 2-Methylbenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 3-Methylbenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 2-Methyl-3-nitrobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.997 |
| 3-Methyl-4-nitrobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.997 |
| 4-Methyl-3-nitrobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.998 |
| 3-Nitrobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.996 |
| 4-Nitrobenzoic acid | Acros Organics | Dried for two days at 333 K | 0.998 |
| 3,5-Dinitrobenzoic acid | Aldrich Chemical Company | Dried for two days at 333 K | 0.997 |
| Toluene | Aldrich Chemical Company | None | 0.998, anhydrous |
| Sodium methoxide, 25 mass % solution in methanol | Aldrich Chemical Company | None | |
| 2-Propanol | Aldrich Chemical Company | None | 0.99 |
| Chemical | Analysis Wavelength | Molar Concentration Range |
|---|---|---|
| 1-Chloroanthraquinone | 337 (nm) | 8.79 × 10−5 to 2.93 × 10−4 |
| 2-Ethylanthraquinone | 325 (nm) | 1.21 × 10−4 to 4.04 × 10−4 |
| Acenaphthene | 289 (nm) | 8.05 × 10−5 to 2.68 × 10−4 |
| Benzil | 390 (nm) | 5.49 × 10−3 to 1.83 × 10−2 |
| Anthracene | 356 (nm) | 6.76 × 10−5 to 2.25 × 10−4 |
| Acetylsalicylic acid | 272 (nm) | 4.19 × 10−4 to 1.40 × 10−3 |
| Diphenyl sulfone | 267 (nm) | 2.71 × 10−4 to 9.03 × 10−4 |
| Salicylamide | 300 (nm) | 1.06 × 10−4 to 3.55 × 10−4 |
| Benzoin | 313 (nm) | 1.11 × 10−3 to 3.71 × 10−3 |
| Xanthene | 280 (nm) | 1.79 × 10−4 to 5.95 × 10−4 |
| Benzoic acid | 275 (nm) | 4.88 × 10−4 to 1.63 × 10−3 |
| 4-tert-Butylbenzoic acid | 275 (nm) | 2.86 × 10−4 to 9.54 × 10−4 |
| 3-Chlorobenzoic acid | 280 (nm) | 4.99 × 10−4 to 1.66 × 10−3 |
| 4-Chlorobenzoic acid | 272 (nm) | 4.60 × 10−4 to 1.53 × 10−3 |
| 2-Chloro-5-nitrobenzoic acid | 280 (nm) | 8.79 × 10−5 to 2.93 × 10−4 |
| 4-Chloro-3-nitrobenzoic acid | 292 (nm) | 3.72 × 10−4 to 1.34 × 10−3 |
| 3,4-Dichlorobenzoic acid | 280 (nm) | 4.60 × 10−4 to 1.53 × 10−3 |
| Hippuric acid | 269 (nm) | 6.74 × 10−4 to 2.25 × 10−3 |
| 2-Methoxybenzoic acid | 295 (nm) | 1.61 × 10−4 to 5.37 × 10−4 |
| 4-Methoxybenzoic acid | 273 (nm) | 9.72 × 10−5 to 3.24 × 10−4 |
| 3,4-Dimethoxybenzoic acid | 286 (nm) | 9.23 × 10−5 to 3.08 × 10−4 |
| 3,4,5-Trimethoxybenzoic acid | 289 (nm) | 1.35 × 10−4 to 4.49 × 10−4 |
| 2-Methylbenzoic acid | 279 (nm) | 4.49 × 10−4 to 1.50 × 10−3 |
| 3-Methylbenzoic acid | 280 (nm) | 3.97 × 10−4 to 1.32 × 10−3 |
| 3-Methyl-4-nitrobenzoic acid | 295 (nm) | 1.73 × 10−4 to 5.78 × 10−4 |
| 4-Methyl-3-nitrobenzoic acid | 295 (nm) | 3.29 × 10−4 to 1.10 × 10−3 |
| 3-Nitrobenzoic acid | 280 (nm) | 1.51 × 10−4 to 5.06 × 10−4 |
| 4-Nitrobenzoic acid | 272 (nm) | 4.51 × 10−5 to 1.50 × 10−4 |
| 3,5-Dinitrobenzoic acid | 267 (nm) | 6.35 × 10−5 to 2.12 × 10−4 |
| Solute | Tmp,initial/K | Tmp,equilibrated/K |
|---|---|---|
| Benzil | 368.5 ± 0.5 | 368.2 ± 0.4 |
| Anthracene | 490.3 ± 0.4 | 490.0 ± 0.5 |
| Acenaphthene | 367.0 ± 0.4 | 367.2 ± 0.5 |
| Xanthene | 374.6 ± 0.5 | 374.3 ± 0.5 |
| 1-Chloroanthraquinone | 435.4 ± 0.5 | 435.2 ± 0.4 |
| Benzoic acid | 395.6 ± 0.4 | 395.8 ± 0.4 |
| 4-tert-Butylbenzoic acid | 441.7 ± 0.6 | 441.6 ± 0.4 |
| 3-Chlorobenzoic acid | 427.9 ± 0.4 | 428.1 ± 0.3 |
| 4-Chlorobenzoic acid | 512.5 ± 0.3 | 512.8 ± 0.4 |
| 3,4-Dichlorobenzoic acid | 479.2 ± 0.5 | 479.1 ± 0.4 |
| 3,4-Dimethoxybenzoic acid | 454.3 ± 0.4 | 454.5 ± 0.5 |
| 3,4,5-Trimethoxybenzoic acid | 445.6 ± 0.6 | 445.8 ± 0.5 |
| 2-Hydroxybenzoic acid | 432.7 ± 0.5 | 432.9 ± 0.5 |
| 2-Methoxybenzoic acid | 374.7 ± 0.5 | 374.8 ± 0.4 |
| 4-Methoxybenzoic acid | 456.6 ± 0.5 | 456.3 ± 0.4 |
| 2-Methylbenzoic acid | 376.5 ± 0.4 | 376.7 ± 0.4 |
| 3-Methylbenzoic acid | 382.4 ± 0.4 | 382.5 ± 0.4 |
| 2-Methyl-3-nitrobenzoic acid | 455.5 ± 0.4 | 455.2 ± 0.5 |
| 3-Methyl-4-nitrobenzoic acid | 490.7 ± 0.5 | 491.0 ± 0.5 |
| 4-Methyl-3-nitrobenzoic acid | 461.2 ± 0.6 | 461.6 ± 0.6 |
| 3-Nitrobenzoic acid | 414.7 ± 0.4 | 414.4 ± 0.5 |
| 4-Nitrobenzoic acid | 512.6 ± 0.5 | 512.5 ± 0.4 |
| 3,5-Dinitrobenzoic acid | 481.4 ± 0.5 | 481.3 ± 0.4 |
| 2-Chloro-5-nitrobenzoic acid | 440.1 ± 0.5 | 440.4 ± 0.5 |
| 4-Chloro-3-nitrobenzoic acid | 456.3 ± 0.5 | 456.5 ± 0.5 |
| 2-Ethylanthraquinone | 383.9 ± 0.5 | 384.2 ± 0.5 |
| Diphenyl sulfone | 398.2 ± 0.4 | 397.9 ± 0.5 |
| Acetylsalicylic acid | 413.7 ± 0.5 | 413.3 ± 0.6 |
| Salicylamide | 413.2 ± 0.5 | 413.4 ± 0.4 |
| Benzoin | 410.4 ± 0.4 | 410.7 ± 0.5 |
| Hippuric acid | 463.2 ± 0.5 | 462.8 ± 0.5 |
| Chemical Name | XS,organic | Chemical Name | XS,organic |
|---|---|---|---|
| 1-Chloroanthraquinone | 0.003494 | 3,4-Dichlorobenzoic acid | 0.01216 |
| 2-Ethylanthraquinone | 0.02086 | 2-Hydroxybenzoic acid | 0.1187 |
| Acenaphthene | 0.09654 | Hippuric acid | 0.0005241 |
| Benzil | 0.09184 | 2-Methoxybenzoic acid | 0.02938 |
| Anthracene | 0.003755 | 4-Methoxybenzoic acid | 0.006635 |
| Acetylsalicylic acid | 0.02041 | 3,4-Dimethoxybenzoic acid | 0.003625 |
| Diphenyl sulfone | 0.02108 | 3,4,5-Trimethoxybenzoic acid | 0.007172 |
| Salicylamide | 0.04114 | 2-Methylbenzoic acid | 0.1170 |
| Benzoin | 0.006353 | 3-Methylbenzoic acid | 0.1114 |
| Xanthene | 0.08530 | 2-Methyl-3-nitrobenzoic acid | 0.02141 |
| Benzoic acid | 0.1295 | 3-Methyl-4-nitrobenzoic acid | 0.008034 |
| 4-tert-Butylbenzoic acid | 0.06369 | 4-Methyl-3-nitrobenzoic acid | 0.01549 |
| 3-Chlorobenzoic acid | 0.04934 | 3-Nitrobenzoic acid | 0.07749 |
| 4-Chlorobenzoic acid | 0.007404 | 4-Nitrobenzoic acid | 0.006436 |
| 2-Chloro-5-nitrobenzoic acid | 0.03879 | 3,5-Dinitrobenzoic acid | 0.02331 |
| 4-Chloro-3-nitrobenzoic acid | 0.01991 |
| Solute | Log K a | Log P b |
|---|---|---|
| tert-Butyl acetate | 3.53 c | 2.09 |
| Benzil | 8.74 | 3.87 |
| Anthracene | 7.90 | 4.87 |
| Acenaphthene | 6.75 | 4.39 |
| Xanthene | 7.51 | 5.01 |
| 1-Chloroanthraquinone | 9.99 | 3.95 |
| Benzoic acid | 6.68 | 1.54 |
| 4-tert-Butylbenzoic acid | 8.79 | 3.56 |
| 3-Chlorobenzoic acid | 7.36 | 2.22 |
| 4-Chlorobenzoic acid | 7.10 | 2.30 |
| 3,4-Dichlorobenzoic acid | 7.67 | 2.93 |
| 3,4-Dimethoxybenzoic acid | 9.37 | 0.92 |
| 3,4,5-Trimethoxybenzoic acid | 10.53 | 1.27 |
| 2-Hydroxybenzoic acid | 7.23 | 1.87 |
| 2-Methoxybenzoic acid | 7.69 | 0.89 |
| 4-Methoxybenzoic acid | 8.19 | 1.49 |
| 2-Methylbenzoic acid | 6.30 | 2.00 |
| 3-Methylbenzoic acid | 7.04 | 2.06 |
| 2-Methyl-3-nitrobenzoic acid | 8.65 | 1.91 |
| 3-Methyl-4-nitrobenzoic acid | 8.37 | 2.00 |
| 4-Methyl-3-nitrobenzoic acid | 9.03 | 1.72 |
| 3-Nitrobenzoic acid | 8.37 | 1.44 |
| 4-Nitrobenzoic acid | 8.56 | 1.66 |
| 3,5-Dinitrobenzoic acid | 9.95 | 1.65 |
| 2-Chloro-5-nitrobenzoic acid | 9.00 | 2.05 |
| 4-Chloro-3-nitrobenzoic acid | 9.38 | 2.17 |
| 2-Ethylanthraquinone | 9.53 | 4.71 |
| Diphenyl sulfone | 10.22 | 2.83 |
| Acetylsalicylic acid | 9.36 | 0.86 |
| Salicylamide | 8.92 | 1.24 |
| Benzoin | 11.07 | 2.34 |
| Hippuric acid | 11.72 | −0.55 |
| Lovastatin | 18.10 | 4.09 |
| Simvastatin | 18.17 | 4.23 |
| Solute | E | S | A | B | L | V |
|---|---|---|---|---|---|---|
| Radon | 0.000 | 0.000 | 0.000 | 0.000 | 0.877 | 0.3840 |
| Hydrogen | 0.000 | 0.000 | 0.000 | 0.000 | −1.200 | 0.1086 |
| Oxygen | 0.000 | 0.000 | 0.000 | 0.000 | −0.723 | 0.1830 |
| Nitrogen | 0.000 | 0.000 | 0.000 | 0.000 | −0.978 | 0.2222 |
| Carbon monoxide | 0.000 | 0.000 | 0.000 | 0.040 | −0.836 | 0.2220 |
| Sulfur dioxide | 0.370 | 0.660 | 0.240 | 0.190 | 0.778 | 0.3465 |
| Ethane | 0.000 | 0.000 | 0.000 | 0.000 | 0.492 | 0.3904 |
| 2-Methylpropane | 0.000 | 0.000 | 0.000 | 0.000 | 1.409 | 0.6722 |
| Pentane | 0.000 | 0.000 | 0.000 | 0.000 | 2.162 | 0.8131 |
| Hexane | 0.000 | 0.000 | 0.000 | 0.000 | 2.668 | 0.9540 |
| Heptane | 0.000 | 0.000 | 0.000 | 0.000 | 3.173 | 1.0949 |
| Octane | 0.000 | 0.000 | 0.000 | 0.000 | 3.677 | 1.2358 |
| Nonane | 0.000 | 0.000 | 0.000 | 0.000 | 4.182 | 1.3767 |
| Octadecane | 0.000 | 0.000 | 0.000 | 0.000 | 8.722 | 2.6448 |
| Nonadecane | 0.000 | 0.000 | 0.000 | 0.000 | 9.226 | 2.7857 |
| Eicosane | 0.000 | 0.000 | 0.000 | 0.000 | 9.731 | 2.9266 |
| Docosane | 0.000 | 0.000 | 0.000 | 0.000 | 10.740 | 3.2084 |
| Tricosane | 0.000 | 0.000 | 0.000 | 0.000 | 11.252 | 3.3493 |
| Tetracosane | 0.000 | 0.000 | 0.000 | 0.000 | 11.758 | 3.4902 |
| Octacosane | 0.000 | 0.000 | 0.000 | 0.000 | 13.780 | 4.0538 |
| 2-Methylpentane | 0.000 | 0.000 | 0.000 | 0.000 | 2.503 | 0.9540 |
| 2,4-Dimethylpentane | 0.000 | 0.000 | 0.000 | 0.000 | 2.809 | 1.0949 |
| 2,5-Dimethyhexane | 0.000 | 0.000 | 0.000 | 0.000 | 3.308 | 1.2358 |
| 2,3,4-Trimethylpentane | 0.000 | 0.000 | 0.000 | 0.000 | 3.481 | 1.2358 |
| Cyclohexane | 0.305 | 0.100 | 0.000 | 0.000 | 2.964 | 0.8454 |
| Ethylcyclhexane | 0.263 | 0.100 | 0.000 | 0.000 | 3.877 | 1.1272 |
| Propene | 0.103 | 0.080 | 0.000 | 0.070 | 0.946 | 0.4883 |
| trans-But-2-ene | 0.126 | 0.080 | 0.000 | 0.050 | 1.664 | 0.6292 |
| Pent-1-ene | 0.093 | 0.080 | 0.000 | 0.070 | 2.047 | 0.7701 |
| 2-Methylprop-1-ene | 0.120 | 0.080 | 0.000 | 0.080 | 1.579 | 0.6292 |
| 3-Methylbut-1-ene | 0.063 | 0.060 | 0.000 | 0.050 | 1.933 | 0.7701 |
| Hept-1-ene | 0.092 | 0.080 | 0.000 | 0.070 | 3.063 | 1.0519 |
| Buta-1,2-diene | 0.320 | 0.230 | 0.000 | 0.100 | 1.543 | 0.5862 |
| 2-Methylbuta-1,3-diene | 0.313 | 0.230 | 0.000 | 0.100 | 2.101 | 0.7271 |
| Hepta-1,6-diene | 0.189 | 0.200 | 0.000 | 0.100 | 3.028 | 1.0089 |
| Dichloromethane | 0.387 | 0.570 | 0.100 | 0.050 | 2.019 | 0.4943 |
| Trichloromethane | 0.425 | 0.490 | 0.150 | 0.020 | 2.480 | 0.6167 |
| Tetrachloromethane | 0.458 | 0.380 | 0.000 | 0.000 | 2.823 | 0.7391 |
| 1,2-Dichloroethane | 0.416 | 0.640 | 0.100 | 0.110 | 2.573 | 0.6352 |
| 1-Chloropropane | 0.216 | 0.400 | 0.000 | 0.100 | 2.202 | 0.6537 |
| 1-Chlorobutane | 0.210 | 0.400 | 0.000 | 0.100 | 2.722 | 0.7946 |
| 2-Chloro-2-methylpropane | 0.142 | 0.300 | 0.000 | 0.030 | 2.273 | 0.7946 |
| Bromoethane | 0.366 | 0.400 | 0.000 | 0.120 | 2.120 | 0.5654 |
| 2-Bromo-2-methylpropane | 0.305 | 0.290 | 0.000 | 0.070 | 2.609 | 0.8472 |
| Iodomethane | 0.676 | 0.430 | 0.000 | 0.120 | 2.106 | 0.5077 |
| Iodoethane | 0.640 | 0.400 | 0.000 | 0.140 | 2.573 | 0.6486 |
| 1,1,2-Triflurotrichlroethane | 0.010 | 0.130 | 0.000 | 0.000 | 2.210 | 0.8107 |
| 1,2-Difluorotetrachlroethane | 0.227 | 0.330 | 0.000 | 0.020 | 3.034 | 0.9154 |
| Tetrahydrofuran | 0.289 | 0.520 | 0.000 | 0.480 | 2.636 | 0.6223 |
| 1,4-Dioxane | 0.329 | 0.750 | 0.000 | 0.640 | 2.892 | 0.6810 |
| 2-Methylpropionaldehyde | 0.144 | 0.620 | 0.000 | 0.450 | 2.120 | 0.6879 |
| Propanone | 0.179 | 0.700 | 0.040 | 0.490 | 1.696 | 0.5470 |
| Butanone | 0.166 | 0.700 | 0.000 | 0.510 | 2.287 | 0.6879 |
| Ethyl acetate | 0.106 | 0.620 | 0.000 | 0.450 | 2.314 | 0.7466 |
| Butyl acetate | 0.071 | 0.600 | 0.000 | 0.450 | 3.353 | 1.0284 |
| Acetonitrile | 0.237 | 0.900 | 0.070 | 0.320 | 1.739 | 0.4042 |
| Propionitrile | 0.162 | 0.900 | 0.020 | 0.360 | 2.082 | 0.5450 |
| Diethylamine | 0.154 | 0.300 | 0.080 | 0.690 | 2.395 | 0.7220 |
| Triethylamine | 0.101 | 0.150 | 0.000 | 0.790 | 3.040 | 1.0538 |
| Nitromethane | 0.313 | 0.950 | 0.060 | 0.310 | 1.892 | 0.4237 |
| N,N-Dimethylformaide | 0.367 | 1.310 | 0.000 | 0.740 | 3.173 | 0.6468 |
| Methanol | 0.278 | 0.440 | 0.430 | 0.470 | 0.970 | 0.3082 |
| Ethanol | 0.246 | 0.420 | 0.370 | 0.480 | 1.485 | 0.4491 |
| 1-Propanol | 0.236 | 0.420 | 0.370 | 0.480 | 2.031 | 0.5900 |
| 1-Pentanol | 0.219 | 0.420 | 0.370 | 0.480 | 3.106 | 0.8718 |
| 1-Hexanol | 0.210 | 0.420 | 0.370 | 0.480 | 3.610 | 1.0127 |
| 2-Propanol | 0.212 | 0.360 | 0.330 | 0.560 | 1.764 | 0.5900 |
| 2-Butanol | 0.217 | 0.360 | 0.330 | 0.560 | 2.338 | 0.7309 |
| 2-Methyl-1-propanol | 0.217 | 0.390 | 0.370 | 0.480 | 2.413 | 0.7309 |
| 3-Methyl-1-butanol | 0.192 | 0.390 | 0.370 | 0.480 | 3.011 | 0.8718 |
| Cyclohexanol | 0.460 | 0.540 | 0.320 | 0.570 | 3.758 | 0.9040 |
| 1,3-Dichloro-2-propanol | 0.546 | 0.930 | 0.420 | 0.540 | 3.650 | 0.8348 |
| Dimethyl sulfoxide | 0.522 | 1.720 | 0.000 | 0.970 | 3.401 | 0.6126 |
| Carbon disulfide | 0.876 | 0.260 | 0.000 | 0.030 | 2.370 | 0.4905 |
| Tetramethyltin | 0.324 | 0.110 | 0.000 | 0.100 | 2.651 | 1.0431 |
| Benzene | 0.610 | 0.520 | 0.000 | 0.140 | 2.786 | 0.7164 |
| Toluene | 0.601 | 0.520 | 0.000 | 0.140 | 3.325 | 0.8573 |
| o-Xylene | 0.663 | 0.560 | 0.000 | 0.160 | 3.939 | 0.9982 |
| m-Xylene | 0.623 | 0.520 | 0.000 | 0.160 | 3.839 | 0.9982 |
| p-Xylene | 0.613 | 0.520 | 0.000 | 0.160 | 3.839 | 0.9982 |
| trans-Stilbene | 1.350 | 1.210 | 0.000 | 0.230 | 7.456 | 1.5630 |
| Acenaphthene | 1.604 | 1.050 | 0.000 | 0.220 | 6.469 | 1.2586 |
| Anthracene | 2.290 | 1.340 | 0.000 | 0.280 | 7.568 | 1.4544 |
| Phenanthrene | 2.055 | 1.290 | 0.000 | 0.290 | 7.632 | 1.4544 |
| Fluoranthene | 2.377 | 1.550 | 0.000 | 0.240 | 8.827 | 1.5846 |
| Pyrene | 2.808 | 1.710 | 0.000 | 0.280 | 8.833 | 1.5846 |
| Chlorobenzene | 0.718 | 0.650 | 0.000 | 0.070 | 3.657 | 0.8388 |
| Aniline | 0.955 | 0.960 | 0.260 | 0.410 | 3.934 | 0.8162 |
| Benzoic acid | 0.730 | 0.900 | 0.590 | 0.400 | 4.657 | 0.9317 |
| 2-Hydroxybenzoic acid | 0.900 | 0.850 | 0.730 | 0.370 | 4.732 | 0.9904 |
| 4-Hydroxybenzoic acid | 0.930 | 0.900 | 0.810 | 0.560 | 4.867 | 0.9904 |
| Methyl 4-hydroxybenzoate | 0.900 | 1.370 | 0.690 | 0.450 | 5.665 | 1.1313 |
| 2-Methylpyridine | 0.598 | 0.750 | 0.000 | 0.580 | 3.422 | 0.8162 |
| 2-Furaldehyde | 0.690 | 1.130 | 0.000 | 0.450 | 3.318 | 0.6929 |
| Phenylacetic acid | 0.730 | 1.080 | 0.660 | 0.570 | 4.962 | 1.0726 |
| 4-Hydroxyphenylacetic acid | 1.030 | 1.450 | 0.940 | 0.740 | 5.902 | 1.1313 |
| 4-Ethoxyacetanilide | 0.940 | 1.480 | 0.480 | 0.860 | 6.893 | 1.4542 |
| Betulin | 1.790 | 2.120 | 0.700 | 1.140 | 17.470 | 3.8670 |
| 3-Nitrophthalic acid | 1.360 | 2.010 | 1.200 | 0.890 | 7.780 | 1.3212 |
| Acetylsalicylic acid | 0.781 | 1.690 | 0.710 | 0.670 | 6.279 | 1.2879 |
| 3-Chlorobenzoic acid | 0.840 | 0.950 | 0.630 | 0.320 | 5.197 | 1.0541 |
| 4-Chlorobenzoic acid | 0.840 | 1.020 | 0.630 | 0.270 | 4.947 | 1.0541 |
| 3-Nitrobenzoic acid | 0.990 | 1.180 | 0.730 | 0.520 | 5.601 | 1.1059 |
| 4-Nitrobenzoic acid | 0.990 | 1.520 | 0.680 | 0.400 | 5.770 | 1.1059 |
| 3,5-Dinitrobenzoic acid | 1.250 | 1.630 | 0.700 | 0.590 | 6.984 | 1.2801 |
| 4-Chloro-3-nitrobenzoic acid | 1.250 | 1.470 | 0.700 | 0.440 | 6.685 | 1.2283 |
| 2-Chloro-5-nitrobenzoic acid | 1.250 | 1.400 | 0.670 | 0.460 | 6.513 | 1.2283 |
| 2-Methoxybenzoic acid | 0.899 | 1.410 | 0.450 | 0.620 | 5.636 | 1.1313 |
| 4-Methoxybenzoic acid | 0.899 | 1.250 | 0.620 | 0.520 | 5.741 | 1.1313 |
| 2-Methylbenzoic acid | 0.730 | 0.840 | 0.420 | 0.440 | 4.677 | 1.0726 |
| 3-Methylbenzoic acid | 0.730 | 0.890 | 0.600 | 0.400 | 4.819 | 1.0726 |
| Ketoprofen | 1.650 | 2.260 | 0.550 | 0.890 | 10.527 | 1.9779 |
| Naproxen | 1.510 | 2.020 | 0.600 | 0.670 | 9.207 | 1.7821 |
| Haloperidol | 1.900 | 1.390 | 0.400 | 1.760 | 12.819 | 2.7980 |
| Paracetamol | 1.060 | 1.630 | 1.040 | 0.860 | 6.430 | 1.1724 |
| 4-Nitrobenzyl chloride | 1.080 | 1.350 | 0.000 | 0.350 | 5.806 | 1.1539 |
| Salicylamide | 1.160 | 1.580 | 0.610 | 0.510 | 5.818 | 1.0315 |
| Benzil | 1.445 | 1.590 | 0.000 | 0.620 | 7.611 | 1.6374 |
| 1-Chloroanthraquinone | 1.900 | 1.790 | 0.000 | 0.570 | 9.171 | 1.6512 |
| Monuron | 1.140 | 1.500 | 0.470 | 0.780 | 7.180 | 1.4768 |
| Diuron | 1.280 | 1.600 | 0.570 | 0.700 | 8.060 | 1.5992 |
| Ferrocene | 1.350 | 0.850 | 0.000 | 0.200 | 5.622 | 1.1209 |
| Diphenyl sulfone | 1.570 | 2.150 | 0.000 | 0.700 | 8.902 | 1.6051 |
| Hexachlorobenzene | 1.490 | 0.990 | 0.000 | 0.000 | 7.390 | 1.4508 |
| Hydroquinone | 1.063 | 1.270 | 1.060 | 0.570 | 4.827 | 0.8338 |
| 1,3-Dicyanobenzene | 0.890 | 1.639 | 0.000 | 0.561 | 5.372 | 1.0258 |
| 1,4-Dicyanobenzene | 0.870 | 1.602 | 0.000 | 0.470 | 5.330 | 1.0258 |
| Benzenesulfonamide | 1.130 | 2.137 | 0.651 | 0.647 | 6.524 | 1.0971 |
| 2-Chlorobenzenesulfonamide | 1.220 | 2.310 | 0.660 | 0.623 | 7.291 | 1.2195 |
| o-Toluenesulfonamide | 1.130 | 2.157 | 0.692 | 0.595 | 7.076 | 1.2380 |
| p-Toluenesulfonamide | 1.130 | 2.203 | 0.680 | 0.679 | 7.108 | 1.2380 |
| Methyl 2-Sulfamoylbenzoate | 1.170 | 2.813 | 0.664 | 0.928 | 8.476 | 1.4533 |
| 2-Chlorothioxanthone | 2.226 | 1.394 | 0.000 | 0.556 | 9.319 | 1.6581 |
| 2-Mercapto-1,3,4-thiadizole | 1.166 | 1.066 | 0.365 | 0.457 | 4.285 | 0.7224 |
| Dapsone | 2.210 | 3.370 | 0.800 | 1.080 | 11.716 | 1.8047 |
| Salicylanilide | 1.868 | 2.161 | 0.895 | 0.361 | 8.915 | 1.4436 |
| Dimethyl terephthalate | 0.788 | 1.426 | 0.000 | 0.567 | 6.519 | 1.4288 |
| 5,6-Dimethoxy-1-indanone | 1.037 | 1.211 | 0.000 | 0.785 | 6.703 | 1.4454 |
| Pyrazinamide | 1.030 | 1.458 | 0.331 | 0.856 | 4.976 | 0.8106 |
| 3-Methyl-4-nitrophenol | 1.070 | 1.300 | 0.740 | 0.320 | 5.731 | 1.0902 |
| 2-Ethoxybenzamide | 0.910 | 1.406 | 0.377 | 0.952 | 6.297 | 1.3133 |
| Chlorpropanamide | 1.224 | 2.234 | 0.734 | 0.988 | 9.712 | 1.8986 |
| Thioxanthen-9-one | 1.940 | 1.441 | 0.000 | 0.557 | 8.436 | 1.5357 |
| 2-Iodoaniline | 1.530 | 1.096 | 0.130 | 0.426 | 5.818 | 1.0744 |
| 4-Iodoaniline | 1.530 | 1.342 | 0.225 | 0.400 | 6.031 | 1.0744 |
| Nicotinamide | 1.010 | 1.277 | 0.621 | 0.958 | 5.067 | 0.9317 |
| 2-Phenylindole | 1.990 | 1.880 | 0.420 | 0.360 | 9.051 | 1.5542 |
| Syringic acid | 1.070 | 1.790 | 0.820 | 0.900 | 7.269 | 1.3896 |
| Kojic acid | 1.130 | 1.589 | 0.706 | 0.939 | 5.594 | 0.9512 |
| Pyrimethamine | 2.230 | 1.863 | 0.392 | 1.101 | 10.508 | 1.8458 |
| 2-Bromodibenzofuran | 2.340 | 1.778 | 0.000 | 0.612 | 10.781 | 1.9218 |
| p-Coumaric acid | 1.330 | 1.453 | 0.841 | 0.674 | 6.795 | 1.2292 |
| 2,4-Dinitroaniline | 1.430 | 2.197 | 0.554 | 0.310 | 7.259 | 1.1646 |
| Terephthaldehyde | 1.030 | 1.235 | 0.000 | 0.566 | 5.235 | 1.0296 |
| 2-Methoxy-4-nitroaniline | 1.220 | 1.680 | 0.170 | 0.460 | 6.474 | 1.1900 |
| 2-Chloro-5-nitroaniline | 1.290 | 1.564 | 0.268 | 0.358 | 6.238 | 1.1128 |
| 1-Methyl-4-(methylsulfonyl)benzene | 0.792 | 1.573 | 0.000 | 0.788 | 6.034 | 1.2791 |
| 1,3-Diphenylguanidine | 1.540 | 1.974 | 0.585 | 0.767 | 9.216 | 1.7215 |
| Tinidazole | 1.400 | 2.768 | 0.000 | 1.348 | 9.402 | 1.6959 |
| Sorafenib | 2.460 | 2.913 | 0.574 | 1.494 | 15.998 | 3.0195 |
| 3,4-Dichlorobenzoic acid | 0.950 | 0.920 | 0.670 | 0.260 | 5.623 | 1.1766 |
| 3,4-Dimethoxybenzoic acid | 0.950 | 1.646 | 0.570 | 0.755 | 6.746 | 1.3309 |
| 3,4,5-Trimethoxybenzoic acid | 1.001 | 1.760 | 0.603 | 0.850 | 7.711 | 1.5309 |
| 4-tert-Butylbenzoic acid | 0.730 | 1.111 | 0.551 | 0.443 | 6.547 | 1.4953 |
| Vanillin | 0.990 | 1.336 | 0.321 | 0.662 | 5.703 | 1.1313 |
| Isovanillin | 1.040 | 1.477 | 0.308 | 0.681 | 5.868 | 1.1313 |
| 2-Ethylanthraquinone | 1.410 | 1.545 | 0.000 | 0.557 | 8.781 | 1.8106 |
| Benzoin | 1.587 | 2.115 | 0.196 | 0.847 | 9.159 | 1.6804 |
| Hippuric acid | 1.170 | 1.839 | 1.207 | 0.918 | 7.375 | 1.3290 |
| 2-Methyl-3-nitrobenzoic acid | 1.040 | 1.396 | 0.541 | 0.532 | 6.332 | 1.2468 |
| 3-Methyl-4-nitrobenzoic acid | 1.040 | 1.336 | 0.525 | 0.500 | 6.266 | 1.2468 |
| 4-Methyl-3-nitrobenzoic acid | 1.040 | 1.461 | 0.659 | 0.521 | 6.434 | 1.2468 |
| Sorbic acid | 0.480 | 0.904 | 0.528 | 0.432 | 4.047 | 0.9424 |
| Maltol | 0.888 | 1.152 | 0.212 | 0.763 | 4.510 | 0.8925 |
| o-Acetoacetanisidide | 1.190 | 2.333 | 0.264 | 1.025 | 8.563 | 1.6108 |
| Isophthalic acid | 1.100 | 1.210 | 0.960 | 0.590 | 5.988 | 1.1470 |
| Vanillyl alcohol | 1.053 | 1.817 | 0.755 | 0.890 | 6.464 | 1.1743 |
| Ethyl vanillin | 1.040 | 1.587 | 0.411 | 0.664 | 6.544 | 1.2722 |
| Vanillic acid | 1.144 | 1.476 | 0.826 | 0.639 | 6.407 | 1.1900 |
| 3,4-Dichloro-1-nitrobenzene | 1.100 | 1.333 | 0.000 | 0.141 | 5.782 | 1.1354 |
| 2,3-Dichloro-1-nitrobenzene | 1.100 | 1.563 | 0.000 | 0.098 | 6.001 | 1.1354 |
| 3,5-Dinitro-2-methylbenzoic acid | 1.310 | 2.120 | 0.750 | 0.650 | 8.040 | 1.4210 |
| Xanthone | 1.640 | 1.173 | 0.000 | 0.563 | 7.466 | 1.4309 |
| Lovastatin | 1.230 | 2.730 | 0.310 | 1.760 | 15.459 | 3.2853 |
| Simvastatin | 1.350 | 2.550 | 0.320 | 1.860 | 15.551 | 3.4268 |
| 2-Bromo-9-fluorenone | 1.840 | 1.425 | 0.000 | 0.399 | 8.415 | 1.5472 |
| Benorilate | 1.897 | 2.916 | 0.484 | 1.364 | 12.564 | 2.2930 |
| Probenecid | 1.206 | 1.951 | 0.701 | 1.080 | 10.369 | 2.1578 |
| 3-Methylflavone-8-carboxylic acid | 2.050 | 1.929 | 0.485 | 1.034 | 10.969 | 2.0259 |
| Metamitron | 1.650 | 2.248 | 0.395 | 1.032 | 6.777 | 1.5003 |
| Solute | Log K a | Log P b | Ref. |
|---|---|---|---|
| Radon | 0.810 | 1.460 | [19] |
| Hydrogen | −1.070 | 0.650 | [19] |
| Oxygen | −0.660 | 0.850 | [19] |
| Nitrogen | −0.760 | 1.040 | [19] |
| Carbon monoxide | −0.600 | 1.020 | [19] |
| Sulfur dioxide | 2.360 | 0.830 | [19] |
| Ethane | 0.490 | 1.830 | [19] |
| 2-Methylpropane | 1.580 | 3.280 | [19] |
| Pentane | 2.090 | 3.790 | [19] |
| Hexane | 2.540 | 4.360 | [19] |
| Heptane | 2.980 | 4.940 | [19] |
| Octane | 3.450 | 5.560 | [19] |
| Nonane | 3.910 | 6.060 | [19] |
| 2-Methylpentane | 2.410 | 4.250 | [19] |
| 2,4-Dimethylpentane | 2.700 | 4.780 | [19] |
| 2,5-Dimethyhexane | 3.160 | 5.180 | [19] |
| 2,3,4-Trimethylpentane | 3.230 | 5.110 | [19] |
| Cyclohexane | 2.760 | 3.660 | [19] |
| Ethylcyclhexane | 3.540 | 5.120 | [19] |
| Propene | 1.110 | 2.080 | [19] |
| trans-But-2-ene | 2.030 | 3.140 | [19] |
| Pent-1-ene | 2.170 | 3.400 | [19] |
| 2-Methylprop-1-ene | 1.870 | 2.730 | [19] |
| 3-Methylbut-1-ene | 2.010 | 3.350 | [19] |
| Hept-1-ene | 2.980 | 4.300 | [19] |
| Buta-1,2-diene | 2.080 | 2.530 | [19] |
| 2-Methylbuta-1,3-diene | 2.410 | 2.910 | [19] |
| Hepta-1,6-diene | 3.370 | 4.220 | [19] |
| Dichloromethane | 2.960 | 2.000 | [19] |
| Trichloromethane | 3.380 | 2.590 | [19] |
| Tetrachloromethane | 3.100 | 3.290 | [19] |
| 1,2-Dichloroethane | 3.460 | 2.190 | [19] |
| 1-Chloropropane | 2.700 | 2.460 | [19] |
| 1-Chlorobutane | 3.160 | 3.040 | [19] |
| 2-Chloro-2-methylpropane | 2.610 | 3.410 | [19] |
| Bromoethane | 2.590 | 2.050 | [19] |
| 2-Bromo-2-methylpropane | 2.970 | 3.570 | [19] |
| Iodomethane | 2.540 | 1.890 | [19] |
| Iodoethane | 2.960 | 2.420 | [19] |
| 1,1,2-Triflurotrichlroethane | 2.490 | 3.790 | [19] |
| 1,2-Difluorotetrachlroethane | 3.390 | 4.030 | [19] |
| Tetrahydrofuran | 3.010 | 0.460 | [19] |
| 1,4-Dioxane | 3.670 | −0.040 | [19] |
| 2-Methylpropionaldehyde | 2.970 | 0.870 | [19] |
| Propanone | 2.860 | 0.030 | [19] |
| Butanone | 3.260 | 0.540 | [19] |
| Ethyl acetate | 3.300 | 1.140 | [19] |
| Acetonitrile | 3.070 | 0.220 | [19] |
| Propionitrile | 3.430 | 0.610 | [19] |
| Diethylamine | 2.750 | −0.240 | [19] |
| Triethylamine | 3.130 | 0.770 | [19] |
| Nitromethane | 3.610 | 0.660 | [19] |
| N,N-Dimethylformaide | 4.470 | −1.260 | [19] |
| Methanol | 2.700 | −1.040 | [19] |
| Ethanol | 3.020 | −0.650 | [19] |
| 2-Propanol | 3.030 | −0.450 | [19] |
| Dimethyl sulfoxide | 4.880 | −2.980 | [19] |
| Carbon disulfide | 2.290 | 2.440 | [19] |
| Tetramethyltin | 2.640 | 4.170 | [19] |
| Benzene | 3.240 | 2.610 | [19] |
| Toluene | 3.690 | 3.040 | [19] |
| trans-Stilbene | 8.240 | 5.720 | [85] |
| Acenaphthene | 6.920 | 4.560 | [19] |
| Anthracene | 8.150 | 5.120 | [19] |
| Phenanthrene | 8.120 | 5.320 | [19] |
| Fluoranthene | 9.280 | 5.840 | [19] |
| Pyrene | 9.280 | 5.780 | [19] |
| Chlorobenzene | 4.150 | 3.330 | [19] |
| Aniline | 5.490 | 1.190 | [19] |
| Benzoic acid | 6.910 | 1.790 | [19] |
| 2-Hydroxybenzoic acid | 7.410 | 2.020 | [19] |
| 4-Hydroxybenzoic acid | 8.110 | 1.330 | [19] |
| Methyl 4-hydroxybenzoate | 8.750 | 1.900 | [19] |
| 2-Methylpyridine | 4.160 | 0.760 | [19] |
| 2-Furaldehyde | 4.620 | 0.790 | [19] |
| Phenylacetic acid | 8.140 | 1.670 | [19] |
| 4-Hydroxyphenylacetic acid | 9.950 | 0.440 | [19] |
| 4-Ethoxyacetanilide | 9.420 | 1.420 | [19] |
| Betulin | 20.410 | 10.020 | [19] |
| 3-Nitrophthalic acid | 12.680 | 0.010 | [19] |
| Acetylsalicylic acid | 9.900 | 1.330 | [19] |
| 3-Chlorobenzoic acid | 7.610 | 2.460 | [19] |
| 4-Chlorobenzoic acid | 7.410 | 2.610 | [19] |
| 3-Nitrobenzoic acid | 8.750 | 1.820 | [19] |
| 4-Nitrobenzoic acid | 8.980 | 2.080 | [19] |
| 3,5-Dinitrobenzoic acid | 10.410 | 2.110 | [19] |
| 4-Chloro-3-nitrobenzoic acid | 9.760 | 2.550 | [19] |
| 2-Chloro-5-nitrobenzoic acid | 9.410 | 2.460 | [19] |
| 2-Methoxybenzoic acid | 8.180 | 1.370 | [19] |
| 4-Methoxybenzoic acid | 8.620 | 1.920 | [19] |
| 2-Methylbenzoic acid | 6.530 | 2.230 | [19] |
| 3-Methylbenzoic acid | 7.260 | 2.280 | [19] |
| Ketoprofen | 13.760 | 3.300 | [19] |
| Naproxen | 12.500 | 3.700 | [19] |
| Salicylamide | 9.230 | 1.630 | [19] |
| Benzil | 9.040 | 4.170 | [19] |
| 1-Chloroanthraquinone | 10.410 | 4.380 | [19] |
| Monuron | 9.580 | 1.950 | [19] |
| Diuron | 10.700 | 2.700 | [19] |
| Ferrocene | 6.020 | 4.100 | [19] |
| Diphenyl sulfone | 10.670 | 3.280 | [19] |
| Hexachlorobenzene | 7.510 | 6.100 | [19] |
| Docosane | 10.010 | 13.580 | [19] |
| Tricosane | 10.540 | 14.260 | [19] |
| Hydroquinone | 9.050 | 0.180 | [19] |
| 1,3-Dicyanobenzene | 7.209 | 1.670 | [39] |
| 1,4-Dicyanobenzene | 7.062 | 2.055 | [34] |
| Benzenesulfonamide | 10.581 | 0.811 | [78] |
| 2-Chlorobenzenesulfonamide | 11.478 | 1.368 | [33] |
| o-Toluenesulfonamide | 11.189 | 1.574 | [28] |
| p-Toluenesulfonamide | 11.252 | 1.163 | [74] |
| Methyl 2-Sulfamoylbenzoate | 13.433 | 0.757 | [77] |
| 2-Chlorothioxanthone | 9.878 | 4.789 | [35] |
| 2-Mercapto-1,3,4-thiadizole | 6.127 | 0.780 | [37] |
| Dapsone | 16.998 | 1.408 | [68] |
| Salicylanilide | 13.001 | 3.502 | [31] |
| Dimethyl terephthalate | 8.015 | 3.373 | [29] |
| 5,6-Dimethoxy-1-indanone | 7.722 | 2.487 | [48] |
| Pyrazinamide | 7.348 | −0.569 | [65] |
| 3-Methyl-4-nitrophenol | 8.881 | 2.550 | [81] |
| 2-Ethoxybenzamide | 8.405 | 0.409 | [82] |
| Chlorpropanamide | 13.734 | 2.351 | [30] |
| Thioxanthen-9-one | 9.155 | 4.087 | [58] |
| 2-Iodoaniline | 6.792 | 2.623 | [46] |
| 4-Iodoaniline | 7.513 | 2.498 | [46] |
| Nicotinamide | 7.874 | −1.148 | [22] |
| 2-Phenylindole | 11.533 | 4.638 | [44] |
| Syringic acid | 11.199 | 0.700 | [80] |
| Kojic acid | 8.951 | −1.167 | [64] |
| Pyrimethamine | 12.767 | 2.501 | [47] |
| 2-Bromodibenzofuran | 11.704 | 5.505 | [50] |
| p-Coumaric acid | 10.061 | 1.187 | [21] |
| 2,4-Dinitroaniline | 10.930 | 2.868 | [51] |
| Terephthaldehyde | 6.294 | 1.703 | [52] |
| 2-Methoxy-4-nitroaniline | 8.569 | 2.742 | [25] |
| 2-Chloro-5-nitroaniline | 8.427 | 2.912 | [20] |
| 1-Methyl-4-(methylsulfonyl)benzene | 7.731 | 1.549 | [79] |
| 1,3-Diphenylguanidine | 12.388 | 2.986 | [45] |
| Tinidazole | 12.262 | 0.329 | [38] |
| Sorafenib | 19.501 | 4.760 | [36] |
| 3,4-Dichlorobenzoic acid | 7.939 | 3.199 | [40] |
| 3,4-Dimethoxybenzoic acid | 9.680 | 1.410 | [41] |
| 3,4,5-Trimethoxybenzoic acid | 11.012 | 1.757 | [42] |
| 4-tert-Butylbenzoic acid | 8.951 | 3.726 | [53] |
| Vanillin | 7.739 | 1.311 | [65] |
| Isovanillin | 7.995 | 1.157 | [86] |
| 2-Ethylanthraquinone | 9.925 | 5.111 | [24] |
| Benzoin | 11.512 | 2.781 | [57] |
| Hippuric acid | 12.276 | 0.001 | [49] |
| 2-Methyl-3-nitrobenzoic acid | 8.951 | 2.214 | [54] |
| 3-Methyl-4-nitrobenzoic acid | 8.743 | 2.379 | [55] |
| 4-Methyl-3-nitrobenzoic acid | 9.485 | 2.173 | [56] |
| Sorbic acid | 6.340 | 1.429 | [60] |
| Maltol | 6.129 | −0.045 | [75] |
| o-Acetoacetanisidide | 11.661 | 1.427 | [63] |
| Isophthalic acid | 9.193 | 0.933 | [69] |
| Vanillyl alcohol | 10.308 | −0.114 | [73] |
| Ethyl vanillin | 9.075 | 1.734 | [72] |
| Vanillic acid | 9.983 | 1.317 | [70] |
| 3,4-Dichloro-1-nitrobenzene | 6.712 | 4.006 | [61] |
| 2,3-Dichloro-1-nitrobenzene | 7.280 | 4.187 | [61] |
| 3,5-Dinitro-2-methylbenzoic acid | 12.058 | 2.102 | [59] |
| Xanthone | 8.034 | 3.624 | [43] |
| Lovastatin | 18.336 | 4.424 | [23] |
| Simvastatin | 18.400 | 4.749 | [88] |
| 2-Bromo-9-fluorenone | 9.139 | 4.841 | [67] |
| Benorilate | 16.329 | 2.278 | [32] |
| Probenecid | 13.750 | 2.976 | [76] |
| 3-Methylflavone-8-carboxylic acid | 13.426 | 3.198 | [84] |
| Metamitron | 11.823 | 0.916 | [87] |
| Solute | Log K a | Log P b | Ref. |
|---|---|---|---|
| Hydrogen | −1.100 | 0.620 | [19] |
| Nitrogen | −0.800 | 1.000 | [19] |
| Nitrous oxide | 0.720 | 0.950 | [19] |
| Carbon monoxide | −0.640 | 0.980 | [19] |
| Pentane | 2.150 | 3.850 | [19] |
| Hexane | 2.630 | 4.450 | [19] |
| Heptane | 3.100 | 5.060 | [19] |
| Octane | 3.560 | 5.670 | [19] |
| Nonane | 4.020 | 6.170 | [19] |
| 2-Methylpentane | 2.490 | 4.330 | [19] |
| 2,4-Dimethylpentane | 2.790 | 4.870 | [19] |
| 2,5-Dimethylhexane | 3.270 | 5.290 | [19] |
| 2,3,4-Trimethylpentane | 3.340 | 5.220 | [19] |
| Cyclohexane | 2.870 | 3.770 | [19] |
| Ethylcyclohexane | 3.660 | 5.240 | [19] |
| 1-Heptene | 3.140 | 4.360 | [19] |
| 1,6-Heptadiene | 3.240 | 4.090 | [19] |
| Carbon tetrachloride | 3.120 | 3.310 | [19] |
| Butyl acetate | 4.090 | 2.150 | [19] |
| 2-Butanol | 3.590 | 0.200 | [19] |
| 2-Methyl-1-propanol | 3.550 | 0.250 | [19] |
| 1-Propanol | 3.410 | 0.150 | [19] |
| 1-Pentanol | 4.600 | 1.250 | [19] |
| 3-Methyl-1-butanol | 4.240 | 1.000 | [19] |
| 1-Hexanol | 5.010 | 1.780 | [19] |
| Cyclohexanol | 5.180 | 1.170 | [19] |
| 1,3-Dichloro-2-propanol | 5.560 | 0.380 | [19] |
| Benzene | 2.840 | 2.210 | [19] |
| Toluene | 4.030 | 3.380 | [19] |
| o-Xylene | 4.560 | 3.820 | [19] |
| m-Xylene | 4.440 | 3.830 | [19] |
| p-Xylene | 4.470 | 3.880 | [19] |
| Octadecane | 8.750 | 11.790 | [19] |
| Nonadecane | 9.280 | 12.490 | [19] |
| Eicosane | 9.470 | 12.780 | [19] |
| Docosane | 10.360 | 13.930 | [19] |
| Tricosane | 10.930 | 14.650 | [19] |
| Tetracosane | 11.260 | 15.100 | [19] |
| Octacosane | 13.090 | 17.430 | [19] |
| Anthracene | 8.160 | 5.130 | [19] |
| Pyrene | 9.290 | 5.790 | [19] |
| Fluoranthene | 9.270 | 5.830 | [19] |
| Acenaphthene | 6.910 | 4.550 | [19] |
| Phenanthrene | 8.090 | 5.290 | [19] |
| Methyl 4-hydroxybenzoate | 8.680 | 1.840 | [19] |
| Benzoic acid | 6.810 | 1.710 | [19] |
| 2-Hydroxybenzoic acid | 7.340 | 1.950 | [19] |
| 4-Hydroxybenzoic acid | 7.890 | 1.110 | [19] |
| trans-Stilbene | 8.210 | 5.690 | [85] |
| Diuron | 10.610 | 2.610 | [19] |
| Monouron | 9.390 | 1.760 | [19] |
| Hexachlorobenzene | 7.620 | 6.120 | [19] |
| Diphenyl sulfone | 10.440 | 3.050 | [19] |
| 4-Nitrobenzyl chloride | 7.090 | 3.320 | [19] |
| Paracetamol | 10.380 | −0.520 | [19] |
| Ferrocene | 6.010 | 4.243 | [27] |
| 3-Chlorobenzoic acid | 7.500 | 2.350 | [19] |
| 4-Chlorobenzoic acid | 7.210 | 2.410 | [19] |
| 3,4-Dichlorobenzoic acid | 7.911 | 3.171 | [40] |
| 3-Nitrobenzoic acid | 8.530 | 1.600 | [19] |
| 4-Nitrobenzoic acid | 8.760 | 1.860 | [19] |
| 3,5-Dinitrobenzoic acid | 10.180 | 1.880 | [19] |
| 3,5-Dinitro-2-methylbenzoic acid | 11.853 | 1.897 | [59] |
| 2-Methylbenzoic acid | 6.420 | 2.120 | [19] |
| 3-Methylbenzoic acid | 7.100 | 2.120 | [19] |
| 3-Methyl-4-nitrobenoic acid | 8.635 | 2.271 | [55] |
| Naproxen | 12.200 | 3.400 | [19] |
| Acetylsalicylic acid | 9.580 | 1.080 | [19] |
| 2-Methoxybenzoic acid | 7.880 | 1.080 | [19] |
| 4-Methoxybenzoic acid | 8.410 | 1.710 | [19] |
| 3,4-Dimethoxybenzoic acid | 9.462 | 1.192 | [41] |
| 3,4,5-Trimethoxybenzoic acid | 10.757 | 1.501 | [42] |
| Benzil | 8.930 | 4.060 | [19] |
| 4-Nitroaniline | 9.290 | 2.100 | [19] |
| Haloperidol | 14.320 | 3.020 | [19] |
| Hydroquinone | 8.960 | 0.140 | [19] |
| 1-Chloroanthraquinone | 10.290 | 4.260 | [19] |
| Salicylamide | 9.010 | 1.410 | [19] |
| 4-Chloro-3-nitrobenzoic acid | 9.390 | 2.360 | [20] |
| 2-Chloro-5-nitrobenzoic acid | 9.130 | 2.180 | [20] |
| Lovastatin | 18.279 | 4.267 | [23] |
| 2-Ethylanthraquinone | 9.865 | 5.042 | [24] |
| Simvastatin | 18.677 | 4.678 | [88] |
| Thioxanthen-9-one | 9.335 | 4.051 | [58] |
| Benzoin | 11.305 | 2.574 | [57] |
| Maltol | 6.033 | −0.156 | [75] |
| Nicotinamide | 7.727 | −1.295 | [26] |
| 2-Methyl-3-nitrobenzoic acid | 8.847 | 2.110 | [54] |
| 4-tert-Butylbenzoic acid | 8.825 | 3.600 | [53] |
| o-Acetoacetanisidide | 11.407 | 1.173 | [63] |
| Xanthone | 7.940 | 3.530 | [43] |
| Vanillyl alcohol | 9.948 | −0.474 | [73] |
| Hippuric acid | 12.082 | −0.193 | [49] |
| 2-Ethoxybenzamide | 8.310 | 0.314 | [83] |
| Chlorpropanamide | 13.479 | 2.096 | [30] |
| 4-Methyl-3-nitrobenzoic acid | 9.342 | 2.063 | [56] |
| Dapsone | 16.416 | 0.826 | [68] |
| Salicylanilide | 12.785 | 3.286 | [31] |
| Dimethyl terephthalate | 7.867 | 3.225 | [29] |
| 5,6-Dimethoxy-1-indanone | 7.398 | 2.163 | [48] |
| Pyrazinamide | 7.108 | −0.809 | [65] |
| 3-Methyl-4-nitrophenol | 8.746 | 2.415 | [81] |
| Tinidazole | 11.922 | −0.011 | [38] |
| 2-Bromo-9-fluorenone | 9.134 | 4.836 | [67] |
| Benorilate | 15.974 | 1.925 | [32] |
| Probenecid | 13.554 | 2.780 | [76] |
| 3-Methylflavone-8-carboxylic acid | 13.151 | 2.923 | [84] |
| Metamitron | 11.593 | 0.686 | [87] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Longacre, L.; Wu, E.; Yang, C.; Zhang, M.; Sinha, S.; Varadharajan, A.; Acree, W.E., Jr. Development of Abraham Model Correlations for Solute Transfer into the tert-Butyl Acetate Mono-Solvent and Updated Equations for Both Ethyl Acetate and Butyl Acetate. Liquids 2022, 2, 258-288. https://doi.org/10.3390/liquids2040016
Longacre L, Wu E, Yang C, Zhang M, Sinha S, Varadharajan A, Acree WE Jr. Development of Abraham Model Correlations for Solute Transfer into the tert-Butyl Acetate Mono-Solvent and Updated Equations for Both Ethyl Acetate and Butyl Acetate. Liquids. 2022; 2(4):258-288. https://doi.org/10.3390/liquids2040016
Chicago/Turabian StyleLongacre, Laine, Emily Wu, Chelsea Yang, Miles Zhang, Sneha Sinha, Advika Varadharajan, and William E. Acree, Jr. 2022. "Development of Abraham Model Correlations for Solute Transfer into the tert-Butyl Acetate Mono-Solvent and Updated Equations for Both Ethyl Acetate and Butyl Acetate" Liquids 2, no. 4: 258-288. https://doi.org/10.3390/liquids2040016
APA StyleLongacre, L., Wu, E., Yang, C., Zhang, M., Sinha, S., Varadharajan, A., & Acree, W. E., Jr. (2022). Development of Abraham Model Correlations for Solute Transfer into the tert-Butyl Acetate Mono-Solvent and Updated Equations for Both Ethyl Acetate and Butyl Acetate. Liquids, 2(4), 258-288. https://doi.org/10.3390/liquids2040016







