Solvent Exchange around Aqueous Zn(II) from Ab Initio Molecular Dynamics Simulations
Abstract
1. Introduction
2. Computational Methods
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIMD | ab initio molecular dynamics |
| CN | coordination number |
| DFT | density functional theory |
| DFTB | density functional tight binding |
| EXAFS | extended X-ray absorption fine structure |
| GTH | Goedecker–Teter–Hutter (pseudopotentials) |
| MD | molecular dynamics |
| MLWF | maximally localized Wannier function |
| ND | neutron diffraction |
| QM | quantum mechanics |
| QM/MM | quantum mechanics/molecular mechanics |
| revPBE | revised Perdew–Burke–Ernzerhof (functional) |
| XRD | X-ray diffraction |
References
- Coleman, J.E. Zinc enzymes. Curr. Opin. Chem. Biol. 1998, 2, 222–234. [Google Scholar] [CrossRef]
- Maret, W. Zinc Biochemistry: From a Single Zinc Enzyme to a Key Element of Life. Adv. Nutr. 2013, 4, 82–91. [Google Scholar] [CrossRef]
- Ohtaki, H.; Radnai, T. Structure and Dynamics of Hydrated Ions. Chem. Rev. 1993, 93, 1157–1204. [Google Scholar] [CrossRef]
- Bakker, H.J. Structural Dynamics of Aqueous Salt Solutions. Chem. Rev. 2008, 108, 1456–1473. [Google Scholar] [CrossRef]
- Marcus, Y. Effect of Ions on the Structure of Water: Structure Making and Breaking. Chem. Rev. 2009, 109, 1346–1370. [Google Scholar] [CrossRef]
- Kristiansson, O.; Eriksson, A.; Lindgren, J. Hydration of Ions in Aqueous Solutions Studied by Infrared Spectroscopy. II. Application. Acta Chem. Scand. A 1984, 38, 613–618. [Google Scholar] [CrossRef][Green Version]
- Stangret, J.; Libuś, Z. Influence of Zn(II), Mn(II), and Mg(II) Cations on the Vibrational Spectra of Water in Aqueous Perchlorate Solutions. Spectrosc. Lett. 1988, 21, 397–412. [Google Scholar] [CrossRef]
- Å. Bergström, P.; Lindgren, J.; Sandström, M.; Zhou, Y. Infrared Spectroscopic Study on the Hydration of Mercury(II), Cadmium(II), and Zinc(II) in Aqueous Solution and in the Hexahydrated Perchlorate Salts. Inorg. Chem. 1992, 31, 150–152. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Pye, C.C. Zinc(II) hydration in aqueous solution. A Raman spectroscopic investigation and an ab-initio molecular orbital study. Phys. Chem. Chem. Phys. 1999, 1, 4583–4593. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Pye, C.C. Zinc(II) Hydration in Aqueous Solution: A Raman Spectroscopic Investigation and An ab initio Molecular Orbital Study of Zinc(II) Water Clusters. J. Solut. Chem. 1999, 28, 1045–1070. [Google Scholar] [CrossRef]
- Mink, J.; Németh, C.; Hajba, L.; Sandström, M.; Goggin, P.L. Infrared and Raman spectroscopic and theoretical studies of hexaaqua metal ions in aqueous solution. J. Mol. Struct. 2003, 661–662, 141–151. [Google Scholar] [CrossRef]
- Wei, Z.F.; Zhang, Y.H.; Zhao, L.J.; Liu, J.H.; Li, X.H. Observation of the First Hydration Layer of Isolated Cations and Anions through the FTIR-ATR Difference Spectra. J. Phys. Chem. A 2005, 109, 1337–1342. [Google Scholar] [CrossRef]
- Miyanaga, T.; Watanabe, I.; Ikeda, S. Amplitude in EXAFS and Ligand Exchange Reaction of Hydrated 3d Transition Metal Complexes. Chem. Lett. 1988, 17, 1073–1076. [Google Scholar] [CrossRef]
- noz Páez, A.M.; Pappalardo, R.R.; Marcos, E.S. Determination of the Second Hydration Shell of Cr3+ and Zn2+ in Aqueous Solutions by Extended X-ray Absorption Fine Structure. J. Am. Chem. Soc. 1995, 117, 11710–11720. [Google Scholar] [CrossRef]
- Kuzmin, A.; Obst, S.; Purans, J. X-ray absorption spectroscopy and molecular dynamics studies of Zn2+ hydration in aqueous solutions. J. Phys. Condens. Matter 1997, 9, 10065–10078. [Google Scholar] [CrossRef]
- D’Angelo, P.; Barone, V.; Chillemi, G.; Sanna, N.; Meyer-Klaucke, W.; Pavel, N.V. Hydrogen and Higher Shell Contributions in Zn2+, Ni2+, and Co2+ Aqueous Solutions: An X-ray Absorption Fine Structure and Molecular Dynamics Study. J. Am. Chem. Soc. 2002, 124, 1959–1967. [Google Scholar] [CrossRef]
- Migliorati, V.; Mancini, G.; Tatoli, S.; Zitolo, A.; Filipponi, A.; De Panfilis, S.; Di Cicco, A.; D’Angelo, P. Hydration Properties of the Zn2+ Ion in Water at High Pressure. Inorg. Chem. 2013, 52, 1141–1150. [Google Scholar] [CrossRef]
- Bol, W.; Gerrits, G.J.A.; Van Panthaleon Van Eck, C.L. The Hydration of Divalent Cations in Aqueous Solution. An X-ray Investigation with Isomorphous Replacement. J. Appl. Cryst. 1970, 3, 486–492. [Google Scholar] [CrossRef]
- Ohtaki, H.; Yamaguchi, T.; Maeda, M. X-Ray Diffraction Studies of the Structures of Hydrated Divalent Transition-Metal Ions in Aqueous Solution. Bull. Chem. Soc. Jpn. 1976, 49, 701–708. [Google Scholar] [CrossRef]
- Licheri, G.; Paschina, G.; Piccaluga, G.; Pinna, G. X-ray Diffraction Study of Aqueous Solutions of ZnSO4. Z. Naturforsch. 1982, 37, 1205–1210. [Google Scholar] [CrossRef]
- Radnai, T.; Palinkas, G.; Caminiti, R. X-Ray Diffraction Study on Hydration and Ion-Pairing in Aqueous ZnSO4 Solution. Z. Naturforsch. 1982, 37, 1247–1252. [Google Scholar] [CrossRef]
- Dagnall, S.P.; Hague, D.N.; Towl, A.D.C. X-ray Diffraction Study of Aqueous Zinc(II) Nitrate. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1982, 78, 2161–2167. [Google Scholar] [CrossRef]
- Powell, D.H.; Gullidge, P.M.N.; Neilson, G.W.; Bellissent-Funel, M.C. Zn2+ hydration and complexation in aqueous electrolyte solutions. Mol. Phys. 1990, 71, 1107–1116. [Google Scholar] [CrossRef]
- Salmon, P.S.; Bellissent-Funel, M.C.; Herdman, G.J. The dynamics of aqueous Zn2+ solutions: A study using incoherent quasi-elastic neutron scattering. J. Phys. Condens. Matter 1990, 2, 4297–4309. [Google Scholar] [CrossRef]
- Mhin, B.J.; Lee, S.; Cho, S.J.; Lee, K.; Kim, K.S. Zn(H2O)62+ is very stable among aqua-Zn(II) ions. Chem. Phys. Lett. 1992, 197, 77–80. [Google Scholar] [CrossRef]
- Bock, C.W.; Katz, A.K.; Glusker, J.P. Hydration of Zinc Ions: A Comparison with Magnesium and Beryllium Ions. J. Am. Chem. Soc. 1995, 117, 3754–3765. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Park, J.K.; Kim, K.S. Ab Initio Study of the Structures, Energetics, and Spectra of Aquazinc(II). J. Phys. Chem. 1996, 100, 14329–14338. [Google Scholar] [CrossRef]
- Hartmann, M.; Clark, T.; van Eldik, R. Theoretical Study of the Water Exchange Reaction on Divalent Zinc Ion using Density Functional Theory. J. Mol. Model. 1996, 2, 354–357. [Google Scholar] [CrossRef]
- Hartmann, M.; Clark, T.; van Eldik, R. Hydration and Water Exchange of Zinc(II) Ions. Application of Density Functional Theory. J. Am. Chem. Soc. 1997, 119, 7843–7850. [Google Scholar] [CrossRef]
- Rotzinger, F.P. Mechanism of Water Exchange for the Di- and Trivalent Metal Hexaaqua Ions of the First Transition Series. J. Am. Chem. Soc. 1997, 119, 5230–5238. [Google Scholar] [CrossRef]
- Pavlov, M.; Siegbahn, P.E.M.; Sandström, M. Hydration of Beryllium, Magnesium, Calcium, and Zinc Ions Using Density Functional Theory. J. Phys. Chem. A 1998, 102, 219–228. [Google Scholar] [CrossRef]
- De, S.; Ali, S.M.; Ali, A.; Gaikar, V.G. Micro-solvation of the Zn2+ ion—A case study. Phys. Chem. Chem. Phys. 2009, 11, 8285–8294. [Google Scholar] [CrossRef] [PubMed]
- Cooper, T.E.; O’Brien, J.T.; Williams, E.R.; Armentrout, P.B. Zn2+ Has a Primary Hydration Sphere of Five: IR Action Spectroscopy and Theoretical Studies of Hydrated Zn2+ Complexes in the Gas Phase. J. Phys. Chem. A 2010, 114, 12646–12655. [Google Scholar] [CrossRef]
- Obst, S.; Bradaczek, H. Molecular Dynamics Simulations of Zinc Ions in Water Using CHARMM. J. Mol. Model. 1997, 3, 224–232. [Google Scholar] [CrossRef]
- Chillemi, G.; D’Angelo, P.; Pavel, N.V.; Sanna, N.; Barone, V. Development and Validation of an Integrated Computational Approach for the Study of Ionic Species in Solution by Means of Effective Two-Body Potentials. The Case of Zn2+, Ni2+, and Co2+ in Aqueous Solutions. J. Am. Chem. Soc. 2002, 124, 1968–1976. [Google Scholar] [CrossRef]
- Arab, M.; Bougeard, D.; Smirnov, K.S. Molecular dynamics study of the structure and dynamics of Zn2+ ion in water. Chem. Phys. Lett. 2003, 379, 268–276. [Google Scholar] [CrossRef]
- Inada, Y.; Mohammed, A.M.; Loeffler, H.H.; Funahashi, S. Water-Exchange Mechanism for Zinc(II), Cadmium(II), and Mercury(II) Ions in Water as Studied by Umbrella-Sampling Molecular-Dynamics Simulations. Helv. Chim. Acta 2005, 88, 461–469. [Google Scholar] [CrossRef]
- Wu, J.C.; Piquemal, J.P.; Chaudret, R.; Reinhardt, P.; Ren, P. Polarizable Molecular Dynamics Simulation of Zn(II) in Water Using the AMOEBA Force Field. J. Chem. Theory Comput. 2010, 6, 2059–2070. [Google Scholar] [CrossRef]
- Yu, H.; Whitfield, T.W.; Harder, E.; Lamoureux, G.; Vorobyov, I.; Anisimov, V.M.; MacKerell, A.D.; Roux, B. Simulating Monovalent and Divalent Ions in Aqueous Solution Using a Drude Polarizable Force Field. J. Chem. Theory Comput. 2010, 6, 774–786. [Google Scholar] [CrossRef]
- Jana, C.; Ohanessian, G.; Clavaguéra, C. Theoretical insight into the coordination number of hydrated Zn2+ from gas phase to solution. Theor. Chem. Acc. 2016, 135, 141. [Google Scholar] [CrossRef]
- Xu, M.; Zhu, T.; Zhang, J.Z.H. Molecular Dynamics Simulation of Zinc Ion in Water with an ab Initio Based Neural Network Potential. J. Phys. Chem. A 2019, 123, 6587–6595. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, A.M.; Loeffler, H.H.; Inada, Y.; Tanada, K.; Funahashi, S. Quantum mechanical/molecular mechanical molecular dynamic simulation of zinc(II) ion in water. J. Mol. Liquids 2005, 119, 55–62. [Google Scholar] [CrossRef]
- Fatmi, M.Q.; Hofer, T.S.; Randolf, B.R.; Rode, B.M. An extended ab initio QM/MM MD approach to structure and dynamics of Zn(II) in aqueous solution. J. Chem. Phys. 2005, 123, 054514. [Google Scholar] [CrossRef] [PubMed]
- Brancato, G.; Rega, N.; Barone, V. Microsolvation of the Zn(II) ion in aqueous solution: A hybrid QM/MM MD approach using non-periodic boundary conditions. Chem. Phys. Lett. 2008, 451, 53–57. [Google Scholar] [CrossRef]
- Rega, N.; Brancato, G.; Petrone, A.; Caruso, P.; Barone, V. Vibrational analysis of x-ray absorption fine structure thermal factors by ab initio molecular dynamics: The Zn(II) ion in aqueous solution as a case study. J. Chem. Phys. 2011, 134, 074504. [Google Scholar] [CrossRef]
- Riahi, S.; Roux, B.; Rowley, C.N. QM/MM Molecular Dynamics Simulations of the Hydration of Mg(II) and Zn(II) Ions. J. Chem. Phys. 2013, 99, 1–9. [Google Scholar] [CrossRef]
- Fujiwara, T.; Mochizuki, Y.; Komeiji, Y.; Okiyama, Y.; Mori, H.; Nakano, T.; Miyoshi, E. Fragment molecular orbital-based molecular dynamics (FMO-MD) simulations on hydrated Zn(II) ion. Chem. Phys. Lett. 2010, 490, 41–45. [Google Scholar] [CrossRef]
- Cauët, E.; Bogatko, S.; Weare, J.H.; Fulton, J.L.; Schenter, G.K.; Bylaska, E.J. Structure and dynamics of the hydration shells of the Zn2+ ion from ab initio molecular dynamics and combined ab initio and classical molecular dynamics simulations. J. Chem. Phys. 2010, 132, 194502. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Wang, R.; Meijer, E.J. Understanding hydration of Zn2+ in hydrothermal fluids with ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2011, 13, 13305–13309. [Google Scholar] [CrossRef]
- Ducher, M.; Pietrucci, F.; Balan, E.; Ferlat, G.; Paulatto, L.; Blanchard, M. van der Waals Contribution to the Relative Stability of Aqueous Zn(2+) Coordination States. J. Chem. Theory Comput. 2017, 13, 3340–3347. [Google Scholar] [CrossRef]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Hassanali, A.A.; Cuny, J.; Verdolino, V.; Parrinello, M. Aqueous solutions: State of the art in ab initio molecular dynamics. Phil. Trans. R. Soc. A 2014, 372, 20120482. [Google Scholar] [CrossRef] [PubMed]
- Marx, D.; Sprik, M.; Parrinello, M. Ab initio molecular dynamics of ion solvation. The case of Be2+ in water. Chem. Phys. Lett. 1997, 273, 360–366. [Google Scholar] [CrossRef]
- Śmiechowski, M.; Forbert, H.; Marx, D. Spatial decomposition and assignment of infrared spectra of simple ions in water from mid-infrared to THz frequencies: Li+(aq) and F-(aq). J. Chem. Phys. 2013, 139, 014506. [Google Scholar] [CrossRef] [PubMed]
- Śmiechowski, M.; Sun, J.; Forbert, H.; Marx, D. Solvation shell resolved THz spectra of simple aqua ions – distinct distance- and frequency-dependent contributions of solvation shells. Phys. Chem. Chem. Phys. 2015, 17, 8323–8329. [Google Scholar] [CrossRef]
- Chaudhari, M.I.; Soniat, M.; Rempe, S.B. Octa-Coordination and the Aqueous Ba2+ Ion. J. Phys. Chem. B 2015, 119, 8746–8753. [Google Scholar] [CrossRef]
- Schienbein, P.; Schwaab, G.; Forbert, H.; Havenith, M.; Marx, D. Correlations in the Solute–Solvent Dynamics Reach Beyond the First Hydration Shell of Ions. J. Phys. Chem. Lett. 2017, 8, 2373–2380. [Google Scholar] [CrossRef]
- Giacobello, F.; Mollica-Nardo, V.; Foti, C.; Ponterio, R.C.; Saija, F.; Trusso, S.; Sponer, J.; Cassone, G.; Giuffrè, O. Hydrolysis of Al3+ in Aqueous Solutions: Experiments and Ab Initio Simulations. Liquids 2022, 2, 26–38. [Google Scholar] [CrossRef]
- Gregory, K.P.; Elliott, G.R.; Wanless, E.J.; Webber, G.B.; Page, A.J. A quantum chemical molecular dynamics repository of solvated ions. Sci. Data 2022, 9, 430. [Google Scholar] [CrossRef]
- Śmiechowski, M. Unusual Influence of Fluorinated Anions on the Stretching Vibrations of Liquid Water. J. Phys. Chem. B 2018, 122, 3141–3152. [Google Scholar] [CrossRef]
- Helm, L.; Merbach, A.E. Water exchange on metal ions: Experiments and simulations. Coord. Chem. Rev. 1999, 187, 151–181. [Google Scholar] [CrossRef]
- Rotzinger, F.P. Treatment of Substitution and Rearrangement Mechanisms of Transition Metal Complexes with Quantum Chemical Methods. Chem. Rev. 2005, 105, 2003–2037. [Google Scholar] [CrossRef] [PubMed]
- Kell, G.S. Density, Thermal Expansivity, and Compressibility of Liquid Water from 0 °C to 150 °C: Correlations and Tables for Atmospheric Pressure and Saturation Reviewed and Expressed on 1968 Temperature Scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
- Pan, P.; Tremaine, P.R. Thermodynamics of aqueous zinc: Standard partial molar heat capacities and volumes of Zn2+(aq) from 10 to 55 °C. Geochim. Cosmochim. Acta 1994, 58, 4867–4874. [Google Scholar] [CrossRef]
- Marcus, Y. The Standard Partial Molar Volumes of Ions in Solution. Part 4. Ionic Volumes in Water at 0–100 °C. J. Phys. Chem. B 2009, 113, 10285–10291. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–22, 19–25. [Google Scholar] [CrossRef]
- Śmiechowski, M. Anion–water interactions of weakly hydrated anions: Molecular dynamics simulations of aqueous NaBF4 and NaPF6. Mol. Phys. 2016, 114, 1831–1846. [Google Scholar] [CrossRef]
- Lagardère, L.; Jolly, L.H.; Lipparini, F.; Aviat, F.; Stamm, B.; Jing, Z.F.; Harger, M.; Torabifard, H.; Cisneros, G.A.; Schnieders, M.J.; et al. Tinker-HP: A massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields. Chem. Sci. 2018, 9, 956–972. [Google Scholar] [CrossRef]
- Laury, M.L.; Wang, L.P.; Pande, V.S.; Head-Gordon, T.; Ponder, J.W. Revised Parameters for the AMOEBA Polarizable Atomic Multipole Water Model. J. Phys. Chem. B 2015, 119, 9423–9437. [Google Scholar] [CrossRef]
- The cp2k Developers Group. cp2k v. 6.0, 2001–2018. Available online: http://www.cp2k.org/ (accessed on 13 September 2022).
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Ben, M.D.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comp. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Marques, M.A.L.; Oliveira, M.J.T.; Burnus, T. Libxc: A library of exchange and correlation functionals for density functional theory. Comp. Phys. Commun. 2012, 183, 2272–2281. [Google Scholar] [CrossRef]
- Marsalek, O.; Markland, T.E. Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects. J. Phys. Chem. Lett. 2017, 8, 1545–1551. [Google Scholar] [CrossRef] [PubMed]
- Duignan, T.T.; Baer, M.D.; Schenter, G.K.; Mundy, C.J. Real single ion solvation free energies with quantum mechanical simulation. Chem. Sci. 2017, 8, 6131–6140. [Google Scholar] [CrossRef] [PubMed]
- Macchieraldo, R.; Esser, L.; Elfgen, R.; Voepel, P.; Zahn, S.; Smarsly, B.M.; Kirchner, B. Hydrophilic Ionic Liquid Mixtures of Weakly and Strongly Coordinating Anions with and without Water. ACS Omega 2018, 3, 8567–8582. [Google Scholar] [CrossRef] [PubMed]
- Ohto, T.; Dodia, M.; Imoto, S.; Nagata, Y. Structure and Dynamics of Water at the Water–Air Interface Using First-Principles Molecular Dynamics Simulations within Generalized Gradient Approximation. J. Chem. Theory Comput. 2019, 15, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Ohto, T.; Dodia, M.; Xu, J.; Imoto, S.; Tang, F.; Zysk, F.; Kühne, T.D.; Shigeta, Y.; Bonn, M.; Wu, X.; et al. Accessing the Accuracy of Density Functional Theory through Structure and Dynamics of the Water–Air Interface. J. Chem. Theory Comput. 2019, 10, 4914–4919. [Google Scholar] [CrossRef]
- Lippert, G.; Hutter, J.; Parrinello, M. A hybrid Gaussian and plane wave density functional scheme. Mol. Phys. 1997, 92, 477–487. [Google Scholar] [CrossRef]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [PubMed]
- Galib, M.; Duignan, T.T.; Misteli, Y.; Baer, M.D.; Schenter, G.K.; Hutter, J.; Mundy, C.J. Mass density fluctuations in quantum and classical descriptions of liquid water. J. Chem. Phys. 2017, 146, 244501. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef] [PubMed]
- Jonchiere, R.; Seitsonen, A.P.; Ferlat, G.; Saitta, A.M.; Vuilleumier, R. Van der Waals effects in ab initio water at ambient and supercritical conditions. J. Chem. Phys. 2011, 135, 154503. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Durrant, T.R.; Murphy, S.T.; Watkins, M.B.; Shluger, A.L. Relation between image charge and potential alignment corrections for charged defects in periodic boundary conditions. J. Chem. Phys. 2018, 149, 024103. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Marzari, N.; Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 1997, 56, 12847–12865. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Racine, J. gnuplot 4.0: A portable interactive plotting utility. J. Appl. Econom. 2006, 21, 133–141. [Google Scholar] [CrossRef]
- Brancato, G.; Barone, V. Free Energy Landscapes of Ion Coordination in Aqueous Solution. J. Phys. Chem. B 2011, 115, 12875–12878. [Google Scholar] [CrossRef] [PubMed]
- Cooper, T.E.; Carl, D.R.; Armentrout, P.B. Hydration Energies of Zinc(II): Threshold Collision-Induced Dissociation Experiments and Theoretical Studies. J. Phys. Chem. A 2009, 113, 13727–13741. [Google Scholar] [CrossRef] [PubMed]
- Marcus, Y. Ionic Radii in Aqueous Solutions. Chem. Rev. 1988, 88, 1475–1498. [Google Scholar] [CrossRef]
- Pestana, L.R.; Mardirossian, N.; Head-Gordon, M.; Head-Gordon, T. Ab initio molecular dynamics simulations of liquid water using high quality meta-GGA functionals. Chem. Sci. 2017, 8, 3554–3565. [Google Scholar] [CrossRef]
- Pestana, L.R.; Marsalek, O.; Markland, T.E.; Head-Gordon, T. The Quest for Accurate Liquid Water Properties from First Principles. J. Phys. Chem. Lett. 2018, 9, 5009–5016. [Google Scholar] [CrossRef]
- Atta-Fynn, R.; Bylaska, E.J.; de Jong, W.A. Free energies and mechanisms of water exchange around Uranyl from first principles molecular dynamics. Mater. Res. Soc. Symp. Proc. 2012, 1383, 113–118. [Google Scholar] [CrossRef]
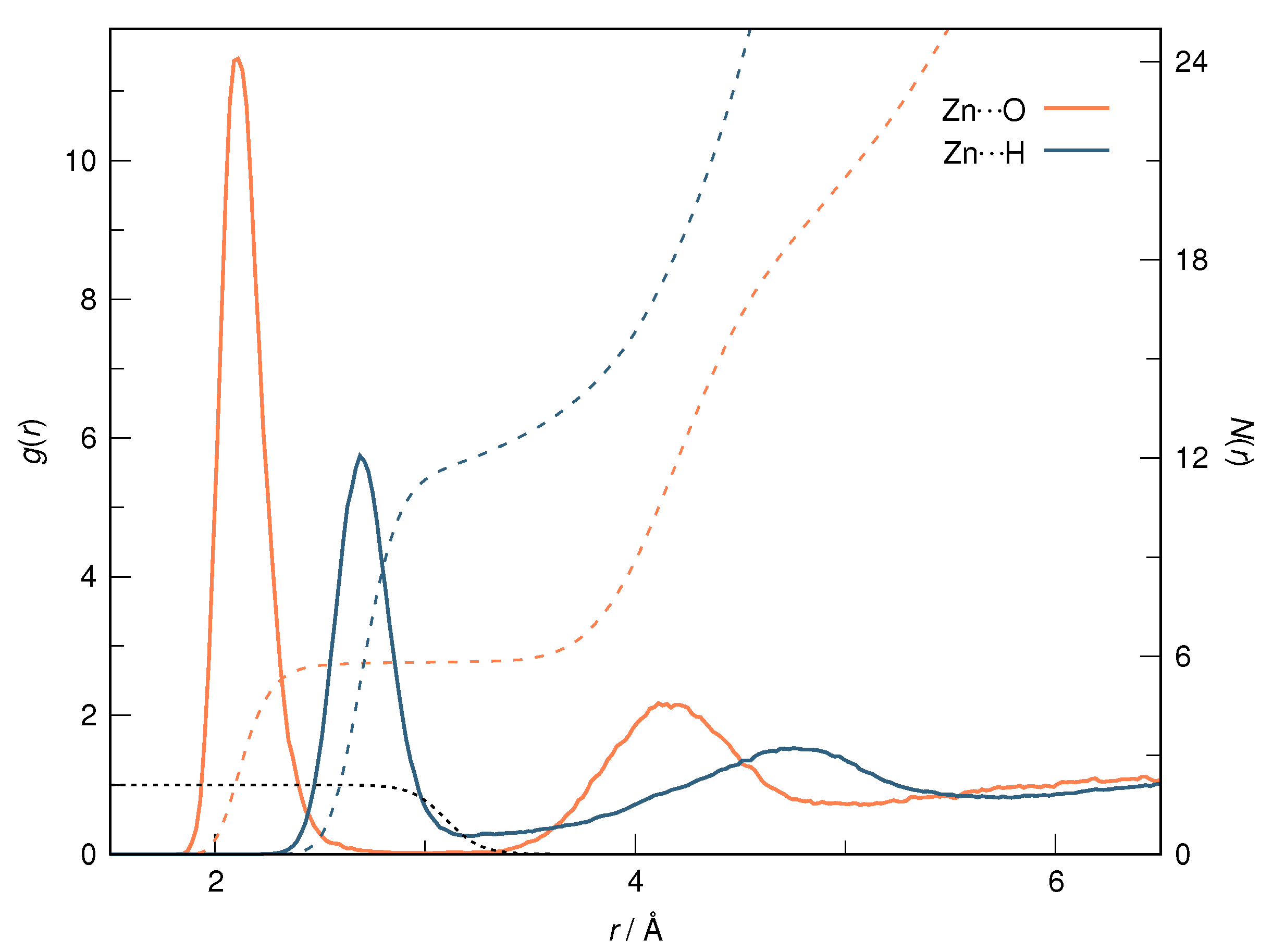
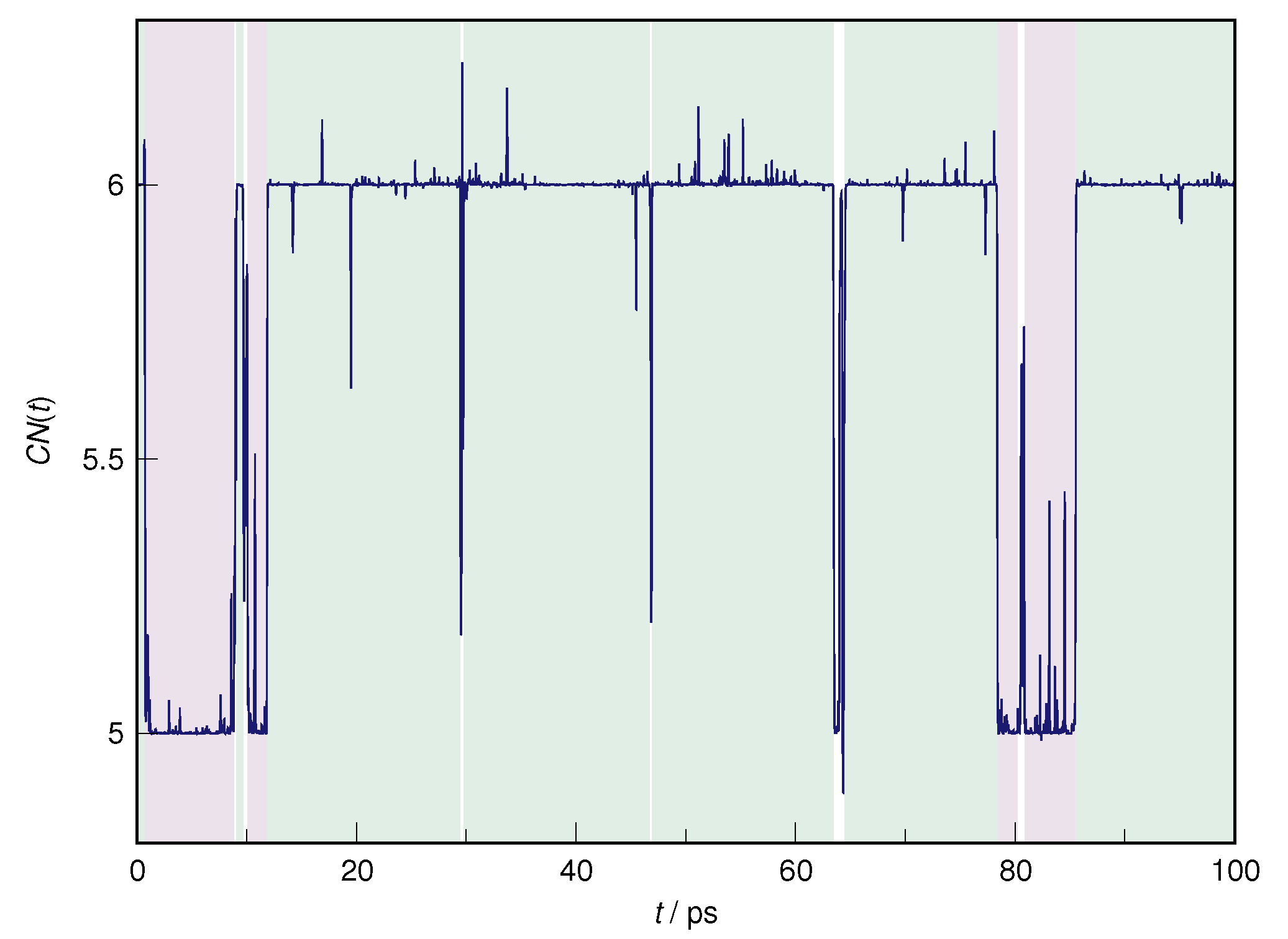
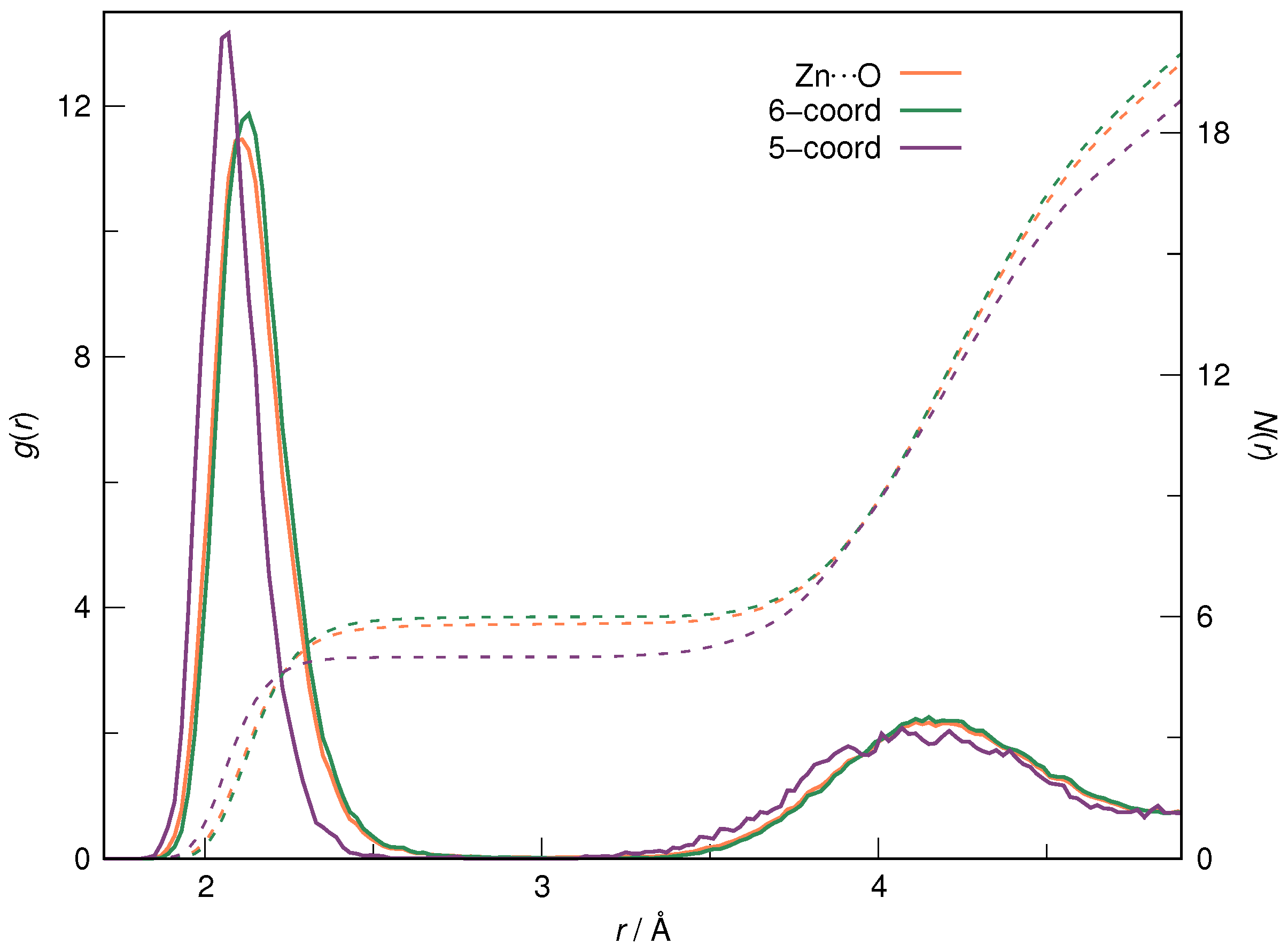
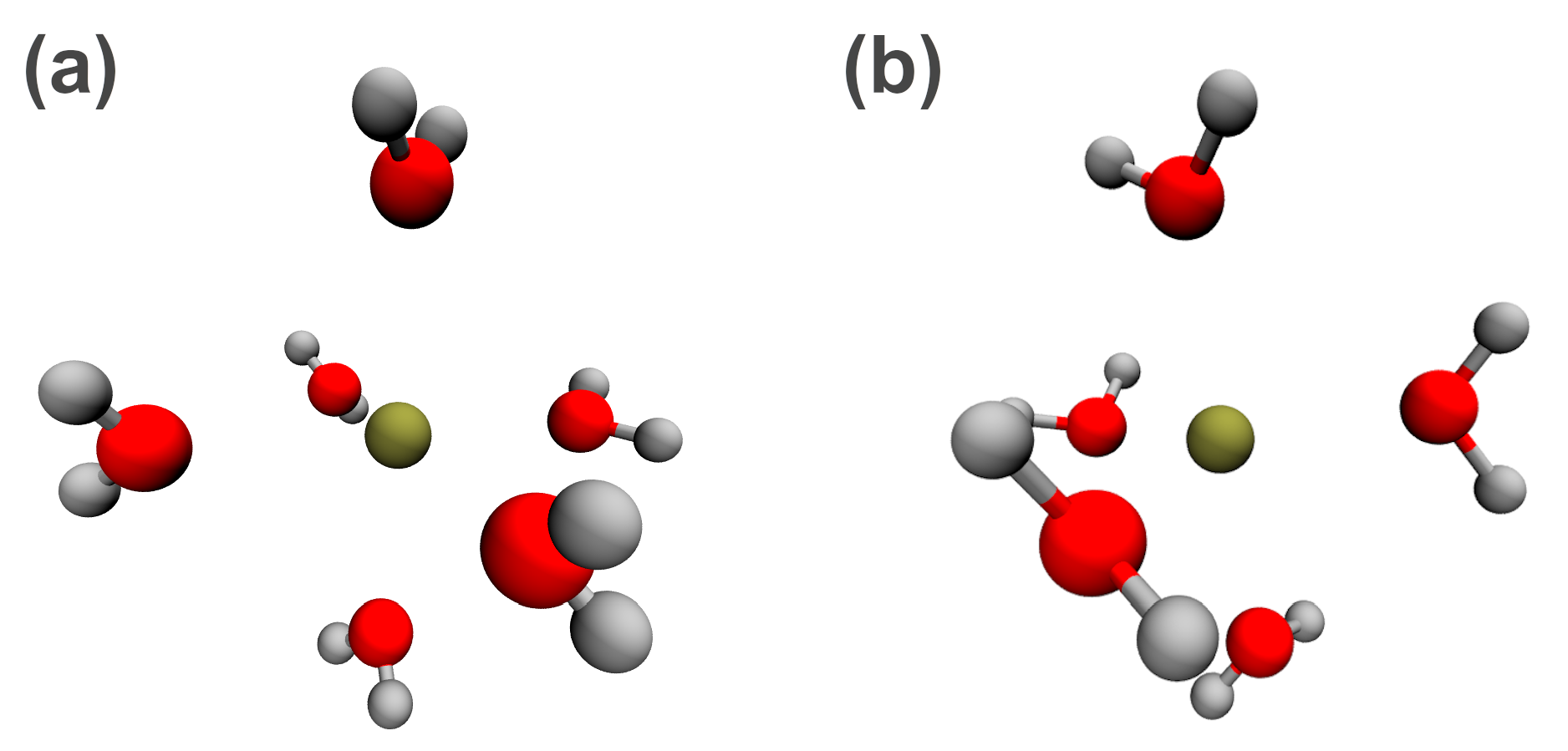
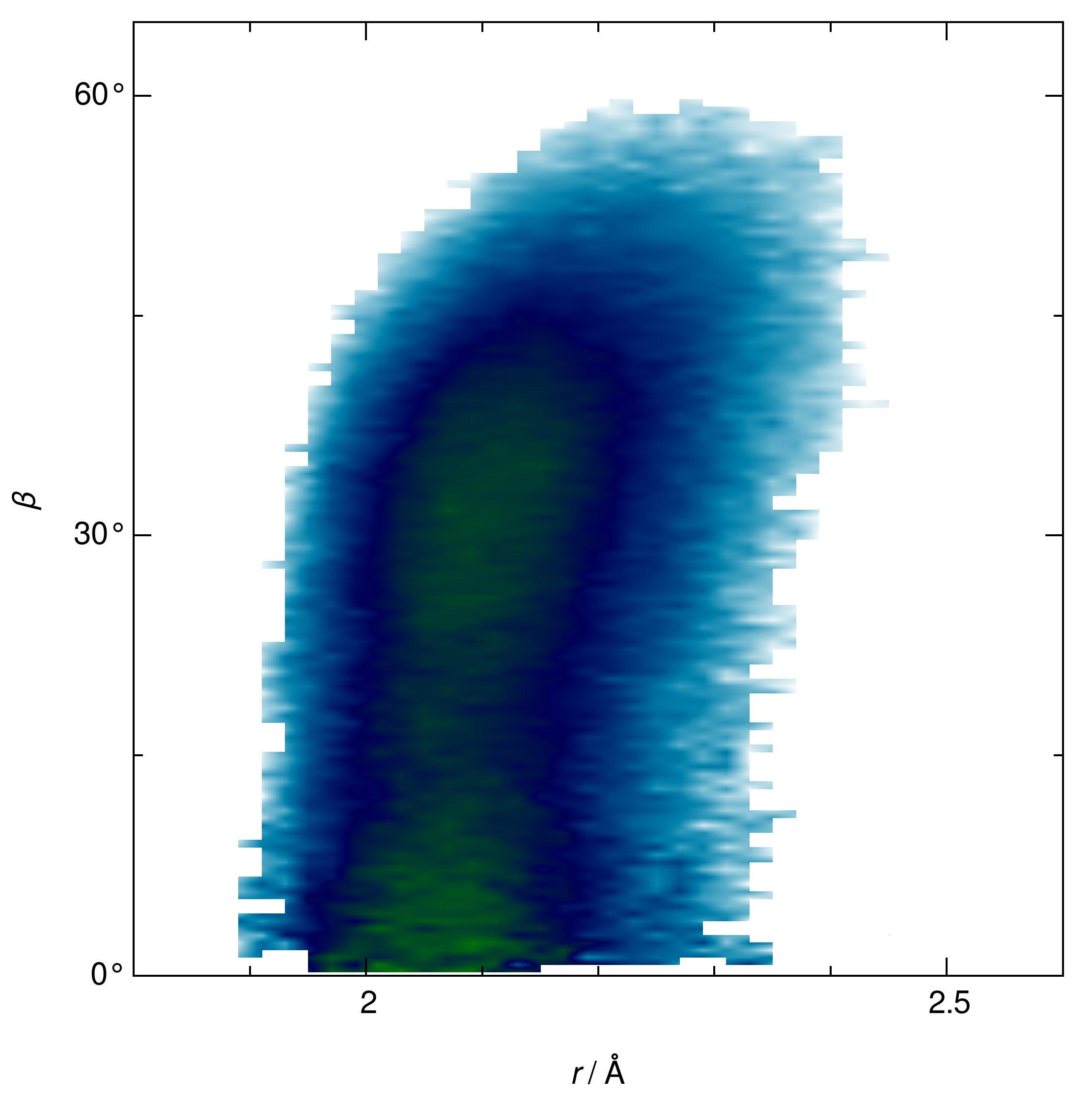
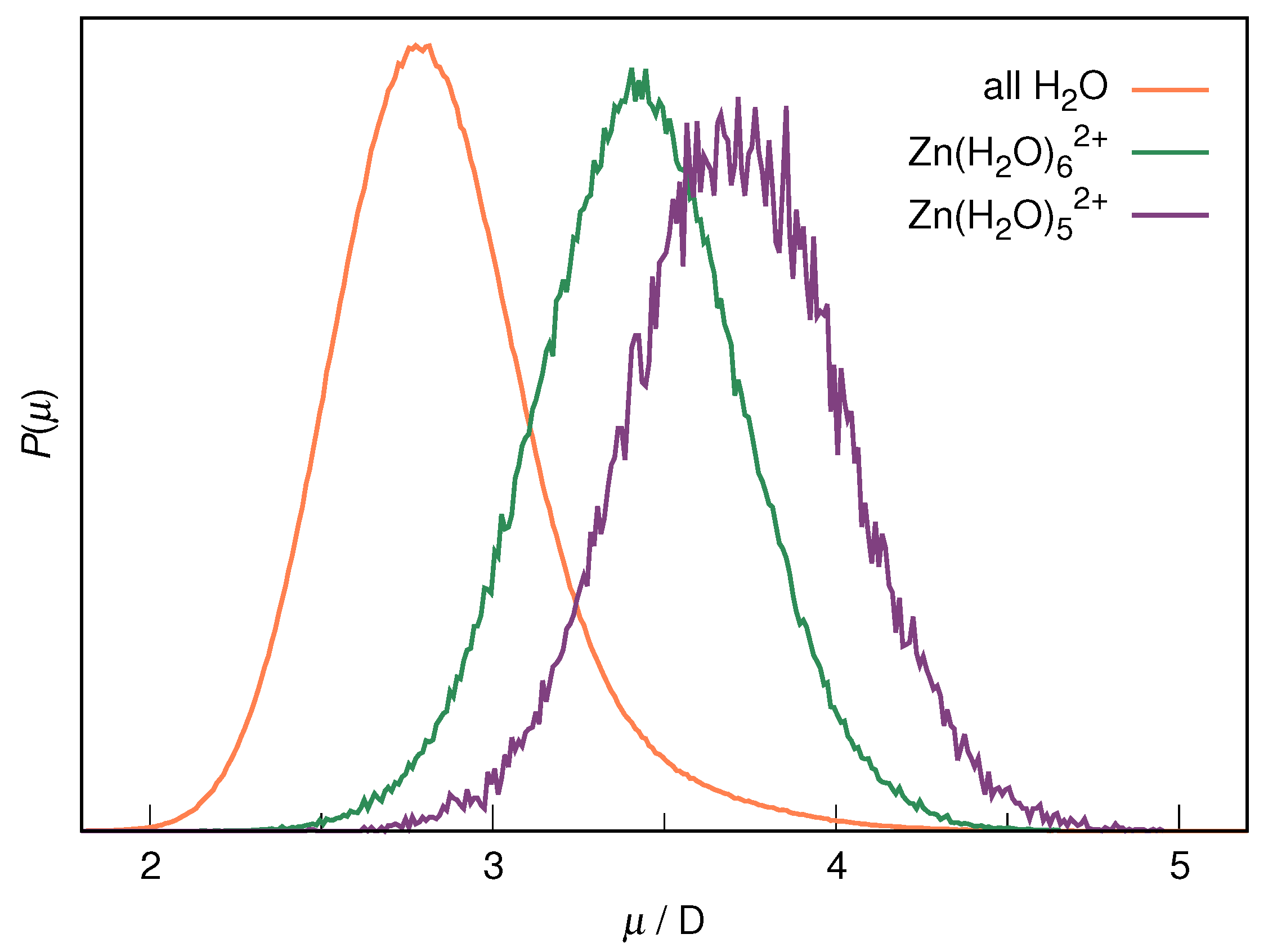
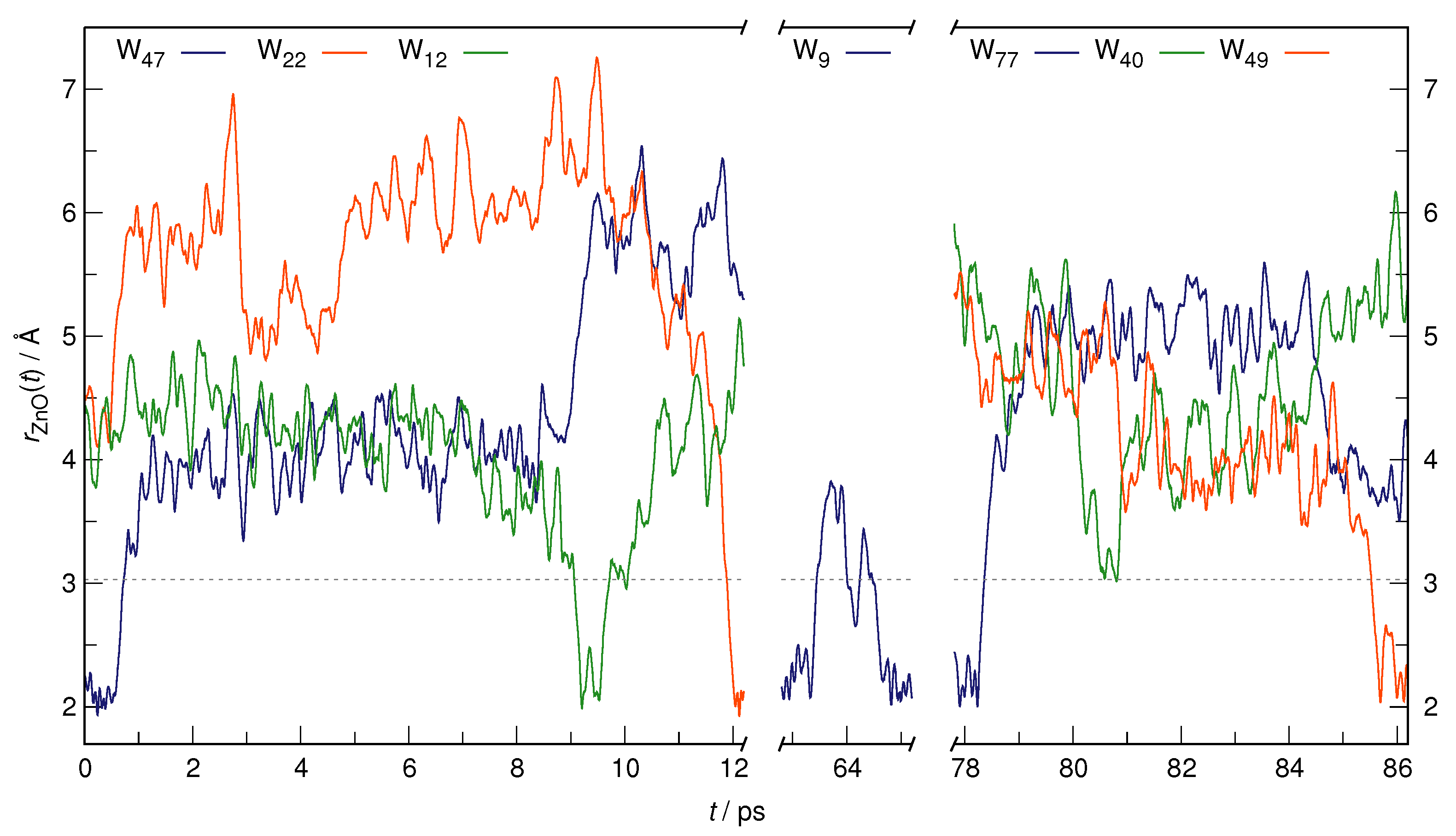
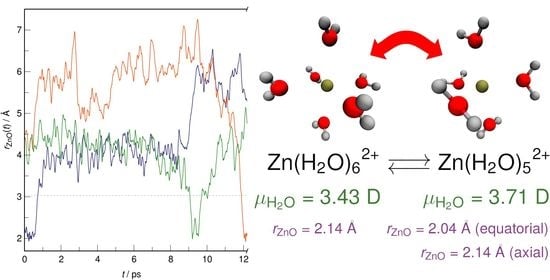
| RDF | 1 | 2 | ||||
|---|---|---|---|---|---|---|
| Zn⋯O | 2.11 | 3.03 | 5.8 | 4.11 | 5.07 | 15.2 |
| Zn⋯H | 2.69 | 3.21 | 12.0 | 4.75 | 5.79 | 28.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malinowski, A.; Śmiechowski, M. Solvent Exchange around Aqueous Zn(II) from Ab Initio Molecular Dynamics Simulations. Liquids 2022, 2, 243-257. https://doi.org/10.3390/liquids2030015
Malinowski A, Śmiechowski M. Solvent Exchange around Aqueous Zn(II) from Ab Initio Molecular Dynamics Simulations. Liquids. 2022; 2(3):243-257. https://doi.org/10.3390/liquids2030015
Chicago/Turabian StyleMalinowski, Adrian, and Maciej Śmiechowski. 2022. "Solvent Exchange around Aqueous Zn(II) from Ab Initio Molecular Dynamics Simulations" Liquids 2, no. 3: 243-257. https://doi.org/10.3390/liquids2030015
APA StyleMalinowski, A., & Śmiechowski, M. (2022). Solvent Exchange around Aqueous Zn(II) from Ab Initio Molecular Dynamics Simulations. Liquids, 2(3), 243-257. https://doi.org/10.3390/liquids2030015