Exploring the Impact of Pedestrian Behavior Parameters on Gap Acceptance in Microsimulation Applications

Abstract

As urban environments become increasingly congested, understanding pedestrian behaviors at intersections is essential for ensuring safety and efficiency. This study explores the complexities of pedestrian behavior in urban traffic networks, focusing on sensitivity analysis using a microscopic simulation tool and a pedestrian module based on the social force model (SFM). By examining nine key pedestrian behavior parameters in isolation, this research identifies their impact on gap acceptance behavior. This exploratory approach highlights how individual parameters, such as Lambda—indicative of a pedestrian’s responsiveness to stimuli from behind—affect the variability in and distribution of gap acceptance times. The findings provide valuable insights into the interplay between pedestrian behavior parameters and their influence on decision-making processes. These results serve as a foundation for refining pedestrian behavior models, offering practical guidance for urban planners, traffic engineers, and policymakers. By emphasizing sensitivity analysis, this study demonstrates the utility of microscopic simulation models in achieving a more profound, nuanced understanding of pedestrian dynamics, contributing to the development of safer and more efficient urban environments.

1. Introduction

Addressing the evolving challenges in urban environments—including demographic shifts, health priorities, and the advent of novel transportation options—necessitates a comprehensive understanding of pedestrian travel behavior and engagement with city landscapes. As urban areas experience increasing pedestrian and vehicular traffic density, accurately modeling pedestrian behavior becomes paramount for planning safe and efficient transportation systems. Reliable models that simulate pedestrian–vehicle interactions are essential for optimizing infrastructure design, improving network operations, and enhancing safety measures. Despite significant progress in transportation modeling, pedestrian behaviors at critical junctures, such as unmarked intersections, remain insufficiently represented in simulation environments.

Microsimulation tools like VISSIM have become widely accepted in urban planning for evaluating transportation systems, particularly pedestrian–vehicle interactions. VISSIM utilizes the social force model (SFM), a mathematical representation of pedestrian dynamics, to simulate pedestrian movements and interactions with vehicles and other pedestrians. These models are invaluable for assessing pedestrian travel times, waiting times, vehicle delays, and safety conflicts. However, the calibration of these models to accurately reflect pedestrian gap acceptance—a key safety behavior—remains underexplored. Gap acceptance, defined as a pedestrian’s decision to cross a roadway based on the available time gap between vehicles, significantly influences the design of pedestrian facilities, signal timings, and vehicle traffic flow. While empirical studies have examined pedestrian gap acceptance, they are often limited by uncontrollable environmental factors and safety constraints. As a result, there is a growing need for controlled, simulation-based studies to investigate the nuances of pedestrian behavior under diverse traffic conditions.

Foundational research has laid the groundwork for understanding pedestrian gap acceptance. DiPietro and King (1970) [1] used time-lapse photography to reveal that factors like pedestrian gender and group size impact gap acceptance decisions. Harrell and Bereska (1992) [2] further emphasized the role of vehicle proximity and speed in pedestrian perceptions of safety at marked crosswalks. More recent studies, such as Yannis et al. (2010) [3], have highlighted the importance of environmental factors like vehicle distance, illegal parking, and pedestrian presence in decision-making at uncontrolled midblock locations. Kadali and Vedagiri (2016) [4] demonstrated that crossing width and traffic conditions significantly influence pedestrian behavior at six-lane unmarked crosswalks, underscoring the need for context-specific models.

Despite these advancements, existing pedestrian modeling systems often fail to capture the dynamic nature of pedestrian–vehicle interactions at intersections. The SFM, although effective for modeling pedestrian avoidance and navigation in dense environments, was not initially designed to address safety behaviors like gap acceptance in mixed-traffic scenarios. This highlights the need to understand the sensitivity of SFM parameters to pedestrian behaviors and their implications for model calibration. Research in this area can bridge the gap between theoretical pedestrian models and their practical applications in urban environments.

Recent studies have introduced innovative methodologies to better understand pedestrian gap acceptance. Alver and Katanalp (2022) [5] used an Analytical Hierarchical Process–Fuzzy Logic (AHP-FL) approach to evaluate pedestrian gap acceptance at semicontrolled midblock crosswalks, emphasizing the influence of vehicle speed and pedestrian characteristics. Similarly, Zhang et al. (2019) [6] found that traffic volume and the number of lanes significantly impact crossing behavior in China. Emerging research, such as Rezwana et al. (2025) [7], utilized virtual reality simulations to explore pedestrian interactions with driverless vehicles (DVs), revealing longer gap acceptance times and heightened stress levels compared to interactions with human-driven vehicles (HDVs). Khaki and Mohammadnazar (2021) [8] developed a probabilistic model that highlighted traffic flow rate and driver yielding behavior as critical determinants of gap acceptance, while Jayaraman et al. (2020) [9] introduced a Behavior-aware Model Predictive Controller (B-MPC) for automated vehicles, enabling long-term predictions of pedestrian crossing behavior.

The current study addresses these gaps by investigating the impact of nine distinct pedestrian behavior parameters within VISSIM’s SFM on gap acceptance. This research provides a granular analysis of their influence on gap acceptance behavior by modifying individual parameters while holding others constant. This approach offers a foundation for calibrating simulation models to more accurately represent real-world pedestrian behavior, facilitating the development of safer and more efficient pedestrian facilities. Ultimately, this study contributes to the growing body of research aimed at refining pedestrian behavior modeling in urban environments, with the goal of enhancing safety, mobility, and urban infrastructure design.

1.1. Overview of the Study and Its Relevance

Pedestrian gap acceptance refers to the decision-making process wherein pedestrians assess available time gaps in vehicle traffic to determine the safety of crossing a roadway or intersection. This behavior is influenced by factors such as pedestrian response time, environmental conditions, and vehicle speeds. Despite its importance, the interaction between pedestrian behavior parameters and gap acceptance within simulation environments remains poorly studied. Prior research has primarily focused on empirical observations or high-level modeling approaches, leaving a critical gap in understanding how parameter adjustments in microsimulation tools affect pedestrian safety outcomes.

This study employs VISSIM’s pedestrian module to evaluate the effects of nine behavioral parameters—including Tau, React to N, A Social (isotropic), B Social (isotropic), Lambda, A Social Mean, B Social Mean, Visual Density, and Noise—on gap acceptance [10]. By isolating the effects of these parameters, this research provides valuable insights for traffic engineers and urban planners seeking to calibrate microsimulation models for specific urban contexts. The findings of this study have broad implications for urban planning and transportation safety. By identifying the key parameters that influence pedestrian gap acceptance, this research contributes to the calibration of microsimulation tools, enabling more accurate predictions of pedestrian–vehicle interactions. These insights can inform the design of safer pedestrian facilities, optimize signal timings, and enhance urban mobility. Furthermore, the study’s methodology provides a framework for future research on pedestrian behavior modeling, particularly in the context of emerging transportation technologies, such as autonomous vehicles. In summary, this study not only addresses a critical gap in pedestrian behavior modeling but also underscores the need for continued exploration of parameter sensitivities in simulation tools. By bridging the gap between theoretical modeling and practical application, this research advances the understanding of pedestrian dynamics in urban environments, paving the way for safer and more efficient transportation systems.

1.2. Problem Statement and Research Objectives

1.2.1. Problem Statement

Pedestrian gap acceptance influences transportation system safety and functionality. Despite the critical role of gap acceptance in urban environments, there is a lack of comprehensive investigation into the diverse pedestrian behavior parameters impacting it. Real-world observational data, while insightful, are subject to uncontrollable variables and safety concerns and do not always allow for detailed, controlled examination of specific behavior parameters. This study uses controlled simulated environments to address these limitations, not to replace real-world observations, but to deepen understanding of pedestrian behavior by manipulating individual parameters and observing the effects on gap acceptance. This approach enables a more nuanced comprehension of pedestrian behavior, which can inform urban planning and traffic regulations.

1.2.2. Research Objectives

This study has the following objectives:

• Develop a method for collecting pedestrian gap acceptance in a simulated environment.
• Quantify the individual effects of nine key pedestrian behavior parameters on gap acceptance in a simulated environment.
• Conduct a detailed statistical analysis of each parameter’s effect on gap acceptance while keeping other parameters constant.
• Inform the design of future pedestrian simulation studies and assist in developing safer and more efficient pedestrian facilities by providing insights into the pedestrian behavior parameters that significantly influence gap acceptance.

1.2.3. Rationale of the Study

• The growing complexities in urban environments, driven by demographic shifts, public health considerations, and the integration of new transportation technologies, have underscored the need for a deeper understanding of pedestrian behavior, particularly at unmarked intersections where pedestrian–vehicle interactions are most frequent and complex. Pedestrian gap acceptance—the decision-making process pedestrians use to determine whether the available time gap between oncoming vehicles is safe for crossing—plays a crucial role in ensuring urban safety and optimizing traffic flow. While microsimulation tools like VISSIM have become essential for modeling pedestrian–vehicle interactions, significant gaps remain in their capacity to accurately replicate pedestrian behavior across diverse traffic conditions.
• Traditional empirical studies have provided valuable insights into pedestrian gap acceptance, but they often face limitations due to uncontrollable environmental factors and safety concerns that hinder comprehensive behavioral analysis. Simulation-based studies offer an effective solution by providing a controlled environment where key variables can be isolated, allowing researchers to explore the nuanced dynamics of pedestrian decision-making. This study aims to overcome the limitations of current microsimulation models by calibrating VISSIM’s social force model (SFM) to better represent pedestrian gap acceptance behavior, thereby improving the accuracy and applicability of pedestrian behavior models in urban planning.
• The SFM has proven effective in modeling pedestrian movements in high-density environments, but it falls short in capturing complex safety behaviors like gap acceptance, especially at intersections where pedestrian–vehicle conflicts are most likely to occur. To address this shortfall, this study conducts a sensitivity analysis on nine key pedestrian behavior parameters—Tau, Lambda, React to N, A Social (isotropic), B Social (isotropic), A Social Mean, B Social Mean, Visual Density, and Noise—to examine their individual and collective impacts on pedestrian gap acceptance. The analysis provides a granular understanding of how each parameter influences pedestrian decisions, allowing for more accurate calibration of simulation models. This approach bridges the gap between theoretical pedestrian modeling and real-world dynamics, equipping urban planners, traffic engineers, and policymakers with data-driven tools for infrastructure planning, traffic safety assessments, and mobility optimization.
• The findings of this study hold significant practical value for urban planners, traffic engineers, policymakers, and transportation safety professionals, offering actionable strategies for improving pedestrian safety and mobility in urban settings. By identifying which pedestrian behavior parameters most significantly influence gap acceptance decisions, this research enables more precise calibration of microsimulation models, leading to better-informed infrastructure designs. For instance, understanding that Tau, which represents pedestrian reaction time, directly affects crossing decisions allows planners to adjust crosswalk designs and signal timings to accommodate varying reaction times, particularly for vulnerable populations like the elderly and children who may require longer crossing periods.
• The study also has substantial implications for traffic safety improvements. By accurately modeling pedestrian gap acceptance, planners can design intersections and midblock crossings that minimize pedestrian–vehicle conflicts, thereby reducing the risk of accidents. Parameters such as Lambda, which measures pedestrian sensitivity to their surroundings, can inform the placement of pedestrian signals, pavement markings, and other visual cues that encourage safer crossing behaviors. Additionally, the research highlights the importance of group dynamics in pedestrian decision-making, as reflected in the React to N parameter, which captures how the presence of other pedestrians influences individual crossing choices. This insight can guide the design of wider crosswalks, pedestrian refuge islands, and other infrastructure features that safely accommodate group crossings and reduce congestion.
• Furthermore, the study’s findings support the development of adaptive traffic management systems that integrate pedestrian behavior data into intelligent transportation systems (ITSs). By incorporating real-time pedestrian flow data and behavioral insights, cities can implement dynamic traffic controls that adjust to varying traffic densities, improving network efficiency and safety. This approach also has significant potential for enhancing the operation of autonomous vehicles (AVs). Understanding pedestrian gap acceptance behaviors enables AV developers to fine-tune algorithms that predict pedestrian movements more accurately, reducing the likelihood of pedestrian–vehicle conflicts and improving AV navigation in urban environments.
• The implications of this study extend beyond traffic management to broader urban mobility and accessibility planning. By accounting for behavioral variability among different pedestrian populations, urban planners can create more inclusive spaces that cater to diverse needs, ensuring that city landscapes are navigable and safe for all users, including children, seniors, and individuals with disabilities. These findings also offer valuable guidance for policymakers seeking to implement evidence-based regulations aimed at improving pedestrian safety, such as establishing minimum visibility standards at crosswalks or mandating pedestrian-friendly signal timings in high-traffic areas.
• Lastly, this study provides a robust foundation for future research in pedestrian behavior modeling. The sensitivity analysis of the nine pedestrian behavior parameters offers a framework for exploring more complex interactions in mixed-traffic environments, guiding the development of holistic urban mobility models that integrate pedestrian, cyclist, and vehicular dynamics. By advancing the accuracy and applicability of pedestrian behavior models in microsimulation tools, this research contributes to the creation of safer, more efficient, and pedestrian-friendly urban spaces, supporting broader goals of sustainable urban development and public health.

2. Background

2.1. Social Force Model

The behavior parameters incorporated in the social force model (SFM) are central to this study’s modeling of pedestrian traffic. In the original model, the SFM is depicted for pedestrian motion dynamics by considering personal motivations and environmental constraints. In this model, the pedestrian α has a preferred velocity $\overrightarrow{w_a}\left(t\right)$ is temporally changed $d\overrightarrow{w_a}/dt$ because of different external forces. Hence, the preferred velocity is described by the vectorial quantity $\overrightarrow{F_a}\left(t\right)$. Here, the force $\overrightarrow{F_a}\left(t\right)$ consists of two other parts: (1) personal desire force $F_p$, and (2) Interaction force $F_{int}$.

$$\begin{gathered} \overrightarrow{F_a}\left(t\right)=All the personal desire related driving Force \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +all other pedestrian related repulsive Force \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +all other stationary object related repulsive Force \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+all the attraction related interaction force \end{gathered}$$

The social force model is defined by

$${\displaystyle \frac{d\overrightarrow{w_a}}{dt}}=\overrightarrow{F_a}\left(t\right)+fluctuations.$$

These parameters control complex and dynamic simulated pedestrian behaviors, though their direct impact on gap acceptance behavior remains insufficiently understood. Nine walking behavior parameters dictate the movement patterns of pedestrians around other individuals and surrounding entities, as outlined below. The impact of each parameter is presented concerning its influence on the social “force” acting upon a pedestrian.

Lambda: Governs the force’s amount of anisotropy because events and phenomena in the back of pedestrians do not influence them (psychologically and socially) as much as if they were in sight. This parameter defines the mean value of the exponential distribution for the desired time gap [10,11].

Tau: represents the relaxation time or inertia related to the response time, as it couples the difference between the desired speed and direction with the current speed and direction for acceleration [10,12].

A and B Social isotropic: Together with Lambda, these parameters influence one of the two forces that form the repulsive force between two pedestrians. These parameters model the isotropic social force of pedestrians, representing how pedestrians interact with each other in a social context [10,13].

A and B Social Mean: The parameter A Social Mean decides the strength of the force, while the parameter B Social Mean determines the range of the force in meters. These parameters depict the social forces that cause pedestrians to form and maintain groups [10,11].

React to N: Sets the maximum number of pedestrians considered for the social force. When calculating the total force for a pedestrian, only the influence exerted by the n closest pedestrians is considered. This parameter determines how many pedestrians in the field of vision a pedestrian takes into account when walking [11].

Noise: Determines the strength of the random force term. The greater this parameter value, the stronger the random force added to the systematically calculated forces if a pedestrian remains below their desired speed for a certain time. This parameter accounts for the variability in pedestrian behavior, allowing for more realistic pedestrian movement simulation [10].

Visual Density: Together with A and B Social Mean, this parameter will determine the time pedestrians require to avoid other pedestrians walking toward them. The distance between two pedestrians (body surface to body surface) [10].

2.2. Limitations of SFM for Gap Acceptance

While the social force model (SFM) has proven effective for modeling pedestrian dynamics in high-density environments such as airports, malls, and public plazas, its application to intersectional gap acceptance behavior presents significant challenges. Originally designed to simulate pedestrian movement with a focus on collision avoidance, personal space maintenance, and social interactions, the SFM does not inherently account for the cognitive processes involved in pedestrian–vehicle interactions, particularly the safety-critical decisions pedestrians make when assessing the timing and distance of oncoming traffic before crossing a roadway.

One of the primary limitations of the SFM in this context is its lack of mechanisms for modeling anticipatory behaviors and risk assessments that are fundamental to pedestrian gap acceptance [14]. The model’s parameters are tailored to reflect social forces and physical constraints, rather than the perceptual and decision-making processes pedestrians use to evaluate traffic gaps. For instance, the Lambda parameter, which measures a pedestrian’s sensitivity to stimuli from behind, is largely irrelevant in crossing scenarios where the focus is on oncoming traffic. Similarly, isotropic social force parameters, designed to model group cohesion and spatial distribution among pedestrians, do not effectively capture individual risk assessments or strategic behaviors pedestrians exhibit at intersections. These gaps limit the model’s capacity to accurately replicate real-world crossing behaviors, especially in complex traffic environments where pedestrians must dynamically assess both vehicle speed and distance.

The implications of these limitations extend directly to current traffic simulation practices. Many urban planning tools and traffic safety studies rely on microsimulation models like VISSIM, which incorporate the SFM to simulate pedestrian movements [13]. However, the inability of the SFM to accurately model gap acceptance behaviors can lead to misleading predictions of pedestrian–vehicle interactions, potentially resulting in suboptimal infrastructure designs and traffic management strategies. For example, if the model underestimates pedestrian hesitation or overestimates crossing aggressiveness, it could lead to inappropriate signal timing recommendations or flawed assessments of pedestrian safety risks at intersections [15]. This disconnect between simulated behaviors and real-world dynamics undermines the reliability of traffic simulations used for safety evaluations, infrastructure planning, and policymaking.

Moreover, the absence of decision-making variables related to pedestrian risk perception and behavioral variability limits the model’s ability to account for demographic differences, such as age, mobility constraints, or cultural attitudes toward risk-taking. This shortfall is particularly critical in cities where diverse pedestrian populations exhibit varying gap acceptance behaviors [15]. Without the ability to model these differences, simulations risk oversimplifying complex pedestrian–vehicle interactions, potentially compromising pedestrian safety in infrastructure designs.

Despite these challenges, the SFM remains a valuable tool for conducting controlled sensitivity analyses in simulated environments. Empirical studies of pedestrian gap acceptance often face practical constraints, including ethical considerations, safety concerns, and environmental variability. Conducting real-world experiments that involve pedestrians crossing active roadways under varying traffic conditions is frequently unfeasible due to safety risks. External factors such as weather conditions, driver behavior, and pedestrian distractions further complicate the reliability of observational data. Simulation models offer a practical alternative in this context, allowing researchers to explore pedestrian behaviors under controlled and repeatable conditions.

The strength of the SFM lies in its ability to serve as a foundational framework for testing parameter sensitivities, even when its parameters are not explicitly designed for gap acceptance studies. Researchers can identify how changes affect pedestrian crossing decisions by systematically isolating and adjusting individual parameters within a microsimulation environment and using this information to calibrate models more accurately. The SFM may not fully capture the cognitive aspects of gap acceptance. These sensitivity analyses provide valuable insights into how the model can be refined or extended to better approximate observed behaviors. This iterative approach helps bridge the gap between theoretical models and real-world applications, enhancing the utility of microsimulation tools for urban planning, traffic safety assessments, and infrastructure optimization.

While the SFM has inherent limitations in modeling pedestrian gap acceptance behavior, its structured framework still offers a basis for understanding and improving pedestrian–vehicle interaction models. Recognizing these limitations is crucial for advancing traffic simulation practices, ensuring that models evolve to incorporate more accurate representations of pedestrian decision-making processes, and ultimately leading to safer, more efficient urban transportation systems.

2.3. Gap Acceptance and Pedestrian Behavior in Microsimulation Models

The 2010 Highway Capacity Manual (HCM) defines critical gap or headway as “the time in seconds below which a pedestrian will not attempt to begin crossing the street”. If the available gap is greater than the critical gap, it is assumed that the pedestrian will cross; if less, it is assumed that the pedestrian will not cross [16]. The term “adequate gap” is used in the Manual on Uniform Traffic Control Devices (MUTCD) and is assumed to be the same as the critical gap in the HCM [17]. The gap can also be defined as an available gap, accepted gap, or rejected gap, depending on the conditions present when a pedestrian attempts to cross [17].

Several methodologies have been developed to determine pedestrian-acceptable gaps. The most common approaches are behavioral analysis and statistical analysis. Behavioral analysis uses mathematical or simulation models to examine pedestrian–vehicle interactions, extracting or calculating acceptable gaps for pedestrians and drivers. Statistical analysis, on the other hand, calculates the probability of gap acceptance based on assumptions about the distribution of arriving vehicles and pedestrian movements. Behavioral analysis provides detailed insights into context-specific interactions, while statistical analysis offers a broader, trend-based perspective on pedestrian behavior [18].

Research into pedestrian gap acceptance has been advanced through both simulation and empirical studies. Simulation efforts, such as those by Schroeder et al. [19], which utilize Cellular Automata for pedestrian–vehicle interaction, and Wilson and Grayson [20], who examine small gap acceptance in traffic flow, provide predictive insights but may not fully capture the complexity of real-world pedestrian behaviors. Empirical studies, including those by Hunt and Abdul Jabbar [21] and Di Pietro and King [1], offer valuable observational data but often lack a comprehensive analysis of environmental factors and decision-making processes. This study bridges these knowledge gaps by leveraging the SFM within VISSIM to examine the impact of behavioral parameters on gap acceptance. By employing a sensitivity analysis framework, this research provides a systematic approach to understanding how pedestrian dynamics can be modeled and calibrated to reflect real-world behaviors, contributing to the broader goals of urban safety and efficiency.

3. Methodology

The methodology begins by establishing a foundational simulation scenario, calibrated to reflect pedestrian dynamics using the standard parameters provided by the social force model (SFM).

The simulated environment emulates a typical urban setting but incorporates deliberate simplifications, such as limiting the scenario to a single-lane, one-way traffic setup. This choice was intentional to isolate the effects of individual parameters on gap acceptance while minimizing confounding variables like multi-lane interactions or bidirectional traffic. Simplifying the scenario ensures a controlled environment for sensitivity analysis, allowing a clearer understanding of how each parameter influences pedestrian behavior.

3.1. Parameter Selection and Justification

To strengthen the methodological framework of this study, the selection of parameters—Lambda, Tau, A Social (isotropic), B Social (isotropic), A Social Mean, B Social Mean, React to N, Visual Density, and Noise—was strategically made to capture key behavioral aspects influencing pedestrian gap acceptance. Each parameter was chosen for its capacity to represent critical decision-making processes and environmental interactions that shape pedestrian behavior, particularly during road crossings in complex urban settings [22].

Tau represents pedestrian reaction time or inertia, directly impacting how quickly a pedestrian responds to external stimuli such as approaching vehicles. This makes Tau a fundamental parameter for assessing gap acceptance, as faster or slower reactions can significantly alter crossing decisions. A shorter Tau may lead to riskier crossings, while a longer Tau often results in more conservative behavior, particularly among vulnerable groups such as children or elderly pedestrians. Although originally designed to measure sensitivity to stimuli from behind, Lambda contributes to overall spatial awareness and situational responsiveness. In high-traffic scenarios, where pedestrians must constantly adjust to dynamic environments, Lambda plays an indirect but vital role in shaping gap acceptance behavior by influencing how pedestrians perceive surrounding movements.

A Social (isotropic) and B Social (isotropic) define the strength and range of isotropic repulsive forces between pedestrians. While these parameters were initially designed to simulate personal space and collision avoidance in dense environments, their relevance extends to pedestrian–vehicle interactions. In crossing scenarios, they influence how pedestrians position themselves relative to both other pedestrians and vehicles, affecting their readiness to cross. This becomes particularly important in crowded intersections where pedestrians must navigate social forces and vehicular gaps. A Social Mean and B Social Mean extend these dynamics by averaging the strength and range of social forces across groups of pedestrians. These parameters help model group cohesion and collective movement, which are critical when groups approach crossings together. High group cohesion can lead to synchronized movements, potentially encouraging pedestrians to cross together, even in smaller or riskier gaps, a behavior frequently observed in urban environments.

React to N quantifies the number of surrounding pedestrians influencing an individual’s crossing decision. This parameter reflects the cognitive load experienced by pedestrians in crowded scenarios and directly impacts their decision-making process. In high-density areas, pedestrians often rely on social cues from others to make crossing decisions, leading to a higher likelihood of group-based behaviors, such as collective risk-taking or hesitation. Visual Density captures the pedestrian’s perception of environmental complexity and spatial crowding. Higher visual density increases cognitive load, which can delay crossing decisions or result in erratic movements. In high-density urban environments, this parameter plays a crucial role in shaping pedestrian behavior, as individuals adjust their movements based on perceived crowding, often opting for longer gaps or waiting for less congested moments to cross. Noise introduces randomness into pedestrian decision-making, reflecting the inherent unpredictability of human behavior. This parameter accounts for real-world inconsistencies, such as distractions, sudden stops, or hesitations, which can significantly affect gap acceptance decisions. Including Noise in the model allows for a more realistic representation of pedestrian behavior, particularly in scenarios where external stimuli or cognitive distractions may influence decision-making.

These parameters were not selected arbitrarily; their ranges were determined through a combination of microsimulation documentation and previous research findings. For example, Lambda values typically range between 0 and 1, as identified in prior studies [23], ensuring that the parameter accurately reflects varying levels of pedestrian sensitivity. Similarly, intermediate values for A Social, B Social, and other parameters were guided by established research [24,25,26,27], ensuring that the sensitivity analysis is grounded in empirical evidence.

By incorporating these parameters, the study captures both the cognitive and social dimensions of pedestrian decision-making, offering a nuanced understanding of gap acceptance behavior. This approach not only refines microsimulation models like VISSIM but also provides urban planners, traffic engineers, and policymakers with actionable insights to improve infrastructure design, optimize traffic management, and enhance pedestrian safety. The deliberate selection and calibration of these parameters ensure that the model reflects real-world complexities, making it a valuable tool for both academic research and practical urban planning applications.

3.2. Simulation Setup

The study utilized PTV VISSIM 10, a widely recognized microsimulation software, leveraging its social force model (SFM) to simulate pedestrian dynamics and interactions with vehicular traffic. The primary objective was to analyze pedestrian gap acceptance at unmarked intersections by systematically varying nine key pedestrian behavior parameters: Tau, Lambda, A Social (isotropic), B Social (isotropic), A Social Mean, B Social Mean, React to N, Visual Density, and Noise. Each parameter was chosen based on its theoretical or indirect relevance to pedestrian gap acceptance, ensuring a comprehensive evaluation of behavioral influences. The simulation environment was designed to reflect a typical urban setting while simplifying the scenario to a single-lane, one-way traffic configuration. This intentional simplification minimized confounding variables, enabling a more precise analysis of the effects of individual parameters on pedestrian behavior. Stochastic modeling was applied to pedestrian speeds, capturing real-world variability in walking paces, with an average walking speed of 4.3 ft/s [28]. Similarly, vehicular speeds followed a stochastic distribution, averaging 25 mph, with traffic volumes set at 600 vehicles per hour and pedestrian volumes at 250 individuals per hour, aligning with typical urban conditions as outlined by the National Association of City Transportation Officials (NACTO).

Calibration was performed by comparing pedestrian crossing speeds and gap acceptance distributions from the simulation to empirical benchmarks (average pedestrian speed: 4.3 ± 0.5 ft/s, as per the previous study [29]. Each parameter was tuned iteratively until simulated behaviors fell within these acceptable thresholds. Intermediate values were selected based on SFM documentation and previous sensitivity analyses [10], aiming for even distribution within the parameter range. The initial setup utilized default VISSIM parameter values, which were then refined based on observed discrepancies between simulated and expected behaviors. Each parameter was tested across four distinct intermediate values, resulting in 41 simulation runs. During these tests, all other parameters were held constant at their baseline values to isolate the impact of each specific variable. Key assumptions streamlined the simulation process while maintaining realism. For instance, pedestrians who began crossing within one second of arriving at the curb were considered not to have engaged in gap acceptance decision-making, as such rapid crossings typically occur without immediate vehicular conflict. This threshold aligns with empirical findings indicating that pedestrian reaction times generally range between 0.874 and 1.147 s.

Data collection within the simulation utilized strategically placed Data Collection Lines (DCLs) at critical points in the interaction zones, allowing precise measurement of pedestrian entry and exit times. The primary metric, gap acceptance, was calculated based on the time between a pedestrian initiating crossing and the arrival of the following vehicle at the crosswalk. This approach provided a detailed and direct assessment of pedestrian crossing decisions, moving beyond the binary accepted/rejected gap frameworks commonly used in previous studies. These methodological details not only enhance the study’s transparency and reproducibility but also offer a robust framework for future research. By providing a comprehensive overview of the simulation setup, calibration processes, and key assumptions, this study serves as a valuable reference for researchers aiming to replicate or extend pedestrian behavior analysis in urban traffic environments.

3.3. Analytical Approach

Simulation results were analyzed to summarize each parameter’s impact on gap acceptance. Key metrics—mean, maximum, minimum, and standard deviation—were calculated for each parameter to identify those with the most significant influence. The analysis included detailed comparative assessments and hypothesis testing to evaluate the statistical significance of parameter effects.

While this study focuses on a simplified scenario, future research will aim to address more complex and realistic conditions. This includes extending the analysis to multi-lane and bidirectional traffic scenarios to capture the intricacies of real-world intersections. Additionally, it will investigate the interactions between multiple parameters to gain a comprehensive understanding of their combined influence on pedestrian behavior. Real-world validation will also be prioritized by comparing simulation outcomes with empirical observations, using field studies to gather data on pedestrian–vehicle interactions under diverse urban conditions, thereby improving model accuracy and reliability. Future work aims to address these areas and refine the applicability of microsimulation models, ensuring they reflect the nuanced dynamics of pedestrian behavior in diverse urban settings.

4. Data Collection

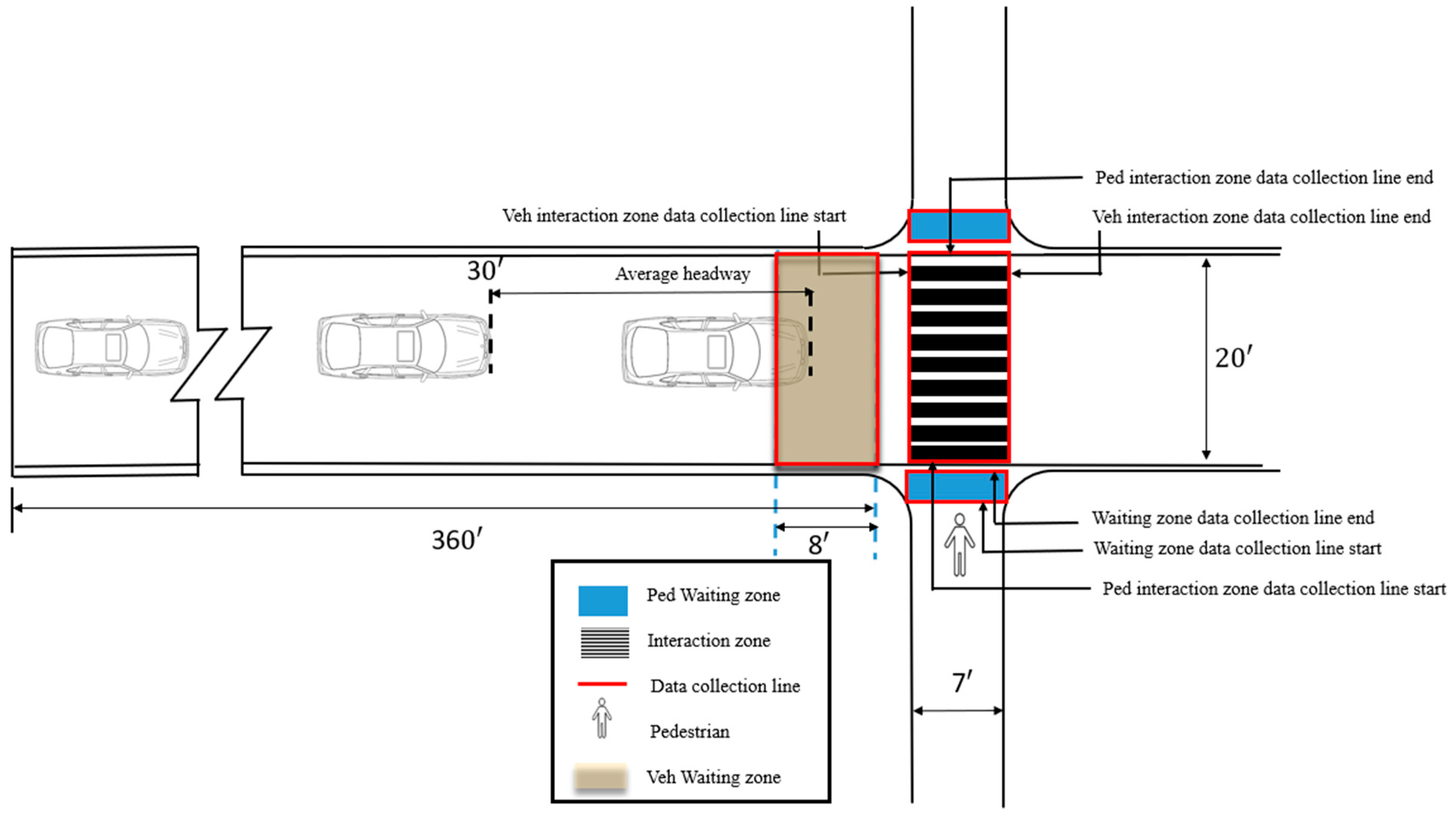
A schematic illustration of the simulation environment developed for measuring pedestrian gap acceptance is provided in Figure 1. In reality, pedestrians usually pause at the roadway/crossing interface (interaction zone) to evaluate the road’s safety [30]. These pedestrians within the simulation halt before the interaction zone, proceeding to cross only when they identified an appropriate gap. To achieve this level of realism, we modified the pre-set rules within the software using the trial-and-error method. The average headway is approximately 30 feet, exhibiting stochastic distribution characteristics [31]. This observation is pivotal in understanding the spatial dynamics and variability in vehicle spacing under the examined traffic conditions. Figure 1 further illustrates the location of Data Collection Lines (DCLs), strategically placed at the boundaries of the interaction zones, and identifies the area where pedestrians and vehicles would wait. The software can record the specific timestamps at these DCLs and the waiting area, which will subsequently be employed to measure accepted gaps. Figure 1 illustrates Data Collection Lines (DCLs) with red lines. The zone designated for pedestrian waiting is highlighted in blue, while the area reserved for vehicle waiting is depicted in brown. This figure is sketched approximately to scale, including the dimensions of the roads.

The measurement of gap acceptance in this research is rooted in existing methods utilized in pedestrian safety studies; however, it provides a more detailed and direct insight into pedestrian crossing behavior [32]. This measure can be considered an expanded version of existing methods, which often focused on pedestrian–vehicle interactions but did not consider the precise moments of crossing initiation (T_p) and the subsequent arrival of vehicles (T_v) [33]. Existing measures of gap acceptance tend to offer a limited understanding of the pedestrian–vehicle interaction, as they usually view the interaction in a binary manner: a gap is either accepted or rejected [24,27]. However, this research provides a granular perspective by considering the time a pedestrian commences crossing and the time of the subsequent vehicle’s arrival at the crosswalk.

This study adopted a structured method to formalize pedestrian gap acceptance decisions mathematically and applied specific assumptions to ensure both accuracy and realism in the analysis. Gap acceptance was quantified by measuring the time interval between a pedestrian’s decision to initiate crossing and the arrival of the next approaching vehicle at the crosswalk. This gap time was calculated using timestamp data collected via strategically placed Data Collection Lines (DCLs) in the simulation environment. The DCLs recorded the precise moment a pedestrian began to cross and the exact time the nearest vehicle passed the crosswalk. The time difference between these two events was the available gap time. A gap was considered “accepted” if the pedestrian initiated the crossing during this interval without conflicting with the approaching vehicle’s trajectory.

A key assumption was introduced to ensure analytical consistency: if a pedestrian’s waiting time before initiating the crossing was less than one second, this instance was not classified as an accepted gap. This threshold was based on established empirical findings, notably the study by Liu et al. [31], which identified pedestrian reaction times ranging from 0.874 s to 1.147 s, with an average close to one second. The one-second cutoff approximates the lower bound of these empirical values, ensuring that the analysis accounts for the cognitive delay inherent in human decision-making. This delay includes the time pedestrians need to perceive a gap, assess its safety, and physically initiate the crossing.

The rationale behind selecting the one-second threshold extends beyond empirical validation and addresses practical considerations of pedestrian behavior. In real-world scenarios, pedestrians rarely react instantaneously upon perceiving a gap. Instead, they require a brief cognitive processing period to assess traffic conditions and determine whether a crossing is safe. Setting the threshold at one second reflects this behavioral nuance and ensures that the simulated gap acceptance decisions align with real-world crossing behaviors. Furthermore, gaps shorter than one second typically do not provide pedestrians with enough time to make informed and safe crossing decisions. Thus, their exclusion from the analysis serves as a conservative measure that prioritizes pedestrian safety. This assumption also helps standardize the analytical approach, reducing the likelihood of including instances where pedestrians might have crossed opportunistically without fully evaluating the safer gap. By focusing on gaps that meet or exceed the one-second threshold, the study captures instances where pedestrians actively engaged in decision-making processes rather than reacting reflexively or by chance.

The primary metric in the study, gap acceptance, was calculated based on the following formula: $G=T_v-T_p$. In this equation, $T_p$ is the time when a pedestrian starts crossing, and $T_v$ is the time at which the next vehicle arrives at the crosswalk. $G$, then, represents the gap measured, i.e., the time a pedestrian has to cross before the next vehicle reaches the crossing zone. Gc is the critical gap threshold, determined through field observations or simulation.

The gap acceptance decision can be mathematically formalized as follows:

$$G_{accepted}=\left\{\begin{array}{c}1, if G\ge G_c\\ 0, if G<G_c\end{array}\right.$$

5. Results

Table 1. Behavior parameter descriptive statistics.

Parameter	Parameter Value	Mean Gap Acceptance Time (G) (s)	Standard Deviation of Gap Time (s)	Minimum Gap Time (s)	Maximum Gap Time (s)
Tau τ	0.05	2.09	0.92	1.01	3.14
	0.2	4.9	1.18	3.07	6.12
	0.4	8.58	1.84	6.09	10.95
	0.6	12.07	2.02	8.65	14.34
	0.8	12.32	3.45	7.13	15.45
Lambda	0.2	11.33	1.59	9.56	13.49
	0.4	8.78	1.37	7.12	10.96
	0.6	6.5	0.82	5.34	7.87
	0.8	4.66	0.93	3.45	6.09
	0.9	4.52	2.46	2.23	8.96
React to N	6	5.62	1.35	4.09	7.74
	8	3.82	1.22	2.23	5.87
	9	9.09	1.46	7.09	11.13
	10	8.27	1.55	6.65	10.76
	12	6.11	2.14	3.45	8.56
Noise	0.1	4.13	1.59	1.65	5.79
	1.2	5.32	1.66	3.28	7.87
	2	6.7	2.09	3.55	9.67
	4	8.37	2.37	4.92	12.56
	6	10.76	3.98	5.02	18.14
Visual Density	1	4.82	1.23	2.34	6.65
	3	6.39	2.37	3.28	9.89
	6	6.94	2.08	3.99	10.23
	13	8.64	2.83	4.99	12.56
	20	9.2	5.39	4.99	20.68
B Social isotropic	1	4.49	1.14	2.23	5.9
	2.8	6.53	2.22	3.28	8.99
	3.5	8.77	4.91	5.07	18.37
	4.8	9.36	3.48	3.71	15.45
A Social isotropic	1.3	5.18	2.07	2.5	7.94
	2.72	7.72	2.19	4.99	11.21
	5	9.17	2.98	6.89	15.01
	7	8.43	2.97	4.8	13.21
A Social Mean	0.2	6.6	1.56	4.99	9.09
	0.4	5.03	1.93	3.02	7.98
	0.6	4.89	1.36	2.99	6.76
	0.8	3.93	1.51	1.56	5.81
	0.9	3.78	1.82	1.12	6.12
B Social Mean	1	4.46	1.24	2.23	5.9
	2.8	6.04	1.84	3.28	8.3
	3.5	5.86	2.12	3.34	9.12
	4.8	5.91	2.22	1.12	9.12

demonstrates a nuanced relationship between pedestrian behavior parameters and gap acceptance times. Notably, higher values of ‘Tau’ indicate an increase in mean gap acceptance time, with ‘Tau’ at 0.8 showing a significant increase in both mean and standard deviation, suggesting greater variability at higher ‘Tau’ values. In contrast, ‘Lambda’ presents a different trend; as the parameter value increases from 0.2 to 0.9, there is a noticeable decrease in mean gap acceptance times, which could imply that pedestrians are less influenced by the directional force component at higher ‘Lambda’ values. For ‘React-to-N’, we see a peak in mean gap acceptance times at values 9 and 10, but this does not follow a linear progression, indicating that the maximum number of pedestrians considered in the social force calculation has a complex impact on gap acceptance times, which may not be directly proportional.

The ‘Noise’ parameter follows a more predictable trend, with increasing values correlating with longer mean gap acceptance times and larger standard deviations. This number suggests that higher levels of randomness in pedestrian movement result in more variable and extended gap acceptance times. With ‘Visual Density’, mean gap acceptance times increase as the Visual Density increases to 13, but then we see a slight decrease when moving to the highest category of 20. This could indicate that high pedestrian densities may lead to quicker gap acceptance times, possibly due to greater pressure or urgency pedestrians feel in these scenarios.

The isotropic parameters (‘B Social isotropic’ and ‘A Social isotropic’) display increasing mean gap times with higher parameter values, hinting at the strengthening of repulsive forces between pedestrians leading to longer gap times. However, ‘A Social isotropic’ shows a slight decrease at the highest value, possibly due to complex interactions at higher levels of social force that a linear model does not capture. The mean parameters (‘A Social mean’ and ‘B Social mean’) also display this non-linear relationship with the gap acceptance times, where higher values do not always result in increased mean times, again suggesting a complex interplay between social forces and pedestrian behavior.

6. Sensitivity Analysis

6.1. Lambda

Figure 2 presents the box plot for gap time across various Lambda values (0.2, 0.4, 0.6, 0.8, and 0.9). A notable trend in the box plots is an apparent inverse correlation, where increasing Lambda corresponds with decreasing mean and median gap time values. This pattern suggests that as the sensitivity to stimuli behind the pedestrian—represented by Lambda—increases, the pedestrian’s gap time, or the time they take to decide when to cross, decreases.

For Lambda at 0.2, the gap acceptance times are quite high, with values ranging up to approximately 13.49 s, which suggests a very cautious approach to crossing when pedestrians have a low sensitivity to stimuli from behind. This can be attributed to pedestrians being less influenced by the approaching traffic from behind and, therefore, taking longer to make crossing decisions due to less perceived pressure. As Lambda increases to 0.4 and 0.6, we see a decrease in gap acceptance times, with the upper range dropping to about 10.96 and 7.87 s, respectively. This decrease indicates that as pedestrians become more sensitive to stimuli from behind, they may feel more pressure from approaching traffic, thus shortening their decision time for crossing. The values here suggest a more moderate level of caution and a more typical range of gap acceptance times. When Lambda reaches 0.8 and 0.9, the gap acceptance times decrease, with the higher values at 6.09 and 8.96 s, respectively. Interestingly, the value of 0.9 presents an anomaly with one of the gap times spiking to 8.96 s, which could indicate an individual instance of increased caution or perhaps an outlier in the data.

We can interpret that a lower Lambda results in higher gap acceptance times, implying that pedestrians are less responsive to the traffic behind them and, therefore, take longer to decide to cross. As Lambda increases, the mean gap acceptance time decreases, which can be correlated with increased attentiveness to traffic conditions behind the pedestrian, leading to quicker crossing decisions. The trend, however, is not strictly linear, as shown by the spike at Lambda 0.9, suggesting that other factors may also influence pedestrian behavior. The findings for the Lambda parameter have practical implications for traffic management and pedestrian safety. Understanding the sensitivity of pedestrians to traffic approaching from behind can inform the design of crossing signals and warnings to ensure they are appropriately timed and positioned to account for different levels of pedestrian attention and reaction times.

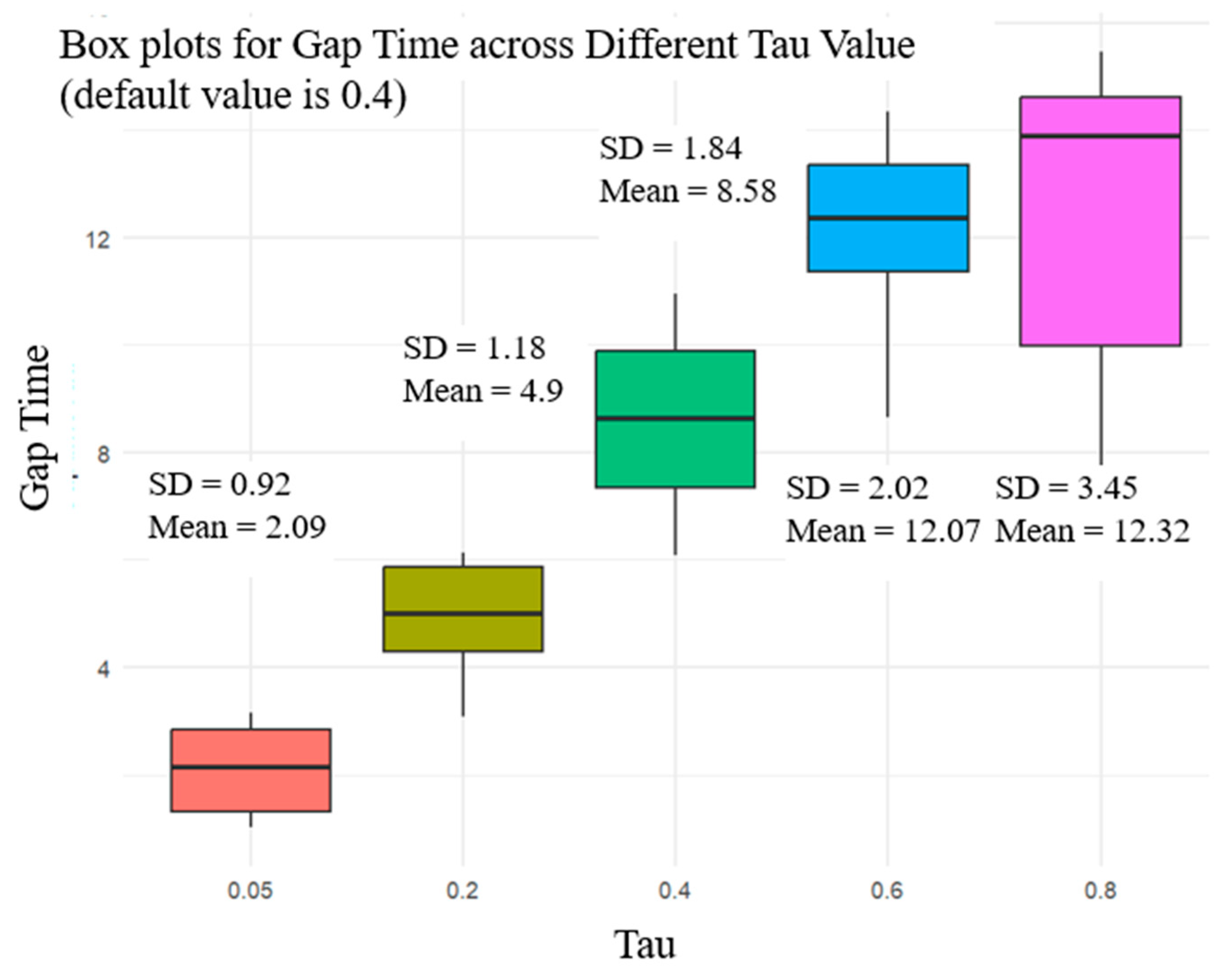
6.2. Tau

Figure 3 shows the box plots of gap time for different ranges of Tau. Analyzing the gap times across varying Tau values from 0.05 to 0.8 reveals a nuanced pattern of gap acceptance. At the lowest Tau value of 0.05, the gap acceptance times are quite low, with a mean of approximately 2.10 s. This suggests that when pedestrians react quickly to changes in their environment (a low Tau), their decisions to cross are made quite promptly. The standard deviation is also relatively low, indicating that the gap acceptance times are consistent among pedestrians. As the Tau value increases to 0.2 and 0.4, there is a noticeable increase in both the mean and the standard deviation of gap acceptance times. For Tau 0.2, the mean is around 4.98 s, and for Tau 0.4, it rises to approximately 8.48 s. This trend continues as Tau increases, which could imply that pedestrians with a higher relaxation time take longer to assess their environment and make a crossing decision. There is also more significant variability in their crossing times. For Tau values of 0.6 and 0.8, we see further increases in gap acceptance times, with means of approximately 12.07 and 12.32 s, respectively. The standard deviation for these values of Tau is quite significant, which suggests a wide range of pedestrian behaviors and decision-making processes at these higher relaxation times.

From these data, we can infer a correlation between Tau and gap acceptance times. As the relaxation time increases, pedestrians take longer to make a crossing decision, and there is more significant variability in their decision times. The distribution of gap acceptance times seems to widen with higher values of Tau, indicating a diversity in pedestrian responses when they have more time to react to their surroundings. This analysis can be highly relevant for urban planning and traffic engineering, as it provides insight into pedestrian behavior in response to traffic conditions. Understanding how pedestrians with different relaxation times interact with traffic can guide the design of crossings and signaling systems to improve safety and flow. The skewness of the data suggests most pedestrians have lower gap acceptance times, but there is a tail of pedestrians who take much longer, especially at higher Tau values. This could indicate a subset of the population that is particularly cautious or requires more time to process the traffic conditions before crossing. The Tau parameter is a crucial factor in understanding pedestrian crossing behavior, with its value directly influencing the time taken to make crossing decisions and the variability in these times among pedestrians.

6.3. A Social Isotropic

Figure 4’s box plot displays the gap time distribution for ‘A Social Isotropic’ values (1.3, 2.72, 5, 7). At a low A Social isotropic value of 1.3, pedestrians are less influenced by isotropic social forces, translating to relatively consistent and shorter gap acceptance times ranging from 2.5 to 7.94 s. This suggests that when pedestrians are less concerned with isotropic social forces, their decision-making is more straightforward, and they can make quicker crossing decisions. As the value increases to 2.72, representing a moderate sensitivity to isotropic social forces, we see a wider spread in gap times, ranging up to 11.21 s. This variance indicates a more complex decision-making process as pedestrians become more attuned to their surroundings, considering the social forces from all directions. The data exhibit even more significant variability at a higher A Social isotropic value of 5, with gap acceptance times reaching 15.01 s. This suggests that as pedestrians become more sensitive to the isotropic social forces, the complexity of their decision-making process increases, and they take more time to assess the overall social environment before crossing. The highest recorded A Social isotropic value of 7 shows a significant range of gap acceptance times, indicating a heightened consideration for isotropic social forces. This value is linked to longer decision times, as seen by a maximum of 13.21 s. This further solidifies the trend that higher sensitivity to isotropic social forces correlates with an increased time to make crossing decisions.

The parameter A Social isotropic in the social force model (SFM) encapsulates how pedestrians interact socially, factoring in isotropic forces around them—those that are equal in all directions. This A Social isotropic parameter analysis reveals its influence on pedestrians’ gap acceptance time, reflecting their readiness to initiate crossing based on social stimuli. The sensitivity analysis demonstrates a direct relationship between the A Social isotropic parameter and pedestrian gap acceptance time. As pedestrians place greater emphasis on isotropic social forces, their gap acceptance time lengthens, suggesting that they require a more favorable social context before deciding to cross. This insight is critical for urban planners and traffic engineers, indicating that pedestrian flow models must account for varying levels of social force sensitivity to predict pedestrian behavior at crossings accurately.

6.4. B Social Isotropic

Figure 5’s box plot displays the gap time distribution for ‘B Social Isotropic’ values (0.1, 0.2, 0.3, 0.4). At a B Social isotropic level of 1, representing a low need for personal space, gap acceptance times are relatively low, with a narrow range from 2.23 to 5.9 s. This suggests that when pedestrians are comfortable being closer to others, they make quicker decisions to cross, likely because they feel less pressure from nearby pedestrians. As B Social isotropic increases to 2.8, indicating a moderate increase in the desire for personal space, there is a slight upward trend in gap acceptance times, with a range now up to 8.99 s. This increase implies that pedestrians are taking more time to evaluate their surroundings and choose a suitable gap to cross, correlating with their increased need for personal space. At B Social isotropic 3.5, there is a notable jump in both the mean and the maximum gap acceptance times, with the maximum reaching 18.37 s. This significant increase indicates that as pedestrians’ preference for personal space increases, their decision time at crossings becomes more cautious and variable. The highest B Social isotropic level of 4.8 shows even more significant variability, with gap times ranging from 3.71 to 15.45 s. This high variability reflects the complex decision-making process when pedestrians need much personal space. Some pedestrians may still cross quickly if they perceive an immediate large gap, while others wait longer, contributing to a broader spread in the observed gap acceptance times.

The B Social isotropic (B Social isotropic) parameter in pedestrian dynamics influences how pedestrians maintain personal space around them, affecting their gap acceptance time—how long they wait before deciding to cross a road. The observed trend suggests a positive correlation between the B Social isotropic parameter and gap acceptance time. As pedestrians’ requirement for personal space increases, they tend to wait longer to find gaps in traffic that accommodate their comfort level. This parameter’s impact on pedestrian behavior is crucial for understanding and modeling pedestrian flow, especially in designing urban spaces and crossings that cater to different personal space needs to ensure smooth pedestrian traffic and safety.

6.5. A Social Mean

Figure 6’s box plot shows the gap time distribution for various ‘A Social Mean’ values (0.2, 0.4, 0.6, 0.8, 0.9), revealing exciting correlations. An inverse relationship is observed between A Social Mean and the mean and median gap time, suggesting that a larger A Social Mean correlates with a shorter gap time. At the lowest value of 0.2, there is a notable spread in gap acceptance times from 4.99 s to 9.09 s. This suggests that even at low levels of the social mean force, pedestrians can experience a broad range of decision times. It might indicate that minimal social grouping tendencies can still influence individual crossing behaviors to varying degrees. As the A Social Mean value increases to 0.4, the range of gap times shifts to between 3.28 and 7.98 s. Compared to the 0.2 group, this reduced maximum time may reflect a degree of group influence, where pedestrians might feel a pull toward conforming to group behaviors, leading to a narrower range of crossing times. Moving up to a value of 0.6, we again observe a lower maximum gap time of 6.76 s. Increasing the social mean force does not necessarily lead to longer gap times. Instead, social forces may provide a reference point for pedestrians, leading to quicker decision-making as the pedestrian navigates through a socially influenced environment. Interestingly, the trend reverses at the higher A Social Mean values of 0.8 and 0.9, where the data show minimum gap times decreasing to as low as 1.56 and 1.12 s, respectively. This drop suggests that at high levels of A Social Mean, pedestrians may be more inclined to cross quickly, possibly due to increased confidence or pressure within larger social groups.

‘A Social Mean’ measures the average social influence or interaction level in pedestrian behavior, with values indicating the degree of social cohesion or interaction among pedestrians in a given setting. This parameter reflects how social norms, group dynamics, or collective behaviors influence individual pedestrian decisions regarding gap acceptance in traffic. This sensitivity analysis indicates a complex relationship between the A Social Mean parameter and pedestrian gap acceptance times. Rather than a linear decrease in gap time with increased A Social Mean value, social forces have a nuanced effect on pedestrian behavior. Group behaviors might influence pedestrians in a way that either hastens or delays their crossing decisions depending on the strength of the social force. This insight can be valuable in developing pedestrian models for urban planning. Understanding social forces’ impact can help design crosswalks and signaling systems that accommodate natural pedestrian behaviors, ensuring safety and efficiency in pedestrian traffic flow.

6.6. B Social Mean

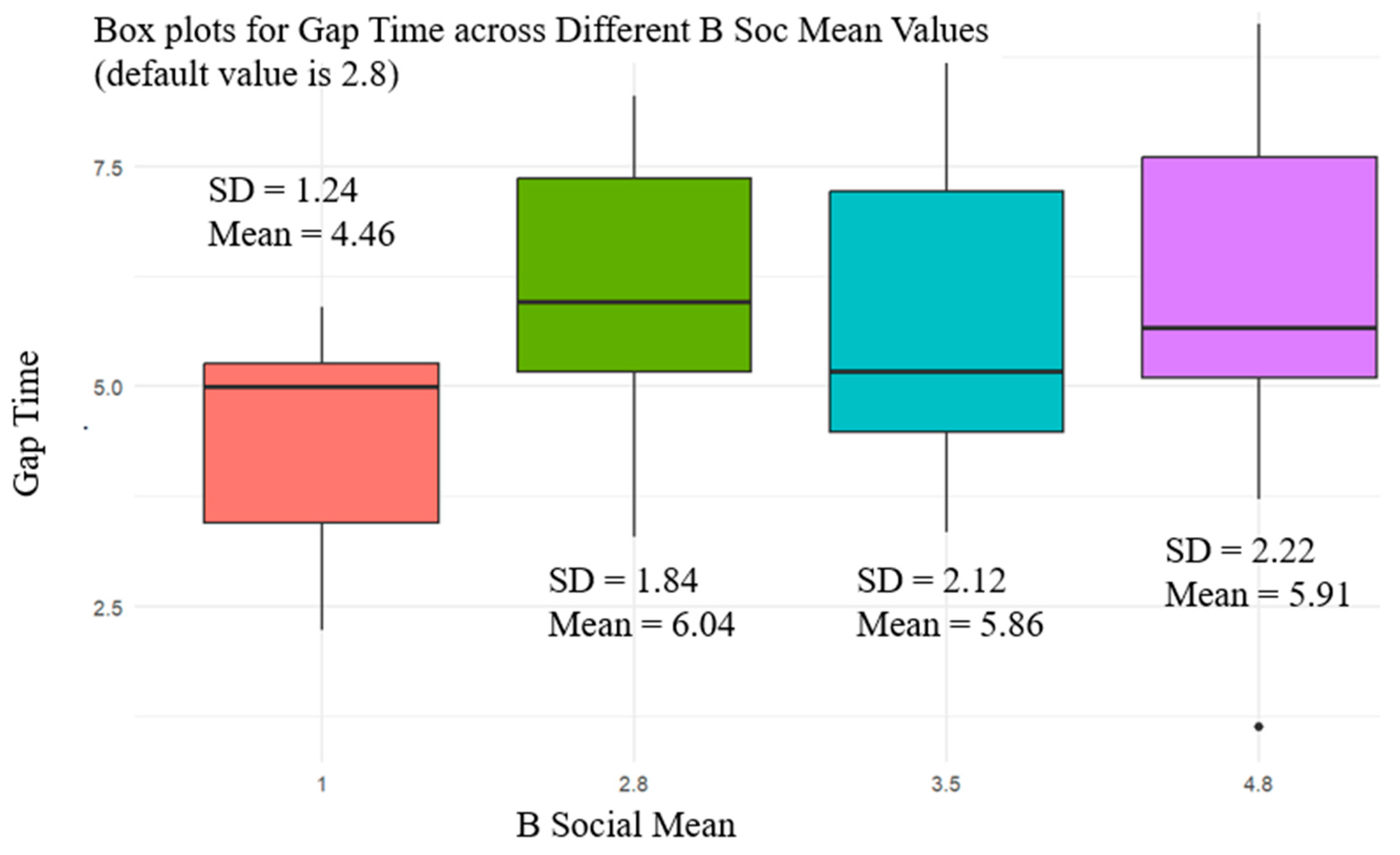
Figure 7’s box plot shows the gap time distribution for various ‘B Social Mean’ values (1.0, 2.8, 3.5, 4.8), revealing correlations. A primary observation is a positive correlation between B Social Mean and the mean and median gap time. As the B Social Mean rises, so do the mean and median gap times, implying a relationship between a higher B Social Mean and a more extended gap time.

For B Social Mean at a value of 1, the gap acceptance times range from 2.23 s to 5.9 s. This demonstrates that even with a minimal level of social force range, pedestrian behaviors vary significantly, implying a diversity in the way individuals respond to potential social grouping at lower force ranges, and increasing the B Social Mean value to 2.8 leads to a broader spread in gap times, extending from 3.28 s to 8.3 s. This increase in minimum and maximum gap times could suggest that a larger range in the social force causes a more significant variance in individual decision times, possibly due to the influence of group dynamics that encourage some pedestrians to wait for others, thereby extending their gap acceptance time. At the higher B Social Mean value of 3.5, an intriguing trend emerges where the minimum gap time decreases to 3.34 s, but the maximum gap time increases to 9.12 s. This result indicates that as a broader range of social forces influence pedestrians, their crossing times become more variable, potentially due to differences in individual comfort levels within groups or varying interpretations of social cues; at the highest observed B Social Mean value of 4.8, the spread in gap times is pronounced, ranging from a low of 1.12 s to a high of 9.12 s. This suggests a non-linear relationship between the range of social force and pedestrian behavior. An extensive range of social influence does not uniformly result in longer decision times. Still, it may create situations where some pedestrians rush to join a group while others delay their crossing to conform to group behaviors.

B Social Mean assesses the average level of social behavior in pedestrian settings, indicating the degree of social influence on pedestrian gap acceptance decisions. Higher ‘B Social Mean’ values may reflect increased social cohesion or peer influence, potentially leading to more collective or cautious crossing behaviors. Conversely, lower values suggest individualistic decision-making, which is less influenced by surrounding social behaviors. The data trend implies that as B Social Mean increases, the variability in gap acceptance times also rises, highlighting the diverse impact of social behaviors on pedestrian crossing decisions in different traffic environments. This analysis of B Social Mean indicates that the range of the social force has a complex impact on pedestrian gap acceptance times. The variability in crossing behaviors underscores the importance of considering individual and group dynamics in pedestrian flow modeling. For urban planners and traffic engineers, these insights can inform the design of crossing environments that better cater to the natural social behaviors of pedestrians, potentially improving both safety and traffic efficiency.

6.7. React to N

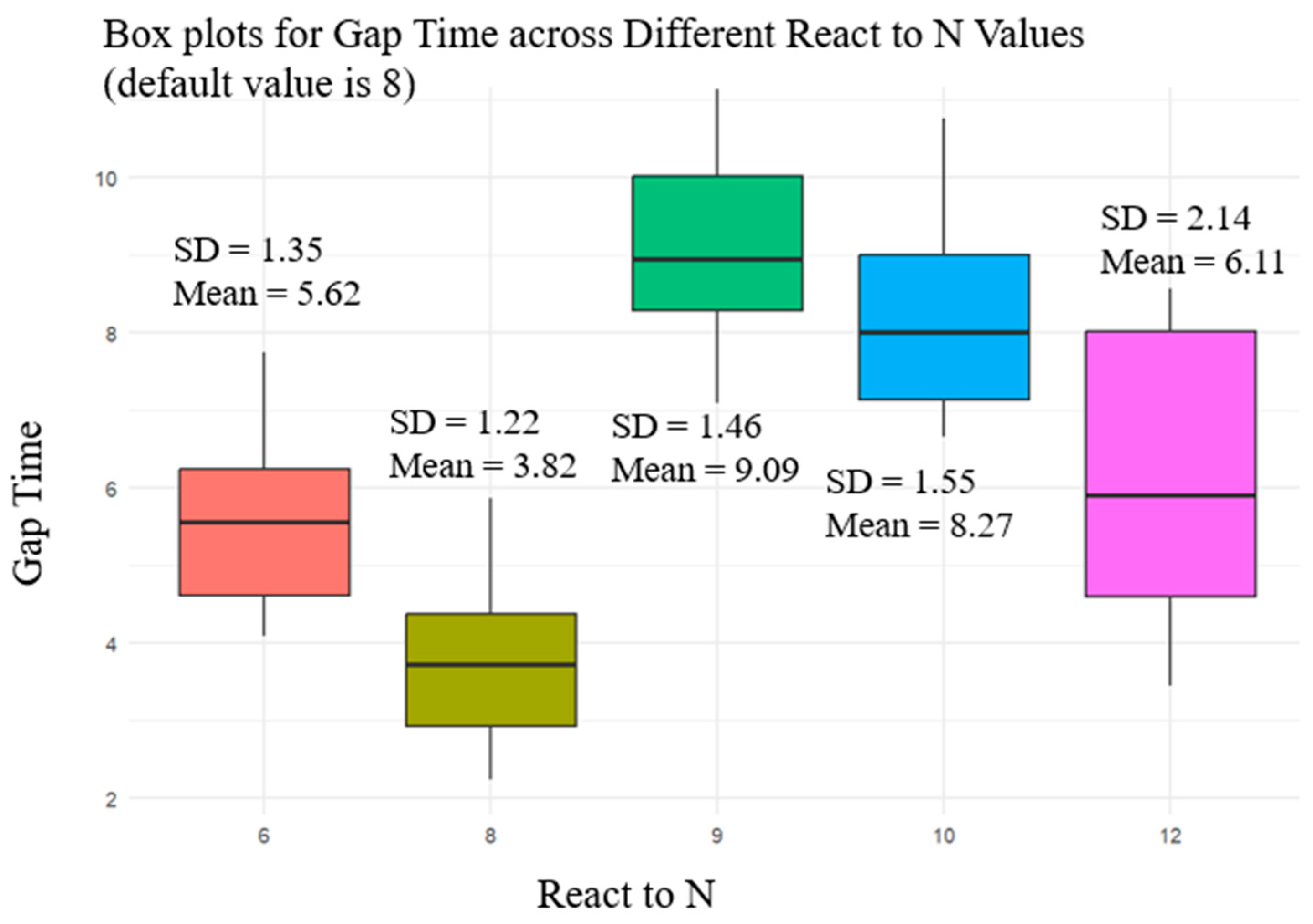
Figure 8 presents box plots for gap time across different ‘React to N’ values (6, 8, 9, 10, 12), illustrating a nuanced relationship between the mean gap time and ‘React to N’ values. At a React-to-N value of 6, the gap acceptance times are moderately varied, ranging from 4.09 to 7.74 s. This suggests that when pedestrians consider a moderate number of their peers, their gap acceptance times can fluctuate but generally remain within a middle range. It implies a level of caution balanced with an awareness of the social group, potentially leading to a collective crossing rhythm in moderate traffic conditions.

When the value of React-to-N increases to 8, we see a surprising dip in gap acceptance times, with values tightening to a lower range between 2.23 and 5.87 s. This could indicate that as pedestrians consider more individuals in their vicinity, there might be a stronger herd effect, leading them to make quicker crossing decisions based on the actions of the larger group. This clustering of lower gap times suggests a potential shift from individual to collective decision-making dynamics. However, an exciting trend reversal occurs at a React-to-N of 9, where gap acceptance times shoot up, peaking at 11.13 s. This increase could indicate that there is a threshold after which considering more pedestrians does not lead to quicker decisions but instead causes hesitation or delay, possibly due to overstimulation or increased complexity in processing the actions of many individuals. The data for a React-to-N of 10 and 12 continue this trend of higher gap acceptance times, with a decrease compared to the React-to-N of 9. The gap times for these values span from 6.65 to 10.76 s and 3.45 to 8.56 s, respectively. These results might suggest an optimal number of individuals a pedestrian can effectively consider before the decision-making process is negatively impacted, either speeding up due to a strong follow-the-crowd instinct or slowing down due to increased processing demands.

Analyzing the React to N parameter gives us insight into pedestrian behavior in response to the number of other pedestrians considered in their decision-making process when crossing. React-to-N defines the number of pedestrians that are accounted for in the social force affecting a given pedestrian. A higher React-to-N value implies that the pedestrian is influenced by a larger number of surrounding individuals when making gap acceptance decisions. React-to-N seems to have a complex relationship with gap acceptance times. The initial decrease and subsequent increase in gap acceptance times as React-to-N values grow suggest a nuanced interaction between individual pedestrian behavior and group dynamics. For urban planners and traffic engineers, these findings can be significant in designing pedestrian crossings and managing crowd movements, especially in busy urban areas with high pedestrian volumes. Understanding at which point collective behavior aids or hinders pedestrian flow could lead to improved safety measures and traffic signaling systems.

6.8. Noise

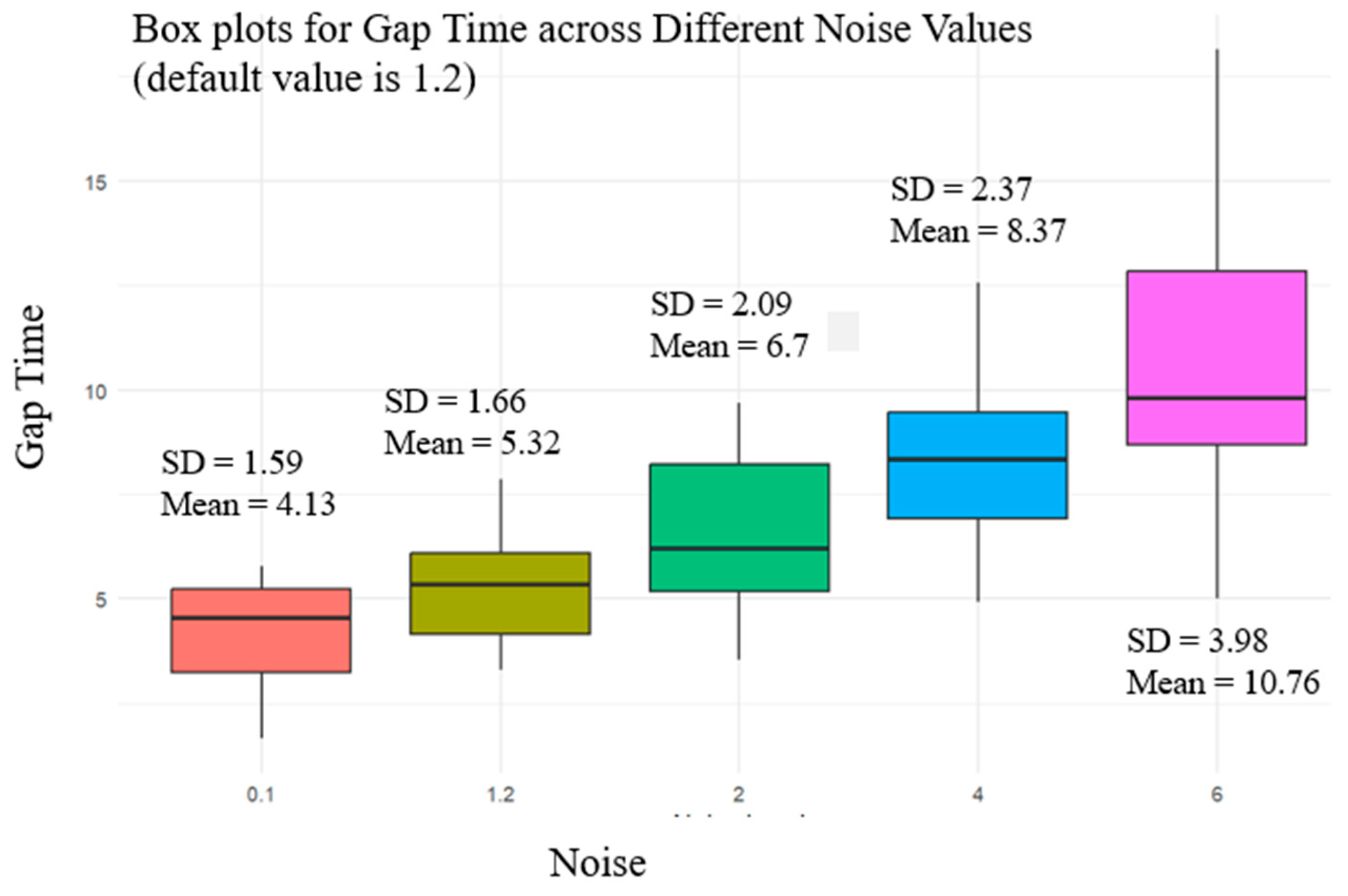
Figure 9 outlines the distribution of gap time across different Noise levels (0.1, 1.2, 2, 4, 6), indicating a correlation between mean gap time and Noise. For a Noise level of 6, the gap acceptance times are high, ranging from 5.02 to 18.14 s, with a significant outlier at 18.14 s. This high variability can be attributed to the model’s assumption that higher Noise leads to more erratic pedestrian behavior. As pedestrians react to a greater degree of randomness in their environment, their gap acceptance times may increase due to uncertainty and hesitation, reflecting a situation where pedestrians might be dealing with unexpected events or distractions. Reducing the Noise to 4 slightly decreases the spread of gap acceptance times, though they still cover a wide range from 4.92 to 12.56 s. This suggests that while lower levels of Noise lead to more predictable behavior than the highest level, there remains a considerable degree of variability in how pedestrians perceive and react to gaps in traffic. At a Noise level of 2, the gap times reduce further, between 3.55 and 9.67 s. This reduced Noise level can be seen as a proxy for a less chaotic environment, where pedestrians can better predict traffic flow and thus make more confident crossing decisions. The lowest Noise levels, 1.2 and 0.1, correspond to the narrowest range of gap acceptance times, from 1.65 to 7.87 s and 2.23 to 5.79 s, respectively. These times reflect a scenario where pedestrians encounter fewer unexpected events and behave more consistently. It suggests that in environments perceived as predictable and stable, pedestrians can make more uniform and quicker crossing decisions.

The ‘Noise’ parameter quantifies ambient Noise levels in pedestrian environments, examining their influence on gap acceptance times. Lower ‘Noise’ values could represent quieter settings, potentially leading to shorter gap acceptance times due to less distraction. At the same time, higher levels might cause longer gap times as Noise increases distraction or stress. The Noise parameter in pedestrian behavior modeling introduces variability into the movement patterns of simulated pedestrians, mimicking the unpredictable nature of human actions. Analyzing gap acceptance times across Noise levels reveals how randomness injected into pedestrian decision-making impacts their crossing behavior.

Higher Noise levels correlate with increased variability and higher gap acceptance times, indicating that pedestrians may be less sure of themselves and more cautious when there is more unpredictability in their environment. On the other hand, lower Noise levels are associated with more consistent and shorter gap acceptance times, suggesting that pedestrians are more decisive and confident when they perceive their environment as being more predictable. This insight has practical implications for urban design and traffic planning. By minimizing environmental factors contributing to uncertainty—erratic traffic flow, unclear signage, or poor visibility—pedestrians can make safer and more efficient crossing decisions.

6.9. Visual Density

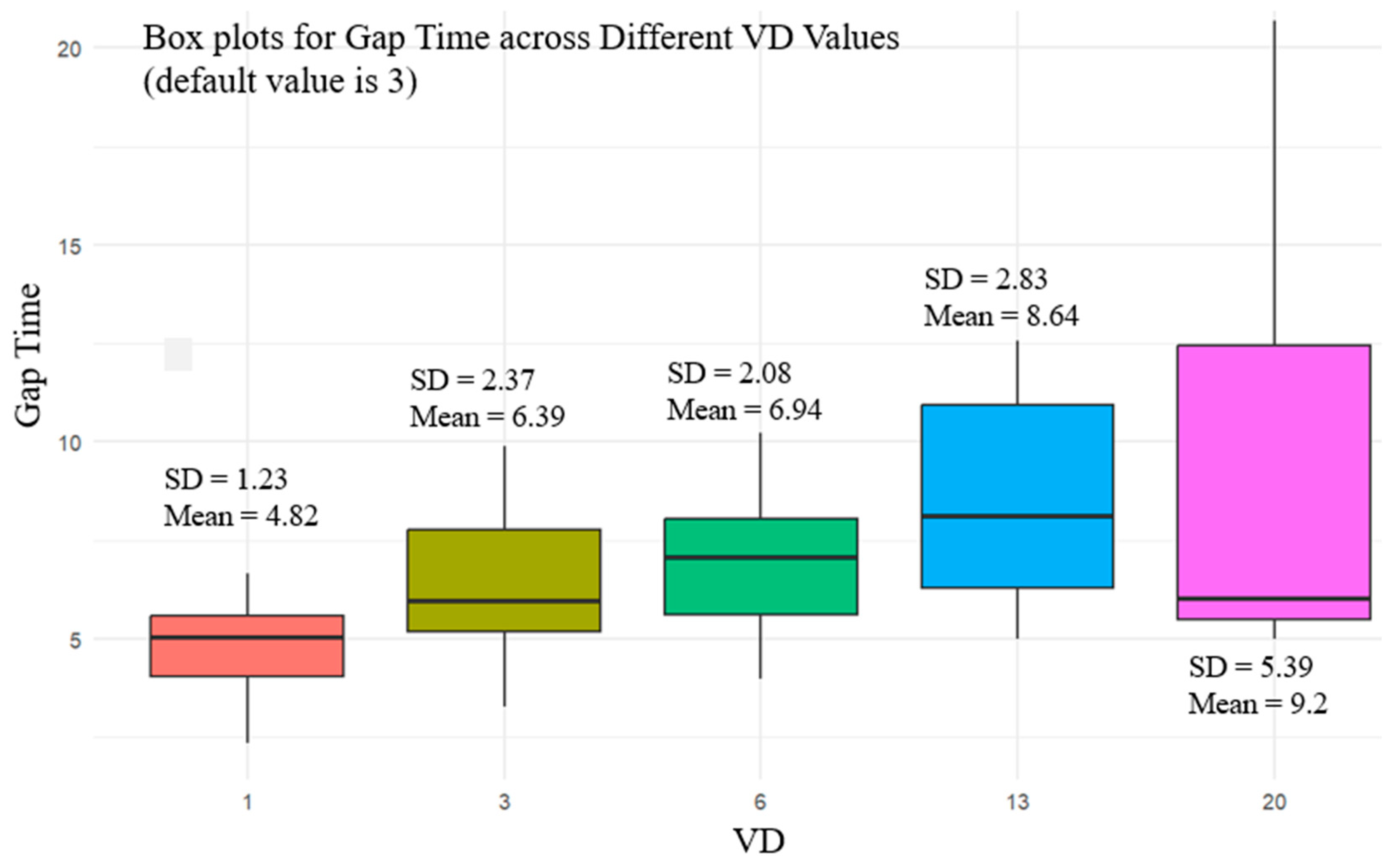
Figure 10 presents the distribution of gap time across varying Visual Density levels (1, 3, 6, 13, 20), highlighting an overall increase in the mean gap time as Visual Density increases. For Visual Density at level 1, representing low pedestrian density, gap acceptance times range from 2.34 to 6.65 s. The lower range of times indicates that pedestrians are likely to cross more quickly when there are fewer individuals around them, with less need to navigate or avoid others. This finding is consistent with intuitive expectations—lower crowd density generally allows for smoother pedestrian movement and quicker decisions at crosswalks. Increasing the Visual Density to level 3 shows a slight upward trend in both the mean gap acceptance times and the range, extending to 9.89 s. This suggests that a moderate increase in crowding begins to impact pedestrian crossing behavior, likely due to the additional attention required to avoid collisions and navigate through the denser pedestrian environment. A more pronounced increase in mean and maximum gap acceptance times is observed at Visual Density level 6, with the maximum time reaching 10.23 s. At this level of crowding, pedestrians must consider more variables when deciding to cross, such as the movement patterns of those around them, which may result in longer deliberation times at the curb.

At high Visual Density levels of 13 and 20, representing very crowded conditions, there is a significant increase in the variability in gap acceptance times, with the maximum values soaring to 12.56 and 20.68 s, respectively. These significant variances indicate that as pedestrian density becomes very high, individual behavior becomes less predictable, with some pedestrians choosing to wait longer to find larger traffic gaps that allow for comfortable crossing amidst the crowd.

The ‘Visual Density’ parameter evaluates the impact of environmental visual complexity on pedestrian gap acceptance times. Higher ‘Visual Density’ values, indicating greater visual clutter, may prolong gap acceptance times as pedestrians navigate more visually dense environments, requiring additional time to process information and assess safety. Conversely, lower ‘Visual Density’ values suggest simpler visual environments, potentially facilitating quicker decision-making and shorter gap acceptance times. The Visual Density parameter indicates that as pedestrian crowding increases, the average time taken to decide when to cross and the variability in these times among different pedestrians also increase. This has implications for traffic flow and pedestrian safety, emphasizing the importance of designing urban spaces that accommodate varying levels of pedestrian traffic without creating undue delays or safety risks.

The sensitivity analysis in this study highlights the significant influence of key social force model (SFM) parameters on pedestrian gap acceptance behavior. Tau (reaction time) emerged as a primary factor, where higher values led to more conservative crossing behavior and longer gap acceptance times, especially relevant for vulnerable populations like the elderly. Lambda (sensitivity to stimuli) showed that increased spatial awareness reduced decision-making time, making it vital for modeling cautious behavior in complex intersections. A Social (isotropic) and B Social (isotropic), governing social repulsive forces, affected pedestrian spacing and crossing dynamics. Higher values resulted in more dispersed pedestrian flows and longer wait times, while lower values encouraged group crossings. The mean social parameters, A Social Mean and B Social Mean, revealed that stronger group cohesion prompted quicker crossings, while larger social force ranges led to more hesitation. React to N, reflecting the number of pedestrians influencing an individual’s decision, showed moderate social influence accelerated crossings, but excessive influence caused hesitation. Noise introduced randomness, increasing variability in gap acceptance and mimicking real-world unpredictability. Visual Density impacted decision times, with higher perceived crowding leading to slower decisions, though extreme density sometimes triggered faster crossings due to social pressure. These findings emphasize the need for dynamic parameter calibration in simulation models to accurately reflect real-world behaviors. Adjusting parameters based on demographics, crowd density, and environmental complexity can enhance the realism and utility of pedestrian traffic simulations, leading to safer and more efficient urban designs.

6.10. Parameter Effects and Behavioral Interpretations

The effects of pedestrian behavior parameters on gap acceptance times, as observed in this study, reflect the internal dynamics of the social force model (SFM). Parameters such as Lambda and Tau demonstrated strong influences—Lambda showed decreasing gap times with higher directional sensitivity, while Tau exhibited increasing gap times with greater response inertia. Noise introduced variability consistent with the model’s treatment of randomness, and Visual Density affected crossing delays as environmental complexity increased. React to N exhibited a non-linear pattern, suggesting sensitivity to modeled social interactions, while A/B Social parameters influenced delay based on the strength and range of the repulsive force. These findings underscore the importance of parameter tuning for accurate microsimulation. Empirical validation is recommended to support the applicability of these simulation-based results in real-world contexts.

6.11. Hypothesis Testing

As each behavioral parameter had multiple levels or categories, we used one-way Analysis of Variance (ANOVA) to determine whether the mean gap acceptance time differed significantly across these levels. ANOVA, an extension of the t-test, is well suited for comparing means across more than two groups [34,35]. Before conducting the ANOVA, we performed assumption-confirmatory tests to verify that the dataset met the necessary conditions for this statistical analysis. The assumption of normality was tested using the Shapiro–Wilk test, homogeneity of variances was assessed with Levene’s test, and independent observations were confirmed during the data collection phase. The dataset met all criteria, making ANOVA an appropriate test [36]. The fundamental hypotheses for all nine pedestrian behavioral parameters (B Social Mean, A Social Mean, B Social isotropic, A Social isotropic, React to N, Visual Density, Noise, τ, and $\lambda$) are consistent.

We can represent this commonality using the behavioral parameter ‘$X_a$’ as a placeholder: The null hypothesis ($H_0$) posits that the means of the gap time are identical across all categories of ‘$X_a$’. In other words, we hypothesize that the specific categorization of ‘$X_a$’ does not influence the gap time. This is a hypothesis of no effect or no difference. The alternative hypothesis ($H_a$), contrarily, assumes that at least one category of ‘$X_a$’ manifests a different mean gap time. This means that the categorization of ‘$X_a$’ does indeed influence the gap time. To apply these hypotheses to each specific behavioral parameter, replace ‘$X_a$’ with the parameter in question. The consistent format of these hypotheses allows for systematically exploring each pedestrian behavioral parameter’s possible effects on the gap time while facilitating a comprehensive comparison of these effects across the different parameters [37].

The results from the ANOVA test provided insights into how pedestrian behavior parameters influence the gap acceptance time. The ‘B Social isotropic’, ‘A Social Mean’, ‘React to N’, ‘Visual Density’, ‘Noise’, ‘Tau’, and ‘Lambda’ parameters were all found to be statistically significant (p < 0.05), which are also given in

Table 2. ANOVA results for gap time across different pedestrian behavioral parameters.

Parameter	F Statistic	p-Value	Significance (p < 0.05)
B Social Mean	1.301	0.293	Not Significant
A Social Mean	3.605	0.0163	Significant
B Social isotropic	4.384	0.0116	Significant
A Social isotropic	3.026	.0523	Not Significant
React to N	12.65	6.35 × 10−6	Significant
Visual Density	2.888	0.0343	Significant
Noise	8.052	0.000103	Significant
Tau	27.79	7.05 × 10−9	Significant
Lambda	22.74	1.88 × 10−8	Significant

. This indicates meaningful differences in the gap times across different levels of these parameters. Hence, these parameters have a consequential effect on the gap times. Conversely, the ‘B Social Mean’ and ‘A Social isotropic’ parameters had p-values greater than 0.05, suggesting that different levels of these parameters do not significantly affect the gap times. Notably, failing to reject the null hypothesis for these parameters does not confirm the absence of an effect, but rather that there is insufficient evidence to conclude that an effect exists.

It is essential to note that while these findings demonstrate statistical significance, they do not necessarily imply practical significance. Future work could explore the effect sizes better to understand the practical implications of these test statistics.

6.12. Post Hoc Analysis (Tukey’s HSD) for Significant Parameters

In this study, one-way Analysis of Variance (ANOVA) was used to evaluate whether changes in individual pedestrian behavior parameters significantly affected the gap acceptance time. While ANOVA can identify whether at least one group differs significantly from the others, it does not indicate which specific groups differ. Therefore, to determine the nature and location of these differences among the multiple levels of each parameter, we conducted post hoc tests using Tukey’s Honestly Significant Difference (HSD) method. This approach enabled pairwise comparisons while controlling for the family wise error rate, ensuring statistical rigor in identifying the parameter levels that contributed most to behavioral variation. Additionally, effect sizes were calculated using partial eta squared (η²) to quantify the magnitude of each parameter’s influence on gap acceptance behavior. While p-values indicate whether an effect exists, effect sizes reveal the practical significance of that effect. In the context of microsimulation modeling, this distinction is crucial.

The post hoc analysis (Tukey’s HSD) revealed significant differences in pedestrian gap acceptance times across key behavioral parameters (

Table 3. Post hoc analysis (Tukey’s HSD).

Parameter	Parameter Value Comparison	Mean Difference in Gap Time (G) (s)	p-Value	Effect Size (Cohen’s d)
$Tau$	0.05 vs. 0.2	2.81	<0.001	1.2 (Large)
	0.05 vs. 0.4	6.49	<0.001	2.8 (Very Large)
	0.05 vs. 0.6	9.98	<0.001	4.2 (Very Large)
	0.05 vs. 0.8	10.23	<0.001	4.3 (Very Large)
	0.2 vs. 0.4	3.68	<0.001	1.6 (Large)
	0.4 vs. 0.6	3.49	0.002	1.5 (Large)
$Lambda$	0.2 vs. 0.4	2.55	0.003	1.1 (Large)
	0.2 vs. 0.6	4.83	<0.001	2.3 (Very Large)
	0.2 vs. 0.8	6.67	<0.001	3.1 (Very Large)
	0.2 vs. 0.9	6.81	<0.001	3.2 (Very Large)
	0.6 vs. 0.8	1.84	0.12	0.8 (Medium)
$React to N$	6 vs. 9	3.47	<0.001	1.9 (Large)
	8 vs. 9	5.27	<0.001	2.3 (Very Large)
	9 vs. 12	2.98	0.008	1.4 (Large)
$Visual Density$	1 vs. 13	3.82	0.012	1.1 (Large)
	1 vs. 20	4.38	0.003	1.3 (Large)
$Noise$	0.1 vs. 6	6.63	<0.001	2.5 (Very Large)
	2 vs. 6	4.06	0.001	1.7 (Large)

). For instance, the Tau parameter, representing pedestrian reaction time, exhibited a strong positive relationship with the gap time. Comparisons showed that higher Tau values (e.g., 0.6 vs. 0.05) corresponded to a markedly larger waiting time, with effect sizes ranging from large (Cohen’s d = 1.2 for 0.05 vs. 0.2) to very large (d = 4.3 for 0.05 vs. 0.8). Similarly, the Lambda, which governs sensitivity to stimuli from behind, demonstrated an inverse trend: higher values (e.g., 0.9 vs. 0.2) significantly reduced gap acceptance times (d = 3.2), suggesting pedestrians with enhanced spatial awareness made quicker crossing decisions. Non-linear effects were observed for React to N, where moderate group influence (e.g., React to N = 9) led to delayed decisions compared to smaller groups (React to N = 6 or 8), with a large effect size (d = 2.3). Parameters such as Noise and Visual Density further underscored environmental complexity, with higher levels exacerbating variability in crossing behavior (d = 2.5 and 1.3, respectively).

These findings emphasize the critical role of parameter-specific calibration in pedestrian behavior models. For instance, the large effect sizes for Tau and Lambda highlight their utility in tailoring simulations to reflect demographic variability, such as slower reaction times among elderly pedestrians or more caution in dense traffic. The non-significant difference between Tau = 0.6 and 0.8 (p = 0.12) suggests a threshold beyond which reaction time adjustments yield diminishing returns, a nuance vital for optimizing signal timings. Similarly, the pronounced impact of Noise and Visual Density underscores the need to design urban spaces that minimize environmental unpredictability, such as clear signage or reduced crowding at crossings. Collectively, these results provide insights for refining microsimulation tools and designing pedestrian-centric infrastructure, ensuring models align with real-world behavioral complexity while enhancing urban safety and efficiency.

7. Discussion

7.1. Parameter Sensitivity and Behavioral Interpretations

This study explored the impact of nine key pedestrian behavioral parameters on gap acceptance times in road-crossing scenarios, leveraging statistical analyses such as ANOVA to identify significant relationships. The findings highlight the influence of several parameters, including ‘A Social Mean’, ‘B Social Isotropic’, ‘React to N’, ‘Visual Density’, ‘Noise’, ‘Tau’ (τ), and ‘Lambda’ (λ). These results provide insights into pedestrian behavior and inform microsimulation model calibration. However, it is critical to address the limitations of behavioral interpretation, particularly for parameters not directly related to gap acceptance.

While parameters like ‘Tau’ and ‘Lambda’ have a clear theoretical connection to pedestrian decision-making—representing response time and sensitivity to environmental stimuli, respectively—others, such as ‘B Social Isotropic’ and ‘React to N,’ serve as proxies for broader social interactions [37]. These parameters capture social forces and group dynamics within the simulation environment but do not inherently reflect individual behavioral traits. For instance, while higher ‘B Social Isotropic’ values suggest extended gap acceptance times due to stronger repulsive social forces, attributing this to increased personal space preferences or social awareness extends beyond the parameter’s modeled intent. Similarly, the non-linear trends observed in ‘React to N’ highlight the complexity of group influences but should not be overstated as direct behavioral tendencies without empirical validation.

7.2. Parameter Sensitivity and Model Calibration

This study aimed to assess parameter sensitivity to guide calibration efforts for pedestrian behavior models. The significant relationships identified through ANOVA provide a foundation for adjusting model parameters to align simulation outputs with observed pedestrian behaviors [38]. For example, the sensitivity of ‘Visual Density’ and ‘Noise’ parameters to gap acceptance times underscores the importance of environmental conditions in shaping pedestrian decisions. These findings support the need for calibrated models that account for variability in pedestrian behavior under different environmental contexts. However, the study’s focus on parameter sensitivity limits its capacity to provide definitive behavioral insights. The relationships identified are specific to the controlled simulation environment and should not be generalized without empirical validation.

To further understand the insight and strength of differences among parameter levels, post hoc analyses using Tukey’s HSD were conducted for all significant ANOVA results. These pairwise comparisons revealed which specific levels of each parameter led to considerable variation in gap times. Additionally, effect sizes were calculated using Cohen’s d, providing insight into the magnitude of each parameter’s influence. Notably, Tau and Lambda exhibited large to very large effect sizes, indicating strong practical implications for simulation calibration. These results highlight parameters that have a meaningful impact on pedestrian decision-making behavior in microsimulation environments. Future research should integrate field studies to test the robustness of these findings and refine the behavioral assumptions underpinning microsimulation models.

7.3. Practical Implications for Urban Planners and Traffic Engineers

The practical implications of this study are significant for urban planners and traffic engineers tasked with designing safe and efficient pedestrian environments. The sensitivity of parameters like ‘Tau’ and ‘Lambda’ to gap acceptance times highlights the need for adaptive traffic management systems that consider pedestrian response times and sensitivity to environmental stimuli. For example, longer pedestrian crossing times in high ‘Visual Density’ scenarios suggest the need for wider crossings or staggered signals to accommodate varying pedestrian speeds and reduce potential conflicts [39].

Additionally, the influence of the ‘Noise’ and ‘React to N’ parameters on decision-making variability emphasizes the importance of designing environments that minimize unpredictability [40]. Clear signage, well-maintained crossings, and consistent traffic flows can mitigate the effects of environmental randomness and enhance pedestrian confidence in decision-making. These insights can inform targeted interventions to improve pedestrian safety and urban mobility, such as optimized signal timings or enhanced crosswalk designs.

7.4. Limitations and Future Directions

This study’s reliance on a simplified scenario provided a controlled environment for conducting parameter sensitivity analysis, effectively isolating the effects of individual pedestrian behavior parameters by minimizing confounding variables. This approach allowed for precise calibration and a clearer understanding of how each parameter influences gap acceptance behavior. However, such simplification inherently limits the generalizability of the findings to the complexities of real-world urban environments, where pedestrians encounter multi-lane, bidirectional traffic flows, varying vehicle types, and diverse crossing conditions.

To address these limitations, future research should expand the scope of analysis to encompass multi-lane and bidirectional traffic scenarios. These more complex settings better reflect the intricacies of real-world intersections, where pedestrian decision-making is influenced by dynamic factors such as opposing vehicle flows, varying traffic densities, and the presence of turning movements. Incorporating these complexities will not only enhance the ecological validity of the findings but also provide a more comprehensive understanding of pedestrian behaviors across diverse urban contexts.

Another critical direction for future research lies in exploring the interactions between behavioral parameters. While this study focused on the isolated effects of individual parameters, pedestrian decision-making is inherently multifaceted, shaped by the interplay of various social, cognitive, and environmental factors. Investigating how combinations of parameters—such as the joint influence of reaction time (Tau) and social pressure (React to N)—affect gap acceptance can reveal emergent behaviors that single-parameter analyses may overlook. This multi-dimensional approach will contribute to the development of more robust and realistic microsimulation models.

Real-world validation remains essential to test the robustness and practical applicability of the simulation findings. Controlled field studies that observe pedestrian behavior under varied traffic conditions will enable the refinement of microsimulation models, ensuring that simulated behaviors align closely with observed patterns. Such empirical validation will also support the calibration of behavioral parameters, reducing the gap between theoretical modeling and practical urban planning applications. These studies should particularly focus on diverse demographic groups and varied urban settings to account for behavioral heterogeneity and cultural differences in pedestrian behavior.

Furthermore, future research should explore the psycho-physiological dimensions of pedestrian decision-making, such as stress responses, cognitive load, and risk perception, which were beyond the scope of this study. Integrating biometric data—like heart rate variability or eye-tracking measures—into pedestrian modeling can provide deeper insights into the cognitive and emotional states that influence crossing decisions, particularly under high-stress or time-constrained conditions.

Ultimately, advancing pedestrian behavior modeling requires a holistic approach that bridges controlled simulation with real-world complexity. By expanding scenario types, investigating parameter interdependencies, and validating findings through empirical studies, future research can contribute to the development of more accurate, reliable, and human-centered microsimulation tools. These enhancements will not only improve the predictive accuracy of pedestrian behavior models but also provide urban planners, traffic engineers, and policymakers with more effective strategies for designing safer and more efficient pedestrian environments.

8. Conclusions

Understanding the intricacies of pedestrian dynamics, particularly in congested urban environments, is essential for advancing transportation planning and safety. This study significantly contributes to pedestrian behavior modeling by systematically exploring the sensitivity of nine key behavioral parameters within the social force model (SFM) and their influence on gap acceptance in microsimulation environments. By isolating and analyzing each parameter, this research offers valuable insights into pedestrian decision-making processes and the broader implications for urban planning, traffic engineering, and simulation modeling.

The primary objective of this study was to investigate parameter sensitivities rather than to develop a fully calibrated pedestrian behavior model. Through rigorous sensitivity analyses and statistical validation using ANOVA, the study identified critical parameters—such as pedestrian response time (Tau), spatial sensitivity (Lambda), and environmental complexity (Visual Density)—as significant influencers of gap acceptance behavior. Tau was shown to directly impact crossing decisions, with higher values correlating with longer and more variable gap acceptance times, mainly affecting vulnerable populations. In contrast, increased Lambda values, indicative of increased spatial awareness, led to quicker crossing decisions. Visual Density further emphasized the role of environmental complexity, where increased crowding prompted longer and more cautious gap acceptance behaviors.

Social dynamics also emerged as influential factors. Parameters like A Social and B Social (both isotropic and mean) demonstrated non-linear effects on pedestrian behavior, with stronger social repulsion forces generally leading to longer gap acceptance times. The React to N parameter, representing the number of nearby pedestrians influencing individual decision-making, revealed complex interactions where moderate social influence accelerated crossing decisions, but excessive influence introduced hesitation and delays. Additionally, Noise, representing randomness in pedestrian behavior, significantly increased variability in gap acceptance times, reflecting real-world unpredictability. The inclusion of post hoc tests and effect size metrics, such as Cohen’s d, strengthened the interpretation of the results by quantifying the practical significance of parameter effects. Parameters like Tau (reaction time) and Lambda (directional sensitivity) demonstrated not only statistical significance but also large effect sizes, underscoring their critical role in shaping pedestrian gap acceptance behavior. These findings reinforce the importance of carefully calibrating key behavioral parameters in microsimulation tools to ensure realistic and reliable modeling of pedestrian–vehicle interactions.

While the simplified traffic setup in this study allowed for controlled sensitivity analysis, it represents a basic environment that may not capture the full complexity of real-world, multi-lane intersections. As such, the findings should be interpreted as an initial step toward understanding how specific pedestrian behavior parameters influence gap acceptance within the social force model framework. These results provide a basis for refining microsimulation tools, such as VISSIM, particularly in enhancing internal model calibration. Although a direct application to urban design or signal timing strategies requires further validation under more complex and realistic conditions, the study highlights parameter sensitivities that could inform future modeling efforts. Continued research in diverse traffic scenarios is needed to assess how these parameter effects translate into practical recommendations for pedestrian safety and infrastructure planning.

However, the study’s reliance on a controlled traffic simulation introduces limitations in capturing the full complexity of real-world pedestrian dynamics. Future research should expand this work by incorporating multi-lane and bidirectional traffic scenarios, as well as exploring interactions between multiple behavioral parameters. Real-world validation through field studies is crucial to ensure the applicability of these findings and to bridge the gap between simulation outputs and actual pedestrian behaviors.

As urban areas continue to grow and integrate emerging transportation technologies, such as autonomous vehicles (AVs), understanding pedestrian behavior remains a critical priority. Accurate microsimulation models will play an increasingly vital role in ensuring pedestrian safety and optimizing urban mobility in mixed-traffic environments. This study serves as a foundational step toward that goal, providing actionable insights to enhance simulation accuracy, inform urban design, and ultimately contribute to the development of safer, more efficient, and pedestrian-friendly urban environments.