Abstract
Terminals are key components of intermodal transport networks, as they are the facilities where freight is transferred between transport modes. The efficiency of such facilities crucially depends on their locations (and sizes), which are typically chosen considering two levels of analysis: local/urban and regional/country. Our focus in this presentation is the regional/country level. At this level, the problems involved in the locational (and sizing) decisions at stake are a particular variety of hub locations problems—a class of problems that has been widely studied through optimization approaches. However, they typically assume that decisions are made in a centralized management context: decision-makers not only choose the locations of intermodal terminals (or hubs), but also fully control their utilization (i.e., which terminal each user will patronize). This signifies that such approaches are not applicable when users–potentially, any companies that move freight–behave according to their own individual interests; that is, they are not applicable in a decentralized management context. In this presentation, we describe an ongoing study where (regional) intermodal terminal location problems are dealt with in this type of context considering terminals of different types and respective capacity and operation ranges. In particular, we present the complex optimization model we have developed to handle such problems, and the (sometimes counterintuitive) results it led to when applied to a case study inspired by the Portuguese reality.
1. Introduction
Freight transport plays an increasingly important role in the global economy, therefore attracting a great deal of attention from transport policy institutions. Amongst the main policy directions explored by these institutions to make freight transport more sustainable is intermodality (or intermodalism). According to Rodrigue [1], this is “the movements of passengers or freight from an origin to a destination relying on several modes of transportation”, when “each carrier is issuing its own ticket (passengers) or contract (freight)”. Slightly different definitions of intermodality (as well as definitions of related concepts such as multimodality and combined transport) are presented and discussed in Agamez-Arias and Moyano-Fuentes [2].
The history of intermodality started to develop fast in the 1960s, coinciding with the rise of containerization in maritime transportation (Donovan [3]). Since then, intermodality policies have been pursued virtually everywhere in the world. This is in particular the cases of the United States after the publication of the Intermodal Surface Transportation Efficiency Act in 1991 (updated in 1998), and of the European Union after the adoption of Council Directive 92/106/EEC in 1992 (whose effects were assessed in the report “Analysis of the EU Combined Transport” prepared in 2015 for the European Commission; see https://ec.europa.eu/transport/themes/logistics/studies_en (accessed on 6 September 2021)).
The key facilities of an intermodal freight transport system are the intermodal terminals. These are the facilities where freight is transferred between transport modes. In addition to loading and unloading operations, intermodal terminals may offer services such as temporary storage or intermediate buffer, and even pre-delivery inspection or enhancement work on the goods being transported (Bektas [4]).
The performance of an intermodal transport system depends heavily on the location and type/capacity of its intermodal terminals. In general, decisions on these issues are taken or at least controlled (through economic activity and/or land use licensing mechanisms) by a governmental entity at the national and/or local level, even if their operation may be later awarded to private concessionaires. The governmental entity is naturally expected to make these decisions in the best public interest, but needs to take into account the fact that, except perhaps in highly centralized economies, terminal users will subsequently take advantage of them or not in their operations according to their own best interest (i.e., to minimize their own terminal and transport costs). There are, therefore, two levels of decision (governmental entity and terminal users) impacting on the performance of the system, and we are in a decision context that, in line with Vasconcelos et al. [5], we designate as decentralized management.
In this paper, we propose an optimization model aimed to assist a governmental entity in the planning (or re-planning) of intermodal terminals at the network level. It is specifically developed for application to rail-road terminals, but could easily be adapted to any other types of terminals. The model allows to determine the optimal locations and types/capacities of the terminals to operate in a territory (e.g., a country or a set of countries willing to share their intermodal transport policy) in a decentralized management context, given the freight flows expected to take place between the regions of that territory in some reference planning year. The objective of the governmental entity is to minimize the (socioeconomic) costs of moving freight and installing, operating and maintaining the terminals.
The model we have developed fits into a growing body of research that has been reviewed in Caris et al. [6] and, more recently and thoroughly, in SteadieSeifi et al. [7], where a long section is devoted to strategic (network-level) planning problems and, more specifically, to the intermodal terminal location problem. It also fits into the research agenda suggested a few years ago by Caris et al. [8] regarding the main decision-support problems raised by intermodal terminals. In this agenda, two specific challenges involving intermodal terminal location problems are highlighted: first, the inclusion of economies of scale in terminal handling costs; second, the connection between terminal location and service design (i.e., the selection of routes on which services are offered and the determination of the characteristics of each service). Both these challenges are, at least to some extent, addressed by our model.
It is important to clarify at the outset that the model we propose is not intended to return the exact location for each intermodal terminal—just the region where, in a subsequent stage, the ideal site for its placement should be looked for, considering all relevant criteria. There is also a significant body of research on the site-level evaluation of the location of intermodal terminals and related facilities (freight villages, logistic centers, etc.), predominantly based on multicriteria decision-aid methods, in some cases combined with fuzzy-set theory approaches. Examples of criteria considered at this level include the contribution to the local economy (particularly to employment), the easiness of access, the impact on the environment, the compatibility with land-use plans, and the complementarity with other policy initiatives. Some of the main references for this research are Kapros et al. [9], Ballis and Mavrota [10], Kayikci [11] and Tadić et al. [12].
The remainder of the paper is organized as follows. In the next section, additional information is provided about rail-road terminals, their types and respective costs. Then, we describe in detail the problem at stake and provide an overview of the related modeling literature. This is followed by the presentation of the optimization model we have developed to address the problem, where we highlight the constraints required to cope with a decentralized management context. The behavior of the model is illustrated and discussed afterward, with reference to a case study inspired by the Portuguese reality. Model solving issues are examined next. In the final section of the paper, we summarize the research conducted so far and indicate directions for our future work on the intermodal terminal location problem in a decentralized management context.
2. Rail-Road Terminals
The basic service performed by rail-road terminals is the transfer of freight (bulk or loading units such as containers) between the rail and the road transport modes, but they can offer various other services. In Figure 1 we display the typical layout of a rail-road terminal showing the various components they may include between the road access area and the rail access area, and in Figure 2 we specify the services provided by intermodal rail terminals (i.e., rail-road terminals but also rail-barge-road, rail-road-sea and rail-road-barge-sea terminals). The types of service offered by these terminals are naturally related to the volumes of freight they handle and to their capacity, and these are in turn related to the costs of building, equipping, operating and maintaining the terminals.
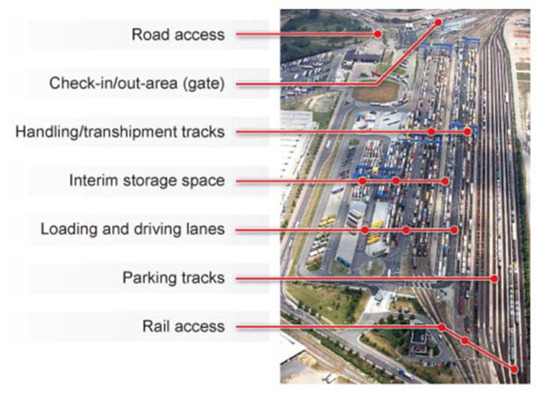
Figure 1.
Typical layout of a rail-road terminal. (Source: https://www.intermodal-terminals.eu/intermodal-terminals, accessed on 6 September 2021).
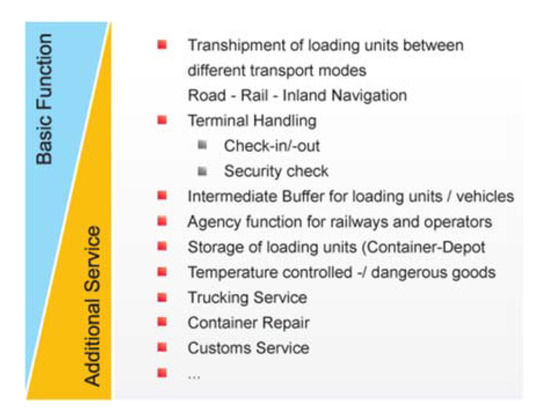
Figure 2.
Services provided by an intermodal rail terminal. (Source: https://www.intermodal-terminals.eu/intermodal-terminals, accessed on 6 September 2021).
The costs of intermodal rail terminals were recently analyzed in detail by Wiegmans and Behdani [13] based on the rather scarce literature available on the subject (a significant part of which is grey literature issued from European Commission projects). The analysis was conducted considering five types of terminals classified according to capacity level: XXL, XL, L, M, and S (Table 1). The capacity of the larger terminals (XXL) can exceed 500,000 TEU/year, whereas the capacity of the smaller terminals (S) is below 10,000 TEU/year (TEU, i.e., twenty-foot equivalent units, is a measure of capacity often used for container terminals). According to Christiansen et al. [14], a 1-TEU container carries up to approximately 28 tons of cargo with a volume of up to 1000 cubic feet. The five-level classification presented above was first proposed by Wiegmans et al. [15], and has been used or served as reference in a number of subsequent studies, being Tadić al. [16] the last to date. In Table 2, we provide information on the physical characteristics and investment costs for terminals of different specific capacities.

Table 1.
Types of intermodal rail terminals.

Table 2.
Costs of intermodal rail terminals.
3. Problem Description
The specific problem we are dealing with in this paper considers a territory (country) divided into regions linked by a road network and a rail network, as exemplified in Figure 3. In this example, there are eight regions represented by the respective centroids (A, B, …, H). The road network connects all the regions, but this is not necessarily the case of the rail network. In some of the regions served by the rail network, there may be already an intermodal terminal, as it occurs with Regions E and G. The other regions where the road network and the rail network intersect (B and H), or at least some of them, are possible locations for new intermodal terminals. The freight tonnages to be moved between every pair of regions, or origin-destination (OD) freight demands, are known in some reference planning year (in the sense that they were estimated with enough accuracy). A part of this freight, because of their nature, will be moved by road only, but the other part may be moved by a combination of road and rail through two intermodal terminals if this is beneficial for the companies operating in the regions. For instance, the freight to be delivered from Region A to Region H can be moved by road through Regions B, D, and F, or it can be moved first by road to the terminal located in Region E, then by rail to the terminal located in Region G, and finally by road again to Region H.
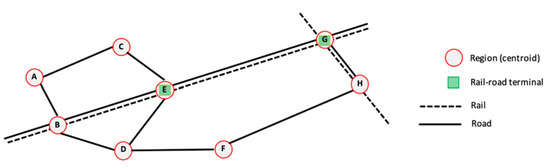
Figure 3.
Rail-road network scheme.
The problem we want to address is that of a governmental entity willing to determine the regions where new rail-road terminals should be located and which should be their type/capacity (and also, possibly, the regions where existing terminals should be closed or their type should be modified), so that the (socioeconomic) costs involved in satisfying all the demands for freight transport in the territory are minimized. The governmental entity at stake can be the ministry in charge of the transport sector or some national or regional agency depending on the political and administrative organization of the country. In any case, this entity is assumed to legitimately represent the public interest. Since all the demands are to be satisfied, it is reasonable to assume that the (socioeconomic) benefits from freight transport are fixed (constant), and the minimization of costs will signify the maximization of net benefits.
The previous explanations clearly suggest that we are dealing with a hub location problem, where, obviously, the hubs are the rail-road terminals. Hub location problems can be classified according to three important criteria. One of them separates single-allocation problems, i.e., each spoke (region) is allocated to one and only one hub, from multiple-allocation problems, i.e., some spokes may be allocated to more than one hub. A second one distinguishes between strict hubbing, i.e., all spokes are allocated to a hub, from non-strict hubbing, i.e., some spokes are not allocated to a hub, being served directly from other regions. The third criterion refers to whether the number of hubs is predetermined (-hub problem, where is the number of hubs), or, alternatively, it is determined endogenously as a function of the costs of installing, operating and maintaining a hub, including the fixed costs (fixed-charge hub problem).
The problem at stake can be classified as a multiple-allocation non-strict hubbing fixed-charge hub location problem. The costs to minimize comprise both internal costs and external costs. The former are the private costs involved in the transport of freight and in the construction, operation and maintenance of the rail-road terminals. The latter correspond to the side effects of transport, i.e., global warming, air pollution, noise, accidents and congestion. In order to achieve an efficient allocation of resources, the external costs of any activities should be internalized, i.e., should be incurred by the economic agents that perform the activities (freight transport in this case), and not by the economic agents that suffer their consequences. For this to happen, governments can levy taxes on freight transport. The internalization of the external costs of transport is often a major policy concern. However, it should be noted that full internalization of external costs would normally require taxes to be different across freight transport firms, which would violate the equality principle adopted in the constitutional law(s) of virtually every country. This means that it would only be possible in a context where a governmental entity could control terminal users up to the point of imposing the transport schemes they should use (i.e., in a context of centralized management). The state-of-the-art on the external costs of freight transport and their internalization is provided in Mostert and Limbourg [17].
The context for the problem we are dealing with is, therefore, that of decentralized management. The governmental entity defines the location and type/capacity of the new rail-road terminals (and also, possibly, the changes to make in the current terminal network) to minimize costs, but taking into account that the potential terminal users in the various regions will decide whether to resort to the terminals or not for minimizing their own costs. Since it is practically impossible to account separately for each terminal user, transport costs need to be estimated based on average transport costs per unit of freight by rail and road. The other costs that terminal users need to cope with are the fees they pay for utilizing the terminals. These fees are set by the governmental entity, and their value could also be determined endogenously to minimize costs (taking into account that these fees are paying a service, and that the service is basically the same in every terminal or, at most, may vary with the type of terminal). Alternatively, it is possible to test several different possible values for the fees, and then choose among them the ones that lead to the lowest costs.
4. Related Work
As stated in the previous section, intermodal terminal location problems are a special type of hub location problems. This means that the vast literature on this problem, reviewed, for instance, by Alumur and Kara [18], Campbell and O’Kelly [19], Farahani et al. [20] and Contreras [21], is, to some extent, related to our work. However, in the following, we will focus solely on the research that specifically addresses intermodal terminal location problems from an optimization perspective (Table 3).

Table 3.
Related work on intermodal terminal location problems (compared to that presented in this paper).
This stream of research has been initiated in the turn of the XXth century with a series of three papers by Arnold and Thomas [22] and Arnold et al. ([23,24]). These authors dealt with the intermodal terminal location problem using two fixed-charge models: a hub location model with four-index flow decision variables ( is equal to one if flow from origin to destination is sent through hubs and in this order, and is equal to zero otherwise); and, to circumvent the difficulties they were facing to handle the huge number of decision variables of the former model, an uncapacitated multi-commodity minimum cost network flow model with three-index decision variables ( is equal to one if the itinerary for hauling the commodity from origin to destination contains arc , and is equal to zero otherwise). However, even when the latter model was used, these authors could only tackle an application to the Iberian Peninsula, involving the location of 13 new intermodal terminals (to complement the current network of 15) through a greedy algorithm.
Several authors who have dealt recently with the intermodal terminal location problem based their work on the hub location model proposed by Arnold et al. [24]. Sörensen et al. [25] focused on the exact same model and presented two metaheuristics to solve it: a GRASP algorithm and an attribute-based hill climbing algorithm, in both cases complemented with a greedy (add-and-remove) algorithm. The GRASP algorithm was later adapted by Sorensen and Vanovermeire [26] to handle a bi-objective hub location model where the objective of terminal operators (minimize terminal costs) was separated from the objective of terminal users (minimize transport costs). Lin et al. [27] proposed an enhanced formulation of the Sorensen et al. [25] model and two simple matheuristics to solve it. The results they have obtained for the same instances clearly outperformed their previous results with respect to solution quality and computational effort. More recently, Lin and Lin [28], addressed the same problem through a new matheuristic within which the selection of terminals and the routing of transport flows are carried out in separate stages. This approach enabled a substantial decrease in the number of decision variables considered in Lin et al. [27] and a reduction of computation time by approximately 50% while keeping solution quality at the same level.
Along the same line of research, it is also worth mentioning the works of Ishfaq and Cox [29] and Santos et al. [30], both dealing with problems somewhat more involved than those tackled by Arnold et al. [24]. The former authors represented their problem with a model based on four-index flow decision variables, and focused, above all, in solution methods. In particular, they proposed a tabu search metaheuristic that performed well in randomly-generated instances of up to 30 possible terminal locations (coincident with demand centers). Santos et al. [30] is, to the best of our knowledge, the first paper where an intermodal terminal location problem is formulated with three-index flow decision variables similar to the ones first proposed by Ernst and Krishnamoorthy [31] and to the ones we use in our model (see Section 5). Hub location models with these types of variables are typically solved faster than with four-index variables. In Santos et al. [30], the application of the model is exemplified for a real-world setting, Belgium, considering two transport modes (road and rail) and 35 possible terminal locations. Finally, we should mention here an article by Ghane-Ezabadi and Vergara [32], where a new formulation for the intermodal terminal location problem is proposed. Using a decomposition-based search algorithm, these authors were able to solve randomly-generated instances of the problem involving the location of 4 terminals in 30 possible locations (in around 20 min).
A feature common to the models dealt with in the papers mentioned above (and several others) is that they apply to a centralized management context. The only authors who have developed an optimization model for an intermodal terminal location problem in a decentralized management context are Vasconcelos et al. [5]. The problem they have tackled is uncapacitated (i.e., it does not take into consideration terminal types/capacities), and the model they formulated relies on a questionable assumption (i.e., firms send their freight either by road only or through pre-defined intermodal road-barge terminals). The application of this model is illustrated with an application to Brazil (12 terminals, 9 of which already in place). Other authors that proposed approaches applicable to a decentralized management context are Limbourg and Jourquin [33] and Zhang et al. ([34,35]). However, in both cases, the problems they have addressed were not formulated as optimization models, and were tackled through heuristics (hill-climbing and genetic algorithms, respectively). Hence, the quality of the solutions found could not be properly assessed (against the global optimum solutions).
5. Optimization Model
The optimization model we have developed for the problem described in Section 3 combines a model applicable to a centralized management context with additional constraints accounting for the decentralized management context. The model and the additional constraints are presented below in separate subsections.
5.1. Centralized Management
In the formulation of the optimization model for the intermodal terminal location problem under centralized management, we will use the following notation:
Indices
i-intermodal terminal type
j, k, g, h-region
Sets
-set of regions;
-set of intermodal terminal types.
Parameters
—freight tonnage originated in Region to move to Region (TEU/year);
—total freight tonnage to be moved from Region (TEU/year);
—generalized transport cost by road/rail between Regions and , considering the time involved in loading and unloading operations (€/TEU/km);
)—travel distance by road/rail between Regions and (km);
—minimum/maximum capacity (or utilization of capacity) for a terminal of Type (TEU/year);
—discounted installation and operation costs for a terminal of Type (€/year);
if a terminal of Type can be installed in Region (the road and rail networks need to intersect in this region), otherwise .
Decision variables
= 1 if a terminal of Type is located at Region , otherwise ;
—proportion of the freight tonnage originated in Region moved to a terminal of Type located in Region (see Figure 4);
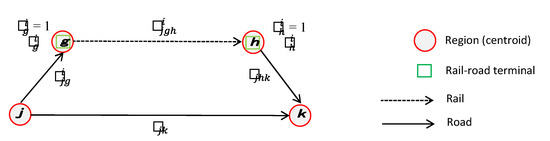
Figure 4.
Location and flow decision variables.
—proportion of the freight tonnage originated in Region moved to a terminal of Type located in Region through a terminal located in Region ;
—proportion of the freight tonnage originated in Region moved to Region through a terminal located in Region ;
—proportion of the freight tonnage originated in Region moved directly (by road) to Region ;
—flow handled in a terminal of Type located in Region .
Using this notation, the optimization model consists of the following objective function and constrains.
Objective function
The objective function (1) of the model represents the total annual costs to be minimized. It comprises five terms. The first one expresses the costs of moving freight by road directly to their destination. The second, third and fourth term describe the transport costs of sending the freight through the intermodal terminals in the three stages of the trip: from the origin to the first terminal, by road; between terminals, by rail; and from the second terminal to the destination, again by road. Finally, the fifth term expresses the intermodal terminal costs. These costs comprise the annual-equivalent installation costs (applicable only in the case of new terminals) and the annual operation and maintenance costs, which are assumed to be fixed for each type of terminal.
Constraints
We will start by the constraints aimed to ensure that freight demands are satisfied, and then move to the constraints that guarantee the continuity of freight flows. Next, we focus on the constraints representing the location of intermodal terminals and, finally, on the capacity constraints.
The demand satisfaction constraints included in the model are of two kinds. Constraints (2) ensure that all the freight originated in a given region, j, will be sent to the destination regions either directly by road (sum of for every Region k) or through a first intermodal terminal (sum of for every terminal g of Type i), whereas constraints (3) guarantee that they will arrive to the right region, k, through a second terminal, h(), or by road ().
The continuity constraints included in the model are also of two kinds: constraints (4) guarantee that the freight arriving to an intermodal terminal located in g either coming from a region, j() or from another terminal, h( is the same that leaves that terminal either to another terminal, ( or to its destination region, k(; constraints (5) guarantee that the freight arriving to an intermodal terminal located in from Region must be sent to another terminal, .
The following constraints, (6)–(10), define the terminal locations. Constraints (6) specify that there can be at most one intermodal terminal in each region, of one of the possible terminal types. Constraints (7) specify the regions where terminals may be installed (e.g., regions where the road and rail terminals intersect). If this is the case, then and only one of the binary variables representing the location of a terminal, , can be equal to 1. Otherwise, and for every terminal of Type i. The remaining constraints of this kind relate intermodal terminal locations with freight flows. Constraints (8) guarantee that freight will not be sent from a region, j to an intermodal terminal g that does not exist (i.e., the sum of is equal to zero), forcing every to be zero. If, instead, a terminal exists, then, at most, all the freight originating in that region will be sent through that terminal. Constraints (9) play a similar role with respect to the freight sent to region k from a terminal located at h. Likewise, constraints (10) ensure that freight can only be moved to a terminal in a given region, h, if a terminal operates in that region.
The capacity constraints specify the maximum and minimum freight tonnage that can be handled by an intermodal terminal. The freight tonnage handled by an intermodal terminal g is given by constraints (11), where the freight coming directly to g from the different regions (sum of ) is added to the freight coming to g through other terminals (sum of . Constraints (12) and (13) ensure that this quantity is within pre-defined limits ( and that depend on the terminal type (i).
Finally, Constraints (14) and (15) represent the domain of the variables.
5.2. Decentralized Management
The optimization model presented in the previous subsection is valid in a centralized management context, when a governmental entity decides not only on the location and capacity of intermodal terminals, but also on how these facilities should be used to minimize total (socioeconomic) terminal and transport costs. In a context of decentralized management, decisions on the use of terminals are made by the companies that move freight to minimize their own transport costs (including the costs of using the terminals). Hence, there are two different types of decisions-makers, with different objective functions. Such optimization models are called bilevel (Colson et al. [36]; Sinha et al. [37]). One of the most frequent approaches to handle bilevel models involves their reduction to a single-level model by replacing the objective function of one type of decision-maker (in this case, the terminal users) with a set of constraints (ensuring that their transport costs are minimized). This is the approach we have followed: the objective-function and constraints of the centralized management model were kept, and new constraints were added to it. These new constraints, as well as the new parameters and decision variables they involve, are presented below.
Parameter
terminal usage flat rate (€/TEU);
Decision variables
if the freight tonnage originated in Region is moved to Region through terminals located in Regions and , otherwise ;
—minimum transport cost for moving freight between Regions and (€/TEU).
Constraints
Constraints (16) specify that only one route will be used to move freight between regions, either by road only ( or through intermodal terminals (one of the binary variables and constraints (17) ensure that this route is the least-cost route. Note that, if intermodal terminals are included in the route, then companies will have to pay their use. We assume this payment is made twice (first, when the freight enters the rail network and, second, when it leaves it), and consists in a flat rate, , per unit of freight tonnage.
The latter constraints (17) are nonlinear, but can be replaced by linear constraints (thus making the model in principle easier to solve). These constraints and the additional decision variables that need to be considered in their formulation are presented below.
Parameter
large number (“big M”).
Decision variables
if the freight tonnage originated in Region is sent to a terminal located in Region , otherwise ;
= 1 if the freight tonnage originated in Region is sent from a terminal located in region to a terminal located in Region , otherwise ;
if the freight tonnage originated in Region is sent from a terminal located in Region to Region , otherwise ;
—cost of a route between Regions and passing through terminals located in Regions and .
Constraints
Two new sets of constraints have to be included in the model to replace constraints (17): the first set identifies the segments included in the least-cost routes between any pair of regions, and the second set computes the costs for making such routes.
We start by the first set:
Constraints (18) indicate whether the freight originated in a given region, j is moved by road directly to some other region, k. Indeed, if then (else, if then . The other constraints in this set apply when freight is moved by road and rail, that is, when intermodal terminals (g and h) are used. Constraints (19) define the first segment of the least-cost route, as if and only if . Constraints (20) and (21) play the same role with respect to the second and third segments, setting the value of variables and . Finally, Constraints (22) and (23) link route information with segment information, since, considered together, they ensure that only if = = .
The set of constraints that computes transport costs is as follows:
Constraints (24) compute transport costs when freight is moved by road only between any pair of regions, j and k, and constraints (25) compute the same when it is moved by road and rail. The costs for routes passing through regions where intermodal terminals are not located must be such that they are never chosen. Constraints (26) and (27) guarantee that the least-cost routes will be selected for any pair of regions, and constraints (28) compute the value of the transport costs (including the usage flat rate paid in the intermodal terminals if road and rail are used).
Finally, the following constraints represent the domain of the variables.
6. Case Study
The results obtained through the application of the optimization model presented in the previous section are explained and discussed below for a case study inspired by the Portuguese reality. The study was carried out based on the 23 NUTS 3 regions of (mainland) Portugal. NUTS are territorial units of three hierarchical levels set up in the European Union in 2003 for statistical and policy purposes; see https://ec.europa.eu/eurostat/web/nuts/background (accessed on 6 September 2021). The level of detail provided by NUTS 3 is very convenient for illustrating the behavior of the proposed model, which is the main reason why we have developed this case study. However, a study based on more detailed geographical units could be performed if necessary. The NUTS 3 regions are represented in Figure 5. The background geographic information used in this figure (as well as in Figures 7–10), was downloaded from https://snig.dgterritorio.gov.pt (accessed on 6 September 2021), the official source for that type of information in Portugal.
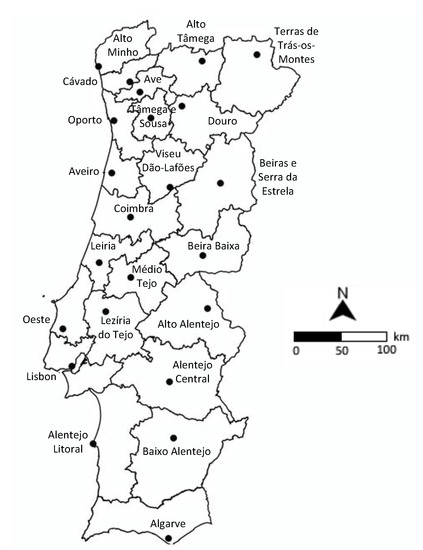
Figure 5.
NUTS 3 regions of mainland Portugal.
The methodology we have followed in the development of the case study is outlined in Figure 6. Its first step consisted in the collection of the data needed to run the optimization model. These data, described in Section 6.1, defines the reference scenario used in the study. Afterward, we applied our model to this scenario and analyzed the respective results, which are presented and discussed in Section 6.2.1. In particular, we examined the impact of the management context (centralized vs. decentralized) on model (optimal) solutions. We next defined six alternative scenarios by considering variations in the most uncertain parameters, i.e., freight demand and transport costs, and applied our model again in the analysis of the sensitivity of solutions to those variations. The results of this analysis is presented in Section 6.2.2.
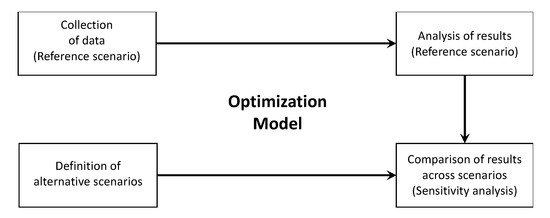
Figure 6.
Methodology applied in the case study.
6.1. Study Data
The application of the optimization model requires the following types of data: (1) locations and types of existing rail-road terminals, as well as of possible new terminals; (2) configuration of the rail and road networks; (3) freight tonnage for each pair of regions; (4) generalized transport costs by rail and road for each pair of regions; (5) intermodal terminal costs, usage fees and freight operation ranges for the different types of terminals.
In contrast to some parts of Central Europe where rail-road terminals are numerous, in Portugal there are only five such facilities. Four of these terminals are located next to the country’s largest ports, also handling maritime freight (Figure 7): Lisbon, of Type XL; Leixões (Oporto), of Type L; and Aveiro and Sines (Alentejo Litoral), both of Type M. The only existing inland terminal is located at Guarda (Beiras e Serra da Estrela), next to the main motorway (A25) and the main rail line (Linha da Beira Alta) connecting Portugal to Spain and the rest of Europe, being also of Type M.
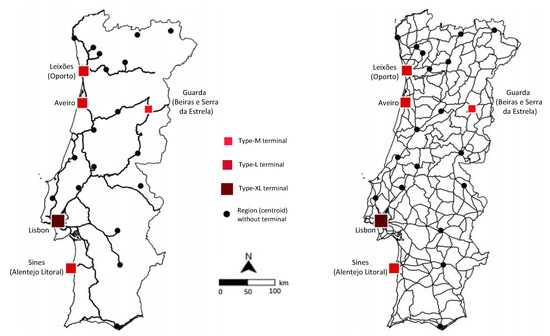
Figure 7.
Rail network (left) and road network (right) of Portugal, and existing rail-road intermodal terminals.
The possible locations for new terminals we have considered in our study, of the same three types (XL, L and M), were the other 16 NUTS 3 regions served simultaneously by the road and rail networks (i.e., all regions except the two that are not connected to the rail network–Alto Tâmega and Trás-os-Montes). Following a massive investment program in road infrastructure undertaken between 1985 and 2016 with a strong support from the European Union, Portugal is now provided with a dense network of good-quality motorways and fast two-way highways that provide easy access even to the remotest parts of the country. In contrast, the rail infrastructure received little attention in the same period, and several lines have been closed. Line closures affected essentially the inland regions, which are now served poorly by the rail network or not served at all. The coastal regions are better served, but the lines that connect them are rather congested, and priority is given to passenger traffic to the detriment of freight transport. Schemes of the rail and road networks are also provided in Figure 7.
The freight tonnages were estimated based on information published by INE, the Portuguese statistics bureau, for the year 2014. According to this information, in that year a total of approximately 130 million tons of freight were moved by rail and road in (mainland) Portugal. Since INE only provides information for the freight tonnages moved between the five NUTS 2 regions (Norte, Centro, Lisboa, Alentejo and Algarve), we had to extrapolate their values for the NUTS 3 regions. This was completed assuming that the freight tonnages moved between the NUTS 2 regions were distributed across NUTS 3 regions proportionally to the products of the populations of these regions. We also assumed that 80% of the total freight was captive of the road mode, and only the remaining 20% could be distributed across the two modes (this is, approximately, the share of the rail mode in France, where a dense network of rail-road terminals is available). It should be noted that, according to our calculations, only around 3% of the total freight tonnages generated by the NUTS 3 regions was moved through the rail network, which may be partly explained by the lack of rail-road terminals affecting the country. We would have liked to make these extrapolations in a more sophisticated manner (see, e.g., Chow et al. [38] and Tavasszy et al. [39]), but this would have been worthless because our results could not be validated (or invalidated) with the data we had available. In favor of our results, it should be said that the freight tonnages we have obtained were considered plausible by experienced freight transport planners in Portugal.
The generalized transport costs were calculated by multiplying an average cost per unit of distance (km) dependent on the transport mode by the distances measured for that mode on the transport network. The computation of accurate generalized transport costs can be a difficult task, as shown, e.g., in Janic [40], Hanssen et al. [41] and Mostert and Limbourg [17]. For our case study, we have used values for the average unit transport costs based on the work of Bína et al. [42]: 3.6 €/TEU/km for road transport, and 2.0 €/TEU/km (57% lower) for rail transport. These values were assumed to capture both internal and external costs.
The intermodal terminal costs were obtained based on Wiegmans and Behdani [40]. For Type-M terminals, the annual fixed costs (annual-equivalent installation costs plus operation and maintenance costs) were taken to be 0.62 × 106 €/year. These terminals were assumed to operate an annual freight tonnage in the range [12.36, 30] TEU/year. The minimum of these two values was obtained so that the profits generated by any terminal would be non-negative assuming a usage flat rate of 50 €/TEU. For Type L terminals, the same costs were 3.06 × 106 €/year, and the freight operation range was [61.15, 100] TEU/year, and for Type XL terminals they were 8.98 × 106 €/year and [179.54, 500] TEU/year. The annual-equivalent installation costs were determined assuming a discount rate of 5%/year and a useful lifetime of the terminals of 30 years.
6.2. Study Results
The results we have obtained for our reference scenario and for their sensitivity to variations in parameters (freight demand and transport costs) are presented below. Due to the data limitations we have recognized in the previous subsection, the practical applicability of these results needs to be taken with caution. A true real-world study would undoubtedly require more accurate data.
6.2.1. Reference Scenario
We will start by presenting and analyzing the global results of the application of the model (e.g., number and location of new intermodal terminals), and then move to more detailed results (e.g., transport cost changes across NUTS 3 regions if model solutions were implemented).
Our results are summarized in Figure 8 and Table 4. There we provide information on the number and types of intermodal terminals to operate, on the freight tonnage to move by rail and road (TEU and TEU × km) and on the respective transport costs, both for the current terminal network (if operated according to our optimization model) and for the optimal terminal network in a centralized and a decentralized management context.
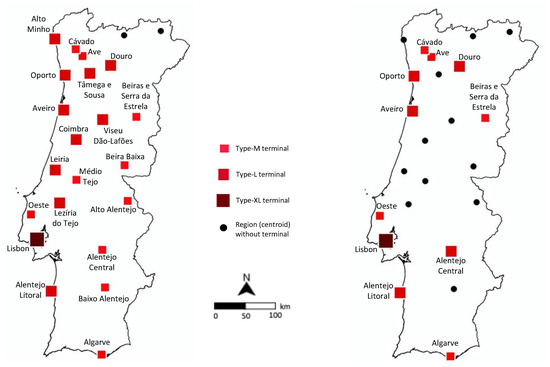
Figure 8.
Optimal locations and types of intermodal terminals under centralized management (left) and under decentralized management (right).

Table 4.
Main features of the current and optimal intermodal terminal networks.
Overall, the most striking result is that the changes to the current network would be much larger in a centralized management context than in a decentralized one; that is, the management context has a prominent influence on the solution to implement. Indeed, in a centralized context, new terminals should be installed in every region served by the rail network where a terminal does not exist at present. This means that sixteen new terminals should be built, being seven of Type L and nine of Type M. In contrast, in a decentralized context, the number of terminals to build would sharply decrease to just six, being two of Type L (located in Alentejo Central and Douro) and four of Type M (in Algarve, Ave, Cávado and Oeste).
Other important results concern the mode shares and the costs. At present, and as shown in Table 4, if the current terminals were operated optimally in a decentralized management context, only 3.2% of the freight tonnage would be moved by rail (note that this percentage is calculated considering also the freight taken as captive of the road mode). This would signify a mode share of 5.0% for rail in terms of TEU × km. Through the construction and operation of new terminals, these percentages could increase to 6.6% and 8.8% respectively. In a centralized management context, they would be much higher, i.e., 15.8% and 14.8%. With respect to total costs (terminal and transport), the impact of the changes would not be impressive in terms of percentages, because the main origins and destinations of freight are already served by terminals. However, in absolute terms, the savings would be very significant: 24 or 90 million € annually, depending on the management context being decentralized or centralized.
Moving now to a more detailed analysis of results and focusing on the decentralized management context, we next discuss how freight transport costs would change across NUT 3 regions if the current intermodal terminal network were replaced by the optimal network. This is shown in Table 5. The regions that would benefit the most from the changes are Algarve (with cost savings of 5.02%), Alentejo Central (3.66%) and Douro (3.06%), i.e., as could be expected, regions where new terminals would be located. However, it should be noted that transport costs would decrease less in some of these regions than in regions that would not receive new terminals; for instance, the savings for Oeste (0.96%) would be clearly lower than those for Alto Alentejo (2.04%). This shows that benefits are not necessarily concentrated in the regions of the new terminals, being instead distributed across regions according to an irregular geographical pattern. In this case, the configuration of the rail and road networks dictates that the lowest cost savings (of only 0.25%) are made by the regions of Beiras e Serra da Estrela and Viseu Dão-Lafões, both situated in the deprived off-coast areas of central Portugal.

Table 5.
Freight transport costs of NUTS 3 before and after the implementation of the optimal intermodal terminal network under decentralized management.
To finalize this subsection, and recalling that our study focused only on the fraction of freight taken as not captive of road transport, we will now look into the freight tonnage that the different intermodal terminals would handle in a decentralized management context, and into the freight transport operations to perform based on these terminals.
Information on freight handling is provided in Table 6. It can be seen there that, if the optimal network were implemented, then the existing terminals would generally operate at least the same freight tonnage as they do in the current network. The exception is the terminal of Oporto, where the tonnage would decrease slightly, from 67.4 × 103 to 65.3 × 103 TEU/year (−3.1%). In contrast, in Alentejo Litoral, it would increase sharply, from 34.6 × 103 to 53.0 × 103 TEU/year (+53.2%). It can also be seen in the same table that all terminals would be operated at a level compatible with their types/capacities. In particular, this signifies that they would all be profitable (i.e., revenues would exceed costs in every terminal).

Table 6.
Freight handled by the intermodal terminals.
The freight transport operations to perform are exemplified for the Douro region, where a new Type-L terminal would be installed. As shown in Figure 9, the freight generated in this region would be delivered to the other regions either by road only or through a combination of road and rail (thus through the new Douro terminal). As could be expected, road (only) would be used for moving freight to close regions without terminal such as Tâmega e Sousa, Alto Tâmega and (the not so close) Beira Baixa. Freight would also be moved by road to the Beiras e Serra da Estrela region, despite there is a terminal, because the rail connection is poor. Freight transport to the majority of regions would be made through the Douro terminal. This is particularly the case of the more distant regions regardless of whether there is or would be a terminal (as in Lisbon, Alentejo Central, Alentejo Litoral and Algarve) or not (as in Baixo Alentejo). The optimal routes for the freight generated in the Douro region that is moved by a combination of rail and road to regions without terminal are displayed in Figure 10. Most of this freight would first be hauled by rail to the terminal of Aveiro and then by road to the destinations (Coimbra, Leiria, Médio Tejo, Lezíria do Tejo and Alto Alentejo). The only regions that would be served through other terminals are Alto Minho and Baixo Alentejo, for which the intermediate terminals would be Oporto and Alentejo Central, respectively. It should be noted that, given the location and capacity of the terminals in the optimal network, these routes would be, in every case, the least cost ones connecting the Douro region to the other regions (as we are considering the management context to be decentralized).
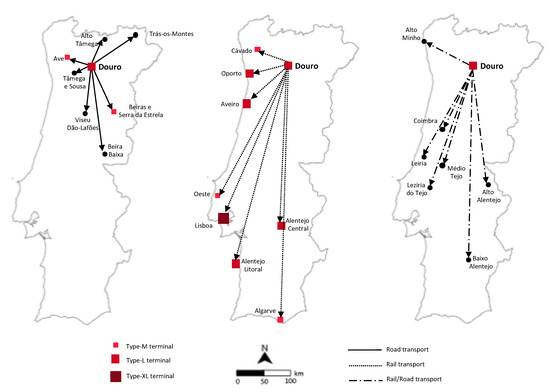
Figure 9.
Optimal transport modes to use in the delivery of freight generated in the Douro Region: road (left), rail (middle) and combination of both modes (right).
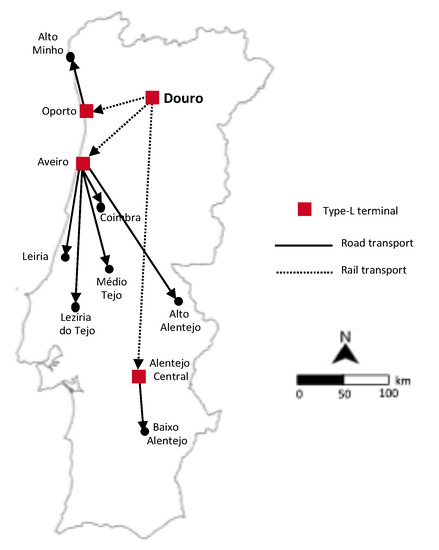
Figure 10.
Optimal routes to deliver freight generated in the Douro Region when both rail and road are used as transport modes.
The analysis of the freight transport operations involving the other intermodal terminals revealed a pattern similar to those based on the Douro terminal. The first aspect to highlight is that road transport would be predominantly used to supply close regions, being always the preferred option for distances of 200 km or less. In contrast, for distances over 400 km, rail would in general be used as transport mode when there is a terminal in the region to where the freight is sent. The exceptions occur in cases, not so rare in Portugal, where the rail distance clearly exceeds the road distance. Finally, for distances between 200 km and 400 km it is almost impossible to typify the optimal transport solutions: they can be road, rail or a combination of both modes depending on the configuration of the terminal network (i.e., the location of other terminals) and on the ratio between road distances and rail distances.
6.2.2. Sensitivity Analysis
For studying the sensitivity of the solutions found for the reference scenario, we analyzed six alternative scenarios. These scenarios are defined in Table 7, being obtained by variations of ±20% in freight demand (in every region), rail transport unit costs and road transport unit costs, one at a time. Such variations were chosen because they are plausible in light of freight transport evolutions occurred in Portugal in recent years, and are large enough to elucidate the behavior of our model (variations of ±2% or even ±5% might not be adequate in this sense).

Table 7.
Alternative scenarios defined for the sensitivity analysis.
The results obtained for these scenarios are summarized in Table 8. It can be seen there that, as could be expected, the increase of freight demand (Scenario S1) would lead to an optimal solution characterized by an increase in the number and capacity of terminals. This increase would be very significant: ten new terminals against only six in the reference scenario (nine of which are Type L instead of just two). Accordingly, the share of freight tonnage to be moved through the intermodal terminals would more than double (from 6.6% to 13.6%). What we did not expect was that the optimal solution for the decrease of freight demand (S2) would also involve the increase in the number and capacity of terminals (seven new terminals, four of which are Type L) and the increase of the intermodal mode share. But this was not the only surprising result. Indeed, we have found out that the optimal solution if rail unit costs were higher (S3) would also be characterized by a larger share of intermodal transport (thus, of rail) than in the reference scenario (7.2% against 6.6%), though naturally not as large as when rail unit costs decrease (S4). The more normal results we obtained were observed when the road transport unit costs increased (S5) and decreased (S6), as, in these scenarios, the share of freight tonnage handled through the intermodal terminals would, respectively, increase (to 14.6%) and decrease (to 5.9%, i.e., slightly). It should be noted that, also in these scenarios, the number and capacity of terminals should be larger than in the optimal solution for the reference scenario. This is explained by the fact that a decentralized management is considered, and we have included in the model constraints guaranteeing that the decisions on the use of terminals are made by the companies that move freight to minimize their own transport costs.

Table 8.
Sensitivity of optimal solutions to variations in freight demand and transport costs in a decentralized management context.
The complex pattern of the variations in optimal solutions can be perceived well in Table 9. It shows the impact of variations in rail transport unit costs between −20% and +20% of the reference value (2.0 €/TEU/km) with steps of 5%. When these costs decrease, nothing strange happens. The rail modal share increases steadily, from 6.6% to 9.9% when the unit costs decrease by 5% and to 10.2% when they decrease by 10%, reaching 14.5% when the decrease is 20%. At the same time, the total costs (terminal and transport) decrease, also steadily, from 2.698 to 2.605 × 109 €/year (i.e., around 3.4%). However, when the rail transport unit costs increase, the change of the rail modal share is very irregular: it decreases to 6.4% when the increase of unit costs is 5%, but when this increase is 10%, counterintuitively, it increases to 8.9%; then, it increases even more, to 10.0%, when the unit costs are 15% higher than the reference value, before decreasing to 7.2% when they are 20% higher. This irregularity is also observed with respect to the total costs, which are higher for the reference value of the rail unit costs than when these costs are 10% and 15% higher (reaching 2.684 and 2.687 × 109 €/year, respectively).

Table 9.
Sensitivity of optimal solutions to variations in rail transport unit costs in a decentralized management context.
Overall, these results clearly indicate that the interplay between the constraints included in the model—in particular, the capacity constraints and the decentralized management constraints—leads to changes in the optimal solutions that are extremely difficult to anticipate.
In order to understand the reasons why optimal solutions vary sometimes in a surprising manner, we have performed a detailed analysis of such solutions when the rail transport unit costs increase by 5% and 10% with respect to their reference value of 2.0 €/TEU/km (all else being as in the reference scenario).
First, we will consider the case of a 5% increase in rail transport unit costs (∆cra = 5%). As shown in Table 10, the optimal solution obtained for the reference scenario (e.g., considering the existing terminal network) would be feasible in this scenario. Naturally, its total costs would be higher than in the reference scenario (2.707 vs. 2.698 × 109 €/year). However, it has been possible to find a better solution by replacing the terminals of Alentejo Central, Algarve and Oeste by terminals in Alto Alentejo and Lezíria do Tejo. In these conditions, the freight processed in the Douro terminal and sent to the terminals replaced would be sent instead to the terminal of Lezíria do Tejo and then distributed from there by road to its destinations. Additionally, the freight to the Alto Alentejo region would be sent directly there by rail, and not by a combination of rail and road (through the terminal of Aveiro). Together, these changes would make the total costs to increase to 2.704 × 109 €/year, that is, a little less than if the terminals were kept in the same locations.

Table 10.
Optimal terminal network in the reference scenario and if rail transport unit costs increase by 5% and 10%.
We now move to the more interesting case of a 10% increase in rail transport unit costs (∆cra = 10%). In this case, the optimal solution obtained for the reference scenario would not be feasible, since the terminals in Alentejo Central, Douro and Oeste would operate below the minimum capacity (see Table 10). This is normal because of the increase in transport costs. However, at the same time, and more importantly, this increase would make it possible to open some terminals that otherwise would operate above the maximum capacity for the respective type. The significant increase in the number of terminals, both of Type L (from 5 to 7) and of Type M (also from 5 to 7), is due to this reason, as we confirmed by verifying that this solution would not be feasible in the conditions of the reference scenario—the maximum capacity of the terminals in Alto Alentejo and Tâmega e Sousa would be exceeded. The end result of these contradictory effects—increase in rail transport unit costs leading to a decrease in the use of rail transport and increase in the number and capacity of terminals leading to an increase in the use of rail transport—is that, altogether, they favor rail transport (whose modal share would increase from 6.6% to 8.2%) and make total costs lower (2.684 × 109 €/year instead of 2.698 × 109 €/year).
7. Model Solving
The various instances of the proposed optimization model dealt with in the case study were implemented in the GAMS modeling language (version 24.0.2) and handled through the ILOG CPLEX optimization solver (version 12.5.0.0) on a computer equipped with an Intel Core i7-5500U 2.66 Ghz processor and 8 GB of RAM.
Owing to the extraordinary advances of (integer linear) optimization in the last decades (see, e.g., Lodi [43]), the model was solved relatively quickly even when the decision context was decentralized. In fact, the computation time required to run each instance was always inferior to 3 min.
Since the problem we have tackled involved only 16 locations for installing possible new terminals, we have carried out a computational study to investigate how the computational effort would vary as a function of problem size. For this, we have used randomly-generated instances defined for rectangle-shaped territories divided into a given number the regions. The size of the territories and the location of the centroids of the regions were chosen at random (provided that the straight-line distance between them was at least 50 km), as well as the GDPs of the regions. Both the size and the GDP of the regions were chosen to follow the same probabilistic distributions as the size and GDP of the NUTS 3 regions of the European Union. Each region (centroid) was assumed to be connected to all other regions by straight-line road and rail segments. The freight tonnage to move between each pair of regions was assumed to be proportional to the product of their GDP and inversely proportional to the straight-line distance between them (i.e., freight demands were calculated according to an unconstrained gravity-type model). The terminal costs and usage rate, the rail and road transport unit costs, and the terminal types and capacity limits were the same as those considered in the reference scenario of the case study presented in the previous section.
In Table 11, we present the results of the application of our model to instances of 15, 20, 25, 30, 35 and 40 regions, considering 5 different (randomly-generated) territories in each case. For each instance, we have allowed a maximum computation time of three hours (180 min).

Table 11.
Results of the computational study.
Three main conclusions may be drawn from the analysis of Table 11, all of them aligned with our expectations. The first is that the instances of our case study were solved much faster than randomly-generated instances of (approximately) the same size (maximum of 3 min against minimum of 35 min). We were not very surprised by this finding because, according to our experience with other models, it is frequent that, when problems have a geographic nature, real-world instances are easier to solve than randomly-generated instances. Another conclusion is that instances defined for a decentralized management context are substantially more difficult to solve than those defined for a centralized management context. For example, the computation time required to solve 15-region instances in the latter context has always been inferior to 1 min, whereas it has always exceeded 35 min in the former. Moreover, in a decentralized management context, it has never been possible to solve to exact optimality any instance of 25 regions or more, and after three hours of computations the optimality gap was still considerable (34.5% in the worst case). In contrast, in a centralized management context, all instances of 30 regions or less were solved to exact optimality in 13 min at most, and, for larger instances, the optimality gap after three hours was 1.3% at most. Finally, the third conclusion is that the computational effort tends to increase quickly with instance size. This is clear in a centralized management context, as 15-region instances always took less than one minute to solve, whereas 40-region instances (those which could be solved in three hours) took on average 73 min. In a decentralized management context, the increase in computational effort can only be assessed through the optimality gap, which was 0% in the 15-region instances and 12.7% on average in the 20-region instances, and reached 33.4% on average in the 40-region instances. This certainly indicates that computation times grow fast with instance size also in this context.
In these conditions, it is quite obvious that, particularly when the management context is decentralized, instances of our model not much larger than the ones we have dealt with in the case study may be difficult (if not impossible) to handle through the ILOG CPLEX optimization solver (and probably any other). This signifies that, for larger instances, faster solution methods will have to be devised, including, e.g., metaheuristic methods.
8. Conclusions
In this paper, we have proposed a new optimization model aimed to assist a governmental entity in the planning or re-planning of intermodal terminals at the network level with the objective of minimizing the total (socioeconomic) terminal and transport costs. The model allows to determine the optimal locations and types/capacities of the terminals to operate in a territory in a decentralized management context, given the freight demands expected to take place between its regions in some reference planning year. In such a context, the governmental entity decides the location and type/capacity of the terminals, but does not control their utilization; i.e., terminal users patronize them or not according to their own best interests. Though, our focus in the paper was placed on rail-road terminal networks, the model can be easily adapted to accommodate any other types of terminals.
The behavior of the model was illustrated and discussed for a case study inspired by the Portuguese reality. The results we have obtained in this study clearly show the influence of the decision context: under decentralized management, the optimal terminal network would involve a much smaller number of terminals than under centralized management (i.e., if the governmental entity could fully control the utilization of the terminals to minimize terminal and transport costs). It should be emphasized here that some of the results we have obtained were rather surprising. For example, we have shown that, under a decentralized management context, an increase in rail transport unit costs may lead to an increase in the optimal number and capacity of terminals, as well as to an increase in the rail modal share, as the decisions on the use of terminals are made by the companies that move freight to minimize their own transport costs.
The case study included in the paper, inspired by the Portuguese reality, demonstrates well the usefulness of the proposed optimization model. In this case, we could solve the model quite fast using ILOG CPLEX even when the management context was decentralized because only 16 regions were considered as possible locations of new terminals (of three types). However, a computational study clearly revealed that larger instances of our model, such as the ones corresponding to mainland Spain (47 NUTS 3 regions) or France (94), would certainly be impossible to handle without resorting to faster solution methods. Consequently, one of the directions of our future work on intermodal terminal location problems will be the development of a metaheuristic method (namely, an evolutionary algorithm) for solving our model.
Another direction we intend to pursue in the future relates to what we recognize to be a limitation of our model, i.e., the assumption that, in a decentralized management context, all freight generated in a region is sent to the other regions through the least-cost route. It is obviously highly unlikely that this happens, and it would definitely be more realistic to assume that routes (and modes) are chosen according to the principle that the less costly is a route, the lower is the probability that this route is chosen. Logit functions are the ones typically used in transport studies to represent this principle. However, they are nonlinear, and therefore the inclusion of such functions in the proposed optimization model will make it more complex and more difficult to solve. The adaption of the metaheuristic we aim to develop for our model may be an idea to explore in this regard.
The third direction we expect to follow in our future research relates to the consideration of uncertainty in freight demand. Indeed, instead of planning the intermodal terminal network for the freight demands expected to take place in some reference planning year, it would certainly be more accurate to decide on the location and type/capacity of terminals taking into account possible scenarios for the evolution of these demands and their respective probabilities. Once again, this would make the proposed optimization model more complex and difficult to solve. Would the gains in optimal solutions justify the additional complexity? This is an important question that we will try to answer through our research.
Author Contributions
Conceptualization, all authors; methodology, all authors; software, E.J.D.; validation, E.J.D.; formal analysis, E.J.D.; investigation, E.J.D.; resources, A.P.A.; data curation, E.J.D.; writing—original draft preparation, E.J.D.; writing—review and editing, A.P.B.-P. and A.P.A.; visualization, E.J.D.; supervision, A.P.B.-P. and A.P.A.; project administration, A.P.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rodrigue, J.-P. The Geography of Transport Systems; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Agamez-Arias, A.D.M.A.; Moyano-Fuentes, J. Intermodal transport in freight distribution: A literature review. Transp. Rev. 2017, 37, 782–807. [Google Scholar] [CrossRef]
- Donovan, A. Intermodal Transportation in Historical Perspective. Transp. Law J. 2000, 27, 317–344. [Google Scholar]
- Bektas, T. Freight Transport and Distribution: Concepts and Optimisation Models; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Vasconcelos, A.D.; Nassi, C.D.; Lopes, L.A.S. The uncapacitated hub location problem in networks under decentralized management. Comput. Oper. Res. 2011, 38, 1656–1666. [Google Scholar] [CrossRef]
- Caris, A.; Macharis, C.; Janssens, G.K. Planning Problems in Intermodal Freight Transport: Accomplishments and Prospects. Transp. Plan. Technol. 2008, 31, 277–302. [Google Scholar] [CrossRef]
- SteadieSeifi, M.; Dellaert, N.P.; Nuijten, W.; Van Woensel, T.; Raoufi, R. Multimodal freight transportation planning: A literature review. Eur. J. Oper. Res. 2014, 233, 1–15. [Google Scholar] [CrossRef]
- Caris, A.; Macharis, C.; Janssens, G.K. Decision support in intermodal transport: A new research agenda. Comput. Ind. 2013, 64, 105–112. [Google Scholar] [CrossRef]
- Kapros, S.; Panou, K.; Tsamboulas, D.A. Multicriteria Approach to the Evaluation of Intermodal Freight Villages. Transp. Res. Rec. 2005, 1906, 56–63. [Google Scholar] [CrossRef]
- Ballis, A.; Mavrotas, G. Freight village design using the multicriteria method PROMETHEE. Oper. Res. 2007, 7, 213–231. [Google Scholar] [CrossRef]
- Kayikci, Y. A conceptual model for intermodal freight logistics centre location decisions. Procedia Soc. Behav. Sci. 2010, 2, 6297–6311. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. A novel hybrid MCDM model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR for city logistics concept selection. Expert Syst. Appl. 2014, 41, 8112–8128. [Google Scholar] [CrossRef]
- Wiegmans, B.; Behdani, B. A review and analysis of the investment in, and cost structure of, intermodal rail terminals. Transp. Rev. 2018, 38, 33–51. [Google Scholar] [CrossRef]
- Christiansen, M.; Fagerholt, K.; Nygreen, B.; Ronen, D. Maritime Transportation. In Transportation (Handbooks in Operations Research and Management Science Volume 14); Barnhart, C., Laporte, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 189–284. [Google Scholar]
- Wiegmans, B.W.; Masurel, E.; Nijkamp, P. Intermodal freight terminals: An analysis of the freight terminal market. Transp. Plan. Technol. 1999, 63, 105–168. [Google Scholar] [CrossRef][Green Version]
- Tadić, S.; Krstić, M.; Brnjac, N. Selection of efficient types of inland intermodal terminals. J. Transp. Geogr. 2019, 78, 170–180. [Google Scholar] [CrossRef]
- Mostert, M.; Limbourg, S. External Costs as Competitiveness Factors for Freight Transport—A State of the Art. Transp. Rev. 2016, 36, 692–712. [Google Scholar] [CrossRef]
- Alumur, S.A.; Kara, B.Y. Network hub location problems: The state of the art. Eur. J. Oper. Res. 2008, 190, 1–21. [Google Scholar] [CrossRef]
- Campbell, J.F.; O’Kelly, M.E. Twenty-Five Years of Hub Location Research. Transp. Sci. 2012, 46, 153–169. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Hekmatfar, M.; Arabani, A.B.; Nikbakhsh, E. Hub location problems: A review of models, classification, solution techniques, and applications. Comput. Ind. Eng. 2013, 64, 1096–1109. [Google Scholar] [CrossRef]
- Contreras, I. Hub location problems. In Location Science; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 311–344. [Google Scholar]
- Arnold, P.; Thomas, I. Localisation des centres de transbordement dans un système multiréseaux: Essai de formalization. L’Espace Geogr. 1999, 3, 193–204. [Google Scholar] [CrossRef]
- Arnold, P.; Peeters, D.; Thomas, I.; Marchand, H. Pour une localisation optimale des centres de transbordement intermodaux entre réseaux de transport: Formulation et extensions. Can. Geogr. Geogr. Can. 2001, 45, 427–436. [Google Scholar] [CrossRef]
- Arnold, P.; Peeters, D.; Thomas, I. Modelling a rail/road intermodal transportation system. Transp. Res. Part E Logist. Transp. Rev. 2004, 40, 255–270. [Google Scholar] [CrossRef]
- Sörensen, K.; Vanovermeire, C.; Busschaert, S. Efficient metaheuristics to solve the intermodal terminal location problem. Comput. Oper. Res. 2012, 39, 2079–2090. [Google Scholar] [CrossRef]
- Sörensen, K.; Vanovermeire, C. Bi-objective optimization of the intermodal terminal location problem as a policy-support tool. Comput. Ind. 2013, 64, 128–135. [Google Scholar] [CrossRef]
- Lin, C.-C.; Chiang, Y.-I.; Lin, S.-W. Efficient model and heuristic for the intermodal terminal location problem. Comput. Oper. Res. 2014, 51, 41–51. [Google Scholar] [CrossRef]
- Lin, C.-C.; Lin, S.-W. Two-stage approach to the intermodal terminal location problem. Comput. Oper. Res. 2016, 67, 113–119. [Google Scholar] [CrossRef]
- Ishfaq, R.; Cox, C.R. Hub location–allocation in intermodal logistic networks. Eur. J. Oper. Res. 2011, 210, 213–230. [Google Scholar] [CrossRef]
- Santos, B.F.; Limbourg, S.; Carreira, J.S. The impact of transport policies on railroad intermodal freight competitiveness—The case of Belgium. Transp. Res. Part D Transp. Environ. 2015, 34, 230–244. [Google Scholar] [CrossRef]
- Ernst, A.; Krishnamoorthy, M. Efficient algorithms for the uncapacitated single allocation p-hub median problem. Locat. Sci. 1996, 4, 139–154. [Google Scholar] [CrossRef]
- Ghane-Ezabadi, M.; Vergara, H.A. Decomposition approach for integrated intermodal logistics network design. Transp. Res. Part E Logist. Transp. Rev. 2016, 89, 53–69. [Google Scholar] [CrossRef]
- Limbourg, S.; Jourquin, B. Optimal rail-road container terminal locations on the European network. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 551–563. [Google Scholar] [CrossRef]
- Zhang, M.; Wiegmans, B.; Tavasszy, L. Optimization of multimodal networks including environmental costs: A model and findings for transport policy. Comput. Ind. 2013, 64, 136–145. [Google Scholar] [CrossRef]
- Zhang, M.; Janic, M.; Tavasszy, L.A. A freight transport optimization model for integrated network, service, and policy design. Transp. Res. Part E Logist. Transp. Rev. 2015, 77, 61–76. [Google Scholar] [CrossRef]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Sinha, A.; Malo, P.; Deb, K. A Review on Bilevel Optimization: From Classical to Evolutionary Approaches and Applications. IEEE Trans. Evol. Comput. 2017, 22, 276–295. [Google Scholar] [CrossRef]
- Chow, J.; Yang, C.H.; Regan, A.C. State-of-the art of freight forecast modeling: Lessons learned and the road ahead. Transportation 2010, 37, 1011–1030. [Google Scholar] [CrossRef]
- Tavasszy, L.A.; Ruijgrok, K.; Davydenko, I. Incorporating Logistics in Freight Transport Demand Models: State-of-the-Art and Research Opportunities. Transp. Rev. 2012, 32, 203–219. [Google Scholar] [CrossRef]
- Janić, M. Modelling the full costs of an intermodal and road freight transport network. Transp. Res. Part D Transp. Environ. 2006, 12, 33–44. [Google Scholar] [CrossRef]
- Hanssen, T.-E.S.; Mathisen, T.A.; Jørgensen, F. Generalized Transport Costs in Intermodal Freight Transport. Procedia Soc. Behav. Sci. 2012, 54, 189–200. [Google Scholar] [CrossRef]
- Bína, L.; Bínová, H.; Březina, E.; Kumpošt, P.; Padělek, T. Comparative model of unit costs of road and rail freight transport for selected European countries. Eur. J. Bus. Soc. Sci. 2016, 3, 127–136. [Google Scholar]
- Lodi, A. Mixed Integer Programming Computation. In 50 Years of Integer Programming 1958–2008: From the Early Years to the State-of-the-Art; Jünger, M., Liebling, T.M., Naddef, D., Nemhauser, G.L., Pulleyblank, W.R., Reinelt, G., Rinaldi, G., Wolsey, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 619–645. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).