Medical Segmentation of Kidney Whole Slide Images Using Slicing Aided Hyper Inference and Enhanced Syncretic Mask Merging Optimized by Particle Swarm Metaheuristics

Abstract

Accurate segmentation of kidney microstructures in whole slide images (WSIs) is essential for the diagnosis and monitoring of renal diseases. In this study, an end-to-end instance segmentation pipeline was developed for the detection of glomeruli and blood vessels in hematoxylin and eosin (H&E) stained kidney tissue. A tiling-based strategy was employed using Slicing Aided Hyper Inference (SAHI) to manage the resolution and scale of WSIs and the performance of two segmentation models, YOLOv11 and YOLOv12, was comparatively evaluated. The influence of tile overlap ratios on segmentation quality and inference efficiency was assessed, with configurations identified that balance object continuity and computational cost. To address object fragmentation at tile boundaries, an Enhanced Syncretic Mask Merging algorithm was introduced, incorporating morphological and spatial constraints. The algorithm’s hyperparameters were optimized using Particle Swarm Optimization (PSO), with vessel and glomerulus-specific performance targets. The optimization process revealed key parameters affecting segmentation quality, particularly for vessel structures with fine, elongated morphology. When compared with a baseline without postprocessing, improvements in segmentation precision were observed, notably a 48% average increase for glomeruli and up to 17% for blood vessels. The proposed framework demonstrates a balance between accuracy and efficiency, supporting scalable histopathology analysis and contributing to the Vasculature Common Coordinate Framework (VCCF) and Human Reference Atlas (HRA).

1. Introduction

The kidney is a vital organ responsible for maintaining systemic homeostasis by regulating blood filtration, fluid balance, electrolyte composition and acid-base status. Each kidney contains around one million nephrons, with each beginning at the glomerulus, a specialized capillary network that serves as the primary blood filtration site. Approximately one-fifth of cardiac output is delivered through the renal vasculature to maintain an adequate glomerular filtration rate [1]. The capillaries, arterioles and venules within the kidney ensure this filtration process and support metabolic demands. Damage to these microvascular structures or to the glomerular filtration barrier can lead to conditions, such as proteinuria, chronic kidney disease, or end-stage renal disease [2]. Additionally, vascular dysfunction and microvascular rarefaction contribute to progressive loss of kidney function [1].

Given the central role of microvascular health in renal pathology, accurate assessment of glomerular and vascular structures is essential for diagnosis and monitoring. High-resolution kidney biopsies remain the clinical gold standard and modern whole slide imaging allows the digitization of entire biopsy slides at subcellular resolution, often producing gigapixel scale images. However, manual analysis methods are labor-intensive, subjective and often inconsistent across imaging conditions [3]. Deep learning methods, particularly convolutional neural networks (CNN), have shown promise in automating such analyses but face computational limitations when processing entire WSIs directly.

One of the key challenges in this context is small object detection. In renal histopathology, microvascular structures occupy small pixel regions and exhibit high morphological variability [4,5]. These factors, along with class imbalance and anatomical complexity [6,7], limit the effectiveness of conventional detection models, as small objects often lack sufficient semantic and contextual features for reliable extraction. To address this, tiling-based inference has become a common approach, where WSIs are divided into smaller patches to allow localized, high-resolution predictions.

A widely adopted tiling strategy is slicing aided hyper inference  [8], which enables large-scale inference by slicing images into overlapping or non-overlapping tiles. However, SAHI introduces postprocessing challenges. Since objects may be fragmented across tiles, a consolidation step is needed to merge redundant or partial detections. Traditional Non-Maximum Suppression (NMS) [9] is commonly used for this purpose but is suboptimal for instance segmentation due to its box-centric logic and inability to preserve full object extent, especially for irregular or boundary-crossing structures [10]. Syncretic NMS [11] improves upon this by merging correlated neighboring detections, yet it still suffers in low-overlap or sparsely tiled settings, which are common in WSI processing.

Recent advances have explored various strategies to improve object detection and segmentation in high-resolution images. The importance of pre- and post-processing in whole slide image analysis pipelines has been highlighted, with tiling and reconstruction steps introducing unique challenges that impact the reliability of clinical predictions [12]. Combining the SAHI algorithm with modern neural networks has been shown to enhance the detection of small objects in high-resolution images, supporting the use of tiling-based inference [13]. However, the fragmentation of objects across tiles remains problematic, particularly for boundary-spanning structures. A hybrid two-stage cascade has been proposed to mitigate segmentation errors in overlapping objects, yet mask inaccuracies persist in complex spatial arrangements, similar to the microvascular structures observed in kidney histology [14]. Optimization-based methods, such as the particle swarm optimization approach for enhancing segmentation accuracy, have also been explored but not systematically applied to the postprocessing of tiled WSI segmentations [15]. Overall, current merging strategies largely rely on heuristic, box-centric approaches that struggle to reconstruct irregularly shaped or elongated objects and lack principled mechanisms for adapting parameters across datasets or imaging conditions. These limitations frequently result in fragmented or incomplete masks, leading to precision losses for fine microvascular structures that cross tile boundaries in renal WSIs.

There is currently no postprocessing framework explicitly designed to address spatial fragmentation and boundary-crossing inconsistencies in tiled WSI instance segmentation. Existing solutions rely on heuristic, non-adaptive methods that fail to accurately reconstruct irregular microvascular objects and cannot dynamically balance segmentation precision with computational efficiency in gigapixel-scale images. This raises the research question: How can mask merging strategies in tiled whole slide image inference be optimized to accurately reconstruct boundary-spanning microvascular structures, maximizing segmentation precision while maintaining computational efficiency beyond what existing postprocessing methods offer?

To address this gap, this work introduces an enhanced syncretic mask merging algorithm specifically designed to handle irregularly shaped, low-density and partially detected microvascular structures in renal WSIs. The approach is integrated into a complete segmentation pipeline that

• Provides a comparative evaluation of YOLOv11 and YOLOv12 instance segmentation models, validated using SAHI tiling on high-resolution kidney WSIs.
• Investigates the impact of tile overlap on segmentation accuracy and identifies optimal overlap configurations.
• Introduces a novel syncretic mask merging algorithm capable of reconstructing fragmented objects more effectively across tile boundaries.
• Proposes and explores the viability of metaheuristics PSO for adaptive tuning of mask merging parameters, aiming to improve segmentation precision while maintaining computational efficiency.

The objective of this study is to develop and evaluate a scalable, accuracy-focused segmentation pipeline tailored for complex microvascular structures in renal WSIs, providing a solution that overcomes the limitations of existing postprocessing techniques.

2. Materials and Methods

This section presents the components of the proposed instance segmentation pipeline, including the base segmentation models, the tiling and inference strategy, the enhanced merging algorithm and the optimization of its hyperparameters.

Among the core components of our pipeline, the segmentation backbone is based on the YOLO architecture, which performs object detection and segmentation using a unified forward pass. The loss function guiding YOLO training combines four terms: localization, object confidence, objectness penalty for background regions and classification. For improved stability, particularly for small, fragmented anatomical features, advanced variants such as Complete Intersection-over-Union (CIoU) loss are used to better align predicted and ground truth boxes [16]. A detailed mathematical description of the YOLO loss function and its role in this study is provided in Appendix A.

SAHI [8] is employed to enable object detection on whole slide images by dividing them into overlapping patches. Each tile is processed independently and predictions are later merged to produce whole-image instance segmentation. Key slicing parameters such as tile size and overlap ratios are explored and tuned to balance efficiency and object continuity. However, due to the challenges of merging fragmented detections near tile borders, especially for irregular objects, we propose a postprocessing algorithm designed to enhance merging accuracy. Further details of the SAHI algorithm and its formal implementation are provided in Appendix B.

To improve postprocessing in tiled inference scenarios, we build upon Syncretic NMS [11], an extension of standard NMS that merges spatially correlated detections to recover more complete object instances. While originally developed for general instance segmentation, its applicability to whole slide images is limited due to challenges such as sparse tile overlap and low IoU across tile boundaries. In this work, we adapt and extend the Syncretic framework to address those issues, enabling robust merging of fragmented microvascular detections across tiles. A detailed description of the original Syncretic NMS algorithm and its merging criteria is provided in Appendix C.

To further improve the accuracy and coherence of reconstructed instances, we introduce a refinement operator $\Phi \left(A\right)$ applied to each cluster A of correlated detections. This operator merges the binary masks of all objects in A using a logical union, followed by a set of morphological operations. These include mask smoothing via morphological closing, hole filling and selective dilation of small or fragmented regions. The purpose is to enhance shape continuity, close gaps introduced by tile boundaries and correct under-segmentation in low-contrast or irregularly shaped structures. The refined object retains its semantic class and has its bounding box and geometry recomputed from the updated mask. The full morphological refinement procedure, along with implementation details and parameters, is provided in Appendix D.

2.1. Dataset and Preprocessing

The dataset used in our work is derived from whole slide images of PAS-stained human kidney tissue, with resolutions from 8704 × 13,824 to 17,408 × 44,544 pixels, representing entire histological slides. It is prepared for the HuBMAP Hacking the Human Vasculature Kaggle competition [17]. Slides represent healthy kidney tissue with a focus on microvascular structures. The training dataset is composed of image tiles originally extracted from WSIs at 40 times magnification, corresponding to a physical area of approximately $128\times 128\mathsf{\mu }$m. These tiles are categorized into three subsets: Dataset 1 (expert-reviewed annotations), Dataset 2 (sparser annotations), and Dataset 3 (unannotated tiles). While Datasets 1 and 2 originate from five donor slides and include polygonal masks for blood vessels, glomeruli and uncertain regions, Dataset 3 is intended for semi-supervised learning and lacks annotations and demographic metadata [18].

A total of 6606 tiles from Datasets 1 and 2 and 1800 self-annotated tiles from Dataset 3 were used to train the YOLOv11 and YOLOv12 models. The data were split into training, validation and test sets as follows: 5575 images (84%) for training, 685 images (10%) for validation and 346 images (5%) for testing. Each image was resized to 640 × 640 pixels and augmented by applying horizontal and vertical flips with a 50% probability each, resulting in three variants per original image. The tissue samples include sections from distinct anatomical regions of the kidney: renal cortex, renal medulla and renal papilla. This segmentation task not only supports basic biological mapping but also enables downstream applications like modeling blood flow, tissue oxygenation and cellular organization. Figure 1 illustrates the dataset structure, showing a full kidney whole slide image and a representative annotated tile extracted for model training.

2.2. Implementation and Training of YOLO Models

Recent YOLO versions have introduced architectural enhancements aimed at improving instance segmentation performance. The YOLOv11 model [19] integrates a transformer-based backbone to enhance global spatial understanding and selectively applies attention mechanisms to enrich feature representations without incurring additional computational cost. Building upon this, the YOLOv12 model [20] introduces area attention and Residual Efficient Layer Aggregation Networks (RELAN). RELAN enhances the model’s ability to capture spatial dependencies by dividing feature maps into regions and aggregating information from multiple network layers using residual connections and a redesigned feature aggregation strategy. This mechanism is implemented via lightweight A2C2f blocks, which aggregate contextual information from adjacent regions using efficient 2D attention and depthwise separable convolutions. This enables more effective fusion of low-level details and high-level semantic features, resulting in improved object detection accuracy and more stable training dynamics.

The PyTorch YOLO (version 8.3.159) segmentation models provided by Ultralytics [21] were utilized. These models use convolutional neural networks as the backbone for feature extraction. Lightweight components such as C3k2 blocks promote feature reuse, while C2PSA attention modules enhance the model’s focus on spatially relevant information. Additionally, multi-scale segmentation heads are employed to refine mask predictions across varying object sizes by leveraging feature maps from different network depths [19]. This multi-scale strategy enables effective detection of both small and large structures, as each head specializes in a specific scale of object representation. Such approaches have been shown to significantly improve segmentation performance in real-time models like YOLO-MS [22]. The contributions of this work are reflected in the adaptation of segmentation backbones and training protocols to the unique demands of tiled inference in whole slide kidney histology, where maintaining boundary continuity and managing fine-scale morphological variation.

Two YOLO-based instance segmentation models are explored in this study: the compact YOLOv11s-seg and the more recent YOLOv12s-seg. The YOLOv11s-seg model comprises 355 layers and approximately 10.1 million parameters (35.6 GFLOPs). Both models were trained on tiled inputs derived from a kidney histology dataset for 100 epochs using Automatic Mixed Precision (AMP). AMP accelerates training by utilizing FP16 operations where safe, while retaining FP32 precision where necessary, thereby reducing memory usage and improving training speed, beneficial for high-resolution images. The AdamW optimizer was used, with learning rate and momentum parameters automatically tuned via Ultralytics’ built-in hyperparameter search. Similarly, the YOLOv12s-seg model, consisting of 533 layers, 9.75 million parameters and 33.6 GFLOPs [20], was trained under the same regime. Both models were trained and evaluated under identical conditions to secure balanced evaluation.

2.3. Inference Strategy with SAHI

In analysis, SAHI $overlap\_ratio$ values in the range from 0 to 0.15 (0–15%) were explored, using increments of 0.025 (2.5%), to evaluate overlap impact on detection continuity across slice boundaries. To reduce computational cost, inference was performed on cropped regions of 3072 × 3072 pixels extracted from the original whole slide images. These regions were subsequently divided into overlapping tiles of 512 × 512 pixels, which were processed through the inference pipeline and postprocessed before comparison against the available ground truth annotations. For evaluation of the proposed segmentation pipeline, standard performance metrics commonly used in medical image analysis were computed [23], including instance-level matching metrics and the results were compared with ground truth annotations. Implementation details are available in Appendix B.

2.4. Proposed Enhanced Syncretic Mask Merging

To overcome the limitations of traditional bounding box-based merging in large-scale image inference, the Syncretic NMS framework is extended with modified merging criteria and a morphological postprocessing procedure. The proposed method is specifically tailored for tiled instance segmentation and introduces object-level reasoning that preserves the continuity of biological structures across tile borders.

The enhanced Syncretic strategy generalizes prior approaches by applying merging to binary object masks rather than bounding boxes, using a flexible mergeability predicate and additional morphological operations to resolve overlapping or fragmented instances across tiles. Specifically, border objects are detected and clustered using a spatial proximity radius, with merging decisions guided by contour similarity $\mathcal{D}(o_m,o_j)$, feature similarity $\mathcal{F}(o_m,o_j)$, bounding box IoU $\mathcal{I}(o_m,o_j)$ and semantic label agreement $\mathcal{L}(o_m,o_j)$. The resulting clusters are fused into unified masks via logical union, followed by contour simplification and polygon extraction. A final morphological refinement stage applies gap closing, hole filling and one pass dilation to improve continuity and recover thin or clipped regions. 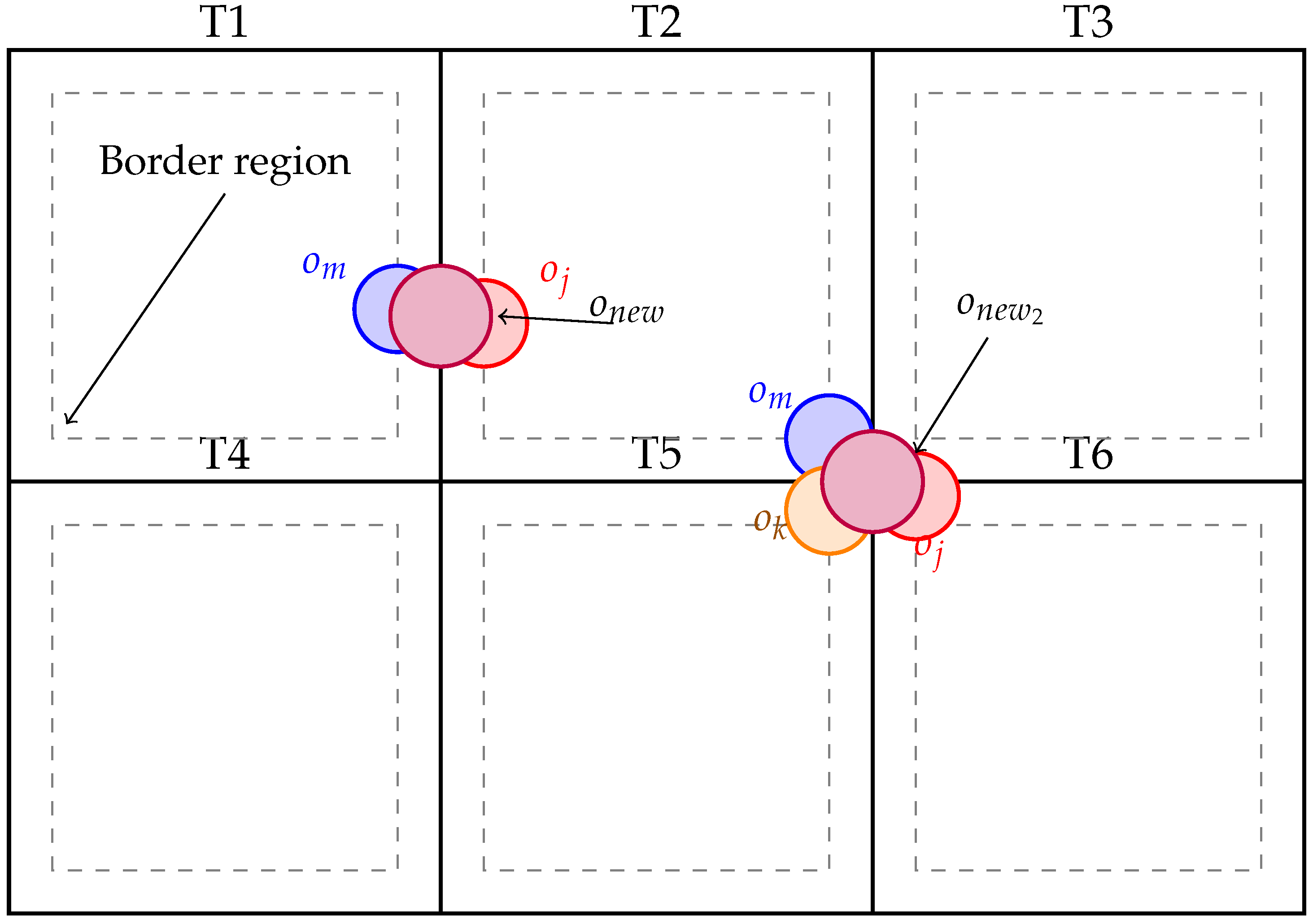Figure 2 illustrates the mask merging process, showing how fragmented instances are accurately grouped and reconstructed across adjacent tiles.

Algorithm 1 operates in two major stages: (1) object-level clustering based on spatial, semantic, and feature similarity, and (2) morphological refinement. First, all detected instances are converted from local tile coordinates into a unified global space. Objects near tile boundaries are designated as merge candidates and grouped into a global candidate set. Merging proceeds iteratively: at each step, the highest confidence object is selected as a seed, and neighboring candidates are evaluated for compatibility using a mergeability predicate $\mathcal{M}$. This predicate considers semantic class consistency, contour proximity, feature vector similarity, and geometric overlap. Compatible objects are grouped into a cluster and merged via the operator $\Phi$, producing a unified mask instance.

Algorithm 1 Enhanced Syncretic Merging Algorithm (adapted from [11])

Require: Tiles ${\left\{T_i\right\}}_{i=1}^n$ with local masks, confidence scores and class labels; tile offsets ${\left\{(x_i,y_i)\right\}}_{i=1}^n$ Ensure: Merged global object set G 1: Convert all objects to global coordinates: ${\widehat{O}}_i\leftarrow \mathtt{ToGlobal}\left(T_i\right)$ 2: Identify candidate objects near tile edges: $O_i^{\mathrm{border}}$ 3: Combine border objects into global pool: $O^{\mathrm{border}}\leftarrow {\bigcup }_i{O}_i^{\mathrm{border}}$ 4: Initialize empty set G 5: Build candidate list B from unmatched objects in $O^{\mathrm{border}}$ 6: while $B\ne \varnothing$ do 7:     Select object $o_m$ with maximum confidence 8:     Initialize set $A\leftarrow \left\{o_m\right\}$ 9:     for each $o_j$ in B near $o_m$ do 10:         if $\mathcal{M}(o_m,o_j)$ holds then 11:            Add $o_j$ to A 12:            Remove $o_j$ from B 13:         end if 14:     end for 15:     $o_{\mathrm{new}}\leftarrow \Phi \left(A\right)$ 16:     $G\leftarrow G\cup o_{\mathrm{new}}$ 17:     Remove $o_m$ from B 18: end while 19: return G

Where:

• $T_i$: The i-th tile in the WSI, with local detections, masks, scores and class labels.
• $(x_i,y_i)$: Tile $T_i$ upper left corner.
• n: Total number of tiles in the WSI.
• $O_i^{border}$: List of border objects in tile $T_i$, whose bounding boxes or masks lie within border_threshold_px of any tile edge.
• $O^{border}$: List of all objects near border ${\bigcup }_{i=1}^n{O}_i^{border}$.
• B: Working candidate list built from unmatched objects in $O^{border}$ at the start of each iteration.
• $o_m$: Object in B with the highest confidence in the current iteration.
• A: Merge group initialized with $o_m$ and extended with nearby compatible objects.
• $o_j$: A candidate object in B evaluated for merging with $o_m$.
• $o_{new}$: New merged object resulting from applying $\Phi \left(A\right)$.
• G: Final list of merged global objects to be returned.
• border_threshold_px: Pixel threshold defining how close an object must be to a tile edge to be considered a border object.
• search_radius: Maximum spatial distance (in pixels) within which object pairs are considered for merging.

The mergeability predicate $\mathcal{M}(o_m,o_j)$ is evaluated using the following criteria:

$$\mathcal{M}(o_m,o_j)=\left[\mathcal{D}(o_m,o_j)\le {\tau }_d\wedge \mathcal{F}(o_m,o_j)\ge {\tau }_f\wedge \mathcal{I}(o_m,o_j)\ge {\tau }_i\wedge \mathcal{L}(o_m,o_j)=1\right]$$

(1)

where:

• $\mathcal{D}(o_m,o_j)$: Euclidean distance between outlines of $o_m$ and $o_j$ [24].
• $\mathcal{F}(o_m,o_j)$: Cosine similarity between shape features of $o_m$ and $o_j$ [25].
• $\mathcal{I}(o_m,o_j)$: IoU score between the $o_m$ and $o_j$ boxes.
• $\mathcal{L}(o_m,o_j)$: Semantic label match indicator, equals 1 if classes match, else 0.

The functions defining the mergeability predicate and their thresholds are as follows: $\mathcal{C}(o_m,o_j)$ in Equation (3) captures contour-based spatial proximity and is constrained by the distance contour_proximity_thresh (${\tau }_d$); $\mathcal{F}(o_m,o_j)$ in Equation (2), measures cosine similarity of features that are over the cosine_sim_thresh (${\tau }_f$); $\mathcal{I}(o_m,o_j)$, representing the IoU between bounding boxes, which must meet the minimum threshold bbox_iou_thresh (${\tau }_i$); $\mathcal{L}(o_m,o_j)$ in Equation (5), a binary indicator ensuring semantic class consistency [26].

$$\mathcal{F}(o_m,o_j)={\displaystyle \frac{F_m·F_j}{\parallel F_m\parallel ·\parallel F_j\parallel }}$$

(2)

$$\mathcal{C}(o_m,o_j)=max\left(\underset{a\in C_m}{max}\underset{b\in C_j}{min}\parallel a-b\parallel ,\underset{b\in C_j}{max}\underset{a\in C_m}{min}\parallel b-a\parallel \right)$$

(3)

$$\mathcal{S}(o_m,o_j)={\displaystyle \frac{|M_m\cap M_j|}{|M_m\cup M_j|}}·s_j$$

(4)

$$\mathcal{L}(o_m,o_j)=\left\{\begin{array}{cc}1,\hfill & ifclass\left(o_m\right)=class\left(o_j\right)\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

(5)

In the Equations (2)–(5), $M_m$ and $M_j$ denote the sets of foreground pixels (or sampled points) from the masks of objects $o_m$ and $o_j$, respectively. $F_m$ and $F_j$ represent their corresponding feature vectors, which may be derived from intermediate neural network embeddings. $C_m$ and $C_j$ are the sets of contour or boundary points extracted from the object masks. The $s_j$ represents the confidence score of object $o_j$ predicted. The operator $\parallel ·\parallel$ refers to the Euclidean norm and $|·|$ denotes the cardinality of a set. The dot product $F_m·F_j$ is used in computing cosine similarity and the intersection and union operators in $\mathcal{S}(o_m,o_j)$ correspond to standard binary mask operations. The proposed merging framework incorporates this refinement operator $\Phi \left(A\right)$ as a final step, ensuring spatial continuity and accurate reconstruction of merged object instances. Implementation details are included in Appendix D.

In terms of computational complexity, the Enhanced Mask Merge algorithm scales as $O(N·k·d)$, where N is the number of border objects, k is the average number of nearby candidates considered for merging and d is the dimensionality of the feature vectors used in similarity evaluation. These feature vectors encode appearance or shape characteristics and are used to compute cosine similarity between objects. In contrast, the Syncretic NMS algorithm does not rely on feature vectors and instead performs pairwise comparisons based solely on geometric overlap and confidence scores. As a result, its worst-case complexity is $O\left(N^2\right)$, since each box may be compared with all others. While Syncretic NMS is simpler and effective for small-scale scenarios, its quadratic growth becomes computationally expensive as N increases. Enhanced Mask Merge, by leveraging spatial locality and feature-based filtering, offers a scalable alternative for large-scale instance merging tasks.

2.5. Evaluation and Hyperparameter Optimization

To evaluate instance segmentation performance, standard object-level metrics commonly used in medical imaging were computed: Accuracy, Precision, Recall and the F1 score. These metrics quantify agreement between predicted and ground truth objects, defined as follows:   

$$\begin{array}{cc}\mathrm{Accuracy}={\displaystyle \frac{CP}{CP+IP+IN}},\hfill & \mathrm{Precision}={\displaystyle \frac{CP}{CP+IP}},\hfill \\ \\ \mathrm{Recall}={\displaystyle \frac{CP}{CP+IN}},\hfill & F1={\displaystyle \frac{2·CP}{2·CP+IP+IN}}\hfill \end{array}$$

(6)

To summarize performance across different IoU thresholds, the average F1 score ($A{P}_{F_1}$) was calculated as follows:

$$A{P}_{F_1}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{F}_1^{(IoU=t_i)}$$

(7)

where $t_i\in \{0.5,0.6,0.7,0.8,0.9\}$ and $N=5$.

Evaluation was performed on a representative subset of 15 WSIs, each covering large, high-resolution tissue sections at 40× magnification. Due to the computational demands of processing WSIs, each image was subdivided into dozens of tiles measuring $512\times 512$ pixels, resulting in a total of several hundred tiles across the evaluation set. To ensure consistency, predictions with confidence scores below 50% were excluded. While the dataset size is limited, it reflects a practical balance between computational feasibility and anatomical coverage.

Hyperparameter optimization was conducted using particle swarm optimization [27]. The Python library pyswarms [28] was used to implement PSO with a swarm of 30 particles and 30 iterations. The inertia weight was fixed at 0.5, while both cognitive and social coefficients were set to 2.0 to balance exploration and convergence. The optimization objective was to maximize the macro-averaged F1 score across both blood vessels and glomeruli.

A set of tunable parameters governing mask refinement and cross-tile merging was explored, including morphological kernel sizes, spatial proximity thresholds, and feature similarity cutoffs. Given the differing geometries of blood vessels and glomeruli, class-specific parameter bounds were introduced. These ranges, shown in

Table 1. Empirically selected hyperparameter ranges for PSO optimization.

Hyperparameter	Overall (Range)	Blood Vessels	Glomeruli
morph_kernel	–	5 to 11	3 to 7
epsilon	–	1.0 to 2.0	0.5 to 1.5
dilation_percentile	5 to 30	Shared	Shared
dilation_kernel	3 to 11	Shared	Shared
contour_proximity_thresh	20.0 to 80.0	Shared	Shared
cosine_sim_thresh	0.80 to 0.95	Shared	Shared
bbox_iou_thresh	0.05 to 0.50	Shared	Shared

, were selected empirically.

This represents a novel approach for tuning postprocessing in tiled whole slide inference, leveraging PSO to optimize a mask merging framework that incorporates spatial proximity, semantic consistency and feature-level similarity. Unlike conventional NMS-based methods, the refinement pipeline is class-aware and scale-sensitive, enabling robust reconstruction of fragmented or elongated structures across tile boundaries.

3. Results

To assess the proposed training strategy and model architectures, an evaluation was conducted across multiple training epochs and inference settings. Loss components for both models consistently decreased across epochs, with no signs of overfitting observed. In the inference phase, both models successfully integrated SAHI, enabling dense and overlapping tile aggregation across high-resolution whole slide images. This approach allowed for precise instance segmentation while maintaining computational efficiency on large-scale histology data.

Table 2. Instance segmentation performance comparison of YOLOv11s-seg and YOLOv12s-seg.

Segment	Instance	Precision (%)	Recall (%)	F1 Score
Blood Vessels	YOLOv11s-seg	73.5	67.2	0.702
	YOLOv12s-seg	65.6	69.8	0.676
Glomeruli	YOLOv11s-seg	90.5	90.8	0.906
	YOLOv12s-seg	91.5	88.6	0.900
Overall	YOLOv11s-seg	82.0	79.0	0.804
	YOLOv12s-seg	77.6	76.9	0.789

presents a comparative evaluation of instance segmentation performance between YOLOv11s-seg and YOLOv12s-seg across key kidney tissue structures.

Both models achieved high segmentation performance for glomerulus, with precision and recall consistently above 88%. Blood vessel segmentation was more variable due to the finer and more diffuse structure of vascular elements. However, YOLOv11s-seg maintained a higher F1 score overall, making it more balanced in performance across both classes.

As shown in

Table 3. Computational efficiency metrics of YOLOv11s-seg and YOLOv12s-seg.

Metric	YOLOv11s-seg	YOLOv12s-seg	Unit
Time per Epoch	2:17	4:38	min:s
Average Inference Time per Tile	6.2	11.7	ms
GPU Memory Utilization	5.5	8.1	GB
Total Training Time (100 epochs)	4:02:00	6:58:19	h:m:s

, YOLOv11s-seg was considerably more efficient, with lower GPU memory usage and faster epoch and inference times. This is particularly important in whole slide image workflows, where inference must be both accurate and fast. The reduced GPU footprint of YOLOv11s-seg also enhances its applicability in clinical or resource-limited deployment environments. Given the strong segmentation performance, compact architecture, and superior computational efficiency, YOLOv11s-seg was selected for downstream tasks, including framework validation and segmentation-based postprocessing.

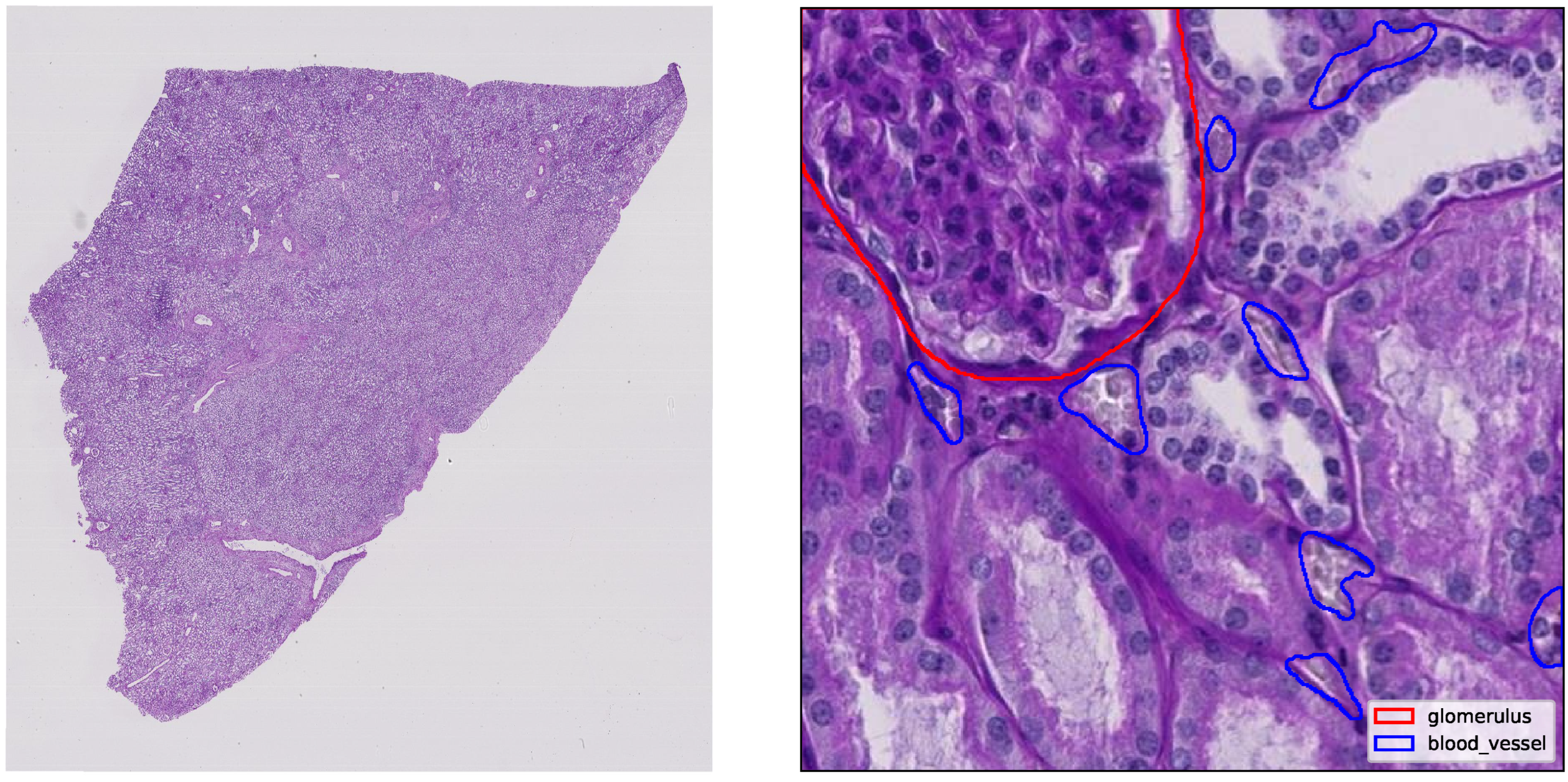
Figure 3 shows the Mask F1 score curve and the mask Precision Recall (PR) curve for YOLOv11s-seg. The F1 curve tracks the harmonic mean of mask precision and recall throughout training. Glomerular segmentation demonstrates particularly strong separation, while blood vessel performance is slightly more variable. Figure 4 presents a representative validation example. The left panel shows ground truth masks for glomeruli and blood vessels overlaid on a histology tile, while the right panel displays YOLOv11s-seg’s predicted masks for the same region. Qualitatively, the model captures the boundaries and structure of glomeruli accurately, with reasonable performance on finer vascular elements.

Despite the architectural enhancements in YOLOv12s-seg, such as A2C2f blocks and deeper layer integration, the model underperformed YOLOv11s-seg in both segmentation quality and computational efficiency. Specifically, YOLOv11s-seg achieved higher mask mAP@0.5 (0.623 vs. 0.585) and overall better balance of precision and recall across key object classes. While glomerular segmentation performance remained strong in both models, YOLOv11s-seg showed slightly higher overall mAP and more consistent recall. The YOLOv12 model also incurred greater computational cost, with significantly slower inference (2×) and deeper network complexity. Moreover, YOLOv12s-seg required over 70% more training time and 47% more GPU memory, while offering no clear benefit in segmentation accuracy. Clearly, the additional complexity of YOLOv12s-seg does not translate into improved performance in this histological context, and simpler CNN-based models like YOLOv11s-seg remain more reliable for resource-constrained biomedical segmentation tasks.

The impact of tile overlap ratio on segmentation performance was evaluated. Experiments were conducted using varying overlap ratios ranging from 0% to 15% in steps of 2.5%. Performance was assessed using the ${AP}_{F_1}$ metric, computed as the mean F1 score across IoU thresholds 0.5–0.9 compared with ground truth. Figure 5 illustrates how segmentation quality, measured via ${AP}_{F_1}$, changes with increasing overlap. The performance improves steadily up to an overlap of approximately 7.5%, after which it plateaus or slightly declines. This suggests moderate overlap helped in restoring instance structures across tiles. As expected, inference time per image increases with larger overlaps due to redundant tile processing. Figure 5 shows a near-linear increase in average runtime from 140 to over 210 s per image as the overlap increases from 7.5% to 15%. Based on the ${AP}_{F_1}$ results, the optimal overlap ratio was found to be approximately 7.5%.

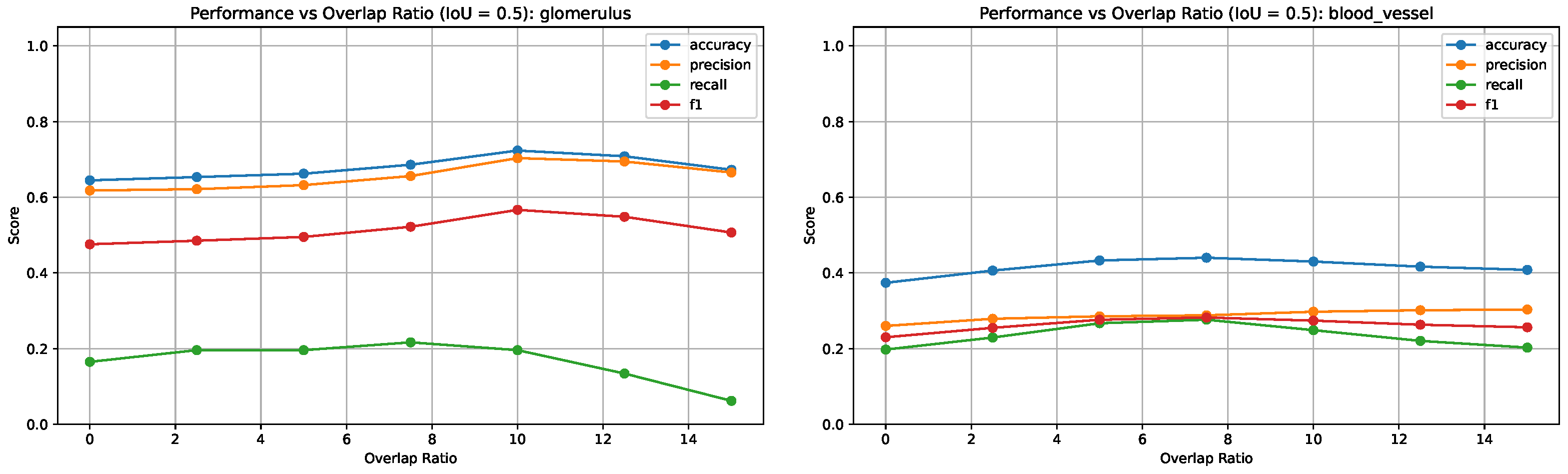
Figure 6 presents F1 scores across all IoU thresholds and overlap ratios for both blood vessels and glomeruli. These plots highlight how stricter IoU thresholds affect the precision/recall tradeoff differently across tissue types, with blood vessels showing more pronounced performance variations due to their elongated and fragmented morphology. Figure 7 shows the variation in segmentation metrics at IoU = 0.5 for both tissue types, highlighting the effect of overlap ratio on detection performance.

Figure 8 illustrates the impact of tile overlap on segmentation quality. The no-overlap result shows fragmented and incomplete segmentations, especially at tile boundaries, while the overlap result yields more continuous and accurate detections. As seen in the figure, the central glomerulus (red) on the left has lost its upper left corner due to the tile boundary truncation. This demonstrates that moderate overlap improves prediction quality and also suggests that further postprocessing is necessary to consolidate segments across tiles, motivating our proposed enhanced mask merging method.

Based on these findings, an overlap ratio in the range of 5–7.5% is recommended for most use cases, as this range offers a favorable balance between segmentation accuracy and inference time. Overlaps within this range consistently improved object continuity across tile boundaries without introducing significant computational overhead for large-scale whole slide image processing. To further refine the segmentation results, postprocessing optimization was conducted using a tile overlap of 7.5%.

Table 4. Best PSO optimized parameters with 7.5% overlap.

Hyperparameter	F1 Score	Blood Vessels	Glomeruli
morph_kernel (vessel)	7	7	7
epsilon (vessel)	1.07	1.10	1.50
morph_kernel (glomerulus)	5	5	7
epsilon (glomerulus)	1.31	1.47	0.95
dilation_percentile	23	5	20
dilation_kernel	5	5	5
contour_proximity_thresh	45.97	56.24	55.46
cosine_sim_thresh	0.94	0.91	0.82
bbox_iou_thresh	0.21	0.12	0.17
F1 Score	0.8138	0.7559	0.8718

presents the best performing hyperparameter configurations, both overall and separately for each class, as determined by peak $F1$ score. The values listed in Table 4 represent the PSO optimized parameters used in the algorithm, with rounded values shown for implementation and original outputs provided in parentheses for reference.

The results show that glomeruli segmentation achieved near-optimal performance with minimal missed instances, while vessel detection remained more challenging due to under-segmentation and fragmentation. The optimized morphological kernel sizes fall within the lower end of their respective ranges, suggesting that moderate morphological closing is generally effective. Polygon approximation parameters (epsilon) support preserving shape detail, with vessels favoring higher values than glomeruli. Clustering thresholds reflect the fragmentary nature of instance predictions: low bbox_iou_thresh values (0.12–0.21) allow for permissive spatial merging, while moderate cosine_sim_thresh values maintain conservative shape agreement. Specifically, a low bbox_iou_thresh value (0.12) allows for permissive spatial merging of partially overlapping vessel fragments, compensating for breakage across tile boundaries. At the same time, a relatively high cosine_sim_thresh (0.91) ensures that only geometrically similar fragments are merged, thus guarding against the erroneous fusion of unrelated vessels. The contour_proximity_thresh values indicate that a spatial clustering radius in the 45–56 pixel range is effective. Importantly, all optimized parameters remained within the empirically defined hyperparameter bounds (Table 1), validating the suitability of the selected search space.

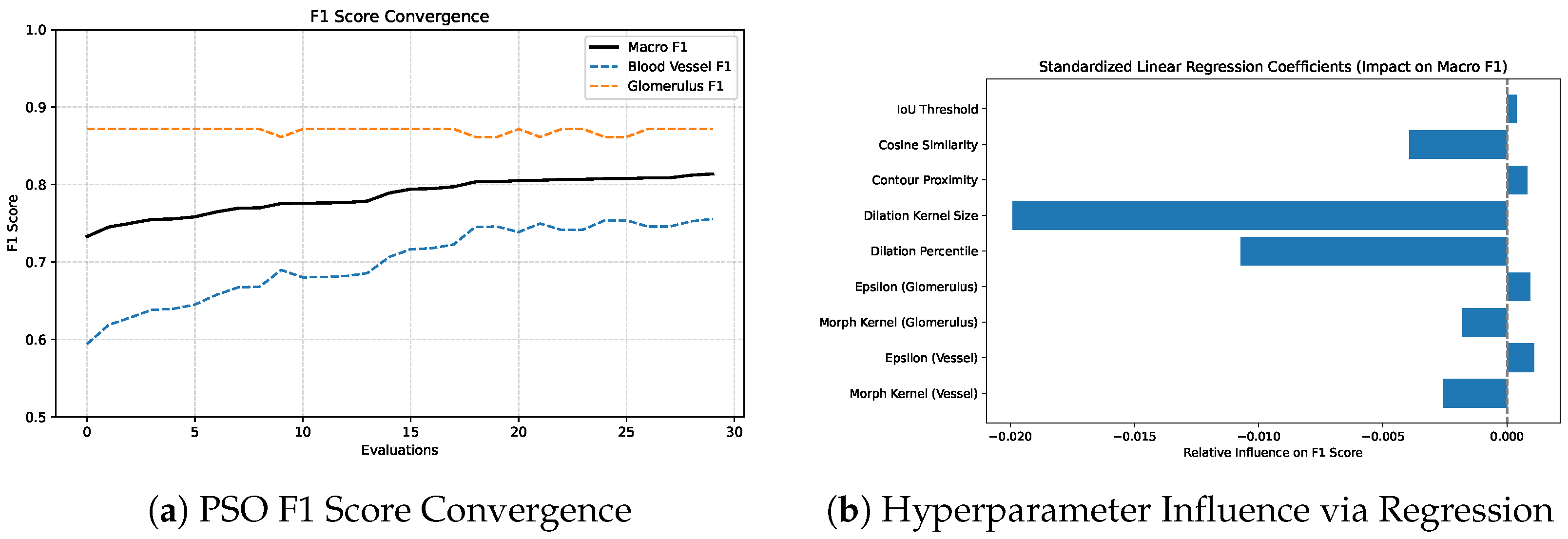
Figure 9 illustrates the convergence of F1 scores during PSO optimization (left) and the relative influence of each hyperparameter on macro F1 as determined by standardized linear regression (right). Regression analysis revealed that dilation_kernel, dilation_percentile and cosine_similarity had the strongest negative influence on macro $F1$. In contrast, parameters such as morphological_kernel (glomerulus), epsilon (glomerulus) and IoU_threshold showed minimal impact within the tested range. The sensitivity analysis and convergence behavior observed in this study not only validate the effectiveness of our optimization strategy but also highlight the practical application of the proposed postprocessing algorithm. By identifying a small subset of hyperparameters with high impact, future tuning efforts can be confidently prioritized around these parameters.

Additionally, qualitative and quantitative evaluations were performed using the best-scoring image from each class. Figure 10 presents side-by-side comparisons between predicted and ground truth instance segmentations for the top-performing image in each class.

Metrics are summarized in

Table 5. Evaluation metrics for the best-performing annotated examples.

Metric	Blood Vessel		Glomerulus
	GT	Pred	GT	Pred
Instance Count	363	340	5	5
True Positives (TP)	299		5
False Positives (FP)	41		0
False Negatives (FN)	64		0
Accuracy	0.740		1.000
Precision	0.879		1.000
Recall	0.824		1.000
F1 Score	0.851		1.000

, including detection counts and evaluation metrics. Ground truth and predicted instance counts are reported separately, while derived metrics such as precision, recall and F1 score were computed against the reference annotations. The results demonstrate the fitness of the proposed merging and cleaning algorithm. Glomerulus segmentation achieved perfect agreement with the ground truth in the best-performing image, whereas blood vessel segmentation, although highly accurate, exhibited slightly lower performance due to the greater structural complexity and fragmentary nature of vascular objects.

Finally,

Table 6. Relative average and maximum improvements ($\Delta$) in segmentation metrics after applying the optimized postprocessing pipeline, computed against baseline predictions from YOLOv11s-seg.

Class	Type	$\mathbf{\Delta }$Accuracy	$\mathbf{\Delta }$Precision	$\mathbf{\Delta }$Recall	$\mathbf{\Delta }{\mathit{F}}_{\mathbf{1}}$
Blood Vessel	Average	0.0437	0.0815	$-0.0058$	0.0360
	Max	0.1051	0.1710	0.0201	0.0872
Glomerulus	Average	0.4234	0.4831	0.0822	0.3571
	Max	0.6944	0.6720	0.5000	0.6652

summarizes the average and maximum improvements (denoted as $\Delta$) in segmentation performance metrics when comparing the proposed optimized pipeline against baseline predictions produced by YOLOv11s-seg without postprocessing. Consistent performance gains were observed across both tissue classes. Notably, glomerulus detection benefited the most, with an average $\Delta F_1$ improvement of 35.7% and a precision gain of 48.3%. These improvements were primarily driven by effective mask merging across tile boundaries, particularly in fragmented or partially visible instances. In contrast, blood vessel segmentation achieved a more moderate average precision gain of 8.15%, while recall decreased slightly by 0.58%, suggesting improved boundary specificity at the cost of missing some peripheral detections. As most vessels were centrally located within tiles, the merging strategy primarily enhanced boundary alignment rather than correcting tile edge artifacts. In contrast, glomeruli more frequently spanned tile borders and thus benefited more substantially from reconstruction. Overall, the strategy proved most beneficial for glomeruli, where mask resolution across tiles had a stronger effect.

A direct comparison with standard NMS or Syncretic-NMS approaches was not included, as these methods are not directly applicable to overleaped tiling pipelines and do not include morphological postprocessing. Similarly, full-resolution inference on high-resolution images was excluded from comparative evaluation, since the underlying models were trained exclusively on smaller tiles extracted from whole slide images and are not optimized for global context.

4. Discussion

The results confirm that the proposed pipeline provides an effective and efficient solution for instance segmentation in tiled kidney whole slide images. Key contributions include adapting YOLO-based segmentation to high-resolution tile inference, incorporating overlap strategies and introducing a PSO-optimized mask merging algorithm.

The proposed framework addresses two major challenges in histological segmentation: object fragmentation across tile borders and morphological variability. By introducing a novel, enhanced mask merging algorithm that extends Syncretic-NMS with shape similarity and contour proximity, the merging step improves instance continuity across tiles. PSO optimization reduces manual tuning by efficiently exploring the postprocessing parameter space. Additionally, SAHI-based tiling enables efficient model training and inference on high-resolution WSIs, while overlap evaluation helps identify optimal configurations for accurate segmentation of complex microvascular structures. These combined strategies lead to substantial improvements in segmentation performance, with notable increases in both precision and F1 score, particularly for instances spanning tile boundaries.

Evaluation was conducted on 15 representative whole slide crops, covering over 600 tiles, which limits statistical generalizability. The merging strategy was tuned at a fixed tile overlap ratio and its sensitivity to this parameter remains untested. Reported gains, including improved glomerular precision, were measured against baseline predictions without postprocessing and were not statistically validated against alternative segmentation or merging baselines.

Despite these limitations, the pipeline’s modular design, low computational overhead and refinement strategy tailored to tiled inference make it broadly applicable to biomedical segmentation tasks. It is compatible with high-resolution WSIs and adaptable to various instance segmentation models, enabling seamless integration into existing workflows across diverse tissue types and imaging conditions. The proposed pipeline is not limited to kidney histology and can be applied to other tiled WSI domains where irregularly shaped or sparsely distributed structures, such as tumors, lesions or vascular abnormalities, require accurate reconstruction across tile boundaries. Its modular architecture allows replacement of the base model and adjustment of mask merging parameters for different tissues, imaging modalities and staining protocols. The low computational cost supports large-scale deployment on clinical repositories and research biobanks, facilitating high-precision segmentation in oncology, neuropathology, dermatopathology and other medical imaging fields where fragmented object detection remains a challenge.

Prior methods have explored tiling [8] or postprocessing [11] independently, but no complete histology-optimized pipeline has been proposed that integrates both. Universal medical segmentation models have been developed to handle diverse modalities, yet tiling-induced inconsistencies remain unresolved [29]. A one-stage framework eliminating grouping postprocessing has been proposed, but it does not address boundary-crossing artifacts [30], while evaluation approaches focusing on precise boundary accuracy do not offer corrective strategies [31]. A scalable tile-based framework for region-merging segmentation in remote sensing images has been introduced, focusing on ensuring result equivalence rather than reconstructing fragmented structures in tiled inference [32]. Object-based tile positioning has been proposed to reduce tile-induced truncation during training on diatom datasets, but this mainly mitigates training artifacts and does not resolve postprocessing inconsistencies during inference [33].

In contrast, this study introduces a tailored segmentation pipeline for renal WSIs that combines YOLO-based tiling inference, a novel syncretic mask merging algorithm and adaptive PSO-driven parameter optimization to directly address spatial fragmentation and boundary inconsistencies, providing a principled and scalable alternative to existing heuristic postprocessing solutions.

5. Conclusions

A complete instance segmentation pipeline was developed for whole slide kidney histology, with a focus on detecting glomeruli and blood vessels. The YOLOv11 and YOLOv12 architectures were evaluated and YOLOv11s-seg was found to offer a superior balance of segmentation accuracy and computational efficiency. Overlapping tile inference was assessed and an overlap range of 5–7.5% was determined to yield the best trade-off between segmentation quality and runtime.

The core contribution of this work lies in the introduction of an Enhanced Syncretic Mask Merging algorithm, combined with a refinement step guided by particle swarm optimization. Morphological, spatial and semantic consistency constraints were applied to resolve fragmented predictions at tile borders. Hyperparameters were optimized in a 9-dimensional search space, with glomeruli segmentation found to be robust across a wide range, while vessel segmentation was more sensitive to tuning, particularly for dilation and shape similarity parameters. Performance gains were measured relative to baseline predictions without postprocessing. An average precision improvement of up to 48% was observed for glomeruli and up to 17% for blood vessels. These improvements were most evident for instances spanning tile boundaries, confirming the utility of overlap merging and refined mask consolidation.

Future research will aim to refine the proposed pipeline by enhancing its adaptability and scalability. This includes validating performance across larger and more diverse datasets, integrating automated methods for selecting overlap and postprocessing parameters and improving resilience to variations in staining and imaging conditions. Comparative studies with other segmentation frameworks and inference strategies will also be pursued to better assess the pipeline’s generalizability and suitability for broader biomedical imaging applications.

Overall, a modular and computationally efficient framework was established for high-resolution histological segmentation. Its applicability to kidney tissue supports initiatives such as the VCCF and the HRA, offering a reproducible solution for detailed tissue annotation at scale. This contributes to more consistent and scalable analysis in biomedical research, supporting advancements in disease understanding and precision diagnostics.