Previous Article in Journal
Skin Lesion Classification Using Hybrid Feature Extraction Based on Classical and Deep Learning Methods
Previous Article in Special Issue
Generative Artificial Intelligence in Healthcare: Applications, Implementation Challenges, and Future Directions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
BioMedInformatics
Volume 5
Issue 3
10.3390/biomedinformatics5030042
biomedinformatics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Deep Learning Treatment Recommendations for Patients Diagnosed with Non-Metastatic Castration-Resistant Prostate Cancer Receiving Androgen Deprivation Treatment

by
Chunyang Li
1,2,*,
Julia Bohman
1,2,
Vikas Patil
1,2,
Richard Mcshinsky
1,2,
Christina Yong
1,2,
Zach Burningham
1,2,
Matthew Samore
1,2 and
Ahmad S. Halwani
1,2,3
1
Department of Internal Medicine, University of Utah, Salt Lake City, UT 84112, USA
2
VA Salt Lake City Health Care System, Salt Lake City, UT 84148, USA
3
Huntsman Cancer Institute, Salt Lake City, UT 84112, USA
*
Author to whom correspondence should be addressed.
BioMedInformatics 2025, 5(3), 42; https://doi.org/10.3390/biomedinformatics5030042
Submission received: 13 June 2025 / Revised: 15 July 2025 / Accepted: 31 July 2025 / Published: 4 August 2025
(This article belongs to the Special Issue Integrating Health Informatics and Artificial Intelligence for Advanced Medicine)
Browse Figures
Versions Notes

Abstract

Background: Prostate cancer (PC) is the second leading cause of cancer-related death in men in the United States. A subset of patients develops non-metastatic, castration-resistant PC (nmCRPC), for which management requires a personalized consideration for appropriate treatment. However, there is no consensus regarding when to switch from androgen deprivation therapy (ADT) to more aggressive treatments like abiraterone or enzalutamide. Methods: We analyzed 5037 nmCRPC patients and employed a Weibull Time to Event Recurrent Neural Network to identify patients who would benefit from switching from ADT to abiraterone/enzalutamide. We evaluated this model using differential treatment benefits measured by the Kaplan–Meier estimation and milestone probabilities. Results: The model achieved an area under the curve of 0.738 (standard deviation (SD): 0.057) for patients treated with abiraterone/enzalutamide and 0.693 (SD: 0.02) for patients exclusively treated with ADT at the 2-year milestone. The model recommended 14% of ADT patients switch to abiraterone/enzalutamide. Analysis showed a statistically significant absolute improvement using model-recommended treatments in progression-free survival (PFS) of 0.24 (95% confidence interval (CI): 0.23–0.24) at the 2-year milestone (PFS rate increasing from 0.50 to 0.74) with a hazard ratio of 0.44 (95% CI: 0.39–0.50). Conclusions: Our model successfully identified nmCRPC patients who would benefit from switching to abiraterone/enzalutamide, demonstrating potential outcome improvements.

1. Introduction

Prostate cancer is the second leading cause of cancer-related death and one of the most commonly diagnosed cancers for men in the United States [1,2]. Disease trajectory shows considerable variation across individuals. It is often asymptomatic in early stages and remains indolent for some patients, while for others it behaves aggressively. There is also heterogeneity in the cancer’s change from indolent to aggressive, with some patients experiencing a quick progression at diagnosis, and others progressing suddenly at different points over time [3,4,5].
Progression of prostate cancer is defined by the disease stage and/or response to prior treatment. Patients with localized disease typically receive definitive treatment such as radical prostatectomy or radiation therapy, after which approximately half of patients will experience disease progression [6,7]. Rising prostate-specific antigen (PSA) levels indicate further progression and inform the decision to initiate treatment of androgen deprivation therapy (ADT). After beginning ADT, patients have a median of 19 months before PSA levels again begin to rise, a phenomenon known as castration resistance [8]. This stage—non-metastatic, castration-resistant prostate cancer (nmCRPC)—is defined differently by varying bodies of experts, but by all definitions involves “castrate” levels of testosterone (<50 ng/mL), a notable rise or rises in the PSA level, and no evidence of metastatic disease on imaging [9,10,11]. Despite being crucial to treatment decisions, there is no consistency in how PSA values are tracked over time, with heterogeneity in when measurements are taken and how key metrics like the PSA doubling time (PSADT) are calculated [4]. Research examining nmCRPC treatment practices and outcomes in the Veterans Health Administration (VHA) suggests that providers often do not calculate PSADT, and that patients are often not started on newer treatments, even when their PSADT meets the criteria for high risk [12].
Patients with nmCRPC experience progression-free survival for an average of 25–30 months prior to developing metastatic disease, and 33% of nmCRPC patients progress to bone metastasis within 2 years [13]. A PSADT less than 10 months has been shown to be a clinically significant threshold for identifying patients at the time of nmCRPC with faster progression to metastasis or death [14,15]. Clinical trials have demonstrated an improvement in clinical outcomes when patients with a PSADT ≤ 10 months are treated with more aggressive treatments such as enzalutamide, apalutamide, darolutamide, and others [16,17,18,19]. Patients with less aggressive disease are often maintained on ADT.
Not all patients have the same level of data available for their PSA values over time, and with different formulations for calculating PSADT based on available PSA data [4], the implementation of clinical decision-making based on PSADT ≤ 10 months in real-world settings fails to reflect the knowledge gleaned from clinical trials. Furthermore, decisions to escalate treatment are subject to a variety of factors often not captured in clinical trials, such as advanced age or other demographics [20]. It is thus crucial to identify individual patient risk among the general population beyond those patients represented in clinical trials and academic medical centers.
Artificial intelligence approaches, such as deep learning (DL), have been proposed as the next frontier in supporting clinical decision-making in medicine [21]. Compared to traditional statistical analysis, survival analysis using artificial intelligence allows for more effective use of longitudinal data, requires no a priori assumptions regarding the model, and can leverage high-dimensional data such as radiology and pathology reports. The feasibility of applying DL has been previously explored in prostate cancer, specifically in the diagnosis of disease using radiographic imaging [22], biopsy information [23], stratification of patient risk based on 3-dimensional prostate gland structures [24], contouring of targets for radiation therapy [25], prediction of aggressive disease from molecular features [26], and prediction of survival after different radiotherapy treatments [27]. No studies have attempted to stratify patient risk at the decision-making stage of nmCRPC using longitudinal yet commonly obtained data that are available through the routine care and treatment of patients.

2. Materials and Methods

This study is approved under IRB# 00129914. The analysis was conducted in AWS VA Enterprise Cloud Prospect. The cohort study follows the Strengthening Reporting of Observational Studies in Epidemiology (STROBE) reporting guidelines.
We created a DL model capable of providing treatment recommendations based on sequential disease-based data. Treatment recommendations were based on model predictions of individual benefits of switching to more aggressive treatments than ADT, thereby providing critical information to nmCRPC patients and their providers for making treatment decisions.
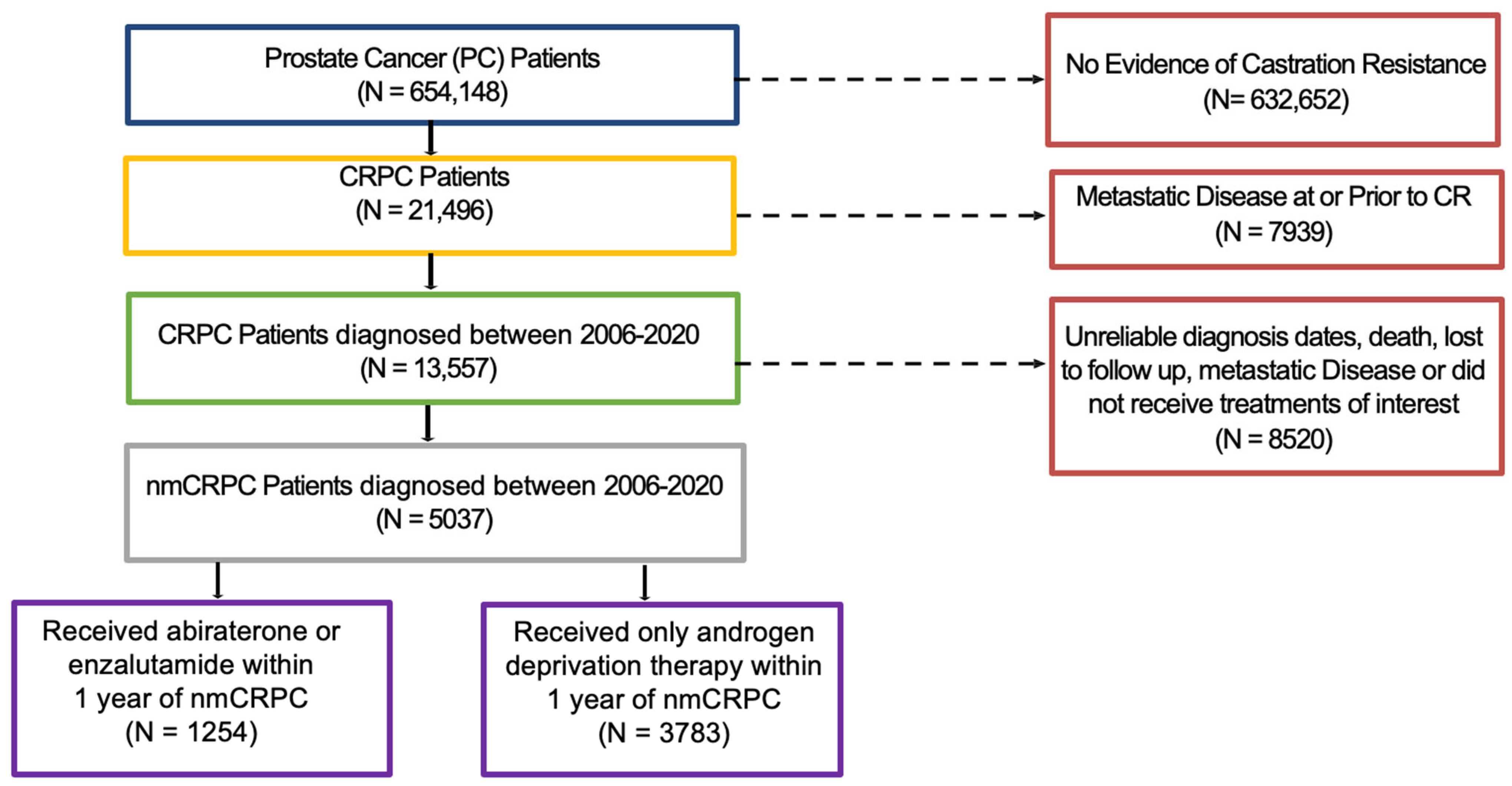
Using data from the VHA and pharmacy dispensation records from Veteran Affairs Corporate Data Warehouse, we identified a nationwide cohort of 13,557 patients diagnosed with prostate cancer from 1 January 2006, through 31 December 2019, who later developed nmCRPC. One year after the start of nmCRPC was selected as the landmark time, and patients who developed metastatic disease or died within that 1-year period were excluded. Figure 1 provides the patient cohort flow diagram.
Features for time to event, or progression-free survival (PFS), included age at nmCRPC date, body mass index (BMI), Gleason score, ethnicity, time from prostate cancer diagnosis to nmCRPC, Charlson comorbidity index (CCI) 6 months prior to nmCRPC date, treatment history, and PSA values. Details about feature processing and handling of missing data are provided in Appendix A.
Data were split into 10 folds for a 10-fold cross-validation, with each fold randomly sampled without replacement and stratified by the treatments patients received over time to ensure that the treatment distribution over time within each fold reflected the original dataset. This split enabled balanced treatment distributions among the training, testing, and validation sets. For each cross-validation iteration, eight folds were used for training, one fold for testing and one fold for validation. This process resulted in 10 validation sets that covered the entirety of the dataset. We evaluated the performance of the model by averaging its performance across these sets.
Our outcome of interest was time to metastatic disease or death from the landmark date of one year post-nmCRPC. Two prediction models were separately trained based on two data cohorts, respectively, defined as patients exclusively treated with ADT and patients treated with abiraterone (abi) or enzalutamide (enza). Each cohort was split into training, testing, and validation sets. For patients who received ADT, the individual event probabilities were obtained by combining the predicted event probabilities for the validation set. Their counterfactual event probabilities (i.e., probability of experiencing the event if they had received abi or enza treatment) were obtained by fitting them into the trained prediction model with the abi or enza cohort 10 times and averaging the predicted probabilities.
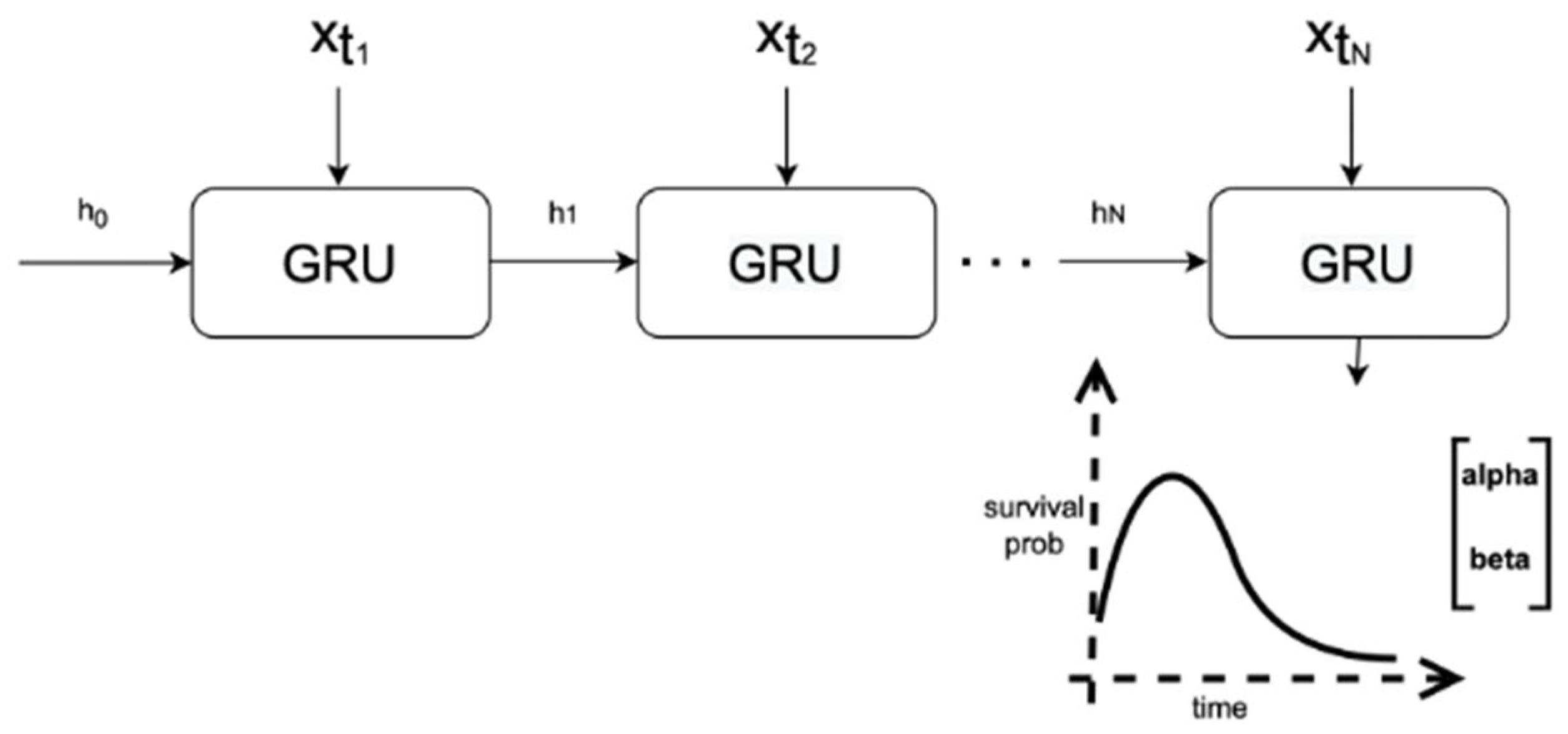
The deep learning architecture used for our predictive models and treatment recommendation model was the Weibull Time to Event Recurrent Neural Network (WTTE-RNN) model [28], a prediction model initially created for web churn using a DL survival analysis approach. Time to the next event is assumed to follow a Weibull distribution, and a recurrent neural network (RNN) model outputs the distribution scale and shape parameters. Figure 2 shows how the model made predictions using our data. We implemented WTTE-RNN using a gated recurrent unit (GRU) as the RNN. Further details concerning model architecture and hyperparameters used can be found in Appendix B.
Model performance was evaluated by the area under the receiver operating characteristic curve (AUROC) and calibration plots. We based our clinical benefit analysis on Mehltretter et al. [29], adapting their approach to fit a survival analysis scenario. Two years post-nmCRPC was chosen as the milestone time point for our event-free survival evaluation.
We compared the predicted event rate under the hypothetical case wherein all patients were assigned the model-recommended treatment (model-recommended treatment event rate) with the predicted event rate under the observed case where patients were treated with ADT (true event rate). We predicted the event rate under every possible treatment for each patient and took the treatment with the highest PFS probability as the model-recommended treatment per patient. To obtain the model-recommended treatment event rate, the data for each patient were adjusted to reflect their model-recommended treatment and then the model predicted the event rate using these adjusted data. We then found the difference between the mean event rate for the true data and the mean model-recommended treatment event rate. As an additional comparison, we plotted the Kaplan–Meier survival curves for the model-recommended treatment–adjusted data versus the true data.
We also compared the PFS among patients who happened to have received the model-recommended treatment, and the PFS among patients whose true treatments differed from the model-recommended treatment. This approach allowed a comparison of the actual event rate between the group that was concordant with model recommendations by chance and the group that was discordant with model recommendations by chance. Analysis of non-hypothetical cases allowed for better measurement of the DL survival model’s ability to correctly identify patients who were assigned ADT but could have benefitted from the receipt of abi or enza. We only included patients from the ADT cohort for this analysis.
A similar analysis was conducted based on the PSADT ≤ 10 months treatment recommendation rule. A binary indicator was created based on PSADT, with 1 representing patients identified as risky (i.e., needing more aggressive treatment) with PSADT ≤ 10 months, and 0 representing patients identified as not risky (i.e., not requiring treatment beyond ADT) with PSADT > 10 months. However, 57.4% of patients were missing PSADT. Missingness in PSADT is common and often indicative of a better underlying condition as it likely was not necessary to measure PSA as frequently for such patients. We compared 3 different approaches for handling missingness in PSADT: a complete case analysis; encoding the binary indicator arising from PSADT as 0 for patients with missing values; and imputing missing values of PSADT using the MissForest package [30]. Patients with a PSADT binary indicator of 1 who were given new treatments, as well as patients who stayed on ADT and had a PSADT binary indicator of 0, were counted as concordant. Patients who were not given new treatments in response to a PSADT indicator of 1 were counted as discordant. We compared the 2-year milestone event rate differences between these concordant and discordant groups for each of the 3 methods for handling missingness of PSADT. Results from comparing event rates in those concordant or discordant with PSADT-based treatment recommendations were compared with results from the DL survival model event rates in those concordant or discordant with model-recommended treatments.

3. Results

Our final cohort consisted of 5037 patients with nmCRPC. Among these, 1254 patients received abi or enza, and 3783 exclusively received ADT within one year of nmCRPC. The median number of records per patient for individuals who received ADT only versus abi/enza within one year of nmCRPC was 9 (IQR: 5–14) versus 21 (IQR: 13–31), respectively, with maximum records of 57 and 82, respectively.
There were 2153 patients (42.7%) who experienced at least one event (i.e., death or metastasis) during the observation period. Of patients who experienced an event, 731 (14.5%) developed metastatic disease and 1842 (36.6%) died during the observation period. The median follow-up time was 2.5 years (interquartile range [IQR]: 1.5–4.3 years). Baseline characteristics of the study cohort are summarized in Table 1. There was a high degree of missingness for the Gleason score. Details around how missing values were filled in are in Appendix A.
The average AUROC for the model trained on the abi/enza cohort at the 2-year milestone was 0.738 (standard deviation [SD]: 0.057), and the average AUROC for the model trained on the ADT cohort at the 2-year milestone was 0.693 (SD: 0.02). We determined variable importance by excluding one variable at a time from the model and comparing each resulting AUROC against the AUROC of the model with all variables included. In these comparisons, the larger the drop in AUROC, the more important the variable. We ran the analysis 100 times and took the average variable importance of each variable, which are displayed in Figure 3. The prediction target for calculating importance was death or metastasis within 2 years of nmCRPC. Treatment was identified as the most important variable, followed by the PSA and BMI for the abi/enza cohort. The treatment feature reflects patients’ treatment history, including the duration of ADT prior to receiving abi/enza, as well as other treatments administered. No information around treatments collected after the time of nmCRPC was included. For the ADT cohort, age was the most important variable, followed by CCI and PSA.
At 2 years, the model recommended that 3254 (86.0%) of 3783 patients stay on ADT for the maximum benefit, and 529 patients (14.0%) would derive a greater benefit from switching to a more aggressive treatment. Patient characteristics of the group recommended to stay on ADT and of those recommended to take abi/enza are detailed in Appendix C.
Within the ADT cohort, the difference between the rate of PFS at the 2-year milestone based on true data versus the data adjusted to reflect model treatment recommendations was 0.1, with a PFS rate of 0.703 for the unadjusted data and a PFS rate of 0.803 for the adjusted data.
The rate of PFS at 2 years among patients concordant with model treatment recommendations, i.e., patients given ADT for whom the model recommended ADT, was 0.74. The rate of PFS at 2 years among patients discordant with model treatment recommendations was 0.50. We observed a significant absolute PFS rate improvement of 0.24 (95% CI: 0.23–0.24), a relative reduction of 47.32%, and an odds ratio of 0.36. The hazard ratio for those whose treatments were concordant versus discordant with the model recommendation was 0.44 (95% CI: 0.39–0.50).
The complete case analysis for adherence to PSADT-based treatment recommendations had a PFS rate at the 2-year milestone of 0.73 among concordant patients and a PFS rate of 0.58 among discordant patients. The absolute improvement was 0.15 (95% CI: 0.08–0.19), a relative improvement of 35.38%, and an odds ratio of 0.52. The hazard ratio for those whose treatment was concordant versus discordant with the PSADT-recommended treatment was 0.69 (95% CI: 0.58–0.82).
In Table 2, we report results for patients concordant/discordant with model-recommended treatments versus patients concordant/discordant with PSADT-based treatment recommendations. The rate improvements and hazard ratios for those whose treatments were concordant/discordant with model-recommended treatments are significantly higher than those concordant/discordant with PSADT-based recommended treatments both in the complete case analysis and using imputed PSADT. Interestingly, imputing the binary indicator arising from a PSADT with 0 yielded better results than using imputed values from MissForest to create the binary indicator.
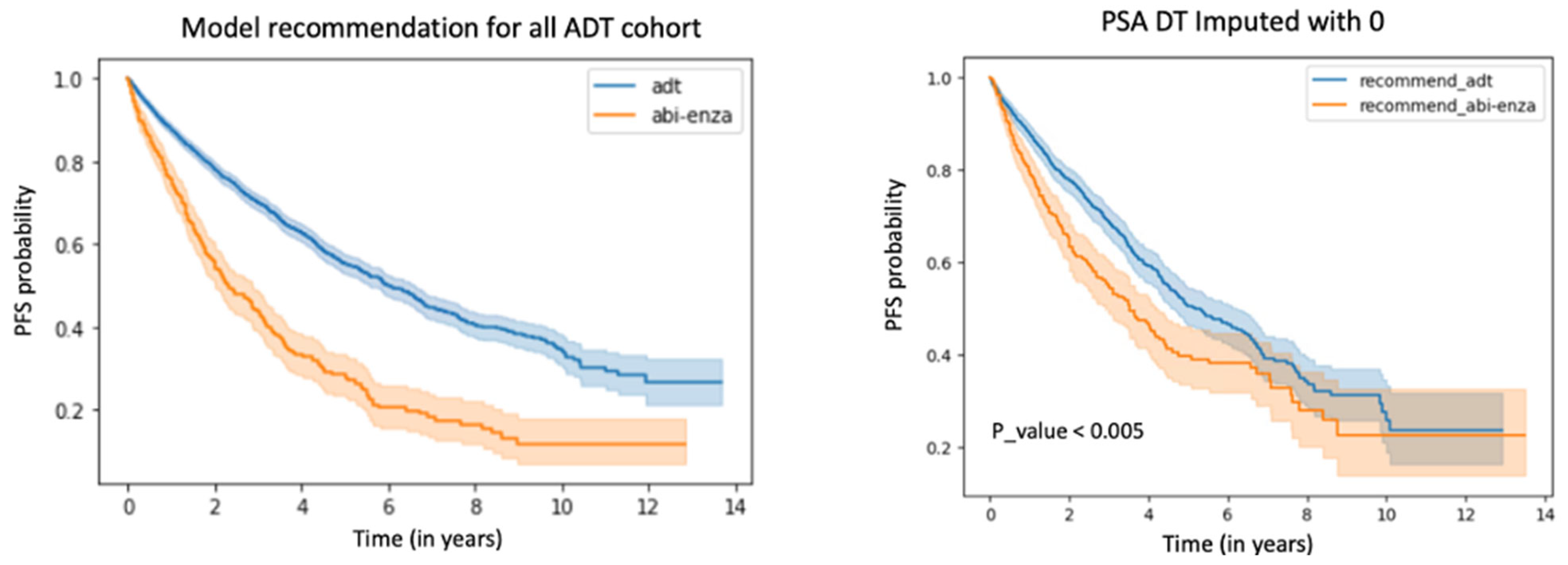
We also compared differences in concordant/discordant patients according to model-recommended treatments versus PSADT-based recommendations by plotting Kaplan–Meier survival curves, as shown in Figure 4. Discordant patients demonstrated worse survival outcomes under both paradigms. Further details comparing PSADT with the DL model are in Appendix D.

4. Discussion

We used DL to create a personalized medicine model that can identify patients with nmCRPC who would likely benefit from switching from ADT to abi or enza. We demonstrated that our model can recommend treatment and potentially improve patient outcomes using a few commonly available and easily extractable clinical features, allowing for easy clinical implementation and interpretation.
The current clinical standard for treatment recommendations is based on PSADT. However, the PSA is not always well measured across patients, and it can be difficult for conventional algorithms to accurately capture how the PSA changes over time and in response to treatment [4]. We aimed to incorporate change in the PSA, alongside treatment, as time-series inputs used to predict individual patients’ outcomes under different treatments received after nmCRPC prognosis, thereby yielding personalized treatment recommendations. We were able to make individualized predictions and recommendations, demonstrating the average potential clinical benefits at a group level as well as examining group differences. We were able to obtain a significantly greater PFS based on concordance with the DL model recommendations compared to concordance with recommendations based on PSADT. Through this thorough investigation of potential clinical benefit, we sought to facilitate an understanding of DL prediction and increase clinician trust in the prognostic products resulting from DL methods.
We adapted the approach applied in Mehltretter et al. [29] to a survival analysis setting using time-series EHR data. We applied WTTE-RNN, a model that has been used effectively in prognosis prediction for breast cancer patients [31] and predicting equipment failure [32]. To our knowledge, ours is the first study to apply this model in prostate cancer. WTTE-RNN can automatically process time-series information, eliminating the need to perform manual feature engineering. In addition, this method provides a fuller picture, capturing more patient-level characteristics than PSADT. The model also offers flexibility in use, since the time-dependent hazards are obtained from Weibull shape and scale parameters; it can provide predictions to an infinite time domain without an increasing number of neuron units that could lead to model overfitting.
As seen in Table 1, there are significant differences in key characteristics like BMI, Gleason score, and PSADT between the ADT cohort versus the abi/enza cohort. Such differences highlight the importance of restricting the analysis of potential benefits from following treatment recommendations based on the DL model to just the ADT cohort.
A limitation of this study is the observational nature of our dataset; patients who received different treatments may have other fundamental differences. Our analysis of potential clinical benefit did not control for potential confounding. While it is suggestive of benefits arising from more aggressive treatments for specific individuals based on deep learning recommendations, it does not definitively prove the existence of clinically significant benefits.
In clinical practice, most patients are treated with ADT after their nmCRPC date. Previous work has found that 60.6% of patients with nmCRPC are treated with ADT in VHA hospitals [12]. Those who are given more aggressive treatments, such as second-generation antiandrogens, are typically patients with severe disease and a less favorable prognosis. This limits possible inferences from our model, and we therefore chose to examine only patients receiving ADT, who likely form a more homogenous cohort.
We have laid critical groundwork for future use of a treatment recommendation model as a tool in a clinical context. An important next step for clinical adoption is further improving the AUROC of the model. Currently the model achieves an AUROC around 0.7, whereas clinicians would require a higher level of accuracy. Incorporating more data features could potentially boost model performance. Future work includes adding more temporal features to the DL model, such as more lab results, clinical visit notes, related ICD codes, etc. With more features available, more investigations could be performed to determine the relative contributions of each set of predictor variables in predicting patient outcomes, as well as increasing model performance. After adding more features, validating the model using an external dataset would be the next step in translating this tool into clinical practice to inform treatment decisions for patients with nmCRPC. Additional steps needed before implementing this model in clinical practice in the general US population would include prospective validation studies using both VHA and non-VHA cohorts, as well as explorations of how clinicians could most effectively and efficiently operationalize the model within a shared decision framework.

5. Conclusions

In this study, we demonstrated that a DL survival model using time-series EHR data to predict the risk of metastatic disease or death in patients with nmCRPC can make individualized treatment recommendations for those exclusively treated with ADT. If incorporated within EHR systems, the model’s predictions and recommendations can provide valuable information to guide clinicians and patients in making treatment decisions.

Author Contributions

Conceptualization, C.L., J.B., Z.B. and A.S.H.; Data curation, V.P. and R.M.; Formal analysis, C.L.; Methodology, C.L.; Supervision, Z.B. and A.S.H.; Writing—original draft, C.L. and J.B.; Writing—review and editing, C.L., J.B., C.Y. and M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study is approved under IRB #00129914.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data include protected health information and are not available. Detailed information on model tuning and implementation is available upon request.

Acknowledgments

We would like to thank Siamack Ayandeh for the creation of the analytics study mart environment and the Veterans Health Administration Office of Research and Development for funding cloud credits.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
abiabiraterone
ADTandrogen deprivation therapy
AUROCarea under the receiving operating characteristic
BMIbody mass index
CCICharlson comorbidity index
CIconfidence interval
DLdeep learning
EHRelectronic heath records
enzaenzalutamide
IQRinterquartile range
nmCRPCnon-metastatic castration resistant prostate cancer
PCprostate cancer
PFSprogression free survival
PSAprostate specific antigen
PSADTprostate specific antigen doubling time
RNNrecurrent neural network
SDstandard deviation
VHAVeterans Health Administration
WTTE-RNNWeibull time to event recurrent neural network

Appendix A

Features for time to event, or progression-free survival (PFS), were either static or time-series. Static features included age at nmCRPC date, body mass index (BMI), Gleason score, ethnicity, time from prostate cancer diagnosis to nmCRPC, and Charlson comorbidity index (CCI) 6 months prior to nmCRPC diagnosis date. Time-series features included treatment, PSA, number of days from prostate cancer diagnosis to the record time, and nmCRPC status. Variation in PSA under various treatments was included to inform the model how aggressive and or refractory the disease was to current treatment at any point in time. We coded the nmCRPC status as a longitudinal indicator with three categories: pre-nmCRPC, onset of nmCRPC, and post-start of nmCRPC. For prediction, time-series data was exclusively taken from the period between the diagnosis of PC to initiation of ADT or abi/enza. Categorical variables were converted to binary indicators, and all variables were standardized to the same unit.
Missing data for static features was imputed using the mean (continuous features) or median/mode (discrete features) values within each fold of the data split. For time-series features, the missing values were filled in using the latest available non-missing value prior to the missing value. If no prior value was available, missing values were imputed with the mean values within each fold. We adopted this imputation approach to avoid temporal information leakage and leakage from the test set to the training set.

Appendix B

The WTTE-RNN model provides a survival function arising from defining a Weibull distribution with the scale and shape parameters, α and β , outputted from the RNN model. The survival function, hazard function, and cumulative hazard are defined as follows:
S t x   =   e x p −   t α β λ t x   =   t α β − 1 ⋅ β α Λ t x   =   t α β
The loss function is defined as log-likelihood loss, derived from the Weibull distribution to account for censored data. Density at points is compared for uncensored data and probability over regions was considered for uncensored data. The optimization problem for the RNN in the continuous and discrete cases is defined as follows:
m a x i m i z e l o w   g L w , y , u , x : =   ∑ t = 0 T u t ⋅ β t ⋅ l o g y t α t   + log β t   −   y t α t β t m a x i m i z e l o w   g L d w , y , u , x : =   ∑ t = 0 T u t ⋅ e x p y t   +   1 α t β t   −   y t α t β t −   1   −   y t   +   1 α t β t
where t is time steps of a sequence, w is parameters for R N N , y t ∈ [ 0 , ∞ ) is time to event at time step t ; u t ∈ { 0,1 } is a censoring indicator with 0 indicating right censoring and 1 otherwise; and x is feature vector. In our case, we discretized time to event into months.
For each individual, WTTE-RNN predicted an a and b describing the individual time to event distribution. Each patient was assigned all treatments: i , j , k etc. For each treatment i , we had an independent event function − E ( t | x ) = 1 − S ( t | x ) = 1 −   e x p − t α β .
We first passed a patient through the trained DL model with treatment i and again with treatment j . The event probabilities E ( t | x , t r t = i ) and E ( t | x , t r t = j ) (defined below) for each treatment at the same pre-defined milestone times were compared. If E t x ,   t r t = i > E ( t | x , t r t = j ) , then treatment i led to a higher risk for the patient than treatment j ; therefore, treatment j was deemed the more beneficial treatment option for the patient.
E t x , t r t = i = 1 −   e x p −   t α i β i E t x , t r t = j = 1 −   e x p −   t α j β j
We used two gated recurrent unit (GRU) layers and the Adam optimizer. Other hyperparameters were tuned according to Table A1.
Table A1. Hyperparmeter tuning.
Table A1. Hyperparmeter tuning.
HyperparameterRangeADT 1 CohortAbi/Enza 2 Cohort
Hidden units(20, 200)8030
Learning rate(0.0001, 0.01)0.010.01
Batch size(64, 1000)500200
1 Androgen deprivation therapy. 2 Abiraterone or enzalutamide.

Appendix C

Table A2 contains characteristics of patients from the ADT cohort recommended by the model to switch to abi/enza versus patients recommended to stay on ADT.
Table A2. ADT cohort characteristics.
Table A2. ADT cohort characteristics.
OverallRecommended
ADT		Recommended Abi/Enza
(N = 3783)(N = 3254)(N = 529)p-Value
Demographics
Race/Ethnicity, N (%)
Non-Hispanic White2033 (56.2)1760 (56.6)273 (53.5)<0.001
Black1177 (32.5)970 (31.2)207 (40.6)
Hispanic252 (7.0)235 (7.6)17 (3.3)
Others158 (4.4)145 (4.7)13 (2.5)
Age at nmCRPC, median [IQR]70.0 [65.0–78.0]69.0 [64.0–75.0]82.0 [75.0–86.0]<0.001
BMI, mean (SD) †29.6 (6.0)30.0 (6.0)27.4 (5.7)<0.001
Clinical Characteristics
Gleason score, median [IQR] ‡7.0 [7.0–8.0]7.0 [7.0–8.0]7.0 [7.0–8.0]0.001
Disease characteristics at nmCRPC
PSA doubling time € <0.001
>10 months1162 (72.5)994 (74.5)168 (62.7)
≤10 months441 (27.5)341 (25.5)100 (37.3)
Metastasis or death, N (%) <0.001
No2351 (62.1)2129 (65.4)222 (42.0)
Yes1432 (37.9)1125 (34.6)307 (58.0)
Footnotes: † 2 missing values. ‡ 478 missing values. € 2180 missing values. IQR = interquartile range; SD = standard deviation; ADT = androgen deprivation therapy; Abi = abiraterone; Enza = enzalutamide.

Appendix D

Table A3 provides median survival times as well as the p-values for log-rank tests corresponding to differences in patients concordant/discordant with model vs. PSADT treatment recommendations.
Table A3. Survival times.
Table A3. Survival times.
ModelMedian Survival Time in YearsLog-Rank p-Value
ConcordantDiscordant
WTTE-RNN 16.012.31<0.005
PSADT 2 complete case5.173.52<0.005
PSADT MissForest imputed5.325.290.64
PSADT 0 imputed5.523.52<0.005
1 Weibull Time to Event Recurrent Neural Network. 2 Prostate specific antigen doubling time.

References

  1. Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef]
  2. Siegel, R.L.; Giaquinto, A.N.; Jemal, A. Cancer statistics, 2024. CA Cancer J. Clin. 2024, 74, 12–49. [Google Scholar] [CrossRef]
  3. Spratt, D.E.; Zumsteg, Z.S.; Feng, F.Y.; Tomlins, S.A. Translational and clinical implications of the genetic landscape of prostate cancer. Nat. Rev. Clin. Oncol. 2016, 13, 597–610. [Google Scholar] [CrossRef] [PubMed]
  4. Rosinha, A.; Rabaca, C.; Calais, F.; Pinto, J.M.; Barreira, J.V.; Fernandes, R.; Ramos, R.; Fialho, A.C.; Palma dos Reis, J. Improving the identification of high-risk non-metastatic castration-resistant prostate cancer patients in clinical practice. Front. Oncol. 2024, 13, 1266369. [Google Scholar] [CrossRef] [PubMed]
  5. Ziaran, S.; Varchulova Novakova, Z.; Bohmer, D.; Danisovic, L. Biomarkers for determination prostate cancer: Implication for diagnosis and prognosis. Neoplasma 2015, 62, 683–691. [Google Scholar] [CrossRef] [PubMed]
  6. Amling, C.L.; Bergstralh, E.J.; Blute, M.L.; Slezak, J.M.; Zincke, H. Defining prostate specific antigen progression after radical prostatectomy: What is the most appropriate cut point? J. Urol. 2001, 165, 1146–1151. [Google Scholar] [CrossRef]
  7. Lee, W.R.; Hanks, G.E.; Hanlon, A. Increasing prostate-specific antigen profile following definitive radiation therapy for localized prostate cancer: Clinical observations. J. Clin. Oncol. 1997, 15, 230–238. [Google Scholar] [CrossRef]
  8. Sharifi, N.; Dahut, W.L.; Steinberg, S.M.; Figg, W.D.; Tarassoff, C.; Arlen, P.; Gulley, J.L. A retrospective study of the time to clinical endpoints for advanced prostate cancer. BJU Int. 2005, 96, 985–989. [Google Scholar] [CrossRef]
  9. Lowrance, W.T.; Murad, M.H.; Oh, W.K.; Jarrard, D.F.; Resnick, M.J.; Cookson, M.S. Castration-resistant prostate cancer: AUA guideline amendment 2018. J. Urol. 2018, 200, 1264–1272. [Google Scholar] [CrossRef]
  10. Scher, H.I.; Morris, M.J.; Stadler, W.M.; Higano, C.; Basch, E.; Fizazi, K.; Antonarakis, E.S.; Beer, T.M.; Carducci, M.A.; Chi, K.N.; et al. Trial design and objectives for castration-resistant prostate cancer: Updated recommendations from the Prostate Cancer Clinical Trials Working Group 3. J. Clin. Oncol. 2016, 34, 1402–1418. [Google Scholar] [CrossRef]
  11. Halwani, A.S.; Rasmussen, K.M.; Patil, V.; Li, C.C.; Yong, C.M.; Burningham, Z.; Gupta, S.; Narayanan, S.; Lin, S.-W.; Carroll, S.; et al. Real-world practice patterns in veterans with metastatic castration-resistant prostate cancer. In Urologic Oncology: Seminars and Original Investigations; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1.e1–1.e10. [Google Scholar]
  12. Halwani, A.S.; Patil, V.; Morreall, D.; Li, C.; Yong, C.; Appukkutan, S.; Partridge, J.; Jhaveri, J.; Rasmussen, K.M. Real-world treatment patterns among veterans with nonmetastatic castration-resistant prostate cancer (nmCRPC). J. Clin. Oncol. 2022, 40, e17042. [Google Scholar] [CrossRef]
  13. Smith, M.R.; Kabbinavar, F.; Saad, F.; Hussain, A.; Gittelman, M.C.; Bilhartz, D.L.; Wynne, C.; Murray, R.; Zinner, N.R.; Schulman, C.; et al. Natural history of rising serum prostate-specific antigen in men with castrate nonmetastatic prostate cancer. J. Clin. Oncol. 2005, 23, 2918–2925. [Google Scholar] [CrossRef] [PubMed]
  14. Arnold, P.; Penaloza-Ramos, M.C.; Adedokun, L.; Rees, S.; Lockhat, M.; Spary, L.; Watkins, A.; Gnanapragasam, V.; Crabb, S.J. Clinical characteristics and outcomes for patients with non-metastatic castration-resistant prostate cancer. Sci. Rep. 2021, 11, 22151. [Google Scholar] [CrossRef] [PubMed]
  15. Smith, M.R.; Saad, F.; Oudard, S.; Shore, N.; Fizazi, K.; Sieber, P.; Tombal, B.; Damiao, R.; Marx, G.; Miller, K.; et al. Denosumab and bone metastasis–free survival in men with nonmetastatic castration-resistant prostate cancer: Exploratory analyses by baseline prostate-specific antigen doubling time. J. Clin. Oncol. 2013, 31, 3800–3806. [Google Scholar] [CrossRef] [PubMed]
  16. Hussain, M.; Fizazi, K.; Saad, F.; Rathenborg, P.; Shore, N.; Ferreira, U.; Ivashchenko, P.; Demirhan, E.; Modelska, K.; Phung, D.; et al. Enzalutamide in men with nonmetastatic, castration-resistant prostate cancer. N. Engl. J. Med. 2018, 378, 2465–2474. [Google Scholar] [CrossRef]
  17. Smith, M.R.; Saad, F.; Chowdhury, S.; Oudard, S.; Hadaschik, B.A.; Graff, J.N.; Olmos, D.; Mainwaring, P.N.; Lee, J.Y.; Uemura, H.; et al. Apalutamide treatment and metastasis-free survival in prostate cancer. N. Engl. J. Med. 2018, 378, 1408–1418. [Google Scholar] [CrossRef]
  18. Fizazi, K.; Shore, N.; Tammela, T.L.; Ulys, A.; Vjaters, E.; Polyakov, S.; Jievaltas, M.; Luz, M.; Alekseev, B.; Kuss, I.; et al. Darolutamide in nonmetastatic, castration-resistant prostate cancer. N. Engl. J. Med. 2019, 380, 1235–1246. [Google Scholar] [CrossRef]
  19. Fizazi, K.; Shore, N.D.; Tammela, T.; Ulys, A.; Vjaters, E.; Polyakov, S.; Jievaltas, M.; Luz, M.; Alekseev, B.; Kuss, I.; et al. Overall survival (OS) results of phase III ARAMIS study of darolutamide (DARO) added to androgen deprivation therapy (ADT) for nonmetastatic castration-resistant prostate cancer (nmCRPC). J. Clin. Oncol. 2020, 38, 5514. [Google Scholar] [CrossRef]
  20. Saad, F.; Bogemann, M.; Suzuki, K.; Shore, N. Treatment of nonmetastatic castration-resistant prostate cancer: Focus on second-generation androgen receptor inhibitors. Prostate Cancer Prostatic Dis. 2021, 24, 323–334. [Google Scholar] [CrossRef]
  21. Giordano, C.; Brennan, M.; Mohamed, B.; Rashidi, P.; Modave, F.; Tighe, P. Accessing artificial intelligence for clinical decision-making. Front. Digit. Health 2021, 3, 645232. [Google Scholar] [CrossRef]
  22. Campanella, G.; Hanna, M.G.; Geneslaw, L.; Miraflor, A.; Werneck Krauss Silva, V.; Busam, K.J.; Brogi, E.; Reuter, V.E.; Klimstra, D.S.; Fuchs, T.J. Clinical-grade computational pathology using weakly supervised deep learning on whole slide images. Nat. Med. 2019, 25, 1301–1309. [Google Scholar] [CrossRef]
  23. Bulten, W.; Pinckaers, H.; van Boven, H.; Vink, R.; de Bel, T.; van Ginneken, B.; van der Laak, J.; de Kaa, C.H.-V.; Litjens, G. Automated gleason grading of prostate biopsies using deep learning. arXiv 2019, arXiv:1907.07980. [Google Scholar] [CrossRef]
  24. Xie, W.; Reder, N.P.; Koyuncu, C.; Leo, P.; Hawley, S.; Huang, H.; Mao, C.; Postupna, N.; Kang, S.; Serafin, R.; et al. Prostate cancer risk stratification via nondestructive 3D pathology with deep learning–assisted gland analysis. Cancer Res. 2022, 82, 334–345. [Google Scholar] [CrossRef]
  25. Almeida, G.; Tavares, J.M.R. Deep learning in radiation oncology treatment planning for prostate cancer: A systematic review. J. Med. Syst. 2020, 44, 179. [Google Scholar] [CrossRef] [PubMed]
  26. Elmarakeby, H.A.; Hwang, J.; Arafeh, R.; Crowdis, J.; Gang, S.; Liu, D.; AlDubayan, S.H.; Salari, K.; Kregel, S.; Richter, C.; et al. Biologically informed deep neural network for prostate cancer discovery. Nature 2021, 598, 348–352. [Google Scholar] [CrossRef] [PubMed]
  27. Hu, L.; Ji, J.; Li, F. Estimating heterogeneous survival treatment effect in observational data using machine learning. Stat. Med. 2021, 40, 4691–4713. [Google Scholar] [CrossRef] [PubMed]
  28. Martinsson, E. WTTE-RNN: Weibull Time to Event Recurrent Neural Network a Model for Sequential Prediction of Time-to-Event in the Case of Discrete or Continuous Censored Data, Recurrent Events or Time-Varying Covariates. Master’s Thesis, University of Gothenburg, Goteborg, Sweden, 2017. [Google Scholar]
  29. Mehltretter, J.; Fratila, R.; Benrimoh, D.; Kapelner, A.; Perlman, K.; Snook, E.; Israel, S.; Miresco, M.; Turecki, G. Differential treatment benefit prediction for treatment selection in depression: A deep learning analysis of STAR*D and CO-MED data. bioRxiv 2019, 4, 679779. [Google Scholar] [CrossRef]
  30. Stekhoven, D.J.; Bühlmann, P. MissForest—Non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef]
  31. Kim, J.-Y.; Lee, Y.S.; Yu, J.; Park, Y.; Lee, S.K.; Lee, M.; Lee, J.E.; Kim, S.W.; Nam, S.J.; Park, Y.H.; et al. Deep learning-based prediction model for breast cancer recurrence using adjuvant breast cancer cohort in tertiary cancer center registry. Front. Oncol. 2021, 11, 596364. [Google Scholar] [CrossRef]
  32. Li, W.; Cai, J.; Li, H.; Yu, F.; Ding, P. Estimation of Equipment Remaining Useful Life based on WTEE-RNN Method. In Proceedings of the 2022 2nd International Conference on Computational Modeling, Simulation and Data Analysis (CMSDA), Zhuhai, China, 2–4 December 2022; pp. 130–134. [Google Scholar]
Biomedinformatics 05 00042 g001
Figure 1. Patient cohort flow diagram.
Figure 1. Patient cohort flow diagram.
Biomedinformatics 05 00042 g001
Biomedinformatics 05 00042 g002
Figure 2. WTTE-RNN model: X t 1 , X t 2 , … ,   X t n are time-dependent features at time t 1 , … ,   t n , while h 0 , h 1 , … , h n are hidden units passed in the gated recurrent unit (GRU). The outputs are scale and shape parameters, α and β , for a Weibull distribution that is used to construct a survival curve for the patient.
Figure 2. WTTE-RNN model: X t 1 , X t 2 , … ,   X t n are time-dependent features at time t 1 , … ,   t n , while h 0 , h 1 , … , h n are hidden units passed in the gated recurrent unit (GRU). The outputs are scale and shape parameters, α and β , for a Weibull distribution that is used to construct a survival curve for the patient.
Biomedinformatics 05 00042 g002
Biomedinformatics 05 00042 g003
Figure 3. Variable importance plot for predicting death or metastasis within 2 years of nmCRPC for the abi/enza cohort (left) and ADT cohort (right). The word “treatment” here refers to treatment history—i.e., the frequency and duration of ADT treatments prior to nmCRPC (and thus prior to receiving abi/enza, for the abi/enza cohort), as well as any other treatments administered before nmCRPC.
Figure 3. Variable importance plot for predicting death or metastasis within 2 years of nmCRPC for the abi/enza cohort (left) and ADT cohort (right). The word “treatment” here refers to treatment history—i.e., the frequency and duration of ADT treatments prior to nmCRPC (and thus prior to receiving abi/enza, for the abi/enza cohort), as well as any other treatments administered before nmCRPC.
Biomedinformatics 05 00042 g003
Biomedinformatics 05 00042 g004
Figure 4. Patient outcome concordant vs. discordant with the recommended treatment for model recommendation (left) and PSADT recommendation (right).
Figure 4. Patient outcome concordant vs. discordant with the recommended treatment for model recommendation (left) and PSADT recommendation (right).
Biomedinformatics 05 00042 g004
Table 1. Baseline characteristics.
Table 1. Baseline characteristics.
OverallADTAbi/Enza
(N = 5037)(N = 3783)(N = 1254)p-Value
Demographics
Race/Ethnicity, N (%)
Non-Hispanic White2828 (56.1)2033 (53.7)795 (63.4)<0.001
Black1477 (29.3)1177 (31.1)300 (23.9)
Hispanic314 (6.2)252 (6.7)62 (4.9)
Others418 (8.3)321 (8.5)97 (7.7)
Age at nmCRPC, median [IQR]71.0 [65.0–78.0]70.0 [65.0–78.0]71.0 [67.0–79.0]<0.001
BMI, mean (SD) †29.8 (6.0)29.6 (6.0)30.4 (5.9)<0.001
Clinical Characteristics
Gleason score, median [IQR] ‡7.0 [7.0–8.0]7.0 [7.0–8.0]8.0 [7.0–9.0]<0.001
Disease characteristics at nmCRPC
PSA doubling time <0.001
>10 months1368 (63.8)1162 (72.5)206 (38.1)
≤10 months776 (36.2)441 (27.5)335 (61.9)
PSA doubling time imputed with MissForest, N (%) <0.001
>10 months3374 (67.0)2733 (72.2)641 (51.1)
≤10 months1663 (33.0)1050 (27.8)613 (48.9)
Metastasis, N (%) <0.001
No4306 (85.5)3442 (91.0)864 (68.9)
Yes731 (14.5)341 (9.0)390 (31.1)
Mortality, N (%) <0.001
Alive3195 (63.4)2522 (66.7)673 (53.7)
Deceased1842 (36.6)1261 (33.3)581 (46.3)
Footnotes: † 2 missing values. ‡ 733 missing values. IQR = interquartile range; SD = standard deviation; ADT = androgen deprivation therapy; Abi = abiraterone; and Enza = enzalutamide.
Table 2. Progression free survival comparison results.
Table 2. Progression free survival comparison results.
Recommendation ModelData CohortRate Improvement
Mean
95% CI 1		Percentage Change
Mean
95% CI		Odds Ratio
Mean
95% CI		Hazard Ratio
Mean
95% CI
DL 3 modelAll ADT 2 patients0.236
[0.231, 0.242]		47.32%
[46.69%, 47.96%]		0.359
[0.352, 0.367]		0.44
[0.39, 0.50]
PSADT 4 available0.215
[0.208, 0.223]		44.17%
[43.17%, 45.17%]		0.396
[0.384, 0.409]		0.48
[0.40, 0.58]
Imputed PSADTImpute 00.133
[0.127, 0.139]		31.79%
[30.72%, 32.86%]		0.559
[0.544, 0.573]		0.69
[0.59, 0.80]
MissForest impute0.016
[0.012, 0.012]		4.90%
[3.66%, 6.15%]		0.932
[0.914, 0.949]		0.97
[0.87, 1.09]
PSADTPSADT available0.149
[0.143, 0.155]		35.38%
[34.28%, 36.48%]		0.517
[0.503,0.531]		0.69
[0.58, 0.82]
1 Confidence interval. 2 Androgen deprivation therapy. 3 Deep learning. 4 Prostate-specific antigen doubling time.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Li, C.; Bohman, J.; Patil, V.; Mcshinsky, R.; Yong, C.; Burningham, Z.; Samore, M.; Halwani, A.S. Deep Learning Treatment Recommendations for Patients Diagnosed with Non-Metastatic Castration-Resistant Prostate Cancer Receiving Androgen Deprivation Treatment. BioMedInformatics 2025, 5, 42. https://doi.org/10.3390/biomedinformatics5030042

AMA Style

Li C, Bohman J, Patil V, Mcshinsky R, Yong C, Burningham Z, Samore M, Halwani AS. Deep Learning Treatment Recommendations for Patients Diagnosed with Non-Metastatic Castration-Resistant Prostate Cancer Receiving Androgen Deprivation Treatment. BioMedInformatics. 2025; 5(3):42. https://doi.org/10.3390/biomedinformatics5030042

Chicago/Turabian Style

Li, Chunyang, Julia Bohman, Vikas Patil, Richard Mcshinsky, Christina Yong, Zach Burningham, Matthew Samore, and Ahmad S. Halwani. 2025. "Deep Learning Treatment Recommendations for Patients Diagnosed with Non-Metastatic Castration-Resistant Prostate Cancer Receiving Androgen Deprivation Treatment" BioMedInformatics 5, no. 3: 42. https://doi.org/10.3390/biomedinformatics5030042

APA Style

Li, C., Bohman, J., Patil, V., Mcshinsky, R., Yong, C., Burningham, Z., Samore, M., & Halwani, A. S. (2025). Deep Learning Treatment Recommendations for Patients Diagnosed with Non-Metastatic Castration-Resistant Prostate Cancer Receiving Androgen Deprivation Treatment. BioMedInformatics, 5(3), 42. https://doi.org/10.3390/biomedinformatics5030042

Article Metrics

Back to TopTop