AI-Driven Bayesian Deep Learning for Lung Cancer Prediction: Precision Decision Support in Big Data Health Informatics
Abstract
1. Introduction
2. Background and Related Work
2.1. Machine Learning Applications in Lung Cancer
- Decision Support via Computer-Aided Systems (CAD): CAD platforms, underpinned by artificial intelligence capabilities, offer invaluable decision-making support throughout the entire spectrum of the lung cancer treatment continuum [52]. Notably, they have the ability to scrutinize computed tomography (CT) scans, pinpointing anomalies and regions indicative of lung damage [52].
- Text-based Lung Cancer Detection: Beyond imaging, machine learning models, especially those anchored on support vector machines (SVMs), have shown promise in refining the diagnosis process using text datasets pertaining to lung cancer.
2.2. Deep Learning Applications in Lung Cancer
- Lung Nodule Detection: Modern deep learning optimized medical imaging instruments provide clinicians with excellent ability to perform timely and accurate pathology classification of lung nodules, a crucial first step of the lung cancer early diagnosis, and improve treatment outcome [57].
- Large-scale Disease Screening: The prospect of harnessing deep learning algorithms for broad-based lung cancer screening initiatives is gaining traction. A comprehensive meta-analysis delineating the utility of these algorithms in lung cancer diagnostics reveals promising outcomes, characterized by high degrees of sensitivity and specificity [58]. This finding is indicative of deep learning’s burgeoning role in shaping future disease screening paradigms.
2.3. Bayesian Methods in Medical Predictions and Medical Informatics
2.4. Sampling Techniques in Bayesian Models
3. Preliminaries
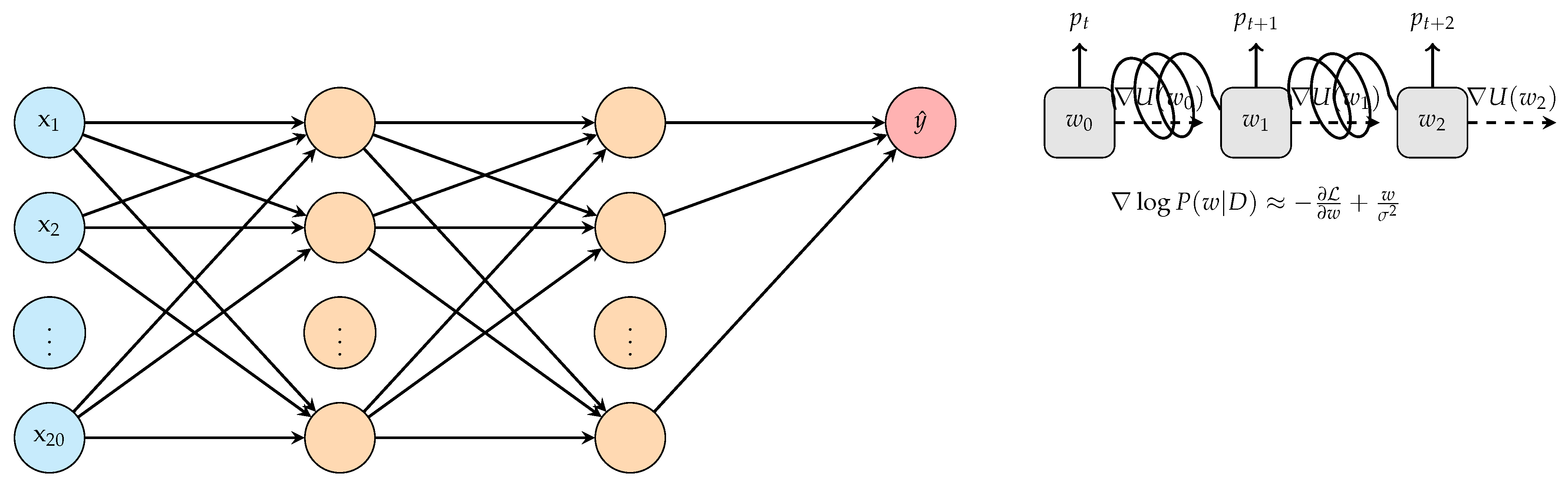
3.1. Bayesian Inference in Deep Learning
- Posterior Distribution of Weights: In the context of Bayesian deep learning, the primary goal is to capture the distribution over the weights, W, of the neural network given the observed data D:where:
- −
- —The likelihood, detailing how well the model explains observed data for a particular set of weights W.
- −
- —The prior distribution over weights, encapsulating our initial beliefs before seeing any data.
- −
- —The evidence or marginal likelihood, a normalizing factor ensuring the resulting posterior distribution integrates to one.
- Predictive Distribution for Unseen Data: An essential component in Bayesian deep learning is modeling predictions for new, unseen data while accounting for uncertainties. The predictive distribution is represented as:where represents the targets, and are the inputs for the new data. This form offers a way to obtain predictive uncertainty estimates, crucial for decisions in sensitive areas like healthcare.
- Modeling with MCMC Sampling: Leveraging Markov Chain Monte Carlo (MCMC) methods, especially Hamiltonian Monte Carlo (HMC), we can draw samples from the desired posterior distribution . This sampling can be represented as:Iterative refinement through MCMC sampling leads to a more nuanced understanding of the weight distributions, thereby enhancing prediction quality.
- Incorporation of Risk Factors: Using a Bayesian neural network (BNN) structure allows the inclusion of risk factors such as smoking, alcohol, and pollution, enabling the model to estimate lung cancer probability:To factor in uncertainties associated with the weights, the model can be extended as:
- Addressing Interactions and Confounding: It is vital to note that real-world data often indicates intricate interactions among various factors. An interaction between smoking and alcohol can be represented as . With these interactions, the BNN model can be reformulated:However, interactions sometimes introduce confounding effects. For instance, genetic predispositions G can impact the relationship between lung cancer and its risk factors. An enhanced model that accounts for this can be depicted as:By being explicit about these relationships, the model attempts to discern genuine risk factor effects from potential confounding influences.
- Enhancing Decision Support via Model Decomposition: Clinicians often require a more granular understanding of the model’s decisions to make informed medical interventions. By employing concepts like the Shapley value from game theory, it is possible to decompose the contributions of each factor to a given prediction. For example:These decomposition techniques offer a way to ascertain the relative impact of each factor in a BNN’s decision, paving the way for more individualized and evidence-backed medical decision-making.
3.2. Hierarchical Modeling in Bayesian Framework
- Hierarchical Bayesian Deep Learning and its Relevance: For such scenarios where data comes from various sources, like different age cohorts or geographic regions, hierarchical Bayesian models (HBMs) are very ’powerful’. The basic idea of HBM is that shared statistical information among these groups can be exploited for better generalization of the model. In the context of lung cancer prediction, an HBM can be mathematically captured as:This formula demonstrates that every individual group can show some type of pattern, and, at the same time, it can exhibit some overall commonalities that offer a valuable tool for prediction.
- Introducing a Comprehensive Set of Risk Factors: A well-rounded view of potential risk factors is crucial. These factors encompass the following:
- −
- S—Smoking habits and frequency;
- −
- A—Intensity and regularity of alcohol consumption;
- −
- P—Cumulative exposure to air pollution;
- −
- E—Exercise regimes, intensity, and consistency;
- −
- D—Dietary choices, frequency, and patterns.
Incorporating these factors, the Bayesian neural network (BNN) prediction model evolves to: - Interactions Among Risk Factors: It is important to recognize that some risk factors may interact in non-trivial ways. One example is that a heavy smoking high-fat diet would exponentially raise cancer risks. Such interactions can be modeled as:By embedding these interactions and accommodating group-level effects, our model becomes richer:
- Prior Knowledge Integration: Established medical knowledge guarantees that incorporation into the model does not render the model to work in a state of nothingness. By integrating priors based on previous research or expert opinion, we align the model closer to real-world expectations:
- Decoding the Black Box: Neural networks, especially deep architectures, can be opaque. Yet, in medical scenarios, understanding why a model makes a particular prediction is crucial. Tools like layer-wise relevance propagation (LRP) shed light on this:Such methods are invaluable in providing clarity and building trust among clinicians.
- Uncertainty as a Guiding Star: One of the defining features of Bayesian approaches is the native incorporation of uncertainty. Instead of a singular prediction, clinicians obtain a probable range, allowing them to assess risk more holistically:Such metrics are crucial for ensuring clinical decisions that are well-informed and supported by evidence.
4. Methodology
5. Patient Data and Dataset Description
5.1. Dataset Characteristics
5.2. Preprocessing Steps
- Handling Missing Data:
- K-nearest neighbors (k = 5) replaced 12% of missing smoking history entries with values through validation by 10-fold cross-validation to check for robustness.
- Normalization:
- A Z-score normalization procedure standardized nodule size distributions with mean = 0 and SD = 1, while Min–Max scaling applied 0–1 range normalization to age data for interpretation purposes.
- Encoding:
- Ordinal categorical features (e.g., malignancy ratings) were label-encoded to preserve ordinal relationships.
- Balancing:
- Four strategies were investigated (None, SMOTE, ADASYN, Cycle-GAN; see Table 4); the final model uses Cycle-GAN, which offered the best recall–precision trade-off.
- Comparative Study of Class-Balancing Strategies:
5.3. Feature Engineering and Selection
- Age: As the only numerical feature, it was crucial to ensure it does not dominate the training process. We normalized age using Min–Max scaling to confine its values within the range [0, 1].
- Most categorical features are related to potential risk factors and have an ordinal nature.
- −
- Features like ‘air pollution’, ‘alcohol use’, and ‘smoking’ may have ordered levels such as Low, Medium, and High.
- −
- For these ordinal features, label encoding was applied to transform them into integer values, ensuring the inherent order is maintained.
- Binary features:
- −
- Features like ‘coughing of blood’, if represented in a yes/no format, were binarized.
5.3.1. Model Predictions and Class Definitions
- Class 0: Benign—Cases where no malignancy is detected.
- Class 1: Moderate Risk—Cases with indeterminate lung nodules that require further evaluation.
- Class 2: Malignant—Cases with high certainty of lung cancer presence.
5.3.2. Complete Feature List and Justification for Deep Neural Network (DNN) Usage
5.3.3. Justification for Using a Deep Neural Network (DNN)
5.3.4. Feature Extraction
5.3.5. Feature Normalization and Transformation
5.3.6. Feature Importance and Selection
- Category-level contribution to prediction:
5.3.7. Clinical Interpretation of Key Predictive Features
- Smoking History: A well-established carcinogenic factor, contributing to chronic inflammation, DNA damage, and increased mutation rates.
- Genetic Risk: Includes hereditary syndromes and specific genetic variants such as EGFR mutations that predispose individuals to lung cancer.
- Age: A proxy for cumulative exposure to environmental risk factors and genetic alterations over time.
- Air Pollution: Particularly fine particulate matter (PM2.5), which has been implicated in oxidative stress and lung tissue remodeling.
- Nodule Shape and Size: Radiologic features strongly associated with malignancy risk, especially irregular, spiculated nodules exceeding 8 mm.
5.4. Bayesian Neural Network Architecture
- Architectural rationale.
5.4.1. Network Layers and Activation Functions
5.4.2. Design Rationale for Architectural Parameters
5.4.3. Bayesian Regularization and Priors
5.5. MCMC Sampling Techniques
5.6. Hamiltonian Monte Carlo
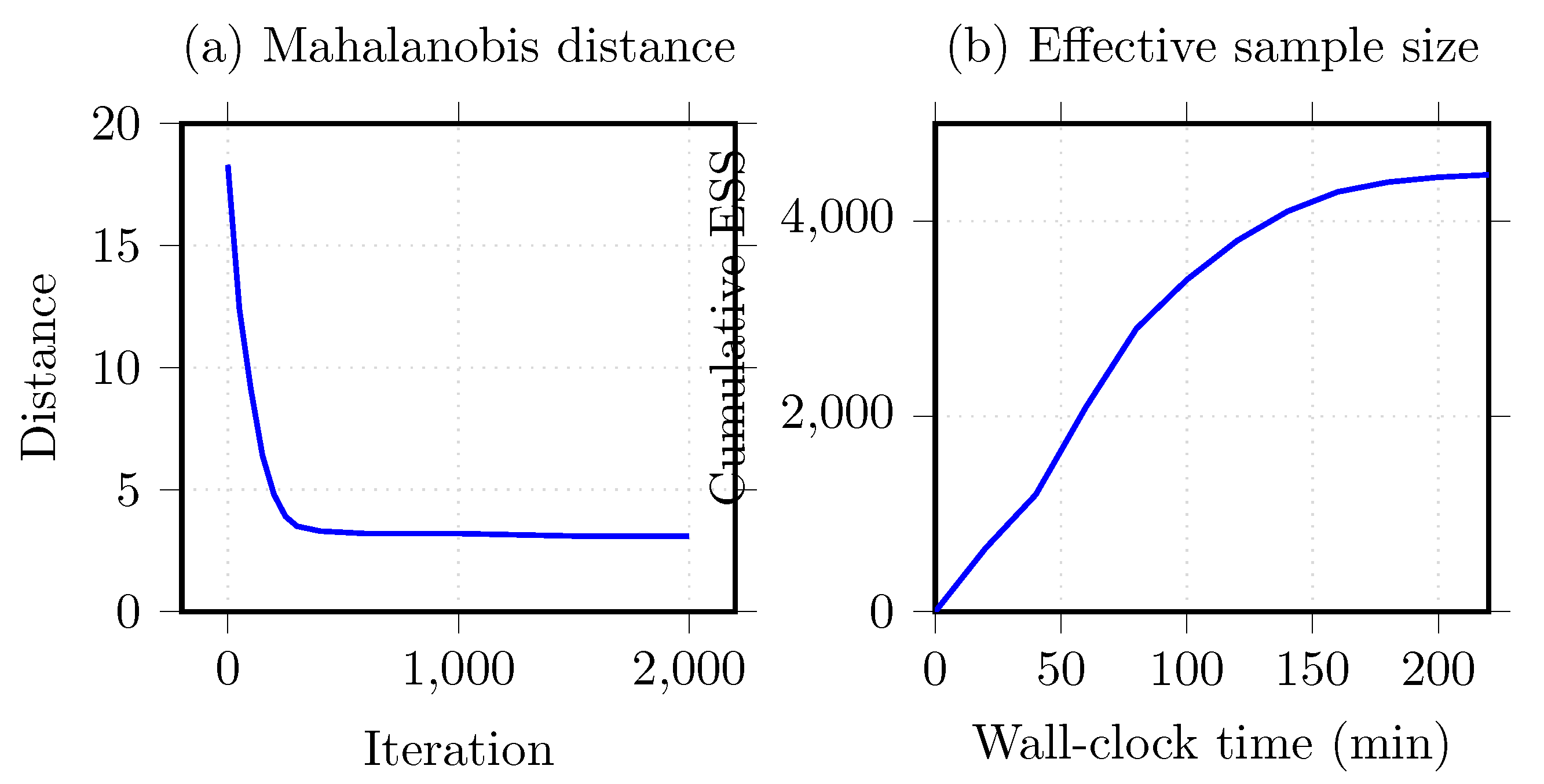
5.7. Convergence Diagnostics
5.8. Model Evaluation and Validation
5.9. Technical Validation Framework
- Clinical Dataset Testing: The model’s applicability should be validated on diverse real-world clinical datasets for different demographics to ensure generalizability.
- Robustness Checks: Testing the model against noisy and incomplete data to obtain a better understanding of stress resilience in various scenarios.
- Interoperability Assessments: Incorporation of integration tests with hospital information systems to verify seamless working within established workflows.
5.9.1. Cross-Validation Strategy
5.9.2. Performance Metrics
- Accuracy: This metric provided a general overview of the model’s performance, capturing the ratio of correct predictions to total predictions.
- Precision: Precision quantified the accuracy of positive predictions. In our context, it measured the proportion of true lung cancer cases among those predicted as such.
- Recall (Sensitivity): Critical in a medical setting, recall captures the proportion of actual lung cancer cases that were correctly identified by the model. A high recall is pivotal to ensure minimal false negatives.
- F1 Score: Harmonizing precision and recall, the F1 score offers a single metric that considers both false positives and false negatives, making it especially pertinent for imbalanced datasets.
5.10. Uncertainty Quantification and Interpretation
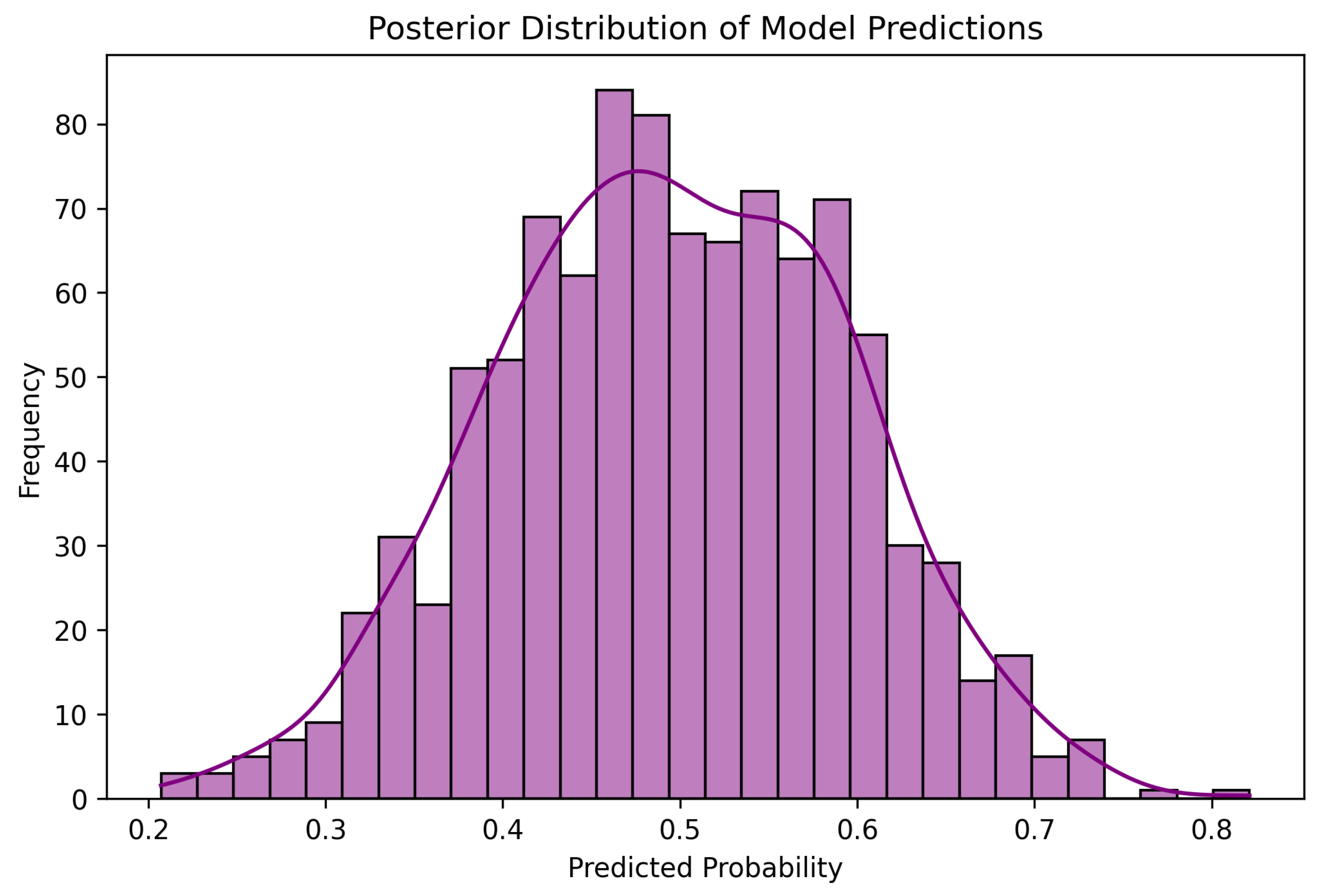
5.10.1. Posterior Predictive Checks
5.10.2. Interpretability Techniques
6. Results
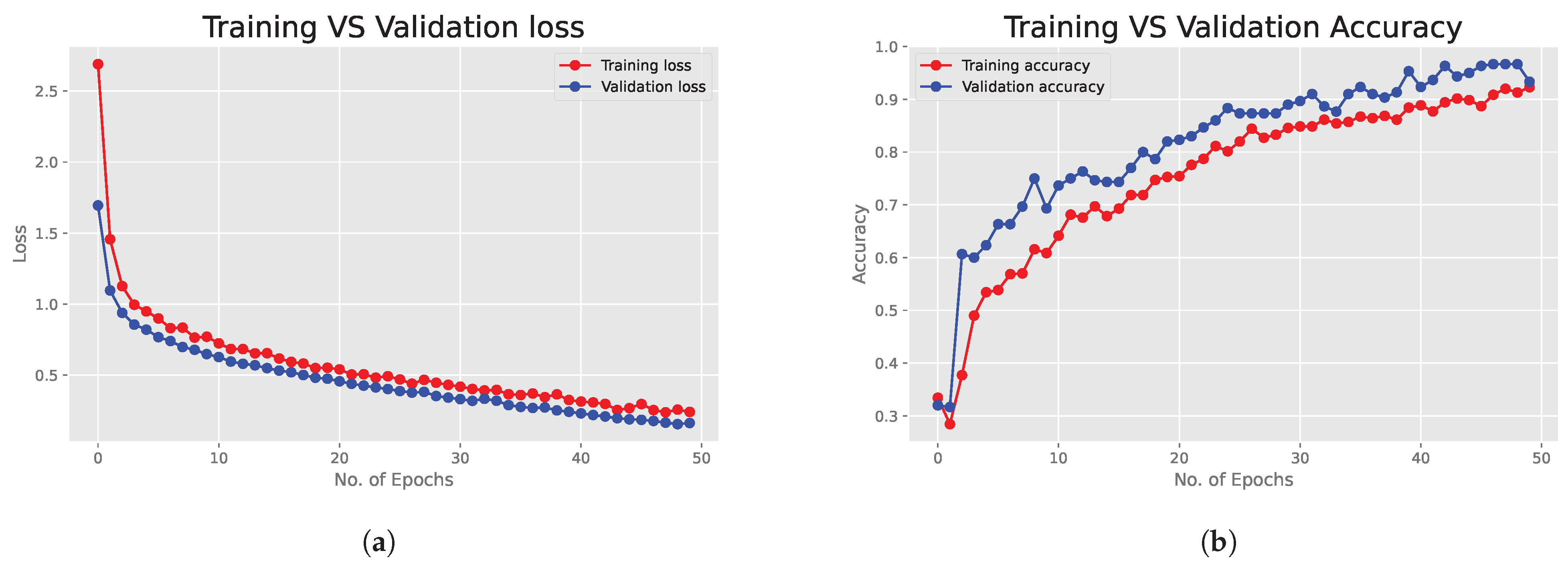
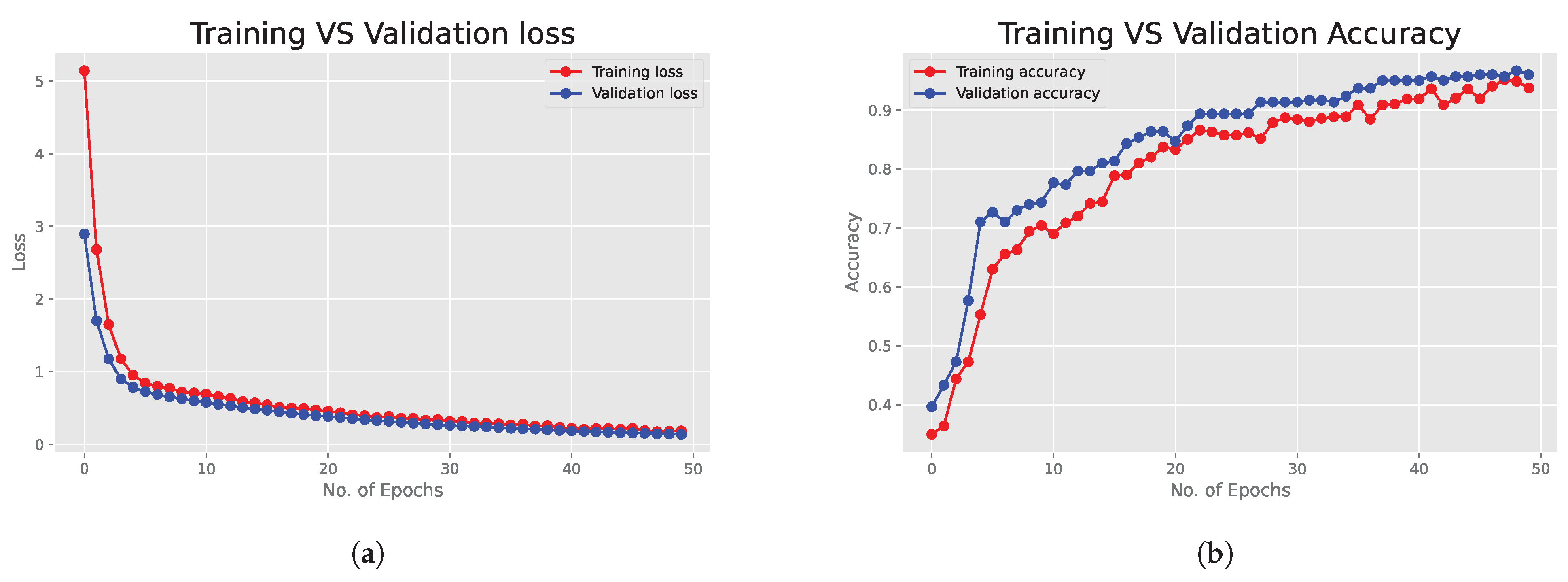
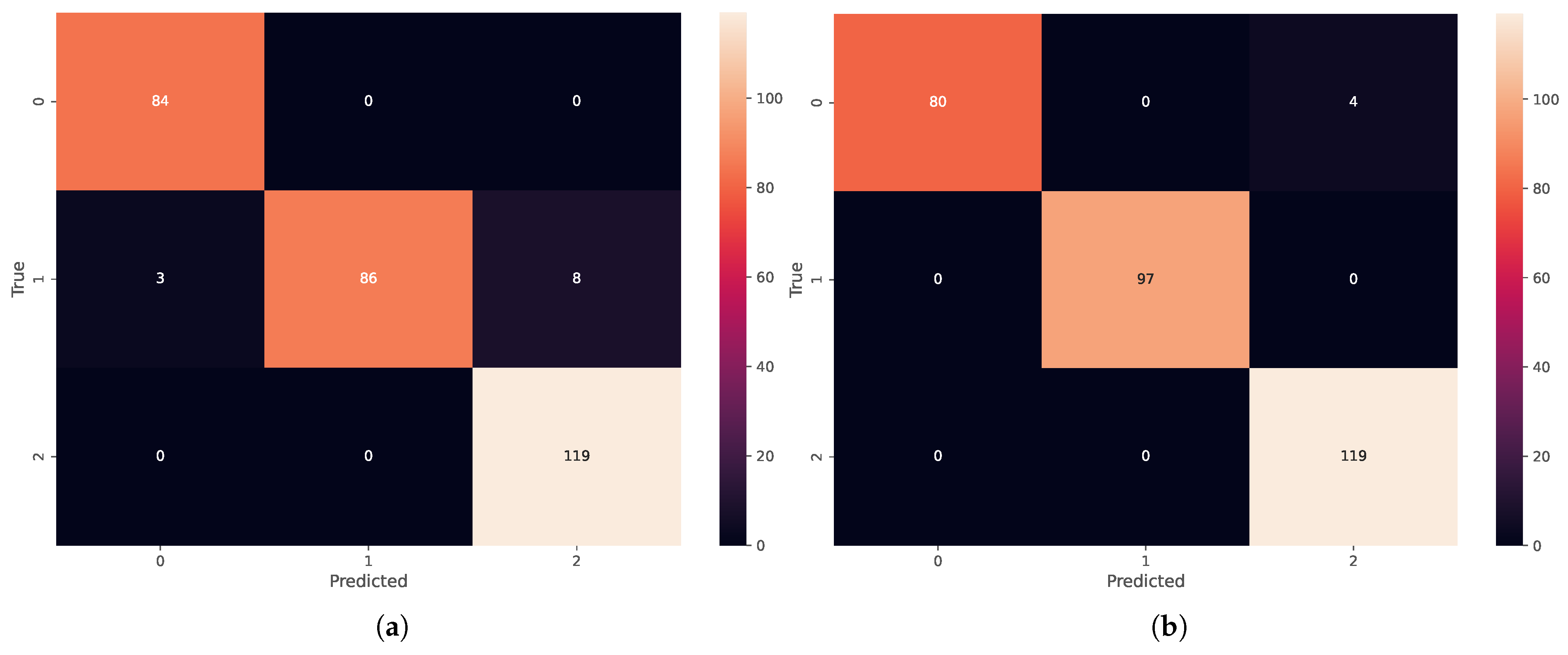
6.1. Deep Neural Network Results
6.2. Bayesian Neural Network Results
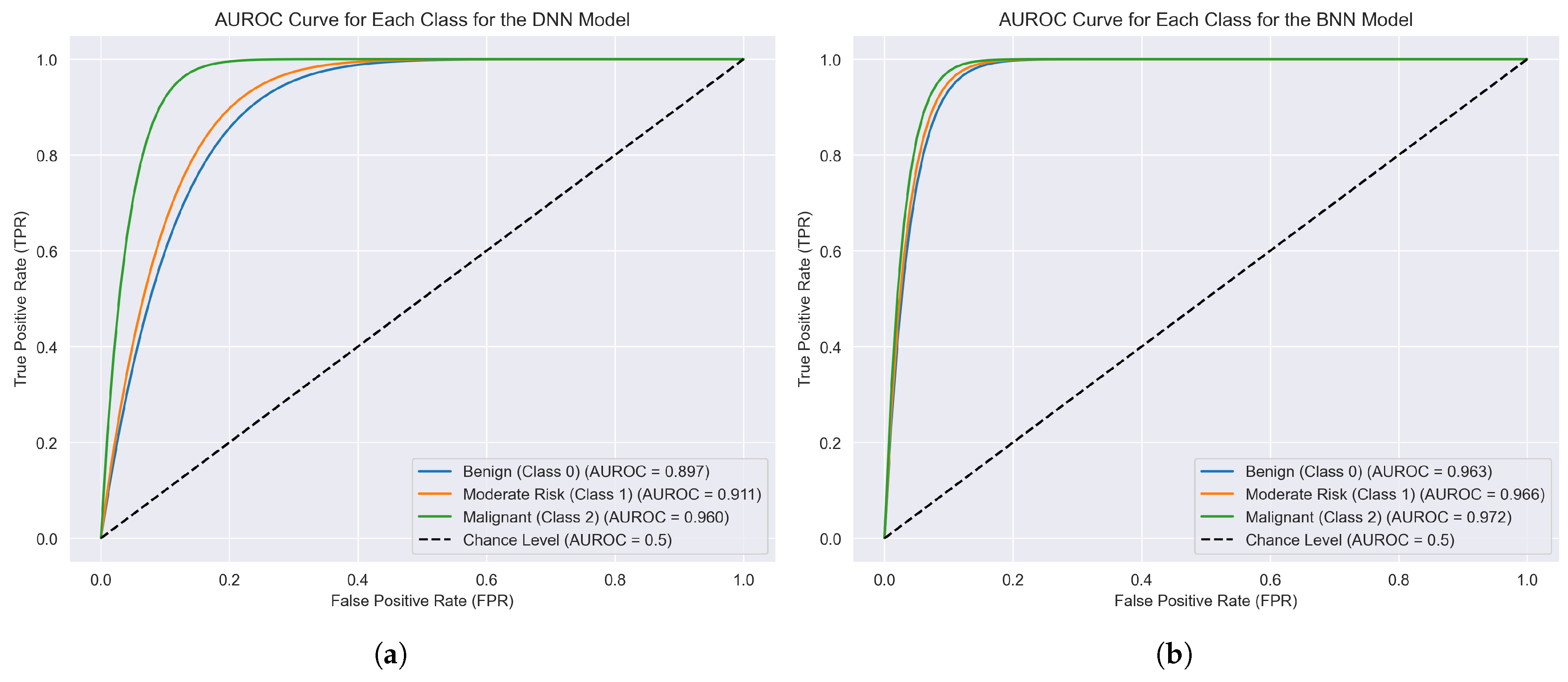
6.3. Performance Metrics and ROC Curves
6.4. Complexity and Computational Cost Analysis
- Deep Neural Networks (DNNs): A traditional DNN, during training, primarily requires forward and backward passes through the network, resulting in a complexity often denoted as , where N signifies the number of training samples, D represents the number of model parameters, and E is the number of training epochs. During inference, only a forward pass is necessary, making DNNs relatively efficient in making predictions once trained.
- Bayesian neural networks (BNNs): Training a BNN is inherently more computationally demanding than a DNN. The additional computational overhead arises from the need to infer a distribution over the model parameters instead of point estimates. When utilizing Markov Chain Monte Carlo (MCMC) methods, such as the Hamiltonian Monte Carlo in our research, the complexity can be approximated as , where S is the number of MCMC samples. The sampling process during both training and inference introduces additional latency in BNNs, making them slower than DNNs for equivalent tasks.
- Feasibility in Real-World Scenarios: Despite the heightened computational burden, BNNs offer considerable advantages, specifically in their ability to quantify uncertainty in predictions. This inherent property of BNNs can be crucial in clinical and medical applications where not only the prediction but also the confidence in the prediction is vital. While DNNs might be chosen for scenarios where speed is paramount, BNNs stand out when uncertainty estimation is a priority.
Deployment in Clinical Environments with Limited Resources
- Approximate Inference Alternatives: As noted, replacing HMC with scalable methods like VI, Monte Carlo Dropout, or Bayes by Backprop can drastically reduce computational load while preserving key Bayesian properties such as posterior-based uncertainty modeling. These methods are particularly suitable for training models on limited hardware, such as standard hospital servers or workstations.
- Model Compression and Optimization: Post-training compression techniques such as pruning, quantization, and knowledge distillation can significantly reduce inference time and memory usage. These methods allow the deployment of BNNs on edge devices without compromising predictive performance or clinical relevance.
- Cloud and Hybrid Architectures: In settings where local infrastructure is constrained, model training can be offloaded to cloud platforms. The trained model—possibly compressed or approximated—can then be deployed locally for inference. For institutions with secure and low-latency cloud access, even hybrid inference setups are viable.
6.5. External Validation and Generalisability
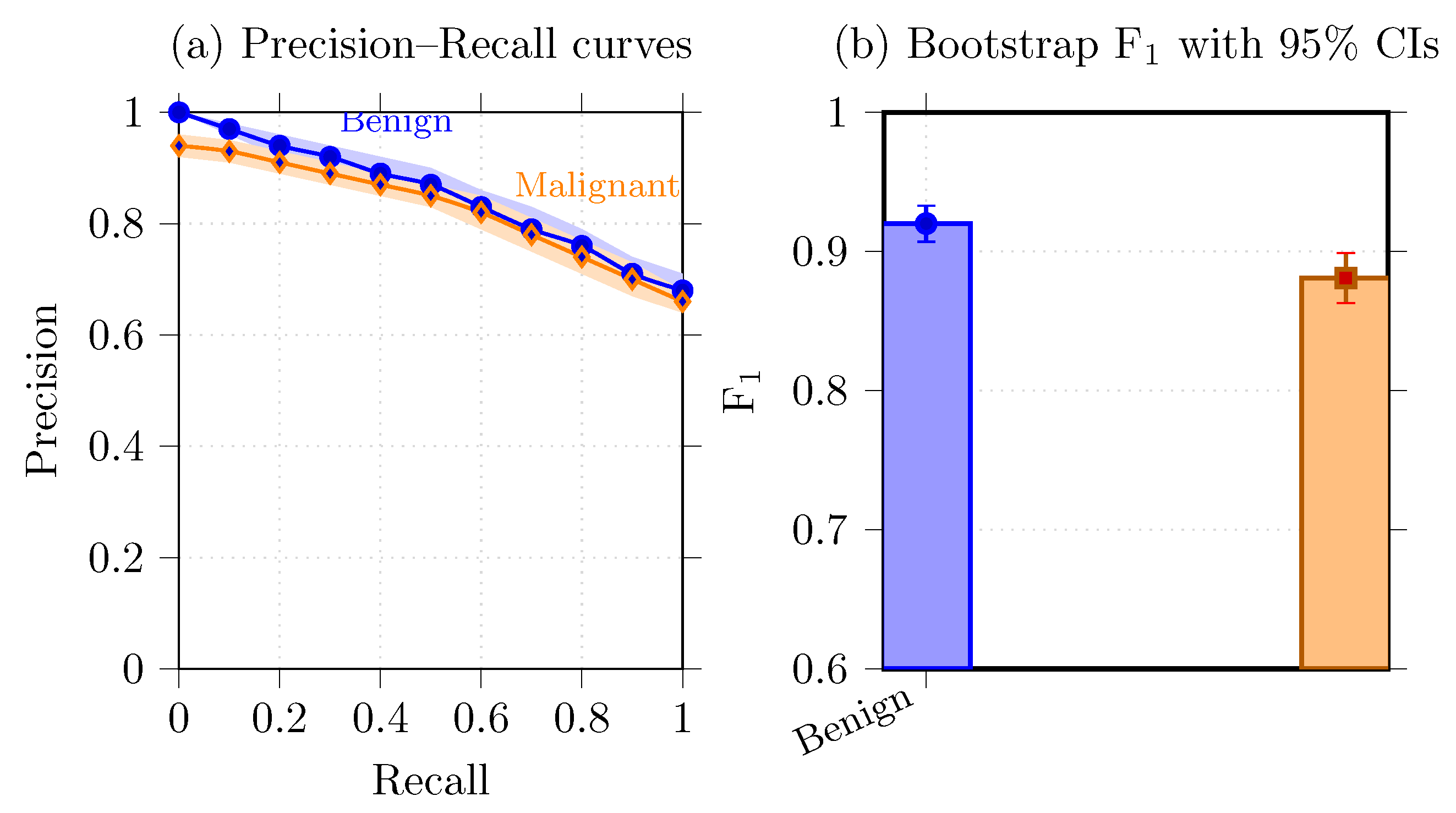
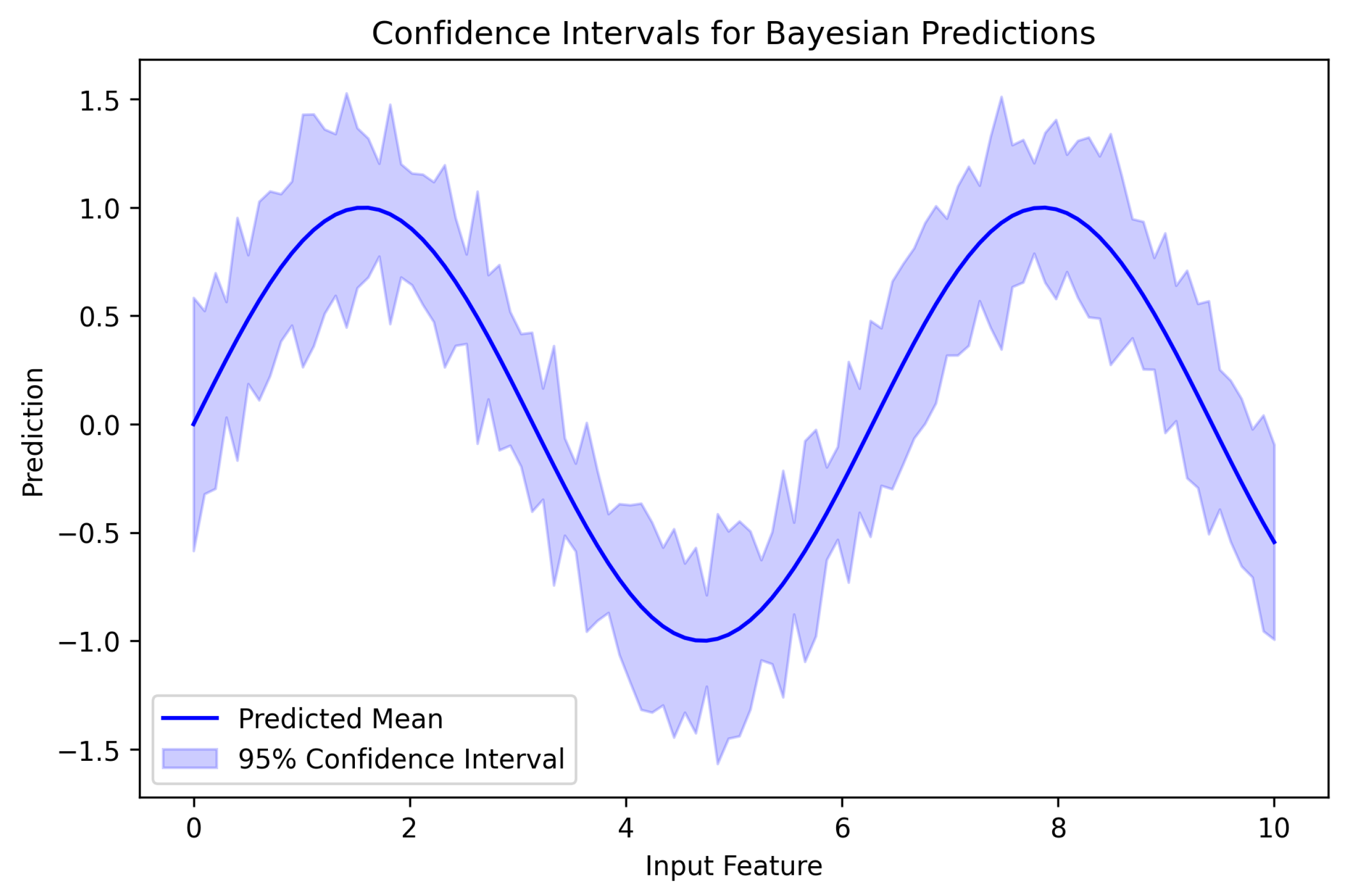
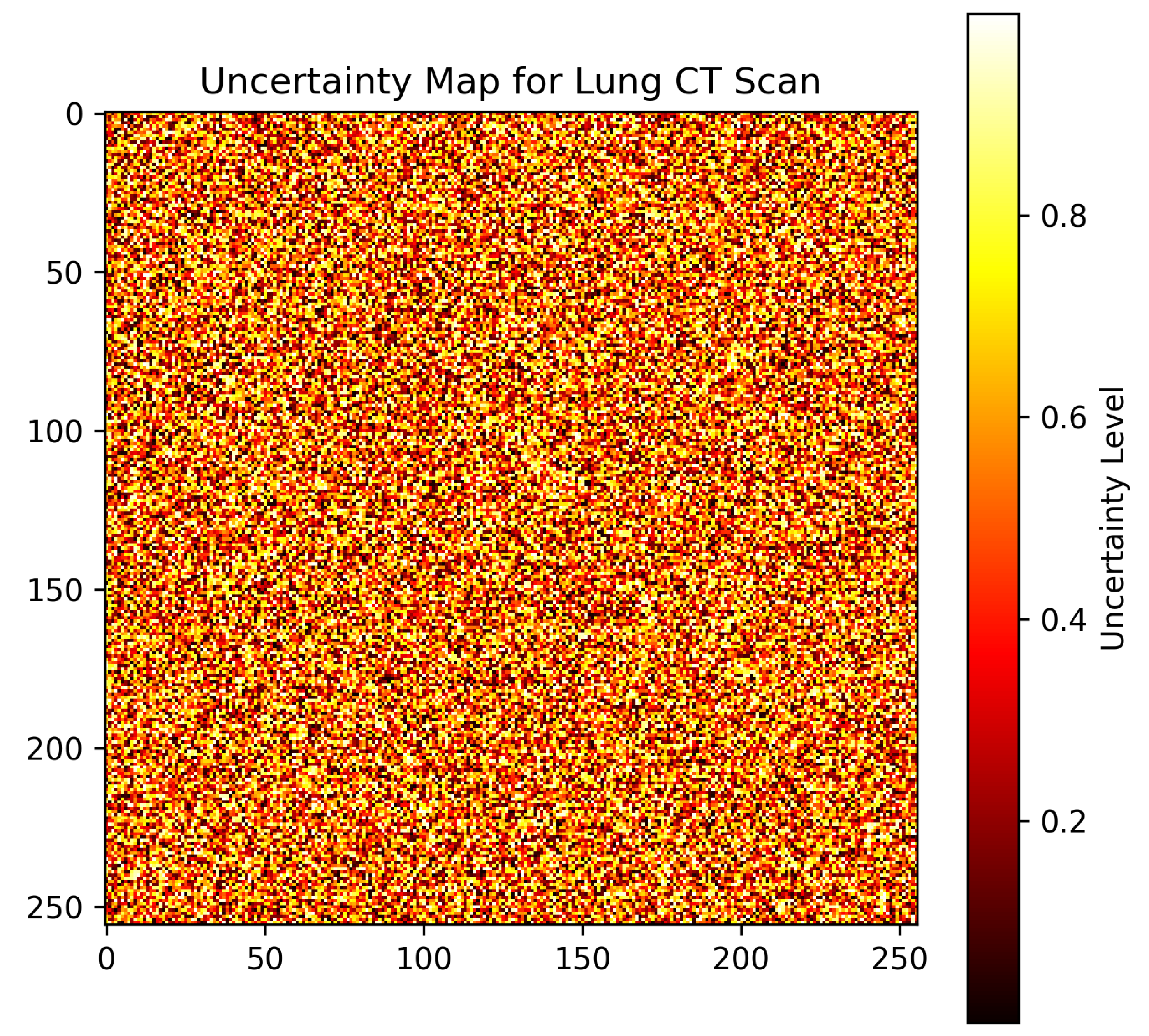
6.6. Precision–Recall Analysis and Uncertainty Visualization
- Bootstrap confidence intervals.
- Precision–recall curves.
- Uncertainty heatmaps.
6.7. Visualizations and Model Interpretation
6.7.1. Confidence Intervals for Predictions
6.7.2. Uncertainty Map for Medical Imaging
6.7.3. Posterior Distribution of Predictions
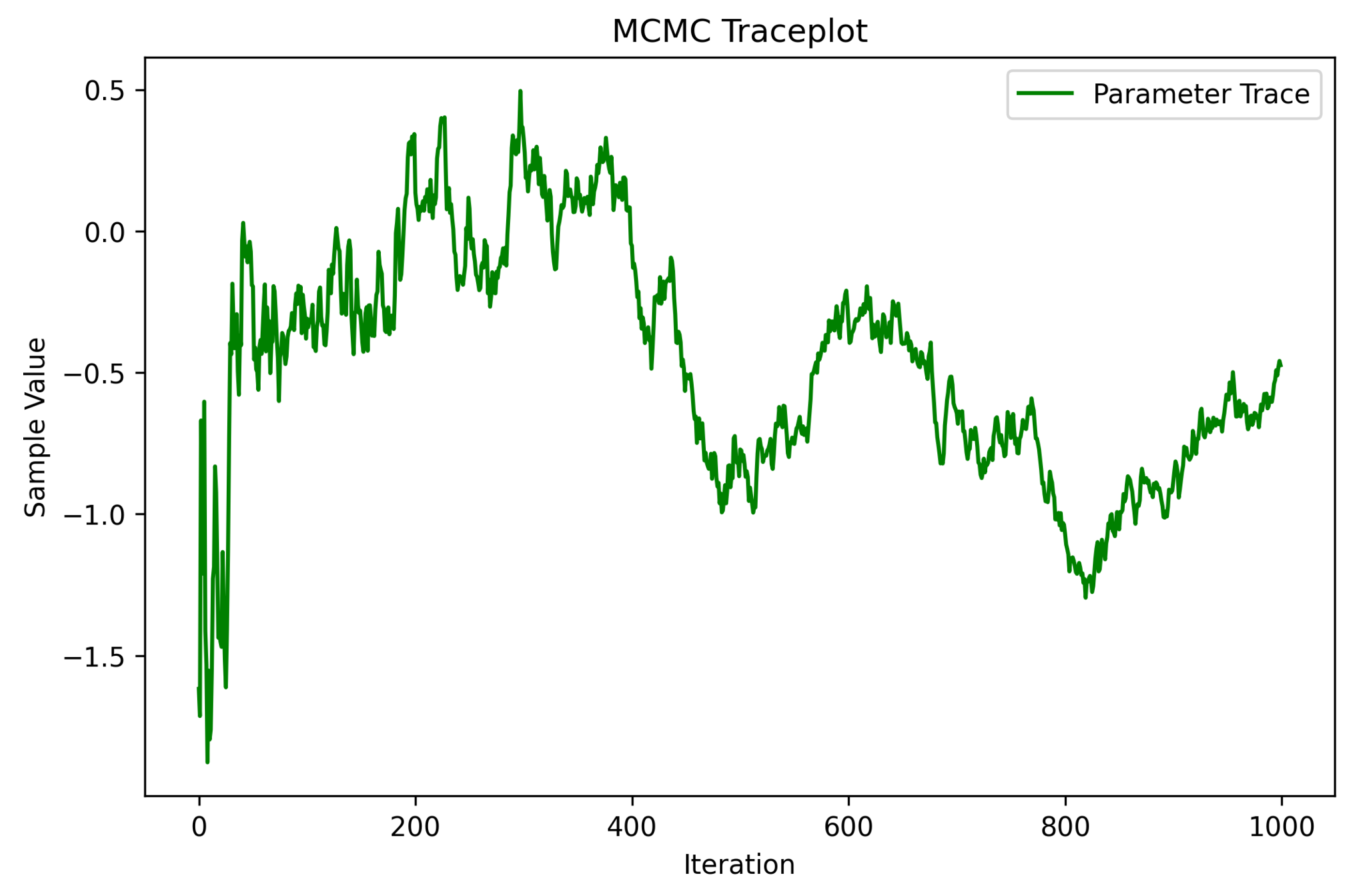
6.7.4. Traceplot for MCMC Sampling
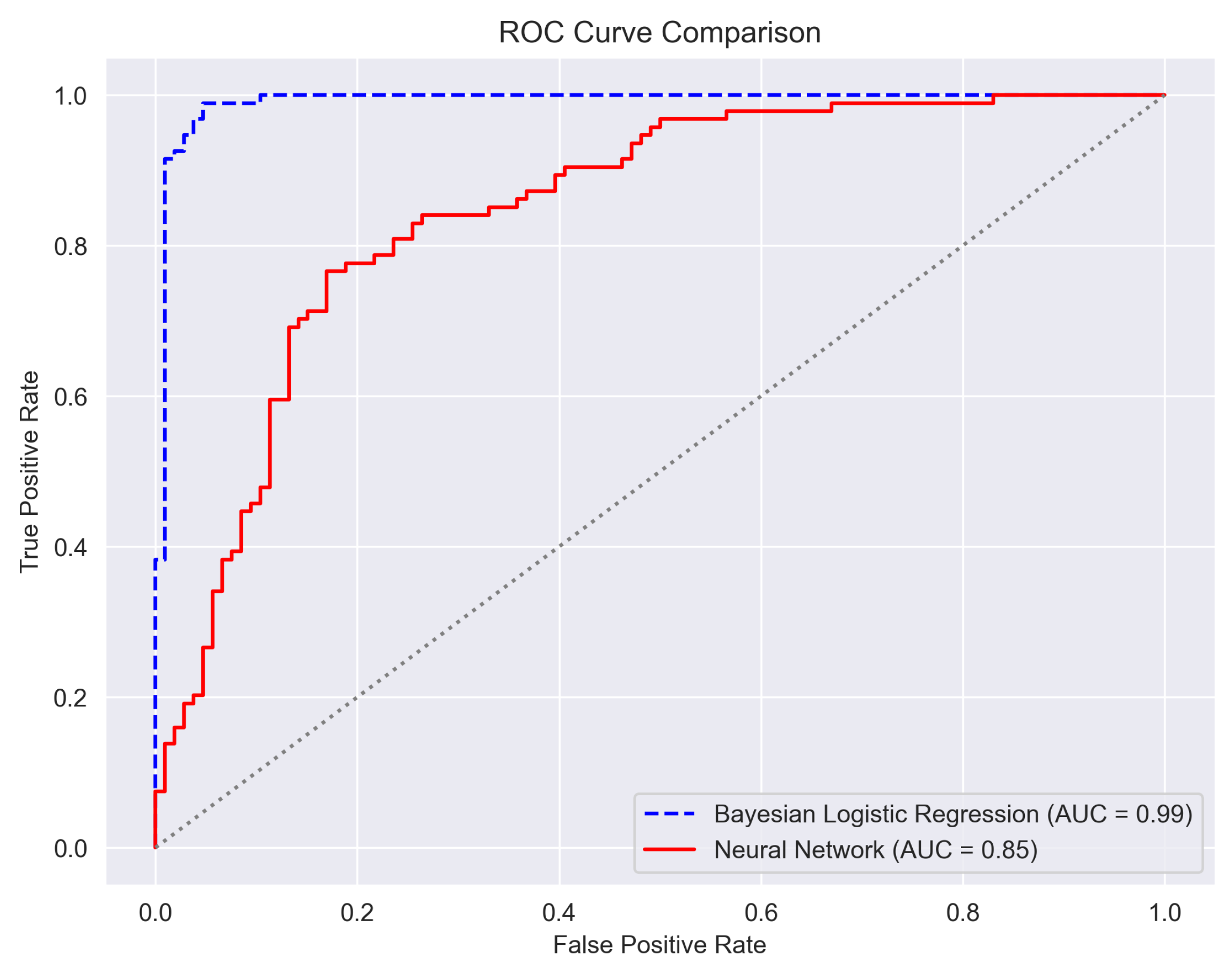
6.8. Horizontal Comparison with Classical Models
Bayesian Neural Network-Only Performance
7. Discussion
7.1. Comparison with Existing Approaches
7.2. Clinical Implications and Practical Implementation
7.3. Clinician-Facing Prototype and Usability Feedback
8. Conclusions and Future Work
8.1. Future Research Directions
8.2. Limitations and Future Enhancements
9. Ethical, Privacy and Fairness Considerations
- Patient privacy.
- Subgroup fairness.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| AUC | Area Under the Curve |
| BNN | Bayesian Neural Network |
| CAD | Computer-Aided Diagnosis |
| CNN | Convolutional Neural Network |
| CT | Computed Tomography |
| DNN | Deep Neural Network |
| DL | Deep Learning |
| HMC | Hamiltonian Monte Carlo |
| LDCT | Low-Dose Computed Tomography |
| LIDC-IDRI | Lung Image Database Consortium and Image Database Resource Initiative |
| LRP | Layer-wise Relevance Propagation |
| MCMC | Markov Chain Monte Carlo |
| ML | Machine Learning |
| PACS | Picture Archiving and Communication System |
| PCA | Principal Component Analysis |
| PPC | Posterior Predictive Check |
| ROC | Receiver Operating Characteristic |
| SMOTE | Synthetic Minority Oversampling Technique |
| SVM | Support Vector Machine |
| VIF | Variance Inflation Factor |
References
- Luo, G.; Zhang, Y.; Etxeberria, J.; Arnold, M.; Cai, X.; Hao, Y.; Zou, H. Projections of lung cancer incidence by 2035 in 40 countries worldwide: Population-based study. JMIR Public Health Surveill. 2023, 9, e43651. [Google Scholar] [PubMed]
- Siegel, R.L.; Miller, K.D.; Fedewa, S.A.; Ahnen, D.J.; Meester, R.G.; Barzi, A.; Jemal, A. Colorectal cancer statistics, 2017. CA Cancer J. Clin. 2017, 67, 177–193. [Google Scholar] [PubMed]
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [PubMed]
- Siegel, R.L.; Giaquinto, A.N.; Jemal, A. Cancer statistics, 2024. CA Cancer J. Clin. 2024, 74, 12–49. [Google Scholar]
- Chiu, H.Y.; Peng, R.H.T.; Lin, Y.C.; Wang, T.W.; Yang, Y.X.; Chen, Y.Y.; Wu, M.H.; Shiao, T.H.; Chao, H.S.; Chen, Y.M.; et al. Artificial Intelligence for Early Detection of Chest Nodules in X-ray Images. Biomedicines 2022, 10, 2839. [Google Scholar] [CrossRef]
- Field, J.K.; Vulkan, D.; Davies, M.P.; Baldwin, D.R.; Brain, K.E.; Devaraj, A.; Eisen, T.; Gosney, J.; Green, B.A.; Holemans, J.A.; et al. Lung cancer mortality reduction by LDCT screening: UKLS randomised trial results and international meta-analysis. Lancet Reg. Health—Eur. 2021, 10, 100179. [Google Scholar]
- Pastorino, U.; Rossi, M.; Rosato, V.; Marchiano, A.; Sverzellati, N.; Morosi, C.; Fabbri, A.; Galeone, C.; Negri, E.; Sozzi, G.; et al. Annual or biennial CT screening versus observation in heavy smokers. Eur. J. Cancer Prev. 2012, 21, 308–315. [Google Scholar]
- Infante, M.; Cavuto, S.; Lutman, F.R.; Brambilla, G.; Chiesa, G.; Ceresoli, G.; Passera, E.; Angeli, E.; Chiarenza, M.; Aranzulla, G.; et al. A randomized study of lung cancer screening with spiral computed tomography: Three-year results from the DANTE trial. Am. J. Respir. Crit. Care Med. 2009, 180, 445–453. [Google Scholar]
- Van Meerbeeck, J.P.; O’Dowd, E.; Ward, B.; Van Schil, P.; Snoeckx, A. Lung cancer screening: New perspective and challenges in Europe. Cancers 2022, 14, 2343. [Google Scholar] [CrossRef]
- van Beek, E.J.; Mirsadraee, S.; Murchison, J.T. Lung cancer screening: Computed tomography or chest radiographs? World J. Radiol. 2015, 7, 189. [Google Scholar]
- Panunzio, A.; Sartori, P. Lung cancer and radiological imaging. Curr. Radiopharm. 2020, 13, 238–242. [Google Scholar] [PubMed]
- Bradley, S.H.; Bhartia, B.S.; Callister, M.E.; Hamilton, W.T.; Hatton, N.L.F.; Kennedy, M.P.; Mounce, L.T.; Shinkins, B.; Wheatstone, P.; Neal, R.D. Chest X-ray sensitivity and lung cancer outcomes: A retrospective observational study. Br. J. Gen. Pract. 2021, 71, e862–e868. [Google Scholar] [PubMed]
- Sicular, S.; Alpaslan, M.; Ortega, F.A.; Keathley, N.; Venkatesh, S.; Jones, R.M.; Lindsey, R.V. Reevaluation of missed lung cancer with artificial intelligence. Respir. Med. Case Rep. 2022, 39, 101733. [Google Scholar] [PubMed]
- Muhammad, K.; Ullah, H.; Khan, Z.A.; Saudagar, A.K.J.; AlTameem, A.; AlKhathami, M.; Khan, M.B.; Abul Hasanat, M.H.; Mahmood Malik, K.; Hijji, M.; et al. WEENet: An intelligent system for diagnosing COVID-19 and lung cancer in IoMT environments. Front. Oncol. 2022, 11, 811355. [Google Scholar]
- Velu, S. An efficient, lightweight MobileNetV2-based fine-tuned model for COVID-19 detection using chest X-ray images. Math. Biosci. Eng. 2023, 20, 8400–8427. [Google Scholar] [CrossRef]
- Ibrahim, D.M.; Elshennawy, N.M.; Sarhan, A.M. Deep-chest: Multi-classification deep learning model for diagnosing COVID-19, pneumonia, and lung cancer chest diseases. Comput. Biol. Med. 2021, 132, 104348. [Google Scholar]
- Malik, H.; Naeem, A.; Naqvi, R.A.; Loh, W.K. DMFL_Net: A Federated Learning-Based Framework for the Classification of COVID-19 from Multiple Chest Diseases Using X-rays. Sensors 2023, 23, 743. [Google Scholar]
- Panda, A.; Kumar, A.; Gamanagatti, S.; Mishra, B. Virtopsy computed tomography in trauma: Normal postmortem changes and pathologic spectrum of findings. Curr. Probl. Diagn. Radiol. 2015, 44, 391–406. [Google Scholar]
- Horry, M.; Chakraborty, S.; Pradhan, B.; Paul, M.; Gomes, D.; Ul-Haq, A.; Alamri, A. Deep mining generation of lung cancer malignancy models from chest X-ray images. Sensors 2021, 21, 6655. [Google Scholar] [CrossRef]
- Pesce, E.; Withey, S.J.; Ypsilantis, P.P.; Bakewell, R.; Goh, V.; Montana, G. Learning to detect chest radiographs containing pulmonary lesions using visual attention networks. Med Image Anal. 2019, 53, 26–38. [Google Scholar]
- Li, X.; Shen, L.; Xie, X.; Huang, S.; Xie, Z.; Hong, X.; Yu, J. Multi-resolution convolutional networks for chest X-ray radiograph based lung nodule detection. Artif. Intell. Med. 2020, 103, 101744. [Google Scholar] [PubMed]
- Marín-Jiménez, I.; Casellas, F.; Cortés, X.; García-Sepulcre, M.F.; Juliá, B.; Cea-Calvo, L.; Soto, N.; Navarro-Correal, E.; Saldaña, R.; de Toro, J.; et al. The experience of inflammatory bowel disease patients with healthcare: A survey with the IEXPAC instrument. Medicine 2019, 98, e15044. [Google Scholar] [PubMed]
- Rawat, D.; Meenakshi; Pawar, L.; Bathla, G.; Kant, R. Optimized Deep Learning Model for Lung Cancer Prediction Using ANN Algorithm. In Proceedings of the 2022 3rd International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 17–19 August 2022; pp. 889–894. [Google Scholar] [CrossRef]
- Malhotra, J.; Malvezzi, M.; Negri, E.; La Vecchia, C.; Boffetta, P. Risk factors for lung cancer worldwide. Eur. Respir. J. 2016, 48, 889–902. [Google Scholar] [PubMed]
- Bailey-Wilson, J.E.; Sellers, T.A.; Elston, R.C.; Evens, C.C.; Rothschild, H. Evidence for a major gene effect in early onset lung cancer. J. La. State Med Soc. 1993, 145, 157–162. [Google Scholar]
- Lorenzo Bermejo, J.; Hemminki, K. Familial lung cancer and aggregation of smoking habits: A simulation of the effect of shared environmental factors on the familial risk of cancer. Cancer Epidemiol. Biomarkers Prev. 2005, 14, 1738–1740. [Google Scholar]
- Bailey-Wilson, J.E.; Amos, C.I.; Pinney, S.M.; Petersen, G.; De Andrade, M.; Wiest, J.; Fain, P.; Schwartz, A.; You, M.; Franklin, W.; et al. A major lung cancer susceptibility locus maps to chromosome 6q23–25. Am. J. Hum. Genet. 2004, 75, 460–474. [Google Scholar]
- Malkin, D.; Li, F.P.; Strong, L.C.; Fraumeni, J.F., Jr.; Nelson, C.E.; Kim, D.H.; Kassel, J.; Gryka, M.A.; Bischoff, F.Z.; Tainsky, M.A.; et al. Germ line p53 mutations in a familial syndrome of breast cancer, sarcomas, and other neoplasms. Science 1990, 250, 1233–1238. [Google Scholar]
- Amos, C.I.; Wu, X.; Broderick, P.; Gorlov, I.P.; Gu, J.; Eisen, T.; Dong, Q.; Zhang, Q.; Gu, X.; Vijayakrishnan, J.; et al. Genome-wide association scan of tag SNPs identifies a susceptibility locus for lung cancer at 15q25. 1. Nat. Genet. 2008, 40, 616–622. [Google Scholar]
- Thorgeirsson, T.E.; Geller, F.; Sulem, P.; Rafnar, T.; Wiste, A.; Magnusson, K.P.; Manolescu, A.; Thorleifsson, G.; Stefansson, H.; Ingason, A.; et al. A variant associated with nicotine dependence, lung cancer and peripheral arterial disease. Nature 2008, 452, 638–642. [Google Scholar]
- Doll, R.; Peto, R.; Boreham, J.; Sutherland, I. Mortality in relation to smoking: 50 years’ observations on male British doctors. BMJ 2004, 328, 1519. [Google Scholar]
- U.S. Department of Health and Human Services. The Health Consequences of Smoking—50 Years of Progress: A Report of the Surgeon General; Centers for Disease Control and Prevention (US): Atlanta, GA, USA, 2014.
- Wynder, E.L. Tobacco as a cause of lung cancer: Some reflections. Am. J. Epidemiol. 1997, 146, 687–694. [Google Scholar] [PubMed]
- IARC Working Group on the Evaluation of Carcinogenic Risks to Humans. Tobacco Smoke and Involuntary Smoking; IARC: Lyon, France, 2004; Volume 83, Available online: https://publications.iarc.who.int/101 (accessed on 3 July 2025).
- Hackshaw, A.K.; Law, M.R.; Wald, N.J. The accumulated evidence on lung cancer and environmental tobacco smoke. BMJ 1997, 315, 980–988. [Google Scholar] [PubMed]
- Boffetta, P. Involuntary smoking and lung cancer. Scand. J. Work. Environ. Health 2002, 28, 30–40. [Google Scholar] [PubMed]
- Stayner, L.; Bena, J.; Sasco, A.J.; Smith, R.; Steenland, K.; Kreuzer, M.; Straif, K. Lung cancer risk and workplace exposure to environmental tobacco smoke. Am. J. Public Health 2007, 97, 545–551. [Google Scholar]
- Boffetta, P.; Trédaniel, J.; Greco, A. Risk of childhood cancer and adult lung cancer after childhood exposure to passive smoke: A meta-analysis. Environ. Health Perspect. 2000, 108, 73–82. [Google Scholar]
- Mayne, S.T.; Buenconsejo, J.; Janerich, D.T. Previous lung disease and risk of lung cancer among men and women nonsmokers. Am. J. Epidemiol. 1999, 149, 13–20. [Google Scholar]
- Wu, A.H.; Fontham, E.T.; Reynolds, P.; Greenberg, R.S.; Buffler, P.; Liff, J.; Boyd, P.; Henderson, B.E.; Correa, P. Previous lung disease and risk of lung cancer among lifetime nonsmoking women in the United States. Am. J. Epidemiol. 1995, 141, 1023–1032. [Google Scholar]
- Gao, Y.T.; Blot, W.J.; Zheng, W.; Ersnow, A.G.; Hsu, C.W.; Levin, L.I.; Zhang, R.; Fraumeni, J.F., Jr. Lung cancer among Chinese women. Int. J. Cancer 1987, 40, 604–609. [Google Scholar]
- Aoki, K. Excess incidence of lung cancer among pulmonary tuberculosis patients. Jpn. J. Clin. Oncol. 1993, 23, 205–220. [Google Scholar]
- IARC Working Group on the Evaluation of Carcinogenic Risks to Humans. Ionizing Radiation, Part 1: X- and Gamma (γ)-Radiation, and Neutrons; IARC Monographs on the Evaluat: Lyon, France, 2000; Volume 75. [Google Scholar]
- Vainio, H.; Bianchini, F. Weight Control and Physical Activity; IARC: Lyon, France, 2002; Volume 6. [Google Scholar]
- Berman, D.W.; Crump, K.S. Update of potency factors for asbestos-related lung cancer and mesothelioma. Crit. Rev. Toxicol. 2008, 38, 1–47. [Google Scholar]
- Gilham, C.; Rake, C.; Burdett, G.; Nicholson, A.G.; Davison, L.; Franchini, A.; Carpenter, J.; Hodgson, J.; Darnton, A.; Peto, J. Pleural mesothelioma and lung cancer risks in relation to occupational history and asbestos lung burden. Occup. Environ. Med. 2016, 73, 290–299. [Google Scholar] [PubMed]
- Steenland, K.; Mannetje, A.; Boffetta, P.; Stayner, L.; Attfield, M.; Chen, J.; Dosemeci, M.; DeKlerk, N.; Hnizdo, E.; Koskela, R.; et al. Pooled exposure–response analyses and risk assessment for lung cancer in 10 cohorts of silica-exposed workers: An IARC multicentre study. Cancer Causes Control 2001, 12, 773–784. [Google Scholar] [PubMed]
- Chen, C.Y.; Huang, K.Y.; Chen, C.C.; Chang, Y.H.; Li, H.J.; Wang, T.H.; Yang, P.C. The role of PM2. 5 exposure in lung cancer: Mechanisms, genetic factors, and clinical implications. EMBO Mol. Med. 2025, 17, 31–40. [Google Scholar] [PubMed]
- Aslani, S.; Alluri, P.; Gudmundsson, E.; Chandy, E.; McCabe, J.; Devaraj, A.; Horst, C.; Janes, S.M.; Chakkara, R.; Nair, A.; et al. Enhancing cancer prediction in challenging screen-detected incident lung nodules using time-series deep learning. arXiv 2022, arXiv:2203.16606. [Google Scholar]
- Hou, K.Y.; Chen, J.R.; Wang, Y.C.; Chiu, M.H.; Lin, S.P.; Mo, Y.H.; Peng, S.C.; Lu, C.F. Radiomics-Based Deep Learning Prediction of Overall Survival in Non-Small-Cell Lung Cancer Using Contrast-Enhanced Computed Tomography. Cancers 2022, 14, 3798. [Google Scholar] [CrossRef]
- Deepa, V.; Fathimal, P. Lung cancer prediction and Stage classification in CT Scans Using Convolution Neural Networks—A Deep learning Model. In Proceedings of the 2022 International Conference on Data Science, Agents & Artificial Intelligence (ICDSAAI), Chennai, India, 8–10 December 2022; Volume 1, pp. 1–5. [Google Scholar] [CrossRef]
- Silva, F.; Pereira, T.; Neves, I.; Morgado, J.; Freitas, C.; Malafaia, M.; Sousa, J.; Fonseca, J.; Negrão, E.; Flor de Lima, B.; et al. Towards Machine Learning-Aided Lung Cancer Clinical Routines: Approaches and Open Challenges. J. Pers. Med. 2022, 12, 480. [Google Scholar] [CrossRef]
- Banerjee, N.; Das, S. Machine Learning for Prediction of Lung Cancer. In Deep Learning Applications in Medical Imaging; IGI Global: Hershey, PA, USA, 2021; pp. 114–139. [Google Scholar]
- Raoof, S.S.; Jabbar, M.A.; Fathima, S.A. Lung Cancer Prediction using Machine Learning: A Comprehensive Approach. In Proceedings of the 2020 2nd International Conference on Innovative Mechanisms for Industry Applications (ICIMIA), Bangalore, India, 5–7 March 2020; pp. 108–115. [Google Scholar] [CrossRef]
- Oentoro, J.; Prahastya, R.; Pratama, R.; Kom, M.S.; Fajar, M. Machine Learning Implementation in Lung Cancer Prediction—A Systematic Literature Review. In Proceedings of the 2023 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Bali, Indonesia, 20–23 February 2023; pp. 435–439. [Google Scholar] [CrossRef]
- Kadir, T.; Gleeson, F. Lung cancer prediction using machine learning and advanced imaging techniques. Transl. Lung Cancer Res. 2018, 7, 304. [Google Scholar]
- Wang, L. Deep Learning Techniques to Diagnose Lung Cancer. Cancers 2022, 14, 5569. [Google Scholar] [CrossRef]
- Forte, G.C.; Altmayer, S.; Silva, R.F.; Stefani, M.T.; Libermann, L.L.; Cavion, C.C.; Youssef, A.; Forghani, R.; King, J.; Mohamed, T.L.; et al. Deep Learning Algorithms for Diagnosis of Lung Cancer: A Systematic Review and Meta-Analysis. Cancers 2022, 14, 3856. [Google Scholar] [CrossRef]
- Adhikari, T.M.; Liska, H.; Sun, Z.; Wu, Y. A Review of Deep Learning Techniques Applied in Lung Cancer Diagnosis. In Signal and Information Processing, Networking and Computers: Proceedings of the 6th International Conference on Signal and Information Processing, Networking and Computers (ICSINC), Guiyang, China, 13–16 August 2019; Springer: Singapore, 2020; pp. 800–807. [Google Scholar]
- Essaf, F.; Li, Y.; Sakho, S.; Kiki, M.J.M. Review on deep learning methods used for computer-aided lung cancer detection and diagnosis. In Proceedings of the 2019 2nd International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 20–22 December 2019; pp. 104–111. [Google Scholar]
- Serj, M.F.; Lavi, B.; Hoff, G.; Valls, D.P. A deep convolutional neural network for lung cancer diagnostic. arXiv 2018, arXiv:1804.08170. [Google Scholar]
- Abdullah, A.A.; Hassan, M.M.; Mustafa, Y.T. A Review on Bayesian Deep Learning in Healthcare: Applications and Challenges. IEEE Access 2022, 10, 36538–36562. [Google Scholar] [CrossRef]
- Vijayaragunathan, R.; John, K.K.; Srinivasan, M. Bayesian approach: Adding clinical edge in interpreting medical data. J. Med Health Stud. 2022, 3, 70–76. [Google Scholar]
- Hadley, E.; Rhea, S.; Jones, K.; Li, L.; Stoner, M.; Bobashev, G. Enhancing the prediction of hospitalization from a COVID-19 agent-based model: A Bayesian method for model parameter estimation. PLoS ONE 2022, 17, e0264704. [Google Scholar]
- Holl, F.; Fotteler, M.; Müller-Mielitz, S.; Swoboda, W. Findings from a Panel Discussion on Evaluation Methods in Medical Informatics. In Informatics and Technology in Clinical Care and Public Health; IOS Press: Amsterdam, The Netherlands, 2022; pp. 272–275. [Google Scholar]
- Ding, N.; Fang, Y.; Babbush, R.; Chen, C.; Skeel, R.D.; Neven, H. Bayesian sampling using stochastic gradient thermostats. Adv. Neural Inf. Process. Syst. 2014, 27, 3203–3211. [Google Scholar]
- Lye, A.; Cicirello, A.; Patelli, E. Sampling methods for solving Bayesian model updating problems: A tutorial. Mech. Syst. Signal Process. 2021, 159, 107760. [Google Scholar]
- Boulkaibet, I.; Marwala, T.; Mthembu, L.; Friswell, M.; Adhikari, S. Sampling techniques in Bayesian finite element model updating. In Topics in Model Validation and Uncertainty Quantification, Volume 4: Proceedings of the 30th IMAC, A Conference on Structural Dynamics, 2012; Springer: New York, NY, USA, 2012; pp. 75–83. [Google Scholar]
- Marin, J.M.; Robert, C.P. Importance sampling methods for Bayesian discrimination between embedded models. arXiv 2009, arXiv:0910.2325. [Google Scholar]
- Karras, C.; Karras, A.; Avlonitis, M.; Sioutas, S. An Overview of MCMC Methods: From Theory to Applications. In Artificial Intelligence Applications and Innovations. AIAI 2022 IFIP WG 12.5 International Workshops; Maglogiannis, I., Iliadis, L., Macintyre, J., Cortez, P., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 319–332. [Google Scholar]
- Karras, C.; Karras, A.; Avlonitis, M.; Giannoukou, I.; Sioutas, S. Maximum Likelihood Estimators on MCMC Sampling Algorithms for Decision Making. In Artificial Intelligence Applications and Innovations. AIAI 2022 IFIP WG 12.5 International Workshops. AIAI 2022; Maglogiannis, I., Iliadis, L., Macintyre, J., Cortez, P., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 345–356. [Google Scholar]
- Karras, C.; Karras, A.; Tsolis, D.; Giotopoulos, K.C.; Sioutas, S. Distributed Gibbs Sampling and LDA Modelling for Large Scale Big Data Management on PySpark. In Proceedings of the 2022 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Ioannina, Greece, 23–25 September 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Vlachou, E.; Karras, C.; Karras, A.; Tsolis, D.; Sioutas, S. EVCA Classifier: A MCMC-Based Classifier for Analyzing High-Dimensional Big Data. Information 2023, 14, 451. [Google Scholar] [CrossRef]
- Vlachou, E.; Karras, A.; Karras, C.; Theodorakopoulos, L.; Halkiopoulos, C.; Sioutas, S. Distributed Bayesian Inference for Large-Scale IoT Systems. Big Data Cogn. Comput. 2023, 8, 1. [Google Scholar]


| Risk Factor Category | Specific Risk Factors (with Description) | References |
|---|---|---|
| Genetic Factors | Family History: Higher likelihood with direct relatives diagnosed | [25,26,27,28] |
| Polymorphisms: Variations in DNA sequence increasing susceptibility | [29,30] | |
| Tobacco Smoking | Cigarettes: Primary contributor to lung cancer risk | [31,32] |
| Other Tobacco Products: Increased risk | [33,34] | |
| Passive Smoking: Non-smokers exposed to smoke also at risk | [35,36,37] | |
| Childhood Exposure: Early exposure can have long-term effects | [38] | |
| Medical Conditions | COPD: Chronic Obstructive Pulmonary Disease, often a precursor | [39,40,41] |
| TB: History of tuberculosis can increase the risk | [42] | |
| Irradiation | High exposure to radiation is a known risk | [43,44] |
| Occupation | Asbestos: Inhalation increases risk, often in industrial jobs | [45,46] |
| Silica: Dust inhalation in certain professions can be harmful | [47] | |
| Environmental Exposures | PM2.5: Air pollution in urban areas | [4,48] |
| Application Area | Specific Bayesian Solution |
|---|---|
| Genomic Data Interpretation | Bayesian sparse learning for identifying significant genetic markers. |
| Treatment Recommendation Systems | Probabilistic matrix factorization to match patients with optimal treatments. |
| Radiology Imaging | Bayesian deep learning for enhanced MRI image reconstruction. |
| Epidemic Outbreak Predictions | Bayesian spatiotemporal modeling for predicting disease spread. |
| Medical Sensor Data | Hierarchical Bayesian modeling for wearable health device data analysis. |
| Healthcare Workflow Optimization | Bayesian networks for optimizing hospital resource allocation. |
| Neuroinformatics | Bayesian non-parametric methods for brain signal analysis. |
| Drug Discovery | Bayesian optimization in high-dimensional drug compound screening. |
| Attribute | Details |
|---|---|
| Source | Publicly available LIDC-IDRI dataset (1010 CT scans) |
| Inclusion Criteria | Patients aged 40–85; nodules ≥3 mm; malignancy confirmed via biopsy |
| Exclusion Criteria | Non-malignant nodules; incomplete clinical records |
| Demographics | Age (mean ± SD: 62.3 ± 9.8), Sex (Male: 58%, Female: 42%) |
| CT Scan Parameters | Slice thickness: 1–3 mm; resolution: 512 × 512 pixels; contrast-enhanced |
| Class Distribution | Benign: 30%, Malignant: 70% (addressed via SMOTE oversampling) |
| Balancing Method | Recallminor | Precision | Macro-F1 | FPR |
|---|---|---|---|---|
| None (baseline) | 0.803 | 0.944 | 0.889 | 0.029 |
| SMOTE | 0.832 | 0.891 | 0.896 | 0.041 |
| ADASYN | 0.836 | 0.887 | 0.897 | 0.039 |
| Cycle-GAN | 0.844 | 0.922 | 0.912 | 0.030 |
| Category | Feature |
|---|---|
| Clinical Features | Age |
| Smoking history (pack-years) | |
| Family history of lung cancer | |
| Chronic respiratory conditions (e.g., COPD) | |
| Exposure to air pollution | |
| Occupational exposure to carcinogens | |
| Previous history of lung infections | |
| Alcohol consumption | |
| BMI (Body Mass Index) | |
| Genetic risk factors (if available) | |
| Imaging Features (from CT Scans) | Nodule size (in mm) |
| Nodule shape (spherical vs. irregular) | |
| Nodule density (solid vs. subsolid) | |
| Nodule margin characteristics (smooth vs. spiculated) | |
| Presence of calcifications | |
| Nodule growth rate (based on previous scans) | |
| Location of nodules in lung lobes | |
| Presence of pleural effusion | |
| Texture-based radiomics features | |
| Vascular involvement |
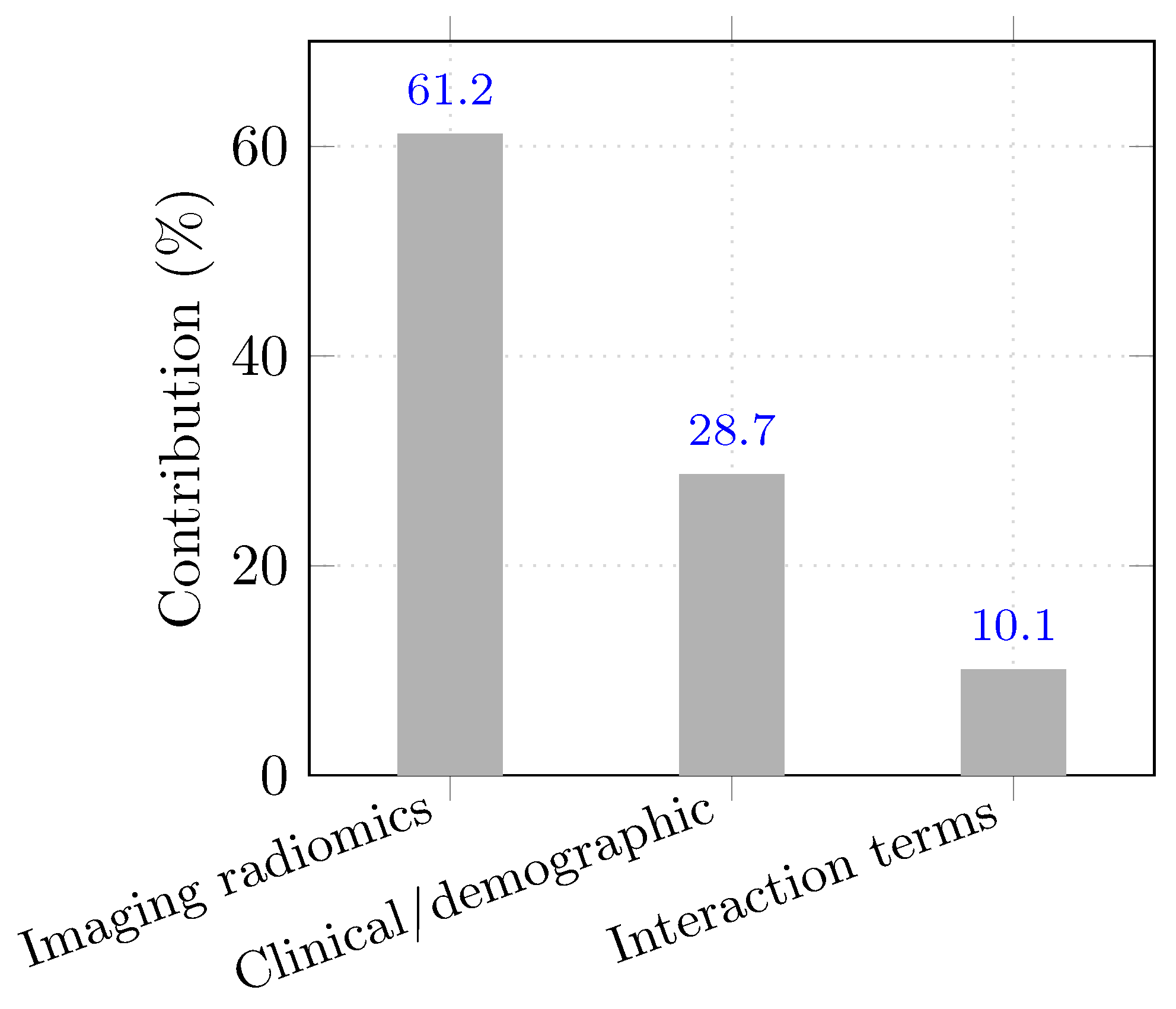
| Category | Variables (n) | Contribution (%) |
|---|---|---|
| Imaging radiomics | 13 | 61.2 |
| Clinical/demographic | 5 | 28.7 |
| Interaction terms | 2 | 10.1 |
| Backbone | AUC | Train Time (h/fold) | GPU Mem (GB) |
|---|---|---|---|
| Two-layer FC (ours) | 0.971 | 3.7 | 14.7 |
| 3D ResNet-18 | 0.973 | 7.5 | 28.9 |
| 3D DenseNet-121 | 0.974 | 8.2 | 32.4 |
| Metric | Value | Note |
|---|---|---|
| Free parameters D | 5254 | Two FC layers |
| Chains/Iterations | 4/2000 | 500 burn-in |
| Wall clock time | 3 h 42 min | All chains, JIT enabled |
| Peak GPU memory | 14.7 GB | CUDA profiler |
| Median ESS | 1184 | Across weights |
| Mean acceptance | 0.82 | After warm-up |
| Max | 1.00 | All <1.01 |
| Inference latency | 22 ms/scan | 100 posterior draws |
| Model size on disk | 250 MB | 100 draws × 5254 fp32 |
| Median ESS | Min ESS | Max | |
|---|---|---|---|
| Layer-1 weights | 1242 | 637 | 1.003 |
| Layer-2 weights | 1153 | 691 | 1.004 |
| Bias parameters | 1304 | 812 | 1.002 |
| All parameters | 1184 | 637 | 1.004 |
| Classes | Precision | Recall | F1 Score | Support |
|---|---|---|---|---|
| 0 | 0.96 | 0.83 | 0.89 | 84 |
| 1 | 0.87 | 0.94 | 0.90 | 86 |
| 2 | 0.98 | 0.99 | 0.97 | 119 |
| Accuracy | 0.93 | 300 | ||
| Macro Avg | 0.93 | 0.92 | 0.93 | 300 |
| Weighted Avg | 0.94 | 0.93 | 0.93 | 300 |
| Classes | Precision | Recall | F1 Score | Support |
|---|---|---|---|---|
| 0 | 1.00 | 0.95 | 0.98 | 84 |
| 1 | 1.00 | 1.00 | 1.00 | 97 |
| 2 | 0.98 | 0.99 | 0.98 | 119 |
| Accuracy | 0.99 | 300 | ||
| Macro Avg | 0.99 | 0.98 | 0.99 | 300 |
| Weighted Avg | 0.99 | 0.99 | 0.99 | 300 |
| Dataset | Subjects (n) | Accuracy | AUC | ECE |
|---|---|---|---|---|
| TCIA QIN-Lung-CT | 204 | 0.92 | 0.94 | 0.031 |
| NLST | 372 | 0.93 | 0.92 | 0.034 |
| PLCO | 248 | 0.91 | 0.94 | 0.029 |
| Class | Precision | Recall | F1 |
|---|---|---|---|
| Benign | 0.938 [0.919, 0.956] | 0.903 [0.884, 0.920] | 0.920 [0.903, 0.936] |
| Malignant | 0.922 [0.901, 0.943] | 0.844 [0.826, 0.862] | 0.881 [0.862, 0.899] |
| Model | Accuracy | AUC | Macro-F | Brier |
|---|---|---|---|---|
| Logistic Regression | 0.81 | 0.86 | 0.78 | 0.180 |
| Random Forest | 0.86 | 0.89 | 0.83 | 0.140 |
| LightGBM | 0.92 | 0.93 | 0.90 | 0.100 |
| XGBoost | 0.91 | 0.93 | 0.89 | 0.110 |
| CatBoost | 0.90 | 0.92 | 0.88 | 0.120 |
| DeepSurv | 0.90 | 0.92 | 0.88 | 0.120 |
| Deep Ensemble (5×) | 0.93 | 0.95 | 0.91 | 0.090 |
| Proposed BNN | 0.991 | 0.990 | 0.987 | 0.020 |
| Class | Precision | Recall | F1 | Support |
|---|---|---|---|---|
| 0 (Benign) | 1.00 | 0.95 | 0.975 | 84 |
| 1 (Malignant) | 1.00 | 1.00 | 1.000 | 97 |
| 2 (Indeterminate) | 0.98 | 0.99 | 0.985 | 119 |
| Overall accuracy | 0.990 | |||
| Macro average | 0.987 | |||
| Weighted average | 0.989 | |||
| Model | Accuracy | Precision | Recall | F1 Score | Uncertainty Quantification | Dataset | Ref. |
|---|---|---|---|---|---|---|---|
| Proposed BNN + HMC | 99% | 0.99 | 0.99 | 0.99 | Yes (HMC, Shapley) | LIDC-IDRI (1010) | This Study |
| 3D CNN (DeepCAD-NLM-L) | 95% | 0.94 | 0.93 | 0.93 | No | LIDC-IDRI (800) | [49] |
| Bayesian CNN (Variational) | 91% | 0.90 | 0.89 | 0.89 | Yes (Variational Inference) | NLST (2000) | [62] |
| Reader | SUS Score | Task Time (min) | Key Comment |
|---|---|---|---|
| R1 | 80 | 4.2 | “Confidence band helps decide follow-up interval.” |
| R2 | 75 | 4.7 | “SHAP list is intuitive; add ICD-10 mappings.” |
| R3 | 78 | 4.1 | “Heatmap draws attention to border voxels.” |
| Median | 78 | 4.3 | - |
| Subgroup | AUC | Macro-F1 | Support |
|---|---|---|---|
| Female | 0.969 | 0.928 | 142 |
| Male | 0.971 | 0.931 | 158 |
| Age ≤ 50 y | 0.962 | 0.923 | 71 |
| Age > 50 y | 0.974 | 0.941 | 229 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amasiadi, N.; Aslani-Gkotzamanidou, M.; Theodorakopoulos, L.; Theodoropoulou, A.; Krimpas, G.A.; Merkouris, C.; Karras, A. AI-Driven Bayesian Deep Learning for Lung Cancer Prediction: Precision Decision Support in Big Data Health Informatics. BioMedInformatics 2025, 5, 39. https://doi.org/10.3390/biomedinformatics5030039
Amasiadi N, Aslani-Gkotzamanidou M, Theodorakopoulos L, Theodoropoulou A, Krimpas GA, Merkouris C, Karras A. AI-Driven Bayesian Deep Learning for Lung Cancer Prediction: Precision Decision Support in Big Data Health Informatics. BioMedInformatics. 2025; 5(3):39. https://doi.org/10.3390/biomedinformatics5030039
Chicago/Turabian StyleAmasiadi, Natalia, Maria Aslani-Gkotzamanidou, Leonidas Theodorakopoulos, Alexandra Theodoropoulou, George A. Krimpas, Christos Merkouris, and Aristeidis Karras. 2025. "AI-Driven Bayesian Deep Learning for Lung Cancer Prediction: Precision Decision Support in Big Data Health Informatics" BioMedInformatics 5, no. 3: 39. https://doi.org/10.3390/biomedinformatics5030039
APA StyleAmasiadi, N., Aslani-Gkotzamanidou, M., Theodorakopoulos, L., Theodoropoulou, A., Krimpas, G. A., Merkouris, C., & Karras, A. (2025). AI-Driven Bayesian Deep Learning for Lung Cancer Prediction: Precision Decision Support in Big Data Health Informatics. BioMedInformatics, 5(3), 39. https://doi.org/10.3390/biomedinformatics5030039








