Machine Learning for Extraction of Image Features Associated with Progression of Geographic Atrophy
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Feature Extraction
- -
- Shape-based (2D) features, which include size, shape, volume, and surface measurements.
- -
- First-order statistics, which describe intensities and distributions.
- -
- Neighbouring Gray Tone Difference Matrix (NGTDM) features, which quantify average gray levels from neighbouring gray levels.
- -
- Gray-Level Dependence Matrix (GLDM) features, which look at gray-level dependencies in an image.
- -
- Gray-Level Run-Length Matrix (GLRLM) features, which quantify gray-level runs, such as consecutive regions of gray levels.
- -
- Gray-Level Co-occurrence Matrix (GLCM) features, which are second-order joint probability functions of an image.
- -
- Gray-Level Size Zone Matrix (GLSZM) features, which quantify gray-level zones.
| Feature Category | Features |
|---|---|
| Shape (2D) | Maximum 2D Diameter Row, Volume, Elongation, Flatness, Maximum 3D Diameter, Least Axis, Surface Volume Ratio, Major Axis, Surface Area, Maximum 2D Diameter Slice, Minor Axis, Maximum 2D Diameter Column, Sphericity |
| Neighbouring Gray Tone Difference Matrix (NGTDM) Features | Busyness, Coarseness, Complexity, Strength, Contrast |
| First-Order Statistics | 10th Percentile, Variance, Interquartile Range, Skewness, Mean, Energy, Uniformity, Root Mean Squared, 90th Percentile, Kurtosis, Mean Absolute Deviation, Range, Total Energy, Maximum, Median, Robust Mean Absolute Deviation, Minimum, Standard Deviation, Entropy |
| Gray-Level Dependence Matrix (GLDM) Features | Gray-Level Non-Uniformity, Dependence Entropy, Small Dependence Low Gray-Level Emphasis, Gray-Level Variance, Dependence Non-Uniformity Normalised, Large Dependence High Gray-Level Emphasis, Large Dependence Emphasis, Large Dependence Low Gray-Level Emphasis, Small Dependence High Gray-Level Emphasis, Dependence Variance, High Gray-Level Emphasis, Dependence Non-Uniformity, Low Gray-Level Emphasis, Small Dependence Emphasis |
| Gray-Level Run-Length Matrix (GLRLM) Features | Gray-Level Non-Uniformity, Run Percentage, Run-Length Non-Uniformity Normalised, Short Run High Gray-Level Emphasis, Long Run Emphasis, Short Run Low Gray-Level Emphasis, Gray-Level Variance, Run-Length Non-Uniformity, Short Run Emphasis, Run Variance, Run Entropy, Gray-Level Non-Uniformity Normalised, Low Gray-Level Run Emphasis, Long Run High Gray-Level Emphasis, Long Run Low Gray-Level Emphasis, High Gray-Level Run Emphasis |
| Gray-Level Co-occurrence Matrix (GLCM) Features | Imc1, Sum Average, Correlation, Idn, Joint Entropy, Difference Entropy, Cluster Tendency, Joint Energy, Difference Variance, Id, Joint Average, Idm, Cluster Shade, Imc2, Inverse Variance, Cluster Prominence, Sum Squares, Sum Entropy, Difference Average, Contrast, Idmn, Maximum Probability, Autocorrelation |
| Gray-Level Size Zone Matrix (GLSZM) Features | Gray-Level Non-Uniformity, Large Area High Gray-Level Emphasis, High Gray-Level Zone Emphasis, Size Zone Non-Uniformity, Small Area High Gray-Level Emphasis, Zone Variance, Gray-Level Variance, Large Area Low Gray-Level Emphasis, Size Zone Non-Uniformity Normalised, Gray-Level Non-Uniformity Normalised, Small Area Emphasis, Large Area Emphasis, Small Area Low Gray-Level Emphasis, Low Gray-Level Zone Emphasis, Zone Percentage, Zone Entropy |
| Clustering Features | Early-Stage Hyperfluorescence Cluster, Late-Stage Hyperfluorescence Cluster, Lesion Cluster |
2.3. Feature Selection
2.4. Mixed-Effects Model
- -
- Deficiencies in statistical power with the use of repeated observations;
- -
- The lack of adaptability due to missing data;
- -
- Disparate methods for treating continuous and categorical responses;
- -
- Dubious methods for modelling heteroscedasticity and non-spherical error variance.
2.5. Measure of Outcome
2.6. Model Diagnostics and Selection
2.7. Prediction Accuracy Using Forecasting Errors
- -
- : The forecast generated for the ith patient at time (i.e., the fitted/predicted value);
- -
- : The observed value for the ith patient at time ;
- -
- : The mean (or centred) value of the outcome measure;
- -
- : The forecast error for the ith patient at a particular time .
3. Results
3.1. Feature Extraction and Selection
3.2. Model Selection








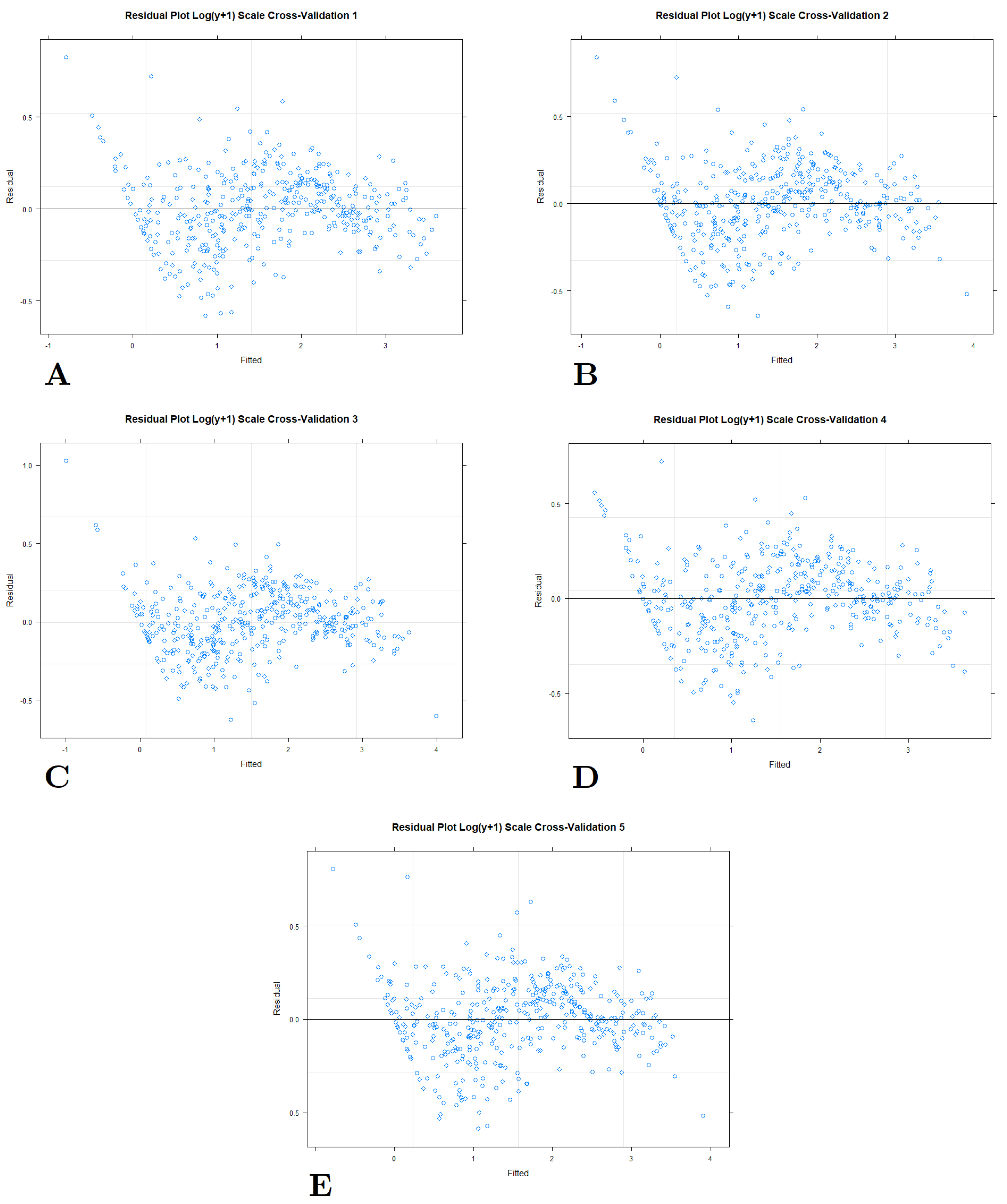
4. Discussion
4.1. Overall Findings
4.2. Testing Models with Different Transformations
4.3. The Most Suitable Model
4.4. Comparisons with the Literature
4.5. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holz, F.G.; Bindewald-Wittich, A.; Fleckenstein, M.; Dreyhaupt, J.; Scholl, H.P.; Schmitz-Valckenberg, S.; Group, F.A.-S. Progression of geographic atrophy and impact of fundus autofluorescence patterns in age-related macular degeneration. Am. J. Ophthalmol. 2007, 143, 463–472. [Google Scholar] [CrossRef]
- Jeong, Y.J.; Hong, I.H.; Chung, J.K.; Kim, K.L.; Kim, H.K.; Park, S.P. Predictors for the progression of geographic atrophy in patients with age-related macular degeneration: Fundus autofluorescence study with modified fundus camera. Eye 2014, 28, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Klein, R.; Meuer, S.M.; Knudtson, M.D.; Klein, B.E. The epidemiology of progression of pure geographic atrophy: The Beaver Dam Eye Study. Am. J. Ophthalmol. 2008, 146, 692–699. [Google Scholar] [CrossRef]
- Lindblad, A.S.; Lloyd, P.C.; Clemons, T.E.; Gensler, G.R.; Ferris, F.L., 3rd; Klein, M.L.; Armstrong, J.R.; Age-Related Eye Disease Study Research Group. Change in area of geographic atrophy in the Age-Related Eye Disease Study: AREDS report number 26. Arch. Ophthalmol. 2009, 127, 1168–1174. [Google Scholar] [CrossRef]
- Pfau, M.; Lindner, M.; Goerdt, L.; Thiele, S.; Nadal, J.; Schmid, M.; Schmitz-Valckenberg, S.; Sadda, S.R.; Holz, F.G.; Fleckenstein, M. Prognostic Value of Shape-Descriptive Factors for the Progression of Geographic Atrophy Secondary to Age-Related Macular Degeneration. Retina 2019, 39, 1527–1540. [Google Scholar] [CrossRef]
- Liefers, B.; Colijn, J.M.; González-Gonzalo, C.; Verzijden, T.; Wang, J.J.; Joachim, N.; Mitchell, P.; Hoyng, C.B.; van Ginneken, B.; Klaver, C.C.W.; et al. A Deep Learning Model for Segmentation of Geographic Atrophy to Study Its Long-Term Natural History. Ophthalmology 2020, 127, 1086–1096. [Google Scholar] [CrossRef]
- Niu, S.; de Sisternes, L.; Chen, Q.; Rubin, D.L.; Leng, T. Fully Automated Prediction of Geographic Atrophy Growth Using Quantitative Spectral-Domain Optical Coherence Tomography Biomarkers. Ophthalmology 2016, 123, 1737–1750. [Google Scholar] [CrossRef]
- Pfau, M.; Möller, P.T.; Künzel, S.H.; von der Emde, L.; Lindner, M.; Thiele, S.; Dysli, C.; Nadal, J.; Schmid, M.; Schmitz-Valckenberg, S.; et al. Type 1 Choroidal Neovascularization Is Associated with Reduced Localized Progression of Atrophy in Age-Related Macular Degeneration. Ophthalmol. Retin. 2020, 4, 238–248. [Google Scholar] [CrossRef]
- Schmidt-Erfurth, U.; Bogunovic, H.; Grechenig, C.; Bui, P.; Fabianska, M.; Waldstein, S.; Reiter, G.S. Role of deep learning quantified hyperreflective foci for the prediction of geographic atrophy progression. Am. J. Ophthalmol. 2020, 216, 257–270. [Google Scholar] [CrossRef]
- Künzel, S.H.; Möller, P.T.; Lindner, M.; Goerdt, L.; Nadal, J.; Schmid, M.; Schmitz-Valckenberg, S.; Holz, F.G.; Fleckenstein, M.; Pfau, M. Determinants of Quality of Life in Geographic Atrophy Secondary to Age-Related Macular Degeneration. Investig. Ophthalmol. Vis. Sci. 2020, 61, 63. [Google Scholar] [CrossRef] [PubMed]
- Pfau, M.; Emde, L.v.d.; Dysli, C.; Möller, P.T.; Thiele, S.; Lindner, M.; Schmid, M.; Rubin, D.L.; Fleckenstein, M.; Holz, F.G.; et al. Determinants of cone- and rod-function in geographic atrophy: AI-based structure-function correlation. Am. J. Ophthalmol. 2020, 217, 162–173. [Google Scholar] [CrossRef]
- Arslan, J.; Benke, K.K. Progression of Geographic Atrophy: Epistemic Uncertainties Affecting Mathematical Models and Machine Learning. Transl. Vis. Sci. Technol. 2021, 10, 3. [Google Scholar] [CrossRef] [PubMed]
- Arslan, J.; Benke, K.K.; Samarasinghe, G.; Sowmya, A.; Guymer, R.H.; Baird, P.N. Model Structure Uncertainty in the Characterization and Growth of Geographic Atrophy. Transl. Vis. Sci. Technol. 2021, 10, 2. [Google Scholar] [CrossRef] [PubMed]
- Ying, G.-s.; Maguire, M.G.; Glynn, R.; Rosner, B. Tutorial on Biostatistics: Linear Regression Analysis of Continuous Correlated Eye Data. Ophthalmic Epidemiol. 2017, 24, 130–140. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- Lippert, C.; Listgarten, J.; Liu, Y.; Kadie, C.M.; Davidson, R.I.; Heckerman, D. FaST linear mixed models for genome-wide association studies. Nat. Methods 2011, 8, 833–835. [Google Scholar] [CrossRef] [PubMed]
- Korte, A.; Vilhjalmsson, B.J.; Segura, V.; Platt, A.; Long, Q.; Nordborg, M. A mixed-model approach for genome-wide association studies of correlated traits in structured populations. Nat. Genet. 2012, 44, 1066–1071. [Google Scholar] [CrossRef] [PubMed]
- Gondro, C.; van der Werf, J.; Hayes, B. Genome-Wide Association Studies and Genomic Prediction; Springer: New York, NY, USA; Heidelberg, Germany; Dordrecht, The Netherlands; London, UK, 2013. [Google Scholar]
- Demidenko, E. Mixed Models: Theory and Application with R; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zhou, X.; Carbonetto, P.; Stephens, M. Polygenic Modeling with Bayesian Sparse Linear Mixed Models. PLoS Genet. 2013, 9, e1003264. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, X.; Bradbury, P.; Yu, J.; Zhang, Y.-M.; Todhunter, R.J.; Buckler, E.S.; Zhang, Z. Enrichment of statistical power for genome-wide association studies. BMC Biol. 2014, 12, 73. [Google Scholar] [CrossRef]
- Rizzo, S.; Botta, F.; Raimondi, S.; Origgi, D.; Fanciullo, C.; Morganti, A.G.; Bellomi, M. Radiomics: The facts and the challenges of image analysis. Eur. Radiol. Exp. 2018, 2, 36. [Google Scholar] [CrossRef]
- Burham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Burnham, K.P. Multimodel Inference: Understanding AIC Relative Variable Importance Values; Colorado State University: Fort Collins, CO, USA, 2015. [Google Scholar]
- van Griethuysen, J.J.M.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.H.; Fillion-Robin, J.C.; Pieper, S.; Aerts, H. Computational Radiomics System to Decode the Radiographic Phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef]
- Arslan, J.; Benke, K. Automation of Cluster Extraction in Fundus Autofluorescence Images of Geographic Atrophy. Appl. Biosci. 2023, 2, 384–405. [Google Scholar] [CrossRef]
- Arslan, J.; Samarasinghe, G.; Sowmya, A.; Benke, K.K.; Hodgson, L.A.B.; Guymer, R.H.; Baird, P.N. Deep Learning Applied to Automated Segmentation of Geographic Atrophy in Fundus Autofluorescence Images. Transl. Vision Sci. Technol. 2021, 10, 2. [Google Scholar] [CrossRef]
- Quinto, B. Next-Generation Machine Learning with Spark: Covers XGBoost, LightGBM, Spark NLP, Distributed Deep Learning with Keras, and More; Elahi, I., Ed.; Apress: New York, NY, USA, 2020. [Google Scholar]
- A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013.
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000. [Google Scholar]
- Dingemanse, N.J.; Dochtermann, N.A. Quantifying individual variation in behaviour: Mixed-effect modelling approaches. J. Anim. Ecol. 2013, 82, 39–54. [Google Scholar] [CrossRef]
- Edwards, L.J.; Muller, K.E.; Wolfinger, R.D.; Qaqish, B.F.; Schabenberger, O. An R2 Statistic for Fixed Effects in the Linear Mixed Model. Stat. Med. 2008, 27, 6137–6157. [Google Scholar] [CrossRef]
- Zhang, Z.; Ersoz, E.; Lai, C.-Q.; Todhunter, R.J.; Tiwari, H.K.; Gore, M.A.; Bradbury, P.J.; Yu, J.; Arnett, D.K.; Ordovas, J.M.; et al. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 2010, 42, 355–360. [Google Scholar] [CrossRef]
- Cheng, J.; Edwards, L.J.; Maldonado-Molina, M.M.; Komro, K.A.; Muller, K.E. Real Longitudinal Data Analysis for Real People: Building a Good Enough Mixed Model. Stat. Med. 2010, 29, 504–520. [Google Scholar] [CrossRef]
- Brown, H.; Prescott, R. Applied Mixed Models in Medicine; John Wiley & Sons Ltd.: West Sussex, UK, 1999. [Google Scholar]
- Ho, R.K.W.; Hu, I. Flexible modelling of random effects in linear mixed models—A Bayesian approach. Comput. Stat. Data Anal. 2008, 52, 1347–1361. [Google Scholar] [CrossRef]
- Schutzenmeister, A.; Piepho, H.-P. Residual analysis of linear mixed models using a simulation approach. Comput. Stat. Data Anal. 2012, 56, 1405–1416. [Google Scholar] [CrossRef]
- Proust, C.; Jacqmin-Gadda, H. Estimation of linear mixed models with a mixture of distribution for the random effects. Comput. Methods Programs Biomed. 2005, 78, 165–173. [Google Scholar] [CrossRef]
- Baayen, R.H.; Davidson, D.J.; Bates, D.M. Mixed-effects modeling with crossed random effects for subjects and items. J. Mem. Lang. 2008, 59, 390–412. [Google Scholar] [CrossRef]
- Chen, Z.; Dunson, D.B. Random Effects Selection in Linear Mixed Models. Biometrics 2003, 59, 762–769. [Google Scholar] [CrossRef]
- Bates, D.; Maechler, M. Package ‘lme4’: Linear Mixed Model Implementation; R Core Team: Vienna, Austria, 2010. [Google Scholar]
- Brader, H.S.; Pistilli, M.; Ying, G.-S.; Maguire, M.G. Early Progression of Geographic Atrophy in the Complications of Age-related macular degeneration Prevention Trial (CAPT). Investig. Ophthalmol. Vis. Sci. 2015, 56, 3790. [Google Scholar]
- Kuha, J. AIC and BIC: Comparisons of Assumptions and Performance. Sociol. Methods Res. 2004, 33, 188–229. [Google Scholar] [CrossRef]
- Wei, J.; Zhou, L. Model selection using modified AIC and BIC in joint modeling of paired functional data. Stat. Probab. Lett. 2010, 80, 1918–1924. [Google Scholar] [CrossRef]
- Galecki, A.; Burzykowski, T. Linear Mixed-Effects Models Using R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kutner, M.; Nachtsheim, C.; Neter, J.; Li, W. Chapter 2: Inference in Regression and Correlation Analysis. In Applied Linear Statistical Models; McGraw-Hill/Irwin: New York, NY, USA, 2005; pp. 63–73. [Google Scholar]
- Fernandez, G.C.J. Residual Analysis and Data Transformations: Important Tools in Statistical Analysis. HortScience 1992, 27, 297–300. [Google Scholar] [CrossRef]
- Cook, R.D.; Weisberg, S. Residuals and Inlfuence in Regression (Monographs on Statistics and Applied Probability); Chapman and Hall: New York, NY, USA, 1982. [Google Scholar]
- Bowerman, B.L.; O’Connell, R.T.; Koehler, A.B. Forecasting, Time Series, and Regression; Brooks/Cole, a Part of Cengage Learning; Thomson Brooks/Cole: Boston, MA, USA, 2005. [Google Scholar]
- Brandimarte, P. Introduction to Distribution Logistics; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Skinner, D.R.; Benke, K.K.; Chung, M.J. Application of adaptive convolution masking to the automation of visual inspection. IEEE Trans. Robot. Autom. 1990, 6, 123–127. [Google Scholar] [CrossRef]
- Conger, A.J. A Revised Definition for Suppressor Variables: A Guide to Their Identification and Interpretation. Educ. Psychol. Meas. 1974, 34, 35–46. [Google Scholar] [CrossRef]

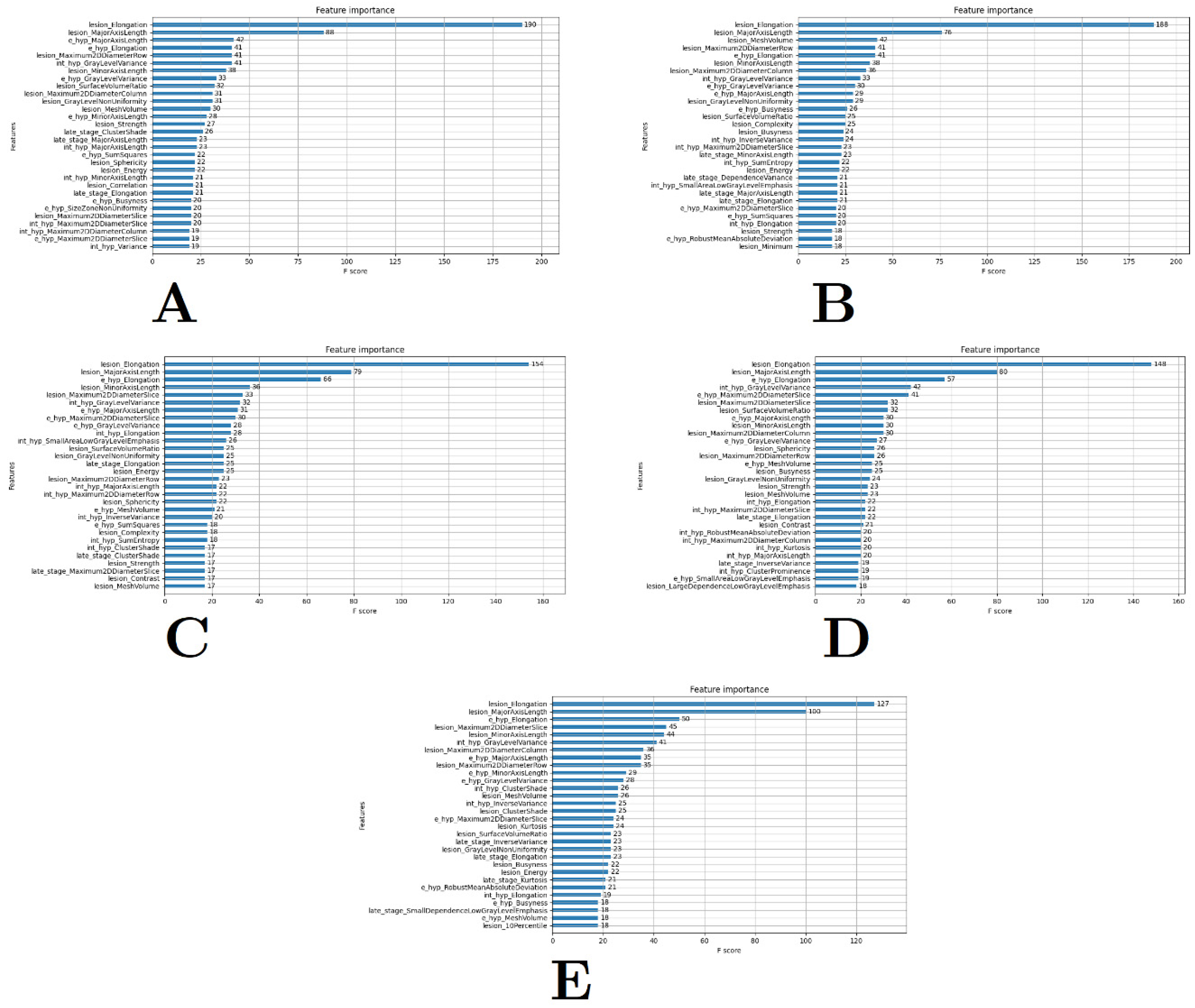



| Top Features Tested |
|---|
| lesion_elongation |
| lesion_majoraxislength |
| e_hyp_majoraxislength |
| e_hyp_elongation |
| lesion_maximum2ddiametercolumn |
| int_hyp_graylevelvariance |
| lesion_minoraxislength |
| e_hyp_graylevelvariance |
| lesion_surfacevolumeratio |
| lesion_graylevelnonuniformity |
| lesion_meshvolume |
| e_hyp_minoraxislength |
| lesion_strength |
| late_stage_majoraxislength |
| int_hyp_majoraxislength |
| e_hyp_sumsquares |
| lesion_sphericity |
| lesion_energy |
| int_hyp_minoraxislength |
| lesion_correlation |
| late_stage_elongation |
| e_hyp_busyness |
| e_hyp_sizezonenonuniformity |
| lesion_maximum2ddiameterslice |
| int_hyp_maximum2ddiameterslice |
| int_hyp_maximum2ddiametercolumn |
| e_hyp_maximum2ddiameterslice |
| int_hyp_variance |
| late_stage_clustershade |
| lesion_maximum2ddiameterrow |
| lesion_complexity |
| lesion_busyness |
| int_hyp_inversevariance |
| late_stage_minoraxislength |
| int_hyp_sumentropy |
| late_stage_dependencevariance |
| int_hyp_smallarealowgraylevelemp |
| int_hyp_elongation |
| e_hyp_robustmeanabsolutedeviation |
| lesion_minimum |
| e_hyp_meshvolume |
| int_hyp_clustershade |
| late_stage_maximum2ddiameterslice |
| lesion_contrast |
| int_hyp_robustmeanabsolutedeviat |
| int_hyp_kurtosis |
| late_stage_inversevariance |
| int_hyp_clusterprominence |
| e_hyp_smallarealowgraylevelempha |
| lesion_largedependencelowgraylevel |
| lesion_kurtosis |
| late_stage_kurtosis |
| late_stage_smalldependencelowgray |
| lesion_10percentile |
| Feature | Model 1.0 | Model 1.1 | Model 1.2 | Model 1.3 | Model 1.4 | Model 1.5 | Model 1.6 | Model 1.7 |
|---|---|---|---|---|---|---|---|---|
| lesion_elongation | x | x | x | x | x | x | x | x |
| lesion_minoraxislength | x | x | x | x | x | x | x | x |
| lesion_meshvolume | x | x | x | x | x | x | x | x |
| lesion_surfacevolumeratio | x | x | ||||||
| lesion_contrast | x | x | x | x | x | x | x | x |
| e_hyp_majoraxislength | x | x | ||||||
| e_hyp_minoraxislength | x | x | ||||||
| e_hyp_busyness | x | x | x | x | x | x | x | x |
| lesion_10percentile | x | x | x | x | x | x | x | x |
| lesion_sphericity | x | x | x | x | x | x | x | x |
| lesion_cluster | x | x | x | x | ||||
| e_hyp_sumsquares | x | x | ||||||
| lesion_correlation | x | x | x | x | ||||
| late_stage_clustershade | x | x | x | x | ||||
| lesion_complexity | x | x | x | x | ||||
| late_stage_minoraxislength | x | x | ||||||
| late_stage_dependencevariance | x | x | x | x | ||||
| late_stage_smalldependencelowgray | x | x | x | x | ||||
| lesion_minimum | x | x | ||||||
| late_stage_maximum2ddiameterslice | x | x |
| Model | p-Value | RMSE | ME | MAE | MAD | AIC | BIC | logLik | DF | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1.2 | 0.83 | 0.96 | 0.981 | <0.001 | 1.32 | −7.3 × 10−15 | 0.94 | 0.999 | 2084.93 | 2169.97 | −1022.46 | 20 |
| Model 1.1 | 0.83 | 0.95 | 0.979 | <0.001 | 1.35 | −1.4 × 10−14 | 0.97 | 1.047 | 2124.56 | 2192.77 | −1046.28 | 16 |
| Model 1.5 | 0.83 | 0.95 | 0.981 | <0.001 | 1.32 | −1.2 × 10−16 | 0.94 | 0.995 | 2094.51 | 2179.55 | −1027.25 | 20 |
| Model 1.6 | 0.82 | 0.95 | 0.978 | <0.001 | 1.40 | −4.3 × 10−15 | 0.99 | 1.063 | 2131.48 | 2186.90 | −1052.74 | 13 |
| Model 1.3 | 0.75 | 0.94 | 0.979 | <0.001 | 1.38 | −6.8 × 10−15 | 0.97 | 0.969 | 2215.01 | 2292.22 | −1089.50 | 18 |
| Model 1.4 | 0.76 | 0.94 | 0.979 | <0.001 | 1.37 | 1.9 × 10−16 | 0.97 | 0.992 | 2215.14 | 2292.35 | −1089.57 | 18 |
| Model 1.0 | 0.76 | 0.94 | 0.978 | <0.001 | 1.42 | −8.6 × 10−15 | 1.01 | 1.027 | 2257.33 | 2317.57 | −1114.67 | 14 |
| Model 1.7 | 0.74 | 0.94 | 0.976 | <0.001 | 1.46 | −5.1 × 10−15 | 1.02 | 1.002 | 2260.57 | 2307.90 | −1119.28 | 11 |
| Feature | Model 1.2 | Model 1.2sq | Model 1.2log |
|---|---|---|---|
| lesion_elongation | x | x | |
| lesion_minoraxislength | x | x | x |
| lesion_meshvolume | x | x | x |
| lesion_contrast | x | x | x |
| e_hyp_busyness | x | x | x |
| lesion_10percentile | x | x | x |
| lesion_sphericity | x | x | x |
| lesion_cluster | x | x | x |
| e_hyp_sumsquares | x | x | |
| lesion_correlation | x | x | |
| late_stage_clustershade | x | ||
| lesion_complexity | x | ||
| late_stage_minoraxislength | x | x | |
| late_stage_dependencevariance | x | x | |
| late_stage_smalldependencelowgray | x | x | x |
| p-Value | RMSE | ME | MAE | MAD | AIC | BIC | logLik | DF | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cross-Validation 1 | Original Area | 0.83 | 0.95 | 0.98 | <0.001 | 1.35 | 0.10 | 0.93 | 2.58 | 1729.33 | 1809.85 | −844.67 | 20 |
| Square-Root Area | 0.89 | 0.96 | 0.93 | <0.001 | 6.15 | 3.37 | 3.54 | 2.92 | 330.47 | 407.01 | −147.24 | 18 | |
| + 1) | 0.89 | 0.96 | 0.88 | <0.001 | 5.87 | 3.78 | 3.86 | 2.62 | 62.86 | 115.10 | −18.43 | 13 | |
| Cross-Validation 2 | Original Area | 0.85 | 0.95 | 0.96 | <0.001 | 1.39 | −0.07 | 1.05 | 3.86 | 1717.88 | 1798.30 | −838.94 | 20 |
| Square-Root Area | 0.89 | 0.96 | 0.95 | <0.001 | 6.49 | 3.60 | 3.73 | 2.52 | 330.47 | 407.01 | −147.24 | 18 | |
| + 1) | 0.89 | 0.95 | 0.92 | <0.001 | 7.74 | 4.84 | 4.89 | 3.11 | 126.84 | 179.37 | −50.42 | 13 | |
| Cross-Validation 3 | Original Area | 0.83 | 0.95 | 0.98 | <0.001 | 1.52 | 0.25 | 1.09 | 2.85 | 1712.43 | 1793.19 | −836.22 | 20 |
| Square-Root Area | 0.89 | 0.96 | 0.94 | <0.001 | 6.33 | 3.89 | 4.02 | 3.08 | 330.47 | 407.01 | −147.24 | 18 | |
| + 1) | 0.88 | 0.95 | 0.91 | <0.001 | 8.66 | 5.49 | 5.54 | 3.14 | 109.04 | 161.41 | −41.52 | 13 | |
| Cross-Validation 4 | Original Area | 0.84 | 0.96 | 0.97 | <0.001 | 1.44 | −0.07 | 1.08 | 4.05 | 1701.23 | 1781.55 | −830.61 | 20 |
| Square-Root Area | 0.89 | 0.96 | 0.94 | <0.001 | 6.94 | 3.93 | 4.11 | 2.78 | 330.47 | 407.01 | −147.24 | 18 | |
| + 1) | 0.89 | 0.95 | 0.90 | <0.001 | 7.23 | 4.11 | 4.21 | 2.24 | 124.57 | 176.81 | −49.28 | 13 | |
| Cross-Validation 5 | Original Area | 0.85 | 0.96 | 0.98 | <0.001 | 1.50 | 0.26 | 1.05 | 4.25 | 1731.18 | 1812.08 | −845.59 | 20 |
| Square-Root Area | 0.89 | 0.96 | 0.93 | <0.001 | 6.84 | 3.82 | 3.95 | 2.93 | 330.47 | 407.01 | −147.24 | 18 | |
| + 1) | 0.89 | 0.95 | 0.88 | <0.001 | 8.04 | 4.66 | 4.73 | 2.68 | 118.31 | 170.48 | −46.15 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arslan, J.; Benke, K. Machine Learning for Extraction of Image Features Associated with Progression of Geographic Atrophy. BioMedInformatics 2024, 4, 1638-1671. https://doi.org/10.3390/biomedinformatics4030089
Arslan J, Benke K. Machine Learning for Extraction of Image Features Associated with Progression of Geographic Atrophy. BioMedInformatics. 2024; 4(3):1638-1671. https://doi.org/10.3390/biomedinformatics4030089
Chicago/Turabian StyleArslan, Janan, and Kurt Benke. 2024. "Machine Learning for Extraction of Image Features Associated with Progression of Geographic Atrophy" BioMedInformatics 4, no. 3: 1638-1671. https://doi.org/10.3390/biomedinformatics4030089
APA StyleArslan, J., & Benke, K. (2024). Machine Learning for Extraction of Image Features Associated with Progression of Geographic Atrophy. BioMedInformatics, 4(3), 1638-1671. https://doi.org/10.3390/biomedinformatics4030089






