Abstract
Ultrasound elastography (USE) or elastosonography is an ultrasound-based, non-invasive imaging method for assessing tissue elasticity. The different types of elastosonography are distinguished according to the mechanisms used for estimating tissue elasticity and the type of information they provide. In strain imaging, mechanical stress is applied to the tissue, and the resulting differential strain between different tissues is used to provide a qualitative assessment of elasticity. In shear wave imaging, tissue elasticity is inferred through quantitative parameters, such as shear wave velocity or longitudinal elastic modulus. Shear waves can be produced using a vibrating mechanical device, as in transient elastography (TE), or an acoustic impulse, which can be highly focused, as in point-shear wave elastography (p-SWE), or directed to multiple zones in a two-dimensional area, as in 2D-SWE. A general understanding of the basic principles behind each technique is important for clinicians to improve data acquisition and interpretation. Major clinical applications include chronic liver disease, breast lesions, thyroid nodules, lymph node malignancies, and inflammatory bowel disease. The integration of artificial intelligence tools could potentially overcome some of the main limitations of elastosonography, such as operator dependence and low specificity, allowing for its effective integration into clinical workflow.
1. Introduction
Elasticity is a mechanical property of tissues that is vitally linked to their microstructure, function, and pathology [1]. In biological tissues, elasticity mainly depends on the composition of the extracellular matrix, which is affected by aging and the development of diseases [2]. Therefore, a pathological process that alters the structure and composition of tissue also affects its elasticity. Intuitively, this is why clinical palpation is still an essential tool for the detection of the disease during physical examination [3].
Elasticity cannot be measured directly using conventional imaging methods; however, several techniques have been developed to obtain an indirect quantitative estimate of this important parameter [1]. Ultrasound elastography (USE) is a promising non-invasive imaging technique that exploits the physical principles and properties of ultrasound to assess the elasticity (or, conversely, the stiffness) of different biological tissues for diagnostic purposes [4,5]. The physical principles at the base of ultrasound imaging can be found here [6].
In the first section of this article, we propose a step-by-step introduction to the basic principles of USE, beginning with the definition of elasticity and its main equations, with the help of some simplified models. Since this article targets clinicians and residents, we avoided differential notation in the equations. We are aware of several limitations to our description, from a formal standpoint. Still, we have tried to achieve a good balance between correctness and ensuring the accessibility of this content for people without advanced mathematical knowledge.
In the second part, we provide a concise overview of the main clinical applications, focusing on the liver, breast, thyroid, lymph nodes, and bowel. For each application, we report some evidence to illustrate how USE could successfully integrate B-mode ultrasound to enhance diagnostic performance [7,8].
USE has many of the advantages of standard ultrasound examination that have contributed to its popularity in recent decades: it is safe, inexpensive, widely available, and quick to perform. However, elastography also inherits important limitations, first of all, its low specificity and operator dependence, which have hindered its large-scale implementation in clinical practice [7,8].
In this landscape, therefore, for each application we finally present some recent evidence of how artificial intelligence, when applied to elastosonography measurements, could partially overcome these limitations, thereby improving its diagnostic performance and effective integration into the clinical practice.
2. Principles of Ultrasound Elastography
The physical principles of the USE are complex: for general, introductory articles, see [5,7]; for intermediate-level reviews, see [9,10]; in-depth accounts can also be found elsewhere [11,12].
2.1. Definition of Elasticity
Since elastosonography is essentially elasticity imaging, it is worth commencing with a definition of elasticity.
In material mechanics, the elasticity of a material is the property that describes its tendency to resume its original size and shape after being subjected to a deforming force, or stress [13,14]. A more detailed account of the elastic properties of tissues may be found in an earlier work [14]. Rubber is an example of a material with the property of being elastic at a high grade.
The opposite of elasticity is plasticity, which is the propensity of a solid to undergo largely irreversible changes in shape, in response to applied forces (for example, clay). In the real world, most materials present a mixture of elastic and plastic properties.
Conversely, stiffness is also defined as the opposite of elasticity and is the ability of a body to oppose the elastic deformation caused by an applied force [13]. Thus, elasticity and stiffness do not describe different properties, but instead convey the same underlying property of “being elastic” from opposite perspectives: a tissue that provides high elasticity has low stiffness (rubber), while a tissue that has high stiffness has low elasticity (steel).
2.2. Longitudinal Elasticity and Young’s Modulus (YM)
In elasticity imaging, researchers are interested in knowing a particular quantity, called Young’s modulus (YM), which expresses the tissue property of their topic of interest, namely, its elasticity. Elastosonography techniques are essentially differentiated on the basis of how they estimate this quantity [7,8].
If an elastic body is not free to move when it is subjected to an external force, it deforms and develops a force that opposes the deformation. Hooke’s law describes the behavior of an elastic spring subjected to a force, F, longitudinally, either in traction or compression (Figure 1) [13]. Hooke’s law states that an elastic body undergoes a deformation that is directly proportional to the force applied to it:
where is the force of retraction of the spring that is equal and opposite to the applied force, represents the elongation undergone by the spring along the -axis (we suppose that the deformation occurs only in one dimension), and represents the longitudinal elasticity coefficient, which depends upon the nature of the material itself and is dimensionally expressed as . This law is valid, of course, within certain limits, beyond which the body loses the capacity to return to its original shape (elastic behavior) and becomes permanently deformed (plastic behavior).
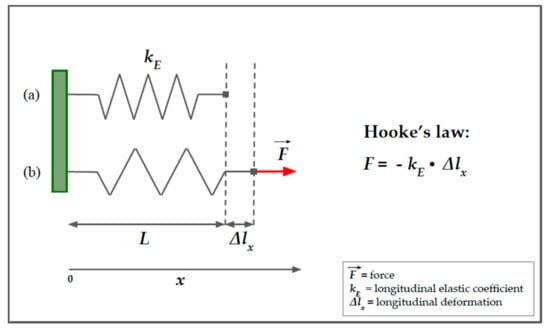
Figure 1.
Spring model of Hooke’s law. A simple helical spring model can be used to represent Hooke’s law. Hooke’s law states that the force (F) required to extend or compress a spring for a certain distance (Δlx) scales linearly to that distance. On the left, the upper part of the image (a) represents the spring in resting conditions, characterized by a longitudinal elasticity constant, kE, that is typical of the spring. The lower part of the image (b) represents the spring in traction due to a force, F, parallel to the x-axis. Δlx represents the longitudinal displacement of the free hand of the spring. The minus sign in the second member of the equation means that we are considering the restoring force exerted by the spring on whatever is pulling its free end since the direction of the restoring force is opposite to that of the displacement.
The formulation of Hooke’s law in Equation (1) is useful to describe the deformation of a spring that is stressed longitudinally, in traction or compression, along the -axis, but it does not fit well with more complex models.
Hereafter, we present a more general formulation of Hooke’s law (Equation (2)) that uses two vector quantities, the stress and the strain [8,13]:
where represents the stress applied, represents the strain, and is a constant, known as Young’s modulus (YM) [8,9,10,11,12,13,14], which simply represents the deformation resistance along the axis of stress. Similarly to the in Equation (1), YM relies on the intrinsic characteristics of the body.
Stress is defined as the ratio between the applied force, F, and the surface, A, on which the force is applied [9,14]:
Its unit of measure is the Pascal, dimensionally defined as .
The longitudinal strain is defined as the ratio between the change in length and the initial length [9,14]:
where is the final length and is the initial length (or ). The strain, unlike the displacement, , in Equation (1), is a dimensionless quantity.
Although Equations (1) and (2) look similar, they are not equivalent (see Figure 2).
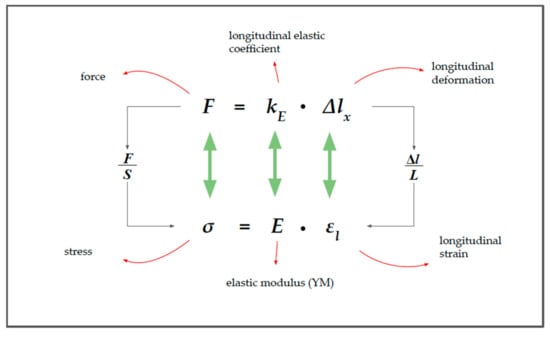
Figure 2.
The relationship between force (F) and stress (σ).
In Equation (2), Young’s modulus () appears in place of the longitudinal coefficient of elasticity (). YM expresses the relationship between the longitudinal stress and the longitudinal deformation (strain), in the case of uniaxial load conditions and in the case of the fully elastic behavior of the material:
As previously stated, YM describes the property of the tissue that is of most interest to us, that is, the way in which it reacts to external mechanical stress. Unlike the longitudinal elasticity coefficient, the accepted measurement unit of YM in the International System is the Pascal .
For a homogeneous isotropic solid, the relation between the stress and the strain can be considered to be linear for small changes (i.e., for strains of less than a few percent); thus, the ratio E is a constant [10]. With the stress increasing from zero, the strain increases rapidly and the elastic modulus becomes progressively greater with the increasing strain [10].
A further complication is that tissue may be viscoelastic, and this issue will be discussed in the next sections.
2.3. Shear Wave and Shear Modulus (G)
Ultrasounds propagate via compression and rarefaction waves, longitudinally, and via shear waves, in which the particles propagate orthogonally to the direction of the ultrasound beam [6,10,13] (Figure 3). The other principal wave modes are surface and plate waves; however, these are hardly relevant to ultrasound propagation in biological soft tissues and, therefore, are not given further consideration here [10].
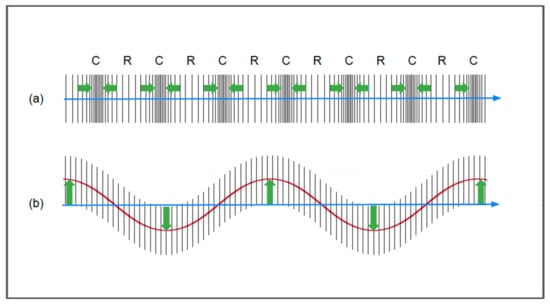
Figure 3.
Longitudinal waves (a) and shear waves (b). The green arrows and the red line in figure (b) show the movement of the molecules with respect to the axis of propagation.
Shear waves are at the basis of shear wave elastography (SWE) methods, in which the physical quantity of interest is the shear wave speed, measured in [m/s]. Young’s modulus of elasticity (E) may then be derived from the shear wave velocity, knowing the relationship between the shear modulus (G) and the elastic modulus (E), using the assumptions of the constant density, homogeneity, isotropy, and incompressibility of the material [7,8,9].
To understand the mechanisms underlying shear wave elastography, we consider a cylindrical model, which represents a portion of tissue. Until now, we have only considered the deformation that occurs along the force axis (longitudinal strain); however, in the absence of volume variations, a cylindrical object becomes thinner and wider when compressed (Figure 4).
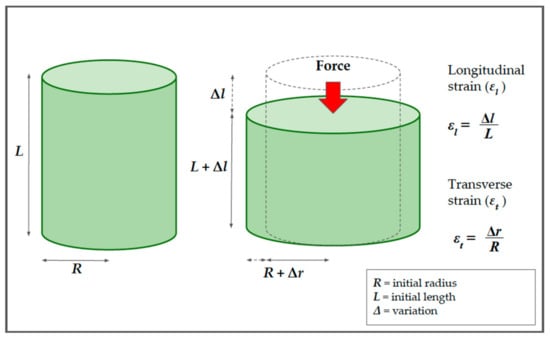
Figure 4.
The relationship between the longitudinal and the transverse strains in solids, using a cylindrical model. Before compression, the cylinder has a length (L) and radius (R). After the application of force (red arrow), the cylinder becomes thinner and wider. The longitudinal strain (εl) is defined as the ratio between the change in length (Δl) and the initial length (L). The transverse strain (εt) is defined as the ratio between the variation of the radius (Δr) and the initial radius (R).
For this cylinder, it is possible to calculate not only the longitudinal strain, , but also the transverse strain, . The percentage change in the radial direction, , is called the transverse strain and, analogously to the longitudinal strain in Equation (2), is defined as reported previously [5,7,10,14]:
where represents the change in width and represents the initial radius.
Since the two components act together, it is possible to calculate the ratio between the longitudinal and transverse deformations. This ratio is named Poisson’s ratio and is indicated by the Greek letter (“ni“) [5,7,10,14]:
The Poisson ratio is important as it represents the degree to which the material shrinks or expands transversely in the presence of longitudinal stress (see Figure 5) [5,7,9,10]. In the case of a virtually incompressible material, it has a value equal to 0.5 [5,7]. This is important because biological tissues react to compression more similarly to our cylinder than to the spring in Figure 1.
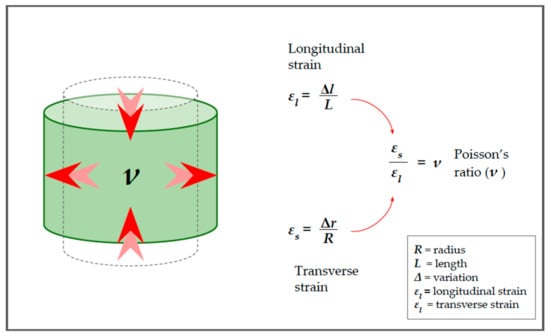
Figure 5.
Poisson’s ratio. The relationship between the longitudinal and transverse deformation is called Poisson’s ratio and depends on the characteristics of the medium. Red arrows in the cylinder highlight the strain direction.
In the cylinder example, we considered transverse strain as being the result of longitudinal compression, and that model is important to understand how the two types of deformations are related. However, it is possible to consider a simplified model in which the transverse strain is produced by a force that acts tangentially to the direction of displacement; in this case, we may speak more properly of shear stress (Figure 6). Similar to the calculations for YM, it is possible to describe a quantity, which we define as G, to indicate the shear modulus [5,7,9,10]. The equation is:
where is the tangential (or shear) stress, is the shear modulus, and represents the shear strain (i.e., the percentage of transverse displacement).
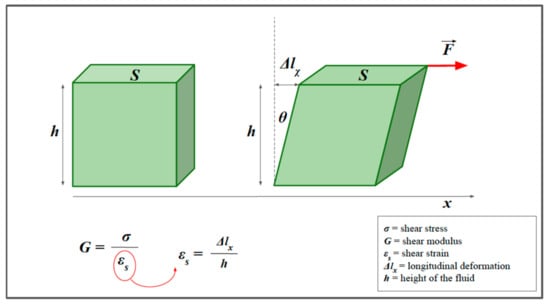
Figure 6.
Shear strain. The model helps to visualize the concept of shear stress. We consider a prism of elastic material and a shear force F (red arrow), applied parallel to the x-axis. Similarly to the calculations for Young’s modulus (E), it is possible to describe a quantity, which we define as G, to indicate the shear modulus. G is the constant of proportionality between the shear stress and the shear strain. The transverse strain can also be expressed as a function of the angle, θ.
The two elastic moduli, E and G, are interrelated. The shear modulus, G, can be derived through the longitudinal modulus, E, and the Poisson’s ratio:
which, by making E explicit, becomes:
Due to the high water content of biological tissues, the Poisson’s ratio is near 0.5, from which [5,7]:
Finally, since biological tissues are not exactly incompressible, we must introduce a third modulus of elasticity, called the bulk modulus (Figure 7), which is a measure of how the volume changes under pressure [5,7,10]:
where and represents the volume strain.
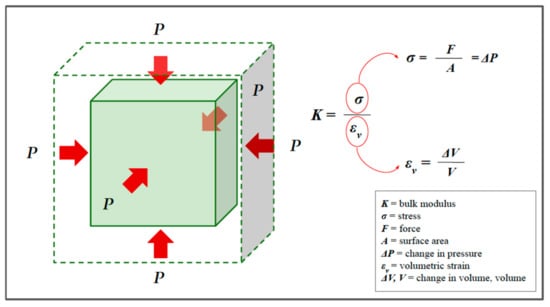
Figure 7.
The bulk modulus, or modulus of compressibility. Red arrows represent the pressure acting on the surface. In the bulk modulus equation the volumetric stress is usually expressed as a pressure P (force to surface area ratio) or, more precisely, the change in pressure.
These three elastic modules are important, not only because they define the deformation of a material subjected to a stress but also because they influence the speed of propagation of mechanical waves in the medium [5,7,9,13,14]. For soft materials, such as rubber or biological tissue, where the bulk modulus is much higher than the shear modulus, Poisson’s ratio is nearly 0.5 [5,7,14].
For a sound wave propagating through biological tissue, which have mechanical properties halfway between solids and liquids, the parameter K allows us (better than parameter E) to estimate the longitudinal propagation speed, , which is given by:
where represents the density of the medium [5,7]. For soft tissues, K must range from about 1800 MPa in fat to about 2800 MPa in muscle [10].
If we consider the speed of the waves propagating in the transverse direction (shear waves), the notation becomes:
where represents the density of the medium [5,7].
According to Equations (13) and (14), the greater the value of K or G (the stiffer the medium is), the faster the waves will propagate [5].
The shear wave velocity in soft tissues is significantly lower (1–10 m/s) than the longitudinal wave velocity and covers a wider range of values. However, in soft tissues, the longitudinal wave velocity is usually approximated to 1540 m/s, comparable to sound velocity in water (1500 m/s), with minimal changes between the different tissues (ranging from 1412 m/s in fat to 1629 m/s in muscle) [10].
This fact has important implications in terms of USE because the differences in the shear wave velocity between soft tissues can be used to obtain information on the elasticity between different tissues, with good contrast resolution [5,7].
2.4. Viscoelastic Models
Until now, we have considered biological tissues as soft solids that are characterized by perfectly elastic behavior, without considering the viscous components. However, since biological tissues are highly hydrated, internal friction forces cannot be neglected [10]. Ignoring the viscosity introduces errors and biases in the context of elasticity estimates [15]. Since biological tissues contain both elastic and viscous components, they are called viscoelastic media.
When shear stress is applied to a fluid, instead of deformation (as with the solid in Figure 6), it produces sliding of the various layers of fluid [13]. This sliding is hindered by internal frictional forces, a property known as viscosity. The dynamic viscosity of a fluid is a measure of its resistance to flow when tangential stress is applied, and this is due to the adjacent layers of fluid moving at different speeds. Shear elasticity in solids and viscosity in fluids are somehow interconnected, but there are differences. Viscosity is a property that manifests itself in a liquid and concerns the speed with which a stress is exerted.
Figure 8 illustrates the concept of viscosity and highlights the similarities with shear strain in a solid.
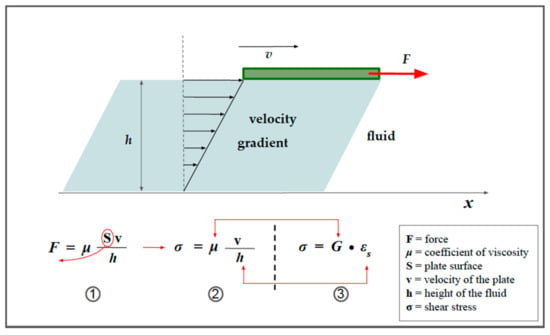
Figure 8.
The concept of viscosity. A green plate flows from left to right on the surface of a fluid (light blue), pulled with a force of intensity, F. If there were no friction present, the plate would move with a uniformly accelerated motion; however, in reality, its speed tends to be constant over time since the force F is balanced by a friction force due to the sliding of the various layers of liquid (under the conditions of laminar motion). The viscous friction force acting on the plate has an intensity that is given by relation 1 and it is directly proportional to the sliding speed (v). From relation 1, it is easy to derive relation 2, as highlighted by the red arrow. It is worth noting that, unlike the shear stress in solids (relation 3), the shear deformation is not expressed as a longitudinal strain, but instead as a gradient of velocity, that is, the change in velocity with respect to the depth of the liquid. Red arrows highlight the similarities.
Shear wave velocity is determined by both elasticity and viscosity [15].
The model presented in Figure 9 (the Kelvin–Voigt model) is used to describe the behavior of solid viscoelastic media. Where the velocity of the applied force is very slow, the effect of viscosity can be ignored. Conversely, if high-frequency vibration is applied, the viscous component will have a greater effect, the magnitude of which will depend on the frequency.
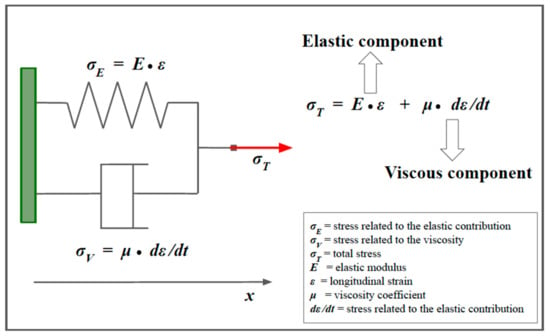
Figure 9.
The Kelvin–Voigt model for viscoelastic materials. The Kelvin–Voigt model is used to describe viscoelastic materials. This model is represented by a purely viscous damper (bottom), connected in parallel to a purely elastic spring (top). The constitutive equation associated with the model is represented on the right. For more explanations, see the main text.
When the Kelvin–Voigt model is used, the following equation is derived to establish the speed of a transverse wave, instead of Equation (14) [5,15,16]:
where G is the shear modulus, is the dynamic viscosity coefficient, and ω is the angular frequency of vibration [15].
Therefore, (1) SWV is determined by both elasticity and viscosity [15,16], and (2) SWV increases at the rate of the square root of the frequency; the higher the frequency, the faster the speed [5,15,16].
In biological tissue characterization applications, G is often in the order of a few thousand and μ is often less than 10. Thus, for a purely elastic material, or when the wave frequency is very low (less than a few Hz), the viscous component can be omitted; the SWV is constant over all frequencies and can be obtained via Equation (14) [15,16].
However, for viscoelastic media, especially when the frequency is very high (higher than a few tens of kHz), the shear wave speed increases monotonically with frequency [15,16,17]. Not only does the velocity increase with the frequency but also the velocity dispersion caused by the viscosity occurs during wave propagation, when the frequency is high in the soft tissues [5,15,16,17].
3. From Basic Physics to Imaging
3.1. From Elasticity to Strain Imaging
Since elasticity concerns the material’s resistance to deformation, the application of an external force is required to measure it: this, in very simple terms, is the underlying principle of strain imaging, which extracts information on tissue elasticity by exploiting the deformation induced by external stress [5,7]. Strain imaging was the first type of ultrasound-based elastography, developed in the 1970s by Dr. Jonathan Ophir [18].
It is divided into two different techniques, according to the modality of the compression [5].
In strain elastography (SE), compression is applied (usually to the skin surface) directly through manual compression or, indirectly, through the heart pulse or respiratory movements [5,7,10,19]. In freehand compression, the ultrasound probe takes on the dual functions of a transducer and a mechanical actuator [19]. The operator manages the transducer to produce a quasi-static load with a compressive stress of up to 3–5% [5]. Force is applied for a length of time that is sufficiently long for the induced tissue strains to effectively become stabilized (quasi-static) [10].
In Acoustic Radiation Force Impulse (ARFI) strain imaging, the tissue deformation is produced through a short-duration (0.1–0.5 ms) high-intensity (spatial peak pulse average = 1400 W/cm2, spatial peak temporal average = 0.7 W/cm2) acoustic “pushing pulse” that produces a small displacement (~10–20 μm) in the normal direction (i.e., perpendicular to the surface) [2,20,21,22]. In this technique, the same transducer is used to generate and analyze tissue displacement.
In theory, YM could be derived from Equation (2), knowing the stress and strain. However, since the stress that is applied manually or physiologically is not quantifiable, SE cannot provide quantitative elasticity measurements of YM, expressed in kPa [23]. However, assuming that the stress that is exerted is uniform, strain imaging provides qualitative information concerning tissue elasticity by comparing the different strains of the insonified adjacent tissue [7,23]. The differential displacement between the adjacent tissues can be evaluated via different techniques, depending on the manufacturer, including spatial-correlation methods, Doppler processing, or a combination of these two methods [5,7,9].
In the spatial correlation method, the strain is inferred from an analysis of the images before and after compression, and by mapping the differences in the speckle pattern within a region of interest (ROI) along the beam axis [5,7,9,24]. Even if it has currently been replaced by other mechanisms, this method is useful for understanding the underlying general principles [5,7,9,24].
In Figure 10A–D is presented a simplified model of its inner workings.
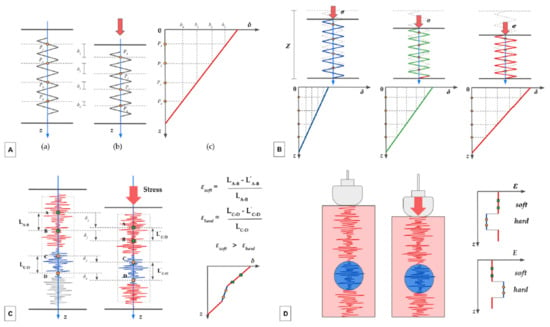
Figure 10.
(A–D). The autocorrelation method.
Assuming that the tissue has a purely elastic behavior and that the displacement occurs only in the longitudinal direction, this deformation can be approximated with a one-dimensional spring model (Figure 10A). Before the compression (a), 4 different points (named P1–P4), located at different depths (z), are identified on the spring. After the compression (b), each point is displaced downward (δ), with the more superficial showing a greater displacement than the deeper ones (δ1 > δ2, δ2 > δ3,…). Intuitively, the displacement is maximum for a point located at the free end of the spring (on the skin) and is virtually zero for a point located at the anchor end. The graph in Figure 10A(c) represents the relationship between the depth (z) and the displacement (δ). The slope of the line expresses the coefficient of elasticity, an intrinsic characteristic of the medium.
Figure 10B shows three spring models, representing biological tissues with different elasticity. Before compression occurs, they have the same initial length (Z), represented with the dotted gray silhouette superimposed. Assuming the stress exerted (red arrows) to be identical, the tissue on the left (blue spring) demonstrates the greatest stiffness, the tissue in the middle (green spring) has intermediate stiffness, and the one on the right (red spring) is the most elastic. In each spring, we depicted four representative points (yellow dots) which were virtually aligned before the compression. The three graphs in the second row represent the relationship between the initial depth of the points and the displacement obtained. Again, the slope of the corresponding graph (same color as the spring) expresses the coefficient of elasticity; it is higher for the blue spring and lower for the red spring.
In Figure 10C, in place of the spring, a speckle pattern is represented along the main axes. The ultrasound beam passes through tissues with different elasticity: points A and B are located in a more elastic part of the tissue (in red), while points C and D are located in a stiffer area (in blue). The system correlates the position of the speckles before and after the compression. For each part of the tissue, the strain (ε) is inferred by considering the differential displacement (displacement in relation to the depth). As is evident, points A and B are displaced proportionally more than points C and D. The strain of the soft tissue (εsoft) is higher than the strain of the hard tissue (εhard). The graph in the bottom right shows the relationship between depth and displacement for different areas of the tissue: this is the result of the combination of two graphs with different slopes, with a stiffer central part and two more elastic parts at the ends.
In Figure 10D, the stiffer area is represented by a nodular lesion (in blue). The two graphs on the right represent the relationship between the strain (ε) (upper graph) and the elastic modulus (E) (lower graph) and the depth (z). Note that there are no units of measurement in the graphs, as the estimate is qualitative (stress is not quantifiable).
The mechanism explained in Figure 10 works as long as the strain is extremely slight, and the window moves while maintaining its speckle pattern. We only consider the displacement in the direction of propagation of the ultrasound beam.
The autocorrelation-based method is the preferred estimator used without considering the lateral displacement [24]. However, each region of interest (ROI) also moves in the transverse direction due to the lateral deformation of the tissues; therefore, an adjustment is needed to estimate the displacement accurately in both the longitudinal and transverse directions.
In the Doppler-based method [5,7], the phase difference between the echo signals obtained by transmitting repeated pulses before and after compression is detected, and an autocorrelation method is used to calculate the displacement [5].
The methods described so far are not suitable for real-time processing because of the amount of computation time required. Concerning their practical application in the clinical setting, since the fluctuations in compression speed are large when manual compression is used, a high degree of accuracy is required to accommodate small displacements. More recently, some authors have developed a new tool, called the combined autocorrelation method (CAM), which combines the merits of the spatial correlation method and phase differences detection [5,24].
3.2. Visualizing SI information
In strain imaging, elasticity information can be displayed in many ways [8].
The main modality is a semi-transparent color map, called an elastogram, which is represented as if superimposed on a B-mode image. Typically, high stiffness is displayed in blue, and low stiffness is displayed in red, although the color scale may vary, depending on the manufacturer or personal preferences [8,23,25,26,27].
In strain imaging, the results may also be expressed through semi-quantitative parameters. The strain ratio is a parameter that is normally used to compare the stiffness of a discrete mass lesion with the adjacent tissue. In the strain ratio, two regions of interest (ROI) are drawn on the target region and an adjacent (usually normal) reference region that is experiencing similar stress. Then, the strain ratio is automatically calculated by the machine as the mean strain in the reference (B), divided by the mean strain in the “lesion” (A) [8,23]. Both ROIs should be placed at the same depth.
A strain ratio > 1 usually indicates that the target lesion compresses less than the normal reference tissue, thus indicating lower strain and greater stiffness (or lower elasticity) [8,23]. The usefulness of this index emerges, for example, for the evaluation of nodular lesions in which the probability of malignancy increases as the deformation ratio increases [24].
Many elasticity scores or grading systems have been proposed to qualitatively classify the elastography color patterns in a wide spectrum of disease processes, including breast imaging [27], thyroid nodules [28,29], and bowel inflammatory disease [30].
The fat-to-lesion strain ratio is the strain ratio between fat and a lesion [31].
Finally, the elastography-based maximum size of the lesion can be compared with the corresponding B-mode image and can be expressed as a ratio as well [32].
A good practical guide written by experts in the field on how to perform deformation elastography is available in a previous work [23].
3.3. From Shear Waves to Shear Wave Imaging
Shear wave imaging focuses on the shear waves created by mechanical excitation in solids, in which the particles move perpendicularly to the direction of propagation [1,9,15]. As previously mentioned, the propagation speed of the shear waves in soft tissue is several orders of magnitude slower than the speed of sound waves in soft tissue, and ranges from 1–10 m/s, compared to 1540 m/s. For this reason, measurement of the shear wave speed is suitable for producing a good contrast resolution for soft tissues. In shear wave imaging, Young’s modulus, E, is calculated from the shear wave speed. Starting from Equation (9) and by making G explicit, we obtain:
However, (Equation (11)), from which we derive:
where the measurement of allows the estimation of and . Density has units in kg/m3 and has units in m/s; therefore, is dimensionally defined as [kg/(m·s2)], which is equivalent to [N/m2] or [kPa], that is, the units of measurement of and . A recent consensus advocates reporting the results as shear wave velocity (SWV) in terms of m/s, as part of a standardized approach [5,33].
From a technical point of view, the calculation of the shear wave speed makes use of so-called time-of-flight (TOF) methods, which perform a linear regression of the wave time arrival with respect to different positions [5,33]. The TOF indicates the measurement of the time taken by an object, a particle, or a wave to travel a certain distance in a given medium; knowing the distance between the two points and the time taken to travel that distance, it is possible to derive the speed.
In shear wave elastography (SWE), the shear wave speed within a location of interest is derived by cross-correlating the time profiles of the shear wave-induced displacement at two neighboring points. Starting from the comparison of these profiles, a mathematical function yields the time taken for the shear wave to travel between the two points, then the shear wave speed is obtained by dividing the distance between the two points by the transit time [5,33]. TOF-based methods employ assumptions about tissue behavior to generate an estimate of the shear wave velocity, including local homogeneity and a known direction of propagation [5,33].
As with strain imaging, shear waves can be generated by different sources, including external vibration and the acoustic radiation force [5,7]. There are currently two technical approaches for SWE: one-dimensional transient elastography (1D-TE) [5,7,34,35] and acoustic radiation force impulse (ARFI) shear wave elastography [5,7,21,36,37,38]. The first commercially available ultrasonic shear wave measurement system was the FibroScanTM (Echosens, Paris, France), which uses the probe as a mechanical actuator [5,34]. The probe produces a controlled mechanical excitation through a piston that punches the surface of the body at a known frequency and amplitude; it is integrated with an ultrasonic transducer to monitor the impulse of the shear waves generated by the piston. This method was designed specifically to measure liver stiffness and does not provide a 2D guide for the operator; it is similar to A-mode imaging. Therefore, the sampling relies on the operator’s knowledge of the gross anatomy of the liver. The analysis of the echo pattern along the A-line allows adjustment of the acoustic window, avoiding the suboptimal ones due to the interference of vascular structures or other causes.
In ARFI-based SWE, an acoustic impulse is used to generate shear waves. Unlike ARFI strain imaging, the tissue displacement itself is not measured; instead, the velocity of the shear waves, which propagate perpendicularly to the direction of the ultrasound beam, is measured. YM can then be derived.
3.4. Visualizing SWE Information
In transient elastography (TE), the ultrasound transducer has a fixed focal configuration; the same probe is used to generate the vibrating stress and to measure the shear wave velocity along the main axes. The FibroScanTM device displays the elastogram, which represents the strains induced in the liver by shear wave propagation as a function of time and depth. An A-mode and M-mode are provided as well, for quality checks of the measurement. The equivalent stiffness in [kPa] is derived from the SWV and can also be visually assessed according to the slope of the elastogram [35].
The lack of a grayscale B-mode makes it difficult to understand where the measurement is performed [35,39]. Other limitations concern the need to recalibrate the spring in the device, at intervals of 6 to 12 months (depending on the type of probe), the reduced feasibility in cases of obesity, and the impossibility of employing the device in patients with ascites [7,39].
ARFI-based SWE is divided into point SWE (pSWE) and two-dimensional SWE (2D-SWE). In pSWE, an ARFI is used to induce tissue displacement in the normal direction in a single focal location (therefore, it is named “point” SWE) [5,36]. SWV may be reported either in [m/s] or converted in [kPa], to provide a quantitative estimation of tissue elasticity. Unlike TE, p-SWE may be performed on a conventional ultrasound device; B-mode image guidance is possible during the measurement since the same probe is used to both generate the shear waves and detect their propagation [5,7,33,36].
In pSWE (Figure 11), the tissue region interrogated by a single, highly focused ultrasound beam is narrow because the shear waves are rapidly attenuated by the internal frictional forces, as they propagate from the excitation region. To derive tissue stiffness over a larger ROI, data from multiple pushes must be combined; this is the basis of two-dimensional shear wave elastography (2D-SWE) [5,7].
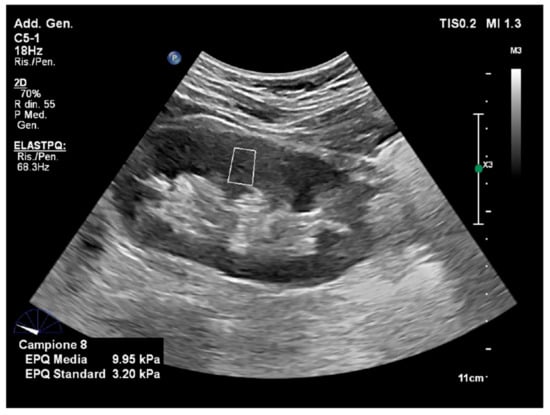
Figure 11.
Point shear wave elastography. The image is obtained with point shear-wave elastography (ElastQ, Philips), using a convex probe in a healthy volunteer. A small ROI (white square) is placed in the middle third of the renal parenchyma. The mean stiffness value was 9.95 kPa.
The technique of 2D-SWE is the latest technological innovation that uses acoustic radiation force to assess tissue elasticity (Figure 12). First, 2D-SWE alternates the multiple perturbations and reading phases, enabling an image of the shear wave speed for analyzing a larger tissue sample. Instead of a single focal location, multiple focal zones are interrogated in rapid succession, faster than the shear wave speed. The need to transmit multiple pulses in sequence to synthesize a single elastographic image results in an increase in the acquisition time. To achieve a larger ROI without increasing the acquisition time, some devices transmit multiple thrust beams at the same time, each constituting an independent source of shear waves [5,7,33]. As they propagate, the wavefronts generated by each thrust eventually meet and pass through each other. The combined wavefronts can assess a much larger region of tissue in a single transmission event. This creates a near-cylindrical shear wave cone, allowing the real-time monitoring of shear waves in the transverse direction for the measurement of shear wave speed and the generation of quantitative elastograms [5,10,33].
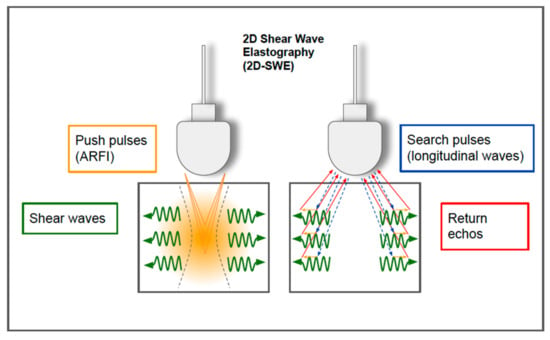
Figure 12.
Two-dimensional shear wave elastography. In 2D-SWE, instead of a single focal location, as in ARFI strain imaging and pSWE, the acoustic radiation force is used to interrogate multiple focal zones in rapid succession, faster than the shear wave speed. In step 1 (on the left), shear waves are generated using acoustic radiation force impulses; they propagate perpendicularly to the primary US wave at a lower velocity. In step 2 (on the right), since the speed of sound in tissue is approximately 1000 times faster than the shear wave speed, fast longitudinal wave excitation (blue and red arrows) can be used to track the displacement (orange small arrows) as the shear waves propagate through the tissue.
In 2D-SWE, a TOF algorithm is used to estimate the local shear wave speed at every location in the shear wave elastography ROI [33]. The speed within a location of interest is derived by correlating the displacement induced by the shear waves at two neighboring points. The cross-correlation function also provides the correlation coefficient, which is used to assess the quality of the measurement.
The quality of the measurement is important in clinical practice [40]. Some vendors provide a color-coded “confidence map” that helps the operator to visually assess the quality of the acquired signals in real time [40] (Figure 13). In this viewing modality, the operator can easily work with the split-screen modality. On one side, the confidence map displays an ROI that is identical to the one of the elastogram, which chromatically represents the quality of the measurements. On the other side, the elastogram provides a chromatic map of elasticity values according to the confidence map, but the filtering thresholds are filtered out and, thus, appear transparent, showing the areas below the threshold. The operator can easily compare the confidence map and the elastogram to select the most suitable tissue areas for the sampling, improving the quality of the examination (Figure 13).
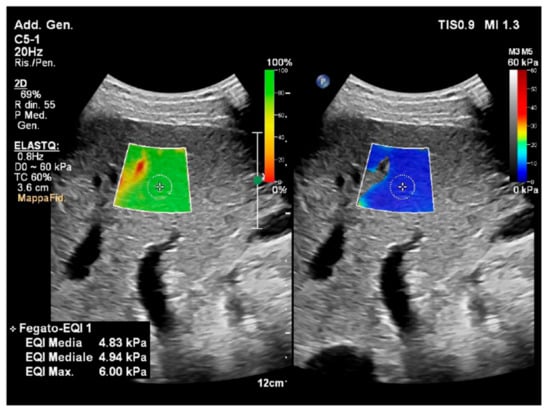
Figure 13.
Confidence map and elastogram in 2D-SWE. The image is obtained via two-dimensional shear-wave elastography (2D-SWE) (ElastQ, Philips), using a convex probe in a healthy volunteer. The confidence map is displayed on the left, setting a threshold of 60%. A standard deviation of 60% or less of the mean value is indicative of a good-quality acquisition. The areas of low quality (red) are filtered out by the system and display as transparent (note that the area in red corresponds to a vascular structure on the B-mode); the yellow color is a warning indicating that the area is not of good quality; the green indicates a good quality of the measurement. On the right, the elastogram depicts a colorimetric map of the stiffness, in which the blue color corresponds to greater elasticity while red represents greater stiffness. In the elastogram on the right, a circular sampling area was inserted to obtain a quantitative measure of the stiffness value in the selected location (mean kPa 4.83). The presence of the confidence map helps the operator to check the quality of the sampling in real time.
Compared to pSWE and TE, this technique includes the real-time visualization of a color elastogram, superimposed on a B-mode image, enabling the operator to be guided by both anatomical and tissue stiffness information [7,39,40]. The optimal depth for sampling is considered to be 4–5 cm from the skin; although most vendors allow measurements up to 8 cm from the transducer, it is proven that the accuracy decreases below 6 cm because of the attenuation of the ARFI pulse [7].
Figure 14 summarizes the different types of USE and some of the commercial devices that are currently available.
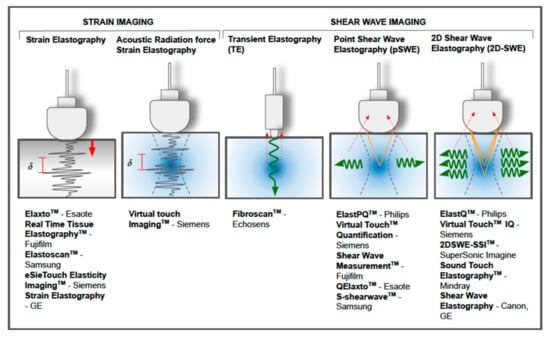
Figure 14.
Different techniques of ultrasound-based elastography and some of the commercial devices that are currently available.
4. Examples of Clinical Applications and Artificial Intelligence Integration
4.1. Liver
Ultrasound elastography has been applied in the staging of liver fibrosis more extensively, compared to other clinical settings. Chronic liver disease results in the development of collagen deposition and hepatic fibrosis, leading to increased parenchymal stiffness. Although biopsy is the gold standard for staging liver fibrosis, it is an invasive method that presents some limitations, including some variability between observers [39]. Many clinical guidelines recommend USE as a noninvasive imaging technique for the non-invasive detection and staging of liver fibrosis [39,40,41,42].
TE was the first modality to be applied systematically and was quickly established as the point-of-care technology for the non-invasive quantitative assessment of liver fibrosis, although it presents some limitations [41,42,43]. The feasibility and results of the p-SWE and 2D-SWE techniques have been extensively investigated and the recommended protocols are reported in the reference guidelines [41]. In addition, the SWE techniques showed excellent reproducibility, provided that the recommendations of the manufacturer and expert recommendations are followed [39].
For example, in patients with chronic viral hepatitis, SWE is the preferred method for first-line assessment for the severity of liver fibrosis in untreated patients and to rule out advanced disease; however, it cannot be used to stage liver fibrosis or rule out cirrhosis in patients with a sustained viral response, due to the loss of accuracy of the cutoffs defined in viremic patients [39].
Measurements are usually taken with the patient holding their breath for a few seconds on a medium apnea, while supine, or slightly rotated in the lateral decubitus, with the right arm raised above the head. Sampling is conducted in the right lobe of the liver. When using SWE techniques, ARFI should be applied perpendicular to the hepatic capsule, to a depth of 4–5 cm deep, ensuring that the ROI and the immediately adjacent areas are free of vascular and biliary structures, along with the rib shadows [5,39]. A detailed account of the main limiting factors can be found in the main reference guidelines [39,41].
With the availability of antiviral therapies, chronic viral hepatitis is slowly but progressively decreasing its burden of disease in favor of non-alcoholic fatty liver disease (NAFLD) as the leading cause of chronic hepatitis in the world and is an emerging issue in public health [44]. NAFLS includes a wide range of conditions, from simple steatosis to nonalcoholic steatohepatitis (NASH).
USE plays a promising role in the non-invasive assessment of these patients [39]. Among the different techniques, SWE showed superior performance in the assessment of liver fibrosis in NAFLD patients and can be used to rule out advanced fibrosis and select patients for further assessment [39,45]. Much effort is directed toward the potential application of USE in patient screening for the quantitative assessment of patients with simple steatosis, in order to perform risk stratification and ensure follow-up.
The controlled attenuation parameter (CAP), expressed in decibels per meter (dB/m), describes the decrease in the amplitude of the ultrasonic signal in the liver and correlates with the degree of hepatic steatosis [46,47]. Its accuracy is not influenced by fibrosis or cirrhosis [39,48]. It is available as an add-on tool in the latest version of the FibroScan 502 Touch System and is considered a standardized and reproducible point-of-care technique that is suitable for detecting fatty liver disease [39]. However, since there is a large overlap between the adjacent grades, there are no reference consensual cut-offs, and quality criteria have not yet been established [39]. Combinational elastography is a new imaging technique available on the Fujifilm Arietta 850 that combines strain and shear wave elastography for the quantification of liver fibrosis and steatosis, which could partially overcome some of the traditional limitations of the studies in this field [39,49].
Artificial intelligence could potentially assist quantitative ultrasound imaging data analysis and integration for the assessment of liver fibrosis and steatosis, aiming to develop individualized classifications and predictive models. However, to date, only a few studies have applied AI in this context [50].
A large recent prospective multicenter study was conducted to assess the accuracy of a deep learning (DL) model in patients with chronic hepatitis B, using 2D-SWE elastograms instead of the traditional 2D-SWE approach, aspartate transaminase-to-platelet ratio index, and fibrosis index, and using liver biopsy as the reference standard [51]. The DL-based model shows the best overall performance in predicting liver fibrosis stages, compared with 2D-SWE and biomarkers; its diagnostic accuracy improved as more images (especially ≥ 3 images) were acquired from each individual [51].
A recent study by Destrempes et al. aimed to develop a quantitative B-mode ultrasound and elastography-based model to improve the classification of steatosis and fibrosis in patients with chronic liver disease, in comparison with SWE alone, adopting histopathology as the reference standard. A random forest model for classification and a bootstrapping technique was used to identify those combinations of parameters that provided the highest diagnostic accuracy. The ML-based model incorporating quantitative US and SWE data shows better accuracy in the classification of liver steatosis and fibrosis when compared to SWE alone [52].
4.2. Breast
USE is a complementary tool for improving the detection and non-invasive characterization of breast lesions, which can help radiologists to enhance patient management [7]. In particular, adding SWE to B-mode US has been shown not only to provide additional diagnostic information but also to reduce the likelihood of unnecessary biopsies [53].
Several tools have been developed to frame benign and malignant breast masses using SE [7]. The most common parameters are the Tsukuba score (elasticity score) [54], the elastography-to-B-mode ratio (width or length ratio, LR) [32], and the strain ratio (SR, or fat–lesion ratio) [55]. The Tsukuba score (a five-point color scale) is based on a tissue stiffness map in and around the lesion, where lower scores (1–3) indicate a lesion that is likely to be benign, while higher scores (4–5) indicate a higher probability of malignancy that requires a biopsy. Several studies have evaluated the performance of deformation elastography, many of which used the Tsukuba score, and showed an aggregate sensitivity and specificity of 83% and 84%, respectively, ranging from approximately 80 to 90% [54].
In the LR, the lesion size measured on the elastogram is divided by the lesion size measured on the B-mode. Since the stromal response to breast cancer also increases the stiffness of the surrounding tissues, the transverse diameter of a malignant lesion appears larger on an elastogram than in the B-mode. One study showed excellent sensitivity and specificity (100% and 95%, respectively) in terms of this score when differentiating benign and malignant breast lesions [32].
The strain ratio of the nodular lesion to the strain in the subcutaneous fat is another important parameter when using strain imaging. Since fat has a constant modulus of elasticity over various compressions, the ratio is a semi-quantitative measure that reflects the relative stiffness of the injury [55].
A meta-analysis including 12 studies (2087 breast lesions) compared the performances of strain ratio (9 studies, 1875 patients) and the length ratio (3 studies, 450 breast lesions), showing that the sensitivity and specificity were good for both parameters (88% and 83%, respectively, for SR and 98% and 72%, respectively, for LR) [56].
A study by Ricci et al. compared the sensitivity and specificity of a B-mode ultrasound, color map, SR, and LR, and found that the combination of these three elastography parameters improved the overall diagnostic performance, compared to these parameters alone [57].
Concerning SWE, a recent meta-analysis of 25 studies including 5147 breast lesions showed pooled sensitivities of 0.94 and 0.97 (p = 0.087), pooled specificities of 0.85 and 0.61 (p = 0.009), and area under the receiver operating characteristic curve (AUC) values of 0.96 and 0.96 (p = 0.095) for the SWE and B-mode combined, compared to the traditional B-mode alone. When SWE was combined with the US B-mode, the B-Rads assignment changed from 4 to 3 in 71.3% of cases, reducing the frequency of unnecessary biopsies by 41.1% [58].
Artificial intelligence tools could further improve the real-time integration and performance of USE in B-mode US.
A recent study by Li et al. evaluated the performance of an AI system that integrates complementary information from the US mode and SWE mode and, thus, enhances the feature representations of each mode image. The diagnostic performance and concordance between expert and inexperienced radiologists in the classification of breast nodules in two operative settings were compared, with an independent diagnosis on the ultrasound; after an interval of 7 days, they performed a secondary diagnosis with the aid of AI (secondary diagnosis mode). A dataset containing 599 images of 91 patients was used, including 64 benign and 27 malignant breast tumors. AI assistance provides a more pronounced improvement in diagnostic performance for inexperienced radiologists; meanwhile, experienced radiologists benefited more from AI in terms of reducing interobserver variability [59].
Another study by Kim et al. investigated the added value of a DL-based CAD tool (S-Detect) on the SWE and B-mode US for the evaluation of 156 breast masses, detected at US screening in 146 women. S-Detect was applied to the most representative images selected on the B-mode US, followed by the application of S-Detect software. Color-coded SWE maps were created for the mass and the normal fat and the lesion-to-fat elasticity ratio was calculated. The BI-RADS score was applied for the final assessment category by three radiologists for the B-mode US alone, B-mode US plus S-Detect, and B-mode US plus SWE. Compared to the B-mode US alone, either the addition of S-Detect or SWE increased the specificity without a significant loss in sensitivity when using either S-Detect or SWE. In two assessments, the AUC of the B-mode plus SWE was higher than in the B-mode plus S-Detect [60].
4.3. Thyroid
Thyroid nodules are a common finding in US B-mode samples and affect up to 68% of the adult population. With the widespread use of imaging in clinical practice, incidental thyroid nodules are being discovered with increasing frequency [61,62]. TI-RADS classification, based on B-mode ultrasound features, is adopted to select nodules for sampling by fine needle aspiration biopsy (FNAB), which is generally used for the confirmation of malignancy. Although FNAB is considered the gold standard for diagnosis, up to 15–30% of samples are considered nondiagnostic or indeterminate due to technical factors, such as insufficient sampling or histological dilemmas between similar histotypes [63]. In addition, the TI-RADS system is characterized by low diagnostic specificity, resulting in the execution of an excess number of invasive examinations [64].
Thyroid elastosonography provides complementary information to B-mode US and FNAB for the evaluation of thyroid nodules. Analogously to the breast scan study, semi-quantitative parameters, such as the thyroid stiffness index (strain in the background normal thyroid/strain in the thyroid nodule) [65], and qualitative parameters, such as the Rago and Asteria criteria, were developed to stratify the risk of malignancy of thyroid nodules, based on the SE results [28,29]. Their application has shown controversial results [7,66].
It has been hypothesized that the diagnostic performance of the combination of US grayscale and SE measurements is greater than that of the individual modalities for malignancy assessment. This hypothesis was supported by a study conducted by Trimboli et al., in which the combination of the two modalities produced a sensitivity of 97% and a negative predictive value of 97%, which are higher than when using the two modalities individually [67].
In contrast, in the study by Moon et al., neither elastography nor the combination of elastography and grayscale US showed better performance for the diagnosis of thyroid tumors than grayscale US [68]. It has been observed that this heterogeneity of results could be due to the different exclusion criteria and the variability in the percentage of malignant nodules [7]. More recently, a multicenter study by Hairu et al., conducted on a total of 1445 thyroid nodules (834 malignant and 611 benign), evaluated the performance of SE in the diagnosis of highly suspect thyroid nodules, based on the 2015 ATA guidelines in the Chinese population, and demonstrated that the combination of the TI-RADS classification and SE led to a significant increase in the sensitivity and NPV (97.1 and 91.9%, respectively), compared with the TI-RADS, in particular in nodules of ≥1 cm [69].
Several studies have suggested that SWE is a promising tool for differentiating malignant and benign thyroid nodules, and some early meta-analyses appeared to support this view of a high-precision diagnostic tool. For example, in the meta-analysis by Zhan et al. (16 studies and 2436 nodules), the overall mean sensitivity and specificity of ARFI for the differentiation of thyroid nodules were 0.80 and 0.85, respectively [70]. In a review by Lin et al. (15 studies and 1867 nodules), the pooled sensitivity, specificity, and area under the summary ROC curve of SWE for detecting malignant thyroid nodules were 84.3%, 88.4%, and 93%, respectively [71]. When adopted as a screening tool, the PPV and NPV were 27.7–44.7% and 98.1–99.1%, respectively, calculated with a malignancy prevalence of 5–10% in the thyroid nodules [71].
However, the comforting results at the population level are less convincing at the individual level, due to the reproducibility problems of the method and the enormous overlap of the elasticity indices, which means that the proposed cut-off levels do not have optimal diagnostic accuracy [7,72,73,74].
A meta-analysis by Hu et al. in 2017 compared the results of RTE and SWE, and concluded that the overall sensitivities of RTE and SWE are approximately comparable in terms of the differentiation between malignant and benign thyroid nodules, while the difference in specificity between these 2 methods was statistically significant; the specificity of RTE was statistically superior to that of SWE.
Several authors have suggested using SWE as an adjunct to the US B-mode to select patients for FNAB or surgery, rather than for use as a separate diagnostic tool. The diagnostic accuracy of SWE as an adjuvant test has been addressed in several studies, but the results have been mixed, and some studies have shown an increase in sensitivity at the expense of specificity [75,76]. However, the most recent evidence seems to suggest that multimodal integration is the way forward. A recent study by Petersen et al. compared the diagnostic performance of the TIRADS system (Kwak-TIRADS, EU-TIRADS), in combination with SWE imaging, for the assessment of 61 thyroid nodules detected in 43 patients (10 malignant and 51 benign). The addition of SWE resulted in an increased accuracy from 65.6% to 82.0% when using Kwak-TIRADS and from 49.2% to 72.1% when using EU-TIRADS, suggesting that the combination of TIRADS and SWE seems to be superior for the risk stratification of thyroid nodules, compared to each method when used in isolation [77].
A 2020 meta-analysis by Filho et al. compared the performance of the SWE of different manufacturers as an independent predictor of malignancy in the diagnostic differentiation of thyroid nodules (TN), obtaining ROC curves between 0.84 and 0.88 [78].
A recent review concludes that the present SWE technology seems not to be robust enough for clinical implementation on a wider scale [74]. However, AI can effectively integrate information in grayscale and elastosonography to improve the classification of thyroid nodules, overcoming some of the natural limitations of the method. For example, in a study of 2050 thyroid nodules, it was shown that a random forest model performed better than a radiologist in the differential diagnosis of thyroid nodules (malignant vs. benign), based on conventional US only (AUC = 0.924 (confidence interval (CI) 0.895–0.953) vs. 0.834 [CI 0.815–0.853]) and based on both conventional US and real-time elastography (AUC = 0.938 [CI 0.914–0.961] vs. 0.843) [79].
A study by Qin et al. proposed a new model based on a convolutional neural network that combines the characteristics of conventional ultrasound and ultrasound elasticity images to form a hybrid functionality space. Experimental results show that the accuracy of the proposed method is 0.947, which is better than that of other single data-source methods under the same conditions [80].
A recent retrospective study by Zhao et al. evaluated the performance of an ML model using a US and SWE image dataset of 743 nodules in 720 patients with biopsy-confirmed thyroid nodules (≥1 cm) and an independent test dataset. The radiomic features extracted from the USA and SWE images were used for the development of ML-assisted radiomics approaches and were then compared with the results obtained via the TI-RADS classification. The ML-assisted visual ultrasound approach performed better than the US approach alone. Furthermore , ML-assisted US + SWE visual approach also resulted in a reduction in the unnecessary FNAB rate, which decreased from 30.0% to 4.5% in the validation dataset and from 37.7% to 4.7% in the test dataset, compared to TI-RADS [81].
The integration of grayscale and elastosonographic modalities could improve the accuracy of the estimation of LN metastases for patients with papillary thyroid cancer. A study by Liu et al. trained and validated an AI model of the support vector machine type, using three feature sets extracted from B-US, SE-US, and a multi-modality containing B-US and SE-US. The results obtained with the multimode set produced a better area under the ROC curve than when using those functions extracted from B-US or SE-US separately [82].
4.4. Lymph Nodes
Both SE and SWE have been successfully applied to improve the diagnostic characterization of lymph nodes and have demonstrated that USE and conventional US can play complementary roles in the differentiation of malignant and benign LNs [7,83]. In addition to the traditional method, endoscopic US (EUS) and endobronchial US (EBUS) have also gained considerable popularity in recent years [84].
In normal LNs, the cortex is usually stiffer than the hilum, and this architecture is generally also preserved in inflammatory LNs. Conversely, malignant carcinoma cells proliferate rapidly and infiltrate the lymph node, distorting the normal architecture and increasing its stiffness [85]. However, focal infiltration may be challenging to detect, and lymphoma may produce soft lymph nodes that can predominantly have similar elasticity to the surrounding tissue, thus representing a specific challenge for this application [7].
Several studies have been published, evaluating the performance of elastosonography in differentiating between benign and malignant LNs, showing sensitivity values ranging from 64.5% to 100% and a specificity ranging from 41.7 to 91.3%, with an overall accuracy ranging from 60% to 96.7% [82].
Again, artificial intelligence (AI) can improve lymph node classification, compared to the radiologists’ evaluation alone.
A study by Tahmasebi et al. assessed the accuracy of image classification software (Google Cloud AutoML Vision, Mountain View, CA) compared to three expert radiologists, regarding a dataset containing ultrasound images of 317 axillary lymph nodes, using the histopathology as a reference standard. They showed that AI has comparable performance to expert radiologists and could be used to predict the presence of metastases in ultrasound images of the axillary lymph nodes [85].
Huang et al. have compared different machine learning models, including ultrasound elastography data, in the prediction of LN metastasis risk for patients with papillary thyroid microcarcinoma. The random forest classifiers show that the better performance had the strongest prediction efficiency, with an AUC of 0.889 (95% CI: 0.838–0.940) and 0.878 (95% CI: 0.821–0.935) in the training set and testing set, respectively [86].
4.5. Bowel
The incidence of inflammatory bowel disease (IBD) is growing worldwide [87]. The main types are ulcerative colitis (UC), which affects only the colon and rectum, and Crohn’s disease (MC), which could potentially affect every part of the digestive tract. IBD has a complex pathogenesis and a wide variety of clinical presentations, with clinical symptoms that often poorly correlate with bowel disease activity [88]. Therefore, both the initial diagnosis and further monitoring may be challenging for the clinicians, requiring the integration of clinical data, laboratory indices, and endoscopic and imaging data, together with a histopathological assessment. However, the assessment of disease activity and intestinal complications is crucial for therapeutic decisions. Several potential noninvasive biomarkers have been proposed for IBD activity assessment, including genetic, serological, fecal, microbial, histological, and immunological biomarkers [89]. In this context, ultrasound elastography could play an important role as a new non-invasive tool to improve patient monitoring [90,91,92].
Several studies have been performed to evaluate the feasibility and diagnostic contribution of elastography data in the assessment of IBD, which are summarized in two recent literature reviews, one by Ślósarz et al., including 12 records, and another by Grazynska, including 15 studies [90,91].
In Crohn’s disease in particular, chronic inflammation leads to the remodeling of the extracellular matrix and fibrosis, which, as is known, is one of the main determinants of tissue stiffness [93,94]. For this reason, much research has focused on the role of elastography in differentiating between inflammations and fibrosis [90]. The development of fibrosis is, in fact, associated with the onset of stenosis, a dreaded complication that can lead to surgery.
Some authors focused on distinguishing fibrotic bowel segments from inflamed ones, based on a qualitative assessment of color patterns in SE, using MRI as a reference standard. Sconfienza et al., for example, proposed a new classification score in which each patient could receive from 8 to 24 points: the terminal ileum was divided into 8 sectors and subsequently graded according to the prevalent color: red = 1 (minimal fibrosis), green = 2 (intermediate fibrosis), and blue = 3 (maximal fibrosis) [30]. Another study by Lo Re et al. evaluated a total of 41 affected bowel segments and 35 unaffected bowel segments in 35 patients, using a SE color-scale and enterography magnetic resonance imaging (E-MRI), showing a significant correlation between the findings of the two methods in distinguishing fibrotic and edematous matter. In particular, the color coding showed a blue color pattern in the fibrotic mesentery and bowel wall and a green color pattern in the edematous tissue [95].
Fraquelli et al. evaluated the role of the semiquantitative parameter strain ratio when discriminating patients with stenosis as candidates for surgery from patients with active non-narrowing/non-penetrating disease. Using histopathological data as a reference standard, they found a significant correlation between strain ratio and fibrosis severity, suggesting that SE shows excellent discriminatory ability in diagnosing severe intestinal fibrosis [96]. However, further studies are needed to consolidate these data, since other authors have not found a significant correlation between the strain ratio and the histopathologic scores of inflammation, fibrosis, or the clinical or biochemical biomarkers [97].
Even if the application of artificial intelligence in the field of inflammatory bowel disease has grown significantly in the past decade [98], demonstrating its great potential in extracting valuable information from multiple data-streams, to the best of our knowledge, there are still as yet no significant studies applying AI to elastosonography data in IBD. Therefore, this could present an interesting field of application for AI to overcome some traditional limitations and finally perfect the full integration of the method in patient management.
5. Conclusions
Elastosonography is a powerful non-invasive method for the assessment of tissue stiffness, which includes a set of different techniques depending on the principles used for elasticity estimation. In this review, we provided a brief introduction to the basic physical principles that underpin ultrasound elastography imaging. Although USE is a promising method, both investigator-dependent and independent factors may affect elasticity measurement. A general understanding of the underlying principles could benefit the entire process of data acquisition and interpretation, enhancing the USE reproducibility. Furthermore, the application of AI can be a precious ally, allowing us to extract more information from elasticity data to improve the diagnostic process and the integration of USE into the clinical workflow.
Author Contributions
Resources, G.M.D. and C.F.; data curation, M.C. (Maurizio Cè), M.C. (Michaela Cellina); writing—original draft preparation, M.C. (Maurizio Cè) and M.C. (Michaela Cellina), C.M.; writing—review and editing, N.C.D., M.C. (Maurizio Cè) and M.C. (Michaela Cellina); supervision, G.O.; project administration, C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parker, K.J.; Taylor, L.S.; Gracewski, S.; Rubens, D.J. A unified view of imaging the elastic properties of tissue. J. Acoust. Soc. Am. 2005, 117, 2705–2712. [Google Scholar] [CrossRef] [PubMed]
- Akhtar, R.; Sherratt, M.J.; Cruickshank, J.K.; Derby, B. Characterizing the elastic properties of tissues. Mater. Today 2011, 14, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Sun, C.; Zhou, Q.; Cheng, C.; Yan, C.; Wang, B. Use of Palpation Imaging in Diagnosis of Breast Diseases: A Way to Improve the Detection Rate. Med. Sci. Monit. 2020, 26, e927553-1–e927553-10. [Google Scholar] [CrossRef] [PubMed]
- Bamber, J.C. Ultrasound elasticity imaging: Definition and technology. Eur. Radiol. 1999, 9 (Suppl. 3), S327–S330. [Google Scholar] [CrossRef] [PubMed]
- Shiina, T.; Nightingale, K.R.; Palmeri, M.L.; Hall, T.J.; Bamber, J.C.; Barr, R.G.; Castera, L.; Choi, B.I.; Chou, Y.-H.; Cosgrove, D.; et al. WFUMB Guidelines and Recommendations for Clinical Use of Ultrasound Elastography: Part 1: Basic Principles and Terminology. Ultrasound Med. Biol. 2015, 41, 1126–1147. [Google Scholar] [CrossRef]
- Hill, C.R.; Bamber, J.C.; ter Haar, G.R. (Eds.) Physical Principles of Medical Ultrasonics; John Wiley: Chichester, UK, 2004. [Google Scholar]
- Sigrist, R.M.S.; Liau, J.; Kaffas, A.E.; Chammas, M.C.; Willmann, J.K. Ultrasound Elastography: Review of Techniques and Clinical Applications. Theranostics 2017, 7, 1303–1329. [Google Scholar] [CrossRef]
- Ozturk, A.; Grajo, J.R.; Dhyani, M.; Anthony, B.W.; Samir, A.E. Principles of ultrasound elastography. Abdom. Radiol. 2018, 43, 773–785. [Google Scholar] [CrossRef]
- Kwon, S.J.; Jeong, M.K. Advances in ultrasound elasticity imaging. Biomed. Eng. Lett. 2017, 7, 71–79. [Google Scholar] [CrossRef]
- Wells, P.N.T.; Liang, H.-D. Medical ultrasound: Imaging of soft tissue strain and elasticity. J. R. Soc. Interface 2011, 8, 1521–1549. [Google Scholar] [CrossRef]
- Li, G.-Y.; Cao, Y. Mechanics of ultrasound elastography. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160841. [Google Scholar] [CrossRef]
- Greenleaf, J.F.; Fatemi, M.; Insana, M. Selected Methods for Imaging Elastic Properties of Biological Tissues. Annu. Rev. Biomed. Eng. 2003, 5, 57–78. [Google Scholar] [CrossRef]
- Halliday, D.; Resnik, R.; Krane, K.S. Physics, 5th ed.; John Wiley: Hoboken, NJ, USA, 2001; Volume 1. [Google Scholar]
- Callister, W.D. Materials Science and Engineering: An Introduction, 2nd ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Zheng, Y.; Zheng, Y.; Chen, X.; Yao, A.; Lin, H.; Shen, Y.; Zhu, Y.; Lu, M.; Wang, T.; Chen, S. (Eds.) Shear Wave Propagation in Soft Tissue and Ultrasound Vibrometry. In Wave Propagation Theories and Applications; IntechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Deffieux, T.; Montaldo, G.; Tanter, M.; Fink, M. Shear Wave Spectroscopy for In Vivo Quantification of Human Soft Tissues Visco-Elasticity. IEEE Trans. Med. Imaging 2009, 28, 313–322. [Google Scholar] [CrossRef]
- Chen, S.; Fatemi, M.; Greenleaf, J.F. Quantifying elasticity and viscosity from measurement of shear wave speed dispersion. J. Acoust. Soc. Am. 2004, 115, 2781–2785. [Google Scholar] [CrossRef]
- Ophir, J.; Céspedes, I.; Ponnekanti, H.; Yazdi, Y.; Li, X. Elastography: A Quantitative Method for Imaging the Elasticity of Biological Tissues. Ultrason. Imaging 1991, 13, 111–134. [Google Scholar] [CrossRef]
- Hall, T.J.; Zhu, Y.; Spalding, C.S. In vivo real-time freehand palpation imaging. Ultrasound Med. Biol. 2003, 29, 427–435. [Google Scholar] [CrossRef]
- Nightingale, K.R.; Palmeri, M.L.; Nightingale, R.W.; Trahey, G.E. On the feasibility of remote palpation using acoustic radiation force. J. Acoust. Soc. Am. 2001, 110, 625–634. [Google Scholar] [CrossRef]
- Nightingale, K.; Soo, M.S.; Nightingale, R.; Trahey, G. Acoustic radiation force impulse imaging: In vivo demonstration of clinical feasibility. Ultrasound Med. Biol. 2002, 28, 227–235. [Google Scholar] [CrossRef]
- Doherty, J.R.; Trahey, G.E.; Nightingale, K.R.; Palmeri, M.L. Acoustic radiation force elasticity imaging in diagnostic ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 685–701. [Google Scholar] [CrossRef]
- Dietrich, C.F.; Barr, R.G.; Farrokh, A.; Dighe, M.; Hocke, M.; Jenssen, C.; Dong, Y.; Saftoiu, A.; Havre, R.F. Strain Elastography—How To Do It? Ultrasound Int. Open 2017, 3, E137–E149. [Google Scholar] [CrossRef]
- Shiina, T.; Nitta, N.; Ueno, E.; Bamber, J.C. Real time tissue elasticity imaging using the combined autocorrelation method. J. Med. Ultrason. 2002, 29, 119–128. [Google Scholar] [CrossRef]
- Garra, B.S.; Cespedes, E.I.; Ophir, J.; Spratt, S.R.; Zuurbier, R.A.; Magnant, C.M.; Pennanen, M.F. Elastography of breast lesions: Initial clinical results. Radiology 1997, 202, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Gennisson, J.-L.; Deffieux, T.; Fink, M.; Tanter, M. Ultrasound elastography: Principles and techniques. Diagn. Interv. Imaging 2013, 94, 487–495. [Google Scholar] [CrossRef] [PubMed]
- Dobruch-Sobczak, K. The differentiation of the character of solid lesions in the breast in the compression sonoelastography. Part II: Diagnostic value of BIRADS-US classification, Tsukuba score and FLR ratio. J. Ultrason. 2013, 13, 31–49. [Google Scholar] [CrossRef] [PubMed]
- Asteria, C.; Giovanardi, A.; Pizzocaro, A.; Cozzaglio, L.; Morabito, A.; Somalvico, F.; Zoppo, A. US-Elastography in the Differential Diagnosis of Benign and Malignant Thyroid Nodules. Thyroid 2008, 18, 523–531. [Google Scholar] [CrossRef]
- Rago, T.; Santini, F.; Scutari, M.; Pinchera, A.; Vitti, P. Elastography: New Developments in Ultrasound for Predicting Malignancy in Thyroid Nodules. J. Clin. Endocrinol. Metab. 2007, 92, 2917–2922. [Google Scholar] [CrossRef]
- Sconfienza, L.M.; Cavallaro, F.; Colombi, V.; Pastorelli, L.; Tontini, G.; Pescatori, L.; Esseridou, A.; Savarino, E.; Messina, C.; Casale, R.; et al. In-vivo Axial-strain Sonoelastography Helps Distinguish Acutely-inflamed from Fibrotic Terminal Ileum Strictures in Patients with Crohn’s Disease: Preliminary Results. Ultrasound Med. Biol. 2016, 42, 855–863. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, C.; Zhan, W.; Jia, X.; Dong, Y.; Yang, Z. Elastography ultrasound for breast lesions: Fat-to-lesion strain ratio vs gland-to-lesion strain ratio. Eur. Radiol. 2014, 24, 3171–3177. [Google Scholar] [CrossRef]
- Barr, R.G. Real-time ultrasound elasticity of the breast: Initial clinical results. Ultrasound Q. 2010, 26, 61–66. [Google Scholar] [CrossRef]
- GE Engineering. 2D Shear Wave Elastography LOGIQ E9/E10/E10s. Uploaded on March 2020. Available online: https://ge-ultrasound.eu/wp-content/uploads/2021/02/1.-LOGIQ-E9-LOGIQ-E10-LOGIQ-E10s_Shear-Wave-Whitepaper_2020_JB29031XX.pdf (accessed on 15 December 2022).
- Sandrin, L.; Fourquet, B.; Hasquenoph, J.-M.; Yon, S.; Fournier, C.; Mal, F.; Christidis, C.; Ziol, M.; Poulet, B.; Kazemi, F.; et al. Transient elastography: A new noninvasive method for assessment of hepatic fibrosis. Ultrasound Med. Biol. 2003, 29, 1705–1713. [Google Scholar] [CrossRef]
- Jung, K.S.; Kim, S.U. Clinical applications of transient elastography. Clin. Mol. Hepatol. 2012, 18, 163–173. [Google Scholar] [CrossRef]
- Sarvazyan, A.P.; Rudenko, O.V.; Swanson, S.D.; Fowlkes, J.; Emelianov, S.Y. Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics. Ultrasound Med. Biol. 1998, 24, 1419–1435. [Google Scholar] [CrossRef]
- Taljanovic, M.S.; Gimber, L.H.; Becker, G.W.; Latt, L.D.; Klauser, A.S.; Melville, D.M.; Gao, L.; Witte, R.S. Shear-Wave Elastography: Basic Physics and Musculoskeletal Applications. Radiographics 2017, 37, 855–870. [Google Scholar] [CrossRef]
- Nightingale, K.; McAleavey, S.; Trahey, G. Shear-wave generation using acoustic radiation force: In vivo and ex vivo results. Ultrasound Med. Biol. 2003, 29, 1715–1723. [Google Scholar] [CrossRef]
- Ferraioli, G.; Wong, V.W.-S.; Castera, L.; Berzigotti, A.; Sporea, I.; Dietrich, C.F.; Choi, B.I.; Wilson, S.R.; Kudo, M.; Barr, R.G. Liver Ultrasound Elastography: An Update to the World Federation for Ultrasound in Medicine and Biology Guidelines and Recommendations. Ultrasound Med. Biol. 2018, 44, 2419–2440. [Google Scholar] [CrossRef]
- Barr, R.G.; Wilson, S.R.; Rubens, D.; Garcia-Tsao, G.; Ferraioli, G. Update to the Society of Radiologists in Ultrasound Liver Elastography Consensus Statement. Radiology 2020, 296, 263–274. [Google Scholar] [CrossRef]
- Ferraioli, G.; Filice, C.; Castera, L.; Choi, B.I.; Sporea, I.; Wilson, S.R.; Cosgrove, D.; Dietrich, C.F.; Amy, D.; Bamber, J.C.; et al. WFUMB Guidelines and Recommendations for Clinical Use of Ultrasound Elastography: Part 3: Liver. Ultrasound Med. Biol. 2015, 41, 1161–1179. [Google Scholar] [CrossRef]
- Friedrich-Rust, M.; Nierhoff, J.; Lupsor-Platon, M.; Sporea, I.; Fierbinteanu-Braticevici, C.; Strobel, D.; Takahashi, H.; Yoneda, M.; Suda, T.; Zeuzem, S.; et al. Performance of Acoustic Radiation Force Impulse imaging for the staging of liver fibrosis: A pooled meta-analysis. J. Viral Hepat. 2011, 19, e212–e219. [Google Scholar] [CrossRef]
- Fraquelli, M.; Rigamonti, C.; Casazza, G.; Conte, D.; Donato, M.F.; Ronchi, G.; Colombo, M. Reproducibility of transient elastography in the evaluation of liver fibrosis in patients with chronic liver disease. Gut 2007, 56, 968–973. [Google Scholar] [CrossRef]
- Muthiah, M.D.; Sanyal, A.J. Burden of Disease due to Nonalcoholic Fatty Liver Disease. Gastroenterol. Clin. N. Am. 2020, 49, 1–23. [Google Scholar] [CrossRef]
- Xiao, G.; Zhu, S.; Xiao, X.; Yan, L.; Yang, J.; Wu, G. Comparison of laboratory tests, ultrasound, or magnetic resonance elastography to detect fibrosis in patients with nonalcoholic fatty liver disease: A metaanalysis. Hepatology 2017, 66, 1486–1501. [Google Scholar] [CrossRef]
- Sasso, M.; Beaugrand, M.; de Ledinghen, V.; Douvin, C.; Marcellin, P.; Poupon, R.; Sandrin, L.; Miette, V. Controlled Attenuation Parameter (CAP): A Novel VCTE™ Guided Ultrasonic Attenuation Measurement for the Evaluation of Hepatic Steatosis: Preliminary Study and Validation in a Cohort of Patients with Chronic Liver Disease from Various Causes. Ultrasound Med. Biol. 2010, 36, 1825–1835. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.-T.; Xiang, L.-L.; Qi, F.; Zhang, Y.-J.; Chen, Y.; Zhou, X.-Q. Accuracy of controlled attenuation parameter (CAP) and liver stiffness measurement (LSM) for assessing steatosis and fibrosis in non-alcoholic fatty liver disease: A systematic review and meta-analysis. Eclinicalmedicine 2022, 51, 101547. [Google Scholar] [CrossRef] [PubMed]
- De Ledinghen, V.; Hiriart, J.B.; Vergniol, J.; Merrouche, W.; Bedossa, P.; Paradis, V. Controlled attenuation parameter (CAP) with the XL probe of the Fibroscan: A comparative study with the M probe and liver biopsy. Dig. Dis. Sci. 2017, 62, 2569–2577. [Google Scholar] [CrossRef] [PubMed]
- Yazaki, T.; Tobita, H.; Sato, S.; Miyake, T.; Kataoka, M.; Ishihara, S. Combinational elastography for assessment of liver fibrosis in patients with liver injury. J. Int. Med. Res. 2022, 50, 3000605221100126. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.L.; Yuen, P.; Ma, A.J.; Chan, A.W.; Leung, H.H.; Wong, V.W. Artificial intelligence in prediction of non-alcoholic fatty liver disease and fibrosis. J. Gastroenterol. Hepatol. 2021, 36, 543–550. [Google Scholar] [CrossRef]
- Wang, K.; Lu, X.; Zhou, H.; Gao, Y.; Zheng, J.; Tong, M.; Wu, C.; Liu, C.; Huang, L.; Jiang, T.; et al. Deep learning Radiomics of shear wave elastography significantly improved diagnostic performance for assessing liver fibrosis in chronic hepatitis B: A prospective multicentre study. Gut 2019, 68, 729–741. [Google Scholar] [CrossRef]
- Destrempes, F.; Gesnik, M.; Chayer, B.; Roy-Cardinal, M.-H.; Olivié, D.; Giard, J.-M.; Sebastiani, G.; Nguyen, B.N.; Cloutier, G.; Tang, A. Quantitative ultrasound, elastography, and machine learning for assessment of steatosis, inflammation, and fibrosis in chronic liver disease. PLoS ONE 2022, 17, e0262291. [Google Scholar] [CrossRef]
- Park, S.-Y.; Kang, B.J. Combination of shear-wave elastography with ultrasonography for detection of breast cancer and reduction of unnecessary biopsies: A systematic review and meta-analysis. Ultrasonography 2021, 40, 318–332. [Google Scholar] [CrossRef]
- Itoh, A.; Ueno, E.; Tohno, E.; Kamma, H.; Takahashi, H.; Shiina, T.; Yamakawa, M.; Matsumura, T. Breast Disease: Clinical Application of US Elastography for Diagnosis. Radiology 2006, 239, 341–350. [Google Scholar] [CrossRef]
- Ueno, E.; Umemoto, T.; Bando, H.; Tohno, E.; Waki, K.; Matsumura, T. New Quantitative Method in Breast Elastography: Fat Lesion Ratio (FLR). In Proceedings of the Radiological Society of North America 2007 Scientific Assembly and Annual Meeting, Chicago, IL, USA, 27 November 2007. [Google Scholar]
- Sadigh, G.; Carlos, R.C.; Neal, C.H.; Dwamena, B.A. Accuracy of quantitative ultrasound elastography for differentiation of malignant and benign breast abnormalities: A meta-analysis. Breast Cancer Res. Treat. 2012, 134, 923–931. [Google Scholar] [CrossRef]
- Ricci, P.; Maggini, E.; Mancuso, E.; Lodise, P.; Cantisani, V.; Catalano, C. Clinical application of breast elastography: State of the art. Eur. J. Radiol. 2014, 83, 429–437. [Google Scholar] [CrossRef]
- Gong, X.; Xu, Q.; Xu, Z.; Xiong, P.; Yan, W.; Chen, Y. Real-time elastography for the differentiation of benign and malignant breast lesions: A meta-analysis. Breast Cancer Res. Treat. 2011, 130, 11–18. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Tan, T.; Chen, K.; Xu, Y.; Wu, R. Application of ultrasonic dual-mode artificially intelligent architecture in assisting radiologists with different diagnostic levels on breast masses classification. Diagn. Interv. Radiol. 2021, 27, 315–322. [Google Scholar] [CrossRef]
- Kim, M.Y.; Kim, S.-Y.; Kim, Y.S.; Kim, E.S.; Chang, J.M. Added value of deep learning-based computer-aided diagnosis and shear wave elastography to b-mode ultrasound for evaluation of breast masses detected by screening ultrasound. Medicine 2021, 100, e26823. [Google Scholar] [CrossRef]
- Kobaly, K.; Kim, C.S.; Mandel, S.J. Contemporary Management of Thyroid Nodules. Annu. Rev. Med. 2022, 73, 517–528. [Google Scholar] [CrossRef]
- Kant, R.; Davis, A.; Verma, V. Thyroid Nodules: Advances in Evaluation and Management. Am. Fam. Physician 2020, 102, 298–304. [Google Scholar]
- Yoon, J.H.; Kim, E.-K.; Kwak, J.Y.; Moon, H.J. Effectiveness and Limitations of Core Needle Biopsy in the Diagnosis of Thyroid Nodules: Review of Current Literature. J. Pathol. Transl. Med. 2015, 49, 230–235. [Google Scholar] [CrossRef]
- Abou Shaar, B.; Meteb, M.; Awad El-Karim, G.; Almalki, Y. Reducing the Number of Unnecessary Thyroid Nodule Biopsies With the American College of Radiology (ACR) Thyroid Imaging Reporting and Data System (TI-RADS). Cureus 2022, 14, e23118. [Google Scholar] [CrossRef]
- Lyshchik, A.; Higashi, T.; Asato, R.; Tanaka, S.; Ito, J.; Mai, J.J.; Pellot-Barakat, C.; Insana, M.F.; Brill, A.B.; Saga, T.; et al. Thyroid Gland Tumor Diagnosis at US Elastography. Radiology 2005, 237, 202–211. [Google Scholar] [CrossRef]
- Azizi, G.; Keller, J.; Lewis, M.; Puett, D.; Rivenbark, K.; Malchoff, C. Performance of Elastography for the Evaluation of Thyroid Nodules: A Prospective Study. Thyroid 2013, 23, 734–740. [Google Scholar] [CrossRef]
- Trimboli, P.; Guglielmi, R.; Monti, S.; Misischi, I.; Graziano, F.; Nasrollah, N.; Amendola, S.; Morgante, S.N.; Deiana, M.G.; Valabrega, S.; et al. Ultrasound Sensitivity for Thyroid Malignancy Is Increased by Real-Time Elastography: A Prospective Multicenter Study. J. Clin. Endocrinol. Metab. 2012, 97, 4524–4530. [Google Scholar] [CrossRef] [PubMed]
- Moon, H.J.; Sung, J.M.; Kim, E.-K.; Yoon, J.H.; Youk, J.H.; Kwak, J.Y. Diagnostic Performance of Gray-Scale US and Elastography in Solid Thyroid Nodules. Radiology 2012, 262, 1002–1013. [Google Scholar] [CrossRef] [PubMed]
- Hairu, L.; Yulan, P.; Yan, W.; Hong, A.; Xiaodong, Z.; Lichun, Y.; Kun, Y.; Ying, X.; Lisha, L.; Baoming, L.; et al. Elastography for the diagnosis of high-suspicion thyroid nodules based on the 2015 American Thyroid Association guidelines: A multicenter study. BMC Endocr. Disord. 2020, 20, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhan, J.; Jin, J.-M.; Diao, X.-H.; Chen, Y. Acoustic radiation force impulse imaging (ARFI) for differentiation of benign and malignant thyroid nodules—A meta-analysis. Eur. J. Radiol. 2015, 84, 2181–2186. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.; Chen, M.; Liu, B.; Wang, S.; Li, X. Diagnostic performance of shear wave elastography in the identification of malignant thyroid nodules: A meta-analysis. Eur. Radiol. 2014, 24, 2729–2738. [Google Scholar] [CrossRef]
- Bardet, S.; Ciappuccini, R.; Pellot-Barakat, C.; Monpeyssen, H.; Michels, J.-J.; Tissier, F.; Blanchard, D.; Menegaux, F.; De Raucourt, D.; Lefort, M.; et al. Shear Wave Elastography in Thyroid Nodules with Indeterminate Cytology: Results of a Prospective Bicentric Study. Thyroid 2017, 27, 1441–1449. [Google Scholar] [CrossRef]
- Swan, K.Z.; Bonnema, S.J.; Jespersen, M.L.; Nielsen, V.E. Reappraisal of shear wave elastography as a diagnostic tool for identifying thyroid carcinoma. Endocr. Connect. 2019, 8, 1195–1205. [Google Scholar] [CrossRef]
- Swan, K.Z.; Nielsen, V.E.; Bonnema, S.J. Evaluation of thyroid nodules by shear wave elastography: A review of current knowledge. J. Endocrinol. Investig. 2021, 44, 2043–2056. [Google Scholar] [CrossRef]
- Park, A.Y.; Son, E.J.; Han, K.; Youk, J.H.; Kim, J.-A.; Park, C.S. Shear wave elastography of thyroid nodules for the prediction of malignancy in a large scale study. Eur. J. Radiol. 2015, 84, 407–412. [Google Scholar] [CrossRef]
- Han, R.-J.; Du, J.; Li, F.-H.; Zong, H.-R.; Wang, J.-D.; Shen, Y.-L.; Zhou, Q.-Y. Comparisons and Combined Application of Two-Dimensional and Three-Dimensional Real-time Shear Wave Elastography in Diagnosis of Thyroid Nodules. J. Cancer 2019, 10, 1975–1984. [Google Scholar] [CrossRef]
- Petersen, M.; Schenke, S.A.; Firla, J.; Croner, R.S.; Kreissl, M.C. Shear Wave Elastography and Thyroid Imaging Reporting and Data System (TIRADS) for the Risk Stratification of Thyroid Nodules—Results of a Prospective Study. Diagnostics 2022, 12, 109. [Google Scholar] [CrossRef]
- Filho, R.H.C.; Pereira, F.L.; Iared, W. Diagnostic Accuracy Evaluation of Two-Dimensional Shear Wave Elastography in the Differentiation Between Benign and Malignant Thyroid Nodules. J. Ultrasound Med. 2020, 39, 1729–1741. [Google Scholar] [CrossRef]
- Zhang, B.; Tian, J.; Pei, S.; Chen, Y.; He, X.; Dong, Y.; Zhang, L.; Mo, X.; Huang, W.; Cong, S.; et al. Machine Learning–Assisted System for Thyroid Nodule Diagnosis. Thyroid 2019, 29, 858–867. [Google Scholar] [CrossRef]
- Qin, P.; Wu, K.; Hu, Y.; Zeng, J.; Chai, X. Diagnosis of Benign and Malignant Thyroid Nodules Using Combined Conventional Ultrasound and Ultrasound Elasticity Imaging. IEEE J. Biomed. Health Inform. 2020, 24, 1028–1036. [Google Scholar] [CrossRef]
- Zhao, C.-K.; Ren, T.-T.; Yin, Y.-F.; Shi, H.; Wang, H.-X.; Zhou, B.-Y.; Wang, X.-R.; Li, X.; Zhang, Y.-F.; Liu, C.; et al. A Comparative Analysis of Two Machine Learning-Based Diagnostic Patterns with Thyroid Imaging Reporting and Data System for Thyroid Nodules: Diagnostic Performance and Unnecessary Biopsy Rate. Thyroid 2021, 31, 470–481. [Google Scholar] [CrossRef]
- Liu, T.; Ge, X.; Yu, J.; Guo, Y.; Wang, Y.; Wang, W.; Cui, L. Comparison of the application of B-mode and strain elastography ultrasound in the estimation of lymph node metastasis of papillary thyroid carcinoma based on a radiomics approach. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1617–1627. [Google Scholar] [CrossRef]
- Wang, B.; Guo, Q.; Wang, J.-Y.; Yu, Y.; Yi, A.-J.; Cui, X.-W.; Dietrich, C.F. Ultrasound Elastography for the Evaluation of Lymph Nodes. Front. Oncol. 2021, 11, 714660. [Google Scholar] [CrossRef]
- Knabe, M.; Günter, E.; Ell, C.; Pech, O. Can EUS Elastography Improve Lymph Node Staging in Esophageal Cancer? Surg. Endosc. 2013, 27, 1196–1202. [Google Scholar] [CrossRef]
- Tahmasebi, A.; Qu, E.; Sevrukov, A.; Liu, J.-B.; Wang, S.; Lyshchik, A.; Yu, J.; Eisenbrey, J.R. Assessment of Axillary Lymph Nodes for Metastasis on Ultrasound Using Artificial Intelligence. Ultrason. Imaging 2021, 43, 329–336. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Y.; Du, H.; Lai, L.; Chen, J.; Zhang, T.; Mao, H. Machine Learning-Based Shear Wave Elastography Elastic Index (SWEEI) in Predicting Cervical Lymph Node Metastasis of Papillary Thyroid Microcarcinoma: A Comparative Analysis of Five Practical Prediction Models. Cancer Manag. Res. 2022, 14, 2847–2858. [Google Scholar] [CrossRef]
- Ng, S.C.; Shi, H.Y.; Hamidi, N.; Underwood, F.E.; Tang, W.; Benchimol, E.I.; Panaccione, R.; Ghosh, S.; Wu, J.C.Y.; Chan, F.K.L.; et al. Worldwide incidence and prevalence of inflammatory bowel disease in the 21st century: A systematic review of population-based studies. Lancet 2018, 390, 2769–2778. [Google Scholar] [CrossRef] [PubMed]
- Actis, G.C.; Pellicano, R.; Fagoonee, S.; Ribaldone, D.G. History of Inflammatory Bowel Diseases. J. Clin. Med. 2019, 8, 1970. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, B.L.; Mazzaro, M.C.; Nagasako, C.K.; Ayrizono, M.D.L.S.; Fagundes, J.J.; Leal, R.F. Assessment of disease activity in inflammatory bowel diseases: Non-invasive biomarkers and endoscopic scores. World J. Gastrointest. Endosc. 2020, 12, 504–520. [Google Scholar] [CrossRef] [PubMed]
- Ślósarz, D.; Poniewierka, E.; Neubauer, K.; Kempiński, R. Ultrasound Elastography in the Assessment of the Intestinal Changes in Inflammatory Bowel Disease—Systematic Review. J. Clin. Med. 2021, 10, 4044. [Google Scholar] [CrossRef] [PubMed]
- Grażyńska, A.; Kufel, J.; Dudek, A.; Cebula, M. Shear Wave and Strain Elastography in Crohn’s Disease—A Systematic Review. Diagnostics 2021, 11, 1609. [Google Scholar] [CrossRef] [PubMed]
- Cebula, M.; Kufel, J.; Grażyńska, A.; Habas, J.; Gruszczyńska, K. Intestinal Elastography in the Diagnostics of Ulcerative Colitis: A Narrative Review. Diagnostics 2022, 12, 2070. [Google Scholar] [CrossRef]
- Alfredsson, J.; Wick, M.J. Mechanism of fibrosis and stricture formation in Crohn’s disease. Scand. J. Immunol. 2020, 92, e12990. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Fowler, K.J.; Ozturk, A.; Bs, C.K.P.; Ba, A.L.L.; Montes, V.; Ba, W.C.H.; Wang, K.; Andre, M.P.; Samir, A.E.; et al. Liver fibrosis imaging: A clinical review of ultrasound and magnetic resonance elastography. J. Magn. Reson. Imaging 2020, 51, 25–42. [Google Scholar] [CrossRef]
- Re, G.L.; Picone, D.; Vernuccio, F.; Scopelliti, L.; Di Piazza, A.; Tudisca, C.; Serraino, S.; Privitera, G.; Midiri, F.; Salerno, S.; et al. Comparison of US Strain Elastography and Entero-MRI to Typify the Mesenteric and Bowel Wall Changes during Crohn’s Disease: A Pilot Study. BioMed Res. Int. 2017, 2017, 4257987. [Google Scholar] [CrossRef]
- Fraquelli, M.; Branchi, F.; Cribiù, F.M.; Orlando, S.; Casazza, G.; Magarotto, A.; Massironi, S.; Botti, F.; Contessini-Avesani, E.; Conte, D.; et al. The Role of Ultrasound Elasticity Imaging in Predicting Ileal Fibrosis in Crohnʼs Disease Patients. Inflamm. Bowel Dis. 2015, 21, 2605–2612. [Google Scholar] [CrossRef]
- Serra, C.; Rizzello, F.; Pratico’, C.; Felicani, C.; Fiorini, E.; Brugnera, R.; Mazzotta, E.; Giunchi, F.; Fiorentino, M.; D’Errico, A.; et al. Real-time elastography for the detection of fibrotic and inflammatory tissue in patients with stricturing Crohn’s disease. J. Ultrasound 2017, 20, 273–284. [Google Scholar] [CrossRef]
- Gubatan, J.; Levitte, S.; Patel, A.; Balabanis, T.; Wei, M.T.; Sinha, S.R. Artificial intelligence applications in inflammatory bowel disease: Emerging technologies and future directions. World J. Gastroenterol. 2021, 27, 1920–1935. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).