Mechanistic Modelling of DNA Damage Repair by the Radiation Adaptive Response Mechanism and Its Significance
Abstract
1. Introduction
2. Modelling of Radiation’s Influence on Cells
3. Radiation Adaptive Response—Enhancement of the Repair Process
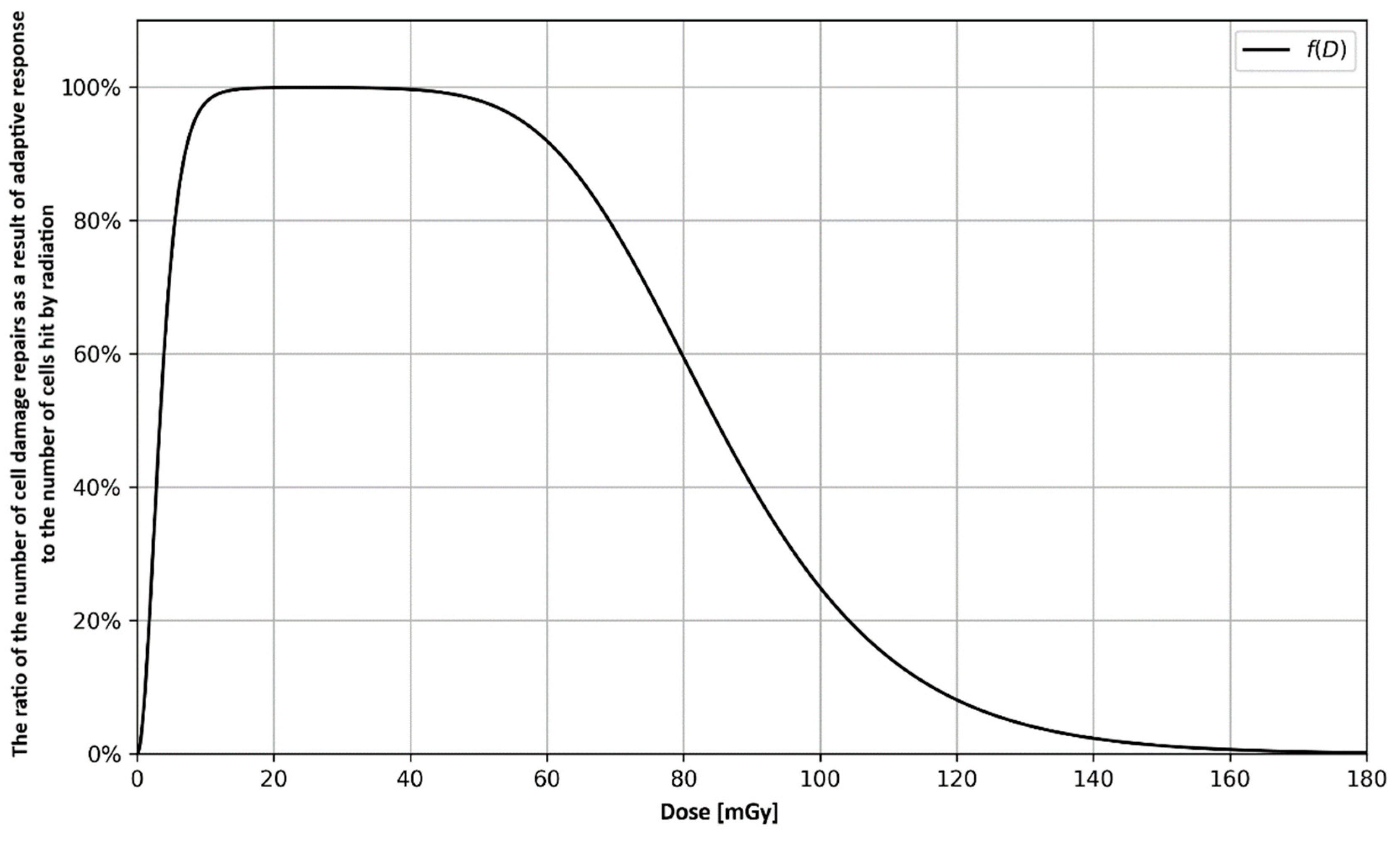
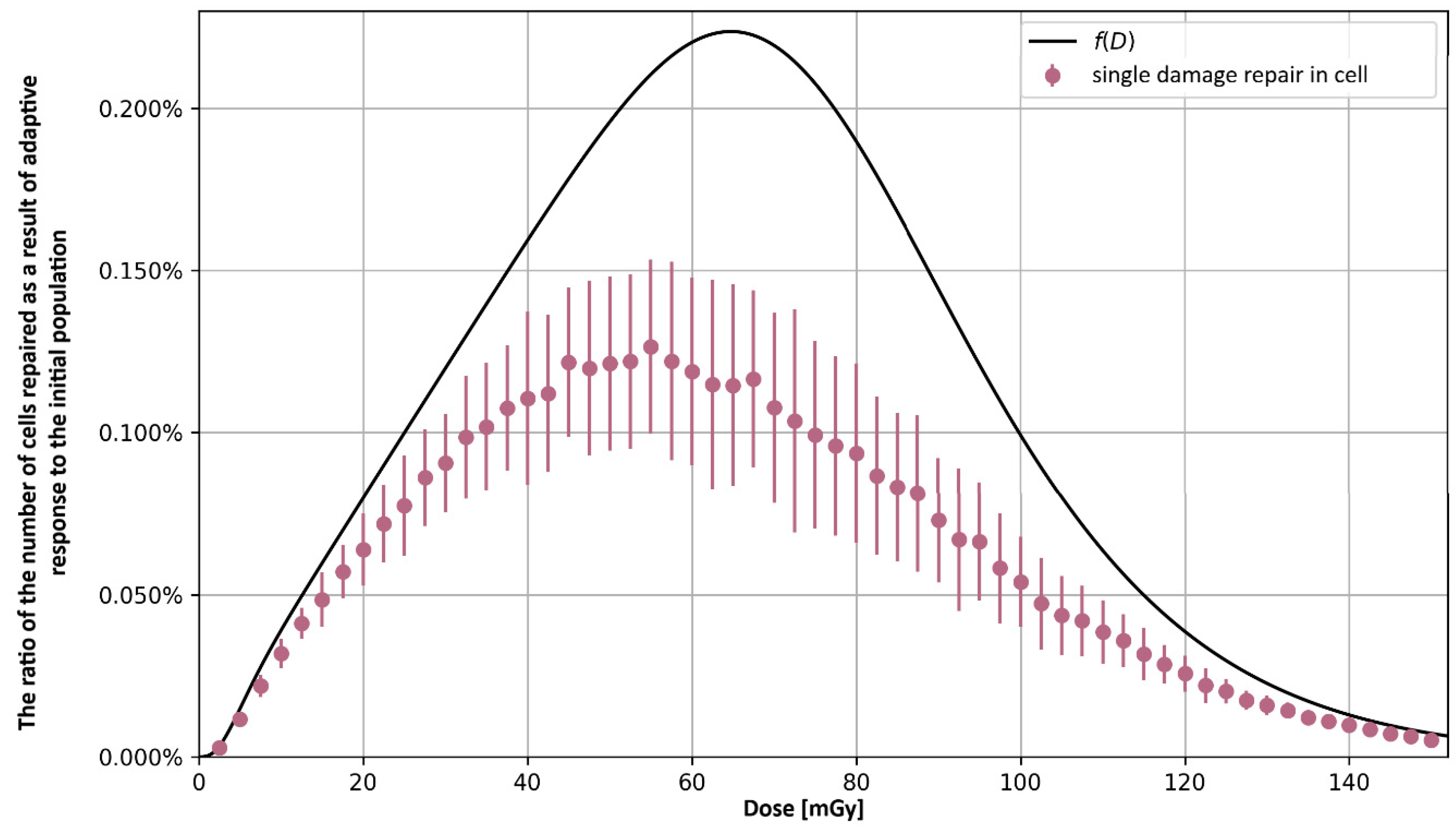
3.1. Analytical Approach
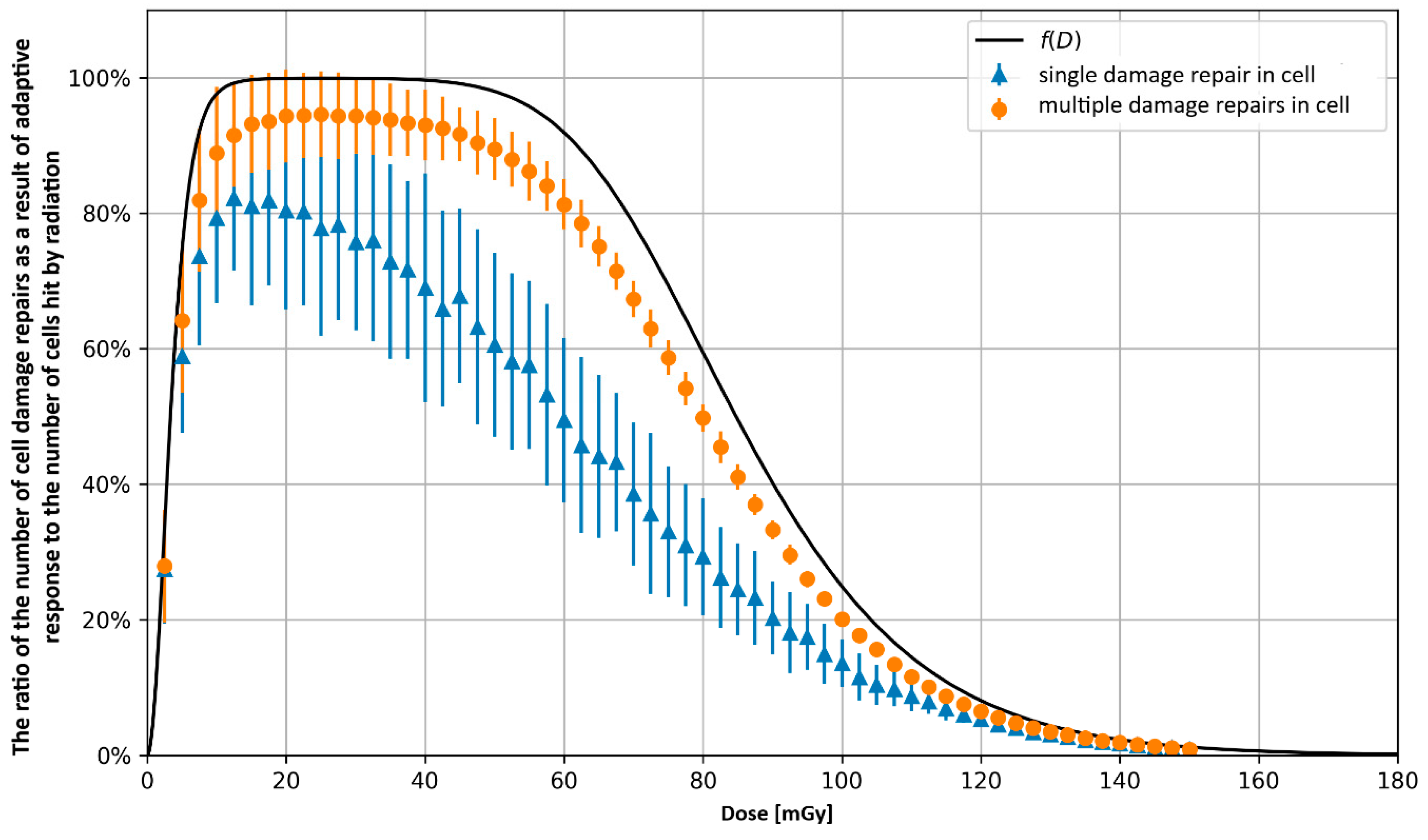
3.2. Monte Carlo Approach—Single Dose
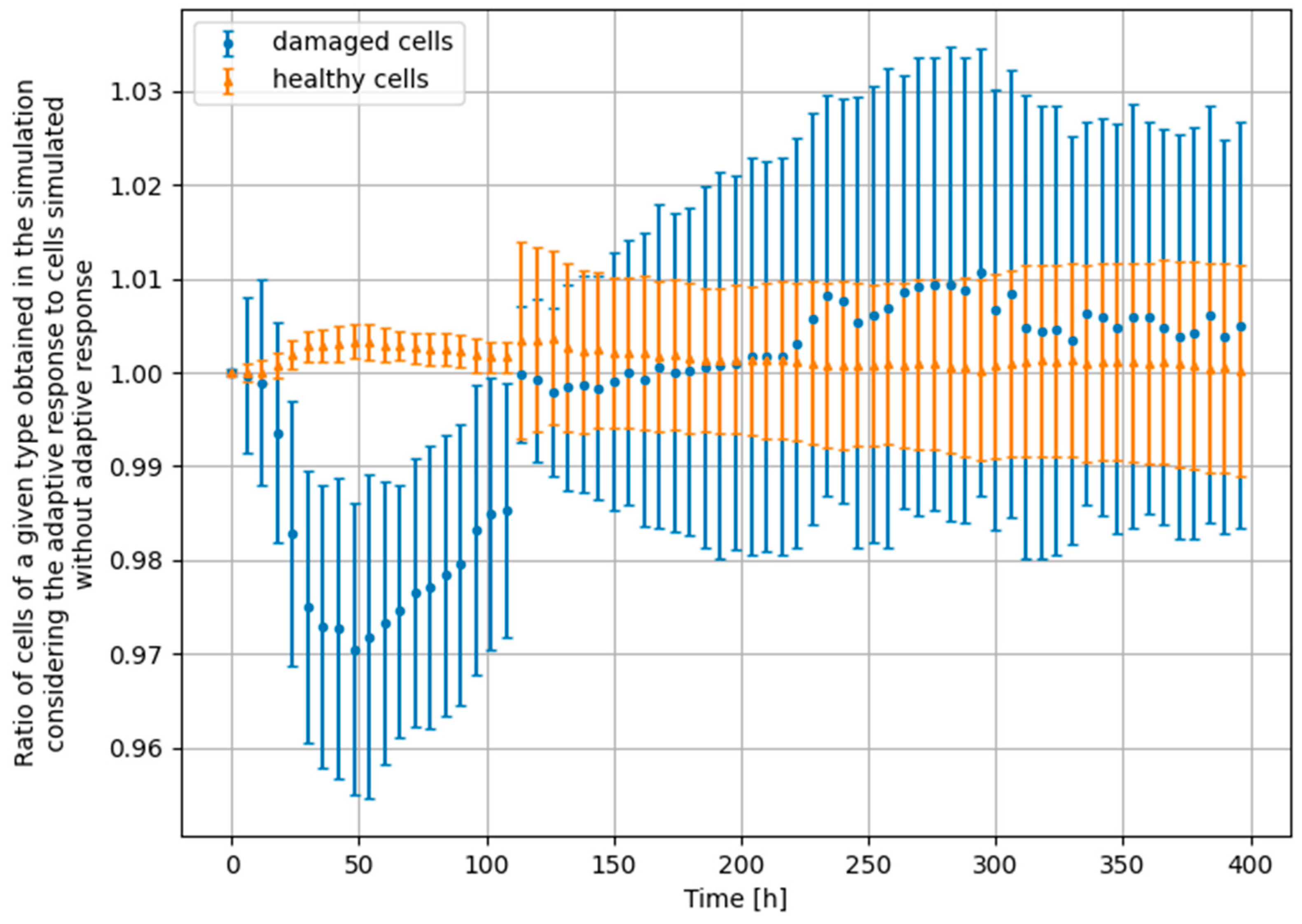
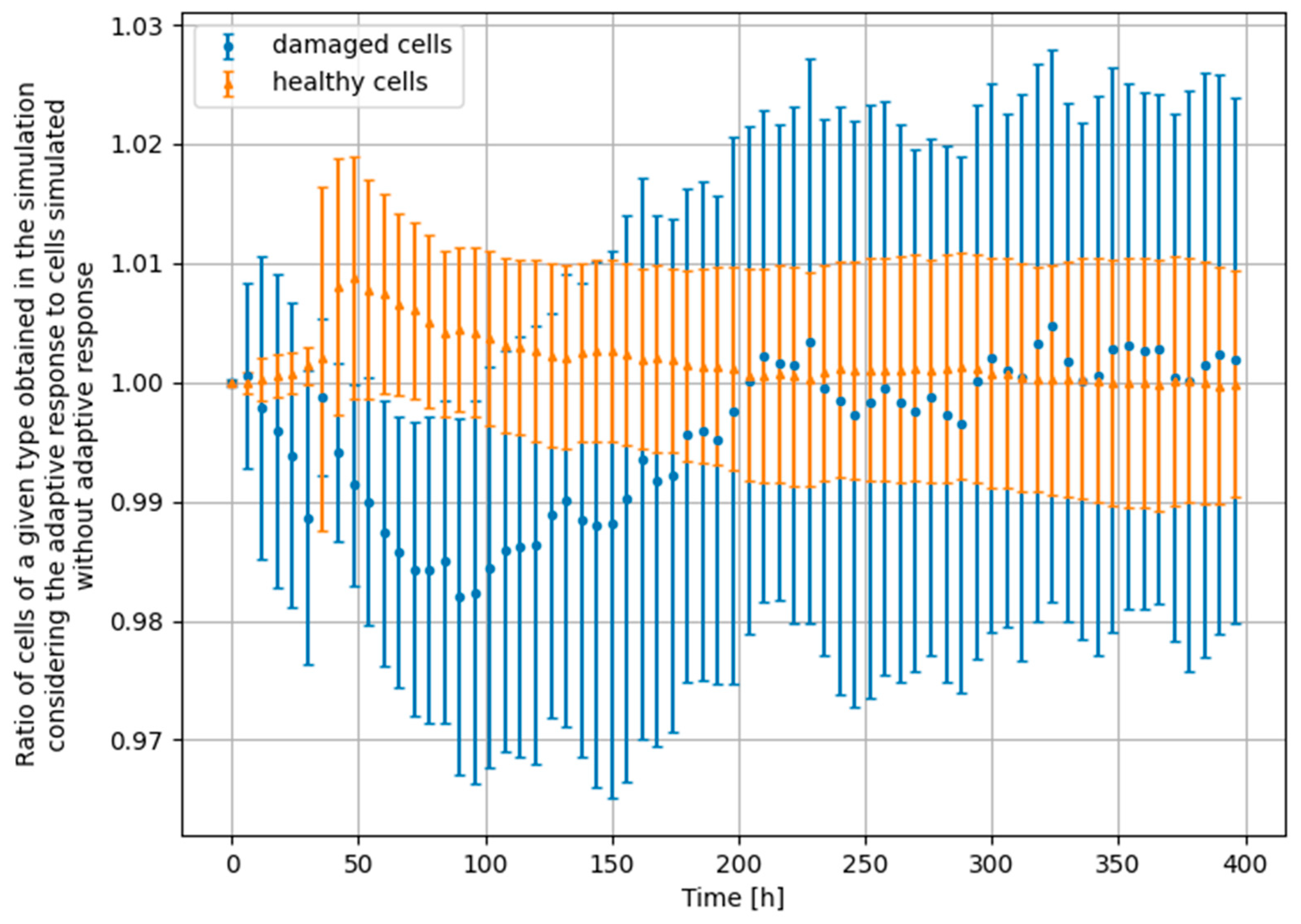
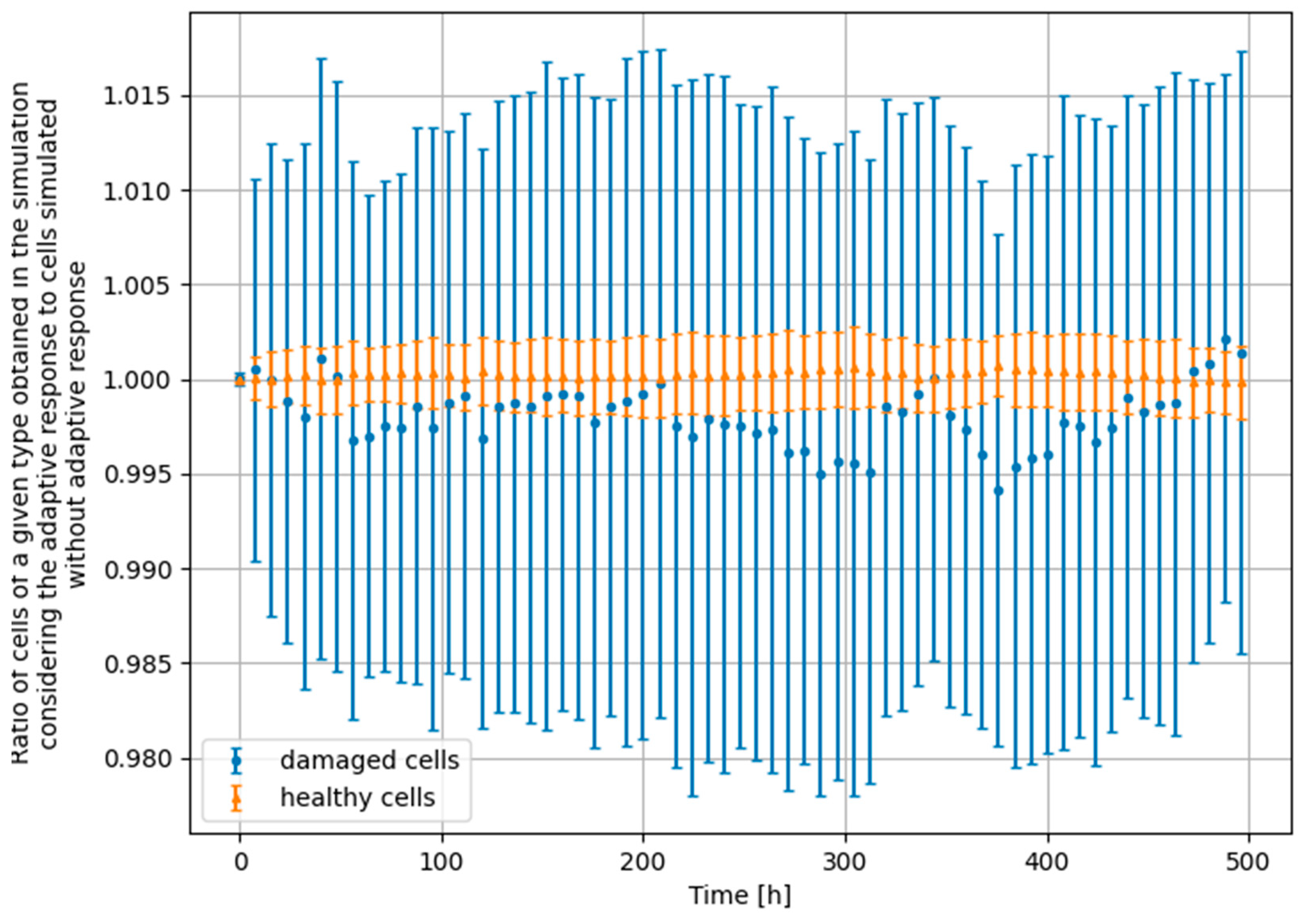
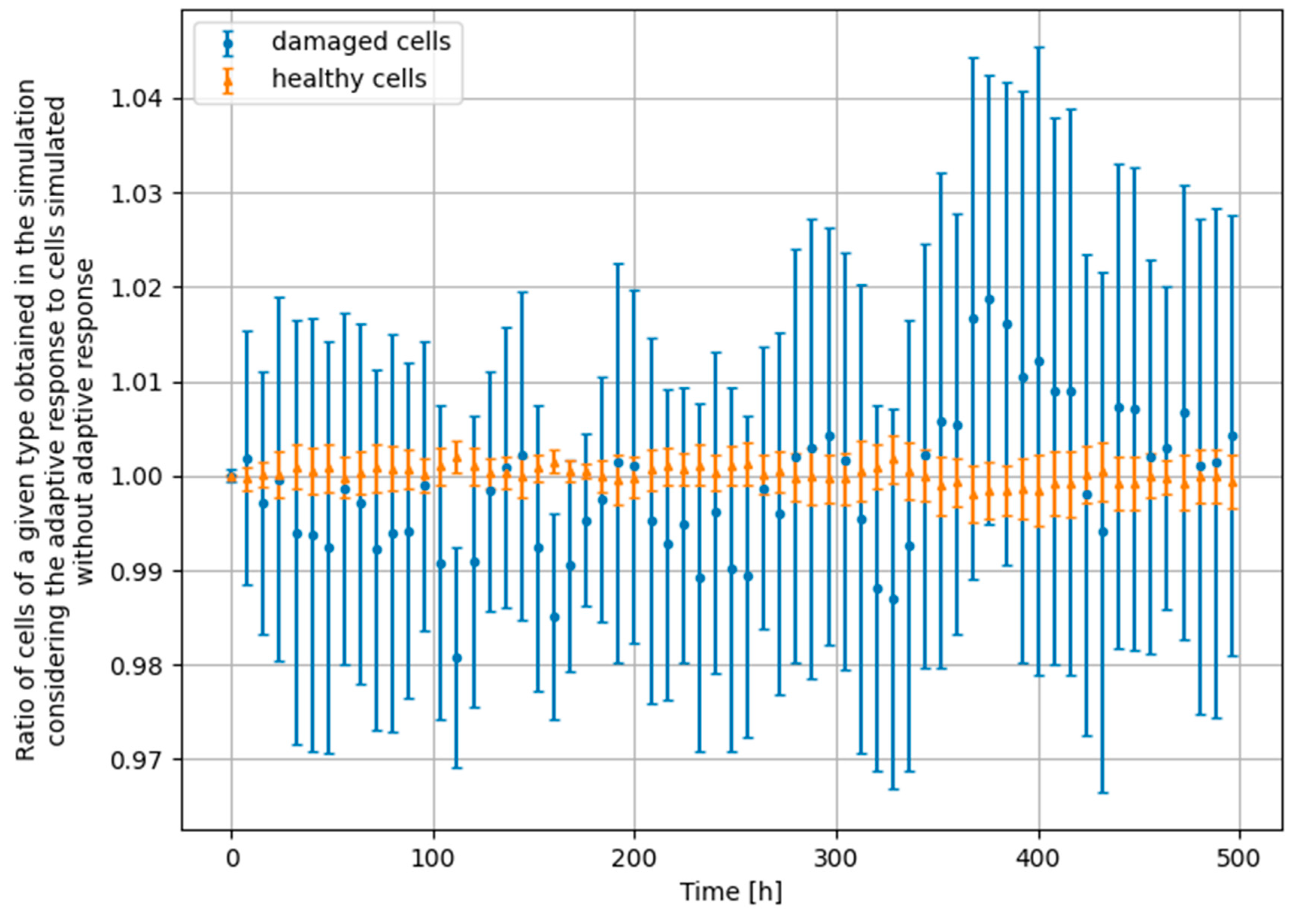
3.3. Monte Carlo Approach—Two Doses
- Scenario no. 1: D1 = 25 mGy, Δt = 24 h, D2 = 1500 mGy
- Scenario no. 2: D1 = 25 mGy, Δt = 24 h, D2 = 4000 mGy
- Scenario no. 3: D1 = 25 mGy, Δt = 100 h, D2 = 1500 mGy
- Scenario no. 4: D1 = 100 mGy, Δt = 24 h, D2 = 1500 mGy
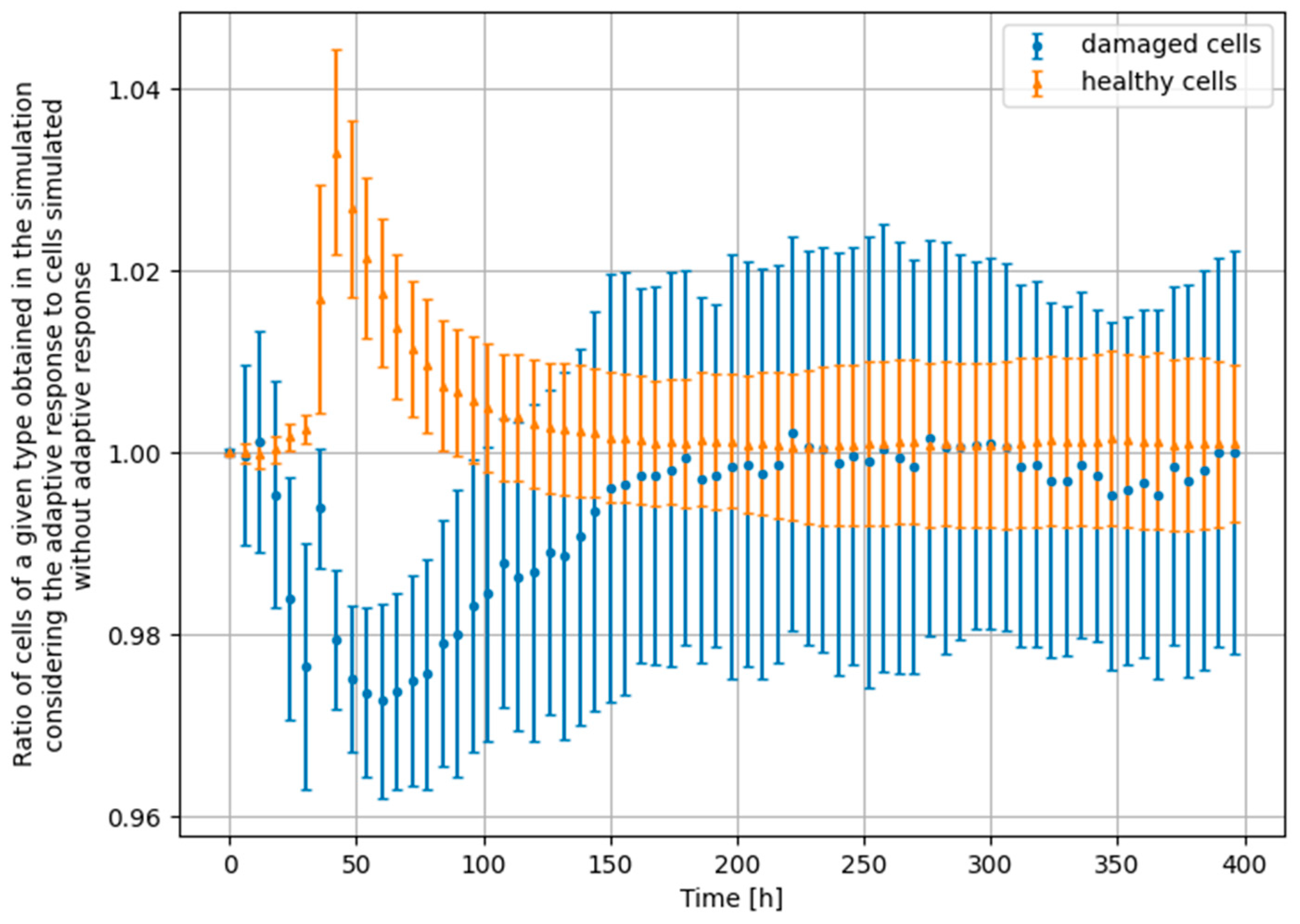
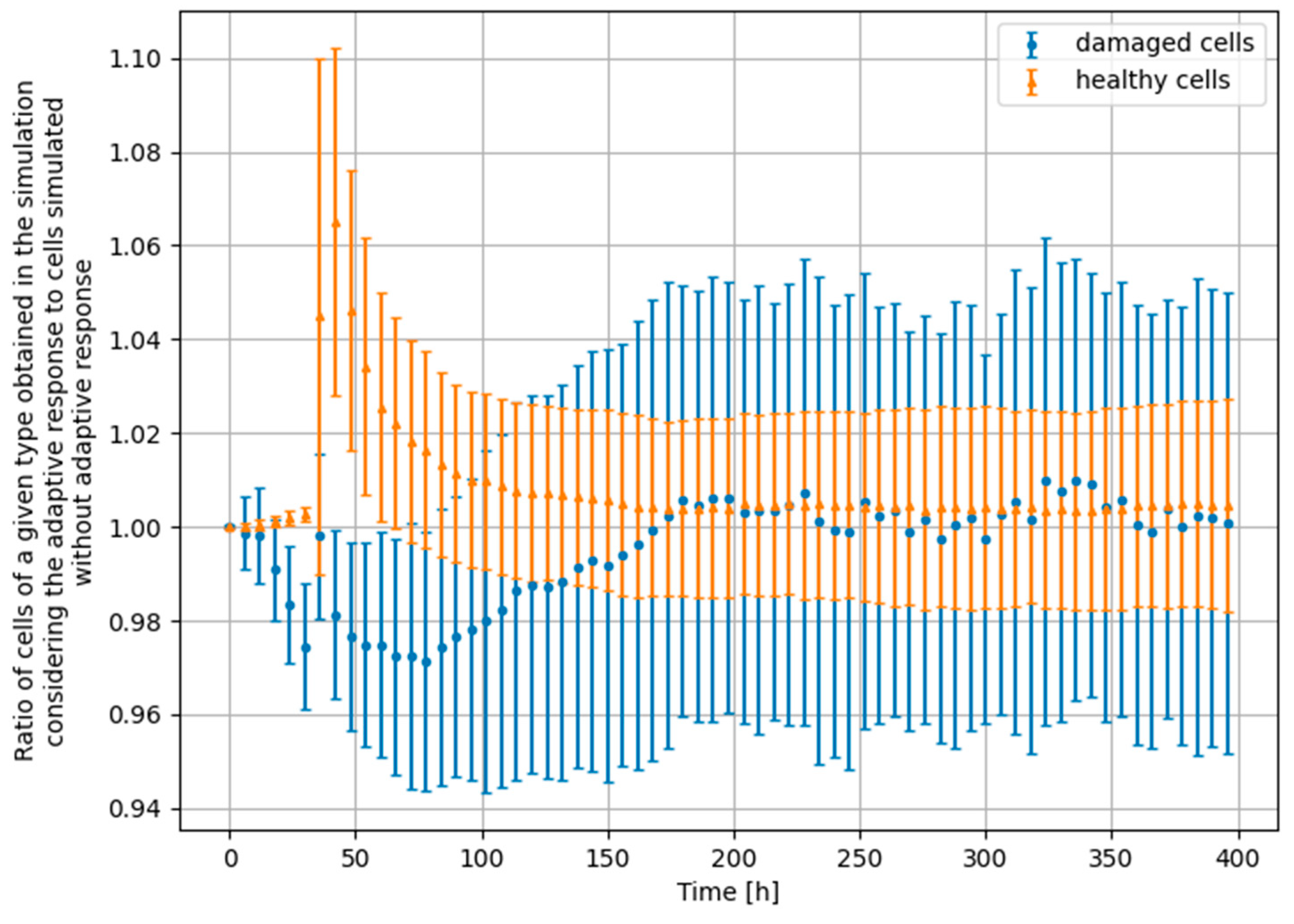
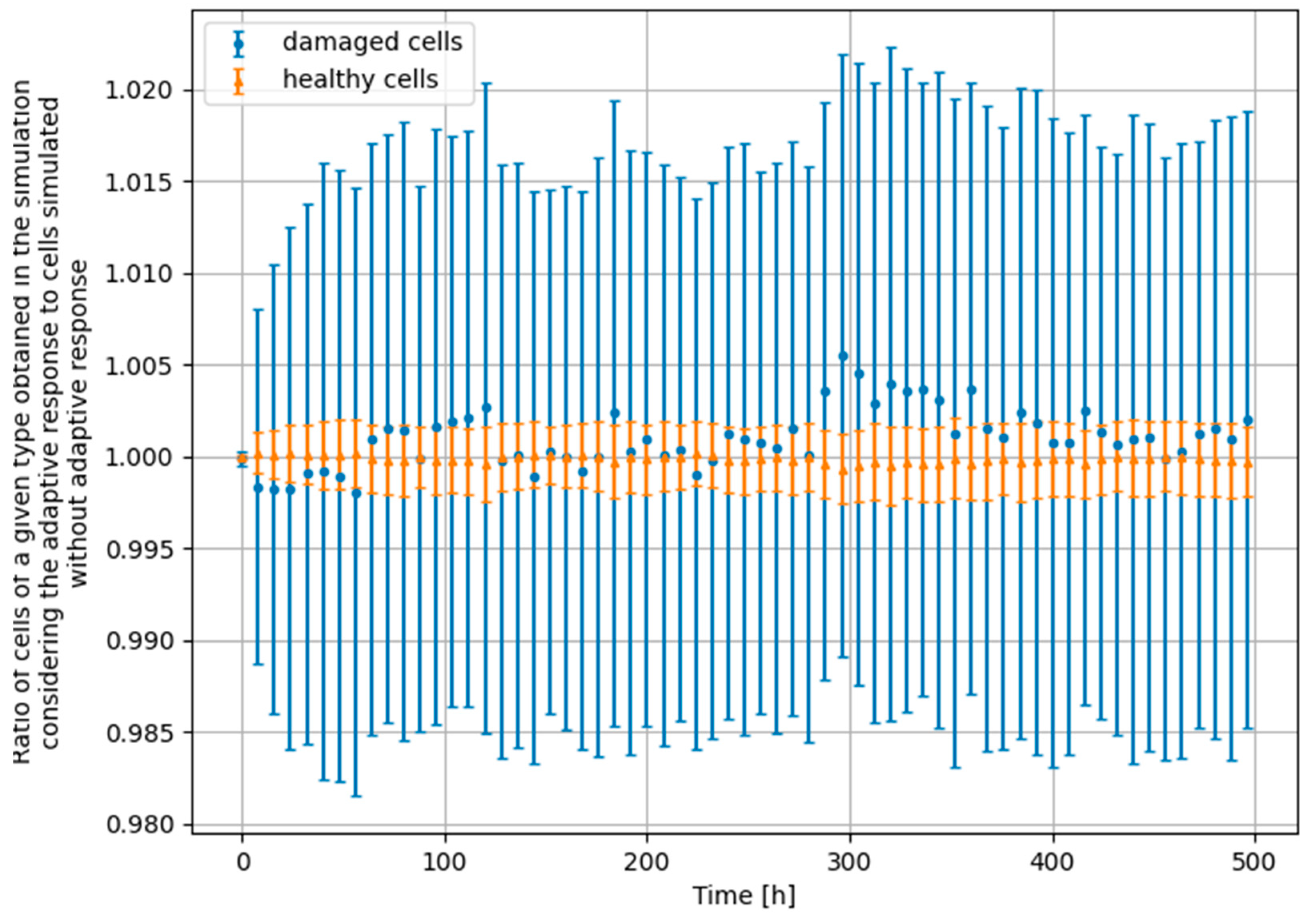
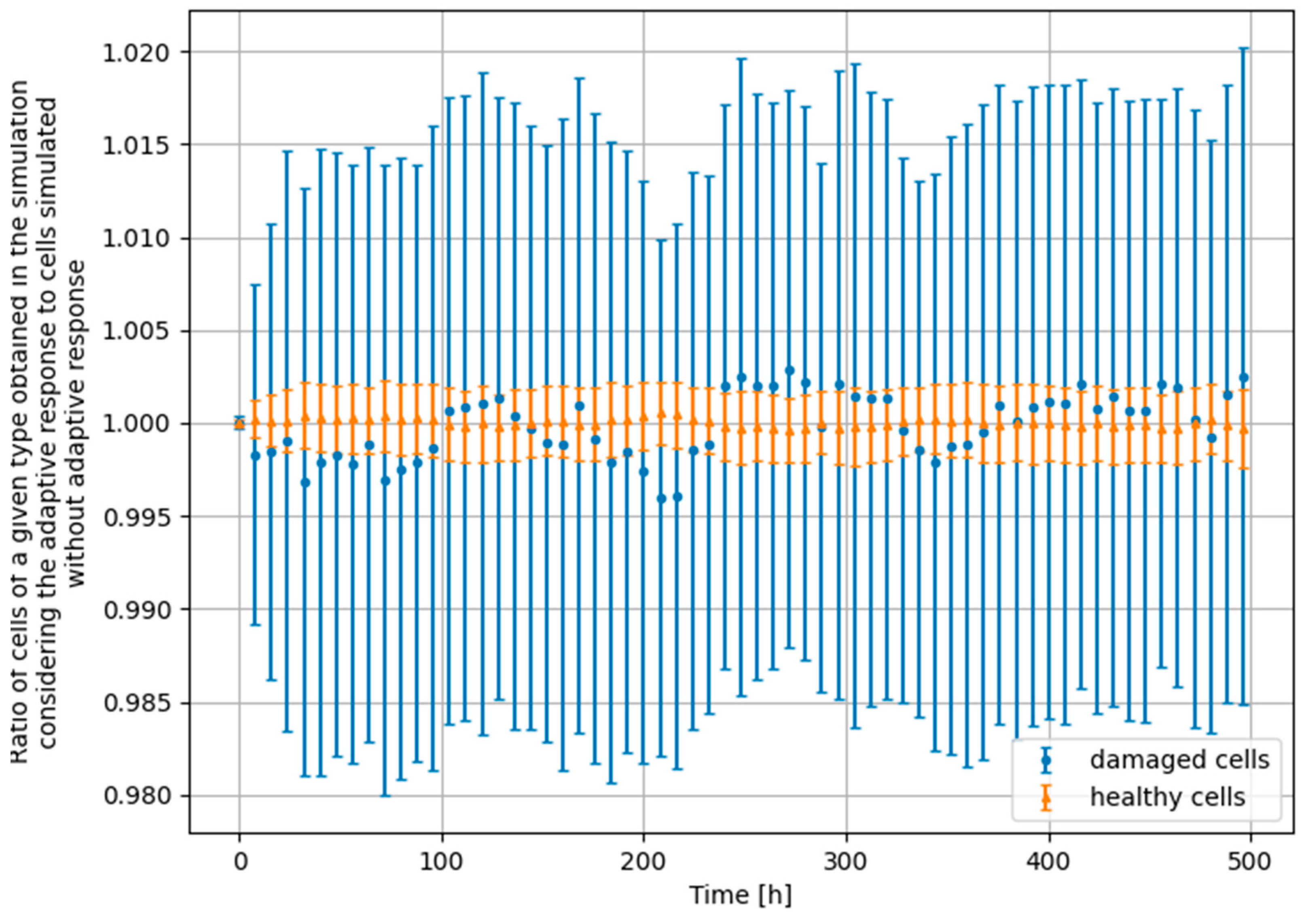
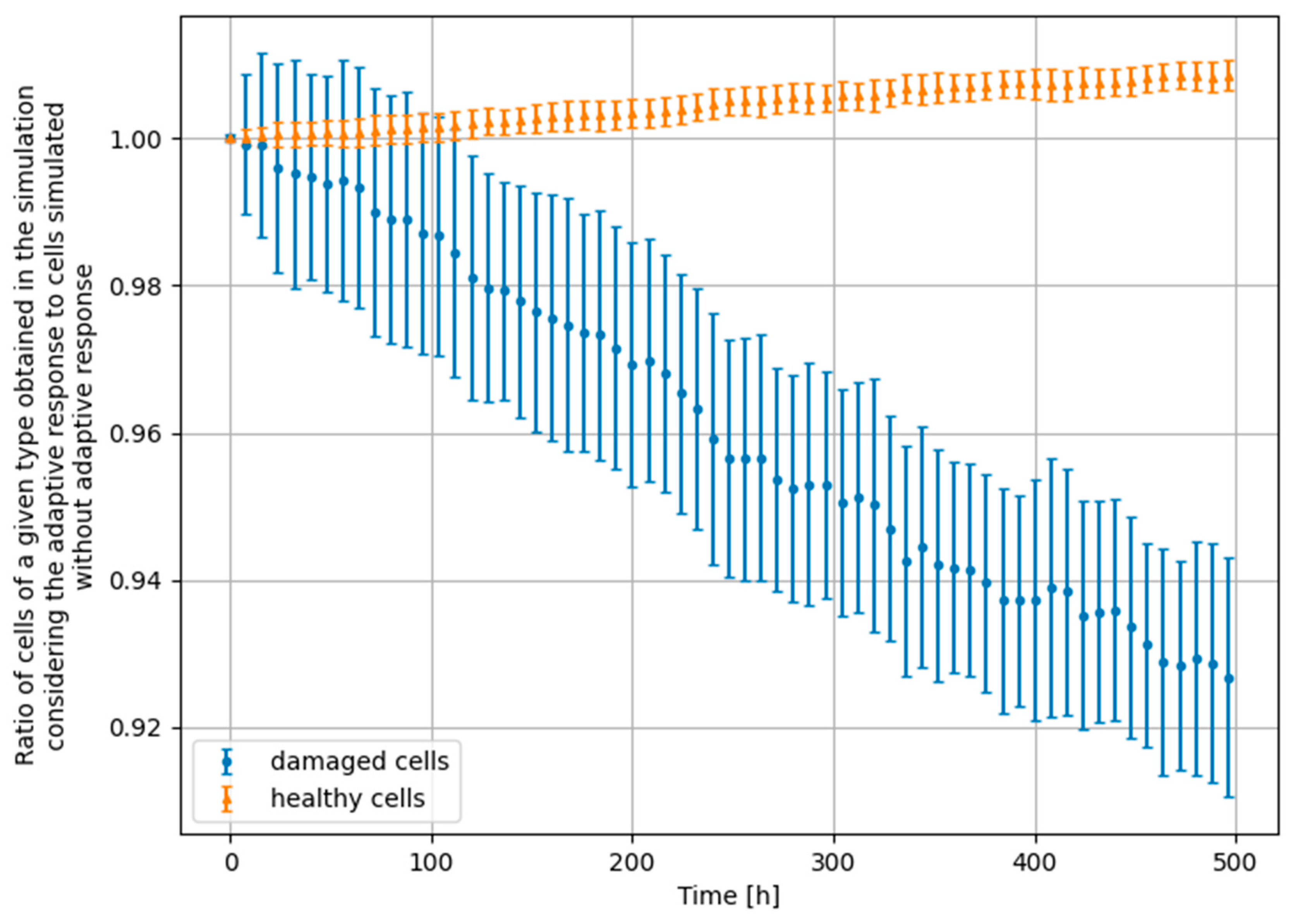
3.4. Monte Carlo Approach—Constant Dose-Rate
4. Significance of the Radioadaptive-Related Repair
5. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fornalski, K.W.; Adamowski, Ł.; Bugała, E.; Jarmakiewicz, R.; Kirejczyk, M.; Kopyciński, J.; Krasowska, J.; Kukulski, P.; Piotrowski, Ł.; Ponikowska, J.; et al. Biophysical modeling of the ionizing radiation influence on cells using the stochastic (Monte Carlo) and deterministic (analytical) approaches. Dose-Response, 2022; in-press (published on-line). [Google Scholar] [CrossRef]
- UNSCEAR (United Nations Scientific Committee on the Effects of Atomic Radiation) Report. Annex B: Adaptive Responses to Radiation in Cells and Organisms. 1994. Available online: https://www.unscear.org/docs/publications/1994/UNSCEAR_1994_Report.pdf (accessed on 13 February 2023).
- Raper, J.R. Effects of total surface beta irradiation. Radiology 1947, 49, 314–324. [Google Scholar] [CrossRef] [PubMed]
- Olivieri, G.; Bodycote, J.; Wolff, S. Adaptive response of human lymphocytes to low concentrations of radioactive thymidine. Science 1984, 223, 594–597. [Google Scholar] [CrossRef] [PubMed]
- Sanders, C.L. Radiation Hormesis and the Linear-No-Threshold Assumption; Springer: New York, NY, USA, 2010. [Google Scholar]
- Wolff, S. The adaptive response in radiobiology: Evolving insights and implications. Environ. Health Perspect. 1998, 106 (Suppl. 1), 277–283. [Google Scholar] [PubMed]
- Aurengo, A.; Averbeck, D.; Bonnin, A.; Le Guen, B.; Masse, R.; Monier, R.; Tubiana, M.; Valleron, A.J.; de Vathaire, F. Dose-effect relationships and estimation of the carcinogenic effects of low doses of ionizing radiation. Rep. Fr. Acad. Sci. Natl. Acad. Med. 2005. Available online: https://www.radiochemistry.org/documents/html/033005_rad.html (accessed on 13 February 2023).
- Brooks, A.L.; Glines, W.M.; Waltar, A. Proceedings of the Joint American Nuclear Society and Health Physics Society Conference: Applicability of Radiation-Response Models to Low-Dose Protection Standards 1–3 October 2018, Pasco, Washington Introduction—Years in the Making. Health Phys. 2020, 118, 229–231. [Google Scholar] [CrossRef] [PubMed]
- Tapio, S.; Jacob, V. Radioadaptive response revisited. Radiat. Environ. Biophys. 2007, 46, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Guéguen, Y.; Bontemps, A.; Ebrahimian, T.G. Adaptive responses to low doses of radiation or chemicals: Their cellular and molecular mechanisms. Cell. Mol. Life Sci. 2019, 76, 1255–1273. [Google Scholar] [CrossRef]
- Feinendegen, L.E. The role of adaptive responses following exposure to ionizing radiation. Hum. Exp. Toxicol. 1999, 18, 426–432. [Google Scholar] [CrossRef]
- Feinendegen, L.E. Low Doses of Ionizing Radiation: Relationship between Biological Benefit and Damage Induction. A Synopsis. World J. Nucl. Med. 2005, 4, 21–34. [Google Scholar]
- Feinendegen, L.E. Quantification of adaptive protection following low-dose irradiation. Health Phys. 2016, 110, 276–280. [Google Scholar] [CrossRef]
- Smirnova, O.A.; Yonezawa, M. Radioprotection effect of low level preirradiation on mammals: Modeling and experimental investigations. Health Phys. 2003, 85, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, O.A.; Yonezawa, M. Radioresistance in mammals induced by low-level chronic irradiation: Modeling and experimental investigations. Health Phys. 2004, 87, 366–374. [Google Scholar] [CrossRef]
- Wodarz, D.; Sorace, R.; Komarova, N.L. Dynamics of cellular responses to radiation. PLoS Comput. Biol. 2014, 10, e1003513. [Google Scholar] [CrossRef] [PubMed]
- Bodgi, L.; Foray, N. The nucleo-shuttling of the ATM protein as a basis for a novel theory of radiation response: Resolution of the linear-quadratic model. Int. J. Radiat. Biol. 2016, 92, 117–131. [Google Scholar] [CrossRef] [PubMed]
- Devic, C.; Ferlazzo, M.L.; Foray, N. Influence of individual radiosensitivity on the adaptive response phenomenon: Toward a mechanistic explanation based on the nucleo-shuttling of ATM protein. Dose-Response 2018, 16, 1559325818789836. [Google Scholar] [CrossRef] [PubMed]
- Esposito, G.; Campa, A.; Pinto, M.; Simone, G.; Tabocchini, M.A.; Belli, M. Adaptive response: Modelling and experimental studies. Radiat. Prot. Dosim. 2011, 143, 320–324. [Google Scholar] [CrossRef]
- Socol, Y.; Shaki, Y.; Dobrzyński, L. Damped-oscillator model of adaptive response and its consequences. Int. J. Low Radiat. 2020, 11, 186–206. [Google Scholar] [CrossRef]
- Fornalski, K.W. Radioadaptation and radioresistance during deep space travels. J. Space Saf. Eng. 2022, 9, 385–389. [Google Scholar] [CrossRef]
- Fornalski, K.W.; Adamowski, Ł.; Dobrzyński, L.; Jarmakiewicz, R.; Powojska, A.; Reszczyńska, J. The radiation adaptive response and priming dose influence: The quantification of the Raper-Yonezawa effect and its three-parameter model for postradiation DNA lesions and mutations. Radiat. Environ. Biophys. 2022, 61, 221–239. [Google Scholar] [CrossRef]
- Dobrzyński, L.; Fornalski, K.W.; Reszczyńska, J.; Janiak, M.K. Modeling cell reactions to ionizing radiation: From a lesion to a cancer. Dose-Response 2019, 17, 1–19. [Google Scholar] [CrossRef]
- Piotrowski, Ł. Modelowanie Odpowiedzi Grupy Komórek na Promieniowanie Jonizujące Metodą Monte Carlo. Bachelor’s Thesis, Faculty of Physics, Warsaw University of Technology, Warsaw, Poland, (supervisor: K.W. Fornalski). 2022. Available online: https://www.researchgate.net/publication/368275322_Modelowanie_odpowiedzi_grupy_komorek_na_promieniowanie_jonizujace_metoda_Monte_Carlo (accessed on 13 February 2023).
- Bugała, E. Modelowanie Radiacyjnej Odpowiedzi Adaptacyjnej dla Obszarów o Podwyższonym tle Promieniowania Jonizującego (in Polish). Master Thesis, Faculty of Physics, Warsaw University of Technology, Warsaw, Poland, (supervisor: K.W. Fornalski). 2022. Available online: https://www.researchgate.net/publication/368139245_Modelowanie_radiacyjnej_odpowiedzi_adaptacyjnej_dla_obszarow_o_podwyzszonym_tle_promieniowania_jonizujacego (accessed on 13 February 2023).
- Fornalski, K.W. Radiation adaptive response and cancer: From the statistical physics point of view. Phys. Rev. E 2019, 99, 22139. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piotrowski, Ł.; Krasowska, J.; Fornalski, K.W. Mechanistic Modelling of DNA Damage Repair by the Radiation Adaptive Response Mechanism and Its Significance. BioMedInformatics 2023, 3, 150-163. https://doi.org/10.3390/biomedinformatics3010011
Piotrowski Ł, Krasowska J, Fornalski KW. Mechanistic Modelling of DNA Damage Repair by the Radiation Adaptive Response Mechanism and Its Significance. BioMedInformatics. 2023; 3(1):150-163. https://doi.org/10.3390/biomedinformatics3010011
Chicago/Turabian StylePiotrowski, Łukasz, Julianna Krasowska, and Krzysztof W. Fornalski. 2023. "Mechanistic Modelling of DNA Damage Repair by the Radiation Adaptive Response Mechanism and Its Significance" BioMedInformatics 3, no. 1: 150-163. https://doi.org/10.3390/biomedinformatics3010011
APA StylePiotrowski, Ł., Krasowska, J., & Fornalski, K. W. (2023). Mechanistic Modelling of DNA Damage Repair by the Radiation Adaptive Response Mechanism and Its Significance. BioMedInformatics, 3(1), 150-163. https://doi.org/10.3390/biomedinformatics3010011






