Analysis of Single-Cell RNA-Sequencing Data: A Step-by-Step Guide
Abstract
:1. Introduction
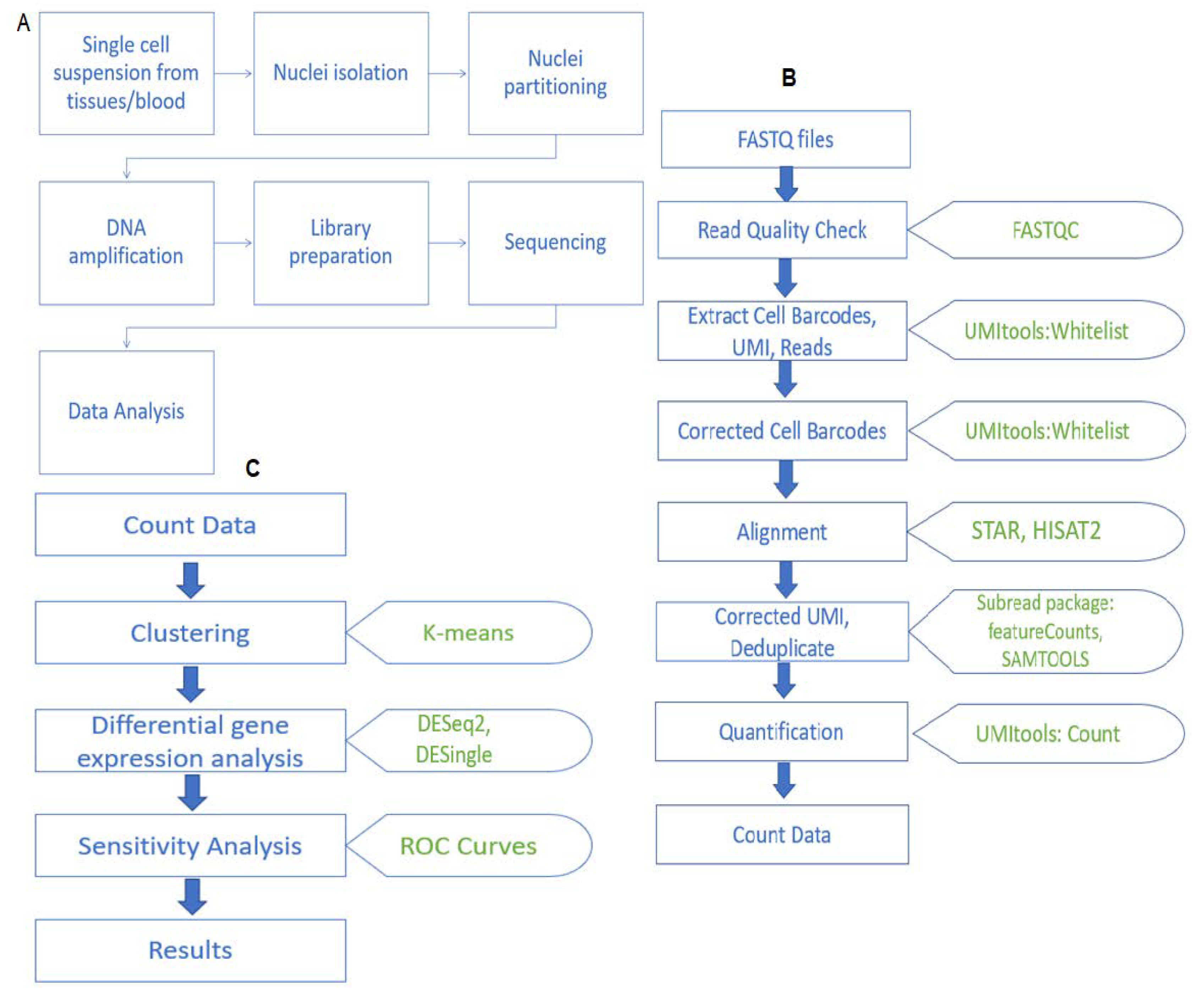
2. Material and Methods
2.1. Data Description
2.2. Raw Data Download
2.3. Data Preprocessing
2.4. Quality Check of Raw Reads
2.5. Extracting the Cell Barcodes, UMIs and Reads
2.6. Mapping to Reference Genome to Obtain Read Counts
2.7. Assigning Reads to Genes
3. Statistical Modeling and Data Analysis
3.1. Mathematical Models for scRNA Count Data
3.1.1. Negative Binomial Model
3.1.2. Zero-Inflated Negative Binomial Model
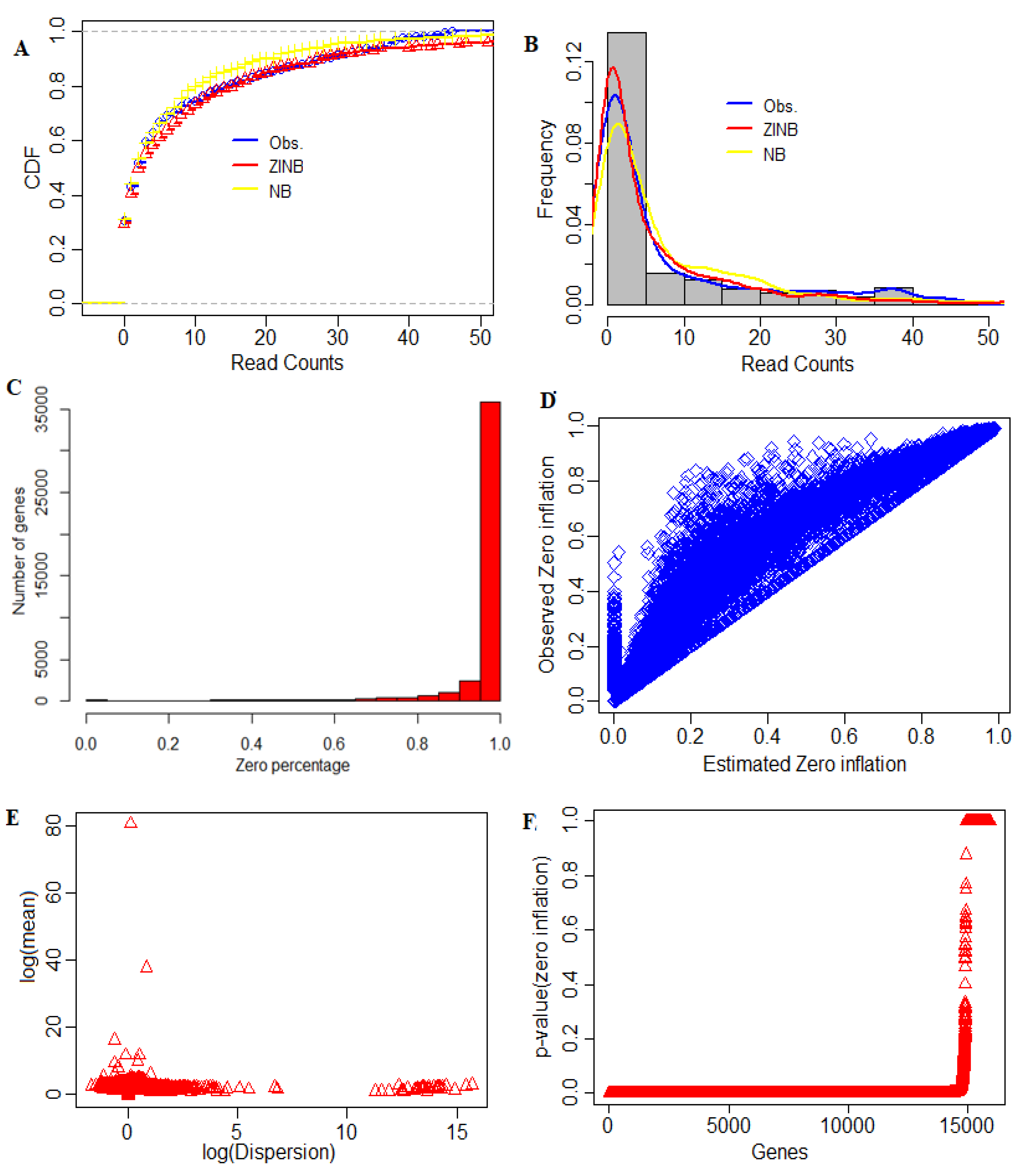
3.2. Zero-Inflation Analysis
3.3. Clustering
3.4. K-means Clustering
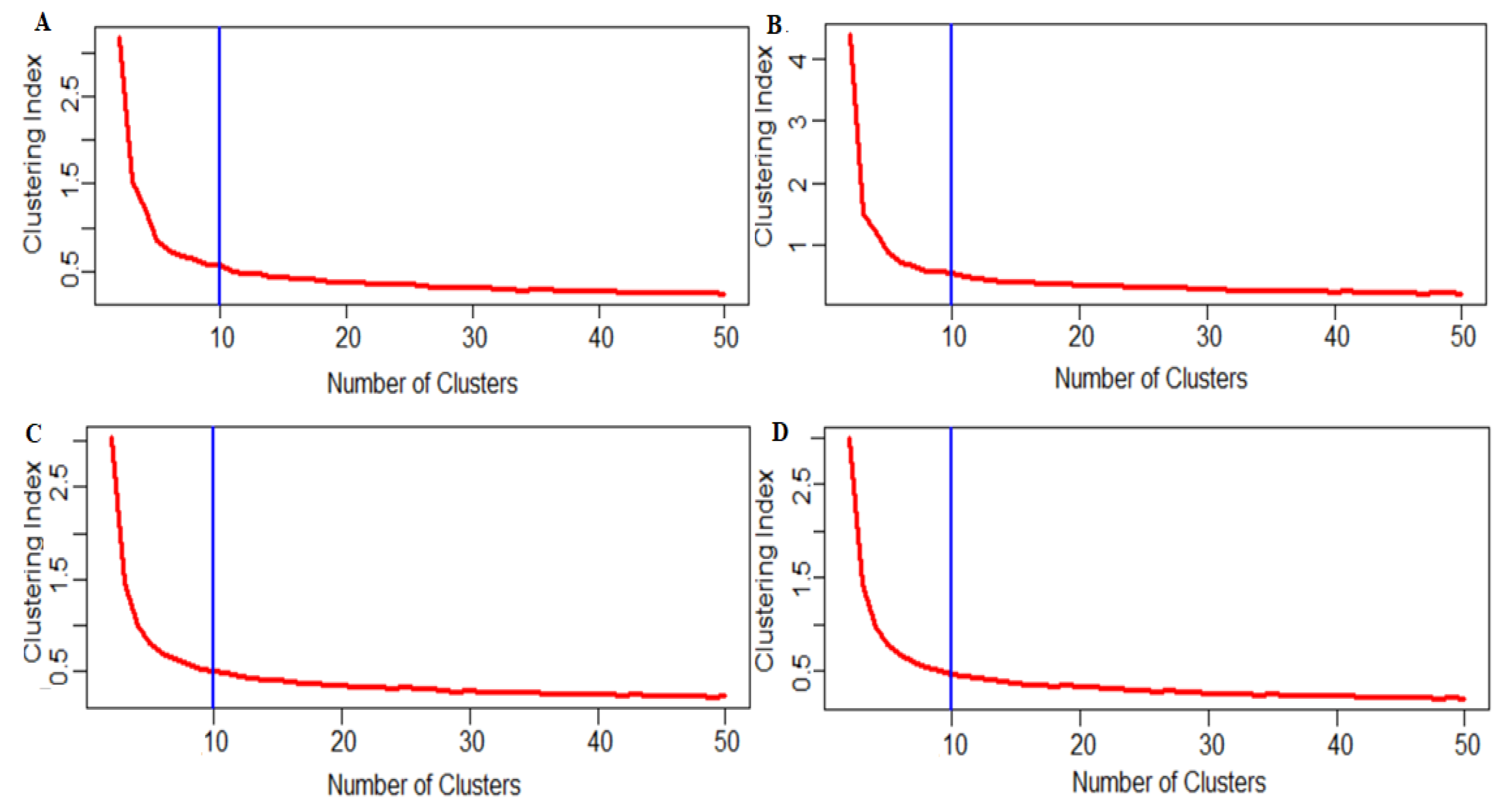
3.5. Determination of the Optimum Number of Clusters
3.6. Differential Gene Expression Analysis
3.7. DESeq2
3.8. DEsingle
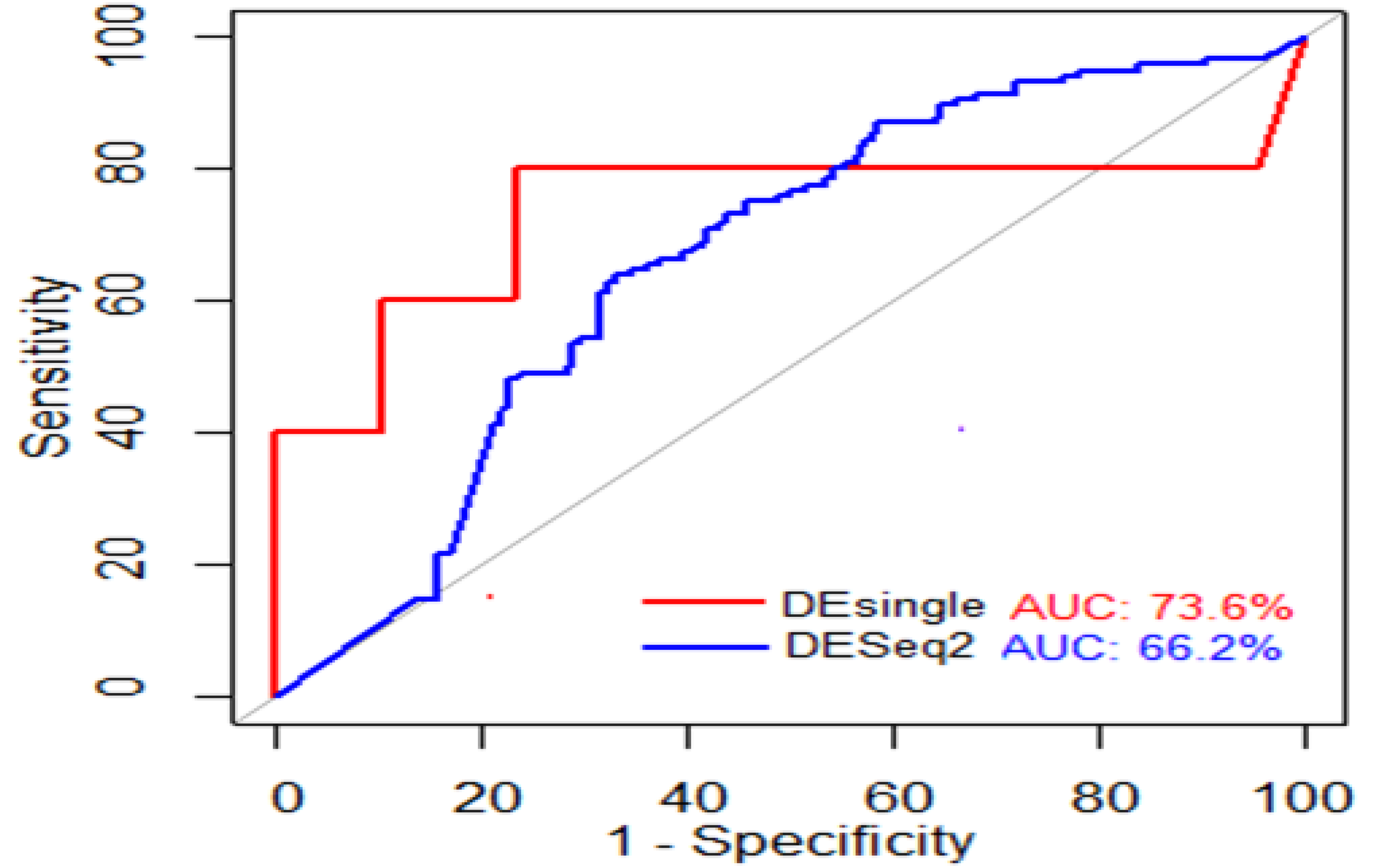
3.9. Performance Evaluation of DE Methods
4. Results and Discussion
4.1. Quality Control
4.2. Extracting UMIs, Cell Barcodes and UMIs
4.3. Mapping
4.4. Quantification
4.5. Determining the Distribution of Zeros in Data
4.6. Distribution of Cell Sequencing Depths
4.7. Clustering Analysis
4.8. Study the Effect of Zero’s Reduction on the Determination of Optimum Cell Clusters
4.9. Case 1: No Reduction
4.10. Case 2: Reduction in the Number of Genes when many Cells have Zero Counts
4.11. Differential Expression Analysis
4.12. Evaluating Performance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vallejos, C.A.; Richardson, S.; Marioni, J.C. Beyond comparisons of means: Understanding changes in gene expression at the single-cell level. Genome Biol. 2016, 17, 1. [Google Scholar] [CrossRef] [Green Version]
- Hwang, B.; Lee, J.H.; Bang, D. Single-cell RNA sequencing technologies and bioinformatics pipelines. Exp. Mol. Med. 2018, 50, 96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lavin, Y.; Kobayashi, S.; Leader, A.; Amir, E.-A.D.; Elefant, N.; Bigenwald, C.; Remark, R.; Sweeney, R.; Becker, C.D.; Levine, J.H.; et al. Innate Immune Landscape in Early Lung Adenocarcinoma by Paired Single-Cell Analyses. Cell 2017, 169, 750–765.e17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, F.; Barbacioru, C.; Wang, Y.; Nordman, E.; Lee, C.; Xu, N.; Wang, X.; Bodeau, J.; Tuch, B.B.; Siddiqui, A.; et al. mRNA-Seq whole-transcriptome analysis of a single cell. Nat. Methods 2009, 6, 377–382. [Google Scholar] [CrossRef]
- Scialdone, A.; Natarajan, K.N.; Saraiva, L.; Proserpio, V.; Teichmann, S.; Stegle, O.; Marioni, J.C.; Buettner, F. Computational assignment of cell-cycle stage from single-cell transcriptome data. Methods 2015, 85, 54–61. [Google Scholar] [CrossRef] [PubMed]
- Picelli, S.; Bjorklund, Å.K.; Faridani, O.; Sagasser, S.; Winberg, G.; Sandberg, R. Smart-seq2 for sensitive full-length transcriptome profiling in single cells. Nat. Methods 2013, 10, 1096–1098. [Google Scholar] [CrossRef] [PubMed]
- Brink, S.C.V.D.; Sage, F.; Vértesy, Á.; Spanjaard, B.; Peterson-Maduro, J.; Baron, C.; Robin, C.; Van Oudenaarden, A. Single-cell sequencing reveals dissociation-induced gene expression in tissue subpopulations. Nat. Methods 2017, 14, 935–936. [Google Scholar] [CrossRef] [PubMed]
- Hashimshony, T.; Senderovich, N.; Avital, G.; Klochendler, A.; de Leeuw, Y.; Anavy, L.; Gennert, D.; Li, S.; Livak, K.J.; Rozenblatt-Rosen, O.; et al. CEL-Seq2: Sensitive highly-multiplexed single-cell RNA-Seq. Genome Biol. 2016, 17, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Macosko, E.Z.; Basu, A.; Satija, R.; Nemesh, J.; Shekhar, K.; Goldman, M.; Tirosh, I.; Bialas, A.R.; Kamitaki, N.; Martersteck, E.M.; et al. Highly Parallel Genome-wide Expression Profiling of Individual Cells Using Nanoliter Droplets. Cell 2015, 161, 1202–1214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zemmour, D.; Zilionis, R.; Kiner, E.; Klein, A.M.; Mathis, D.; Benoist, C. Single-cell gene expression reveals a landscape of regulatory T cell phenotypes shaped by the TCR. Nat. Immunol. 2018, 19, 291–301. [Google Scholar] [CrossRef] [PubMed]
- Jaitin, D.A.; Kenigsberg, E.; Keren-Shaul, H.; Elefant, N.; Paul, F.; Zaretsky, I.; Mildner, A.; Cohen, N.; Jung, S.; Tanay, A.; et al. Massively parallel single-cell RNA-seq for marker-free decomposition of tissues into cell types. Science 2014, 343, 776–779. [Google Scholar] [CrossRef] [PubMed]
- Ramsköld, D.; Luo, S.; Wang, Y.-C.; Li, R.; Deng, Q.; Faridani, O.; Daniels, G.A.; Khrebtukova, I.; Loring, J.F.; Laurent, L.; et al. Full-length mRNA-Seq from single-cell levels of RNA and individual circulating tumor cells. Nat. Biotechnol. 2012, 30, 777–782. [Google Scholar] [CrossRef] [Green Version]
- Ziegenhain, C.; Vieth, B.; Parekh, S.; Reinius, B.; Guillaumet-Adkins, A.; Smets, M.; Leonhardt, H.; Enard, W. Comparative Analysis of Single-Cell RNA Sequencing Methods. Mol. Cell 2017, 65, 631–643.e4. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Gerstein, M.; Snyder, M. RNA-seq: A revolutionary tool for transcriptomics. Nat. Rev. Genet. 2009, 10, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejczyk, A.; Kim, J.K.; Svensson, V.; Marioni, J.; Teichmann, S.A. The technology and biology of single-cell RNA sequencing. Mol. Cell 2015, 58, 610–620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.; Rai, A.; Merchant, M.L.; Cave, M.C.; Rai, S.N. A Comprehensive Survey of Statistical Approaches for Differential Expression Analysis in Single-cell RNA Sequencing Studies. Genes 2021, 12, 1947. [Google Scholar] [CrossRef]
- Bacher, R.; Kendziorski, C. Design and computational analysis of single-cell RNA-sequencing experiments. Genome Biol. 2016, 17, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brennecke, P.; Anders, S.; Kim, J.K.; Kolodziejczyk, A.; Zhang, X.; Proserpio, V.; Baying, B.; Benes, V.; Teichmann, S.; Marioni, J.; et al. Accounting for technical noise in single-cell RNA-seq experiments. Nat. Methods 2013, 10, 1093–1095. [Google Scholar] [CrossRef] [PubMed]
- Blower, M.D.; Jambhekar, A.; Schwarz, D.S.; Toombs, J. Combining Different mRNA Capture Methods to Analyze the Transcriptome: Analysis of the Xenopus laevis Transcriptome. PLoS ONE 2013, 8, e77700. [Google Scholar] [CrossRef]
- Hicks, S.C.; Townes, F.W.; Teng, M.; Irizarry, R. Missing data and technical variability in single-cell RNA-sequencing experiments. Biostatistics 2018, 19, 562–578. [Google Scholar] [CrossRef]
- Haque, A.; Engel, J.; Teichmann, S.A.; Lönnberg, T. A practical guide to single-cell RNA-sequencing for biomedical research and clinical applications. Genome Med. 2017, 9, 75. [Google Scholar] [CrossRef] [PubMed]
- Qiu, P. Embracing the dropouts in single-cell RNA-seq analysis. Nat. Comm. 2020, 11, 1169. [Google Scholar] [CrossRef] [Green Version]
- Lafzi, A.; Moutinho, C.; Picelli, S.; Heyn, H. Tutorial: Guidelines for the experimental design of single-cell RNA sequencing studies. Nat. Protoc. 2018, 13, 2742–2757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luecken, M.D.; Theis, F.J. Current best practices in single-cell RNA-seq analysis: A tutorial. Mol. Syst. Biol. 2019, 15, e8746. [Google Scholar] [CrossRef]
- Andrews, T.S.; Kiselev, V.Y.; McCarthy, D.; Hemberg, M. Tutorial: Guidelines for the computational analysis of single-cell RNA sequencing data. Nat. Protoc. 2021, 16, 1–9. [Google Scholar] [CrossRef]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miao, Z.; Deng, K.; Wang, X.; Zhang, X. DEsingle for detecting three types of differential expression in single-cell RNA-seq data. Bioinformatics 2018, 34, 3223–3224. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Su, S.; Dong, X.; Amann-Zalcenstein, D.; Biben, C.; Seidi, A.; Hilton, D.J.; Naik, S.H.; Ritchie, M.E. scPipe: A flexible R/Bioconductor preprocessing pipeline for single-cell RNA-sequencing data. PLoS Comput. Biol. 2018, 14, e1006361. [Google Scholar] [CrossRef]
- Tian, L.; Dong, X.; Freytag, S.; Cao, K.-A.L.; Su, S.; JalalAbadi, A.; Amann-Zalcenstein, D.; Weber, T.S.; Seidi, A.; Jabbari, J.S.; et al. Benchmarking single cell RNA-sequencing analysis pipelines using mixture control experiments. Nat. Methods 2019, 16, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Cock, P.J.; Fields, C.J.; Goto, N.; Heuer, M.L.; Rice, P.M. The Sanger FASTQ file format for sequences with quality scores, and the Solexa/Illumina FASTQ variants. Nucleic Acids Res. 2010, 38, 1767–1771. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sequence Read Archives. Available online: https://trace.ncbi.nlm.nih.gov/Traces/sra/sra.cgi?view=software (accessed on 10 November 2020).
- Leinonen, R.; Sugawara, H.; Shumway, M.; on behalf of the International Nucleotide Sequence Database Collaboration. The Sequence Read Archive. Nucleic Acids Res. 2010, 39, D19–D21. [Google Scholar] [CrossRef] [Green Version]
- Andrews, S. FastQC-A Quality Control Tool for High throughput Sequence Data. 2014. Available online: http://www.bioinformatics.babraham.ac.uk/projects/fastqc/ (accessed on 10 November 2020).
- Smith, T.; Heger, A.; Sudbery, I. UMI-tools: Modeling sequencing errors in Unique Molecular Identifiers to improve quantification accuracy. Genome Res. 2017, 27, 491–499. [Google Scholar] [CrossRef] [Green Version]
- “GRC and Collaborators”. Genome Reference Consortium. Available online: https://www.ncbi.nlm.nih.gov/grc/credits/ (accessed on 19 October 2020).
- Harrow, J.; Frankish, A.; Gonzalez, J.M.; Tapanari, E.; Diekhans, M.; Kokocinski, F.; Aken, B.L.; Barrell, D.; Zadissa, A.; Searle, S.; et al. GENCODE: The reference human genome annotation for The ENCODE Project. Genome Res. 2012, 22, 1760–1774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dobin, A.; Davis, C.A.; Schlesinger, F.; Drenkow, J.; Zaleski, C.; Jha, S.; Batut, P.; Chaisson, M.; Gingeras, T.R. Gingeras, STAR: Ultrafast universal RNA-seq aligner. Bioinformatics 2013, 29, 15–21. [Google Scholar] [CrossRef]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R.; 1000 Genome Project Data Processing Subgroup. The Sequence Alignment/Map format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef] [Green Version]
- Liao, Y.; Smyth, G.K.; Shi, W. featureCounts: An efficient general-purpose program for assigning sequence reads to genomic features. Bioinformatics 2014, 30, 923–930. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Ewing, B.; Hillier, L.; Wendl, M.C.; Green, P. Base-calling of automated sequencer traces using Phred. I. Accuracy assessment. Genome Res. 1998, 8, 175–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Batut, B.; Hiltemann, S.; Bagnacani, A.; Baker, D.; Bhardwaj, V.; Blank, C.; Bretaudeau, A.; Brillet-Guéguen, L.; Čech, M.; Chilton, J.; et al. 2018 Community-Driven Data Analysis Training for Biology. Cell Syst. 2018, 6, 752–758.e1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dobin, A.; Gingeras, T.R. Mapping RNA-seq Reads with STAR. Curr. Protoc. Bioinform. 2015, 51, 1–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- GENOCODE. Available online: https://www.gencodegenes.org/human/stats.html (accessed on 15 November 2020).
- Robinson, M.D.; McCarthy, D.J.; Smyth, G.K. EdgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 2010, 26, 139–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hardcastle, T.; Kelly, K. BaySeq: Empirical Bayesian Methods for Identifying Differential Expression in Sequence Count Data. BMC Bioinform. 2010, 11, 422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.V.; Li, J.J. An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat Commun. 2018, 9, 997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lun, A.T.L.; Bach, K.; Marioni, J.C. Pooling Across Cells to Normalize Single-Cell Rna Sequencing Data with Many Zero Counts. Genome Biol. 2016, 17, 75. [Google Scholar] [CrossRef] [PubMed]
- Žurauskienė, J.; Yau, C. PcaReduce: Hierarchical clustering of single-cell transcriptional profiles. BMC Bioinform. 2016, 17, 140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.; Rai, S.N. SwarnSeq: An improved statistical approach for differential expression analysis of single-cell RNA-seq data. Genomics 2021, 113, 1308–1324. [Google Scholar] [CrossRef]
- Das, S.; Rai, S.N. Statistical methods for analysis of single-cell RNA-sequencing data. MethodsX 2021, 8, 101580. [Google Scholar] [CrossRef]
- Shalek, A.K.; Satija, R.; Shuga, J.; Trombetta, J.J.; Gennert, D.; Lu, D.; Chen, P.; Gertner, R.S.; Gaublomme, J.T.; Yosef, N.; et al. Single-cell RNA-seq reveals dynamic paracrine control of cellular variation. Nature 2014, 510, 363–369. [Google Scholar] [CrossRef] [Green Version]
- Pierson, E.; Yau, C. Zifa: Dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biol. 2015, 16, 241. [Google Scholar] [CrossRef] [Green Version]
- Scholtens, D.; von Heydebreck, A. Analysis of Differential Gene Expression Studies. In Bioinformatics and Computational Biology Solutions Using R and Bioconductor; Gentleman, R., Carey, V.J., Huber, W., Irizarry, R.A., Dudoit, S., Eds.; Statistics for Biology and Health; Springer: New York, NY, USA, 2005. [Google Scholar] [CrossRef]

| Name | Version | Description | Reference |
|---|---|---|---|
| FastQC | v0.11.9 | FastQ Quality Check | [33] |
| UMI-tools | 1.0.0 | Tools for handling Unique Molecular Identifiers | [34] |
| Human genome | Grch38/hg 38 | Human genome reference file | [35] |
| GTF | Release 35 | Gene Transfer Format | [36] |
| STAR | 2.7 | Spliced Transcripts Alignment to a Reference | [37] |
| SAM tools | 1.4 | SAMtools software package | [38] |
| Subread package | 2.0.1 | The package used by SAMtools | [39] |
| Stats R package | 3.6.1 | Package for k-means clustering | [40,41] |
| DESeq2 | 1.28.1 | DE analysis tool for RNA-seq | [26] |
| DEsingle | 1.8.2 | DE analysis tool for scRNA-seq | [27] |
| Case Type | Percentage Reduction | No. of Optimal Clusters | No. of Genes |
|---|---|---|---|
| Case 1 | No reduction | 10 | 42,406 |
| Case 2 | 80% | 10 | 2415 |
| Case 2 | 60% | 10 | 1201 |
| Case 2 | 50% | 10 | 879 |
| Case 2 | 30% | 10 | 454 |
| Level of Significance | DEsingle Genes | DESeq2 Genes | Common Genes |
|---|---|---|---|
| 1% | 634 | 79 | 25 |
| 0.1% | 401 | 75 | 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malhotra, A.; Das, S.; Rai, S.N. Analysis of Single-Cell RNA-Sequencing Data: A Step-by-Step Guide. BioMedInformatics 2022, 2, 43-61. https://doi.org/10.3390/biomedinformatics2010003
Malhotra A, Das S, Rai SN. Analysis of Single-Cell RNA-Sequencing Data: A Step-by-Step Guide. BioMedInformatics. 2022; 2(1):43-61. https://doi.org/10.3390/biomedinformatics2010003
Chicago/Turabian StyleMalhotra, Aanchal, Samarendra Das, and Shesh N. Rai. 2022. "Analysis of Single-Cell RNA-Sequencing Data: A Step-by-Step Guide" BioMedInformatics 2, no. 1: 43-61. https://doi.org/10.3390/biomedinformatics2010003
APA StyleMalhotra, A., Das, S., & Rai, S. N. (2022). Analysis of Single-Cell RNA-Sequencing Data: A Step-by-Step Guide. BioMedInformatics, 2(1), 43-61. https://doi.org/10.3390/biomedinformatics2010003







