Roles of Earth’s Albedo Variations and Top-of-the-Atmosphere Energy Imbalance in Recent Warming: New Insights from Satellite and Surface Observations
Abstract
1. Introduction
2. Data and Methods
2.1. Satellite and Surface Datasets
2.2. Modeling the Response of Global Surface Air Temperature to Solar Forcing
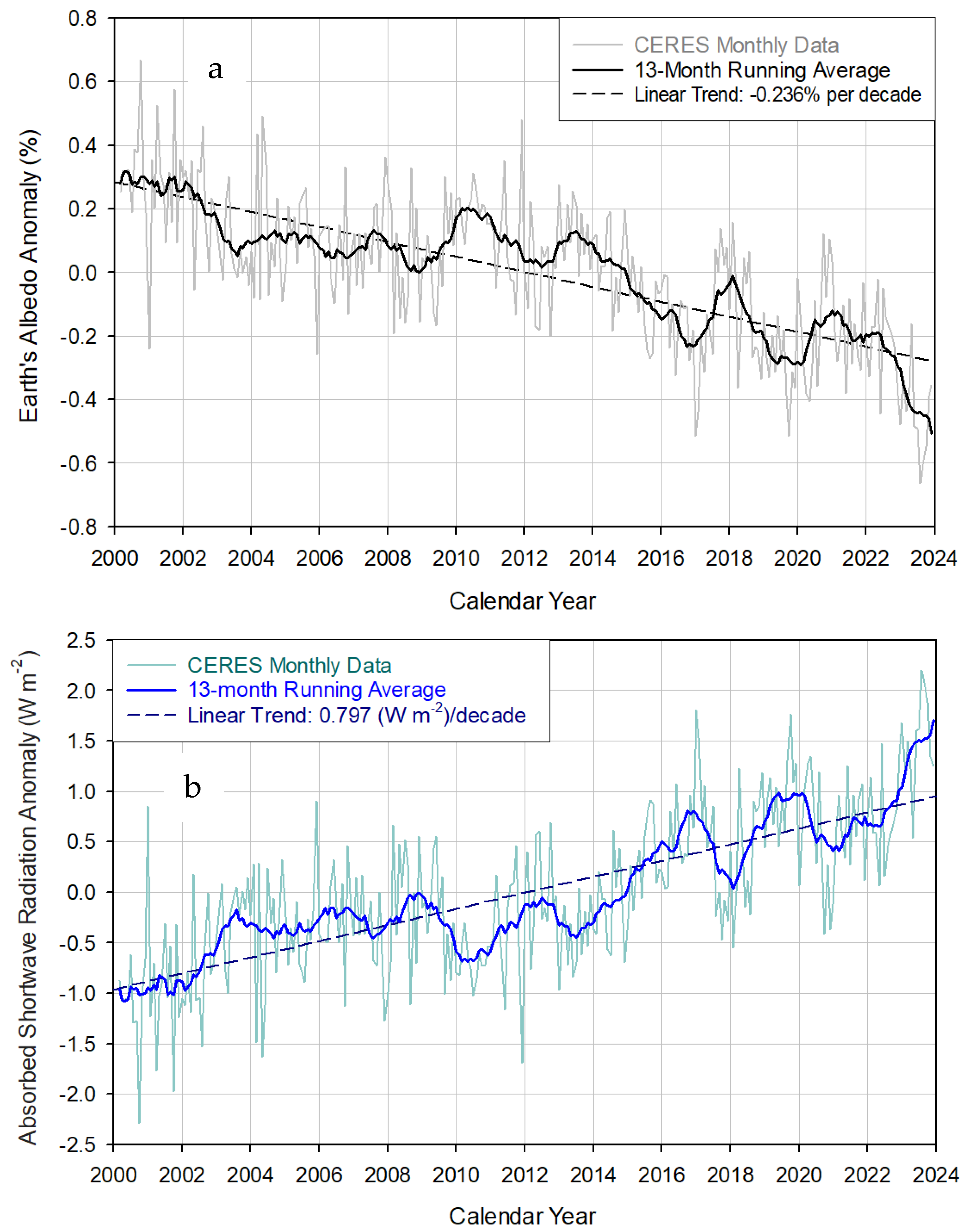
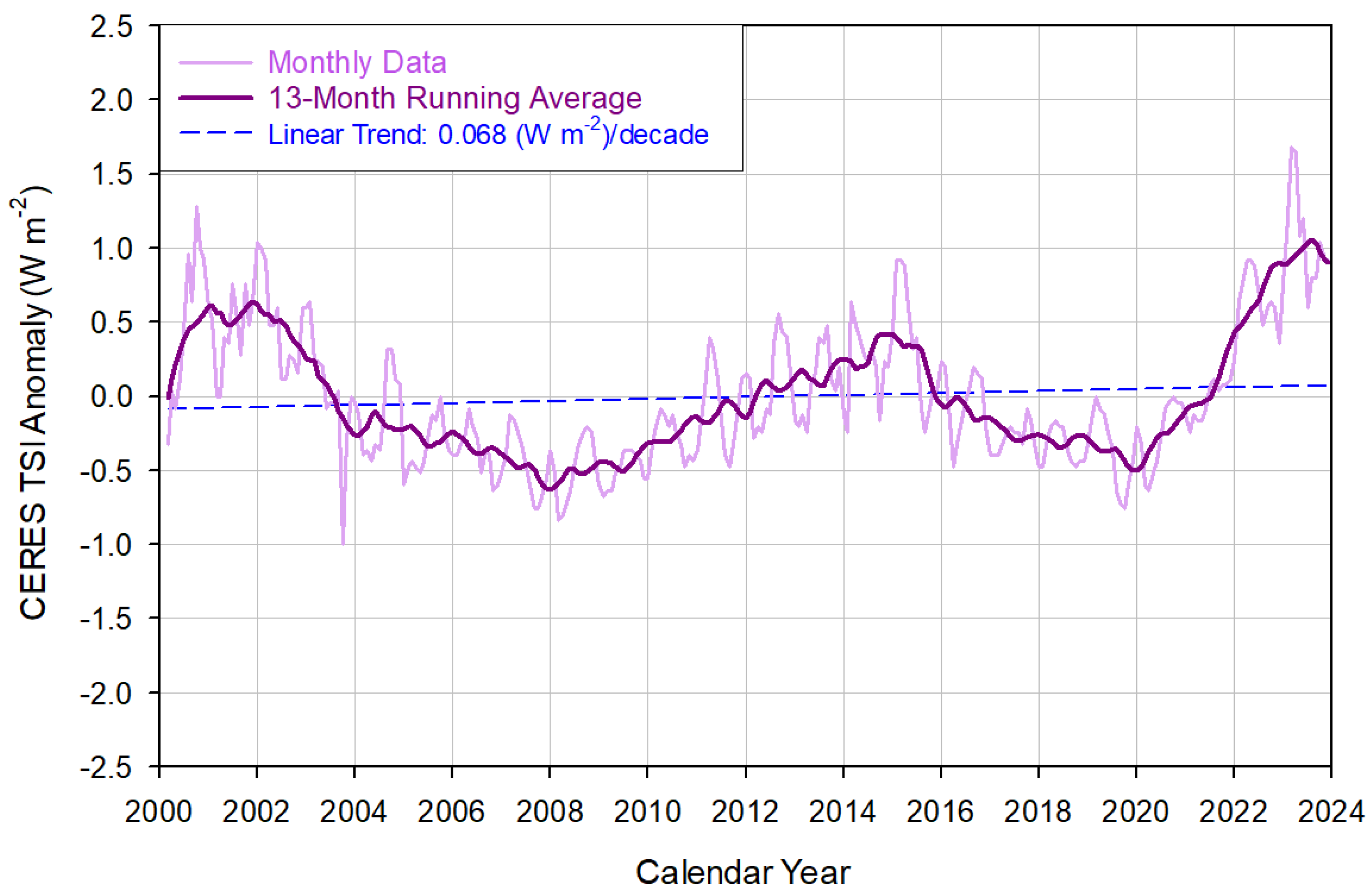
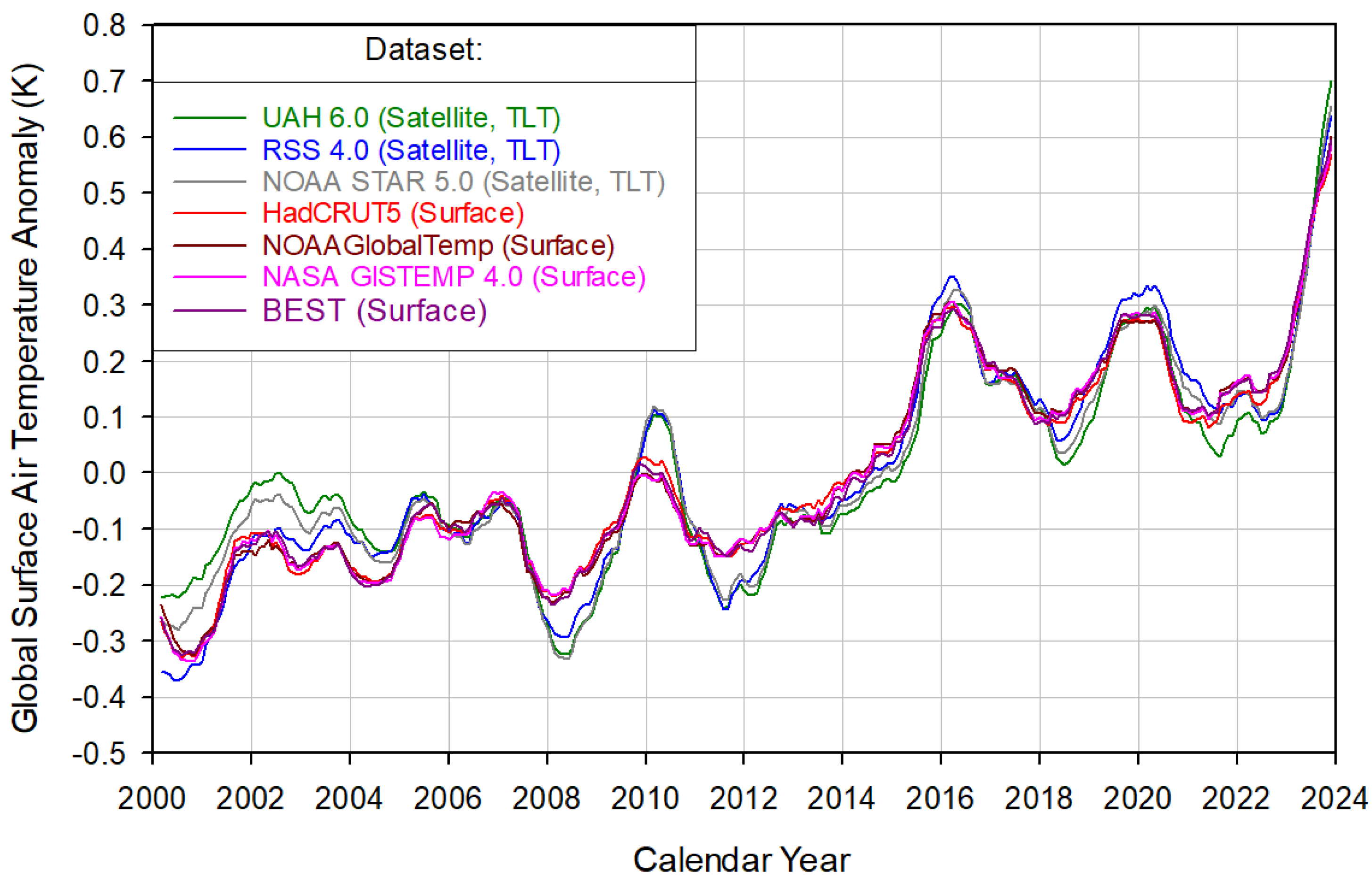
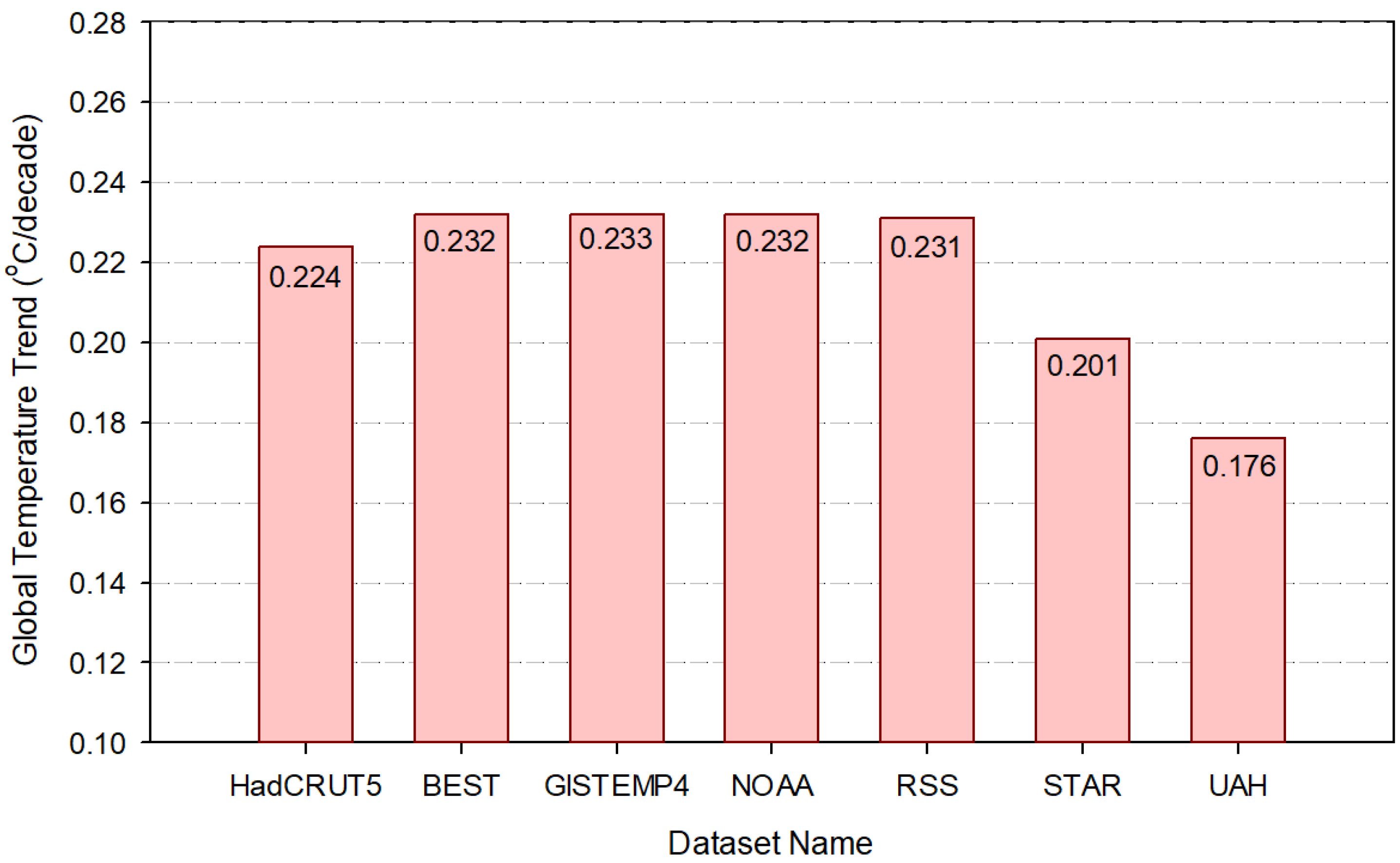
3. Results
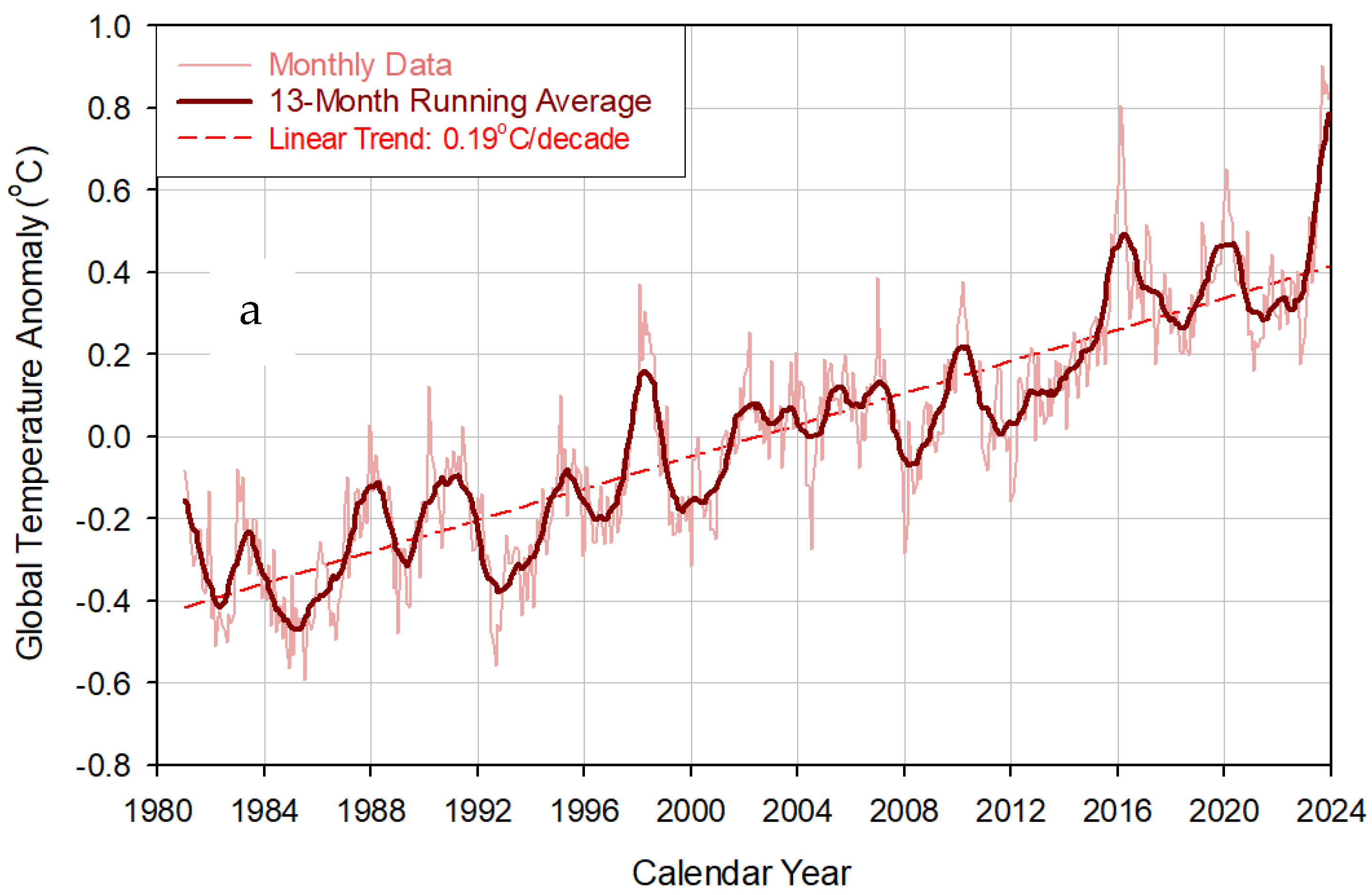
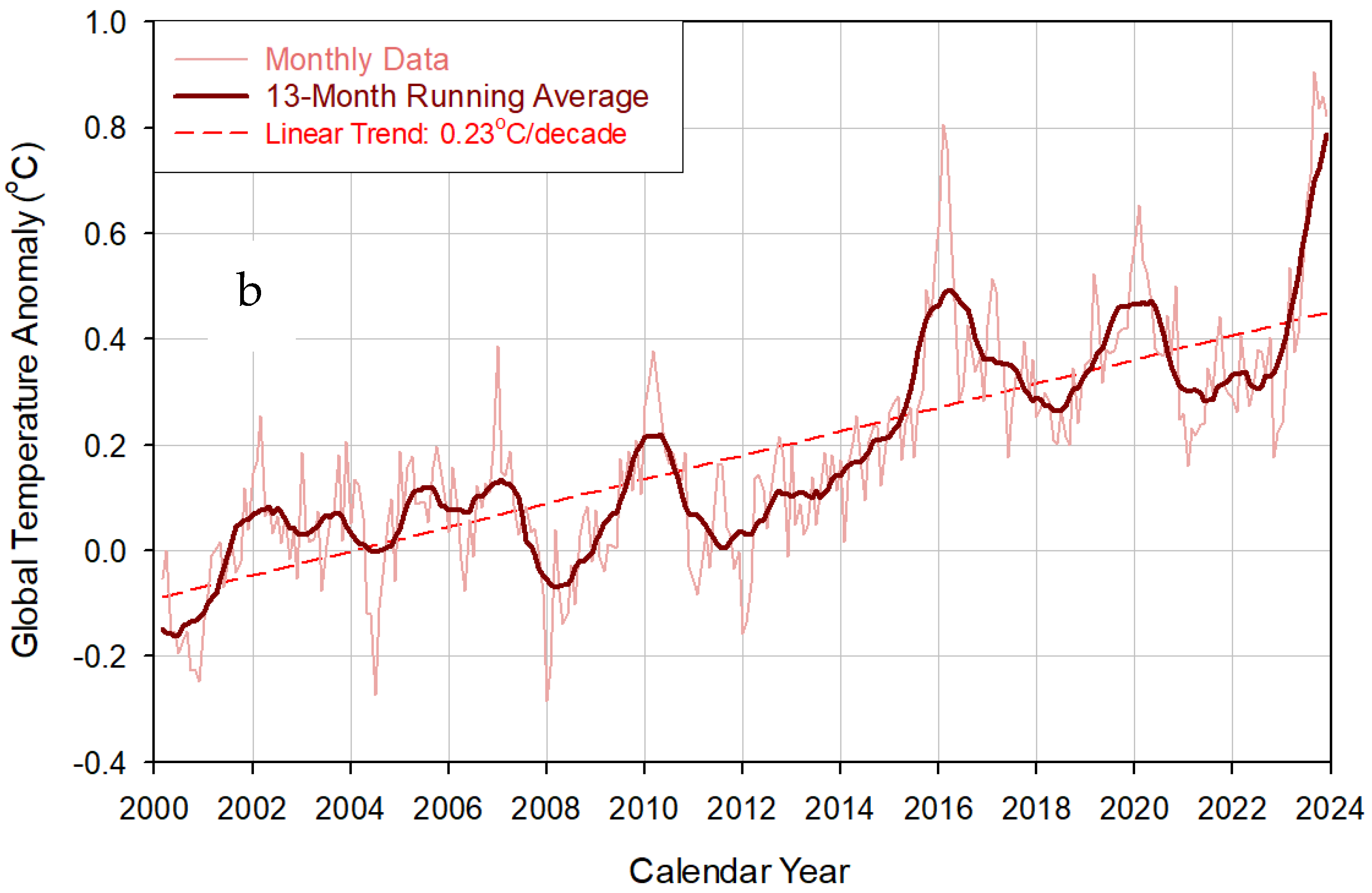
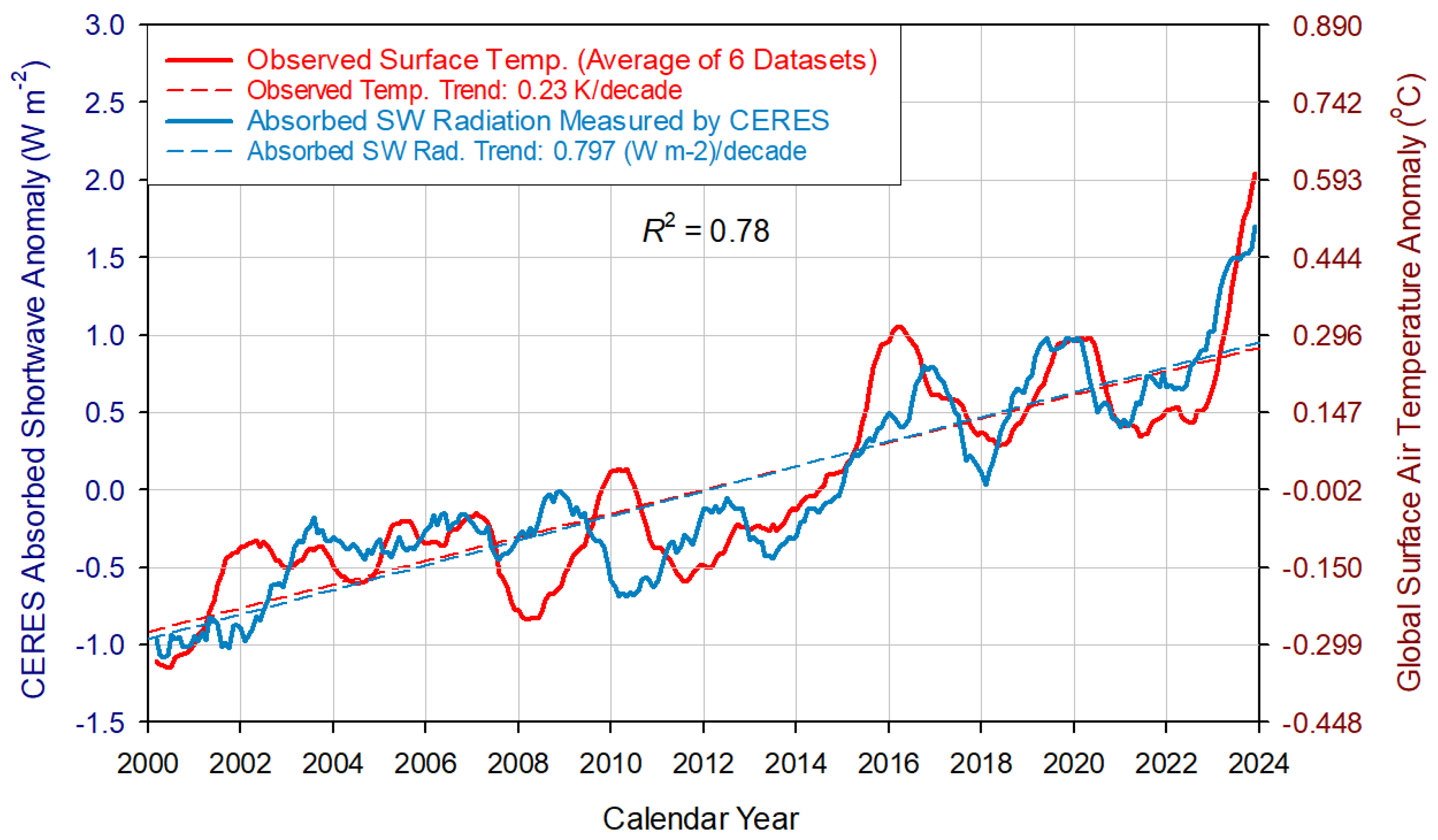
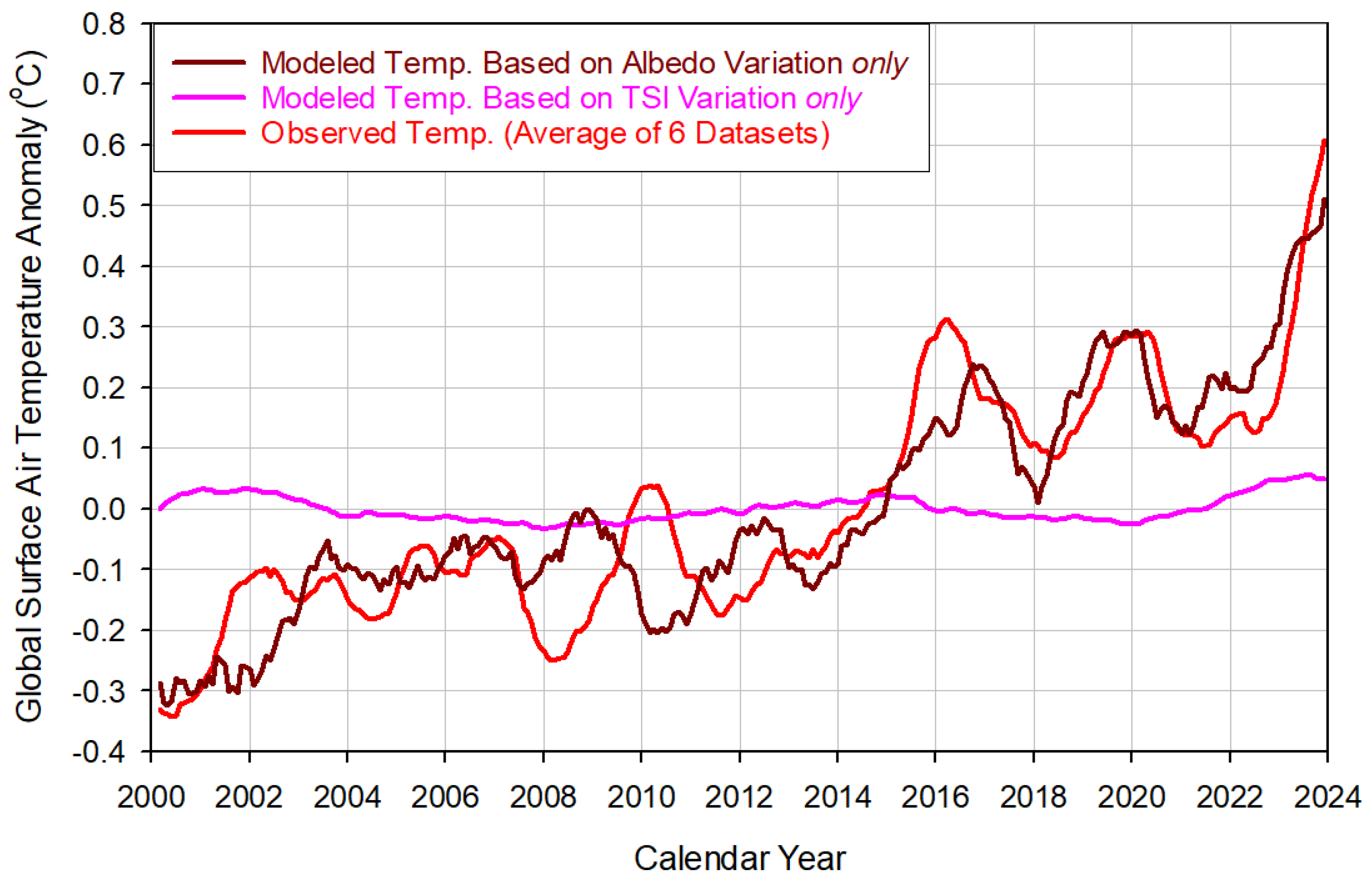
3.1. Drivers of Recent Warming
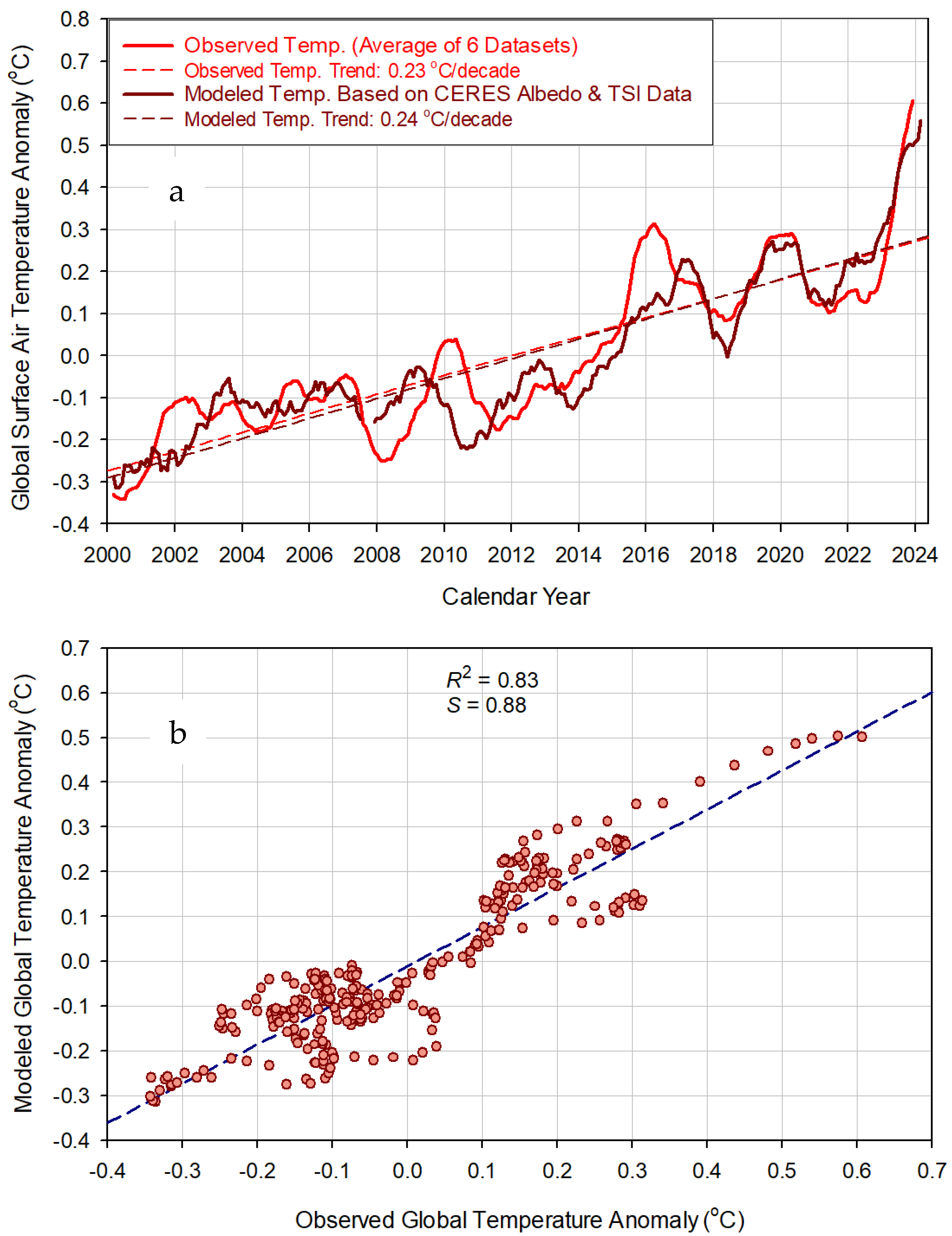
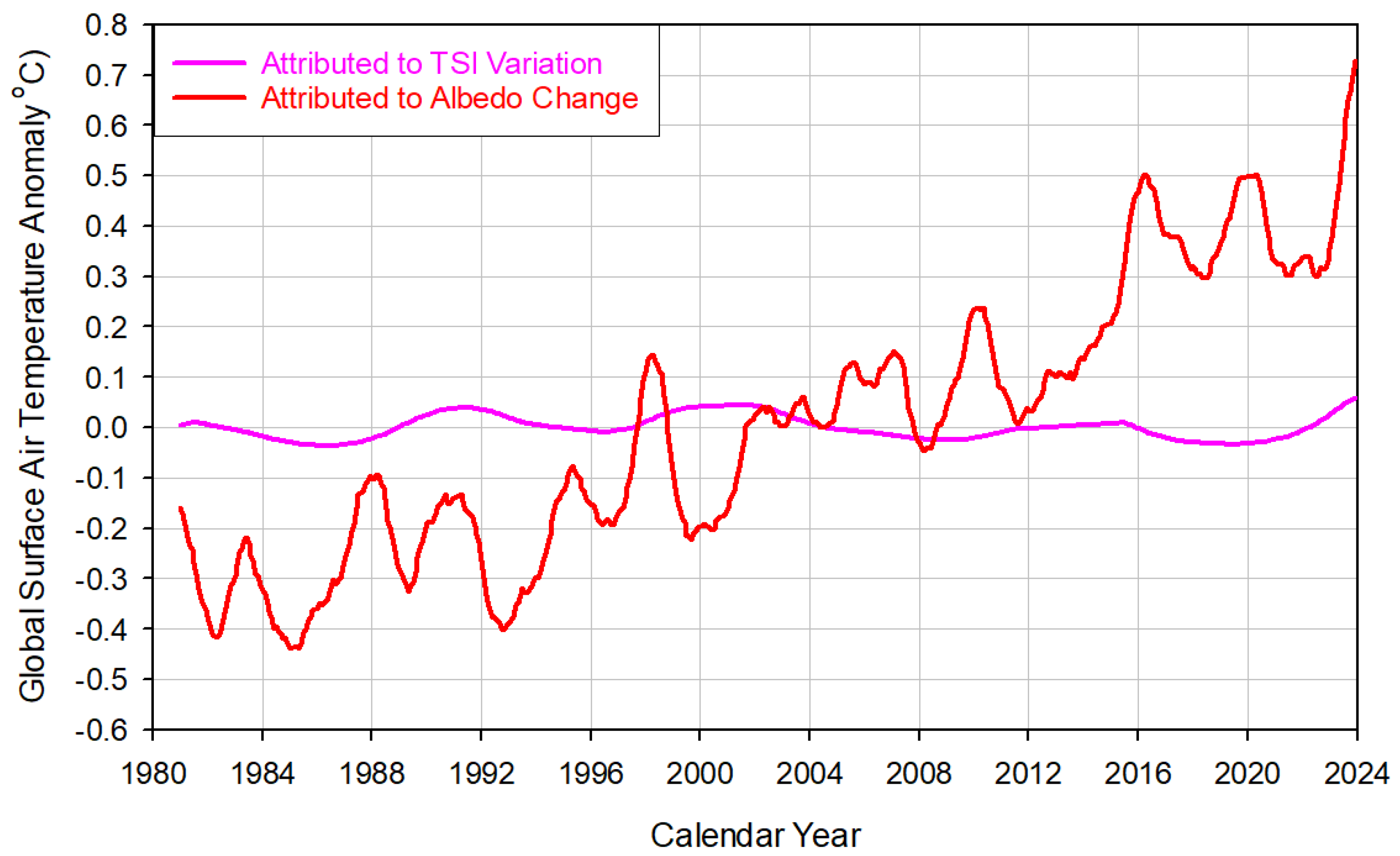
3.2. Contributions of TSI and Albedo Variations to Recent Warming
4. Discussion
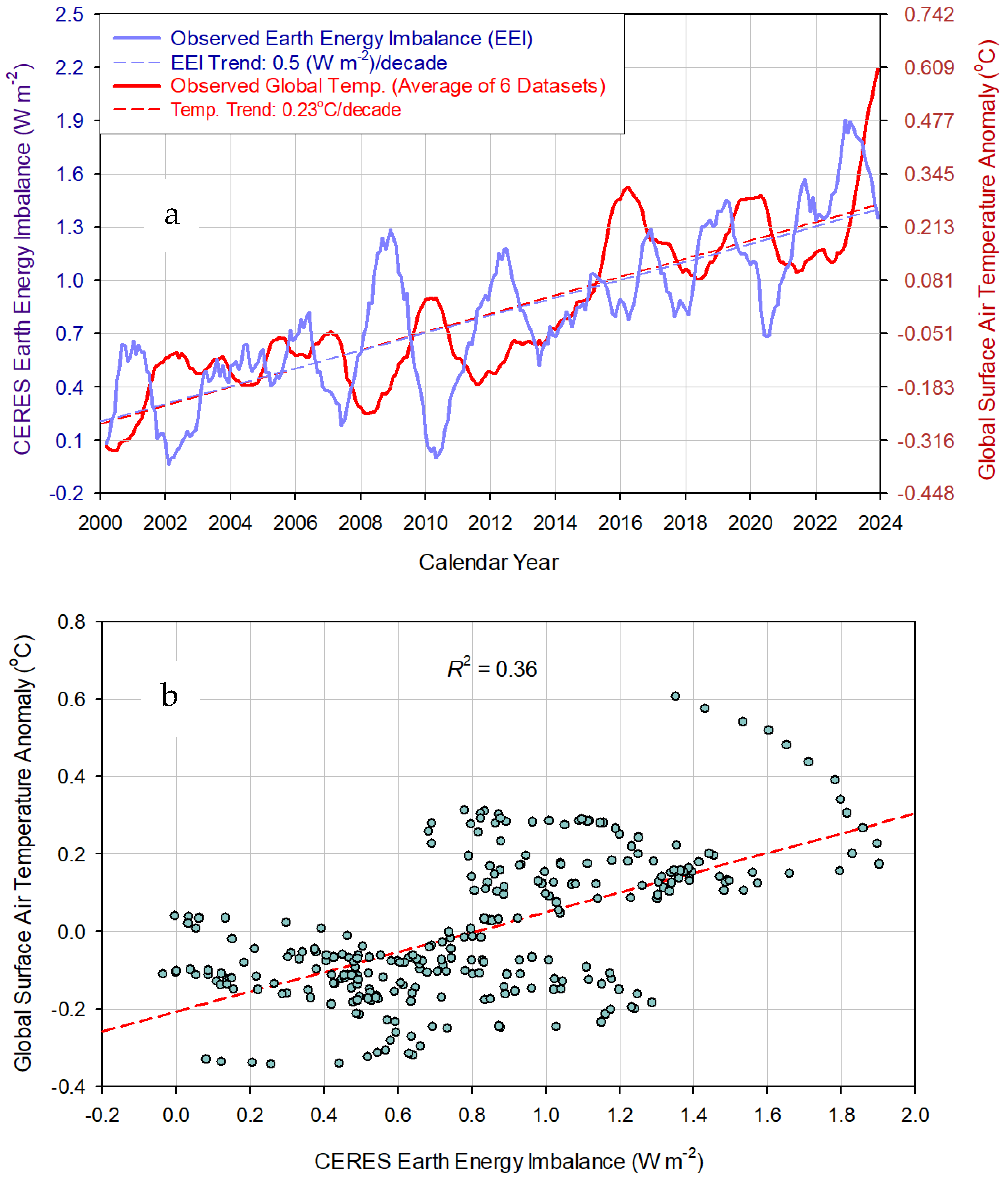
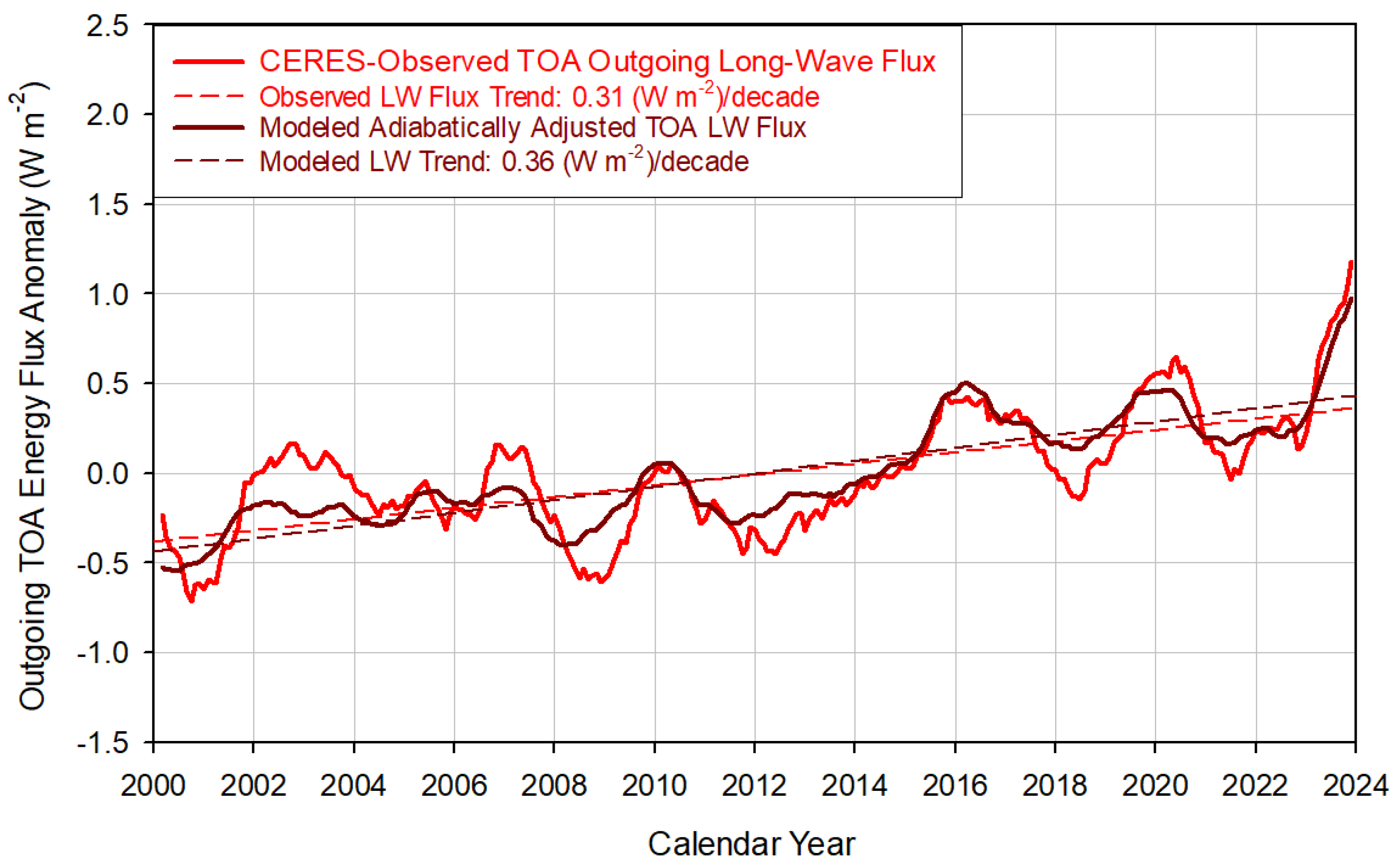
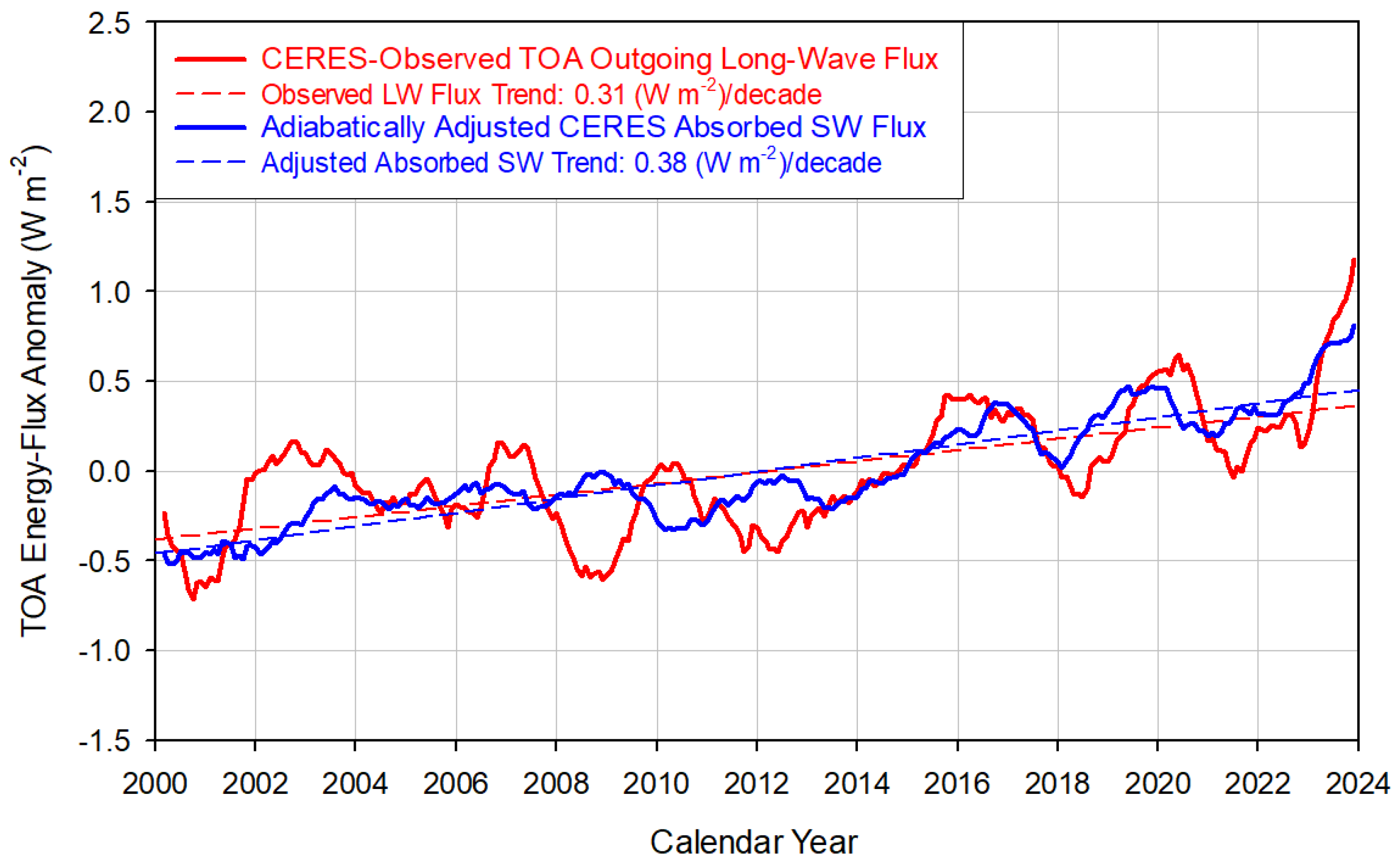
4.1. The Earth Energy Imbalance
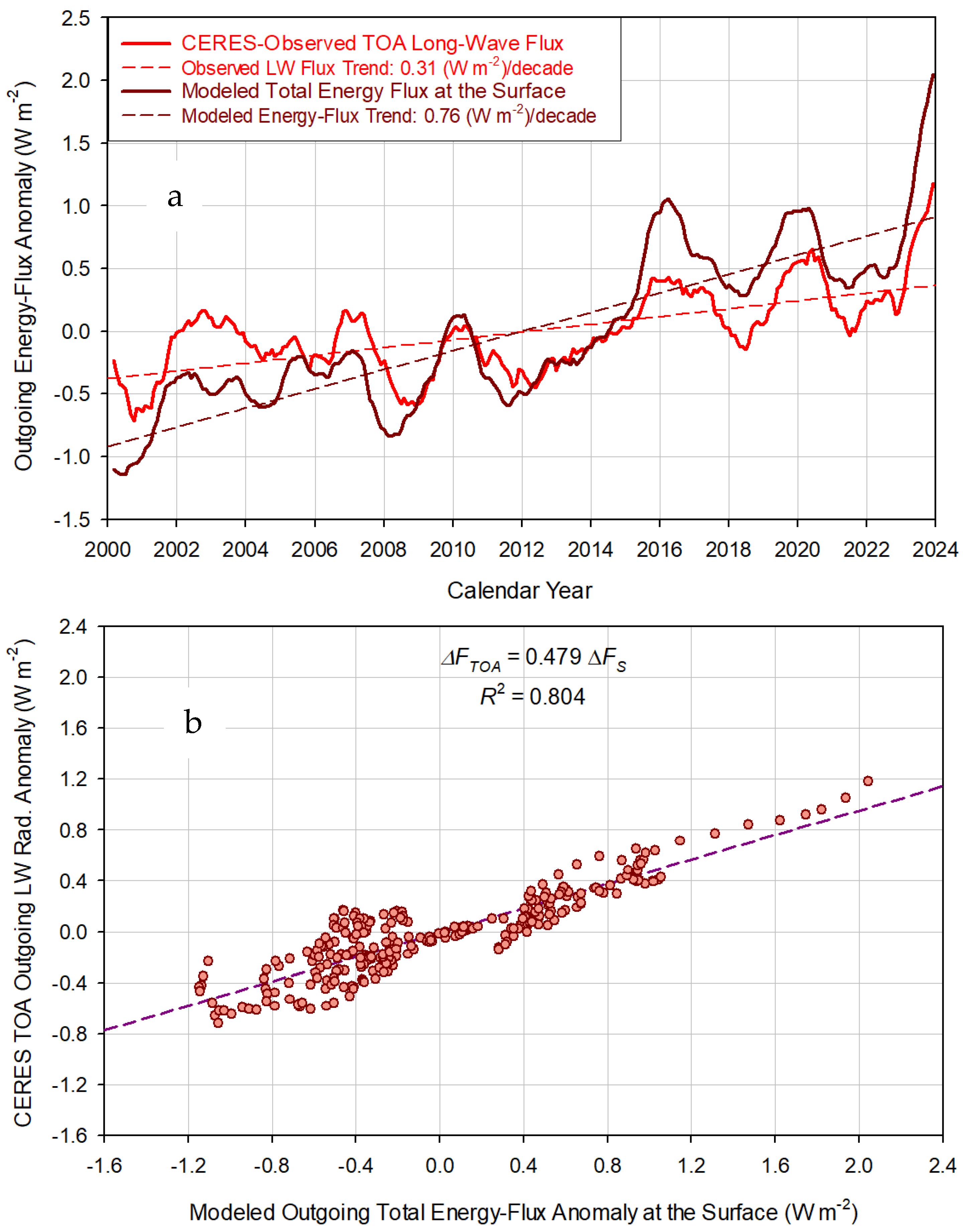
4.2. Physical Nature of the Earth Energy Imbalance
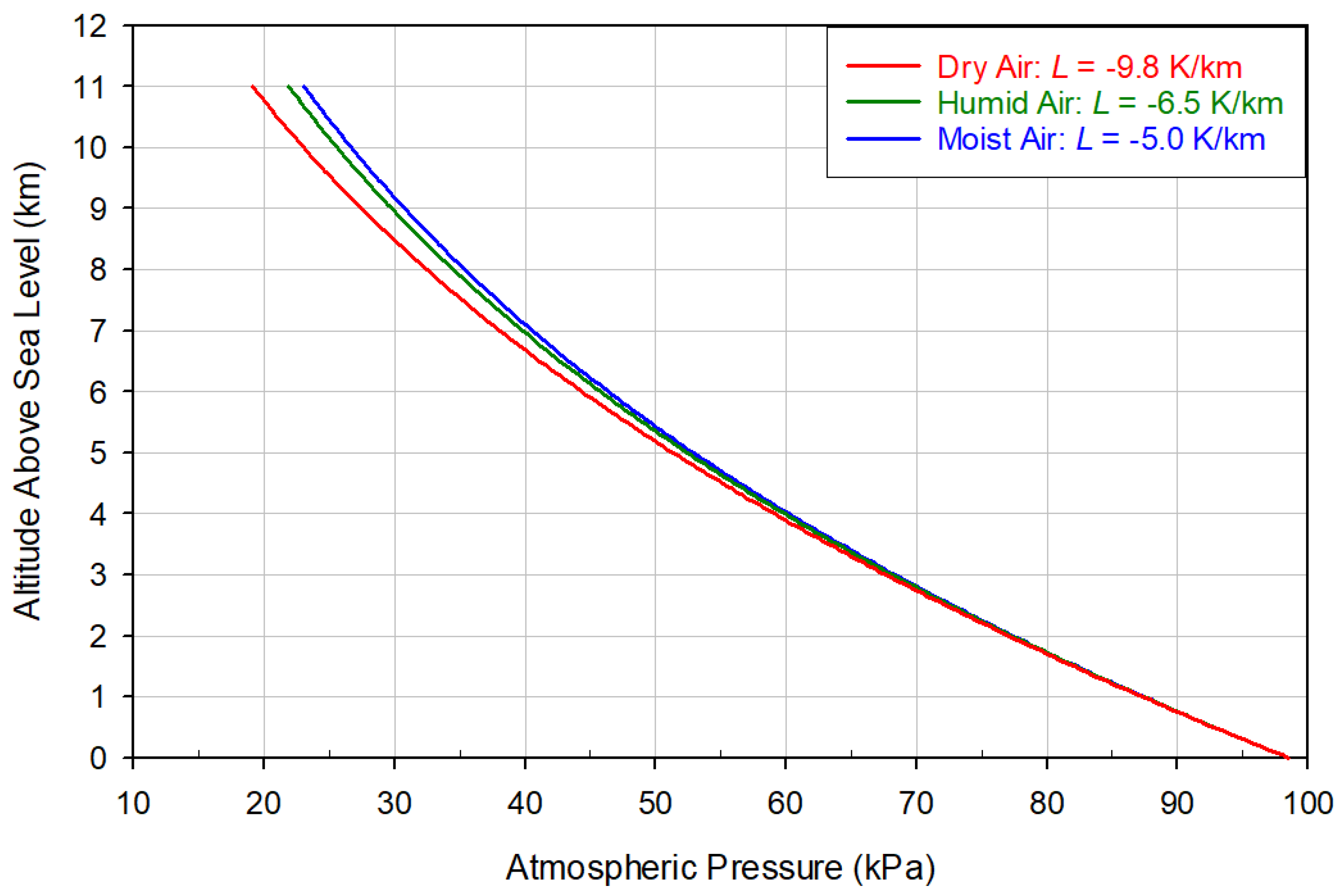
The Earth Energy Imbalance Explained by Thermodynamic Theory
4.3. Recapitulation of Findings about the Earth Energy Imbalance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; 2391p. [Google Scholar] [CrossRef]
- Forster, P.; Storelvmo, T.; Armour, K.; Collins, W.; Dufresne, J.L.; Frame, D.; Lunt, D.; Mauritsen, T.; Palmer, M.; Watanabe, M.; et al. The Earth’s Energy Budget, Climate Feedbacks, and Climate Sensitivity. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 923–1054. [Google Scholar] [CrossRef]
- Stanhill, G.; Achiman, O.; Rosa, R.; Cohen, S. The cause of solar dimming and brightening at the Earth’s surface during the last half century: Evidence from measurements of sunshine duration. J. Geophys. Res. Atmos. 2014, 119, 10902–10911. [Google Scholar] [CrossRef]
- Yuan, M.; Leirvik, T.; Wild, M. Global trends in downward surface solar radiation from spatial interpolated ground observations during 1961–2019. J. Clim. 2021, 34, 9501–9521. [Google Scholar] [CrossRef]
- Loeb, N.G.; Thorsen, T.J.; Norris, J.R.; Wang, H.; Su, W. Changes in Earth’s energy budget during and after the “pause” in global warming: An observational perspective. Climate 2018, 6, 62. [Google Scholar] [CrossRef]
- Loeb, N.G.; Wang, H.; Rose, F.G.; Kato, S.; Smith Jr, W.L. Decomposing shortwave top-of-atmosphere and surface radiative flux variations in terms of surface and atmospheric contributions. J. Clim. 2019, 32, 5003–5019. [Google Scholar] [CrossRef]
- Loeb, N.G.; Wang, H.; Allan, R.P.; Andrews, T.; Armour, K.; Cole, J.N.S.; Dufresne, J.; Forster, P.; Gettelman, A.; Guo, H.; et al. New generation of climate models track recent unprecedented changes in Earth’s radiation budget observed by CERES. Geophys. Res. Lett. 2020, 47, e2019GL086705. [Google Scholar] [CrossRef]
- Loeb, N.G.; Johnson, G.C.; Thorsen, T.J.; Lyman, J.M.; Rose, F.G.; Kato, S. Satellite and ocean data reveal marked increase in Earth’s heating rate. Geophys. Res. Lett. 2021, 48, e2021GL093047. [Google Scholar] [CrossRef]
- Dübal, H.-F.; Vahrenholt, F. Radiative energy flux variation from 2001–2020. Atmosphere 2021, 12, 1297. [Google Scholar] [CrossRef]
- Stephens, G.L.; Hakuba, M.Z.; Kato, S.; Gettelman, A.; Dufresne, J.-L.; Andrews, T.; Cole, J.N.S.; Willen, U.; Mauritsen, T. The changing nature of Earth’s reflected sunlight. Proc. Roy. Soc. A 2022, 478, 20220053. [Google Scholar] [CrossRef]
- Cheng, L.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Abraham, J.; Zhu, J. Improved estimates of ocean heat content from 1960 to 2015. Sci. Adv. 2017, 3, e1601545. [Google Scholar] [CrossRef]
- Nikolov, N.; Zeller, K. New insights on the physical nature of the atmospheric Greenhouse Effect deduced from an empirical planetary temperature model. Environ. Pollut. Clim. Change 2017, 1, 112. [Google Scholar] [CrossRef]
- Volokin, D.; ReLlez, L. On the average temperature of airless spherical bodies and the magnitude of Earth’s atmospheric thermal effect. SpringerPlus 2014, 3, 723. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical assessment of the role of the Sun in climate change using balanced multi-proxy solar records. Geosci. Front. 2023, 14, 101650. [Google Scholar] [CrossRef]
- Jones, P.D.; Harpham, C. Estimation of the absolute surface air temperature of the Earth. J. Geophys. Res. Atmos. 2013, 118, 3213–3217. [Google Scholar] [CrossRef]
- Wong, E.W.; Minnett, P.J. The response of the ocean thermal skin layer to variations in incident infrared radiation. J. Geophys. Res. Ocean. 2018, 123, 2475–2493. [Google Scholar] [CrossRef]
- Akbari, E.; Alavipanah, S.K.; Jeihouni, M.; Hajeb, M.; Haase, D.; Alavipanah, S. A review of ocean/sea subsurface water temperature studies from remote sensing and non-remote sensing methods. Water 2017, 9, 936. [Google Scholar] [CrossRef]
- Treguier, A.M.; Montégut, C.d.B.; Bozec, A.; Chassignet, E.P.; Fox-Kemper, B.; Hogg, A.M.; Iovino, D.; Kiss, A.E.; Le Sommer, J.; Li, Y.; et al. The mixed layer depth in the Ocean Model Intercomparison Project (OMIP): Impact of resolving mesoscale eddies. Geosci. Model Dev. 2023, 16, 3849–3872. [Google Scholar] [CrossRef]
- Forster, P.M.; Smith, C.J.; Walsh, T.; Lamb, W.F.; Lamboll, R.; Hauser, M.; Ribes, A.; Rosen, D.; Gillett, N.; Palmer, M.D.; et al. Indicators of Global Climate Change 2022: Annual update of large-scale indicators of the state of the climate system and human influence. Earth Syst. Sci. Data 2023, 15, 2295–2327. [Google Scholar] [CrossRef]
- Schmidt, G. Climate models can’t explain 2023’s huge heat anomaly—We could be in uncharted territory. Nature 2024, 627, 467. [Google Scholar] [CrossRef]
- Zhang, Y.; Rossow, W.B. Global radiative flux profile data set: Revised and extended. J. Geophys. Res. Atmos. 2023, 128, e2022JD037340. [Google Scholar] [CrossRef]
- Shaviv, N.J. Using the oceans as a calorimeter to quantify the solar radiative forcing. J. Geophys. Res. 2008, 113, A11101. [Google Scholar] [CrossRef]
- Voiculescu, M.; Usoskin, I.; Condurache-Bota, S. Clouds blown by the solar wind. Environ. Res. Lett. 2013, 8, 045032. [Google Scholar] [CrossRef][Green Version]
- Lam, M.M.; Chisham, G.; Freeman, M.P. Solar wind-driven geopotential height anomalies originate in the Antarctic lower troposphere. Geophys. Res. Lett. 2014, 41, 6509–6514. [Google Scholar] [CrossRef]
- Svensmark, J.; Enghoff, M.B.; Shaviv, N.; Svensmark, H. The response of clouds and aerosols to cosmic ray decreases. J. Geophys. Res. Space Physics. 2016, 121, 8152–8181. [Google Scholar] [CrossRef]
- Svensmark, H.; Svensmark, J.; Enghoff, M.B.; Shaviv, N.J. Atmospheric ionization and cloud radiative forcing. Sci. Rep. 2021, 11, 19668. [Google Scholar] [CrossRef]
- Kumar, V.; Dhaka, S.K.; Hitchman, M.H.; Yoden, S. The influence of solar-modulated regional circulations and galactic cosmic rays on global cloud distribution. Sci. Rep. 2023, 13, 3707. [Google Scholar] [CrossRef]
- Miyahara, H.; Kusano, K.; Kataoka, R.; Shima, S.; Touber, E. Response of high-altitude clouds to the galactic cosmic ray cycles in tropical regions. Front. Earth Sci. 2023, 11, 1157753. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Balmaseda, M.A. Earth’s Energy Imbalance. J. Clim. 2014, 27, 3129–3144. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; von Schuckmann, K.; Cheng, L. Insights into Earth’s energy imbalance from multiple sources. J. Clim. 2016, 29, 7495–7505. [Google Scholar] [CrossRef]
- Raghuraman, S.P.; Paynter, D.; Ramaswamy, V. Anthropogenic forcing and response yield observed positive trend in Earth’s energy imbalance. Nat. Commun. 2021, 12, 4577. [Google Scholar] [CrossRef] [PubMed]
- von Schuckmann, K.; Cheng, L.; Palmer, M.D.; Hansen, J.; Tassone, C.; Aich, V.; Adusumilli, S.; Beltrami, H.; Boyer, T.; Cuesta-Valero, F.J.; et al. Heat stored in the Earth system: Where does the energy go? Earth Syst. Sci. Data 2020, 12, 2013–2041. [Google Scholar] [CrossRef]
- von Schuckmann, K.; Minière, A.; Gues, F.; Cuesta-Valero, F.J.; Kirchengast, G.; Adusumilli, S.; Straneo, F.; Ablain, M.; Allan, R.P.; Barker, P.M.; et al. Heat stored in the Earth system 1960–2020: Where does the energy go? Earth Syst. Sci. Data 2023, 15, 1675–1709. [Google Scholar] [CrossRef]
- Raval, A.; Ramanathan, V. Observational determination of the greenhouse effect. Nature 1989, 342, 758–761. [Google Scholar] [CrossRef]
- Schmidt, G.A.; Ruedy, R.A.; Miller, R.L.; Lacis, A.A. Attribution of the present-day total greenhouse effect. J. Geophys. Res. 2010, 115, D20106. [Google Scholar] [CrossRef]
- Knight, R. All about polytropic processes. Phys. Teach. 2022, 60, 422. [Google Scholar] [CrossRef]
- Andrews, D.G. An Introduction to Atmospheric Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; pp. 24–26. [Google Scholar]
- Pierrehumbert, R.T. Principles of Planetary Climate; Cambridge University Press: Cambridge, UK, 2010; 652p. [Google Scholar]
- Dufresne, J.-L.; Eymet, V.; Crevoisier, C.; Grandpeix, J.-Y. Greenhouse effect: The relative contributions of emission height and total absorption. J. Clim. 2020, 33, 3827–3844. [Google Scholar] [CrossRef]
- Schmithüsen, H.; Notholt, J.; König-Langlo, G.; Lemke, P.; Jung, T. How increasing CO2 leads to an increased negative greenhouse effect in Antarctica. Geophys. Res. Lett. 2015, 42, 10422–10428. [Google Scholar] [CrossRef]
- Sejas, S.A.; Taylor, P.C.; Cai, M. Unmasking the negative greenhouse effect over the Antarctic Plateau. npj Clim Atmos Sci. 2018, 1, 17. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.-P.; Paige, D.A.; Greenhagen, B.T.; Sefton-Nash, E. The global surface temperatures of the Moon as measured by the Diviner Lunar Radiometer Experiment. Icarus 2017, 283, 300–325. [Google Scholar] [CrossRef]
- Hansen, J.E.; Sato, M.; Simons, L.; Nazarenko, L.S.; Sangha, I.; Kharecha, P.; Zachos, J.C.; von Schuckmann, K.; Loeb, N.G.; Osman, M.B.; et al. Global warming in the pipeline. Oxf. Open Clim. Change 2023, 3, kgad008. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolov, N.; Zeller, K.F. Roles of Earth’s Albedo Variations and Top-of-the-Atmosphere Energy Imbalance in Recent Warming: New Insights from Satellite and Surface Observations. Geomatics 2024, 4, 311-341. https://doi.org/10.3390/geomatics4030017
Nikolov N, Zeller KF. Roles of Earth’s Albedo Variations and Top-of-the-Atmosphere Energy Imbalance in Recent Warming: New Insights from Satellite and Surface Observations. Geomatics. 2024; 4(3):311-341. https://doi.org/10.3390/geomatics4030017
Chicago/Turabian StyleNikolov, Ned, and Karl F. Zeller. 2024. "Roles of Earth’s Albedo Variations and Top-of-the-Atmosphere Energy Imbalance in Recent Warming: New Insights from Satellite and Surface Observations" Geomatics 4, no. 3: 311-341. https://doi.org/10.3390/geomatics4030017
APA StyleNikolov, N., & Zeller, K. F. (2024). Roles of Earth’s Albedo Variations and Top-of-the-Atmosphere Energy Imbalance in Recent Warming: New Insights from Satellite and Surface Observations. Geomatics, 4(3), 311-341. https://doi.org/10.3390/geomatics4030017







