Gibbs Quantum Fields Computed by Action Mechanics Recycle Emissions Absorbed by Greenhouse Gases, Optimising the Elevation of the Troposphere and Surface Temperature Using the Virial Theorem

Abstract

Atmospheric climate science lacks the capacity to integrate thermodynamics with the gravitational potential of air in a classical quantum theory. To what extent can we identify Carnot’s ideal heat engine cycle in reversible isothermal and isentropic phases between dual temperatures partitioning heat flow with coupled work processes in the atmosphere? Using statistical action mechanics to describe Carnot’s cycle, the maximum rate of work possible can be integrated for the working gases as equal to variations in the absolute Gibbs energy, estimated as sustaining field quanta consistent with Carnot’s definition of heat as caloric. His treatise of 1824 even gave equations expressing work potential as a function of differences in temperature and the logarithm of the change in density and volume. Second, Carnot’s mechanical principle of cooling caused by gas dilation or warming by compression can be applied to tropospheric heat–work cycles in anticyclones and cyclones. Third, the virial theorem of Lagrange and Clausius based on least action predicts a more accurate temperature gradient with altitude near 6.5–6.9 °C per km, requiring that the Gibbs rotational quantum energies of gas molecules exchange reversibly with gravitational potential. This predicts a diminished role for the radiative transfer of energy from the atmosphere to the surface, in contrast to the Trenberth global radiative budget of ≈330 watts per square metre as downwelling radiation. The spectral absorptivity of greenhouse gas for surface radiation into the troposphere enables thermal recycling, sustaining air masses in Lagrangian action. This obviates the current paradigm of cooling with altitude by adiabatic expansion. The virial-action theorem must also control non-reversible heat–work Carnot cycles, with turbulent friction raising the surface temperature. Dissipative surface warming raises the surface pressure by heating, sustaining the weight of the atmosphere to varying altitudes according to latitude and seasonal angles of insolation. New predictions for experimental testing are now emerging from this virial-action hypothesis for climate, linking vortical energy potential with convective and turbulent exchanges of work and heat, proposed as the efficient cause setting the thermal temperature of surface materials.

1. Introduction

In previous articles [1,2], we showed how the Carnot cycle can be analysed by action mechanics, regarding caloric as Gibbs field quanta [2]. Action mechanics provides a more holistic account of molecular action and form. It relies on Planck’s material quantum of action (ħ) as a measure of the molecules’ characteristic action, a function of their momentum and radial motion (mvrδφ) [2]. The quantum energy levels for each species of molecule and environmental states of temperature and pressure are a cumulative logarithmic function of translational, rotational, vibrational or other internal actions [1,2]. The thermodynamic properties of the gas molecules are easily calculated from these molecular actions [2], temperature and pressure, allowing the absolute classical entropy and absolute Gibbs energy of atmospheric gases to be calculated correctly to four significant figures [1].

Action mechanics is consistent with statistical mechanics, reinterpreting Willard Gibbs’ phase space of momentum and position as the least action space. Carnot [3] anticipated the Gibbs free energy as specific kinds of caloric at hotter or colder temperatures, with engine power dependent on the fall between them. His expressions that “the quantity of heat due to the change in volume of a gas is greater as the temperature is higher” and “The fall of caloric produces more motive power at inferior than at superior temperatures” are consistent with modern quantum theory.

These statements indicate that variations in the Gibbs energy are a function of both volume and temperature with the maximum work possible when the temperature difference between the hot source and the cooling sink is greatest, with the latter as low as possible. In action mechanics, the maximum work possible is estimated as the variation in the Gibbs energies of the heating isothermal gas and of the cooled isothermal gas [2]. Based on this principle, Carnot remarked that coal could potentially achieve a temperature difference of 1000 °C, whereas the steam engines then current were designed to work over a range of temperatures of only 60 °C [3].

Carnot’s viewpoint of the role of caloric in motive power can be identified with variations in the Gibbs field energies for each of the four phases of the engine cycle. This will be proven by direct reference to Carnot’s Mendoza-edited manuscript [3], also using the original in French, and by the model programs developed in this study. However, Mendoza’s viewpoint that caloric can be equated closely to entropy is rejected. On the contrary, despite recent support for this errant opinion, caloric’s physical description by Carnot equates best to thermal energy, not entropy as defined by Clausius and Boltzmann. It is a pure number with characteristic units of heat capacity per degree of temperature (J/°K) but actually dimensionless as the quotient of extensive energy (J) divided by intensive energy (T = mv²/3k) for translational heat governed by Boyle’s law, unlike heat as Joules of energy.

Isothermally, the enthalpy of gas molecules remains constant. Carnot showed [3] in 1824 that the property of heat transformations [4], later defined by Clausius in 1865 [5] as entropy, was a function not only of the temperature but also the diminishing density of each molecule, expressed as the logarithm of its volume. He defines that where “the density of air is less…. its capacity to store heat is a little greater”. We have confirmed this for the Gibbs potential elsewhere [1]. Carnot was already aware of the conservation of total kinetic and potential field energy in natural systems and its relation to working engines.

This conservation principle was known since Leibniz explained it before 1700 as a diagram in his Discourse on Metaphysics where the vis viva was stored reversibly in an inertial potential, described brilliantly later as energy by Emilie du Chatelet. So, both the first and the second energy principles emerged from Carnot’s work published in 1824 [3]. The storage of heat, defined by Clausius [5] as the Carnot principle, is a function of state that measures supportive internal work or is dissipated externally more generally. In quantum state terms, the negative Gibbs energy tends to become greater, achieving a higher quantum number that can be measured as scalar action, estimated as a logarithmic function of the quantum number [2,6].

A Carnot heat engine cycle (Figure 1) involves charging a working fluid with heat at a high temperature, isothermally expanding while performing external work, then continued expansion adiabatically as the temperature decreases, compensated by the increased dilution of each molecule. Carnot’s stage three of compression by the engine’s inertia isothermally removes less heat at a lower temperature. The cycle is concluded by continued adiabatic compression restoring the original temperature and pressure. Carnot explained this process exactly [3] using the varying caloric content, referring to two heating stages of the working fluid (a + b) and two cooling stages (b′ + a′) in the cycle. Acting together, these four phases ensure that the cycle is reversible, inferring that the magnitude of the maximum work possible is given by (a − a′) or (b′ − b). Figure 1 emphasises the continuous inertial action of Carnot’s cycle.

A key conclusion in the reversible Carnot cycle as explained by Clausius [4] is that the entropy change for heat transfer inwards in stage 1 (+q/T₁) is equal to the entropy change for heat transfer outwards in stage 3 (−q/T₃), so that the variation in scalar action in stage 1 reversed is equal to that in stage 3, whereas the change in the Gibbs energy in each stage is proportional to the temperature. Carnot was also aware that the maximum engine power possible was not achievable. The mechanism of two isothermal heat transfers across a fall in temperature linked by adiabatic expansions and compressions is an ideal proposal not possible in practice. Real engine systems are neither isothermal nor adiabatic and include frictional losses dissipating work energy.

In this article, Carnot’s treatise of 1824 on the motive power of heat is related to meteorological processes in the real troposphere. Can more be done to relate Carnot’s principles to atmospheric and meteorological science? Perhaps it can, particularly when the principles of least action initiated by Leibniz and expressed in Lagrange’s calculus of variations [7] are integrated, requiring action mechanics to simplify calculations.

Just as for the Carnot cycle in real engines, there is dissipation of energy during all these cycles, so the Lagrangian relationship does not achieve equality between the two terms of the Euler–Lagrange equation [7,8]. In fact, this dissipative frictional property is important for heating the Earth’s surface in anticyclones from heat stored as work [6], which we will show is facilitated by greenhouse gases.

In meteorology, currently, a lapse rate in temperature for dry air calculated by an adiabatic isolation of 9.8 °C per km is regarded as expressing an adiabatic expansion. This implies that a convective expansion into the troposphere is consistent with the isentropic stage of a Carnot cycle. However, is this true?

It will be shown for a dry atmosphere as theoretical methods that the decrease in temperature with altitude is near 6.5–6.9 °C per km, a result that is consistent with the virial theorem, a phenomenon concerning kinetic and potential energy well known in physics.

2. Theoretical Methods

Applying the Carnot cycle to tropospheric mechanics requires the calculation of the entropy and Gibbs energy of an ideal gas using action mechanics [1,2]. Also, a new method is needed to incorporate gravitational potential into atmospheric dynamics. This requires the novel use of Lagrange’s virial theorem to estimate lapse rates in temperature with altitude [9]. Essentially, the virial theorem shows that the mean vis viva ($\sum _1^{n}m{v}^2$) in a set of interacting material particles subject to central forces is equal to their average potential energy. Thus, the mean kinetic energy (T = Σmv²/2) in such a Lagrangian system is half the mean potential energy, to be discussed in Section 2.4.

$${\sum }_1^n(m{v}^2)/2=T$$

(1)

2.1. Action Mechanics

Action mechanics [2] is a reinterpretation of the partition functions given in textbooks on statistical mechanics as estimates of scalar action, with units measured with Planck’s material quantum of action (ħ). It seeks to provide quantum thermodynamics. For diatomic gases like N₂ and O₂, comprising 99% of the atmosphere, the macroscopic variables of temperature and volume or density express entropy (S) as the absorption of heat with increasing temperature(ST). Terrill Hill’s statistical mechanics [9] have been integrated in simplified form [1,2,6] as functions of scalar action. The abbreviations for translational action (@_t) and rotational action (@_r) are scalars [1] designated as having dimensions similar to the vector angular momentum with rotational action (@_r = Iω/σ), including a factor for symmetry (σ) and a corrective term for the ratio of the mean velocity to the root-mean-square velocity. Then, a factor of inversed 2³ is included, preventing the double counting of molecular couples separated by 2r assuming a cubic array (z_{t =} 2³(1.0854)³ = 10.22). The factor of 1.0854 was logically validated as a correction when found to be the inverse ratio for the mean velocity of particles compared to the root-mean-square velocity from the Maxwell–Boltzmann distribution [1]. Then, the terms in Equations (2) and (4) from statistical mechanics for translation and rotation [9] can be expressed in Equations (3) and (5) as terms of scalar action in quantum fields shown by quantum numbers, yielding field energies able to be expressed as mean values establishing the temperature for individual molecular quantum fields [2,6].

Equating Terms for Statistical Mechanics and Scalar Action

The expression for translational entropy given in Hill [9] in Equation (2) was set [1] as equivalent to scalar action (mrv), shown in Equation (3). Rotational entropy is even more readily converted by (4), with the composite entropy by temperature shown in (5). The exponential term provides enthalpy for a diatomic gas, one term contributing about one-fifth to entropy as a heat requirement from absolute zero. Most of the entropy shown as $(3kT{I}_t{)}^{\frac{3}{2}}/{(ħ}^3{z}_t$) is negative Gibbs energy, a focus of Boltzmann’s interest in his lectures on gas theory. This heat requirement proven by third-law experiments for atmospheric gases corresponds to heat for the phase changes of melting and vapourisation. No separate mathematical derivation is required for these simple substitutions in Hill’s statistical mechanics expressions for diatomic gases like dinitrogen, N₂, 78% of the atmosphere, for translation and rotation, shown in Equations (2) and (4).

$$S=Nkln[({\displaystyle \frac{2\pi mkT}{h^2}}{)}^{\frac{3}{2}}kT{e}^{\frac{5}{2}}/p]$$

(2)

$$\begin{gathered} S_{t}T=RTln[e^{\frac{5}{2}}(3kT{I}_t{)}^{\frac{3}{2}}/({ħ}^3{z}_t)]=RTln[e^{\frac{5}{2}}{(mrv)}^3/({ħ}^3{z}_t)] \\ =RT[e^{\frac{5}{2}}{(@}^3/{ħ}^3)]\mathrm{where}{@}^3=[{\displaystyle \frac{(mrv{)}^3}{z_t}}] \end{gathered}$$

(3)

$$\begin{gathered} S_{r}T=\mathit{NkTln}\left({\displaystyle \frac{{8\pi }^{2}kTIe}{\sigma h^2}}\right) \\ =NkTln\left({\displaystyle \frac{2kTIe}{\sigma {ħ}^2}}\right)=NkTlne{({@}_r/ħ)}^2=RTlne(j_r{)}^2 \end{gathered}$$

(4)

$$\Sigma ST=RTln[e^{\frac{7}{2}}{(n}_t{)}^3(j_r{)}^2]$$

(5)

In Figure 2, the expressions for the translational and rotational entropy of diatomic molecules are considered as external and internal fields containing quanta sustaining thermodynamic states also generating temperature as half the mean vis viva.

In these equations for linear diatomic gases (Figure 2), simpler equivalences for the macroscopic properties of temperature and pressure are shown as logarithmic ratios of action (@/ħ), using Planck’s reduced constant (ħ) in the denominator to measure the levels of the translational or rotational quantum states [1,6]. Here, the symbol e^n/2 indicates a mathematical exponent for internal kinetic or pressure–volume energy, and the subscripts refer to translation (t) and rotation (r), with the three moments of rotational inertia (I_A, I_B, I_C) for 3-dimensional molecules, suitable for computing water, nitrous oxide and methane as polyatomic molecules (see Tables S2 and S3 in Supplementary Materials). By contrast, CO₂ is more simply computed as a symmetrical linear rotator. This is statistical mechanics recast in a simpler, more realistic, form [2,7], as suggested in Figure 2. The heat capacity exponential term depends on whether the system volume is constant (C_v) or able to expand at atmospheric pressure (C_p). Using these @ symbols is justified by the ease of manipulation, also recognising that these symbols include corrections for molecular symmetry or mean velocity so that the quantum information from molecular properties is applied accurately.

By modifying Willard Gibbs’ statistical mechanics of extension in phase [10] using action mechanics [1,2,6], it is then possible to estimate absolute values for action and entropy, the quantum state numbers per molecule and the mean translational, rotational and vibrational quanta in the field. Equation (6) gives a formula for estimating the mean molecular properties for entropic energy per mole as ST, energy [C_vT, J] or enthalpy [H, C_pT, J] and Gibbs energy [−G, −g_t J], using lower case as the energy per monatomic molecule. In a variable-pressure volume system performing reversible mechanical work, like the Carnot cycle, for estimating the molecular kinetic energy, c_pT must be replaced by c_vT with c_v equal to 3/2 for a monatomic gas like argon. In a sealed cylinder, no work is performed against the atmosphere, with the internal field energy varying with internal pressure reversibly, with respect to the back pressure from the external work. For maximum efficiency, the whole cycle must be performed reversibly, as Carnot defined.

s_tT = c_vT + kTln[e(@_t/ћ)³] = c_vT + kT + kTln[(n_t)] = h − g_t

(6)

Effectively the Sackur–Tetrode Equation (6), the Gibbs field energy [10] per molecule (g_t) for translation is zero at absolute zero temperature and action, becoming progressively more negative as the temperature increases and the Gibbs field spontaneously gains quantum energy (−g_t). This is consistent with the Maxwell relationship that ΔG equals ΔH − TΔS and that spontaneous reactions have negative changes in Gibbs energy, as when entropy increases. In this article, we will illustrate how the absolute value of the Gibbs field energy can easily be calculated. The Gibbs field is the milieu in which the kinetic potential of material particles is caused by the impulsive quanta in transit. However, the Gibbs vibrational zero-point energy for the chemical bonding of hv/2 and electronic energy, not considered in this article, are positive.

In principle, this procedure, successfully used previously [2,6], applies throughout this article. Here, this is based on achieving a field condition where the time-integrated momentum exchange from impulses caused by the quantum field (Σhv_i/c) and the reversible momentum exchange for the material particles (Σmv_i) are equal, within the same Brownian [11] or random walk matrix. Per se, neither material particles nor quanta exchange momentum directly, and particles only do so in collisions by way of far swifter intervening field quanta. The rate of action impulses, keeping the material particles separated, is effectively magnified by the factor c/v_i; so, a simple comparison of the ratio of momenta, hv_i/cmv_i or h/λ_imv_i, will be greater by this factor.

2.2. In the Atmosphere, the Internal Pressure of the Ideal Gas Law Balances Gravitational Pressure

In the following analysis, the molecular pressure (p) for gases is a statistical mean value for each species from the ideal gas law, shown in Equation (7), where N is the number of molecules per unit volume (1/a³) and kT is equal to mv²/3, as translational kinetic energy, equal to mv²/2.

p = kT/a³ = NkT

(7)

This ideal relationship between pressure and temperature was only recently made available to Carnot for his theory. Here, kT is equivalent to the root-mean-square velocity in mv²/3, with a being the mean cubic separation of molecules (r = a/2); each molecule is regarded as confined to its mean specific volume of a³. It is important to understand that the surface pressure balances thermodynamic pressure with the gravitational pressure exerted by the weight of the atmosphere. This is recognised in meteorology as the hydrostatic principle. Consequently, molecular pressure can be balanced in Equation (8).

p = NkT = Mg/a²

(8)

Here, M is the total mass of atmospheric gases per unit area for each molecule at the surface, with a weight or vertical force Mg. We have related this to the scalar action per molecule area previously [3].

2.3. The Laplace Equation Only Applies to an Isothermal Atmosphere

The well-known Laplace barometric formula for the atmosphere given in Equation (9) might be regarded as suitable for studying the troposphere.

p_h/p_o = n_h/n_o = e^−mgh/kT

(9)

The gas pressure at an altitude h (p_h) is compared to that at the base level (p_o). This is frequently given as a ratio of the number of molecules per unit volume at each altitude h (n_h/n_o). So, taking natural logarithms, we can write Equation (10).

kTln(n_h/n_o) = −mgh

(10)

This gravitational formula was confirmed in 1910 for isothermal conditions using Brownian particles by Perrin [11], who also verified Einstein’s theory of translational and rotational Brownian motion. This classical work of Einstein and Perrin on Brownian motion provided the original inspiration for developing action mechanics [1,2,6]. Despite its strong mathematical tradition [12], the well-known flaw of the Laplace formula is its failure to correspond to the reality that temperature declines with altitude in the troposphere.

In this article, a second novel approach will be employed, additional to heat–work Carnot cycles in the troposphere. The temperature gradient with tropospheric altitude will be linked to the reversible interaction between thermodynamics and gravitational work. Furthermore, this temperature gradient exists in a static atmosphere, even in the absence of adiabatic expansion or compression. Thus, for a mole of monatomic molecules in a canonical ensemble as defined by Gibbs [13], the following concise relationship involving a function of relative action (@/ħ) was shown to hold. The action term involved (@_t) for translation is equal to [(3 kTI_t)^1/2/z_t], where I_t indicates the translational molecular inertia (I_t = mr_t²) with z_t correcting for the mean velocity rather than the root-mean-square velocity.

ST = RTln[e^5/2(@/ħ)³]

(11)

The total field thermal energy, kinetic and potential, shown by the entropy Rln[e^5/2(@/ħ)³] at the temperature T is simply their product, RTln[e^5/2(@/ħ)³]. As a result, for monatomic molecules, argon, neon or helium, in the atmosphere, based on temperature change alone, we might expect to have the following difference in absolute thermal energy content sT per molecule at the Earth’s surface and at an altitude h_n.

s_oT_o – s_nT_n = kT_oln[e^5/2(@_to/ħ)³] − kT_nln[e^5/2(@_tn/ħ)³]

(12)

This equation for variation in entropic energy with tropospheric altitude must be adjusted to account for the conversion of thermodynamic to gravitational energy. It proposes to achieve this with the aid of Clausius’s virial theorem [13], applied to the atmosphere as a gravitationally bound system of particles. This second novelty predicts a new barometric equation for the atmosphere in steady-state equilibrium with thermal energy flow.

2.4. The Principle of Least Action Causing Virial Theorem Lapse Rates

In Lagrange’s calculus of variations [7] for a system of N point particles, the scalar moment of inertia is defined by Equation (13), where m_k and r_k represent the mass and position of the kth particle.

$$I={\sum }_{k=1}^N{m}_k{r}_k^2$$

(13)

The scalar A is then defined by Equation (14) with dimensions of momentum by position, or action.

$$A={\sum }_{k=1}^N{p}_k{r}_k$$

(14)

Assuming the masses are constant, A is also one-half the time derivative of the moment of inertia.

$$\begin{gathered} \frac{1}{2}{\displaystyle \frac{dI}{dt}}=\frac{1}{2}{\displaystyle \frac{d}{dt}}{\sum }_{k=1}^N{m}_k{r}_k{r}_k \\ \hspace{1em}={\sum }_{k=1}^N{p}_k{r}_k=A \end{gathered}$$

(15)

The time derivative of A performed by parts on momentum or impulse and position is given [8] by Equation (16).

$${\displaystyle \frac{dA}{dt}}=2T+{\sum }_{k=1}^N{F}_k.r_k$$

(16)

Here, T is kinetic energy $(\Sigma m{v}^2/2$), and the second term of force by position is torque, or the virial acting to vary angular momentum, as action generalised between pairs of k particles. The virial theorem, based on the principle of least action, implies that ${\displaystyle \frac{dA}{dt}}$ = 0 in a conservative system. Then, $2T=-\sum _{k=1}^N{F}_k.r_k$, twice the mean kinetic energy equal to the negative of the torque or potential energy. Consistent with Lagrange’s identity for gravitating systems, Clausius’s virial theorem [13] stated later that the mean kinetic energy (+mv²/2) of particles in a gravitationally bound system should be equal in magnitude to half their mean potential energy (−mv²).

The virial theorem is employed to explain the evolution of stars made up of hydrogen atoms, their eventual collapse into heavier atoms and their ultimate explosion. Perhaps surprisingly, for reasons explained by Kennedy [14], the virial theorem can also be applied to the atmosphere assuming transient reversible states related to molecular equilibrium between gravity and thermodynamics. This automatically requires a temperature gradient with altitude, independently of the chaotic effects of convective expansion or compression. This version of the virial theorem requires that the decreasing kinetic energy (δT) of air molecules with altitude (δh) indicates only half the thermal energy required for the gravitational work of convection (mgδh/2) and that the remaining heat is provided by the exchange of quanta (also mgδh/2) as negative variations in Gibbs energy, a field potential allowed by their degrees of freedom of action. The equality of half the change in potential energy (mgδh) and a negative change in kinetic energy is seen between particles in different gravitational potentials, like hydrogen atoms in stars, molecules in the atmosphere that are clearly not in orbital motion [14]. The absorption of a quantum of energy by the H atom lowers the electron’s kinetic energy equal to the quantum, thus reversibly raising the potential energy by twice the quantum (2 hv).

This unique application of the virial theorem for the troposphere yields a simple equation relating changes in the mean molecular kinetic energy (nkδT/2) with changes in altitude, as half the change in gravitational potential energy (−mgδh/2).

$$\begin{gathered} -nk\delta T/2=mg\delta h/2 \\ -{\displaystyle \frac{\delta T}{\delta h}}={\displaystyle \frac{mg}{nk}}={\displaystyle \frac{mg}{2C_v}} \end{gathered}$$

(17)

Equation (17) provides a remarkably simple means of calculating the virial lapse rate of temperature with the change in height (h), based on a steady-state molecular equilibrium between thermal and gravitational states. Here, m is the mean molecular weight of the gases in Daltons (28.97 for air) number-density-weighted, where n is the number of degrees of kinetic freedom of k/2, being 3 for argon and 5 for diatomic or linear molecules like N₂, O₂ and CO₂, plus a factor for the freedom of vibrational kinetic motion for CO₂, giving an n of about 5.4 on the Earth’s surface. This application of the virial theorem proposes that this change in the gravitational potential energy (mgδh/2) comprises the net change in energy with height as the functional virial or potential energy for all six or more degrees of freedom, translation, rotation and vibration [14]. Previously, the use of the virial theorem was restricted to the quantum states of the electron in the hydrogen atom or monatomic states typical of stars or gas considered as isothermal to calculate a mean value of kinetic energy, rather than the gravitational levels of the troposphere proposed in the virial-action theory. Here, it is effectively extended to rotational and vibrational degrees of freedom, applying the theorem to different altitudes and temperatures, as given by the lapse rate of Equation (17).

The mean lapse rate then depends on the composition of gases and their kinetic properties as degrees of freedom for energy. The code for a program (Baromet10/Cal) to calculate exact lapse rates from composition, different degrees of freedom and gravity is given in the Supplementary Materials. The virial-action theorem applies because the molecules in the air are not simply suspended in a gravity field with potential energy (mgh) equal to their kinetic energy (1/2 mv²) if they fall. In part, they all have a Gibbs energy quantum field. To fall, they must gain this kinetic energy while losing quantum state field energy of equal magnitude. A principle of quantum mechanics is that the absorption of a quantum reduces the kinetic energy of an electron equal to the quantum with an increase in potential energy twice the quantum. On emission, the electron gains the same amount of kinetic energy as the quantum emitted, a decrease in potential energy of twice the quantum. Perfect gas molecules with increases in volume affecting translational action or in temperature affecting translational, rotational and vibrational action are also subject to virial action as electrons in the hydrogen atom.

2.5. A Comment on Adiabatic Lapse Rates

By contrast, the adiabatic lapse rate theory used in climate science from the 19th century is based on the notion of the isentropic convection of a parcel of air. The validity of its mathematical and physical derivation is critiqued below, but it is described by the following Equation (18).

$$\begin{gathered} -\delta T/\delta h=mg/c_p \\ -\delta T{c}_p=mg\delta h \end{gathered}$$

(18)

An adiabat for dry air (9.8 C/km) can be calculated using Equation (18), where c_p is the molecular heat capacity at constant pressure and m is the molecular mass. It is more customary in climate science to use a mass-weighted heat capacity per kg as C_p. This accounts for the fact that this dry adiabat is rarely observed, usually being measured from meteorological balloons nearer 6.5, although the release of heat from the condensation of water is invoked, reducing cooling and lowering the lapse rate [14]. We dispute this interpretation, being a minor effect only.

2.6. Gravity and Thermodynamics of Monatomic Gases

Based on the action method we developed for calculating entropy [2], the following equation describes differences in the entropic energy sT between a molecule transported from the base level h_o to an altitude h_n for a monatomic gas like argon. Considering the reversible exchange of two molecules at two altitudes varying both in gravitational potential and in entropic energy, we propose the following expression balancing gravity with thermodynamics for a monatomic gas with three degrees of translational freedom.

mgδh_o−n = [3 kT_o − 3 kT_n] < = >   kT_oln[e^5/2(@_to/ħ)³] − kT_nln[e^5/2(@_tn/ħ)³]

(19)

This unique relationship between gravity and thermodynamics is considered to describe a heat–work process for a particular species of molecule at the Earth’s surface h_o elevated to height h_n. Equation (6) would give a correct description of the molecular energy with entropy (sT) only for conditions of unchanged gravitational potential at h_o and h_n. The differences between the entropic terms and kinetic terms 3 kT_o − 3 kT_n = mgδh_o-n = (mv_o² − mv_n²) at each gravitational altitude provide a balanced equation accounting for the increased work in gravitational potential energy mgh (vis viva = mv_o² − mv₁²) and the corresponding decrease in thermal sensible heat and work heat in the molecular system.

For Equation (19), the question of where the sources of energy in the 3 kδT transferred with increased height are to be found must be asked. While one half is plainly kinetic energy, it is proposed that the second half must be a thermodynamic property of state, with heat released as the chemical free energy increases with height acting as the source for the second half of the increased gravitational potential energy.

For the application of the virial theorem to the atmosphere [14], half the change in gravitational potential (mgh_n) was taken as equal to the difference in kinetic energy (3 kT_n − 3 kT_o)/2—recalling that a negative change in kinetic energy occurs as the molecular gravitational potential increases in the atmosphere. A rising molecule uses the thermal energy associated with its entropy, for both potential and kinetic absorption of heat, to perform cooling gravitational work, increasing its free energy; a descending molecule uses its gravitational potential to generate heat as both kinetic and actinic emissions, increasing the kinetic energy but reducing its free energy by the increased absorption of quanta, as suggested in Figure 2. Reversibility must guarantee that an air molecule at all altitudes will tend to have the same capacity to perform work.

We can rearrange Equation (19) to the following form in (20) to illustrate these effects.

mgh_o−n = 3 kT_o − 3 kT_n ⇔ kT_olne^5/2[(@_to/ħ)³] − kT_nlne^5/2[(@_tn/ħ)³]

(20)

Balancing the thermal terms, together with work against the atmosphere, the reversible transition is given by Equation (21).

mgh_0−n = kT_oln[(@_to/ħ)³] − kT_nln[(@_tn/ħ)³] − 3/2k(T_o − T_n) + k(T_o − T_n)

(21)

Given the ease of calculation of the terms of Equation (21), at the surface, we can solve for the change in number density and pressure with height by the following equation.

kT_nln[(@_tn/ħ)³] = kT_oln[(@_to/ħ)³] − 1/2k(T_o − T_n) − mgh_n

(22)

Expressed in positive Gibbs energy terms, we have Equation (23).

mgh_n = kT_nln[(ħ/@_tn)³] − kT_oln[(ħ/@_to)³] − 1/2k(T_o − T_n)

(23)

Expressed as Helmholtz energies, Equation (17) becomes

mgh_0−n = kT_nln[(ħ/@_tn)³/e] − kT_oln[(ħ/@_to)³/e] − 3/2k(T_o − T_n)

(24)

The two negative processes in energy on the right-hand side of Equation (20) translate to positive changes in potential energy on the left-hand side. Furthermore, the first logarithmic free energy term is numerically negative, given the inversed relative action, and the second at the surface is positive but of greater magnitude since @_to is less than @_tn. Overall, the difference between the two free energy terms is negative but, in terms of the quanta of energy released, can be equated to gravitational work mgh_n. But for monatomic gases, the virial theorem requires that mgh_n must also equal the magnitude of −3/2k(T_o − T_n). This property of a reversal in sign for kinetic energy is part of the nature of increasing potential energy.

2.7. Earth’s Diatomic Virial-Action Troposphere

Diatomic molecules in the Earth’s atmosphere have been proposed to reversibly exchange kinetic energy plus Gibbs energy with gravitational energy [14]. Molecule A ascending gains gravitational energy mgh, and molecule B descending gains the same kinetic energy as A loses (mgh/2) as well as losing the free field energy that molecule A gains as it becomes colder. These logarithmic changes in action state involve the absorption or the emission of radiation, used to perform gravitational work. In effect, the increase in free energy of an ascending molecule releases the quantum of heat needed for gravitational work, consistent with the virial theorem.

Comparing a molecule at the surface with one at altitude h_n, the increase in gravitational potential energy must equal the sum of the decrease in enthalpy (expressed positively) and the change in Gibbs energy, which is expressed positively, given that T_o is greater than T_n. Since the action depends on pressure or the number density only at constant temperature, this result suggests that Perrin’s confirmation of the Laplace barometric equation on a microscope stage was achieved under isothermal conditions, dictated by the temperature of the suspending fluid. Perrin [11] used an eyepiece blind with a pinhole to limit counts to a small number (less than 5) appearing in a single field of view. His counts of gum particles simulated monatomic particles, as predicted by Einstein, in the small volume of fluid focused by the objective.

As well as the change in action potential, to estimate the entropy change δs per molecule between the surface and an altitude of h_n, we include the enthalpy change and not just kinetic energy. The enthalpy for a monatomic gas includes both the kinetic energy 3/2 kT as well as an additional kT term to allow for the pressure–volume work that must be performed against the Earth’s atmospheric pressure at any altitude.

                 δsT = kTln[e^7/2(@_tn/ħ)³(@_r/ħ)²Q_e] − kTln[e^7/2(@_to/ħ)³(@_r/ħ)²Q_e]
= kTn[(n_tn/n_to)³(j_r)²]

(25)

The translational action @_n equal to (3 kT_nI_tn)^1/2/z_t is a function of both temperature and radial separation. The increase in the logarithmic action with decreased pressure at higher altitude is more than balanced by the linear lapse rate decrease in temperature. Thus, the translational action and entropy increase with altitude, although the entropic energy given by sT decreases.

Applying the virial theorem to ascertain temperature gradients, action mechanics [15] has provided the following equation, enabling the interaction between thermodynamics and gravity to be studied. By solving for the translational action (@_tn) at any altitude (h_n), the virial-action Equation (26) allows pressure, number density, Gibbs energies for translation and rotation, temperature and entropy to be easily calculated using simple numerical computation [1]. The equation may also be written as follows:

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}mg{\delta h}_{o-n}=3.5k(T_n-T_o)+\{k{T}_o\mathit{ln}[({@}_{to}/\hslash {)}^3{Q}_e]-k{T}_n\mathit{ln}[({@}_{tn}/\hslash {)}^3-\{k{T}_o\mathit{ln}[({@}_{ro}/\hslash {)}^2/{\sigma }_r] \\ -k{T}_n\mathit{ln}[({@}_{rn}/\hslash {)}^2/{\sigma }_r] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=3.5k\left(T_n-T_o\right)+\left\{k{T}_o\mathit{ln}[{n_{to}}^3{Q}_e\right]-k{T}_n\mathit{ln}[{n_{tn}}^3{Q}_e]\}-\{k{T}_o\mathit{ln}[{n_{ro}}^2{\sigma }_r]-k{T}_n\mathit{ln}[{n_{rn}}^2] \end{gathered}$$

(26)

In principle, we can express this gravitational, thermal and statistical configuration of energy in tropospheric profiles more simply in Equation (27), the virial-action gravitation equation.

$$mg\delta h_n=3.5k\delta T+\delta g_t-\delta g_r=\delta h_{\mathrm{o}-\mathrm{n}}+\delta g_t-\delta g_r$$

(27)

In Figure 3, $\delta g_t$ and $\delta g_r$ represent variations in the mean molecular Gibbs energy required for the operation of the virial theorem under gravity, and δT is (T_n − T_o). Though surprising, the variation in the rotational Gibbs energy ($\delta g_r$) is invariably opposed to variation in the translational Gibbs energy. This is a new variational principle in the interaction between gravity and thermodynamics recognised in this requirement. The location for the internal rotational energy establishing the diatomic molecule’s inertia differs from the external inertia of translation action and energy. This reverse variation was justified (27) by operating on Venus and Mars [15]. Both the rotational (g_r/T) and vibrational (g_vib/T) Gibbs energy per degree increase with altitude as the temperature falls (i.e., as rotational entropy declines), but the translational entropy increases because the decrease in pressure increases radial separation (+δr_t) faster than the velocity decreases (−δv) as temperature falls.

Equation (27) expresses a variational process in the distribution of action and its energetic cost rather than a summation of energy. Rotational action and its quantum number state decrease with altitude, while translational action and its quantum number state increase, offsetting each other as the least action. Since the action ratios (@/ħ) and their logarithmic derivative, entropy, provide a measure of the quanta of energy needed to sustain the molecular system in the action field, we find that reduced rotational action releases heat for gravitational work; by contrast, even though increasing translational action with altitude as the temperature falls requires more quanta each of unit action, this need is offset by a longer radius of action compared to rotation and the quanta of lower frequency and momentum involved. Thus, the yield of translational quanta for each rotational (or vibrational) quantum of energy released increases with altitude. In energy terms, translational quanta are less expensive than rotational or vibrational quanta, but the rotational quanta of Figure 2 sustain rotational action, apparently without impulsive force in collisions, in contrast to translational and vibrational action.

2.8. The Global Virial-Action Heat Cycle Hypothesis

A cross-sectional illustration of cyclonic rotation, clockwise in the southern hemisphere, is shown in Figure 4. A linear virial-action increase in temperature consistent with Equation (17) is shown as the thermal gradient to about 10 km, while the pressure gradient decreases exponentially with altitude, proportional to the weight of the atmosphere at higher altitude.

In Figure 4, a humid central low-pressure zone is considered convective from the warmed surface; this variation is induced by a diurnal cycle with noon central. Four stages for a hypothetical Carnot cycle can be identified with analogies to the cycle illustrated in Figure 1. As a real system, this cannot perform as an ideal Carnot cycle with 100% efficiency proportional to the temperature gradient with heat in and heat out of equal entropy change. Nevertheless, temporal phases can be recognised in the troposphere corresponding to Carnot’s description of the heating and cooling of the working fluid. For each km of elevation in thermal convection, the temperature falls by an amount twice the fall in kinetic energy, as predicted by the virial-action theorem, with colder air emitting long-wavelength radiation to space. The pressure gradient is shown falling non-linearly as a function of temperature and volume, according to the perfect gas law low in Equation (6). The linear decline in temperature with altitude ensures that there is an exponential fall in pressure, a function of weight per unit area or the rate of translational inertia (Σmr²ω) [2]. Indicated in Figure 4 is the role of heat radiation from the surface as a hot source for heating the atmosphere in Carnot stage 1, with thermal energy being exchanged convectively with gravitational potential energy in stage 2 according to Equation (22), giving global cooling, eventually generating outgoing longwave radiation as stage 3 in the upper troposphere of reduced density.

Table 1. US Airforce tropospheric profiles showing virial-action lapse rates in temperature to the tropopause.

Profile		15N Tropical	45N Mid-Latitude Jul	45N Mid-Latitude Jan	60N Sub-Arctic Jul	60N Sub-Arctic Jan	US Standard
Surface	Temp K	299.7	294.2	272.2	287.2	257.2	288.2
	1 Pressure	1.013	1.013	1.018	1.010	1.013	1.013
	2 Density	24.50	24.96	27.11	25.49	28.56	25.48
Tropopause	Temp K	203.7	215.8	219.7	225.2	217.2	216.8
	Pressure	0.132	0.179	0.257	0.268	0.283	0.227
	Density	4.70	6.01	8.47	8.62	9.44	7.59
Ratio	Pressure	0.13	0.18	0.25	0.27	0.28	0.24
S/T	Density	0.19	0.24	0.31	0.34	0.30	0.33
Altitude	Km	15	13	10	10	9	11
δT/δh		6.6	6.5	5.3	6.2	4.4	6.5

¹ bars; ² N × 10¹⁸/cm³; US Standard is a composite with most values given in the more complete Table S1 (in Supplementary Material) nearer 6.5 at low altitude.

summarises United States Airforce Geophysics Laboratory (AFGL) comprehensive atmospheric profiles [15] compiled from 0 to 120 km. These profiles are included in the Supplementary Materials, showing surface data near zero altitude up to the tropopause, 0.2 to 0.3 of the atmospheric surface pressure or density in Table 1. Below the altitude chosen as the tropopause, the fall in temperature is regular at all latitudes, about midway between 6 and 7 °C or degrees K for each change in altitude per km. The composite US Standard is 6.5 °C per km between 288 and 217 °C and an altitude of 11 km. These data allowed the testing of the virial-action hypothesis for temperature lapse rates in previous publications [15], including tests on other planets such as Venus and Mars.

The height of the tropopause below which the temperature declines linearly with altitude is obvious for the study of the AFGL profiles [15]. At the tropopause, the temperature variation falls to zero, indicating a mixing or overturning zone for air, above which is the stratosphere. The changes with altitude are not the adiabatic, isentropic stages two and four of the Carnot cycle shown in Figure 1. There, no heat can leave or enter. Instead, the changes in temperature result from either work on another resisting system causing cooling or warming by compression. As heat and work processes, these can occur when there is no significant change in the gravitational potential.

The governing virial-action Equations (25)–(27) are the basis for the simple computer programs prepared in previous studies [6,14] providing ideal solutions for atmospheric profiles. A logical program of 6000–9000 steps included in the Supplementary Materials (Baromet10/Cal) was constructed (Figure 5) in a machine code interpreter, now in the public domain as Astrocal, formerly marketed by Vernon Hester, Philadelphia, PA. Anyone interested in obtaining working copies of these programs operated in an emulator under Hester’s Multidos 5.11 on a Windows platform should register with the website www.ackle.au. Versions of the programs can then be easily prepared in more accessible computer codes such as the statistical program R or Python.

In the Results and Discussion, the application of the ideal virial-action equations to heat cycles interacting with gravity will be conducted and tested for Earth systems. The results for the real troposphere will be shown as consistent with these equations, although the range of local and regional variations consistent with intense periodic convection and cyclonic influences obviously overlie this configurational framework.

3. Results and Discussion

3.1. Estimating Virial-Action Lapse Rates in Atmospheres as a Function of Composition

Estimates for virial-action dry lapse rates using Equation (17) for the troposphere on Earth for the mixture of predominant gases in the atmosphere are given in

Table 2. Atmospheric virial gradients in temperature with altitude.

Gas Phase	Molecular Weight m Daltons	Surface Gravity g	Degrees of Freedom n	δT/h = mg/nk × 105 K/cm
Earth		9.8066
Air (N2 + O2 + A)	28.97	“	4.98 (1% argon)	6.901 *
Argon	40.01	“	3.00	15.864
Carbon dioxide	44.01	“	5.41	9.650
Water	18.02	“	6.00	3.573
Venus		8.87
Carbon dioxide	44.01	“	6.37 at 0 km	7.462
Carbon dioxide	44.01	“	5.71 at 50 km	8.264
Mars		3.711
Carbon dioxide	44.01	“	5.11 at 0 km	3.866
Water	18.02	“	6.11 at 0 km	1.324

* The actual lapse rate observed in the Earth’s atmosphere is about 6.5 K per km [15], possibly affected by some heat released on the condensation of water from the convection of humid air at altitude. Determination of values for atmospheres on Venus and Mars is described elsewhere [14]. For air on Earth, δT/h = mg/nk = [(28.97 × 1.67 × 10⁻²⁷) × 9.8066/(4.98 × 1.3806 × 10⁻²³) = 6.901 °C per km. The symbol (“) means the force of gravity experienced on each planet is the same for each gas.

. Given that water in a humid equatorial atmosphere can reach 100,000 ppmv, or 10%, the lapse rate will be reduced from 6.894 to 6.562. This is close to the observed values for the US Standard atmosphere by the US Airforce [15]. The values shown in Table 2 are taken from Kennedy [14] for the other two rocky planets, with their atmospheres also shown, consistent with observations. The rate in air is estimated using a program in the Supplementary Materials for the three predominant gases, N₂, O₂ and argon. Since CO₂ is only 0.0004 atm, one-twenty-fifth of argon, its lapse rate of 9.65 °C per km has little effect on Earth, although on planet Venus, it is decisive.

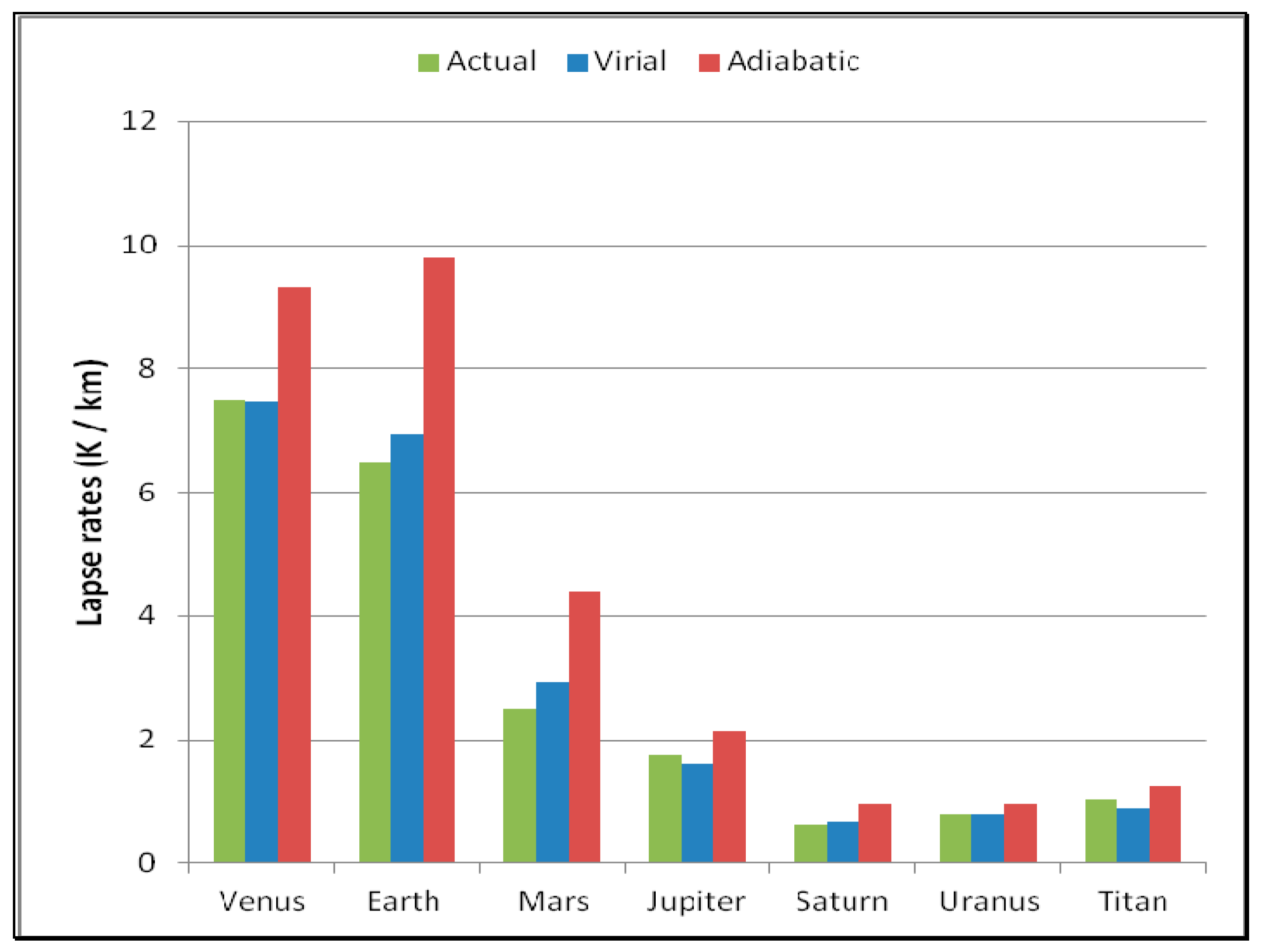
Figure 6 shows comparisons between the actual, virial and adiabatic lapse rates on planets with an atmosphere, with data described in more detail previously [14]. The observed lapse rates [15] correspond much more closely to the virial-action lapse rates than to adiabatic expansions into the atmosphere. By comparison, the adiabatic lapse rate favoured by meteorologists plays little role in climate modelling, given its variability locally. Verification that the virial form shown in Table 1 occurs generally on all planets [14] should give confidence for the meteorological modelling of tropospheric configurations with altitude on Earth.

3.2. Carnot Heat Engine Cycles Between 288.15 and 208.15 K at Constant Gravity

For relevance to the troposphere, a Carnot cycle in this temperature range is considered appropriate. The Carnot engine cycle starts at the highest pressure and temperature, conditions conducive to driving a work process. In stage 1 of Figure 3, the volume per molecule increases from the minimum, relieving the high pressure, which tends to cool the gas as work is performed by expansion, but remaining at the same temperature (isothermal), with heat being provided by the hot source (a). At some arbitrary point, the source is insulated from the gas cylinder, and expansion continues with an external pressure exactly matching that in the cylinder until it reaches about 0.1 atm pressure and 208.15 K, like conditions at the tropopause. Inertia from the cycling engine shown in Figure 1 then recompresses the gas at a constant external temperature with the insulation removed, until the entropy change (δs = δq/δT) is equal to that of the original heating. With insulation restored, the engine then recompresses the gas in the cylinder to the same volume, pressure and temperature as at the beginning of the cycle. Then, as Carnot showed, the maximum work possible for each cycle is given by the difference between the heat input in stage 1 and the output (a′) removed at the minimum temperature of stage 3.

The outputs for a Carnot cycle using either argon at 0.01 atm or N₂ at 1 atm as working fluid are shown in

Table 3. Action thermodynamics of the Carnot cycle for working fluids of argon and nitrogen molecules.

Property	Stage 1	Stage 2	Stage 3	Stage 4
Kelvin temperature variation	288–288	288–208	208–208	208–288
Argon (Ar) (0.01 atm)	Isothermal	Isentropic	Isothermal	Isentropic
Radius (a/2 = r, nm)	7.799825	10.88553	12.80769	9.17711
Pressure (kT/a3, hPa)	1.04797	3.85527	1.70982	4.647769
Translational action (@t, J.sec × 10−32)	10.15313	14.16984	14.16984	10.15313
Mean quantum number (nt = @t,/)	962.7548	1343.6326	1343.6326	962.7548
Negative Gibbs energy (−gt, J × 10−20)	8.19898 (δ2-1 = a)	8.59681 (δ3-2 = b′)	6.21005 (δ4-3 = a′)	5.9227 (δ1-4 = b)
Mean quantum (hv, J × 10−23)	8.51617	6.39818	4.62184	6.15182
Energy density (gt/a3, J/m3 × 105)	21.59810	8.33102	3.69481	9.57877
Quantum frequency (v, Hz × 1010)	12.8522	9.65589	6.97510	9.28406
Wavelength (m × 10−3)	2.33260	3.10476	4.29804	3.22911
Nitrogen (N2) translational
Radius (a/2 = r, m × 10−9)	1.680421	2.345217	3.075281	2.20353
Pressure (kT/a3, Pa × 105)	1.047973	0.385527	0.123512	0.33573
Translational action (@t, J.sec × 10−33)	18.30132	25.54155	28.44610	20.39685
Mean quantum number (nt)	173.539	242.194	269.925	193.410
Neg. Gibbs energy (−gt, J × 10−20)	6.15407	6.55190	4.82634	4.53896
Mean quantum (hv, J × 10−21)	0.354621	0.27052	0.34461	0.2346
Energy density (gt/a3, J/m3 × 106)	1.62113	6.34934	2.07431	0.530281
Quantum frequency (v, Hz × 1011)	5.35181	4.08263	2.69842	0.67921
Wavelength (m × 10−4)	5.60170	7.34312	11.10992	4.41385
Nitrogen rotational
Negative rotational Gibbs energy (−gr, J × 10−20)	1.56165	1.56165	1.5534	1.5534
Mean quantum number (jr)	7.1187	7.1187	6.0504	6.0504
Mean quantum (hv, J × 10−21)	2.19373	2.19373	1.71002	1.71000
Frequency (v, Hz × 1012)	3.31069	3.31069	2.58070	2.58070
Wavelength (m × 10−5)	9.05529	9.05529	11.61670	11.61670
nt3 × jr2 × 108	2.648495	7.19936	7.19936	2.64849

Codes a, b, a′ and b′ chosen by Carnot are shown as differences in negative Gibbs energy between stages shown. Carnot8/cal inputs were F = 288.15 K, R = 208.15 K, P = 0.01 atm or 1.0 atm, H = 1.5 or 2.5 (N₂), M = 40 or 14 and N = 14 and R = 1.38 × 10⁻⁸ (N₂).

. Note that the increase in the negative Gibbs energy (−δg_t = a) between isothermal stages 1 and 2 at high temperature is almost twice as much as the isothermal decrease between stages 3 and 4 (−δg_t = −a′) at low temperature. These bracketed letters were used by Carnot in 1824 [3]. As explained by Carnot (on page 31 in French edition), (a + b) must equal (a′ + b′), balancing the two heating stages for the working fluid cycle and the two cooling stages, respectively. Therefore, the difference between the variations (a − a′) or (b′ − b) is the maximum work possible at a given temperature range. Carnot insists that the first two sets be equal so that “after a complete cycle of operations the gas is brought back exactly to its primitive state”. The total heat input from the hot source, that is, stage 1 plus engine inertia in Figure 1, must equal the maximum external work performed (a − a′) as hot source heat in minus cold heat out plus the external work performed, either as torque sustaining fly wheel momentum or any increased gravitational potential.

Table 3 also shows how other parameters associated with the cycle vary during each stage of the cycle. This includes variations in the pressure, temperature, action, entropy and Gibbs energy and mean values for quanta in the Gibbs energy of molecules in the cycle. This quantum field was considered as caloric by Carnot, drawing attention to its characteristic properties of state for each stage of the cycle. The Gibbs field quanta are regarded as causing the vis viva of the working fluid and its kinetic energy by exerting torques [2,4], as indicated in the Lagrangian analysis indicated in Equation (14) as the second derivative of the inertia of independent particles. The heat input at a given temperature indicates the entropy change involved (δq/T), enabling the effective torque maintaining the mean kinetic energy constant for different molecules. Clausius [4] referred to this field energy performing work on the fluid in the engine as the ergal in his early research but later preferred his entropy or transformation terminology, indicating this was equivalent to the external work. In fact, this action of absorbed heat exerts a field pressure needed to produce a translational configuration of the molecules able to sustain the external work, such as lifting a weight or pumping water upwards by evacuation. In textbook accounts of the Carnot cycle, this expansion work phase is described as the integral of the dV/V differential expressing the external work without reference to the working fluid’s details. In action mechanics, this is described as a differential increase in action with changes in the negative Gibbs energy, as in line 5 in the argon table.

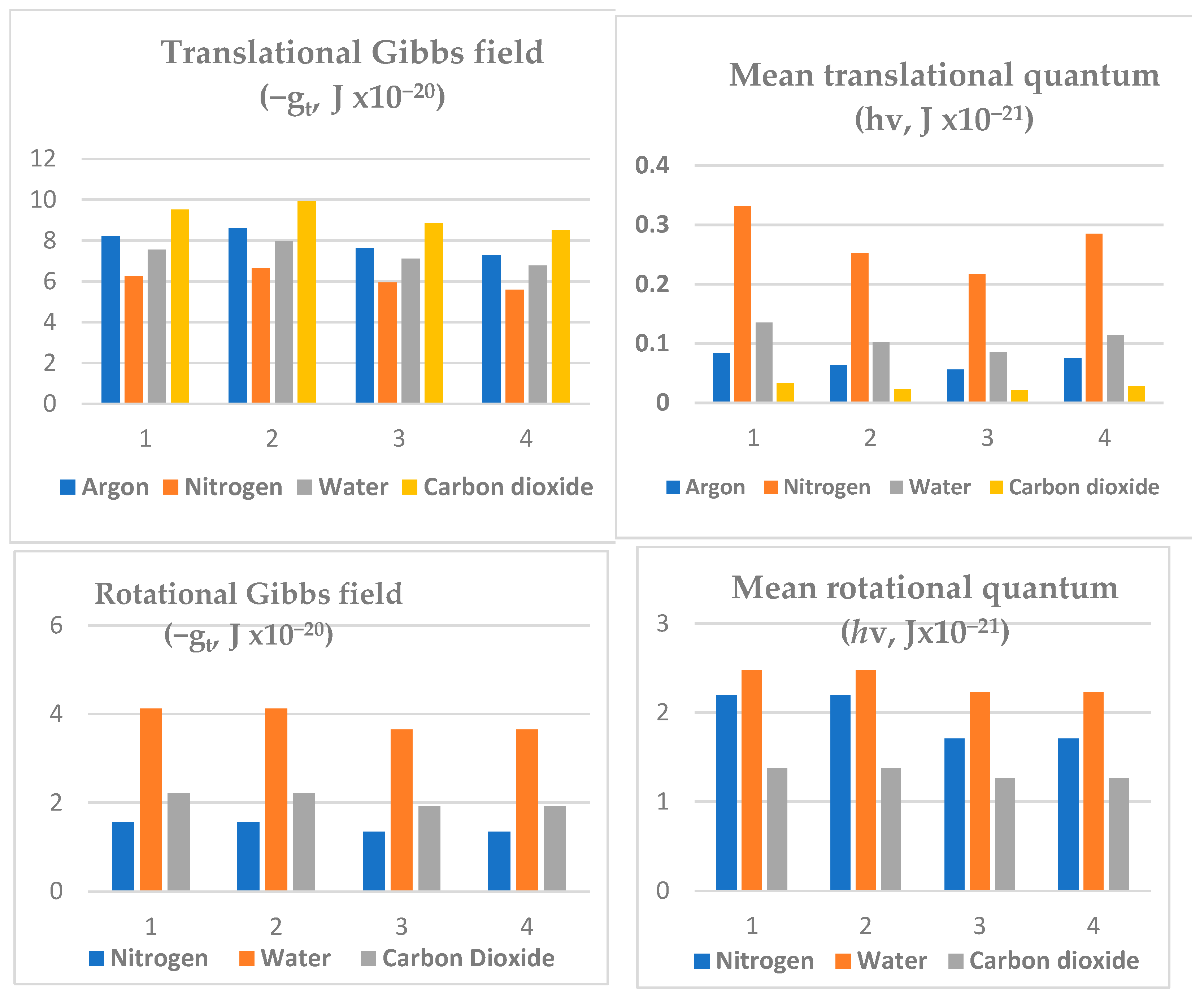
For argon in Table 3, code a is 0.398, a′ is 0.287, code b′ is 2.387 and b is 2.276. Every cycle of the engine can perform the same amount of work, allowing the rate of work or power to be estimated. It is of interest that the difference in the Gibbs energies for inputs and outputs is the same for argon and N₂, although the adiabatic expansion between stage 2 and 3 extends the cylinder further because of the release of internal rotational quanta in the diatomic gas. This is no advantage in work performed since all the rotational energy consumed during expansion (b′) is needed to reheat the gas on recompression (b).

Only the variations in the translational Gibbs energy participate in the work process because both rotational and vibrational internal energies vary only with temperature and not with volume. It is remarkable that even Carnot’s codes for variation in the caloric at different stages of the engine cycle correspond exactly to variations in the Gibbs energy in a quantum field or as changes in the gravitational potential, shown in Table 1 for both gases. Of course, the subsequent theoretical work of Clausius, Gibbs, Boltzmann, Planck and Einstein was needed to establish this link.

Schrödinger’s classic text Statistical Thermodynamics [16] provides a theoretical basis validating action mechanics estimates of Gibbs energy; this is displayed in Table 3, where the Gibbs field is also partitioned into translational quanta in line 7 for argon. These apply to monatomic gases like argon but also to all gas molecules for the translational partition, certainly when too cold for rotation and vibration if polyatomic. In a chapter entitled The n-particle problem, Irwin equates the translational quantum field, as shown in Equation (28), with the thermodynamic potential of Gibbs.

$$\begin{gathered} e^{{\displaystyle \frac{hv}{kT}}}={\displaystyle \frac{(\frac{2\pi mkT}{h^2}{)}^{\frac{3}{2}}V}{n}} \\ =(mrv{)}^3/({ħ}^3{z}_t)={@}^3/{ħ}^3={{\mathrm{n}}_{\mathrm{t}}}^3=1/\xi \end{gathered}$$

(28)

Then,

$$\begin{gathered} nkTln\xi =E+RT-ST \\ =G(\text{the thermodynamic potential or Gibbs energy}) \end{gathered}$$

(29)

Note that the Gibbs energy will be negative, indicating spontaneity; ST must exceed (E + RT) [1]. Schrödinger had no hesitation in applying quantum theory to translational action in a zone where mechanics are classical at ambient temperature [6].

The Carnot cycle simulation shown in Table 3 for the atmospheric gases argon and nitrogen can be extended to greenhouse gases, water vapour and CO₂, its thermal effect to be examined in later sections. However, the variation in spectral properties is shown in Figure 7. The mean values of quantum properties in a cycle corresponding to an average global surface temperature of 288.15 K and at 5 km of 255.65 K have been estimated with the same Astrocal program (Carnot8/Cal) described in the Supplementary Materials. In all cases, the translational energies are in the mm wavelength zone with frequencies near 10¹¹ around 100 GHz. The rotational properties for N_2, the predominant gas in air, are also given in Table 3. However, the power of action mechanics to provide access to significant rotational spectra is revealed in the data generated for water vapour and CO₂. The Gibbs energy values can be resolved for the Earth’s surface spectrum for less than 100 μm for water molecules for its three inertial moments rotating as an asymmetric top.

By contrast, the simpler rotational spectrum for the linear symmetrical top CO₂ with a wavelength near 150 μm is greater than the predominant surface emission spectrum. A significant role for the water rotational spectral absorptions is evident in Figure 7. Earlier, we showed with accuracy [1] that the vibrational entropy of water vapour is negligible by comparison with CO₂, the latter with its major absorption and emission at 15 μm or 667 cm⁻¹. The vibrational spectrum for water with much shorter wave numbers of 1595, 3652 and 3756 can retain only 1% of the entropy for CO₂ per molecule, with correspondingly lower pressure of up to two orders of magnitude less. The far greater number density of water molecules in the troposphere at lower altitudes up to 5 km explains its predominant role in establishing the natural greenhouse warming on Earth, by comparison to CO₂.

This unique ability of action mechanics to easily estimate accurate mean values for the rotational Gibbs field energies is impressive, verifying its theoretical basis [1,2]. We intend to further investigate this capacity. The contrast in rotational energies between water vapour and CO₂, given that the quantum values for water lie in the Earth’s infrared emission zone, offers the potential for a better understanding of greenhouse processes.

3.3. Virial-Action Atmospheres on Earth

In

Table 4. Virial-action mechanics profile on Earth estimated for mean values of atmospheric molecules.

Altitude (km)	Temp K	Estimate of Pressure ×10−6 Pascals	Estimate of Density ×10−25 per m3	Solved Negative Translational Gibbs Energy kTln(nt)3Qe/zt ×1020 J per Molecule	Estimated from Negative Rotational Gibbs Energy −gr = kTln[(nr)2/σr] ×1020 J per Molecule	Temp K USAF	USAF Model 6 Pressure ×10−6 Pascals
0	288.2	1.01282	2.545887	6.3252617	1.5965459	288.2	1.0130
1	281.3	0.89895	2.315004	6.1968176	1.5489674	281.7	0.8988
2	274.4	0.79384	2.095675	6.0686066	1.5016219	275.2	0.7950
Lumns	267.5	0.69722	1.888033	5.9406345	1.4545154	266.7	0.7012
4	260.6	0.60880	1.692180	5.8129076	1.4076540	262.2	0.6166
5	253.7	0.52826	1.508188	5.6854323	1.3610441	255.7	0.5405
6	246.8	0.45527	1.336097	5.5582154	1.3146928	249.2	0.4722
7	239.9	0.38496	1.175904	5.4312642	1.2686071	242.7	0.4111
8	233.0	0.33059	1.027566	5.3045863	1.2227945	236.2	0.3565
9	226.1	0.27817	0.890993	5.1781896	1.1772636	229.7	0.3080
10	219.2	0.23187	0.766044	5.0520831	1.1320224	223.3	0.2650

The key outcomes are the correspondence of the temperature and pressure gradients taken from the US Airforce data set in Table S1 and that estimated by action mechanics shown in columns two and three in Table 4. The Gibbs energy changes are linear with altitude.

, the thermodynamic properties of air with properties averaged for nitrogen and oxygen with root-mean-square velocities characteristic of a surface temperature of 288.15 K are shown. These data were calculated using numerical computation, as outlined in Figure 5, for each height. A comparison between data generated by the action barometric model and actual field observations collated by the United States Air Force [15] is also shown in Table 4, with close agreement, although the temperature fall is disrupted near the troposphere possibly because of atmospheric dynamics.

The data sets in Table 4 and

Table 5. Mean variations in gravitational and thermodynamic molecular properties with tropospheric altitude on Earth.

Altitude (km)	Estimated Gravitational Potential Energy mghn ×1022 J per Molecule	Estimated Decreasing Enthalpy 3.5 kδT = δh ×10−22 J per Molecule	Estimated Rotational Gibbs Energy δ[kTln(nr)2/σr] = −δgr × 1022 per Molecule	Solved Translational Gibbs Energy δ[kTln(nt)3/zt] = −δgt × 1022 J per Molecule	Solved Cumulative Translational Gibbs Energy
0	0
1	4.75679	−3.32976	−4.75783	−12.84441	−12.84438
2	9.51359	−6.65951	−9.49241	−12.82111	−25.66551
3	14.27038	−9.98927	−14.20306	−12.79721	−38.46271
4	19.02718	−13.31903	−18.88920	−12.77269	−51.23541
5	23.78397	−16.64878	−23.55018	−12.74753	−63.98294
6	28.54077	−19.97854	−28.18532	−12.72169	−76.70463
7	33.29756	−23.30829	−32.79389	−12.69512	−89.39975
8	38.05436	−26.63805	−37.37514	−12.66779	−102.06754
9	42.81115	−29.96781	−41.92824	−12.63967	−114.70720
10	47.56795	−33.29756	−46.45235	−12.61065	−127.31787

The governing algorithm for diatomic or other linear molecules is that mgh_n-o + 3.5 kδT_o-n = δ[kT_o-nln(n_t)³_o-n/z_t] − δ[kT_o-nln(n_r)²_o−n/σ_r] = δg_t − δg_r. Computed as mean-molecular-weight molecule of 28.97 Daltons.

were computed using the virial-action gravitation Equation (27), assuming a base temperature of 288.15 K and the Earth’s average pressure at sea level, with gravity (g) 9.8066, using the program Baromet10/Cal. A standard diatomic molecule of mass 29 with a bond length of 1.13 × 10⁻¹⁰ cm, a rotational symmetry of 2 and a Q_e value of 1.41 to account for oxygen’s spin multiplicity of 3 was used. However, the same data could have been produced using the respective proportions of nitrogen and oxygen. Minor gases, including argon, were ignored in the calculation. The plot was made by solving Equation (20), as follows: kT_nln[(@_tn/ħ)³Q_e/z_t] = 3.5k(T_n − T_o) + kT_oln[(@_to/ħ)³Q_e/z_t] − kT_oln[(@_ro/ħ)²/σ_r] + kT_nln[(@_rn/ħ)²/σ_r] − mgh_n. A data set including the variation in gravitational potential is shown in Table 5, confirming virial-action Equation (27). 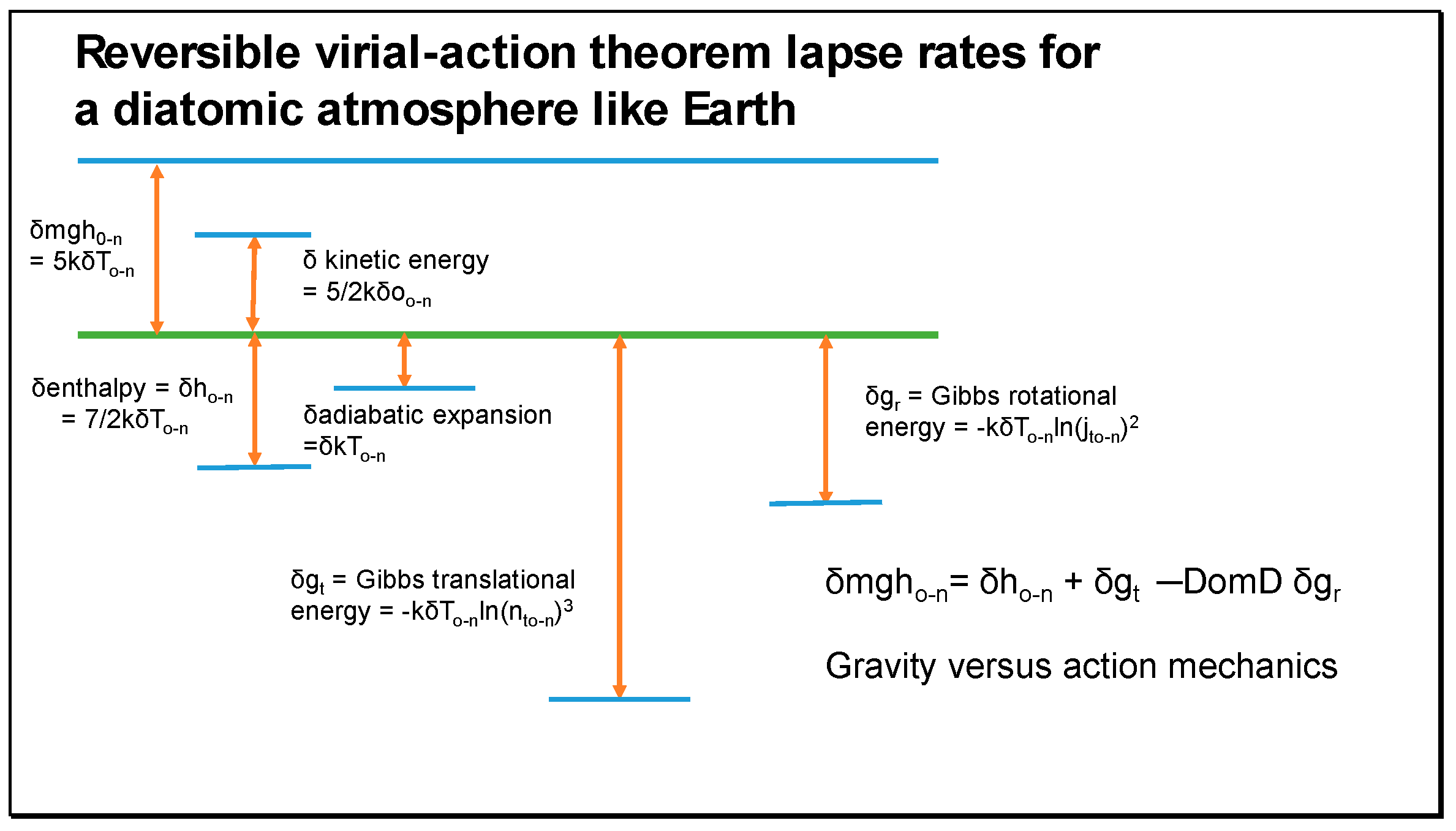In Table 5, the close correspondence between the increasing gravitational potential and decreasing rotational Gibbs energy is significant. The inertial effect of rotation in diatomic molecules effectively renders the molecules weightless. The rotational Gibbs field reduces with altitude as the atmosphere becomes colder, being replaced with increasing gravitational potential, explaining Equation (27). Its vibrational component expressed as a harmonic oscillator has no such inertial or centrifugal component and cannot compensate mechanically for gravity.

3.4. Comparing the Mechanics of Earth Atmospheres with and Without Greenhouse Gases

The greenhouse effect on Earth is responsible for an increase in the surface temperature of about 33 K, from −18 °C as a mean value or 255 K [17]. Using the virial-action plot (Baromet10/cal), Figure 8 shows atmospheric profiles for contrasting atmospheres, both with the US Standard [15] proportions of major gases but only one (mean values) augmented with greenhouse gases raising the surface temperature to 32 °C. A mean incoming solar radiation of 341 Watts per square metre applies to both. However, as a black body on the surface, no radiation will be absorbed in the atmosphere, requiring that a black body temperature of 255 K radiates with the same intensity as the incoming radiation, without significant absorption in the atmosphere, having an albedo of zero. Despite this, it is assumed that sufficient heat transfer from the surface to sustain the Gibbs fields of the atmospheric molecules will still occur, taking much longer to equilibrate but with no recycling in the absence of heat engines in the atmosphere. Assuming the same weight of the atmosphere, the surface pressure must be the same, balanced thermodynamically, but the pressure will decrease more rapidly on the black body surface. In the figure, the gravitational energy per molecule would increase with altitude in a linear manner similar to temperature, as both forms of Gibbs energies rise according to the formula given in Equation (27).

A comparison of profiles at different latitudes generated with the program Baromet10/Cal is shown in Figure 9. The equatorial bulge compared to the mean of the polar profiles shown is obvious. The tropopause is typified with a transition to little or no temperature change, suggesting that the quantum exchange of mechanical Gibbs energy with gravity is uncoupled. The thermal dynamics of the troposphere in actual profiles are strong functions of diurnal or seasonal conditions, accounting for variations likely to be observed from these ideal plots, a result of convection and advection. However, the virial-action model developed from our Carnot heat cycle using action mechanics can provide a more secure basis for tropospheric dynamics in future research. Despite the Earth operating with equal inputs and outputs of radiant energy, the greenhouse enhancement in the surface temperature provides Carnot heat energy.

3.5. How Closely Do Anticyclones and Cyclones Function as Carnot Heat Engines?

Just as in the case of real heat engines, because of friction, the maximum power sustaining action in the troposphere must be imperfect. In a perfect cycle, factors like the rates of heat transfer are not limiting; there is no friction generating waste heat loss, nor is there the chaotic loss of heat in the working fluid by turbulence [6]. The principle of least action regarding the action mechanics of particles in the working fluid applies. By contrast, tropospheric work processes are largely dissipative but continuously replenished with new energy. The internal work of the troposphere is a function of the increase in entropy of the radiant energy emitted from the Sun at almost 6000 K and the outgoing longwave radiation (OLR) emitted above the surface of the tropopause as infrared or microwave radiation at about 255 K. The average surface temperature near 288 K is a result of greenhouse warming.

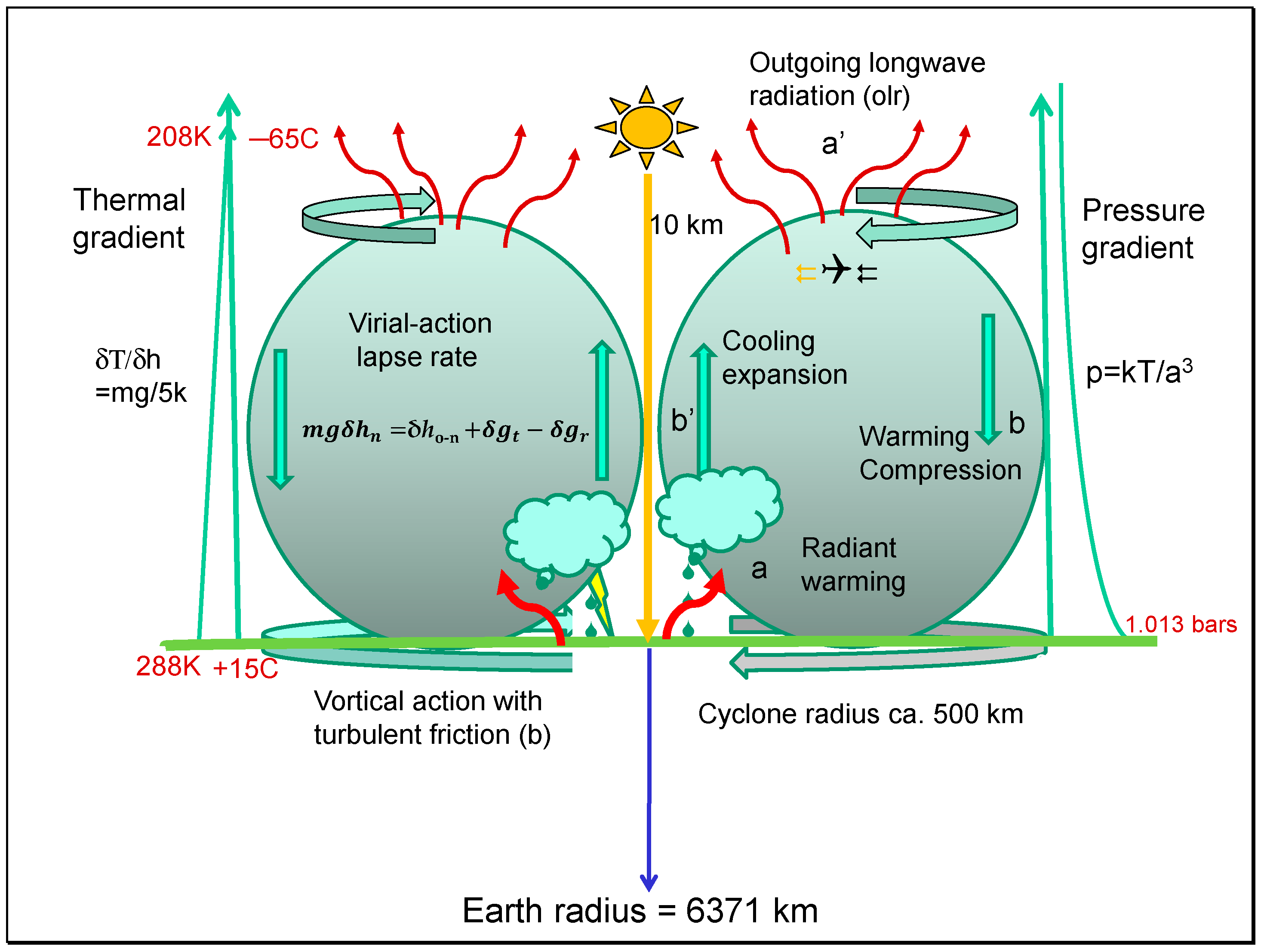
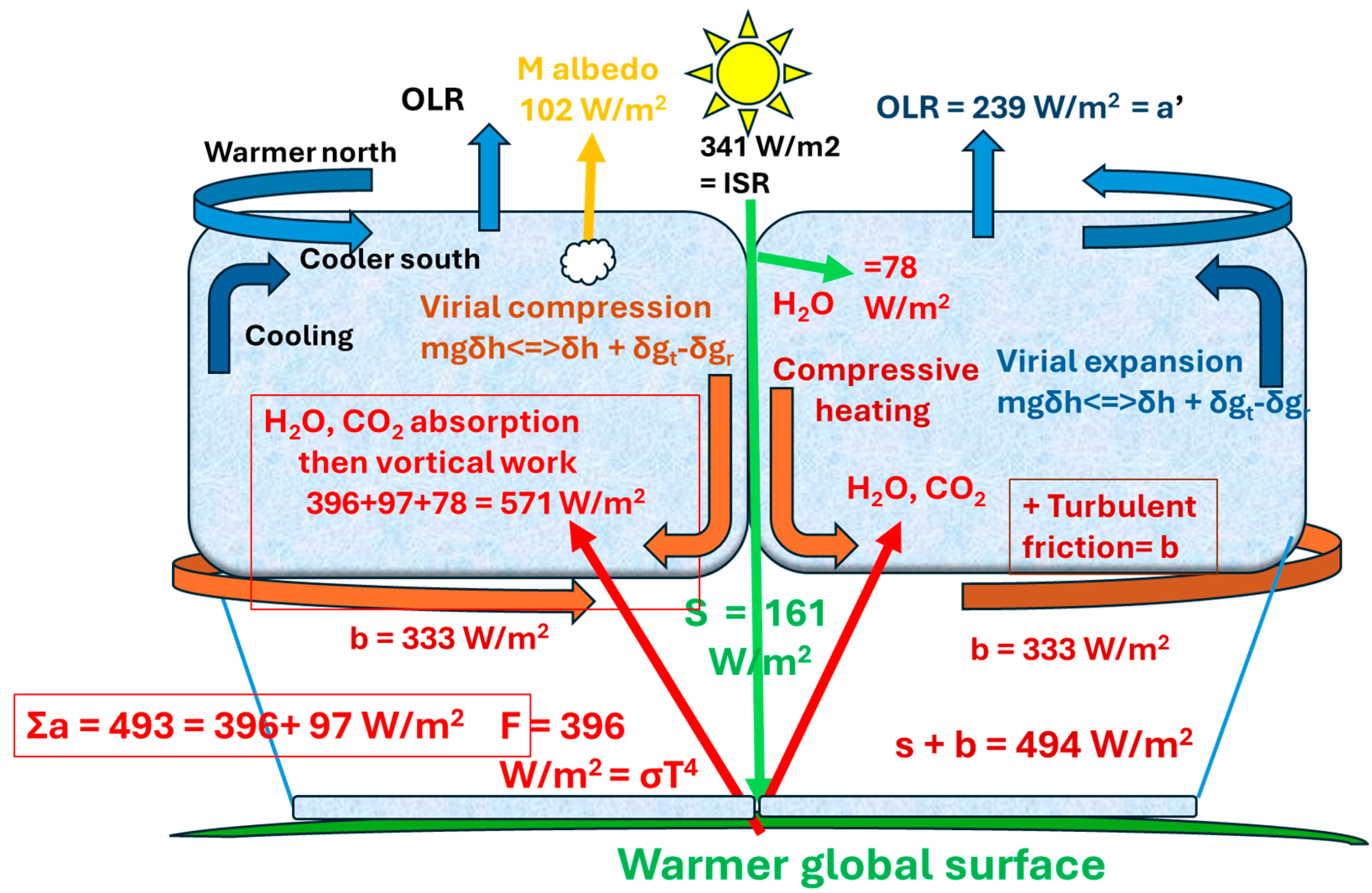
In Figure 10, the Earth’s surface on land and sea provides the warmer heat source for radiant energy, sustaining the troposphere up to the colder tropopause. The Trenberth model for greenhouse warming [17] involves the difference between black body radiation from the surface (R = σT⁴) and outgoing longwave radiation (OLR ≡ a′). One of Carnot’s insights for reversibility in the engine working fluid was the need for the equality of heating (Σa + A = 396 + 97 + 78 = 571 W/m²) and cooling processes (b′ + a′ = 333 + 239 = 572 W/m²), as shown in Figure 10. For warming, the troposphere is partly heated by solar absorption by water in air (A = 78 W/m²), with the latent heat of evapotranspiration at the surface (e = 78 W/m²) with heat release by condensation, under cooling convection. Thermals also conduct from the surface (c = 19 W/m²). For 239 W/m² of absorbed solar radiation, a total of 571 W/m² is absorbed in the troposphere, and 239 is emitted through the tropopause to space. About 332 or 333 W/m² is available for frictional dissipation at the surface by turbulent heat release rather than by radiation. The greenhouse effect can be considered as (161 + 333) or 494 W/m² or a trebling of the total direct heat received at the surface while still allowing 239 W/m² of outgoing longwave radiation. Just considering the enhanced radiation from the surface because of a greenhouse effect and subtracting the OLR suggests a lower black body yield of 157 W/m² (R-OLR = 157 W/m²). It is important to understand that, in terms of the work potential, the rating power or Joules per sec (W/m²) takes no heed of the quality of the work achieved; 239 W/m² for the incoming solar radiation (ISR) and the same value for power as OLR cannot be compared for the kinds of work achieved given the large variation in the impulsive momentum between the two kinds of quanta concerned.

By contrast, there is a low likelihood of fully adiabatic expansions or compressions in the troposphere, given that radiative processes that transfer energy occur everywhere there are greenhouse gases with high emissivity. Cooling expansions and warming compressions with changes in altitude exist, but we claim these represent virial-action thermal and gravitational transitions, as already discussed. Heat and work processes in the troposphere also differ from heat engines in the smaller range of pressure variation, particularly in anticyclones. The ranges of pressures shown in Table 3 for argon and nitrogen gases in the Carnot cycle are 7–10-fold for an 80 K temperature gradient. As a result, winds flowing to balance relatively low pressure gradients are far gentler. Wind droughts are more typical of periods of higher pressure [18], explaining why wind turbines generating electricity perform weakly. In high-pressure anticyclonic zones with pressure above 1013 hPa (1.0 atm) up to 1030 hPa, descending compressing air still absorbs surface radiation with similar warming rates; the higher pressure is then relieved by radial Coriolis flow from horizontal rarefaction to zones of lower peripheral pressure.

In cyclonic zones with pressure falling as low as 900 hPa, the surface radiation also has intensity with Planck spectrum peaks defined by the varying temperature. Stronger winds flow to the centre of these depressions with vertical expansion rarefying air, cooling it quickly, and the likelihood of exceeding 100% relative humidity with the precipitation of rain is far greater. Black body radiation from the surface may be absorbed as a function of the concentration and absorptivity in the troposphere of greenhouse gases such as water, CO₂, CH₄ and N₂O. Having been excited to a higher quantum state, all these polar gases dissipate their vibrationally excited states almost immediately, warming other air molecules through collision processes [19]. Near-surface warming can perform work sustaining 10 tonnes per square metre of the atmosphere, like phase 1 in a horizontal piston, increasing action and entropy. In sub-tropical or tropical marine environments, the cyclonic motion is enhanced by the release of infrared radiation from the condensation of water vapor by gravitationally cooling convection near a central eyewall. Surface evaporation by solar heating provides this source of latent energy. Similar though less intense processes can occur on land, provided there exists surface water.

In both cases of air cells of low and high pressure, vortical action provides an additional degree of freedom for the storage of Gibbs energy, sustaining mass action. This work process can be calculated using action mechanics, as described elsewhere [2]. The conservation of vortical action was used to explain the mechanical intensification of tropical cyclones [7], using the latent heat of water vapour to sustain vortical rotation, a higher level of Gibbs field energy. For vortical action, quantum levels are partitioned by the reduced Planck’s constant of action (h/2π = 1.054 × 10⁻³⁴) (n_t = mrv/ћ), assuming a symmetry factor of 2. The vortical Gibbs energy for the matter per cell (M/a³) is then estimated using the logarithm of the quantum number multiplied by the appropriate torque factor (Σmv²). The total vortical Gibbs energy is obtained from the product of the number of molecules per cubic metre. This is then extended by altitude.

3.6. Greenhouse Gas Enhancement of Surface Temperature by Vortical Action

This work process requires the significant absorption of heat radiated from the surface, mainly by water and carbon dioxide, without significant rises in temperature. Greenhouse gases like H₂O and CO₂ act like temporary capacitors, rapidly giving up their energised state by absorbing quanta of infrared energy emitted from the surface. This process occurs for CO₂ molecules in collisions with water molecules after only about 105 collisions, dissipating this into translational kinetic energy from a collision rate of 10¹⁰ per sec. Nitrous oxide has the same dissipation rate with water, and methane and CO₂ persist in an excited state for 406 collisions according to the experiments of Leffler and Grunwald [19]. In the southern hemisphere, this powers anticlockwise anticyclone motion because the absorption of surface emission by GHGs is greater further north (Figure 9), increasing pressure as the inertial Coriolis effect guides the air flow; this veers in the direction of the Earth’s motion in both hemispheres, moving away from the equator as latitudes increase. The increased translational and rotational energy provide the freedom for low-frequency vortical action and energy (hv) [6], providing a mechanism for the turbulent release of heat as radiation (T) near the surface. Given the negative surface gradient in temperature as solar intensity (S) declines, greenhouse gas activity will be greater nearer the equator, providing a pressure gradient from north to south in the southern hemisphere, as indicated in Figure 10.

The release of radiation by friction nearer the surface, consistent with gravitational potential, does not conflict with the second law of thermodynamics, solving objections to downwelling radiation warming from a colder source. As shown in the Carnot cycle, any increase in the freedom of relative translational motion of molecules increases the heat capacity of the gas phase. For anticyclones, this allows turbulent friction processes nearer the surface to release heat within the boundary layer of the lower atmosphere (Σhv), to the extent of about 332 watts per m² [6,17] as a global average, rather than by direct radiation from a colder atmosphere to the surface, more in accordance with the second law of thermodynamics. The decreasing wind speed near the surface regarded as vorticity represents the loss of power with wind speed as frictional heat is released in turbulence, warming the air and causing spectral radiation proportional to the temperature. If the Earth had no greenhouse gases in its atmosphere, the surface radiation would be emitted directly to space, and the profile with height would require slow heating by conduction.

The vortical translational energy in anticyclones and cyclones must be consistent with the global Kiehl–Trenberth heat flow budget [17] for black body radiation from the surface into the atmosphere, where some is absorbed as infrared radiation by greenhouse gases. The Kiehl–Trenberth budget proposes that 332 W per m² of downwelling radiation is then returned from the heated atmosphere, greater than direct solar radiation alone would sustain. In action mechanics, it is proposed that frictional turbulence near the surface returns absorbed radiation instead of net radiation from higher in a colder atmosphere to the surface, with vortical action in anticyclones generated as work processes in the air, facilitated by Coriolis accelerations in each hemisphere.

While the rates of energy flow can be indicated as a power function of W/m², the chemical potential of the Gibbs field is important for function. In the Carnot cycle illustrated in Figure 1 and the data in Table 2, the differences in the variation in the Gibbs energy in the isothermal stages are the maximum work potential (a − a′). Direct sunlight falling on chlorophyll provides low-entropy quanta emitted at the temperature of the Sun with a short mean wavelength of 500 nm, generating high action impulses. Radiation emitted from the Earth’s surface has a longer wavelength of about 10 micrometres, and that from the tropopause is even less impulsive at around 15 micrometres, with rotational energy exciting water molecules up to 100 micrometres. While the total energy as Joules per sec must be conserved, the quality of the quanta very much determines the work potential.

A wind speed of 10 m per sec is predicted to contain vortical energy [6] of 1.47 × 10³ J per m³ of air in wind, many times greater than the wind’s kinetic energy, with an additional 2.4 MJ per m³ of thermal energy required for the air to be heated from absolute 0 K to 298 K [1]. In a previous paper [6], we explained how vortical energy as the latent heat of condensation of water and the conservation of momentum can power the intensification of tropical cyclones. It is important to be aware that the Trenberth diagram gives details of mean global energy flows per square metre of the Earth’s surface, irrespective of wavelength. In terms of heat energy performing work in Carnot cycles, as shown in Figure 4 and Figure 9, the variation in the Gibbs energy as the kinetic potential must be considered separately. The sunlight within plants decomposing water into oxygen and reducing CO₂ to carbohydrates has wavelengths of less than 1 micrometre. The heat energy radiated from the Earth’s surface near 10 micrometres at a higher temperature than the black body temperature of 255 K, at a mean value of 288 K (a), is able to power anticyclones and cyclones [6] in vortical motion as winds often in laminar flow without turbulence. Radiation into space occurs (a′) near the black body temperature at the tropopause, identified in Table 1 at different latitudes and in Figure 9.

3.7. Estimates of Gibbs Energies for Atmospheric Gases

In

Table 6. Profile conditions and Gibbs energy per molecule for tropospheric gases, including greenhouse gases.

Atmospheric Gas	Temperature T	Density n/m3	Pressure P	Translational Gibbs Energy −gt	Rotational Gibbs Energy −gr	Vibrational Gibbs Energy −gc
	Kelvin	=1/a3	Dynes/cm2	J/molecule	J/molecule	J/molecule
Water 0.0004 atm		×10−21	×10−2	×1020 J	×1020 J	×1023
0 km	288.1500	10.1835493	4.0512848	9.016585189	2.07234140	1.24028461
5 km	270.3356	6.1502476	2.2954659	8.611636060	1.90849468	0.72861960
Water 0.016 atm		×10−17	×10−4	×1020 J	×1020 J	×1023
0 km	288.1500	4.07341976	1.6205139	7.549051568	2.072341403	1.24028461
5 km	270.3356	3.13706846	1.1708526	7.144102429	1.908494677	0.72861960
CO2 0.0004 atm		×10−15	×10−2	×1020	×1020	×1021
0 km	288.1500	10.1835494	4.0512848	9.549961720	2.24865929	1.79371631
5 km	239.6064	0.87391569	0.2890965	8.661879002	1.80880709	0.62083771
N2 0.78 atm		×10−19	×10−5	×1020	×1020	×1025
0 km	288.1500	1.98579213	7.9000053	6.266476733	1.561650059	3.89511735
5 km	254.8849	1.20911641	4.2548799	5.652889568	1.338200586	0.82971538
O2 0.21 atm		×10−18	×10−5	×1020	×1020	×1023
0 km	288.1500	5.34636343	2.1269245	7.30523956	1.69715480	1.32545576
5 km	250.1497	2.09532214	0.7236454	6.59208978	1.42449783	0.39379343
Argon 0.01 atm		×10−17	×10−4	×1013
0 km	288.1500	2.5458873	1.0128212	8.21253258	0	0
5 km	250.1497	2.09532214	0.7236454	6.59208978	0	0
N2 + O2 + Ar 1.0 atm		×1019	×105	×1020	×1020
0 km	288.150	2.54588734	10.128212	6.324644044	1.596607545	negligible
5 km	253.7317	1.50945891	5.287750	5.685466013	1.361338787

, Gibbs energies have been determined for the major tropospheric gases, including key greenhouse gases. Of these, only CO₂ has significant vibrational potential energy in ambient conditions. The very stable bonds of hydrogen in water and high zero-point potential energies for unpolarised N₂ and O₂ molecules show there is no infrared absorption by these gases, or by monatomic argon. Only molecules with a significant magnetic moment from asymmetry freely exchange quanta. Water is greenhouse-active in terms of rotational quanta. It is capable of primary excitation by solar energy at its vibrational frequencies or by quanta emitted when water condenses in the atmosphere, as in tropical cyclones, as we have discussed elsewhere [6,20,21]. However, its function as a greenhouse gas has by far the largest effect in the atmosphere. Varying with temperature, this form of entropy does not vary with concentration. When water is at the same pressure as CO₂, its vibrational Gibbs energy (half its total) is more than 100 times less.

The results obtained from the program Entropy8/Cal in the Supplementary Materials for atmospheric gases are given in Table 6. Gases without greenhouse properties have little or no vibrational entropy above absolute zero temperature [20]. CO₂ is outstanding in this degree of freedom, although at tropospheric temperature, it has only minor activation of this property. The major greenhouse gas at lower altitudes only has about 1% as much vibrational excitation at tropospheric temperatures.

This information on atmospheric gases is significant in function. CO₂ is distributed evenly in the troposphere, both by altitude and latitude, and it has no significant potential gradients. Therefore, it has little effect on weather, despite its significant role in climate. Methane and nitrous oxide are two more impermanent greenhouse gases. Water is by far the most significant for warming, given that all three of its phases are common on the Earth’s surface. Its rapid condensation when convecting upwards in storms may lead to cavities in the air into which about 10 tonnes of air falls, perhaps generating thunderclaps and lightning from compressive reactions and friction.

Uniquely amongst greenhouse gases, water can undergo all three of its phase transitions at surface conditions, offering prospects for surface temperature management [22]. Our previous research [1] showed that of the major greenhouse gases, only CO₂ and nitrous oxide (N₂O) have significant excitation of the temperature-dependent vibrational energy and Gibbs energy. Water and methane, while vibrationally active at shorter infrared wavelengths, also provide capacitance for trapping specific wavelengths of surface radiation, discharging this almost immediately by collisions, generating translational energy, as explained above [18]. Similar rapid discharges of this heat trapping capacity will occur with all greenhouse gases. By raising the temperature, this will mean subsequent radiation will be a function of the virial-action temperature at any altitude. Radiation from the surface absorbed by molecules with high optical density therefore heats the troposphere and contributes to the gravitational work of sustaining the troposphere at altitude. In a diurnal cycle, the variation in surface temperature as the intensity of sunlight increases with the Earth’s rotation will result in gravitational elevation. The chaotic nature of meteorological conditions for convective and advective flows in the troposphere will mean that these reversible processes for virial-action and heat–work processes will also be erratic in nature.

Like vibration, the rotational energy per molecule is dependent on temperature only, irrespective of the density of the molecules, although the total energy stored does depend on concentration. Table 6 shows that at 0.016 atm, water is 50 times as dense as CO₂ and therefore stores almost the same total vibrational energy per unit volume of air. Of course, water also stores far more rotational energy and, from its ability to condense, can release far more radiant heat from its latent energy store, mainly by sacrificing its translational entropy [1,6,21]. Of the total translational negative Gibbs energy shown in the table as mixed oxygen, nitrogen and argon, we have estimated there is 1.066503 × 10¹⁰ J of energy stored per square metre up to 10 km, equivalent to 87 days of solar radiation at 161 W per m², or 311 days of the mean radiation from the surface of 396 W/m² at 288 K, according to the Stefan–Boltzmann equation after greenhouse enhancement.

3.8. What Carnot Meant by Heat and Caloric

It is of interest to discuss whether Carnot distinguished between the terms chaleur and calorique he used in describing heat. He seems to suggest a specific nature for caloric, characteristic of a physical state of the working fluid in different conditions of temperature and volume, similar to how we show the forms can be considered as different quantum states in Table 3. Mendoza, in a footnote in the edition [4] he edited, equated caloric with entropy. Hermann and Pohlig [23] have recently discussed which physical quantity deserves the name for the quantity of heat, deciding that Freeman Dyson’s 1954 definition as disordered energy is most accurate. They decided that entropy is the best name. We agree, as long as it is considered as a capacity factor consistent with its physical dimensions of Joules per degree Kelvin. In discussing the thermal capacity of solids, Feldhof [24] considers entropy capacity as key to thermal processes. This may be true for materials as a second derivative, but it is important to be aware that entropy itself is a capacity factor for energy per degree.

The importance of the virial theorem was accepted by Ludwig Boltzmann [25], as derived from the Lagrangian calculus of variations. In his lectures on gas theory, he set an important foundation for statistical and action mechanics, pointing out on numerous occasions that entropy (and thus Gibbs energy) was controlled by volume and temperature, the latter to the exponential power 3/2, that is, f(VT^3/2). This is also obvious in the statistical mechanics Equations (2) and (4) from which the action mechanics equations for estimating entropy and Gibbs energy are developed. His derivation of the virial theorem [25] owes much to Clausius but with a strong emphasis on the principle of stationary action on which the absolute determination of negative Gibbs energy is based.

Given that we have shown that Carnot’s formula [4] for caloric in contrast to heat is equal to the variation in Gibbs energy considered as quanta, it seems that the rejection of Carnot’s version of caloric in the 19th century was premature. Clearly, his term meant ordered energy, whereas entropy means energy that is disordered or distributed into many different quantum states, as a function of environmental conditions.

4. Conclusions

This article sought to show how lessons from Carnot’s foundation of theoretical thermodynamics in his heat engine cycle can be applied to the working fluid of the atmosphere. A classical quantum approach enabled the partitioning of the mean heat energy per molecule shown in Equations (3) and (5) from the statistical mechanics of diatomic molecules like N₂. The subsequent development of Equation (27) using virial theorem action mechanics provided a link between the mean variation in molecular gravitational energy with height (mgδh), enthalpy (5/2 kδT) and translational and rotational Gibbs energy per molecule (δg_t and δg_r). The integration achieved in this equation between atmospheric thermodynamics and gravitational potential is unique. Note that the Gibbs energy increases as the Gibbs field energy decreases as temperature declines with altitude. Negative Gibbs energy corresponds to increases in entropy and temperature as the Gibbs field is populated with quanta.

Although mgδh is legitimate as an approximate measure for potential energy, giving the equivalent kinetic energy as δh decreases, this is not true for particle masses subject to higher orbital or quantum states. In such cases, the potential energy increases by twice as much, equal to the size of the quantum of radiation causing the elevation in orbital energy plus the decrease in kinetic energy. This principle is expressed in the virial theorem not only for the quantum mechanics of electronic orbits but also the variation in the rotational energy of molecules with temperature [14]. Indeed, Table 4 shows the equivalence of mgδh_n and δg_r per molecule for increased altitude δh.

The change in gravitational energy is actually mgδh_n plus the rotational energy released at the same elevation to a colder altitude. The virial theorem also requires that the following equation must hold relating the equality for reversible changes with altitude as a result of diminished temperature. A similar change will take place with the rotational Gibbs energy of N₂ in the isentropic state of a Calvin cycle with no change in gravitational potential. Enthalpy decreases with altitude as the temperature becomes colder. Translational Gibbs energy increases with altitude, releasing quantum field energy, supporting the second half of the required gravitational energy of mgδh.

mgδh_n + δg_r = 3/2 kδT + δg_t

(30)

This novel achievement is based on extensive research published on entropy [1,2,6]. This advance draws partly on details of Carnot’s analysis of achieving maximum power in heat engines. For example, the recent development of the high-pressure pyrolytic combustion of coal as applied in Japan is consistent with Carnot’s argument in 1824 that then-current steam engines utilised a temperature range of less than 100 °C, when a 1000 °C range could be available with coal as a heat source. It is reassuring to know that Carnot’s concept of variations in caloric in the engine cycle that we have examined in detail is identical to the variations in negative Gibbs energy.

The proposal to use a virial-action solution for the lapse rate of temperature in the atmosphere was made previously [14], shown as functionally accurate on several planets in the solar system. The atmosphere is supported only because of the continuous inflow of solar heat, sustained in the troposphere by the virial-action hypothesis. These results may be found useful by meteorologists to better understand the causes of weather and the Trewartha approach to climatic zones based on fluxes of energy and changes in the phase state of water.

The global Earth does not operate as a reversible heat engine performing external work. On the contrary, solar energy is dissipated almost completely, from solar quanta emitted equivalent in energy to 6000 K to about 300 K from the Earth. Heat flow and work processes on Earth occur within the working fluids, as shown in Figure 4 and Figure 10. Radiant emissions from the Earth’s surface recycled by absorption by greenhouse gases like water and carbon dioxide perform work on the gases of the atmosphere by collisions, dissipating most of these quanta to longer wavelengths in the Gibbs fields of the predominant air molecules, N₂, O₂ and argon. Temperature differences at different latitudes set up the Lagrangian action circulation of air masses influenced by Coriolis inertia as anticyclones and cyclones, discussed previously [6], as the vortical action mechanics of the troposphere. Rather than warming the surface by radiation from emissions from greenhouse gases in the troposphere, layered stacks of Carnot cycles can generate work in the troposphere, without a temperature increase, except near the surface, where vorticity generates heat release from frictional turbulence.

Rather than by downwelling radiation, greenhouse heat transfer to the surface occurs in stacked aerial Carnot cycles with energy transferred in warming Gibbs fields, the reversal of Equation (27). Obviously, as greenhouse gases are warmed with decreasing altitude, they will radiate appropriately for the local temperature.

These reversible Carnot heat cycles modified by gravity have greater capacity for resilience in terms of storing heat as work without changes in temperature, or its reversal as storage by surface frictional turbulence. Furthermore, the dynamic release of heat from turbulence caused by the pressure from mass collisions of air remains to be investigated. There are clear differences between the Manabe [26] convective–radiative and the virial-action models for the warming of tropospheric systems, as shown in Table 6. Radiation does play a key role in heating the troposphere by longwave radiation with the recycling of this energy captured by greenhouse gases, predominantly by water and CO₂. However, virial-action mechanics as the prime cause of the surface temperature balancing thermodynamic and gravitational pressures [2] offer new prospects for advances in climate science. For example, predictions of increasing greenhouse gas contents like water could be calculated using the virial-action model. The cooling surface effects of landscape smoothing reforestation and reducing surface roughness can also be estimated. The impacts of wind turbines and windfarms on the environment may have been underestimated. Evidence is emerging of serious wake effects causing the drying of the landscape following other effects on climatic warming [27,28].

In a final word, Sadi Carnot, in discounting cooling by radiation to space, asks, “is it not to the cooling of the air by dilatation that the cold of the higher regions of the atmosphere must be attributed?”. Adiabatic expansion with no change in the gravitational potential (caloric stage 2, −b′) in his engine cycle gave cooling by the internal fluid performing external work. This cooling in Figure 1 expands the working fluid to its maximum volume and lowest density, also shown in the Carnot cycle experiment in Table 3. While the internal work of Clausius’s ergal [4] is shown as a decrease in the Gibbs energy per molecule in the isothermal expansion of the working fluid to a higher quantum state, by contrast, the increase in translational action as the atmospheric gas expands in convection results from an increase in Lagrangian inertia, shown in Equation (16) for the virial-action theorem. Here, gravitational work is performed with altitude cooling the air.

Regarding the popular opinions on the cause of environmental cooling, Carnot refutes these [3], p16, saying, “mais cette explication se trouve dėtruite si l’on remarque qu’á égale hauteur le froid règne aussi bien et mème avec plus d’intensité sur les plaines élevées que le Sommet des montagnes”. Carnot attributes the equality in coldness on high plains and mountain tops of equal height to be a result of the loss of heat in the working fluid by performing work against gravity, rather than an escape of heat to space. This is Carnot’s main message regarding heat–work reversibility. Of course, high plains can exhibit inverted temperature gradients, warmer at height, because of the absence of water in the atmosphere to trap radiation, the surface becoming colder.

As Carnot showed clearly, heat can be stored as work with no increase in the temperature, re-emerging later as heat from compression, or surface friction. Defined by Clausius as the second law of thermodynamics, heat cannot be transferred to a warmer surface from a cooler troposphere if equilibrated for temperature. A Trenberth model [17] that shows that 333 MW/m² of energy is downwelling radiation, compensating for the need for subsequent radiation of 396 W/m² from the surface, must be corrected. We conduct this by proposing that the vortical advection and convective work sustaining the kinetic motion of anticyclones and cyclones [6] is dissipated by frictional vorticity, releasing turbulent heat of similar power to the greenhouse absorption.