Investigation of the Charging and Discharging Cycle of Packed-Bed Storage Tanks for Energy Storage Systems: A Numerical Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Set-Up and Methodology
2.2. Numerical Model
2.3. Materials Properties
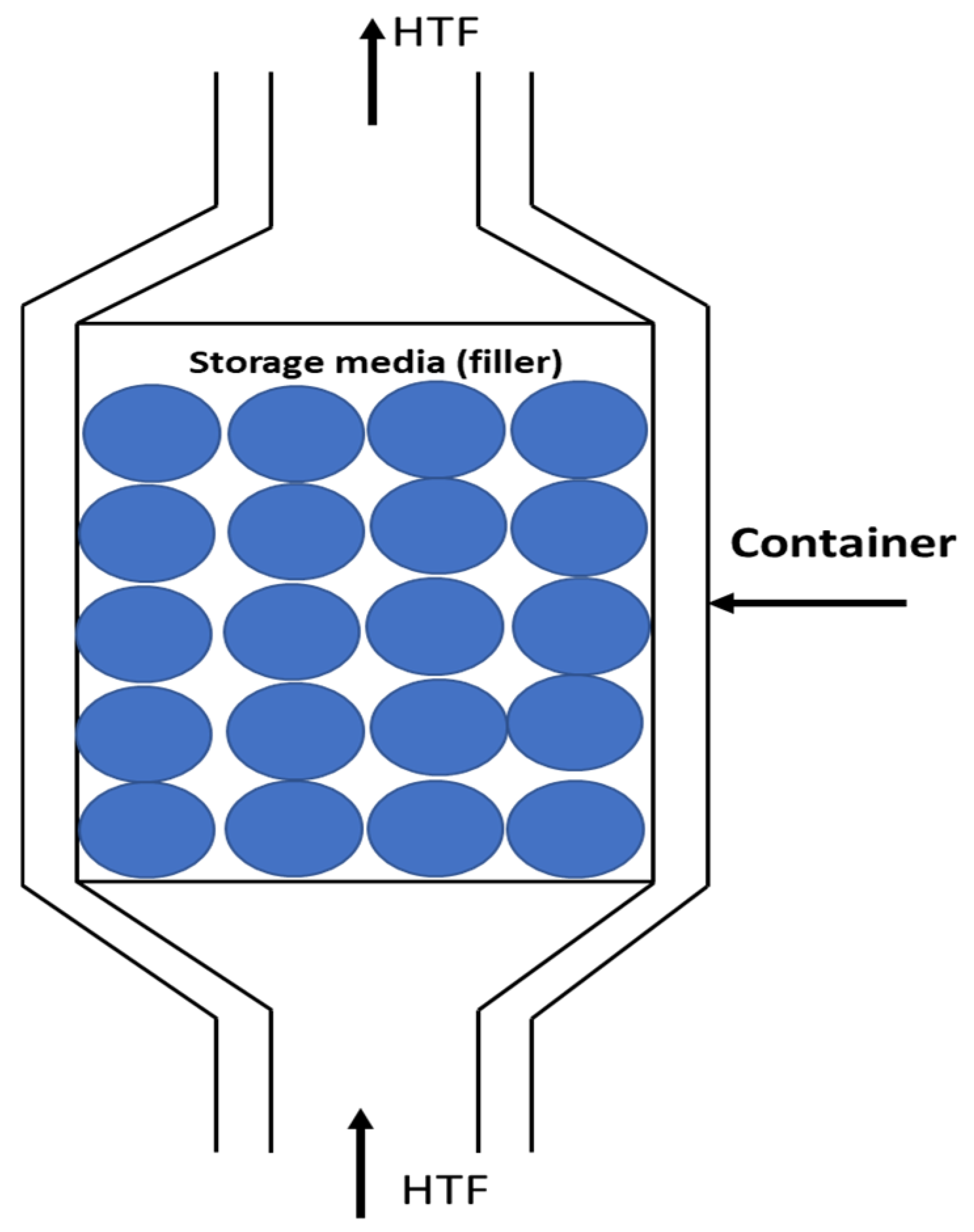
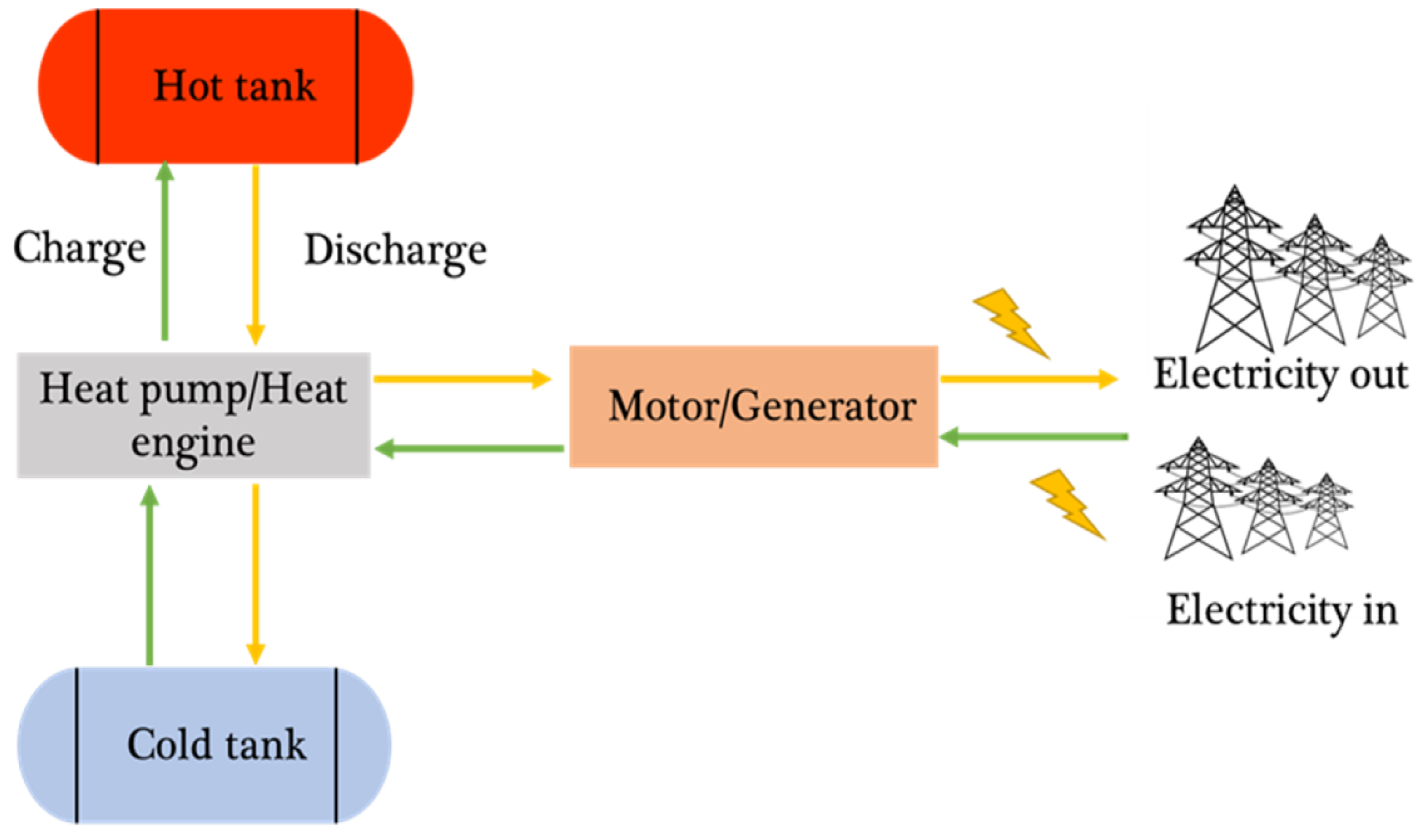
2.4. Modeling Hot/Cold Thermal Energy Storage
3. Results and Discussion
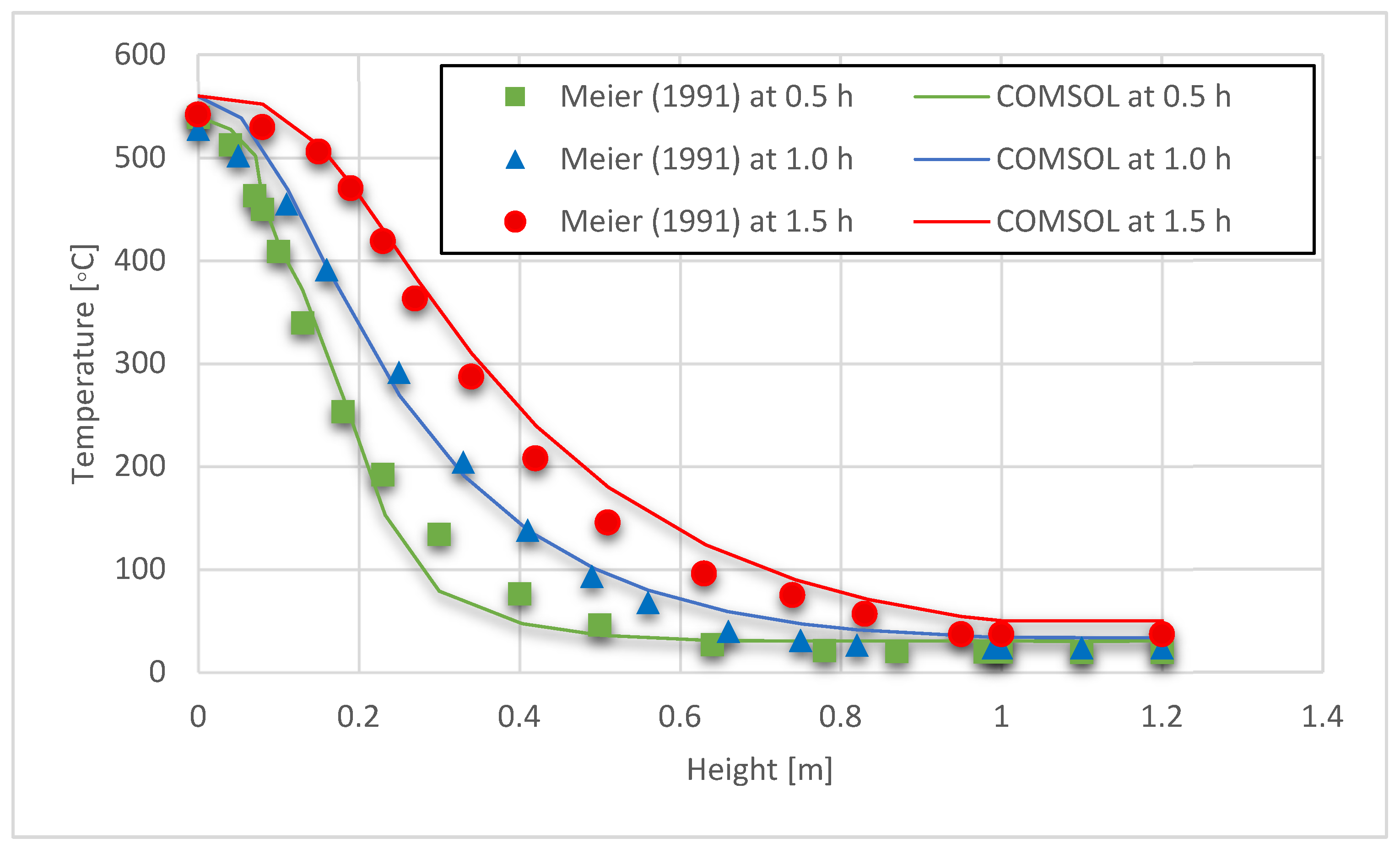
3.1. Model Validation
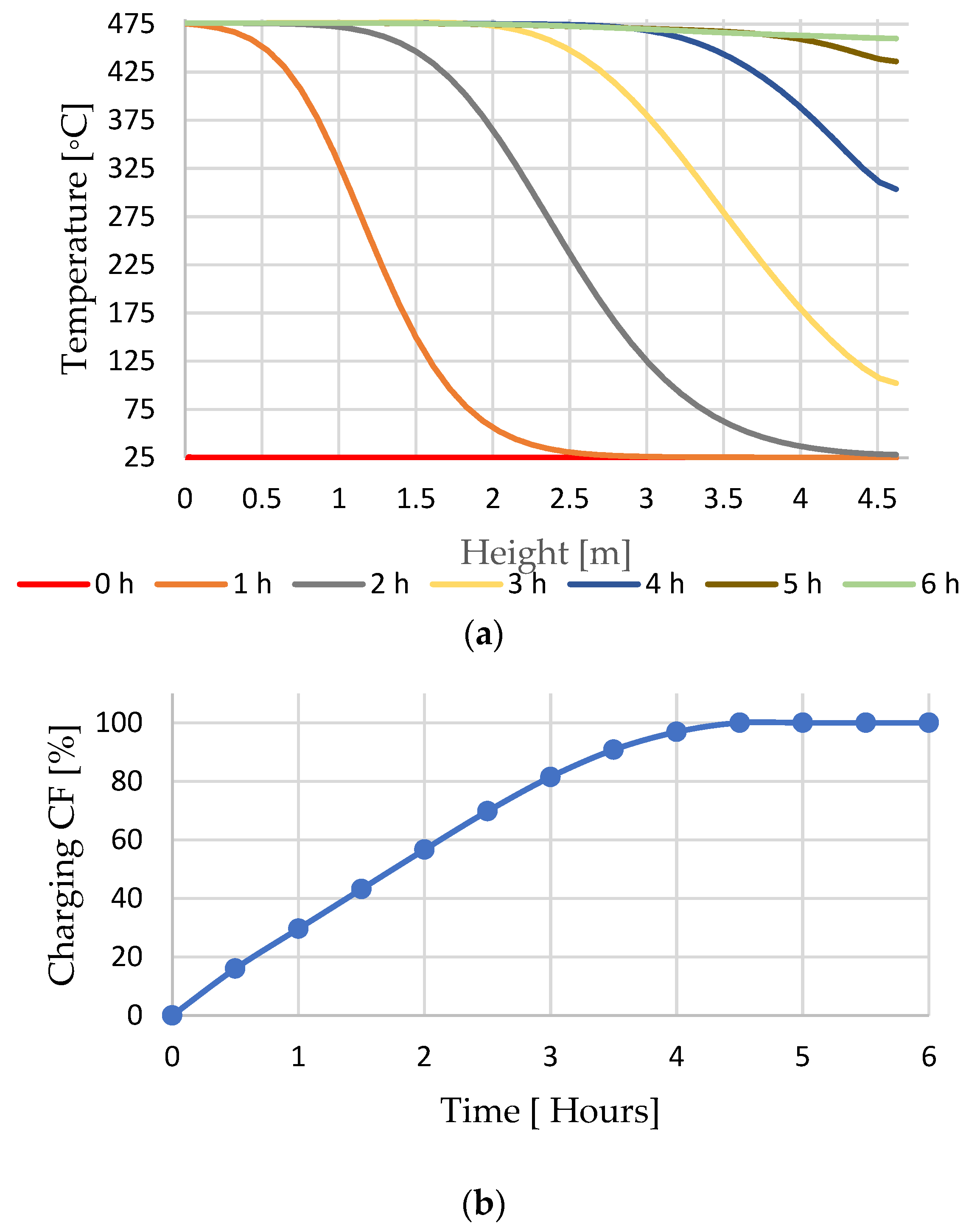
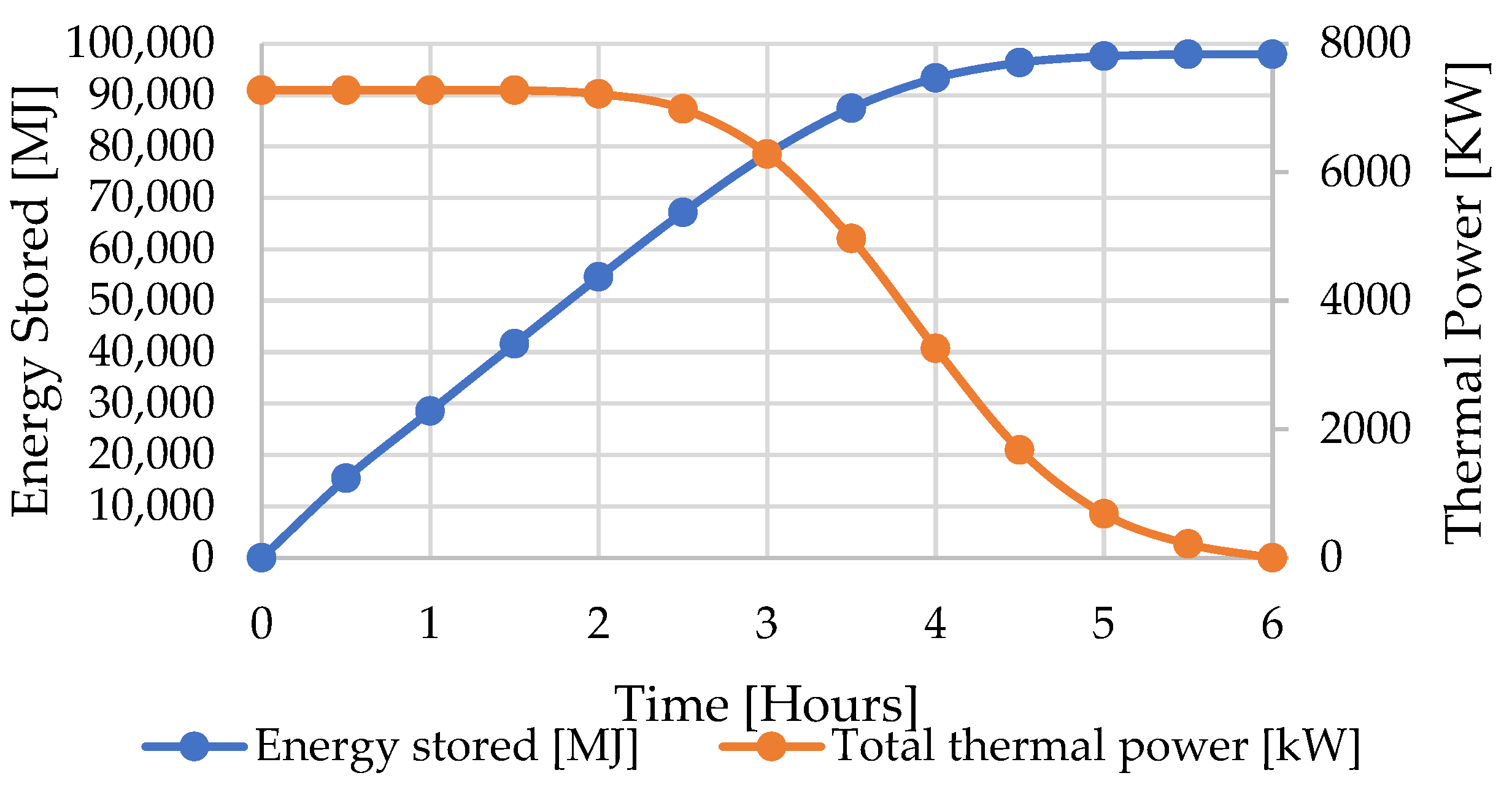
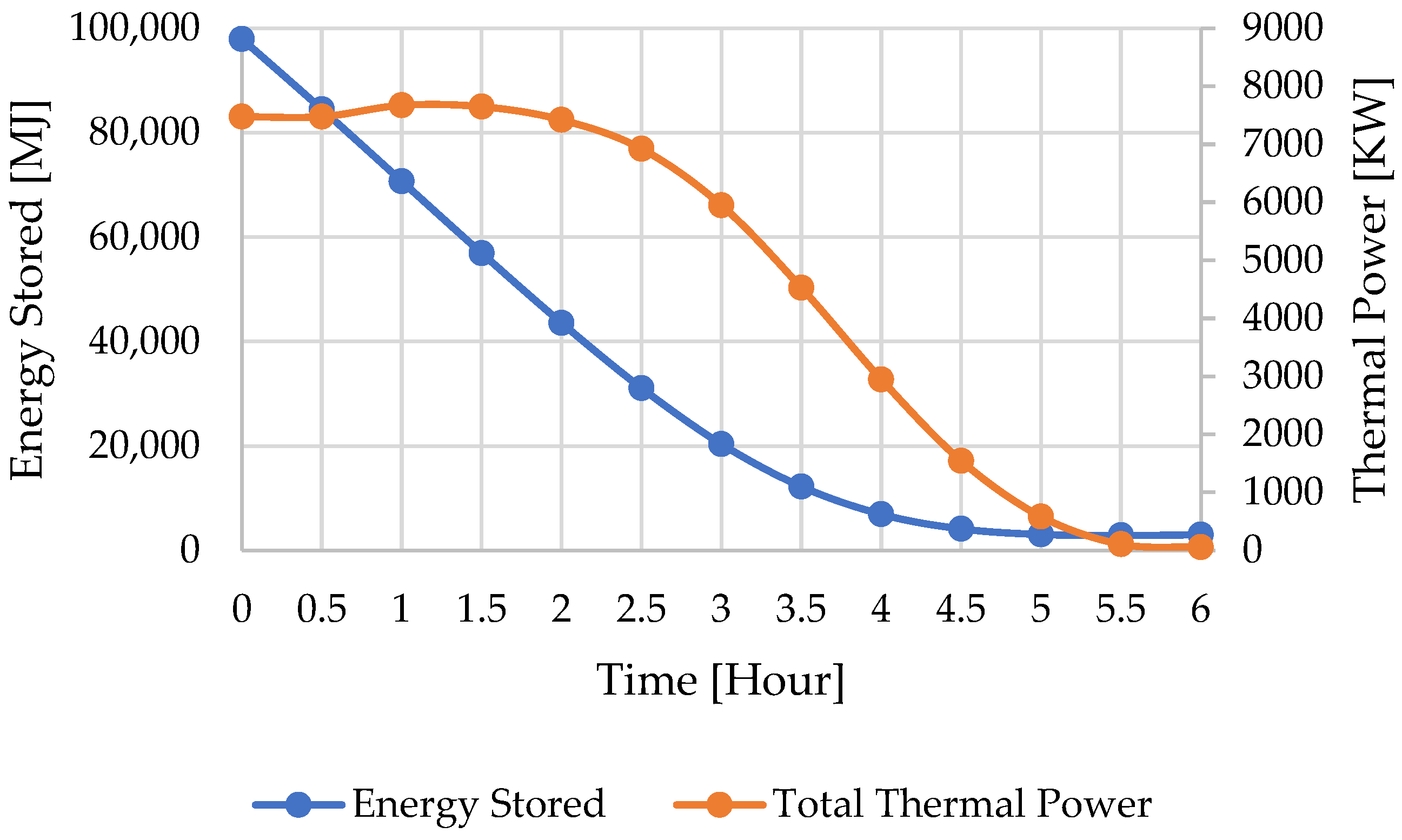
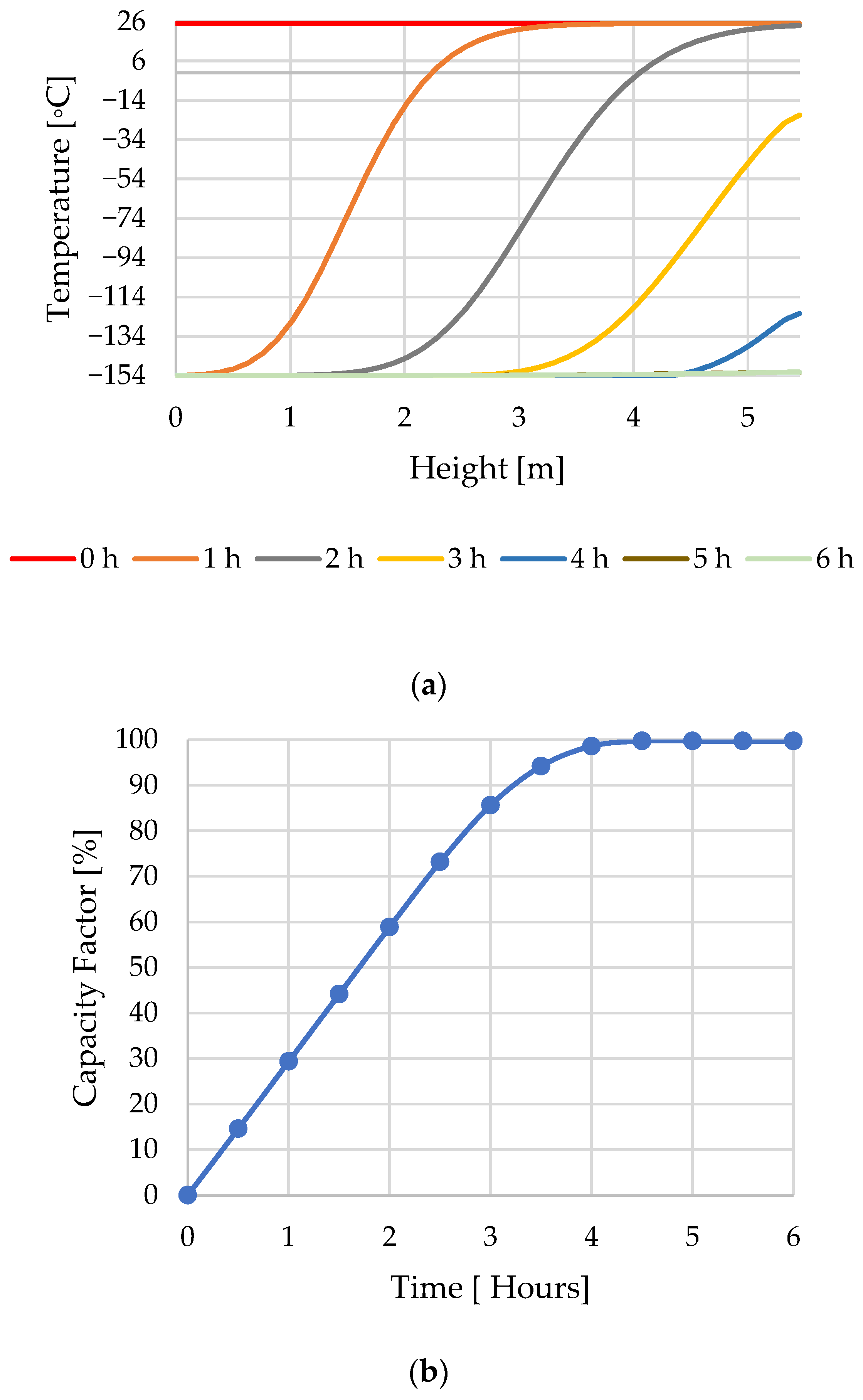
3.2. Hot Storage Charging Cycle
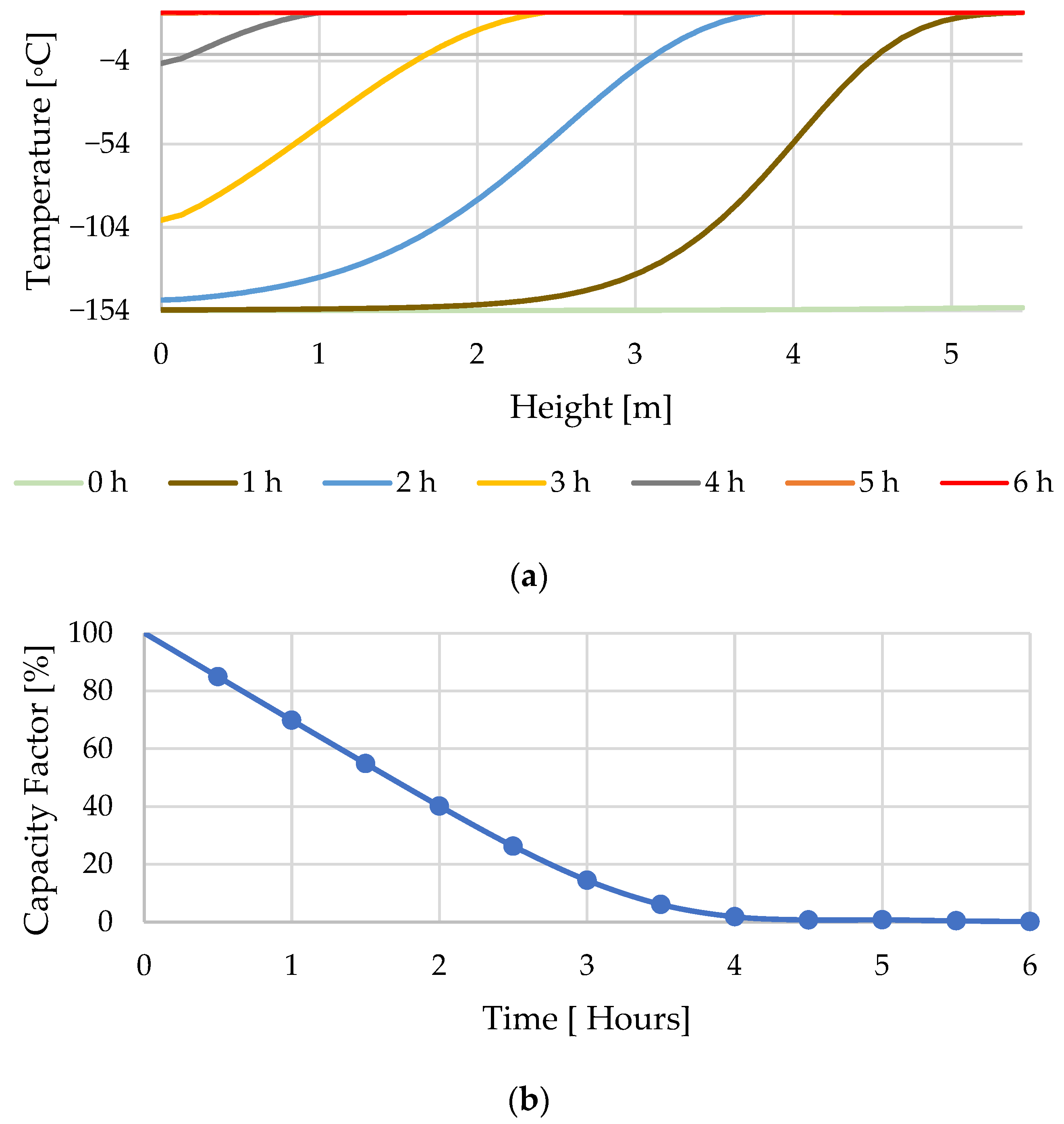
3.3. Hot Storage Discharging Cycle
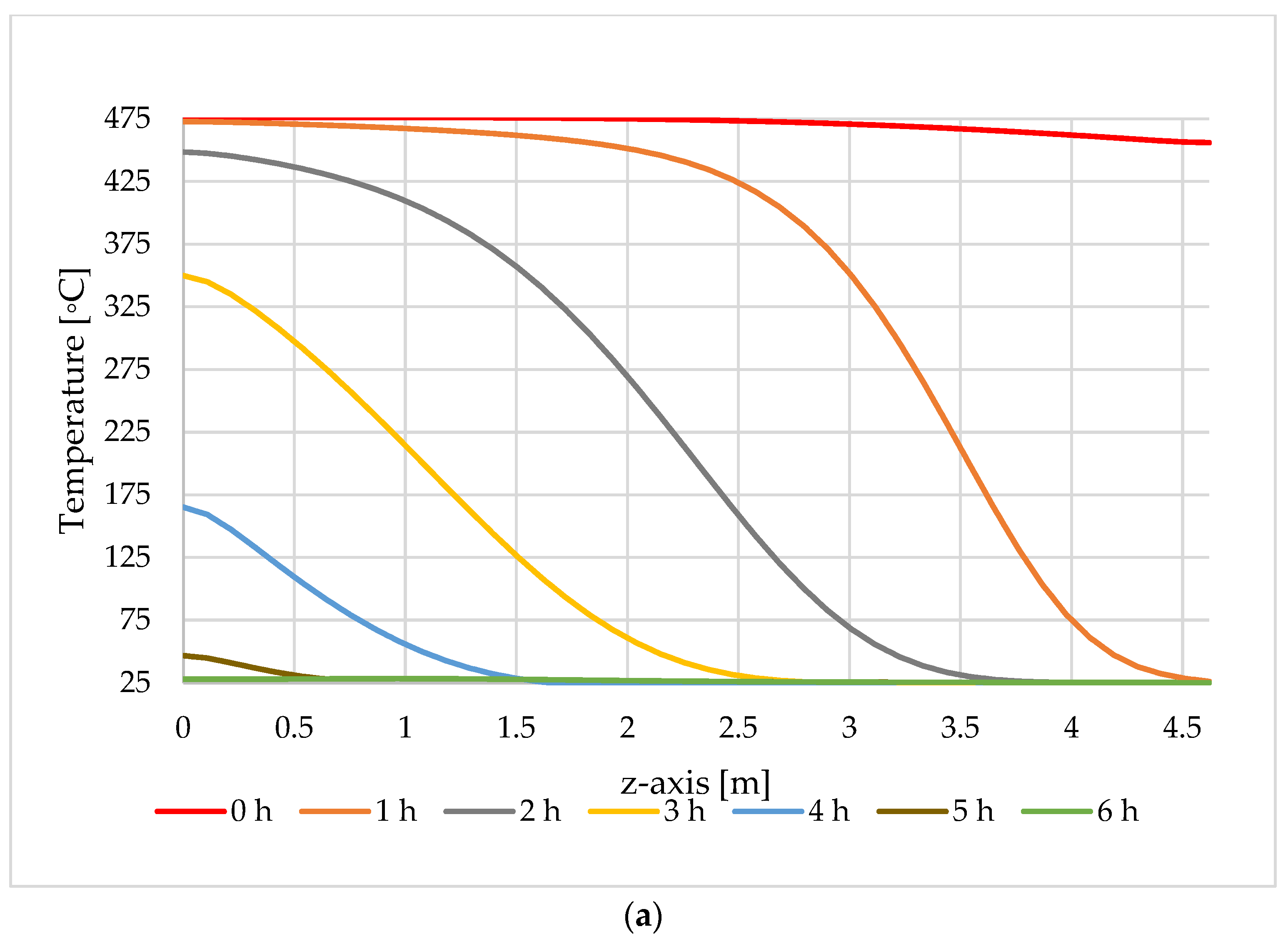
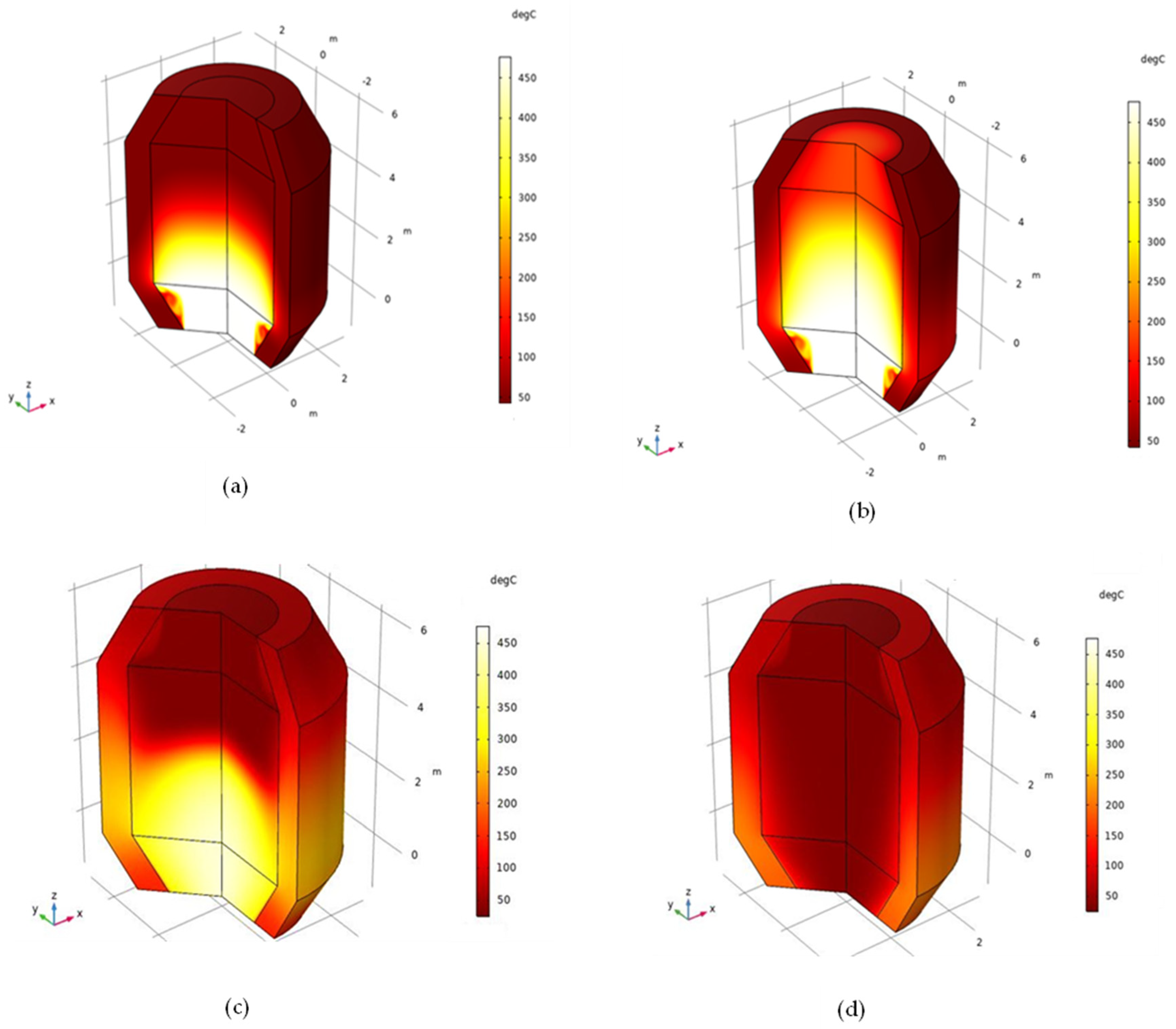
3.4. Temperature Profile
3.5. Cold Storage Charging Cycle
3.6. Cold Storage Discharging Cycle
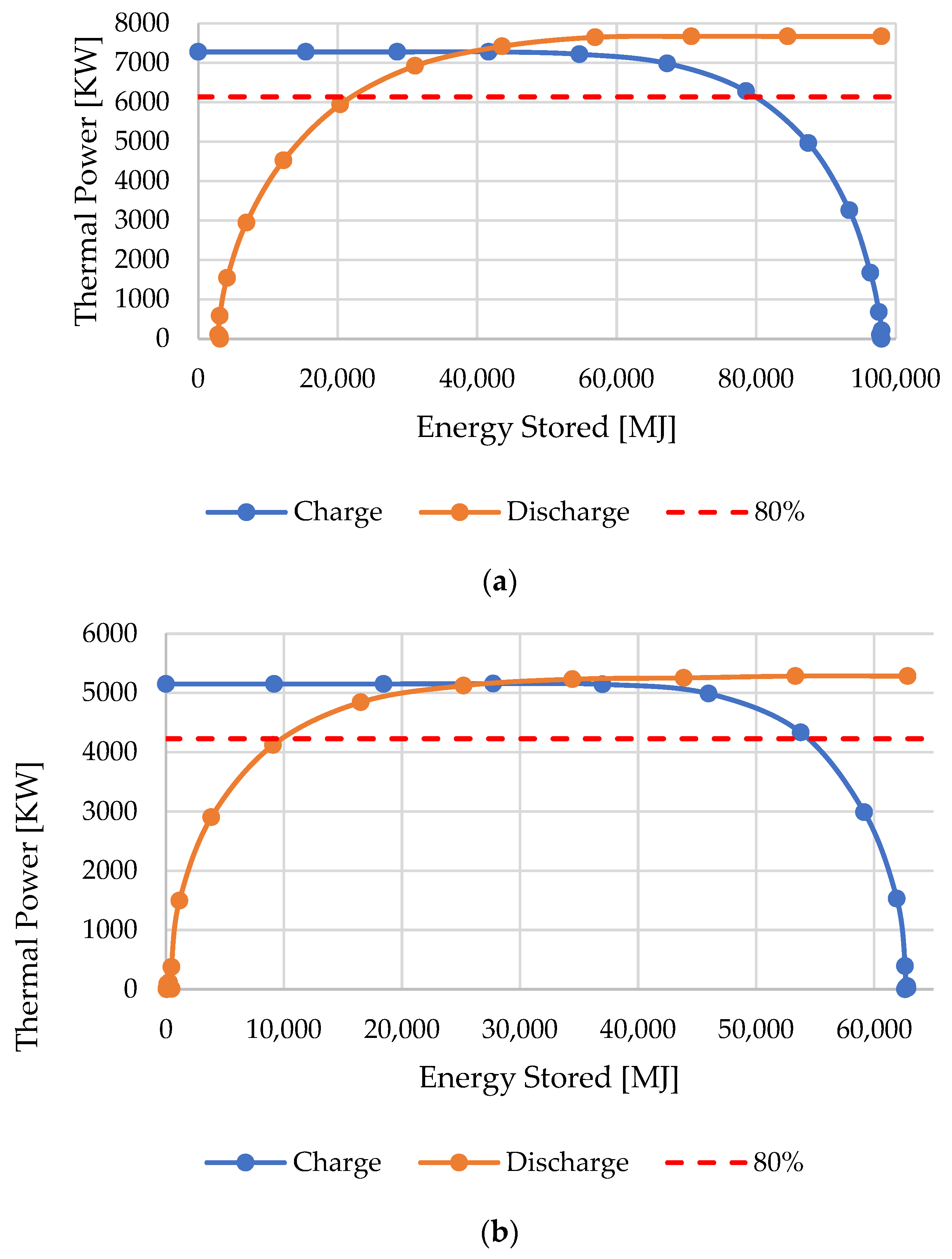
3.7. The Packed-Bed Operation Range
4. Conclusions
Future Work and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Roman symbols | ||
| AA | Advanced-Adiabatic | CF | Capacity factor |
| CAES | Compressed-Air Energy Storage | cf | Coefficient of friction |
| HTF | Heat Transfer Fluid | Cf | Forcheimer parameter |
| LAES | Liquid-Air Energy Storage | Cp | Heat Capacity |
| PBSS | Packed-Bed Storage System | D | Packed Bed Diameter |
| PHES | Pumped Heat Energy Storage | dp | Particle diameter |
| PTES | Pumped Thermal Energy Storage | Estored | Energy Stored |
| RTE | Round Trip Efficiency | g | Acceleration of gravity |
| TES | Thermal Energy Storage | H | Packed-Bed height |
| Greek symbols | K | Thermal conductivity | |
| α | Thermal diffusivity | l | Length scale |
| ɛ | Porosity (void fraction) | Mass flowrate | |
| ɳ | Efficiency | P | Operating Pressure |
| θ | Volume fraction | PTH | Thermal Power |
| porous media viscosity | q | Conductive heat fluxes | |
| ρ | Density | Q | Heat sources |
| τ | Viscous stress tensor | qsf | Interstitial convective heat transfer coefficient |
| Subscripts | S | Seebeck coefficient | |
| ch | Charging | t | Time |
| dis | Discharging | T | Temperature |
| f | Fluid | u | Superficial velocity |
| HT | Heat Transfer | v | Interstitial velocity |
| i | Initial | Viscous dissipation | |
| s | Solid | Thermoelastic damping | |
| TH | Thermal | ||
References
- White, A.; Parks, G.; Markides, C.N. Thermodynamic analysis of pumped thermal electricity storage. Appl. Therm. Eng. 2013, 53, 291–298. [Google Scholar] [CrossRef]
- Rabi, A.M.; Radulovic, J.; Buick, J.M. Pumped Thermal Energy Storage Technology (PTES): Review. Thermo 2023, 3, 396–411. [Google Scholar] [CrossRef]
- McTigue, J.D.; White, A.J.; Markides, C.N. Parametric studies and optimisation of pumped thermal electricity storage. Appl. Energy 2015, 137, 800–811. [Google Scholar] [CrossRef]
- Mercangöz, M.; Hemrle, J.; Kaufmann, L.; Z’gRaggen, A.; Ohler, C. Electrothermal energy storage with transcritical CO2 cycles. Energy 2012, 45, 407–415. [Google Scholar] [CrossRef]
- Elsihy, E.S.; Wang, X.; Xu, C.; Du, X. Numerical investigation on simultaneous charging and discharging process of molten-salt packed-bed thermocline storage tank employing in CSP plants. Renew. Energy 2021, 172, 1417–1432. [Google Scholar] [CrossRef]
- Barbour, E.; Mignard, D.; Ding, Y.; Li, Y. Adiabatic Compressed Air Energy Storage with packed bed thermal energy storage. Appl. Energy 2015, 155, 804–815. [Google Scholar] [CrossRef]
- Geissbühler, L.; Becattini, V.; Zanganeh, G.; Zavattoni, S.; Barbato, M.; Haselbacher, A.; Steinfeld, A. Pilot-scale demonstration of advanced adiabatic compressed air energy storage, Part 1: Plant description and tests with sensible thermal-energy storage. J. Energy Storage 2018, 17, 129–139. [Google Scholar] [CrossRef]
- Alva, G.; Liu, L.; Huang, X.; Fang, G. Thermal energy storage materials and systems for solar energy applications. Renew. Sustain. Energy Rev. 2017, 68, 693–706. [Google Scholar] [CrossRef]
- Rabi’, A.M.; Radulovic, J.; Buick, J.M. Packed Bed Thermal Energy Storage System: Parametric Study. Thermo 2024, 4, 295–314. [Google Scholar] [CrossRef]
- Alva, G.; Lin, Y.; Fang, G. An overview of thermal energy storage systems. Energy 2018, 144, 341–378. [Google Scholar] [CrossRef]
- Gil, A.; Medrano, M.; Martorell, I.; Lázaro, A.; Dolado, P.; Zalba, B.; Cabeza, L.F. State of the art on high temperature thermal energy storage for power generation. Part 1—Concepts, materials and modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–55. [Google Scholar] [CrossRef]
- Medrano, M.; Gil, A.; Martorell, I.; Potau, X.; Cabeza, L.F. State of the art on high-temperature thermal energy storage for power generation. Part 2—Case studies. Renew. Sustain. Energy Rev. 2010, 14, 56–72. [Google Scholar] [CrossRef]
- Balakrishnan, A.R.; Pei, D.C.T. Heat Transfer in Gas-Solid Packed Bed Systems. 2. The Conduction Mode. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 40–46. [Google Scholar] [CrossRef]
- Almendros-Ibáñez, J.; Fernández-Torrijos, M.; Díaz-Heras, M.; Belmonte, J.; Sobrino, C. A review of solar thermal energy storage in beds of particles: Packed and fluidized beds. Sol. Energy 2019, 192, 193–237. [Google Scholar] [CrossRef]
- Zanganeh, G.; Pedretti, A.; Haselbacher, A.; Steinfeld, A. Design of packed bed thermal energy storage systems for high-temperature industrial process heat. Appl. Energy 2015, 137, 812–822. [Google Scholar] [CrossRef]
- de Gracia, A.; Cabeza, L.F. Numerical simulation of a PCM packed bed system: A review. Renew. Sustain. Energy Rev. 2017, 69, 1055–1063. [Google Scholar] [CrossRef]
- Elouali, A.; Kousksou, T.; El Rhafiki, T.; Hamdaoui, S.; Mahdaoui, M.; Allouhi, A.; Zeraouli, Y. Physical models for packed bed: Sensible heat storage systems. J. Energy Storage 2019, 23, 69–78. [Google Scholar] [CrossRef]
- Sanderson, T.; Cunningham, G. Performance and efficient design of packed bed thermal storage systems. Part 1. Appl. Energy 1995, 50, 119–132. [Google Scholar] [CrossRef]
- Ge, Y.; Zhao, Y.; Zhao, C. Transient simulation and thermodynamic analysis of pumped thermal electricity storage based on packed-bed latent heat/cold stores. Renew. Energy 2021, 174, 939–951. [Google Scholar] [CrossRef]
- Gallo, A.B.; Simõões-Moreira, J.R.; Costa, H.K.M.; Santos, M.M.; Moutinho dos Santos, E.M. Energy storage in the energy transition context: A technology review. Renew. Sustain. Energy Rev. 2016, 65, 800–822. [Google Scholar] [CrossRef]
- Petrollese, M.; Cascetta, M.; Tola, V.; Cocco, D.; Cau, G. Pumped thermal energy storage systems integrated with a concentrating solar power section: Conceptual design and performance evaluation. Energy 2022, 247, 123516. [Google Scholar] [CrossRef]
- Mazzucco, G.; Xotta, G.; Salomoni, V.; Giannuzzi, M.; Maiorana, C. Solid thermal storage with PCM materials. Numerical investigations. Appl. Therm. Eng. 2017, 124, 545–559. [Google Scholar] [CrossRef]
- Benato, A.; Stoppato, A. Pumped Thermal Electricity Storage: A technology overview. Therm. Sci. Eng. Prog. 2018, 6, 301–315. [Google Scholar] [CrossRef]
- Farres-Antunez, P.; McTigue, J.D.; White, A.J. A pumped thermal energy storage cycle with capacity for concentrated solar power integration. In Proceedings of the 2019 Offshore Energy and Storage Summit (OSES), Brest, France, 10–12 July 2019; pp. 1–10. [Google Scholar]
- Singh, H.; Saini, R.; Saini, J. A review on packed bed solar energy storage systems. Renew. Sustain. Energy Rev. 2010, 14, 1059–1069. [Google Scholar] [CrossRef]
- Esence, T.; Bruch, A.; Molina, S.; Stutz, B.; Fourmigué, J.-F. A review on experience feedback and numerical modeling of packed-bed thermal energy storage systems. Sol. Energy 2017, 153, 628–654. [Google Scholar] [CrossRef]
- Saez, A.E.; McCoy, B.J. Dynamic response of a packed bed thermal storage system—A model for solar air heating. Sol. Energy 1982, 29, 201–206. [Google Scholar] [CrossRef]
- Beasleyt, D.E.; Clark, J.A. Transient response of a packed for thermal energy storage bed. Int. J. Heat Mass Transf. 1984, 27, 1659–1669. [Google Scholar] [CrossRef]
- Singh, H.; Saini, R.; Saini, J. Performance of a packed bed solar energy storage system having large sized elements with low void fraction. Sol. Energy 2013, 87, 22–34. [Google Scholar] [CrossRef]
- Anderson, R.; Bates, L.; Johnson, E.; Morris, J.F. Packed bed thermal energy storage: A simplified experimentally validated model. J. Energy Storage 2015, 4, 14–23. [Google Scholar] [CrossRef]
- Mctigue, J.D.; White, A.J. A comparison of radial-flow and axial-flow packed beds for thermal energy storage. Appl. Energy 2018, 227, 533–541. [Google Scholar] [CrossRef]
- Peng, H.; Shan, X.; Yang, Y.; Ling, X. A study on performance of a liquid air energy storage system with packed bed units. Appl. Energy 2018, 211, 126–135. [Google Scholar] [CrossRef]
- Hänchen, M.; Brückner, S.; Steinfeld, A. High-temperature thermal storage using a packed bed of rocks—Heat transfer analysis and experimental validation. Appl. Therm. Eng. 2011, 31, 1798–1806. [Google Scholar] [CrossRef]
- Laubscher, H.F.; von Backström, T.W.; Dinter, F. Developing a cost effective rock bed thermal energy storage system: Design and modelling. AIP Conf. Proc. 2017, 1850, 080015. [Google Scholar] [CrossRef]
- Zanganeh, G.; Pedretti, A.; Zavattoni, S.; Barbato, M.; Steinfeld, A. Packed-bed thermal storage for concentrated solar power—Pilot-scale demonstration and industrial-scale design. Sol. Energy 2012, 86, 3084–3098. [Google Scholar] [CrossRef]
- Zanganeh, G.; Pedretti, A.; Zavattoni, S.; Barbato, M.; Haselbacher, A.; Steinfeld, A. Design of a 100 MWhth Packed-bed Thermal Energy Storage. Energy Procedia 2014, 49, 1071–1077. [Google Scholar] [CrossRef]
- Marti, J.; Geissbühler, L.; Becattini, V.; Haselbacher, A.; Steinfeld, A. Constrained multi-objective optimization of thermocline packed-bed thermal-energy storage. Appl. Energy 2018, 216, 694–708. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Y.; Bai, F.; Wang, Z. Experimental and numerical investigation of a packed-bed thermal energy storage device Capital cost expenditure of high temperature latent and sensible thermal energy storage systems Experimental and Numerical Investigation of a Packed-bed Thermal Energy. AIP Conf. Proc. 2017, 1850, 080027. [Google Scholar] [CrossRef]
- Ortega-Fernández, I.; Zavattoni, S.A.; Rodríguez-Aseguinolaza, J.; D’AGuanno, B.; Barbato, M.C. Analysis of an integrated packed bed thermal energy storage system for heat recovery in compressed air energy storage technology. Appl. Energy 2017, 205, 280–293. [Google Scholar] [CrossRef]
- Schlipf, D.; Faust, E.; Schneider, G.; Maier, H. First operational results of a high temperature energy storage with packed bed and integration potential in CSP plants. AIP Conf. Proc. 2017, 1850, 080024. [Google Scholar] [CrossRef]
- White, A.J.; McTigue, J.D.; Markides, C.N. Analysis and optimisation of packed-bed thermal reservoirs for electricity storage applications. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 739–754. [Google Scholar] [CrossRef]
- Meier, A.; Winkler, C.; Wuillemin, D. Experiment for modelling high temperature rock bed storage. Sol. Energy Mater. 1991, 24, 255–264. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Z.; He, Y.; Li, X.; Bai, F. Sensitivity analysis of the numerical study on the thermal performance of a packed-bed molten salt thermocline thermal storage system. Appl. Energy 2012, 92, 65–75. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Porous Media Flow Module. Available online: https://doc.comsol.com/5.6/doc/com.comsol.help.porous/PorousMediaFlowModuleUsersGuide.pdf (accessed on 17 July 2025).
- Nandi, B.R.; Bandyopadhyay, S.; Banerjee, R. Numerical modeling and analysis of dual medium thermocline thermal energy storage. J. Energy Storage 2018, 16, 218–230. [Google Scholar] [CrossRef]
- Bennett, J.P. High-Temperature Properties of Magnesia-Refractory Brick Treated With Oxide and Salt Solutions; United States Department of the Interior, Bureau of Mines: Washington, DC, USA, 1985. [Google Scholar]
- Rao, L.H.; Dirbude, S. Numerical modelling and optimization of packed-bed thermal-energy storage system. J. Phys. Conf. Ser. 2022, 2178, 012003. [Google Scholar] [CrossRef]

| TES System | CAES | PHES | PTES |
|---|---|---|---|
| Cost [USD/kWh] | 2.5 | 5–100 | 25–250 |
| RTE [%] | 50–70 | 60–80 | 40–70 |
| Energy Density [kWh/m3] | 10 | 1.4 | 50 |
| Packed Bed Storage Media | Filler Cost [$/Ton] | Advantages | Limitations |
|---|---|---|---|
| AL2O3 | 1500 | Good thermal shock resistance and high temperature stability. | Material cost and processing are expensive and heavy. |
| Concrete | 500 | Good availability, easy to shape, and moderate cost | Thermal cracking risk and degradation at higher temperatures (>400 °C). |
| Natural rocks | 200 | Widely available and very low cost | Potential cracking and limited mechanical strength at very high temperatures. |
| Magnesia bricks | 1000 | Corrosion-resistant and excellent high-temperature stability | Manufacturing complexity and higher cost than natural rock. |
| Molten Salts | 1500 | Fluid simplifies heat transfer; High heat capacity. | Relatively expensive; corrosion issues; freezing risk (~220 °C). |
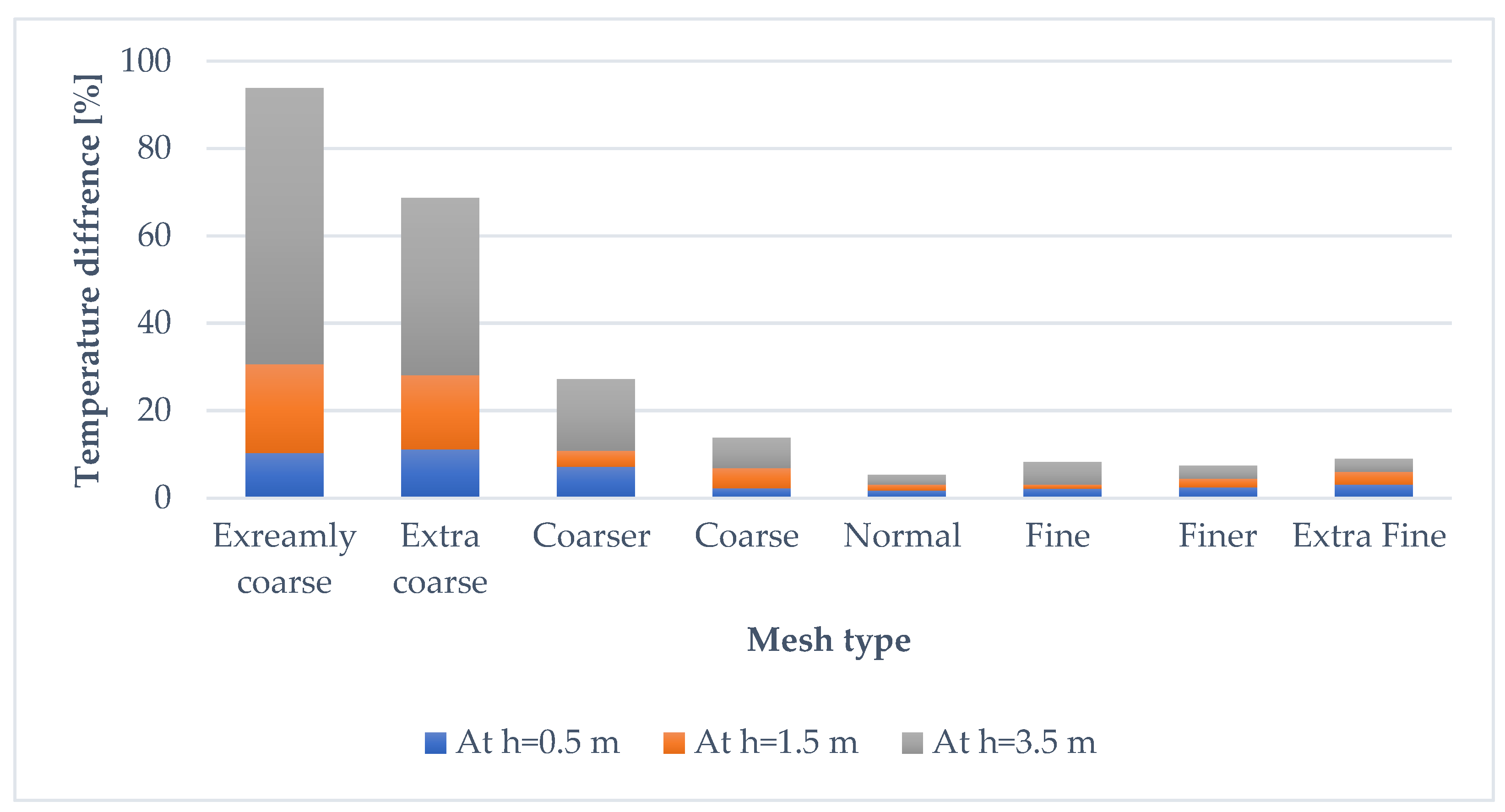
| Mesh Type | Extremely Coarse | Extra Coarse | Coarser | Coarse | Normal | Fine | Finer | Extra Fine | Extremely Fine |
|---|---|---|---|---|---|---|---|---|---|
| Number of elements | 375 | 596 | 933 | 1754 | 2634 | 4377 | 10,571 | 24,688 | 45,622 |
| Simulation time [min] | 2.0 | 4.0 | 7.9 | 20.2 | 37.2 | 79.7 | 299.5 | 1069.8 | 2680.6 |
| Storage Tank | Symbol | Unit | Value |
|---|---|---|---|
| PTES (Hot reservoir) | |||
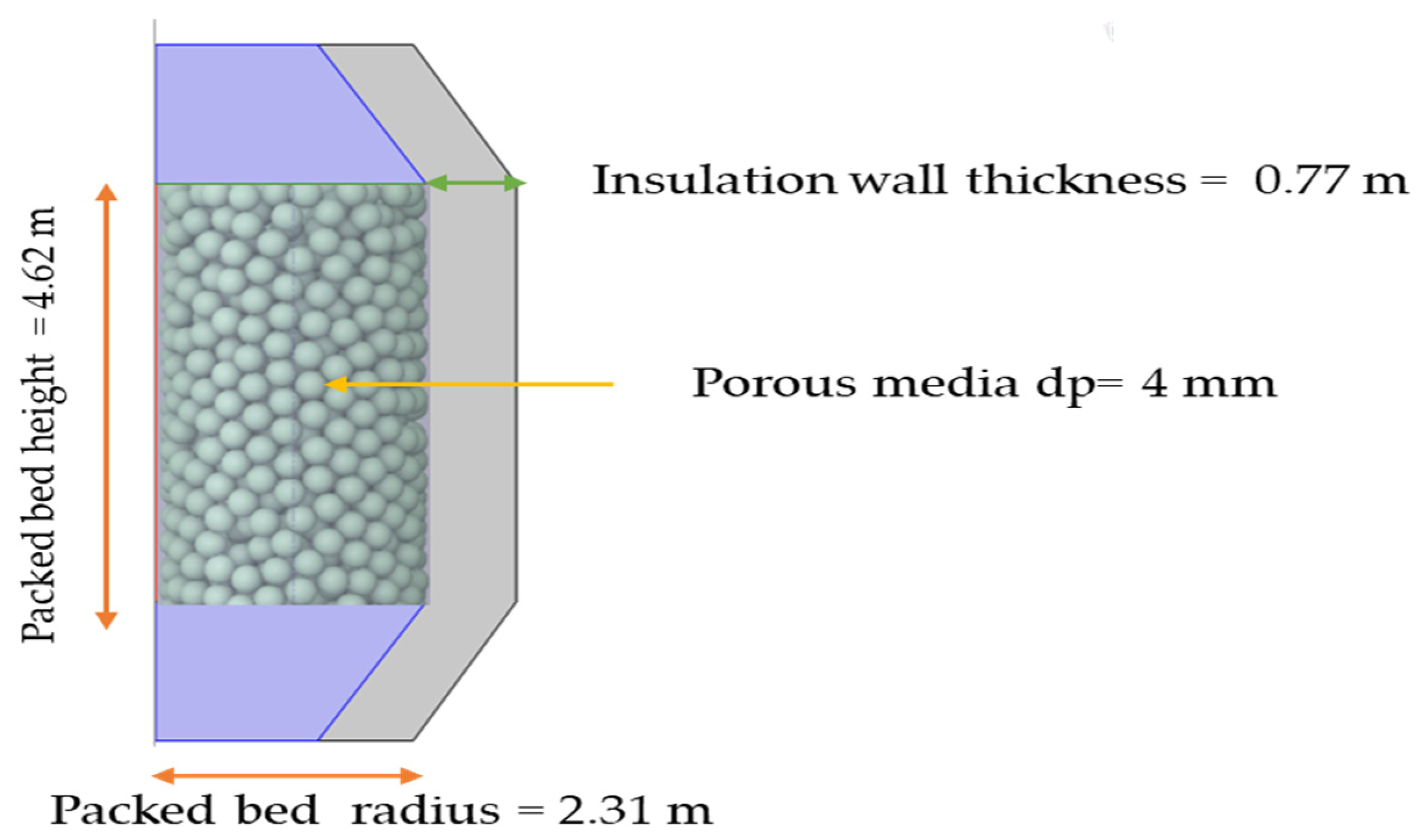
| Tank Diameter | D | [m] | 4.62 |
| Tank Hight | H | [m] | 4.62 |
| Charging Temperature | Tch | [°C] | 476.00 |
| Discharging Temperature | Tdis | [°C] | 25.00 |
| PTES (Cold reservoir) | |||
| Tank Diameter | D | [m] | 5.45 |
| Tank Hight | H | [m] | 5.45 |
| Charging Temperature | Tch | [°C] | −154.00 |
| Discharging Temperature | Tdis | [°C] | 25.00 |
| Design Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Medium particle diameter/size | dp | [mm] | 4 |
| Solid storage material | --- | --- | Magnesia |
| Void fraction (porosity) | ɛ | --- | 0.20 |
| Thermo-Physical Properties | |||
| Cp, s | [J/kg·K] | 1150 | |
| [kg/m3] | 3000 | ||
| Ks | [W/m. K] | 5.0 | |
| Chemical Properties | |||
| Magnesium | (MgO) | [%] | 89.10 |
| Iron oxide | (Fe2O3) | [%] | 1.83 |
| Alumina | (AL2O3) | [%] | 0.38 |
| Chromium oxide | (Cr2O3) | [%] | 0.42 |
| Silica | (SiO2) | [%] | 7.40 |
| Calcia | (CaO) | [%] | 0.87 |
| Melting temperature | [°C] | 1600 | |
| Storage Tank | Symbol | Unit | Value |
|---|---|---|---|
| Tank Diameter | D | m | 0.70 |
| Tank Hight | H | m | 1.93 |
| Charging Temperature | Tch | °C | 600 |
| Discharging Temperature | Tdis | °C | 27 |
| Particle Diameter | dp | mm | 2.00 |
| Mass flow rate | kg/s | 1.10 | |
| Porosity | ɛ | - | 0.45 |
| Solid storage material | --- | --- | Rock |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabi’, A.M.; Radulovic, J.; Buick, J.M. Investigation of the Charging and Discharging Cycle of Packed-Bed Storage Tanks for Energy Storage Systems: A Numerical Study. Thermo 2025, 5, 24. https://doi.org/10.3390/thermo5030024
Rabi’ AM, Radulovic J, Buick JM. Investigation of the Charging and Discharging Cycle of Packed-Bed Storage Tanks for Energy Storage Systems: A Numerical Study. Thermo. 2025; 5(3):24. https://doi.org/10.3390/thermo5030024
Chicago/Turabian StyleRabi’, Ayah Marwan, Jovana Radulovic, and James M. Buick. 2025. "Investigation of the Charging and Discharging Cycle of Packed-Bed Storage Tanks for Energy Storage Systems: A Numerical Study" Thermo 5, no. 3: 24. https://doi.org/10.3390/thermo5030024
APA StyleRabi’, A. M., Radulovic, J., & Buick, J. M. (2025). Investigation of the Charging and Discharging Cycle of Packed-Bed Storage Tanks for Energy Storage Systems: A Numerical Study. Thermo, 5(3), 24. https://doi.org/10.3390/thermo5030024







