Dynamic Exergy Analysis of Heating Surfaces in a 300 MW Drum-Type Boiler
Abstract
1. Introduction
2. Methods
2.1. Heating Surfaces of a Drum-Type Boiler
2.2. Mathematical Model
2.3. Exergy Analysis
2.3.1. Exergy Type
2.3.2. Exergy Balance
2.3.3. Exergy Destruction
2.4. Research Framework
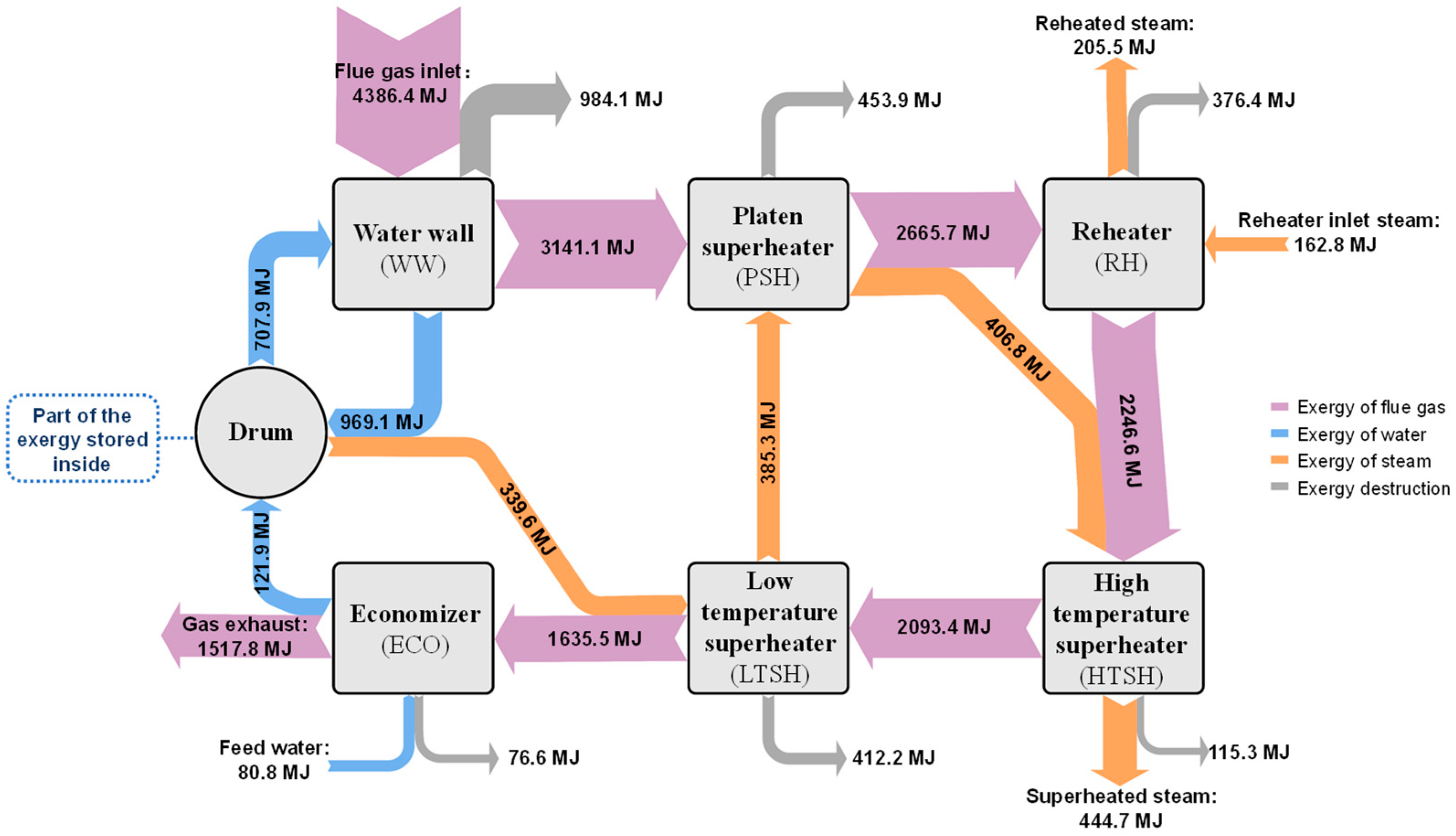
3. Results
3.1. Steady-State Analysis
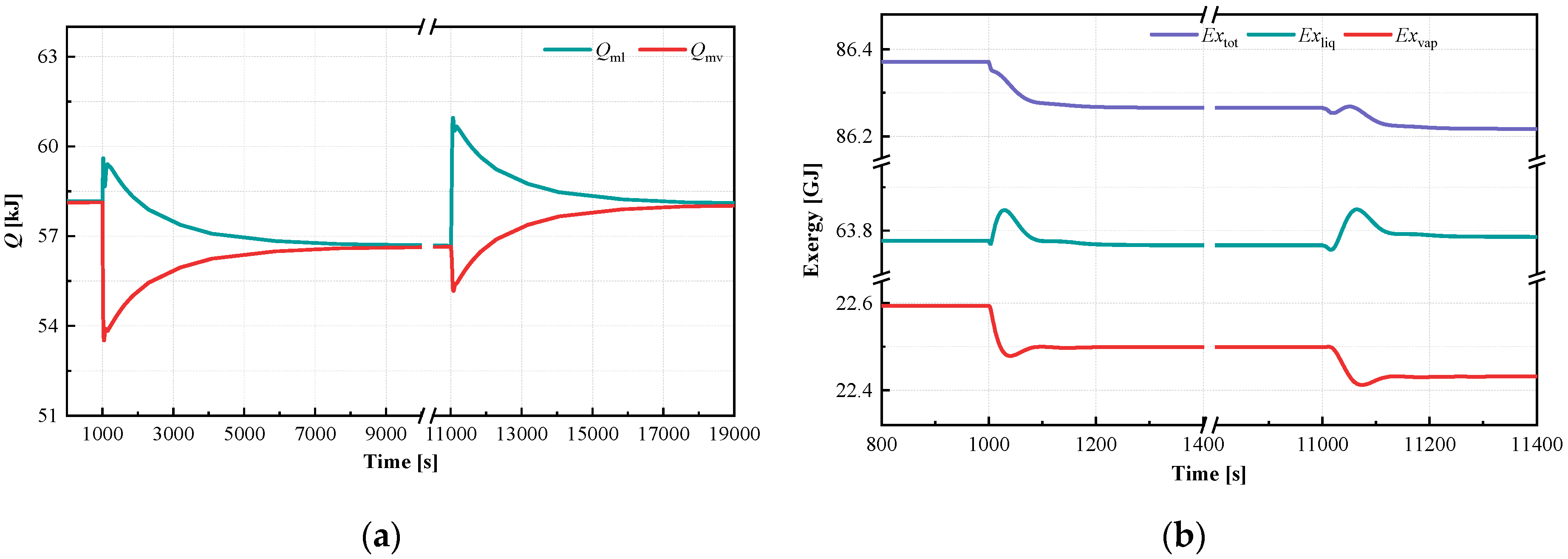
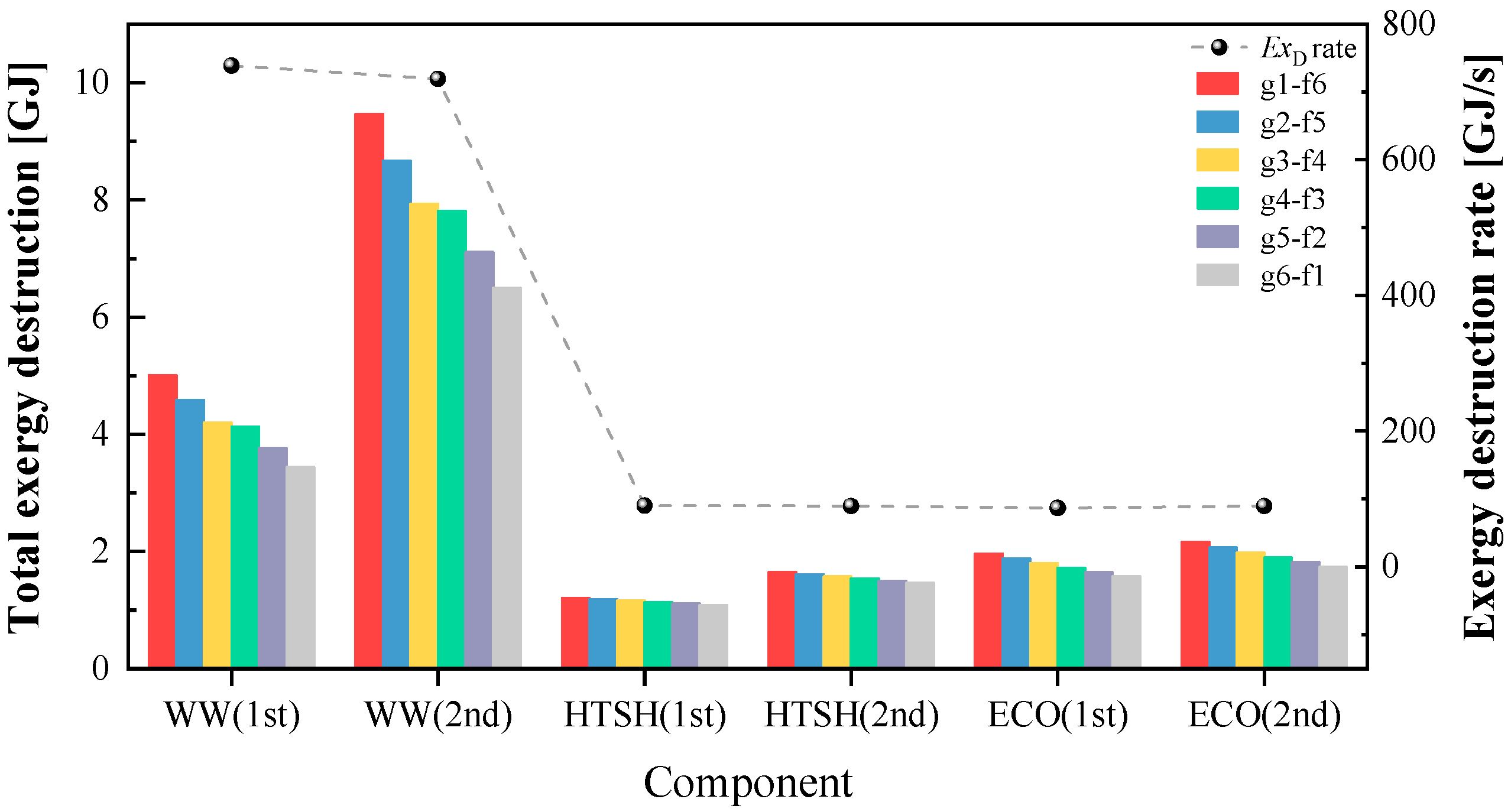
3.2. Dynamic Exergy Assessment
3.2.1. Drum
3.2.2. Heating Surfaces
4. Conclusions
- (1)
- During steady-state operation, the evaporator and superheater unit contribute to 81.3% of the total exergy destruction in the boiler heat networks. Notably, the water wall, platen superheater, and low-temperature superheater exhibit the highest proportions of irreversible loss within the boiler heat exchange networks.
- (2)
- The thermal inertia induced by the drum wall results in a significant delay in energy changes, with a dynamic period of up to 5000 s. Consequently, the phenomenon leads to delayed exergy fluctuations of liquid and steam in the drum.
- (3)
- The dynamic exergy analysis highlights that the water wall demonstrates the highest total dynamic exergy destruction of 9.5 GJ. Despite the water wall components having the shortest dynamic process, the exergy destruction per unit time surpasses that of other components by 7.9–8.5 times, reaching up to 738.8 GJ/s.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ai | heat transfer area, m2 |
| cvg,i | specific heat capacity of flue gas volume segment i, kJ/(kg·K) |
| E | energy, kJ |
| Ex | exergy, kJ |
| ex | specific exergy, kJ/kg |
| H | enthalpy, kJ |
| h | specific enthalpy, kJ/kg |
| ki | heat transfer coefficient, W/(m2·K) |
| Lm,i | length of the metal segment i, m |
| M | mass, kg |
| m | mass flow rates, kg/s |
| Qm,i | energy of heat transfer, W |
| r | radius, m |
| S | entropy, kJ/K |
| Ti | temperature of segment i, K |
| Φi | heat flux, W |
| ρcm | density of the metal, kg/m3 |
Abbreviations
| WW | Water wall |
| PSH | Platen superheater |
| HTSH | High-temperature superheater |
| LTSH | Low-temperature superheater |
| RH | Reheater |
| ECO | Economizer |
References
- Energy Institute Statistical Review of World Energy 2024. Available online: https://www.energyinst.org/statistical-review (accessed on 26 December 2021).
- Guo, M.; Hao, Y.; Nižetić, S.; Lee, K.Y.; Sun, L. Modelica-Based Heating Surface Modelling and Dynamic Exergy Analysis of 300 MW Power Plant Boiler. Energy Convers. Manag. 2024, 312, 118557. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M.; Yan, J. Flexibility and Efficiency Co-Enhancement of Thermal Power Plant by Control Strategy Improvement Considering Time Varying and Detailed Boiler Heat Storage Characteristics. Energy 2021, 232, 121048. [Google Scholar] [CrossRef]
- Wang, Y.; Lou, S.; Wu, Y.; Wang, S. Flexible Operation of Retrofitted Coal-Fired Power Plants to Reduce Wind Curtailment Considering Thermal Energy Storage. IEEE Trans. Power Syst. 2020, 35, 1178–1187. [Google Scholar] [CrossRef]
- Guo, M.; Hao, Y.; Lu, Y.; Sun, L. Long-Short Term Memory Modeling and Performance Analysis of Extended-State Kalman Filter-Based Energy-Saving Model Predictive Control for Supercritical Unit. Appl. Therm. Eng. 2025, 272, 126202. [Google Scholar] [CrossRef]
- Noroozian, A.; Mohammadi, A.; Bidi, M.; Ahmadi, M.H. Energy, Exergy and Economic Analyses of a Novel System to Recover Waste Heat and Water in Steam Power Plants. Energy Convers. Manag. 2017, 144, 351–360. [Google Scholar] [CrossRef]
- Ouyang, T.; Xie, S.; Pan, M.; Qin, P. Peak-Shaving Scheme for Coal-Fired Power Plant Integrating Flexible Carbon Capture and Wastewater Treatment. Energy Convers. Manag. 2022, 256, 115377. [Google Scholar] [CrossRef]
- Chandrasekharan, S.; Panda, R.C.; Swaminathan, B.N.; Panda, A. Operational Control of an Integrated Drum Boiler of a Coal Fired Thermal Power Plant. Energy 2018, 159, 977–987. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, Z.; Bollas, G.M. Dynamic Modeling, Simulation and Optimization of a Subcritical Steam Power Plant. Part I: Plant Model and Regulatory Control. Energy Convers. Manag. 2017, 145, 324–334. [Google Scholar] [CrossRef]
- Stanger, L.; Schirrer, A.; Benedikt, F.; Bartik, A.; Jankovic, S.; Müller, S.; Kozek, M. Dynamic Modeling of Dual Fluidized Bed Steam Gasification for Control Design. Energy 2023, 265, 126378. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, L.; Liu, M.; Wang, J.; Yan, J. Performance Analysis of Coal-Fired Power Plants Integrated with Carbon Capture System under Load-Cycling Operation Conditions. Energy 2023, 276, 127532. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, M.; Liu, Y.; Wang, D.; Zhuang, Z.; Quan, M. Energy, Exergy, and Economic Analysis of a Centralized Solar and Biogas Hybrid Heating System for Rural Areas. Energy Convers. Manag. 2023, 276, 116591. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Caliskan, H.; Altuntas, O.; Hepbasli, A. Novel Combined Extended-Advanced Exergy Analysis Methodology as a New Tool to Assess Thermodynamic Systems. Energy Convers. Manag. 2021, 236, 114019. [Google Scholar] [CrossRef]
- Zhang, Q.; Yi, H.; Yu, Z.; Gao, J.; Wang, X.; Lin, H.; Shen, B. Energy-Exergy Analysis and Energy Efficiency Improvement of Coal-Fired Industrial Boilers Based on Thermal Test Data. Appl. Therm. Eng. 2018, 144, 614–627. [Google Scholar] [CrossRef]
- Hashemi Beni, M.; Emami, S.; Meghdadi Isfahani, A.H.; Shirneshan, A.; Kalbasi, R. Transient Simulation and Exergy Analysis of a D-Type Steam Boiler with Natural Circulation during Cold Start: A Case Study. Appl. Therm. Eng. 2022, 210, 118367. [Google Scholar] [CrossRef]
- Huang, G.; Huang, C.; Liu, H.; Huang, H.; Shang, W.; Wang, W. Exergy Analysis of Off-Design Performance in Solar-Aided Power Generation Systems: Evaluating the Rationality of Using Part-Load Operation Solution of Coal-Fired Plants. Energy 2024, 302, 131749. [Google Scholar] [CrossRef]
- Zhang, H.; Hao, R.; Liu, X.; Zhang, N.; Guo, W.; Zhang, Z.; Liu, C.; Liu, Y.; Duan, C.; Qin, J. Thermodynamic Performance Analysis of an Improved Coal-Fired Power Generation System Coupled with Geothermal Energy Based on Organic Rankine Cycle. Renew. Energy 2022, 201, 273–290. [Google Scholar] [CrossRef]
- Cheng, X.; Liang, X. Heat Transfer Entropy Resistance for the Analyses of Two-Stream Heat Exchangers and Two-Stream Heat Exchanger Networks. Appl. Therm. Eng. 2013, 59, 87–93. [Google Scholar] [CrossRef]
- Guo, M.; Hao, Y.; Lee, K.Y.; Sun, L. Extended-State Kalman Filter-Based Model Predictive Control and Energy-Saving Performance Analysis of a Coal-Fired Power Plant. Energy 2025, 314, 134169. [Google Scholar] [CrossRef]



| Medium | Stream Location | T [℃] | P [bar] | [kg/s] | h [kJ/kg] | s [kJ/kg·K] |
|---|---|---|---|---|---|---|
| Flue gas | Furnace inlet | 1600.0 | 1.25 | 400.0 | 12031.5 | 8.78 |
| Platen superheater inlet | 1083.1 | 1.18 | 400.0 | 8794.2 | 8.35 | |
| Platen superheater outlet | 892.3 | 1.13 | 400.0 | 7545.0 | 8.15 | |
| Reheater outlet | 690.5 | 1.11 | 400.0 | 6465.4 | 8.04 | |
| High-temperature superheater outlet | 623.8 | 1.05 | 400.0 | 6029.3 | 7.86 | |
| Economizer inlet | 424.4 | 1.03 | 400.0 | 4795.7 | 7.56 | |
| Exhaust gas | 375.5 | 1.01 | 400.0 | 4469.2 | 7.45 | |
| Water | Economizer outlet | 273.6 | 186.56 | 258.0 | 1199.4 | 2.97 |
| Water wall inlet | 291.8 | 186.54 | 294.7 | 1407.3 | 3.34 | |
| Water wall outlet | 351.0 | 187.99 | 1278.7 | 1677.8 | 3.78 | |
| Steam | Drum outlet | 359.3 | 186.54 | 1278.7 | 1919.6 | 3.91 |
| Platen superheater inlet | 355.1 | 176.14 | 294.7 | 2449.3 | 3.84 | |
| Platen superheater outlet | 390.6 | 175.88 | 294.7 | 2795.3 | 5.56 | |
| Low-temperature superheater outlet | 495.6 | 175.73 | 294.7 | 3191.8 | 6.13 | |
| Reheater inlet | 541.0 | 175.29 | 294.7 | 3398.5 | 6.39 | |
| Reheater outlet | 325.0 | 36.60 | 146.8 | 3038.8 | 6.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, C.; Zhu, J.; Wang, H.; Dai, C.; Sun, L. Dynamic Exergy Analysis of Heating Surfaces in a 300 MW Drum-Type Boiler. Thermo 2025, 5, 17. https://doi.org/10.3390/thermo5020017
Wang X, Wang C, Zhu J, Wang H, Dai C, Sun L. Dynamic Exergy Analysis of Heating Surfaces in a 300 MW Drum-Type Boiler. Thermo. 2025; 5(2):17. https://doi.org/10.3390/thermo5020017
Chicago/Turabian StyleWang, Xing, Chun Wang, Jiangjun Zhu, Huizhao Wang, Chenxi Dai, and Li Sun. 2025. "Dynamic Exergy Analysis of Heating Surfaces in a 300 MW Drum-Type Boiler" Thermo 5, no. 2: 17. https://doi.org/10.3390/thermo5020017
APA StyleWang, X., Wang, C., Zhu, J., Wang, H., Dai, C., & Sun, L. (2025). Dynamic Exergy Analysis of Heating Surfaces in a 300 MW Drum-Type Boiler. Thermo, 5(2), 17. https://doi.org/10.3390/thermo5020017





