1. Introduction
Phase change materials (PCMs) have attracted significant attention in various fields where energy storage or thermal management is needed. PCMs possess the ability to store and release thermal energy during phase transitions, making them useful for applications requiring efficient thermal regulation. However, the relatively low thermal conductivity of PCMs limits the charging and discharging rates, leading to reduced overall efficiency [
1]. In recent years, researchers have explored innovative strategies to enhance the thermal conductivity of PCMs by incorporating them into porous metallic or carbon matrices, such as metal foams. These porous structures provide efficient pathways for heat conduction and offer a promising solution to overcome the inherent limitations of low thermal conductivity in PCMs [
2]. Metal or carbon foams belong to the class of materials called cellular solids [
3] and are characterized by a random network of interconnected metallic struts and open pores. By infiltrating the PCM into the interconnected pores of the metal foam, high effective thermal conductivity (ETC) can be achieved due to the increased contact area between the PCM and the metallic matrix. This enhanced thermal conductivity allows for faster heat transfer, thereby improving the performance of PCMs in applications such as thermal energy storage and thermal management systems.
Due to the many recent advancements in manufacturing techniques, particularly through additive manufacturing techniques, novel cellular solids are continuously being developed [
4]. Lattice structures are three-dimensional structures composed of repeating unit cells. Lattice structures can be classified as surface-based or strut-based. The surface-based ones are often inspired by so-called triply periodic minimal surfaces (TPMS). Due to their large surface area, such lattices are often investigated for applications such as heat exchangers [
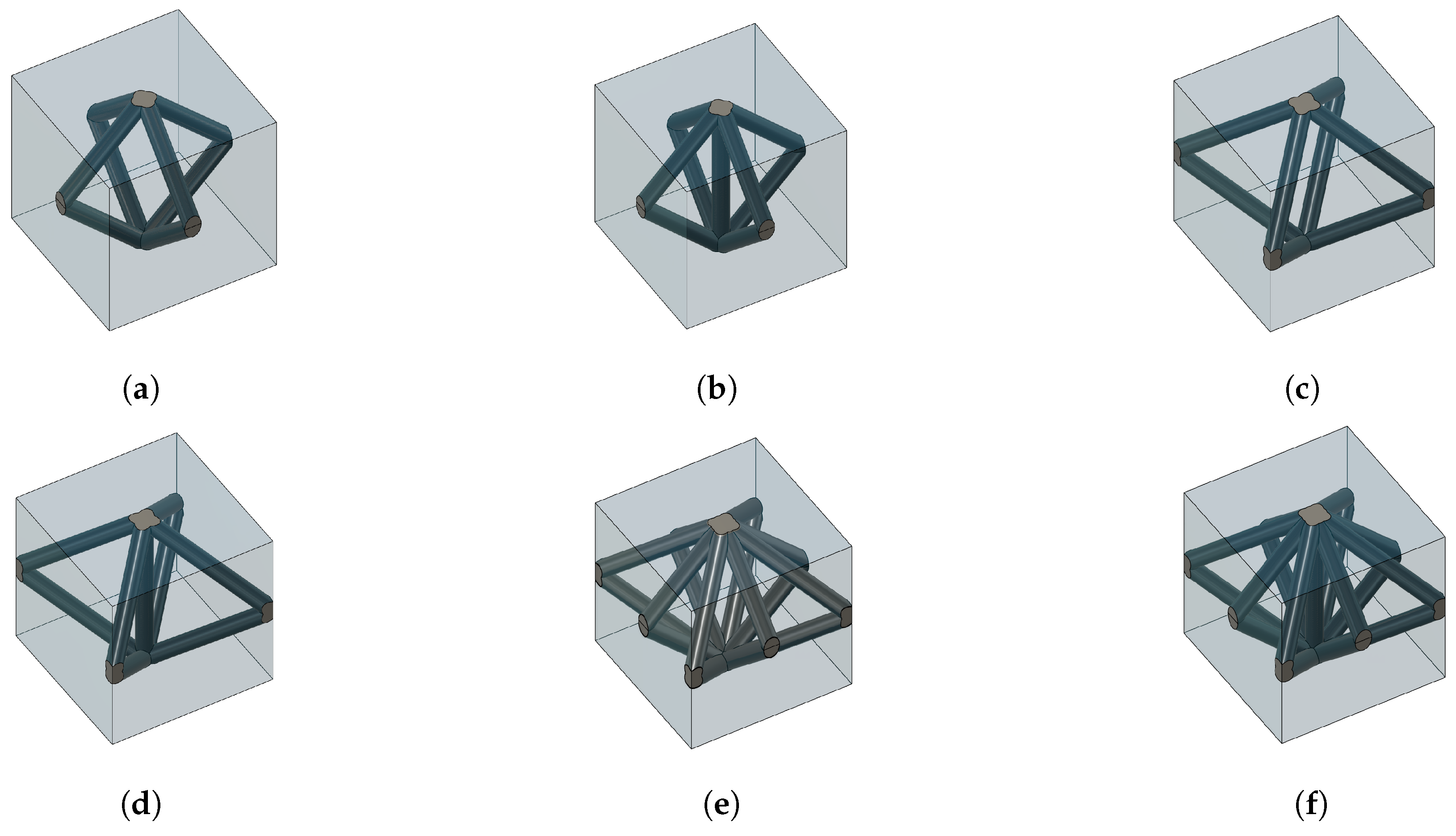
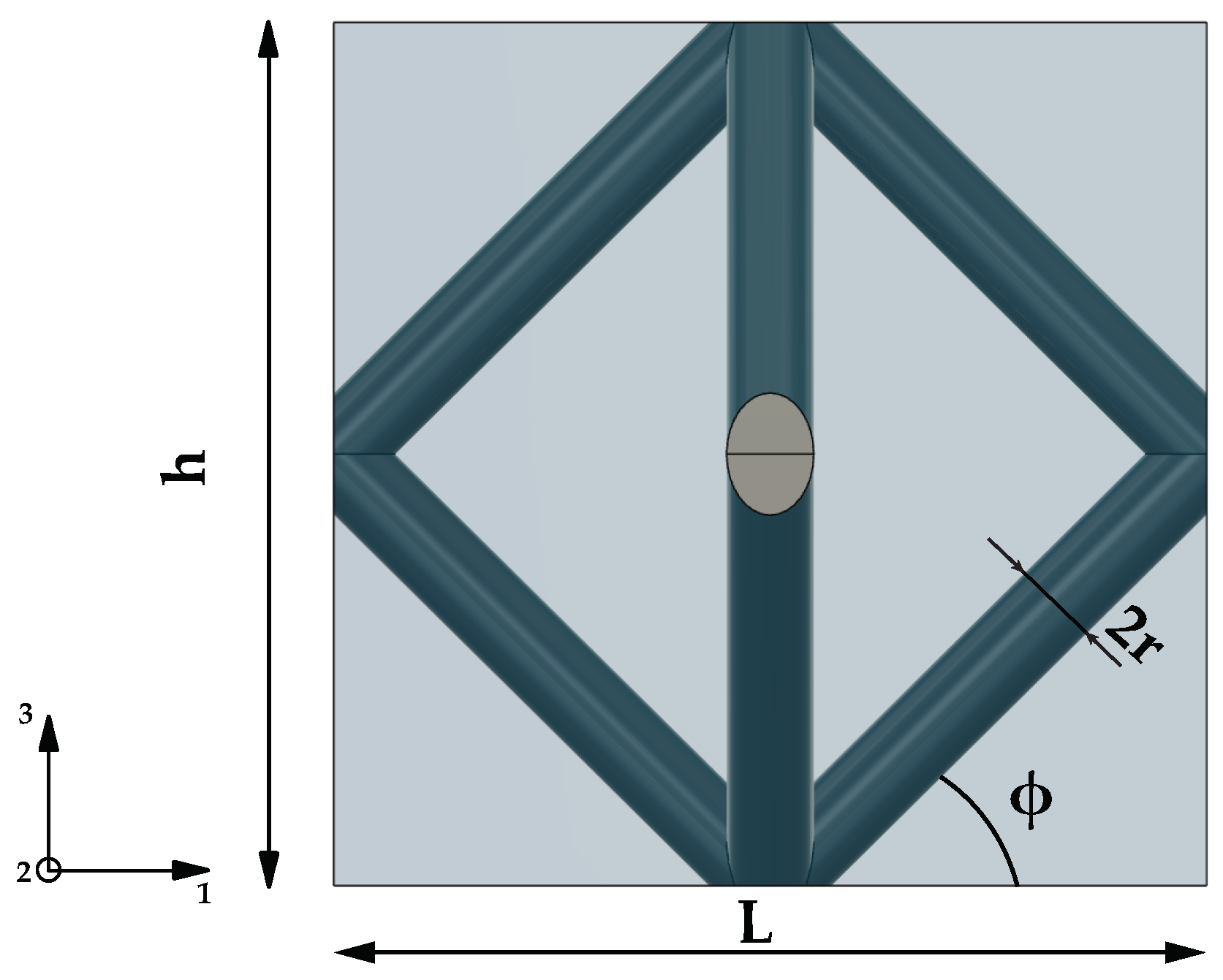
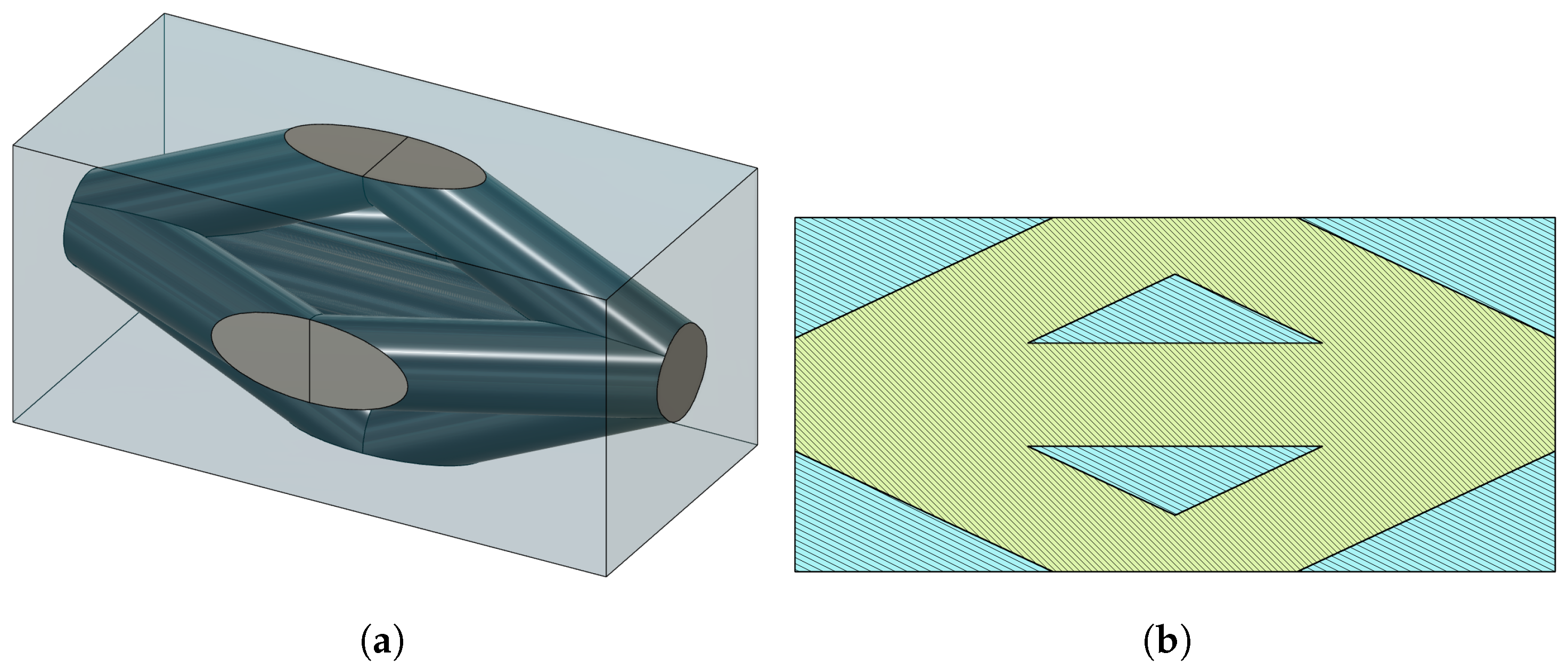
5]. The unit cells of strut-based lattices are prismatic, and the struts join different vertices via segments lying either on the face diagonals of the prism (face-centered) or via volume diagonals (body-centered). A schematic representation of the most common ones is given in
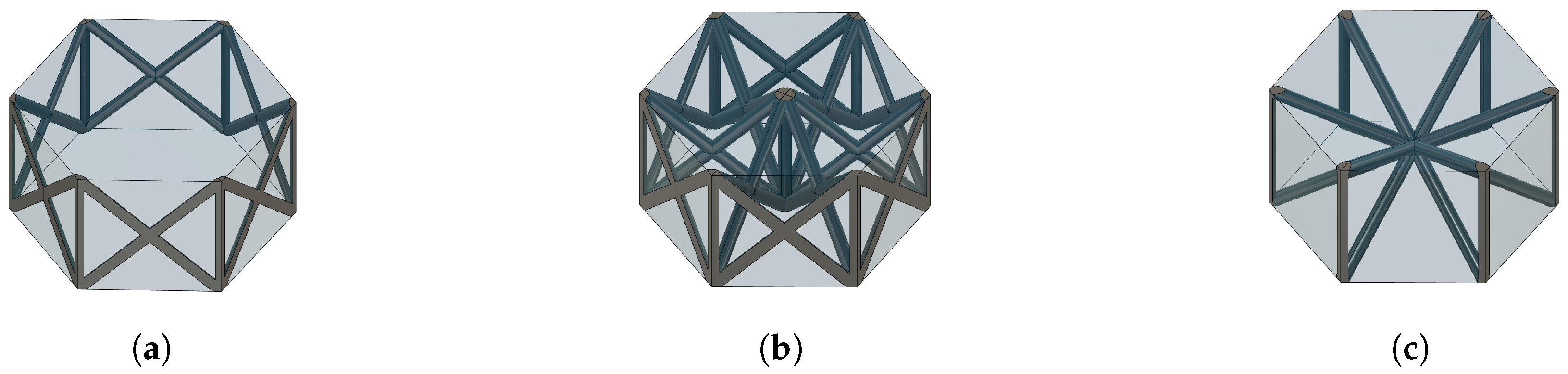
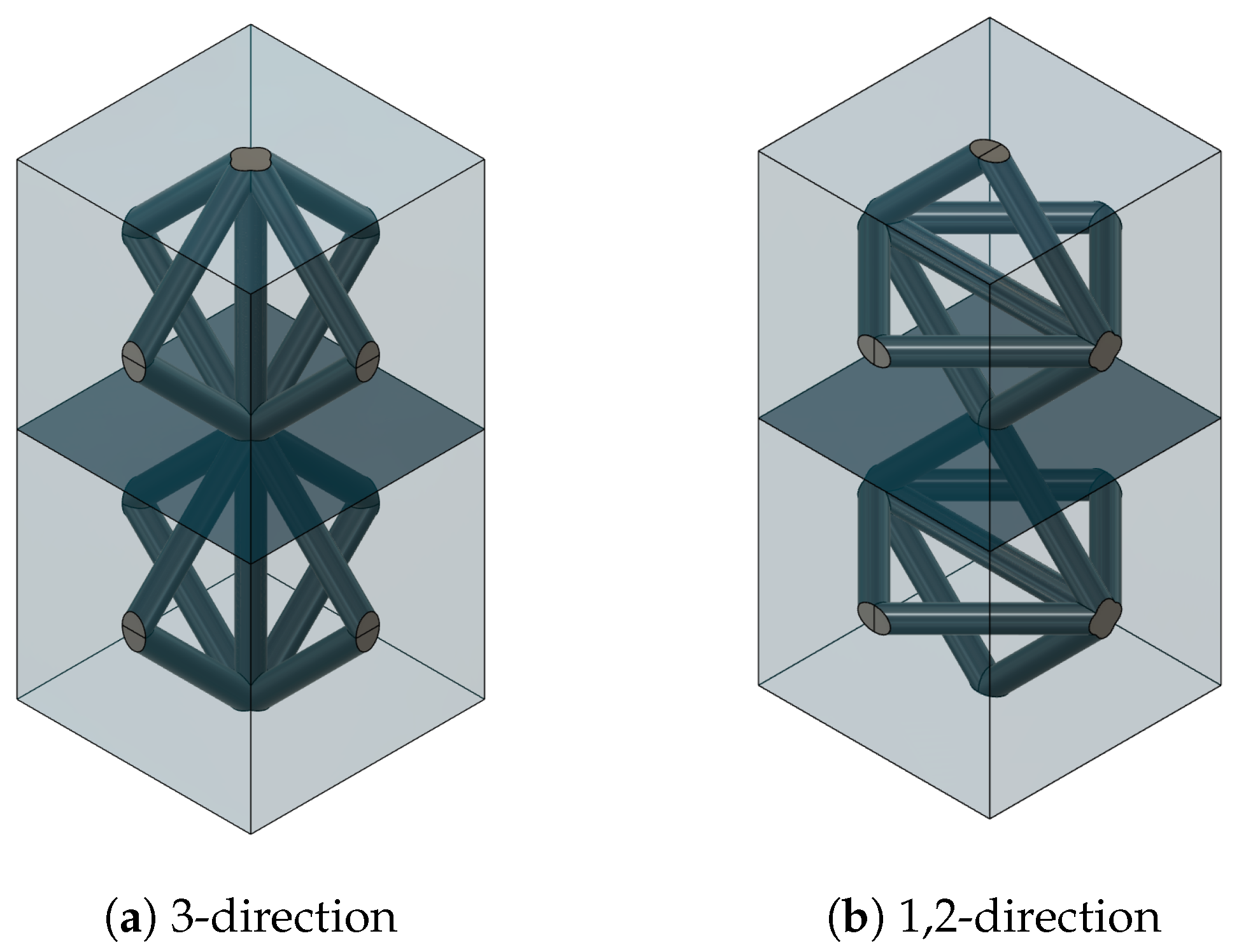
Figure 1, while novel unit cells with a hexagonal shape are shown in
Figure 2. These are also studied in this work.
These structures can be tailored to exhibit specific geometries and properties, including enhanced thermal conductivity. Moreover, the versatility in design made possible by additive manufacturing techniques enables the fine-tuning of the lattice parameters, such as the strut diameter, strut angle, cell size, porosity, and the overall structural geometry. This fine-tuning aims to maximize the enhancement in thermal conductivity.
Several authors have investigated, both numerically and experimentally, the thermal performance of composites composed of strut-based lattice structures and PCMs. Righetti et al. [
6] analyzed the effect of varying cell sizes for different
bcc lattice samples with the same porosity. They concluded that the melting time was the lowest for the sample with the smallest cell size. In prior research, the authors of this work empirically demonstrated that the impact of the cell topology on the thermal behavior of the composite is a primary factor. They also found that, in comparison to metal foams, the effect of natural convection on the thermal performance of lattice structure–PCM composites is enhanced. This is mainly attributed to the geometries of some lattice structures, which can exhibit larger pore sizes for the same porosity [
7]. While architectured lattice structures are becoming increasingly popular, the description of the effective thermophysical properties has been approached by only a few authors and it still represents a challenge. The effective density and heat capacity can be determined with the help of simple volumetric mixing laws [
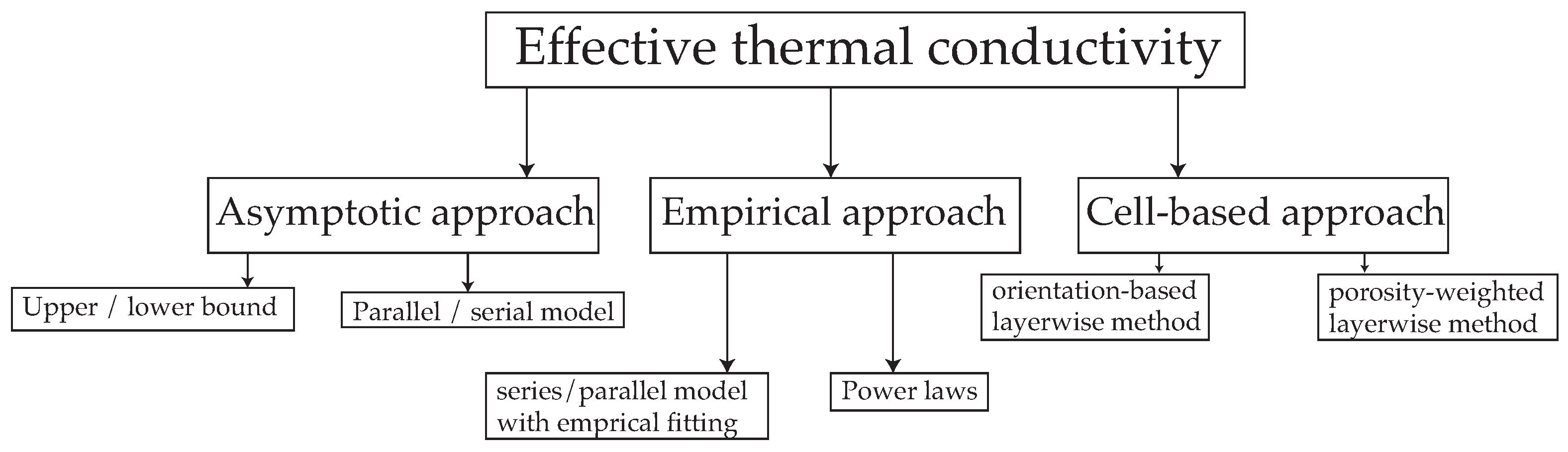
8]. However, the effective thermal conductivity is strongly dependent on the geometry of the porous material. The methods to determine the effective thermal conductivity of a lattice structure are similar to the ones developed in the last few decades to describe foams. These can be divided into three categories: asymptotic, empirical, and cell-based approaches [
9], as schematically shown in
Figure 3.
The asymptotic approach, mainly attributed to Maxwell, univocally relates the effective thermal conductivity to the porosity and sets upper and lower bounds to the effective thermal conductivity. According to Ranut et al. [
9], the method is poor in predicting the ETC. However, several authors have adapted this method by using empirical correction factors. Calmidi and Mahajan [
10] fitted the parallel model with a coefficient
A and an exponential factor
n. Bhattachaeya et al. [
11] used both parallel and serial models to assess the contribution of each model to the effective thermal conductivity (ETC) of high-porosity metal foams. Mendes et al. [
12] examined different methods of calculating the upper bound and lower bound, such as the Hashin–Shtrikman bounds [
13] or the effective medium theory, along with a combination of these methods. They obtained good results with certain combinations of the different bound methods. Wang et al. [
14] investigated the effective thermal conductivity of sandwich panels based on lattice cores for high-temperature applications and delivered a power law correlation for the effective thermal conductivity. Similarly, several authors have developed correlations based on power laws to describe the effective thermal conductivity for a variety of lattice structures, both with and without PCMs as fillers [
15,
16,
17]. The empirical models demonstrate a high level of accuracy in estimating the effective thermal conductivity (ETC) for various material combinations. Nonetheless, these models exhibit limited flexibility when it comes to accommodating different geometries. For small changes in the matrices, new empirical factors have to be determined to make the equations match reality. To improve the flexibility of ETC models, cell-based approaches were introduced by Calmidi and Mahajan [
10] to describe the effective thermal conductivity of metal foams approximating random cells with hexagons. Using this method, the effect of the geometry of the porous medium can be considered. However, due to the randomness of the foam geometry, empirical factors are usually used to adapt the models to the experimental or numerical results. The thermal network method is frequently used to calculate the conductivity of different layers in series. Alternatively, the conductivity can be determined with a porosity-weighted approach [
10,
18], which does not take into account the strut or the ligament orientation, unlike the strut orientation-based methods [
19,
20,
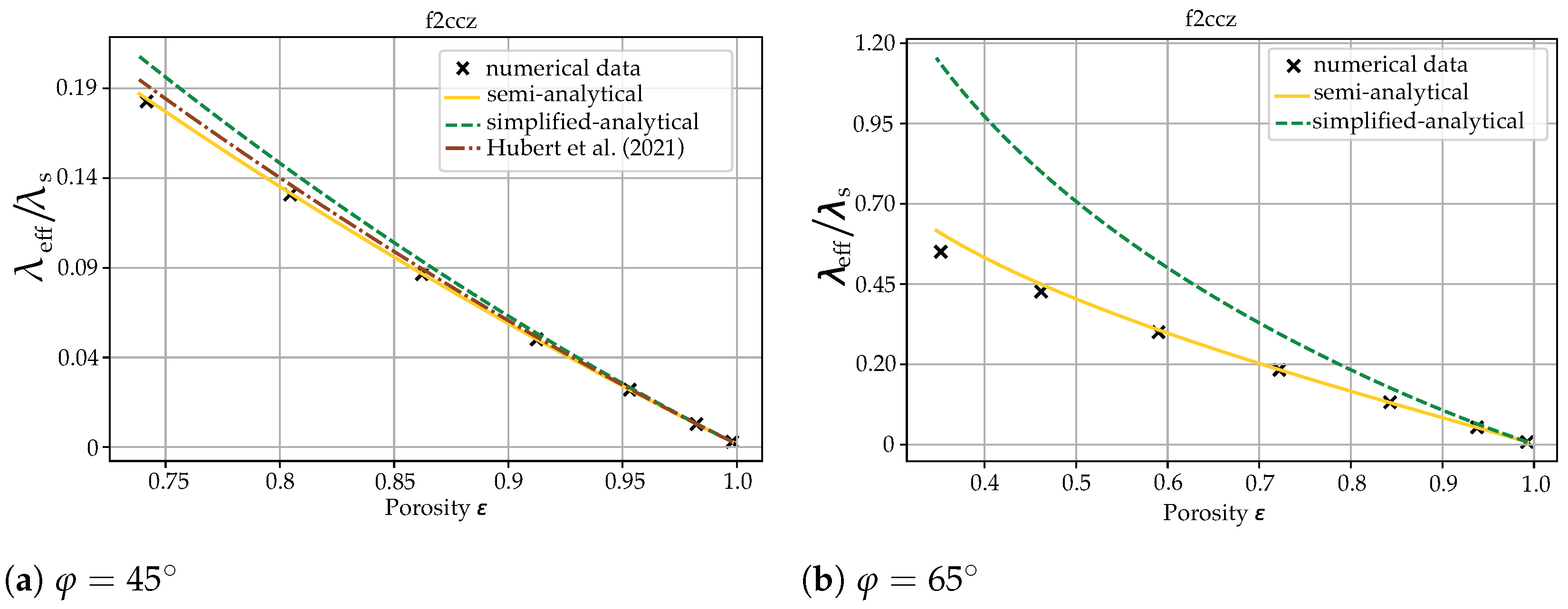
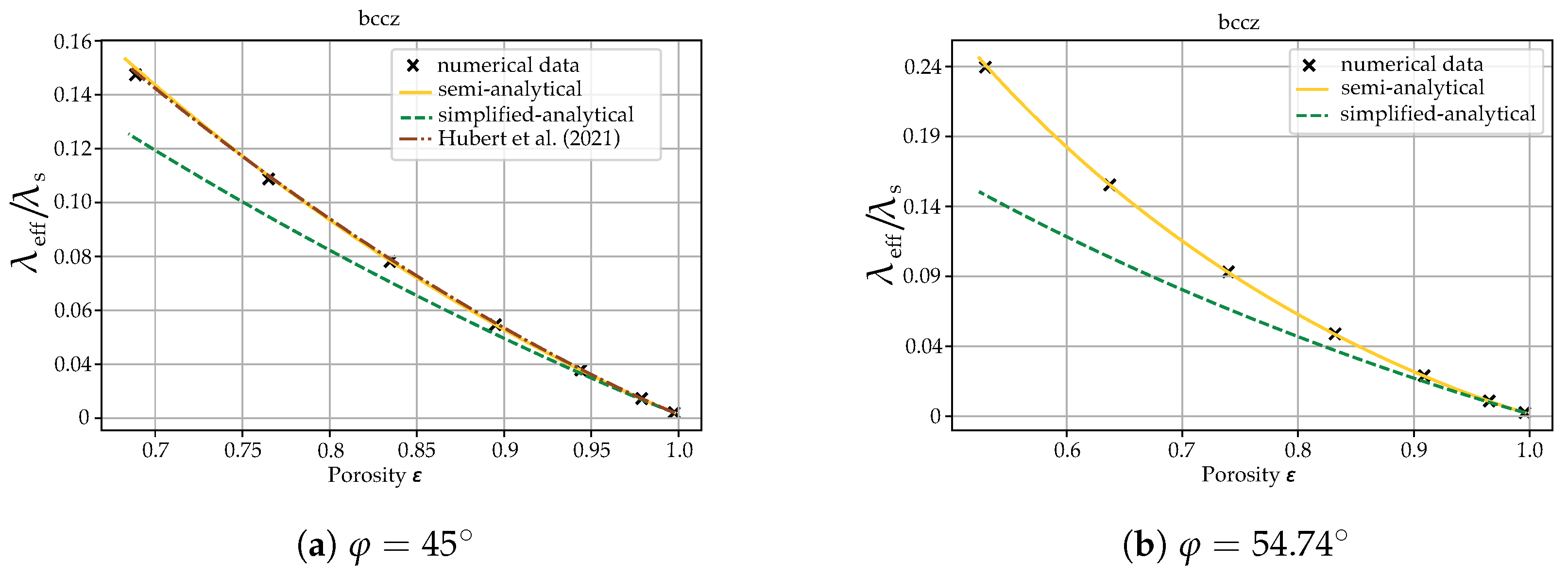
21]. To model the structure precisely, the ligament orientation needs to be respected, as a longer distance of the ligament leads to higher thermal resistance. Due to the high regularity and periodicity of the geometry of a lattice structure, cell-based models can offer high reliability and robustness to predict the ETC, and they are theoretically superior to purely empirical methods. To the authors’ knowledge, only Hubert et al. [
22] have used a cell-based approach to obtain the ETC of a lattice structure with a PCM as a filler. They used fitting coefficients to model the complex intersections between struts and nodes at which struts cross each other. Such coefficients are determined from experimental data and are different for different topologies. The nodes are modeled as cubic elements, with their dimensions determined by the empirical coefficients provided experimentally. The model presented in [
22] is capable of modeling the ETC for the
,
,
, and
cell topologies, taking into account different porosities and with a fixed aspect ratio of 1. However, the number of investigated cell types is limited. There is a large number of cell topologies and new cell shapes, such as hexagonal cells (
Figure 2), which can offer a higher packaging density of struts with respect to cubic unit cells. Furthermore, the model in [
22] only applies to cubic cells, i.e. the aspect ratio between edge lengths is 1. Variations in the aspect ratio lead to different strut angles and thus to significant changes in the ETC. This is especially interesting for multifunctional use cases. The aspect ratio, being an additional parameter, enables more flexibility in tailoring the material properties. Additionally, in [
22], the idealization of the cell nodes is based only on empirical factors. In this work, instead, a novel model is presented. Generic topological parameters are introduced, which allows one to consider a much wider spectrum of geometries with respect to previous works.
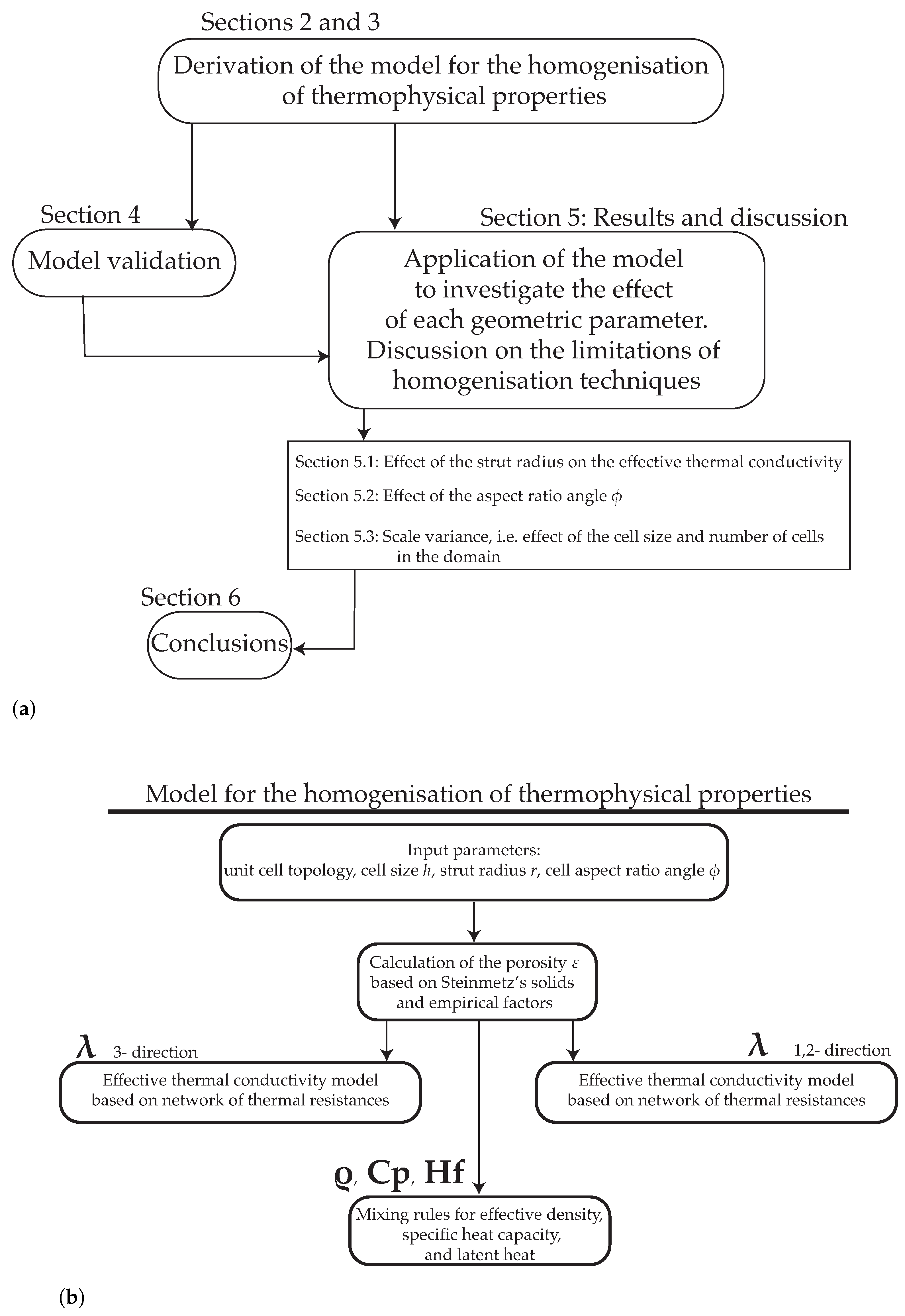
The work is structured as schematically shown in
Figure 4.
Section 2 focuses on deriving formulae to describe the geometry of the lattice unit cells based on the input parameters (
Figure 4b).
In order to more accurately describe the nodes at the intersection of the struts, Steinmetz’s solids are used [
23]. Due to the complex geometry of the cells and in order to account for eventual manufacturing imperfections, the analytical formulae that derive the unit cell porosity are accompanied by empirical factors obtained via numerical investigations. In particular, the model introduced here has the capability to individually analyze the impact of various geometric parameters. These parameters include the cell height, cell aspect ratio (strut angle), strut radius, and cell type. In addition to cubic or parallelepiped unit cells (
Figure 1, cells based on hexagonal prisms are treated as well (
Figure 2). Although less investigated, such unit cells exhibit the highest packaging density for cylindrical struts in the z direction, which enables the most efficient arrangement of conductive struts for a given porosity. Once the porosity is determined as a function of all the other geometric parameters, the effective thermal conductivity (ETC) can be calculated. The derivation of the ETC, described in
Section 3, is based on a network of thermal resistances composed of nodes and struts. The same approach is used to obtain both the ETC in the direction of z struts (3-direction) and in the orthogonal direction (1,2-direction). Simple volume mixing rules are presented in
Section 4, where the validation of the presented model is discussed.
Section 5 (
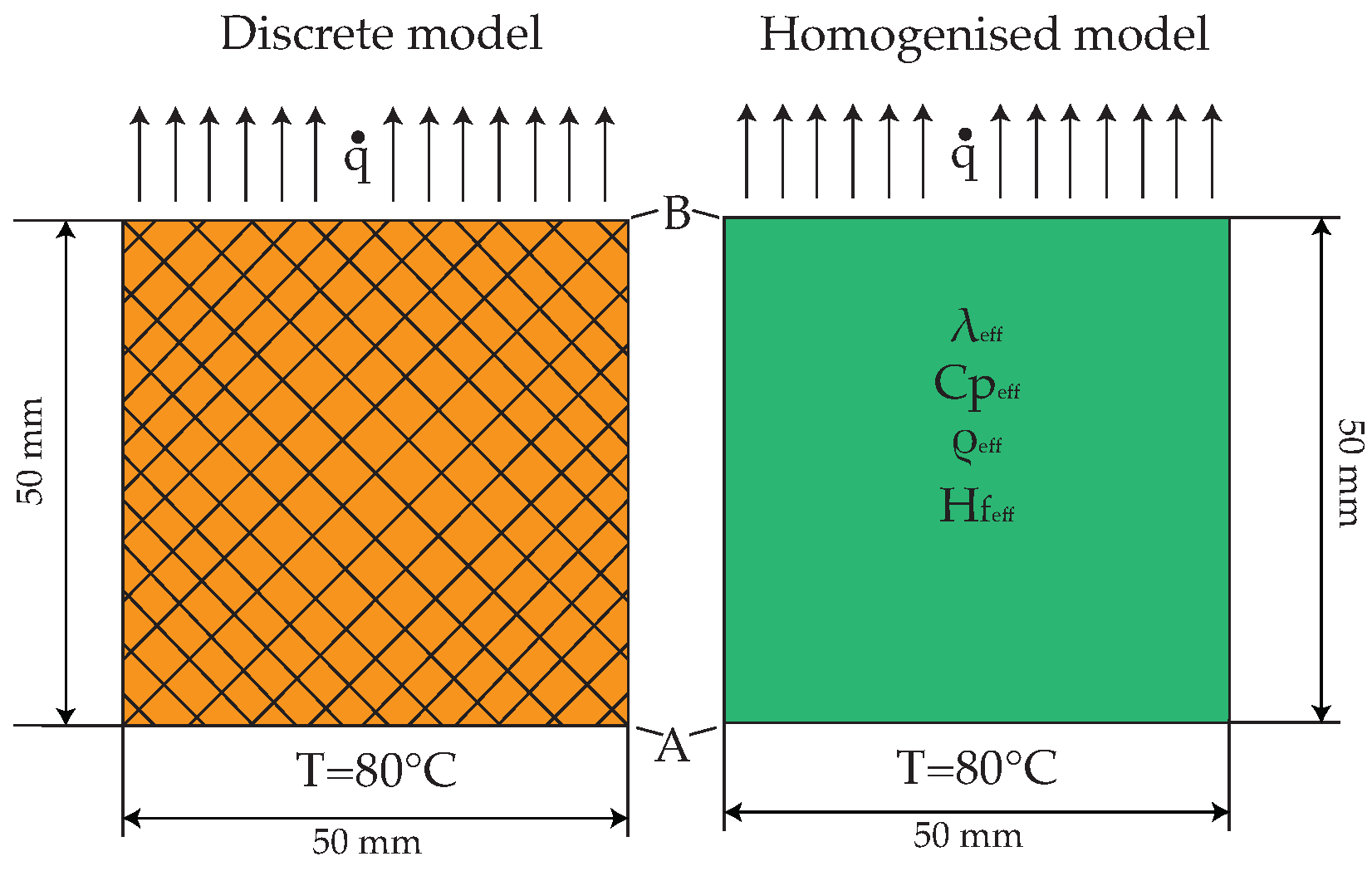
Figure 4a) presents an analysis of the quantitative results, with a major focus on the effect of each geometric parameter on the variation in the effective thermal conductivity. Furthermore, the validity of the homogenization techniques, which come with the use of effective thermophysical properties, is discussed. In particular, the scale variance is addressed. According to several authors [
12,
20], if convection and radiation can be neglected, the ETC of a cellular solid with a filler (e.g., a PCM) can be considered scale-invariant, i.e., a variation in the cell size and strut radius maintaining the same porosity does not lead to a variation in the ETC. While this can be a valid assumption, the transient thermal behavior of the composite is affected by the cell size and by the number of cells present in the domain. Therefore, this work presents the first approach to account for scale variance when treating the composite by means of effective thermophysical properties.
2. Derivation of the Lattice Cell Geometric Properties
To effectively characterize various cell topologies and make meaningful comparisons between them, it is essential to take into account all geometric parameters within a lattice structure. These variables are the cell height
h, the cell width
L, the aspect ratio of the cell height
h to the cell width
L expressed by the angle
, the strut radius
r, and the cell type. For face-centered (fc) cells,
corresponds to the strut angle. For body-centered (bc) cells, the strut angle
follows from Equation (
1). For hexagonal cells,
corresponds to the ratio of cell height to edge length
. The face-centered struts thus have an angle of
, while the body-centered strut angle
is calculated using Equation (
2). The following cell types are investigated:
,
,
,
,
,
,
,
,
. In
Figure 5, definitions of the geometric variables of a unit cell are shown.
Prior to introducing the analytical models employed in this study, it is pertinent to elucidate their domain of applicability. In order to consider the composite material as a cellular solid infiltrated by a PCM, it is necessary that the unit cells are open on all sides. This condition imposes constraints on the geometric parameters of each individual unit cell. It is important to note that the range of validity varies due to the different topological configurations. For instance, unit cells with a relatively low number of struts, such as the
topology, maintain their status as open cells at porosities below those required for densely packed unit cells, i.e., the
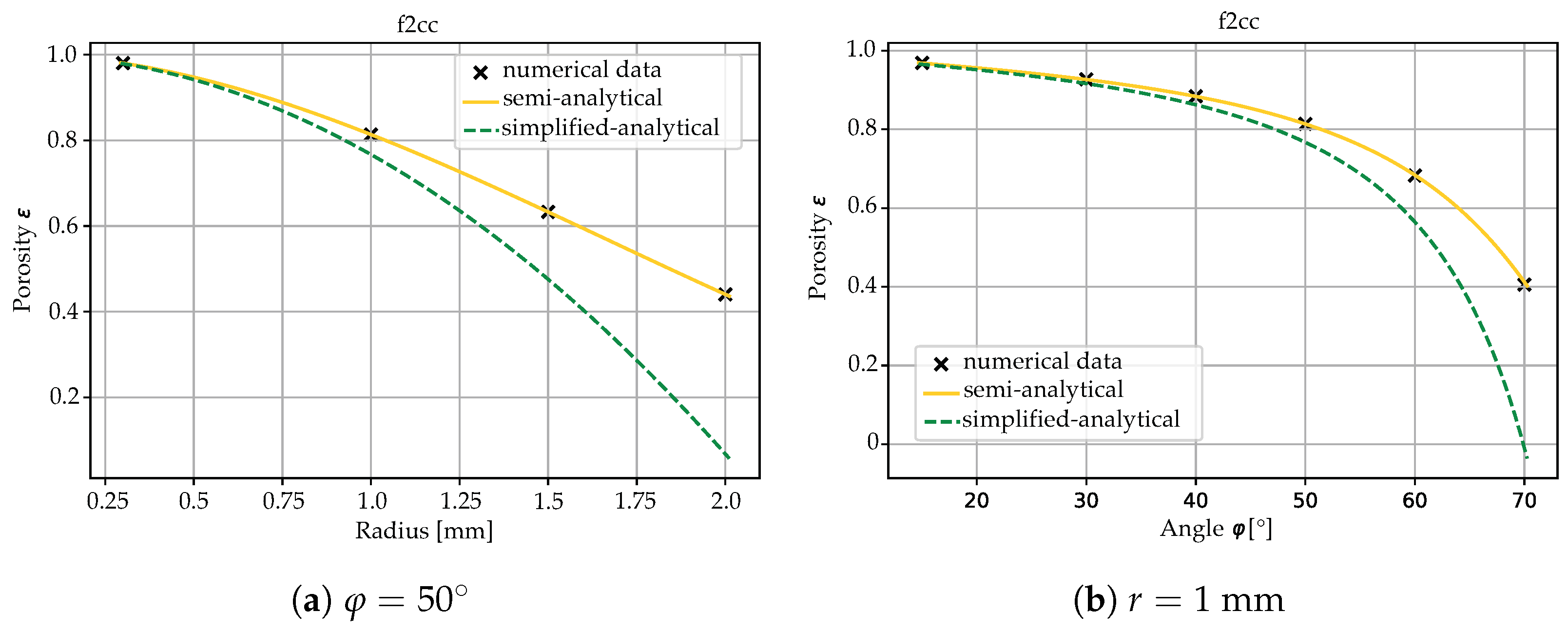
topology. In summary, the semi-analytical models employed for porosity calculations have been determined to consistently hold true for porosities
and aspect ratio angles
. Conversely, the simplified models outlined in
Section 3.4 are applicable only when dealing with porosities exceeding 0.9 and aspect ratio angles up to
. Furthermore, the equations used for the semi-analytical estimation of the ETC exhibit validity within a narrower range of porosities (
) and aspect ratio angles (
). For a comprehensive examination of the scope of validity of the presented models, we refer the reader to
Section 4.
2.1. Derivation of the Porosity
For the exact calculation of the ETC, knowledge of the lattice porosity is necessary. The struts are modeled as cylinders. The volume of the cylinder depends on several parameters, introduced in Equation (
3). The strut’s length is related to the cell size
h and to the strut type, which is taken into account by making use of the strut angle
. The angle
corresponds to the angle between the horizontal plane (1,2-plane in
Figure 5) and the strut. For face-centered (fc) struts, i.e., struts that run across the cell sides, this is the angle
. For body-centered (bc) struts, which run through the center of the cell, this corresponds to the angle
or
. For z struts,
.
The intersection of two struts creates a generic angle
between the two struts.
Table 1 shows the values of
for simple intersections. The volume of the intersection can be described via Steinmetz’s solid, shown in
Figure 6. Its volume is
Four-fold intersections occur at the top and bottom interfaces of most cells and in the central nodes of body-centered cells. Their volume is calculated according to Equation (
5). The equation contains two double intersections from Equation (
4), and the overlap between them is subtracted in the last term. The last term corresponds to the volume of a four-fold Steinmetz solid.
Eight-fold intersections result from a combination of two four-fold intersections, as indicated in Equation (
6). These intersections occur at the interfaces of the cell types
and
. Here, a body-centered four-fold intersection and a face-centered four-fold intersection are added together for the calculation. The overlap of these two volumes is subtracted from the sum. The subtracted volume can be approximated by a six-fold Steinmetz’s solid, as its volume can be determined analytically and it deviates only slightly from the volume of the eight-fold body [
23]. However, as Steinmetz’s solids have analytical solutions only for a constrained amount of intersection angles, the intersection of the fc and bc struts with each other is not taken into account in the subtracting term, leading to inaccuracies that must be corrected with an empirical coefficient.
The porosity
results from the proportion of the lattice volume
to the total volume
according to Equation (
7).
The volume fraction
is simply the strut volume compared to the total volume and can be calculated from Equation (
8).
The strut volume is calculated via the cylinder volume of a strut together with the number of fc struts,
, the number of bc struts,
, and the number of z struts,
, minus the volumes of the intersections. In general, Equation (
9) applies to all cell types. This is composed of Equation (
3) with the three different strut types that occur in the cells. The volumes from Equation (
4) are subtracted with the respective strut intersection angles that occur.
The first term in the square brackets of Equation (
9) models the number of struts with their respective cylinder volumes. The second term subtracts the intersections. The factors
,
,
, and
are associated with the number of volumes that need to be subtracted because of the intersection of the struts. The factors can either be derived geometrically or determined empirically. At some intersections, multiple struts cross. In the case of the cell
, for example, nine struts cross at one intersection. This leads to intersection volumes that cannot be determined analytically. Therefore, for such cases, a semi-empirical approach is used to determine the intersection volumes of the struts that need to be subtracted from the cylinder volumes of the struts. The factors
are empirically determined and serve as coefficients to adjust or correct the model introduced in this context. The factors
and
take into account intersections of equal struts. The factors
and
account for the number of intersections between diagonal struts and z struts.
To obtain an appropriate value of the porosity, the cell topology is accounted for by making use of the coefficients
. A
cell has four fc struts, no bc struts, and a single z strut. Thus,
four fc struts
and one z strut
. As
does not contain bc struts, also the factors
and
are set to zero. The empirical factors are fitted and evaluated based on the volume measurement functions of CAD-generated geometries. Such factors can be adapted in the future to account for different manufacturing tolerances.
Table 2 shows the fitted factors of the respective cells with the numerically obtained volumes. A gradient descent algorithm is used to find appropriate values for the parameters
. The root mean squared error (RMSE) of the derived equations is shown in
Table 2. The empirical fits show very good approximation over a wide porosity range with errors below 1%. The equations can be used for porosities of
. Once this threshold is reached, the pores created by the cells are no longer open.
6. Conclusions
In this work, the effective thermophysical properties of composites based on PCMs embedded with metallic lattice structures are described. Generic geometric parameters are introduced in order to allow the free treatment of all geometric variables and the future topology optimization of such composites. For this purpose, a semi-analytical model for the calculation of the effective thermal conductivity is introduced. The nodes at which the lattice struts cross are described via semi-analytical expressions derived from the use of Steinmetz’s solids. This allows an accurate description of both the porosity of the unit cells and their effective thermal conductivity for a variety of geometric parameters. In the general case, empirical factors must be introduced as analytical solutions for the description of Steinmetz’s solids are limited. Additionally, due to wide manufacturing tolerances, the structures will exhibit non-negligible deviations from the theoretical volume, especially at the nodes where the struts cross. Thus, the empirical factors introduced here can be calibrated in the future depending on the different manufacturing parameters. The model is validated against the existing literature of both previously existing models, which are, however, limited in the number of geometric parameters and experimental results.
A variety of unit cells are considered in a wide range of porosities, i.e., from = 0.65 to = 0.99. The main findings of this work are listed below.
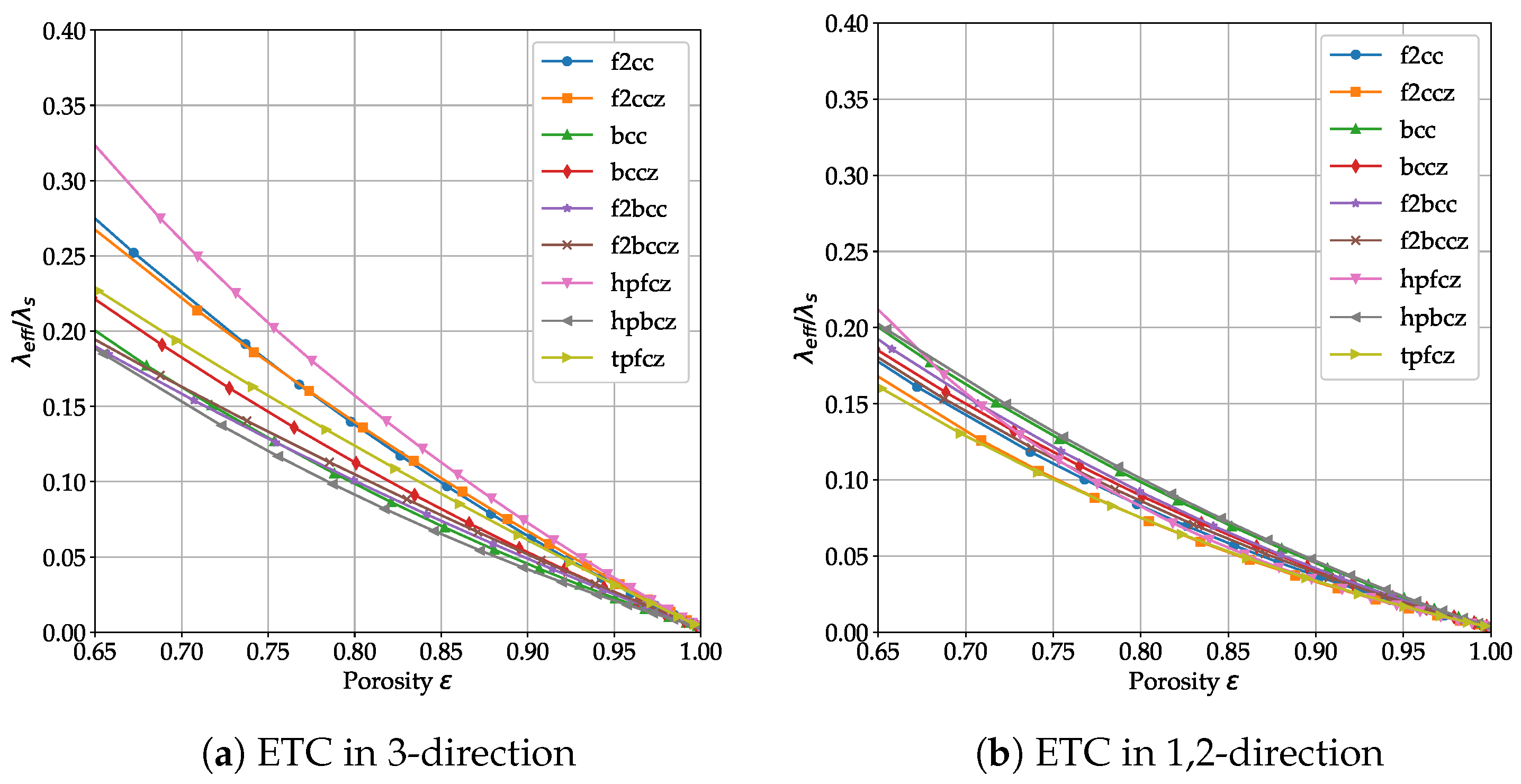
The cells exhibiting the highest effective thermal conductivity in the 3-direction, i.e., the direction of the z struts, at a given porosity, are the face-centered ones, i.e., ,, , .
In the 1,2-direction, the effective thermal conductivity is obviously reduced for all cells presenting a z strut, and the trends are partially inverted. Body-centered lattices exhibit higher effective thermal conductivity than face-centered ones. Hexagonal cells exhibit the peculiarity of showing the highest and the lowest effective thermal conductivities. The consistently shows the highest value in the 3-direction, while the exhibits the lowest value. In the 1,2-direction, the trend is reversed and the shows the highest effective thermal conductivity.
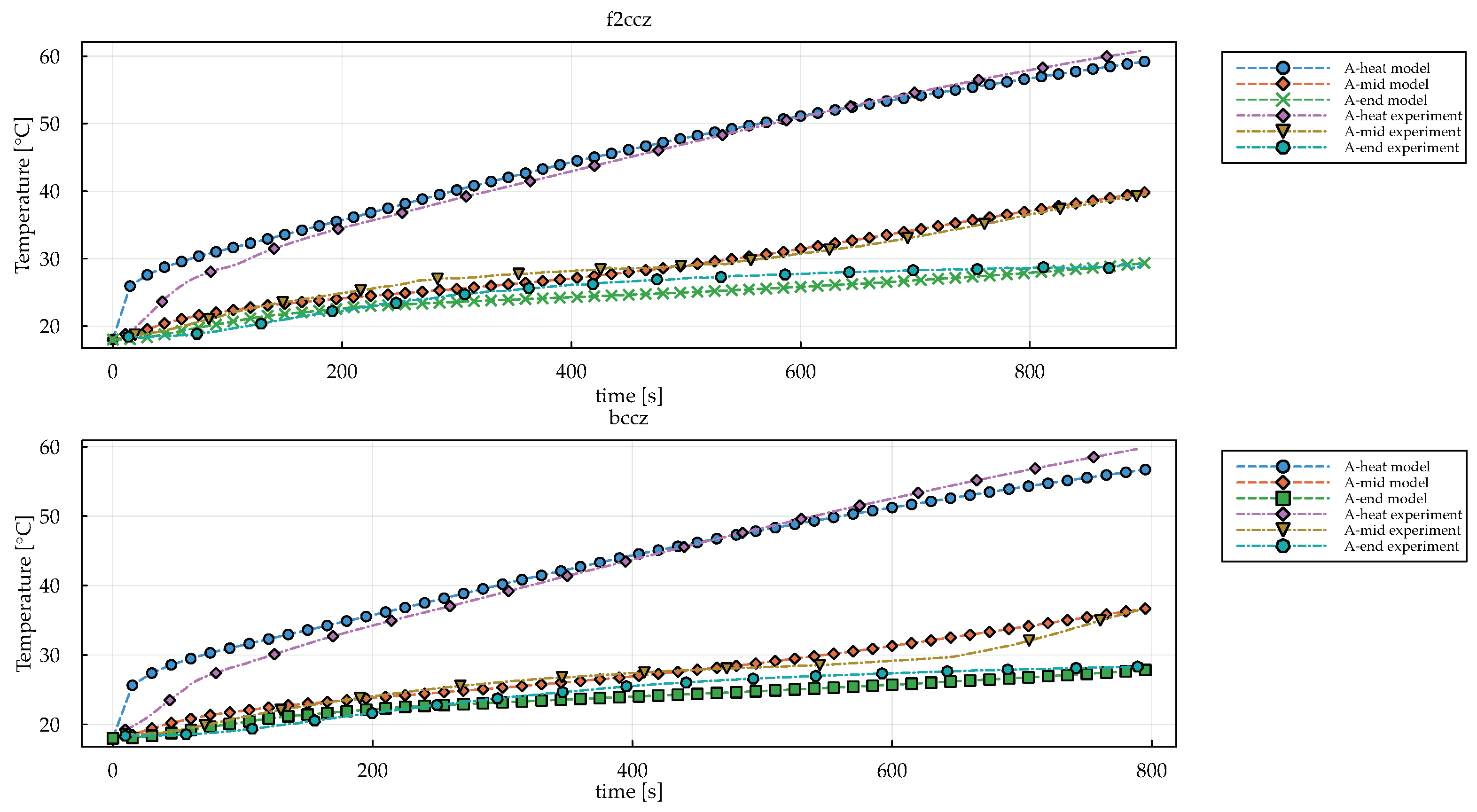
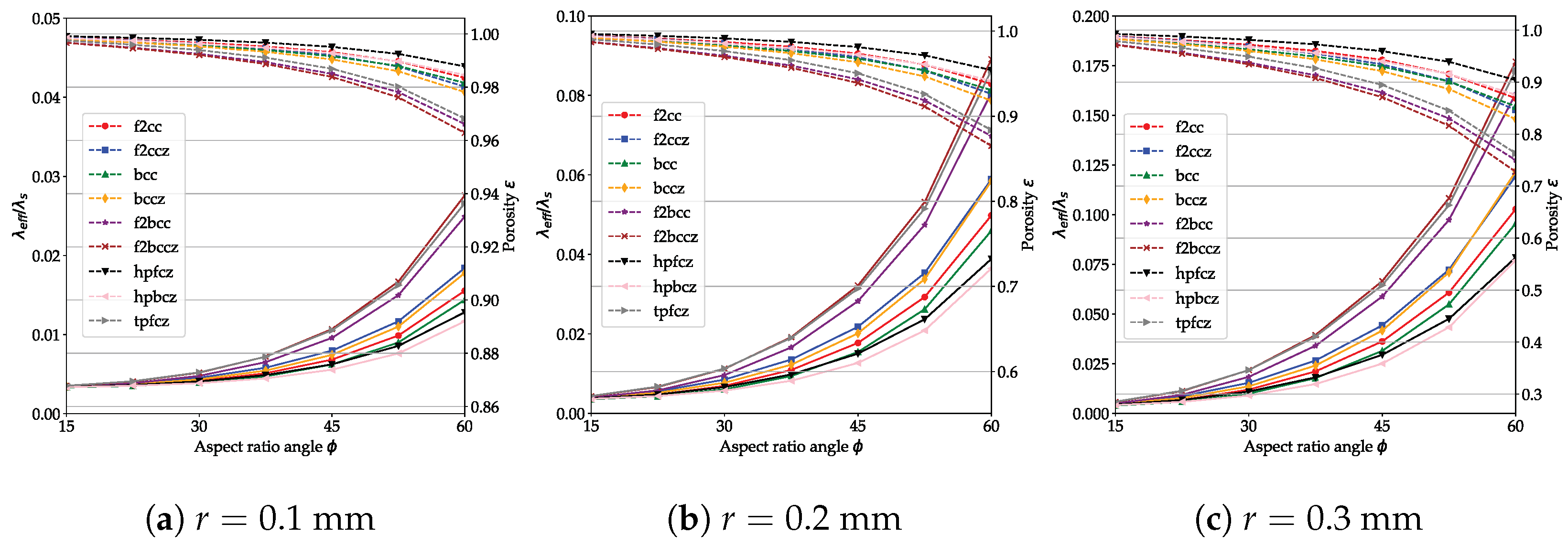
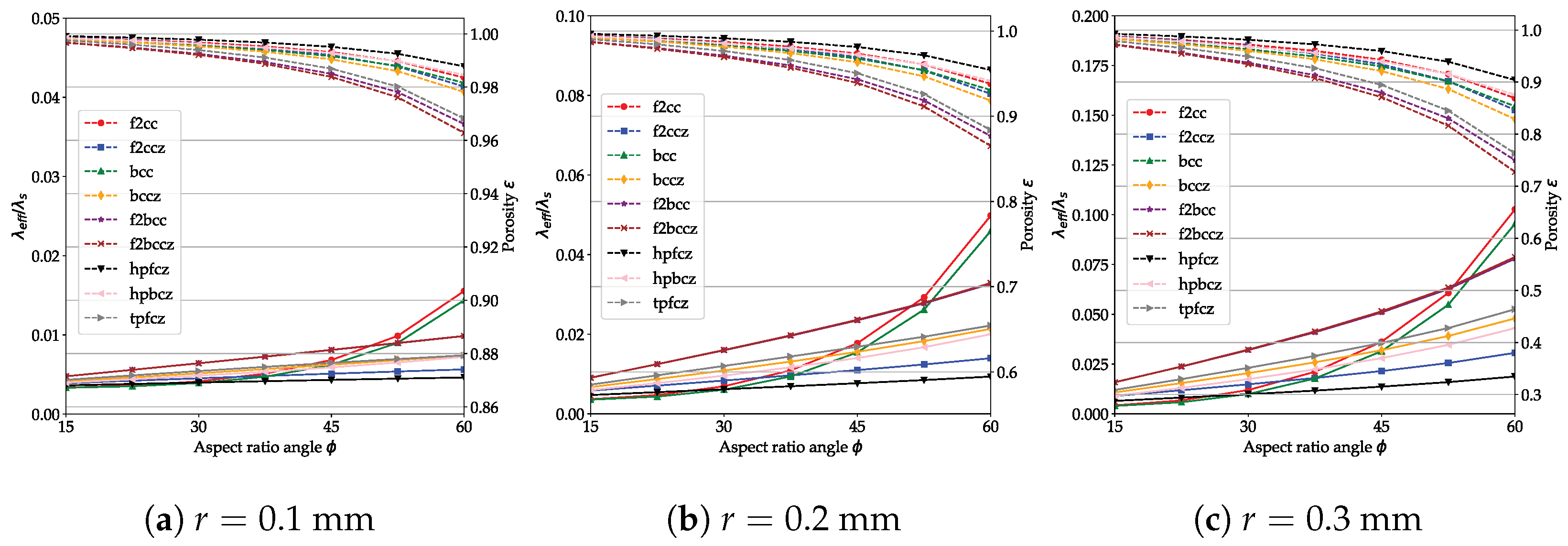
In general, an increase in the aspect ratio, i.e., increasing the strut angle, leads to higher effective thermal conductivities for unit cells with porosity within ca. 75%.
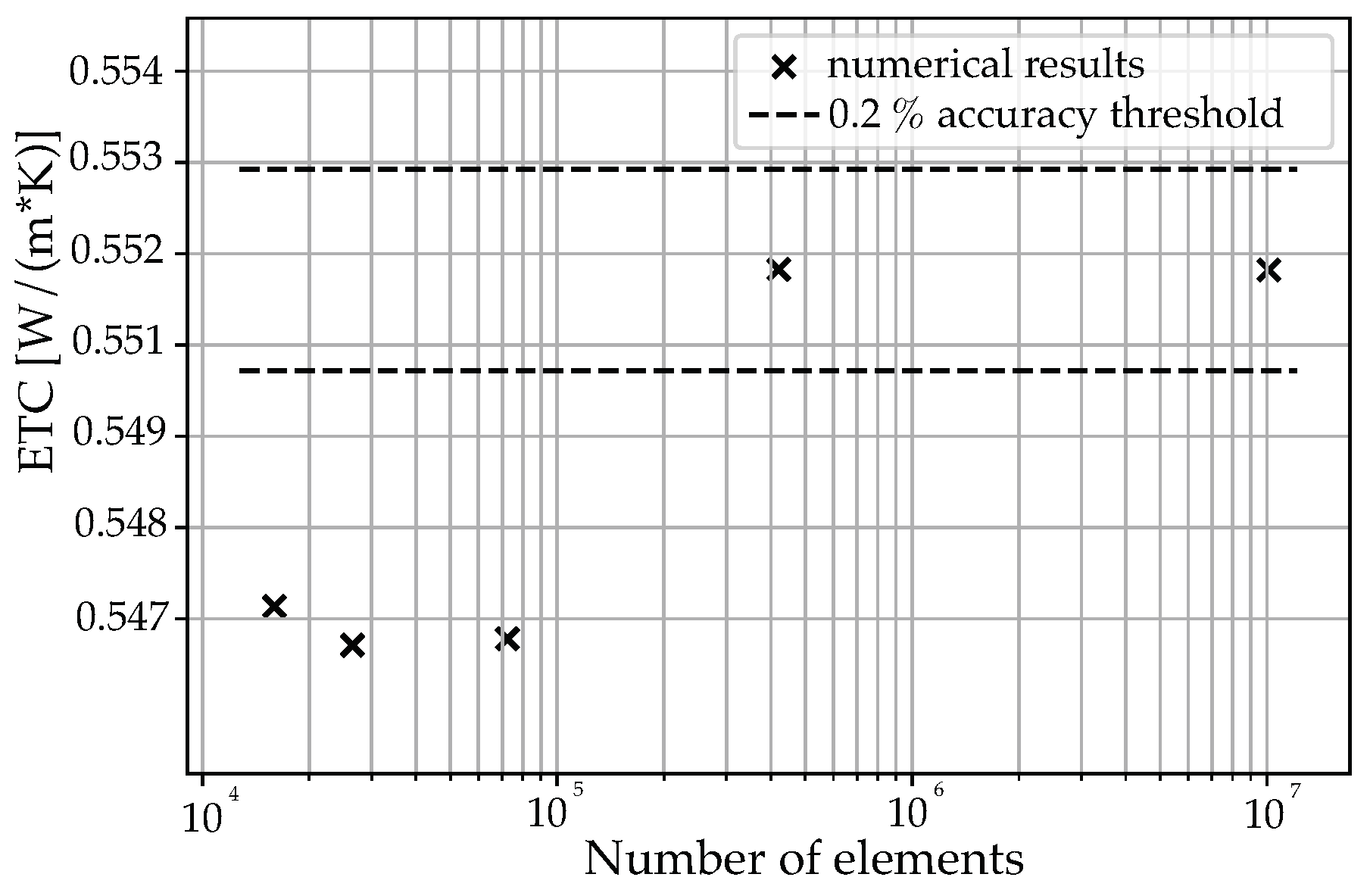
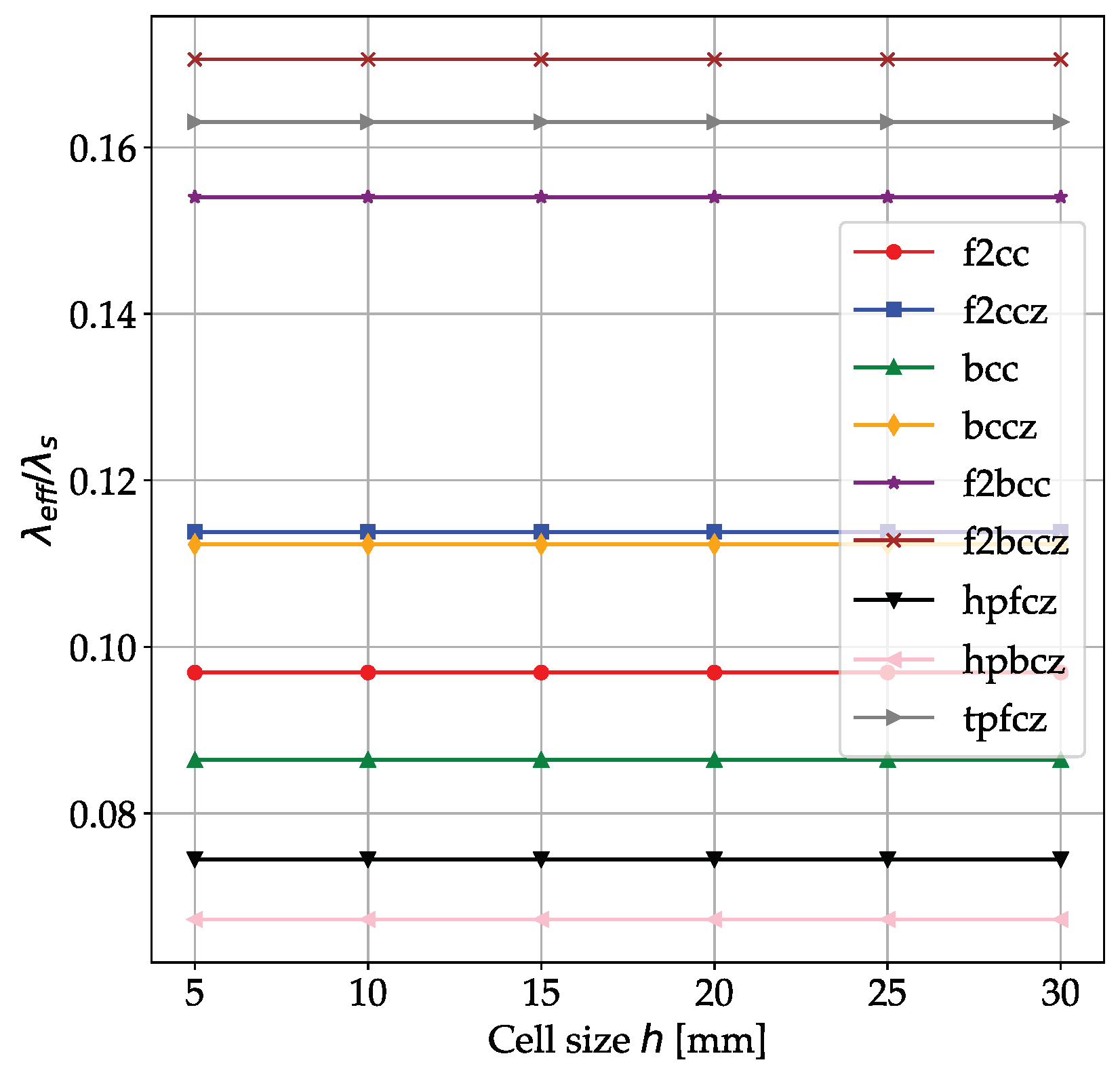
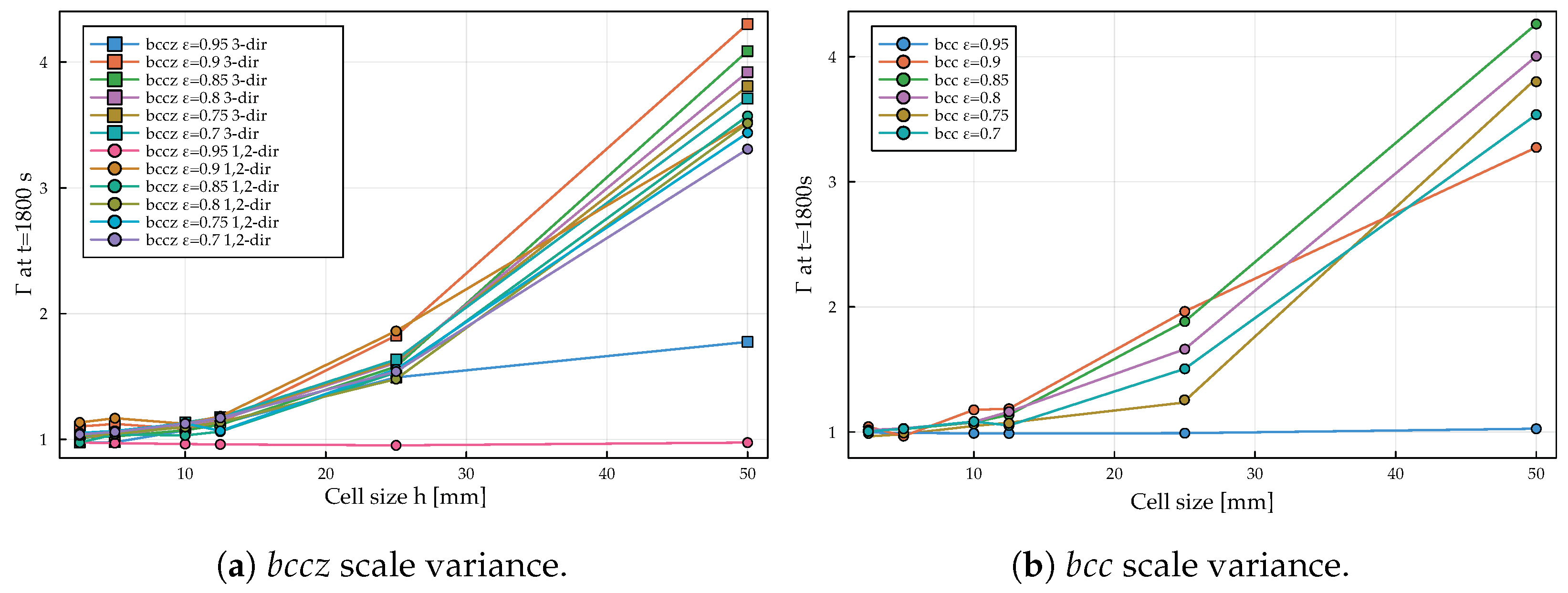
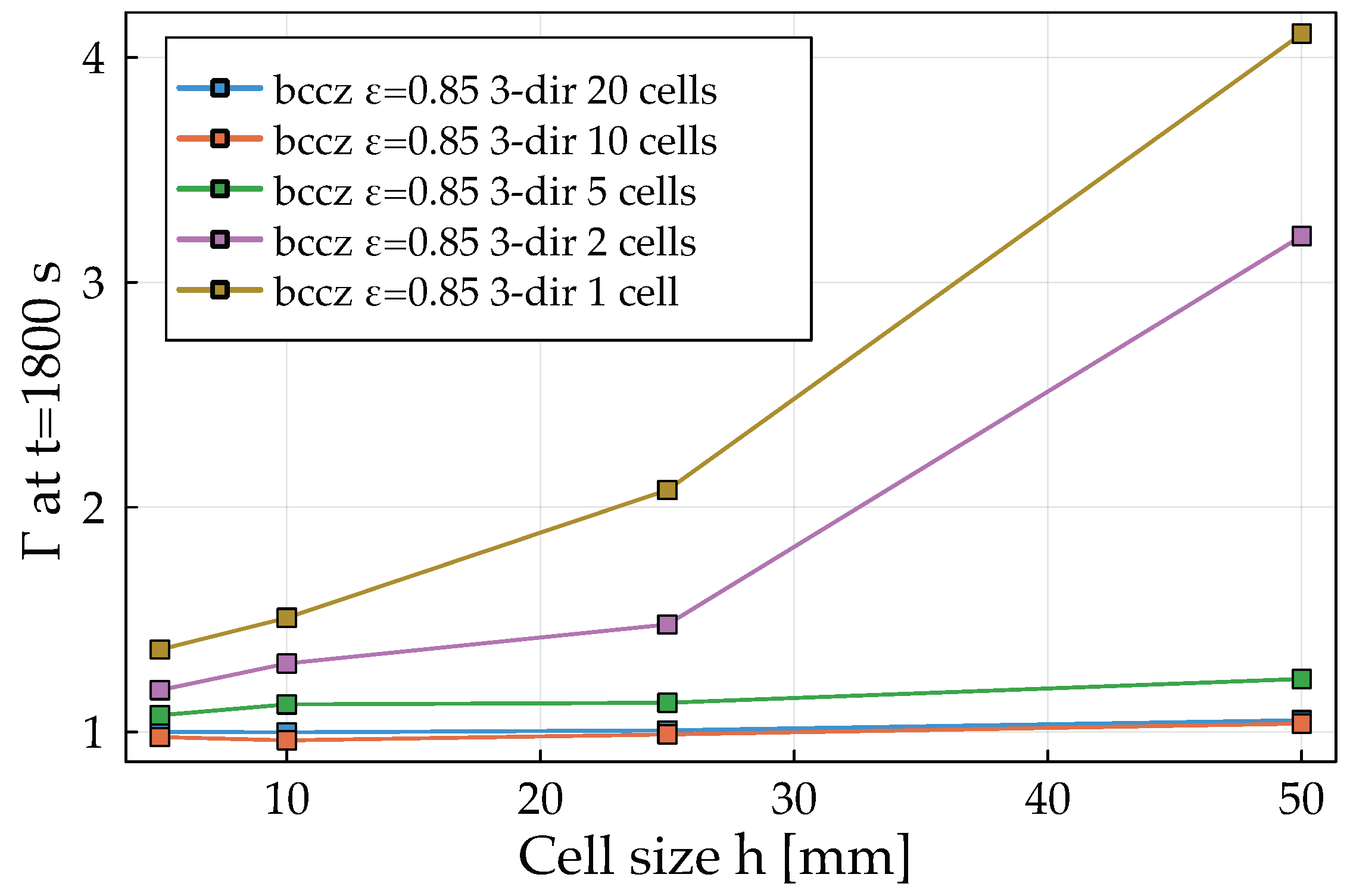
The effect of the cell size, also called scale variance, indirectly affects the accuracy of the proposed analytical equations. Indeed, if the domain volume is fixed, the variation in the cell size directly influences the number of cells that can fit within such a volume. The number of cells directly affects the transient thermal behavior. A minimum number of cells of 10 is identified as appropriate to describe the transient thermal behavior of the analyzed composites via homogenized models based on effective thermophysical properties. If this threshold is maintained, the cell size has no effect on the transient thermal behavior of the composite. Otherwise, a coupled effect of the reduction in the number of cells and of increasing the cell size can be evidenced. Additionally, the porosity has a direct influence on the scale variance. Indeed, at high porosities, the scale variance, related to the variable
of Equation (
37), is reduced, while it increases with decreasing porosity.
All in all, the relations delivered in the present work can be flexibly used to estimate the effective thermophysical properties of a variety of composite PCMs. Care should be taken when dealing with a low number of cells and large cell sizes, as homogenization techniques start to fail.
Future works shall address the extension of the presented methodology to additional strut-based cellular solids, in order to extend the comparability of the thermal performance among the different manufacturable geometries. Additionally, prospective activities shall focus on developing methods to perform the same analysis with surface-based lattices, i.e., TPMS. Furthermore, it is well known that natural convection in the melt does have a measurable effect on the speed and shape of the expanding melting front of the PCM, thus affecting the transient thermal performance of the composite. With variable geometric parameters and, in particular, varying the cell size, the influence of natural convection becomes increasingly relevant due to the variation in the permeability of the lattice structure. Future works should extend the presented homogenization approaches to include this additional phenomenon.