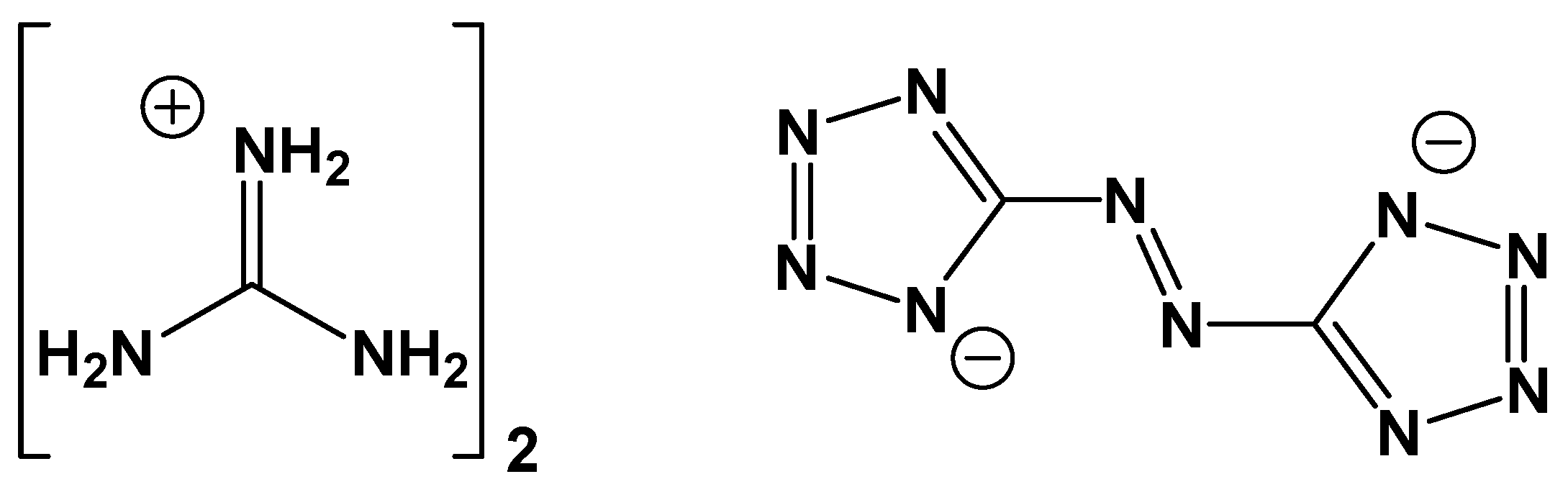
Enthalpy of Formation of the Nitrogen-Rich Salt Guanidinium 5,5′-Azotetrazolate (GZT) and a Simple Approach for Estimating the Enthalpy of Formation of Energetic C, H, N, O Salts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Combustion Calorimetry
2.2. Computational Work
3. Results and Discussion
3.1. Enthalpy of Formation of GZT in Solid Phase
3.2. Computational Results for GZT
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Klapotke, T.M. Chemistry of High-Energy Materials, 6th ed.; De Gruyter Textbook: Berlin, Germany, 2022. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Silva, A.L.R.; Gonçalves, J.M.; Morais, V.M.F.; Ribeiro da Silva, M.D.M.C. Thermodynamic properties of 2-mercapto-, 2,5-dimethyl- and 2-mercapto-5-methyl-1,3,4-thiadiazole. J. Chem. Thermodyn. 2022, 165, 106644. [Google Scholar] [CrossRef]
- Silva, A.L.R.; Costa, V.M.S.; Ribeiro da Silva, M.D.M.C. Experimental and Theoretical Investigation on the Thermochemistry of 3-Methyl-2-benzoxazolinone and 6-Nitro-2-benzoxazolinone. Molecules 2022, 27, 24. [Google Scholar] [CrossRef]
- Silva, A.L.R.; Ribeiro da Silva, M.D.M.C. Effects of the functional groups amino and nitro on the reactivity of benzoxazoles and comparison with homologous benzothiazoles. J. Phys. Org. Chem. 2020, 34, e4118. [Google Scholar] [CrossRef]
- Byrd, E.F.C.; Rice, B.M. A comparison of methods to predict solid phase heats of formation of molecular energetic salts. J. Phys. Chem. A 2009, 113, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.L.R.; Almeida, A.R.R.P.; Ribeiro da Silva, M.D.M.C.; Reinhardt, J.; Klapötke, T.M. On the Enthalpy of Formation and Enthalpy of Sublimation of Dihydroxylammonium 5,5′-bitetrazole-1,1′-dioxide (TKX-50). Prop. Explos. Pyrotech. 2023, 48, e202200361. [Google Scholar] [CrossRef]
- Fischer, N.; Fischer, D.; Klapotke, T.M.; Piercey, D.G.; Stierstorfer, J. Pushing the limits of energetic materials—The synthesis and characterization of dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate. J. Mater. Chem. 2012, 22, 20418–20422. [Google Scholar] [CrossRef]
- Klapötke, T.M.; Cudziło, S.; Trzciński, W.A. An Answer to the Question about the Energetic Performance of TKX-50. Prop. Explos. Pyrotech. 2022, 47, e202100358. [Google Scholar] [CrossRef]
- Sinditskii, V.P.; Filatov, S.A.; Kolesov, V.I.; Kapranov, K.O.; Asachenko, A.F.; Nechaev, M.S.; Lunin, V.V.; Shishov, N.I. Combustion behavior and physico-chemical properties of dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate (TKX-50). Thermochim. Acta 2015, 614, 85–92. [Google Scholar] [CrossRef]
- Paraskos, A. Tracking Sensitive Intermediates by In Situ FTIR for the Safe Synthesis of Energetic Materials. In METTLER TOLEDO R&D and Process Development in the Pharmaceutical and Chemical Industries Seminar; The Hyatt New Brunswick: New Brunswick, NJ, USA, 2016. [Google Scholar]
- Kon’kova, T.S.; Matyushin, Y.N.; Vakhtina, A.I.; Miroshnichenko, E.A.; Asachenko, A.F.; Dzevakov, P.B.; Shishov, N.I. Proceedings of the All-Russian Scientific and Technical Conference ‘Advances Special Chemistry and Chemical Technology; The Russian University of Chemical Technology: Moscow, Russia, 2015. [Google Scholar]
- Keicher, T.; Antes, J.; Gerber, P.; Hafner, S.; Schaller, U. TKX-50—The new kid on the block. In Proceedings of the ICT-Symposium: Treib- und Explosivstoffworkshop, Fraunhofer ICT, Pfinztal, Germany, 20–21 November 2018. [Google Scholar]
- Glasser, L.; Jenkins, H.D.B.; Klapötke, T.M. Is the Volume-Based Thermodynamics (VBT) Approach Valid for the Estimation of the Lattice Enthalpy of Salts Containing the 5,5′-(Tetrazolate-1 N-oxide) Dianion? Z. Anorg. Allg. Chem. 2014, 640, 1297–1299. [Google Scholar] [CrossRef]
- Christopher, I.L.; Michalchuk, A.A.L.; Pulham, C.R.; Morrison, C.A. Towards computational screening for new energetic materials: Calculation of heat of formation and determination of bond strengths by local mode analysis. Front. Chem. 2021, 9, 726357. [Google Scholar] [CrossRef]
- Gao, H.; Ye, C.; Pikarski, C.M.; Shreeve, J.M. Computational characterization of energetic salts. J. Phys. Chem. C 2007, 111, 10718–10731. [Google Scholar] [CrossRef]
- Khakimov, D.V.; Pivina, T.S. Calculated enthalpies of formation of 5,5′-bitetrazole salts. Mendeleev Commun. 2016, 26, 134–135. [Google Scholar] [CrossRef]
- Hammerl, A.; Hiskey, M.A.; Holl, G.; Klapötke, T.M.; Polburn, K.; Stierstorfer, J.; Weigan, J.J. Azidoformamidinium and Guanidinium 5,5′-Azotetrazolate Salts. Chem. Mater. 2005, 17, 3784–3793. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Ribeiro da Silva, M.D.M.C.; Pilcher, G. The construction, calibration and use of a new high-precision static-bomb calorimeter. Rev. Port. Quim. 1984, 26, 163–172. [Google Scholar]
- Ribeiro da Silva, M.A.V.; Ribeiro da Silva, M.D.M.C.; Pilcher, G. Enthalpies of combustion of 1,2-hydroxybenzene and of six alkylsubstituted 1,2-dihydroxybenzenes. J. Chem. Thermodyn. 1984, 16, 1149–1155. [Google Scholar] [CrossRef]
- Hubbard, W.N.; Scott, D.W.; Waddington, G. Standard states and corrections for combustions in a bomb at constant volume. In Experimental Thermochemistry. Measurement of Heats of Reaction, 1st ed.; Rossini, F.D., Ed.; Interscience Publishers, Inc.: New York, NY, USA, 1956; Volume 1, pp. 75–128. [Google Scholar]
- Montgomery, J.A., Jr.; Frisch, M.J.; Ochterski, J.W.; Petersson, G.A. A complete basis set model chemistry. VII. Use of the minimum population localization method. J. Chem. Phys. 2000, 112, 6532–6542. [Google Scholar] [CrossRef]
- Pickard, C.F., IV; Pokon, E.K.; Liptak, M.D.; Shields, G.C. Comparison of CBS-QB3, CBS-APNO, G2, and G3 thermochemical predictions with experiment for formation of ionic clusters of hydronium and hydroxide ions complexed with water. J. Chem. Phys. 2005, 122, 024302. [Google Scholar] [CrossRef]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I.; Bailey, S.M.; Churney, K.L.; Nuttall, R.L. The NBS Tables of Chemical Thermodynamics Properties. J. Phys. Chem. Ref. Data 1982, 11 (Suppl. S2), 2-37–2-380. [Google Scholar]
- NIST Computational Chemistry Comparison and Benchmark Database; Russell Johnson, D., III (Ed.) NIST Standard Reference Database Number 101, Release 16a; 2013. Available online: http://cccbdb.nist.gov/ (accessed on 1 October 2022).
- Acree, W., Jr.; Chickos, J.S. Phase transition enthalpy measurements of organic and organometallic compounds. Sublimation, vaporization and fusion enthalpies from 1880 to 2015. Part 1. C1–C10. J. Phys. Chem. Ref. Data 2016, 45, 033101. [Google Scholar] [CrossRef]
- NIST Webbook. Available online: https://webbook.nist.gov/chemistry/ (accessed on 10 October 2022).
- Domalski, E.S. Selected Values of Heats of Combustion and Heats of Formation of Organic Compounds Containing the Elements C, H, N, O, P and S. J. Phys. Chem. Ref. Data 1972, 1, 221–277. [Google Scholar] [CrossRef]
- Keshavarz, M.H. Energetic Materials Designing Bench (EMDB), version 2.0; Malek Ashtar University of Technology (MUT): Shahin Shar, Iran, 2021. [Google Scholar]
- Wahler, S.; Klapötke, T.M. Research output software for energetic materials based on observational modelling 2.1 (RoseBoom2.1©). Mater. Adv. 2022, 3, 7976–7986. [Google Scholar] [CrossRef]
- Hiskey, M.A.; Goldman, N.; Stine, J.R. High-nitrogen energetic materials derived from azotetrazolate. J. Energ. Mater. 1998, 16, 119–127. [Google Scholar] [CrossRef]
- Abe, M.; Ogura, T.; Miyata, Y.; Okamoto, K.; Date, S.; Kohga, M.; Hasue, K. Evaluation of Gas Generating Ability of Some Tetrazoles and Copper (II) Oxide Mixtures Through Closed Vessel Test and Theoretical Calculation. Sci. Technol. Energ. Mater. 2008, 69, 183–190. [Google Scholar]
- Sinditskii, V.P.; Bogdanova, L.E.; Kapravnoa, K.O.; Levshenkov, A.I.; Kolesov, V.I. High-Energy Salts of 5,5′-Azotetrazole. I. Thermochemistry and Thermal Decomposition. Combust. Expl. Shock Waves 2019, 55, 308–326. [Google Scholar] [CrossRef]
- Rossini, F.D. Assignment of uncertainties to thermochemical data. In Experimental Thermochemistry. Measurement of Heats of Reaction, 1st ed.; Rossini, F.D., Ed.; Interscience Publishers, Inc.: New York, NY, USA, 1956; Volume 1, pp. 297–325. [Google Scholar]
- Olofson, G. Assignment of uncertainties. In Combustion Calorimetry, 1st ed.; Sunner, S., Mansson, M., Eds.; Pergamon Press: Oxford, UK, 1979; Volume 1, pp. 137–159. [Google Scholar]
- Cox, J.D.; Wagman, D.D.; Medvedev, V.A. CODATA Key Values for Thermodynamics; Hemisphere: New York, NY, USA, 1979. [Google Scholar]
- Dorofeeva, O.V.; Ryzhova, O.N.; Sinditskii, V.P. Enthalpy of formation of guanidine and its amino and nitro derivatives. Struct. Chem. 2015, 26, 1629–1640. [Google Scholar] [CrossRef]
- Schaller, U.; Keicher, T.; Weiser, V.; Krause, H.; Schlechtriem, S. Synthesis, Characterization and Combustion of Triazolium Based Salts. In Proceedings of the Insensitive Munitions and Energetic Materials Technology Symposium, Munich, Germany, 11–14 October 2010. [Google Scholar]
- Kon’kova, T.S.; Matyushin, Y.N.; Miroshnichenko, E.A.; Voon’ev, A.B. Thermochemical properties of dinitramidic acid salts. Russ. Chem. Bull. Int. Ed. 2009, 58, 2020–2027. [Google Scholar] [CrossRef]
- Kon’kova, T.S.; Matyushin, Y.N. Thermochemical properties of the salts of picric and dinitrobenzoic acids. Russ. Chem. Bull. 1998, 47, 2387–2390. [Google Scholar] [CrossRef]
- Schmitt, R.J.; Bottaro, J.C.; Penwell, P.E. The Development of New Protecting/Leaving Groups and Application to the Synthesis of Cage Nitramines; SRI International Project 6654; US Office of Naval Research: Arlington, VA, USA, 1993. [Google Scholar]
- Östmark, H.; Bemm, U.; Langlet, A.; Sanden, R.; Wingborg, N. The Properties of Ammonium Dinitramide (AN): Part 1, Basic Properties and Spectroscopic Data. J. Energet. Mater. 2000, 18, 123–138. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Tarchoun, A.F.; Boukeciat, H.; Trache, D. Insight into the Thermodynamic Properties of Promising Energetic HNTO·AN Co-Crystal: Heat Capacity, Combustion Energy, and Formation Enthalpy. Energies 2022, 15, 6722. [Google Scholar] [CrossRef]
- Kon’kova, T.S.; Matyushin, Y.N. Combined study of thermochemical properties of nitroform and its salts. Russ. Chem. Bull. 1998, 47, 2371–2374. [Google Scholar] [CrossRef]
- Miroshnichenko, E.A.; Kon’kova, T.S.; Matyushin, Y.N. Thermochemistry of Primary Nitramines. Dokl. Phys. Chem. 2003, 392, 253–255. [Google Scholar] [CrossRef]
- Coops, J.; Jessup, R.S.; van Nes, K. Calibration of calorimeters for reactions in a bomb at constant volume. In Experimental Thermochemistry. Measurement of Heats of Reaction, 1st ed.; Rossini, F.D., Ed.; Interscience Publishers, Inc.: New York, NY, USA, 1956; Volume 1, pp. 27–58. [Google Scholar]
- Washburn, E.W. Standard states for bomb calorimetry. J. Res. Nat. Bur. Stand. 1933, 10, 525–558. [Google Scholar]
- Hurst, J.E.; Harrison, B.K. Estimation of liquid and solid heat capacities using a modified Kopps’rule . Chem. Eng. Commun. 1992, 112, 21–30. [Google Scholar]
| m(cpd)/g a | 0.25140 |
| m(fuse)/g b | 0.00252 |
| m(n-hexadec.)/g c | 0.25210 |
| Ti/K d | 298.1508 |
| Tf/K d | 299.1933 |
| ΔTad/K e | 0.95580 |
| εi/J·K−1 f | 16.31 |
| εf /J·K−1 f | 17.15 |
| −ΔU(IBP)/J g | 15,310.98 |
| ΔU(HNO3)/J h | 60.36 |
| ΔU(ign)/J i | 0.69 |
| ΔUΣ/J j | 5.11 |
| −ΔU(n-hexadec.)/J k | 11,883.16 |
| −ΔU(fuse)/J l | 40.92 |
| −Δcu°/(J·g−1) m | 13,211.73 |
| Δcu°/(J·g−1) | −13,205.4 |
| −13,225.8 | |
| −13,206.6 | |
| −13,223.6 | |
| −13,188.9 | |
| −13,211.7 | |
| <Δcu°>/(J·g−1) | −(13,210.3 ± 5.5) a |
| −3755.0 ± 3.2 | −3742.6 ± 3.2 | 453.6 ± 3.2 |
| Salt | / kJ·mol−1 | (base)/ kJ·mol−1 | (acid)/ kJ·mol−1 | /kJ·mol−1 |
|---|---|---|---|---|
| NH3OH+NO3− | −366.5 [24] | NH2OH(s) = −114.2 [24] | HNO3(l) = −174.10 [24] | −78.2 |
| NH4+NO3− | −365.56 [24] | NH3(g) = −46.11 [24] | HNO3(l) = −174.10 [24] | −145.35 |
| C(NH2)3+NO3− | −386.94 [24] | guanidine(s) = −56.1 [24] | HNO3(l) = −174.10 [24] | −156.8 |
| AG+NO3− | −278.7 [37] | AG(s) = +58.5 [37] | HNO3(l) = −174.10 [24] | −163.1 |
| DAG+NO3− | −157.3 [24] | DAG(s) = +167.4 [37] | HNO3(l) = −174.10 [24] | −150.6 |
| TAG+NO3− | −50.2 [37] | TAG(s) = +287.7 [37] | HNO3(l) = −174.10 [24] | −163.8 |
| 5-AT+NO3− | −27.6 [24] | 5-AT(s) = +207.9 [24] | HNO3(l) = −174.10 [24] | −61.4 |
| N2H5+NO3− | −251.58 [24] | N2H4(l) = +50.63 [24] | HNO3 (l) = −174.10 [24] | −128.1 |
| (H2N)2COH+NO3− | −564.0 [24] | urea(cr) = −333.51 [24] | HNO3(l) = −174.10 [24] | −56.39 |
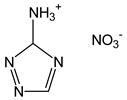 3-amino-1,2,4-triazolium+NO3− | −171.1 [24] | 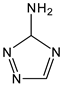 3-amino-1,2,4-triazole (s) = +77.0 [24] | HNO3(l) = −174.10 [24] | −74 |
| Anilinium+NO3− | −182. [27] | aniline (l) = +31.3 [27] | HNO3(l) = −174.10 [24] | −40 |
| EtNH3+NO3− | −366.9 [24] | EtNH2(l) = −74.1 [24] | HNO3(l) = −174.10 [24] | −118.7 |
| Me2NH2+NO3− | −352.0 [24] | Me2NH(l) = −43.9 [27] | HNO3(l) = −174.10 [24] | −134.0 |
| Me3NH+NO3− | −343.9 [24] | Me3N(l) = −46.0 [24] | HNO3(l) = −174.10 [24] | −123.8 |
| MeNH3+NO3− | −354.4 [24] | MeNH2(l) = −47.3 [24] | HNO3(l) = −174.10 [24] | −132.6 |
| Et2NH2+NO3− | −418.8 [24] | Et2NH(l) = −103.3 [24] | HNO3(l) = −174.10 [24] | −141.7 |
| Et3NH+NO3− | −447.7 [37] | Et3N(l) = −169.0 [27] | HNO3(l) = −174.10 [24] | −104.6 |
 4-amino-1,2,4-triazolium nitrate | +2 [38] | 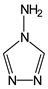 4-amino-1,2,4-triazole(s) = +223.13 [39] | HNO3(l) = −174.10 [24] | −47.03 |
| Compound | (Jenkins) | CBS-4M/Jenkins | Salt | Neutral Adduct | Average of Salt + Adduct | 80:20 | Exptl. Value | Δ (Exptl. and 80:20 Values) |
|---|---|---|---|---|---|---|---|---|
| TKX-50 | 2 × +685.8 1 × +566.8 −1488.95 | +449.45 | +168.1 | +302.3 | +235.2 | +194.94 | +193 (average) [7] | +1.94 |
| TKX-50 | 2 × +685.8 1 × +566.8 −1488.95 | +449.45 | +156.2 | +290.4 | +223.3 | +183.04 | +193 (average) [7] | −9.96 |
| GZT | 2 × 570.31 1 × +770.5 −1287.98 | +623.14 | +380.6 | +521.2 | +450.9 | +408.72 | +410 [31] +452 [32] +387 [33] | −1.28, −43.28, +21.72 |
| AG2AzT | 2 × 669.73 1 × +770.5 −1246.01 | +863.95 | +597.2 | +739.9 | +668.55 | +625.74 | +462 [31], +434 [32], +782 [32] | +163.74, +191.74 −156.26 |
| DAG2AzT | 2 × 814.9 1 × +770.5 −1215.11 | +1185.19 | +840 | +1021.23 | +930.62 | +876.25 | +709 [32] | +167.25 |
| TAG2AzT | 2 × 923.88 1 × +770.5 −1177.40 | +1440.9 | +11,054.2 | +1199.6 | +1126.9 | +1083.28 | +1075 [31], +1065 [32] | +8.28, +18.28 |
| (NH4)2AzT | 2 × 634.6 1 × +770.5 −1467.43 | +572.27 | +423.48 | +610.8 | +517.14 | +460.94 | +443.9 [32] +452 [32] | +17.04, +8.94 |
| (N2H5)2AzT | 2 × +772.48 1 × +770.5 — | density unknown | +651.5 | +794.4 | +722.95 | +680.08 | +659 [32] | +21.08 |
| G2CO3 | 2 × +570.31 1 × −247.78 −1415.0 | −522.16 | −1033.58 | −889.1 | −961.34 | −1004.68 | −971.1 [27] | −33.58 |
| (NH4)2SO4 | 2 × +634.6 1 × −608.8 −1806.74 | −1146.34 | −1196.9 | −948.97 | −1072.94 | −1147.31 | −1180.9 [24] | +33.59 |
| (NH3OH)2SO4 | 2 × +685.8 1 × −608.8 −1712.2 | −949.2 | −1200.0 | −1076.09 | −1138.05 | −1175.2 | −1181.98 [24] | +6.78 |
| (NH4)2C2O4 | 2 × +634.6 1 × −566.21 — | density unknown | −1210.2 | −981.43 | −1095.82 | −1164.45 | −1123.0 [24] | −41.45 |
| Compound | (Jenkins) | CBS-B3/ Jenkins | Salt | Neutral Adduct | Average of Salt + Adduct | 80:20 | Exptl. Value | Δ (Exptl. and 80:20 Values) |
|---|---|---|---|---|---|---|---|---|
| TKX-50 | 2 × +669.2 1 × +541.05 −1488.95 | +390.5 | +168.3 | +240.49 | +204.4 | +182.74 | +193 (average) [7] | −10.26 |
| TKX-50 | 2 × +669.2 1 × +541.05 −1488.95 | +390.5 | +168.3 | +252.39 | +210.3 | +185.12 | +193 (average) [7] | −7.88 |
| GZT | 2 × 570.31 1 × +790.5 −1287.98 | +643.14 | +374.2 | +532.37 | +453.3 | +405.83 | +410 [31], +452 [32], +387 [33] | −4.17, +18.83, −46.17 |
| AG2AzT | 2 × 668.9 1 × +790.5 −1246.01 | +882.29 | −509.8 | +737.9 | +664.4 | +620.22 | +462 [32], +434 [32], +782 [32] | +158.22, +186.22, −161.78 |
| DAG2AzT | 2 × 813.1 1 × +790.5 −1215.11 | +1201.59 | +833.6 | +885.56 | +859.6 | +843.99 | +709 [32] | +134.99 |
| TAG2AzT | 2 × 920.8 1 × +790.5 −1177.40 | +1454.7 | +1047.8 | +1167.04 | +1107.42 | +1071.65 | +1075 [31], +1065 [32] | −3.35, +6.65 |
| (NH4)2AzT | 2 × 632.12 1 × +790.5 −1467.43 | +587.31 | +417.08 | +623.03 | +520.1 | +458.27 | +443.9 [32], +452 [32], +551 [32] | +14.37, +6.27, −92.73 |
| (N2H5)2AzT | 2 × 765.52 1 × +790.5 - | density unknown | +645.06 | +784.88 | +714.97 | +673.02 | +659 [32] +858 [32] | +14.02, −184.98 |
| G2CO3 | 2 × +570.31 1 × −232.2 −1415.0 | −505.68 | −1044.6 | −902.36 | −973.48 | −1016.15 | −971.1 [27] | −45.05 |
| (NH4)2SO4 | 2 × +632.12 1 × −607.3 −1806.74 | −1149.8 | −1196.9 | −989.22 | −1093.1 | −1155.36 | −1180.9 [24] | +25.54 |
| (NH3OH)2SO4 | 2 × +669.2 1 × −607.3 −1712.2 | −981.1 | −1200.0 | −1143.6 | −1171.8 | −1188.72 | −181.98 [24] | −6.74 |
| Compound | (Jenkins) | CBS-4M/Jenkins | Salt | Neutral Adduct | Average of Salt + Adduct | 80:20 | Exptl. Value | Δ (Exptl. and 80:20 Values) |
|---|---|---|---|---|---|---|---|---|
| NH4+C(NO2)3− | +634.59 −219.3 −531.92 | −116.6 | −239.7 | −113.7 | −176.7 | −214.5 | −197.9 [39] | −16.6 |
| NH4+N3− | +634.59 +188.96 −660.0 | +163.55 | +72.54 | +202.56 | +137.55 | +98.54 | +115.6 [24] | −17.06 |
| NH4+HCO2− | +634.59 −481.0 −638.99 | −485.4 | −616.18 | −495.3 | −555.74 | −592.0 | −567.48 [24] | −24.52 |
| NH4+HCO3− | +634.59 −735.70 −639.70 | −740.81 | −891.11 | −740.29 | −815.7 | −860.9 | −849.4 [24] | −11.5 |
| NH4+CH3COO− | +634.59 −523.13 −591.78 | −480.32 | −675.96 | −558.97 | −617.47 | −652.6 | −616.14 [24] | −36.46 |
| NH4+picrate− | +634.59 −376.1 −480.15 | −221.6 | −409.36 | −288.01 | −348.69 | −385.09 | −400.9, −389, −377.2 [40] | +15.31, +3.91, −7.89 |
| NH4+3,5-dinitrobenzoate− | +634.59 −546.2 −486.10 | −397.7 | −624.06 | −571.44 | −597.75 | −613.5 | −500.8 [40] | −112.7 |
| NH4+N(NO2)2− | +634.59 −123.93 −585.49 | −74.83 | −137.06 | +1.09 | −67.99 | −109.43 | −148 [41,42] | +38.57 |
| NH4+H2NCOO− | +634.59 −521.5 −617.47 | −504.38 | −738.46 | −518.3 | −628.38 | −694.43 | −645.05 [24] | −49.38 |
| NH4+H2NCOO− | +634.59 −521.5 −617.47 | −504.38 | −626.16 | −630.6 | −628.4.23 | −627.0 | −645.05 [24] | +18.05 |
| (H2N)3C+picrate− | +570.31 −376.1 −444.73 | −250.5 | −430.8 | −384.8 | −407.8 | −421.6 | −396.6 [43] | −25.0 |
| (H2N)3C+N(NO2)2− | +570.31 −123.93 −529.24 | −82.86 | −158.5 | −90.08 | −124.29 | −166.4 | −157.8, −170.3 [39] | −8.6, +3.9 |
| (H2N)3C+3,5-dinitrobenzoate− | +570.31 −546.2 −460.0 | −435.9 | −645.5 | −588.5 | −617 | −634.1 | −593.5 [40] | −40.6 |
| AG+N(NO2)2− | +669.73 −123.93 — | density unknown | −50.9 | +17.81 | −16.45 | −37.16 | −44 [39] | +6.84 |
| TAG+N(NO2)2− | +923.88 −123.93 −488.07 | +311.88 | +178.3 | +263.7 | +221 | +195.38 | +182.9 [39] | −12.48 |
| N2H5+C(NO2)3− | +772.48 −219.3 −532.0 | +21.18 | −125.67 | −7.2 | −66.44 | −101.98 | −71.69, −76.9 [44] | −30.29, −25.08 |
| N2H5+NTO− | +772.48 −203.49 −545.0 | +23.98 | −206.87 | −125.2 | −166.04 | −190.54 | −231.4 [43] | +40.86 |
| N2H5+N(NO2)2− | +772.48 −123.93 −568.86 | +79.69 | −23.07 | +83.47 | +30.2 | −1.76 | −13.6 [39] | +11.84 |
| N2H5+CH3NNO2− | +772.48 −106.49 — | density unknown | −128.76 | −34.18 | −81.47 | −109.84 | −74.43 [45] | −35.41 |
| NH3OH+N(NO2)2− | +685.76 −123.93 — | density unknown | −138.6 | −64.67 | −101.64 | −123.81 | −139 [41,42] | +15.19 |
| Compound | (Jenkins) | CBS-4M / Jenkins | Salt | neutral Adduct | Average of Salt + Adduct | 80:20 | Exptl. Value | Δ (Exptl. and 80:20 Values) |
|---|---|---|---|---|---|---|---|---|
| NH4+C(NO2)3− | +632.12 −243.16 −531.92 | −142.96 | −239.66 | −144.95 | −192.31 | −220.72 | −197.9 [44] | −22.82 |
| NH4+N3− | +632.12 +190.84 −660.0 | +163.0 | +82.38 | +193.7 | +138.04 | +104.6 | +115.6 [24] | +11 |
| NH4+HCO2− | +632.12 −481.0 −638.99 | −482.5 | −616.18 | −505 | −560.59 | −593.94 | −567.48 [24] | −26.46 |
| NH4+HCO3− | +632.12 −735.70 −639.70 | −742.92 | −891.11 | −743.57 | −817.34 | −861.60 | −849.4 [24] | −12.2 |
| NH4+CH3COO− | +632.12 −511.21 −591.78 | −470.87 | −675.96 | −560.12 | −618.04 | −652.79 | −616.14 [24] | −36.65 |
| NH4+picrate− | +632.12 −376.1 −480.15 | −240.01 | −409.36 | −324.91 | −367.14 | −392.47 | −400.9, −389 [40] −377.2 | +8.43, −3.47, −15.27 |
| NH4+N(NO2)2− | +632.12 −123.93 −585.49 | −95.75 | −157.33 | −59.27 | −108.3 | −137.72 | −148 [41,42] | +10.28 |
| NH4+H2NCOO− | +632.12 −521.5 −617.45 | −501.63 | −741.21 | −524.89 | −633.1 | −697.9 | −645.05 [24] | −52.9 |
| NH4+H2NCOO− | +632.12 −521.5 −617.45 | −501.63 | −629.91 | −637.19 | −633.6 | −636.5 | −645.05 [24] | +8.55 |
| (H2N)3C+N(NO2)2− | +570.31 −123.93 −529.24 | −101.31 | −178.77 | −123.39 | −151.08 | −167.69 | −157.8, −170.3 [39] | −9.89, +2.61 |
| N2H5+C(NO2)3− | +765.52 −243.16 −532.0 | −9.64 | −125.67 | −51 | −88.34 | −110.74 | −71.69, −76.9 [44] | −39.05, −33.84 |
| N2H5+NTO− | +765.52 −204.4 −545.0 | +16.1 | −206.87 | −135.01 | −170.94 | −192.50 | −231.4 [43] | +38.9 |
| N2H5+N(NO2)2− | +765.52 −142.38 −568.86 | +54.32 | −43.34 | +33.8 | −4.77 | −27.91 | −13.6 [39] | −14.31 |
| N2H5+CH3NNO2− | +765.52 −113.42 — | density unknown | −138.47 | −47.71 | −93.09 | −120.32 | −74.43 [45] | −45.89 |
| NH3OH+N(NO2)2− | +669.15 −142.38 — | density unknown | −158.87 | −104.19 | −131.53 | −147.93 | −139 [41,42] | −8.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, A.L.R.; León, G.P.; Ribeiro da Silva, M.D.M.C.; Klapötke, T.M.; Reinhardt, J. Enthalpy of Formation of the Nitrogen-Rich Salt Guanidinium 5,5′-Azotetrazolate (GZT) and a Simple Approach for Estimating the Enthalpy of Formation of Energetic C, H, N, O Salts. Thermo 2023, 3, 549-565. https://doi.org/10.3390/thermo3040033
Silva ALR, León GP, Ribeiro da Silva MDMC, Klapötke TM, Reinhardt J. Enthalpy of Formation of the Nitrogen-Rich Salt Guanidinium 5,5′-Azotetrazolate (GZT) and a Simple Approach for Estimating the Enthalpy of Formation of Energetic C, H, N, O Salts. Thermo. 2023; 3(4):549-565. https://doi.org/10.3390/thermo3040033
Chicago/Turabian StyleSilva, Ana L. R., Gastón P. León, Maria D. M. C. Ribeiro da Silva, Thomas M. Klapötke, and Jelena Reinhardt. 2023. "Enthalpy of Formation of the Nitrogen-Rich Salt Guanidinium 5,5′-Azotetrazolate (GZT) and a Simple Approach for Estimating the Enthalpy of Formation of Energetic C, H, N, O Salts" Thermo 3, no. 4: 549-565. https://doi.org/10.3390/thermo3040033
APA StyleSilva, A. L. R., León, G. P., Ribeiro da Silva, M. D. M. C., Klapötke, T. M., & Reinhardt, J. (2023). Enthalpy of Formation of the Nitrogen-Rich Salt Guanidinium 5,5′-Azotetrazolate (GZT) and a Simple Approach for Estimating the Enthalpy of Formation of Energetic C, H, N, O Salts. Thermo, 3(4), 549-565. https://doi.org/10.3390/thermo3040033









