Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy” Part IV
Abstract
1. Introduction
2. Experimental Data and Computational Methods
2.1. Experimental Data
j = 1,N
2.2. Computational Methods
3. Breakdown of the GC Approach When Achieving Chemical Accuracy
3.1. Ring Strain
3.1.1. Ring Strain Evaluated from Group Contribution Involving Experimental Heats of Formation
Σ Group Contribution of constituting Groups + strain energy
| Cycloalkanes/Cycloalkenes | Exp. Rossini et al. [31,32,33,34,35,36] | Exp. Origin see Table S3 | Model dHf | Model-Exp + G4 Ring Strain | G4 Ring Strain | G4 dHf | Boltzmann-Averaged G4 dHf | Final Model-Exp. (or G4) |
|---|---|---|---|---|---|---|---|---|
| cyclopropane | 53.3 ± 0.6 | −61.89 | 0.2 | 115.4 | 53.7 | −0.6 | ||
| cyclobutane | 28.4 ± 0.6 | −82.52 | −0.9 | 110.0 | 27.8 | −0.3 | ||
| cyclopentane | −77.3 ± 0.8 | −103.15 | 3.6 | 29.4 | −73.4 | 0.7 | ||
| cyclohexane | −123.2 ± 0.8 | −123.78 | 0.6 | 1.2 | −121.1 | −4.2 | ||
| methylcyclopropane | 25.0 | −91.62 | −0.6 | 116 | 24.3 | −0.9 | ||
| ethylcyclopropane | 3.2 | −112.25 | −1.1 | 114.4 | 2.1 | 2.3 | 3.8 | |
| propylcyclopropane | −132.88 | 0.0 | 113.5 | −19.4 | −18.4 | 1.5 | ||
| isopropylcyclopropane | −137.98 | 4.3 | 113.2 | −29.1 | −28.4 | 6.1 | ||
| methylcyclobutane | −6.8 | −112.25 | 1.1 | 106.5 | −5.8 | −5.0 | −4.2 | |
| ethylcyclobutane | −26.3 | −132.88 | −1.8 | 104.8 | −28.1 | −27.1 | −2.5 | |
| propylcyclobutane | −153.51 | −0.1 | 103.7 | −49.7 | −47.9 | −1.5 | ||
| isopropylcyclobutane | −158.61 | 4.3 | 102.9 | −60.0 | −59.0 | 3.7 | ||
| methylcyclopentane | −106.7 ± 0.8 | −132.88 | 1.5 | 27.7 | −102.4 | −102.7 | −4.0 | |
| ethylcyclopentane | −127.1 ± 1.0 | −153.51 | 0.8 | 27.2 | −126.2 | −125.7 | −0.8 | |
| propylcyclopentane | −148.2 ± 1.3 | −174.14 | −0.1 | 25.8 | −148.1 | −147.4 | 0.5 | |
| isopropylcyclopentane | −179.24 | 4.2 | 27.5 | −155.9 | −153.6 | 3.2 | ||
| methylcyclohexane | −154.9 ± 1.0 | −153.51 | 0.0 | −1.4 | −154.8 | −2.2 | ||
| propylcyclohexane | −193.4 ± 1.3 | −194.77 | −2.4 | −0.9 | −195.4 | −194.3 | −3.0 | |
| isopropylcyclohexane | −199.87 | 4.1 | 6.4 | −197.6 | −197.5 | −5.9 | ||
| 1,1-dimethylcyclopropane | −8.2 ± 1.2 | −123.98 | 1.6 | 114.1 | −11.5 | 2.5 | ||
| cis-1,2-dimethylcyclopropane | 0.7 | −117.55 | 3.8 | 122.1 | 0.3 | −2.8 | ||
| trans-1,2-dimethylcyclopropane | −3.2 | −117.55 | 2.0 | 116.3 | −5.4 | 2.9 | ||
| 1,1-dimethylcyclobutane | −143.61 | 2.6 | 104.1 | −42.1 | 0.8 | |||
| cis-1,2-dimethylcyclobutane | −138.18 | 4.2 | 109.1 | −33.3 | −2.9 | |||
| trans-1,2-dimethylcyclobutane | −138.18 | 4.1 | 102.2 | −40.1 | 3.7 | |||
| cis-1,3-dimethylcyclobutane | −138.18 | 4.1 | 103.4 | −38.9 | 3.0 | |||
| trans-1,3-dimethylcyclobutane | −138.18 | 4.2 | 106.9 | −35.5 | −0.4 | |||
| 1,1-dimethylcyclopentane | −138.3 ± 1.2 | −165.24 | −0.2 | 26.7 | −140.1 | −139.4 | −0.4 | |
| 1,2-dimethylcyclopentane cis | −129.5 ± 1.3 | −158.81 | 2.2 | 31.5 | −131.4 | −130.2 | −2.8 | |
| 1,3-dimethylcyclopentane trans | −135.9 ± 1.2 | −158.81 | 5.1 | 28 | −134.8 | 3.6 | ||
| 1,2-dimethylcyclopentane trans | −136.7 ± 1.3 | −158.81 | 3.3 | 25.4 | −137.5 | 4.4 | ||
| 1,3-dimethylcyclopentane cis | −133.7 ± 1.5 | −158.81 | 1.8 | 26.9 | −136 | 1.4 | ||
| cis-1,3-dimethylcyclohexane | −179.44 | 4.0 | −4 | −187.4 | 4.4 | |||
| trans-1,4-dimethylcyclohexane | −179.44 | 4.1 | −3.6 | −187.1 | 4.1 | |||
| cis-1,3,5-trimethylcyclohexane | −212.97 | 0.5 | −6.5 | −220 | 3.4 | |||
| methylenecyclopropane | 201 | 28.74 | −4.0 | 157.7 | 190.4 | |||
| methylenecyclobutane | 121.6 | 8.11 | 3.3 | 116.8 | 120.3 | |||
| methylenecyclopentane | 12 ± 1.1 | −12.52 | 2.6 | 27.1 | 10.0 | |||
| cyclopropene | 277 | 50.87 | −0.9 | 230.4 | 282.2 | |||
| cyclobutene | 157 | 30.24 | −0.1 | 130.1 | 160.4 | |||
| cyclopentene | 33 | 9.61 | 1.9 | 25.3 | 35.1 | |||
| cyclohexene | −5.3 | −11.02 | 0.0 | 5.7 | −5 | |||
| 4-methylcyclopentene | −16.12 | 4.2 | 25.6 | 5.3 | 5.1 | |||
| 3-methylcyclopentene | 8 ± 2 | −16.12 | 0.4 | 24.5 | 5.1 | 5.7 | ||
| 1-methylcyclopentene | −4 ± 2 | −3.80 | −32.75 | −5.3 | 23.5 | −4.4 | ||
| 1-methylcyclopropene | 243.6 | 8.51 | −5.6 | 223.9 | 238.0 |
3.1.2. Discussion and Conclusions on How to Tackle Ring Strain
- -
- The isopropylcycloalkanes seem systematically off the GC prediction by 4.2 kJ/mol (Table 1, column 5). The Boltzmann-averaged G4 enthalpies did show some improvement but not for all. One could introduce an additional parameter correcting all isopropylalkanes by 4.2 kJ/mol and obtain very good agreement between the model and the experiment. However, as the deviation is not much beyond chemical accuracy and we do not have more than four experimental values, it seems more appropriate to suggest further studies including other substituted cycloalkanes before introducing an additional parameter. Therefore, at present, the isopropylalkanes are excluded from the conclusions on the other cycloalkanes discussed below.
- -
- For cyclopropane, a single alkyl substitution has a small influence on the ring strain, which is around 115 kJ/mol independent of the alkyl chain length. When we consider all cyclopropanes in Table 1, we do not see very large deviations. It should be mentioned here that, in part, we cannot compare with experimental data and need to rely on a mix of experimental and G4-calculated data. When we take the GC model value and add a ring strain of 115 kJ/mol for all substituted cyclopropanes, we obtain heats of formation within chemical accuracy from the G4-computed result. This even applies for cis-1,2-dimethylcyclopropane for which the G4 ring strain as such was calculated as 122 kJ/mol and therewith is clearly larger than for all other cyclopropanes.
- -
- For cyclobutane, the ring strain slowly drops with the lengthening of the alkyl chain, 6 kJ/mol from cyclobutane up till propylcyclobutane, but levels off with longer alkyl chain length. For the mono- and di-methyl-substituted cyclobutanes, the ring strain is roughly constant and around 103 kJ/mol. Again, the exception is cis-1,2-dimethylcyclobutane, with a G4-calculated ring strain of 109.1 kJ/mol being somewhat higher than those for other substituted cyclobutanes, but the overall result is still, albeit just, within chemical accuracy. The GC model does not (yet) discriminate between cis and trans in the current context. Still, when we take the GC model value and add a ring strain of 102.5 kJ/mol for the substituted cyclobutanes, we obtain a heat of formation within chemical accuracy from the G4-computed result. Only cyclobutane itself needs to be considered separately, but this is not a problem because for the isolated species, we can adopt the experimental value anyway.
- -
- For cyclopentane, the ring strain is almost constant with the lengthening of the alkyl chain.
- -
- For both the mono- as well as the dimethylcyclopentanes, we see pretty good agreement (column 4 in Table 1), but the G4 strain energies vary. Here, we observed a somewhat higher value for the G4-calculated ring strain for cis-1,2-dimethylcyclopentane. When we add to the pure GC approach, a strain energy of 26.5 kJ/mol throughout, we obtain chemical accuracy for all named species. Note that for most species, we rely on available experimental heat of formation data.
- -
- For the alkyl-substituted cyclohexanes, we observe similar trends as for the cyclopentanes: the results presented in Table 6 in [7] reveal, upon considering our GC model, that we find a very constant ring strain of −2 kJ/mol (note that it is indeed a minus sign!) for the series methylcyclohexane up till tetradecylcyclohexane, compared to 0.4 kJ/mol for the parent cyclohexane. Interestingly, the G4 results also suggest a small but negative ring strain for n-alkylcyclohexanes (see Table 1).
3.2. Selection of the Group Size: Problems with Systems Not Obeying ’Simple’ GC
3.3. Steric Hindrance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Krevelen, D.W.; Chermin, H.A.G. Estimation of the free enthalpy (Gibbs free energy) of formation of organic compounds from group contributions. Chem. Eng. Sci. 1951, 1, 66–80, Erratum in 1952, 1, 238. [Google Scholar] [CrossRef]
- Cohen, N.; Benson, S. Estimation of the heats of formation of organic compounds. Chem. Rev. 1993, 93, 2419–2438. [Google Scholar] [CrossRef]
- Joback, K.G.; Reid, R.C. Estimation of Pure-Component Properties from Group-Contributions. Chem. Eng. Commun. 1987, 57, 233–243. [Google Scholar] [CrossRef]
- Marrero, J.; Gani, R. Group-contribution based estimation of pure component properties. Fluid Phase Equilibria 2001, 183–184, 183–208. [Google Scholar] [CrossRef]
- Hukkerikar, A.S.; Meier, R.J.; Sin, G.; Gani, R. A method to estimate the enthalpy of formation of organic compounds with chemical accuracy. Fluid Phase Equilibria 2013, 348, 23–32. [Google Scholar] [CrossRef]
- Aouichaoui, A.R.N.; Fan, F.; Mansouri, S.S.; Abildskov, J.; Sin, G. Combining Group-Contribution Concept and Graph Neural Networks Toward Interpretable Molecular Property Models. J. Chem. Inf. Model. 2023, 63, 725–744. [Google Scholar] [CrossRef]
- Meier, R.J. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy”. ChemEngineering 2021, 5, 24. [Google Scholar] [CrossRef]
- Meier, R.J. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy” Part II. AppliedChem 2021, 1, 111–129. [Google Scholar] [CrossRef]
- Meier, R.J. Group contribution revisited: The enthalpy of formation of organic compounds with “chemical accuracy” Part III. AppliedChem 2022, 2, 213–228. [Google Scholar] [CrossRef]
- Kadda, A.; Mustapha, B.A.; Yahiaoui, A.; Khaled, T.; Hadji, D. Enthalpy of Formation Modeling Using Third Order Group Contribution Technics and Calculation by DFT Method. Int. J. Thermodyn. (IJoT) 2020, 23, 34–41. [Google Scholar] [CrossRef]
- ICS23 Software Package Which Includes the Marrero-Gani Method as Well as the Constantinou-Gani Approach and Also Provides Results Based on the Joback and Reid GC Method. Available online: https://www.kt.dtu.dk/english/research/kt-consortium/software (accessed on 21 February 2023).
- NIST Data Base. Available online: https://webbook.nist.gov/ (accessed on 16 March 2023).
- Chan, B. High-Level Quantum Chemistry Reference Heats of Formation for a Large Set of C, H, N, and O Species in the NIST Chemistry Webbook and the Identification and Validation of Reliable Protocols for Their Rapid Computation. J. Phys. Chem. A 2022, 126, 4981–4990. [Google Scholar] [CrossRef]
- Parthiban, S.; Martin, J.M.L. Assessment of W1 and W2 theories for the computation of electron affinities, ionization potentials, heats of formation, and proton affinities. J. Chem. Phys. 2001, 114, 6014. [Google Scholar] [CrossRef]
- Karton, A.; Daon, S.; Martin, J.M.L. W4-11: A high-confidence benchmark dataset for computational thermochemistry derived from first-principles W4 data. Chem. Phys. Lett. 2011, 510, 165–178. [Google Scholar] [CrossRef]
- Simmie, J.M.; Somers, K.P. Benchmarking compound methods (CBSQB3, CBS-APNO, G3, G4, W1BD) against the active thermochemical tables: A litmus test for cost-effective molecular formation enthalpies. J. Phys. Chem. A 2015, 119, 7235–7246. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian 4 theory using reduced order perturbation theory. J. Chem. Phys. 2007, 127, 1241. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, B.; Redfern, P.C.; Assary, R.S.; Curtiss, L.A. Accurate quantum chemical energies for 133,000 organic molecules. Chem. Sci. 2019, 10, 7449. [Google Scholar] [CrossRef] [PubMed]
- Konnova, M.E.; Li, S.; Bösmann, A.; Müller, K.; Peter Wasserscheid, P.; Andreeva, I.V.; Turovtzev, V.V.; Zaitsau, D.H.; Pimerzin, A.A.; Verevkin, S.P. Thermochemical Properties and Dehydrogenation Thermodynamics of Indole Derivates. Ind. Eng. Chem. Res. 2020, 59, 20539–20550. [Google Scholar] [CrossRef]
- Ghahremanpour, M.M.; van Maaren, P.J.; Ditz, J.C.; Lindh, R.; van der Spoel, D. Large-scale calculations of gas phase thermochemistry: Enthalpy of formation, standard entropy, and heat capacity. J. Chem. Phys. 2016, 145, 114305. [Google Scholar] [CrossRef]
- Gao, Y.; He, T.; Li, X.; You, X. Effect of hindered internal rotation treatments on predicting the thermodynamic properties of alkanes. Phys. Chem. Chem. Phys. 2019, 21, 1928–1936. [Google Scholar] [CrossRef]
- Rablen, P. A Procedure for Computing Hydrocarbon Strain Energies Using Computational Group Equivalents, with Application to 66 Molecules. Chemistry 2020, 2, 22. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Rablen, P.R. Increase in Strain Energy during Conversion of [4.4.4.5]Fenestrane to [4.4.4.4]Fenestrane: A Method for Estimating the Heats of Formation of Hydrocarbons and Their Derivatives from Ab Initio Energies. J. Org. Chem. 2020, 85, 4981–4987. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Peterson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Peterson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Saeys, M.; Reyniers, M.-F.; Marin, G.B.; VanSpeybroeck, V.; Waroquier, M. Ab Initio Calculations for Hydrocarbons: Enthalpy of Formation, Transition State Geometry, and Activation Energy for Radical Reactions. J. Phys. Chem. 2003, 107, 9147–9159. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Safronov, S.P.; Samarov, A.A.; Vostrikov, S.V. Hydrogen Storage: Thermodynamic Analysis of Alkyl-Quinolines and Alkyl-Pyridines as Potential Liquid Organic Hydrogen Carriers (LOHC). Appl. Sci. 2021, 11, 11758. [Google Scholar] [CrossRef]
- Wavefunction Inc. Spartan’10; Wavefunction Inc.: Irvine, CA, USA, 2010; Available online: https://www.wavefun.com/ (accessed on 21 February 2023).
- Anslyn, E.V.; Dougherty, D.A. Modern Physical Organic Chemistry; University Science Books: Sausalito, CA, USA, 2006; ISBN 1-891389-31-9. [Google Scholar]
- Knowlton, J.W.; Rossini, F.D. Heats of Combustion and Formation of Cyclopropane. J. Res. Natl. Bur. Stand. 1949, 43, 113–115. [Google Scholar] [CrossRef]
- Prosen, E.J.; Johnson, W.H.; Rossini, F.D. Heats of formation and combustion of the normal alkylcyclopentanes and cyclohexanes and the increment per CH2 group for several homologous series of hydrocarbons. J. Res. NBS. 1946, 37, 51–56. [Google Scholar] [CrossRef]
- Kilpatrick, J.E.; Werner, H.G.; Beckett, C.W.; Pitzer, K.S.; Rossini, F.D. Heats, Equilibrium Constants, and Free Energies of Formation of the Alkylcyclopentanes and Alkylcyclohexanes. J. Res. Natl. Bur. Stand. 1947, 39, 523–543. [Google Scholar] [CrossRef]
- Labbauf, A.; Rossini, F.D. Heats of combustion, formation, and hydrogenation of 14 selected cyclomonoolefin hydrocarbons. J. Phys. Chem. 1961, 65, 476–480. [Google Scholar] [CrossRef]
- Johnson, W.H.; Prosen, E.J.; Rossini, F.D. Heats of Combustion and Isomerization of the Six C7H14 Alkylcyclopentanes. J. Res. NBS 1949, 42, 251–255. [Google Scholar] [CrossRef]
- Good, W.D.; Moore, R.T.; Osborn, A.G.; Douslin, D.R. The enthalpies of formation of ethylcyclobutane, methylenecyclobutane, and 1,1-dimethylcyclopropane. J. Chem. Thermodyn. 1974, 6, 303–310. [Google Scholar] [CrossRef]
- Prosen, E.J.; Rossini, F.D. Heats of combustion and formation of the paraffin hydrocarbons at 25 °C. J. Res. Natl. Bur. Stand. 1945, 34, 263–269. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Fenoglio, R.A. Heats of formation of C4H6 hydrocarbons. J. Am. Chem. Soc. 1968, 90, 3395–3397. [Google Scholar] [CrossRef]
- Constantinou, L.; Gani, R. New group contribution method for estimating properties of pure compounds. AIChE J. 1994, 40, 1697–1710. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Vladimir, V.; Turovtsev, V.V.; Andreeva, I.V.; Orlovd, Y.D.; Pimerzin, A.P. Webbing a network of reliable thermochemistry around lignin building blocks: Tri-methoxybenzenes. RSC Adv. 2021, 11, 10727–10737. [Google Scholar] [CrossRef]
- Bystrom, K. The stabilization energy of 1,3,5-triazine derived from measurements of the enthalpies of combustion and sublimation. J. Chem. Thermodyn. 1982, 14, 865–870. [Google Scholar] [CrossRef]
- Iniguez, J.C.; Lopez, M.E.; McEachern, D.M. Vapor pressure and sublimation enthalpy of s-triazine. Rev. Soc. Quim. Mex. 1982, 26, 122–124. [Google Scholar]
- VanSpeybroeck, V.; Gani, R.; Meier, R.J. The calculation of thermodynamic properties of molecules. Chem. Soc. Rev. 2010, 39, 1764–1779. [Google Scholar] [CrossRef]
- Pedley, J.B.; Naylor, R.D.; Kirby, S.P. Thermochemical Data of Organic Compounds, 2nd ed.; Chapman & Hall: New York, NY, USA, 1986; pp. 1–792. ISBN 0412271001. [Google Scholar]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel’yanenko, V.N.; Diky, V.; Muzny, C.D.; Chirico, R.D.; Frenkel, M. New Group-Contribution Approach to Thermochemical Properties of Organic Compounds: Hydrocarbons and Oxygen-Containing Compounds. J. Phys. Chem. Ref. Data 2013, 42, 033102. [Google Scholar] [CrossRef]
- Prosen, E.J.; Johnson, W.H.; Rossini, F.D. Heats of combustion and formation at 25 °C of the alkylbenzenes through C10H14, and of the higher normal monoalkylbenzenes. J. Res. NBS 1946, 36, 455–461. [Google Scholar] [CrossRef]
- Brown, H.C.; Domash, L. Steric effects in displacement reactions. XI. The heats of reaction of diborane with pyridine bases. Steric strains in homomorphs of o-t-butyltoluene and hemimellitene. J. Am. Chem. Soc. 1956, 78, 5384–5386. [Google Scholar] [CrossRef]
- Roganov, G.N.; Pisarev, P.N.; Emel’yanenko, V.N.; Verevkin, S.P. Measurement and Prediction of Thermochemical Properties. Improved Benson-Type Increments for the Estimation of Enthalpies of Vaporization and Standard Enthalpies of Formation of Aliphatic Alcohols. J. Chem. Eng. Data 2005, 50, 1114–1124. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
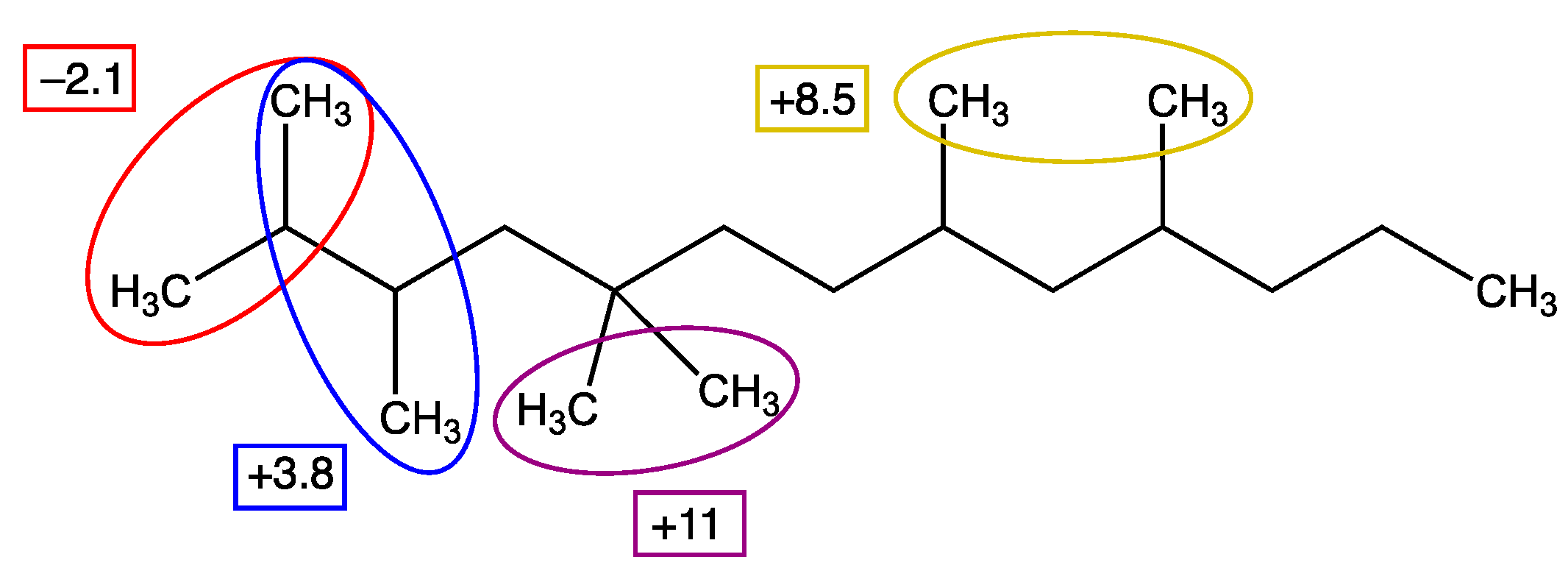



| Pyridines and Quinolines | Verevkin et al. [28] | Model dHf | Model-Exp | ABS (Model-Exp) |
|---|---|---|---|---|
| pyridine | 140.4 ± 0.7 | 142 * | 1.60 | 1.60 |
| 2-methylpyridine | 99.2 ± 0.8 | 99.64 | 0.44 | 0.44 |
| 3-methylpyridine | 106.4 ± 0.6 | 105.64 | −0.76 | 0.76 |
| 4-methylpyridine | 104.1 ± 0.9 | 105.64 | 1.54 | 1.54 |
| 2,3-dimethylpyridine | 68.3 ± 14 | 63.28 | −5.02 | 5.02 |
| 2,4-dimethylpyridine | 63.9 ± 0.9 | 63.28 | −0.62 | 0.62 |
| 2,5-dimethylpyridine | 66.5 ± 1.1 | 63.28 | −3.22 | 3.22 |
| 2,6-dimethylpyridine | 58.7 ± 1.6 | 57.28 | −1.42 | 1.42 |
| 3,4-dimethylpyridine | 70.7 ± 1.1 | 75.78 | 5.08 | 5.08 |
| 3,5-dimethylpyridine | 72.8 ± 1.0 | 75.78 | 2.98 | 2.98 |
| 2-ethylpyridine | 75.6 ± 3.5 | 79.01 | 3.41 | 3.41 |
| 3-ethylpyridine | 82.9 ± 3.5 | 85.01 | 2.11 | 2.11 |
| 4-ethylpyridine | 80.6 ± 3.5 | 85.01 | 4.41 | 4.41 |
| quinoline | 200.5 ± 1.0 | 197 * | −3.50 | 3.50 |
| 2-methylquinoline | 156.6 ± 0.9 | 160.64 | 4.04 | 4.04 |
| 4-methylquinoline | 158.6 ±2.7 | 160.64 | 2.04 | 2.04 |
| 6-methylquinoline | 157.3 ± 2.4 | 160.64 | 3.34 | 3.34 |
| 8-methylquinoline | 164.8 ± 1.3 | 160.64 | −4.16 | 4.16 |
| 2,6-dimethylquinoline | 121.3 ± 0.9 | 124.28 | 2.98 | 2.98 |
| 2,7-methylquinoline | 119.8 ± 3.1 | 124.28 | 4.48 | 4.48 |
| 2-phenylquinoline | 286.6 ± 4.5 | 287.5 | 0.90 | 0.90 |
| averaged absolute difference | 2.76 |
| Experimental dHf Difference kJ/mol | DFT Calculated Energy Difference kJ/mol | |
|---|---|---|
| 2-methylhexane and 3-methylhexane | 2.7 | 4.5 |
| 2,2-dimethylhexane and 2,3-dimethylhexane | 10.8 | 10.0 |
| 2,2-dimethylhexane and 2,4-dimethylhexane | 5 | 2.8 |
| 2,2-dimethylhexane and 2,5-dimethylhexane | 2 | −1.5 |
| 2,3-dimethylhexane and 2,4-dimethylhexane | 5.5 | 7.2 |
| 2,2,5-trimethylhexane and 2,3,4-trimethylhexane | 19 | 18.8 |
| 2,2,3,3,4-pentamethylpentane and 2,2,3,4,4-pentamethylpentane | 0.2 | 1.7 |
| t-Butyl Benzenes | Prosen and Rossini 1946 [47] | Brown et al. 1956 [48] | Model dHf | Model-Exp | ABS (Model-Exp) |
|---|---|---|---|---|---|
| t-butylbenzene | −22.7 ± 1.4 | −24.08 | −1.38 | 1.38 | |
| 4-tert-butyltoluene | −57 ± 2 | −53.94 | 3.06 | 3.06 | |
| 3-tert-butyltoluene | −54 ± 2 | −53.94 | 0.06 | 0.06 | |
| 2-tert-butyltoluene | −33 ± 2 | −27.94 | 5.06 | 5.06 | |
| averaged absolute difference | 2.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meier, R.J.; Rablen, P.R. Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy” Part IV. Thermo 2023, 3, 289-308. https://doi.org/10.3390/thermo3020018
Meier RJ, Rablen PR. Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy” Part IV. Thermo. 2023; 3(2):289-308. https://doi.org/10.3390/thermo3020018
Chicago/Turabian StyleMeier, Robert J., and Paul R. Rablen. 2023. "Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy” Part IV" Thermo 3, no. 2: 289-308. https://doi.org/10.3390/thermo3020018
APA StyleMeier, R. J., & Rablen, P. R. (2023). Group Contribution Revisited: The Enthalpy of Formation of Organic Compounds with “Chemical Accuracy” Part IV. Thermo, 3(2), 289-308. https://doi.org/10.3390/thermo3020018







