The Status of Pyrolysis Kinetics Studies by Thermal Analysis: Quality Is Not as Good as It Should and Can Readily Be

Abstract

This paper is a literature survey that focuses on the present development of thermokinetic publications. It demonstrates that in recent years pyrolysis kinetics has turned into a major application of the thermokinetics. Analysis of the respective publications suggests that too often their quality leaves much to be desired because of the poor choices of the kinetic methods and experimental conditions. It is explained that the proper choices can be made by following the recommendations of the International Confederation for Thermal Analysis and Calorimetry (ICTAC). To help with improving the quality of the kinetic results, the ICTAC recommendations are condensed to a few easy to follow principles. These principles focus on selecting proper computational methods, collecting better experimental data, and efficiently reporting the results. The paramount computational principle is to avoid using the methods that evaluate the activation energy and other kinetic parameters from the data measured at a single heating rate. It is shown that the kinetic parameters evaluated by such methods can give rise to striking examples of failure when estimating the thermal stability at ambient temperature. Because of the vital importance of pyrolysis kinetics studies from an ecological and economical perspective, a substantial improvement of their quality is currently needed.

1. Introduction

Thermal analysis is an invaluable tool to obtain the raw data for kinetic analysis of a target process. This field, also called thermokinetics, involves studies of widely differing subjects, e.g., crystallization, polymerization, pyrolysis and thermal decomposition processes [1,2,3,4]. The importance of thermokinetic analysis for plastic pyrolysis and scale-up has been already recognized [5,6,7,8]. The outcome of thermokinetic analysis, description of the process in terms of kinetic parameters and (often) reaction model, is in turn used in optimization of the thermochemical conversion conditions and other modeling efforts.

Conceptually, thermokinetic analysis relies on the thermal analysis methods and, thus, inherits their problems. One rather basic problem is the dual role of thermal analysis, which is used “as a set of research methods as well as for routine industrial monitoring… In the latter case, the operator does not in general want to have to make choices, and a fixed system is more appropriate” [9]. Unfortunately, the routine analysis approach shows its presence in kinetics as a tendency to perform kinetic analysis in sort of an automated mode, following some oversimplified algorithms (e.g., ASTM standards for kinetic analysis [10,11]). However, reactions of real-life systems usually involve several reaction steps and other complicating factors, such as phase transitions. Untangling the kinetic complexities of multi-step processes almost unavoidably turns kinetic analysis into a research activity even if the original purpose was routine. Although kinetic research does not have simple rules or algorithms that would automatically lead to a good result, there are some principles and practices, which can assist in significantly improving the chances of conducting successful kinetic analysis. Over the years, the thermal analysis and kinetics community has publicized such practices in the form of the ICTAC Kinetics Committee recommendations [1,12,13,14].

In this paper, we identify the trends in the current development of the thermokinetics by using bibliometric analysis tools [15]. Then, we analyze how the recent thermokinetic publications conform to the ICTAC recommendations. The hypothesis based on the authors’ personal experience as reviewers and readers of modern literature is that the development of the field is uneven, and that the quality of a significant fraction of publications does not reach the expected and readily accomplishable level. Finally, we formulate some easy to follow principles that will aid in improving the quality of the current thermokinetic research.

2. Results and Discussion

2.1. Overview of Thermokinetic Research Development

First, we gather the relevant data by searching the documents having the words “kinetic” and those related to thermal analysis (“thermal analysis”, “calorimetry”, etc.) in the title, abstract, and keywords from the Dimensions database [16]. Inspection of the results has revealed that some terms have to be added to the search query to exclude irrelevant research from the output [17]. Figure 1 illustrates that number of scientific publications on the topic grows over the years, reaching 1630 documents in 2021. For comparison, the search results with the same query from the Scopus database is also given. It also shows the expansion, with 1039 documents in 2021. The difference stems from different coverages by these two databases [18]. We use the output of the Dimensions database in discussion below, as its coverage is generally broader, and the usage of its output in bibliometric software (viz., VOSviewer [19]) is more straightforward.

The increase in thermokinetic publications described by unrestricted exponential growth model is approximately 6% per year. This growth rate results in a doubling of the number of documents every 12 years. To compare, the recent calculation of the production growth rate over different scientific fields shows a 4.1% rate and a doubling period of 17 years [20]. Thus, the acceleration of thermokinetic research is nearly equal to that found for thermophysical properties publications (7% [21]), and it considerably exceeds the overall growth rate of modern science in general.

Figure 2 shows the collaboration between authors from different countries in 2000 and 2021. The figure clearly shows that research in the field has become more global. It also shows that the center of the research activities in the field has shifted markedly from the USA and Europe to Asia.

Figure 3 and Figure 4 show the results of co-word analysis of publications from 2000 and 2021, respectively. Each circle (node) in figure represents the popular term (keyword) extracted from title and abstract of the analyzed documents. Thesaurus file was prepared to exclude the non-informative terms (e.g., “ability”, “addition”) and merge the synonym terms (e.g., “thermogravimetry”, “thermogravimetric analysis”, “TG”, and “TGA”). The size of circle is proportional to the occurrence of a specific term, also words are automatically grouped in thematic clusters. Three thematic clusters are observed for research from 2000. The cluster filled by the blue color is linked with investigations of crystallization and glass transition of mainly polymers. The green cluster comprises the research where differential scanning calorimetry (DSC) is involved, the keywords associated with a process are polymerization and curing, and the third thematic cluster, marked as red, is dedicated to research with thermogravimetric analysis (TGA) as a primary tool, and main processes are pyrolysis and degradation.

Figure 4 shows how thermokinetic research has developed over time. By 2021 the cluster focused on pyrolysis studies becomes more dominant. Key words of this (red) cluster are “TGA” (prevailing thermoanalytical method), heating rate (as most studies involve linear heating temperature program), “FWO” (Flynn–Wall–Ozawa kinetic method), “waste” (a lot of studies are focused on waste disposal by pyrolysis). On the other hand, the second dominant cluster (green, Figure 4) comprises studies mainly using DSC, and auxiliary techniques (“SEM” for scanning electron microscopy, “XRD” for X-ray diffraction analysis etc.), the keywords associated with subjects are “alloy”, “glass”, “polymer”.

To further explore the rise of thermokinetic studies focused on pyrolysis, we analyze the document sources.

Table 1. Number of documents and citations by journal title, for thermokinetic papers published at 2000 and 2021 (only top ten journals by publications number are shown).

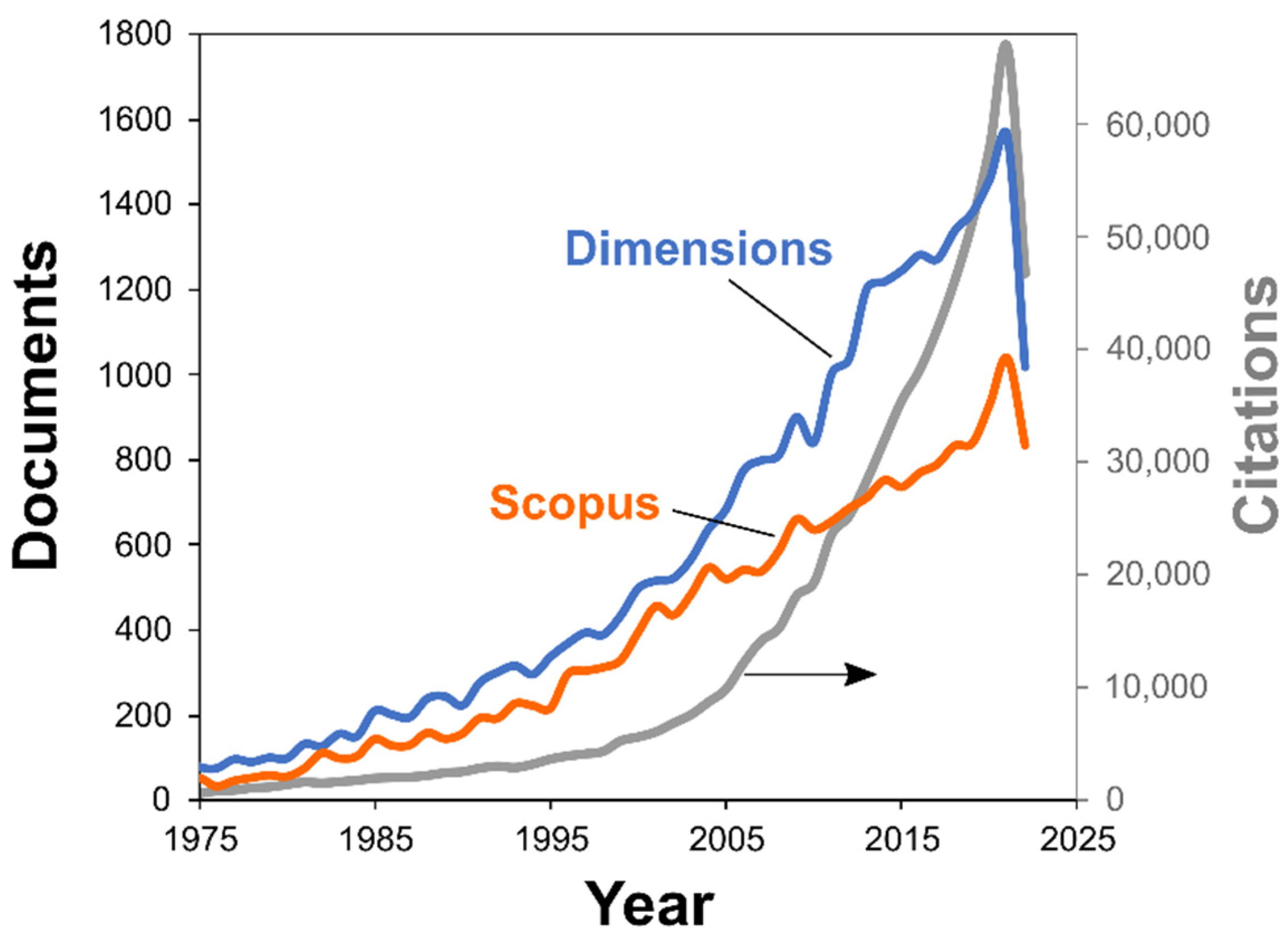
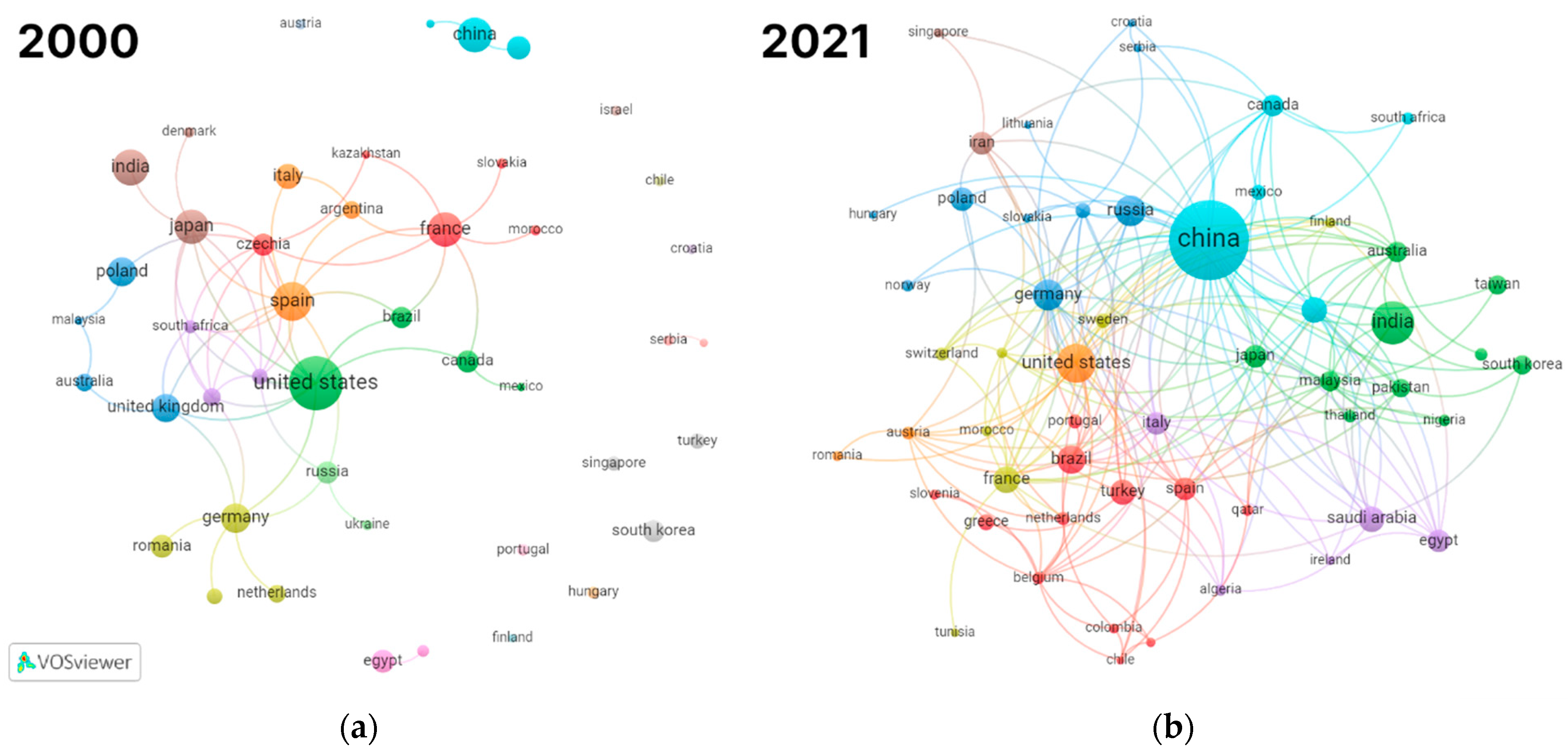
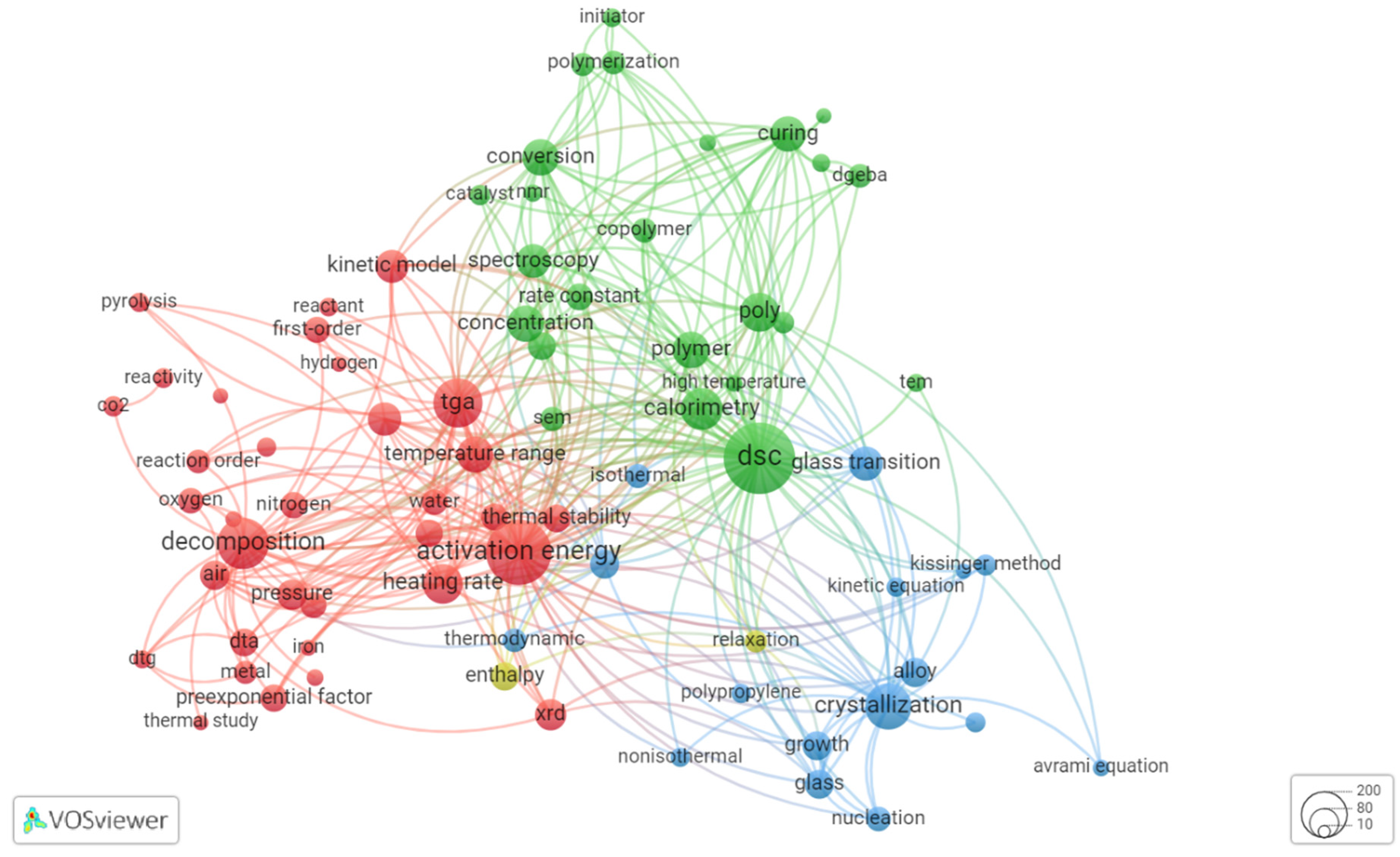
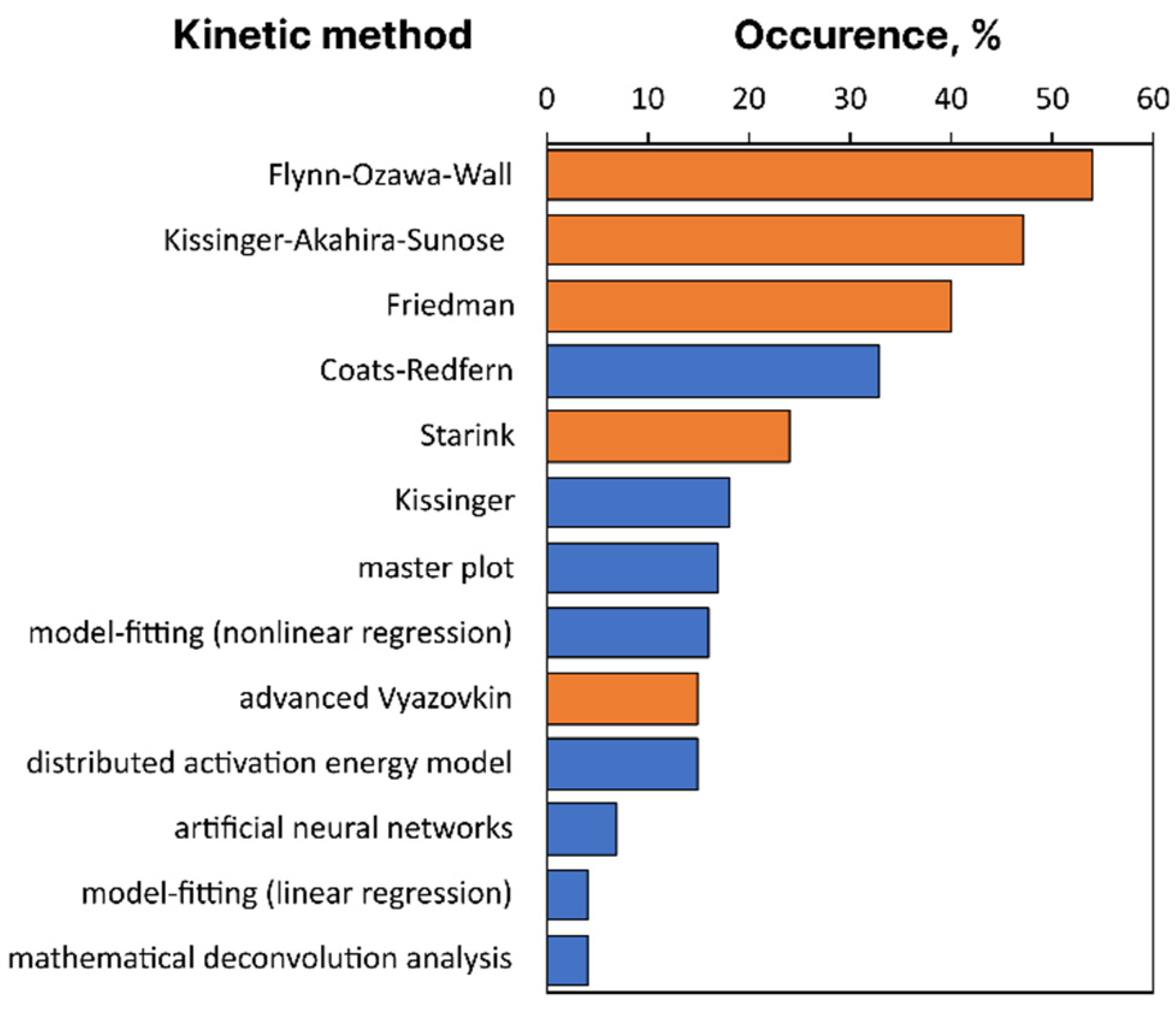
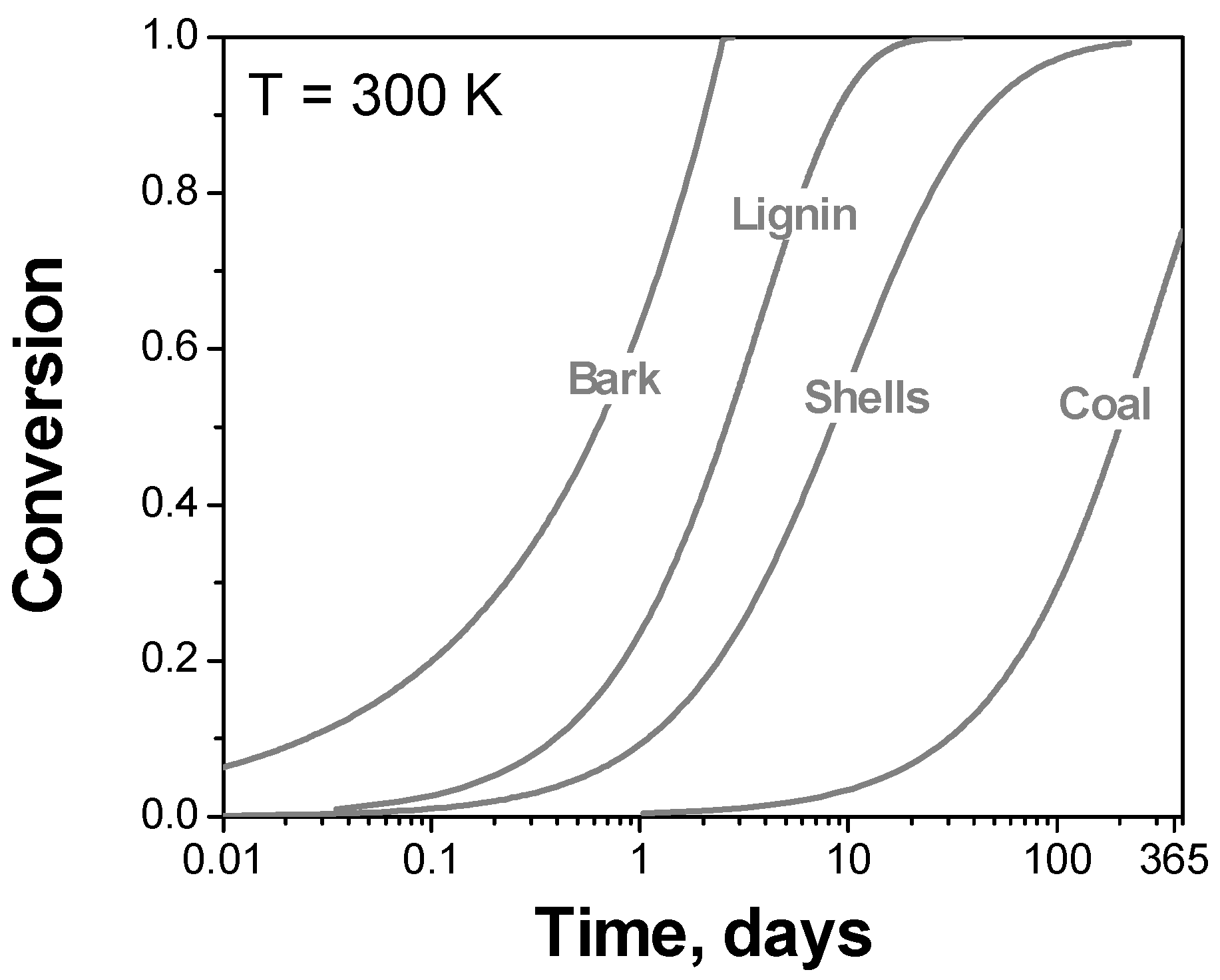
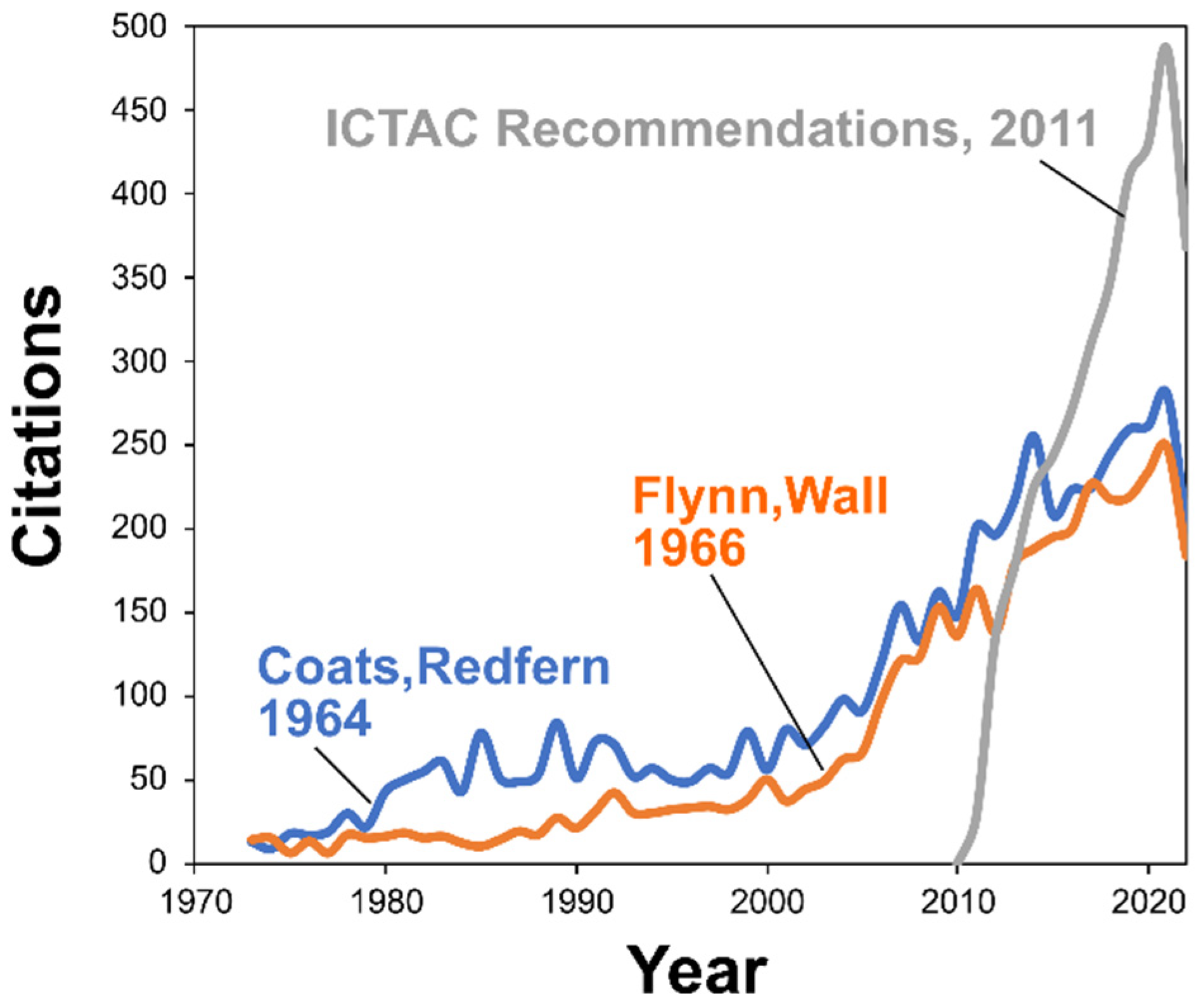
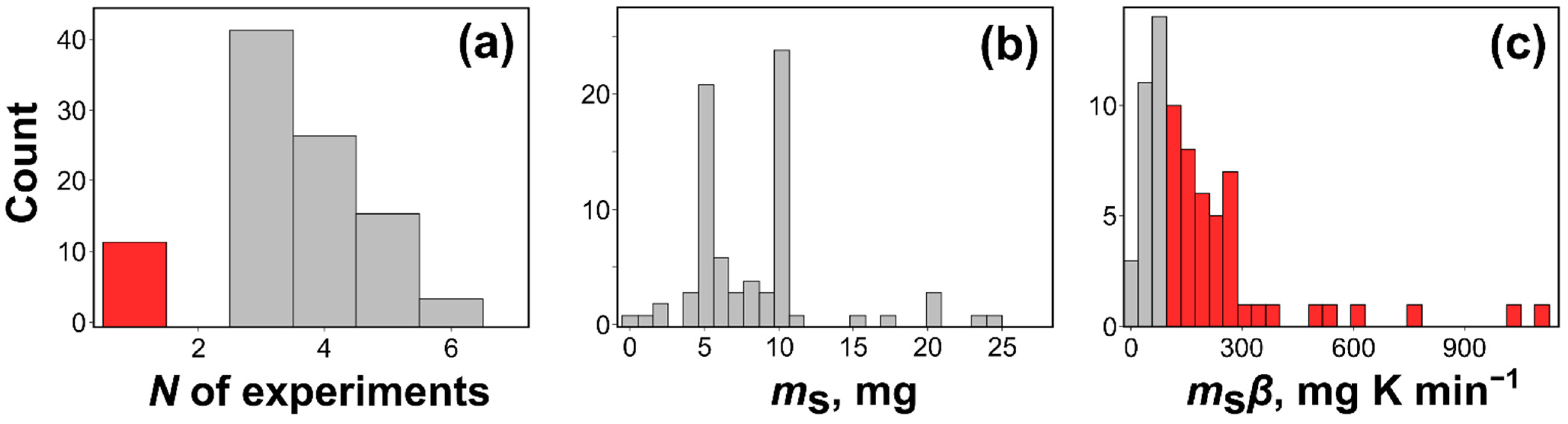
2000			2021
Source Title	Documents	Citations	Source Title	Documents	Citations
Journal of Thermal Analysis and Calorimetry	114	2072	Journal of Thermal Analysis and Calorimetry	94	182
Thermochimica Acta	68	3957	Thermochimica Acta	66	213
Journal of Applied Polymer Science	31	818	Polymers	44	147
Polymer	26	1307	Fuel	41	367
Polymer Degradation and Stability	10	668	Materials	31	62
Journal of Polymer Science Part B Polymer Physics	10	349	ACS Omega	28	52
European Polymer Journal	8	189	Biomass Conversion and Biorefinery	26	98
Polymer Engineering & Science	8	158	Bioresource Technology	21	185
Macromolecules	7	473	Journal of Analytical and Applied Pyrolysis	19	125
Materials Science and Engineering A	7	301	Journal of Applied Polymer Science	19	35
Total (2000)	597	20163	Total (2021)	1630	5509

gives the number of documents and citations by journal title, for documents from 2000 and 2021. As accepted in bibliographic analysis [22,23], we assume that citations reflect the importance and impact of publication. For papers from 2000, most of thermokinetic papers and citations come from two renowned thermal analysis journals, Journal of Thermal Analysis and Calorimetry (JTAC) and Thermochimica Acta (TCA), and the rest from the journals dedicated to polymers. At 2021 the spectrum of journals becomes more diverse, there are journals focused on material science, fuel, biomass in addition to polymer and thermal analysis journals. The number of publications in “traditional” thermokinetic journals, i.e., JTAC and TCA, remains roughly the same, but much more research is published in journals non-specialized in thermal analysis. Quantitatively, JTAC and TCA together account for 30% of research papers or citations in 2000, whereas in 2021 this number drops to less than 10%.

Now, let us come back to the keyword networks (Figure 3 and Figure 4) and search for the terms relevant to kinetic methods used in these studies. Cluster of crystallization studies (blue circles of Figure 3) contain two keywords, relevant to kinetic methods: “Kissinger method” and “Avrami equation”. Indeed, when analyzing DSC profiles of crystallization the Kissinger equation [24] and Avrami reaction model [25,26] are the most popular approaches. Red cluster of studies from 2000 relevant to decomposition, pyrolysis and degradation studies includes the following thermokinetic keywords: “first-order”, “reaction order”. It means that these studies often consider the reaction rate to be proportional to the fraction of remaining reactant raised to the power n:

$$\frac{d\alpha }{dt}=k\left(T\right){\left(1-\alpha \right)}^n$$

(1)

where k(T) is the rate constant and α is the reactant conversion. This way of kinetic description stems from homogeneous gas-phase kinetics and, thus, reaction order n should take reasonable (e.g., integer) values. Optimization of Equation (1) for real-life heterogeneous processes typically results in deviations of n from the mechanistically explainable values. Among the suggested reasons of this are the particle size distribution in the sample [27], heterogeneities in particle morphologies [28], and fractal dimensions effects [29]. Overall, summarizing the past research on the heterogeneous kinetics, we can state that the use of the reaction order model is a rather poor way of describing such kinetics because the proper reaction models are more diverse and complex [12,14].

2.2. Typical Problems of Kinetic Computations

Now let us focus on the keywords relevant to kinetic methods from the 2021 publications (Figure 4). These are the methods that play a central role in the study, as they are explicitly given in the abstracts of the analyzed publications. First, it should be noted, that the number of the keywords, associated with the kinetic methods has increased compared to 2000, i.e., more diverse methods are used. Second, the isoconversional methods become widespread (“KAS” is abbreviation of the Kissinger–Akahira–Sunose method [30], “FWO”—for the Flynn–Wall–Ozawa method [31,32] and others). Additionally, the third general observation is that among the frequently used kinetic methods there are many that are known [12] to be of low accuracy (e.g., Flynn–Ozawa–Wall method). Below we will discuss briefly the shortcomings of some still widely used methods and propose their more advanced replacements. Note, that there is a consensus in the thermal analysis community on the topic of proper kinetic computations [33,34,35,36,37] and it is in detail covered by the ICTAC Kinetics Committee recommendations [12,14]. Although the details covered are very important, the recommendations can be reduced to a few simple principles that will put one on the path to performing reasonable kinetic computations.

The number one principle is to avoid kinetic methods that are designed for estimating the kinetic parameters from a single heating rate run. Instead, employ the methods that estimate the kinetic parameters by simultaneously using data obtained at several different heating rates (or, more generally, temperature programs), which is the second principle that follows logically from the first one. These methods can be model-fitting or isoconversional (model-free). Since the latter are used much more frequently a couple more principles need to be formulated that are specific to isoconversional methods. There are many integral isoconversional methods; do not use more than one and compare them, instead use only one but make sure it is accurate. This is the third principle. The fourth principle: if the isoconversional activation energy varies significantly with conversion, do not replace the dependence with a single average value, instead focus your analysis on the multistep nature of the process. Unfortunately, our bibliographic analysis suggest that these simple principles are frequently ignored in thermokinetic studies of pyrolysis processes. Therefore, we feel that the following discussion is appropriate.

To have a more quantitative picture, we have analyzed the full-texts of 100 most cited thermokinetic publications from the dataset, published in 2021, and manually identified the kinetic methods used therein. The maximum number of citations for considered documents is 50, the minimum is 10. Figure 5 shows the occurrence of specific kinetic methods in descending order among these publications. Isoconversional methods filled by orange indeed are most popular, in agreement with visual observation from keyword network, Figure 4.

Most of the analyzed papers compare more than one isoconversional method ignoring that the methods only differ in accuracy so that nothing of kinetic relevance can be learned from their comparison. Now, let us briefly comment on the key basics and problems of widely applied thermokinetic methods.

We start with the Kissinger method [24], implemented in ASTM E698 standard [10]. Its equation can be written as [12]:

$$ln\left(\frac{\beta }{T_p^2}\right)=ln\left[-\frac{AR}{E_a}{f}^{\prime }\left({\alpha }_p\right)\right]-\frac{E_a}{R{T}_p}$$

(2)

where f(α) is the differential reaction model and R is the gas constant. The method uses only a minor piece of the available thermal analysis data, a shift of the peak temperature T_p with the heating rate β, to yield the activation energy E_a and preexponential factor A. Strictly speaking, the Kissinger equation is valid for single-step first-order reactions, but often the resulting activation energy can be linked to the rate-limiting step of more complex processes [38]. The variation of the conversion degree at the DSC peak temperature can be considered as a measure of the reaction complexity and accuracy of the Kissinger method results [34]. Modifications of the Kissinger method allowing one to obtain the information relevant to the reaction model have been suggested by Burnham [39] and Farjas et al. [11,40]. A recent review [41] surveys the application of the Kissinger method to various processes and highlights associated problems, including the inability of the method to detect the multi-step kinetics and its inapplicability to the processes during cooling, such as melt crystallization. Overall, the Kissinger method is rarely a good choice for proper kinetic analysis.

Isoconversional methods are the most popular way of kinetic analysis of complex thermal behavior (Figure 5). Theoretical analysis of isoconversional kinetic methods, as well as their application to various thermally-induced processes can be found in a book by Vyazovkin [42]. The immediate outcome of isoconversional analysis is a plot of the activation energy (i.e., E_a) versus conversion degree α. For an ideal single-step reaction E_a should be practically constant with the reaction progress. In practice, E_a can be considered constant if within the range α = 0.1–0.9 the difference between the maximum and minimum value of E_a is less than 10–20% of the average E_a value [14]. Only in this situation one can be justified by replacing the observed weak dependence of E_a on α with the average E_a value. However, a larger variation of E_a with α is frequently found that is usually associated with the multi-step character of the process. It should be stressed, that in the majority of analyzed papers the detected significant variation is neglected by averaging E_a over the α range and reporting the mean activation energy. Note that such procedure cannot be justified statistically because by its meaning the mean value is the most probable value of the dataset. That is, the mean E_a makes sense only when the E_a values are scattered randomly over the α range, but no sense when E_a shows significant systematic variation with α. Needless to say that the mean value also has no physical meaning in the case of a multi-step process because such a process is governed by more than one energy barrier, i.e., more than a single E_a value. Furthermore, exploring a systematic dependence of E_a on α can furnish the mechanistic information on the analyzed process [43]. Averaging obviously eliminates this information.

Depending on the form of the base kinetic equation used, the isoconversional methods are of either differential or integral type. The classical differential isoconversional method was proposed by Friedman [44]:

$$ln{\left(\frac{d\alpha }{dt}\right)}_{\alpha ,i}=ln\left[Af\left(\alpha \right)\right]-\frac{E_a}{R{T}_{\alpha ,i}}$$

(3)

Integral isoconversional methods, in turn, rely on the integral form of the kinetic equation, and use different approximations of the so-called temperature integral (${{\displaystyle \int }}_{T_0}^{T}exp\left(-E_a/\left[RT\right]\right)dT$ for linear temperature rise programs). General form of integral isoconversional methods is:

$$ln\left(\frac{{\beta }_i}{T_{\alpha ,i}^c}\right)=const-B\frac{E_a}{R{T}_{\alpha ,i}}$$

(4)

Crude approximation of temperature integral [45] results in C = 0 and B = 1.052 and the Flynn–Ozawa–Wall method [31,32], which is used in the ASTM E1641 standard [46]. More accurate approximation employs C = 2 and B = 1, and yields the Kissinger–Akahira–Sunose method [30]. Even greater accuracy is offered by the Starink method [47], having C = 1.92 and B = 1.0008. Concluding discussion of this group of the methods we should recall the ICTAC Kinetics committee recommendations that the Flynn-Ozawa-Wall method “is very inaccurate and should not be used without performing an iterative correction procedure for the value of E_a” [12]. Contrary to this recommendation, one can see from Figure 5 that this method is the most popular among the kinetic methods used in 2021 within the selected set of publications.

To eliminate the inaccuracy of the integral methods, Vyazovkin suggested a method, which uses numerical integration instead of approximation of the temperature integral [48]. An advancement of this method eliminates ubiquitous integration over 0–α region that is a cause of a systematic error when E_a varies significantly with α [49]. Note that all the methods represented by Equation (4) are based on the integration over 0–α region and, thus, prone to the aforementioned systematic error in E_a. This error is eliminated only if integration is performed over small Δα segments, i.e., in the piecewise manner. For instance, the Vyazovkin method uses a set of n experiments performed under arbitrary thermal programs T(t) and obtains the activation energy E_a at a particular conversion degree α by minimizing function [49]:

$$\mathsf{\Phi }\left(E_{\mathsf{\alpha }}\right)={{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j\ne i}^n\frac{J\left[E_{\mathsf{\alpha }},T_i\left(t_{\mathsf{\alpha }}\right)\right]}{J\left[E_{\mathsf{\alpha }},T_j\left(t_{\mathsf{\alpha }}\right)\right]}$$

(5)

The function J used in Equation (5) is the integral over small Δα segments and determined as:

$$J\left[E_{\mathsf{\alpha }},T\left(t_{\mathsf{\alpha }}\right)\right]={{\displaystyle \int }}_{t_{\mathsf{\alpha }-\mathsf{\Delta }\mathsf{\alpha }}}^{t_{\mathsf{\alpha }}}exp\left[\frac{-E_{\mathsf{\alpha }}}{RT\left(t\right)}\right]dt$$

(6)

The Vyazovkin method has been followed by the development of many isoconversional methods that use the piecewise integration. From the computational standpoint, the simplest of them is that by Ortega [50]. While not as accurate, it still permits eliminating the systematic error in E_a when E_a varies significantly with α, and, thus, delivers better accuracy than any of the methods based on Equation (4).

In connection with the aforementioned issue of properly treating the isoconversional values of the activation energy, one should certainly realize the necessity of evaluating and reporting the values of the preexponential factor. The latter are frequently missing from the pyrolysis publications. This is very unfortunate because not all changes in the reactivity or, more generally, in the reaction rate can be explained by changes in the activation energy. As a matter of fact, many of the reactivity changes can be exclusively due to changes in the preexponential factor [51]. It means that in terms of the activated complex theory these changes are driven by the activation entropy rather than the activation enthalpy. The activation entropy changes in the case of the biomass pyrolysis are discussed at length elsewhere [52]. Here, it should only be mentioned that generally the most appropriate method of estimating the isoconversional values of the preexponential factor is by applying the compensation effect to the isoconversional values of the activation energy [53]. This is because the method is applicable to both single- (E_a does not vary with α) and multi- (E_a varies with α) processes [54]. The high accuracy of this method in the case of multistep processes has recently been demonstrated [55]. It is worthy of note that this method is only one of many important applications of the so-called isokinetic or entropy-enthalpy compensation relationships [56].

To conclude the discussion of isoconversional methods we again recall the statement from the ICTAC Kinetics committee recommendations: “The concurrent use of two or more such equations (i.e., methods) only reveals the trivial difference in the E_a values computed by the methods of different accuracy” [12]. As our analysis of the selected publications shows, the majority of them, in turn, report the results of two or more isoconversional methods (e.g., [57,58,59]). This practice provides no kinetic insights, and the application of only one accurate method (e.g., the differential one of Friedman or integral of Ortega or Vyazovkin) is recommended.

Another powerful group of kinetic methods recommended by the ICTAC Kinetics Committee [14] comprises model-fitting techniques. In its advanced version the parameters of one or, usually, several reaction steps are optimized using nonlinear regression focusing attention on the connectivity between the steps (e.g., consecutive or competitive reactions) and reaction models for the steps (e.g., nucleation-growth or diffusional models) [14,35,37,60,61]. To our surprise, instead of utilizing the aforementioned modern and advanced procedure, 33% of analyzed publications report using the Coats–Redfern model-fitting procedure [62]. It has been repeatedly shown [63,64,65] that this procedure is generally incapable of estimating the correct values of the kinetic triplet (E_a, A, reaction model). In its core, the procedure boils down to fitting single heating rate data, and, all such procedures do not permit obtaining reliable kinetic parameters [64]. Thus, the ICTAC Kinetics Committee has recommended to avoid altogether the methods that are designed to evaluate kinetic parameters from single heating rate measurements [12].

To be fair, not all publications employing the Coats–Redfern method use it as the only computational technique of kinetic analysis. Roughly one fifth of these publications also include the results obtained with isoconversional methods, which generally produce acceptable data. Still, it is alarming that the majority of these papers (i.e., ~26 out of 33%) report kinetic results that are dubious at best.

To better illustrate the size and essence of the problem with using the single heating rate kinetics, we refer the readers to the most recent publications in a renowned journal, dedicated specifically to pyrolysis, the Journal of Analytical and Applied Pyrolysis. In the years 2021 and 2022 there have been at least 17 papers [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82] published that employ a single heating rate method as the only computational technique of kinetic analysis. The failure of such analysis to produce trustworthy kinetic parameters can be exemplified by using several of the aforementioned publications [72,73,75,80]. As an example, we consider estimating the thermal stability of the investigated compounds at an ambient temperature of 27 °C. This is readily accomplished by substituting the reported kinetic parameters into the following equation [64]:

$$t_{\alpha }=\frac{g\left(\mathsf{\alpha }\right)}{A\exp \left(\frac{-E}{RT}\right)}$$

(7)

where g(α) is the integral reaction model, and t_α is time to reach the extent of decomposition α at temperature T. The results obtained are both striking and illuminating. First, if the reported kinetic parameters are correct, the two natural wood species, Jasminum nudiflorum Lindl. bark [75] and tea oil camellia shells [72], should be very thermally unstable at 27 °C (Figure 6). The bark would decompose nearly completely in two days, whereas the shells would lose approximately 50% of their mass for a little over than 1 week. This obviously contradicts the well-known thermal stability of wooden species and, if was true, would be impossible to miss in practical handling of these materials. Similarly, if one uses the reported [73] kinetic triplet, lignin should almost entirely decompose at an ambient temperature for less than 3 weeks. If this was true, its major application as a fuel would be impossible. In reality, lignin does not undergo any significant decomposition on continuous heating below 200 °C [83]. Lastly, the kinetic parameters reported [80] for raw sample of the Shengdong coal predict that at an ambient temperature it would decompose by ~70% in one year. This result is clearly at odds with the common knowledge about coal stability.

One of the most recent kinetic approaches is a set of techniques based on artificial neural networks (7% of analyzed publications). The applications of neural networks to thermal analysis and kinetic research has recently been reviewed [84]. The general conclusion from the review is that in the field of thermokinetics, the most promising usage of neural networks is a trained black-box, that allows to bypass the traditional determination of the kinetic parameters. Obtained in such way non parametric kinetic description of the process can be used in more complex model, accounting for the heat and mass balance of the system. A more traditional use of neural networks that targets estimating the kinetic parameters is still in its infancy [85,86,87] and yet unsuitable for analysis of multi-step kinetics, which are the most common kinetics encountered in the processes of decomposition and pyrolysis.

Another recent kinetic method is based on the separation of the overlapping rate peaks, also known as mathematical deconvolution approach [88]. Experimental reaction rate data representing a series of discernible peaks is deconvoluted into separate peaks. Several mathematical forms for peak shape are used, the most common one is the Fraser–Suzuki function [89]. Deconvoluted peaks from raw data acquired at different heating rates are in turn analyzed by isoconversional and model-fitting kinetic methods [14]. Oftentimes, the deconvoluted peaks show a behavior characteristic of a single-step process. However, this method is based on the assumption that the reaction steps are independent of each other. When the reaction steps are not independent (e.g., competing or consecutive reaction steps) and their relative contributions to the overall rate change significantly with the heating rate, the kinetic analysis of deconvoluted peaks tends to yield incorrect kinetic parameters and reaction model [34].

The previously mentioned rapid growth of the field can certainly be a factor causing a decrease in the quality of kinetic publications. As thermal analysis instruments become more widespread, thermokinetic analysis more frequently accompanies the material science studies. Research becomes more global (Figure 2) and more workers without sufficient thermoanalytical and kinetic background become involved in research. Without sufficient knowledge and expertise in thermal analysis and kinetics, the published research frequently suffers from substandard amateurish data analysis. While evaluation of the quality of kinetic publications can be subjective, there are some features that allow for solid conclusions: incorrect procedure of kinetic analysis, usage of inaccurate kinetic methods, and unawareness of the broader literature on the topic. As an example of the latter, the ICTAC Kinetics Committee recommendations [25] unequivocally advise against using the Flynn–Ozawa–Wall method as well as single heating rate methods such as that by Coats and Redfern. The former (FWO) uses a very crude approximation of the temperature integral that can introduce 20–30% error in the E_a value, whereas the latter (CR) relies on the single heating rate data analysis and can introduce an error in E_a in excess of 100%. In spite of the clear ICTAC recommendations, the applications of poor kinetic methods continue to grow as can be visualized by observing the citation dynamics of original publications of the Flynn–Ozawa–Wall and Coats–Redfern methods (Figure 7). Such dynamics looks especially shocking when compared to the citation dynamics of the ICTAC recommendations for performing kinetic computations [12] (Figure 7). The document is one of the most cited in the field so that disregarding its advices appears more like intentional neglect than accidental unawareness of its existence.

2.3. Typical Problems of Data Collecting and Reporting

No matter how well kinetic computations are done, they cannot produce good results from poor thermal analysis data. The data obviously should be representative of the process, repeatable, and free of detrimental effects. Various aspects of proper data collection have been well covered in the ICTAC recommendations [13]. Without delving into details of these extensive recommendations, it is possible to state one major principle of the data collection. This is to use the slowest heating rates and the smallest samples masses possible to avoid the self-heating/cooling and to generally minimize the adverse heat and mass transfer phenomena [13,91,92,93,94].

Considering the sensitivity of modern TGA and DSC instruments, one typically needs no more than 5 mg of a sample. There is also rarely a need to use heating rates faster than 20 °C min⁻¹. On the whole, smaller sample sizes allow one to use faster heating rates and vice versa. As a rule of a thumb, the product of the sample mass and heating rate (m_s·β) should be kept under 100 mg K min⁻¹ [13]. This rule is upheld by simulation work for degradation of polymers [95]. The value of the product is, of course, enthalpy dependent. The 100 mg K min⁻¹ is a reasonable value for processes whose enthalpy change is in the range of hundreds J g⁻¹. In the case of energetic materials, which decompose releasing thousands J g⁻¹ the recommended sample masses are less than 1 mg and heating rates slower than 5 K min⁻¹ so that m_s·β ≤ 5 mg K min⁻¹.

Figure 8 illustrates the analysis of the discussed publications, viz., distribution of the sample masses, and the product of the sample mass and heating rate values (m_s·β [mg K min⁻¹]). Figure 8b gives the distribution of the sample masses selected by the authors to obtain the thermal analysis data. The distribution shows two maxima, at 5 and 10 mg. Clearly, the majority of the authors select excessively large sample masses. Even more instructive is the distribution of the mass heating rate products (Figure 8c). It is seen that the majority of studies have been conducted at m_s·β ≥ 100 mg K min⁻¹, i.e., under the conditions when the heat and mass transfer phenomena are likely to have a non-negligible contribution to the chemical kinetics. In such a situation, the regular kinetic computations, which do not account for the aforementioned phenomena, yield erroneous values of the Arrhenius parameters. In particular, the error in the activation energy can readily reach tens of % [13].

Another important issue is the number of experiments used for evaluating the Arrhenius parameters. Figure 8a shows that some authors still use single heating rate data for such evaluations. As discussed in the previous section, the respective procedures do not permit obtaining correct kinetic parameters. On the other hand, most studies deal with only three heating rates that is a minimum appropriate number. However, one must realize that three experiments are appropriate only for nearly perfect measurements. Three experiments give rise to the Arrhenius type of plot that has three points (n = 3). To justify the use of this plot for estimating the Arrhenius parameters it has to be proven statistically as linear. This plot has n–2, i.e., 1 degree of freedom. To prove its linearity with 95% confidence probability, the respective Pearson’s correlation coefficient, r has to be equal to or larger than the critical value 0.9969 [96,97] (i.e., r² ≥ 0.9938), which is rarely accomplishable in routine measurements. Thus, careful studies tend to employ four, five or even more different heating rates (or temperatures for isothermal measurements), so that the corresponding critical values of r are significantly smaller. It is also a good idea to use a broad range of the heating rates by selecting the fastest so that it is approximately 10 times larger than the slowest. This secures a sufficiently broad temperature range required for proper kinetic analysis [13,98].

Let us now focus on reporting. The issue of good practices for reporting of thermal analysis is addressed at length in some early publications [9,99]. The simple basic principle is that the thermal analysis data used in kinetic computations should be repeatable and the repeatability should be explicitly stated in a paper. That is, running an experiment more than once should yield kinetic curves that are the same within the experimental error. In addition, the kinetic experiments should be described in sufficient detail. It means that a paper should report enough experimental details for other workers to reproduce the described experiments.

We analyze the experimental sections of the same top 100 thermokinetic publications from 2021 to see the level of detail of the descriptions of the measurements.

Table 2. Analysis of experimental section of top 100 by citations thermokinetic papers, published in 2021: thermal analysis and kinetic details.

Specific Aspect of Thermal Analysis Measurement	Percent of Studies Where It Is Reported
Sample mass	79
Crucible type	8
Software used for kinetic analysis	12
Gaseous atmosphere (gas type)	95
Calibration info	8
Purge gas flow rate	86
Repeatability of measurements	37

summarizes the percentage of studies where a certain experimental detail is reported. Expectedly, for papers mostly focusing on pyrolysis kinetics, the gas type within the furnace, gas flow rate, and sample mass are provided in a majority of the studies. However, few papers report the crucible (pan) type. The latter includes the material, e.g., aluminum, platinum, alumina, etc. It also includes the configuration, i.e., open, closed, or pierced. Just as important is information on how the instrument used was calibrated in terms of temperature, mass, and/or enthalpy. Yet, this information is as underreported as that on crucible type (Table 2).

In addition to reproducibility of experiments discussed above, the results of kinetic computations should be reproducible, too [100]. It means that the sufficient amount of detail of kinetic computations should be reported. This includes the methods of kinetic evaluations with proper literature references as well as the software used to implement the methods. As seen in Table 2, only 12% of analyzed papers mention the software. Some methods, similar to that of Friedman or Ortega, are reduced to linear regression and readily implemented with simple spreadsheet software. Others, such as the Vyazovkin method or the method of fitting of multi-step models are more computationally involved and require the use of specialized software. The latter can be available commercially, oftentimes from the instrument manufacturers. It is important to note the most recent trend in developing and sharing the open-source thermokinetic software or packages. The examples are ThermV v0.2 [101], THINKS [102], takos [103], Kinetic Calculation [104], mixchar [105], and pICNIK [106]. We hope that these free tools will become more widely used by researchers and make the calculation procedures more transparent.

3. Conclusions

Analysis of pyrolysis literature has helped to visualize the development of thermokinetic publications over the recent years. Based on the intensity of the research efforts one can conclude that pyrolysis kinetics has become important and, in some aspects, the dominant application of the thermokinetics. At the same time, our analysis of the kinetic methods and experimental conditions used shows that the quality of the respective publication leaves much to be desired. The quality should and can be improved by following the best practices well-established and publicized by the thermal analysis and kinetics community. As discussed above, these practices translate into a few simple principles that follow from ICTCA recommendations. We expect that implementation of these principles will be helpful to many to start on the right path toward better quality studies of the pyrolysis kinetics.