Effective Cooling System for Solar Photovoltaic Cells Using NEPCM Impingement Jets
Abstract
1. Introduction
2. Physical and Mathematical Model
Problem Definition
3. Governing Equations
- -
- Continuity equation
- -
- Momentum equation
- -
- Energy equation
- -
- Volume fraction equation
4. Thermo-Physical Properties
5. Thermal Assessment
6. Numerical Setup
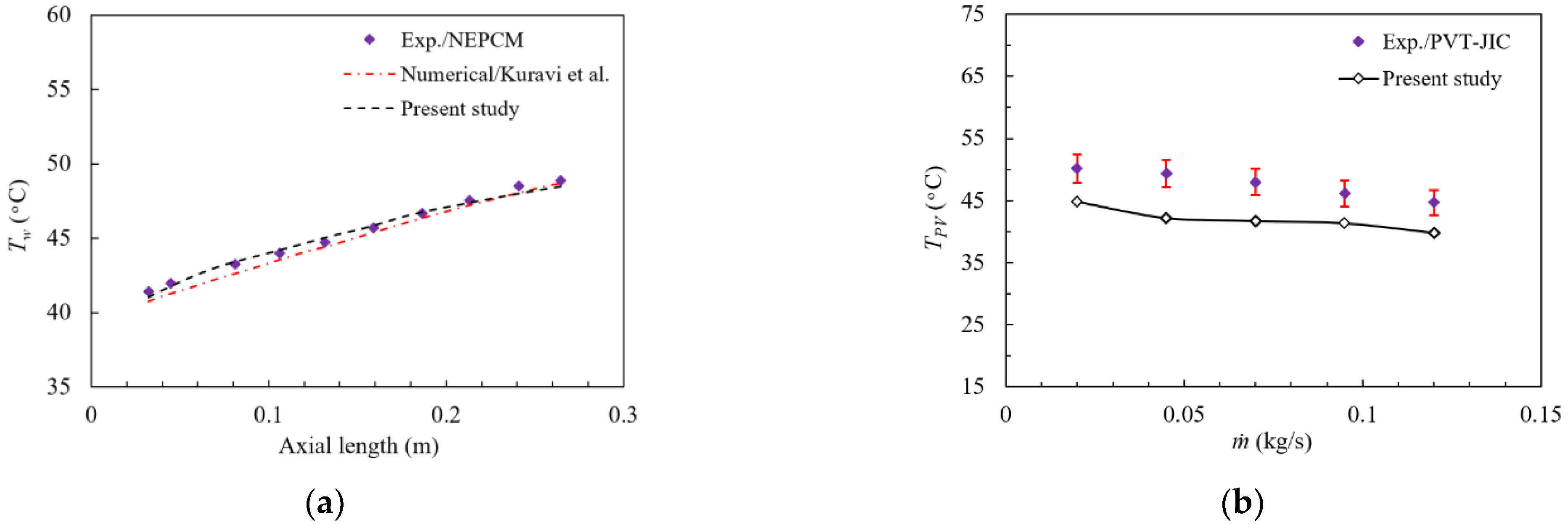
7. Numerical Validation
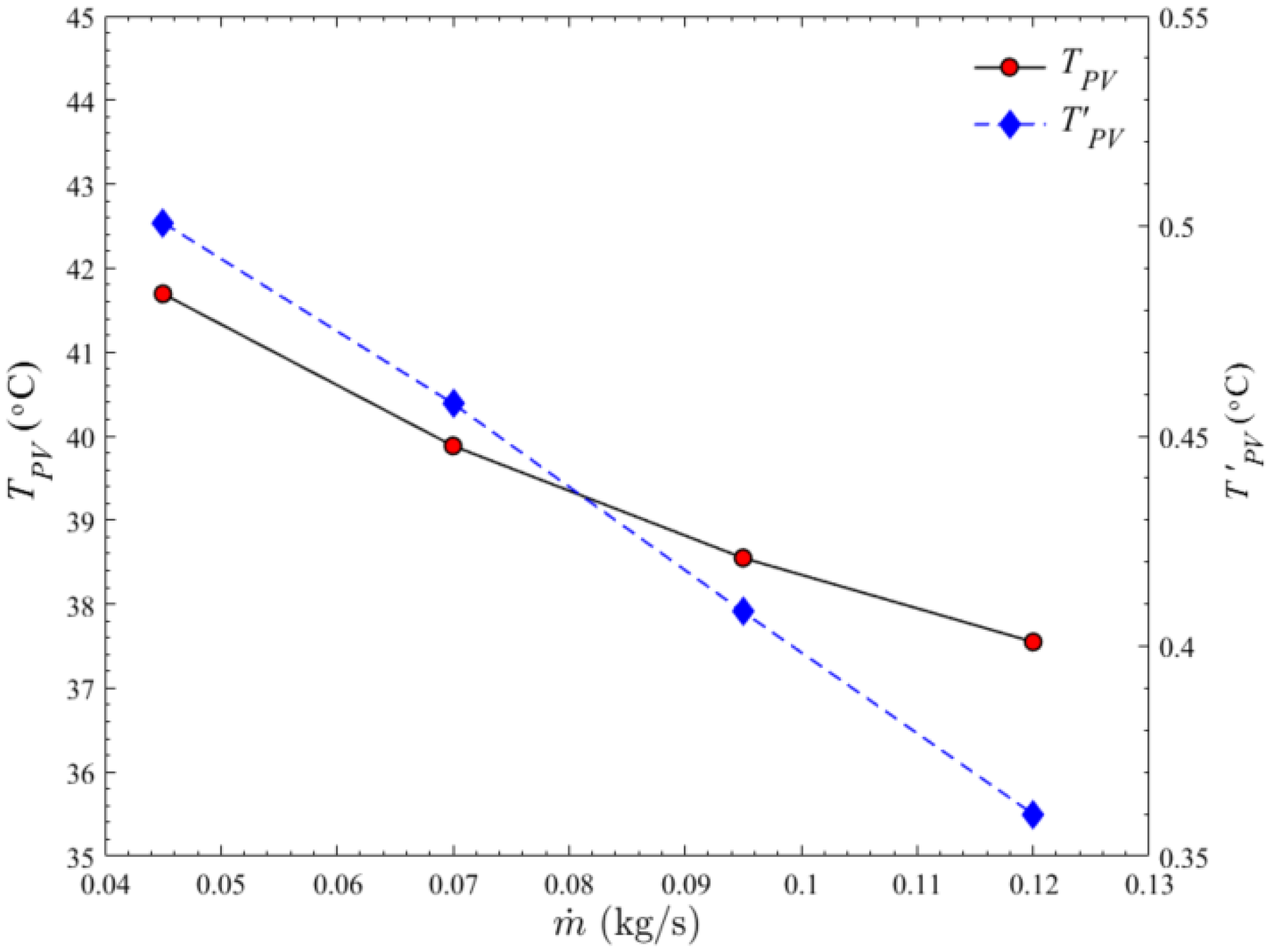
8. Results and Discussion
9. Conclusions
- While the conventional PV efficiency under the solar irradiation of 1000 W/m2 reached 13.3%, using the NEPCM-JIC system with the mass flow rate of 0.045 kg/s, the jet-to-surface spacing of 30 mm, and 8 active nozzles increased the efficiency to 15.26%.
- Using the NEPCM slurry in the JIC system instead of pure water reduced the PV temperature by 1.3 °C under the same conditions.
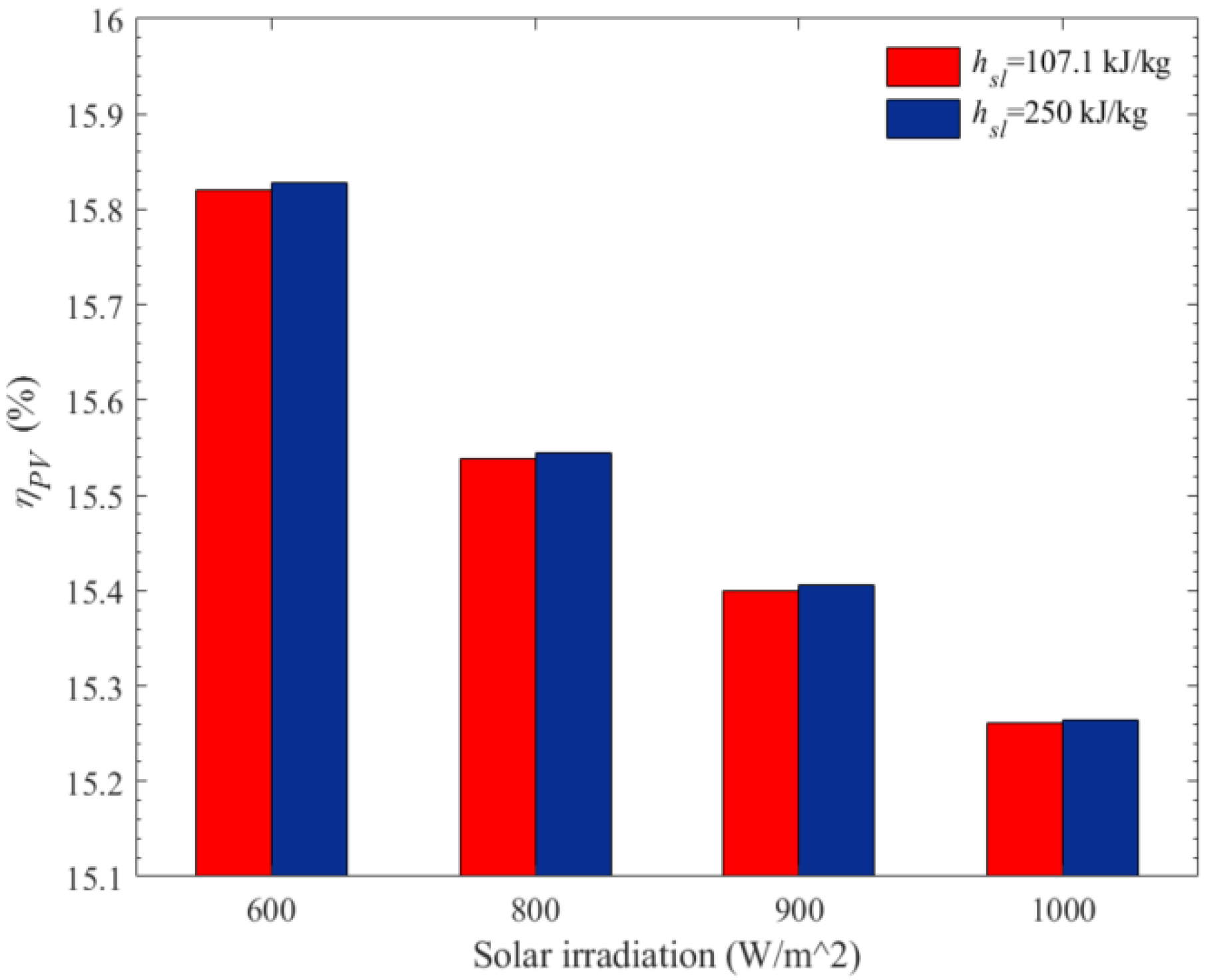
- Increasing solar irradiation led to higher surface temperature and lower efficiency. The PV efficiency was maximised under irradiation of 600 W/m2 and the latent heat of 250 kJ/kg.
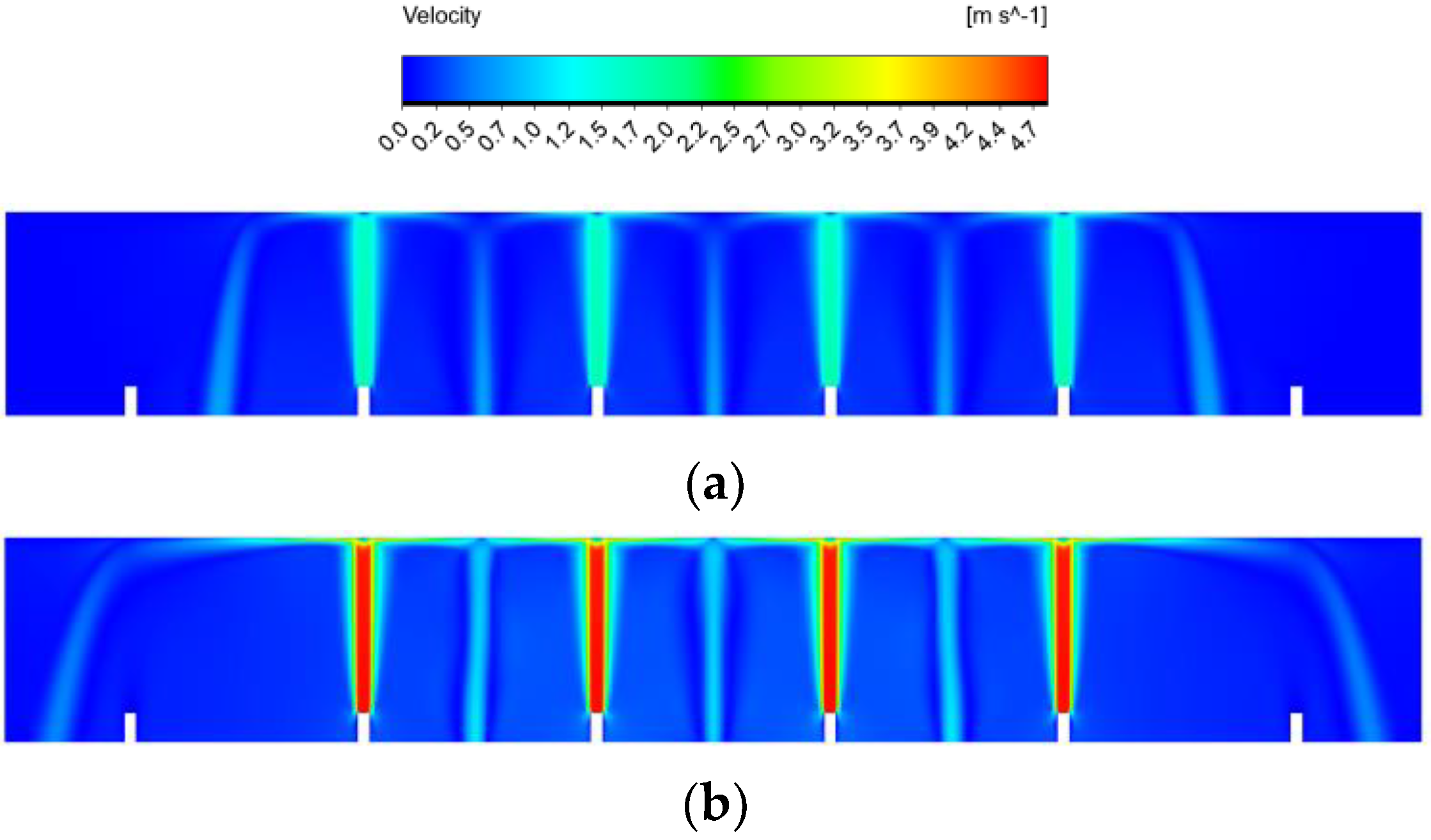
- The PV temperature was significantly reduced when the mass flow rate increased. In addition, the temperature uniformity and output power were improved by increasing the mass flow rate.
- Smaller jet-to-surface distances improved the PV output power, and the minimum PV temperature of 33.8 °C was obtained at H = 5.1 mm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahimi, M.; Valeh-E-Sheyda, P.; Parsamoghadam, M.A.; Masahi, M.M.; Alsairafi, A.A. Design of a self-adjusted jet impingement system for cooling of photovoltaic cells. Energy Convers. Manag. 2014, 83, 48–57. [Google Scholar] [CrossRef]
- Javidan, M.; Moghadam, A.J. Experimental investigation on thermal management of a photovoltaic module using water-jet impingement cooling. Energy Convers. Manag. 2021, 228, 113686. [Google Scholar] [CrossRef]
- Poulek, V.; Matuška, T.; Libra, M.; Kachalouski, E.; Sedláček, J. Influence of increased temperature on energy production of roof integrated PV panels. Energy Build. 2018, 166, 418–425. [Google Scholar] [CrossRef]
- Khodadadi, M.; Sheikholeslami, M. Numerical simulation on the efficiency of PVT system integrated with PCM under the influence of using fins. Sol. Energy Mater. Sol. Cells 2021, 233, 111402. [Google Scholar] [CrossRef]
- Salem, M.; Ali, R.; Elshazly, K. Experimental investigation of the performance of a hybrid photovoltaic/thermal solar system using aluminium cooling plate with straight and helical channels. Sol. Energy 2017, 157, 147–156. [Google Scholar] [CrossRef]
- Nahar, A.; Hasanuzzaman, M.; Rahim, N. Numerical and experimental investigation on the performance of a photovoltaic thermal collector with parallel plate flow channel under different operating conditions in Malaysia. Sol. Energy 2017, 144, 517–528. [Google Scholar] [CrossRef]
- Awad, M.; Radwan, A.; Abdelrehim, O.; Emam, M.; Shmroukh, A.N.; Ahmed, M. Performance evaluation of concentrator photovoltaic systems integrated with a new jet impingement-microchannel heat sink and heat spreader. Sol. Energy 2020, 199, 852–863. [Google Scholar] [CrossRef]
- Olawole, O.C.; Joel, E.S.; Ikono, U.I.; Moses, C.; Oyedepo, S.O.; De, D.K.; Nguyen, H.M.; Omeje, M.; Akinpelu, A.; Fobagboye, L.; et al. Innovative methods of cooling solar panel: A concise review. J. Physics Conf. Ser. 2019, 1299, 012020. [Google Scholar] [CrossRef]
- Zenhäusern, D.; Bamberger, E.; Baggenstos, A.; Häberle, A. PVT Wrap-Up: Energy Systems with Photovoltaic Thermal Solar Collectors; SwissEnergy: Bern, Switzerland, 2017. [Google Scholar]
- Sorensen, H.; Zondag, H. PV Catapult/European Collaboration for Identification of PV Research and Markets Opportunities, Socio-Economics, Studies, Performance Assessment and Dissemination of PV and PV–Thermal Technology. Available online: https://www.wip-munich.de/projects/project-pv-catapult/ (accessed on 21 September 2022).
- Zondag, H.A.; Vries, D.; van Steenhoven, A.A.; van Helden, W.G.; van Zolingen, R.J. Thermal and electrical yield of a combi-panel. In Proceedings of the ISES Bi-Annual Conference on CD-ROM, Jerusalem, Israel, 4–9 July 1999. [Google Scholar]
- Michael, J.J.; Iniyan, S.; Goic, R. Flat plate solar photovoltaic–thermal (PV/T) systems: A reference guide. Renew. Sustain. Energy Rev. 2015, 51, 62–88. [Google Scholar] [CrossRef]
- Nadda, R.; Kumar, A.; Maithani, R. Efficiency improvement of solar photovoltaic/solar air collectors by using impingement jets: A review. Renew. Sustain. Energy Rev. 2018, 93, 331–353. [Google Scholar] [CrossRef]
- Bahaidarah, H.M. Experimental performance evaluation and modeling of jet impingement cooling for thermal management of photovoltaics. Sol. Energy 2016, 135, 605–617. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Lee, A. Investigation of nanoparticle effects on jet impingement heat transfer: A review. J. Mol. Liq. 2020, 316, 113819. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Salehi, F.; Sheikholeslami, M.; Lee, A. A computational study on nanofluid impingement jets in thermal management of photovoltaic panel. Renew. Energy 2022, 189, 970–982. [Google Scholar] [CrossRef]
- Javidan, M.; Moghadam, A.J. Effective cooling of a photovoltaic module using jet-impingement array and nanofluid coolant. Int. Commun. Heat Mass Transf. 2022, 137, 106310. [Google Scholar] [CrossRef]
- Khanjari, Y.; Pourfayaz, F.; Kasaeian, A.B. Numerical investigation on using of nanofluid in a water-cooled photovoltaic thermal system. Energy Convers. Manag. 2016, 122, 263–278. [Google Scholar] [CrossRef]
- Mustafa, W.; Othman, M.; Fudholi, A. Numerical investigation for performance study of photovoltaic thermal nanofluids system. Int. J. Appl. Eng. Res. 2017, 12, 14596–14602. [Google Scholar]
- Wu, W.; Bostanci, H.; Chow, L.; Ding, S.; Hong, Y.; Su, M.; Kizito, J.; Gschwender, L.; Snyder, C. Jet impingement and spray cooling using slurry of nanoencapsulated phase change materials. Int. J. Heat Mass Transf. 2011, 54, 2715–2723. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, T.; Chen, D.; Hong, F.; Cheng, P. Confined jet array impingement cooling with spent flow distraction using NEPCM slurry. Int. Commun. Heat Mass Transf. 2016, 77, 140–147. [Google Scholar] [CrossRef]
- Rehman, T.-U.; Ali, H.M. Experimental study on the thermal behavior of RT-35HC paraffin within copper and Iron-Nickel open cell foams: Energy storage for thermal management of electronics. Int. J. Heat Mass Transf. 2020, 146, 118852. [Google Scholar] [CrossRef]
- Rehman, T.-U.; Ali, H.M. Thermal performance analysis of metallic foam-based heat sinks embedded with RT-54HC paraffin: An experimental investigation for electronic cooling. J. Therm. Anal. 2020, 140, 979–990. [Google Scholar] [CrossRef]
- Bouadila, S.; Baddadi, S.; Rehman, T.-U.; Ayed, R. Experimental investigation on the thermal appraisal of heat pipe-evacuated tube collector-based water heating system integrated with PCM. Renew. Energy 2022, 199, 382–394. [Google Scholar] [CrossRef]
- Rehman, T.-U.; Ambreen, T.; Niyas, H.; Kanti, P.; Ali, H.M.; Park, C.-W. Experimental investigation on the performance of RT-44HC-nickel foam-based heat sinks for thermal management of electronic gadgets. Int. J. Heat Mass Transf. 2022, 188, 122591. [Google Scholar] [CrossRef]
- Kuravi, S.; Kota, K.M.; Du, J.; Chow, L.C. Numerical Investigation of Flow and Heat Transfer Performance of Nano-Encapsulated Phase Change Material Slurry in Microchannels. J. Heat Transf. 2009, 131, 062901. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Salehi, F.; Lee, A. Performance of nano encapsulated phase change material slurry heat transfer in a microchannel heat sink with dual-circular synthetic jets. Int. J. Heat Mass Transf. 2022, 184, 122265. [Google Scholar] [CrossRef]
- Rehman, M.M.U.; Qu, Z.; Fu, R.; Xu, H. Numerical study on free-surface jet impingement cooling with nanoencapsulated phase-change material slurry and nanofluid. Int. J. Heat Mass Transf. 2017, 109, 312–325. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Zolfagharian, M.M.; Mujumdar, A.S.; Zargarabadi, M.R.; Abdulahzadeh, M. Heat transfer under composite arrangement of pulsed and steady turbulent submerged multiple jets impinging on a flat surface. Int. J. Therm. Sci. 2014, 86, 139–147. [Google Scholar] [CrossRef]
- Evans, D.; Florschuetz, L. Cost studies on terrestrial photovoltaic power systems with sunlight concentration. Sol. Energy 1977, 19, 255–262. [Google Scholar] [CrossRef]
- Evans, D.L. Simplified method for predicting photovoltaic array output. Sol. Energy 1981, 27, 555–560. [Google Scholar] [CrossRef]
- Goel, M.; Roy, S.; Sengupta, S. Laminar forced convection heat transfer in microcapsulated phase change material suspensions. Int. J. Heat Mass Transf. 1994, 37, 593–604. [Google Scholar] [CrossRef]
- Liu, L.; Jia, Y.; Lin, Y.; Alva, G.; Fang, G. Performance evaluation of a novel solar photovoltaic–thermal collector with dual channel using microencapsulated phase change slurry as cooling fluid. Energy Convers. Manag. 2017, 145, 30–40. [Google Scholar] [CrossRef]
- Glaspell, A.W.; Rouse, V.J.; Friedrich, B.K.; Choo, K. Heat transfer and hydrodynamics of air assisted free water jet impingement at low nozzle-to-surface distances. Int. J. Heat Mass Transf. 2019, 132, 138–142. [Google Scholar] [CrossRef]
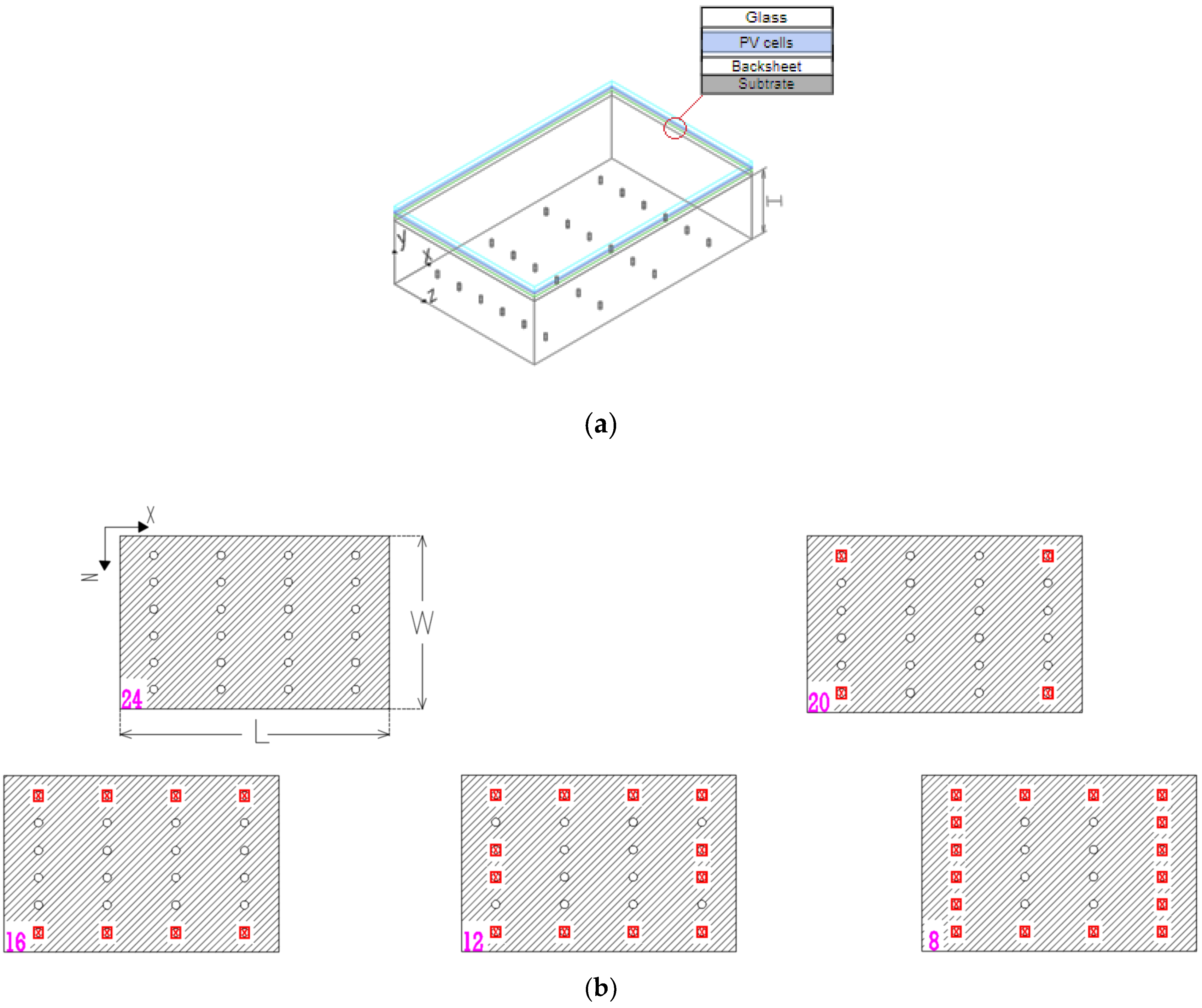

| Glass | PV Cells | Tedlar | Substrate | |
|---|---|---|---|---|
| Thickness, t, (mm) | 4 | 0.3 | 0.5 | 0.5 |
| Thermal conductivity, k, (W/mk) | 1 | 148 | 0.033 | 202 |
| Specific heat capacity, Cp, (J/kg·K) | 500 | 677 | 1250 | 903 |
| Density, ρ, (kg/m3) | 2450 | 2330 | 1200 | 2702 |
| Absorptivity, α | 0.05 | 0.9 | 0.128 | - |
| Transmissivity, τ | 0.92 | 0.09 | - | - |
| Emissivity, ε | 0.85 | - | - | - |
| Materials | ρ (kg/m3) | k (W/m·K) | Cp (J/(K·kg)) |
|---|---|---|---|
| Water | 997 | 0.61 | 4180 |
| Octadecane (core) | 850 | 0.34 | 1800 |
| Polystyrene (shell) | 1260 | 0.21 | 2130 |
| Parameter | Variation Range | |
|---|---|---|
| Solar irradiation (W/m2) | I | 600–1000 |
| Latent heat (kJ/kg) | hsl | 107.1–250 |
| Inlet mass flow rate (kg/s) | ṁ | 0.045–0.12 |
| Number of nozzles | N | 8–24 |
| Jet-to-surface spacing (mm) | H | 5.1–55 |
| Properties | Correlation | ||
|---|---|---|---|
| Density | where c is the volumetric concentration of particles. | ||
| Dynamic viscosity | |||
| Thermal conductivity | |||
| and | |||
| where and are the shear rate magnitude and thermal diffusivity, respectively [27]. | |||
| Specific heat capacity | = 0 or 1 where is the mass concentration of particles. is the latent heat, is the solidus temperature, and is the melting range. | ||
| ṁ (kg/s) | %P(max)increase |
|---|---|
| 0.045 | 14.99 |
| 0.07 | 16.01 |
| 0.095 | 16.76 |
| 0.12 | 17.32 |
| Nozzle No. | TPV (°C) | |
|---|---|---|
| 8 | 37.55 | 15.56 |
| 12 | 34.88 | 15.76 |
| 16 | 34.77 | 15.77 |
| 20 | 34.75 | 15.78 |
| 24 | 34.31 | 15.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadpour, J.; Salehi, F.; Lee, A. Effective Cooling System for Solar Photovoltaic Cells Using NEPCM Impingement Jets. Thermo 2022, 2, 383-393. https://doi.org/10.3390/thermo2040026
Mohammadpour J, Salehi F, Lee A. Effective Cooling System for Solar Photovoltaic Cells Using NEPCM Impingement Jets. Thermo. 2022; 2(4):383-393. https://doi.org/10.3390/thermo2040026
Chicago/Turabian StyleMohammadpour, Javad, Fatemeh Salehi, and Ann Lee. 2022. "Effective Cooling System for Solar Photovoltaic Cells Using NEPCM Impingement Jets" Thermo 2, no. 4: 383-393. https://doi.org/10.3390/thermo2040026
APA StyleMohammadpour, J., Salehi, F., & Lee, A. (2022). Effective Cooling System for Solar Photovoltaic Cells Using NEPCM Impingement Jets. Thermo, 2(4), 383-393. https://doi.org/10.3390/thermo2040026














