Parametrization of the NRTL Model with a Multiobjective Approach: Implications in the Process Simulation
Abstract
1. Introduction
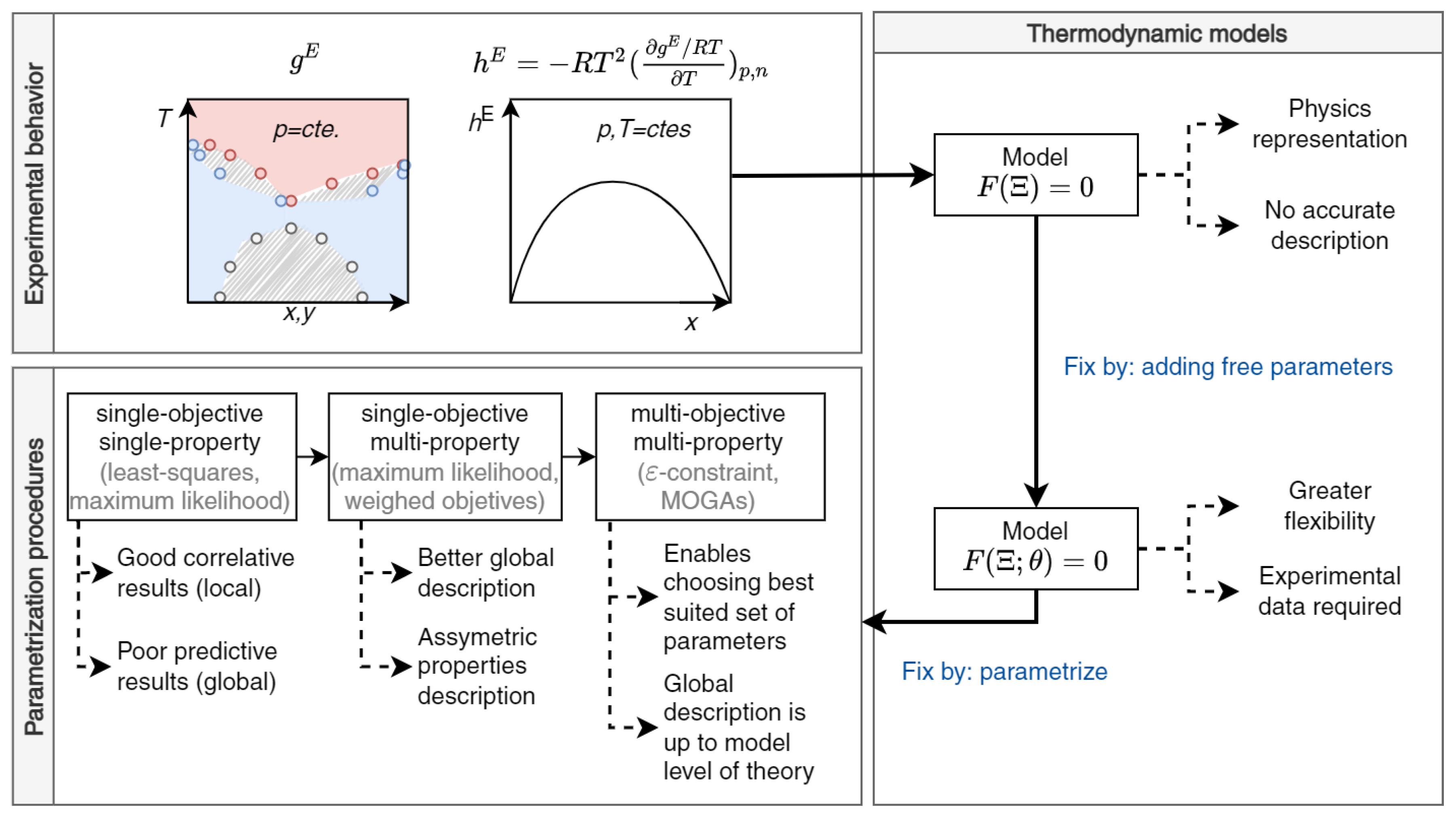
2. Parametrization of Thermodynamic Models
2.1. Conventional Procedure
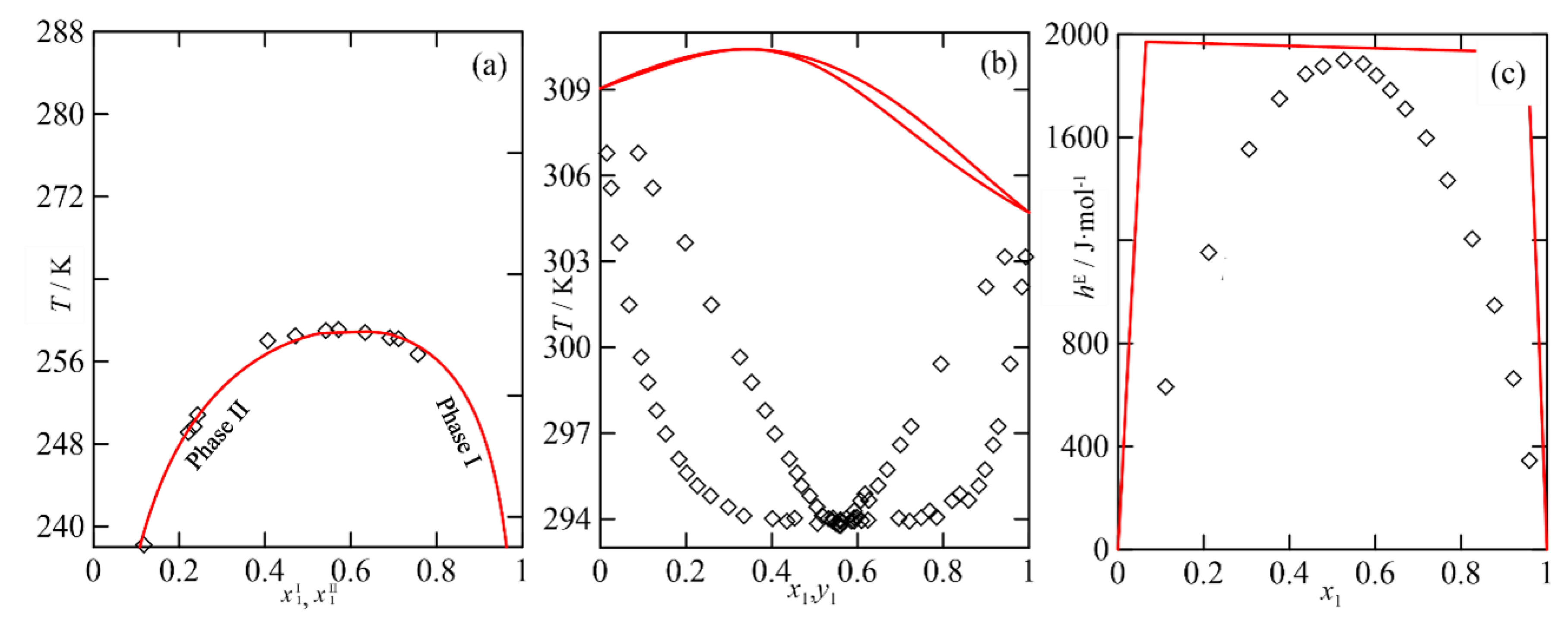
A Practical Case of Parametrization with the NRTL Model
2.2. Multi-Property Approach
The Multi-Property Approach in the NRTL Parametrization
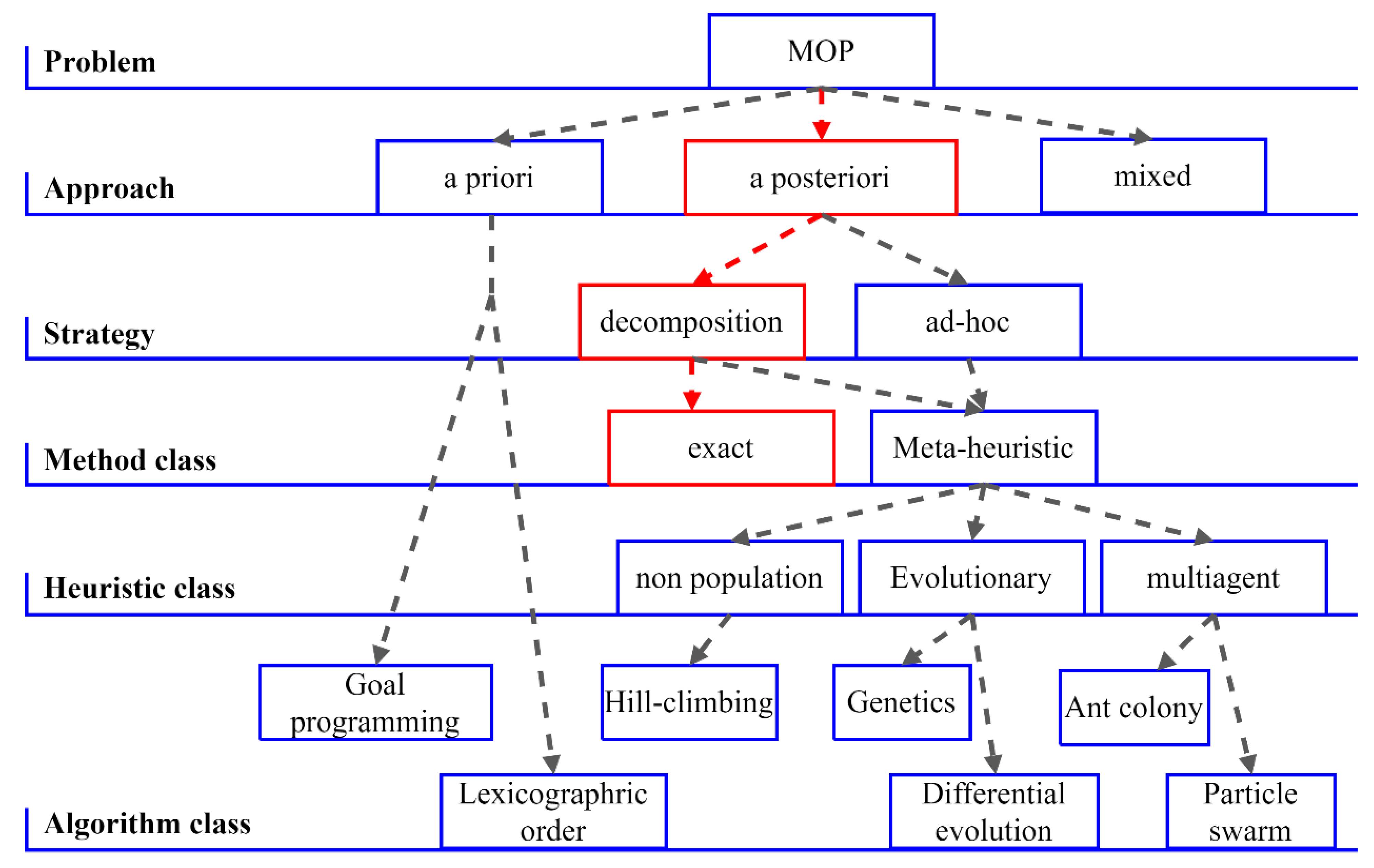
2.3. Multi-Objective Resolution of the Multi-Property Approach
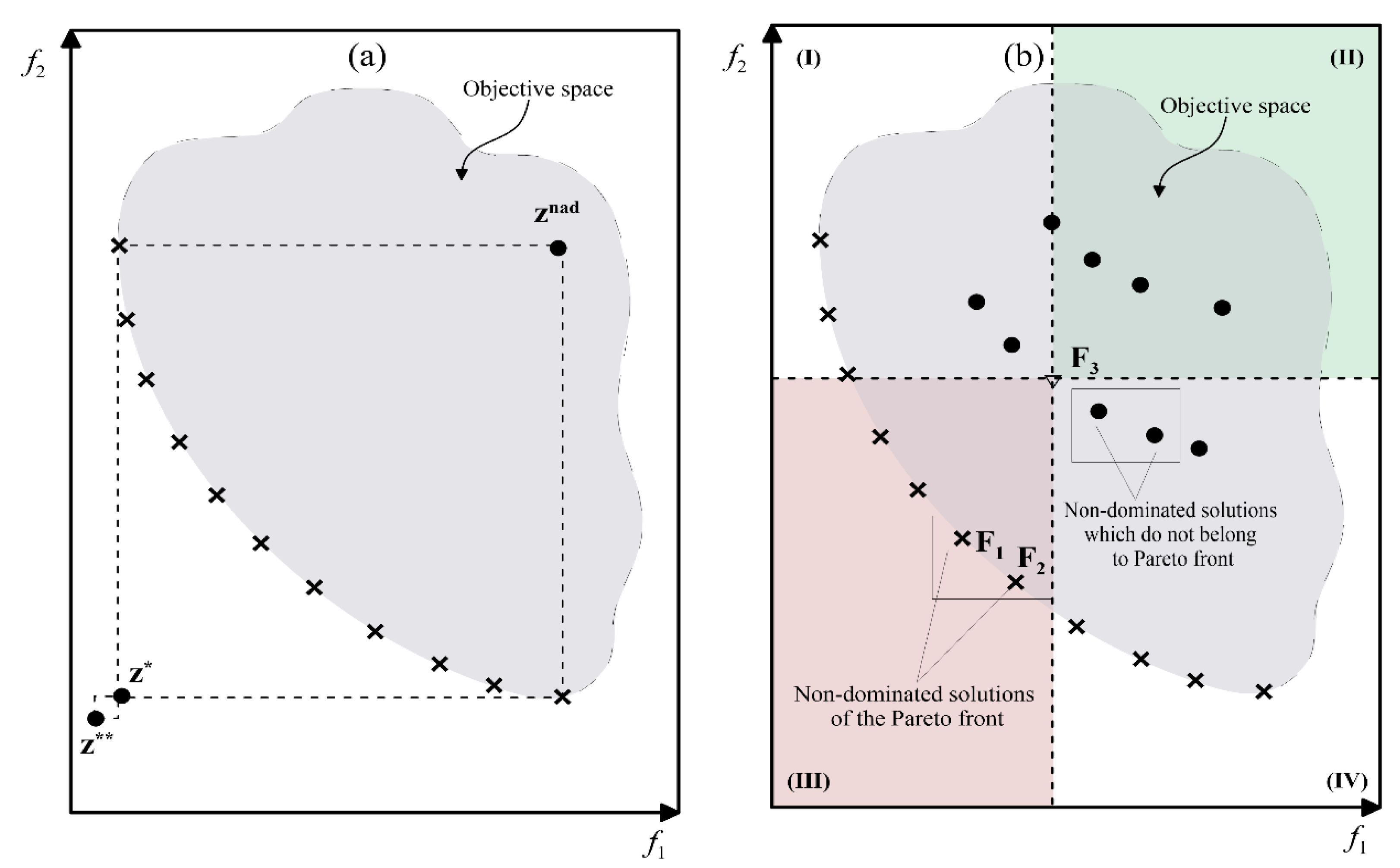
2.3.1. The Optimum in MOP
2.3.2. Resolution of the MOP
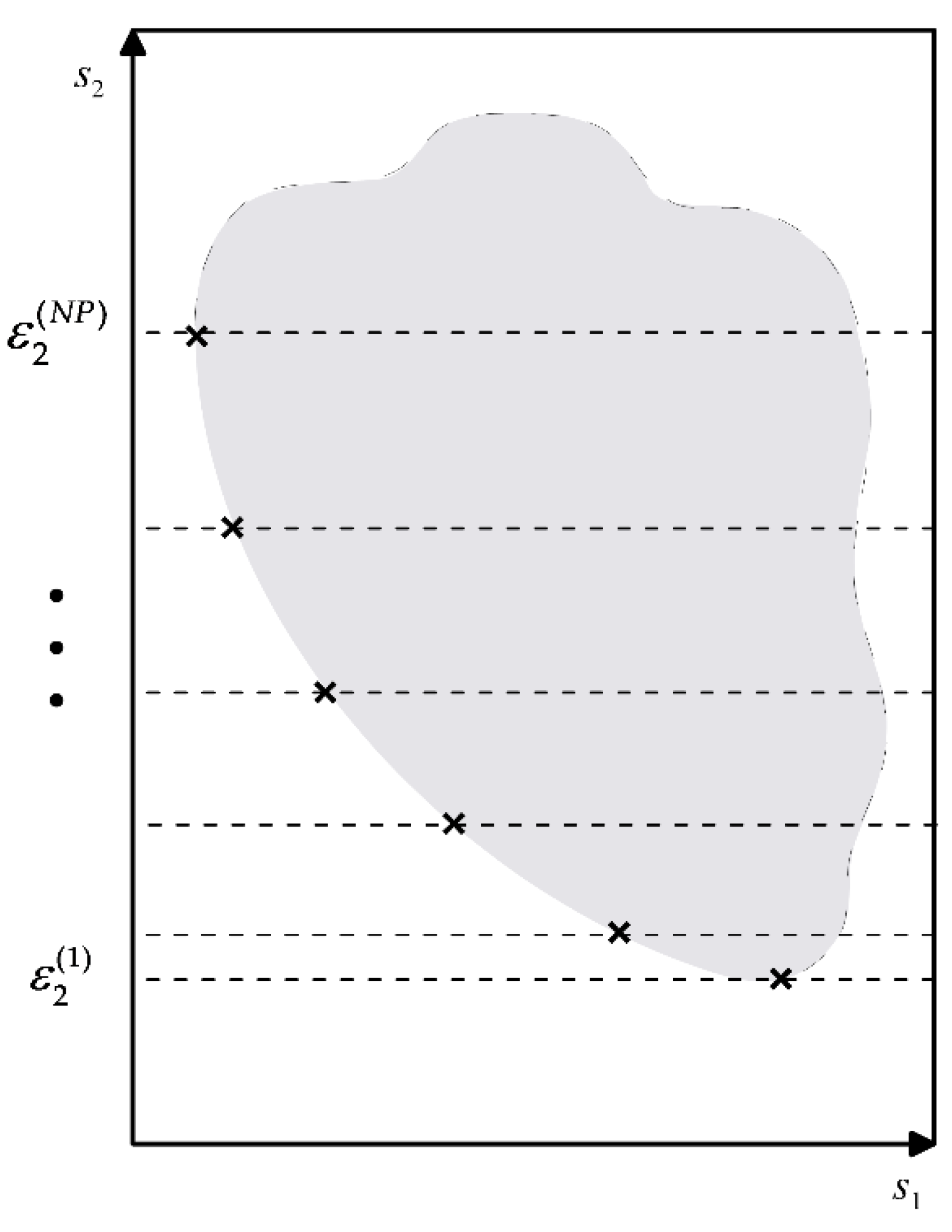
2.3.3. Resolution by ε-Constraint Decomposition
2.3.4. Resolution of the Multi-Property Problem as an MOP
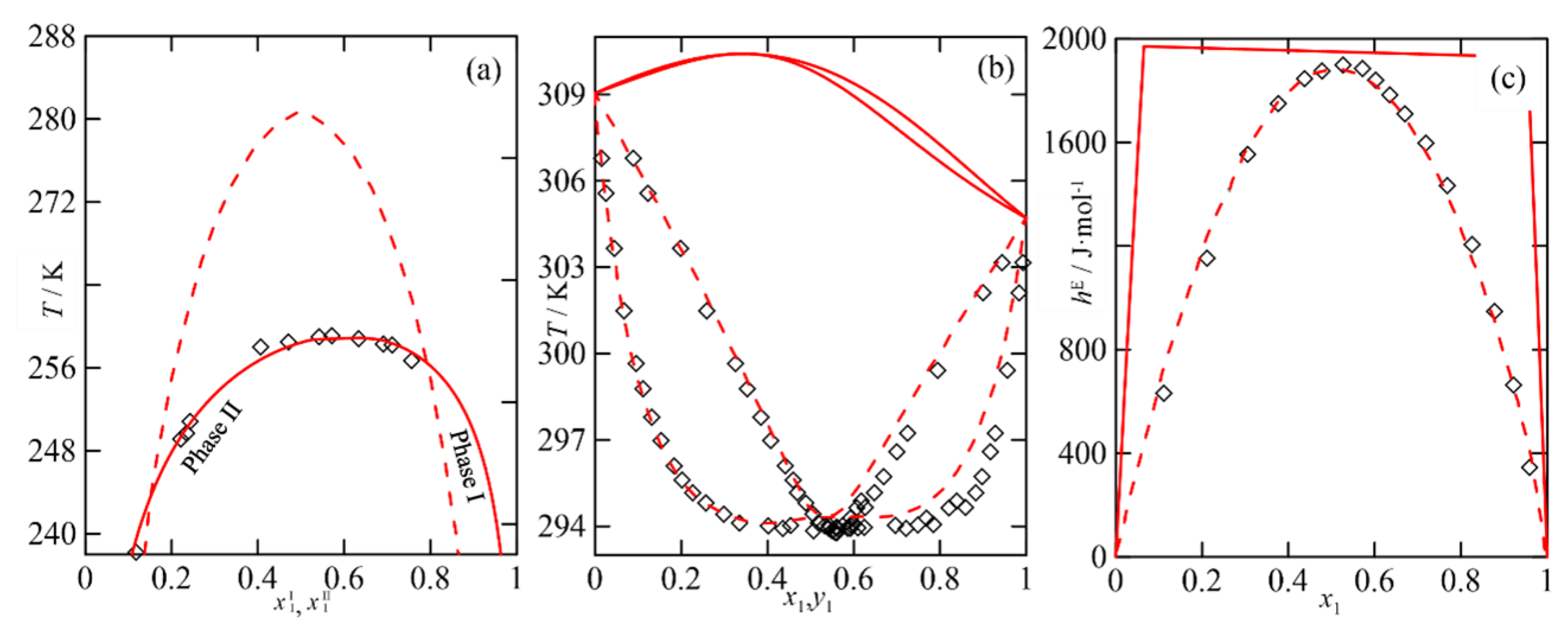
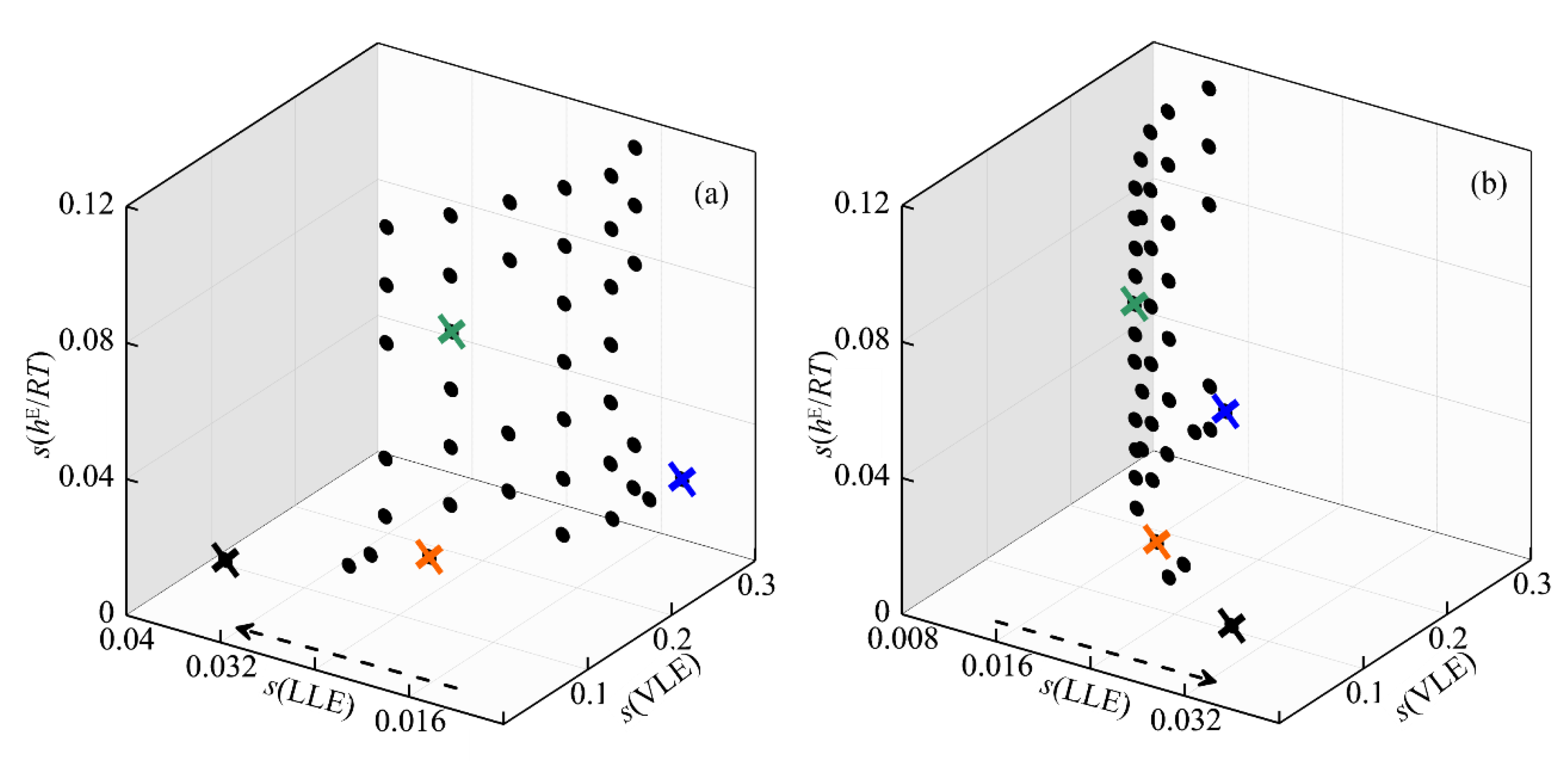
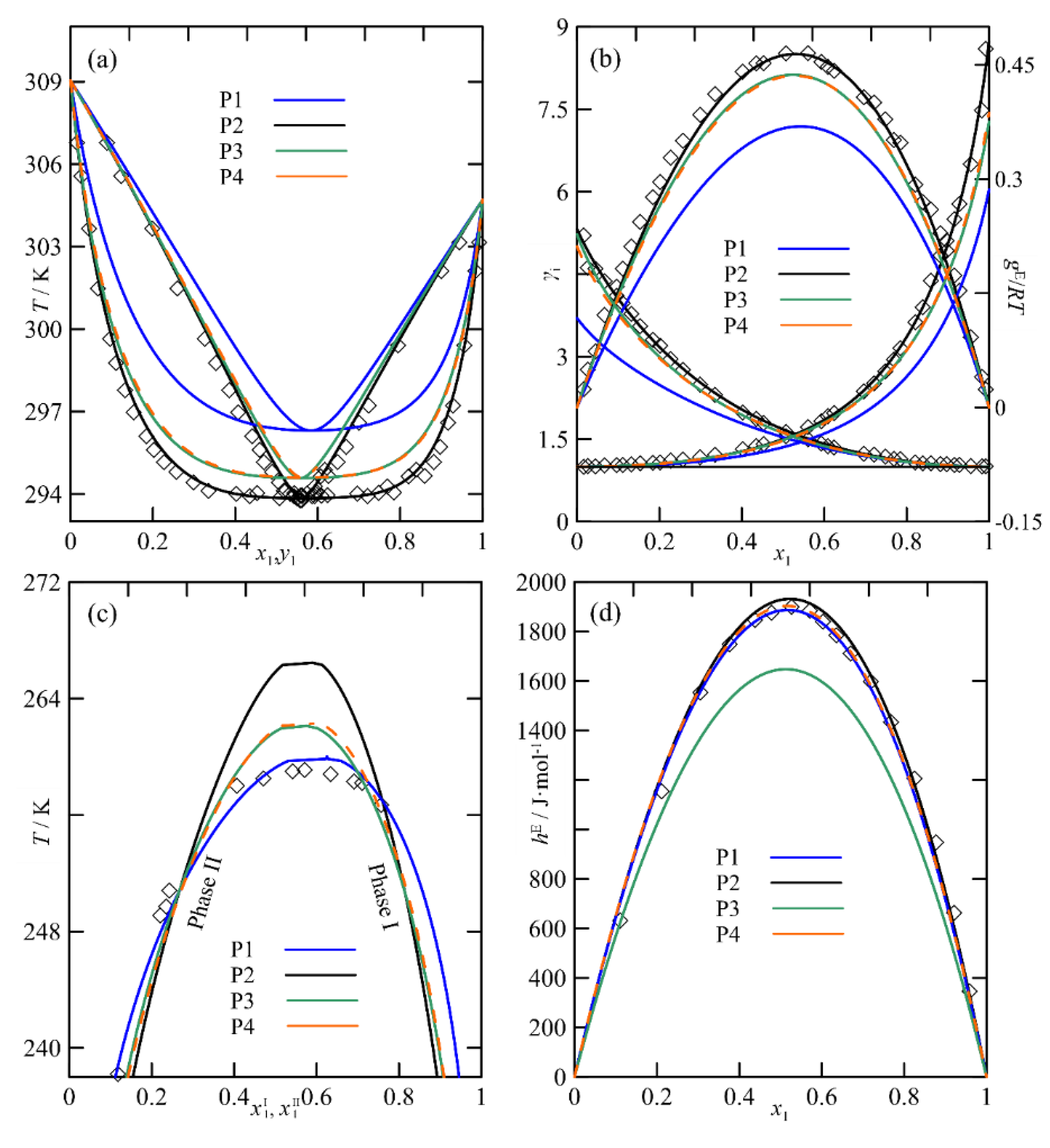
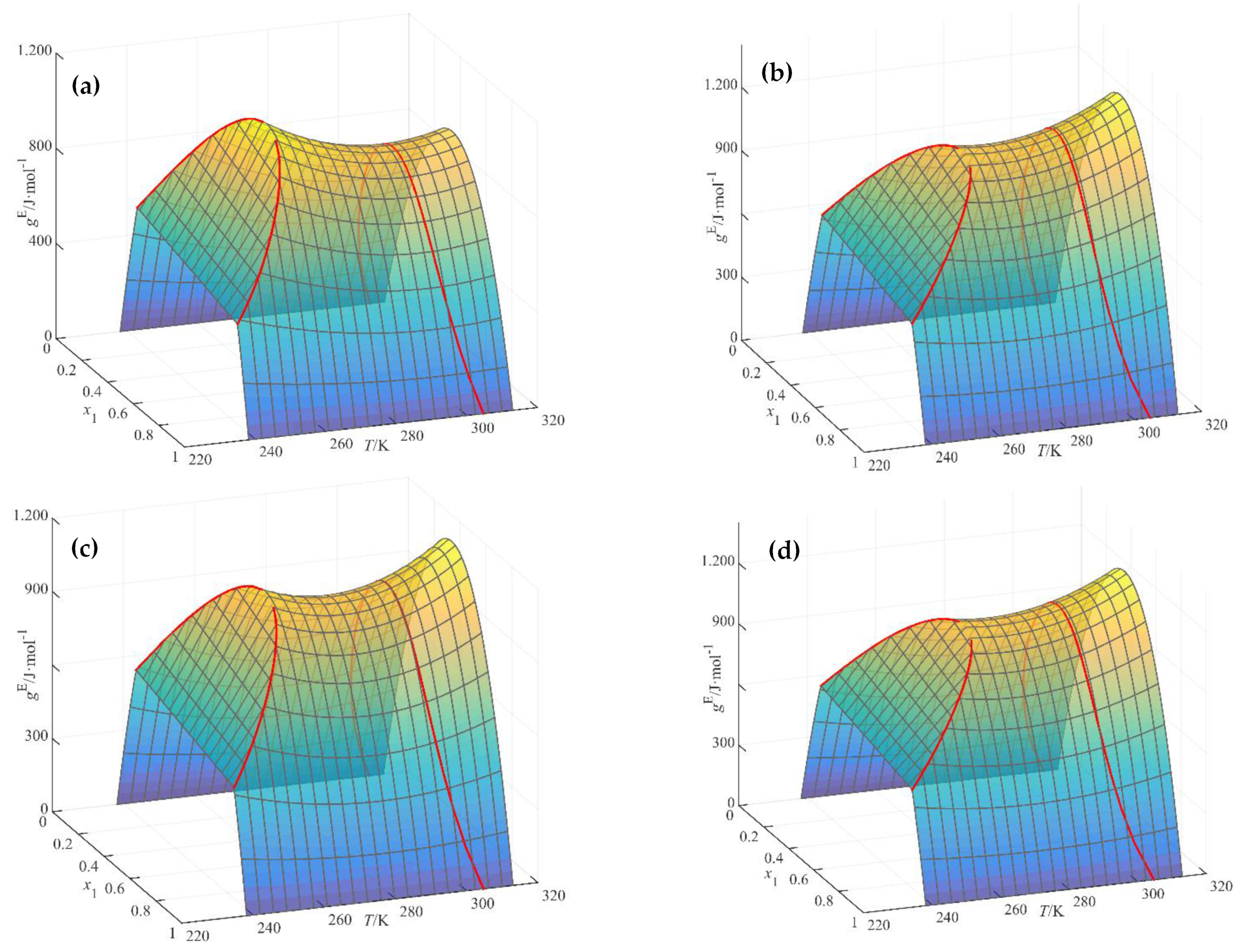
2.3.5. Multi-Objective Modelling Using NRTL
2.4. Comments on the Strategies of Analyzed Modelling
3. Influence of Modelling on the Simulation of a Separation Process
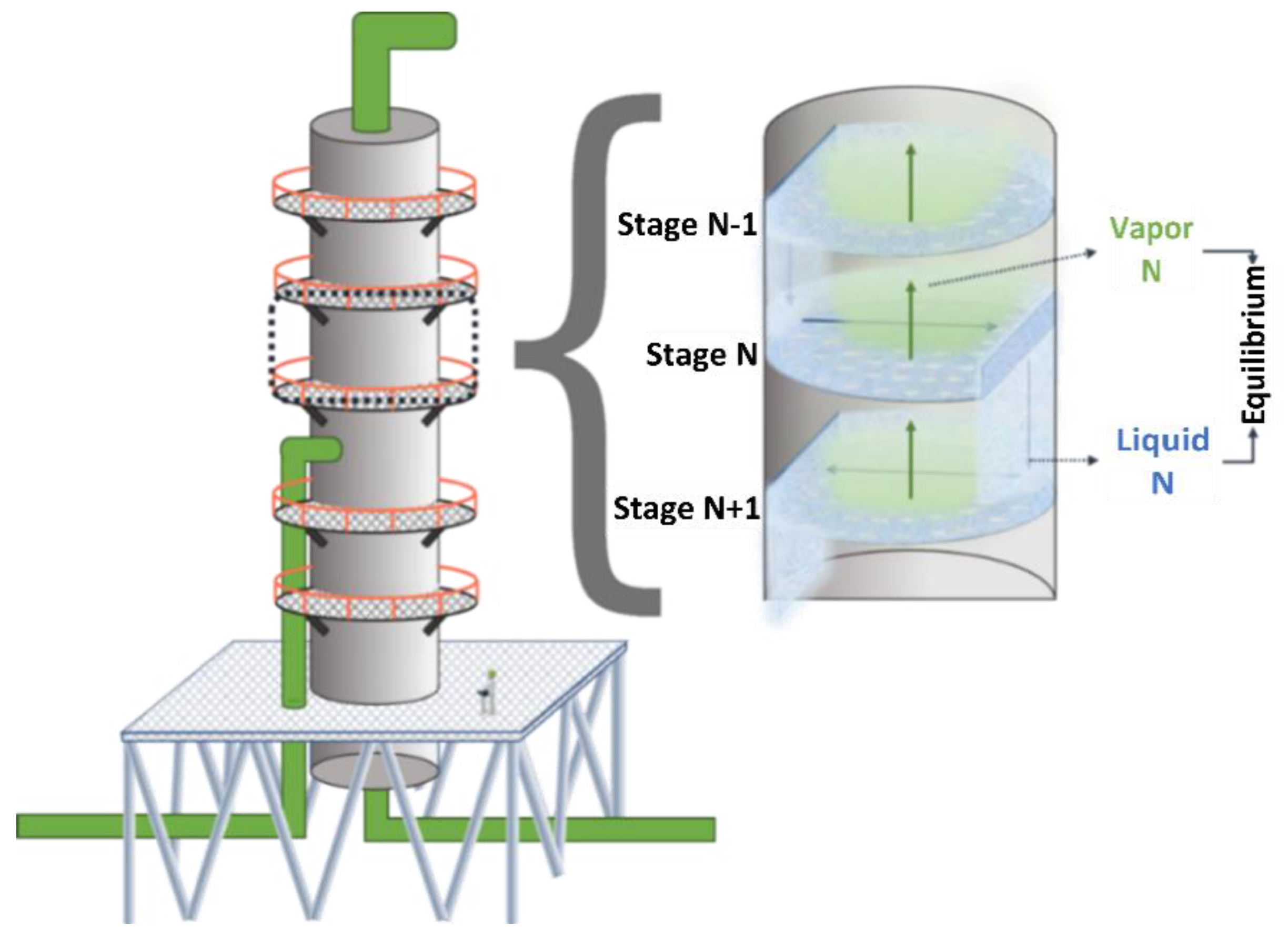
3.1. Description of the Separation Process
- -
- Distillation column C-1: recovery of pentane in bottom streams;
- -
- Distillate, stream 3: product under conditions close to azeotrope;
- -
- Distillates of C-1 and C-2 (x1 ≈ xaz) are blended and sent to E-1;
- -
- E-1 exchanger cools to form two immiscible liquid phases;
- -
- Decanter S-1 separates the immiscible liquid phases;
- -
- Stream 5 (x1 < xaz) is recirculated to column C-1;
- -
- Stream 6 (x1 > xaz) feeds column C-2;
- -
- The ester is obtained by the C-2 bottom.
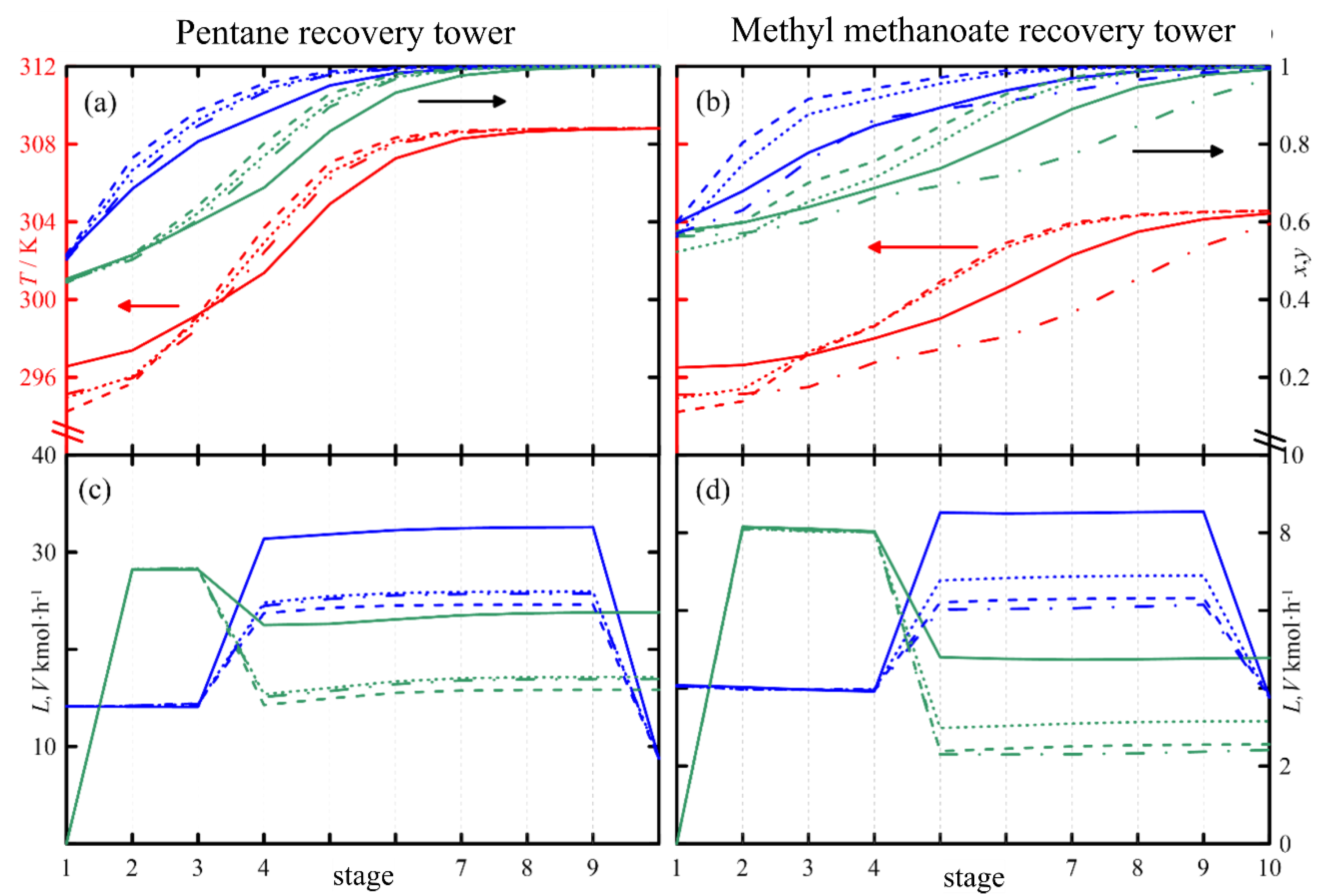
3.2. Results of the Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| A | linear constraint coefficient matrix |
| b | RHS linear constraint vector |
| excess heat capacity, J·mol−1K−1 | |
| g | nonlinear inequality constraint (Equation (1)) /molar Gibbs function (J·mol−1) (Equation (A1)) |
| gE | molar Gibbs excess function (J·mol−1) |
| NRTL binary interaction parameters (Equation (A8)) | |
| h | molar enthalpy J·mol−1/nonlinear equality constraint (Equation (1)) |
| hE | molar excess enthalpy, J·mol−1 |
| M/(Mx, My) | number of properties in the multi-property formulation/apply to ML model fitting (Equation (3)) |
| P | domain of model parameters |
| P* | Pareto set (Equation (13)) |
| p | system pressure, kPa |
| PF* | Pareto front (Equation (14)) |
| R | universal gas constant, 8314 J·mol−1K−1/reflux ratio |
| sY(·) | root mean squared error applied to generic property Y |
| sML(·) | maximum likelihood objective function (Equation (1)) |
| T | temperature, K |
| TE-out, | heat exchanger outlet temperature, K |
| ΔTE | temperature difference between cold inlet and hot outlet |
| uY | Experimental uncertainty of generic property Y (Equation (3)) |
| v | molar volume, m3mol−1 |
| vE | molar excess volume, m3mol−1 |
| wm | weighing factor of m-th generic property in error function calculation |
| x, xi, xaz | liquid-phase molar fraction vector /i-th element/composition coordinate of the azeotropic point |
| Y | generic property |
| y | vapor-phase molar fraction vector |
| Greek letters | |
| α12/α | non-randomness parameter (Equation (A5))/1st liquid phase identifier (I) |
| β | 2nd liquid phase identifier (II) |
| δ(·) | generic error metric |
| εY | ε-constraint boundary for generic property Y (Equation (15)) |
| Γij | NRTL pairwise interaction potential (Equation (A6)) |
| γ | activity coefficients |
| Θ | model vector of parameters |
| Ξ | thermodynamic canonical set |
| NRTL pairwise interaction energies (Equations (A6) and (A8)) | |
| Ω | feasible space |
| Acronyms | |
| APV88 | Aspen© NRTL parametrization using MLE |
| D/F | Distillate to feed ratio |
| FO | objective functions vector (Equation (10)) |
| LLE | liquid–liquid equilibria |
| NRTL | Non-Random Two Liquids model, Appendix A |
| MOP | Multi-objective problem |
| P1, P2, P3, P4 | NRTL parametrization obtaining after solving MOO, stated by Equation (15) |
| SLE | solid–liquid equilibria |
| UCST | upper critical solubility temperature |
| VLE | vapor–liquid equilibria |
Appendix A
Non-Random Two Liquids (NRTL) Molecular Model

References
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics, 7th ed.; McGraw-Hill: Boston, MA, USA, 2005. [Google Scholar]
- Wankat, P.C. Separations Process Engineering: Includes Mass Transfer Analysis, 3rd ed.; Prentice Hall: Boston, MA, USA, 2012. [Google Scholar]
- Prausnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Ortega, J.; Espiau, F.; Wisniak, J. New parametric model to correlate the Gibbs excess function and other thermodynamic properties of multicomponent systems. Application to binary systems. Ind. Eng. Chem. Res. 2010, 49, 406–421. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Valderrama, J.O. The state of the cubic equations of state. Ind. Eng. Chem. Res. 2003, 42, 1603–1618. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like Screening Model for Real Solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Lin, S.-T.; Sandler, S.I. A priori phase equilibrium prediction from a segment contribution solvation model. Ind. Eng. Chem. Res. 2002, 41, 899–913. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. SAFT: Equation-of-state solution model for associating fluids. Fluid Phase Equilib. 1989, 52, 31–38. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Application of the Perturbed-Chain SAFT Equation of State to Associating Systems. Ind. Eng. Chem. Res. 2002, 41, 5510–5515. [Google Scholar] [CrossRef]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Boston, MA, USA, 1998. [Google Scholar] [CrossRef]
- Pérez-Fortes, M.; Schöneberger, J.C.; Boulamanti, A.; Tzimas, E. Methanol synthesis using captured CO2 as raw material: Techno-economic and environmental assessment. Appl. Energy 2016, 161, 718–732. [Google Scholar] [CrossRef]
- Forte, E.; Burger, J.; Langenbach, K.; Hasse, H.; Bortz, M. Multi-criteria optimization for parameterization of SAFT-type equations of state for water. AIChE J. 2018, 64, 226–237. [Google Scholar] [CrossRef]
- Sosa, A.; Fernández, L.; Gómez, E.; Macedo, E.A.; Ortega, J. A practical fitting method involving a trade-off decision in the parametrization procedure of a thermodynamic model and its repercussion on distillation processes. In Distillation—Modeling, Simulation and Optimization; Steffen, V., Ed.; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Sosa, A.; Fernández, L.; Ortega, J.; Jiménez, L. The parametrization problem in the modeling of the thermodynamic behavior of solutions. An approach based on information theory fundamentals. Ind. Eng. Chem. Res. 2019, 58, 12876–12893. [Google Scholar] [CrossRef]
- Lee, Y.S.; Graham, E.J.; Galindo, A.; Jackson, G.; Adjiman, C.S. A comparative study of multi-objective optimization methodologies for molecular and process design. Comput. Chem. Eng. 2020, 136, 106802. [Google Scholar] [CrossRef]
- Forte, E.; Kulkarni, A.; Burger, J.; Bortz, M.; Küfer, K.-H.; Hasse, H. Multi-criteria optimization for parametrizing excess Gibbs energy models. Fluid Phase Equilib. 2020, 522, 112676. [Google Scholar] [CrossRef]
- Franzosini, P.; Geangu-Moisin, A.; Ferloni, P. Some Remarks on methylformate + n-alkanes Binary Systems. Z. Naturforsch. A 1970, 25, 457–458. [Google Scholar] [CrossRef][Green Version]
- Fernández, F.; Ortega, J.; Sabater, G.; Espiau, F. Experimentation and thermodynamic representations of binaries containing compounds of low boiling points: Pentane and alkyl methanoates. Fluid Phase Equilib. 2014, 363, 167–179. [Google Scholar] [CrossRef][Green Version]
- Gmehling, J.; Onken, U.; Rarey-Nies, J.R.; Arlt, W.; Weidlich, U.; Grenzheuser, P.; Kolbe, B. Vapor-liquid Equilibrium Data Collection DECHEMA Chemistry Data Series; DECHEMA: Frankfurt, Germany, 1977; Volume 1–8. [Google Scholar]
- Marina, J.M.; Tassios, D.P. Effective local compositions in phase equilibrium correlations. Ind. Eng. Chem. Process. Des. Dev. 1973, 12, 67–71. [Google Scholar] [CrossRef]
- Fredenslund, A.A.; Gmehling, J.; Rasmussen, P. Vapor-Liquid Equilibria Using UNIFAC. A Group-Contribution Method; Elsevier: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Britt, H.I.; Luecke, R.H. The estimation of parameters in nonlinear, implicit models. Technometrics 1973, 15, 233–247. [Google Scholar] [CrossRef]
- Anderson, T.F.; Abrams, D.S.; Grens, E.A. Evaluation of parameters for nonlinear thermodynamic models. AIChE J. 1978, 24, 20–29. [Google Scholar] [CrossRef]
- Ortega, J.; Espiau, F. A new correlation method for vapor−liquid equilibria and excess enthalpies for nonideal solutions using a genetic algorithm. Application to ethanol+an n-alkane mixtures. Ind. Eng. Chem. Res. 2003, 42, 4978–4992. [Google Scholar] [CrossRef]
- Fernández, L.; Ortega, J.; Pérez, E.; Toledo, F.J.; Canosa, J. multiproperty correlation of experimental data of the binaries propyl ethanoate + alkanes (pentane to decane). New experimental information for vapor–liquid equilibrium and mixing properties. J. Chem. Eng. Data 2013, 58, 686–706. [Google Scholar] [CrossRef]
- Espiau, F.; Ortega, J.; Penco, E.; Wisniak, J. Advances in the correlation of thermodynamic properties of binary systems applied to methanol mixtures with butyl esters. Ind. Eng. Chem. Res. 2010, 49, 9548–9558. [Google Scholar] [CrossRef]
- Ríos, R.; Ortega, J.; Sosa, A.; Fernández, L. Strategy for the management of thermodynamic data with application to practical cases of systems formed by esters and alkanes through experimental information, checking-modeling, and simulation. Ind. Eng. Chem. Res. 2018, 57, 3410–3429. [Google Scholar] [CrossRef]
- Espiau, F.; Ortega, J.; Fernández, L.; Wisniak, J. Liquid–liquid equilibria in binary solutions formed by [pyridinium-derived][F4 B] ionic liquids and alkanols: New experimental data and validation of a multiparametric model for correlating LLE data. Ind. Eng. Chem. Res. 2011, 50, 12259–12270. [Google Scholar] [CrossRef]
- Ko, M.; Im, J.; Sung, J.Y.; Kim, H. Liquid-liquid equilibria for the binary systems of sulfolane with alkanes. J. Chem. Eng. Data 2007, 52, 1464–1467. [Google Scholar] [CrossRef]
- Pareto, V. Cours d’économie Politique; Librairie Droz: Geneva, Switzerland, 1964. [Google Scholar]
- Mavrotas, G. Effective implementation of the e-constraint method in Multi-Objective Mathematical Programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Coello, C.; Lamont, G.; Van Veldhuisen, D. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Belotti, P.; Kirches, C.; Leyffer, S.; Linderoth, J.; Luedtke, J.; Mahajan, A. Mixed-integer nonlinear optimization. Acta Numer. 2013, 22, 1–131. [Google Scholar] [CrossRef]
- Sahinidis, N.V. BARON: A general purpose global optimization software package. J. Glob. Optim. 1996, 8, 201–205. [Google Scholar] [CrossRef]
- Černý, V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Mishra, D.K.; Shinde, V. A review of global optimization problems using meta-heuristic algorithm. In Nature-Inspired Optim. Algorithms; Khamparia, A., Khanna, A., Bao Le, N., Nhu Gia, N., Eds.; De Gruyter: Berlin, Germany, 2021; pp. 87–106. [Google Scholar] [CrossRef]
- Kraft, D. Algorithm 733; TOMP-Fortran modules for optimal control calculations. ACM Trans. Math. Softw. 1994, 20, 262–281. [Google Scholar] [CrossRef]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package, Version 2.6.1; GitHub: San Francisco, CA, USA, 2019. [Google Scholar]
- Seader, J.D.; Henley, E.J. Separation Process Principles, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]


| −7.261/−6.811 | 2375.23/1878.42 | 0/0 | 0/0 | 0.2 |
| s(LLE) | s(VLE) | s(hE/RT) | ||
| 0.0142 | 0.2994 | 0.0179 |
| 1.18 × 106/29.28 | −2.87 × 107/105.6 | −2.09 × 105/−5.37 | 3.93 × 102/9.40×10−3 | 0.002 |
| s(LLE) | s(VLE) | s(hE/RT) | ||
| 0.098 | 0.815 | 0.017 |
| P1 | 20.000/18.845 | 2376.45/1879.56 | −7.817/−6.099 | 0.0691/0.0247 | 0.0308 |
| P2 | 12.746/24.428 | 2379.16/1882.88 | −8.113/−6.249 | 0.1145/−0.0038 | 0.0144 |
| P3 | 34.675/30.078 | 2377.47/1880.99 | −10.000/−10.000 | 0.1381/−0.0095 | 0.0027 |
| P4 | 30.764/31.139 | 2377.50/1881.07 | −9.999/−9.445 | 0.1325/−0.0053 | 0.0041 |
| s(LLE) | s(ELV) | s(hE/RT) | |||
| P1 | 0.0137 | 0.2995 | 0.0203 | ||
| P2 | 0.0338 | 0.0310 | 0.0175 | ||
| P3 | 0.0201 | 0.1079 | 0.0860 | ||
| P4 | 0.0220 | 0.1079 | 0.0180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, L.; Ortega, J.; Sosa, A. Parametrization of the NRTL Model with a Multiobjective Approach: Implications in the Process Simulation. Thermo 2022, 2, 267-288. https://doi.org/10.3390/thermo2030019
Fernández L, Ortega J, Sosa A. Parametrization of the NRTL Model with a Multiobjective Approach: Implications in the Process Simulation. Thermo. 2022; 2(3):267-288. https://doi.org/10.3390/thermo2030019
Chicago/Turabian StyleFernández, Luis, Juan Ortega, and Adriel Sosa. 2022. "Parametrization of the NRTL Model with a Multiobjective Approach: Implications in the Process Simulation" Thermo 2, no. 3: 267-288. https://doi.org/10.3390/thermo2030019
APA StyleFernández, L., Ortega, J., & Sosa, A. (2022). Parametrization of the NRTL Model with a Multiobjective Approach: Implications in the Process Simulation. Thermo, 2(3), 267-288. https://doi.org/10.3390/thermo2030019






