Abstract
It is shown that the inert properties of a stationary random process can be expressed in terms of the ratio of its correlation interval to the doubled variance Dx. When using a fixed value of Planck’s constant h as a proportionality factor, the ratio has the dimension of a kilogram and can be used as an equivalent of a mass standard. It is proposed to use thermal (i.e., Johnson–Nyquist) noise as a reference Gaussian stationary random process. The theoretical substantiation of the project for the creation of “thermoelectric semiconductor ampere-balances” for balancing the inert mass of a quasi-ideal silicon-28 ball is also given. Combining these two projects can provide the basis for a stable and reproducible mass standard.
1. Introduction
The decisions of the 26th General Conference on Weights and Measures (GCWM), dedicated to the “Revision of the International System of Units (SI)”, summed up the implementation of the program for “immaterial” definitions of standards of basic physical quantities.
Starting from 20 May 2019 to implement the new definition of units of measurement, it is necessary to use any equations of physics that relate the mass, Planck’s constant h = 6.62607015 × 10−34 Js, the speed of light in a vacuum c = 299,792,458 m/s, the frequency of the hyperfine transition of the ground state of the cesium-133 atom vCs = 9,192,631,770 Hz, the elementary charge e = 1.602,176,634 × 10−19 C, the Boltzmann constant kB = 1.380649 × 10−23 J/K and the Avogadro constant NA = 6.02214076 × 1023 mol−1.
One of the main directions in the implementation of the mass standard based on the new definition of SI is the development of two projects: “Kibble balance” and “Counting atoms in a quasi-ideal ball of silicon-28 (28Si)” (hereinafter “Counting atoms”) [1,2]. This area of research is also called «The X-ray-crystal-density (XRCD) method».
“Kibble balance” is based on the relationship between gravitational mass and Planck’s constant [3,4,5].
where j is an integer associated with the Landau factor in the quantum Hall effect;
d is an integer associated with the Shapiro steps in the Josephson effect;
f is the excitation frequency of the transition between two superconductors in the Josephson effect;
v is the speed of movement of the winding in a constant magnetic field;
is the free fall acceleration at the location of the watt balance.
“Counting atoms” (or XRCD method) is due to the proportionality between the inert mass of 28Si and the Avogadro constant [1]
where mSi is the atomic mass of 28Si; vSi is the number of moles of 28Si in 1 kg.
These projects are related to each other, because without quasi-ideal 28Si balls having a mass of 1 kg with a relative error of about 10–8, it is impossible to compare the readings of “Kibble balances” located in various laboratories around the world. On the other hand, without the “Kibble balance”, it is impossible to verify the equivalence of the inert mass of a quasi-ideal 28Si ball to its gravitational mass [1].
In other words, the weight of each quasi-ideal 28Si ball must be balanced by Kibble balances with a maximum allowable uncertainty of no more than 10−8 kg. In this case, quasi-ideal 28Si balls, which should be included in the Kibble balance, can be used to compare the readings of similar watt-balances located in different places on the planet.
The presence of only one Kibble scale on the planet will lead to similar problems with the international prototype of the kilogram held by the International Bureau of Weights and Measures.
Both of the above projects are an undoubted progress in the field of practical metrology, because their accuracy increases by an order of magnitude the accuracy of the international prototype of the kilogram, stored in the International Bureau of Weights and Measures. Furthermore, these projects are reproducible in any laboratory in the world based on the above fundamental physical principles and fixing the numerical values of the constants h and NA.
At the same time, these projects have a number of shortcomings [1].
The Kibble balance is one of the most complex measuring systems in the world, because in addition to using the superconducting Josephson effect and the quantum Hall effect, it is necessary to measure with high accuracy the speed v of the coil in a uniform magnetic field, as well as the free fall acceleration at the location of the watt-balance.
The disadvantages of the silicon ball include the possibility of contamination of its surface. In addition, 28Si crystals are never perfect and monoisotopic [1]. Therefore, it is necessary to take into account corrections for the content of impurities, for defects in the 28Si crystal lattice (vacancies and interstices), for the formation of an oxide film, and for adsorbed water molecules by the surface layer of the silicon ball. It is also necessary to take into account the mass defect related to the binding energy of the atoms of the 28Si single crystal [1].
This article proposes a different, stochastic approach to determining the mass standard, based on the relationship between the ratio of the main averaged characteristics of a stationary random process and the ratio of Planck’s constant to the mass of a particle participating in this process.
2. Relationship between Mass, Planck’s Constant and the Characteristics of a Stationary Random Process
The article [6] considers a stationary random process associated with the change in the projection of the location of a chaotic wandering particle (such as a Brownian particle) with time t (see Figure 1).
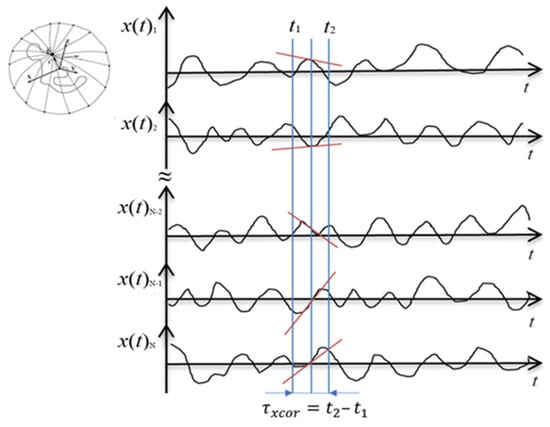
Figure 1.
N realizations of a stationary random process with an autocorrelation interval τx ≈ τxcor. These implementations can be interpreted, for example, as changes over time t of the projection onto the X axis of the location of a particle randomly wandering in a closed region of 3-dimensional space.
As a result of the analysis of this stationary random process x(t) in [6], the following procedure was developed for obtaining the probability density function (PDF) ρ(x′) of the derivative of this process with a known one-dimensional PDF ρ(x) of the process itself:
- (a)
- The initial one-dimensional PDF ρ(x) of a stationary random process is represented as a product of two probability amplitudes (PAs):
- (b)
- two Fourier transforms are performed:
- (c)
- The desired PDF of the derivative of the studied stationary random process is found:where, according to Equation (52) in [6],
- σx is the standard deviation of the original stationary random process x(t);
- τx is autocorrelation interval of the same random process (see Figure 1).
For example, consider a Gaussian stationary random process x(t). In each section ti of this process, the random variable x is distributed according to the Gaussian law:
where σx2 = Dx and ax are the variance and expected value, resp., of the random process x(t) under study.
According to Equation (3), we represent PDF (8) as a product of two probability amplitudes
where
Let us substitute PA (9) into Equations (4) and (5):
and perform the
In accordance with Equation (6), we multiply the PAs (12) and (13), as a result we get
is the PDF of the derivative of the stationary Gaussian random process x(t).
In quantum mechanics, for the transition from the coordinate representation of the position of the particle
A similar procedure is applied to its momentum representation
where in the non-relativistic case (i.e., at low particle speeds compared to the speed of light)
is the x-component of the particle’s momentum, which is related to its velocity vx (i.e., the derivative of its coordinate x with respect to time);
is the reduced Planck constant.
ℏ = h/2π
The PDF of the x-component of the particle momentum is equal to
If the position of the particle is described by the Gaussian PDF (8), then performing actions (15)–(20) we obtain
Taking into account Equation (18), we have the PDF of the derivative of the random process under study:
Comparing the PDFs of the derivatives (14) and (22), we find that if the stochastic and quantum mechanical approaches considered above refer to the same stationary random process, then
Let us write this relation taking into account Equation (7):
Both sides of this ratio have the dimension of kinematic viscosity [m2/s].
Relationship (24) implies a connection between the inertial mass of a chaotically wandering particle, the reduced Planck constant and the main characteristics of a stationary random process in which this particle participates:
It can be seen from Equation (25) that the ratio determines the inert properties of a chaotically wandering particle. The larger the autocorrelation interval of the random process under study, the smoother the change in the direction of particle motion (i.e., the more inert). On the other hand, the greater the dispersion (characterizing the average deviation of a wandering particle from the average value), the less its resistance (inertia).
Thus, the inert properties of a chaotically wandering particle are directly proportional to and inversely proportional to .
3. Statistical Approach to the Determination of the Mass Standard
Let us rewrite relation (25) taking into account (19):
The use of relation (26) to determine the mass standard is fully consistent with the resolutions of the 26th GCWM. Indeed, in this expression there is a direct relationship between the mass and Planck’s constant h.
Therefore, if in nature there is a sufficiently stable stationary random process x(t) with PDF close to Gaussian, then it can be taken as a standard and put as the basis for determining the standard of inertial mass.
To do this, it is necessary to make two representative samples from this process: xk1 (into section t1) and xk2 (into section t2) (see Figure 1), at a distance between sections (where is an estimate of the autocorrelation interval), at which Pearson’s autocorrelation coefficient is less than some critical parameter steadily tending to zero () (see Figure 2):
were , —expected value and variance in cross section t1;
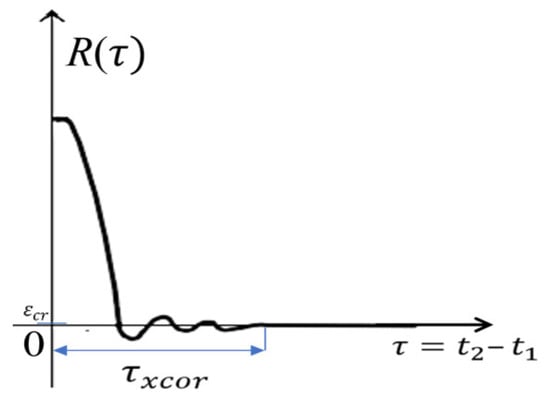
Figure 2.
The autocorrelation interval. is the time interval between the values of the correlation function R(τ = 0) and R(, where is a small critical parameter steadily tending to zero ( → 0).
, —expected value and variance in cross section t2.
For a stationary random process, the following conditions are met:
Therefore, Equation (26) can be represented as an approximate equality
To use Equation (29) as an equivalent of the mass standard, it is necessary to:
- 1.
- Choose a stable stationary random process with PDF close to a Gaussian distribution, which can be carried out in any metrological laboratory;
- 2.
- Estimate its variance (with a confidence level corresponding to nσx = n, where n is any natural number providing a given level of accuracy);
- 3.
- Estimate the correlation interval at a fixed value of the critical parameter .
4. Reference Thermal Noise
The thermal noise of the resistor c (i.e., the Johnson-Nyquist noise) is proposed as a reference stationary random process with an almost-Gaussian PDF.
The spectral density of the squared average electromotive force (EMF) of thermal noise has the form [7]
where T is the temperature and R is the resistance.
The graph of this function is shown in Figure 3.
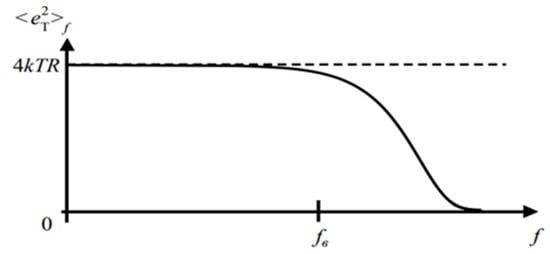
Figure 3.
The spectral density of squared average EMF of the thermal noise.
The autocorrelation function of thermal noise can be obtained using the inverse Fourier transform
However, in the frequency range for which the inequality
spectral density (30) can be considered constant, i.e., frequency independent (Nyquist formula) [7]:
Therefore, thermal noise in a wide range from 0 Hz to the upper frequency of the
can be viewed as white noise with an autocorrelation function:
where δ(τ) is the delta function;
is the variance of the considered stationary random process (i.e., thermal noise).
We multiply Equation (35) by a constant value, composed of the fundamental physical constants
As a result, we get the value
Its reciprocal
Therefore, the value (38) can be put in accordance with relation (24)
This relation allows expressing the mass in terms of thermal noise parameters (i.e., a stable, stationary random process):
For the most accurate determination of the resistance R, we can use the quantum Hall effect [8,9]
where j is an integer associated with the Landau filling factor.
Substituting Equation (41) into relation (40), we obtain
This relation corresponds to the formula of A. Einstein for the equivalence of the energy E and the mass
At the same time, the equivalence of mass m = 1 kg corresponds to a large value of thermal energy
However, the International System of Units (SI) allows the use of fractional quantities. Therefore, fraction of 1 kg can be taken as the equivalent of the mass standard.
Formally, with fixed values of the fundamental constants kB and c, nothing prevents us from taking as a mass standard the value corresponding to the temperature, for example, the triple point of water Ti = 273.16 K, or any other referent thermal scale points, for example, the crystallization point of aluminum Ti = 933.473 K or the crystallization point of copper Ti = 1357.77 K. Then expression (42) for j = 1 takes the form
It remains to solve the problem of transferring this unit to measuring instruments.
5. Thermoelectric Semiconductor Ampere Balance
For the above task, it is proposed to use an ampere-balance, in which the counterweight to the gravitational mass is created by a heated looped conductor located in a constant magnetic field.
In such a looped conductor, there should be thermal noise with a spectral current density [7]
where is one of the reference points of the temperature scale.
Rk = Lρ is the resistance of the looped conductor (L is the length of the conductor, i.e., the circumference; ρ is the linear resistance of the conductor).
However, thermal noise in a conductor is a Gaussian multidirectional random process (Figure 4).
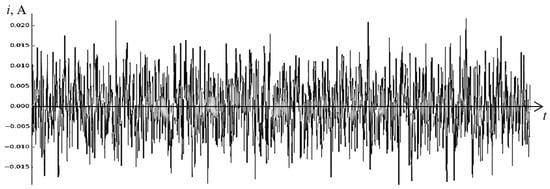
Figure 4.
Thermal noise in a looped conductor with resistance Rk..
Therefore, it should be expected that in a constant magnetic field such a looped conductor, on average, will remain motionless.
In this regard, it is proposed to use a semiconductor ring with an equivalent circuit shown in Figure 5.
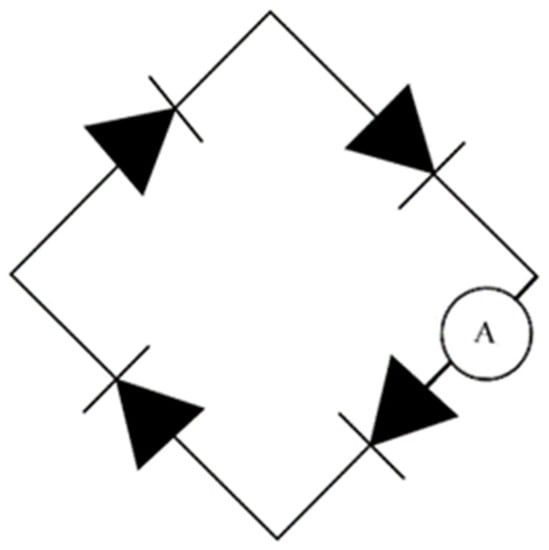
Figure 5.
The semiconductor ring equivalent circuit.
The idea of the semiconductor ring shown in Figure 5 belongs to the MAI master Alexander Bindiman.
In this case, it can be assumed that in such a looped semiconductor, an average direct current should circulate (see Figure 6), approximately equal to the standard deviation of thermal noise.
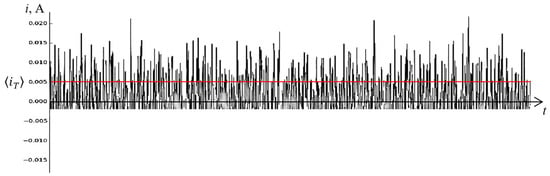
Figure 6.
Expected thermal noise in a semiconductor ring.
On closer examination, it should be taken into account that there are potential barriers (i.e., p-n junctions) in a semiconductor ring; therefore, a shot noise component can also exist in it, and other quantum effects are also possible. If such quantum effects are discovered, then the measurement accuracy will increase significantly.
The thermoelectric effect can be enhanced by stacking n semiconductor rings isolated from each other. In this case, the total average noise current of a stack of semiconductor rings can be estimated by the expression
It is possible that in thin semiconductor rings (several Angstroms thick) located in a constant magnetic field, high-temperature quantum effects, such as the quantum Hall effect, can be observed. If such an effect is detected, then Rk will be determined by an expression like (41), while the accuracy of determining the thermal current (48) will increase significantly:
If this hypothesis is experimentally confirmed, then this thermoelectric effect can be used to create semiconductor ampere scales designed to transfer a unit of weight to a reference (or model) measuring instrument. The scheme of such semiconductor thermoelectric ampere scales is shown in Figure 7.
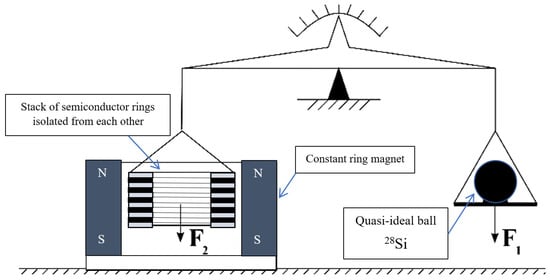
Figure 7.
The scheme of thermoelectric semiconductor ampere-balances for transferring a measure of mass to a reference or exemplary measuring instrument (in particular, a quasi-ideal silicon ball).
In such scales, the gravity force acting on an exemplary load (in this case, a quasi-ideal silicon ball) is compensated by the Ampere force
where is the coefficient of proportionality, which functionally depends on the magnetic induction B created by the constant ring magnet (Figure 7) and the length of the active part of the semiconducting ring l:
The equality of forces F1 and F2, taking into account expression (49), leads to the relation
As a reference (or exemplary) measuring instrument, a quasi-ideal 28Si ball with a mass of 1 can be used, with the help of which a unit of mass can be transferred to other measuring instruments, according to an appropriate verification scheme, and comparison of readings with thermoelectric semiconductor ampere-scales located in various laboratories of the world.
Based on expression (51), we can take as a mass standard the value corresponding to the temperature, for example, of zinc crystallization Ti = 692.677 K:
Let B = 1 T, l = 1 m, g = 9.81 m/s2 and n = 1. Then
In order for the right side of Equation (52) to be equal to 1 g, it is necessary that the stack of isolated looped semiconductors consists of layers. Indeed, substituting the given value of n into Equation (52):
If it is possible to obtain a thickness of one insulated semiconductor layer of the order of 1.4 Å = 1.4 10−10 m, then a stack of such layers will turn out to be a height of the order of
The creation of such a stack of isolated looped semiconductors is at the edge of the possibilities of modern nanotechnology. It is possible to increase the thickness of the semiconductor layer with a significant increase in B and Ti, and a decrease in Rk. For example, at Rk = 100 Ω, B = 1T and Ti = 692.677 K, we obtain the value
which is more than two orders of magnitude larger than (53). Therefore, the thickness of the looped semiconductor layer in a stack 1 m high can be increased by approximately two orders of magnitude up to ~10−8 m.
Unfortunately, at this stage of the study, it is impossible to establish the main limitations of the proposed method. The main metrological characteristics of the thermoelectric semiconductor ampere-balances can be established only during the experimental implementation of this project.
6. Conclusions
Fixing the numerical values of the fundamental physical constants h, e, kB, c and NA on the basis of the resolutions of the 26th GCWM opens up wide possibilities for applying various physical principles to determine the standards of physical quantities.
In particular, this article proposes to use the possibility of expressing the ratio of the Planck constant to the mass of a particle through the ratio of the main averaged characteristics of a Gaussian stationary random process: the doubled variance to the autocorrelation coefficient of this process (24). Whence follows the desired dependence (29)
As a realization of this idea, the theoretical possibility of using thermal noise as a Gaussian stationary random process is considered.
As a result, it is shown that, based on Equation (51), it is possible to take as a mass standard the value corresponding to the thermodynamic temperature, for example, the triple point of water Ti = 273.16 K (or any other reference point on the temperature scale, for example, aluminum crystallization point Ti = 933.473 K, or zinc crystallization point Ti = 692.677 K):
This effect is barely perceptible. For example, at Ti = 692.677 K, B = 1T, l = 1 m, = 9.81 m/s2, n = 1 and j = 1, according to (53), . However, it all depends on what value to take as the mass standard. For example, if we take the Planck mass Mp = 2.176434 × 10−5g as a standard, then by selecting the parameters Ti, B, l, n and j, you can achieve m ≈ Mp with a given accuracy at a quite acceptable temperature, magnetic field and thickness of the looped semiconductor layer of the stack (Figure 7).
It is possible that the creation of thermoelectric semiconductor ampere-balances will turn out to be a no less complex and expensive project than the Kibble balance. However, the hope for success is inspired by the fact that in Equation (57), there are fewer parameters to be measured and controlled than in Equation (1). In addition, the measurement of magnetic thrust in the thermoelectric method is carried out in one stage, and in the Kibble balance, the fictitious power is obtained in two stages.
At the same time, the “thermal electric effect” proposed for study is associated with the creation of traction without energy supply from an external power source. In this case, for the occurrence of accelerated motion of a stack of looped semiconductors (Figure 7), it is sufficient to have a constant magnetic field and an environment with a high temperature.
The measuring setup shown in Figure 7 involves the development of two projects: (1) the creation of thermoelectric semiconductor ampere-balances; and (2) the creation of a quasi-ideal silicon-28 ball with an inertial mass of about 1 g.
Only by combining these two projects into one project will it be possible to provide verification schemes with an accuracy corresponding to the requirements of the 26th GCWM, and to compare the readings of thermoelectric semiconductor ampere-balances located in various laboratories of the world.
Combining these two projects can provide the basis for a stable and reproducible mass standard, since these projects can complement each other and increase the accuracy of measurements due to mutual balancing.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Moscow Aviation Institute.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
For the discussion of the issues raised in this article, I express my gratitude to the Deputy Director of VNIIMS L.K. Isaev; David Reid; Ph.D, senior researcher M.A. Butyugin; head of the VNIIMS department B.A. Ipolitov, Ph.D; senior researcher V.I. Chesnokov; D.V. Gritsaenko; and A.P. Bindiman.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mana, G.; Schlamminger, S. The kilogram: Inertial or gravitational mass? arXiv 2022, arXiv:2201.12136. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Ivashchuk, V.D.; Kalinin, M.I.; Khrushchev, V.V. Evolution of the System of Measurement Units. Toward a Future Revision of the International System of Units (SI)/Legislative and Applied Metrology, No. 2. 2018. Available online: https://www.vniims.ru/activities/redakcionno-izdatelskaya-deyatelnost/zakon_and_prikl/archive/main_2_2018.php (accessed on 6 July 2022).
- Kibble, B.P.; Robinson, I.A.; Belliss, J.H. A Realization of the SI Watt by the NPL Moving-coil Balance. Metrologia 1990, 27, 173. [Google Scholar] [CrossRef]
- Schlamminger, S.; Haddad, D. The Kibble balance and the kilogram. Comptes Rendus Physique 2019, 20, 55–63. [Google Scholar] [CrossRef]
- Li, S.S.; Zhang, Z.H.; Zhao, W.; Li, Z.K.; Huang, S.L. Progress on accurate measurement of the Planck constant: Watt balance and counting atoms. Chin. Phys. B 2014, 24, 010601. [Google Scholar] [CrossRef][Green Version]
- Batanov-Gaukhman, M. Derivation of The Generalized Time-Independent Schrödinger Equation. The New Stochastic Quantum Mechanics: “Think and Calculate”. Av. Cienc. Ing. 2020, 11, Articulo 6. Available online: https://www.executivebs.org/publishing.cl/avances-en-ciencias-e-ingenieria-vol-11-nro-4-ano-2020-articulo-6/ (accessed on 2 July 2022).
- Yakimov, A.V. Physics of Noise and Fluctuations of Parameters. Nizhny Novgorod State University. N.I. Lobachevsky-th, 85C. 2013. Available online: http://www.unn.ru/books/met_files/Yakimov_Noise.pdf (accessed on 22 June 2022).
- Verin, O.G. Quantum Hall Effect and Superconductivity. 2019. Available online: http://www.sciteclibrary.ru/yabb26.pdf (accessed on 13 June 2022).
- Gavrilenko, V.I.; Ikonnikov, A.V. Quantum Hall Effect. Nizhny Novgorod State University. N.I. Lobachevsky. 2010. Available online: http://www.unn.ru/books/met_files/QHE.pdf (accessed on 4 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).