Implicit Equation for Photovoltaic Module Temperature and Efficiency via Heat Transfer Computational Model
Abstract
:1. Introduction
1.1. Photovoltaic (PV) Panel Operating Temperature
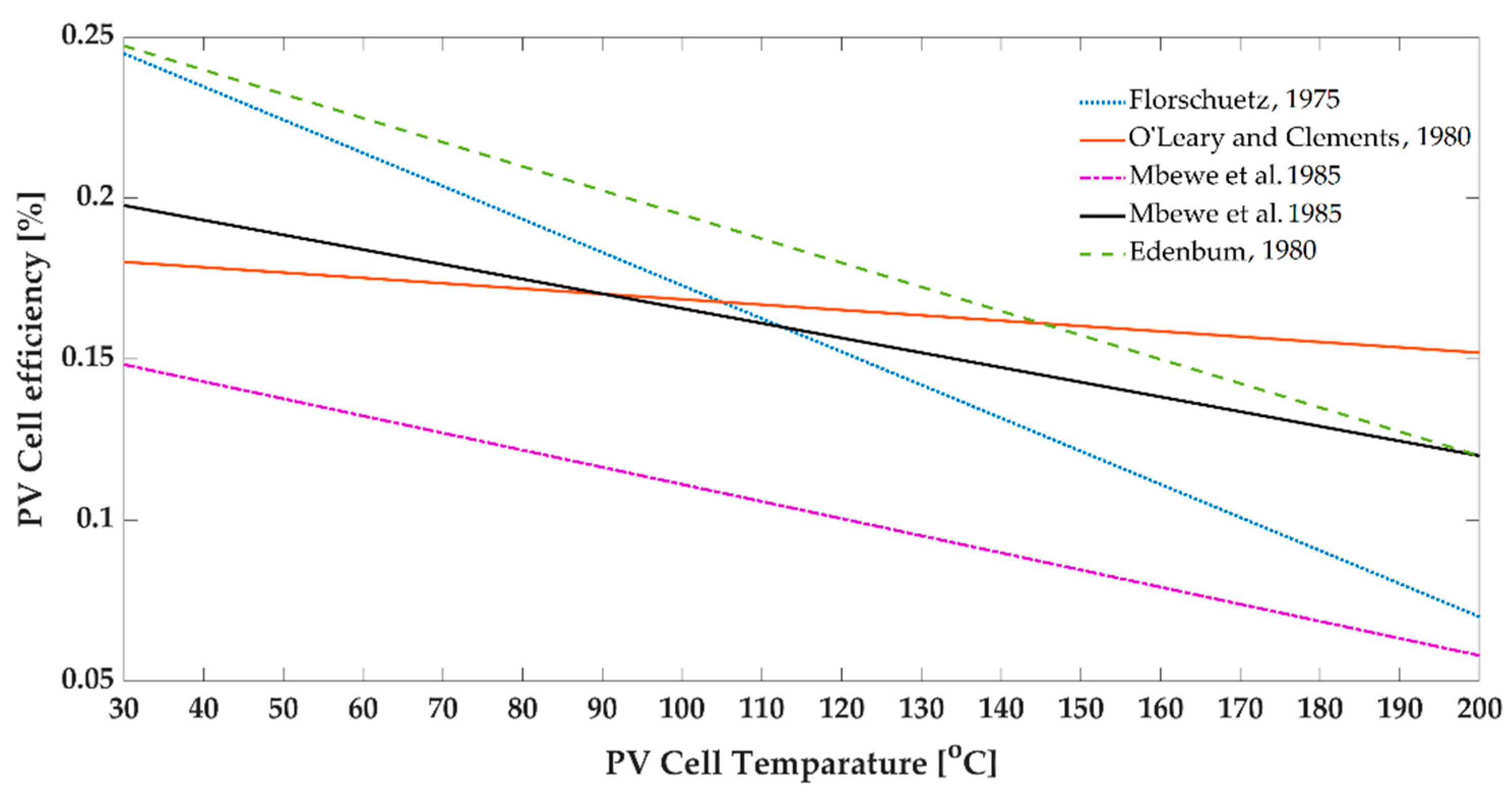
1.2. Heat Transfer Model of Thermal Collectors and Solar Panels
1.3. Aim of This Study
2. Methods
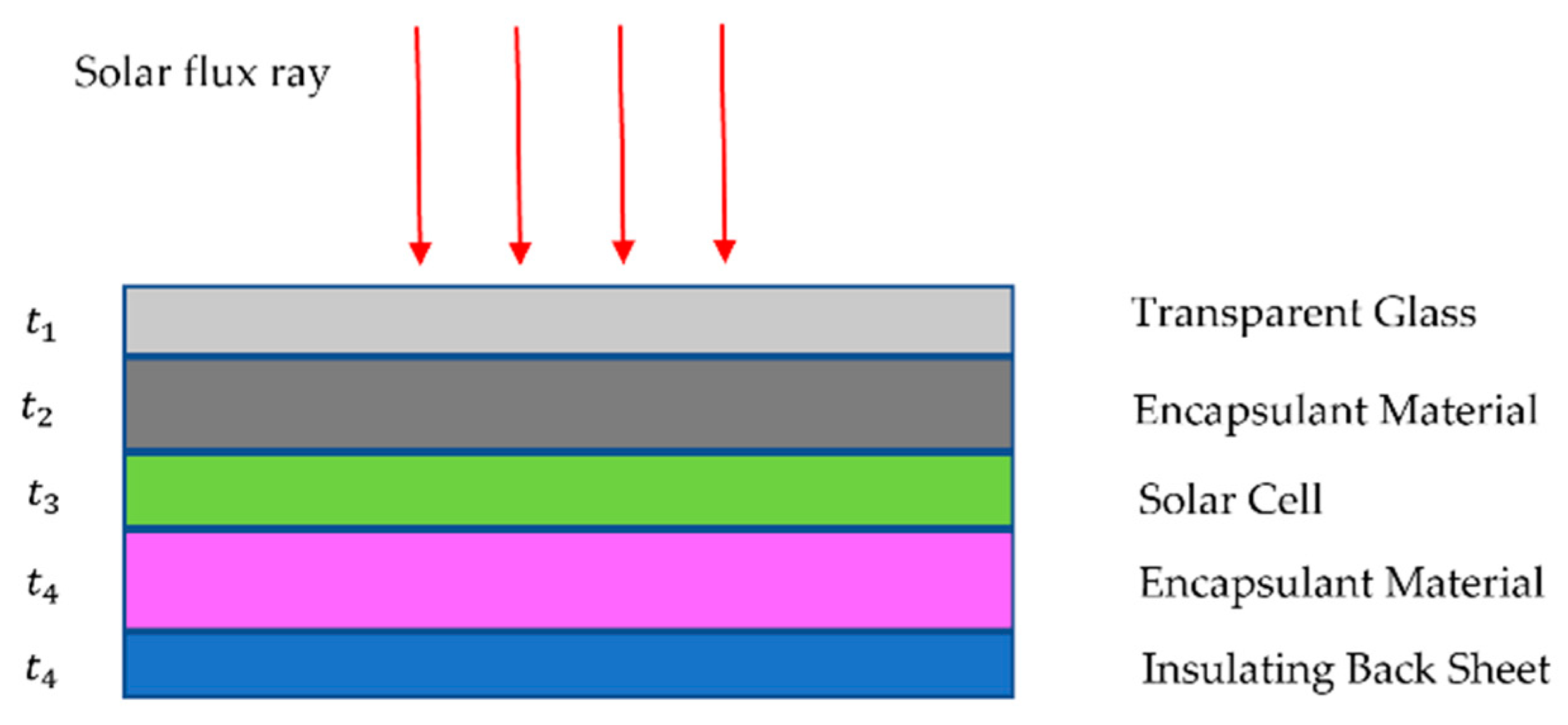
2.1. PV Module Structure and Setup
2.2. Environment Surrounding the PV Module
2.3. Theory
2.3.1. Solar Flux on the PV Module
2.3.2. Radiation to/from the PV Module
2.3.3. PV Module Output
2.3.4. Wind Speed Effect on the PV Module
2.3.5. Heat Transfer Convection in the PV Module
2.3.6. PV Module Heat Transfer Model
- -
- Solar flux.
- -
- Solar beam orientation.
- -
- PV module tilt angle.
- -
- Airflow properties, most of which function as ambient temperature.
- -
- PV module operating temperature related to ambient temperature.
- -
- PV module temperature is a function of the PV module area.
- -
- There is a functionality between the PV module operating temperature and the PV module efficiency.
2.3.7. Numerical Solution
3. Results
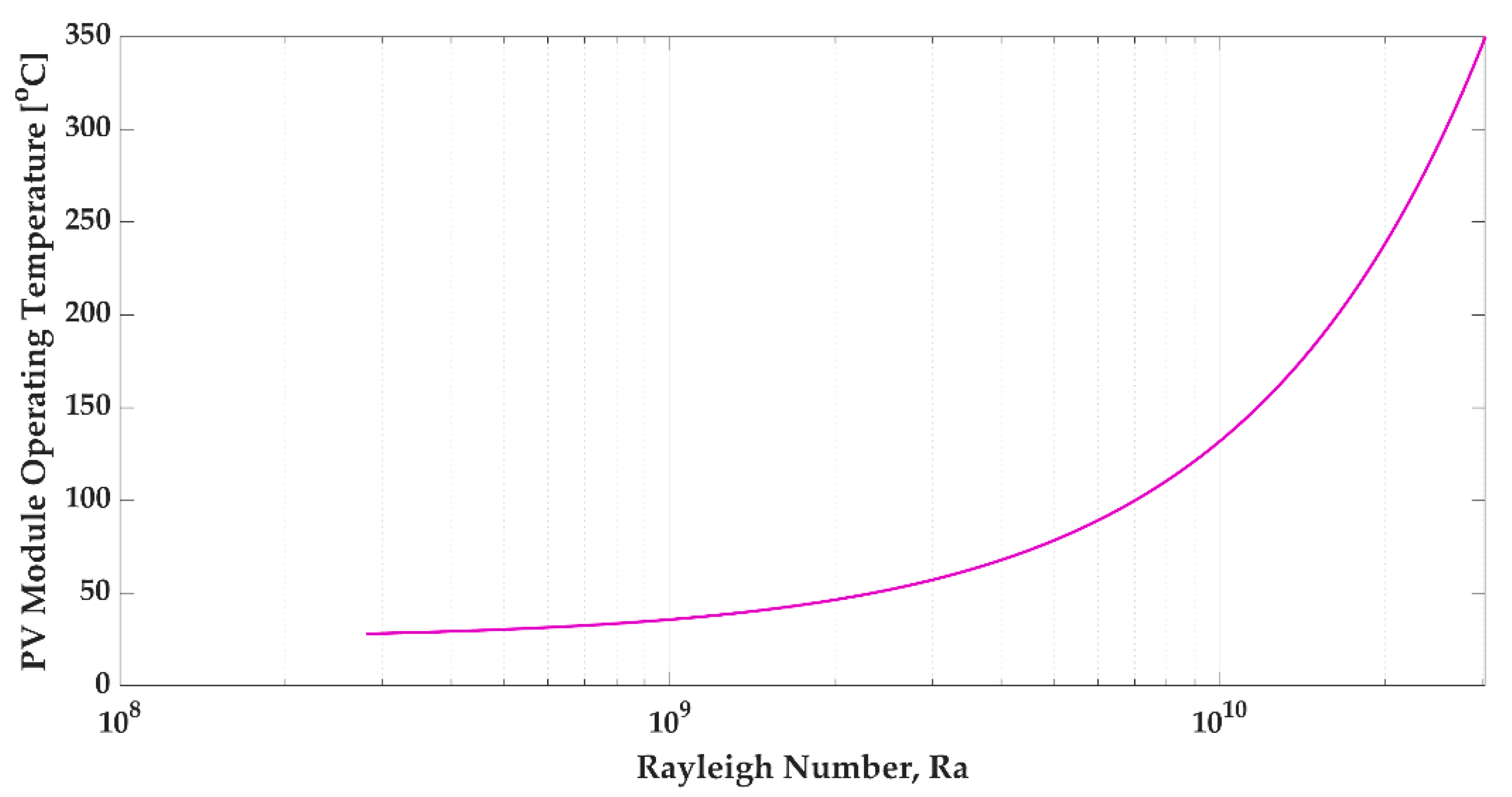
3.1. Rayleigh Number Evaluation
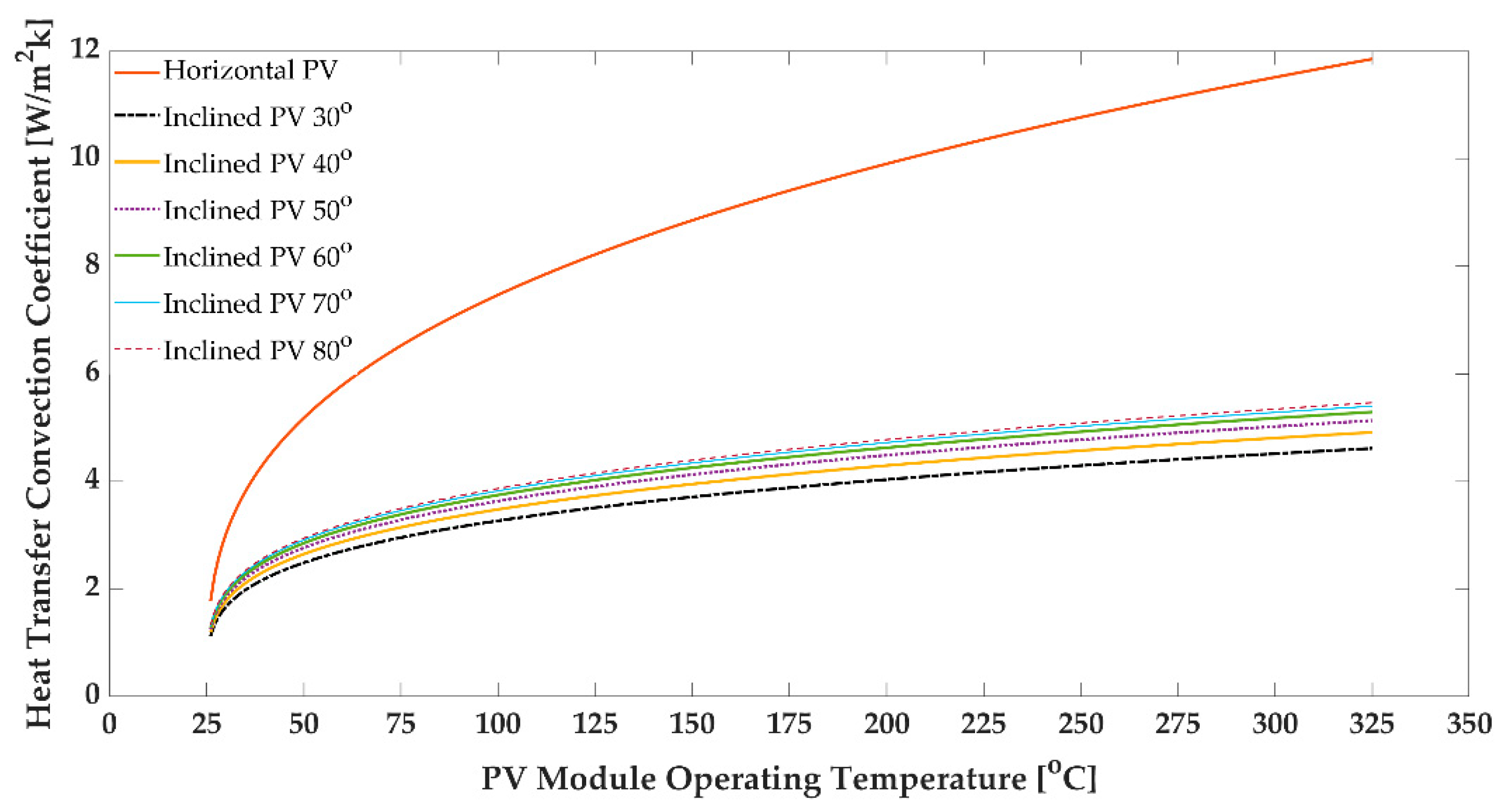
3.2. Convection Heat Transfer Coefficient on the PV Module
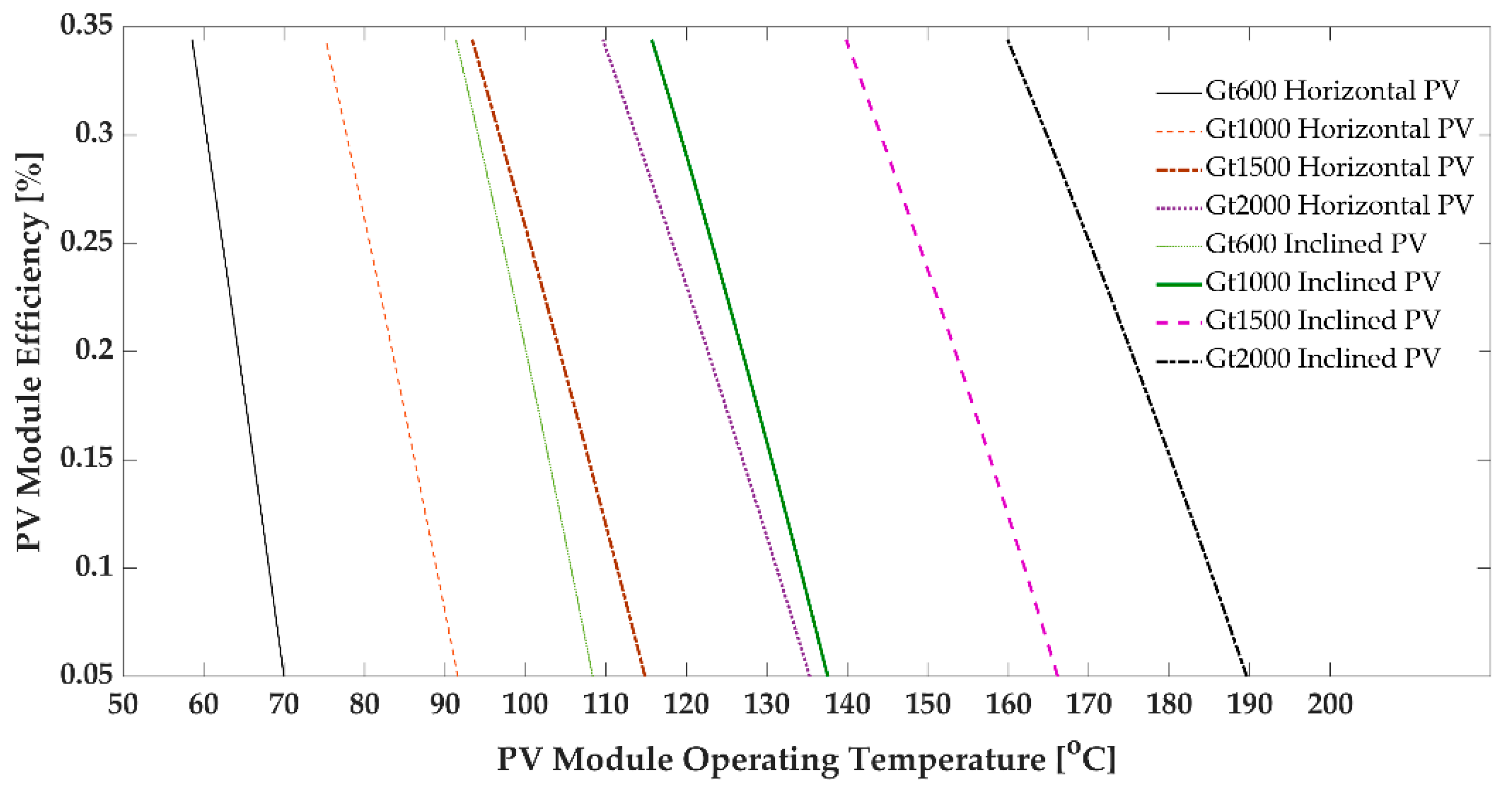
3.3. PV Module Efficiency and Temperature
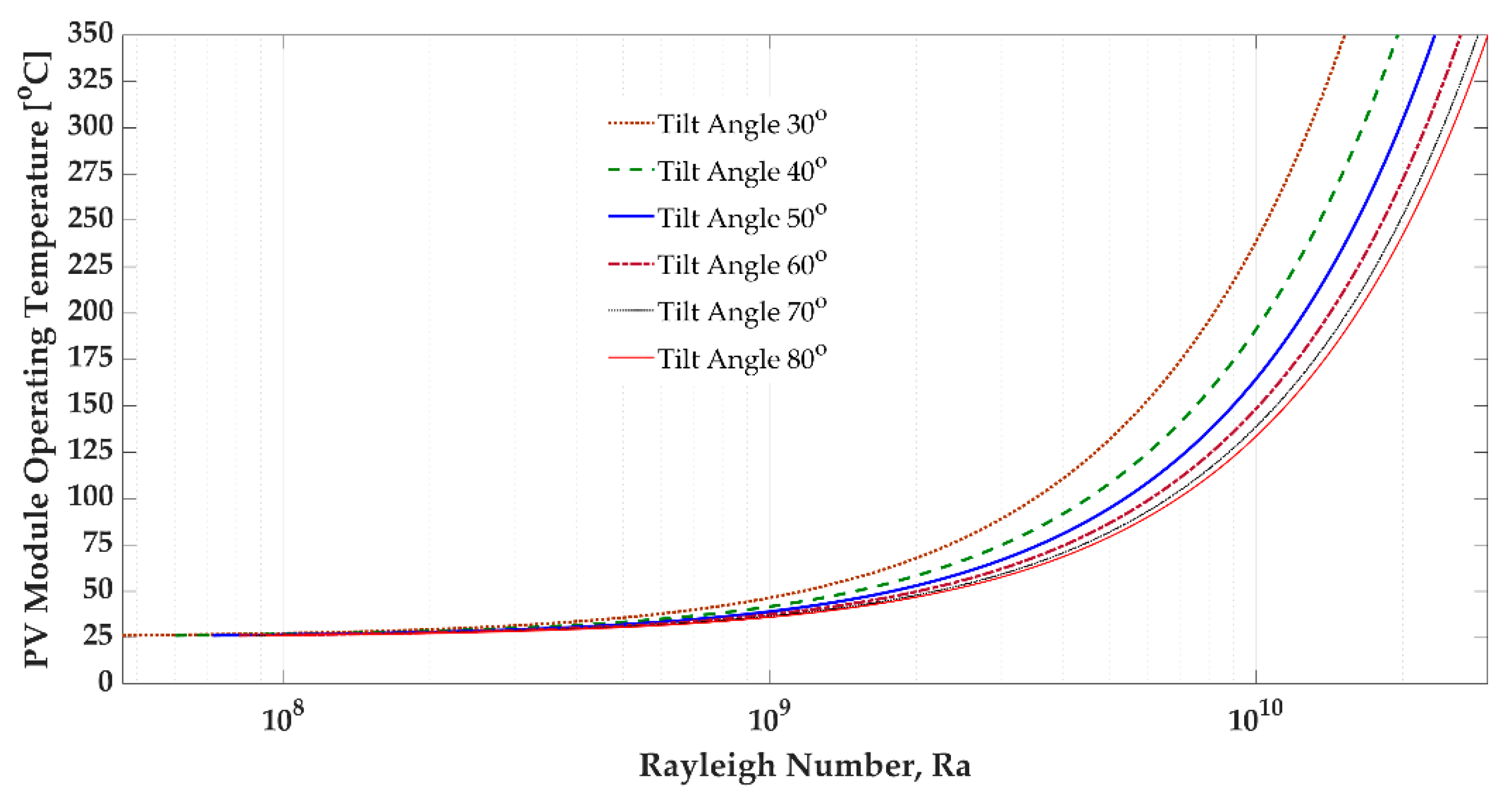
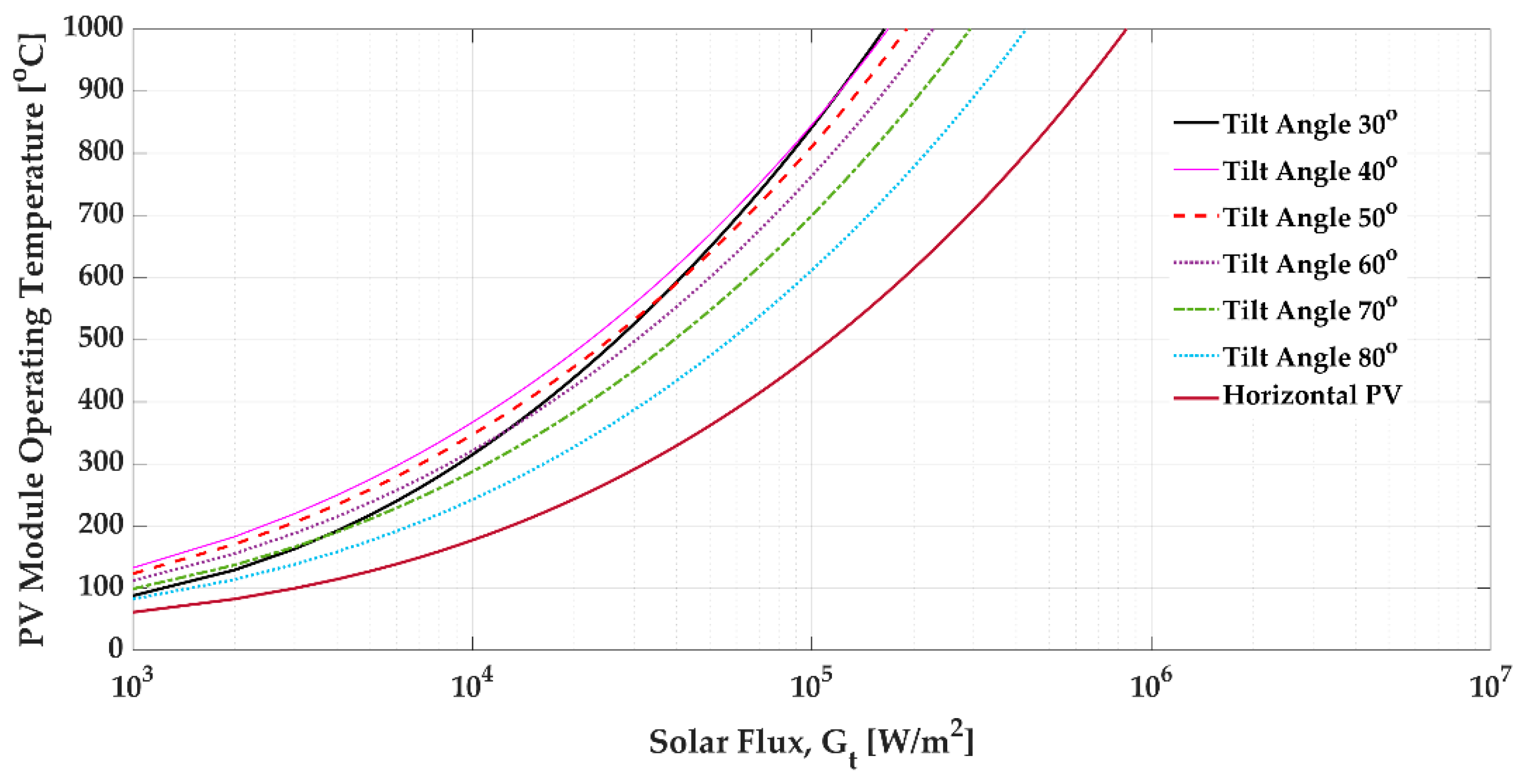
3.4. PV Module Tilt Angle and Temperature
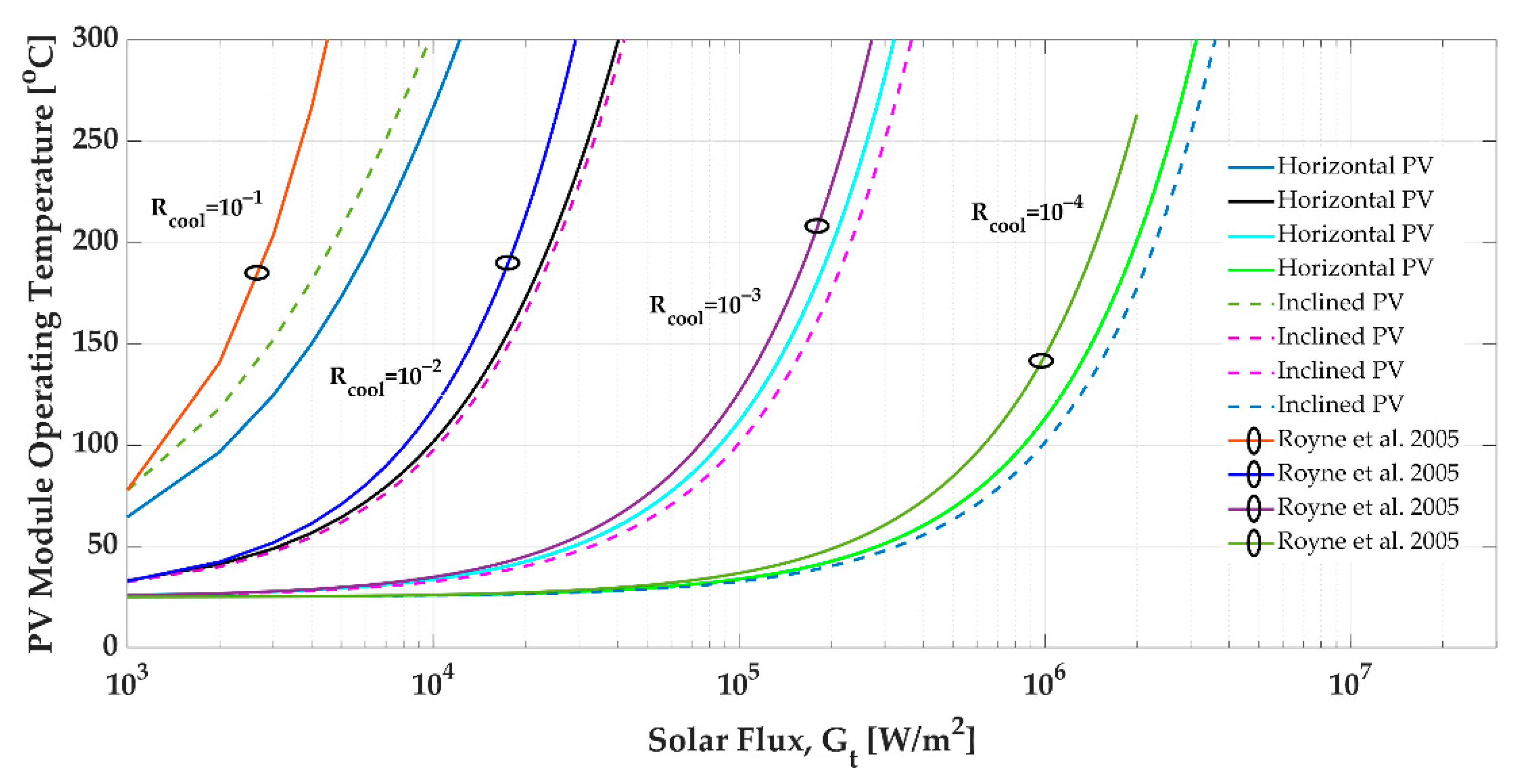
3.5. PV Module Temperature and Cooling Systems
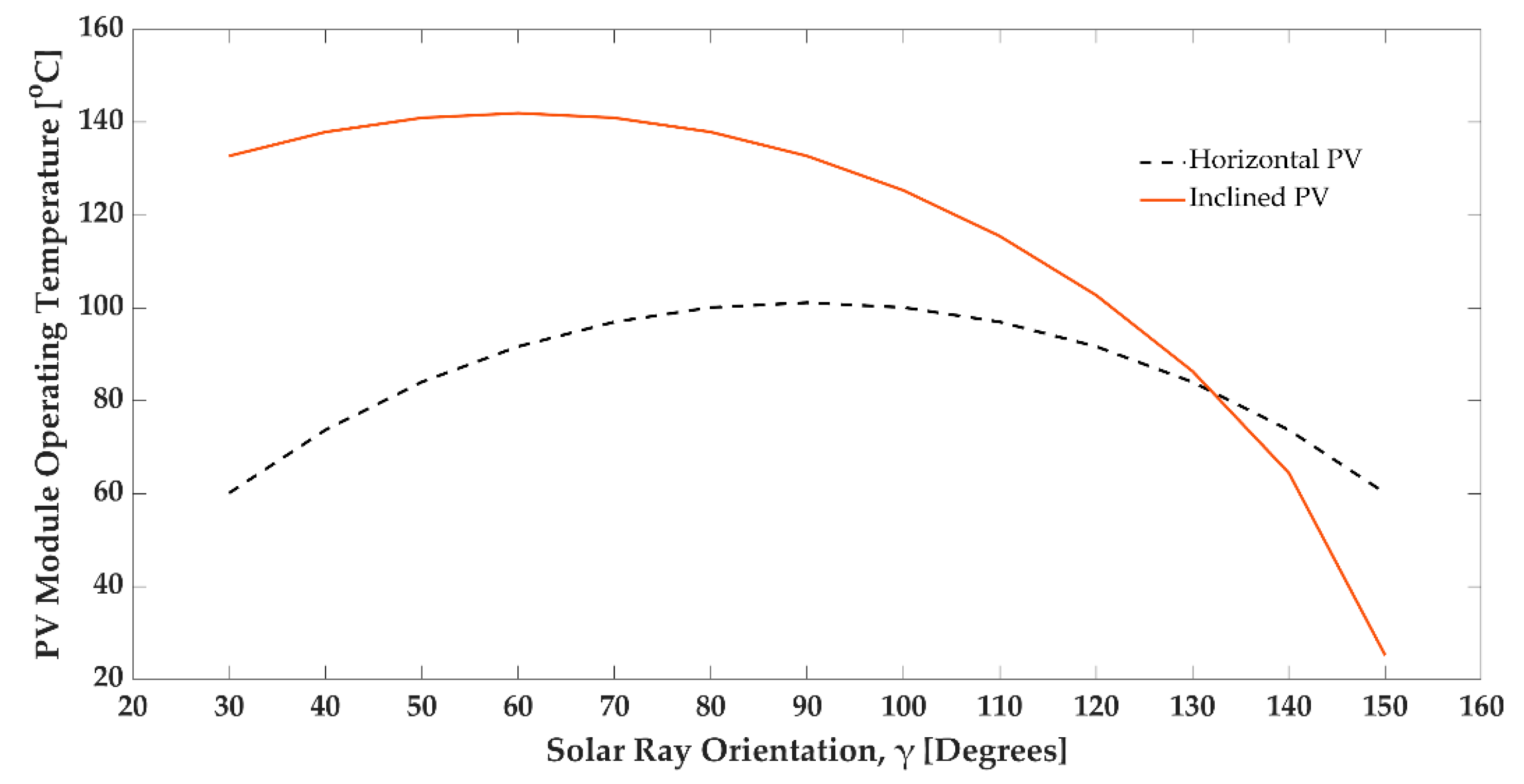
3.6. Solar Orientation and PV Module Temperature
- -
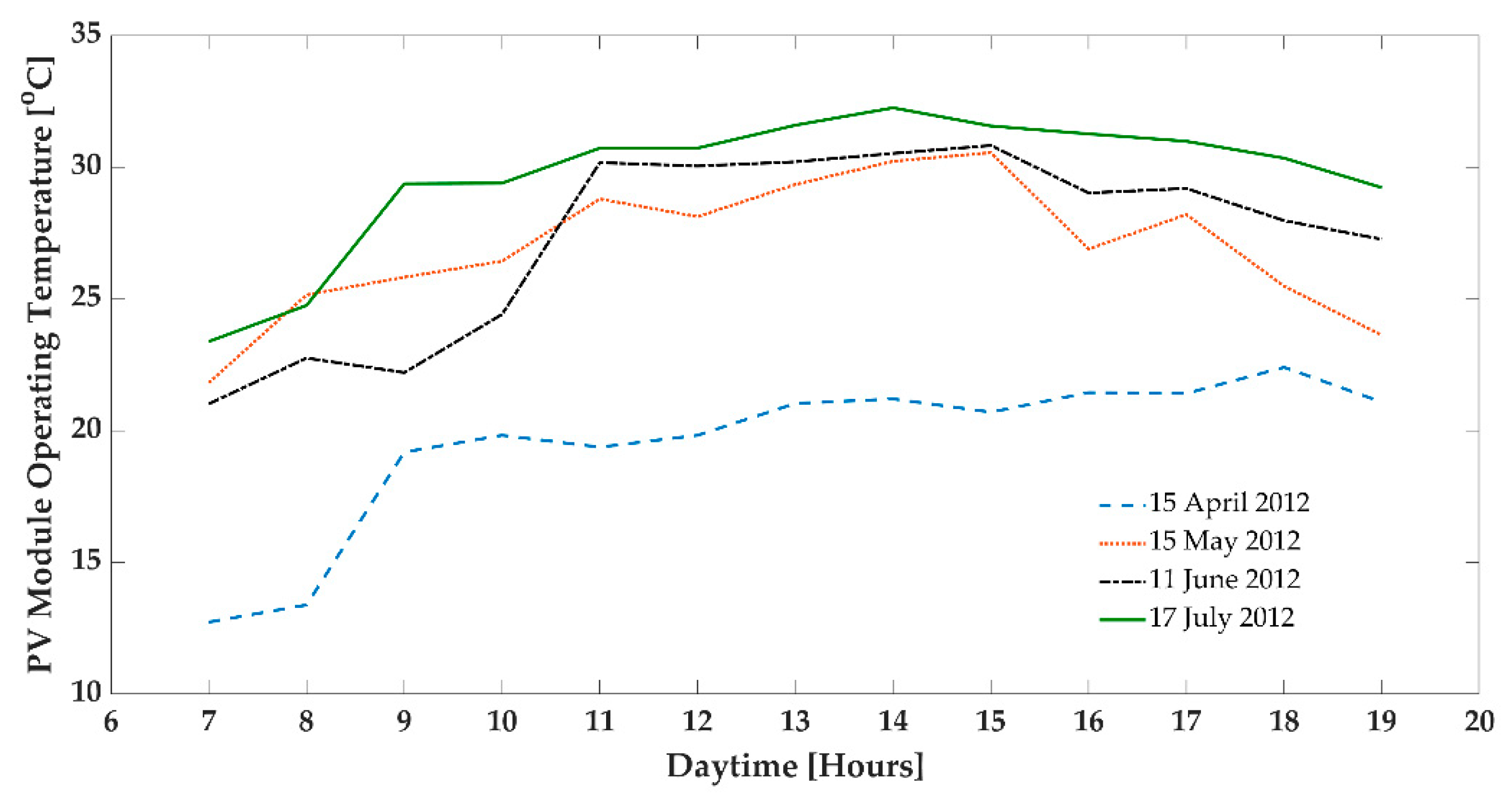
- The ambient temperature is not constant, and it changes during the daytime.
- -
- The sky can sometimes be cloudy, causing changes to the solar flux.
- -
- Humidity changes cause differences in temperature.
- -
- For wind speeds > 5 m/s, forced convection can occur, affecting PV module temperature.
- -
- Air pollution can affect heat transfer.
4. Discussion
5. Conclusions
- -
- The proposed equation has an implicit scheme that determines the environmental and operational characterizations of PV modules.
- -
- PV module efficiency is a linear function of PV module temperature, and it depends on the solar flux.
- -
- The PV panel temperature changes with tilt angle.
- -
- The PV module temperature depends on the solar angle of incidence.
- -
- The inclined PV module becomes hotter than a flat PV panel owing to convection heat transfer, assuming no forced convection and no conduction vis-a-vis a cooling system with a non-isolated backside PV module.
- -
- The optimum operating condition is available with an inclined PV module, and the flat panel has minimum energy generation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamuyu, W.C.L.; Lim, J.R.; Won, C.S.; Ahn, H.K. Prediction Model of Photovoltaic Module Temperature for Power Performance of Floating PVs. Energies 2018, 11, 447. [Google Scholar] [CrossRef] [Green Version]
- Hassanian, R.; Riedel, M.; Yeganeh, N.; Unnthorsson, R. A Practical Approach for Estimating the Optimum Tilt Angle of a Photovoltaic Panel for a Long Period—Experimental Recorded Data. Solar 2021, 1, 5. [Google Scholar] [CrossRef]
- Mbewe, D.J.; Card, H.C.; Card, D.C. A model of silicon solar cells for concentrator photovoltaic and photovoltaicthermal system design. Sol. Energy 1985, 35, 247–258. [Google Scholar] [CrossRef]
- Dalal, V.L.; Moore, A.R. Design considerations for high-intensity solar cells. J. Appl. Phys. 1977, 48, 1244–1251. [Google Scholar] [CrossRef]
- Luque, A.; Sala, G.; Arboiro, J.C. Electric and thermal model for non-uniformly illuminated concentration cells. Sol. Energy Mater. Sol. Cells 1998, 51, 269–290. [Google Scholar] [CrossRef]
- SunPower. Application Notes for HED312 Silicon Concentrator Solar Cell; Sunpower: San Jose, CA, USA, 2002. [Google Scholar]
- Horne, W.E. Solar Energy System. US Patent US5269851, 14 December 1993. [Google Scholar]
- Anton, I.; Sala, G.; Pachon, D. Correction of the Voc vs. temperature dependence under non-uniform concentrated illumination. In Proceedings of the 17th European Photovoltaic Solar Energy Conference, Munich, Germany, 22–26 October 2001; pp. 156–159. [Google Scholar]
- Mathur, R.K.; Mehrotra, D.R.; Mittal, S.; Dhariwal, S.R. Thermal non-uniformities in concentrator solar cells. Sol. Cells 1984, 11, 175–188. [Google Scholar] [CrossRef]
- Sanderson, R.W.; Odonnel, D.T.; Backus, C.E. The effects of nonuniform illumination and temperature profiles on silicon solar cells under concentrated sunlight. In Proceedings of the 14th IEEE PVSC, San Diego, CA, USA, 7–10 January 1980; pp. 431–436. [Google Scholar]
- Chenlo, F.; Cid, M. A linear concentrator photovoltaic module: Analysis of non-uniform illumination and temperature effects on efficiency. Sol. Cells 1987, 20, 27–39. [Google Scholar] [CrossRef]
- Dinesh, S.B.; Sunil, V.P.; Jayashree, G. Performance Evaluation of Photovoltaic Solar Panel Using Thermoelectric cooling. Int. J. Eng. Res. 2014, 3, 536–539. [Google Scholar]
- Amelia, A.R.; Irwan, Y.M.; Leow, W.Z.; Irwanto, M.; Safwati, I.; Zhafarina, M. Investigation of the Effect Temperature on Photovoltaic (PV) Panel Output Performance. Int. J. Adv. Sci. Eng. Inf. Technol. 2016, 6, 682–688. [Google Scholar]
- Thong, L.W.; Murugan, S.; Ng, P.K.; Sun, C.C. Analysis of Photovoltaic Panel Temperature Effects on Its Efficiency. In Proceedings of the 2nd International Conference on Electrical Engineering and Electronics Communication System, Ho Chi Minh, Vietnam, 18–19 November 2016. [Google Scholar]
- Skoplaki, E.; Palyvos, J.A. Operating temperature of photovoltaic modules: A survey of pertinent correlations. Renew. Energy 2009, 34, 23–29. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Ross, R. Interface design Considerations for terrestrial solar cell modules. In Proceedings of the 12th IEEE Photovoltaic Specialists Conference, Baton Rouge, LA, USA; 1976; pp. 801–806. [Google Scholar]
- Buresch, M. Photovoltaic Energy Systems; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Nordmann, T.C.L. Understanding temperature effects on PV system performance. In Proceedings of the 3rd World Conference On Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003. [Google Scholar]
- Markvart, T. Solar Electricity; Wiley: Chichester, UK, 2000. [Google Scholar]
- Bloem, J. Evaluation of a PV-integrated building application in a well wellcontrolled. Build. Environ. 2008, 43, 205–216. [Google Scholar] [CrossRef]
- Whitaker, C.; Wrasman, B.; Risser, V. Photovoltaic array thermal behaviour. In Proceedings of the 6th E.C. Photovoltaic Solar Energy Conference, London, UK, 15–19 April 1985. [Google Scholar]
- Stultz, J.; Wen, L. Thermal Performance Testing and Analysis of Photovoltaic Modules in Natural Sunlight. DOE/JPL LSA Task Report 5101-31; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1977. [Google Scholar]
- ASTM. Method for Determining the Nominal Operating Cell Temperature (NOCT) of An Array or Module. E1036M, Annex A.1, in ASTM; ASTM International: West Conshohocken, PA, USA, 1999; p. 544. [Google Scholar]
- Palyvos, J. A survey of wind convection coefficient correlations for building envelope energy systems, modeling. Appl. Therm. Eng. 2009, 28, 801–808. [Google Scholar] [CrossRef]
- Gopinathan, K.K. Optimization of tilt angle of solar collector for maximum irradiation on sloping surfaces. Sol. Energy 1991, 10, 51–61. [Google Scholar] [CrossRef]
- Khalil, A.; Alnajjar, A. Experimental and theoretical investigation of global and diffuse solar radiation in the United Arab Emirates. Renew. Energy 1995, 6, 537–543. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J. Optimum fixed orientations and benefits of tracking for capturing solar radiation in the continental United States. Renew. Energy 2011, 36, 1145–1152. [Google Scholar] [CrossRef] [Green Version]
- Tamimi, A. Modeling of optimum inclination angles of solar systems for Amman, Jordan. J. Renew. Sustain. Energy 2011, 3, 43109. [Google Scholar] [CrossRef]
- Dhouib, A.; Filali, S. Operating temperatures of photovoltaic panels. Energy Environ. 1990, 1, 494–498. [Google Scholar]
- Anja, R.; Christopher, J.D.; Mills, D.R. Cooling of photovoltaic cells under concentrated illumination: A critical review. Sol. Energy Mater. Sol. Cells 2005, 86, 451–483. [Google Scholar]
- Yunus, C.; Afshin, G. Heat and Mass Transfer: Fundamentals and Applications, 6th ed.; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Frank, P.I.; David, P.D.T.L.B.; Adrienne, S.L. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Jack, H. Heat Transfer; McGraw-Hill Education: New York, NY, USA, 2009. [Google Scholar]
- Ozisik, M. Necati. Heat Transfer: A Basic Approach; McGraw-Hill College: New York, NY, USA, 1984. [Google Scholar]
- Luque, A. Solar Cells and Optics for Photovoltaic Concentration; Hilger, A., Ed.; Philadelphia: Bristol, UK, 1989. [Google Scholar]
- Wen, L. An Investigation of the Effect of Wind Cooling on Photovoltaic Arrays, JPL Internal Report No. 5101-201; Jet Propulsion Laboratory: Pasadena, CA, USA, 1982. [Google Scholar]
- McAdams, W.H. Heat Transmission, 3rd ed.; McGraw-Hill Book Co., Inc.: New York, NY, USA, 1954. [Google Scholar]
- Veldhuis, J.; Nobre, A.; Reindl, T.; Rüther, R.; Reinders, A.H.M.E. The influence of wind on the temperature of PV modules in tropical environments, evaluated on an hourly basis. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 824–829. [Google Scholar]
- Ali, M.; Iqbal, M.H.; Sheikh, N.A.; Hafiz, M.; Ali, M.; Manzoor, S.; Khan, M.M.; Tamrin, K.F. Performance Investigation of Air Velocity Effects on PV Modules under Controlled Conditions. Int. J. Photoenergy 2017, 2017, 3829671. [Google Scholar] [CrossRef]
- Giuseppina, C.; Valerio, L.B.; Vincenzo, F.; Marco, T. Assessment of the Operating Temperature of Crystalline PV Modules Based on Real Use Conditions. Int. J. Photoenergy 2014, 2014, 718315. [Google Scholar]
- Burak, V.S.; Volkov, S.V.; Martynenko, O.G.; KhramtsovI, P.P.; Shikh, A. Free-convective heat transfer on a vertical surface with heat-flux discontinuity. Int. J. Heat Mass Transf. 1995, 38, 155–161. [Google Scholar] [CrossRef]
- Zariffeh, M.D.E.K. Laminar free convection on an inclined flat plate or a vertical cylinder with prescribed wall heat flux. Int. J. Heat Mass Transf. 1981, 24, 1071–1075. [Google Scholar] [CrossRef]
- Hassan, K.-E.; Mohamed, S. Natural convection from isothermal flat surfaces. Int. J. Heat Mass Transf. 1970, 13, 1873–1886. [Google Scholar] [CrossRef]
- Husar, R.; Sparrow, E. Patterns of free convection flow adjacent to horizontal heated surfaces. Int. J. Heat Mass Transf. 1968, 11, 1206–1208. [Google Scholar] [CrossRef]
- Lewandowski, W.; Kubski, P.; Khubeiz, J. Natural convection heat transfer from round horizontal plate. Wärme-Und Stoffübertrag. 1992, 27, 281–287. [Google Scholar] [CrossRef]
- Rotem, Z.; Claassen, L. Natural convection above unconfined horizontal surfaces. J. Fluid Mech. 1969, 38, 173–192. [Google Scholar] [CrossRef]
- Pera, L.; Gebhart, B. Natural convection flows adjacent to horizontal surfaces resulting from the combined buoyancy effects of thermal and mass diffusion. Int. J. Heat Mass Transf. 1972, 15, 269–278. [Google Scholar] [CrossRef]
- Pera, L.; Gebhart, B. Natural convection boundary layer flow over horizontal and slightly inclined surfaces. Int J. Heat Mass Transf. 1973, 16, 1131–1146. [Google Scholar] [CrossRef]
- Fujii, T.; Imura, H. Natural-convection heat transfer from a plate with arbitrary inclination. Int J. Heat Mass Transf 1972, 15, 755–767. [Google Scholar] [CrossRef]
- Tetsu, F.; Hiroshi, H.; Itsuki, M. A theoretical study of natural convection heat transfer from downward-facing horizontal surfaces with uniform heat flux. Int. J. Heat Mass Transf. 1973, 16, 611–627. [Google Scholar] [CrossRef]
- Lewandowski, W.; Radziemska, E.; Buzuk, M.; Bieszk, H. Free convection heat transfer and fluid flow above horizontal rectangular plates. Appl. Energy 2000, 66, 177–197. [Google Scholar] [CrossRef]
- Pretot, S.; Zeghmati, B.; Le, P.G. Theoretical and experimental study of natural convection on a horizontal plate. Appl. Energy 2000, 20, 873–891. [Google Scholar] [CrossRef]
- Martorell, I.; Herrero, J.; Grau, F. Natural convection from narrow horizontal plates at moderate Rayleigh numbers. Int. J. Heat Mass. Transf. 2003, 46, 2389–2402. [Google Scholar] [CrossRef]
- Kozanoglu, B.; Lopez, J. Thermal boundary layer and the characteristic length on natural convection over a horizontal plate. Heat Mass Transf. 2007, 43, 333–339. [Google Scholar] [CrossRef]
- Lloyd, J.; Moran, W. Natural convection adjacent to horizontal surface of various planforms. J. Heat Transf 1974, 96, 443–447. [Google Scholar] [CrossRef]
- Al-Arabi, M.; El-Riedy, M. Natural convection heat transfer from isothermal horizontal plates of different shapes. Int. J. Heat Mass Transf. 1976, 19, 1399–1404. [Google Scholar] [CrossRef]
- Kitamura, K.; Kimura, F. Heat transfer and fluid flow of natural convection adjacent to upward-facing horizontal plates. Int. J. Heat Mass Transf. 1995, 38, 3149–3159. [Google Scholar] [CrossRef]
- Kitamura, K.; Kimura, F. Fluid flow and heat transfer of natural convection over upward-facing, horizontal heated circular disks. Heat Transf.-Asian Res. 2008, 37, 339–351. [Google Scholar] [CrossRef]
- Wragg, A.; Loomba, R. Free convection flow patterns at horizontal surfaces with ionic mass transfer. Int. J. Heat Mass Transf. 1970, 13, 439–442. [Google Scholar] [CrossRef]
- Yousef, W.; Tarasuk, J.; McKeen, W. Free convection heat transfer from upward-facing isothermal horizontal surfaces. J. Heat Transf. 1982, 104, 493–500. [Google Scholar] [CrossRef]
- Chang, T.P. Study on the optimal tilt angle of solar collector according to different. Int. J. Appl. Sci. Eng. 2008, 6, 151–161. [Google Scholar]
- Assi, A.; Jama, M. Estimation of solar radiation using sun hours in the Emirate of Abu Dhabi—UAE. In Proceedings of the 11th World Renewable Energy Congress, Abu Dhabi, United Arab Emirates, 25–30 September 2010. [Google Scholar]
- Islam, M.; Kubo, I.; Ohadi, M.; Alili, A. Measurement of solar energy radiation in Abu Dhabi. Appl. Energy 2009, 86, 511–515. [Google Scholar] [CrossRef]
- Rusheng, T.; Tong, W.U. Optimum tilt angle for solar collectors used in China. Appl. Energy 2004, 79, 239–248. [Google Scholar]
- Ulgen, K. Optimum tilt angle for solar collectors, Energy Sources A Recovery Util. Environ. Eff. 2006, 28, 1171–1180. [Google Scholar]
- Mamun, M.A.A.; Islam, M.M.; Hasanuzzaman, M. Jeyraj Selvaraj, Effect of tilt angle on the performance and electrical parameters of a PV module: Comparative indoor and outdoor experimentalS investigation. Energy Built Environ. 2021, in press.



| Description | Character | Unit | Value |
|---|---|---|---|
| PV solar absorptivity | - | 1 | |
| PV module surface | 1 | ||
| Stefan–Boltzmann constant | |||
| PV surface emissivity | - | 0.855 | |
| Ambient temperature | °C | 25 | |
| Air effective thermal conductivity | |||
| PV module length | 1 | ||
| Gravity acceleration | 9.81 | ||
| Volumetric thermal expansion coefficient | |||
| Air thermal diffusivity | |||
| Air kinematic viscosity | |||
| Air Prandtl number | - | 0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassanian, R.; Riedel, M.; Helgadottir, A.; Yeganeh, N.; Unnthorsson, R. Implicit Equation for Photovoltaic Module Temperature and Efficiency via Heat Transfer Computational Model. Thermo 2022, 2, 39-55. https://doi.org/10.3390/thermo2010004
Hassanian R, Riedel M, Helgadottir A, Yeganeh N, Unnthorsson R. Implicit Equation for Photovoltaic Module Temperature and Efficiency via Heat Transfer Computational Model. Thermo. 2022; 2(1):39-55. https://doi.org/10.3390/thermo2010004
Chicago/Turabian StyleHassanian, Reza, Morris Riedel, Asdis Helgadottir, Nashmin Yeganeh, and Runar Unnthorsson. 2022. "Implicit Equation for Photovoltaic Module Temperature and Efficiency via Heat Transfer Computational Model" Thermo 2, no. 1: 39-55. https://doi.org/10.3390/thermo2010004
APA StyleHassanian, R., Riedel, M., Helgadottir, A., Yeganeh, N., & Unnthorsson, R. (2022). Implicit Equation for Photovoltaic Module Temperature and Efficiency via Heat Transfer Computational Model. Thermo, 2(1), 39-55. https://doi.org/10.3390/thermo2010004









