Thermodynamic Modeling of the Uranium–Tellurium System: Estimation of the Uncertainties by a Bayesian Approach
Abstract
:1. Introduction
2. State of the Art on the U–Te System and Selection of the Data for the Assessment
2.1. Crystal Structure Data
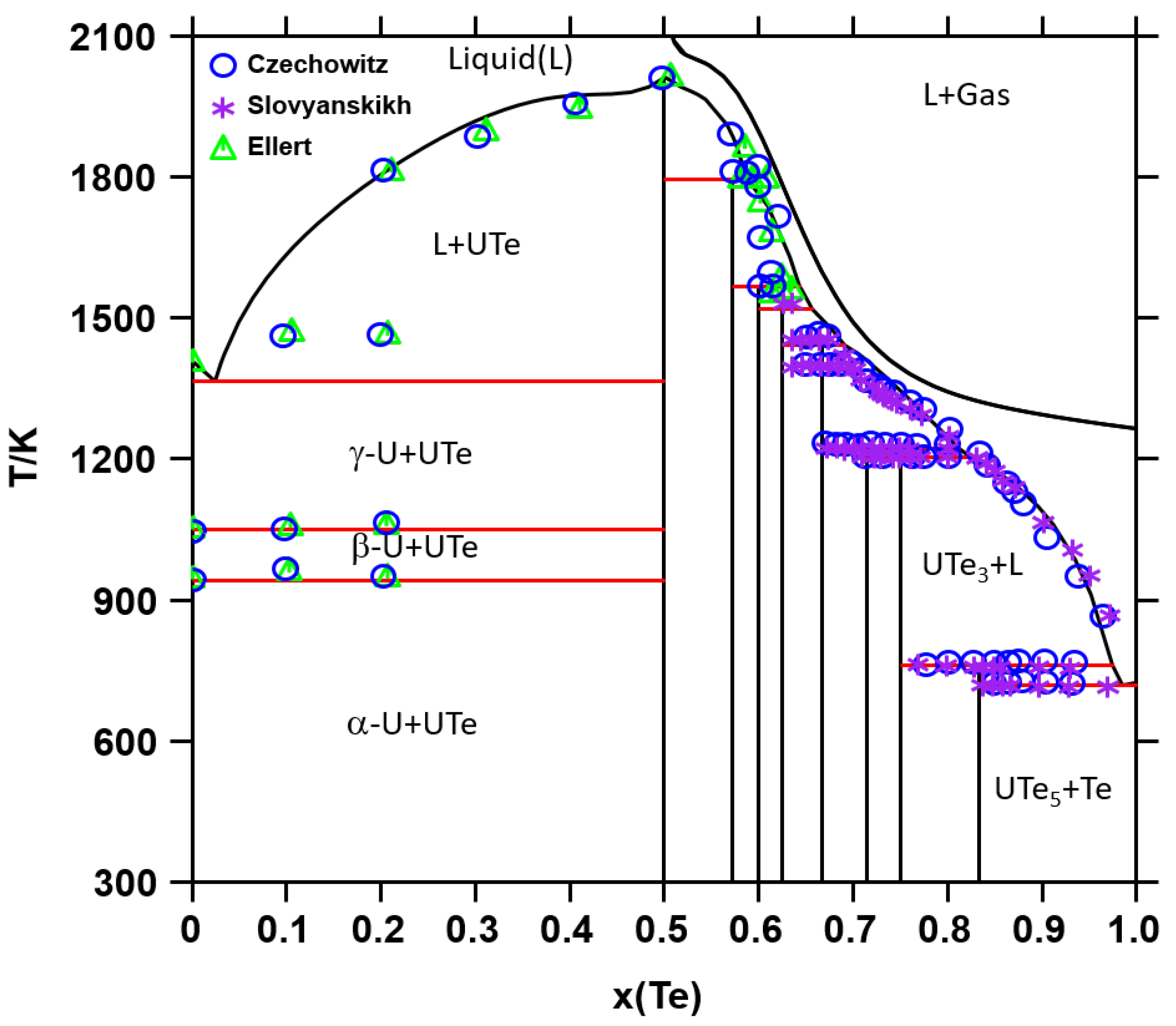
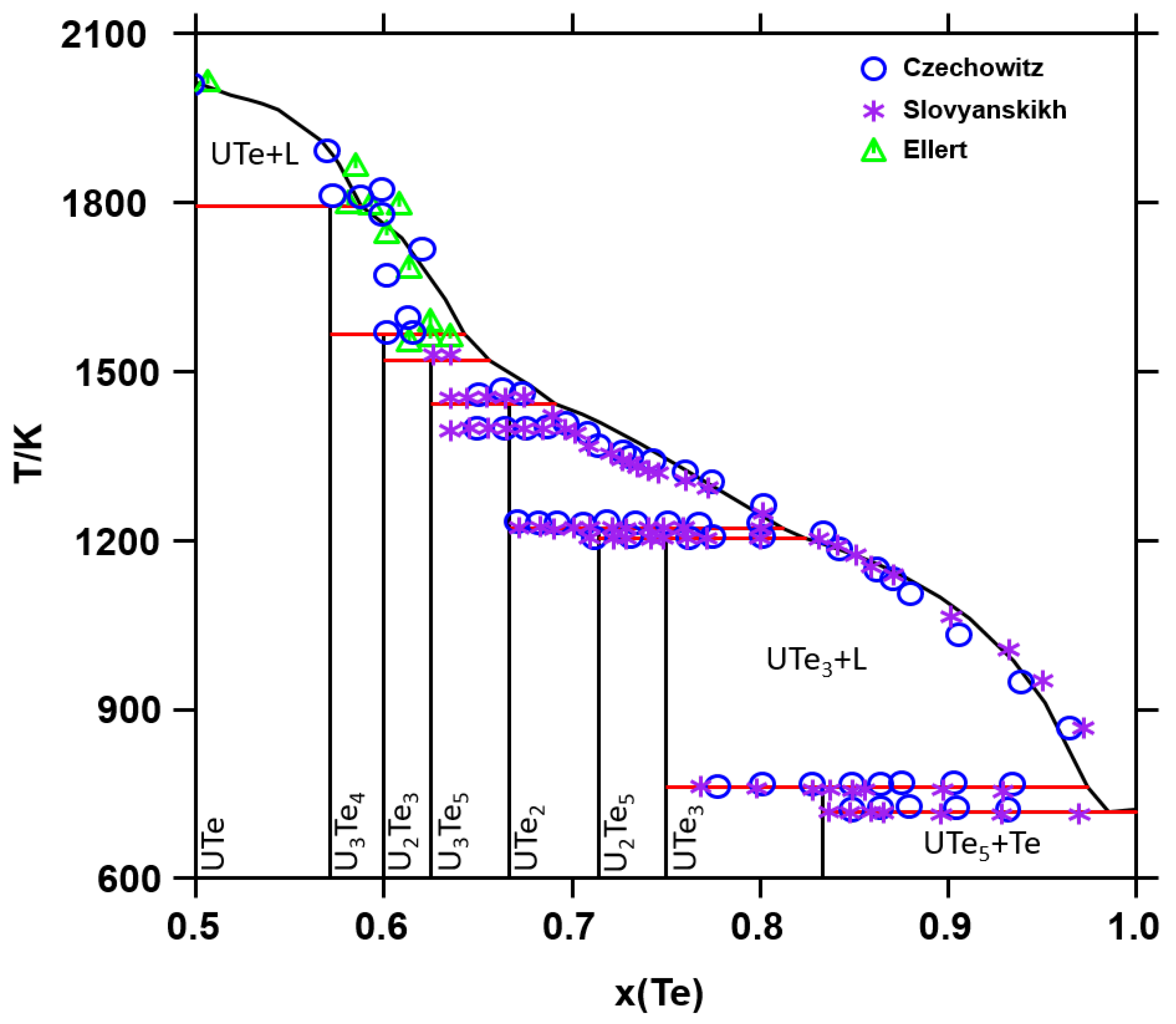
2.2. Phase Diagram Data
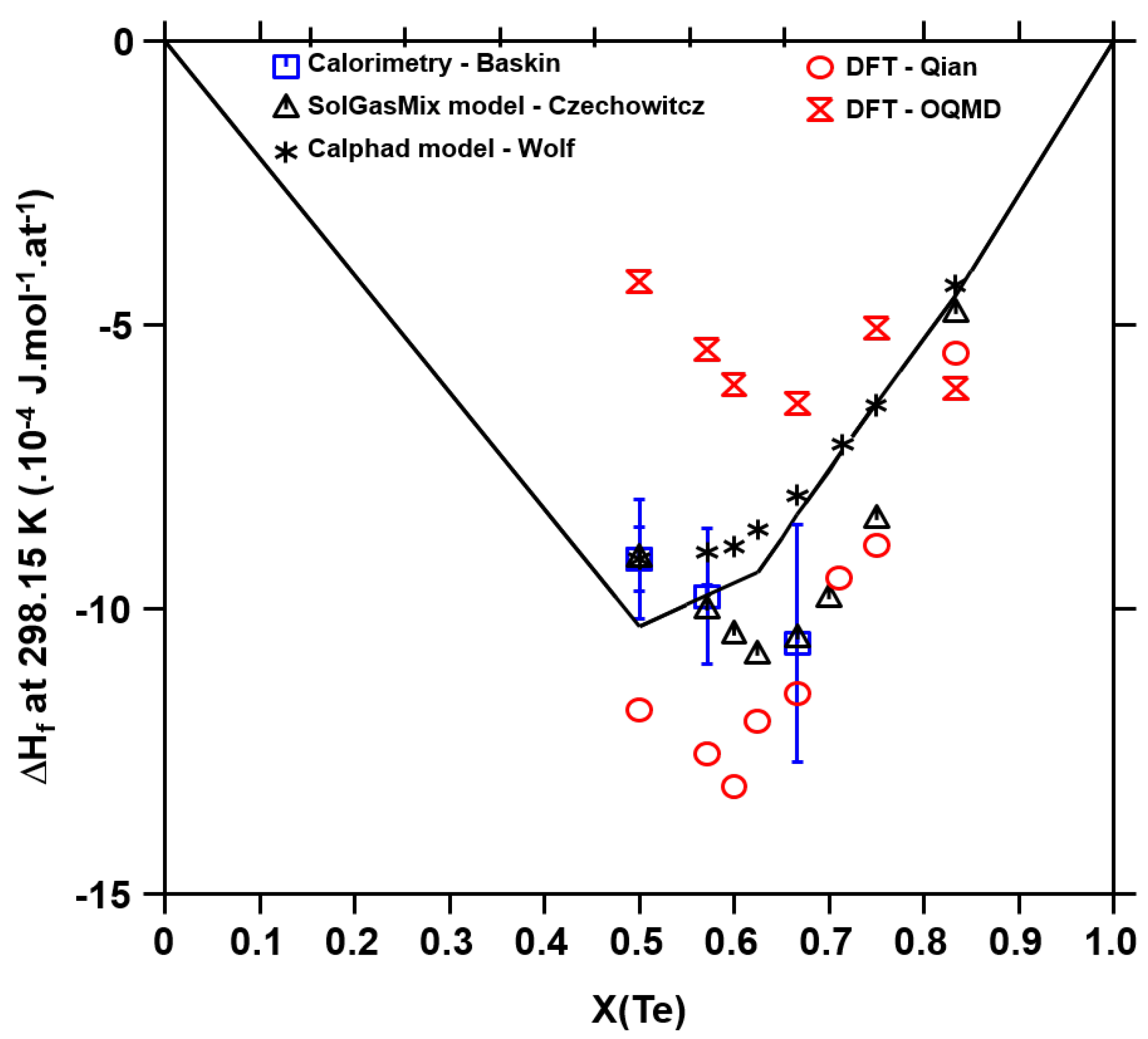
2.3. Thermodynamic Data
3. Thermodynamic Modeling with the CALPHAD Method
3.1. Gibbs Energy Models
3.2. Optimization Procedure
4. Use of Conjugate Prior Distribution for CALPHAD Modeling
4.1. Bayesian Inference
4.2. Conjugate Prior Probability Distribution
4.3. Uncertainty on the Calculated Thermodynamic Quantities
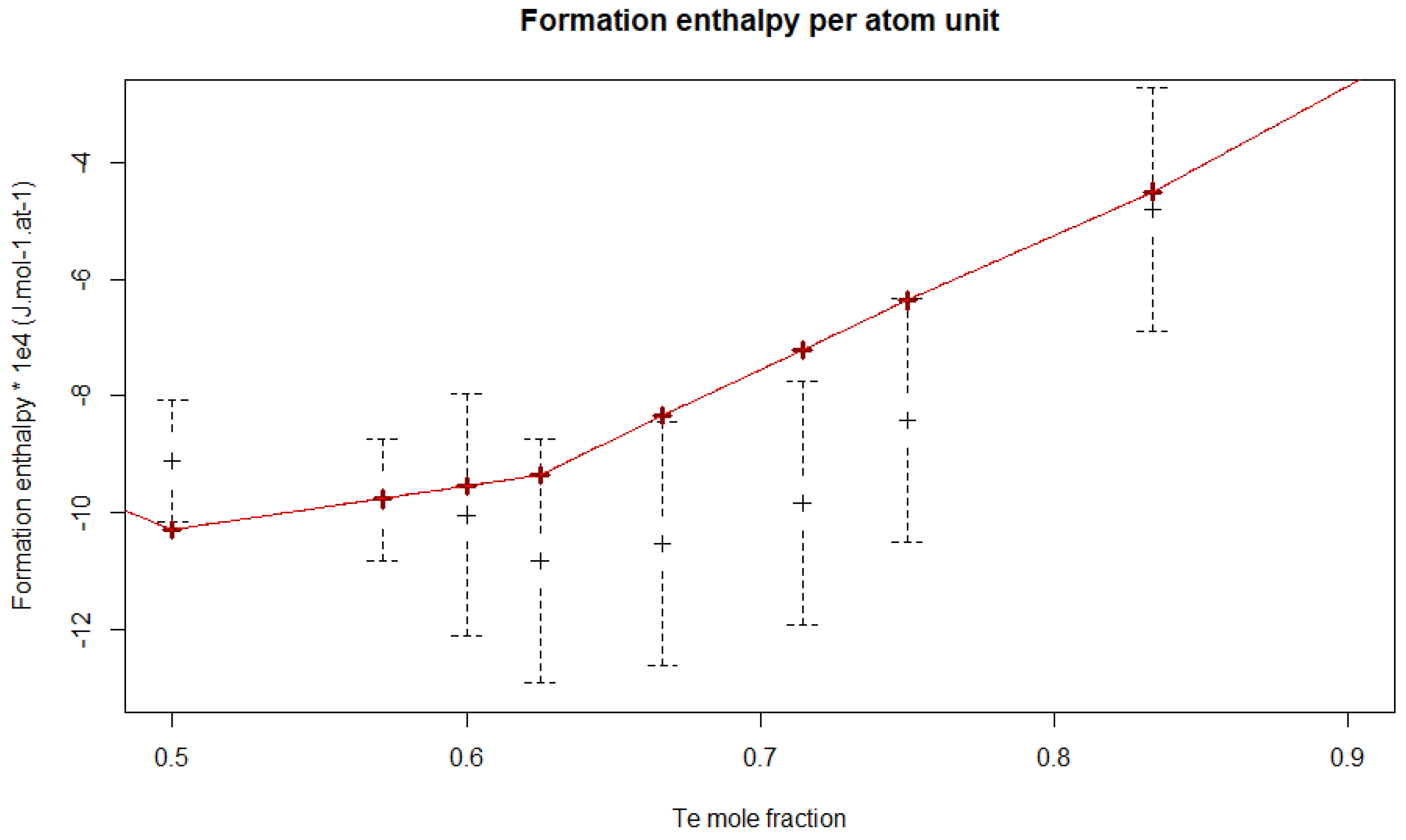
4.3.1. Enthalpy of Formation
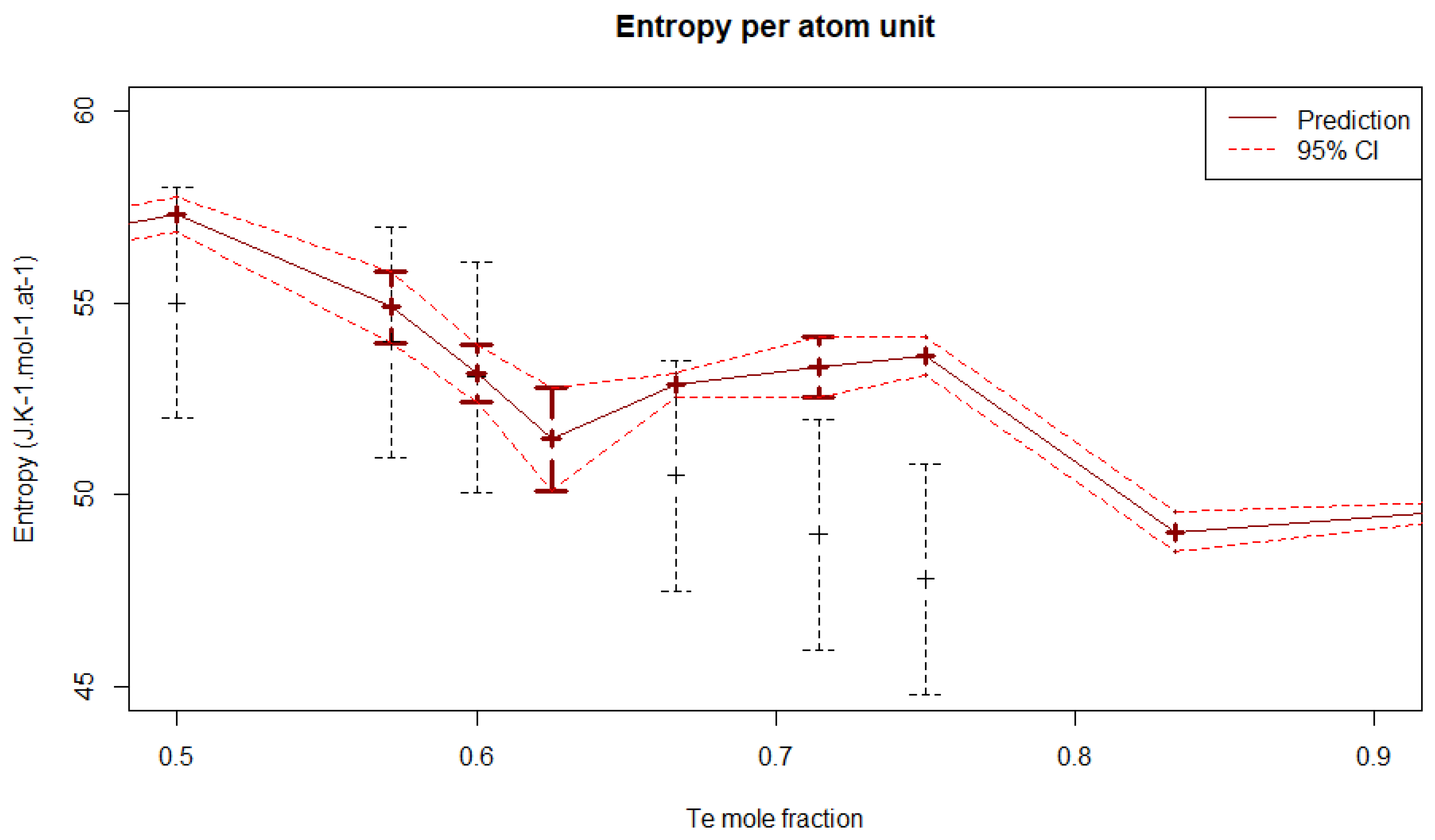
4.3.2. Entropy
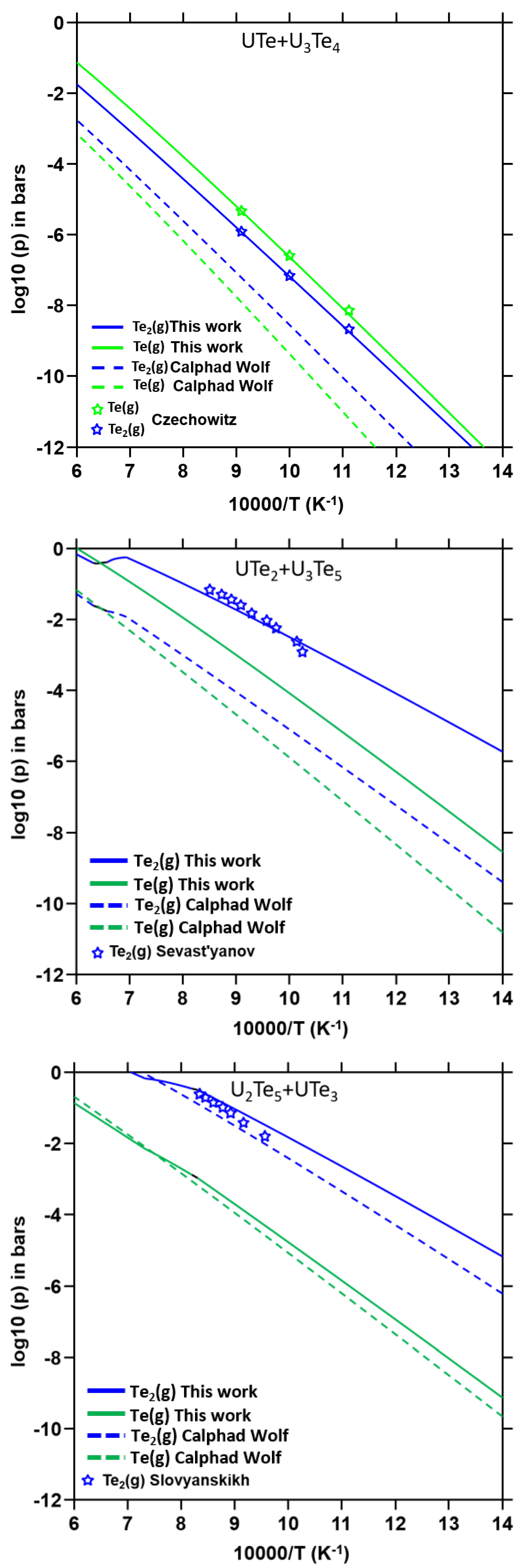
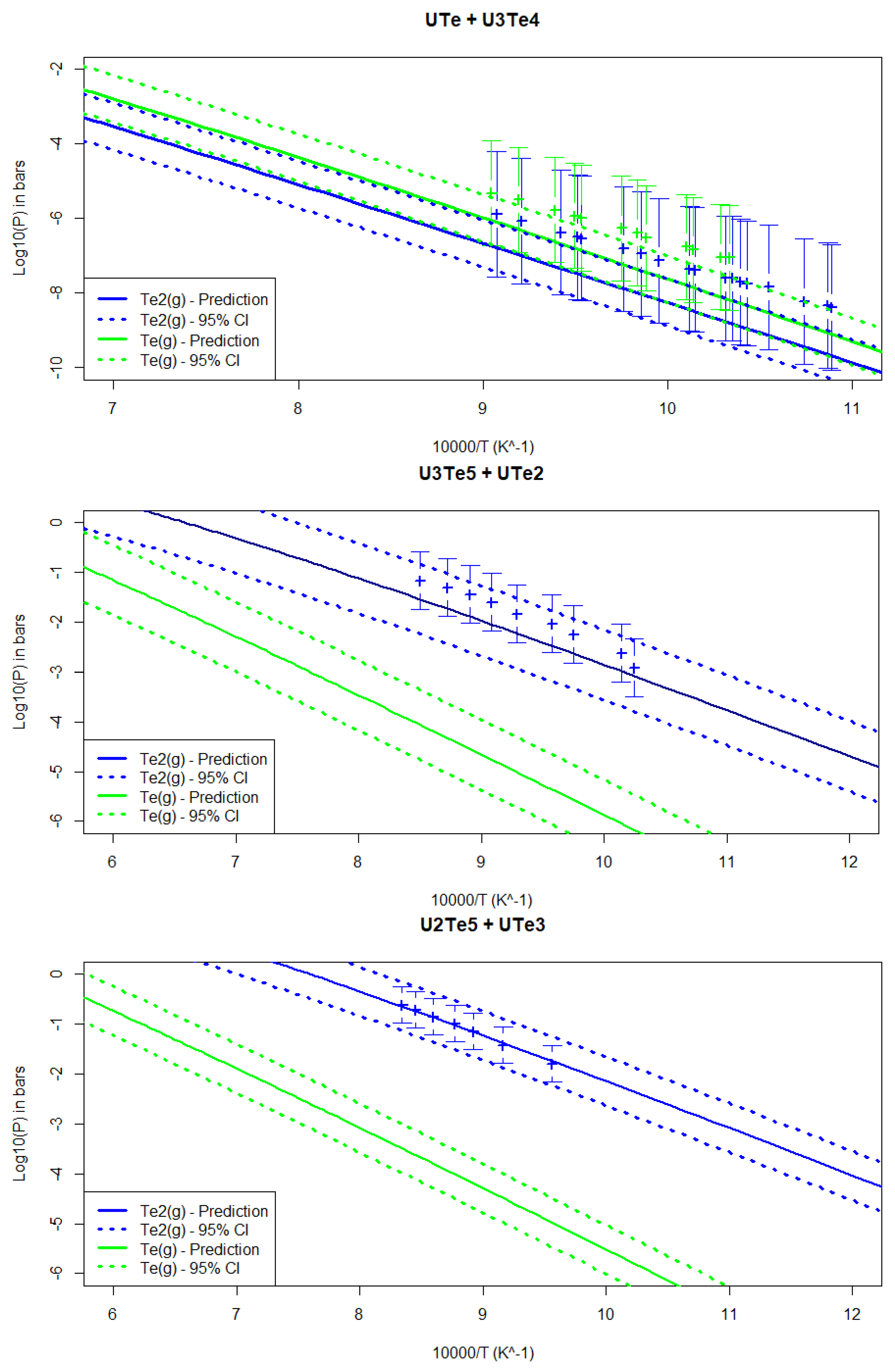
4.3.3. Partial Pressures for the Two-Phase Regions
4.4. Uncertatinty on the Calculated Phase Diagram
5. Results and Discussion
5.1. CALPHAD Assessment
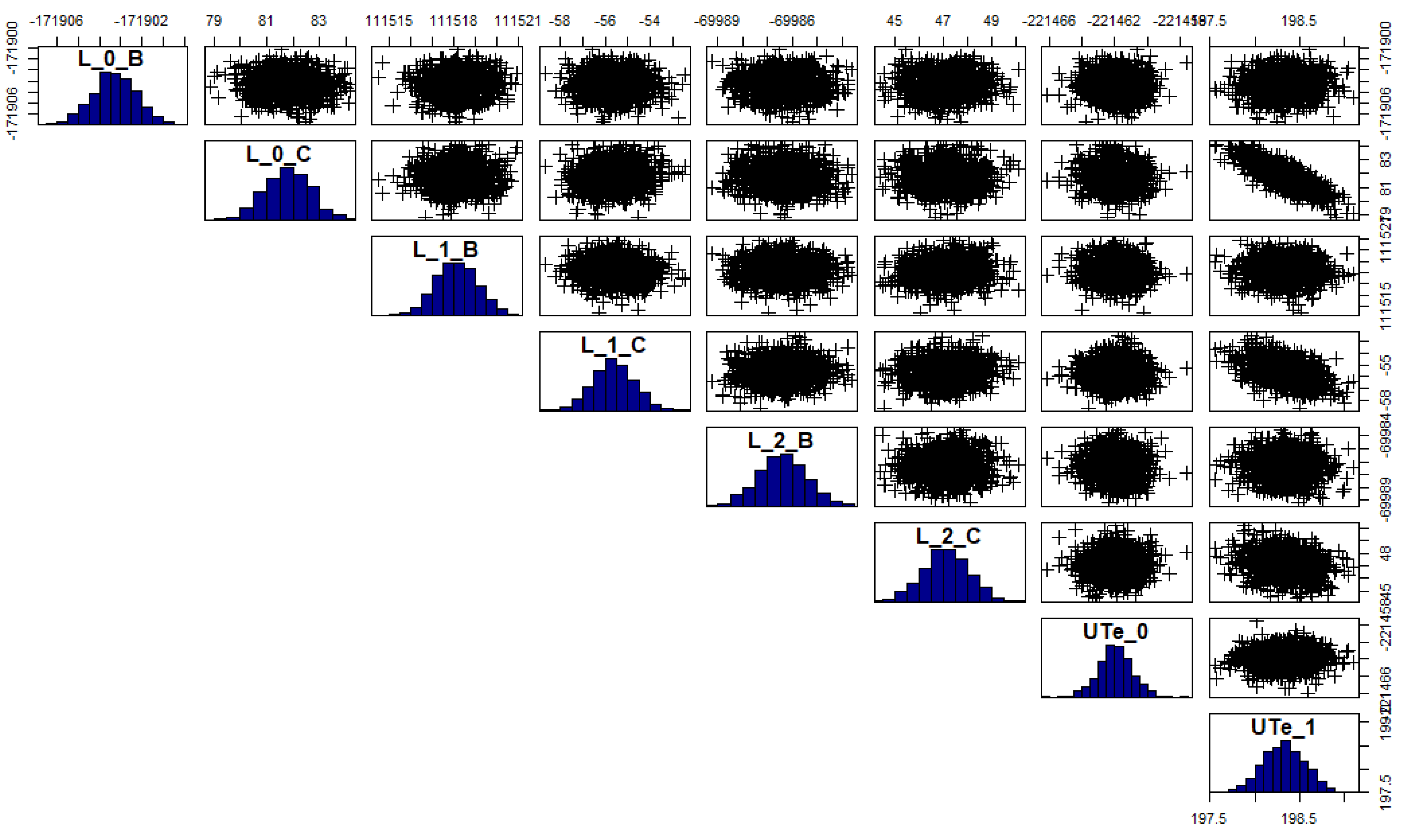
5.2. Uncertainty Propagation with the Bayesian Approach
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Reduction of the Number of Parameters
Appendix A.1. Degree of Freedom and System Dimension Reduction
Appendix A.2. Reduced Prior Probability Distribution and Relations with the Initial Set of Parameters
Appendix B. Additional Table: Correlation Values for the Posterior Probability Distribution
| 1 | −0.015 | −0.010 | −0.012 | −0.046 | 0.030 | 0.034 | 0.028 | −0.010 | 0.034 | 0.052 | 0.031 | |
| 1 | −0.009 | 0.036 | −0.078 | −0.033 | −0.002 | −0.688 | −0.012 | −0.368 | −0.018 | −0.100 | ||
| 1 | 0.021 | −0.006 | 0.002 | 0.039 | −0.007 | 0.020 | −0.006 | 0.055 | −0.006 | |||
| 1 | −0.033 | −0.040 | 0.018 | −0.296 | −0.024 | −0.002 | 0.061 | 0.137 | ||||
| 1 | 0.012 | 0.074 | 0.063 | 0.055 | 0.032 | −0.018 | 0.008 | |||||
| 1 | 0.030 | −0.143 | 0.019 | 0.013 | −0.010 | 0.047 | ||||||
| 1 | −0.014 | 0.036 | −0.003 | 0.020 | 0.000 | |||||||
| 1 | 0.008 | 0.854 | −0.010 | 0.661 | ||||||||
| 1 | −0.002 | −0.011 | −0.006 | |||||||||
| 1 | −0.003 | 0.953 | ||||||||||
| 1 | −0.003 | |||||||||||
| 1 | ||||||||||||
| 0.020 | 0.027 | −0.015 | 0.017 | −0.044 | 0.016 | −0.018 | 0.014 | 0.020 | 0.017 | |||
| −0.011 | 0.121 | −0.034 | 0.463 | 0.021 | 0.615 | −0.007 | 0.687 | 0.004 | 0.682 | |||
| 0.001 | −0.008 | 0.037 | −0.012 | 0.005 | −0.017 | −0.014 | −0.020 | 0.027 | −0.022 | |||
| 0.010 | 0.147 | −0.023 | 0.093 | 0.017 | −0.133 | −0.055 | −0.292 | 0.022 | −0.389 | |||
| 0.015 | −0.010 | 0.013 | −0.036 | −0.031 | −0.041 | −0.011 | −0.041 | −0.009 | −0.037 | |||
| 0.020 | −0.001 | −0.015 | −0.094 | 0.001 | −0.052 | 0.038 | −0.009 | 0.010 | 0.104 | |||
| −0.008 | −0.002 | 0.013 | −0.005 | 0.035 | −0.008 | −0.004 | −0.009 | 0.083 | −0.008 | |||
| 0.030 | 0.514 | 0.067 | 0.245 | −0.055 | 0.126 | 0.010 | 0.037 | 0.003 | 0.008 | |||
| −0.009 | −0.010 | 0.003 | −0.013 | −0.005 | −0.008 | −0.006 | −0.004 | −0.009 | 0.000 | |||
| 0.045 | 0.870 | 0.063 | 0.648 | −0.059 | 0.489 | −0.003 | 0.351 | 0.018 | 0.295 | |||
| −0.020 | −0.004 | −0.020 | −0.013 | −0.036 | −0.029 | 0.037 | −0.039 | 0.001 | −0.045 | |||
| 0.047 | 0.975 | 0.053 | 0.826 | −0.054 | 0.674 | −0.011 | 0.530 | 0.023 | 0.462 | |||
| 1 | 0.043 | −0.039 | 0.034 | 0.002 | 0.025 | 0.040 | 0.018 | 0.021 | 0.017 | |||
| 1 | 0.046 | 0.931 | −0.049 | 0.810 | −0.014 | 0.680 | 0.024 | 0.606 | ||||
| 1 | 0.029 | −0.009 | 0.026 | 0.003 | 0.020 | −0.016 | 0.017 | |||||
| 1 | −0.038 | 0.955 | −0.015 | 0.869 | 0.021 | 0.797 | ||||||
| 1 | −0.034 | −0.018 | −0.027 | 0.033 | −0.025 | |||||||
| 1 | −0.001 | 0.977 | 0.014 | 0.937 | ||||||||
| 1 | 0.006 | −0.070 | 0.021 | |||||||||
| 1 | 0.009 | 0.987 | ||||||||||
| 1 | 0.003 | |||||||||||
| 1 |
References
- Samuelsson, K.; Dumas, J.C.; Sundman, B.; Lainet, M. An improved method to evaluate the “Joint Oxyde-Gaine” formation in (U,Pu)O2 irradiated fuels using the GERMINAL V2 code coupled to Calphad thermodynamic computations. EPJ Nucl. Sci. Technol. 2020, 6, 47. [Google Scholar] [CrossRef]
- Samuelsson, K.; Dumas, J.C.; Sundman, B.; Lamontagne, J.; Guéneau, C. Simulation of the chemical state of high burnup (U,Pu)O2 fuel in fast reactors based on thermodynamic calculations. J. Nucl. Mater. 2020, 532, 151969. [Google Scholar] [CrossRef]
- Guéneau, C.; Dupin, N.; Kjellqvist, L.; Geiger, E.; Kurata, M.; Gossé, S.; Corcoran, E.; Quaini, A.; Hania, R.; Smith, A.L.; et al. TAF-ID: An international thermodynamic database for nuclear fuels applications. Calphad 2021, 72, 102212. [Google Scholar] [CrossRef]
- Lukas, H.L.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Paulson, N.H.; Bocklund, B.J.; Otis, R.A.; Liu, Z.-K.; Stan, M. Quantified uncertainty in thermodynamic modeling for materials design. Acta Mater. 2019, 174, 9–15. [Google Scholar] [CrossRef] [Green Version]
- Paulson, N.H.; Jennings, E.; Stan, M. Bayesian strategies for uncertainty quantification of the thermodynamic properties of materials. Int. J. Eng. Sci. 2019, 142, 74–93. [Google Scholar] [CrossRef] [Green Version]
- Paulson, N.H.; Zomorodpoosh, S.; Roslyakova, I.; Stan, M. Comparison of statistically-based methods for automated weighting of experimental data in CALPHAD-type assessment. Calphad 2020, 68, 101728. [Google Scholar] [CrossRef]
- Thermo-Calc Software, Version 2021a. Available online: https://thermocalc.com/ (accessed on 15 January 2021).
- Okamoto, H. Te-U (Tellurium-Uranium). J. Phase Equilibria 1993, 14, 129–130. [Google Scholar] [CrossRef]
- Herrmannsdörfer, T.; Fischer, P.; Mattenberger, K.; Vogt, O. Temperature dependences of rhombohedral lattice distortion and of ferromagnetic uranium ordering in the uranium monochalcogenides. J. Alloys Compd. 2006, 414, 14–19. [Google Scholar] [CrossRef]
- Tougait, O.; André, G.; Bourée, F.; Noël, H. Neutron diffraction study of magnetic ordering of two binary uranium tellurides U3Te5 and U2Te3. J. Alloys Compd. 2001, 317–318, 227–232. [Google Scholar] [CrossRef]
- Stöwe, K. Contributions to the Crystal Chemistry of Uranium Tellurides. III. Temperature-Dependent Structural Investigations on Uranium Ditelluride. J. Solid State Chem. 1996, 127, 202–210. [Google Scholar] [CrossRef]
- Solvyanskikh, V.K.; Yarembash, E.I.; Ellert, G.V.; Eliseev, A.A. On the system U-Te. Izv. Akad. SSSR Ser. Neor. Materialy 1968, 4, 543–545. [Google Scholar]
- Solvyanskikh, V.K.; Rozanov, I.A.; Gracheva, N.V. The S-Te-U. Russ. J. Inorg. Chem. 1977, 22, 893–896. [Google Scholar]
- Tougait, O.; Potel, M.; Noël, H. Characterization of the Binary Uranium and Thorium Tellurides U7Te12 and Th7Te12. Inorg. Chem. 1998, 37, 5088–5091. [Google Scholar] [CrossRef]
- Tougait, O.; Potel, M.; Padiou, J.; Noël, H. Crystal structure and properties of the binary uranium telluride U2Te5. J. Alloys Compd. 1997, 262–263, 320–324. [Google Scholar] [CrossRef]
- Boehme, D.R.; Nichols, M.C.; Snyder, R.L.; Matheis, D.P. An investigation of the tellutium-rich uranium tellurides using X-ray powder diffraction. J. Alloys Compd. 1992, 179, 37–59. [Google Scholar] [CrossRef]
- Ellert, G.V.; Sevast’yanov, V.G.; Solvyanskikh, V.K. The Se-U and Te-U Systems. Russ. J. Inorg. Chem. 1975, 20, 120–124. [Google Scholar]
- Czechowicz, D.G. Combustion Synthesis and Characterization of Uranium and Thorium Tellurides: LA-10559-T. Master’s Thesis, Los Alamos National Laboratory, Los Alamos, NM, USA, 1985. [Google Scholar]
- Wolf, A. Modellierungen zur Kristallzüchtung von CrSb2 und UPTe, Ein Beitrag zur Rationale Syntheseplanung; Springer: Wiesbaden, Germany, 2017. [Google Scholar] [CrossRef]
- Westrum, E.F.; Gronvold, F. Chemical Thermodynamics of the Actinide Element Chalcogenides. In Proceedings of the Symposium on Thermodynamics of Nuclear Materials (IAEA), Vienna, Austria, 21–25 May 1962. [Google Scholar]
- Czechowicz, D.G. A Study of vaporization Thermodynamics in the Uranium-Tellurium System: LA-10621-T. Master’s Thesis, Los Alamos National Laboratory, Los Alamos, NM, USA, 1986. [Google Scholar]
- Baskin, Y.; Smith, S.D. Enthalpy of formation data on compounds of uranium with groups VA and VIA elements. J. Nucl. Mater. 1970, 37, 209–222. [Google Scholar] [CrossRef]
- Mills, K.C. Thermodynamic Data for Inorganic Sulphides, Selenides and Tellurides; Butterworth & Co.: London, UK, 1974. [Google Scholar]
- Qian, S.; Qiu, R.; Tang, J.; Chen, J.; Liu, P.; Ao, B. Theoretical Assignment of Oxidation State of Uranium in Binary, Ternary, and Quaternary Tellurides. J. Phys. Chem. 2021, 125, 1029–1040. [Google Scholar] [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Solvyanskikh, V.K.; Ellert, G.V.; Yarembash, E.S. Transport mechanism and kinetics in Uranium chalcogenides. Izv. Akad. SSSR Ser. Neor. Mater. 1967, 3, 1133. [Google Scholar]
- Sevast’yanov, V.G.; Solvyanskikh, V.K.; Ellert, G.V. Equilibria in the USx–Br2 and USex–Br2 system. Zh. Neorg. Khim. 1971, 16, 3357. [Google Scholar]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Hillert, M.; Jansson, B.; Sundman, B.; Agren, J. A two-sublattice model for molten solutions with different tendency for ionization. Metall. Trans. 1985, 16, 661. [Google Scholar] [CrossRef]
- SSUB5: SGTE Substances Database, Version 5.2. Available online: https://thermocalc.com/products/databases/general-alloys-and-pure-substances/ (accessed on 15 January 2016).
- Guillaumont, R. Update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium and Technetium; OECD Nuclear Energy Agency, Data Bank: Issy-les-Moulineaux, France, 2003. [Google Scholar]
- Chatterjee, N.D.; Krüger, R.; Haller, G.; Olbricht, W. The bayesian approach to an internally consistent thermodynamic database: Theory, database, and generation of phasediagrams. Contrib. Mineral. Petrol. 1998, 133, 149–168. [Google Scholar] [CrossRef]
- Duong, T.C.; Hackenberg, R.E.; Landa, A.; Honarmandi, P.; Talapatra, A.; Volz, H.M.; Llobet, A.; Smith, A.I.; King, G.; Bajaj, S.; et al. Revisiting thermodynamics and kinetic diffusivities of uranium–niobium with bayesian uncertainty analysis. Calphad 2016, 55, 219–230. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, E. Reconstruction Fonctionnelle et Analyse D’incertitude dans le Cadre d’un Problème Inverse de Thermodynamique Chimique. Ph.D. Thesis, Université Paul Sabatier Toulouse 3, Toulouse, France, 2020. [Google Scholar]
- Robert, C.P. The Bayesian Choice: A Decision-Theoretic Motivation; Springer: New York, NY, USA, 1994. [Google Scholar]
- Azaïs, J.M.; Bardet, J.M. Le Modèle Linéaire par L’exemple. Régression, Analyse de la Variance et Plans d’Expériences. Illustrations Numériques avec les Logiciels R, SAS et Splus; Dunod: Paris, France, 2006. [Google Scholar]
- Sundman, B.; Lu, X.G.; Ohtani, H. The implementation of an algorithm to calculate thermodynamic equilibria for multi-component systems with non-ideal phases in a free software. Comput. Mater. Sci. 2015, 101, 127–137. [Google Scholar] [CrossRef]
- The OpenCalphad Repository. Available online: http://github.com/sundmanbo/opencalphad (accessed on 12 December 2018).



| Compounds | Composition At. % Te | Space Group | Reference |
|---|---|---|---|
| -U | 0 | Okamoto (1993) [9] | |
| -U | 0 | Okamoto (1993) [9] | |
| -U | 0 | Clcl | Okamoto (1993) [9] |
| UTe | 9 | Okamoto (1993) [9] | |
| UTe | 50 | Fm-3m | Hermannsdörfer et al. (2006) [10] |
| UTe | 57.1 | I-43d | Solvyanskikh et al. (1977) [14] |
| UTe | 60 | Pnma | Tougait et al. (2001) [11] |
| UTe | 62.5 | Pnma | Tougait et al. (2001) [11] |
| UTe | 63.2 | Tougait et al. (1998) [15] | |
| -UTe | 66.7 | Unknown | Okamoto (1993) [9] |
| -UTe | 2 | 2 | Stöwe (1996) [12] |
| UTe | 71.4 | C12m1 | Tougait et al. (1997) [16] |
| UTe | 75 | Stöwe (1996) [12] | |
| UTe | 77.8 | Unknown | Okamoto (1993) [9] |
| UTe | 83.3 | Pnma | Boehme et al. (1992) [17] |
| Te | 100 | Okamoto (1993) [9] |
| Composition Range At. % Te | Method | Reference | Comments |
|---|---|---|---|
| 58–100 | DTA, XRD | Slovyanskikh et al. (1968) [13] | Selected |
| 0–65 | DTA, XRD | Ellert et al. (1975) [18] | Selected |
| 0–100 | Review | Czechowitz (1985) [19] | Not selected |
| 0–100 | Review | Okamoto (1993) [9] | Not selected |
| 100 | Calphad model | Wolf (2017) [20] | Not selected |
| Thermodynamic Data | Phases | Method | Reference | Comments |
|---|---|---|---|---|
| Estimation | Westrum 1962 [21] | Selected | ||
| , | Baskin and Smith 1970 [23] | Selected | ||
| Estimation Solgasmix | Czechowicz 1985 [19] | |||
| */ | Slovyanskikh et al., 1967 [27] | Selected | ||
| */ | Sevast’yanov et al., 1971 [28] | Selected | ||
| , | / | KEMS | Czechowicz 1986 [22] | Selected |
| Calphad model | Wolf 2017 [20] | Only selected | ||
| DFT+U | Qian et al., 2021 [25] | Not selected | ||
| DFT | OQMD [26] | Not selected |
| Phase | Parameter Name | Assessment Value | Posterior Mean Value | Posterior Standard Deviation |
|---|---|---|---|---|
| Liquid | B | −171,903.278 | −171,903.269 | 1.000 |
| C | 81.899 | 81.836 | 0.840 | |
| B | 111,518.216 | 111,518.211 | 1.000 | |
| C | −55.379 | −55.635 | 0.965 | |
| B | −69,986.365 | −69,986.364 | 1.000 | |
| C | 46.920 | 47.115 | 0.994 | |
| UTe | −221,461.935 | −221,461.944 | 1.000 | |
| 198.439 | 198.314 | 0.236 | ||
| UTe | −736,731.990 | −736,731.991 | 1.000 | |
| 689.583 | 689.274 | 0.478 | ||
| UTe | −514,925.773 | −514,925.777 | 1.000 | |
| 494.721 | 494.781 | 0.379 | ||
| UTe | −808,509.276 | −808,509.286 | 1.000 | |
| 796.312 | 796.470 | 0.686 | ||
| UTe | −272,474.416 | −272,474.408 | 1.000 | |
| 288.876 | 288.996 | 0.160 | ||
| UTe | −556,197.559 | −556,197.562 | 1.000 | |
| 656.416 | 656.504 | 0.402 | ||
| UTe | −283,794.079 | −283,794.075 | 1.000 | |
| 367.797 | 367.730 | 0.250 | ||
| UTe | −312,579.609 | −312,579.607 | 1.000 | |
| 557.353 | 557.329 | 0.269 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guéneau, C.; Lawrence, E.; Klein, T.; Gamboa, F. Thermodynamic Modeling of the Uranium–Tellurium System: Estimation of the Uncertainties by a Bayesian Approach. Thermo 2022, 2, 15-38. https://doi.org/10.3390/thermo2010003
Guéneau C, Lawrence E, Klein T, Gamboa F. Thermodynamic Modeling of the Uranium–Tellurium System: Estimation of the Uncertainties by a Bayesian Approach. Thermo. 2022; 2(1):15-38. https://doi.org/10.3390/thermo2010003
Chicago/Turabian StyleGuéneau, Christine, Eva Lawrence, Thierry Klein, and Fabrice Gamboa. 2022. "Thermodynamic Modeling of the Uranium–Tellurium System: Estimation of the Uncertainties by a Bayesian Approach" Thermo 2, no. 1: 15-38. https://doi.org/10.3390/thermo2010003
APA StyleGuéneau, C., Lawrence, E., Klein, T., & Gamboa, F. (2022). Thermodynamic Modeling of the Uranium–Tellurium System: Estimation of the Uncertainties by a Bayesian Approach. Thermo, 2(1), 15-38. https://doi.org/10.3390/thermo2010003







