Abstract
The development of instrumentation has allowed thermal analysis to become a widely used method not only in calorimetry but also in the field of non-isothermal kinetics that, however, provides a simplified philosophy of measurements. From the beginning, a methodology is used describing the course of reaction in a simplified temperature regime measured in an inert sample. In a most common case of DTA, the degree of reaction is subtracted from the partial areas of the as-cast peak in the unified mode of the peak linear background. Usually, the effect of thermal inertia, resulting from the reality of heat transfer and changing the peak background to a non-linear s-shaped form, is not incorporated. Therefore, the question of whether or not to include this effect of thermal inertia has become a current underlying problem of thermo-analytical kinetics. The analysis of the rectangular input heat pulses and their DTA responding fundamentally point to the need to include it thus becoming essential and not negligible. In the case of parallel evaluations, the effect of inertia can be partially compensated for each other such as in the Kissinger evaluation method. The study presents a broad overview of the thermo-analytical methodology used and points to the often-neglected literature. However, standard mainstream kinetics procedures need be fixed, and an improved solution found to account for the effect of heat transfer and dissipation, which is becoming the focus of thermal analysis methods of future and also the intention of this review.
1. Introduction
The field of thermal analysis naturally contains the incorporative concept of heat (in the sense of the words: light, fire, caloric and recently even a kind of movable energy) that has long been recognized as a basic element of integration in the way of the organization of matter and society [1]. Within the chronicle of interactions of society with fire, we can roughly distinguish about four periods. Perhaps the longest age can be named the period without fire, as the first human beings were afraid of its effects, followed by periods of exercising fire, incinerating fire and today use of fire, which falls in the recent epoch of technology. Heat can be seen in two leanings: as a working tool widely used in power processing and or as an analytical agent, which is capable of detecting its own actions, which is the case of any derived thermo-analytical approach [1,2,3,4]. Unavoidable temperature differences during installation and measurements lead to irreversible heat flows, which we encounter in all areas of thermal applications from house construction to experimental study of the thermal behavior of samples. However, although the belonging laws of thermodynamics deal with the transfer of energy, they only apply to systems that are thermally static—in equilibrium. They can be used to predict the amount of energy required modifying a system from one equilibrium state to another, but they do not serve to predict the speed with which these (time related) changes can occur. This can be extended to the environment of a constant heating, i.e., invariable first time derivatives when thermodynamic laws and quantities yet remain valid [4]. However, the sphere of thermal analysis involves but simplifies heat impact from the very beginning [5,6,7] to be just responsible for the temperature detection only. Adequate phenomenology—which would really study heat transfer processes—becomes a suitable tool for off-equilibrium conditions within the thermodynamic principles applicable in non-isothermal conditions [4], providing analytical methods that would also allow predicting the effect of heat transfer rate, including inertia (as shown next).
Interpretation of the allied effects of thermal inertia is then given as the degree of deceleration with which the body temperature approaches the ambient temperature, or as the resistance of the material to temperature changes [8], defined as √(λ ρ Cp). This term is often called as the volumetric heat inertia, where λ is thermal diffusivity, ρ density, and Cp heat capacity. Otherwise this heat capacity is often referred to as thermal mass in the spheres of architecture and civil engineering, referring to the heat store capability of buildings [9]. It is clear that a process deceleration due to thermal inertia has become an integral part of the general processes associated with heat transfer and dissipation falling into the realm of thermal analysis where it is taken wrongly into consideration as a heating rate imbalance [10].
2. Thermal Inertia and Newton’s Law of Cooling
Thermal inertia generally results in the process of thermally induced change in the heat capacity of the sample body. Inherent time-dependent heat transfer can be simply derived from the well-known Newton’s law of cooling [11]. It provides the commonly known relation ΔT(t) ≅ ΔT(t)0 exp (−t/τ) where ΔT(t)0 and ΔT(t) are the initial and actual temperature differences, with the latter decaying exponentially as a function of time, t, where τ takes on a value known as a thermal inertia function.
Nevertheless, the inertia persists regardless of size, e.g., we can account for both large and small cars that are broken after crashing due to their motion inertia so that the larger car has more damage than the smaller one, however, it is always regarded as a property of their momentum. It is similar for a thermo-analytical sample, too, where, however, it is always necessary to take into account the relationship of the actual heat inertia to the measured quantity (ΔH). It means that for a large sample the ΔH is larger and more influenced by inertia than with a smaller sample, so we must always consider cross-correlation comparable for both size cases. In addition, it is necessary to take into account the evident and experimentally proven effect of inertia against the background of the DTA peak. This effect becomes significant if a single peak is utilized for the determining the degree of conversion by means of areas proportionality and then analyzed for possible overlapping of multiple reactions. It is clear that the inertia brings an opposite effect at the beginning and at the end of the peak and its incorporation can affect the analysis of the peak partitioning due to inertia correction and its nonlinearity, which cannot be compensated by a single thermal inertia constant, τ, often underlaid as a calorimetric cooling constant.
While no one would question the validity of mechanical momentum, heat inertia has remained forgotten, and it continues to be neglected in the sphere of thermo-analytical kinetics. Some kineticists believe that its incorporation would be too complicated and would disrupt computational throughput. Others try to find possible reasons for its negligibility or inconclusiveness. Further, it has been said that as thermal inertia has not been applied in kinetics over the past 300 years, there is no reason to apply it now or in the future [11] as it will complicate calculations. Still others use philosophical resignation, saying that science is never accurate, and it only approximates the truth—as an excuse for knowingly using inaccurate and simplified thermodynamic models while the ways to correct them has been known for a long time [11,12,13]. If Newton, Fourier, Carnot and Tian were proponents of simplified continuity and motivated by today’s job security, i.e., the need to maintain easier approaches, they would not bother to examine the impractical complexities and ineffectual intricacies of heat transfer, which form an inseparable basis for thermal analysis [14,15,16,17].
Although thermal analysis has thermal in its name, its practical application factually circumvents incorporation of thermal transfer relations. It manifests itself in the endless discussion of whether or not thermal inertia has an effect on the specific evaluation of thermo-analytical kinetics, which seems unceasing [11,12,13,14]. In [14], it was said that the effects of heat transfer in general are diminished by using smaller sample masses (m) and slower heating rates (β). It is clear that more equilibrated conditions keep reducing the effect of thermal inertia approaching stationarity. It also follows in [14] that the result of the ICTA kinetic committee work [15] says nothing more that is logically obvious, i.e., that the kinetics are less affected by heat transfer the closer they are to the equipoise (isothermal) regime, e.g., introduced by decelerate heating. The remark in [13] also points to the negligibility of thermal inertia due to the decreasing sample size that was previously exposed on the samples of large and small cars in collision. This is because, for both larger and smaller sizes, the heat transfer is real even if corresponding to the size and involved heat capacity but affects the goal of measuring the determination of enthalpy changes.
We can briefly contemplate where the basic misinterpretations in thermo-analytical determinations are critical:
(i) In the case of standard differential measurements, the temperature of the inert sample, which is following the surrounding thermostat controlled from the outside program, is taken as the feedback temperature (T) of measurement. However, the actual (reaction true) sample temperature (Ttrue) is correct only when the controlled temperature is added by the difference (ΔT) due to the reaction detected between the sample and its inertia that is read correctly as (T + ΔT), cf. Figure 1 left.
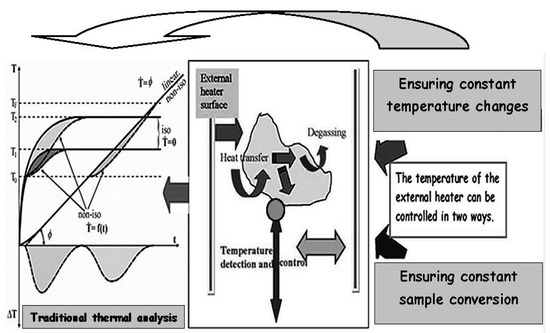
Figure 1.
Schematic view of any (thermo-analytically) placed sample studied inside a heated furnace showing possible internal and external flows which thus forms the basis of the methodology of thermal analysis studying heat processes (middle). According to the method of the given measurement, i.e., detection of the measured quantity, we can distinguish two types of thermal analysis. In the classical design, the furnace temperature is regulated and the degree of sample conversion is measured, while in the second less common mode, the sample conversion is kept constant by changing the ambient temperature, which is also measured as the indicated response temperature. Both methods actually deal with heat transfer and the inclusion and description of this transfer in the standard thermo-analytical literature is missing. The main simplification of the standard method of daily thermal analysis (left) is the unification of the temperature of the external source (heated furnace, inert sample) with the actual reaction temperature of the studied sample, which is considered usable and rationally true despite its inaccuracy. The (left) shown curves trace true-life measurements of temperature where the shaded area represents the deviation of programed temperature from that factually measured. This shows the magnitude of the discrepancy between the programed temperature (which is traditionally used as representative) and the actual value (which is, in fact, mostly ignored via simplification [13]).
(j) In such common differential measurements, the rising temperature is under the inhibition due to thermal inertia, which in turn becomes compensated in the descending part (usually behind the maximum of the temperature difference ΔT). However, the total area remains the same, which is important for calorimetry. Nevertheless, the degree of conversion on the basis of such an s-shaped produced background when derived from the area partiality is affected. Such values differ significantly from the simplified case based on the linear background thus ignoring heat inertia. This cannot be corrected simply just by the application of a single calorimetric-like constant, τ, derived from a one-way cooling process.
3. Historical Kinetics by Thermal Analysis
Thermal analysis has a long tradition whose theoretical foundations date back to the early 1960s, such as the books [16,17] that already contained some basis of heat transfer phenomena. The principle of thermal measurements shows Figure 1, where the method based on constant heating became the basis for the rapid development of this measuring technique. It is based on detecting changes in various measurable variables such as temperature, mass, length, electric a magnetic data, etc. [16,17], the most commonly used is thermogravimetry (TG) and differential thermal analysis (DTA). The portrayal of individual methods, their advantages and drawbacks, sensitivities and calibrations was not the purpose of this paper and, moreover, lies outside the area of interests of readers because it is well described in the manuals of individual instrument manufacturers. Specificity of differential measurements (DTA) involves a twin practice containing an associable sample together with an analogous inert where the temperature of the inert sample is shared with the temperature of the external thermostat (heated furnace). In many years of practice in the study of reactions, the instantaneous inert temperature is practically taken as the usable reaction temperature, although the actual reaction temperature varies by the temperature difference between the inert and reacting samples. This is usually sufficient with regard to its use in qualitative and quantitative analysis, but in the field of the study of kinetics we thus commit a certain inaccuracy, which we conceal in our simplistic approach, in other words, we lie a bit to ourselves. The other approach based as an alternative of constant heating is keeping the constant rate of reaction conversion, which is a particular technique the specificity of which are described elsewhere [18,19,20].
Another important factor of thermal analysis is the study of heat transfer and its effect on the actual temperature of the sample, noticed as early as 1968 [21]. This results in the process of changing the heat capacity of the sample, which shows some thermal inertia due to thermally forced change of motional inertia of inherent particles (atoms, molecules). This is often overlooked, although these effects were the basis of the theoretic works of the greats of thermal history [16,17]. While no one would question the validity of mechanical momentum, heat inertia resulting from the time-honored Newton cooling law [11,22] has remained forgotten and is continuously neglected in thermo-analytical kinetics, which has a long and abundant publication history, e.g., [23,24,25,26,27,28]. Therefore, it needs to be emphasized again that some noniothermal kineticists believe that inertia amalgamation would be too intricate upsetting computational throughput or attempt to find possible reasons for bringing its inaptitude. Others undergo hypothetical capitulation as an excuse for knowingly using inaccurate and simplified models while the ways to correct them has been known for a long time [29,30] although unintentionally complicated.
4. Physical Meaning of the Phenomenon Called Thermal Inertia and Reaction Kinetics by Thermal Analysis
The current mainstream in thermo-analytical kinetics [5,15,26,27] has been largely hostile to the use of physical phenomena associated with heat transfer and subsequently exhibiting the effects of thermal inertia revealed by Newton in his law of cooling at the turn of the 18th century [22,31]. The kinetic mainstream based on the above-mentioned association of the inertia temperature with the reaction temperature of the sample and the neglect of heat transfer processes has a long tradition, although it had its critics at the beginning [17]. However, this simplified approach has become widely used and has its well-appreciated results based on the wise manipulation of mathematical equations modeling kinetic sub-processes [25,32]. Unfortunately, its supporters do not admit their possible variability due to non-reactive effects of heat transfer. At the extreme, the promoters of the mainstream go so far as to neglect the results of their competitors; likewise, the review article [15] did not read the previously published article [32]. As a result, in a recent publication the mainstream promoter attempts to find a variety of reasons to reveal that the effect of thermal inertia is justifiably considered negligible. This motivation can be divided into two categories. The first shows the true physical significance of thermal inertia as such, and the second examines its effect on the value of a frequently published kinetic value called activation energy, E. Let us try to analyze them in detail.
First, it should be emphasized that many critics do not sufficiently understand the physical concept of thermal inertia, which is obviously dependent on the sample heat capacity, Cp, being an extensive property as well as on the time derivative of the change of measured temperature difference, ΔT/dt. It has already been publicized in early papers [4,6] and books [24,25] that show the relation between heat inertia and the term Cp ΔT/dt, where ΔT is the experimentally detected difference between the sample and reference temperatures.
Like enthalpy H, which is the energy measurement in a studied thermodynamic system (in joule, J) the heat capacity Cp is a physical property of matter defined as the amount of heat to be supplied to a given material to produce a unit change in its temperature (in joule per Kelvin, J/K). Its significance lies in the thermally initiated mechanical changes of the vibrational and rotational inertia of the structural units (molecules, atoms) forming the structure of matter, i.e., to their three-dimensional molecular motion. Dividing the heat capacity by the amount of substance gives the specific heat capacity (e.g., in J/(K kg)), which then becomes its corresponding intensive property.
We have to again remind of the above mentioned competitive interpretation of thermal inertia, which is given as the degree of deceleration with which the body temperature approaches the ambient temperature, or as the resistance of the material to temperature changes [9,10]. It is clear that any thermal inertia interpretation has become an inseparable and integral part of the procedural fortitude associated with heat transfer and dissipation in various domains of technological [9] and scientific [33,34] applications, as an integral part of the literature [35,36,37].
5. Impact of Thermal Inertia in Thermal Analysis and Calorimetry
The term thermal inertia has been long known [38], although it is sometimes referred to as a heating rate imbalance [10]. Thus, it is often misinterpreted as a sample-dependent quantity so that its impact can be reduced by miniaturizing the samples. With the size of the sample, its strength decreases, which, however, goes hand in hand with the decreasing sensitivity of the detection of the desired (measured) quantity (as enthalpy). With the introduction of microprocessors [39] it became particularly important, as the instrumental capabilities have deepened to the point that they are able to detect sudden temperature changes even in millisecond processes [40,41]. The inertia effect, however, has not been and cannot be eliminated in this way and often is not considered at all [42]. Similar questioning applies to the meaning of temperature measured during fast thermal changes as discussed in detail in papers [43,44,45], which, while being thermo-analytically authoritative [45], fall outside of this article’s purpose.
In our sophisticated age of computers that bring the latest scientific knowledge, the lack of awareness of basic thermo-analytical theories [4,6]—particularly that of heat transfer physics [31,36]—as applied in nonisothermal kinetics is surprising, although in engineering thermodynamics heat transfer [35,36,37] is a matter of course. Obviously, the ignorance or reluctance concerning incorporation of the influence of Newton’s law of cooling into the dynamics of thermal kinetics is almost scandalous [4,13,24,28]. The editors and journalists, however, mostly reiterate the view that after hundreds of years it is not clear whether someone would be interested in these complications at present [11], as they could greatly obscure the simplified concept of thermo-analytical kinetics.
Recalling again that the impact of thermal inertia and its transfer delaying effect has long been well known from Newton’s famous law of cooling [22,29,30,31] and its real authority was long recognized in the field of calorimetry [46]. It is worth noting that the famous Tian’s equation already contains the inertia term Cp ΔT/dt. Its significance is indisputable especially in determining the so-called calorimetric cooling constants clearly showing that the heat transfer to the heated/cooled sample is not instantaneous and that its description requires introduction of an explicit time indicating an increase or decrease in temperature in the exponential manner.
In this context, it is necessary to mention yet again the use of a rectangular heat pulse introduced as a model thermal effect applied to the sample site. This calibration procedure, first used by its originator Tian and variously repeated many times [47,48,49,50,51,52,53], reveals its impact on the distortion of the input pulse. It is well illustrated by the dissipation process of heat transfer showing that the shape of the rebuild peak during measurement differs significantly from the original input to by tens of percent (see Figure 2). It is obvious that the process of mathematical correction (called rectification) of the measured peak back to the originally introduced one is symmetrical and does not affect the total area of the peak (good for calorimetry). The shape distortion is remarkable in the rising and falling parts and reaches approximately one third of the areas of both the growing and declining areas, thereby strongly influencing the shape of the peak. In some very fast heat dissipation hydration processes, it has been shown that the effect of thermal inertia can in the initial phase deflect calorimetric data to large errors [53,54].
Above all, however, it is important to realize that the shape of the peak began to be used to determine the kinetics of the reaction under study, which is based on the partial division of respective areas. The impact of thermal inertia on the kinetics from thermo-analytical measurements was first pointed out as early as in 1949 by Vold [38] and subsequently analyzed in [4,11,24,28,29,30,53,54,55,56,57,58].
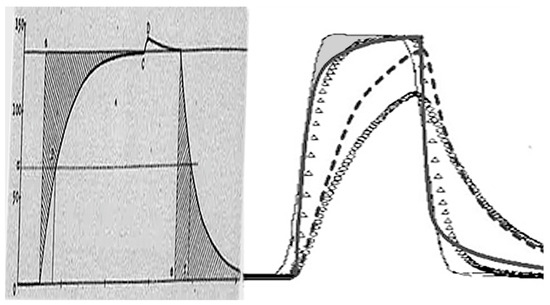
Figure 2.
Historical replica of a calibrating pulse of heat transferred from Tian’s 1933 publication compared with rectangular heat pulse artificially inserted recently into the sample by either method: electrically by resistant heating inside the sample carried out under steady heating and (j) external heat irradiation onto the sample surface during the isothermal regime. Both pulses are normalized on the <ΔT vs. t> axis as to fine-tuning the same shape regarding the inserted rectangular pulse (thin solid). The as-measured DTA response peak (dashed line, resistant heating) was mathematically corrected on the heat inertia effect by the differential method to yield the rectified peak (full line) [11,48]. The as-measured DTA feedback on the externally applied heat-pulse (small-circle line) was corrected by the standard Netzsch instrumental software [49] based on integral method providing a rectified peak (small-triangles line). Both rectifications encompass the same character of the necessary adjustment showing the necessity of corrections for kinetic interpretations due to radical changes in the ratio of partial areas used to determine the degree of conversion. It is clear that the effect of thermal inertia is non-linear (s-shaped) and therefore cannot be compensated [12,14] for a kinetic analysis of a singular peak by a single multiple coefficient often known as calorimetric constant, τ, derived from the fading part of a thermal record [46]. Shaded area of rectangular misfit on the right curves associates to unenclosed effects of temperature gradients in the sample body.
6. DTA Equation and Thermal Inertia Effect in Kinetics
Of course, the important question remains concerning how far the unaccounted thermal inertia influences the kinetic analysis, although it is clear that the thermal inertia has a major impact on the distortion of the subsequently measured process as shown even historically [28,45]. This is a crucial question because it concerns all data published so far. Attempted devaluation of the importance of thermal inertia has been common [12,14] on the basis of the publication [56], but the author forgot to note that its essence is based on yet previous work [55] that has already been analyzed in our papers [29,30] and chapters [57,58].
In particular, Borchart and Danniels [55] used DTA to study kinetics of homogeneous reactions in well stirred liquid samples and started with the abovementioned Vold’s balance, see their equation {3} in Reference [38] (note that {} are transferred notions):
where dH is the change of enthalpy and K is the apparatus constant. The correction with respect to heat inertia is also included in their equation {13} taken over from [38] expressing the rate constant k of a homogeneous reaction as:
where A is total area of DTA peak and a is an acting part of this area for time interval t − t0 and this correction is included in auxiliary equations {12} to {15} taken again over from Reference [38].
dH = CP dΔT + K.ΔT dt
k = (CP(dΔT/dt) + KΔT)/(K(A − a) − CPΔT)
However, the heat inertia term was then neglected in the original equations {17}, {19}, {21} and {22} in accordance with the argument [55] citing “... the quantities (CP dΔT/dt) and CPΔT are usually an order of magnitude smaller than the quantities to which they are added and subtracted”. They results show, however, that term “CP dΔT/dt varies from 0.634... to −2.70” while the term KΔT “varies from 4.67 to 13.1 going through a maximum of 28.1”. For that reason the above neglecting seems to be rather erroneous because the heat inertia term shows a more significant influence as being asymmetrical on the level approaching the curve inflection points, i.e., differing at least 20% from the original signal. The shape of the kinetic curve and the derived kinetic parameters become thus extremely sensitive to this heat inertia consequence especially given by the s-shaped peak background.
In [12], it is argued that by not accounting for thermal inertia by the Kissinger evaluation method [59,60,61] an error in the calculated activation energy up to 20 percent is discharged, which is seen to be negligible. The Kissinger evaluation is a rather simplified approach that received many mathematical upgradings but not too many improvements regarding the impact of heat inertia [60]. Using runs for different heating, β, the Kissinger procedure is estimating activation energy, E, as a slope of approximating line in the plot of ln(β/Tmr2) against −1/RTmr where Tmr is substituted by temperature TmΔ at which an extreme of the peak on DTA curve is reached. It means the temperature difference ΔT = TS − TR between the sample under study (S) and the reference sample (R) attained its extreme value under the constant heating rate, β, for which the condition is valid as dΔmΔT/dt = 0. However, Kissinger’s assumption [59] that the temperature TmΔ (in the point where temperature difference ΔT reaches the extreme value = ΔmΔT) is identical with temperature Tmr where the reaction rate r = dα/dt reaches its maximum is not correct at all. This identity can be assumed justifiable only for curves obtained by compensating DSC (Perkin–Elmer) method [28]. The same inequality Tmr ≠ TmΔ is also relevant to the spontaneous heat flux DSC (calibrated DTA where the spontaneous heat flux q is given as q = K ΔT). The correct equation for a DTA curve ΔT(t,TR) in the simplest form (after subtracting of the baseline BL:ΔTS = ΔT − BL) is as:
where K (dimension W/K) means thermal conductance between the sample environment and the sample holder, Cs (J/K) the heat capacity of the sample under study including its holder, ΔH is integral enthalpy (J) of the process under study and Rt ≡ 1/K is called thermal resistance.
KΔT = CS(dΔT/dt) − ΔH(dα/dt)
or ΔT = Rt [CS(dΔT/dt) − ΔH(dα/dt)]
or ΔT = Rt [CS(dΔT/dt) − ΔH(dα/dt)]
When using both the series of parallel data obtained when changing the heating rate and the corresponding method in the kinetic evaluation under the isoconversion manner, mutual compensation of thermal inertia obviously occurs, so that the evaluated activation energies compensate each other and thus bring less errors than using separate curve analyses. The publication [12] shows an E-error of up to 20 percent, thus seeming less negligible in this respect; this of course requires a deeper analysis of such serial measurements and should become the task of the ICTAC kinetic committee [15], which is not trivial and lies against the interests of the kinetic mainstream. The Kissinger method [59] is still the focus of interest and under the analysis of validity conditions, especially for those for which it was not originally derived [61,62,63,64]. In particular, it is used instead of traditional “cold” crystallization of glasses during heating to crystallize melts during opposite cooling, when it is necessary to integrate thermodynamic parameters [63], which is often forgotten. The method itself is not completely accurate, but it is sufficient for orientation analysis, within the use of which, using a series of parallel measurements, it can be assumed that the effect of arterial inertia is attenuated [13].
7. Discussion and Conclusions
A detailed description of the individual measurement techniques was not the intention of this review and is well included in more details in a number of books [2,16,17,18,27] dealing with thermo-analytical methodic. However, another and no less important topic of dynamic data interpretation is the significance of the resolved values of the activation energies themselves, which are often the main topic of various kinetic studies. It turns out that the use of Arrhenius exponentials to calculate kinetic parameters is often problematic [65,66,67,68], and the associated values of activation energies can take on fictitious values [67,68]. Overestimation of activation energy values [69,70] is therefore often inappropriate, and publications based only on the indication of activation energy values can be even misleading or demonstrating E-data as decorative figures. The solution for these problems will certainly be the task of the ICTAC Kinetic Committee, which should get rid of the current mainstream tendencies and really deal with the issues related to the main content of thermal analysis, i.e., heat transfer and dissipation. These questions are elaborated in more detail in the author’s new book [28].
It is obvious that the long underestimated effect of thermal inertia is a key factor in thermal analysis because it as such must primarily address heat transfer issues. This issue is receiving more and more attention, as shown previously [34,35,36]; in the future it may affect the development of mainstream kinetics itself [15], which so far tends to avoid solving these issues. Of course, discussions and sometimes controversial articles belong to the solution of the topic of thermo-analytical kinetics and it is up to the readers how far they connect to it. The rejection of the effect of thermal inertia often stems from a misunderstanding of its action, especially in the kinetic processing of individual DTA peaks. Vyazovkin [12,14] has argued that thermal inertia can be neglected using a calorimetric constant, τ, but forgets that calorimetric constants are derived from declining part of thermal measurements and therefore cannot be applied to the whole nonlinear (s-shaped, see Figure 2) background of the peak from which the degree of conversion is derived. When using parallel processes, such as isoconversional or cross-heating, it turns out that the thermal inertia is partially compensated for by each source, but this has yet to be proven.
It has also been said [14] that the full incorporation of heat effects would be the best solution if we lived in an ideal world, but that we do not, so simplification must be allowed. Accordingly, the exclusion of heat transfer corrections in the recent practice of thermo-analytical kinetics is a predictable and considerable interpretation, which, however, does not mean that the published results are incorrect. They are simply those that correspond to the magnitude of such simplification, and their way of modeling shows nevertheless the excellence of theoretical procedures, such as [71,72], when applied during associated analyses. Therefore, there is no need to worry that the recognition of the effect of heat transfer, including thermal inertia, will hamper the already published kinetic results, which is also a matter of concern for those who try to denigrate thermal inertia. On the other hand, there rises a necessity to appreciate and incorporate in the future such studies that have already addressed the issues of transfer and incorporated their impact into their conclusions as shown in various papers [73,74,75,76,77,78,79,80,81]. It would be good to think about them and incorporate their different approaches to the analysis of classical thermo-analytical kinetics.
At present, non-isothermal kinetics has become the focus of attention, with a number of review papers published [82,83,84,85], but with almost none of them questioning the influence of thermal inertia as one of the missing key factors. Thermo-analytical methods that actually deal with heat transfer and the inclusion and description of this transfer in the standard thermo-analytical literature are so far mostly absent. The articles describing the transfer imbalance due to heating are sporadic [77,78,79,80,81], as also are discussions on the correct determination and interpretation of thermo-analytically off-equilibrium temperature [45]. Therefore, a rather more detailed depiction and transfer of the thermal problem to the pages of journals is required that directly deals with heat transfer [31,53,79,80]; this has still been lacking in traditional thermo-analytical journals and so we gladly welcomed the new thermo-journal attitude [84].
Perhaps it is interesting to add that it turns out that thermal inertia retains its importance in the microworld, where it intersects with the interpretation of thermal diffusivity [86]. We have previously addressed a similar problem in the field of quantum diffusion [87], which falls outside the scope of this review but shows the generality of the problem being solved above.
Funding
This research received no external funding.
Institutional Review Board Statement
To be excluded.
Informed Consent Statement
Informed content was obtained from all subjects involved in the references.
Data Availability Statement
To be excluded.
Acknowledgments
The studies were supported by the Institute of New Technologies—Research center of the West Bohemian University in Plzeň as well as the Department of Material Engineering and Chemistry, Faculty of Civil Engineering of the Czech Technical University in Prague namely accentuating assistance of Robert Černý.
Conflicts of Interest
The author declares no conflict of interest.
References
- Šesták, J.J.; Mackenzie, R.C. Heat/fire concept and its journey from prehistoric time into the third millennium. J. Therm. Anal. Calorim. 2001, 64, 129–147. [Google Scholar] [CrossRef]
- Mackenzie, R.C. History of thermal analysis. Thermochim. Acta 1984, 73, 251. [Google Scholar] [CrossRef]
- Lombardi, G.; Šesták, J. Ten years since Robert C. Mackenzie’s death: A tribute to the thermal analysis founder. J. Therm. Anal. Calorim. 2011, 105, 783–791. [Google Scholar] [CrossRef]
- Šesták, J. Thermodynamic basis for the theoretical description and correct interpretation of thermoanalytical experiments. Thermochim. Acta 1979, 28, 197–227. [Google Scholar] [CrossRef]
- Šesták, J.; Hubík, P.; Mareš, J.J. Historical roots and development of thermal analysis and calorimetry. In Glassy, Amorphous and Nano-Crystalline Materials; Šesták, J., Mareš, J.J., Hubík, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Šesták, J. Thermal science and analysis: History, terminology, development and the role of personalities. J. Therm. Anal. Calorim. 2013, 113, 1049–1054. [Google Scholar] [CrossRef]
- Šesták, J.; Mareš, J.J. From caloric to statmograph and polarography. J. Therm. Anal. Calorim. 2007, 88, 763–771. [Google Scholar] [CrossRef]
- Wang, J.; Bras, L.; Sivandran, G.; Knox, R.G. A simple method for the estimation of thermal inertia. Geophys. Res. Lett. 2010, 37, L05404. [Google Scholar] [CrossRef]
- Verbeke, S.; Audenaert, A. Thermal inertia in buildings: A review. Renew. Sustain. Energy Rev. 2018, 82, 2300–2318. [Google Scholar] [CrossRef]
- Danley, R.L. New heat flux DSC measurement technique. Thermochim. Acta 2003, 395, 201–208. [Google Scholar] [CrossRef]
- Šesták, J. Ignoring heat inertia impairs accuracy of determination of activation energy in thermal analysis. Int. J. Chem. Kinet. 2019, 51, 74–80. [Google Scholar] [CrossRef]
- Vyazovkin, S. How much is the accuracy of activation energy selected by ignoring thermal inertia? Int. J. Chem. Kinet. 2020, 52, 23–28. [Google Scholar] [CrossRef]
- Šesták, J. The evaluation of non-isothermal thermoanalytical kinetics is simplified without the description of heat transfers, such as thermal inertia, which is not negligible, as indicated by Vyazovkin. Int. J. Chem. Kinet. 2021, 53, 1050–1057. [Google Scholar] [CrossRef]
- Vyazovkin, S. When can the effect of thermal inertia be considered negligible? Int. J. Chem. Kinet. 2021. in print. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Perez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics: Review. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Piloyan, G.O. Introduction to the Theory of Thermal Analysis; Izd. Nauka: Moskva, Russia, 1964. (In Russian) [Google Scholar]
- Garn, P.D. Thermal Analysis of Investigation; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Sørensen, O.T.; Rouquerol, J. Sample Controlled Thermal Analysis; Kluwer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Málek, J.; Šesták, J.; Rouquerol, F.; Rouquerol, J.; Criado, J.M.; Ortega, A. Reaction Kinetics by Method of Constant Rate Thermal Analysis. J. Therm. Anal. 1992, 35, 111. [Google Scholar]
- Criado, J.M.; Pérez-Maqueda, L.A.; Koga, N. Sample Controlled Thermal Analysis (SCTA) as a Promising Tool for Kinetic Characterization of Solid-State Reaction and Controlled Material Synthesis. In Thermal Physics and Thermal Analysis; Šesták, J., Mareš, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 2; pp. 11–43. [Google Scholar]
- Gray, A.P. Simple Generalized Theory for Analysis of Dynamic Thermal Measurements. In Analytical Calorimetry; Porter, R.S., Johnson, J.F., Eds.; Plenum Press: New York, NY, NSA, 1968; Volume 1, pp. 210–218. [Google Scholar]
- Winterton, R.H.S. Early study of heat transfer: Newton and Fourier. Heat Trans. Eng. 2001, 22, 3–11. [Google Scholar] [CrossRef]
- Vyazovkin, S. A unified approach to kinetic processing of nonisothermal data. Int. J. Chem. Kinet. 1996, 28, 95–101. [Google Scholar] [CrossRef]
- Šesták, J. Thermophysical Properties of Solids: Theoretical Thermal Analysis; Elsevier: Amsterdam, The Netherlands, 1984; Russian translation by Mir, Moscow 1988. [Google Scholar]
- Šesták, J. Rationale and fallacy of thermoanalytical kinetic patterns. J. Therm. Anal. Calorim. 2012, 110, 5–16. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J.; Šimon, P. Some fundamental and historical aspects of phenomenological kinetics in solid-state studied by thermal analysis. In Thermal Analysis of Micro-, Nano- and Non-Crystalline Materials; Šesták, J., Šimon, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 1; pp. 1–45. [Google Scholar]
- Vyazovkin, S.; Koga, N.; Schick, C. (Eds.) Handbook of Thermal Analysis and Calorimetry, Volume 6: Recent Advances, Techniques and Applications; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Šesták, J. Thermal Analysis and Thermodynamic Properties of Solids; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780323855372. [Google Scholar]
- Holba, P.; Šesták, J. Heat inertia and its role in thermal analysis. J. Therm. Anal. Calorim. 2015, 121, 303–307. [Google Scholar] [CrossRef]
- Šesták, J. Are nonisothermal kinetics fearing historical Newton’s cooling law, or are just afraid of inbuilt complications due to undesirable thermal inertia? J. Therm. Anal. Calorim. 2018, 134, 1385–1393. [Google Scholar] [CrossRef]
- Davidzon, M.J. Newton’s cooling law and its interpretation. Int. J. Heat Mass Trans. 2012, 55, 5397–5402. [Google Scholar] [CrossRef]
- Šesták, J. The quandary aspects of non-isothermal kinetics beyond the ICTAC kinetic committee recommendations. Thermochim. Acta 2015, 611, 26–35. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Song, X.N.; Liu, D. Asymptotic analysis for effect of thermal inertia on thermal behaviors. Acta Phys. Sin. 1013, 62, 2300–2330. [Google Scholar]
- Rubi, M.J.; Perez-Madrid, A. Inertial effects in non-equilibrium thermodynamics. Physica A 1999, 264, 492–502. [Google Scholar] [CrossRef][Green Version]
- Zemansky, M.V. Heat and Thermodynamics; McGraw-Hill/Kogakuscha: Tokyo, Japan, 1968. [Google Scholar]
- Cengel, Y.A. Introduction to Thermodynamics and Heat Transfer; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 2016. [Google Scholar]
- Vold, M.J. Differential Thermal Analysis. Anal. Chem. 1949, 21, 683–688. [Google Scholar] [CrossRef]
- Lerchner, J.A.; Wolf, G.; Wolf, J. Recent developments in integrated circuit calorimetry. J. Therm. Anal. Calorim. 1999, 57, 241. [Google Scholar] [CrossRef]
- Minakov, A.A.; Schick, C. Ultrafast thermal processing and nanocalorimetry at heating and cooling rates up to 1 MK/s. Rev. Sci. Instr. 2007, 78, 073902e10. [Google Scholar] [CrossRef] [PubMed]
- Minakov, A.A.; Schick, C. Dynamics of the temperature distribution in ultra-fast thin-film calorimeter sensors. Thermochim. Acta 2015, 603, 205–217. [Google Scholar] [CrossRef]
- Ding, J.; Yu, L.; Wang, X.; Xu, Q.; Yang, S.; Ye, S.; Jiang, J. A kinetic-based approach in accelerating rate calorimetry with the varying thermal inertia consideration. J. Therm. Anal. Calorim. 2020, 141, 783–796. [Google Scholar] [CrossRef]
- Šesták, J. Measuring “hotness”, should the sensor’s readings for rapid temperature changes be named “tempericity”? J. Therm. Anal. Calorim. 2016, 125, 991–999. [Google Scholar] [CrossRef]
- Holba, P. The Šesták’s proposal of term “tempericity” for non-equilibrium temperature and modified Tykodi’s thermal science classification with regards to the methods of thermal analysis. J. Therm. Anal. Calorim. 2017, 127, 2553–2559. [Google Scholar] [CrossRef]
- Šesták, J. Do we really know what temperature is: From Newton’s cooling law to an improved understanding of thermal analysis. J. Therm. Anal. Calorim. 2020, 142, 913–926. [Google Scholar] [CrossRef]
- Holman, S.W. Calorimetry: Methods of Cooling Correction. Proc. Am. Acad. Arts Sci. 1895, 31, 245–254. [Google Scholar] [CrossRef]
- He, H.; Dyck, M.F.; Horton, R.; Ren, T.; Bristow, K.L.; Si, B. Development and Application of the Heat Pulse Method for Physical Measurements. Rew. Geophys. 2017, 56, 567–620. [Google Scholar] [CrossRef]
- Svoboda, H.; Šesták, J. A new approach to DTA calibration by predetermined amount of Joule heat. In Proceedings of the 4th ICTA, Thermal Analysis, Budapest, Hungary, 8–13 July 1974; pp. 726–731. [Google Scholar]
- Kaisersberger, E.; Moukhina, E. Temperature dependence of the time constants for deconvolution of heat flow curves. Thermochim. Acta 2009, 492, 101–109. [Google Scholar]
- Barale, S.; Vincent, L.; Sauder, G.; Sbirrazzuoli, N. Deconvolution of calorimeter response from electrical signals for extracting kinetic data. Thermochim. Acta 2015, 615, 30–37. [Google Scholar] [CrossRef]
- Watanabe, H.; Morimoto, K.; Watanabe, M.; Kato, M.; Konashi, K. Multi-stepwise pulse calorimetry for accurate, efficient measurements of thermophysical properties over a wide temperature range. Thermochim. Acta 2020, 693, 178763. [Google Scholar] [CrossRef]
- Righini, F.; Bussolino, C.; Spišiak, J. Pulse calorimetry at high temperatures. Thermochim. Acta 2000, 347, 93–102. [Google Scholar] [CrossRef]
- Kočí, V.; Kočí, J.; Maděra, J.; Černý, R. Assessment of fast heat evolving processes using inverse analysis of calorimetric data. J. Heat Mass Trans. 2017, 115, 831–838. [Google Scholar] [CrossRef]
- Kossoy, A. Effect of thermal inertia-induced distortions of DSC data on the correctness of the kinetics evaluated. J. Therm. Anal. Calorim. 2021, 143, 599–608. [Google Scholar] [CrossRef]
- Borchardt, H.J.; Danniels, F. The Application of Differential Thermal Analysis to the Study of Reaction Kinetics. J. Am. Chem. Soc. 1957, 79, 41–46. [Google Scholar] [CrossRef]
- Kirsh, Y. On the kinetic analysis of DTA curves. Thermochim. Acta. 1988, 135, 97–101. [Google Scholar] [CrossRef]
- Holba, P.; Šesták, J.; Sedmidubský, D. Heat transfer and phase transition at DTA experiments. In Thermal Analysis of Micro-, Nano- and Non-Crystalline Materials; Šesták, J., Šimon, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 5; pp. 99–134. [Google Scholar]
- Holba, P.; Šesták, J. The role of heat transfer and analysis ensuing heat inertia in thermal measurements and its impact to non-isothermal kinetics. In Thermal Analysis and Thermal Physics; Šesták, J., Hubík, P., Mareš, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 15; pp. 319–344. [Google Scholar]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Holba, P.; Šesták, J. Imperfections of Kissinger evaluation method and crystallization kinetics. Glass Phys. Chem. 2014, 40, 486–495. [Google Scholar] [CrossRef]
- Šesták, J.; JHolba, P. Imperfections of Kissinger Evaluation Method and the Explanation of Crystallization Kinetics of Glasses and Melts. In Thermal Analysis and Thermal Physics; Šesták, J., Mareš, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 10; pp. 213–236. [Google Scholar]
- Farjas, J.; Sánchez-Rodriguez, D.; Eloussifi, H.; Roura, P. Thermal Gradients in Thermal Analysis Experiments. In Thermal Physics and Thermal Analysis; Šesták, J., Hubík, P., Mareš, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 16; pp. 345–362. [Google Scholar]
- Avramov, I.; Šesták, J. Generalized Kinetics of Overall Phase Transition Useful for Crystallization When Assuming Heat Inertia. Cond-mat.stat-mech 2019. Available online: https://arXiv.org &>physics&> arXiv1510.02250 (accessed on 8 October 2015).
- Šesták, J. Doubts about the popular Kissinger method of kinetic evaluation and its applicability for crystallization of cooling melts requiring equilibrium temperatures. J. Therm. Anal. Calorim. 2020, 142, 2095–2098. [Google Scholar] [CrossRef]
- Šimon, P. Single-step kinetics approximation employing nonarrhenian temperature function. J. Therm. Anal. Calorim. 2005, 79, 703–709. [Google Scholar]
- Šimon, P.; Thomas, P.; Dubaj, T.; Cibulková, Z. The mathematical incorrectness of the integral isoconversional methods in case of variable activation energy and the consequences. J. Therm. Anal. Calorim. 2014, 115, 853–859. [Google Scholar] [CrossRef]
- Galway, A.K. What theoretical and/or chemical significance is to be attached to the magnitude of an activation energy determined for solid-state reactions? J. Therm. Anal. Calorim. 2006, 86, 267–286. [Google Scholar] [CrossRef]
- Galwey, A.K.; Brown, M.E. Application of the Arrhenius equation to solid-state kinetics:can this be justified? Thermochim. Acta 2002, 386, 91–98. [Google Scholar] [CrossRef]
- Vyazovkin, S. On the phenomenon of variable activation energy for condensed phase reactions. New J. Chem. 2000, 24, 913–917. [Google Scholar] [CrossRef]
- Vyazovkin, S. A time to search: Finding the meaning of variable activation energy. Phys. Chem. Chem. Phys. 2016, 18, 18643–18656. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kinetic effects of pressure on decomposition of solids. Inter. Rew. Phys. Chem. 2020, 39, 35–66. [Google Scholar] [CrossRef]
- Koga, N.; Sakai, Y.; Fukuda, M.; Hara, D.; Tanaka, Y. Universal Kinetics of the Thermal Decomposition of Synthetic Smithsonite over Different Atmospheric Conditions. J. Phys. Chem. C 2021, 125, 1384–1402. [Google Scholar] [CrossRef]
- Wu, X.; Chen, L.; Rao, G.; Chen, W.; Yin, R. Impact of inertia factors on the adiabatic decomposition of ethyl benzene. J. Chem. 2020, 2020, 9845894. [Google Scholar] [CrossRef]
- Heitman, J.L.; Horton, R.; Ren, T.; Nassar, I.N.; Davis, D.D. A test of coupled soil heat and water transfer prediction under transient boundary temperatures. Soil Sci. Soc. Am. J. 2008, 72, 1197–1207. [Google Scholar] [CrossRef]
- Smits, K.M.; Cihan, A.; Sakaki, T.; Illangasekare, T.H. Evaporation from soils under thermal boundary conditions: Experimental and modeling investigation to compare equilibrium- and nonequilibrium-based approaches. Water Resour. Res. 2011, 47, W05540. [Google Scholar] [CrossRef]
- Mianowski, A. Analysis of the Thermokinetics Under Dynamic Conditions by Relative Rate of Thermal Decomposition. J. Therm. Anal. Calorim. 2001, 63, 765–776. [Google Scholar] [CrossRef]
- Ferkl, P.; Hrma, P.; Kloužek, J.; Vernerova, M.; Kruger, A.; Pokorný, R. Model for batch-to-glass conversion: Coupling the heat transfer with conversion kinetics. J. Assian. Ceram. Soc. 2021. in print. [Google Scholar] [CrossRef]
- Patisson, F.; Galant, M.; Francois, T.; Ablitzer, D. A nonisothermal nonequilibrium and nonequimolar transient kinetic model for gas-solid reactions. Chem. Eng. Sci. 1998, 53, 697–708. [Google Scholar] [CrossRef]
- Lamberti, G.; De Santis, F. Heat transfer and crystallization kinetics during fast cooling of polymer films. Heat Mass Transf. 2007, 43, 1143–1150. [Google Scholar] [CrossRef]
- Misyura, S.Y. Different modes of heat transfer and crystallization in a drop of NaCl solution: The influence of key factors on the crystallization rate and the heat transfer coefficient. Int. J. Therm. Sci. 2021, 159, 106602. [Google Scholar] [CrossRef]
- Yasnó, J.P.; Conconi, S.; Visintin, A. Non-isothermal reaction mechanism and kinetic analysis for the synthesis of monoclinic lithium zirconate during solid-state reaction. J. Anal. Sci. Technol. 2021, 12, 15–19. [Google Scholar] [CrossRef]
- Skrdla, P.J. Critical Review: Can we trust kinetic methods of thermal analysis? Analyst 2020, 145, 745–749. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kissinger Method in Kinetics of Materials: Things to Beware and Be Aware of. Molecules 2020, 25, 2813. [Google Scholar] [CrossRef]
- Sapunov, V.N.; Saveljev, E.A.; Voronov Valtiner, M.; Linert, W. The basic theorem of temperature-dependent processes. Thermo 2021, 1, 4. [Google Scholar] [CrossRef]
- Zhang, X. Applications of Kinetic Methods in Thermal Analysis: A Review. Eng. Sci. 2021, 14, 1–13. [Google Scholar]
- Smarlak, M. On the inertia of heat. Eur. Phys. J. Plus. 2012, 127, 72–79. [Google Scholar] [CrossRef][Green Version]
- Mareš, J.J.; Šesták, J.; Hubík, P. Transport Constitutive Relations, Quantum Diffusion and Periodic Reactions. In Glassy, Amorphous and Nano-Crystalline Materials: Thermal Physics, Analysis, Structure and Properties; Šesták, J., Mareš, J., Hubík, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 14; pp. 227–245. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).