Dielectric Properties of Textile Materials: Analytical Approximations and Experimental Measurements—A Review
Abstract
:1. Introduction
2. General Theory of Dielectrics
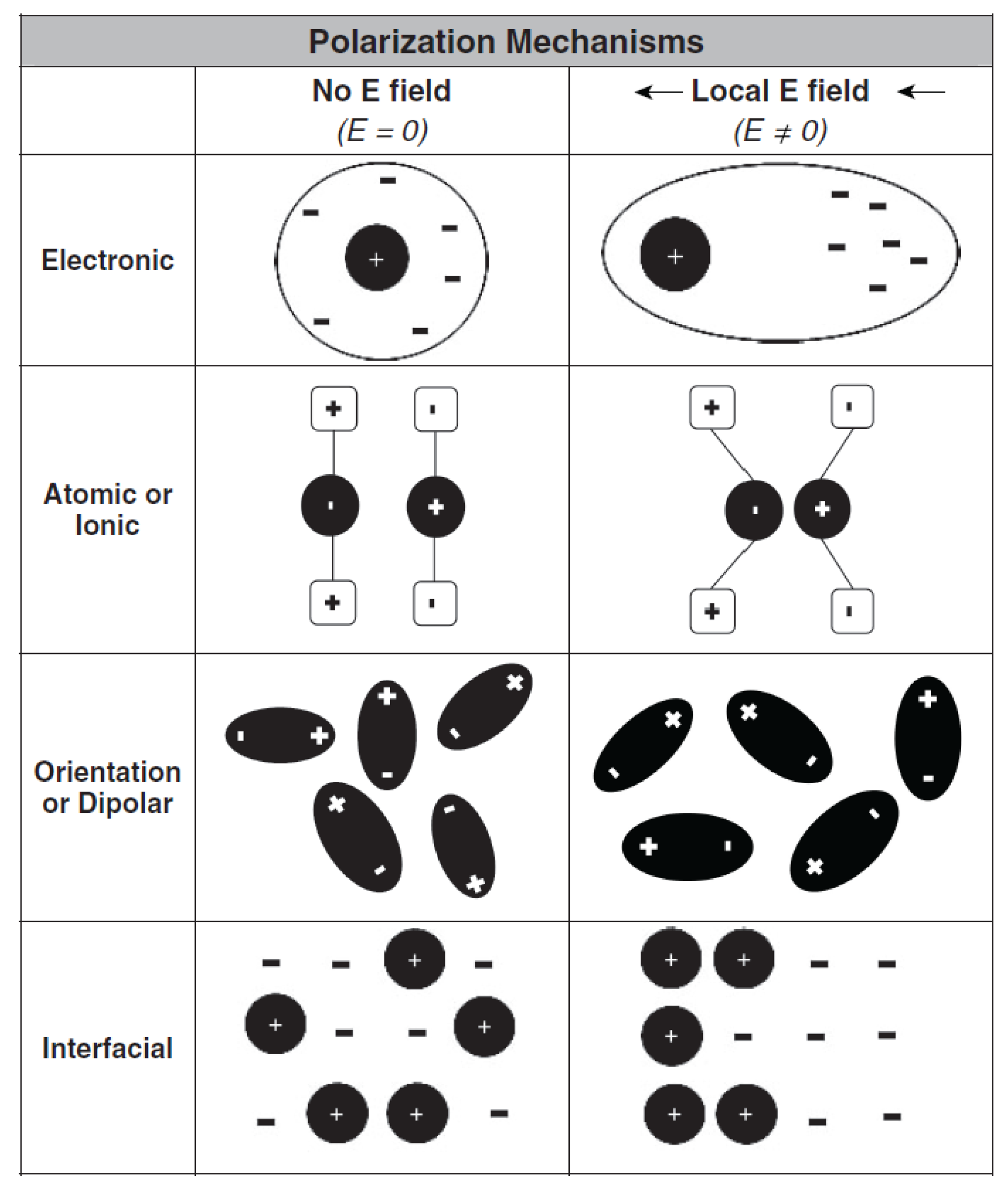
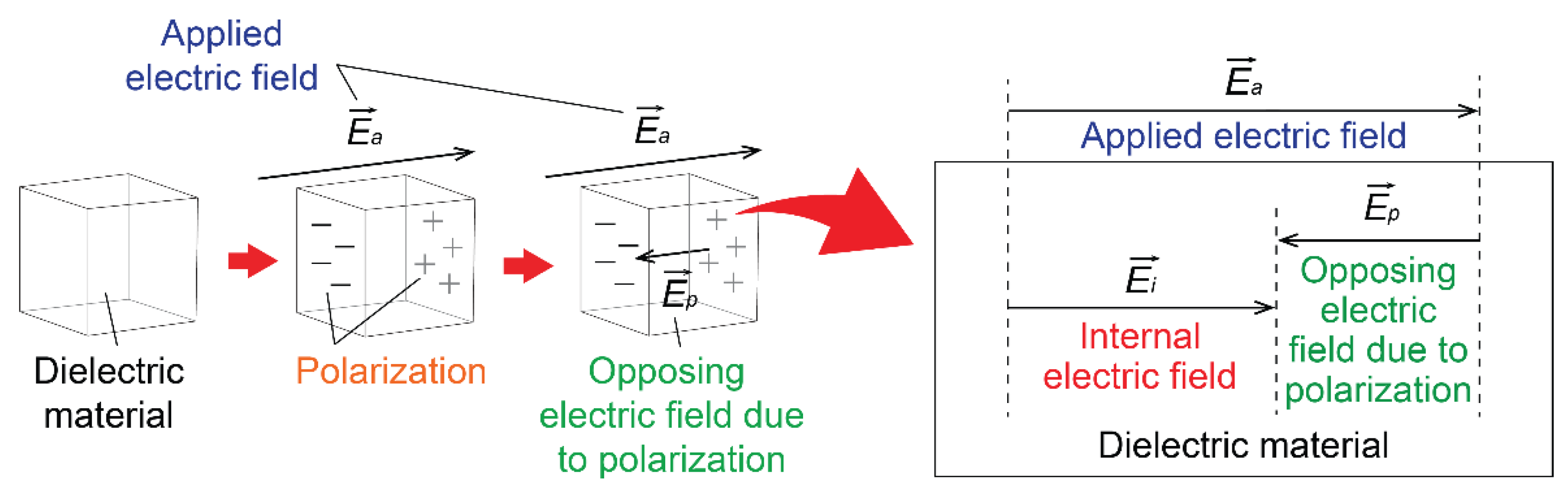
2.1. Dielectrics and Polarization Mechanisms
2.2. Permittivity
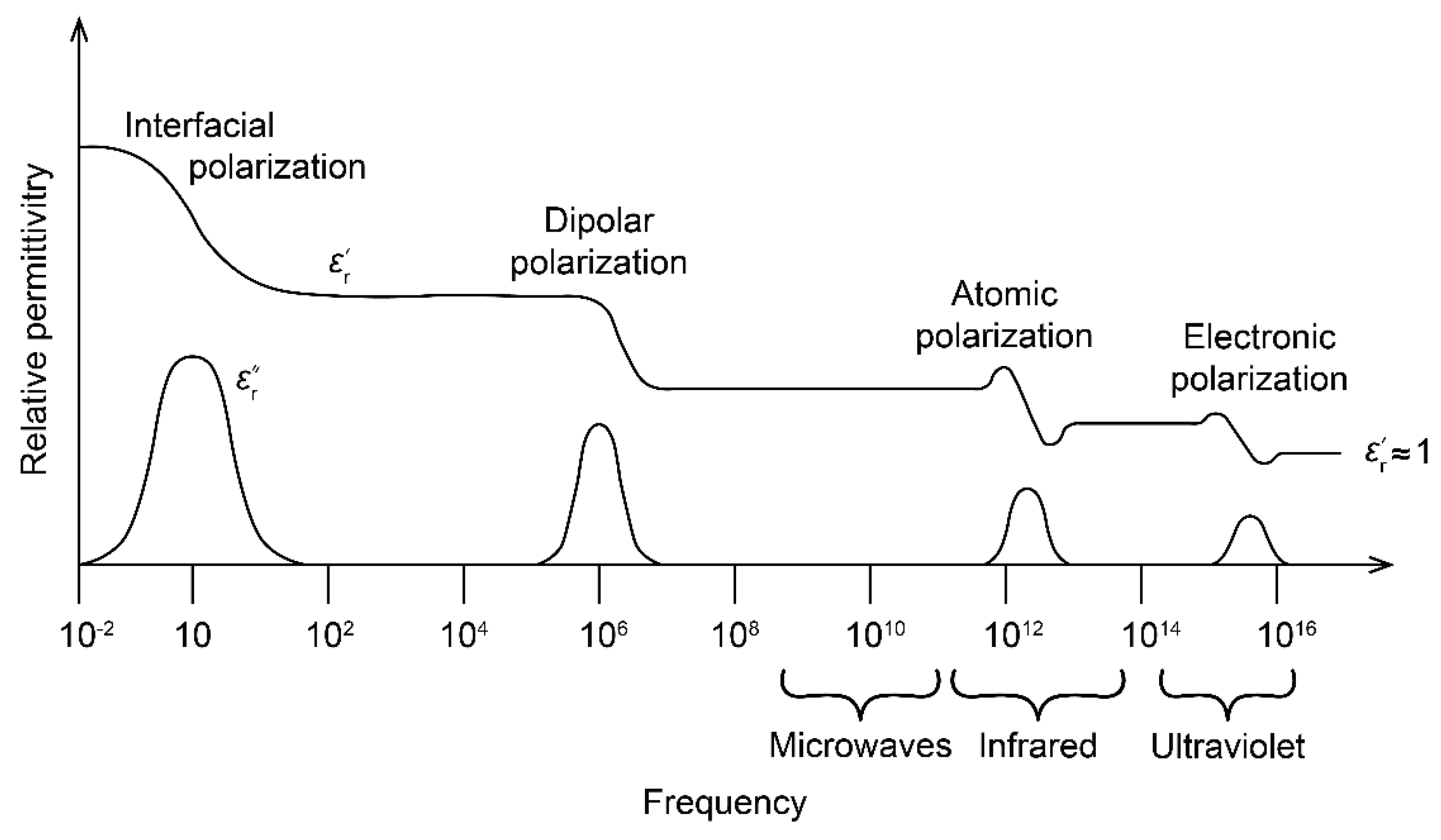
2.3. Dispersion
2.4. Anisotropy
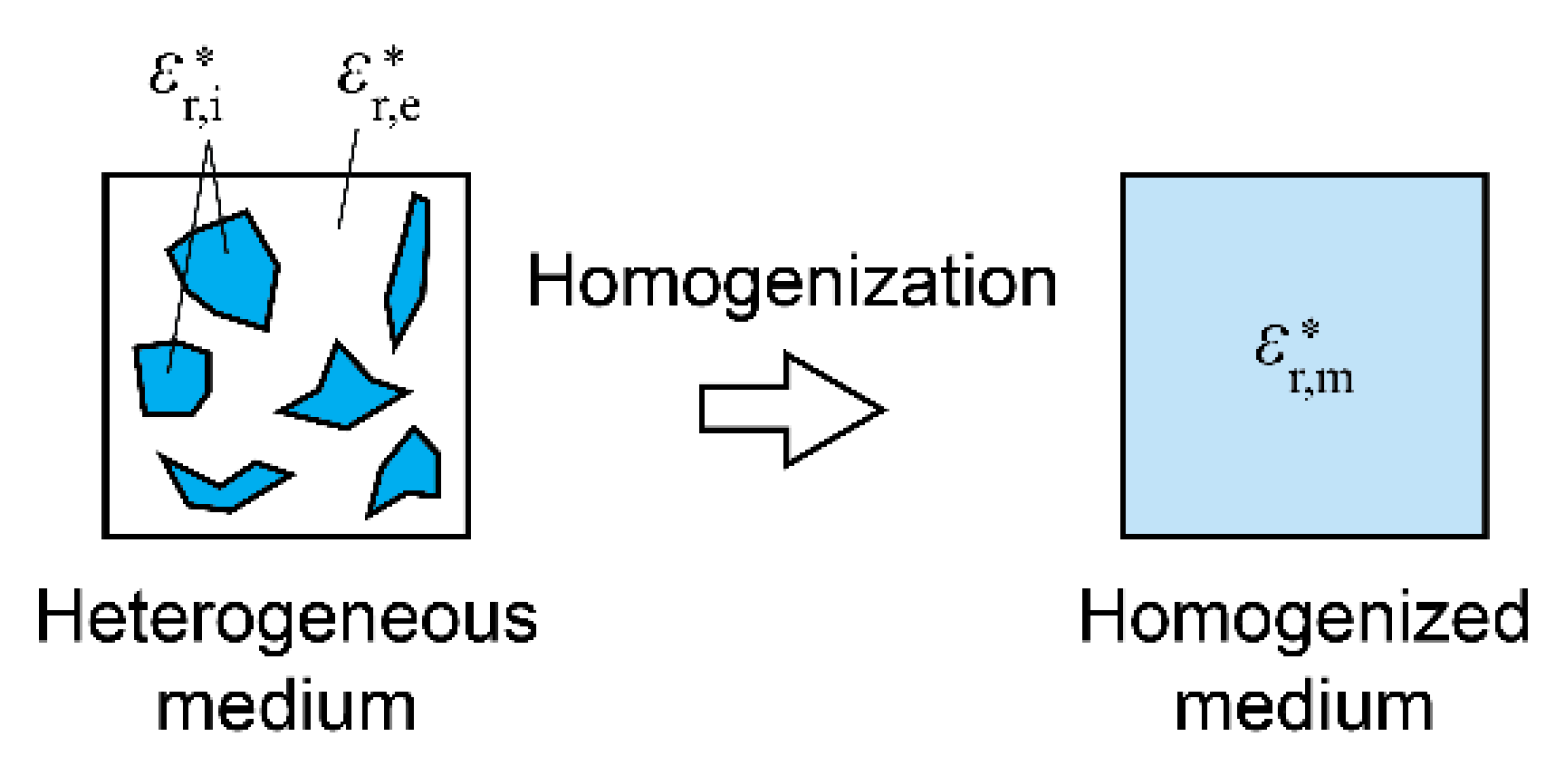
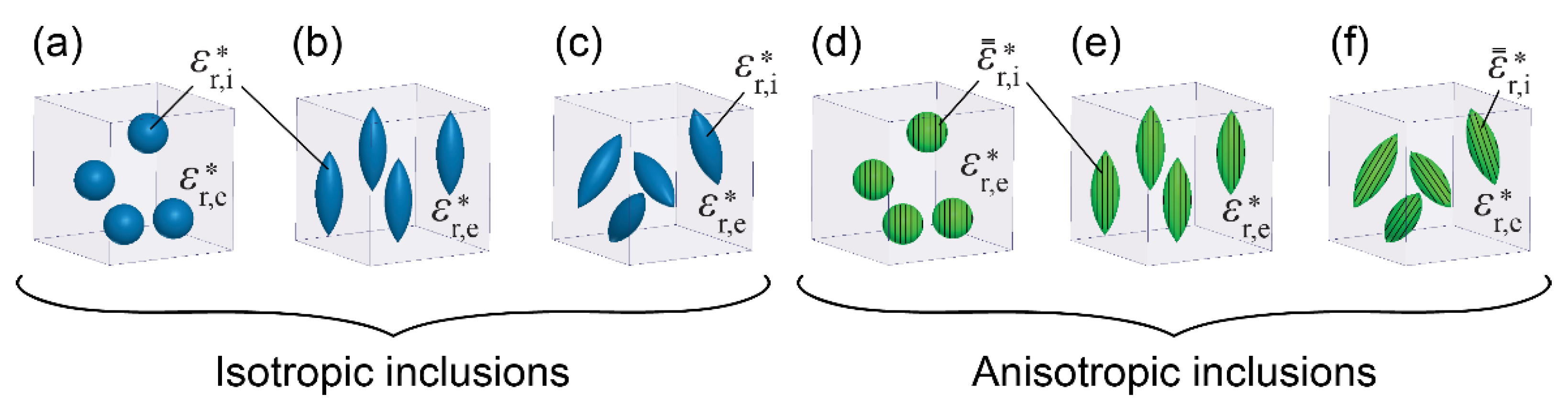
2.5. Inhomogenity and Homogenization
2.6. Dielectric Mixture Theory
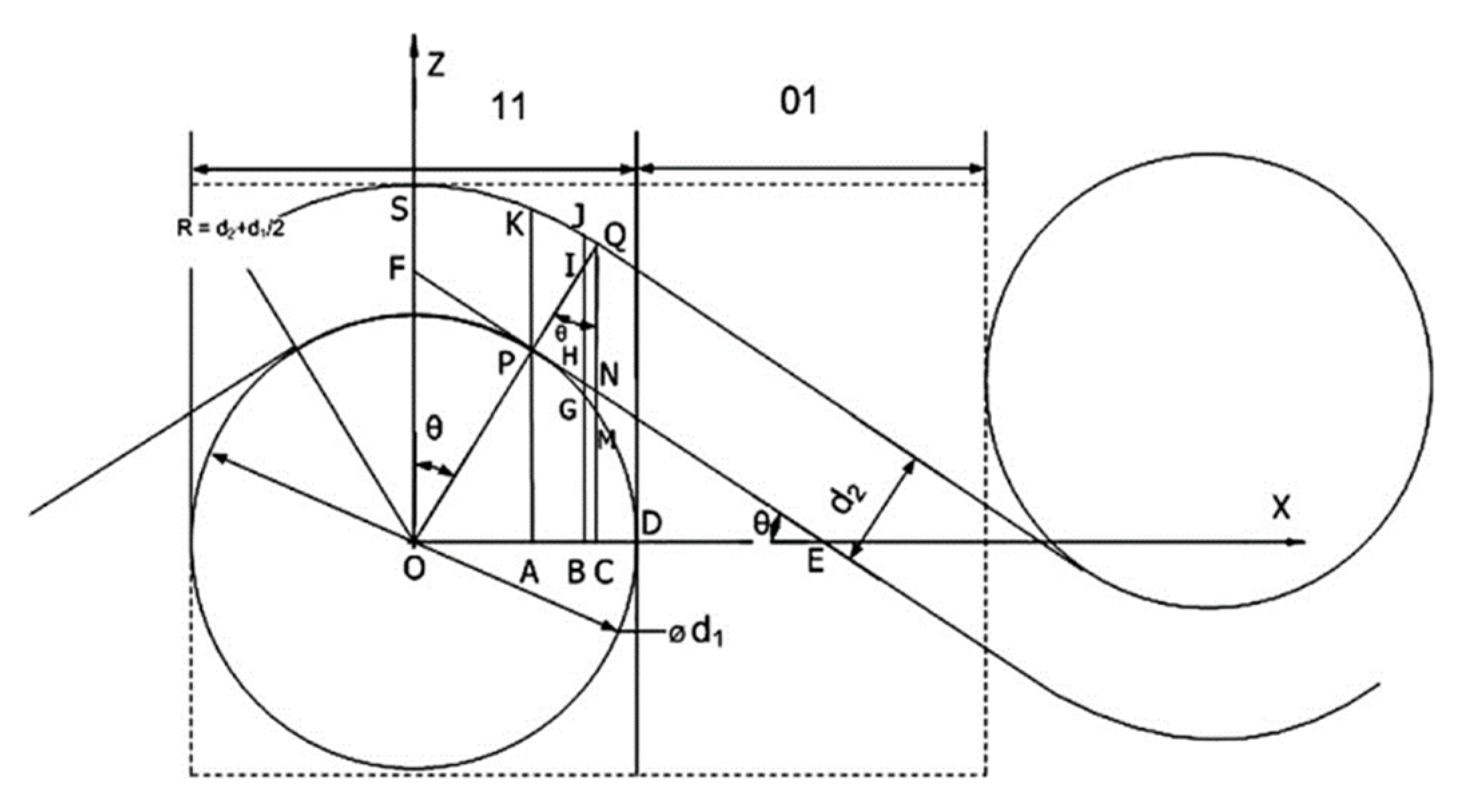
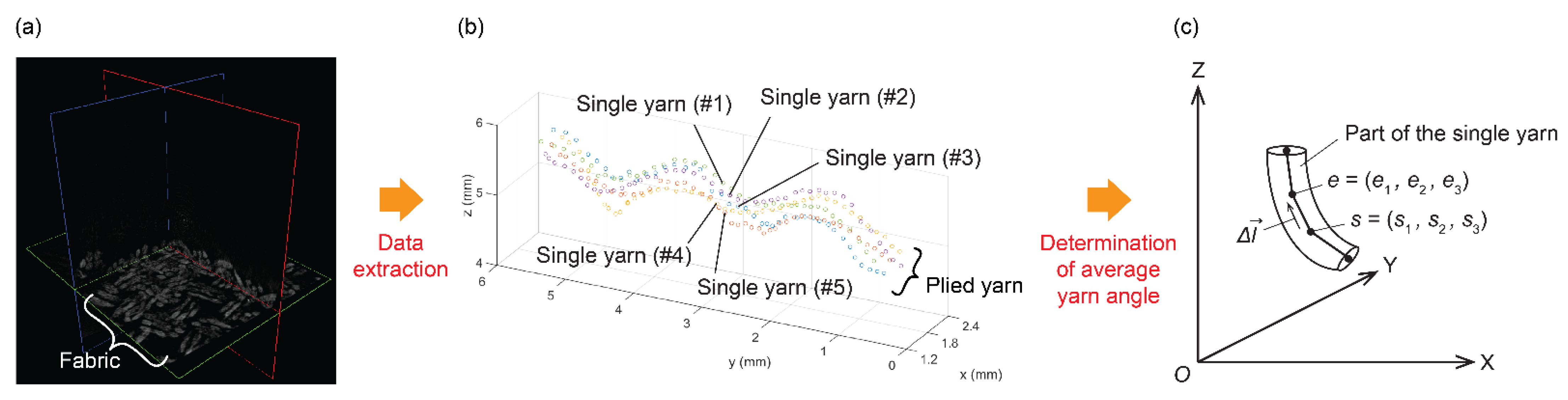
3. Dielectric Properties of Fabrics—The Air-Fiber System
4. Dielectric Properties of Fabrics—The Air-Fiber-Moisture System
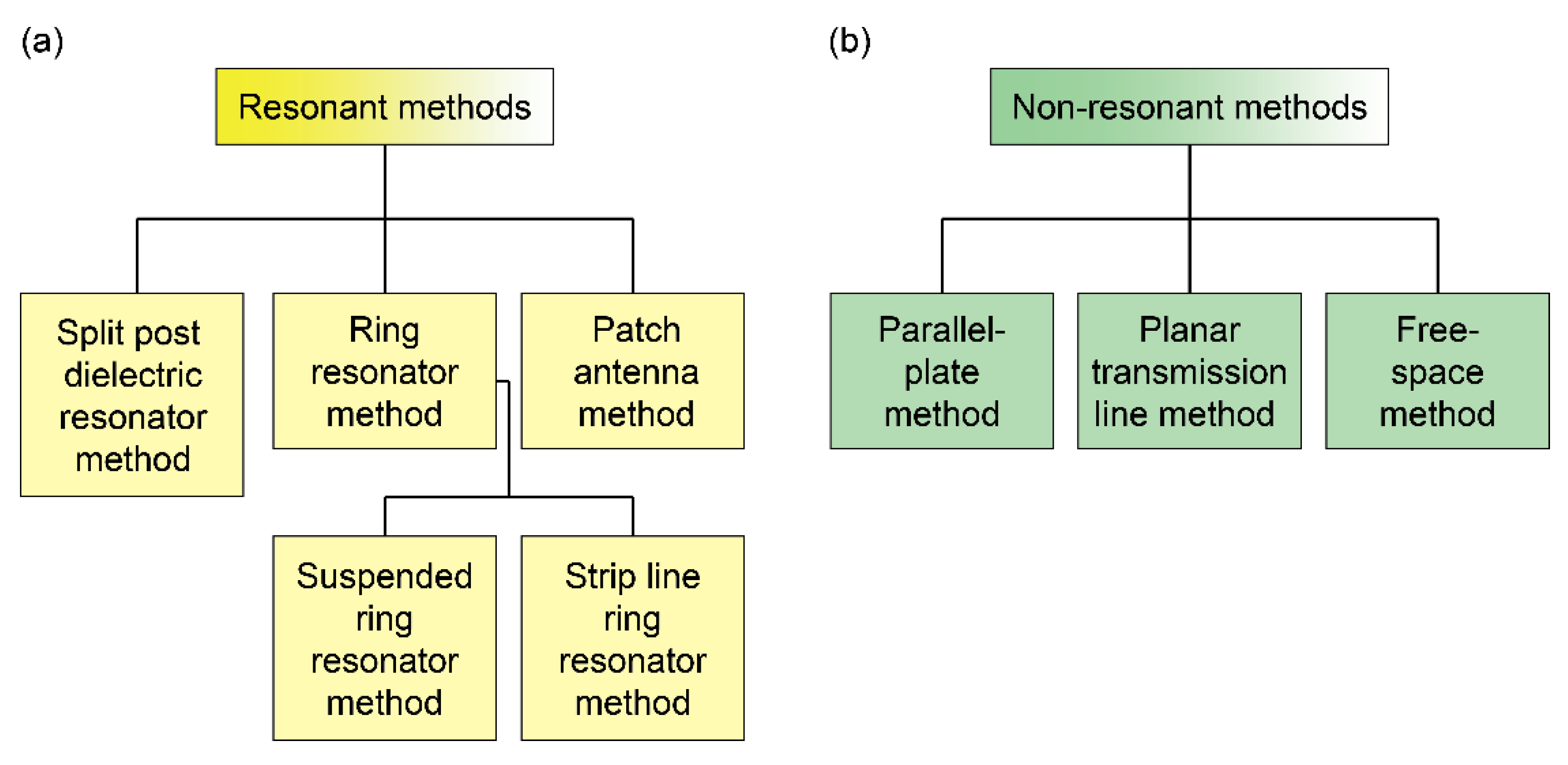
5. Measurement Methods
5.1. Resonant Methods
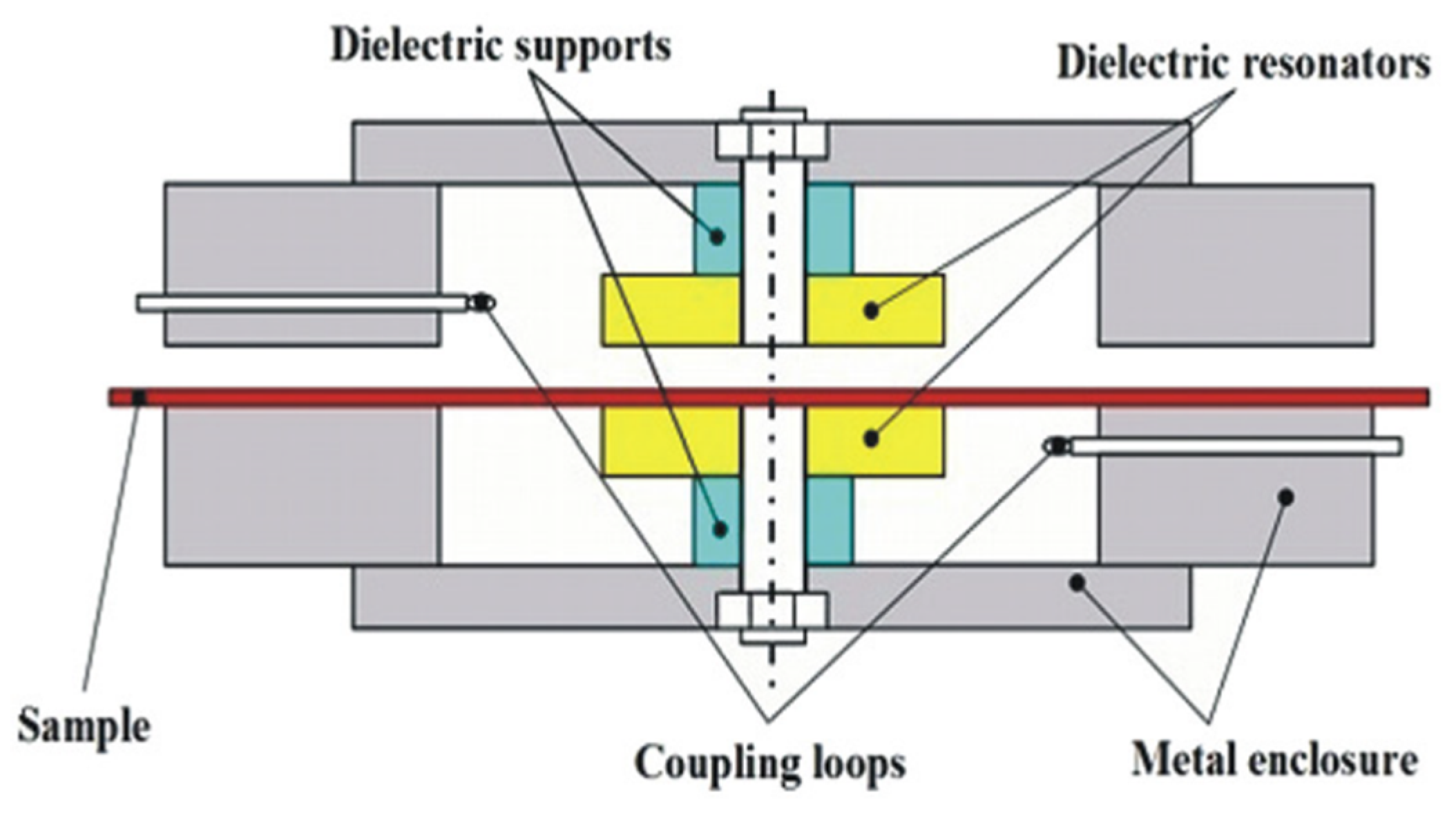
5.1.1. Split Post Dielectric Resonator Method
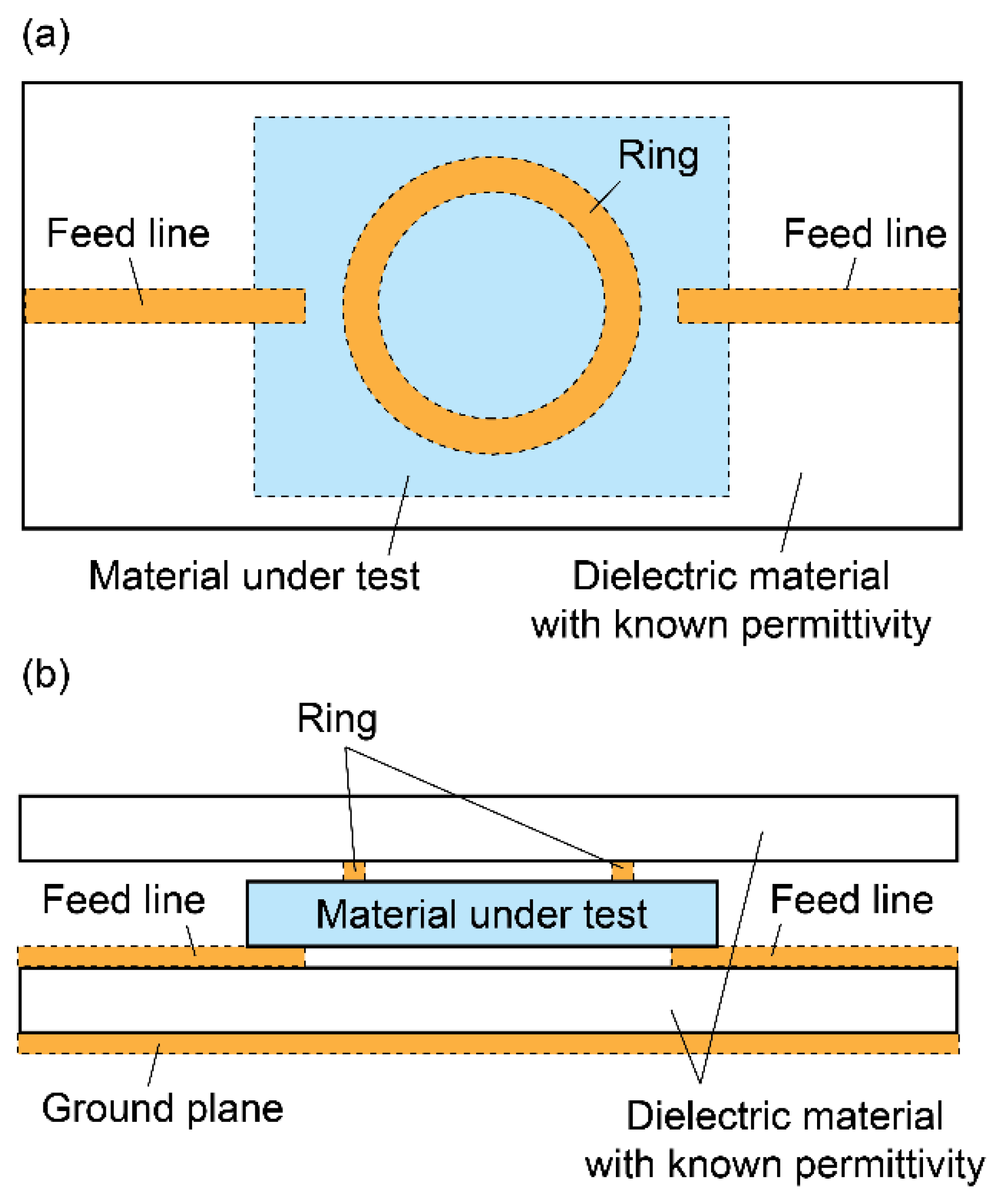
5.1.2. Ring Resonator Method
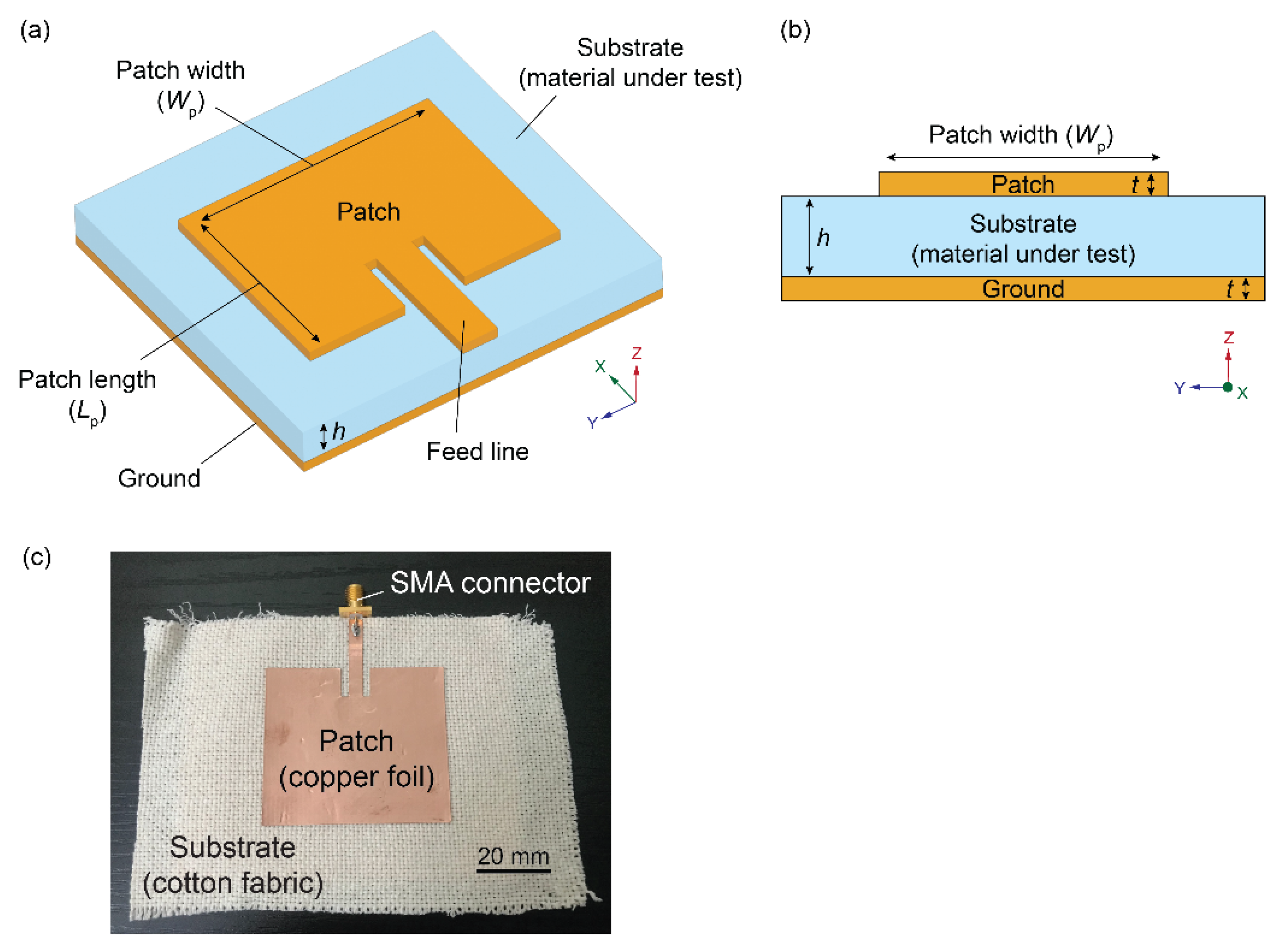
5.1.3. Patch Antenna Method
5.2. Non-Resonant Methods
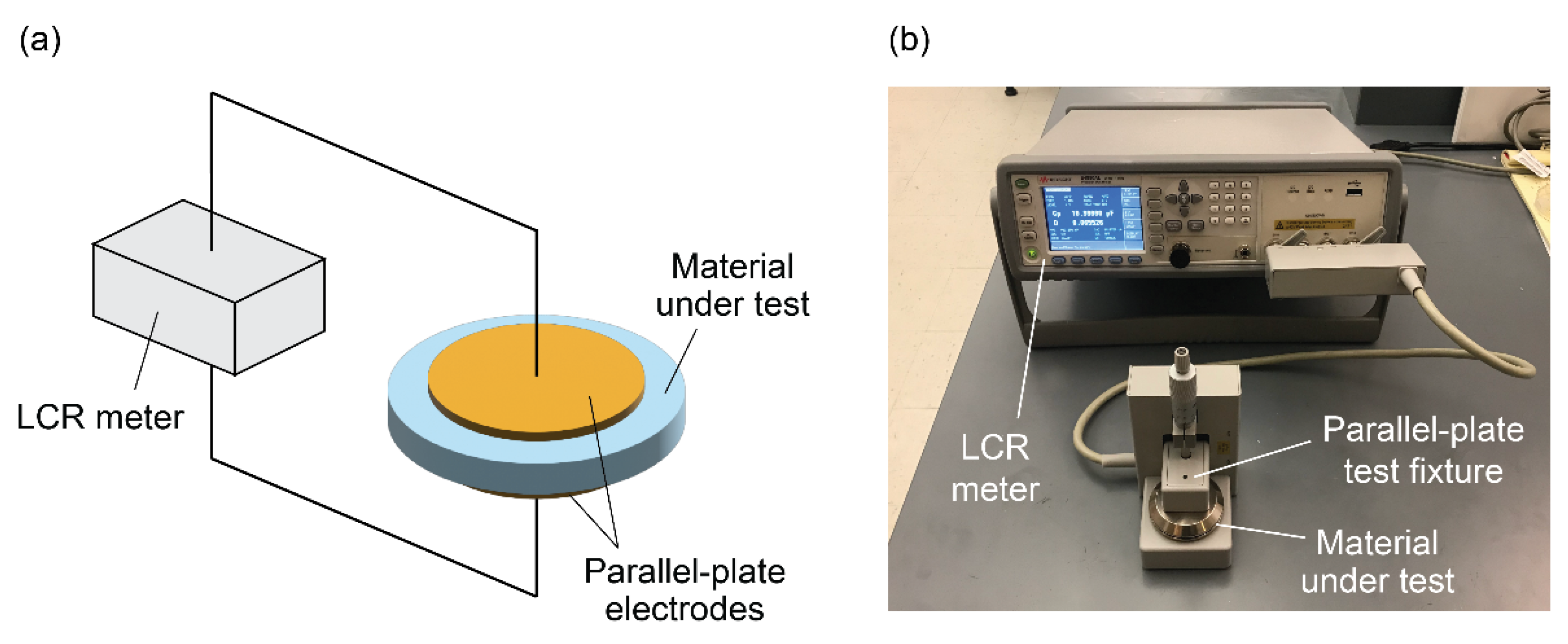
5.2.1. Parallel-Plate Method
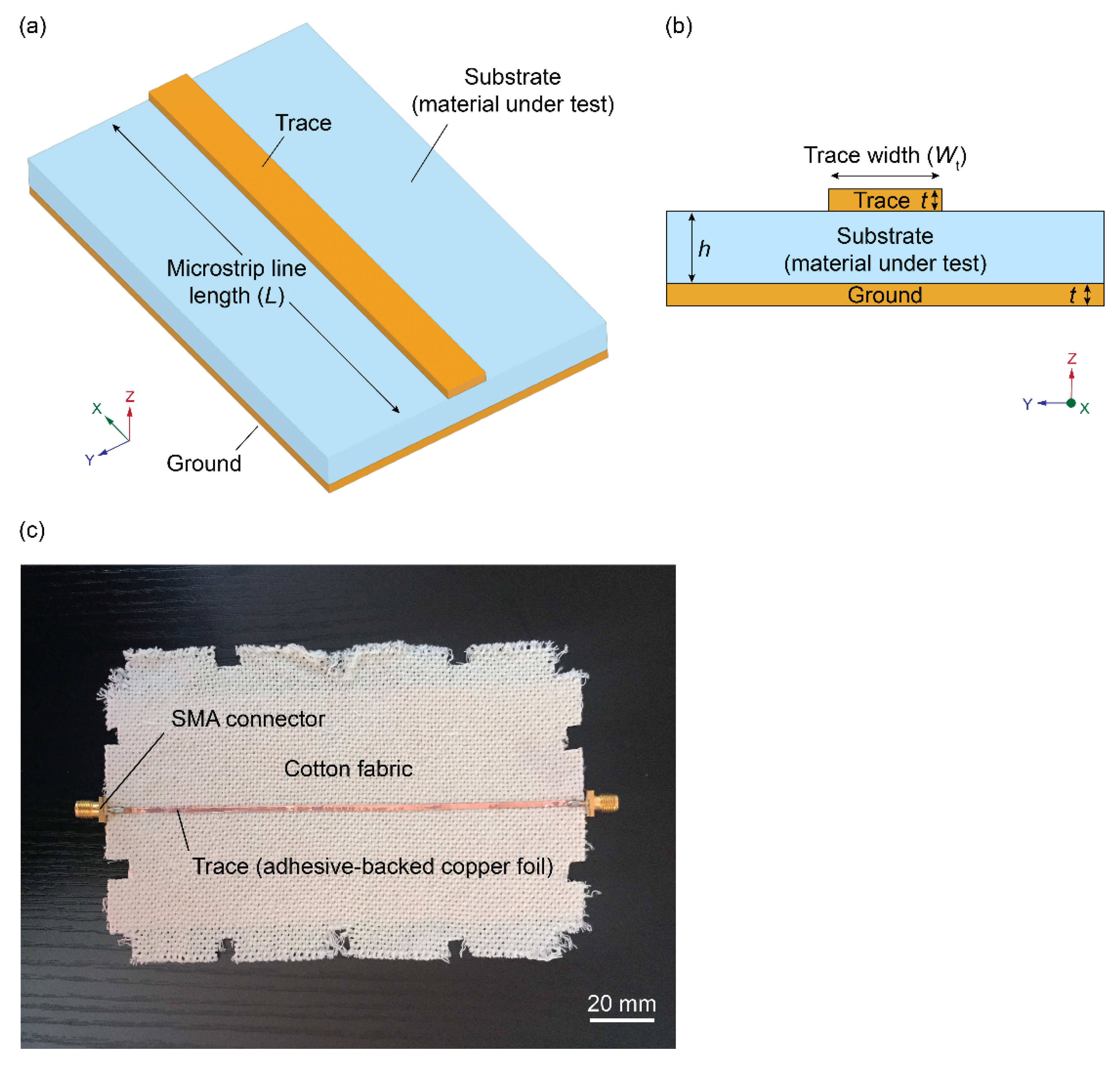
5.2.2. Planar Transmission Line Method
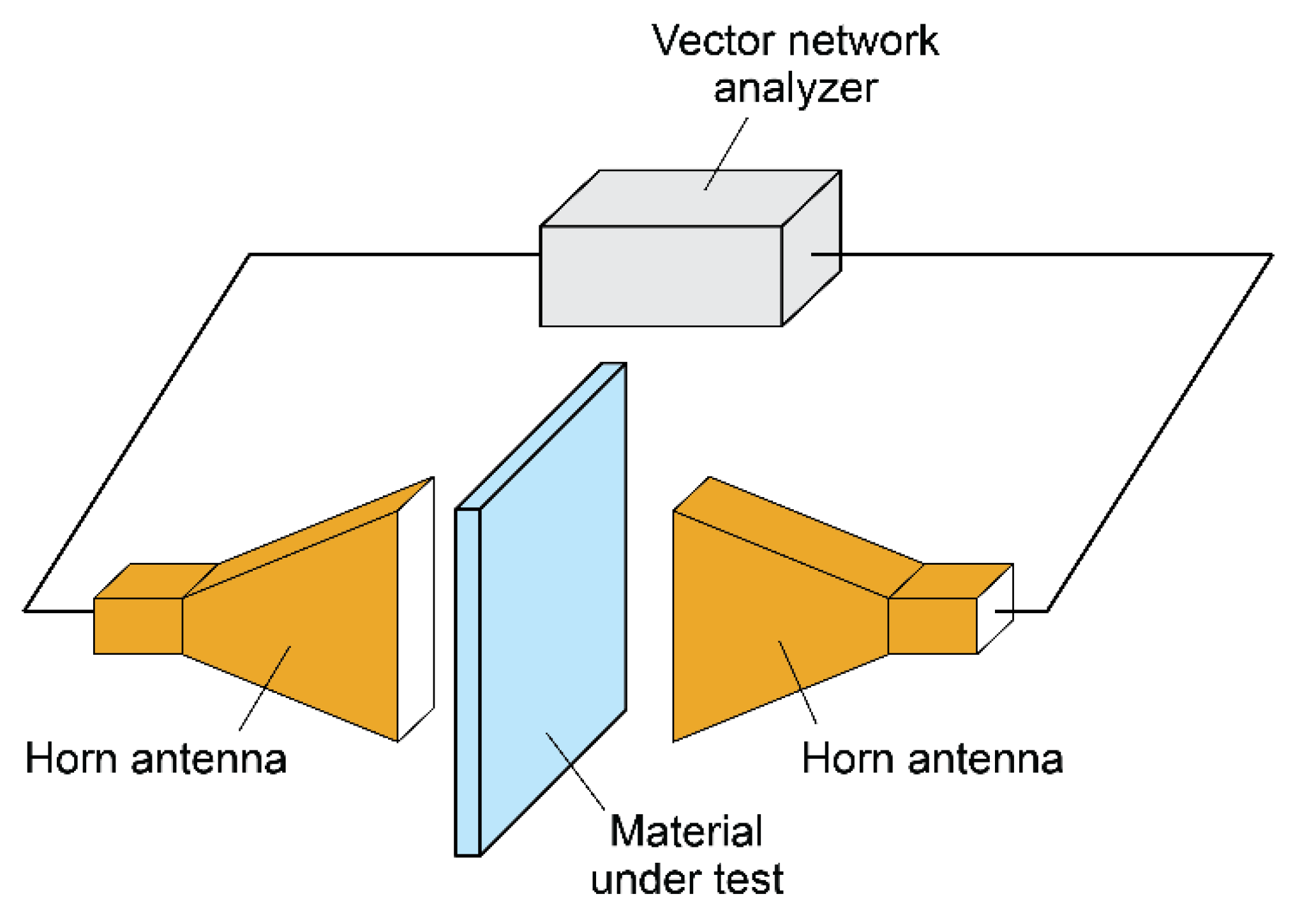
5.2.3. Free-Space Method
6. Conclusions
Funding
Conflicts of Interest
Appendix A
| Fabric Specification | Measurement Conditions | Dielectric Properties | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Composition | Construction | Solid Volume Fraction | Frequency (Hz) | Temperature (°C) | Relative Humidity (%) | Moisture Content (wt%) | Real Part | Imaginary Part | Loss Tangent | |
| Cotton | Plain weave | 0.134 * | 1 × 106 | 21 | 40 | – | 5.59 | 0.352 ‡ | 0.063 | [73] |
| 60 | 6.12 | 0.514 ‡ | 0.084 | |||||||
| 80 | 7.08 | 0.722 ‡ | 0.102 | |||||||
| Cotton | Twill weave | 0.293 * | 2.45 × 109 | – | – | – | 1.71 | 0.034 ‡ | 0.020 | [16] |
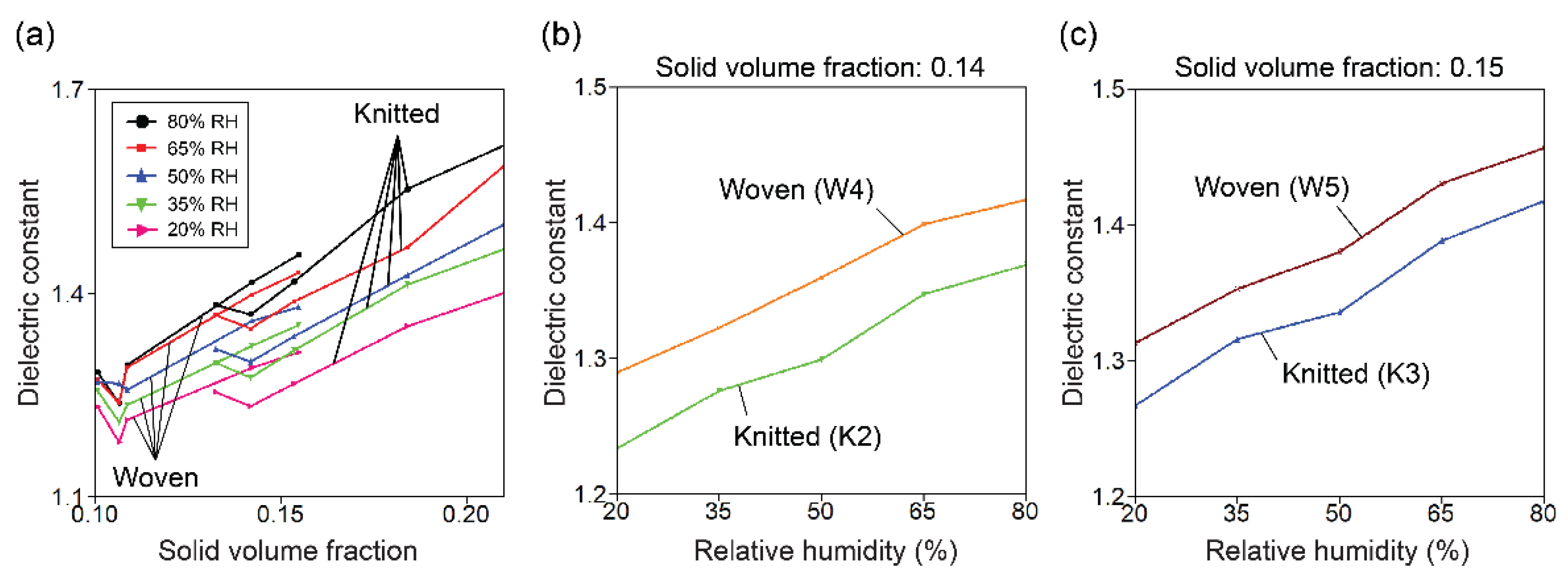
| Cotton | Plain weave | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 80 ± 2.5 | 8.42 | 1.28 | – | – | [7] |
| Plain weave | 0.11 | 1.24 | – | – | ||||||
| Plain weave | 0.11 | 1.29 | – | – | ||||||
| Plain weave | 0.14 | 1.42 | – | – | ||||||
| Plain weave | 0.15 | 1.46 | – | – | ||||||
| Cotton | Plain weave | 0.10 | ~2.45 × 109 | 21 ± 2 | 65 ± 5 | 7.57 | 1.27 | – | – | [7] |
| Plain weave | 0.11 | 1.24 | – | – | ||||||
| Plain weave | 0.11 | 1.29 | – | – | ||||||
| Plain weave | 0.14 | 1.40 | – | – | ||||||
| Plain weave | 0.15 | 1.43 | – | – | ||||||
| Cotton | Plain weave | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 50 ± 2.5 | 6.43 | 1.27 | – | – | [7] |
| Plain weave | 0.11 | 1.27 | – | – | ||||||
| Plain weave | 0.11 | 1.26 | – | – | ||||||
| Plain weave | 0.14 | 1.36 | – | – | ||||||
| Plain weave | 0.15 | 1.38 | – | – | ||||||
| Cotton | Plain weave | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 35 ± 2.5 | 5.27 | 1.26 | – | – | [7] |
| Plain weave | 0.11 | 1.21 | – | – | ||||||
| Plain weave | 0.11 | 1.24 | – | – | ||||||
| Plain weave | 0.14 | 1.32 | – | – | ||||||
| Plain weave | 0.15 | 1.35 | – | – | ||||||
| Cotton | Plain weave | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 20 ± 2.5 | 3.77 | 1.23 | – | – | [7] |
| Plain weave | 0.11 | 1.18 | – | – | ||||||
| Plain weave | 0.11 | 1.21 | – | – | ||||||
| Plain weave | 0.14 | 1.29 | – | – | ||||||
| Plain weave | 0.15 | 1.31 | – | – | ||||||
| Cotton | Plain knit (single jersey) | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 80 ± 2.5 | 8.42 | 1.38 | – | – | [7] |
| Plain knit (single jersey) | 0.11 | 1.37 | – | – | ||||||
| Plain knit (single jersey) | 0.11 | 1.42 | – | – | ||||||
| Plain knit (single jersey) | 0.14 | 1.55 | – | – | ||||||
| Plain knit (single jersey) | 0.15 | 1.62 | – | – | ||||||
| Cotton | Plain knit (single jersey) | 0.10 | ~2.45 × 109 | 21 ± 2 | 65 ± 5 | 7.57 | 1.37 | – | – | [7] |
| Plain knit (single jersey) | 0.11 | 1.35 | – | – | ||||||
| Plain knit (single jersey) | 0.11 | 1.39 | – | – | ||||||
| Plain knit (single jersey) | 0.14 | 1.47 | – | – | ||||||
| Plain knit (single jersey) | 0.15 | 1.59 | – | – | ||||||
| Cotton | Plain knit (single jersey) | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 50 ± 2.5 | 6.43 | 1.32 | – | – | [7] |
| Plain knit (single jersey) | 0.11 | 1.30 | – | – | ||||||
| Plain knit (single jersey) | 0.11 | 1.34 | – | – | ||||||
| Plain knit (single jersey) | 0.14 | 1.43 | – | – | ||||||
| Plain knit (single jersey) | 0.15 | 1.50 | – | – | ||||||
| Cotton | Plain knit (single jersey) | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 35 ± 2.5 | 5.27 | 1.30 | – | – | [7] |
| Plain knit (single jersey) | 0.11 | 1.28 | – | – | ||||||
| Plain knit (single jersey) | 0.11 | 1.32 | – | – | ||||||
| Plain knit (single jersey) | 0.14 | 1.41 | – | – | ||||||
| Plain knit (single jersey) | 0.15 | 1.47 | – | – | ||||||
| Cotton | Plain knit (single jersey) | 0.10 | ~2.45 × 109 | 21 ± 0.2 | 20 ± 2.5 | 3.77 | 1.25 | – | – | [7] |
| Plain knit (single jersey) | 0.11 | 1.23 | – | – | ||||||
| Plain knit (single jersey) | 0.11 | 1.27 | – | – | ||||||
| Plain knit (single jersey) | 0.14 | 1.35 | – | – | ||||||
| Plain knit (single jersey) | 0.15 | 1.40 | – | – | ||||||
| Flax | Plain weave | 0.235 * | 1 × 106 | 21 | 40 | – | 4.22 | 0.156 ‡ | 0.037 | [73] |
| 60 | 4.43 | 0.177 ‡ | 0.040 | |||||||
| 80 | 6.20 | 0.360 ‡ | 0.058 | |||||||
| Jute | Plain weave | 0.223 * | 1 × 106 | 21 | 40 | – | 2.99 | 0.093 ‡ | 0.031 | [73] |
| 60 | 3.90 | 0.137 ‡ | 0.035 | |||||||
| 80 | 4.95 | 0.233 ‡ | 0.047 | |||||||
| Hemp | Plain weave | 0.249 * | 1 × 106 | 21 | 40 | – | 4.08 | 0.114 ‡ | 0.028 | [73] |
| 60 | 4.50 | 0.162 ‡ | 0.036 | |||||||
| 80 | 4.77 | 0.248 ‡ | 0.052 | |||||||
| Wool | Plain weave | 0.303 * | 1 × 106 | 21 | 40 | – | 4.11 | 0.115 ‡ | 0.028 | [73] |
| 60 | 4.65 | 0.214 ‡ | 0.046 | |||||||
| 80 | 5.70 | 0.296 ‡ | 0.052 | |||||||
| Polyester | 2 × 2 rib knit | – | 1.13 × 103 | 20 ± 1 | 65 ± 2 | – | 4.06 | 1.67 | 0.46 | [110] |
| Polyester | Plain weave | 0.387 * | 1 × 106 | 21 | 40 | – | 3.20 | 0.058 ‡ | 0.018 | [73] |
| 60 | 3.39 | 0.088 ‡ | 0.026 | |||||||
| 80 | 3.66 | 0.117 ‡ | 0.032 | |||||||
| Polyester | 3D spacer knit | 0.0706 * | 2.25× 109 | – | – | – | 1.10 | 0.006 ‡ | 0.005 | [83] |
| Polyester | 3D spacer knit | 0.0821 * | 2.25× 109 | – | – | – | 1.10 | 0.007 ‡ | 0.006 | |
| Polyester | 3D spacer knit | 0.0745 * | 2.25× 109 | – | – | – | 1.12 | 0.019 ‡ | 0.017 | |
| Polyester | 3D spacer knit | 0.0982 * | 2.25× 109 | – | – | – | 1.13 | 0.020 ‡ | 0.018 | |
| Polyester | 3D spacer knit | 0.0627 * | 2.25× 109 | – | – | – | 1.11 | 0.004 ‡ | 0.004 | |
| Polyester | Plain weave | 0.43 † | 2.26 × 109 | – | – | – | 1.55 | 0.013 ‡ | 0.009 | [111] |
| Polyester | Felt | – | 2.45 × 109 | – | – | – | 1.2 | 0.028 ‡ | 0.023 | [24] |
| Polyester | Woven | – | – | – | – | 1.5 | 0.042 ‡ | 0.028 | ||
| Polyester | – | – | 2.45 × 109 | – | – | – | 1.44 | – | – | [89] |
| Polyester | Fleece | 0.103 * | 2.45 × 109 | – | – | 0.40 § | 1.15 | 0.000 ‡ | 0.000 | [16] |
| High density polyethylene | Plain weave | 0.1326 | 1 × 103 | – | – | – | 1.12 | – | – | [39] |
| Plain weave | 0.1633 | 1 × 103 | – | – | – | 1.14 | – | – | ||
| Plain weave | 0.1190 | 1 × 103 | – | – | – | 1.10 | – | – | ||
| Plain weave | 0.2560 | 1 × 103 | – | – | – | 1.23 | – | – | ||
References
- Bal, K.; Kothari, V.K. Measurement of Dielectric properties of textile materials and their applications. Indian J. Fibre Text. Res. 2009, 34, 191–199. [Google Scholar]
- Ivanovska, A.; Cerovic, D.; Maletic, S.; Jankovic Castvan, I.; Asanovic, K.; Kostic, M. Influence of the alkali treatment on the sorption and dielectric properties of woven jute fabric. Cellulose 2019, 26, 5133–5146. [Google Scholar] [CrossRef]
- Ivanovska, A.; Cerovic, D.; Tadic, N.; Jankovic Castvan, I.; Asanovic, K.; Kostic, M. Sorption and dielectric properties of jute woven fabrics: Effect of chemical composition. Ind. Crops Prod. 2019, 140, 111632. [Google Scholar] [CrossRef]
- Cerovic, D.D.; Petronijevic, I.; Dojcilovic, J.R. Influence of temperature and fiber structure on the dielectric properties of polypropylene fibrous structures. Polym. Adv. Technol. 2014, 25, 338–342. [Google Scholar] [CrossRef]
- Mukai, Y.; Suh, M. Structure-Microwave Dielectric Property Relationship in Cotton Fabrics. In Proceedings of the Techtextil North America, Raleigh, NC, USA, 26–28 February 2019. [Google Scholar]
- Mukai, Y.; Dickey, E.C.; Suh, M. Low Frequency Dielectric Properties Related to Structure of Cotton Fabrics. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 291–298. [Google Scholar] [CrossRef]
- Mukai, Y.; Suh, M. Relationships between Structure and Microwave Dielectric Properties in Cotton Fabrics. Mater. Res. Express 2020, 7, 015105. [Google Scholar] [CrossRef] [Green Version]
- Sihvola, A.H. Electromagnetic Mixing Formulas and Applications; IEE Electromagnetic Waves Series 47; Institution of Electrical Engineers: London, UK, 1999; ISBN 978-0-85296-772-0. [Google Scholar]
- Gandhi, K.L. Yarn Preparation for Weaving: Winding. In Woven Textiles; Elsevier: Amsterdam, The Netherlands, 2020; pp. 35–79. ISBN 978-0-08-102497-3. [Google Scholar]
- Carvalho, V.; Cardoso, P.; Belsley, M.; Vasconcelos, R.M.; Soares, F.O. Development of a Yarn Evenness Measurement and Hairiness Analysis System. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; pp. 3621–3626. [Google Scholar]
- Ghosh, A.; Mal, P. Testing of Fibres, Yarns and Fabrics and Their Recent Developments. In Fibres to Smart Textiles; Patnaik, A., Patnaik, S., Eds.; CRC Press: Boca Raton, FL, USA, 2019; pp. 221–256. ISBN 978-0-429-44651-1. [Google Scholar]
- Thilagavathi, G.; Karthik, T. Process Control and Yarn Quality in Spinning; Woodhead Publishing India in Textiles; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-93-80308-18-0. [Google Scholar]
- Ott, P.; Schmid, P. Verfahren und Vorrichtung zur Erkennung von Fremdstoffen in Einem Bewegten, Festen, Länglichen Prüfgut. European Patent EP2108949A1, 7 June 2006. [Google Scholar]
- ASTM D1425; Standard Test Method for Evenness of Textile Strands Using Capacitance Testing Equipment. ASTM International: West Conshohocken, PA, USA, 2014.
- Salvado, R.; Loss, C.; Gonçalves, R.; Pinho, P. Textile Materials for the Design of Wearable Antennas: A Survey. Sensors 2012, 12, 15841–15857. [Google Scholar] [CrossRef]
- Hertleer, C.; Laere, A.V.; Rogier, H.; Langenhove, L.V. Influence of Relative Humidity on Textile Antenna Performance. Text. Res. J. 2010, 80, 177–183. [Google Scholar] [CrossRef]
- Xu, F.; Zhu, H.; Ma, Y.; Qiu, Y. Electromagnetic performance of a three-dimensional woven fabric antenna conformal with cylindrical surfaces. Text. Res. J. 2017, 87, 147–154. [Google Scholar] [CrossRef]
- Mukai, Y.; Bharambe, V.T.; Adams, J.J.; Suh, M. Effect of bending and padding on the electromagnetic performance of a laser-cut fabric patch antenna. Text. Res. J. 2019, 89, 2789–2801. [Google Scholar] [CrossRef]
- Mukai, Y.; Suh, M. Development of a Conformal Woven Fabric Antenna for Wearable Breast Hyperthermia. Fash. Text. 2021, 8, 1–12. [Google Scholar] [CrossRef]
- Locher, I.; Klemm, M.; Kirstein, T.; Trster, G. Design and Characterization of Purely Textile Patch Antennas. IEEE Trans. Adv. Packag. 2006, 29, 777–788. [Google Scholar] [CrossRef] [Green Version]
- Mukai, Y.; Suh, M. Development of a Conformal Textile Antenna for Thermotherapy. In Proceedings of the Fiber Society’s Fall 2018 Technical Meeting and Conference, Davis, CA, USA, 29–31 October 2018. [Google Scholar]
- Mukai, Y.; Suh, M. Conformal Cotton Antenna for Wearable Thermotherapy. In Proceedings of the Fiber Society’s Spring 2019 Conference, Hong Kong, China, 21–23 May 2019. [Google Scholar]
- Jia, X.; Tennant, A.; Langley, R.J.; Hurley, W.; Dias, T. Moisture effects on a knitted waveguide. In Proceedings of the 2016 Loughborough Antennas & Propagation Conference (LAPC), Loughborough, UK, 14–15 November 2016; pp. 1–3. [Google Scholar]
- Adami, S.-E.; Proynov, P.; Hilton, G.S.; Yang, G.; Zhang, C.; Zhu, D.; Li, Y.; Beeby, S.P.; Craddock, I.J.; Stark, B.H. A Flexible 2.45-GHz Power Harvesting Wristband With Net System Output From −24.3 dBm of RF Power. IEEE Trans. Microw. Theory Tech. 2018, 66, 380–395. [Google Scholar] [CrossRef] [Green Version]
- Chi, Y.-J.; Lin, C.-H.; Chiu, C.-W. Design and modeling of a wearable textile rectenna array implemented on Cordura fabric for batteryless applications. J. Electromagn. Waves Appl. 2020, 34, 1782–1796. [Google Scholar] [CrossRef]
- Wagih, M.; Hilton, G.S.; Weddell, A.S.; Beeby, S. Broadband Millimeter-Wave Textile-Based Flexible Rectenna for Wearable Energy Harvesting. IEEE Trans. Microw. Theory Tech. 2020, 68, 4960–4972. [Google Scholar] [CrossRef]
- Zhang, R.Q.; Li, J.Q.; Li, D.J.; Xu, J.J. Study of the Structural Design and Capacitance Characteristics of Fabric Sensor. Available online: http://www.scientific.net/AMR.194-196.1489 (accessed on 6 June 2018).
- Seyedin, S.; Zhang, P.; Naebe, M.; Qin, S.; Chen, J.; Wang, X.; Razal, J.M. Textile strain sensors: A review of the fabrication technologies, performance evaluation and applications. Mater. Horiz. 2019, 6, 219–249. [Google Scholar] [CrossRef]
- Bansal, N.; Ehrmann, A.; Geilhaupt, M. Textile Capacitors as Pressure Sensors. In Proceedings of the Aachen-Dresden International Textile Conference, Dresden, Germany, 27–28 November 2014. [Google Scholar]
- Ma, L.; Wu, R.; Patil, A.; Zhu, S.; Meng, Z.; Meng, H.; Hou, C.; Zhang, Y.; Liu, Q.; Yu, R.; et al. Full-Textile Wireless Flexible Humidity Sensor for Human Physiological Monitoring. Adv. Funct. Mater. 2019, 29, 1904549. [Google Scholar] [CrossRef]
- Ng, C.; Reaz, M. Characterization of Textile-Insulated Capacitive Biosensors. Sensors 2017, 17, 574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Yu, Y.; Zhao, X. The influence of the ratio of graphite to silver-coated copper powders on the electromagnetic and mechanical properties of single-layer coated composites. J. Text. Inst. 2021, 112, 1709–1716. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Y.; Zhao, X. The influence of wave-absorbing functional particles on the electromagnetic properties and the mechanical properties of coated fabrics. J. Text. Inst. 2021, 1–21. [Google Scholar] [CrossRef]
- Yamada, Y. Textile-Integrated Polymer Optical Fibers for Healthcare and Medical Applications. Biomed. Phys. Eng. Express 2020. [Google Scholar] [CrossRef]
- Yamada, Y.; Suh, M. Textile Materials for Mobile Health: Opportunities and challenges. In Proceedings of the WTiN Innovate Textile & Apparel Virtual Trade Show, Online, 15–30 October 2020. [Google Scholar]
- Wang, L.; Fu, X.; He, J.; Shi, X.; Chen, T.; Chen, P.; Wang, B.; Peng, H. Application Challenges in Fiber and Textile Electronics. Adv. Mater. 2020, 32, 1901971. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.M.; Hossain, M.M. Nanomaterials-patterned flexible electrodes for wearable health monitoring: A review. J. Mater. Sci. 2021, 56, 14900–14942. [Google Scholar] [CrossRef] [PubMed]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Bal, K.; Kothari, V.K. Permittivity of woven fabrics: A comparison of dielectric formulas for air-fiber mixture. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 881–889. [Google Scholar] [CrossRef]
- Mukai, Y.; Suh, M. Effect of Fabric Construction, Thread Count and Solid Volume Fraction on the Dielectric Properties of Cotton Fabrics. In Proceedings of the Fiber Society’s Fall 2018 Technical Meeting and Conference, Davis, CA, USA, 29–31 October 2018. [Google Scholar]
- Mukai, Y. Dielectric Properties of Cotton Fabrics and Their Applications. Doctoral Dissertation, North Carolina State University, Raleigh, NC, USA, 2019. [Google Scholar]
- Giordano, S. Effective medium theory for dispersions of dielectric ellipsoids. J. Electrost. 2003, 58, 59–76. [Google Scholar] [CrossRef]
- Bunget, I.; Popescu, M. Physics of Solid Dielectrics; Materials Science Monographs 19; Elsevier: Amsterdam, The Netherlands, 1984; ISBN 978-0-444-99632-9. [Google Scholar]
- Gupta, M.; Wong, W.L. Microwaves and Metals; John Wiley & Sons: Singapore; Hoboken, NJ, USA, 2007; ISBN 978-0-470-82272-2. [Google Scholar]
- Kasap, S.O. Principles of Electronic Materials and Devices, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2006; ISBN 978-0-07-295791-4. [Google Scholar]
- Kremer, F.; Schönhals, A. Broadband Dielectric Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-540-43407-8. [Google Scholar]
- Balanis, C.A. Advanced Engineering Electromagnetics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-58948-9. [Google Scholar]
- Oughstun, K.; Cartwright, N. On the Lorentz-Lorenz formula and the Lorentz model of dielectric dispersion. Opt. Express 2003, 11, 1541. [Google Scholar] [CrossRef]
- Patel, D.; Shah, D.; Hilfiker, J.; Linford, M. Characterization of Thin Films and Materials: A Tutorial on Spectroscopic Ellipsometry (SE) 5. Vac. Technol. Coat. 2019, 20, 34–37. [Google Scholar]
- Onimisi, M.Y.; Ikyumbur, J.T. Comparative Analysis of Dielectric Constant and Loss Factor of Pure Butan-1-ol and Ethanol. Am. J. Condens. Matter Phys. 2015, 5, 69–75. [Google Scholar]
- Hanai, T. Dielectric Theory on the Interfacial Polarization for Two-Phase Mixtures. Bull. Inst. Chem. Res. Kyoto Univ. 1962, 39, 341–367. [Google Scholar]
- Sillars, R.W. The properties of a dielectric containing semiconducting particles of various shapes. Inst. Electr. Eng-Proc. Wirel. Sect. Inst. 1937, 12, 139–155. [Google Scholar] [CrossRef]
- Arous, M.; Amor, I.B.; Kallel, A.; Fakhfakh, Z.; Perrier, G. Crystallinity and dielectric relaxations in semi-crystalline poly(ether ether ketone). J. Phys. Chem. Solids 2007, 68, 1405–1414. [Google Scholar] [CrossRef]
- Hikosaka, S.; Ishikawa, H.; Ohki, Y. Effects of crystallinity on dielectric properties of poly(L-lactide). Electron. Commun. Jpn. 2011, 94, 1–8. [Google Scholar] [CrossRef]
- Pelster, R. Dielectric relaxation spectroscopy in polymers: Broadband ac-spectroscopy and its compatibility with TSDC. In Proceedings of the 10th International Symposium on Electrets (ISE 10), Proceedings (Cat. No.99 CH36256), Athens, Greece, 22–24 September 1999; pp. 437–444. [Google Scholar]
- Bahl, I.J.; Trivedi, D.K. A designer’s guide to microstrip line. Microwaves 1977, 174–182. [Google Scholar]
- Natarajan, R. Power System Capacitors; Power Engineering 26; CRC Press: Boca Raton, FL, USA, 2005; ISBN 978-1-57444-710-1. [Google Scholar]
- Bal, K.; Kothari, V.K. Study of dielectric behaviour of woven fabric based on two phase models. J. Electrost. 2009, 67, 751–758. [Google Scholar] [CrossRef]
- Driscoll, T.; Basov, D.N.; Padilla, W.J.; Mock, J.J.; Smith, D.R. Electromagnetic characterization of planar metamaterials by oblique angle spectroscopic measurements. Phys. Rev. B 2007, 75, 115114. [Google Scholar] [CrossRef] [Green Version]
- Khoshman, J.M.; Kordesch, M.E. Vacuum Ultra-Violet Spectroscopic Ellipsometry Study of Sputtered BeZnO Thin Films. Optik 2011, 122, 2050–2054. [Google Scholar] [CrossRef]
- Jean-Mistral, C.; Sylvestre, A.; Basrour, S.; Chaillout, J.-J. Dielectric properties of polyacrylate thick films used in sensors and actuators. Smart Mater. Struct. 2010, 19, 075019. [Google Scholar] [CrossRef]
- Li, S.; Chen, R.; Anwar, S.; Lu, W.; Lai, Y.; Chen, H.; Hou, B.; Ren, F.; Gu, B. Applying effective medium theory in characterizing dielectric constant of solids. In Proceedings of the 2012 International Workshop on Metamaterials (Meta), Nanjing, China, 8–10 October 2012; pp. 1–3. [Google Scholar]
- Zhuromskyy, O. Applicability of Effective Medium Approximations to Modelling of Mesocrystal Optical Properties. Crystals 2016, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Tinga, W.R.; Voss, W.A.G.; Blossey, D.F. Generalized approach to multiphase dielectric mixture theory. J. Appl. Phys. 1973, 44, 3897–3902. [Google Scholar] [CrossRef]
- Garnett, J.C.M.; Larmor, J. XII. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Sihvola, A. Homogenization principles and effect of mixing on dielectric behavior. Photonics Nanostruct.-Fundam. Appl. 2013, 11, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Morton, W.E.; Hearle, J.W.S. Physical Properties of Textile Fibres; Woodhead Publishing: Sawston, UK, 2008; ISBN 978-1-84569-220-9. [Google Scholar]
- Balls, W.L. Dielectric Properties of Raw Cotton. Nature 1946, 158, 9–11. [Google Scholar] [CrossRef]
- Humlicek, J. Data Analysis for Nanomaterials: Effective Medium Approximation, Its Limits and Implementations. In Ellipsometry at the Nanoscale; Losurdo, M., Hingerl, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 145–178. ISBN 978-3-642-33955-4. [Google Scholar]
- Markel, V.A. Introduction to the Maxwell Garnett approximation: Tutorial. J. Opt. Soc. Am. A 2016, 33, 1244. [Google Scholar] [CrossRef] [Green Version]
- Peirce, F.T. 5—The Geometry of Cloth Structure. J. Text. Inst. Trans. 1937, 28, T45–T96. [Google Scholar] [CrossRef]
- Bal, K.; Kothari, V.K. Dielectric behaviour of polyamide monofilament fibers containing moisture as measured in woven form. Fibers Polym. 2014, 15, 1745–1751. [Google Scholar] [CrossRef]
- Cerovic, D.D.; Dojcilovic, J.R.; Asanovic, K.A.; Mihajlidi, T.A. Dielectric investigation of some woven fabrics. J. Appl. Phys. 2009, 106, 084101. [Google Scholar] [CrossRef]
- Igarashi, T.; Hoshi, M.; Nakamura, K.; Kaharu, T.; Murata, K. Direct Observation of Bound Water on Cotton Surfaces by Atomic Force Microscopy and Atomic Force Microscopy–Infrared Spectroscopy. J. Phys. Chem. C 2020, 124, 4196–4201. [Google Scholar] [CrossRef] [Green Version]
- Sakabe, H.; Ito, H.; Miyamoto, T.; Inagaki, H. States of Water Sorbed on Wool as Studied by Differential Scanning Calorimetry. Text. Res. J. 1987, 57, 66–72. [Google Scholar] [CrossRef]
- Skaar, C. Wood-Water Relations; Springer Series in Wood Science; Springer: Berlin/Heidelberg, Germany, 1988; ISBN 978-3-642-73685-8. [Google Scholar]
- Buchner, R.; Barthel, J.; Stauber, J. The dielectric relaxation of water between 0 °C and 35 °C. Chem. Phys. Lett. 1999, 306, 57–63. [Google Scholar] [CrossRef]
- Hippel, A.R. von The dielectric relaxation spectra of water, ice, and aqueous solutions, and their interpretation. I. Critical survey of the status-quo for water. IEEE Trans. Electr. Insul. 1988, 23, 801–816. [Google Scholar] [CrossRef]
- Sugimoto, H.; Takazawa, R.; Norimoto, M. Dielectric relaxation due to heterogeneous structure in moist wood. J. Wood Sci. 2005, 51, 549–553. [Google Scholar] [CrossRef]
- Kuttich, B.; Grefe, A.-K.; Kröling, H.; Schabel, S.; Stühn, B. Molecular mobility in cellulose and paper. RSC Adv. 2016, 6, 32389–32399. [Google Scholar] [CrossRef] [Green Version]
- Cerovic, D.D.; Asanovic, K.A.; Maletic, S.B.; Dojcilovic, J.R. Comparative study of the electrical and structural properties of woven fabrics. Compos. Part B Eng. 2013, 49, 65–70. [Google Scholar] [CrossRef]
- Gezici-Koç, Ö.; Erich, S.J.F.; Huinink, H.P.; van der Ven, L.G.J.; Adan, O.C.G. Bound and free water distribution in wood during water uptake and drying as measured by 1D magnetic resonance imaging. Cellulose 2017, 24, 535–553. [Google Scholar] [CrossRef] [Green Version]
- Loss, C.; Gonçalves, R.; Pinho, P.; Salvado, R. Influence of some structural parameters on the dielectric behavior of materials for textile antennas. Text. Res. J. 2018. [Google Scholar] [CrossRef]
- Mukherjee, P.K. Dielectric properties in textile materials: A theoretical study. J. Text. Inst. 2018, 110, 1–4. [Google Scholar] [CrossRef]
- Mukherjee, P.K.; Das, S. Improved analysis of the dielectric properties of textile materials. J. Text. Inst. 2021, 112, 1890–1895. [Google Scholar] [CrossRef]
- Jilani, M.T.; Rehman, M.Z.; Khan, A.M.; Khan, M.T.; Ali, S.M. A Brief Review of Measuring Techniques for Characterization of Dielectric Materials. Int. J. Inf. Technol. Electr. Eng. 2012, 1, 5. [Google Scholar]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; Wiley: Chichester, UK, 2004. [Google Scholar]
- Baker-Jarvis, J. Dielectric and Conductor-Loss Characterization and Measurements on Electronic Packaging Materials; NIST Technical Note 1520; U.S. Department of Commerce, National Institute of Standards and Technology: Boulder, CO, USA, 2001.
- Sankaralingam, S.; Gupta, B. Determination of Dielectric Constant of Fabric Materials and Their Use as Substrates for Design and Development of Antennas for Wearable Applications. IEEE Trans. Instrum. Meas. 2010, 59, 3122–3130. [Google Scholar] [CrossRef]
- Mazierska, J.; Krupka, J.; Jacob, M.V.; Ledenyov, D. Complex permittivity measurements at variable temperatures of low loss dielectric substrates employing split post and single post dielectric resonators. In Proceedings of the 2004 IEEE MTT-S International Microwave Symposium Digest (IEEE Cat. No.04CH37535), Fort Worth, TX, USA, 6–11 June 2004; pp. 1825–1828. [Google Scholar]
- Kowerdziej, R.; Krupka, J.; Nowinowski-Kruszelnicki, E.; Olifierczuk, M.; Parka, J. Microwave complex permittivity of voltage-tunable nematic liquid crystals measured in high resistivity silicon transducers. Appl. Phys. Lett. 2013, 102, 102904. [Google Scholar] [CrossRef]
- Krupka, J.; Nguyen, D.; Mazierska, J. Microwave and RF methods of contactless mapping of the sheet resistance and the complex permittivity of conductive materials and semiconductors. Meas. Sci. Technol. 2011, 22, 085703. [Google Scholar] [CrossRef]
- Krupka, J. Microwave Measurements of Electromagnetic Properties of Materials. Materials 2021, 14, 5097. [Google Scholar] [CrossRef]
- Waldron, I. Ring Resonator Method for Dielectric Permittivity Measurement of Foams. Master’s Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2006. [Google Scholar]
- Yang, L.; Rida, A.; Vyas, R.; Tentzeris, M.M. RFID Tag and RF Structures on a Paper Substrate Using Inkjet-Printing Technology. IEEE Trans. Microw. Theory Tech. 2007, 55, 2894–2901. [Google Scholar] [CrossRef] [Green Version]
- Waldron, I.; Makarov, S.N. Measurement of dielectric permittivity and loss tangent for bulk foam samples with suspended ring resonator method. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 3175–3178. [Google Scholar]
- Tu, H.; Zhang, Y.; Hong, H.; Hu, J.; Ding, X. A strip line ring resonator for dielectric properties measurement of thin fabric. J. Text. Inst. 2021, 112, 1772–1778. [Google Scholar] [CrossRef]
- Shimin, D. A New Method for Measuring Dielectric Constant Using the Resonant Frequency of a Patch Antenna. IEEE Trans. Microw. Theory Tech. 1986, 34, 923–931. [Google Scholar] [CrossRef]
- Rabih, A.A.S.; Begam, K.M.; Ibrahim, T.; Burhanudin, Z.A. Dielectric Properties of Properly Slaughtered and Non-properly Slaugheterd Chicken. J. Med. Res. Dev. 2014, 3, 15. [Google Scholar]
- Pizzitutti, F.; Bruni, F. Electrode and interfacial polarization in broadband dielectric spectroscopy measurements. Rev. Sci. Instrum. 2001, 72, 2502–2504. [Google Scholar] [CrossRef]
- Chassagne, C.; Dubois, E.; Jiménez, M.L.; van der Ploeg, J.P.M.; van Turnhout, J. Compensating for Electrode Polarization in Dielectric Spectroscopy Studies of Colloidal Suspensions: Theoretical Assessment of Existing Methods. Front. Chem. 2016, 4. [Google Scholar] [CrossRef]
- Ishai, P.B.; Talary, M.S.; Caduff, A.; Levy, E.; Feldman, Y. Electrode polarization in dielectric measurements: A review. Meas. Sci. Technol. 2013, 24, 102001. [Google Scholar] [CrossRef]
- Klein, R.J.; Zhang, S.; Dou, S.; Jones, B.H.; Colby, R.H.; Runt, J. Modeling electrode polarization in dielectric spectroscopy: Ion mobility and mobile ion concentration of single-ion polymer electrolytes. J. Chem. Phys. 2006, 124, 144903. [Google Scholar] [CrossRef] [PubMed]
- Gupta, K.C.; Ramadoss, R.; Zhang, H. RF and microwave network characterization-a concept-map-based tutorial. IEEE Trans. Microw. Theory Tech. 2003, 51, 1326–1329. [Google Scholar] [CrossRef]
- Ravelo, B.; Thakur, A.; Saini, A.; Thakur, P. Microstrip Dielectric Substrate Material Characterization with Temperature Effect. Appl. Comput. Electromagn. Soc. 2015, 30, 1322–1328. [Google Scholar]
- Maloratsky, L.G. Reviewing The Basics Of Microstrip Lines A. Microw. RF 2000, 39, 79–88. [Google Scholar]
- Rocha, L.S.; Junqueira, C.C.; Gambin, E.; Nata Vicente, A.; Culhaoglu, A.E.; Kemptner, E. A free space measurement approach for dielectric material characterization. In Proceedings of the 2013 SBMO/IEEE MTT-S International Microwave & Optoelectronics Conference (IMOC), Rio de Janeiro, Brazil, 4–7 August 2013; pp. 1–5. [Google Scholar]
- Fwen, W.; Ping, S.; Abd Malek, M.F.; Hasss, N. Alternatives for PCB Laminates: Dielectric Properties’ Measurements at Microwave Frequencies. In Dielectric Material; Silaghi, M.A., Ed.; InTech: Rijeka, Croatia, 2012; ISBN 978-953-51-0764-4. [Google Scholar]
- Pometcu, L.; Sharaiha, A.; Benzerga, R.; Tamas, R.D.; Pouliguen, P. Method for material characterization in a non-anechoic environment. Appl. Phys. Lett. 2016, 108, 161604. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, X. Influence of the Yarn Fineness and Stitch Length of Polyester Knitted Fabric on the Dielectric Constant. Fibres Text. East. Eur. 2019, 27, 63–66. [Google Scholar] [CrossRef]
- Mukai, Y.; Bharambe, V.T.; Adams, J.J.; Suh, M. Effect of Bending and Padding on the Electromagnetic Performance of a Laser-Cut Woven Fabric Patch Antenna. In Proceedings of the Textiles Research Open House, Raleigh, NC, USA, 16 April 2018. [Google Scholar]
- Shao, X.; Qiu, Y.; Wang, Y. Theoretical modeling of the tensile behavior of low-twist staple yarns: Part II–theoretical and experimental results. J. Text. Inst. 2005, 96, 69–76. [Google Scholar] [CrossRef]
- Van de Velde, K.; Kiekens, P. Development of a Flax/Polypropylene Composite with Optimal Mechanical Characteristics by Fiber and Matrix Modification. J. Thermoplast. Compos. Mater. 2002, 15, 281–300. [Google Scholar] [CrossRef]
- Van de Velde, K.; Kiekens, P. Influence of Fibre and Matrix Modifications on Mechanical and Physical Properties of Flax Fibre Reinforced Poly(propylene). Macromol. Mater. Eng. 2001, 286, 237–242. [Google Scholar] [CrossRef]
- Dalbehera, S.; Acharya, S.K. Study on mechanical properties of natural fiber reinforced woven jute-glass hybrid epoxy composites. Adv. Polym. Sci. Technol. 2014, 4, 1–6. [Google Scholar]
- Wang, L.; Kumar, R.; Zhang, L. Investigation into hemp fiber- and whisker-reinforced soy protein composites. Front. Chem. China 2009, 4, 313–320. [Google Scholar] [CrossRef]
- Li, Y.V. Proteins and Protein-Based Fibers. In ACS Symposium Series; Yang, Y., Xu, H., Yu, X., Eds.; American Chemical Society: Washington, DC, USA, 2014; Volume 1175, pp. 21–36. ISBN 978-0-8412-2990-7. [Google Scholar]
- Xiang, P.; Kuznetsov, A.V.; Seyam, A.-F.M. Simulation of Fiber Entanglement by Modeling Vorticity in Water Flow Field. Text. Res. J. 2007, 77, 312–329. [Google Scholar] [CrossRef]
- Shaikh, T.N.; Bhattacharya, S.S. Deriving an empirical formula to determine the optimum level of false-twist in mechanically-crimped textured polyester yarn. Text. Res. J. 2011, 81, 1995–2005. [Google Scholar] [CrossRef]
- Mao, N.; Russell, S.J. Fibre to Fabric: Nonwoven Fabrics-ScienceDirect. In Textiles and Fashion; Woodhead Publishing Limited: Sawston, UK, 2015; pp. 307–335. ISBN 978-0-85709-561-9. [Google Scholar]
- ASTM D2495-17; Standard Test Method for Moisture in Cotton by Oven-Drying. ASTM International: West Conshohocken, PA, USA, 2012.


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, Y. Dielectric Properties of Textile Materials: Analytical Approximations and Experimental Measurements—A Review. Textiles 2022, 2, 50-80. https://doi.org/10.3390/textiles2010004
Yamada Y. Dielectric Properties of Textile Materials: Analytical Approximations and Experimental Measurements—A Review. Textiles. 2022; 2(1):50-80. https://doi.org/10.3390/textiles2010004
Chicago/Turabian StyleYamada, Yusuke. 2022. "Dielectric Properties of Textile Materials: Analytical Approximations and Experimental Measurements—A Review" Textiles 2, no. 1: 50-80. https://doi.org/10.3390/textiles2010004
APA StyleYamada, Y. (2022). Dielectric Properties of Textile Materials: Analytical Approximations and Experimental Measurements—A Review. Textiles, 2(1), 50-80. https://doi.org/10.3390/textiles2010004






