1. Introduction
A textile is a flexible material made by creating an interlocking network of yarns. Yarns are produced by several spinning technologies from length-limited or endless fibers (from either natural or synthetic sources) into long and twisted lengths. Through a defined interlocking of one or several yarn systems, a 2D or 3D textile is formed by means of textile technologies, e.g., weaving, weft knitting, warp knitting or braiding. A technical textile is a textile product manufactured for non-aesthetic purposes, where function is the primary criterion. For an extensive introduction to technical textiles, see, e.g., [
1,
2]. Technical textiles include textiles for automotive applications, medical textiles (e.g., implants and bandages), geotextiles (reinforcement of embankments), agrotextiles (textiles for crop protection), protective clothing with thermophysiological effect (e.g., heat and radiation protection for fire fighter clothing), functional and sports clothing as well as light-weight constructions.
The functional and especially the mechanical behavior of a textile can be modeled as thin plates or shells. In particular, the effective bending and tensile behavior as well as the folding or wrinkling of a textile can be described by the mechanical theory of plates and shells [
3,
4]. The underlying textile structure, i.e., the woven or knitted fabric made of threads, determines the mechanical behavior and can be analyzed rigorously with the help of asymptotic analysis and homogenization theory [
5,
6,
7].
In general, the functional behavior of the textile is determined by the functional behavior of the different yarns and the structure of the interlocking network. The yarns can be characterized by their thickness, cross-section and tensile properties. Often, the textile structure is periodic in the plane and specified by the textile manufacturing process. The arrangement of the yarns and the friction between the yarns in contact determine the resulting material behavior [
8,
9], where simulation validates industrial experiments.
In this paper, an application of the mathematical framework of homogenization and asymptotic analysis is presented, which enables to quantify the mechanical behavior of textiles as well determining the sensitive and influencing parameters. These quantifications are critical for the computation of buckling pre-strain in yarns and of folding shear angles in non-stretchable textiles.
Currently, the state of the art for the prediction of the textile folding under compression or shear is mostly by trial and error through expensive experiments. Some recent modelling works use ANSYS, LS-DYNA and ESI-Software for simulations [
10,
11]. Although those commercial tools include many possibilities to simulate shells and their buckling, the main modelling issue of textiles, especially in the non-crimp regime, is the contact between yarns. The contact changes the macroscopic behavior of the pre-forming textiles (see, e.g., advanced modelling papers [
12,
13,
14,
15] and the contact issues between yarns in [
16]). Yarn contacts cause higher gradients and rotations along one or multiple directions to join the constitutive equations [
6,
7,
11,
12,
13,
14], which is, according to the authors, beyond the state of the art in the commercial software tools.
In several papers of the Boisse group, different types of loading and problems with textiles were considered [
15,
16,
17,
18]. In our work, sharp bounds for the change of the limiting textile plate-like behavior are provided, e.g., at changing magnitude of the loading or strength of the contact (if the yarns are almost glued or can slide almost without friction).
The aim of our research is to give ranges of applicability of each homogenized model [
5,
6,
7,
19] and to extend the available computational tools by correct simulation of different single- and multi-layer textiles and different applications with them [
8,
9].
The derived mathematical framework is exemplified by our recent numerical simulations for multiple different textiles. Additionally, our currently developed simulation tool, TexMath (Version 0.4.0) [
20], is presented, which allows us to systematically optimize textiles with respect to their desired functional behavior [
21,
22,
23].
2. Simulation of Textiles with Stretchable Yarns
If the yarns are stretchable, stretching is coupled with the bending of the textile shell due to the strong frictional contact or adhesion. The coupling results in folding under tension. This effect is known as von Karman regime of shells, and it is derived from the yarn properties by asymptotic analysis [
7]. This paper and a complementary structure optimization of the folding or buckling under tension [
23] fully describe the folding mechanisms of textile strips under tension driven by the stretchable yarns integrated in a textile pattern.
A computational algorithm for textiles made of stretchable yarns with frictional contact and sliding at their crossing areas, with redistribution of the meshes due to the relaxation of the pre-stress in nodes caused by the sliding, is presented in [
8,
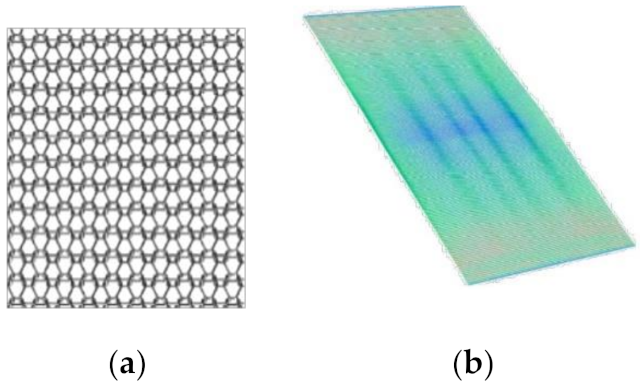
9]. The general model is applicable to woven fabrics made of stretchable yarns as well as knitted fabrics, as presented in
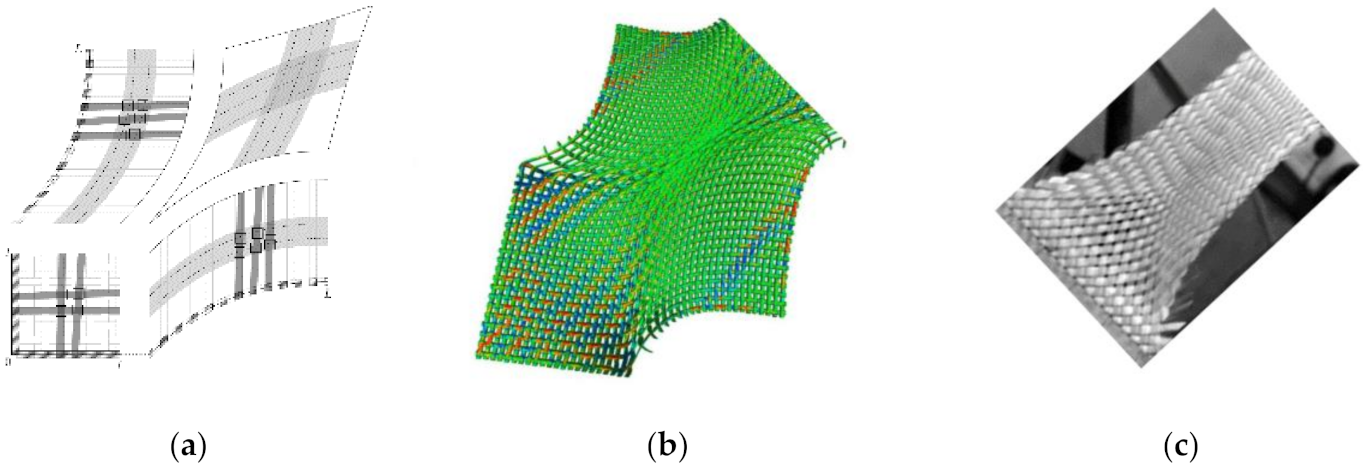
Figure 1.
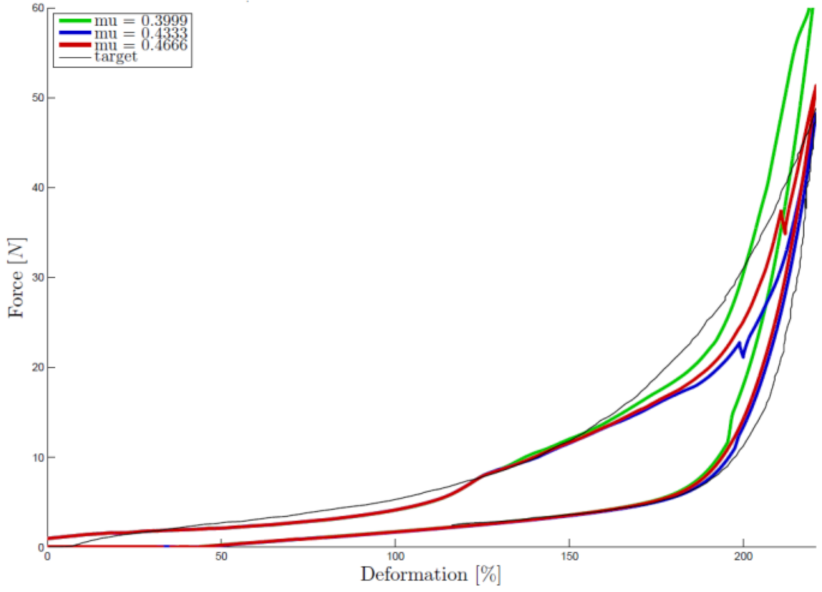
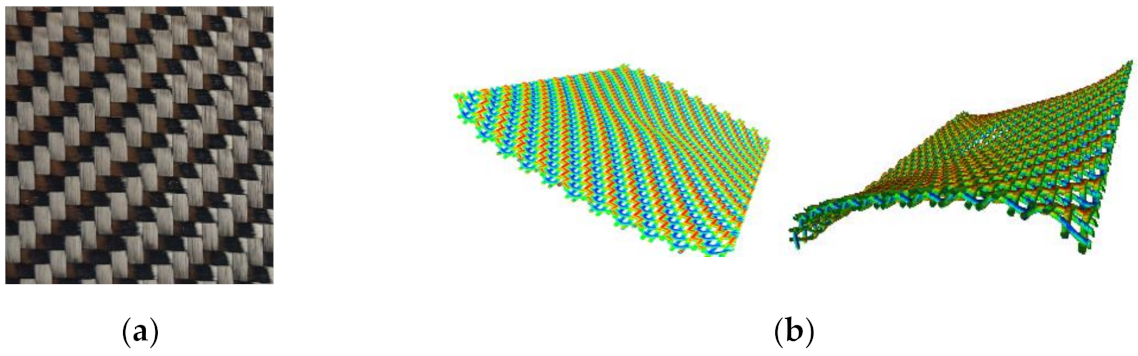
In
Figure 2 below, the algorithm is applied to a weft knitted textile sheet to simulate the loading-unloading under unit-axial tension. The simulation results are compared with experimental measurements. The simulation is performed with varying friction coefficient μ.
In [
21], structure (pattern) optimization with state constraints (a desired stress or pressure profile in the fabric) for knitted fabrics is presented. In the paper, meshes in the knitting pattern are parametrized in a very simple way, corresponding to the knitting machine control parameters such as the stich-height, distance between needles and pre-stress in the yarns during the production in the machine. This allows to simulate the production, to relax to the table-measure with relaxation of the pre-stresses in the yarns between nodes and to find the residual pre-stress in nodes. Afterwards, the knitted fabric can be virtually put on a given body in an appropriate format (e.g., common for CAD-software).
3. Control Parameters for Textile Folding
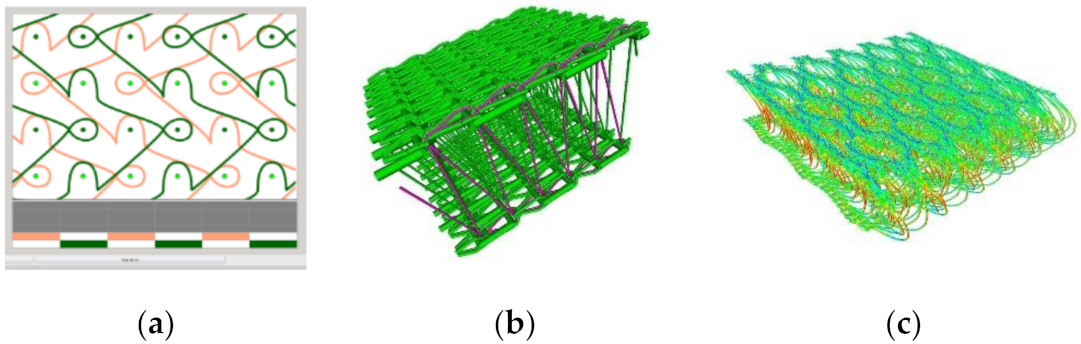
Textile behavior under mechanical loading is influenced by multiple different aspects. The most important aspects considered in our research are: (i) elastic energy of yarns: linear (as in
Section 4)–nonlinear (as in
Section 2); (ii) order of the possible sliding in terms of the geometric parameters, the distance between yarns and their thickness, compared to the order of elastic strains-energy (“weak” or “strong” contact, [
5,
6]); (iii) influence of the boundary fixation (see
Figure 3).
(iv) issue, if the radius of yarns is one order of magnitude smaller compared to the distance between them; (v) tension in yarns during the production (see
Figure 4), which defines whether, after the relaxation, yarn’s mean axis stays straight or oscillates, how big this crimp is, whether the averaged aces of the oscillating weft or warp belong to the mean plane of the effective plate, or if it is situated above or below this plane.
(vi) pre-stress in yarns, induced by thermo- (see
Figure 5), electric- or moisture extension-swelling under some in-plane restrictions of the complete fabric.
All the mentioned aspects play a crucial role in our numerical simulations and are considered in our modular software, TexMath (Version 0.4.0), which is further described in
Section 6.
4. Asymptotic Modeling of Woven Textiles with Not Very Stretchable Yarns and High Friction or Weak Contact
In this section, the results obtained in [
5,
6] are emphasized and explained. These papers are dedicated for the modeling and asymptotic investigation of a linear elasticity problem on woven textile structures. The textiles are made of long and thin fibers, forming a periodic squared domain.
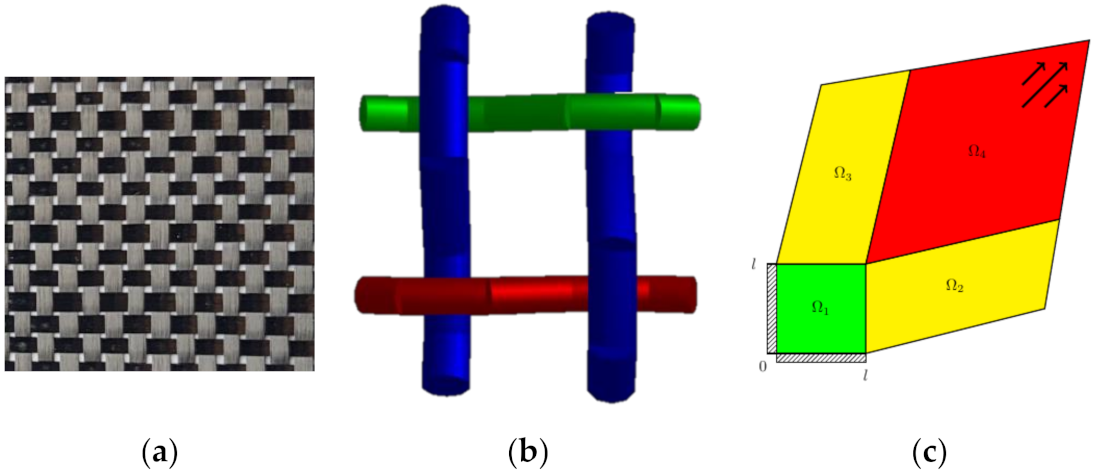
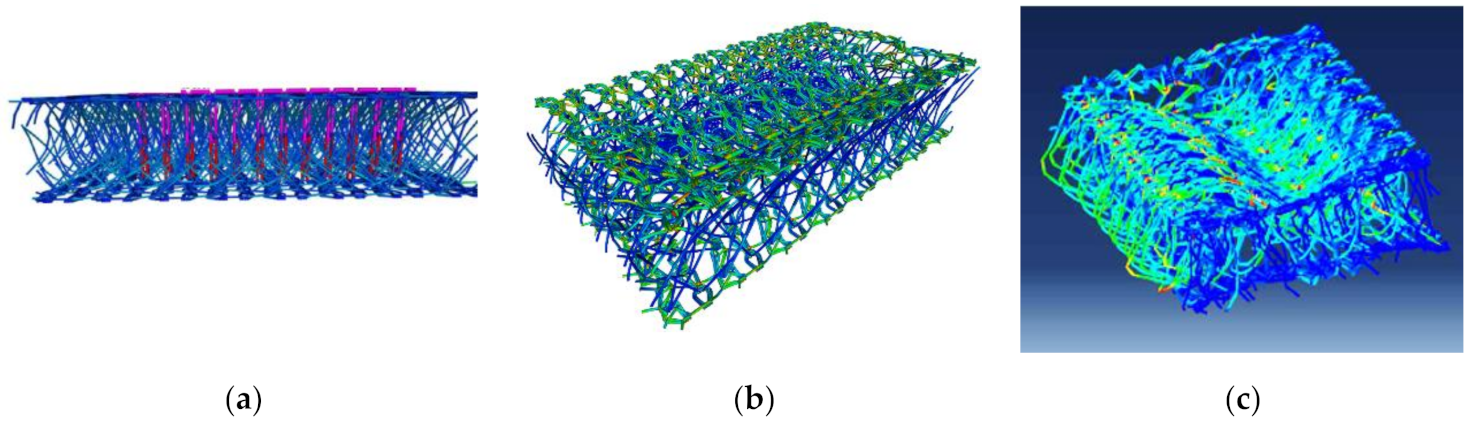
The domain is clamped only partially (see
Figure 6c), and an in-plane sliding between the fibers is bounded by a contact function, which is related to the friction between yarns. It is expressed in the powers of the distance between two weft or two warp yarns. Both partial clamp and loose contact result in a domain split with different behaviors in each of the four parts schematically shown in
Figure 6c.
In [
5,
6,
7], two small parameters were introduced, which denote the radius of yarns and the distance between them. Homogenization and dimension reduction is used to derive the macroscopic behavior in each textile part. In the papers, the limit in the contact elasticity problem on the yarn’s structure (a fabric) with respect to both small geometric parameters is investigated. In the limit, different limiting plate-behaviors for different scaling regimes are obtained, i.e., if sliding or elastic deformation dominates. The applied forces are chosen in a way to stay in the elastic regime without large stretching in the yarns.
Practically, this means that one needs to measure the applied forces and tractions and estimate them in terms of powers of the radius or distance between yarns, in order to apply the correct simulation model.
The main results of these papers are illustrated in
Figure 7;
Figure 8. In the case that sliding dominates the elastic energy of the yarns, the macroscopic effective solution results in two macroscopic plates. The plates are spanned on only weft or only warp yarns with high gradients just along the yarns in each plate. Both are coupled by the macroscopic contact condition including the in-plane rotations. Paper [
6] provides the critical shear angles for woven textiles, computed only from the weaving pattern and fiber cross-sections.
Table 1 shows the experimental validation of the theoretical prediction in [
6]. The computational errors are 1–2%, which corresponds to an angle difference of 3°.
The experimental validation was performed by RWTH Aachen Institute of Textile Technology. The sensitivity study of the shear angles to the textile design can be found in [
24]. Further technical details for
Table 1 on rowing cross-sections, distances between rowing axes and rowing stiffness are listed in [
24].
In paper [
7], a homogenization algorithm is proposed, which computes the effective pre-strain in textiles from known pre-strain in the single yarns. Furthermore, simple formulas are presented, which allow to compute the effective pre-strain that is critical for buckling of a fabric under tension: the buckling across the tension direction or under compression (buckling in the compressed direction). The effective pre-strain (that is) critical for buckling is computed from the fabric’s effective bending and tension properties, as well as its length and width.
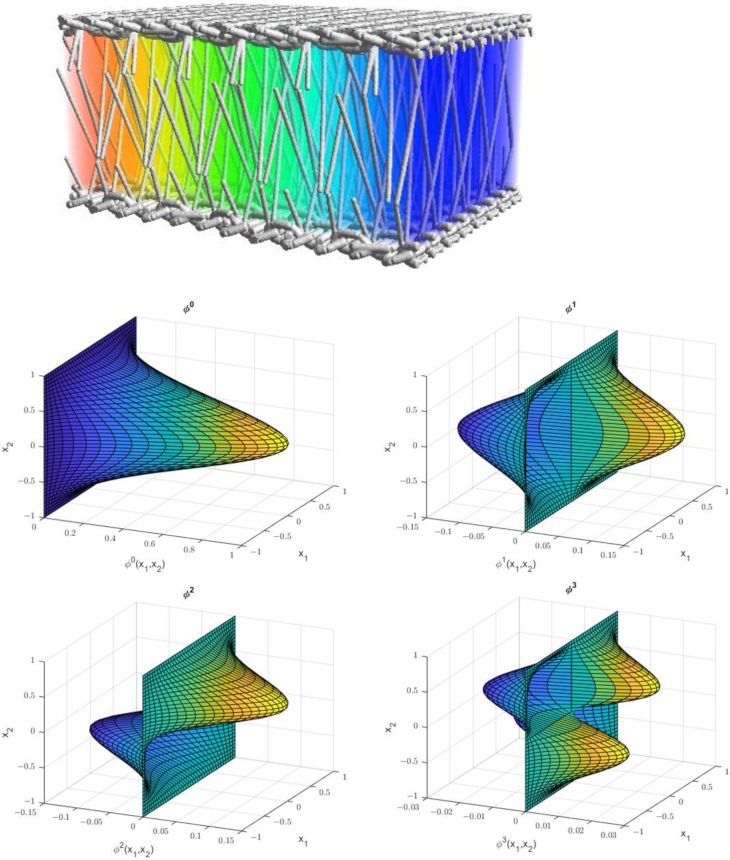
5. Simulation of Spacer Fabrics with a Significant Dimension Reduction
Due to their 3D structure, spacer fabrics possess outstanding properties, such as compressive elasticity and permeability, resulting in enhanced functionality of the products manufactured from them. Especially warp knitted spacer fabrics are already established as foam alternatives, upholstery pads and pressure-elastic components with rear-ventilation effect, as well as filter materials and reinforcing materials for composites. In [
25], a simulation of the compressional elastic, relaxation and permeability properties of spacer fabrics was proposed. The detailed structural modeling helps to better understand the energy-driven processes in warp knitted spacer fabrics and the basic underlying mechanisms. Such simulations can be used for function-adapted product developments and replace the previous extremely time-consuming and costly experimental technology.
One focus of our current research is to find an optimum for local reinforcement of warp knitted spacer fabrics using seams. The local reinforcement should provide desired compression stiffness and a desired curvature of the fabric between two seams. The aim here is to develop a method to variably design the distance between the knitted surfaces in the seam area and to achieve a defined curvature by finding the optimal seam characteristics (height, width and so on) and distance between the seams.
Unlike previous sections, where an overview about particular algorithms and results from other papers was given and illustrated by some qualitative examples, a particular example is considered in this section. A warp knitted spacer fabric with closed structure and thickness of 20 mm is investigated. Seams of types of double quilt stiches with varying stitch parameters were inserted using an “M-Type“ Delta machine (Dürkopp-Adler AG, Bielefeld, Germany). The tension in the sewing yarn as well as the stitch length are known and can be varied.
Using the TexMath module MeshUp (
Figure 9), the spacer fabric was digitalized in the computer in the stage as it comes from the machine. Afterwards, it was virtually extended in the plane and then compressed. All the performed deformations were carried out within the TexMath module FiberFEM for mechanical simulation of textiles. At the end of the mentioned steps, the yarns are already pre-strained. This is the preparation step for the insertion of stitches in the 3D structures.
Figure 10 shows the process of the seam insertion under given machine parameters, reasoning the seam-yarn pre-stress. Using the known pre-strain in the seam, it was placed in the digitalized fabric; see
Figure 11a. The compression is simulated as the next step by FiberFEM. To simulate further compression under large tension in the seam, the commercial tool, ABAQUS, was used; see
Figure 11c.
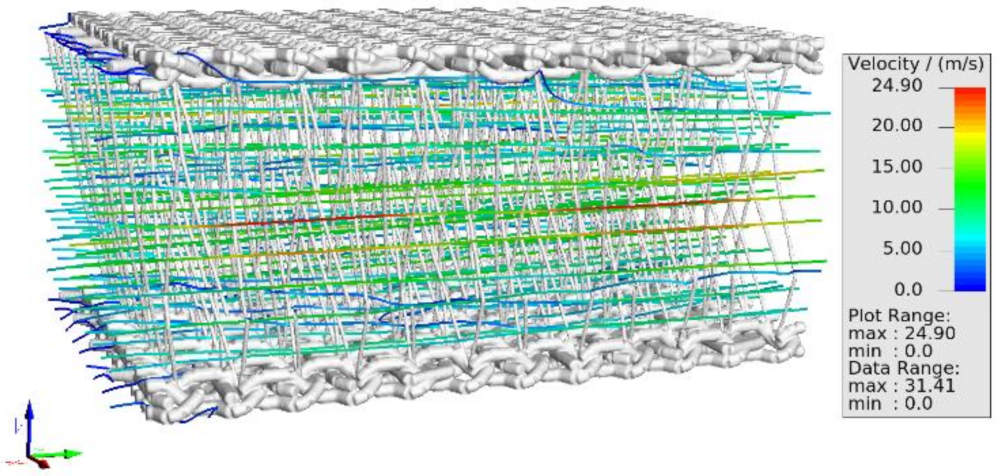
In another focus of our current research, horizontal non-viscous fluid flow through a spacer fabric is considered, see
Figure 12. The spacer fabric is insulated at the top and bottom. Periodicity of the fabric allows to reduce the problem to one periodicity cell for simulation. The deflection of the monofilaments connecting the knitted layers caused by fluid-solid interaction is of special interest.
In [
25], the stationary Stokes flow through spacer fabrics in the compressed and non-compressed state of the fabric was already simulated; see
Figure 13. The simulations were performed in the Software GeoDict (
www.geodict.com). However, the fluid–solid interaction was not considered there. The spacer fabric was assumed to be rigid, and the flow through the uncompressed fabric was simulated first (the first row in
Figure 13). Afterwards, the fabric was compressed with TexMath, and the Stokes flow in the compressed structure was simulated, again, assuming it to be rigid for this simulation.
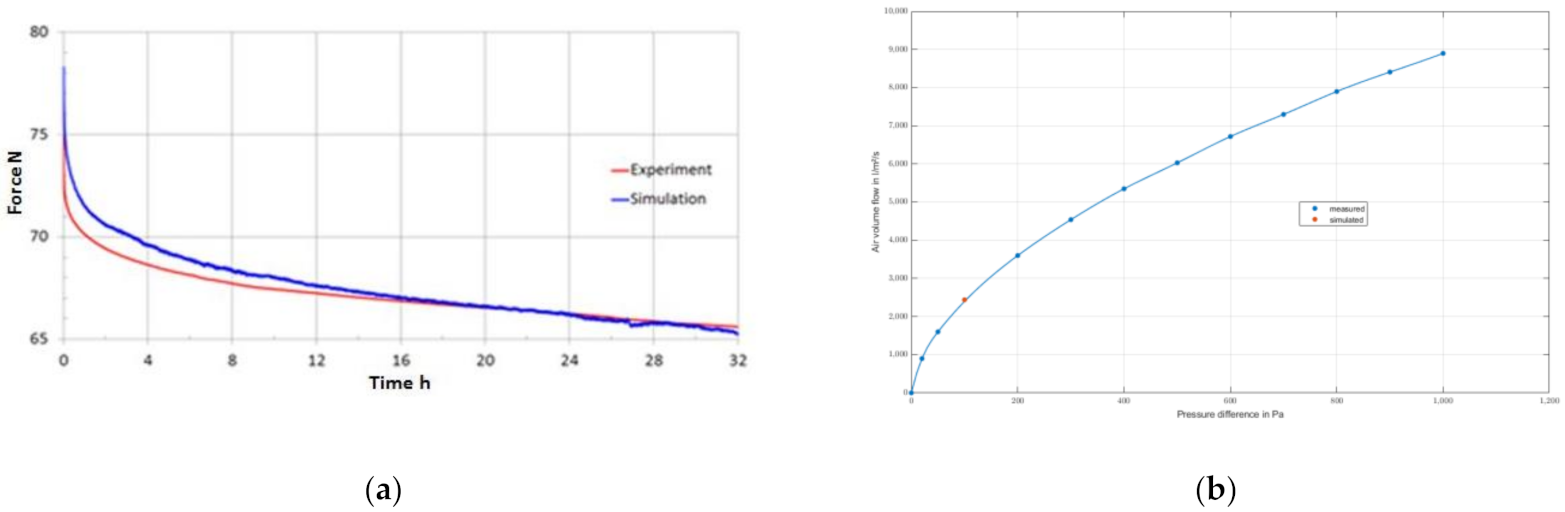
In
Figure 14, the experimental validation from [
25] is recalled.
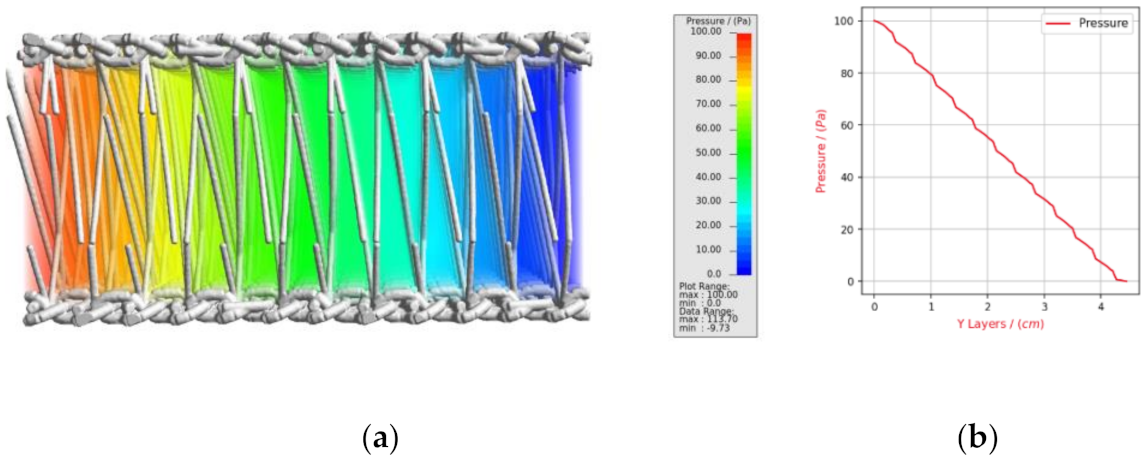
Examining the pressure distribution in the fluid computed within the assumption of rigid beams in one time-step by GeoDict, one can observe that it jumps over vertical lattices as shown in
Figure 15 below.
Our first algorithmic idea for the computation of the monofilament deflection is to restrict the pressure jump in the fluid to the 1-dimensional center axes of the monofilaments for each time step. The reduction approach is sketched in
Figure 16. The result is a force
that acts on the monofilament axes and that can be expressed in a few nodal points along the axes.
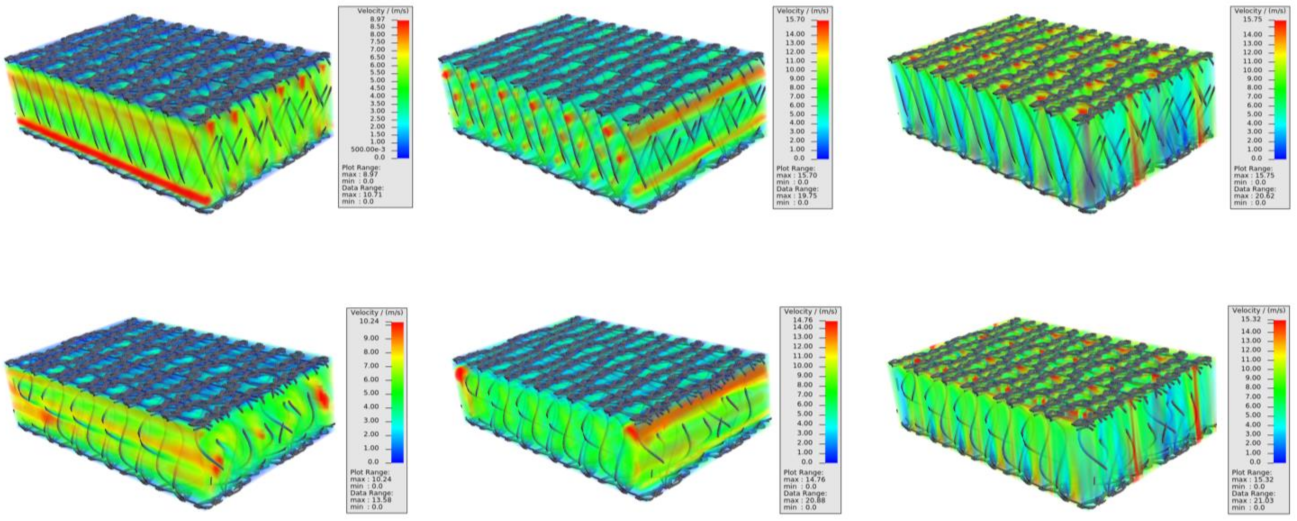
The computed force is then used as an artificial right-hand side in the linear elasticity problem for the monofilament deflection. This problem can be solved efficiently with the TexMath module FiberFEM. The simulation results for a spacer fabric with varying yarn radii are presented in
Figure 17.
Although, some time ago, such an iterative coupling of separate fluid and solid evolutions was considered state of the art in the solution accuracy and resolving of single fibers, it was time costly and not very precise in the sense of the statement of a coupled fluid–solid interaction problem.
Therefore, the coupled fluid–solid problems are solved simultaneously in a second approach. An asymptotic dimension reduction in thin beams and the coupling of 3D and 1D problems are employed. The idea is to reduce the problem to finding the displacement field, velocity field and fluid pressure only in some nodes/points along the monofilament axes. Afterwards, the solution fields are extended inside the monofilament and inside the fluid domain, to be able to reconstruct the solution in each point of the coupled, geometrically multi-scale domain.
As stated, the correct modeling is a main and delicate question. Exactly as in the previous sections, the relation between the textile thickness and applied forces will determine if the textile will behave as a stretchable membrane or as a bending-resistant plate or shell. In fact, here, in the fluid–solid interaction, the relation between the yarn’s stiffness and the fluid viscosity plays a crucial role. If their relation is proportional to the yarn’s thickness, the frictional forces at the monofilaments will rise their tension, and they all together will work like an extensional membrane. However, if the monofilaments are much stiffer than the fluid, as in the case of the spacer fabric infiltrated by water (this corresponds to the cubic yarn-thickness in their relation), the forest of monofilaments will bend and the curvature of the monofilaments will be proportional to the pressure jump in a non-local (such as memory or relaxation) setting [
19].
The problem described in [
19] is initially formulated with 3D fields, i.e., velocity and displacements, which can be restricted to the 2D mean surface of the monofilament axes. Our numerical approach uses a finite element method that further reduces the problem to a few nodes along the axes. The arising test functions are illustrated in
Figure 18. In between two adjacent monofilament forests, linear interpolation is applied.
After solving the finite element formulation, the global nodal solution is extended to the 3D beam domain by an interpolation technique described in [
6]. The extension is then used to reconstruct the fluid velocity and pressure in the whole fluid domain. The numerical implementation is currently in progress and will be the subject of future publications.
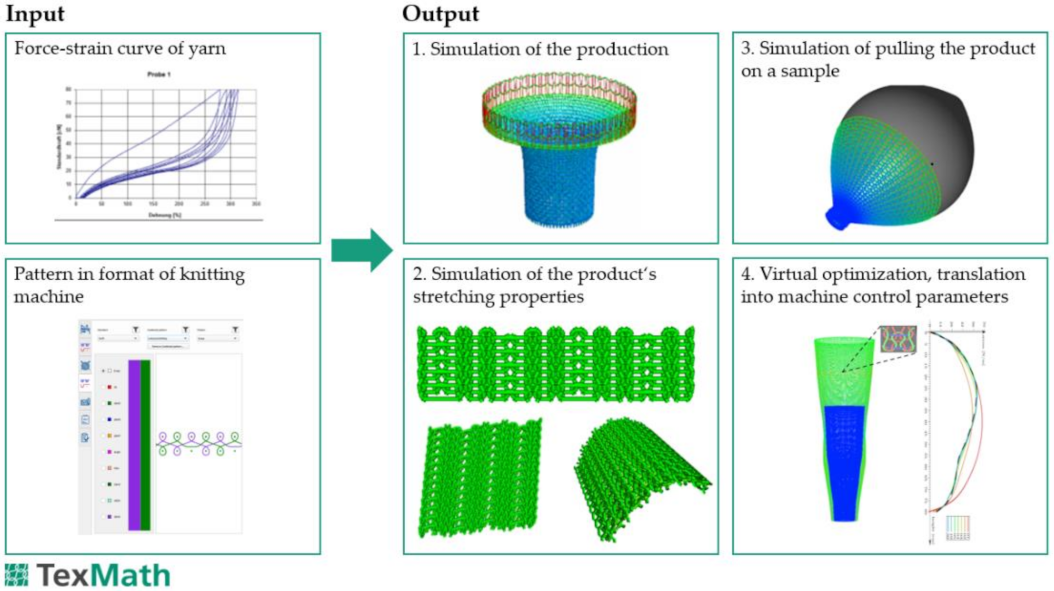
6. Textile Simulation and Optimization within the TexMath Software Tool
Our software tool, TexMath [
20], is a modular program for simulating mechanical material properties and optimizing textile products as well as multi-scale problems for textile applications. One area of application for the TexMath software is the optimization of compression textiles for the medical sector or for sports. For optimal effectiveness, the fit of the material is particularly important.
As a practical example, the optimal design of a knitted bandage with predefined compression properties was considered. The textile has to develop a given pressure profile on the body. In [
21], an efficient two-scale optimization algorithm, based on modern numerical methods and newest developments in homogenization approaches, is proposed. This multiscale optimization method is implemented and combined in TexMath. The design process is illustrated in
Figure 19. As a first step, the knitting process is simulated with TexMath. The resulting virtual bandage is then loaded in another simulation and put on a virtual arm or leg. The calculated pressure profile makes it possible to evaluate the compression properties of the bandage in advance and also to directly control the knitting machine according to the optimal design.
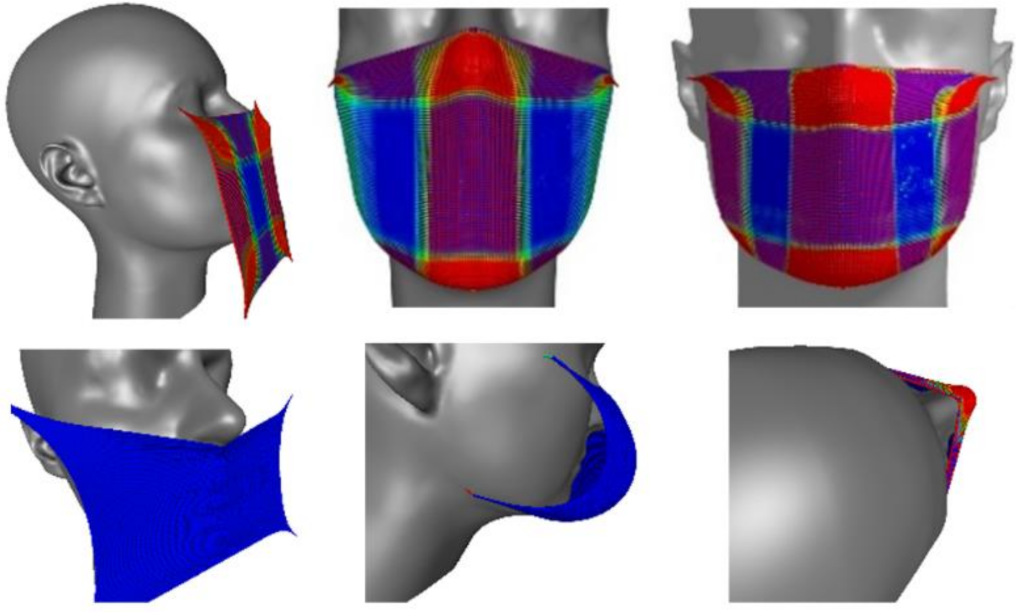
In a second example, the process of putting on a medical mask produced from knitted fabric is simulated. The simulation results are presented in
Figure 20.
The second row of figures, in
Figure 20, demonstrates an advantage of the simulation with the full yarn resolution: it allows to control the fabric behavior by changing the production pre-strain in the yarns. The left mask is produced with a high pre-stress and it slides at the unsupported boundary and high-curvature regions of the body. Its macroscopic behavior corresponds to an elastic membrane, working only on tension. One sees small folding under the nose, which is of the same nature as in
Figure 1. The second mask in the second row of
Figure 20 is produced with fewer pre-stress, hence being denser. Macroscopically, it behaves similar to a shell that works rather on bending than on tension. Its behavior corresponds to
Figure 8.
TexMath can also be used to design and simulate spacer textiles, as seen in the previous section. The goal is to optimize them in advance in terms of structure and infiltration properties.
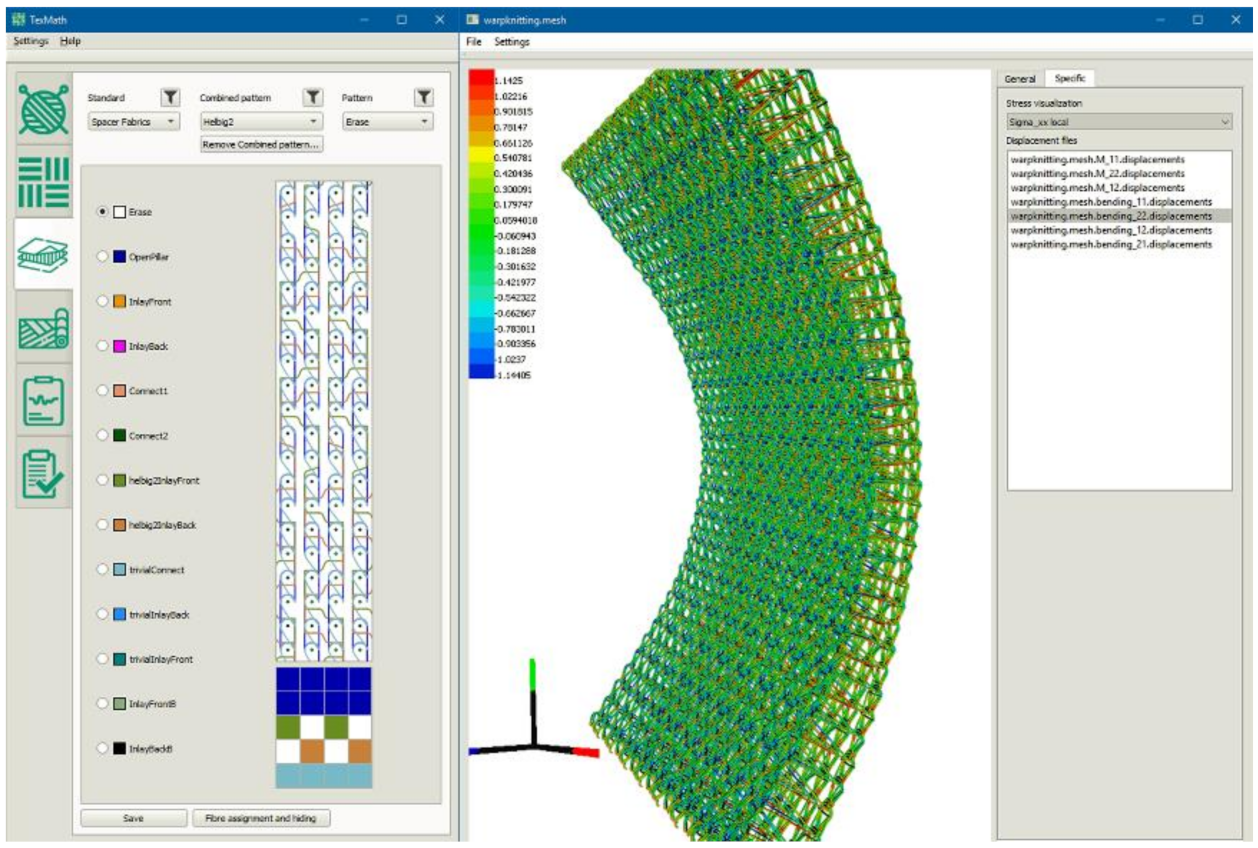
A demo version of the software program will soon be available. The newly developed input interface is particularly user-friendly. The textile class (i.e., knitted, warp-knitted, woven and spacer fabrics) can be easily set. The new graphic interface allows simple and fast configuration, see
Figure 21.
The experimental validation of simulations by the TexMath software can be found in [
9] for weft knitted, in [
25] for spacer fabrics and in reports of a joint AIF-project “OptiDrape” with the Textile institute ITA in Aachen for woven simple and twill patterns with different shifts and pre-forming textiles; see [
24].
7. Conclusions
In this paper, an overview of our recent publications concerning different aspects of the simulation of textiles was provided. Modeling approaches and results in the mathematical analysis for textiles with stretchable yarns, as well as for textiles with not very stretchable yarns and high friction or weak contact were presented. Moreover, our latest research in the simulation of spacer fabrics, which will be the topic of future publications, were shown. Additionally, examples for the numerical simulation and design optimization process within our software tool, TexMath, were provided. As only a survey and interpretation of some mathematical investigations was given, we refer the interested reader to our presented papers for detailed results and further information.