Abstract
Pesticides leaching and run-off to nearby freshwater sources are a major ecological concern. The emergence of herbicide-resistant weeds led to the increased usage of fomesafen, a diphenyl ether herbicide inhibiting protoporphyrinogen oxidase (PPO). This recent rise in demand and use for this molecule invariably increases the chance of this herbicide entering freshwater environments and affecting non-target organisms. However, there is still a lack of information in the literature regarding the impact of this herbicide on the physiology of freshwater phytoplankton. This study aimed to determine the impact of five concentrations (0, 5, 10, 40, 320 µg · L−1) of a fomesafen-based herbicide (Reflex®) on the physiology of two species of green microalgae (Raphidocelis subcapitata FACHB-271; Chlamydomonas snowii) and one cyanobacterial species (Microcystis aeruginosa CPCC 632). While physiological biomarkers (growth, photosynthesis, pigment content, oxidative stress and morphology) of R. subcapitata were significantly affected by the fomesafen treatments, no significant effects were observed in the physiology of C. snowii and M. aeruginosa. We hypothesize that this difference in fomesafen resistance is most likely due to intracellular morphological and genetic differences between species. Modeling of fomesafen uptake in R. subcapitata showed that alteration of cell biovolume is unlikely to be an efficient mechanism modulating fomesafen toxicity and that potential fomesafen efflux or breakdown would need to be very fast (and operate at a high energy cost) in order to protect against uptake and toxicity. This study provides new insights into the sensitivity of different algae species toward fomesafen as well as the associated cellular toxicity mechanisms.
Keywords:
fomesafen; PPO-inhibitor; Reflex®; chlorophytes; cyanophytes; growth; photosynthesis; Chl a; ROS; biovolume; cell complexity 1. Introduction
The protoporphyrinogen oxidase (PPO) inhibitor fomesafen (5-[2-chloro-4-(trifluoromethyl) phenoxy]-N-(methylsulfonyl)-2-nitrobenzamide) is used as an herbicide to control weeds in soybean, potatoes and cotton cultures. A growing number of studies now highlights the effectiveness of tank-mixing fomesafen to prevent the emergence of glyphosate-resistant weeds such as the Palmer amaranth (Amaranthus palmeri; [1,2]) and the common waterhemp (Amaranthus rudis; [3]) which has motivated its use in agriculture. This increase in its usage combined to the resulting runoffs and leaching to aquatic systems, increase the risk of affecting non-target organisms, such as phytoplankton. Fomesafen toxicity to photosynthetic organisms results from the impairment of the chlorophyll biosynthesis pathway by inhibiting PPO [4]. This herbicide competes with protoporphyrinogen IX (PPGIX) for the active site of PPO resulting in an accumulation of free PPGIX. Subsequent leakage of PPGIX in the extraplastidic space results in its non-enzymatic oxidation into protoporphyrin IX (PPIX). Upon illumination, PPIX, formed outside the PPO complex, photoreacts and generates singlet oxygens, which lead to oxidative damages which can ultimately affect photosynthetic pigments and membrane integrity [4]. Although fomesafen was shown to affect growth and survivability of higher plants [5,6,7,8], very few studies focused on the precise underlying physiological effects such as oxidative stress generation and chlorophyll production or degradation. Moreover, some tested the impact of fomesafen on phytoplanktonic species [9,10,11], but these studies mostly discussed the influence of fomesafen on community structure, biomass and primary productivity while largely overlooking its impacts on physiological processes. At maximum annual application rates for commercial agriculture operations (0.31 lbs a.i per acre for snap beans, 0.375 lbs a.i per acre for soybeans and 0.5 lbs a.i. per acre for cotton), expected environmental concentrations of fomesafen in nearby surface water are predicted to be found in the range of 2–25 µg · L−1 [12]. In 2020, fomesafen was detected in 30% of surface water samples analyzed by the Minnesota Department of Agriculture with a maximum concentration of 2.17 µg · L−1 [13]. Very little toxicological information exists in the literature on the effect of fomesafen on green microalgae and cyanobacteria. In the green microalgae, R. subcapitata, biomass was the only physiological endpoint tested against the impact of fomesafen which revealed a NOAEC of 10 µg a.i. L−1 and EC50 of 92 μg a.i. L−1 (MRID46673804, [12]). In cyanobacteria (unknown species), a LC50 of 71 mg a.i. L−1 was determined on biomass (MRID46673807, [12]) and Yu et al. [14] reported that 20 mg L−1 fomesafen induced a 44% growth reduction for M. aeruginosa. Thus, there is an urgent need to further evaluate the toxicity of fomesafen on perhaps more sensitive physiological endpoints than growth in green algae and cyanobacterial model species.
Model species such as Raphidocelis subcapitata and Microcystis aeruginosa are commonly selected in toxicological studies as they possess a relatively high growth rate and typically show sensitivity to a wide range of contaminants. In this context, the present study aimed to investigate the impact of five concentrations (0, 5, 10, 40, 320 µg · L−1 fomesafen active ingredient (a.i.)) of a routinely used fomesafen-based herbicide (Reflex®) on the physiology (growth, photosynthesis, pigment content, oxidative stress) and morphology of two species of chlorophytes (Raphidocelis subcapitata and Chlamydomonas snowii) and one cyanobacteria (Microcystis aeruginosa). By using these species, we aimed to reveal if this herbicide can affect physiological endpoints other than biomass growth in freshwater photosynthetic microorganisms at expected environmental concentrations, as well as testing the effect of higher concentrations to better understand the mode of action of fomesafen on the physiology of freshwater phytoplankton. Finally, we intend to model the uptake of fomesafen in R. subcapitata to provide additional possible explanations behind the observed fomesafen-induced physiological consequences.
2. Results
2.1. Growth Rate and Photosynthesis
In comparison with the control, exposure of R. subcapitata to the fomesafen-based herbicide led to a significant decrease in growth of 15% (p < 0.0001) and 54% (p < 0.0001) for 40 and 320 µg · L−1, respectively. Cultures of C. snowii and M. aeruginosa were unaffected at any of the tested concentrations (Figure 1).
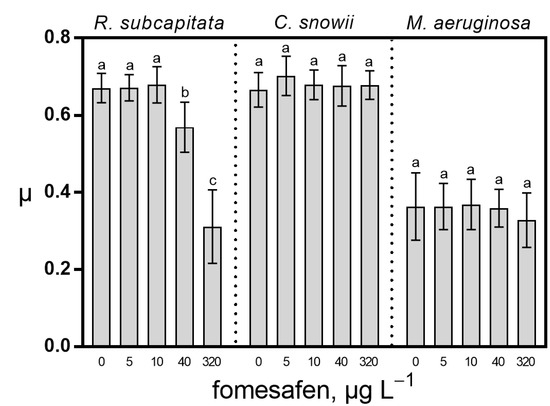
Figure 1.
Growth rate (µ) for R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.). Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tukey–Kramer HSD test.
Compared to the control, exposure of R. subcapitata to 320 µg · L−1 fomesafen-based herbicide led to a 12% decrease in the maximal PSII quantum yield (ϕM) (p < 0.01), while this herbicide had no effect on ϕM for C. snowii and M. aeruginosa (Figure 2A). For the same comparison, exposure of R. subcapitata to 10 and 320 µg · L−1 led to a 5% increase (p < 0.001) and a 21% decrease (p < 0.01) in operational PSII quantum yield (ϕ’M), respectively (Figure 2B). Compared to the control, exposure of C. snowii to 5, 10, 40 and 320 µg · L−1 led to a slight but significant increase in ϕ’M of 4% (p < 0.05) for all concentrations (Figure 2B). Similarly, exposure of M. aeruginosa to 320 µg · L−1 led to a 3% increase in ϕ’M (p < 0.01) in comparison to the control (Figure 2B).
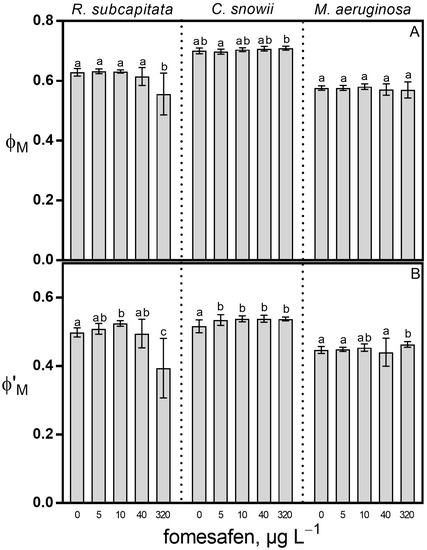
Figure 2.
(A) maximal (ϕM) and (B) operational (ϕ’M) PSII quantum yields of R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.). Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tukey–Kramer HSD test or the Kruskal–Wallis test on ranked means.
Among the studied species, R. subcapitata was shown to be the only one affected by the fomesafen-based herbicide when the PSII energy fluxes are considered (Figure 3). Concentrations of fomesafen of 10, 40 and 320 µg · L−1 yielded a significant increase of the effective antenna size per active reaction center (ABS/RC) of 10% (p < 0.05), 17% (p < 0.01) and 85% (p < 0.01) for 10, 40 and 320 µg · L−1, respectively (Figure 3A). Exposure to 10, 40 and 320 µg · L−1 fomesafen resulted in a respective 9% (p < 0.05), 10% (p < 0.01) and 40% (p < 0.05) rise in trapped energy flux (TR0/RC) compared to the control (Figure 3B). Concomitantly to these changes, exposure to 5, 10 and 40 µg · L−1 fomesafen led to a respective 13% (p < 0.05), 16% (p < 0.05) and 12% (p < 0.05) increase in electron transport flux per reaction center (ET0/RC) compared to the control (Figure 3C). In parallel, the effective dissipation of active RC (DI0/RC) more than doubled for R. subcapitata in comparison with the control following exposure to the highest fomesafen concentration (121%, p < 0.001) (Figure 3D).
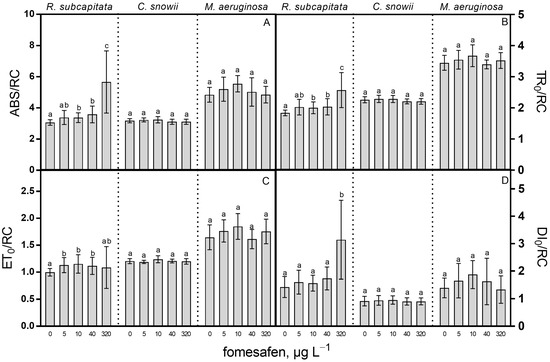
Figure 3.
(A) ABS/RC (effective antenna size per active reaction center (RC)), (B) TR0/RC (trapped energy flux per RC), (C) ET0/RC (electron transport flux per RC), and (D) DI0/RC (effective dissipation of an active RC) of R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.). Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tukey–Kramer HSD test or the Kruskal–Wallis test on ranked means.
The relative energy dissipation pathways of R. subcapitata, C. snowii and M. aeruginosa showed higher sensitivity to the presence of fomesafen compared to the maximal and operational PSII quantum yields (Figure 4). Relative to the control, the qPrel values of R. subcapitata M. aeruginosa were affected by the fomesafen treatment (Figure 4A). R. subcapitata exposed to 10 µg · L−1 produced a significant increase in qPrel (12%, p < 0.05) while treatment of R. subcapitata and M. aeruginosa with 320 µg · L−1 of fomesafen induced a respective decrease of 15% (p < 0.01) and increase of 6% (p < 0.01) in this parameter when compared to the control. The qNrel values of all three species were also affected by the herbicide treatment (Figure 4B). Compared to the control, exposure of R. subcapitata to fomesafen produced a significant decrease in qNrel at 10 µg · L−1 (67%, p < 0.001) and a significant increase at 320 µg · L−1 (70%, p < 0.05). In comparison with the control, exposure of C. snowii to 40 and 320 µg · L−1 caused a respective 45% (p < 0.05) and 50% (p < 0.05) increase in this parameter. For M. aeruginosa, qNrel was significantly decreased following exposure to 10 (11%, p < 0.05), 40 (16%, p < 0.001) and 320 µg · L−1 (16%, p < 0.001) in comparison with the control. Moreover, exposure of C. snowii and M. aeruginosa to the fomesafen-based herbicide significantly altered UQFrel (Figure 4C). In relation to the control, treatment of C. snowii with 40 and 320 µg · L−1 led to significant decrease in UQFrel of 27% (p < 0.05) and 30%. (p < 0.05), respectively, while exposure of M. aeruginosa to 40 µg · L−1 fomesafen led to a 45% (p < 0.01) increase in this parameter.
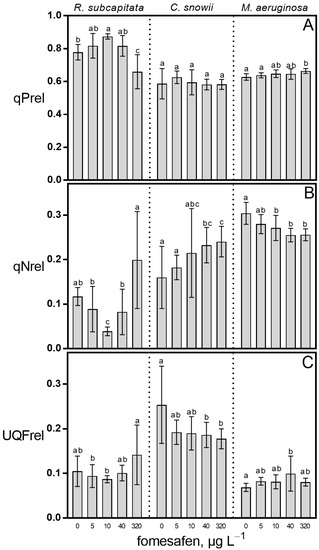
Figure 4.
(A) Relative photochemical quenching (qPrel), (B) relative non-photochemical quenching (qNrel) and (C) relative unquenched fluorescence (UQFrel) of R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.). Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tukey–Kramer HSD test or the Kruskal–Wallis test on ranked means.
Measurement of cyclic electron transport of R. subcapitata showed that electron transport around PSI upon illumination increased significantly following exposure to 10 µg · L−1 (110%, p < 0.01) and 40 µg · L−1 (247%, p < 0.05) fomesafen in comparison with the control (Table 1). Results for C. snowii and M. aeruginosa revealed no clear trend (data not shown).

Table 1.
Cyclic electron transport for R. subcapitata following 72 h exposure to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.). N.d. stands for not determined as the cell densities of the cultures were insufficient to obtain a signal at the highest fomesafen-based herbicide concentration. Means ± standard deviation of nine replicates. Means connected by the same letters are not significantly different by the Tukey–Kramer HSD test.
2.2. Pigment Content
As expected, due to the mode of action of the fomesafen, the Chl a content of the two microalgal cultures was significantly impacted (Figure 5A). In relation to the control, the Chl a content of R. subcapitata diminished when exposed to 40 µg · L−1 (18%, p < 0.05) and 320 µg · L−1 (27%, p < 0.001). For C. snowii, the concentration of Chl a also significantly decreased in relation to the control after exposure to 10 (15%, p < 0.01), 40 (11%, p < 0.05) and 320 µg · L−1 (18%, p < 0.001). In contrast, the Chl a content of M. aeruginosa was not affected by the fomesafen-based herbicide at tested concentrations. The Car content of the green microalgal species was also impacted by the herbicide (Figure 5B). In relation to the control, lower Car content was measured in R. subcapitata following exposure to 320 µg · L−1 (32%, p < 0.0001). C. snowii showed a decrease in Car content in comparison with the control following exposure to 10 (16%, p < 0.001), 40 (14%, p < 0.01) and 320 µg · L−1 (20%, p < 0.0001) fomesafen. Exposure of M. aeruginosa to the fomesafen-based herbicide had no impact on the Car content at every tested concentration.
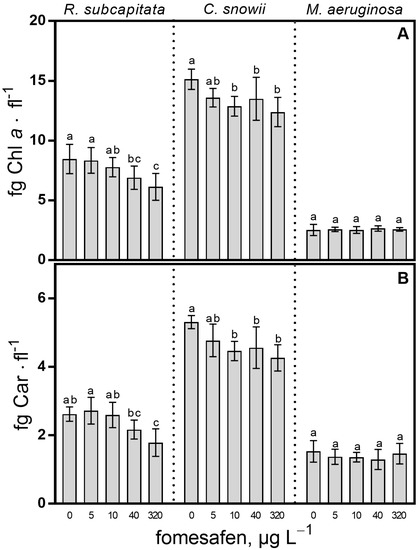
Figure 5.
(A) Chl a and (B) Car content per cell and normalized to biovolume for R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.). Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tukey–Kramer HSD test or the Kruskal–Wallis test on ranked means.
2.3. Oxidative Stress and Cell Complexity
To investigate the impact of fomesafen on intracellular reactive oxygen species (ROS) content we measured DCFH conversion to the fluorescent DCF (Figure 6A). Compared to the control, exposure to fomesafen caused a significant increase in ROS content for R. subcapitata at 320 µg · L−1 (178%, p < 0.0001). We also showed that the fomesafen formulation had no effect on cellular ROS content for C. snowii and M. aeruginosa. The relationship between exposure to fomesafen and ROS-induced change in intracellular complexity (interpreted as a change in the mean SSC parameter) was also investigated (Figure 6B). In relation to the control, cellular complexity of R. subcapitata was found to be affected by the herbicide treatment as shown through a significant increase of SSC following exposure to 320 µg · L−1 (33%, p < 0.001). The fomesafen treatment did not affect mean SSC of C. snowii and M. aeruginosa.
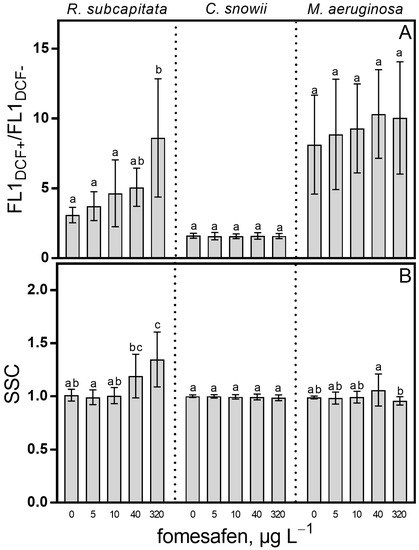
Figure 6.
(A) Intracellular ROS content (FL1DCF+/FL1DCF-) and (B) cell complexity (SSC) of R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen (0, 5, 10, 40 and 320 µg · L−1). ROS content was measured as mean FL1 fluorescence of DCF positive cells divided by background mean FL1 fluorescence of fresh control culture. Cell complexity is represented by the mean side scatter parameter (SSC). Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tuker-Kramer HSD test or the Kruskal–Wallis test on ranked means.
2.4. Cell Biovolume
Cells of R. subcapitata showed a significant increase in biovolume following exposure to 40 µg · L−1 (31%, p < 0.001) and 320 µg · L−1 (51%, p < 0.001) fomesafen in comparison with the control. The fomesafen treatment had no effect on the biovolume of C. snowii and M. aeruginosa (Figure 7).
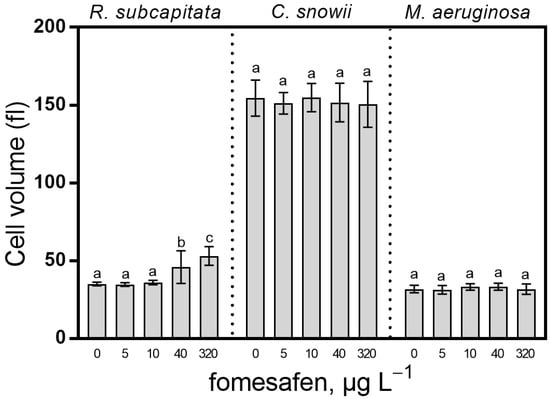
Figure 7.
Cell volume of R. subcapitata, C. snowii and M. aeruginosa after 72 h exposure to five concentrations of fomesafen a.i. (0, 5, 10, 40 and 320 µg · L−1). Cell biovolume is expressed as mean femtoliter ± SD; n = 9. Bars indicate the means ± standard deviation of nine replicates. Means followed by the same letter are not significantly different by the Tukey–Kramer HSD test or the Kruskal–Wallis test on ranked means.
2.5. Modeling of Fomesafen Uptake
Considering that R. subcapitata was the only species which exhibited an effect on growth and biovolume following the fomesafen treatment, this species was selected to model the intracellular concentration of fomesafen over time. Figure 8 shows the modeled cellular fomesafen concentration in R. subcapitata as a function of time assuming no active fomesafen efflux, Equation (6)). For all the fomesafen concentrations (5, 10, 40 and 320 µg · L−1), a steady-state is reached or approached quickly, i.e., after around 1 min. Modeling with a low initial measured cell radius (solid lines) or a high final measured cell radius (dash lines) show that increasing cell radius and volume decreases transitorily by at most 20% the amount of fomesafen taken up by the cell.
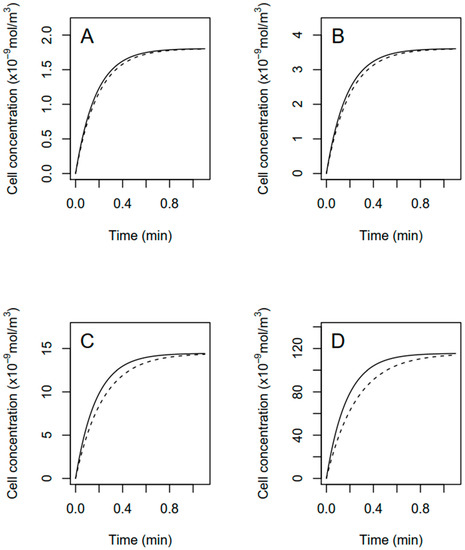
Figure 8.
Modeled cellular concentration of fomesafen in R. subcapitata exposed to 5, 10, 40 and 320 μg · L−1 (panel (A–D)) total fomesafen until approaching steady-state. Computations assume that all fomesafen taken up is tightly bound in the cell, i.e., negligible active fomesafen efflux from the cell. Solid lines assumed a low constant cell biovolume equal to the mean measured initial cell biovolume. Dashed lines assume a high constant mean cell biovolume measured after 72 h of exposure.
Figure 9 shows the same modeling exercise than in Figure 8 although a ke of the same order of magnitude of the rate constant of fomesafen uptake (Ar × Pbl) has been chosen. In this case, fomesafen is considered to be excreted or detoxified from the cell. The trend in the curves of Figure 8 and Figure 9 are similar over time, but the steady-state fomesafen cellular concentration can be significantly decreased due to inclusion of active fomesafen efflux or metabolism.
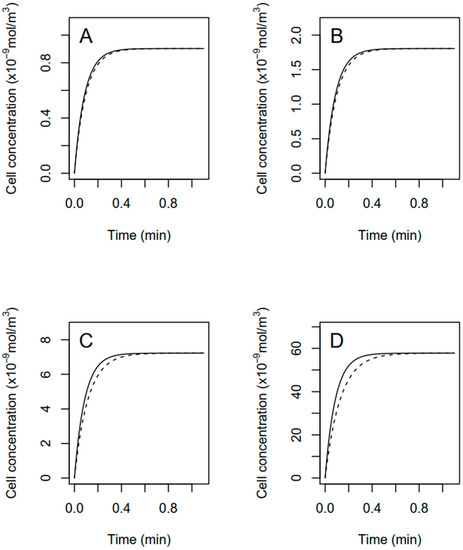
Figure 9.
Modeled cellular concentration of fomesafen in R. subcapitata exposed to 5, 10, 40 and 320 μg · L−1 (panel (A–D)) total fomesafen until approaching steady-state. Computations assume that fomesafen can be actively excreted or metabolized from the cell with an assumed high-rate constant for fomesafen loss on the order of the modeled uptake rate constant. Solid lines assumed a low constant cell biovolume equals to the mean measured initial cell biovolume. Dashed lines assume a high constant mean cell biovolume measured after 72 h of exposure.
3. Discussion
Our results showed that the lowest studied concentrations of fomesafen (5 and 10 µg · L−1) generally had low to no impact on the physiological parameters we investigated. Exposure to these concentrations had no influence on growth, ϕM, UQFrel, DI0/RC, ROS content, SSC and cell biovolume for any of the three species studied. In contrast, the two highest concentrations studied (40 and 320 µg · L−1) elicited obvious responses with clear trends for the most of the parameters evaluated, most notably for green microalgae.
3.1. Fomesafen-Based Herbicide Toxicity to Phytoplankton Physiology
Exposure to high fomesafen concentrations relative to expected environmental concentrations was performed to better understand the mechanism of action of a fomesafen-based herbicide and its physiological consequences on two green microalgae and one cyanobacteria. Results presented here showed that the physiological impacts of the two higher concentrations of fomesafen selected for this study (40 and 320 µg · L−1) differed greatly between the tested phytoplankton species.
Exposure to the fomesafen-based herbicide significantly impaired the growth of R. subcapitata, while C. snowii and M. aeruginosa remained largely unaffected (Figure 1). These results are in accordance with USEPA literature which indicates that the biomass-NOAEC for R. subcapitata is 10 µg · L−1 fomesafen (MRID46673804, [12]) and that cyanobacteria is naturally resistant to very high concentrations of fomesafen (MRID46673807, [12]). Here, more insight on how a fomesafen-based herbicide may impact or not the growth of phytoplankton was obtained through analysis of photosynthetic efficiency and related physiological processes.
Inhibition of growth is most likely to be related to the known impacts of PPO-inhibitors on chlorophyll production [10,15]. As observed, exposure of R. subcapitata and C. snowii to the fomesafen-based herbicide induced a significant decrease in Chl a and Car contents. Since these pigments are essential constituents of photosystem antennas and reaction centers, any decrease in their concentrations may result in an impact on the photosynthetic efficiency. Another known consequence of the exposure to fomesafen is the liberation of PPGIX from the PPO complex which leads to ROS production [15]. As expected, our results demonstrate that exposure to high concentrations of fomesafen-based herbicide enabled strong intracellular generation of ROS for R. subcapitata. Typically, this result can be observed if ROS production overpasses the oxidative stress defense mechanisms usually triggered under stress conditions [16,17,18]. In these conditions, the already synthesized chlorophylls, proteins and lipids can suffer oxidative damages leading to destruction of the reaction centers, disruption of the photosynthetic (and ultimately cell) membrane integrity. This phenomenon is typically followed by a decrease in photosynthetic activity and, eventually, the phytoplankton death [4]. The presence of higher concentrations of antioxidant molecules such as carotenoids for C. snowii may explain (without excluding other antioxidant defence mechanisms) the unchanged level of ROS and cell complexity following exposure to the fomesafen-based herbicide in comparison to R. subcapitata. The lack of increase in ROS content for M. aeruginosa following the fomesafen treatment can alternatively mean that, for this species, ROS content is not affected by fomesafen or that fomesafen-induced ROS production does not surpass the physiological threshold, thereby avoiding oxidative damages. The rise in the relative cell complexity measured for R. subcapitata exposed to high concentrations of fomesafen suggests oxidative degradation of intracellular components. Similar results of higher complexity and degradation of intracellular components (interpreted from higher cell complexity) in presence of ROS was observed in Tetraselmis suecica, another microalgae, exposed to 5 µg · L−1 diuron [19].
The observed decrease in the maximal and operational PSII quantum yields (ϕM and ϕ’M) following exposure of R. subcapitata to the fomesafen-based formulation may be explained by the concomitant decrease in pigment concentrations and the increase in ROS content. The lower photochemical quantum yields recorded following the fomesafen treatment may be due to a decrease in light capture efficiency by open PSII RCs. This is further evidenced by an increase in ABS/RC which may result from a higher number of inactivated reaction centers, a decrease in pigment content, a lower amount of active PSII RC or a combination of these three possibilities. Similarly, the lower TR0/RC and DI0/RC observed in our exposure conditions could also have originated from a lower amount of active reaction centers [20]. These observed changes in energy fluxes may be explained, respectively by the observed lower Chl a and Car contents. For R. subcapitata, electron transport in active RC (ET0/RC) remained unchanged for all tested concentrations. A stable ET0/RC can be expected after a decrease in pigment content if it results in a proportional decrease in electron transfer and available open reaction centers. Such conditions would preserve the ratio between outflux of electrons from reduced quinone A (QA−) toward the plastoquinone (PQ) pool and the actual number of active PSII.
The relative quenching coefficients can effectively reveal the proportion in which each quenching mechanisms are being actively solicited by photosynthetic organisms in a stressful situation [21,22]. Perturbations of the energy distribution pathways following exposure of R. subcapitata to the fomesafen-based herbicide is demonstrated by the lower relative photochemical quenching (qPrel) and the increase of the relative non-photochemical quenching (qNrel) and unquenched fluorescence (UQFrel). As we observed with the operational PSII quantum yield (ϕ’M), qPrel was only affected when treated at the higher concentrations of the fomesafen-based herbicide. Furthermore, the higher qNrel for R. subcapitata in presence of fomesafen can be attributed to the phytoplankton ubiquitous response to physiological stressors [17,18]. Indeed, under these conditions, phytoplankton will dissipate excess light energy through non-photochemical quenching mechanisms related to the xanthophyll cycle, state transition and photoinhibition [23,24]. Higher UQFrel values following herbicide exposure indicate the inability of the PSI to drain electrons efficiently from PSII [22]. Overall, the fomesafen-induced changes in photochemical yields, PSII energy fluxes and energy dissipation processes may be attributed to structural modification at the PSII antenna level.
In freshwater phytoplankton, the roles of cyclic photophosphorylation are not yet fully understood but enhancement of this process is often observed in response to a physiological stress such as the presence of herbicide which limits linear photosynthetic electron flow [25,26]. It is suggested that to maintain optimal ATP-to-NADPH stoichiometry when electron flow between PSII and PSI is hampered, photosynthetic organisms may increase the proportion of cyclic electron flow around PSI [27,28]. This mechanism is also thought to prevent consequences of the over excitation of the PSII by assisting in the generation of a transthylakoidal proton gradient necessary to activate thermal energy dissipation, a key non-photochemical quenching mechanism [17,29] and by increasing ATP production to repair photodamages on PSII [30,31]. It appears that R. subcapitata enhanced cyclic electron transport around PSI (Table 1) and qNrel (Figure 4B) in an attempt to counteract the lower ϕM (Figure 2A), ϕ’M (Figure 2B) and qPrel (Figure 4A) after being exposed to increasing concentrations of fomesafen-based herbicide.
Exposure to the fomesafen-based herbicide significantly increased the cell volume for R. subcapitata. The biovolume of many phytoplanktonic species, including R. subcapitata, is known to increase in the presence of pesticides such as paraquat [32] and chlorpyrifos [33]. In contrast, a decrease in biovolume have been observed with diuron [19] and atrazine [34,35]. Therefore, current literature points toward a complex interaction between toxicants and a change in cell biovolume and the function of such phenomenon remains unclear and species-specific. The increased median biovolume of R. subcapitata cells following exposure to the fomesafen-based herbicide (Figure 7) lead to a lower surface/volume ratio (obtained with larger cells), which might decrease the relative contact of the intracellular machinery with the contaminant depending on intracellular changes in cell morphology and fomesafen intracellular distribution. Hence, since cell biovolume of C. snowii is larger than that of R. subcapitata, one may hypothesize that this is a factor explaining the higher resistance of C. snowii than R. subcapitata as postulated by Kent and Currie [36], who established that cell biovolume plays a significant role in the interaction between various phytoplankton species and lipophilic pesticides which subsequently affect microorganism sensitivity. However, modeling of fomesafen uptake in R. subcapitata (with a cell biovolume around 3 times lower than that of C. snowii based on Figure 7 in the next section rather suggests that this effect is limited in steady-state.
Caquet et al. [10] demonstrated that chlorophytes and cyanobacteria react differently to fomesafen (40 µg · L−1) where the growth of the chlorophytes was affected while the cyanobacterial cells (smaller cells compared to the chlorophytes) continued to grow upon exposure. Moreover, Yu et al. [14] reported that an exposure for three days to very high concentration of fomesafen (20 mg L−1) was needed to induce 44% inhibition in the growth of M. aeruginosa (FACHB-905). It was also reported that there is a wide variation in fomesafen toxicity between green microalgae (EC50—growth of 92 µg · L−1, MRID 46673804) and cyanobacteria (LC50—growth of 71 mg L−1, MRID 46673807) [12]. Although fomesafen targets PPO which is an essential enzyme for photopigment biosynthesis in both green microalgae and cyanobacteria, Kato et al. [37] suggested that a unique and unidentified bacterial gene encoding PPO in cyanobacteria may confer a natural resistance to PPO-inhibiting herbicides.
3.2. Modeling of Fomesafen Uptake in R. subcapitata
Modeling of fomesafen uptake by R. subcapitata indicates that an increase in cell volume only postpone by a few seconds the time needed to reach a steady-state in fomesafen uptake through small modulation of cell permeability. This indicates that modification of biovolume is unlikely to be an efficient protection mechanism against fomesafen in this species, at least at constant external fomesafen concentrations (i.e., non-transitory conditions) where steady-state is rapidly achieved. Instead, detoxification of fomesafen might occur via rapid (active) excretion or metabolism, but the kinetics of breakdown or efflux will have to be fast to significantly decrease the steady-state cellular fomesafen concentration, i.e., with rate constants of fomesafen loss (Ar × Pbl = m2 · m−3 × m · h−1 = h−1) comparable to rate constants of uptake (312–345 h−1), i.e., a turnover rate of complete cellular fomesafen detoxification in the order of a few seconds would be needed to decrease fomesafen uptake.
The modeling scenarios in view of potential detoxification mechanisms are interesting when compared to measured toxicity data in R. subcapitata. Indeed, the proportionately higher toxicity measured at 72 h (on growth rate and photosynthesis) for an increase in fomesafen concentrations between the 40 μg · L−1 and 320 μg · L−1 treatment in comparison with the increase between the 10 μg · L−1 and 40 μg · L−1 treatment could be due, in part, to an higher potential detoxification at lower fomesafen concentration since excreting or metabolizing rapidly would indeed be less energy costly (and be more plausible) at a lower cellular fomesafen concentration than at a higher cellular concentration.
Note however, that our model assumes a constant pH throughout the exposure, whereas significant rise in pH can occur over time in algal batch cultures of R. subcapitata due to photosynthesis. Indeed, a mean rise in pH by 0.2 units in control cultures of R. subcapitata occurred after 3 days of growth in our experiments. This significant rise in pH over time can decrease the proportion of protonated neutral fomesafen species and decrease fomesafen uptake. This effect should be less important at 320 μg · L−1 fomesafen rather than at the three other concentrations because of lower algal growth and photosynthesis. Hence, this would further strengthen fomesafen uptake and potential toxicity at 320 μg · L−1 total fomesafen in the culture compared to that at 40 μg · L−1 total fomesafen in the medium.
From these observations, our study gives new insight into the presence and quantitative importance of potential cellular mechanisms explaining the presence of positive feedback of a pesticide on growth and PSII inhibition. Although most physiological consequences presented here resulted from exposure to high pesticide concentrations unlikely to be found in waterbodies, the observed effects could be detected where much higher pesticide concentrations are expected such as in agricultural drainage ditches. In sum, this study shows that exposure to the pesticide Reflex®, a fomesafen-based herbicide, can induce differential physiological responses amongst non-target photosynthetic microorganisms. Such a contrasting effect across species highlights the need to investigate an array of phytoplanktonic species and physiological endpoints to confidently evaluate the toxicity of fomesafen toward photosynthetic microorganisms.
4. Material and Methods
4.1. Phytoplanktonic Cultures and Growth Conditions
Prior to this experiment, axenic cultures of Raphidocelis subcapitata (FACHB-271), Chlamydomonas snowii (taken from a culture collection of species isolated in our laboratory from the Choinière reservoir in Quebec, Canada [38]) and Microcystis aeruginosa (CPCC 632) were regularly transferred (every 3 to 5 days) to maintain exponential growth. Cultures were transferred in 100 mL of fresh Bold’s Basal Medium at pH of 6.8 prepared according to Stein [39]. Cultures were adapted for at least three weeks in a growth chamber at 24 °C with a 14/10 h light-dark cycle at 100 µmol photons m−2s−1 supplied by white fluorescent lamps (Philips F72T8/TL841/HO, New York, NY, USA) and incandescent bulbs (Philips 60 W, New York, NY, USA). To account for total pigment and enzymatic content differences between species, the number of cells of C. snowii and M. aeruginosa needed for physiological analysis was normalized by the mean biovolume of R. subcapitata.
4.2. Herbicide Solutions and Fomesafen Exposure
Stock solution of the herbicide formulation (22.8% sodium salt of fomesafen, i.e., 240 g fomesafen a.i. per liter, Reflex®, Syngenta, Greensboro, NC, USA) (thereafter called fomesafen-based herbicide) was prepared in nanopure water. Cultures of each species were submitted for 72 h to five concentrations of fomesafen-based herbicide (Reflex®; 0, 5, 10, 40 and 320 µg · L−1 fomesafen a.i.) in nine replicates before sampling for analysis. Exposures to the fomesafen-based herbicide were performed in the same growth conditions as previously described.
4.3. Growth and Cell Biovolume Assessments
Cell density and mean cell biovolume were obtained using a particle analyzer (Multisizer 3, Beckman Coulter Inc., Fullerton, CA, USA). From the plot of ln (cell · ml−1) in relation to time (days), the average growth rate (µ, days−1) was calculated using µ = ln·(Dt/D0)/t; D = cell ml−1 at time (t); D0 = cell ml−1 when the exposure period started [40]. The phytoplankton mean cell volume was expressed in femtoliter (fl).
4.4. Photosystem II Energy Flux Analysis
Prior to the analysis, each culture was sampled and dark-acclimated for 15 min to allow complete oxidation of PSII reaction centers. Then, measurement of the fast polyphasic chlorophyll fluorescence kinetic was performed using a Plant Efficiency Analyzer fluorometer with the liquid compartment (PEA, Hansatech Ltd., King’s Lynn, Norfolk, UK). The parameters ABS/RC, TR0/RC, ET0/RC and DI0/RC resulting from the analysis of PSII energy fluxes were calculated according to Force et al. [20].
4.5. Photosynthetic Electron Transport and Fluorescence Quenching Analysis
Efficiency of PSII reaction center was measured according to Schreiber et al. [41] by using a Water-PAM fluorometer (Heinz Walz, GmbH, Effeltrich, Germany). Each sample was dark acclimated (15 min), and then the minimum (F0) and maximum (FM) fluorescent levels were determined under modulating light (2 µmol m−2 s−1) and saturating light (700 ms, 3000 µmol m−2s−1), respectively. A combination of a continuous actinic light (125 µmol m−2 s−1) and saturating pulses (700 ms, 3000 µmol m−2 s−1, every 60 s) was used to obtain the steady state (FS) and the maximum fluorescence (F’M) levels for light acclimated samples. After obtaining FS and F’M, the actinic light was then turned off to measure the minimal fluorescence level a light-acclimated sample (F’0). Chlorophyll a fluorescence variables were obtained according to equations found in Table 2.

Table 2.
List of Chl a fluorescence variables with their respective formula.
4.6. Photosystem I Cyclic Electron Flow Measurement
We estimated the proportion of cyclic electron flow around PSI during photosynthesis following an adapted procedure from Joliot and Joliot [44]. Cyclic electron flow around PSI was measured using a Joliot Type Spectrophotometer (JTS-10, Spectrologix, Knoxville, TN, USA). Prior to the analysis, cultures were dark-acclimated for 15 min. First, an actinic far-red light-emitting-diode (LED) at 720 nm excited the sample for 5 s through a 705 nm interference filter. During this time, a low-energy array of detection LED at 705–740 nm periodically radiated probing flashes through the culture sample from which the change in absorbance is recorded by a measurement photodiode. Cut-off filters were placed in front of the measurement and a reference photodiode to ensure that only recordings of wavelengths over 695 nm were taken and to filter out the actinic light. Thus, the change in absorbance of the sample at 700 nm was recorded and interpreted as the change in rates of oxidation and reduction of P700. The main data extracted from this analysis was the half-time at which oxidized P700 is completely re-reduced. The half-time of P700+ re-reduction was extracted using the JTS-10 operating software. This procedure allowed to estimate the proportion of cyclic electron flow around PSI in a state of photosynthesis during which cyclic and linear electron flow both operate at a significant rate [31]. This procedure was then repeated a second time on the same sample but following a step of actinic light illumination for 3 min at 630 nm. This light-acclimation step leads to the activation of the Benson-Calvin cycle during which the linear electron flow is largely predominant over cyclic electron transport [31]. The electron turnover rates of PSI were calculated using the formula: K (turnover of PSI in electrons per second) = 0.693/half-time of P700+ re-reduction in seconds [45]. Using K determined from the half-time of P700+ re-reduction extracted from light acclimated and dark-acclimated-sample measurements, we could estimate the relative fraction of PSI participating in linear and cyclic electron flow during photosynthesis following exposure to fomesafen. The fraction of cyclic electron flow around PSI is then expressed as percentage compared to the control.
4.7. Pigment Content Analysis
Following the 72 h exposure to fomesafen-based herbicide, samples were collected under dim green light on 0.2 µm polyvinylidene fluoride filters (Xingya Puryfying Materials factory, Shanghai, China) then quickly frozen in liquid nitrogen and kept at −80 °C until extraction of the pigments. Pigments were extracted in ethanol 95% at 78 °C for 5 min. Samples were then stored 24 h at −20 °C to complete the extraction. Absorbance spectra (400–700 nm) of the pigment extracts was measured with a Cary 300 ultraviolet-visible (UV-Vis) spectrophotometer (Varian Australia Pty Ltd., Mulgrave, VIC, Australia). Pigment contents were calculated according to formulas found in Lichtenthaler [46]. Results are expressed as femtograms (fg) of pigment per cell per biovolume unit (fl).
4.8. Reactive Oxygen Species Content and Cell Complexity Determination
The impact of fomesafen on intracellular ROS concentration was revealed following Stachowski-Haberkorn et al. [19] using a cell-permeable non-selective optical probe, 2′,7′-dichlorodihydrofluorescein diacetate (H2DCF-DA, Sigma-Aldrich, St. Louis, MO, USA) and flow cytometry (BD Accuri™ C6 Plus, BD Biosciences, Becton-Dickinson, Franklin Lakes, NJ, USA). H2DCF-DA permeates in the cells where it is converted by esterases to the non-permeable 2′,7′-dichlorodihydrofluorescein (H2DCF) which is further converted into 2′,7′-dichlorofluorescein (DCF) following contact with ROS. DCF emits green fluorescence which can be measured by flow cytometry through the FL1 channel (FL1, 533/30 nm). H2DCF-DA was added to aliquots of fresh cultures to obtain a final concentration of 80 μM (0.8% DMSO) and incubated in the dark at room temperature for 30 min prior to the analysis. Data obtained from this analysis were presented as FL1 value of H2DCF-DA stained cells divided by the background FL1 fluorescence of fresh cells. The side scatter parameter (SSC) was also analyzed to measure the effect of fomesafen on intracellular complexity. Cell complexity results were expressed as SSC ratio (SSCfomesafen-treated cells/SSCcontrol).
4.9. Modeling Fomesafen Uptake in Phytoplankton
Fomesafen exists in two chemical species, one acid species with no net electrical charges and one anionic species (Figure 10). At a pH relevant of a culture medium (around 7), only a small proportion of fomesafen will be neutral. Even though at pH higher than pKa (3.0; [47]), the anionic form predominates over the neutral form, the neutral form is expected to be taken up passively through lipid bilayers and hence probably rapidly as expected for neutral hydrophilic or hydrophobic compounds [48,49,50]. Here, we assume that the neutral species is the only form taken up by the cell since, to our knowledge, no known transporters have been proved to transport fomesafen in green algae or cyanobacteria.
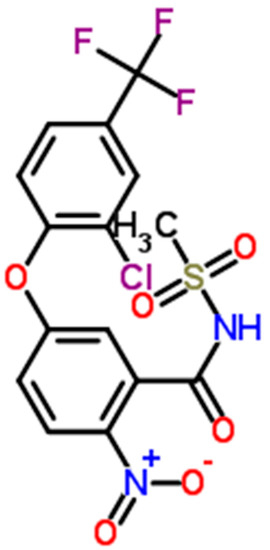
Figure 10.
Chemical structure of fomesafen. This molecule has partial charges on the NO2 group, but is mostly neutral (i.e., with no net electrical charges) at pH < pKa. The N-acyl sulfonamide functional group is ionisable with a pKa = 3.0 [47].
To model fomesafen uptake, the permeability of fomesafen (Pm) through the algal outer cell membrane was first computed using the empirical equation of Walter and Gutknecht [51] describing lipid bilayer permeability of non-electrolytes.
where Kow is the measured octanol-water partition coefficient of fomesafen [52]. This Pm in cm · s−1 is converted to units of m · h−1.
Second, the diffusion coefficient of fomesafen (D) was computed using the empirical equation of Hayduk and Laudie [53].
where cP is the viscosity of water at 25 °C (centipoise) and Vm is the molar volume of fomesafen (cm3 · mol−1). The D (in cm2 · s−1) is then converted in m2 · h−1.
Third, the permeability of the unstirred boundary layer (Pbl) surrounding the cell was estimated using:
where L is the length of the boundary layer surrounding the cell (in m), which is assumed to be equal to the equivalent cell radius [50,54].
Pbl = D/L
Note that calculated Pm is more than 200 times higher than the calculated Pbl in all model cases below. Therefore, the limiting step for fomesafen uptake is the diffusion in the external boundary layer and we will thus consider here Pbl as an estimate of fomesafen permeability in the boundary layer.
Fourth, the rate of change in the cellular fomesafen concentration (mol · m−3 · h−1) can be expressed with the following two differential equations assuming no active fomesafen efflux from the cells (i.e., all fomesafen taken up is tightly bound inside the cell) (Equation (4)) or assuming that all fomesafen taken up can actively diffuse back in the culture medium (Equation (5)):
where cellfo is the cellular fomesafen concentration (mol · m−3), foprot is the concentration of protonated fomesafen in solution (mol · m−3) at a given pH obtained with the Anderson-Hasselbach equation, f is the initial fraction of algal cell volume relative to the volume of the culture medium (0.0035 m3 of algae/m3 of medium), Ar is the algal cell surface: volume ratio (m2 · m−3), μ is the algal growth rate (h−1) and ke is the active efflux or detoxification rate constants (h−1). Note that on the right hand side of Equation (4), the first term represents the uptake rate of the neutral fomesafen species for a given fomesafen concentration in the medium and the second term () takes into account growth biodilution on the cellular fomesafen concentrations. The right hand side of Equation (5) also includes a third term () expressing fomesafen efflux rate or detoxification rate from the cell. Note that potential depletion over time in the fomesafen concentration in the medium is considered through the term ().
Since calculated depletion of fomesafen in the culture medium was always smaller than 5% and since fomesafen loss due to biodilution was negligible compared to fast fomesafen uptake rate, Equations (4) and (5) reduced to:
For the calculations of foprot, the model assumes that the pH in the culture medium remains the same throughout the exposure for simplicity (but see the discussion section below for further details). Additionally, we assume negligible pH gradients in the algal boundary layer (i.e., no significant effect of the boundary layer on fomesafen speciation and uptake) as expected for small green algae with carbon concentrating mechanisms. Indeed, the external carbonic anhydrase of another green algae (C. reinhardtii) has been shown to be present in great excess to that necessary for optimal CO2 uptake rate for air-equilibrated cells [55], suggesting that green algal cells can effectively maintain the equilibrium between HCO3− and CO2 at the cell surface.
In brief, the general modeling procedure we used in the present study involved calculating the membrane and boundary layer permeability using the mean measured initial or final cell radius for each fomesafen concentrations and then, solving the differential equations (Equations (6) and (7)) incorporating the mean measured specific growth rate for each fomesafen concentrations as well as the cellular permeability computed for the initial or final cell radius with or without active efflux.
The simulations of fomesafen uptake were run and associated figures were plotted using the R software version 3.6.0 [56]. The differential equations (Equations (6) or (7)) were solved using the R package deSolve [57] considering 10,000-time steps of 0.36 s until approaching steady-state (1 min). The mean code running time is 5.4 ± (SD) 0.3 s (n = 20) on a 3.1 GHz Intel Core i5 MacBook pro. All scripts and functions are freely available on GitHub (https://github.com/michellavoie4/Fomesafen_Model, accessed on 27 November 2022).
4.10. Statistical Analysis
Data for the physiological analysis were expressed as mean ± standard deviation (n = 9), statistical analysis were performed using JMP (JMP®, version 13.2.0, SAS Institute Inc., Cary, NC, USA) and the figures were constructed using GraphPad Prism 7.0 (GraphPad, San Diego, CA, USA). The Shapiro–Wilk test and Brown-Forsythe test were employed to reveal if data sets followed a normal distribution and were of equal variance, respectively. Datasets that did not respect those conditions were transformed in ranks. Significant differences of the mean or ranked mean of treated cultures were compared to their respective control by a one-way ANOVA followed by post hoc Tukey–Kramer HSD multiple comparison test or using the Kruskal–Wallis test for ranked data.
Author Contributions
Conceptualization, J.N., M.L. and P.J.; methodology, J.N., M.L. and P.J.; validation, J.N., M.L., M.P.G. and P.J.; formal analysis, J.N. and M.L.; investigation, J.N. and M.L.; writing―original draft preparation, J.N. and M.L.; writing―review and editing, J.N., M.L., M.P.G. and P.J.; visualization, J.N. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
The financial means to complete this study was provided by the Natural Sciences and Engineering Research Council of Canada (NSERC) obtained by Philippe Juneau. Also, this research was supported by the Canada First Research Excellence Fund-Sentinel North program of Université Laval (Excellence postdoctoral fellowship to Michel Lavoie) and by the National Sciences and Engineering Research Council of Canada-NSERC (postdoctoral fellowship to Michel Lavoie). Marcelo Pedrosa Gomes received research productivity grants from the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, Brazil).
Data Availability Statement
The data supporting the findings of this paper are available on request from the corresponding author.
Acknowledgments
The authors would like to thank Marie-Claude Perron, Kui Xu, Guo-Zheng Dai, Juan Du, Disney Izquierdo, Catherine Ayotte and Jean-François Paquin for their advice, helpful discussions and help on technicalities throughout this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bond, J.A.; Oliver, L.R.; Stephenson, D.O. Response of Palmer Amaranth (Amaranthus palmeri) Accessions to Glyphosate, Fomesafen, and Pyrithiobac. Weed Technol. 2006, 20, 885–892. [Google Scholar] [CrossRef]
- Chahal, P.S.; Varanasi, V.K.; Jugulam, M.; Jhala, A.J. Glyphosate-Resistant Palmer Amaranth (Amaranthus palmeri) in Nebraska: Confirmation, EPSPS Gene Amplification, and Response to POST Corn and Soybean Herbicides. Weed Technol. 2017, 31, 80–93. [Google Scholar] [CrossRef]
- Sarangi, D.; Sandell, L.D.; Kruger, G.R.; Knezevic, S.Z.; Irmak, S.; Jhala, A.J. Comparison of Herbicide Programs for Season-Long Control of Glyphosate-Resistant Common Waterhemp (Amaranthus rudis) in Soybean. Weed Technol. 2017, 31, 53–66. [Google Scholar] [CrossRef]
- Matringe, M.; Camadro, J.M.; Labbe, P.; Scalla, R. Protoporphyrinogen oxidase as a molecular target for diphenyl ether herbicides. Biochem. J. 1989, 260, 231–235. [Google Scholar] [CrossRef] [PubMed]
- Bridges, D.; Stephenson, M. Weed Control and Tobacco (Nicotiana tabacum) Tolerance with Fomesafen. Weed Technol. 1991, 5, 868–872. [Google Scholar] [CrossRef]
- Kleifeld, Y.; Blumenfeld, T.; Herzlinger, G.; Graph, S.; Buxbaum, H.; Bargutti, A. The use of fomesafen for pre-emergence weed control in cotton. Phytoparasitica 1988, 16, 133–144. [Google Scholar] [CrossRef]
- Kurtz, M.E. Kenaf tolerance to acifluorfen, cyanazine, diuron, fluometuron, fomesafen, lactofen, or prometryn applied postemergence-directed. Ind. Crops Prod. 1996, 5, 119–124. [Google Scholar] [CrossRef]
- Soltani, N.; Shropshire, C.; Sikkema, P.H. Effects of post-emergence application of bentazon and fomesafen on eight market classes of dry beans (Phaseolus vulgaris L.). Crop Prot. 2006, 25, 826–830. [Google Scholar] [CrossRef]
- Caquet, T. Use of carbon and nitrogen stable isotope ratios to assess the effects of environmental contaminants on aquatic food webs. Environ. Pollut. 2006, 141, 54–59. [Google Scholar] [CrossRef]
- Caquet, T.; Deydier-Stephan, L.; Lacroix, G.; Le Rouzic, B.; Lescher-Moutoué, F. Effects of fomesafen, alone and in combination with an adjuvant, on plankton communities in freshwater outdoor pond mesocosms. Environ. Toxicol. Chem. 2005, 24, 1116–1124. [Google Scholar] [CrossRef]
- Perschbacher, P.W.; Stone, N.; Ludwig, G.M.; Guy, C.B., Jr. Evaluation of effects of common aerially-applied soybean herbicides and propanil on the plankton communities of aquaculture ponds. Aquaculture 1997, 157, 117–122. [Google Scholar] [CrossRef]
- USEPA. Environmental fate, ecological risk and endangered species assessment in support of the registration review of fomesafen sodium (PC123802). In Environmental Fate and Effects Division Environmental Risk Branch I; United States Environmental Protection Agency: Washington, DC, USA, 2008. [Google Scholar]
- Minnesota Department of Agriculture (MDA). Water Quality Monitoring Report; MDA: St. Paul, MN, USA, 2020. Available online: https://www.mda.state.mn.us/pesticide-fertilizer/water-monitoring-reports-and-resources (accessed on 15 March 2022).
- Yu, X.B.; Hao, K.; Ling, F.; Wang, G.X. Aquatic environmental safety assessment and inhibition mechanism of chemicals for targeting Microcystis aeruginosa. Ecotoxicology 2014, 23, 1638–1647. [Google Scholar] [CrossRef] [PubMed]
- Boger, P.; Wakabayashi, K. Peroxidizing Herbicides (I): Mechanism of Action. Z. Nat.-Sect. C J. Biosci. 1995, 50, 159–166. [Google Scholar] [CrossRef][Green Version]
- Ledford, H.K.; Niyogi, K.K. Singlet oxygen and photo-oxidative stress management in plants and algae. Plant Cell Environ. 2005, 28, 1037–1045. [Google Scholar] [CrossRef]
- Niyogi, K.K. Photoprotection revisited: Genetic and molecular approaches. Annu. Rev. Plant Biol. 1999, 50, 333–359. [Google Scholar] [CrossRef]
- Niyogi, K.K. Safety valves for photosynthesis. Curr. Opin. Plant Biol. 2000, 3, 455–460. [Google Scholar] [CrossRef] [PubMed]
- Stachowski-Haberkorn, S.; Jérôme, M.; Rouxel, J.; Khelifi, C.; Rincé, M.; Burgeot, T. Multigenerational exposure of the microalga Tetraselmis suecica to diuron leads to spontaneous long-term strain adaptation. Aquat. Toxicol. 2013, 140–141, 380–388. [Google Scholar] [CrossRef]
- Force, L.; Critchley, C.; van Rensen, J.J. New fluorescence parameters for monitoring photosynthesis in plants. Photosynth. Res. 2003, 78, 17–33. [Google Scholar] [CrossRef]
- Buschmann, C. Variation of the Quenching of Chlorophyll Fluorescence under Different Intensities of the Actinic Light in Wildtype Plants of Tobacco and in an Aurea Mutant Deficient of LightHarvesting-Complex. J. Plant Physiol. 1995, 145, 245–252. [Google Scholar] [CrossRef]
- Juneau, P.; Green, B.R.; Harrison, P.J. Simulation of Pulse-Amplitude-Modulated (PAM) fluorescence: Limitations of some PAM-parameters in studying environmental stress effects. Photosynthetica 2005, 43, 75–83. [Google Scholar] [CrossRef]
- Allen, J.F.; Forsberg, J. Molecular recognition in thylakoid structure and function. Trends Plant Sci. 2001, 6, 317–326. [Google Scholar] [CrossRef]
- Govindjee, G. A Role for a Light-Harvesting Antenna Complex of Photosystem II in Photoprotection. Plant Cell 2002, 14, 1663–1668. [Google Scholar] [CrossRef]
- Alric, J. Cyclic electron flow around photosystem I in unicellular green algae. Photosynth. Res. 2010, 106, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Bendall, D.S.; Manasse, R.S. Cyclic photophosphorylation and electron transport. Biochim. Biophys. Acta 1995, 1229, 23–38. [Google Scholar] [CrossRef]
- Alric, J.; Lavergne, J.; Rappaport, F. Redox and ATP control of photosynthetic cyclic electron flow in Chlamydomonas reinhardtii (I) aerobic conditions. Biochim. Biophys. Acta 2010, 1797, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Finazzi, G.; Furia, A.; Barbagallo, R.P.; Forti, G. State transitions, cyclic and linear electron transport and photophosphorylation in Chlamydomonas reinhardtii. Biochim. Biophys. Acta Bioenerg. 1999, 1413, 117–129. [Google Scholar] [CrossRef]
- Munekage, Y.; Hojo, M.; Meurer, J.; Endo, T.; Tasaka, M.; Shikanai, T. PGR5 is involved in cyclic electron flow around photosystem I and is essential for photoprotection in Arabidopsis. Cell 2002, 110, 361–371. [Google Scholar] [CrossRef]
- Huang, W.; Yang, Y.-J.; Zhang, S.-B.; Liu, T. Cyclic Electron Flow around Photosystem I Promotes ATP Synthesis Possibly Helping the Rapid Repair of Photodamaged Photosystem II at Low Light. Front. Plant Sci. 2018, 9, 239. [Google Scholar] [CrossRef]
- Joliot, P.; Joliot, A. Cyclic electron transfer in plant leaf. Proc. Natl. Acad. Sci. USA 2002, 99, 10209–10214. [Google Scholar] [CrossRef]
- Franqueira, D.; Cid, A.; Torres, E.; Orosa, M.; Herrero, C. A comparison of the relative sensitivity of structural and functional cellular responses in the alga chlamydomonas eugametos exposed to the herbicide paraquat. Arch. Environ. Contam. Toxicol. 1999, 36, 264–269. [Google Scholar] [CrossRef]
- Asselborn, V.; Fernández, C.; Zalocar, Y.; Parodi, E.R. Effects of chlorpyrifos on the growth and ultrastructure of green algae, Ankistrodesmus gracilis. Ecotoxicol. Environ. Saf. 2015, 120, 334–341. [Google Scholar] [CrossRef] [PubMed]
- DeLorenzo, M.E.; Leatherbury, M.; Weiner, J.A.; Lewitus, A.J.; Fulton, M.H. Physiological factors contributing to the species-specific sensitivity of four estuarine microalgal species exposed to the herbicide atrazine. Aquat. Ecosyst. Health Manag. 2004, 7, 137–146. [Google Scholar] [CrossRef]
- Tang, J.; Hoagland, K.D.; Siegfried, B.D. Uptake and bioconcentration of atrazine by selected freshwater algae. Environ. Toxicol. Chem. 1998, 17, 1085–1090. [Google Scholar] [CrossRef]
- Kent, R.A.; Currie, D. Predicting algal sensitivity to a pesticide stress. Environ. Toxicol. Chem. 1995, 14, 983–991. [Google Scholar] [CrossRef]
- Kato, K.; Tanaka, R.; Sano, S.; Tanaka, A.; Hosaka, H. Identification of a gene essential for protoporphyrinogen IX oxidase activity in the cyanobacterium Synechocystis sp. PCC6803. Proc. Natl. Acad. Sci. USA 2010, 107, 16649–16654. [Google Scholar] [CrossRef]
- Deblois, C.P.; Marchand, A.; Juneau, P. Comparison of photoacclimation in twelve freshwater photoautotrophs (chlorophyte, bacillaryophyte, cryptophyte and cyanophyte) isolated from a natural community. PLoS ONE 2013, 8, e57139. [Google Scholar] [CrossRef]
- Stein, J. Handbook of Phycological Methods: Culture Methods and Growth Measurements; Cambridge University Press: London, UK, 1973; p. 448. [Google Scholar]
- Wood, A.; Everroad, R.C.; Wingard, L.M. Measuring Growth Rates in Microalgal Cultures. In Algal Culturing Techniques; Andersen, R.A., Ed.; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Schreiber, U.; Schliwa, U.; Bilger, W. Continuous recording of photochemical and non-photochemical chlorophyll fluorescence quenching with a new type of modulation fluorometer. Photosynth. Res. 1986, 10, 51–62. [Google Scholar] [CrossRef]
- Kitajima, M.; Butler, W. Quenching of chlorophyll fluorescence and primary photochemistry in chloroplasts by dibromothymoquinone. Biochim. Biophys. Acta BBA Bioenerg. 1975, 376, 105–115. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.-M.; Baker, N.R. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta BBA Gen. Subj. 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Joliot, P.; Joliot, A. Quantification of cyclic and linear flows in plants. Proc. Natl. Acad. Sci. USA 2005, 102, 4913–4918. [Google Scholar] [CrossRef]
- Du, J.; Qiu, B.; Gomes, M.P.; Juneau, P.; Dai, G. Influence of light intensity on cadmium uptake and toxicity in the cyanobacteria Synechocystis sp. PCC6803. Aquat. Toxicol. 2019, 211, 163–172. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. Chlorophylls and Carotenoids: Pigments of Photosynthetic Biomembranes. In Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1987; Volume 148, pp. 350–382. [Google Scholar]
- Weber, J.B. Ionization and sorption of fomesafen and atrazine by soils and soil constituents. Pestic. Sci. 1993, 39, 31–38. [Google Scholar] [CrossRef]
- Boullemant, A.; Lavoie, M.; Fortin, C.; Campbell, P.G. Uptake of Hydrophobic Metal Complexes by Three Freshwater Algae: Unexpected Influence of pH. Environ. Sci. Technol. 2009, 43, 3308–3314. [Google Scholar] [CrossRef] [PubMed]
- Lavoie, M.; Duval, J.F.L.; Raven, J.A.; Maps, F.; Béjaoui, B.; Kieber, D.J.; Vincent, W.F. Carbonate Disequilibrium in the External Boundary Layer of Freshwater Chrysophytes: Implications for Contaminant Uptake. Environ. Sci. Technol. 2018, 52, 9403–9411. [Google Scholar] [CrossRef] [PubMed]
- Lavoie, M.; Galí, M.; Sévigny, C.; Kieber, D.J.; Sunda, W.G.; Spiese, C.E.; Maps, F.; Levasseur, M. Modelling dimethylsulfide diffusion in the algal external boundary layer: Implications for mutualistic and signalling roles. Environ. Microbiol. 2018, 20, 4157–4169. [Google Scholar] [CrossRef]
- Walter, A.; Gutknecht, J. Permeability of small nonelectrolytes through lipid bilayer membranes. J. Membr. Biol. 1986, 90, 207–217. [Google Scholar] [CrossRef]
- Tomlin, C. Entry 571. In The Pesticide Manual: A World Compendium; The British Crop Protection Council: Farnham, UK; The Royal Society of Chemistry: London, UK, 1994; pp. 832–833. [Google Scholar]
- Hayduk, W.; Laudie, H. Prediction of diffusion coefficients for nonelectrolytes in dilute aqueous solutions. AIChE J. 1974, 20, 611–615. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.; Riebesell, U. Diffusion and reactions in the vicinity of plankton: A refined model for inorganic carbon transport. Mar. Chem. 1997, 59, 17–34. [Google Scholar] [CrossRef]
- Rawat, M.; Moroney, J.V. The regulation of carbonic anhydrase and ribulose-1,5-bisphosphate carboxylase/oxygenase activase by light and CO2 in Chlamydomonas reinhardtii. Plant Physiol. 1995, 109, 937–944. [Google Scholar] [CrossRef][Green Version]
- R Core Team: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 27 November 2022).
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving differential equations in R: Package deSolve. J. Stat. Softw. 2010, 33, 1–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).