Effects of Colloidal Silica Grouting on Geotechnical Properties of Liquefiable Soils: A Review
Abstract
:1. Introduction
2. Overview of Literature on the Use of Colloidal Silica Grouting
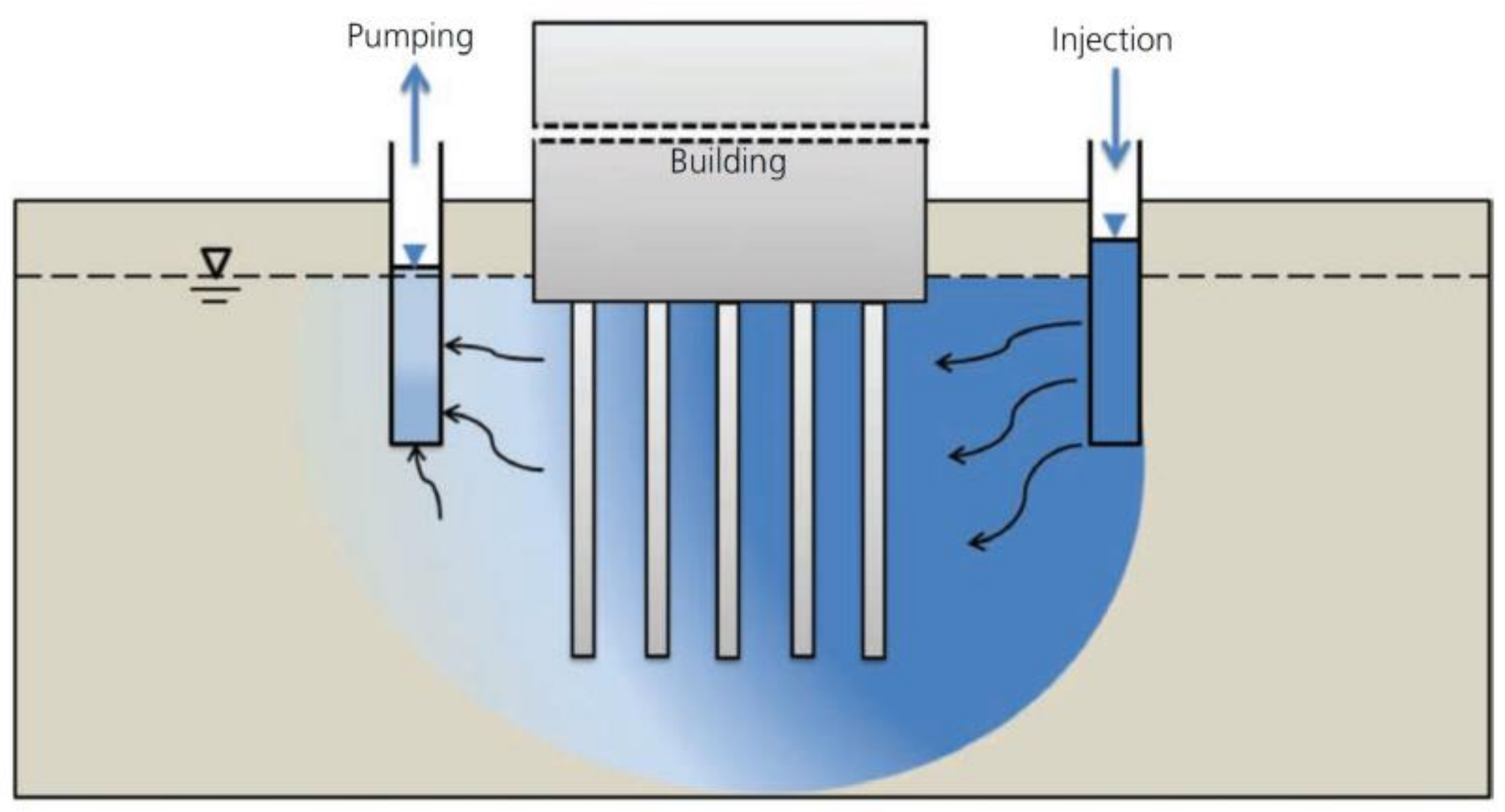
3. Colloidal Silica: An Overview
3.1. Main Characteristics and Gelation Process
3.2. Pure Silica Gel Properties
4. Transport of Colloidal Silica Grout through Porous Media
5. Influence of Colloidal Silica Treatment on Soil Behavior—Laboratory Investigations
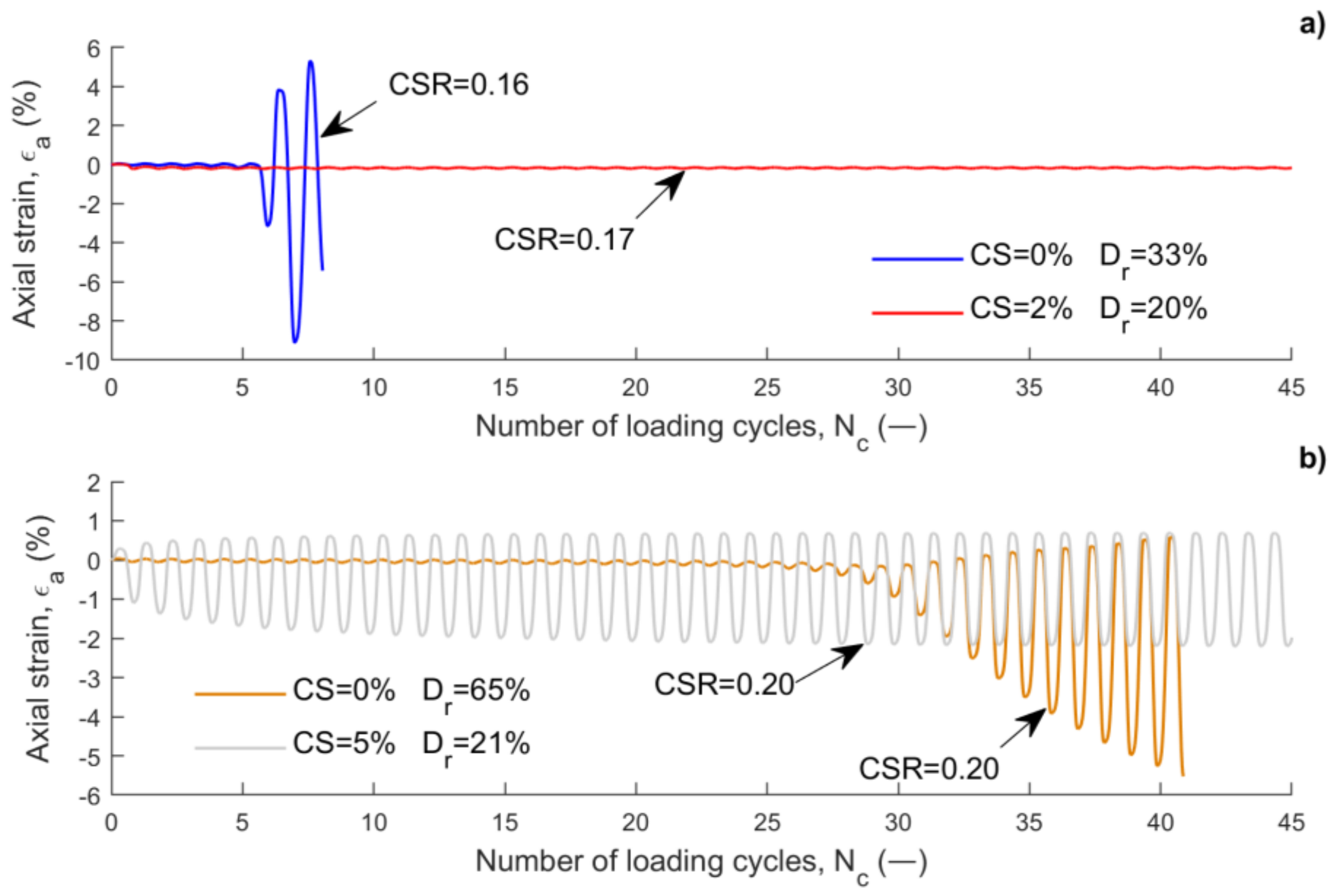
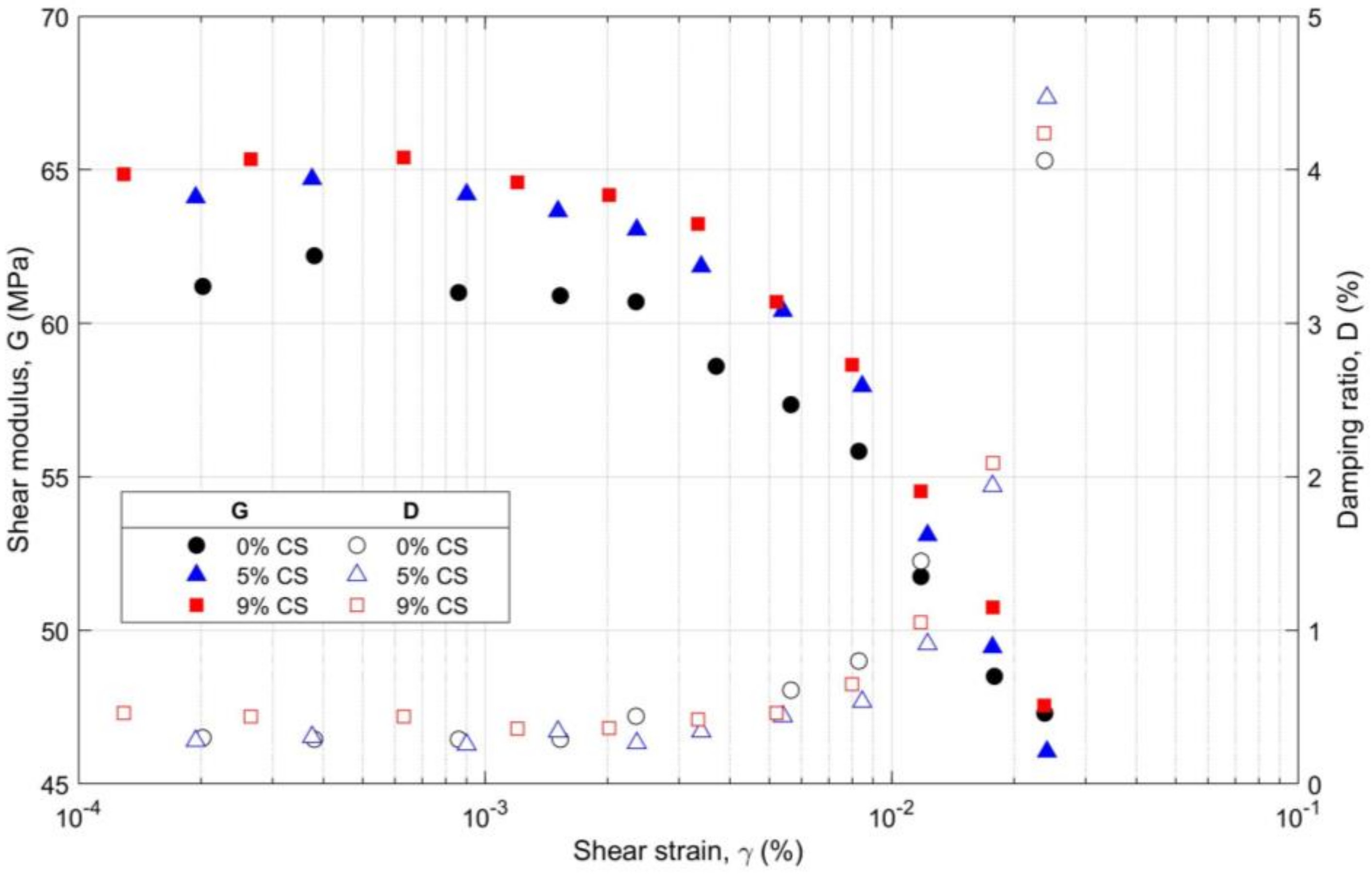
5.1. Mechanical Behavior under Dynamic and Cyclic Loading Conditions
5.1.1. High Strain Levels and Liquefaction
5.1.2. From Low to Medium Strain Levels
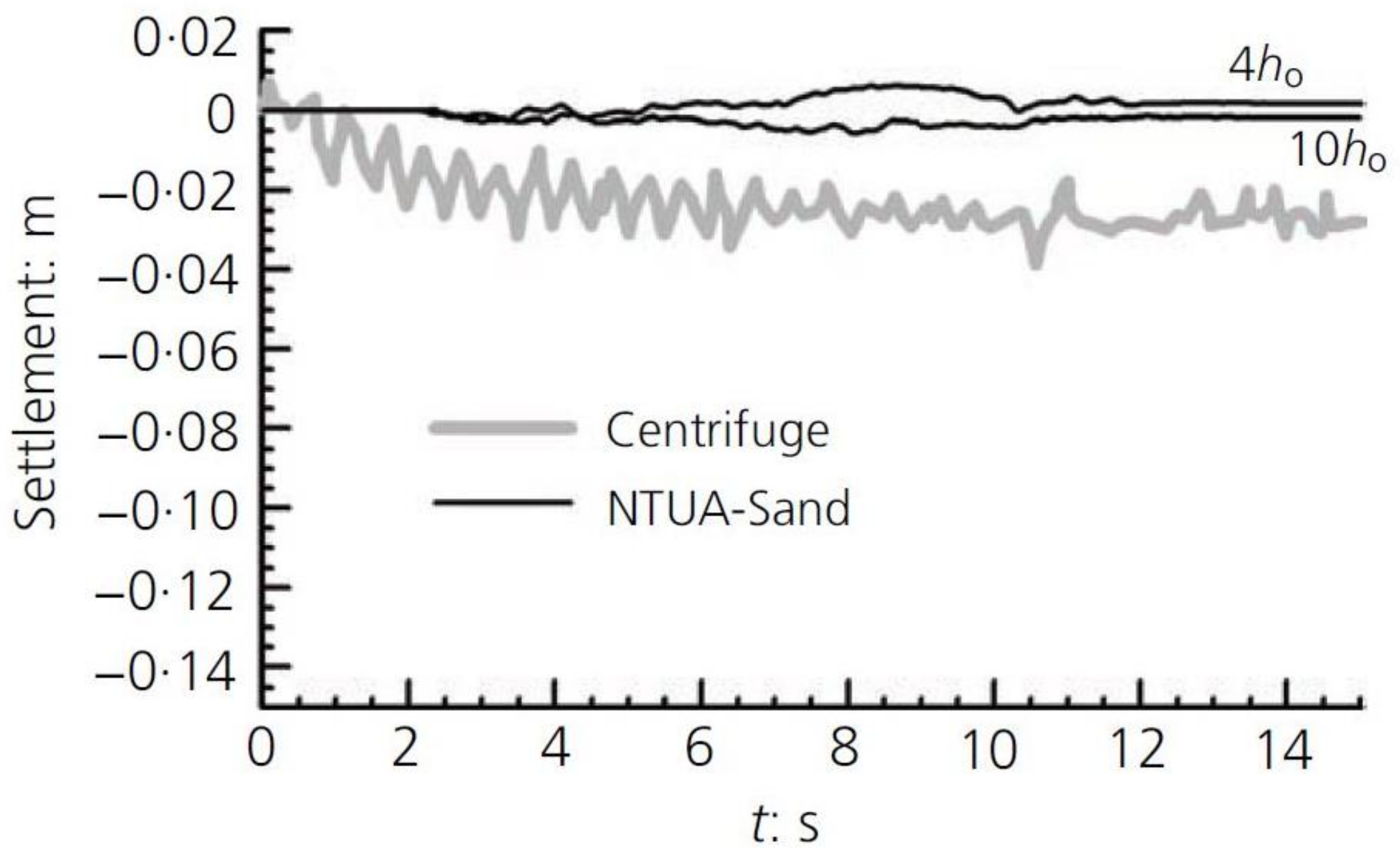
5.1.3. Physical Modeling Tests
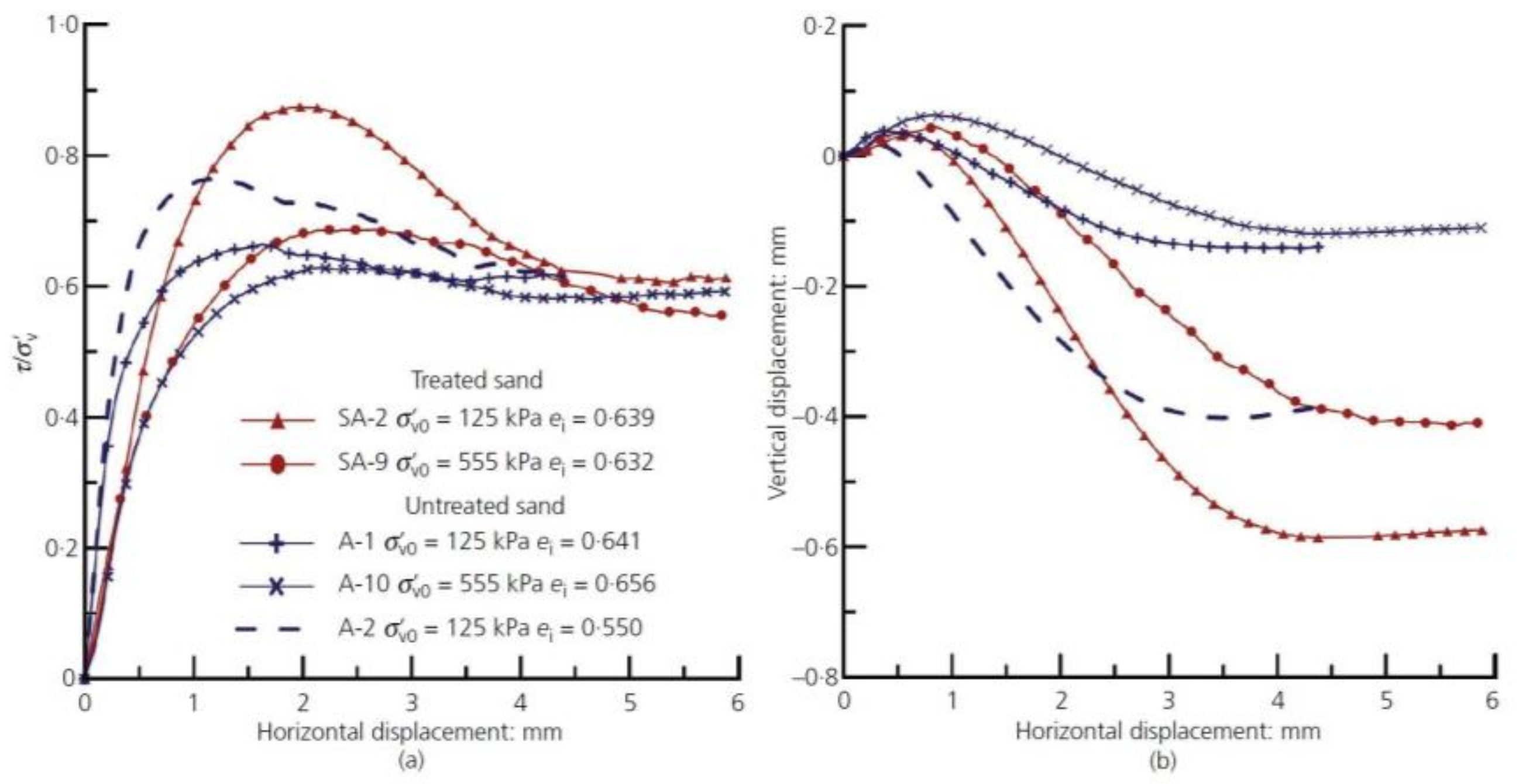
5.2. Mechanical Behavior under Static Loading Conditions
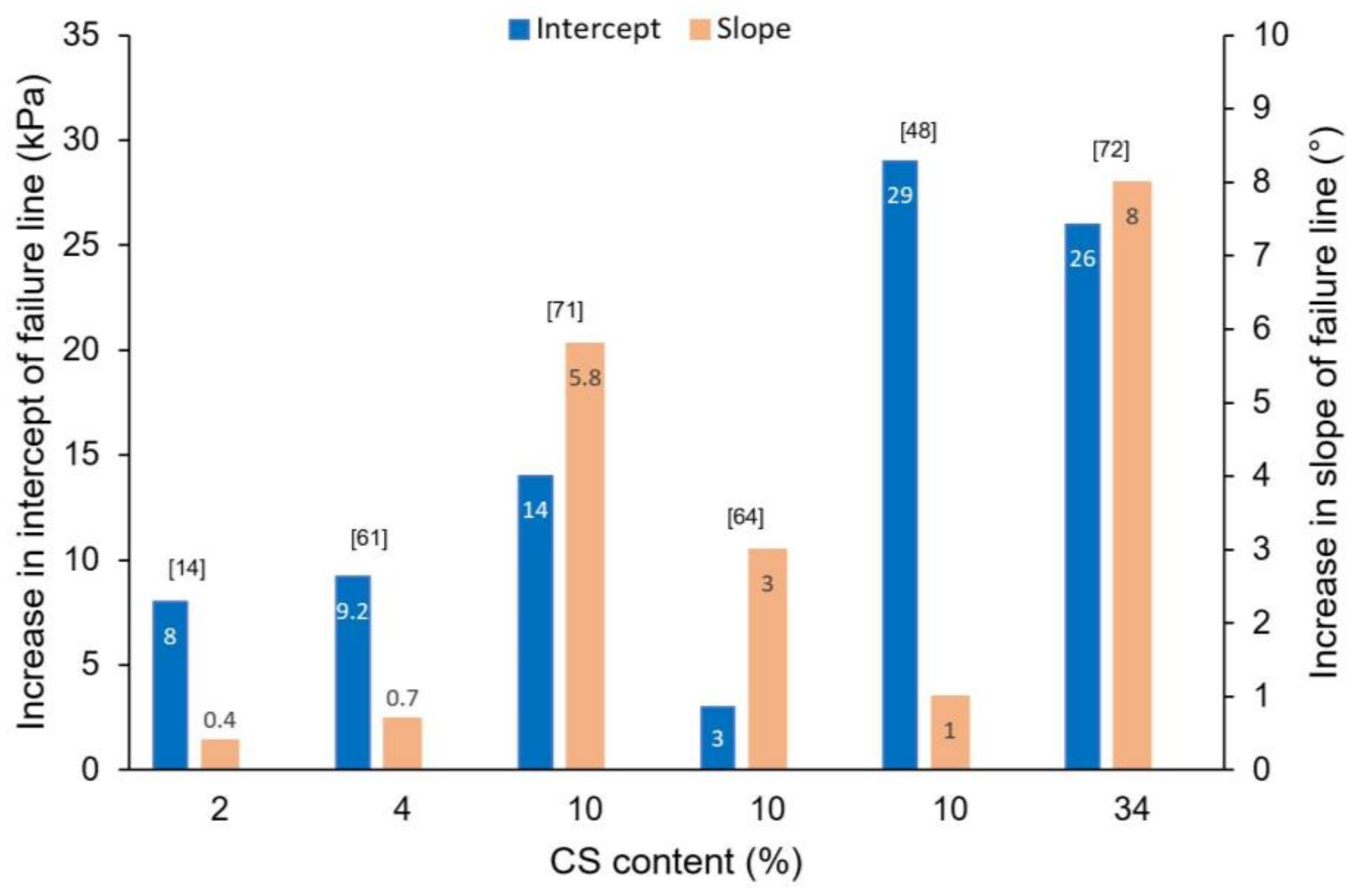
5.2.1. Monotonic Loading
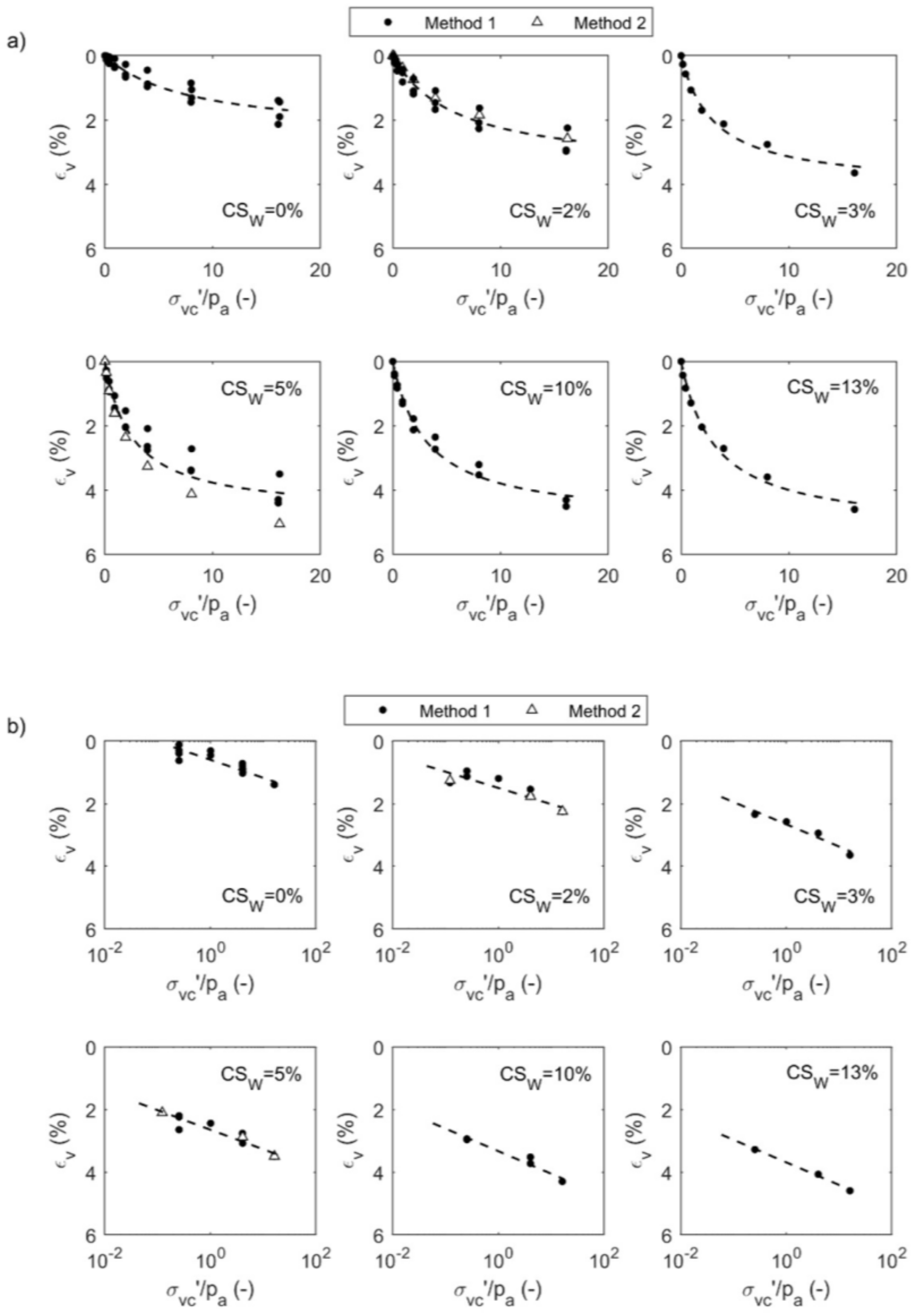
5.2.2. Soil Compressibility
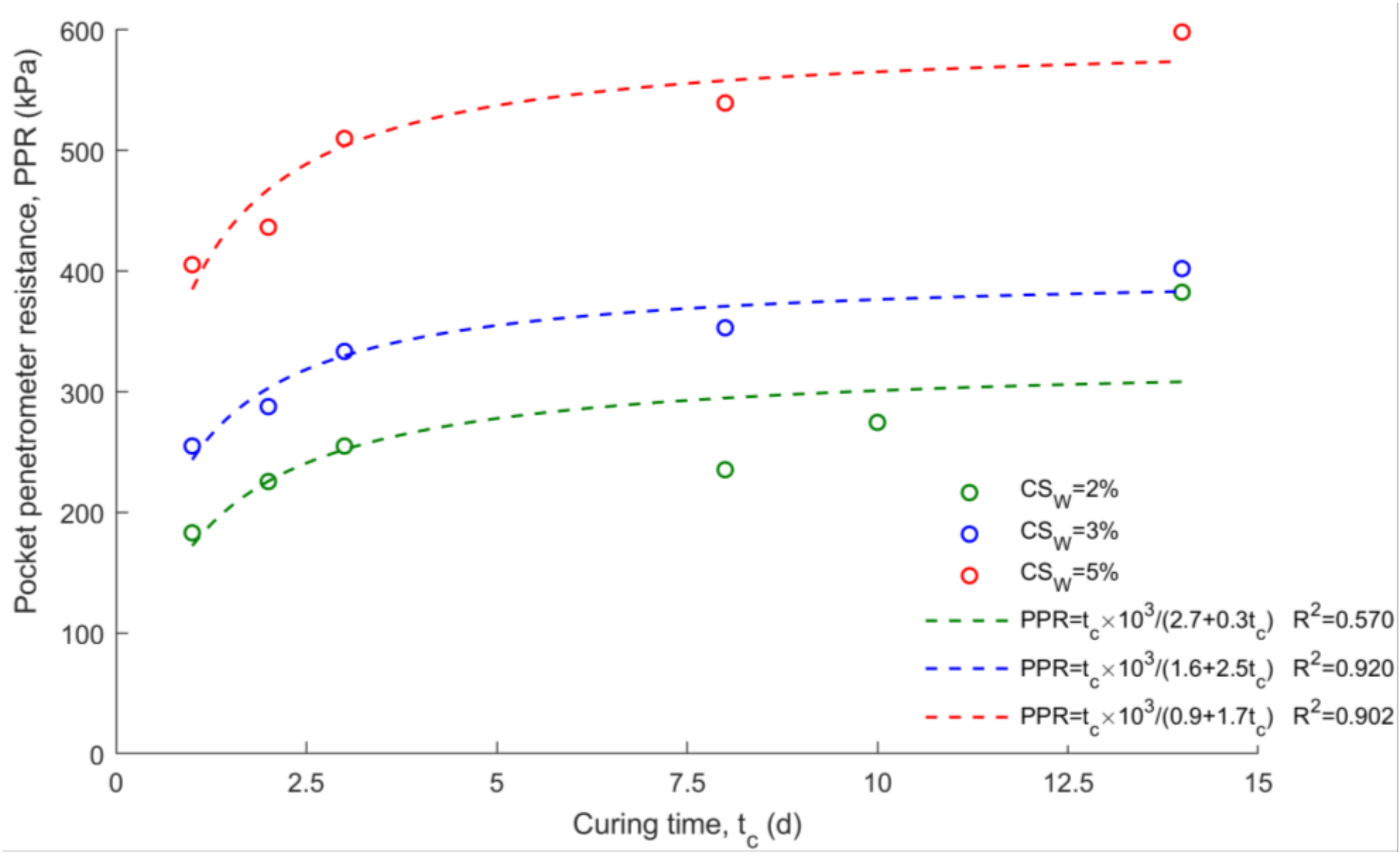
5.3. Effects of Gel Age on the Mechanical Behavior of Stabilized Soil
5.4. Hydraulic Conductivity
6. In-Field Colloidal Silica Grouting for Liquefaction Mitigation
Grouting Performance Evaluation
7. Mechanism of Soil Improvement
8. Numerical Modeling of CS Grouted Materials
9. Summary and Conclusions
- CS grout can be successfully transported through porous media; however, the effects related to grout viscosity increase over time and grout sinking need to be considered in design;
- CS grouting improves the liquefaction resistance of liquefiable soil;
- CS grouting enhances the soil strength under monotonic loading conditions;
- The strength of the treated material increases with the increase in both CS content and gel aging;
- The treated soil shows enhanced dilative behavior under monotonic loading conditions;
- The mechanism of soil improvement has not been fully clarified yet;
- The effects of CS grouting at low-medium strain levels have not been fully clarified yet;
- The compressibility of the treated material seems to be greater than that of the untreated one, at least for the CS contents that would be cost-effective for liquefaction mitigation;
- The CS treatment produces a significant decrease in soil hydraulic conductivity;
- Field experiences of CS grouting demonstrated the feasibility of this improvement method;
- Appropriate constitutive models able to simulate the behavior of the CS-treated material have not been developed yet;
- The effects of CS grout on soil compressibility;
- The effects of CS grout on damping ratio;
- The sinking phenomenon in the grout delivery process;
- The development of adequate constitutive laws to describe the behavior of the stabilized soil;
Author Contributions
Funding
Conflicts of Interest
References
- Hausmann, M.R. Engineering Principles of Ground Modification; McGraw-Hill: New York, NY, USA, 1990; ISBN 9780070272798. [Google Scholar]
- Karol, R.H. Chemical Grouting and Soil Stabilization, Revised and Expanded; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Han, J. Principles and Practice of Ground Improvement; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- DeJong, J.T.; Mortensen, B.M.; Martinez, B.C.; Nelson, D.C. Bio-mediated soil improvement. Ecol. Eng. 2010, 36, 197–210. [Google Scholar] [CrossRef]
- European Commission. Commission Recommendation of 18 October 2011 on the Definition of Nanomaterial. Off. J. Eur. Union 2011, 38–40, 2011/696/EU. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2011:275:0038:0040:EN:PDF (accessed on 20 November 2021).
- Huang, Y.; Wang, L. Experimental studies on nanomaterials for soil improvement: A review. Environ. Earth Sci. 2016, 75, 496–510. [Google Scholar] [CrossRef]
- Ghasabkolaei, N.; Janalizadeh Choobbasti, A.; Roshan, N.; Ghasemi, S.E. Geotechnical properties of the soils modified with nanomaterials: A comprehensive review. Arch. Civ. Mech. Eng. 2017, 17, 639–650. [Google Scholar] [CrossRef]
- Krishnan, J.; Shukla, S. The behaviour of soil stabilised with nanoparticles: An extensive review of the present status and its applications. Arab. J. Geosci. 2019, 12, 436. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, C.; Zhao, M.; Guo, W.; Luo, Q. Comparison of nanomaterials with other unconventional materials used as additives for soil improvement in the context of sustainable development: A review. Nanomaterials 2021, 11, 15. [Google Scholar] [CrossRef] [PubMed]
- Kananizadeh, N.; Ebadi, T.; Ehsan, S.; Rizi, M.; Khoshniat, S.A. Behavior of nanoclay as an additive in order to reduce Kahrizak landfill clay permeability. In Proceedings of the 2nd International Conference on Environmental Science and Technology, Singapore, 26–28 February 2011; pp. 26–28. [Google Scholar]
- Nikookar, M.; Bahari, M.; Nikookar, H.; Arabani, M. The Strength Characteristics of Silty Soil Stabilized Using Nano-Clay. In Proceedings of the 7th Symposium on Advances in Science & Technology (7thSASTech), Bandar-Abbas, Iran, 7–8 March 2013. [Google Scholar]
- Ng, C.W.W.; Coo, J.L. Hydraulic conductivity of clay mixed with nanomaterials. Can. Geotech. J. 2015, 52, 808–811. [Google Scholar] [CrossRef]
- Persoff, P.; Apps, J.; Moridis, G.; Whang, J.M. Effect of dilution and contaminants on sand grouted with colloidal silica. J. Geotech. Geoenv. Eng. 1999, 125, 461–469. [Google Scholar] [CrossRef] [Green Version]
- Ciardi, G.; Bardotti, R.; Vannucchi, G.; Madiai, C. Effects of high-diluted colloidal silica grouting on the behaviour of a liquefiable sand. Geotech. Res. 2020, 7, 193–208. [Google Scholar] [CrossRef]
- Rabbani, M.M.; Ahmed, I.; Park, S.J. Application of nanotechnology to remediate contaminated soils. In Environmental Remediation Technologies for Metal-Contaminated Soils; Hasegawa, H., Rahman, I., Rahman, M., Eds.; Springer: Tokyo, Japan, 2016; pp. 219–229. ISBN 9784431557593. [Google Scholar]
- Persoff, P.; Moridis, G.J.; Apps, J.; Pruess, K.; Muller, S.J. Designing injectable colloidal silica barriers for waste isolation at the Hanford site. In Proceedings of the 33rd Hanford Symposium on Health and Environment—In Situ Remediation: Scientific Basis for Current and Future Technologies, Part 1, Pasco, WA, USA, 7–11 November 1994; pp. 87–101. [Google Scholar]
- Moridis, G.J.; Apps, J.; Persoff, P.; Myer, L.; Muller, S.; Yen, P.; Pruess, K. A field test of a waste containment technology using a new generation of injectable barrier liquids. In Proceedings of the Spectrum 96, Seattle, WA, USA, 18–23 August 1996. [Google Scholar]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock—New design criteria tested in the field, Part II. Tunn. Undergr. Space Technol. 2008, 23, 9–17. [Google Scholar] [CrossRef]
- Butrón, C.; Gustafson, G.; Fransson, Å.; Funehag, J. Drip sealing of tunnels in hard rock: A new concept for the design and evaluation of permeation grouting. Tunn. Undergr. Space Technol. 2010, 25, 114–121. [Google Scholar] [CrossRef]
- El Mohtar, C.S.; Bobet, A.; Santagata, M.C.; Drnevich, V.P.; Johnston, C.T. Liquefaction mitigation using bentonite suspensions. J. Geotech. Geoenv. Eng. 2013, 139, 1369–1380. [Google Scholar] [CrossRef] [Green Version]
- Ochoa-Cornejo, F.; Bobet, A.; Johnston, C.T.; Santagata, M.; Sinfield, J.V. Cyclic behavior and pore pressure generation in sands with laponite, a super-plastic nanoparticle. Soil Dyn. Earthq. Eng. 2016, 88, 265–279. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wen, Z.; Wang, L.; Zhu, C. Centrifuge testing of liquefaction mitigation effectiveness on sand foundations treated with nanoparticles. Eng. Geol. 2019, 249, 249–256. [Google Scholar] [CrossRef]
- Gallagher, P.M.; Mitchell, J.K. Influence of colloidal silica grout on liquefaction potential and cyclic undrained behavior of loose sand. Soil Dyn. Earthq. Eng. 2002, 22, 1017–1026. [Google Scholar] [CrossRef]
- Conlee, C.T.; Gallagher, P.M.; Boulanger, R.W.; Kamai, R. Centrifuge modeling for liquefaction mitigation using colloidal silica stabilizer. J. Geotech. Geoenv. Eng. 2012, 138, 1334–1345. [Google Scholar] [CrossRef]
- Gallagher, P.M.; Pamuk, A.; Abdoun, T. Stabilization of liquefiable soils using colloidal silica grout. J. Mater. Civ. Eng. 2007, 19, 33–40. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, Z. Recent developments of soil improvement methods for seismic liquefaction mitigation. Nat. Hazards 2015, 76, 1927–1938. [Google Scholar] [CrossRef]
- Krishnan, J.; Shukla, S. Seismic Mitigation Liquefaction—An Extensive Study on New Concepts; Lecture Notes in Civil Engineering Book Series; Springer: Singapore, 2021; Volume 117, pp. 369–379. [Google Scholar]
- DeJong, J.T.; Fritzges, M.B.; Nüsslein, K. Microbially induced cementation to control sand response to undrained shear. J. Geotech. Geoenv. Eng. 2006, 132, 1381–1392. [Google Scholar] [CrossRef]
- Montoya, B.M.; DeJong, J.T.; Boulanger, R.W. Dynamic response of liquefiable sand improved by microbial-induced calcite precipitation. Géotechnique 2013, 63, 302–312. [Google Scholar] [CrossRef]
- Xiao, P.; Liu, H.; Stuedlein, A.W.; Evans, T.M.; Xiao, Y. Effect of relative density and biocementation on cyclic response of calcareous sand. Can. Geotech. J. 2019, 56, 1849–1862. [Google Scholar] [CrossRef] [Green Version]
- Yegian, M.K.; Eseller-Bayat, E.; Alshawabkeh, A.; Ali, S. Induced-Partial saturation for liquefaction mitigation: Experimental investigation. J. Geotech. Geoenv. Eng. 2007, 133, 372–380. [Google Scholar] [CrossRef] [Green Version]
- Okamura, M.; Takebayashi, M.; Nishida, K.; Fujii, N.; Jinguji, M.; Imasato, T.; Yasuhara, H.; Nakagawa, E. In-Situ desaturation test by air injection and its evaluation through field monitoring and multiphase flow simulation. J. Geotech. Geoenv. Eng. 2011, 137, 643–652. [Google Scholar] [CrossRef]
- He, J.; Chu, J.; Ivanov, V. Mitigation of liquefaction of saturated sand using biogas. Géotechnique 2013, 63, 267–275. [Google Scholar] [CrossRef]
- Zornberg, J.G.; Cabral, A.R.; Viratjandr, C. Behaviour of tire shred sand mixtures. Can. Geotech. J. 2004, 41, 227–241. [Google Scholar] [CrossRef]
- Mashiri, M.S.; Vinod, J.S.; Sheikh, M.N. Liquefaction potential and dynamic properties of Sand-Tyre Chip (STCh) mixtures. Geotech. Test. J. 2016, 39, 69–79. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: New York, NY, USA, 1996. [Google Scholar]
- Towhata, I.; Kabashima, Y. Mitigation of seismically-induced deformation of loose sandy foundation by uniform permeation grouting. In Proceedings of the Earthquake Geotechnical Engineering Satellite Conference, XVth International Conference on Soil Mechanics and Geotechnical Engineering, Istanbul, Turkey, 27–31 August 2001; pp. 313–318. [Google Scholar]
- Liao, H.J.; Huang, C.C.; Chao, B.S. Liquefaction Resistance of a Colloid Silica Grouted Sand. In Proceedings of the 3rd International Conference on Grouting and Ground Treatment, New Orleans, LA, USA, 10–12 February 2003; pp. 1305–1313. [Google Scholar]
- Díaz-Rodríguez, J.A.; Antonio-Izarraras, V.M. Mitigation of liquefaction risk using colloidal silica stabilizer. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Zhao, M.; Liu, G.; Zhang, C.; Guo, W.; Luo, Q. State-of-the-Art of colloidal silica-based soil liquefaction mitigation: An emerging technique for ground improvement. Appl. Sci. 2020, 10, 15. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, J.; Shukla, S. The utilisation of colloidal silica grout in soil stabilisation and liquefaction mitigation: A state of the art review. Geotech. Geol. Eng. 2021, 39, 2681–2706. [Google Scholar] [CrossRef]
- Seright, R.S. Reduction of gas and water permeabilities using gels. SPE Prod. Facil. 1995, 10, 103–108. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, P.M. Passive Site Remediation for Mitigation of Liquefaction Risk; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2000. [Google Scholar]
- Iler, R.K. The Chemistry of Silica: Solubility, Polymerization, Colloid and Surface Properties and Biochemistry of Silica; John Wiley and Sons Inc.: New York, NY, USA, 1979. [Google Scholar]
- Bergna, H.E.; Roberts, W.O. (Eds.) Colloidal Silica: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Agapoulaki, G.I.; Papadimitriou, A.G. Rheological properties of colloidal silica grout for passive stabilization against liquefaction. J. Mater. Civ. Eng. 2018, 30, 4018251. [Google Scholar] [CrossRef]
- Díaz-Rodríguez, J.A.; Antonio-Izarraras, V.M.; Bandini, P.; López-Molina, J.A. Cyclic strength of a natural liquefiable sand stabilized with colloidal silica grout. Can. Geotech. J. 2008, 45, 1345–1355. [Google Scholar] [CrossRef]
- Porcino, D.; Marcianò, V.; Granata, R. Static and dynamic properties of a lightly cemented silicate-grouted sand. Can. Geotech. J. 2012, 49, 1117–1133. [Google Scholar] [CrossRef]
- Salvatore, E.; Modoni, G.; Mascolo, M.C.; Grassi, D.; Spagnoli, G. Experimental evidence of the effectiveness and applicability of colloidal nanosilica grouting for liquefaction mitigation. J. Geotech. Geoenv. Eng. 2020, 146, 04020108. [Google Scholar] [CrossRef]
- Krishnan, J.; Sharma, P.; Shukla, S.; Pancholi, V.; Dwivedi, V.K. Cyclic behaviour and durability analysis of sand grouted with optimum colloidal silica content. Arab. J. Sci. Eng. 2020, 45, 8129–8144. [Google Scholar] [CrossRef]
- Gallagher, P.M.; Finsterle, S. Physical and numerical model of colloidal silica injection for passive site stabilization. Vadose Zo. J. 2004, 3, 917–925. [Google Scholar] [CrossRef]
- Gallagher, P.M.; Lin, Y. Colloidal silica transport through liquefiable porous media. J. Geotech. Geoenv. Eng. 2009, 135, 1702–1712. [Google Scholar] [CrossRef]
- Gallagher, P.M.; Koch, A.J.; Pamuk, A.; Abdoun, T.H.; Mitchell, J.K. Centrifuge Model of Passive Site Remediation. In Proceedings of the 7th U.S. National Conference on Earthquake Engineering (7NCEE), Boston, MA, USA, 21–25 July 2002. [Google Scholar]
- Gallagher, P.M.; Koch, A.J. Model Testing of Passive Site Stabilization: A New Grouting Technique. In Grouting and Ground Treatment; ASCE: Reston, VA, USA, 2003; pp. 1478–1489. [Google Scholar]
- Axelsson, M. Mechanical tests on a new non-cementitious grout, silica sol: A laboratory study of the material characteristics. Tunn. Undergr. Space Technol. 2006, 21, 554–560. [Google Scholar] [CrossRef]
- Butrón, C.; Axelsson, M.; Gustafson, G. Silica sol for rock grouting: Laboratory testing of strength, fracture behaviour and hydraulic conductivity. Tunn. Undergr. Space Technol. 2009, 24, 603–607. [Google Scholar] [CrossRef]
- Agapoulaki, G.I.; Papadimitriou, A.G. Rheological properties of colloidal silica as a means for designing passive stabilization of liquefiable soils. In Proceedings of the 16th European Conference on Soil Mechanics and Geotechnical Engineering, Edinburgh, UK, 13–17 September 2015; pp. 2331–2336. [Google Scholar]
- Sögaard, C.; Funehag, J.; Abbas, Z. Silica sol as grouting material: A physio-chemical analysis. Nano Converg. 2018, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.J.; Cummins, H.Z.; Morris, J.F. Structural and rheological evolution of silica nanoparticle gels. Soft Matter 2010, 6, 5425–5433. [Google Scholar] [CrossRef]
- Kodaka, T.; Oka, F.; Ohno, Y.; Takyu, T.; Yamasaki, N. Modeling of cyclic deformation and strength characteristics of silica treated sand. In Geomechanics: Testing, Modeling and Simulation; ASCE: Reston, VA, USA, 2005; pp. 205–216. [Google Scholar]
- Kodaka, T.; Ohno, Y.; Takyu, T. Cyclic shear characteristics of treated sand with colloidal silica grout. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; pp. 401–404. [Google Scholar]
- Pamuk, A.; Gallagher, P.M.; Zimmie, T.F. Remediation of piled foundations against lateral spreading by passive site stabilization technique. Soil Dyn. Earthq. Eng. 2007, 27, 864–874. [Google Scholar] [CrossRef]
- Mollamahmutoglu, M.; Yilmaz, Y. Pre- and post-cyclic loading strength of silica-grouted sand. Proc. Inst. Civ. Eng. Geotech. Eng. 2010, 163, 343–348. [Google Scholar] [CrossRef]
- Porcino, D.; Marcianò, V.; Granata, R. Undrained cyclic response of a silicate-grouted sand for liquefaction mitigation purposes. Geomech. Geoengin. 2011, 6, 155–170. [Google Scholar] [CrossRef]
- Vranna, A.; Tika, T. Undrained Monotonic and Cyclic Behaviour of a Silty Sand Stabilized with Colloidal Silica. In Proceedings of the 6th International Conference on Earthquake Geotechnical Engineering, Christchurch, New Zealand, 1–4 November 2015. [Google Scholar]
- Vranna, A.; Tika, T. Laboratory improvement of liquefiable sand via colloidal silica and weak cementation. Proc. Inst. Civ. Eng. Gr. Improv. 2019, 174, 240–251. [Google Scholar] [CrossRef]
- Ciardi, G.; Bardotti, R.; Vannucchi, G.; Madiai, C. Effects of high-diluted colloidal silica grout on the mechanical behavior of a liquefiable sand. In Proceedings of the 7th International Conference on Earthquake Geotechnical Engineering, Roma, Italy, 17–20 June 2019; pp. 1820–1827. [Google Scholar]
- Vranna, A.; Tika, T.; Papadimitriou, A. Laboratory investigation into the monotonic and cyclic behaviour of a clean sand stabilised with colloidal silica. Géotechnique 2020. (ahead of print). [Google Scholar] [CrossRef]
- Vranna, A.; Tika, T. The mechanical response of a silty sand stabilized with colloidal silica. Geotechnics 2021, 1, 243–259. [Google Scholar] [CrossRef]
- Pavlopoulou, E.M.; Georgiannou, V.N. Effect of colloidal silica aqueous gel on the monotonic and cyclic response of sands. J. Geotech. Geoenv. Eng. 2021, 147, 04021122. [Google Scholar] [CrossRef]
- Georgiannou, V.N.; Pavlopoulou, E.M.; Bikos, Z. Mechanical behaviour of sand stabilised with colloidal silica. Proc. Inst. Civ. Eng. Geotech. Res. 2017, 4, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wong, C.; Pedrotti, M.; El Mountassir, G.; Lunn, R.J. A study on the mechanical interaction between soil and colloidal silica gel for ground improvement. Eng. Geol. 2018, 243, 84–100. [Google Scholar] [CrossRef] [Green Version]
- Nouri Delavar, I.; Noorzad, R. Drained shear strength parameters of silty sand grouted by colloidal silica. Int. J. Geotech. Eng. 2020, 14, 1–8. [Google Scholar] [CrossRef]
- Triantafyllos, P.K.; Georgiannou, V.N.; Pavlopoulou, E.-M.; Dafalias, Y.F. Strength and dilatancy of sand before and after stabilisation with colloidal-silica gel. Géotechnique 2021. (ahead of print). [Google Scholar] [CrossRef]
- Krishnan, J.; Sharma, P.; Shukla, S. Experimental investigations on the mechanical properties of sand stabilized with colloidal silica. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 1737–1758. [Google Scholar] [CrossRef]
- Ghadr, S.; Assadi-Langroudi, A.; Hung, C.; O’Kelly, B.C.; Bahadori, H.; Ghodsi, T. Stabilization of sand with colloidal nano-silica hydrosols. Appl. Sci. 2020, 10, 5192. [Google Scholar] [CrossRef]
- Spencer, L.M.; Rix, G.J.; Gallagher, P.M. Dynamic properties of colloidal silica gel and sand mixtures. In Proceedings of the 4th International Conference on Earthquake Geotechnical Engineering, Thessaloniki, Greece, 25–28 June 2007. [Google Scholar]
- Spencer, L.; Rix, G.J.; Gallagher, P.M. Colloidal silica gel and sand mixture dynamic properties. In Proceedings of the Geotechnical Earthquake Engineering and Soil Dynamics Congress IV, Sacramento, CA, USA, 18–22 May 2008. [Google Scholar]
- Batilas, A.; Pantazopoulos, I.; Athanasopoulos, G. Effects of colloidal silica grouting on the dynamic properties of sandy soils. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Gallagher, P.M.; Lin, Y. Column Testing to determine Colloidal Silica Transport Mechanisms. In Proceedings of the Geo-Frontiers Congress 2005, Austin, TX, USA, 24–26 January 2005. [Google Scholar]
- Hamderi, M.; Gallagher, P.M. Pilot-Scale modeling of colloidal silica delivery to liquefiable sands. Soils Found. 2015, 55, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Bolisetti, T.; Reitsma, S.; Balachandar, R. Experimental investigations of colloidal silica grouting in porous media. J. Geotech. Geoenv. Eng. 2009, 135, 697–700. [Google Scholar] [CrossRef]
- Gallagher, P.M.; Conlee, C.T.; Rollins, K.M. Full-Scale field testing of colloidal silica grouting for mitigation of liquefaction risk. J. Geotech. Geoenv. Eng. 2007, 133, 186–196. [Google Scholar] [CrossRef] [Green Version]
- Rasouli, R.; Hayashi, K.; Zen, K. Controlled permeation grouting method for mitigation of liquefaction. J. Geotech. Geoenv. Eng. 2016, 142, 04016052. [Google Scholar] [CrossRef]
- Andrianopoulos, K.I.; Agapoulaki, G.I.; Papadimitriou, A.G. Simulation of seismic response of passively stabilised sand. Geotech. Res. 2016, 3, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Moridis, G.J.; Persoff, P.; Apps, J.A.; Myer, L.; Pruess, K.; Yen, P. A field test of permeation grouting in heterogeneous soils using a new generation of barrier liquids. In Proceedings of the Environmental Remediation’ 95 Conference, Denver, CO, USA, 13–18 August 1995. [Google Scholar]
- Whang, J.M. Chemical-Based barrier materials. In Assessment of Barrier Containment Technologies for Environmental Remediation Applications; Rumer, R.R., Mitchell, J.K., Eds.; National Technical Information Service: Springfield, VA, USA, 1995; pp. 211–247. [Google Scholar]
- Jurinak, J.J.; Summers, L.E. Oilfield applications of colloidal silica gel. SPE Prod. Eng. 1991, 6, 406–412. [Google Scholar] [CrossRef]
- Noll, M.R.; Bartlett, C.; Dochat, T.M. In Situ permeability reduction and chemical fixation using colloidal silica. In Proceedings of the Sixth National Outdoor Action Conference on Aquifer Restoration, Ground Water Monitoring, and Geophysical Method, National Ground Water Association, Las Vegas, NV, USA, 11–13 May 1992; pp. 443–457. [Google Scholar]
- Durmusoglu, E.; Yavuz Corapcioglu, M. Experimental study of horizontal barrier formation by colloidal silica. J. Environ. Eng. 2000, 126, 833–841. [Google Scholar] [CrossRef]
- Towhata, I. Geotechnical Earthquake Engineering; Wei, W., Borja, R.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Higgo, J.J.W.; Williams, G.M.; Harrison, I.; Warwick, P.; Gardiner, M.P.; Longworth, G. Colloid transport in a glacial sand aquifer. Laboratory and field studies. Colloids Surfaces A Physicochem. Eng. Asp. 1993, 73, 179–200. [Google Scholar] [CrossRef]
- Saiers, J.E.; Hornberger, G.M.; Harvey, C. Colloidal silica transport through structured, heterogeneous porous media. J. Hydrol. 1994, 163, 271–288. [Google Scholar] [CrossRef]
- Johnson, P.R.; Sun, N.; Elimelech, M. Colloid transport in geochemically heterogeneous porous media: Modeling and measurements. Environ. Sci. Technol. 1996, 30, 3284–3293. [Google Scholar] [CrossRef]
- Fujita, Y.; Kobayashi, M. Transport of colloidal silica in unsaturated sand: Effect of charging properties of sand and silica particles. Chemosphere 2016, 154, 179–186. [Google Scholar] [CrossRef]
- Noll, M.R.; Epps, D.E.; Bartlett, C.L.; Chen, P.J. Pilot field application of a colloidal silica gel technology for in situ hot spot stabilization and horizontal grouting. In Proceedings of the 7th National Outdoor Action Conference, National Ground Water Association, Las Vegas, NV, USA, 25–27 May 1993; pp. 207–219. [Google Scholar]
- Hamderi, M.; Gallagher, P.M. An optimization study on the delivery distance of colloidal silica. Sci. Res. Essays 2013, 8, 1314–1323. [Google Scholar]
- Weggel, J.R.; Gallagher, P.; Lin, Y. Analytical model for transport of dilute colloidal silica dispersions through porous media. J. Geotech. Geoenv. Eng. 2018, 144, 4018082. [Google Scholar] [CrossRef]
- Agapoulaki, G.I.; Papadimitriou, A.G.; Kandris, K.; Pantazidou, M. Permeation potential of colloidal silica for passive stabilization of liquefiable soils. In Proceedings of the XVI ECSMGE Geotechnical Engineering for Infrastructure and Development, Edinburgh, UK, 13–17 September 2015; pp. 2201–2206. [Google Scholar]
- Weggel, J.R.; Gallagher, P.; Lin, Y. Closure to “Analytical Model for Transport of Dilute Colloidal Silica Dispersions through Porous Media” by J. Richard Weggel, Patricia Gallagher, and Yuanzhi Lin. J. Geotech. Geoenv. Eng. 2019, 145, 07019014. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y. Colloidal Silica Transport Mechanisms for Passive Site Stabilization of Liquefiable Soils; Drexel University: Philadelphia, PA, USA, 2006. [Google Scholar]
- Ishihara, K. Soil Behaviour in Earthquake Geotechnics; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Castro, G. Liquefaction and cyclic mobility of saturated sands. J. Geotech. Eng. Div. 1975, 101, 551–569. [Google Scholar] [CrossRef]
- Castro, G.; Poulos, S.J. Factors affecting liquefaction and cyclic mobility. J. Geotech. Eng. Div. 1977, 103, 501–516. [Google Scholar] [CrossRef]
- Castro, G.; Enos, J.L.; France, J.W.; Poulos, S.J. Liquefaction induced by cyclic loading. NASA STI/Recon Tech. Rep. N 1982, 83, 13308. [Google Scholar]
- Japanese Geotechnical Society. Remedial Measures against Soil Liquefaction: From Investigation and Design to Implementation; Japanese Geotechnical Society, Ed.; Balkema: Rotterdam, NL, USA, 1998. [Google Scholar]
- Ciardi, G. Effects of High-Diluted Colloidal Silica Mixtures on the Mechanical Behavior of Potentially Liquefiable Sand; University of Florence/Technische Universität Braunschweig: Florence, Italy, 2019. [Google Scholar]
- Taboada, V. Centrifuge Modeling of Earthquake-Induced Lateral Spreading Using a Laminar Box. Ph.D. Thesis, Department of Civil Engineering, Rensselaer Polytechnic Institute, Troy, NY, USA, 1995. [Google Scholar]
- Pedrotti, M.; (University of Strathclyde, Glasgow, UK). Personal communication, 2018.
- Sharma, P.; Krishnan, J.; Shruti, S. A Feasibility Study of Colloidal Silica as Stabilizing Material for Passive Site Remediation. In Advances in Civil Engineering; Springer: Singapore, 2021; Volume 83, pp. 333–347. [Google Scholar]
- Moradi, G.; Seyedi, S. Effect of sampling method on strength of stabilized silty sands with colloidal nano silica. J. Civ. Eng. Res. 2015, 5, 129–135. [Google Scholar]
- Yonekura, R.; Miwa, M. Fundamental properties of sodium silicate based grout. In Proceedings of the Eleventh South East Asian Geotechnical Conference, Singapore, 4–8 May 1993; pp. 439–444. [Google Scholar]
- Oka, F.; Yashima, A.; Tateishi, A.; Taguchi, Y.; Yamashita, A. A cyclic elasto-plastic constitutive model for sand considering a plastic-strain dependence of the shear modulus. Géotechnique 1999, 49, 661–680. [Google Scholar] [CrossRef]
- Andrianopoulos, K.I.; Papadimitriou, A.G.; Bouckovalas, G.D. Bounding surface plasticity model for the seismic liquefaction analysis of geostructures. Soil Dyn. Earthq. Eng. 2010, 30, 895–911. [Google Scholar] [CrossRef]
- Papadimitriou, A.G.; Limnaiou, T.; Kympouri, M. Mitigation of liquefaction-induced pipeline uplift using passive stabilization. In Proceedings of the 7th International Conference on Earthquake Geotechnical Engineering, Roma, Italy, 17–20 June 2019; pp. 4327–4334. [Google Scholar]






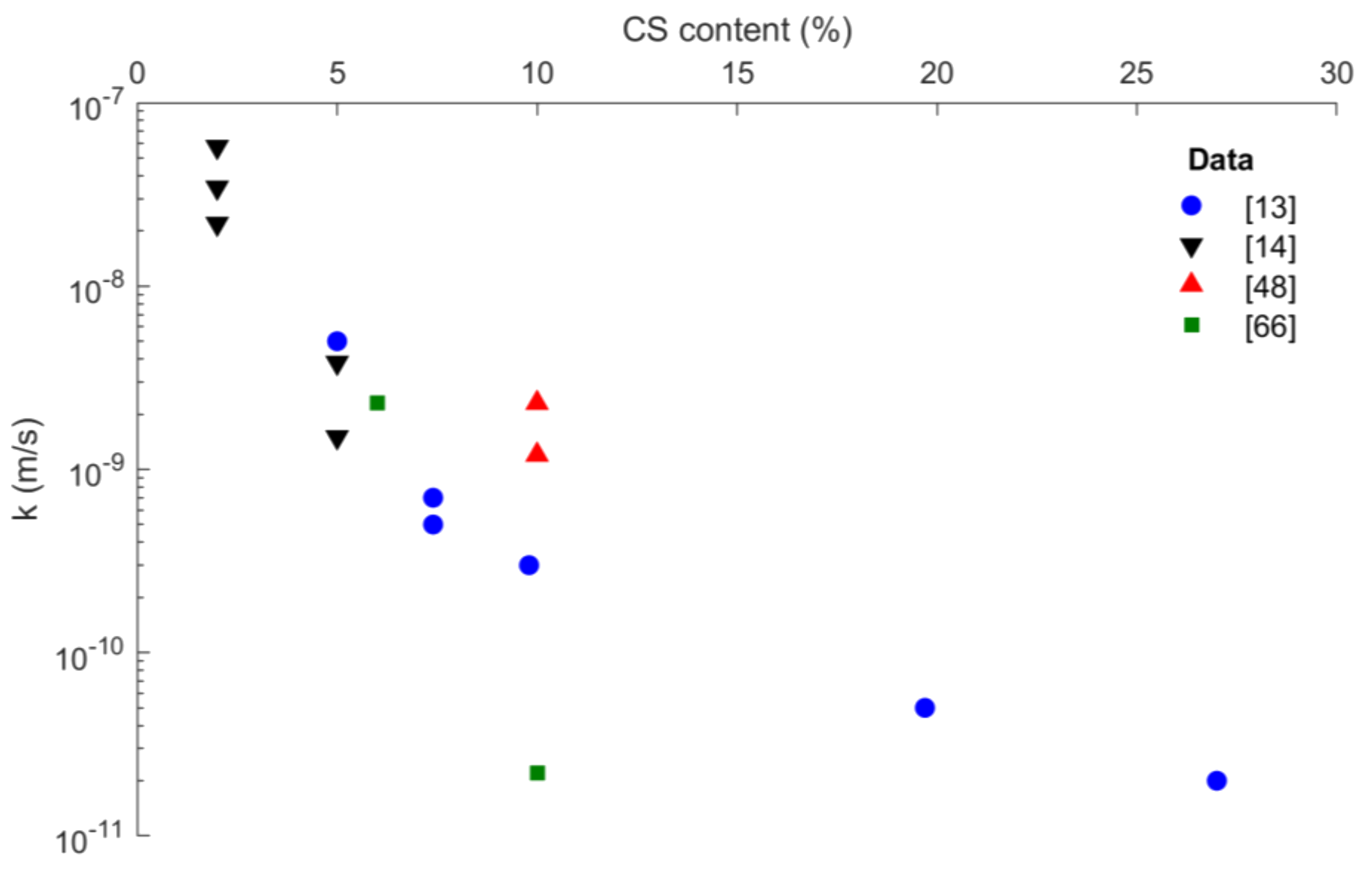
| Reference | Tested Soil(s) | Test Type | Specimen Formation, Testing Details | Main Findings |
|---|---|---|---|---|
| [17] | Hanford sand, Los Banos sand (from quarry) | Flexible wall permeameter | Three kinds of samples:
(1) prepared by pouring sand into liquid grout; (2) prepared by grout injection into sandpacks; (3) collected from field | Sands with initial k ≈ 10−4 m/s could attain a final hydraulic conductivity of ≈10−10 m/s after CS grouting |
| [13] | Monterey silica sand No. 0/30 (D50 = 0.49 mm) and Trevino sandy loam (52% sand, 42% silt and 6% clay, by fraction) | Falling head permeability test | Soil and grout mixed in a cylinder mold | k ranged from ≈5 × 10−9 m/s for 5% CS content up to ≈2 × 10−11 m/s for 27.5% CS content (Monterey sand); k ranged from ≈1.5 × 10−9 m/s for 5% CS content up to ≈1.5 × 110−10 m/s for 27.5% CS content (Trevino loam) |
| [48] | Ticino silica sand (D50 = 0.6 mm, Cu = 1.3, Gs = 2.68) | Constant-flow permeability test | Grout permeation | k ranged from 1.2 × 10−9 m/s to 2.3 × 10−9 m/s for 10% CS content |
| [72] | Leighton Buzzard sand (D50 = 1.2 mm, Cu = 1.26, Gs = 2.65) | Oedometer | See Section 5.2.2 (Permeability estimated from the consolidation times in oedometer tests) | k values ≈ 10−10 m/s for grouted sand |
| [66] | M31 quartz sand (D50 = 0.31 mm, Cu = 1.50, Gs = 2.655) | Triaxial permeability | Grout permeation. Dr = 40%, 100/50 mm height/diameter | K = 2.3 × 10−9 m/s and k = 2.2 × 10−11 m/s for CS contents 6% and 10%, respectively |
| [14] | Silica sand (D50 = 0.30 mm, Cu = 1.6, Gs = 2.65, SP) | Falling head | Dry sand tamped in layers. Dr ≈ 50–64%, 100/50 mm height/diameter, gel time ≈ 2 h, curing time 1 d. CS content: 2, 5%. Specimens were first water-saturated and then injected with grout under gravity; k measurements before and after treatment | 104 (105) fold k reduction for 2% (5%) CS grouted material |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciardi, G.; Vannucchi, G.; Madiai, C. Effects of Colloidal Silica Grouting on Geotechnical Properties of Liquefiable Soils: A Review. Geotechnics 2021, 1, 460-491. https://doi.org/10.3390/geotechnics1020022
Ciardi G, Vannucchi G, Madiai C. Effects of Colloidal Silica Grouting on Geotechnical Properties of Liquefiable Soils: A Review. Geotechnics. 2021; 1(2):460-491. https://doi.org/10.3390/geotechnics1020022
Chicago/Turabian StyleCiardi, Giovanni, Giovanni Vannucchi, and Claudia Madiai. 2021. "Effects of Colloidal Silica Grouting on Geotechnical Properties of Liquefiable Soils: A Review" Geotechnics 1, no. 2: 460-491. https://doi.org/10.3390/geotechnics1020022
APA StyleCiardi, G., Vannucchi, G., & Madiai, C. (2021). Effects of Colloidal Silica Grouting on Geotechnical Properties of Liquefiable Soils: A Review. Geotechnics, 1(2), 460-491. https://doi.org/10.3390/geotechnics1020022






