Next Article in Journal
Effect of Relative Isometric Strength on Countermovement Jump Performance in Professional and Semi-Professional Soccer Players
Previous Article in Journal
Comparison of Gait Parameters Collected Across Two Commercially Available Gait Systems in Older Adults
Previous Article in Special Issue
Exploring the Effect of Prolonged Ankle Plantar-Flexed Standing on Postural Control, Balance Confidence, Falls Efficacy, and Perceived Balance in Older Adults
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomechanics
Volume 5
Issue 2
10.3390/biomechanics5020031
biomechanics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of Simulated Hyper-Gravity on Lower Limb Kinematics and Electromyography During Walking

by
Christopher A. Malaya
1,2,*,
Pranav J. Parikh
2,
Dean L. Smith
3 and
Charles S. Layne
2
1
Grail Laboratory, Parker University, Dallas, TX 75229, USA
2
Center for Neuromotor and Biomechanics Research, Department of Health and Human Performance, University of Houston, Houston, TX 77204, USA
3
Department of Kinesiology, Nutrition, and Health, Miami University, Oxford, OH 45056, USA
*
Author to whom correspondence should be addressed.
Biomechanics 2025, 5(2), 31; https://doi.org/10.3390/biomechanics5020031
Submission received: 25 January 2025 / Revised: 10 April 2025 / Accepted: 13 April 2025 / Published: 4 May 2025
(This article belongs to the Special Issue Gait and Balance Control in Typical and Special Individuals)
Browse Figures
Versions Notes

Abstract

:
Background: Gravity profoundly influences human locomotion. Studies examining the effects of hyper-gravity on gait have largely relied on added external mass, potentially confounding results with changes in inertia and center of mass. This study attempted to isolate the effects of increased gravitational load on kinematics and electromyography during walking at several different levels of load. Methods: Fifteen healthy adults were exposed to simulated gravitational loads ranging from 100% to 130% of body weight using a novel harness and spring-based system that increased weight without the addition of external mass and without altering limb inertia. Participants walked on a treadmill at a self-selected speed through incremental loading and unloading. Lower limb kinematics and electromyography data were recorded. Traditional measures of gait, as well as more dynamical measures, including angle–angle analysis and phase portraits, were examined. Results: Data demonstrated that a 130% load is sufficient to induce kinematic changes at the hip and knee; however, these changes become significant only during the transition from 130% to lower load levels. Ankle kinematics and electromyography appeared to be unaffected. Conclusions: These findings suggest that the presence of external mass and alterations in limb inertias should be considered seriously as independent variables in future loading studies, and that weight and mass may need to be considered as separate effectors during locomotion. This study also found that the act of loading and unloading elicit distinct responses in the joints of the lower extremities, as well as that it may induce an adaptative after-effect.

1. Introduction

Gravity is a ubiquitous natural phenomenon that pervades every aspect of human experience on Earth. While the acceleration caused by gravity (g) varies from 9.763 to 9.833 m per second squared (m/s2) depending on your terrestrial location, “standard g” is often modeled—and assumed—at 9.81 m/s2 [1]. Though humans experience this acceleration as their own weight—the force borne of their own mass accelerating—the influence of our gravitational environment extends far beyond perception and weightiness. Gravity guides the formation of human bone structure and density [2], influences the discharge rates and amplitudes of cortical and spinal neurons [3], and can alter cellular morphology and metabolism [4]. However, there is arguably no system, structure or behavior affected so demonstrably by gravity as that of human locomotion.
Locomotion studies utilizing environments with increased gravitational effects (hyper-gravity) are extremely limited. Previous work investigating the effects of increased weight on human locomotion have found changes in trunk angles, hip, and ankle range of motion and cadence [5], as well as equilibrium points, stability, efficiency, gait speed, and walk-to-run transitions [6,7,8]. However, the studies contained by these reviews utilized the addition of mass to participant’s bodies in order to increase weight. While the goal of these studies was to examine the effects of externally carried loads, it highlights an important confound as these—and similar studies—relate to the effects of hyper-gravity. The addition of external mass changes an individual’s center of mass location [9], induces a stabilizing forward lean [10,11], and adds impactful, unevenly distributed inertial differences to a body [12,13]. These factors, while related to mass and weight, may be unrelated or tangential to purely gravitational constraints. Therefore, the extent to which these changes are driven by increased weight versus increased inertia on the limbs and trunk remains unknown.
Similarly, it is unclear if the kinematic and electromyographic changes seen during loading are due entirely to the relative load on an individual, or if the previous level of load may work as a factor in these responses. In humans, hysteresis—the dependence of a system on its previous states—has been a dynamic factor exhibited at the cellular level [14,15,16,17], scaling all the way up to cortical networks [18,19], proprioception [20,21] and gait [22,23,24,25,26].
It is possible that the same level of load could elicit different kinematic and EMG changes, depending on whether an individual increased or decreased their relative weight to reach it. However, very few studies have sought to examine hysteresis in human gait through manipulation of the gravitational load. Without a clear understanding as to the specific and exact role of loading and unloading, as well as specific increases in load and mass in these adaptations, it is difficult, if not impossible, to optimize load carriage for real world conditions and outcomes. In this study, we sought to investigate the effects of increased gravitational loading on kinematic and electromyographic variables without the addition of external mass. Specifically, we were interested in examining the kinematics and neuromuscular activity of individuals in simulated gravitational environments ranging from 100%, up to 130% of gravitational load. In this study, these questions were approached through the use of zero-dimensional (traditional kinematic and electromyographic measures) and one-dimensional (angle-angle diagrams and phase portraits) analyses. Previous use of these methods in this lab has found that they provide complementary information not otherwise apparent given the use of a single set of measures [27,28].

2. Methods

2.1. Participants

This study examined 15 healthy adults (25.3 ± 4.7 years; 67.1 ± 4.0 inches; 172.3 ± 42.0 lbs.; 53% female). Participants were not knowingly pregnant and did not have a history of, or any current systemic, degenerative or neuromusculoskeletal injuries or disease that could affect their ability to walk with differential loading for 15 min. This study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board at the University of Houston (IRB#:00002971). Informed consent was obtained from all participants prior to enrollment in the study.

2.2. Kinematic Sensors

Participants were fitted with seven inertial measurement units (IMUs; XSens Awinda—Movella Inc., Henderson, NV, USA) arranged in a lower-body configuration. These sensors were placed bilaterally over the insteps of both feet, as well as anteriorly over the tibia at mid-shank and laterally over the mid-thigh. The final sensor was placed over the sacrum, centered at the S2 tubercle. All XSens sensors were secured by proprietary neoprene straps with non-slip, rubber backings.

2.3. Electromyographic Sensors

Four dry surface electromyographic (EMG) sensors (Model SX230—Biometrics Ltd., Newport, RI, USA) were adhered—using hypo-allergenic, double-sided tape—over the right rectus femoris, biceps femoris, medial gastrocnemius and tibialis anterior. These sensors were placed over the belly of each respective muscle—conduction surfaces in line with the muscle fibers—after any body hair in that location was shaved, and the area was cleaned and scrubbed with an alcohol wipe. Sensor placements were performed in accordance with recommendations by the Surface Electromyography for the Non-Invasive Assessment of Muscles (SENIAM) group. The control system (DataLOG MWX8—Biometrics Ltd., Newport, RI, USA) was mounted on each participant’s low back using a stretchable, Velcro band around their waist.

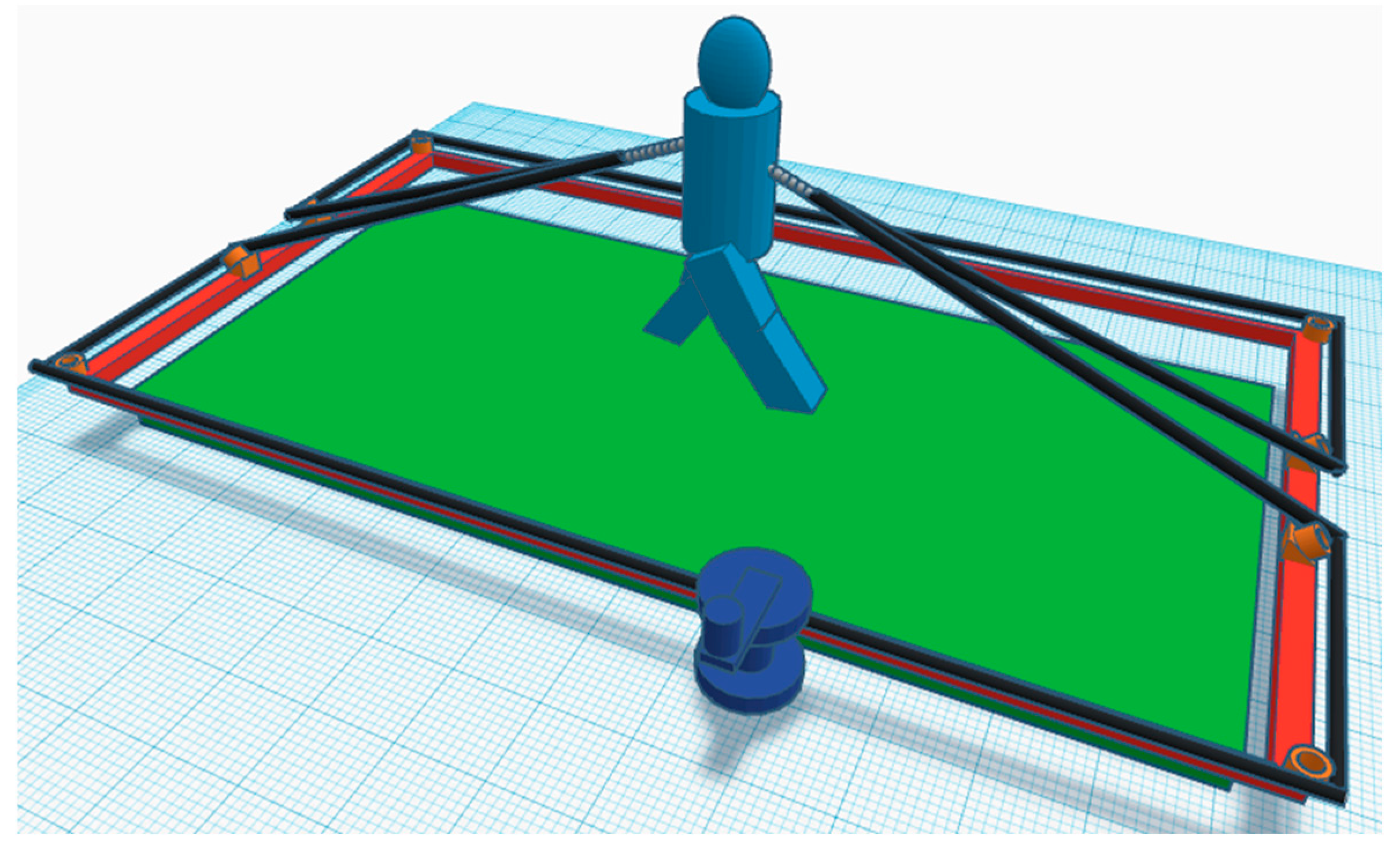
2.4. Loading System and Walking Protocol

Participants were asked to wear a climbing harness with front and back D-ring attachments over their clothing. This harness allowed the participants to be attached to the loading system at two points of equal height, thereby creating an equivalent angle in the front and back ropes that would tether them to the system. This had the intended effect of canceling out any anterior or posterior forces from the system, leaving only a vertical component of load. Similarly, the loading system was connected to the harness by two springs, which allowed individuals in a small degree of normal displacement that would not be available if they were only connected to a taut rope. The entire harness, after being connected to the rope system, added 4 lbs. of weight distributed over the shoulders of the participant (see Figure 1). The entire loading system was built around a treadmill with embedded force plates (Bertec Corporation, Columbus, OH, USA); as such, after donning the harness and being connected to the loading system, an individual’s weight could be calculated and loading parameters for 100%, 110%, 120%, and 130% of normal body weight were established.
Participants were asked to walk at 100% of their normal load for 5 min at a self-selected, comfortable speed (mean speed: 0.78 ± 0.11 m/s). This gave each participant time to become familiar with the loading system, as well as for their gait to stabilize. Following the acclimation period, participants were loaded in 10% increments up to 130% of their body weight, spending 1 full minute at each level. After completing the full minute at 130% of body weight, the protocol was reversed, with participants walking for one minute at 120%, 110%, and 100% of normal load. For all levels of loading and unloading, the treadmill speed remained at the same speed each participant had selected earlier. There was no rest given in between each level besides the time it took to adjust the system to the desired load (≈10 s). Kinematic and EMG data were recorded for the final minute of the acclimatization period, as well as the full minute of walking at all levels of loading and unloading.

2.5. Data Processing

Kinematic data were streamed wirelessly from the XSens IMUs at 60 Hz to a computer running a data collection software suite (MVN Awinda ver. 2022.1). This software collected and internally calculated joint angles for the hip, knee, and ankle, bilaterally. Joint angle waveforms were separated into strides and normalized to 100 points using the peak knee as a reference. Mean, maximum, and minimum angles, as well as range of motion (ROM) were extracted for all joints. Data were exported, separated into strides using peak knee as the reference point, and statistically analyzed in MATLAB (R2019b: 9.7.0.1296695) using custom scripting.
Four channels of EMG data were simultaneously recorded by the waist-mounted control unit, as well as streamed to a computer running a data collection software suite (DataLOG ver: 10.27—Biometrics Ltd., Newport, RI, USA). The 12 g DataLOG control unit was set to sample at 1000 Hz, and provided 1000× amplification gain as well as an automatic anti-aliasing filter prior to streaming. Data collected were exported into MATLAB for processing. Each channel was individually bandpass filtered (20 to 450 Hz) using a 2nd order Butterworth filter. Waveforms were then full wave rectified and enveloped using a low pass filter with an additional 2nd order Butterworth filter utilizing a cutoff frequency of 40 Hz [29]. EMG data were separated into strides and normalized to 100 points using the kinematic peak knee timestamps as a reference. After processing, peak values, root-mean-square (RMS) and integrated areas were calculated for all muscles. We calculated RMS as the square root of the mean of all values squared for each trial. This provides a metric representing the amplitude of the EMG signal [30]. We also calculated integrated areas for each trial to appraise the total electrical signal or drive from the central nervous system to the motorneuron [31,32,33,34].
This study made use of both zero- and one-dimensional analyses, representing traditional kinematic and electromyographic measures as well as phase portraits and angle-angle diagrams. These were created to examine the state spaces of and coordination between the joints of the lower extremity, respectively. Areas were calculated from mean phase portraits using a custom MATLAB script in order to quantify and compare the range of available behaviors.

2.6. Statistical Analysis

Kinematic and electromyographic variables were tested for normality and sphericity using the Kolmogorov–Smirnov and Shapiro–Wilk tests, as well as Mauchly’s test, respectively. Mean, maximum, minimum angles, and range of motion for each joint, as well as peak value, RMS, and integrated areas were compared across all levels of loading using repeated measure ANOVAs. Post hoc testing was performed with paired t-tests, as appropriate.

3. Results

Kolmogorov–Smirnov and Shapiro–Wilk tests revealed all data were normally distributed and Mauchly’s test showed sphericity was preserved.

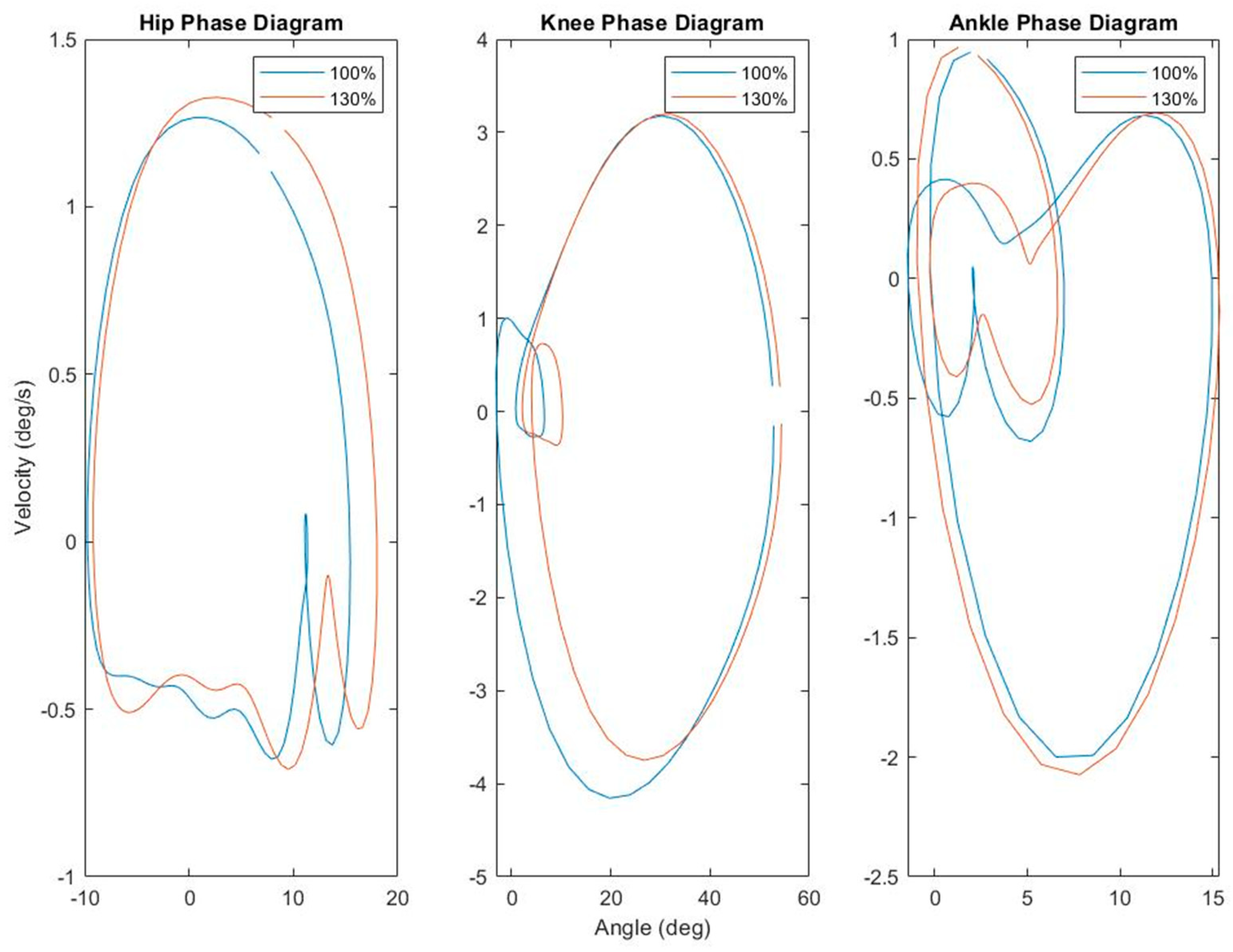
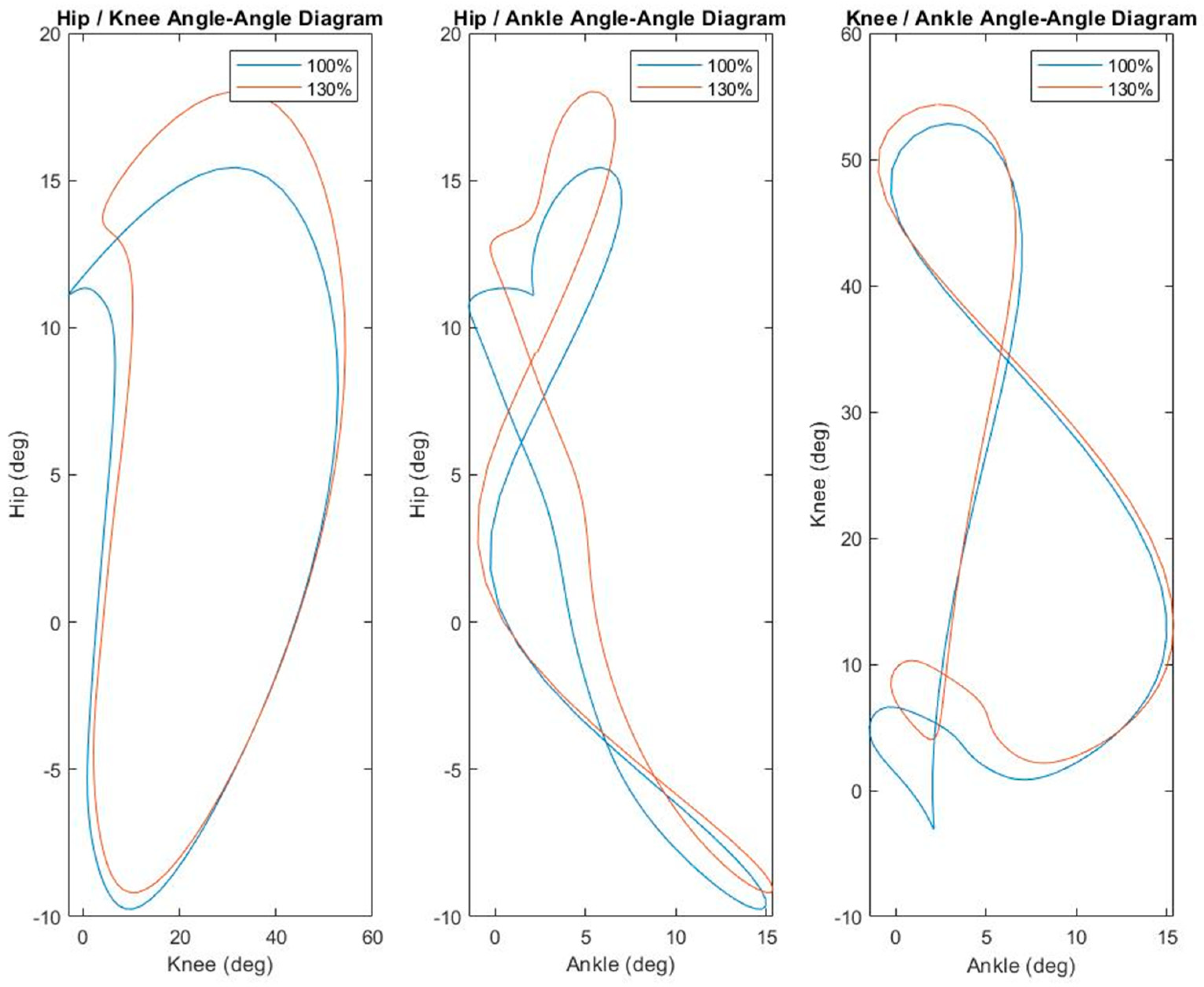
3.1. Kinematics

Hip, knee, and ankle average joint angle waveforms by loading level are presented in Figure 2. Results from repeated measures ANOVA showed loading level had a statistically significant effect on hip mean (F(6,84) = 2.447, p = 0.0314) and max (F(6,84) = 3.073, p = 0.0091) values, as well as knee mean (F(6,84) = 3.172, p = 0.0074), and min (F(6,84) = 4.647, p = 0.0004) values. Pairwise comparisons for the hip and knee are depicted in Table 1. No differences in the ankle variables or any ROM values were found to be significant.

3.2. Electromyography

There were no significant differences in levels of load for peak muscle activity, root-mean-square, or integrated areas for any muscle. Mean and standard deviation EMG values by muscle, variable, and condition can be found in the Supplementary Materials.

4. Discussion

This study examined the effects of simulated gravitational loading (in this case, increased weight without the addition of extra, external mass) between 100% and 130% of body weight on kinematics and electromyographic variables during walking. We were interested in investigating if 130% of body weight was a sufficient load to induce kinematic and EMG changes, as well as examining the individual effects of increased weight without the addition of external mass. Our data revealed that 130% load is sufficient to elicit kinematic changes; however, these changes only appear significant when unloading from 130% to lesser loads. This suggests that walking at 130% and then unloading leads to gait alterations, while simply loading up to 130% does not. It is thus potentially the act of loading or unloading that can elicit changes at these levels, in addition to the actual borne weight.
Preceding studies have demonstrated that human proprioception diminishes in hypogravitational environments [35,36,37]. Indeed, anticipatory postural adjustments disappear below normal gravitational conditions [38] and kinesthetic responses to vibration diminish [39], with these changes being displayed not only kinematically, but also in the human cortical waveforms [40,41]. These studies indicate that alterations in human proprioception due to hypogravity are far reaching, and prevalent. This study found that increased loading at 130% of body weight was sufficient to elicit kinematic changes, but these changes were only clear as participants were unloaded to 120% of their body weight. To be clear, all levels of load from 100% increasing to 130% were not statistically distinct, yet 130% was significantly different from 120% in the knee and hip as participants were unloaded. This suggests that the level of load may not be the only operative factor in our findings; rather, the acts of loading or unloading may elicit distinct kinematic responses. Studies examining the drivers of hysteresis found that hysteretic effects were highest in the situations in which sensory information was the weakest [42] and that perceptual judgements are affected by the lack of or availability of information about an impending action [22].
In the case of this study, movement from a higher level of load (130%) to a lower level of load (120%) would reduce the relative amount of available sensory information. This, in turn, would invoke hysteretic changes in which participants based their expectation of movement in the new environment less on actual environmental cues, and instead more on internal models and expectation.
This concept is supported by Kostyukov and Cherkassky [43], which found muscle spindle discharge rates were higher after stimulation rate increases, and lower after decreases. It is also possible that some of these effects are modified by plantar pressure. Work by Kozlovskaya et al. [44] found that the removal of plantar support led to reflexive decreases in muscle activity and the eventual atony of extensor musculature with concurrent reductions in proprioception [45,46]. Exposure over longer time frames has led to decreased muscle strength-speed properties and motor control alterations [47,48]. Further, some of these alterations were entirely mitigated with plantar pressure stimulation [49]. As load increases, the relative increase in environmental-based proprioceptive information will drive gait behaviors more strongly; on the contrary, as the relative availability of proprioceptive information decreases, the reduction of sensory information will facilitate the use of information from previous levels of loading. This suggests that the effects of unloading, and loading are kinematically distinct, and should likely not be considered equivalent factors, even if used to reach the same level of load.
Phase portraits graphically represent all of the potential states of a dynamic system [50]. In this case, phase portraits depict all of the potential positions (i.e., angles) of a joint, as well as their velocities at that moment. A direct comparison of the portraits for 100% and 130% load (see Figure 3) shows that the movement structure of the joints is mostly preserved, with some stretching and translation as load increases. In combination with the angle-angle diagrams (see Figure 4), we can also see that the coordination between the joints is relatively similar, but also expanded and translated. This suggests that walking-type gait is relatively robust from 100% to 130% of body weight. Interestingly, this mirrors previous investigations of unloading down from full body weight and strengthens the idea that gait is a behavior centered around and suited to our particular gravitational environment. While this study did not present enough load to examine if an entirely new locomotive behavior would emerge at very high percentages of body weight (analogous and opposite to the sub-volitional shift into bounding-type gait found on the moon, for example), the durability of walking-type locomotion appears to be strong up to a 130% load.
We also calculated the areas encircled by our phase portraits for every level of load by joint (see Figure 5). These areas are the two-dimensional spaces created by the outermost set of lines on each graph. These values provide a quantification of the state space of each joint at each level of load; in that way, they can be considered a means to numerically compare the contraction or expansion of the state space between different conditions. In this study, examination of the phase portrait areas of the knee reveals steady contraction of the state space as we increased to 130% of load, before a more than 10% expansion at 120% unloading. Interestingly, this expansion then contracts as we continue to unload, eventually settling at a smaller area than even the original (100%) load condition. The hip areas, on the contrary, consistently expand as we increase to a 120% load—drop slightly at 130%—before contracting significantly as we unload back to a 120% load. Analogously to the knee, the area of the hip phase portrait then continues increasing as load decreases, eventually ending at a larger area than even the original (100%) load condition. This suggests a crucially interesting relationship between the hip and the knee: as the range of available configurations of the hip expands, the knee, inversely, contracts. Similarly, as the hip contracts, the knee expands, and vice versa.
A consideration of the total areas across all three joints (see Table 2) finds a similar trend to the above. As loading increases to 130%, the overall summed areas of the three joints contract slightly before an almost 10% increase with unloading from 130% to 120%. This area remains relatively stable with unloading to 110% and then drops 4% with a return to 100% load. This, and the previous trending (in the hip and knee) highlight two primary ideas. First, this supports the previous assertion that loading and unloading do not appear to be equivalent phenomena. Second, while it is possible that there is an inflection point at 110% with unloading, it is also possible—given the similarity of 120% and 110% when unloading—that this is extinction of a loading induced after-effect. This has major implications for populations in which load-carriage is common in that effective increases or decreases in weight can alter kinematics and movement structure, possibly even for time beyond the actual adding or subtracting of weight. Correspondingly, whether the individual was loaded or unloaded to a certain weight appears to induce specific changes that are not equal across similar loading levels.
Interestingly, the kinematic changes seen in this study were not reflected in EMG data, in which no changes were found across any levels of load. This suggests that muscle activity and kinematic variables can decouple and respond to changes in load differentially. While previous investigations have found that kinematics can be accurately predicted from EMG data alone [51], others have found that kinematic and EMG variables correlate differentially depending on the activity being performed [52]. The results of this study suggest that loading and unloading are activities in which these variables do not track well with each other. It is important to note that this is also potentially due the absence of external mass. In this study, changes in limb inertia and center of gravity were bypassed through the use of our novel loading system. In this way, and in relation to load added over body weight, kinematic variables appear more sensitive than EMG to loading and unloading, and perhaps—given the results of other studies with positive EMG findings—EMG is more sensitive to changes stemming from changes in external mass/inertia. Alternatively, as we only recorded EMG data from four muscles, it is possible that other muscles exhibited changes in response to the loading protocol but were not captured.
The results of this study have important implications for our understanding of the role that gravity plays in human locomotion. This study found that an increase in load can specifically affect both the knee and hip joints, as well as supporting the concept that loading and unloading are independent activities with specific responses. Even the same level of load, reached from higher or lower levels of weight, can elicit different responses. In that way, increases in load appear to drive fewer hysteric changes than decreases (due to the relative availability of proprioceptive sensory information); as such, researchers should take care to ensure that their participants are responding to the correct level of load and should increase their load to the desired level, rather than unweight them.
There are also implications for using this system in long-duration spaceflight, where gravity may not be available to facilitate loading and gait. Indeed, the use of this system in a spacecraft could allow astronauts to maintain healthy levels of load for bone health and venous pumping, despite the absence of gravity, though research would clearly be needed to investigate this.
This study is not without limitations. There is a potential for this system to have influenced gait in some way, though no participant stated they felt the system interfered with their gait, arm swing, or ability to walk on the treadmill at any time. Similarly, participants were queried at all levels of load, and none expressed discomfort or fatigue with the system or any level of load. This study also did not compare its findings to more traditional loading studies examining the effects of external load on gait. As such, it is currently unclear how the effects seen in this study might compare with a heavy backpack or weight vest, for instance. However, while such a comparison was outside the scope of this study, future work should undoubtedly examine this. As the levels of load were not randomized, it is also possible that data could have been influenced by an order effect. This is a constraint of the system itself (individuals need to pass through any lower level of load in order to reach a specific level) which other potential users should be aware of.
This study was a novel investigation of an easily reproducible loading system that can increase the load of an individual, without the addition of external mass. Increased gravitational loading up to 130% of normal body weight can alter hip and knee kinematics but does not appear to affect the ankle joint nor does it appear to elicit changes in electromyographic variables. These findings suggest that the presence of external mass and alterations in limb inertias should be considered seriously as independent variables in future loading studies, and that weight and mass may need to be considered as separate effectors during locomotion. This study also found that the act of loading and unloading elicit distinct responses in the joints of the lower extremities, as well as that it may induce an adaptative after-effect.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/biomechanics5020031/s1, Table S1: EMG Peak by Muscle and Condition; Table S2: EMG RMS by Muscle and Condition; Table S3: EMG AUC by Muscle and Condition.

Author Contributions

All authors were involved in conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, writing—review and editing visualization, supervision, project administration. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board at the University of Houston (IRB#:00002971).

Informed Consent Statement

Informed consent was obtained from all participants involved in the study.

Data Availability Statement

Data can be made available upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hirt, C.; Claessens, S.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. New ultrahigh-resolution picture of Earth’s gravity field. Geophys. Res. Lett. 2013, 40, 4279–4283. [Google Scholar] [CrossRef]
  2. Wolff, J. Das Gesetz der Transformation der Knochen; Hirchwild: Berlin, Germany, 1892. [Google Scholar]
  3. Krasnov, I.B. Gravitational neuromorphology. Adv. Space Biol. Med. 1994, 4, 85–110. [Google Scholar] [PubMed]
  4. Tairbekov, M.G. Kletka kak gravitatsionno-zavisimaia biomekhanicheskaia sistema [The cell as a gravity-dependent biomechanic system]. Aviakosm. Ekolog. Med. 2000, 34, 3–17. [Google Scholar] [PubMed]
  5. Liew, B.; Morris, S.; Netto, K. The effect of backpack carriage on the biomechanics of walking: A systematic review and preliminary meta-analysis. J. Appl. Biomech. 2016, 32, 614–629. [Google Scholar] [CrossRef] [PubMed]
  6. Arellano, C.J.; O’Connor, D.P.; Layne, C.; Kurz, M.J. The Independent Effect of Added Mass on the Stability of the Sagittal Plane Leg Kinematics during Steady-State Human Walking. J. Exp. Biol. 2009, 212 Pt 12, 1965–1970. [Google Scholar] [CrossRef] [PubMed]
  7. Arellano, C.J.; Layne, C.S.; O’Connor, D.P.; Scott-Pandorf, M.; Kurz, M.J. Does Load Carrying Influence Sagittal Plane Locomotive Stability? Med. Sci. Sports Exerc. 2009, 41, 620–627. [Google Scholar] [CrossRef]
  8. Boffey, D.; Harat, I.; Gepner, Y.; Frosti, C.L.; Funk, S.; Hoffman, J.R. The physiology and biomechanics of load carriage performance. Mil. Med. 2019, 184, e83–e90. [Google Scholar] [CrossRef]
  9. Singh, T.; Koh, M. Effects of backpack load position on spatiotemporal parameters and trunk forward lean. Gait Posture 2009, 29, 49–53. [Google Scholar] [CrossRef]
  10. Atwells, R.L.; Birrell, S.A.; Hooper, R.H.; Mansfield, N.J. Influence of carrying heavy loads on soldiers’ posture, movements and gait. Ergonomics 2006, 49, 1527–1537. [Google Scholar] [CrossRef]
  11. Polcyn, A.F.; Bensel, C.K.; Harman, E.A.; Obusek, J.P. The Effects of Load Weight: A Summary Analysis of Maximal Performance, Physiological, and Biomechanical Results from Four Studies on Load–Carriage Systems; United States Army Research Institute of Environmental Medicine Technical Report: Natick, MA, USA, 2001. [Google Scholar]
  12. Haddox, A.G.; Hausselle, J.; Azoug, A. Changes in segmental mass and inertia during pregnancy: A musculoskeletal model of the pregnant woman. Gait Posture 2020, 76, 389–395. [Google Scholar] [CrossRef] [PubMed]
  13. Jensen, R.K.; Nassas, G. Growth of segment principal moments of inertia between four and twenty years. Med. Sci. Sports Exerc. 1988, 20, 594–604. [Google Scholar] [CrossRef] [PubMed]
  14. Villalba-Galea, C.A. Hysteresis in voltage-gated channels. Channels 2017, 11, 140–155. [Google Scholar] [CrossRef]
  15. Villalba-Galea, C.A.; Chiem, A.T. Hysteretic Behavior in Voltage-Gated Channels. Front. Pharmacol. 2020, 11, 579596. [Google Scholar] [CrossRef] [PubMed]
  16. Wei, J.Y.; Simon, J.; Randić, M.; Burgess, P.R. Joint angle signaling by muscle spindle receptors. Brain Res. 1986, 370, 108–118. [Google Scholar] [CrossRef]
  17. Xiao, Y.-F.; Chandler, N.; Dobrzynski, H.; Richardson, E.S.; TenBroek, E.M.; Wilhelm, J.J.; Sharma, V.; Varghese, A.; Boyett, M.R.; Iaizzo, P.A.; et al. Hysteresis in human HCN4 channels: A crucial feature potentially affecting sinoatrial node pacemaking. Sheng Li Xue Bao 2010, 62, 1–13. [Google Scholar]
  18. Kim, H.; Moon, J.-Y.; Mashour, G.A.; Lee, U. Mechanisms of hysteresis in human brain networks during transitions of consciousness and unconsciousness: Theoretical principles and empirical evidence. PLoS Comput. Biol. 2018, 14, e1006424. [Google Scholar] [CrossRef]
  19. Sayal, A.; Sousa, T.; Duarte, J.V.; Costa, G.N.; Martins, R.; Castelo-Branco, M. Identification of competing neural mechanisms underlying positive and negative perceptual hysteresis in the human visual system. Neuroimage 2020, 221, 117153. [Google Scholar] [CrossRef] [PubMed]
  20. Artz, N.J.; Adams, M.A.; Dolan, P. Sensorimotor function of the cervical spine in healthy volunteers. Clin. Biomech. 2015, 30, 260–268. [Google Scholar] [CrossRef]
  21. Weiler, H.T.; Awiszus, F. Influence of hysteresis on joint position sense in the human knee joint. Exp. Brain Res. 2000, 135, 215–221. [Google Scholar] [CrossRef]
  22. Abdolvahab, M.; Carello, C. Functional distance in human gait transition. Acta Psychol. 2015, 161, 170–176. [Google Scholar] [CrossRef]
  23. Aoi, S.; Yamashita, T.; Tsuchiya, K. Hysteresis in the gait transition of a quadruped investigated using simple body mechanical and oscillator network models. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 83 Pt 1, 061909. [Google Scholar] [CrossRef] [PubMed]
  24. Aoi, S.; Katayama, D.; Fujiki, S.; Tomita, N.; Funato, T.; Yamashita, T.; Senda, K.; Tsuchiya, K. A stability-based mechanism for hysteresis in the walk-trot transition in quadruped locomotion. J. R. Soc. Interface 2013, 10, 20120908. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
  25. Mohler, B.J.; Thompson, W.B.; Creem-Regehr, S.H.; Pick, H.L., Jr.; Warren, W.H., Jr. Visual flow influences gait transition speed and preferred walking speed. Exp. Brain Res. 2007, 181, 221–228. [Google Scholar] [CrossRef]
  26. Thorstensson, A.; Roberthson, H. Adaptations to changing speed in human locomotion: Speed of transition between walking and running. Acta Physiol. Scand. 1987, 131, 211–214. [Google Scholar] [CrossRef] [PubMed]
  27. Layne, C.S.; Malaya, C.A.; Young, D.R.; Suter, B.; Holder, J.L., Jr. Comparison of Treadmill Gait Between a Pediatric-Aged Individual with SYNGAP1-Related Intellectual Disability and a Fraternal Twin. Front. Hum. Neurosci. 2022, 16, 918918. [Google Scholar] [CrossRef] [PubMed]
  28. Layne, C.S.; Malaya, C.A.; Ravindran, A.S.; John, I.; Francisco, G.E.; Contreras-Vidal, J.L. Distinct Kinematic and Neuromuscular Activation Strategies During Quiet Stance and in Response to Postural Perturbations in Healthy Individuals Fitted With and Without a Lower-Limb Exoskeleton. Front. Hum. Neurosci. 2022, 16, 942551. [Google Scholar] [CrossRef]
  29. Winter, D.A.; Rau, G.; Kadefors, R.; Broman, H.; De Luca, C.J. Units, Terms and Standards in the Reporting of EMG Research. A Report of the Ad Hoc Committee of the International Society of Electrophysiological Kinesiology; Boston University: Boston, MA, USA, 1980. [Google Scholar]
  30. Cifrek, M.; Medved, V.; Tonković, S.; Ostojić, S. Surface EMG based muscle fatigue evaluation in biomechanics. Clin. Biomech. 2009, 24, 327–340. [Google Scholar] [CrossRef]
  31. Barton, P.M.; Hayes, K.C. Neck flexor muscle strength, efficiency, and relaxation times in normal subjects and subjects with unilateral neck pain and headache. Arch. Phys. Med. Rehabil. 1996, 77, 680–687. [Google Scholar] [CrossRef]
  32. Carpentier, A.; Duchateau, J.; Hainaut, K. Motor unit behaviour and contractile changes during fatigue in the human first dorsal interosseus. J. Physiol. 2001, 534 Pt 3, 903–912. [Google Scholar] [CrossRef]
  33. Linssen, W.H.J.P.; Stegeman, D.F.; Joosten, E.M.G.; Notermans, S.L.H.; van’t Hof, M.A.; Binkhorst, R.A. Variability and interrelationships of surface EMG parameters during local muscle fatigue. Muscle Nerve 1993, 16, 849–856. [Google Scholar] [CrossRef]
  34. van der Hoeven, J.H.; van Weerden, T.W.; Zwarts, M.J. Long-lasting supernormal conduction velocity after sustained maximal isometric contraction in human muscle. Muscle Nerve 1993, 16, 312–320. [Google Scholar] [CrossRef] [PubMed]
  35. Bringoux, L.; Blouin, J.; Coyle, T.; Ruget, H.; Mouchnino, L. Effect of gravity-like torque on goal-directed arm movements in microgravity. J. Neurophysiol. 2012, 107, 2541–2548. [Google Scholar] [CrossRef] [PubMed]
  36. Lackner, J.R.; DiZio, P. Gravitoinertial force level affects the appreciation of limb position during muscle vibration. Brain Res. 1992, 592, 175–180. [Google Scholar] [CrossRef]
  37. Young, L.R.; Oman, C.M.; Merfeld, D.; Watt, D.; Roy, S.; DeLuca, C.; Balkwill, D.; Christie, J.; Groleau, N.; Jackson, D.K.; et al. Spatial orientation and posture during and following weightlessness: Human experiments on Spacelab Life Sciences 1. J. Vestib. Res. 1993, 3, 231–239. [Google Scholar] [CrossRef]
  38. Mouchnino, L.; Cincera, M.; Fabre, J.C.; Assaiante, C.; Amblard, B.; Pedotti, A.; Massion, J. Is the regulation of the center of mass maintained during leg movement under microgravity conditions? J. Neurophysiol. 1996, 76, 1212–1223. [Google Scholar] [CrossRef] [PubMed]
  39. Roll, R.; Gilhodes, J.C.; Roll, J.P.; Popov, K.; Charade, O.; Gurfinkel, V. Proprioceptive information processing in weightlessness. Exp. Brain Res. 1998, 122, 393–402. [Google Scholar] [CrossRef]
  40. Mouchnino, L.; Lhomond, O.; Morant, C.; Chavet, P. Plantar Sole Unweighting Alters the Sensory Transmission to the Cortical Areas. Front. Hum. Neurosci. 2017, 11, 220. [Google Scholar] [CrossRef]
  41. Saradjian, A.H.; Tremblay, L.; Perrier, J.; Blouin, J.; Mouchnino, L. Cortical facilitation of proprioceptive inputs related to gravitational balance constraints during step preparation. J. Neurophysiol. 2013, 110, 397–407. [Google Scholar] [CrossRef]
  42. Thiel, S.D.; Bitzer, S.; Nierhaus, T.; Kalberlah, C.; Preusser, S.; Neumann, J.; Nikulin, V.V.; van der Meer, E.; Villringer, A.; Pleger, B. Hysteresis as an implicit prior in tactile spatial decision making. PLoS ONE 2014, 9, e89802. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
  43. Kostyukov, A.I.; Cherkassky, V.L. Interaction of the movement-dependent, extrafusal and fusimotor after-effects in the firing of the primary spindle endings. Neuroscience 1997, 76, 1257–1266. [Google Scholar] [CrossRef]
  44. Kozlovskaya, I.B.; Sayenko, I.V.; Sayenko, D.G.; Miller, T.F.; Khusnutdinova, D.R.; Melnik, K.A. Role of support afferentation in control of the tonic muscle activity. Acta Astronaut. 2007, 60, 285–294. [Google Scholar] [CrossRef]
  45. Shenkman, B.S.; Kozlovskaya, I.B. Cellular responses of human postural muscle to dry immersion. Front. Physiol. 2019, 10, 187. [Google Scholar] [CrossRef] [PubMed]
  46. Shenkman, B.S.; Grigoriev, A.I.; Kozlovskaya, I.B. Gravity mechanisms in tonic motor system. Neurophysiological and Muscle Aspects. Hum. Physiol. 2017, 43, 578–590. [Google Scholar] [CrossRef]
  47. Saveko, A.; Brykov, V.; Kitov, V.; Shpakov, A.; Tomilovskaya, E. Adaptation in Gait to Lunar and Martian Gravity Unloading During Long-Term Isolation in the Ground-Based Space Station Model. Front. Hum. Neurosci. 2022, 15, 742664. [Google Scholar] [CrossRef]
  48. Shpakov, A.V.; Artamonov Voronov, A.A.; Melnik, K.A. Influence of immersion hypokinesia on kinematic and electromyographic characteristics of human locomotion. Aviakosm. Ekolog. Med. 2008, 5, 24–29. [Google Scholar]
  49. Litvinova, K.S.; Vikhlyantsev, I.M.; Kozlovskaya, I.B.; Podlubnaya, Z.A.; Shenkman, B.S. Effects of artificial support stimulation on fiber and molecular characteristics of soleus muscle in men exposed to 7-day dry immersion. J. Gravit. Physiol. 2004, 11, 131–132. [Google Scholar]
  50. Stergiou, N. Innovative Analyses of Human Movement; Human Kinetics: Champaign, IL, USA, 2004. [Google Scholar]
  51. Manzano, M.; Serrancolí, G. A factorization-based algorithm to predict EMG data using only kinematics information. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3463. [Google Scholar] [CrossRef]
  52. Mauntel, T.C.; Cram, T.R.; Frank, B.S.; Begalle, R.L.; Norcross, M.F.; Blackburn, J.T.; Padua, D.A. Kinematic and neuromuscular relationships between lower extremity clinical movement assessments. Sports Biomech. 2018, 17, 273–284. [Google Scholar] [CrossRef]
Biomechanics 05 00031 g001
Figure 1. Loading system. In this figure, the participant (light blue humanoid) walks over an instrumented treadmill (green). They are connected to the rope system (black) by two springs (silver) that attach to a harness (not pictured). The ropes distribute vertical tension by way of 8 pulleys (orange) arranged around a metal frame (red). The tension in the rope system can be modulated by way of a crank pulley (dark blue) and vertical load is calculated by kinetic sensors embedded in the treadmill.
Figure 1. Loading system. In this figure, the participant (light blue humanoid) walks over an instrumented treadmill (green). They are connected to the rope system (black) by two springs (silver) that attach to a harness (not pictured). The ropes distribute vertical tension by way of 8 pulleys (orange) arranged around a metal frame (red). The tension in the rope system can be modulated by way of a crank pulley (dark blue) and vertical load is calculated by kinetic sensors embedded in the treadmill.
Biomechanics 05 00031 g001
Biomechanics 05 00031 g002
Figure 2. Hip, knee, and ankle joint angles by loading level. Each plot contains the kinematic waveforms for its respective loading (in red) and unloading (in blue) condition, along with a 2-standard deviation shaded area around each waveform. All 130% load conditions are in black to avoid any confusion, as only a single waveform is present.
Figure 2. Hip, knee, and ankle joint angles by loading level. Each plot contains the kinematic waveforms for its respective loading (in red) and unloading (in blue) condition, along with a 2-standard deviation shaded area around each waveform. All 130% load conditions are in black to avoid any confusion, as only a single waveform is present.
Biomechanics 05 00031 g002
Biomechanics 05 00031 g003
Figure 3. Phase portrait comparisons of 100% and 130% load. This graph displays phase portraits for the hip, knee, and ankle. Though there is some expansion of the range of available behaviors for the hip and knee—suggesting they are most sensitive to loading—the ankle appears to be mostly unaffected by the increase in load.
Figure 3. Phase portrait comparisons of 100% and 130% load. This graph displays phase portraits for the hip, knee, and ankle. Though there is some expansion of the range of available behaviors for the hip and knee—suggesting they are most sensitive to loading—the ankle appears to be mostly unaffected by the increase in load.
Biomechanics 05 00031 g003
Biomechanics 05 00031 g004
Figure 4. Angle-angle diagram comparisons of 100% and 130% load. This graph shows that the coordination strategies between the joints of the lower extremities are mostly preserved as load was increased. It is important to note, however, that there was distinct stretching and skewing of the shapes for all three graphs. This suggests that, although the general coordinative structure of movement between these joints was similar, they were not unaffected by load. Indeed, even 130% of body weight was enough to shift some aspects of the coordinative structure of the hip, knee, and ankle.
Figure 4. Angle-angle diagram comparisons of 100% and 130% load. This graph shows that the coordination strategies between the joints of the lower extremities are mostly preserved as load was increased. It is important to note, however, that there was distinct stretching and skewing of the shapes for all three graphs. This suggests that, although the general coordinative structure of movement between these joints was similar, they were not unaffected by load. Indeed, even 130% of body weight was enough to shift some aspects of the coordinative structure of the hip, knee, and ankle.
Biomechanics 05 00031 g004
Biomechanics 05 00031 g005
Figure 5. Phase portraits with calculated areas. The top row represents the hip phase portraits, the middle row is the knee phase portraits, and the bottom row is the ankle phase portraits. The area value represents the two-dimensional area—in pixels—occupied by each shape. These values can be considered a quantitative estimation of the range of available behaviors across each loading condition.
Figure 5. Phase portraits with calculated areas. The top row represents the hip phase portraits, the middle row is the knee phase portraits, and the bottom row is the ankle phase portraits. The area value represents the two-dimensional area—in pixels—occupied by each shape. These values can be considered a quantitative estimation of the range of available behaviors across each loading condition.
Biomechanics 05 00031 g005
Table 1. Hip and knee joint angles—pairwise comparisons.
Table 1. Hip and knee joint angles—pairwise comparisons.
Condition μ ° ± std p Value
HipMean1004.6 ± 7.60.1241
1105.2 ± 5.90.4919
1204.8 ± 8.60.0647
1306.4 ± 8.5
120 U2.6 ± 8.30.0138 *
110 U4.5 ± 7.00.0642
100 U5.3 ± 6.50.3423
Max10019.3 ± 10.90.0463 *
11020.5 ± 10.20.4931
12020.3 ± 12.10.1595
13022.0 ± 13.5
120 U16.7 ± 12.90.0311 *
110 U19.2 ± 11.00.0488 *
100 U21.2 ± 9.80.6390
KneeMean10015.1 ± 5.10.0001 *
11016.2 ± 4.90.0068 *
12016.4 ± 4.60.0113 *
13017.8 ± 4.9
120 U16.1 ± 3.80.1316
110 U15.4 ± 5.10.0082 *
100 U16.7 ± 4.70.1020
Min100−3.1 ± 5.30.0012 *
110−1.7 ± 4.20.0055 *
120−1.1 ± 3.70.0027 *
1301.0 ± 3.9
120 U−2.2 ± 6.30.0554
110 U−2.6 ± 5.60.0081 *
100 U−0.6 ± 4.80.0782
* denotes significance (p < 0.05). All pair-wise comparisons depicted represent the specified measure at that level of load versus 130% load. “U” denotes the specified level of load as it was unloaded to.
Table 2. Summed areas of phase portraits and percentage change.
Table 2. Summed areas of phase portraits and percentage change.
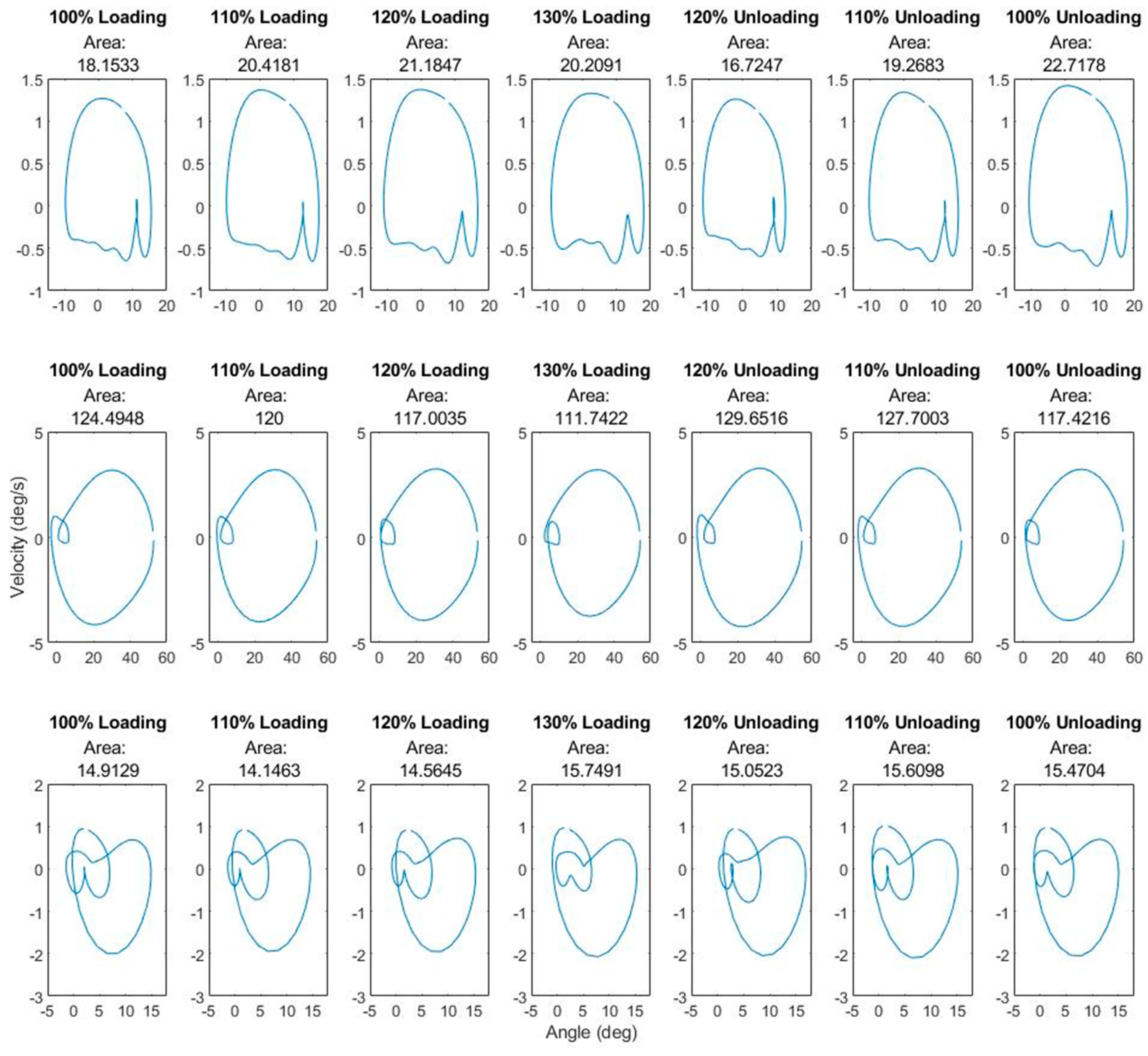
Condition% LoadSummed Areas of Hip, Knee and Ankle Phase Portraits% Change from Previous Level of Loading
Loading100%157.561
110%154.564−2%
120%152.753−1.1%
130%147.700−3.3%
Unloading120%161.429+9.2%
110%162.578+0.7%
100%155.610−4.2%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Malaya, C.A.; Parikh, P.J.; Smith, D.L.; Layne, C.S. Effects of Simulated Hyper-Gravity on Lower Limb Kinematics and Electromyography During Walking. Biomechanics 2025, 5, 31. https://doi.org/10.3390/biomechanics5020031

AMA Style

Malaya CA, Parikh PJ, Smith DL, Layne CS. Effects of Simulated Hyper-Gravity on Lower Limb Kinematics and Electromyography During Walking. Biomechanics. 2025; 5(2):31. https://doi.org/10.3390/biomechanics5020031

Chicago/Turabian Style

Malaya, Christopher A., Pranav J. Parikh, Dean L. Smith, and Charles S. Layne. 2025. "Effects of Simulated Hyper-Gravity on Lower Limb Kinematics and Electromyography During Walking" Biomechanics 5, no. 2: 31. https://doi.org/10.3390/biomechanics5020031

APA Style

Malaya, C. A., Parikh, P. J., Smith, D. L., & Layne, C. S. (2025). Effects of Simulated Hyper-Gravity on Lower Limb Kinematics and Electromyography During Walking. Biomechanics, 5(2), 31. https://doi.org/10.3390/biomechanics5020031

Article Metrics

Back to TopTop