Abstract
This paper explores the adaptation of pseudo-rigid-body models (PRBMs) for simulating large geometric nonlinear deflections in passive exoskeletons, expanding upon their traditional application in small compliant systems. Utilizing the AnyBody modeling system, this study employs force-dependent kinematics to reverse the conventional simulation process, enabling the calculation of forces from the deformation of PRBMs. A novel approach, termed “Constraint Force”, is introduced to facilitate this computation. The approach is thoroughly validated through comparative analysis with laboratory trials involving a beam under bending loads. To demonstrate the functionality, the final segment of this study conducts a biomechanical simulation incorporating motion capture data from a lifting test, employing a novel passive exoskeleton equipped with flexible spring elements. The approach is meticulously described to enable easy adaptation, with an example code for practical application. The findings present a user-friendly and visually appealing simulation solution capable of effectively modeling complex mechanical load cases. However, the validation process highlights significant systematic errors in the direction and amplitude of the calculated forces (20% and 35%, respectively, in the worst loading case) compared to the laboratory results. These discrepancies emphasize the inherent accuracy challenges of the “Constraint Force” approach, pointing to areas for ongoing research and enhancement of PRBM methods.
1. Introduction
1.1. Introducing Biomechanical Simulations
Biomechanical simulations serve as a pivotal tool in the intersection of engineering and biology, offering insights into the mechanical behaviors of biological systems under various conditions. These simulations employ principles from physics and engineering to model and analyze the movements and interactions of biological structures, providing a deeper understanding of their functional mechanics.
Biomechanical simulation has seen remarkable improvements, driven by heightened interest [] and technological advancements. These simulations are critical in understanding internal biomechanical processes that are inaccessible through traditional experimental observations, such as internal stress distributions, strain, and energy within biological tissues. Numerical simulation technologies can undertake detailed parametric analyses efficiently and cost-effectively, adjusting various model parameters, including materials, sizes, and gravitational effects, to perform large-scale comparative analyses []. This capability is particularly valuable in the development and validation of exoskeletons [,,,,,,], which are designed to interact complexly with the human body.
1.2. Passive Exoskeletons in Biomechanical Simulations
Passive exoskeletons, designed to mitigate work-related musculoskeletal disorders (WMSDs), present a significant advancement in enhancing workforce health and productivity. These disorders constitute one of the most significant burdens on the health of employees engaged in physically demanding jobs. Passive exoskeletons offer a viable solution by supporting the body’s musculoskeletal system without the need for active power sources, thus reducing fatigue and the likelihood of injuries while improving overall work efficiency. Traditionally, biomechanical simulations of exoskeletons have predominantly utilized models with rigid elements. While these models are beneficial in understanding the biomechanics of human–exoskeleton interactions under controlled scenarios, they fall short of accurately capturing the nuanced behaviors of systems that incorporate flexible components. This limitation is critical as passive exoskeletons often employ flexible beams to store and release energy, a key feature that enhances their functionality and user comfort. Moreover, the interest in passive exoskeletons extends due to their cost-effectiveness and lightweight nature, essential for widespread adoption in industrial settings. Notable examples of such exoskeletons include Skelex 360-XFR by Skelex B.V., Laevo Flex by Laevo Exoskeletons, Hapo and Hapo MS by ErgoSanté Ergonomie Solidaire, VT-Lowe’s developed by the Department of Mechanical Engineering at Virginia Tech College of Engineering, and SPEXOR by the Robotics and Multibody Mechanics Research Group. These models highlight the diverse applications of passive exoskeletons and underscore the need for advanced simulation techniques that can effectively model these devices’ dynamic and flexible properties.
1.3. Advances in the Simulation of Flexible Beams in Biomechanical Applications
Biomechanical simulations have progressively incorporated more complex models to simulate the behavior of flexible beams and other related components. Various publications have explored different methodologies for more accurate simulations of these elements, reflecting their real-world dynamic behavior more closely. One approach involves using the AnyBody modeling system (AnyBody) to simulate flexible elements. This method sequences multiple segments, calculating the deformation of each segment under geometrically linear conditions [].
In the realm of biomechanical simulations, the PRBM has demonstrated considerable utility across various applications, enhancing the understanding of flexible dynamics within these systems. For instance, PRBMs have been effectively employed in designing compliant leg exoskeleton focused on gravity compensation []. Similarly, the method has been adapted to replace slender beams with chains of rigid segments, which allows for detailed simulation of how these beams flex and bend under load []. This methodology has also been applied to the J-type bionic foot, requiring precise deformation calculations to simulate accurately the complex movements associated with human foot mechanics []. Further, PRBMs have been utilized to analyze circular beams in compliant mechanisms []. Another innovative application includes the simulation of flexible objects, such as cables, in robot manipulation tasks, which are essential for developing robots capable of interacting with their environments naturally and effectively [].
These examples illustrate the breadth of PRBM applications in biomechanical simulations, highlighting its role in bridging the gap between theoretical models and practical, real-world functionalities. However, the traditional approach within these studies has been to calculate deformations based on predetermined forces. This method does not account for scenarios where the actual forces might be unknown or difficult to measure directly. Thus, there remains an unexplored potential in reversing this process—using observed deformations to calculate the unknown forces. This work’s pivotal achievement, the reversal, is realized using integrated iterative methods, specifically force-dependent kinematics (FDK), to calculate the force-dependent kinematics of segments in the human body.
1.4. The Pseudo-Rigid-Body Model Approach
The PRBM represents a new approach in biomechanical simulations, addressing significant limitations posed by traditional rigid body models that fail to simulate large deformations characterized by geometric nonlinearities accurately. The PRBM’s theoretical foundation is deeply rooted in classical mechanics, specifically the principles initially articulated by Bernoulli and subsequently refined by Euler in what is now known as Euler–Bernoulli Beam Theory []. According to this theory, the curvature at any given point along a deflected beam is proportionally related to the bending moment at that point.
Exploiting this fundamental principle, the PRBM methodology replaces a continuous flexible beam with an assembly of discrete rigid segments interconnected by joints, as seen in Figure 1. The deflection of the beam is thus modeled through deformations localized at these joints, with the curvature being quantitatively represented by the angular displacement between successive segments. This proportional relationship between the angular displacement and the bending moments faithfully adheres to Bernoulli’s original postulate, thereby preserving the physical accuracy of the simulation.
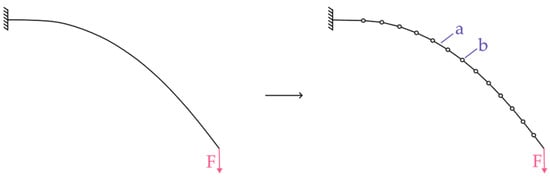
Figure 1.
The basic idea of a pseudo-rigid-body model (PRBM). A continuous flexible beam is replaced with a chain of rigid segments (a) connected with joints (b). Every joint has a torsion stiffness in the direction of bending.
One of the earliest implementations of the PRBM involved a rudimentary torsion spring system composed of a single joint and two segments, predominantly utilized within compliant mechanisms in two-dimensional applications []. These applications traditionally required the computation of deformations from a known set of forces; however, applying the PRBM in biomechanical scenarios often necessitates reversing of this process. Specifically, it requires the determination of unknown forces based on observed deformations, a complex computational challenge that demands iterative resolution methods. Modern simulation platforms such as AnyBody have integrated capabilities that facilitate these sophisticated calculations, thus enhancing the practical utility of the PRBM in complex biomechanical analyses.
To achieve an accurate simulation that mirrors real-world behaviors, the torsional stiffness of the joints within the PRBM must be meticulously calibrated to align with the mechanical properties of the actual beam being modeled. This critical calibration process involves rigorous empirical testing and iterative adjustments to the model parameters to ensure that the simulated deformations accurately reflect the expected physical outcomes under analogous load conditions.
1.5. Methodological Framework and Purpose
This chapter outlines the structured approach adopted in this work to simulate forces arising from significant deflections of flexible beams using the AnyBody software v.7.4.2, leveraging the PRBM technique previously explained. The workflow begins with the determination of the Stiffness Coefficient of the torsional joints, a parameter that needs to match the physical properties of the actual beam being modeled. This initial step sets the groundwork for subsequent simulations and requires validation to ensure its accuracy and reliability in reflecting real-world behaviors.
Following the calibration of the Stiffness Coefficient, the next phase involves doping a specific method to implement the PRBM concept within the AnyBody software. This process utilizes the software’s force-dependent kinematics (FDK) capabilities, allowing for iterative deformation calculations from applied forces. An integral component of this implementation is introducing a novel method called the Constraint Force approach. This technique involves applying forces in a controlled manner to deform the PRBM according to the simulated conditions, thereby enabling the model to approximate the actual mechanical response of the beam under load.
The accuracy and of the Constraint Force method must then be thoroughly validated. This validation process is crucial to confirm that the model not only behaves as expected under theoretical conditions but also provides reliable and accurate results that can be replicated in practical applications. A purely numerical analysis is carried out to validate the constraint force. A PRBM is deflected by an initial force and then compared to assess the accuracy with which the constraint force can reproduce this initial deformation.
To demonstrate the practical applicability and versatility of the PRBM approach, it is applied to a newly developed, patented passive exoskeleton design. This implementation showcases the model’s potential in an exoskeleton application, highlighting its utility not just in theoretical simulations but also in enhancing the design and functionality of biomechanical devices. The simulation is carried out purely numerically, a comparison with measured values will be published in a separate publication.
Summarizing this work, this paper introduces a novel application of PRBM in biomechanical simulations, explicitly targeting the simulation of large geometric nonlinear deflections in passive exoskeletons. The primary purpose of this study is to expand the conventional use of PRBMs beyond small compliant systems, addressing the complex dynamics of exoskeleton interactions with the human body. Employing the AnyBody software and integrating FDK, this research reverses the traditional simulation process to calculate forces from observed deformations, thereby enhancing the understanding of internal biomechanical processes. A significant portion of this work focuses on developing and validating a new method, the Constraint Force, designed to facilitate the PRBM idea within the simulation software. Despite revealing certain limitations and systematic errors in the validation process, this method demonstrates substantial potential for a broad range of applications, emphasizing its adaptability and the ease of incorporating additional forces into the model. This study aims to contribute to the field of biomechanics by providing a more versatile and visually intuitive simulation tool, encouraging further exploration and refinement in the modeling of complex biomechanical systems.
Moreover, the scope of this approach extends beyond the specific case of exoskeletons. It holds promise for a broad spectrum of applications where it is critical to understand the interaction between structural flexibility and applied forces. To facilitate wider adoption and implementation of this methodology, an AnyScript file complete with an example has been made publicly available on GitHub. This resource is intended to assist others in deploying this innovative approach in their own projects, thereby broadening the impact and utility of the PRBM method in various scientific and engineering domains.
2. Materials and Methods
2.1. Measurement of the Stiffness Coefficient
The measurement of the Stiffness Coefficient is the initial step in utilizing the PRBM approach. This section details the experimental setup and methodology used to measure the stiffness characteristics of the beam, which will be later used for the torsional springs in the joints within the simulation model.
The experiment utilizes a fiberglass beam in an exoskeleton prototype, measuring 24 × 4 mm. To prepare for testing, the beam is carefully marked with equidistant dots along its side, each 80 mm apart. It is securely mounted with a free length of 800 mm. To measure the deflection, the beam is subjected to four distinct loads, each carefully selected to represent typical forces the beam might encounter during the regular operation of an exoskeleton. A camera (Sony ZV-E10) captures a 4000 × 6000 pixel picture from a 4.5 m distance of the deflected beam, as seen in Figure 2. The photographs are then analyzed in Matlab R2021a, and a conversion of the pixels into meters using the checkered background is performed. Each point indicated on the bar is digitally traced. Vector calculation is executed to determine the angle of deflection in each traced point, and the angle of the two straight lines from the nearest points is formed. Additionally, the torque resulting from the bending load, calculated via the lever arm effect at every point, is calculated. The lever arm is defined as the distance from each point to the force application point at the tip of the beam perpendicular to the direction of force application. These two values at every point are plotted against each other to visualize the beam’s response to load, as seen in Figure 3. The Stiffness Coefficient is calculated using the linear least square method applied to all points from the three load cases. Therefore, a slope and Stiffness Coefficient of 1.44 Nm/° is calculated for this specific beam.

Figure 2.
Laboratory setup for deforming the flexible beam under defined loads.
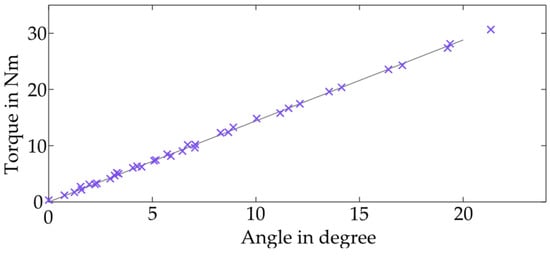
Figure 3.
The Stiffness Coefficient is fitted with the least square method (gray) to the data from three trails under different load condition. The purple data points are each associated with the respective parameters in a joint.
This coefficient, which quantifies the beam’s resistance to bending, is crucial in the PRBM setup. The aim is to establish a linear relationship between the applied loads and the resultant deflections, indicative of the beam’s consistent mechanical behavior. This linear relationship is confirmed through a detailed graph, which visually substantiates the beam’s linear stiffness characteristic.
2.2. Implemention of the PRBM in the AnyBody Modeling Software
The PRBM, while conceptually straightforward, presents several intricacies when implemented within the AnyBody software. The core idea of the PRBM in this work is to compute the forces resulting from deformations, essentially reversing the workflow of previous studies. To achieve this, the force-dependent kinematics (FDK) method is employed. FDK, detailed comprehensively in [], with its mathematical formulation provided in [], is pivotal for enabling the simulation of forces based on observed deformations.
The beam from the laboratory bending tests was reconstructed as a PRBM for implementation within the AnyBody software. Stiff segments, each 80 mm in length, were connected by torsion springs, which used the previously determined Stiffness Coefficient. The rotation of these torsion springs was designated as a degree of freedom within the FDK solver, allowing the FDK algorithm to iteratively determine their deformation. The configuration enables the PRBM to be subjected to loads or deformations.
Initially, one might attempt to define the start and end points of the PRBM beam, attaching it directly to segments of the human body model or using motion-tracking data to move it. However, this results in a closed kinematic loop, where the FDK solver struggles to find a physically plausible solution due to the circular dependency of the segment positions. A resulting deformation of this setup is documented in Appendix A. However, applying a force to the PRBM leads to physically explainable and visually accurate results of the beam under load. This application of force to deform the PRBM is refined into a concept termed Constraint Force. The methodology involves using the known final position of the beam’s deformation to backtrack and calculate the necessary force to achieve this state. Instead of directly positioning or deforming the PRBM, a force is applied that constrains the PRBM into the desired deformation. This force is called the Constraint Force. It is assumed that the Constraint Force is exactly as great as the force generated by the deformation.
Adjusting the force vector of the Constraint Force is governed by the principle of a proportional controller (P-controller). Although the advantages of using a more advanced controller, e.g., a PID-Controller, are acknowledged [], the software architecture does not support multi-step iterative integration, necessitating a more straightforward controller to ensure ease of use.
The distance between the tip of the beam and its target position, or the control error , dictates the adjustment of the Constraint Force. The adjustment’s magnitude is controlled by the Gain Factor , where a larger pulls the tip closer to the target position, without ever fully reaching it []. However, if the simulation begins with a substantial control error , where the PRBM is initially undeformed, the resulting initial force can be tremendous, potentially leading to unrealistic static equilibriums. To mitigate this, the P-controller is modified by integrating a Ramp Factor , which controls the escalation of force at the start of the simulation process. This prevents abrupt initial force spikes and maintains a high enough to allow precise movement of the beam’s tip towards the target. This controller’s mathematical formulation and subsequent adjustments are further explained in Appendix B. Figure 4 provides a simple visual example of how the Constraint Force method progressively aligns the PRBM to the desired position.
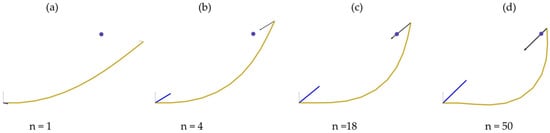
Figure 4.
Functional principle of the Constraint Force. The tip of the PRBM is pulled to the defined point (gray) by the Constraint Force (black). The reaction force in the fixed bearing (blue) is also shown. The Constraint Force starts to deform at (a) and pulls the PRBM closer and closer to the target point in the course of (b–d). The iteration step of the simulation is indicated below the image in each case.
While the detailed coding and application of the FDK within AnyBody are not elaborated here, a code example that illustrates the practical implementation of this simulation technique can be found in the Supplementary Materials at the end of this paper. This additional resource ensures that users can replicate and adapt the PRBM approach within their own projects, thereby enhancing the utility and applicability of the AnyBody software in complex biomechanical analyses.
2.3. Validation of the PRBM Method
The proposed PRBM approach requires rigorous validation to ensure its accuracy and effectiveness before integration into more complex exoskeleton simulations. This validation involves using a simplified model to initially test the PRBM, allowing for easier identification and correction of any discrepancies. Two primary sources of error are scrutinized: inaccuracies in the measured Stiffness Coefficient and deviations in the magnitude and direction of the Constraint Force. Each potential source of error is validated sequentially, beginning with tests on the Stiffness Coefficient to confirm its correspondence with empirical data and adjusting as necessary. Following this, the accuracy of the Constraint Force is assessed by examining the effects of variations in its magnitude and direction on the simulation outcomes.
2.3.1. Validation of the Stiffness Coefficient
Validating the PRBM, the initial step involves verifying whether the implementation of the experimentally measured Stiffness Coefficient accurately reproduces the observed deformations. A Stiffness Coefficient of 1.44 Nm/° was determined during laboratory trials and subsequently implemented into a PRBM setup within the AnyBody simulation software. This setup mirrored the laboratory conditions, and the simulations were conducted with four different force applications that matched those used in the lab trials. The deformations observed in the laboratory, tracked via markers on the beam, were then superimposed onto the deformations simulated by the PRBM for comparison. In all instances, the PRBM exhibited greater deformation than observed in the physical trials, indicating a need for adjustment. Consequently, the Stiffness Coefficient was incrementally increased in each scenario until the simulated deformations aligned with those recorded during the lab experiments. The detailed results of these adjustments and their validation are documented in Section 3.1.1, which provide a visual representation of the comparative deformations before and after the adjustments to the Stiffness Coefficient.
2.3.2. Validation of the Constraint Force
The second aspect of validation for the PRBM focuses on the efficacy and accuracy of the Constraint Force controller. To validate this component, an initial force is applied to deform a simplified version of the PRBM, and the position of the tip is precisely recorded. Subsequently, a Constraint Force is exerted to reposition the tip to the previously recorded point, aiming to replicate the same deformation pattern. The magnitude of the initial force is then compared with that of the Constraint Force to determine if there are any discrepancies between them. This validation process is detailed exhaustively in Appendix C to maintain the conciseness and clarity of this article. This validation’s comprehensive results and illustrative graphics are presented in Section 3.1.2.
2.4. Implementation of a Passive Exoskeleton
Following the validation of the PRBM approach, the feasibility of using this method to simulate flexible exoskeletons is demonstrated using a newly developed prototype. This prototype highlights both the challenges and solutions in implementing the PRBM in practical applications. Designed to support the wearer during lifting and carrying tasks, the exoskeleton is entirely passive and utilizes flexible beams to store energy efficiently during these activities. This prototype is illustrated in Figure 5, where it is shown to effectively intercept loads at the wearer’s hands and redirect these forces toward the ground. It combines rigid and flexible elements in a non-anthropomorphic design, which includes rearward-projecting spring elements that provide a unique combination of structural rigidity and flexibility. Operating solely through passive mechanisms, the prototype facilitates movement and enhances posture stability during use, making it particularly suitable for industrial applications. A detailed discussion of the principle of action utilized by this prototype will be addressed in a separate publication, focusing mainly on the forces and moments it exerts on the human body.
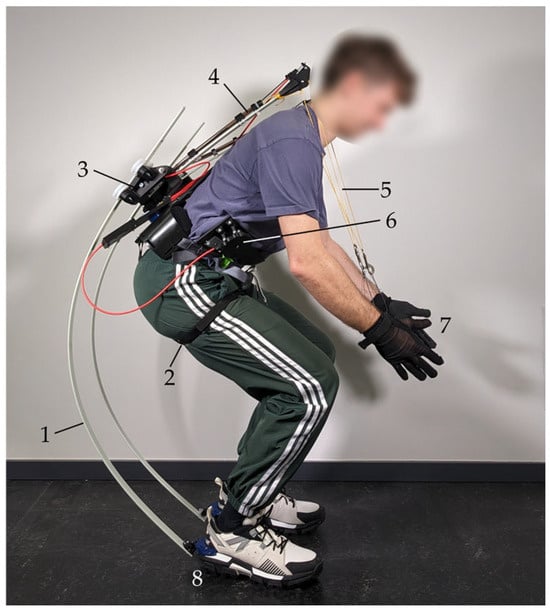
Figure 5.
Overview of the components of the exoskeleton prototype: 1—lower spring elements; 2—leg straps; 3—back attachment; 4—upper spring elements; 5—strings; 6—actuation lever; 7—gloves; 8—foot attachment.
A laboratory experiment was conducted to gather the input data required for simulation. Four distinct lifting motions from a motion capture trial with one subject using the exoskeleton were recorded with a “Plug-in-gait” marker set. These motions were recorded by 16 Qualisys Miqus cameras operating at a frame rate of 200 Hz, with calibration achieved using a 600 mm Wand Kit, resulting in a standard error of 0.295 mm. The motion capture template was used for the simulation with AnyBody, and the ground reaction forces were calculated using the software.
Integrating the simplified model of the PRBM into the exoskeleton model posed minimal difficulties; however, several new challenges emerged, particularly concerning the interface between the human and the exoskeleton. To simplify the interface, the exoskeleton was attached to the pelvis segment, offering a kinematically straightforward connection point while also connecting to the segments at the hands and feet. In Figure 6, the locations and orientations of the torsional springs calculated by the force-dependent kinematics (FDK) are depicted for both the back interface and one of the lower spring elements. The pivotal joint connecting the exoskeleton to the human pelvis was engineered to have a stiffness of 3 Nm/° in the sagittal plane, marked as 1. Additionally, the attachment of the PRBM to the rigid part of the exoskeleton features a sideways (frontal plane) stiffness of 2 Nm/°, identified as 2, and the pivotal joint where the Stiffness Coefficient—validated earlier in Section 2.3.1 and set at 1.6 Nm/°—is applied and is marked as 3. These specifications are crucial for transferring the mechanical functionality of the exoskeleton from the real world into the simulation.
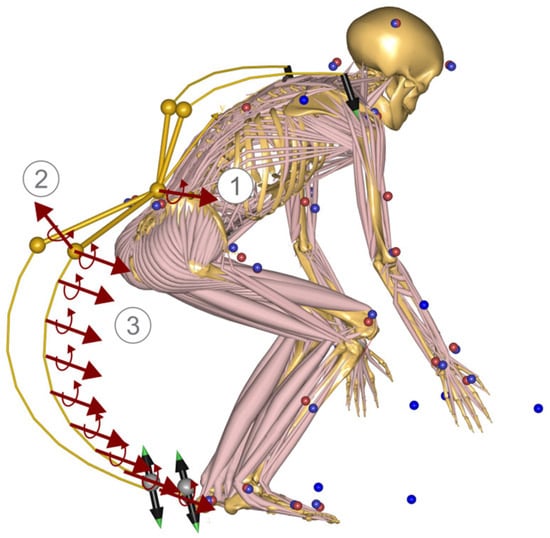
Figure 6.
Specification of the degrees of freedom that were assigned with a Stiffness Coefficient by a force-dependent kinematic (FDK): 1—degrees of freedom of connection to the pelvis in sagittal plane; 2—degrees of freedom of sideway deformation of the PRBM; 3—PRBM degrees of freedom of the lower spring elements. Blue dots are recorded markers from MoCap measurements, red dots are digitally fitted markers.
An additional force is introduced at the onset of the simulation process to initially direct the PRBM towards the correct bending direction, after which this force is deactivated. This initial guiding force acts as a corrective measure, steering the PRBM away from potential buckling and ensuring it starts from a kinematically viable position. Once the PRBM is correctly aligned and the simulation progresses past the initial stages where stability is most likely, this force is no longer necessary and can be safely faded out.
3. Results
3.1. PRBM Validation
The developed PRBM approach is validated in two ways. The first, validating the Stiffness Coefficient, is described in Section 2.3.1, and the results are presented here. The second, validating the Constraint Force, is described in Section 2.3.2. The full results and graphs are shown in Appendix C.
3.1.1. Stiffness Coefficient
In validating of the Stiffness Coefficient, the primary objective was to determine whether the measured coefficient could accurately produce the desired deformation in a PRBM. Figure 7 illustrates the comparative results of four different load cases, depicting both the laboratory tests and the simulation data. In these visual representations, solid lines indicate the actual beam, gray lines represent the PRBM, and black circles mark the joints of the PRBM. It was observed that the PRBM exhibited more significant deformation than the physical beam in laboratory settings. To align the deformations of the PRBM with those of the actual beam, it was necessary to individually adjust the Stiffness Coefficient for each load case, with the required adjustments specified next to each beam in Figure 7. These adjustments varied in magnitude across different load scenarios. Subsequent graphical representations with the adjusted Stiffness Coefficients showed that the PRBM, now with increased stiffness, closely followed the beam’s deformation patterns, with only slight deviations in areas of high curvature. To further refine the model’s accuracy, the Stiffness Coefficient was uniformly increased to 1.6 Nm/°, reflecting an overall adjustment of 11.2%. This revised Stiffness Coefficient has been adopted for subsequent simulations within the exoskeleton framework, enhancing the fidelity and applicability of the model in realistic biomechanical scenarios.
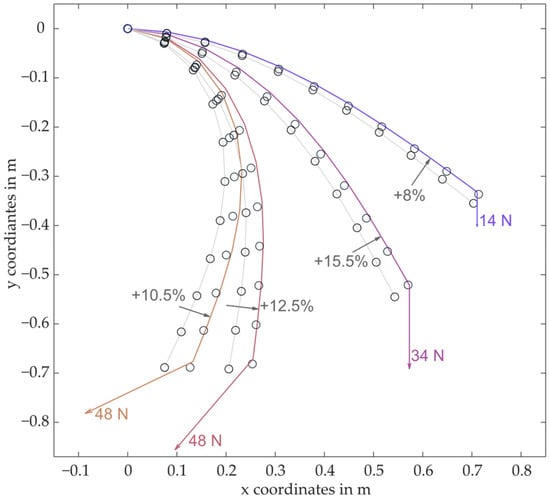
Figure 7.
Comparison of the measured deformation of a beam in the lab (colored line) with the simulation of the deformation using PRBM (gray line) under four different loads. The black circles represent the joint between the rigid segments of the PRBM.
3.1.2. Constraint Force Controller
The subsequent phase of the validation process involved a critical assessment of the control scheme implemented for the Constraint Force within the PRBM. This evaluation, detailed in Appendix C, involved examining the precision of the Constraint Force, mainly focusing on deviations in both the magnitude and direction of the force. The simulation parameters were meticulously adjusted to mirror those of a human motion capture session to achieve a realistic simulation environment. Notably, the deviations between the expected and actual forces exerted by the Constraint Force varied significantly, ranging from nearly negligible to as much as 20% across different loading scenarios. The smallest deviations were observed when the PRBM was subjected to moderate loads, approximately 20 N, where both the magnitude and directional deviations were minimal. In contrast, higher loads consistently resulted in a directional error of about −12.5%, while smaller loads saw errors escalate to 35%. These discrepancies underscore the sensitivity of the Constraint Force to various simulation parameters, complicating the accurate replication of these dynamics in an exoskeleton simulation. Given the complexity and variability of these errors, the exact quantification of deviations remains elusive, suggesting that the results from the exoskeleton simulations should be interpreted with caution. This analysis highlights the inherent challenges in fine-tuning the control mechanisms to realistic biomechanical interactions within the PRBM approach.
3.2. Simulation of a Passive Exoskeleton
The culmination of this research article is integrating the developed PRBM approach into a biomechanical simulation, utilizing motion capture data derived from a lifting trial with the exoskeleton. The primary objective of this phase is to demonstrate the practical application of the approach in full-body simulations that incorporate real motion capture data. Notably, the simulation demands considerable computational resources, requiring approximately nine hours on a modern CPU (i7-12800H 2.40 GHz), significantly longer than the approximately 5 min for a simulation conducted without the exoskeleton.
Figure 8 provides a detailed step-by-step graphical depiction of the biomechanical simulation using the AnyBody software, showcasing the application of the PRBM. The sequence initiates with the exoskeleton in an initial state, where a bending force is applied to the lower spring elements of the PRBM, causing them to deflect backward. As the simulation progresses to the second iteration step, the Constraint Force is systematically increased through a Ramp Factor , which starts to bend the spring elements towards the attachment points. By the fourth iteration step, the Constraint Force has effectively repositioned the spring elements to align with the attachment of the lower spring elements to the foot attachment. As the simulation continues, the PRBM elements undergo further deformation, adapting dynamically to the movement of the human model. In the thirteenth step, forces acting on the hands are activated, simulating the act of lifting. By the eighteenth step, the human model begins to straighten up as the box is lifted higher. In the twenty-second iteration step, there is additional stress on the lower spring elements, leading to increased compression. This necessitates a reduction in the Constraint Force, executed via a RampDown Factor by the twenty-eighth step to prevent high forces.
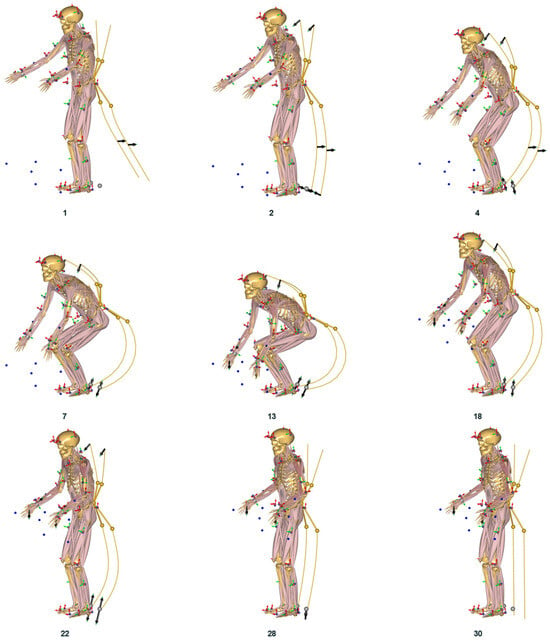
Figure 8.
Step-by-step illustration of the exoskeleton simulation, the number below the image indicates the respective iteration step. A person lifts a box with the help of the exoskeleton. At the beginning of the simulation, the lower spring elements are deflected by the bending force. At the end of the simulation, the Constraint Force is slowly reduced.
The simulation concludes at the thirtieth step, where the Constraint Force is completely withdrawn, allowing the exoskeleton to return to a neutral state, closely mirroring the physical response expected in an actual lifting scenario. This detailed visualization not only underscores the intricate interactions within the biomechanical simulation but also highlights the computational and practical challenges involved in accurately modeling such complex dynamic systems.
4. Discussion
The principal objective of this work was to explore how flexible beams could be simulated in biomechanical contexts, particularly focusing on passive exoskeletons experiencing geometric nonlinear bending. This study introduced a novel and versatile approach, deliberately structured and articulated in a simplified manner to enhance the accessibility and usability of the technique for a broad spectrum of exploratory simulations.
4.1. Constraint Force Control Error
In the development of the PRBM method for biomechanical simulations, significant challenges have emerged, particularly concerning the control scheme of Constraint Force. The validation trials revealed deviations of the Constraint Force of up to 20% in the force amplitude and up to 35% in the force direction, highlighting substantial uncertainties in the PRBM approach. Such discrepancies pose challenges in predicting how these errors might translate into simulations involving more complex structures, like exoskeletons, and in assessing the residual errors that may persist.
Bending tests, designed to replicate the deformation observed in flexible rods of the exoskeleton during lifting tests, aimed to facilitate comparable validation outcomes. Despite these efforts, the potential for significant inaccuracies remains, especially as errors could accumulate detrimentally in overall biomechanical simulations under more complex load conditions typical of exoskeleton usage. Consequently, assigning a specific level of error in such scenarios becomes impractical, necessitating a cautious interpretation of simulation results. Given the variability observed, it is prudent to assume that similar errors manifest in the simulations, and therefore, findings from the current controller configuration should be treated as provisional guidelines rather than definitive outcomes. This cautious approach is essential to ensure the reliability and applicability of biomechanical simulations in practical scenarios.
The implementation primarily utilizes a P-Controller, chosen for its simplicity. However, its inherent limitations are well-documented [], suggesting that a more advanced controller like a PID-Controller could improve outcomes. However, the program’s architecture precludes integration over multiple iteration steps. The simplicity of the simulation, as outlined in the objectives of this paper, is a crucial requirement. Implementing a more complex controller, such as a PID-Controller, would necessitate exporting the computation variables to an external software where input variables for subsequent steps could be calculated. Such an implementation is far from trivial and contradicts the emphasis on simplicity mentioned earlier. This approach would fundamentally alter the usability and accessibility of the simulation, deviating from the initial design principles aimed at maintaining straightforward operation and user-friendliness.
Moreover, the long durations required for simulations pose practical challenges, as frequent manual adjustments to the exoskeleton and human–exoskeleton interfaces are necessary to avoid unstable positions, further complicating the simulation process.
4.2. Stiffness Coefficient
In this study, the Stiffness Coefficient was experimentally determined and its accuracy assessed in a simulation. Initial findings indicated that the calculated Stiffness Coefficient was consistently lower than required, though the underlying reasons for this discrepancy remain unclear. The deviation of all laboratory-measured values in the same direction may indicate a systematic error in the measurements. The test setup and the digital evaluation were then carefully examined, but no identifiable errors were found. The underlying mechanisms show an interesting pattern and require further in-depth investigation. Furthermore, varying load conditions produced differing deviations, adding complexity to understanding how the Stiffness Coefficient behaves under different mechanical stresses. The stiffness coefficient was adjusted upward to better align with the measured deformations observed during physical testing and address these inconsistencies in this paper.
The variability in outcomes underlines the need for a more robust method of determining the Stiffness Coefficient. Current methodologies may not adequately account for the complex interactions and properties of materials used. Future research could therefore benefit from developing an empirical approach to derive the Stiffness Coefficient directly from the Young’s Modulus of the material. This approach potentially provides a more direct and reliable means of calculating the coefficient, ensuring that simulations more accurately reflect the true mechanical properties of the materials and structures being modeled. This would require a large number of bending tests with different beam geometries and materials and a subsequent detailed data analysis. Such advancements would enhance the predictive capabilities of simulations with flexible elements, contributing significantly to the fields of biomechanics and material science.
4.3. Rigid Segment Length
The segment length of the PRBM represents a critical factor in the accuracy and efficiency of biomechanical simulations, warranting further investigation. In this study, the segment length was determined intuitively, striking a balance between closely following the deformation of the modeled structure and minimizing the propagation of calculation errors linked to the Stiffness Coefficient across the PRBM joints. Due to the intuitive selection process, the effect of varying segment lengths on the simulation outcomes was not explicitly analyzed in this work, highlighting a gap in the research.
The optimization of segment length in PRBM applications emerges as a compelling area for future studies. Optimizing this parameter could enhance the model’s fidelity and computational efficiency, especially in complex simulations involving significant deformations and interactions of multiple body segments. Further research could build on existing studies, such as those outlined in reference [], which have previously addressed aspects of segment length. Investigating these dynamics could lead to more refined models that better replicate physical behaviors and improve the predictive capabilities of biomechanical simulations.
4.4. Exoskeleton Simulation
The simulation of a flexible exoskeleton, despite its inherent inaccuracies, introduces a novel approach that significantly broadens the potential applications within the field, making it a noteworthy development for dissemination. According to the authors, this initiative marks the first known attempt to simulate a flexible exoskeleton, demonstrating its ease of use and versatility in application.
To substantiate the validity of this simulation, the exoskeleton was outfitted with sensors to measure forces and moments during physical trials. These measurements revealed considerably lower forces and moments than those predicted in the simulation, hypothesized to result from the rigid connections of the exoskeleton to the human body within the simulated environment. In real-world conditions, the exoskeleton exhibited more flexibility. The back attachment demonstrated the ability to bend under load, dynamics that the current simulation model could not replicate, resulting in exaggerated forces acting directly on the pelvis segment. The results from this innovative study are planned for publication in a forthcoming article, which will further detail these findings.
This endeavor underscores the complexities in simulating human–exoskeleton interactions, echoing broader challenges in biomechanical simulations related to the human–machine interface as discussed in reference []. Addressing these challenges is crucial for advancing the field and ensuring that simulations can accurately mirror real-world dynamics. This study serves as a critical step toward enhancing our understanding and implementation of biomechanical models, particularly in the context of flexible exoskeletons. It highlights the need for continued research and development in this area.
4.5. Kinematic Unstable Positions
One significant challenge in the exoskeleton simulation, mainly due to their numerous degrees of freedom, is the occurrence of kinematically unstable positions. These instabilities often manifest at the beginning of the simulation when the PRBM only slightly deformed. The FDK springs at the interface between the human and the exoskeleton are stiffer than those in the PRBM. They are stiffer so the exoskeleton bends under the load and does not just twist around the interface. If the exoskeleton only twists, the entire system is often pulled into a position from which it then buckles. In this position, the solver is not able to find a feasible solution within a reasonable timeframe, which is defined as less than 12 h per simulation step. These scenarios are problematic, as they do not accurately represent the realistic interactions between the exoskeleton and its user, potentially stalling the simulation process by creating situations where the solver becomes stuck, requiring manual intervention to proceed. Two examples of kinematically unstable positions are shown in Appendix D.
To mitigate this issue, a bending force was introduced to strategically deflect the lower spring elements. This preemptive adjustment ensures that the elements are initially bent in the correct direction, thereby preventing buckling from occurring at the outset. Such adjustments are crucial for maintaining the integrity of the simulation and may be necessary in other scenarios to achieve a more stable and realistic simulation outcome. In principle, we recommend integrating the FDK degrees of freedom into the simulation step by step and not all of them from the beginning. This makes it easier to determine when the PRBM system has too many FDK degrees of freedom and no equilibrium can be found. These workarounds highlight the need to control better simulation parameters and mechanisms to replicate biomechanical systems’ dynamic and complex interactions involving flexible elements.
4.6. Further Limitations
The relevant limitations have already been mentioned in the respective sections of this chapter. However, one more must be added. To enable a more precise calculation, it can be assumed that shorter segments must be used. This means that the calculation effort increases accordingly. Currently, it is not possible to speed up the computation time in the AnyBody software, since the computation is performed iteratively and cannot be distributed across parallel cores. The only option at this time is a processor with a faster single thread performance.
5. Conclusions
In conclusion, this study introduces a straightforward and user-friendly method for simulating flexible elements using the PRBM approach. While the PRBM methodology represents a significant advancement, it has its limitations. The validation phase highlighted considerable deviations that affect the reliability of simulations with flexible elements, indicating that the calculated forces derived from this approach must be interpreted with caution. Despite these challenges, the visually appealing results offer a distinct advantage over other methods, enhancing the interpretability and presentation of largely deformed elements in the context of biomechanical simulations.
One of the primary strengths of the PRBM approach is its ability to address problems that lack closed-form solutions, beneficial for structures subjected to complex load cases. This capability is demonstrated in Figure 9, which shows a PRBM configured with two forces, illustrating the model’s adaptability. This adaptability extends to three-dimensional applications, with the force-dependent kinematics (FDK) capable of handling degrees of freedom in two directions, further broadening the practical applications of this approach.

Figure 9.
The approach can be used in many other ways, e.g., a beam with two forces (black arrows).
There is also promising potential that this methodology could be adapted for various shapes and joint types, enhancing its versatility across different fields of biomechanical research. The wide spectrum of applications and ease of implementation of additional forces make the PRBM approach particularly valuable. This simplicity, combined with the method’s potential for expansion and refinement, suggests considerable opportunity for further development and application in more complex and diverse scenarios. Ultimately, the PRBM approach holds great promise for advancing biomechanical simulations, offering a novel tool that can significantly contribute to the field by providing solutions to previously intractable problems.
Supplementary Materials
An example code can be downloaded at: https://github.com/CoRoLab-Berlin/Pseudo_Rigid_Body_Flexible_Beam and from https://www.mdpi.com/article/10.3390/biomechanics4030040/s1.
Author Contributions
Conceptualization, Y.H. and S.G.; methodology, Y.H. and S.G.; software, Y.H. and M.W.; validation, Y.H. and M.B.; formal analysis, Y.H.; investigation, Y.H. and M.B.; resources, I.B. and S.G.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H., M.W., M.B., I.B. and S.G.; visualization, Y.H.; supervision, I.B. and S.G.; project administration, I.B. and S.G.; funding acquisition, I.B. and S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institut für angewandte Forschung Berlin e.V., the APC was funded by the HTW Berlin.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Berliner Hochschule für Technik.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Raw data were generated at CoRoLab and HumanVR of the Berliner Hochschule für Technik, Germany. Derived data supporting the findings of this study are available from the corresponding author S.G. on request.
Acknowledgments
We would like to thank John Rasmussen from Aalborg University and Divyaksh Subhash Chander from AnyBody for their highly valuable support.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
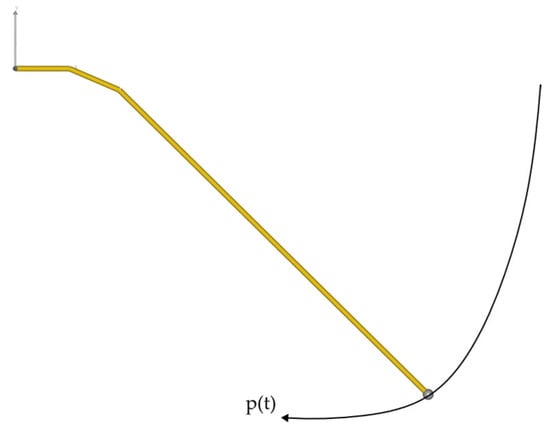
Figure A1.
The deformation of the PRBM when the position of the tip is specified directly. The gray point moves along a defined path p(t). The tip of the PRBM is connected to the point with a spherical joint (6 DOF). This creates a closed kinematic loop and the force-dependent kinematics (FDK) can not solve the system in physically correct way, as seen in the way the beam is bend.
Appendix B
The Constraint Force is specified as for every simulation step n as:
| Constraint force in x and y direction in N | |
| Gain Factor in N/m | |
| Ramp Factor, dimensionless | |
| Control error in x and y direction in m |
| Current iteration step | |
| Length of the ramp in iteration steps |
Appendix C
The second source of inaccuracy pertains to the introduced Constraint Force, where deviations can occur both in the direction and magnitude of the force. Validating this aspect is only slightly more complex than validating the Stiffness Coefficient and is conducted entirely within AnyBody. To verify whether the calculated Constraint Force corresponds to the target force, a PRBM without the Constraint Force controller is initially loaded with a defined force. The coordinates of the tip of the deformed PRBM are recorded. Subsequently, the Constraint Force is implemented to pull the tip towards the saved coordinates. The target force and the Constraint Force are then compared. This process is repeated for various forces. Figure A2 illustrates this for forces ranging from 10 N to 100 N applied at a 45° angle. The number of iteration steps within the simulation is 20, aligning with a typical count for biomechanical simulations. The length of the Constraint Force ramp is = 10 steps. Given the low number of iteration steps, a permanent control error remains, both in direction and magnitude of the force.
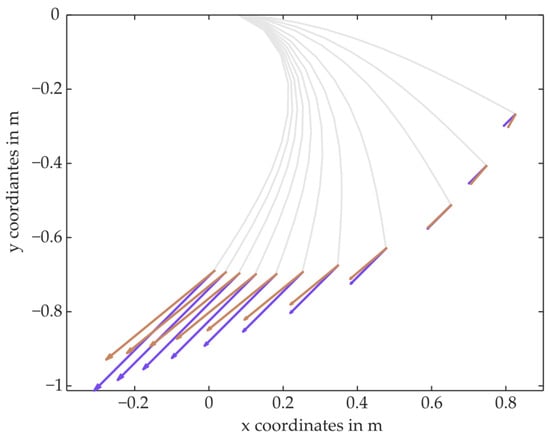
Figure A2.
Comparison of the constraint force (orange) with a target force (purple).
In the Figure A3 the control deviation is plotted as the deviation of the absolute force of the Constraint Force for the different loads (x-axis). The control deviation in the cases of low loads is not pronounced, but then loads increase, it reaches almost 20%. The control deviation of the direction of the Constraint Force is shown below that in Figure A4. The error initially starts around 35% for low forces and then drops to around −12% and remains constant there.
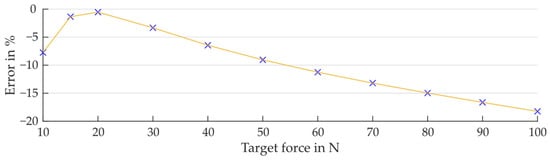
Figure A3.
Remaining control error of the absolute force of the Constraint Force.
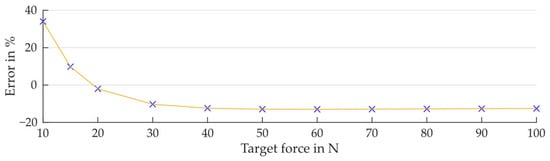
Figure A4.
Remaining control error of the direction of the Constraint Force.
Appendix D
Additional DOFs are included in the system by using FDK. This makes it more difficult for the system to find an equilibrium solution. Some of the equilibrium positions that are found by the AnyBody software are physically permissible and are one of the possible solutions. In reality, however, this solution would not occur because the position is kinematically unstable. The real system would switch to another solution. Two such unstable solutions are shown in Figure A5. One for the lower PRBM and one for the upper PRBM. To avoid this problem, an initial force was applied in the simulation of the lifting process that deflects the PRBM to the kinematically stable position.
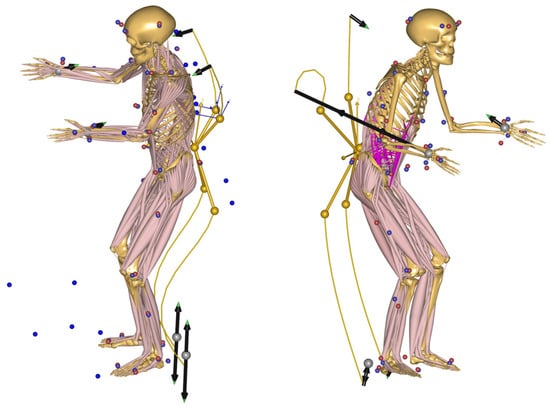
Figure A5.
Two examples of kinematically unstable positions of the PRBM.
References
- Uhlrich, S.D.; Uchida, T.K.; Lee, M.R.; Delp, S.L. Ten steps to becoming a musculoskeletal simulation expert: A half-century of progress and outlook for the future. J. Biomech. 2023, 154, 111623. [Google Scholar] [CrossRef] [PubMed]
- Ni, Y.; Gao, Y.; Yao, J. Introduction to Musculoskeletal System. In Biomechanical Modelling and Simulation on Musculoskeletal System; Fan, Y., Wang, L., Eds.; Springer: Singapore, 2021; pp. 1–34. [Google Scholar] [CrossRef]
- Molz, C.; Yao, Z.; Sänger, J.; Gwosch, T.; Weidner, R.; Matthiesen, S.; Wartzack, S.; Miehling, J. A Musculoskeletal Human Model-Based Approach for Evaluating Support Concepts of Exoskeletons for Selected Use Cases. Proc. Des. Soc. 2022, 2, 515–524. [Google Scholar] [CrossRef]
- Aftabi, H.; Nasiri, R.; Ahmadabadi, M.N. Simulation-based biomechanical assessment of unpowered exoskeletons for running. Sci. Rep. 2021, 11, 11846. [Google Scholar] [CrossRef] [PubMed]
- Fritzsche, L.; Galibarov, P.E.; Gärtner, C.; Bornmann, J.; Damsgaard, M.; Wall, R.; Schirrmeister, B.; Gonzalez-Vargas, J.; Pucci, D.; Maurice, P.; et al. Assessing the efficiency of exoskeletons in physical strain reduction by biomechanical simulation with AnyBody Modeling System. Wearable Technol. 2021, 2, e6. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.S.; Mohammadi, M.; Rasmussen, J.; Andreasen Struijk, L.N.S. Simulation-based design optimization of a wrist exoskeleton. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, Australia, 24–27 July 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Madinei, S.; Nussbaum, M. Estimating lumbar spine loading when using back-support exoskeletons in lifting tasks. J. Biomech. 2023, 147, 111439. [Google Scholar] [CrossRef] [PubMed]
- Tröster, M.; Wagner, D.; Müller-Graf, F.; Maufroy, C.; Schneider, U.; Bauernhansl, T. Biomechanical Model-Based Development of an Active Occupational Upper-Limb Exoskeleton to Support Healthcare Workers in the Surgery Waiting Room. Int. J. Environ. Res. Public Health 2020, 17, 14. [Google Scholar] [CrossRef] [PubMed]
- Auer, S.; Tröster, M.; Schiebl, J.; Iversen, K.; Chander, D.S.; Damsgaard, M.; Dendorfer, S. Biomechanical assessment of the design and efficiency of occupational exoskeletons with the AnyBody Modeling System. Z. Für Arbeitswissenschaft 2022, 76, 440–449. [Google Scholar] [CrossRef]
- Musso, M.; Oliveira, A.S.; Bai, S. Modeling of a Non-Rigid Passive Exoskeleton-Mathematical Description and Musculoskeletal Simulations. Robotics 2022, 11, 147. [Google Scholar] [CrossRef]
- Hao, G.; Yu, J.; Li, H. A brief review on nonlinear modeling methods and applications of compliant mechanisms. Front. Mech. Eng. 2016, 11, 119–128. [Google Scholar] [CrossRef]
- Saggere, L.; Kota, S. Synthesis of Planar, Compliant Four-Bar Mechanisms for Compliant-Segment Motion Generation. J. Mech. Des. 2001, 123, 535–541. [Google Scholar] [CrossRef]
- Li, N.; Liu, C.; Jiang, H. Dynamics modeling for curved-type fully compliant mechanism based on pseudo-rigid-body modeling. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 2302–2307. [Google Scholar] [CrossRef]
- Xu, H.; Gan, J.; Zhang, X. A generalized pseudo-rigid-body PPRR model for both straight and circular beams in compliant mechanisms. Mech. Mach. Theory 2020, 154, 104054. [Google Scholar] [CrossRef]
- Chang, P.; Padır, T. Model-Based Manipulation of Linear Flexible Objects: Task Automation in Simulation and Real World. Machines 2020, 8, 46. [Google Scholar] [CrossRef]
- Timošenko, S.P. History of Strength of Materials: With a Brief Account of the History of Theory of Elasticity and Theory of Structures; Courier Corporation: North Chelmsford, MA, USA, 1983. [Google Scholar]
- Howell, L.L.; Midha, A.; Norton, T.W. Evaluation of Equivalent Spring Stiffness for Use in a Pseudo-Rigid-Body Model of Large-Deflection Compliant Mechanisms. J. Mech. Des. 1996, 118, 126–131. [Google Scholar] [CrossRef]
- Andersen, M.S. Introduction to Musculoskeletal Modelling; Woodhead Publishing Series in Biomaterials; Woodhead Publishing: Cambridge, UK, 2021; pp. 41–80. [Google Scholar] [CrossRef]
- Andersen, M.S.; de Zee, M.; Damsgaard, M.; Nolte, D.; Rasmussen, J. Introduction to Force-Dependent Kinematics: Theory and Application to Mandible Modeling. J. Biomech. Eng. 2017, 139, 9. [Google Scholar] [CrossRef]
- Reuter, M.; Zacher, S. Regelungstechnik für Ingenieure: Analyse, Simulation und Entwurf von Regelkreisen; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2008. [Google Scholar] [CrossRef]
- Scherb, D.; Wartzack, S.; Miehling, J. Modelling the interaction between wearable assistive devices and digital human models—A systematic review. Front. Bioeng. Biotechnol. 2022, 10, 1044275. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).