Femoral Bone Strength Prediction Using Isotopological B-Spline-Transformed Meshes
Abstract
1. Introduction
2. Materials and Methods
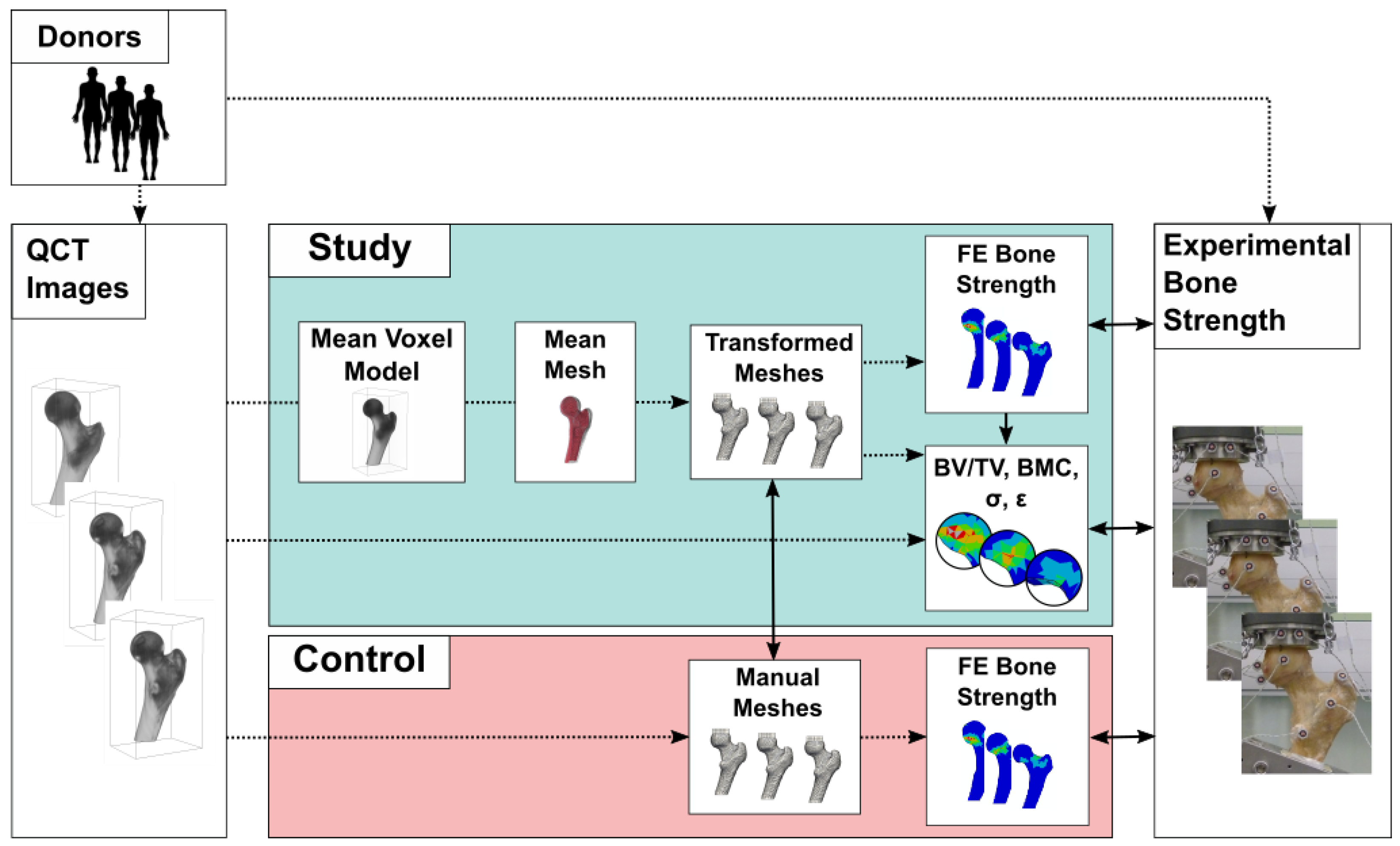
2.1. Overview
2.2. Data
2.3. Finite Element Models
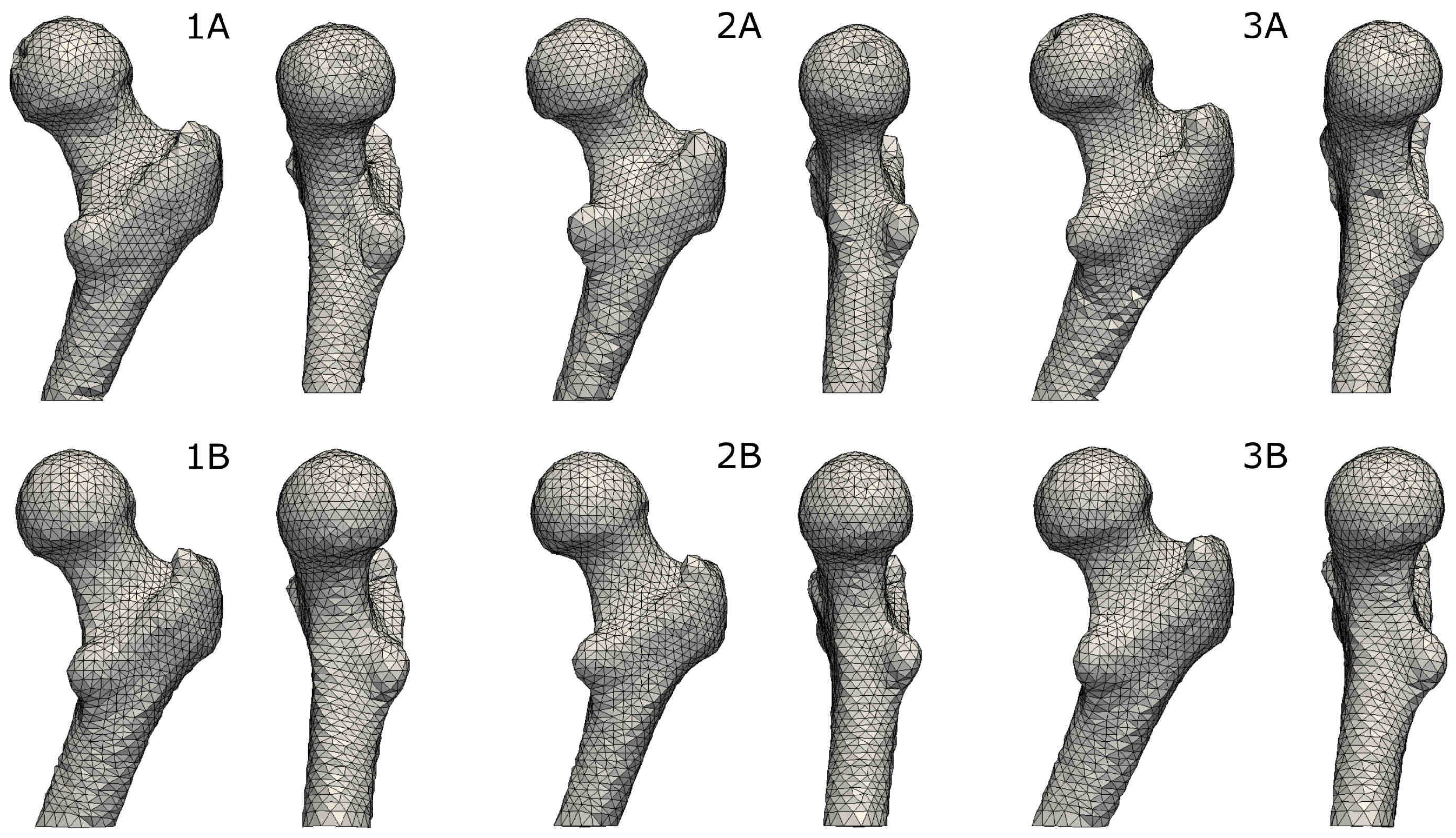
2.4. Mesh Transformation
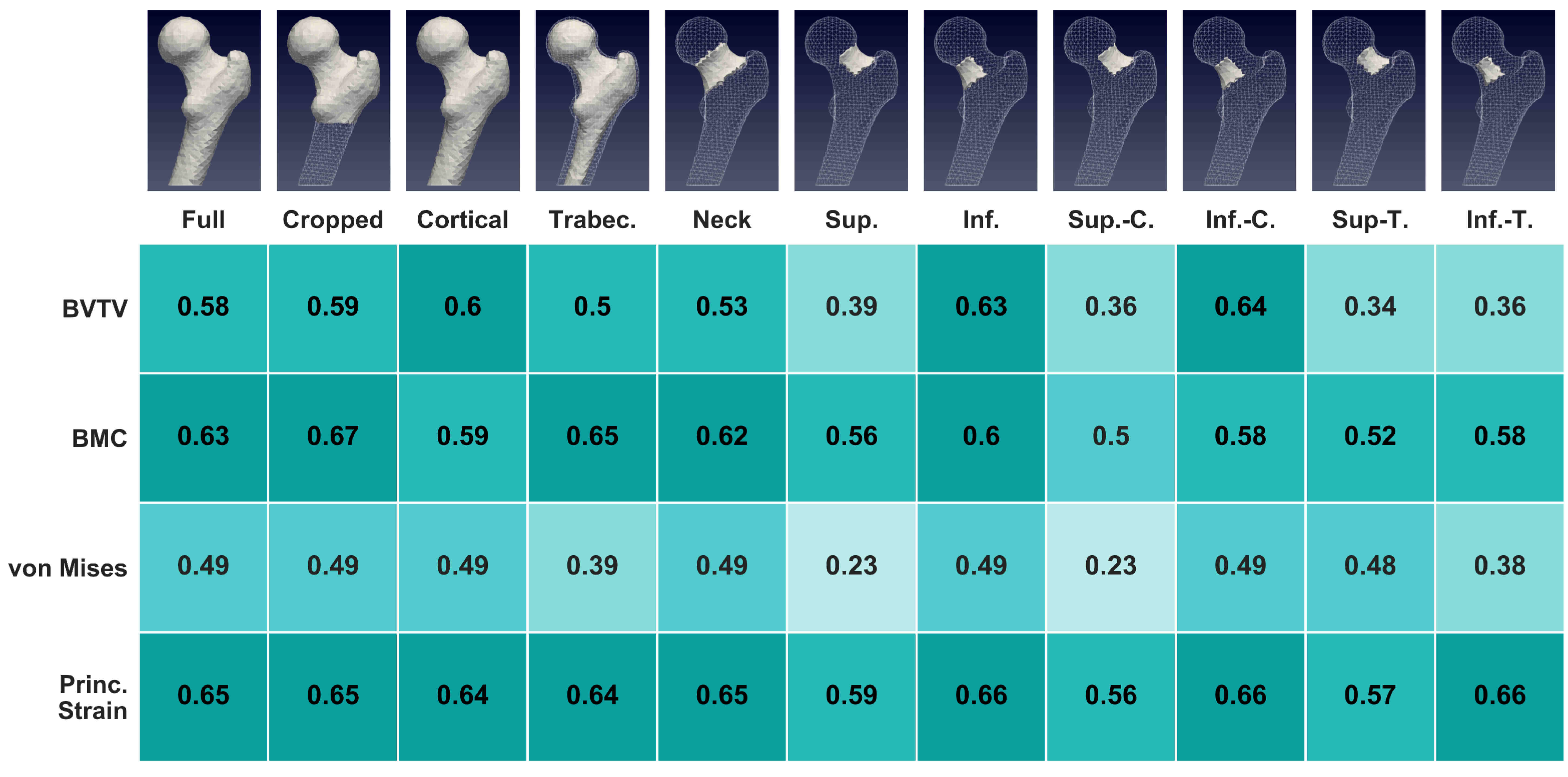
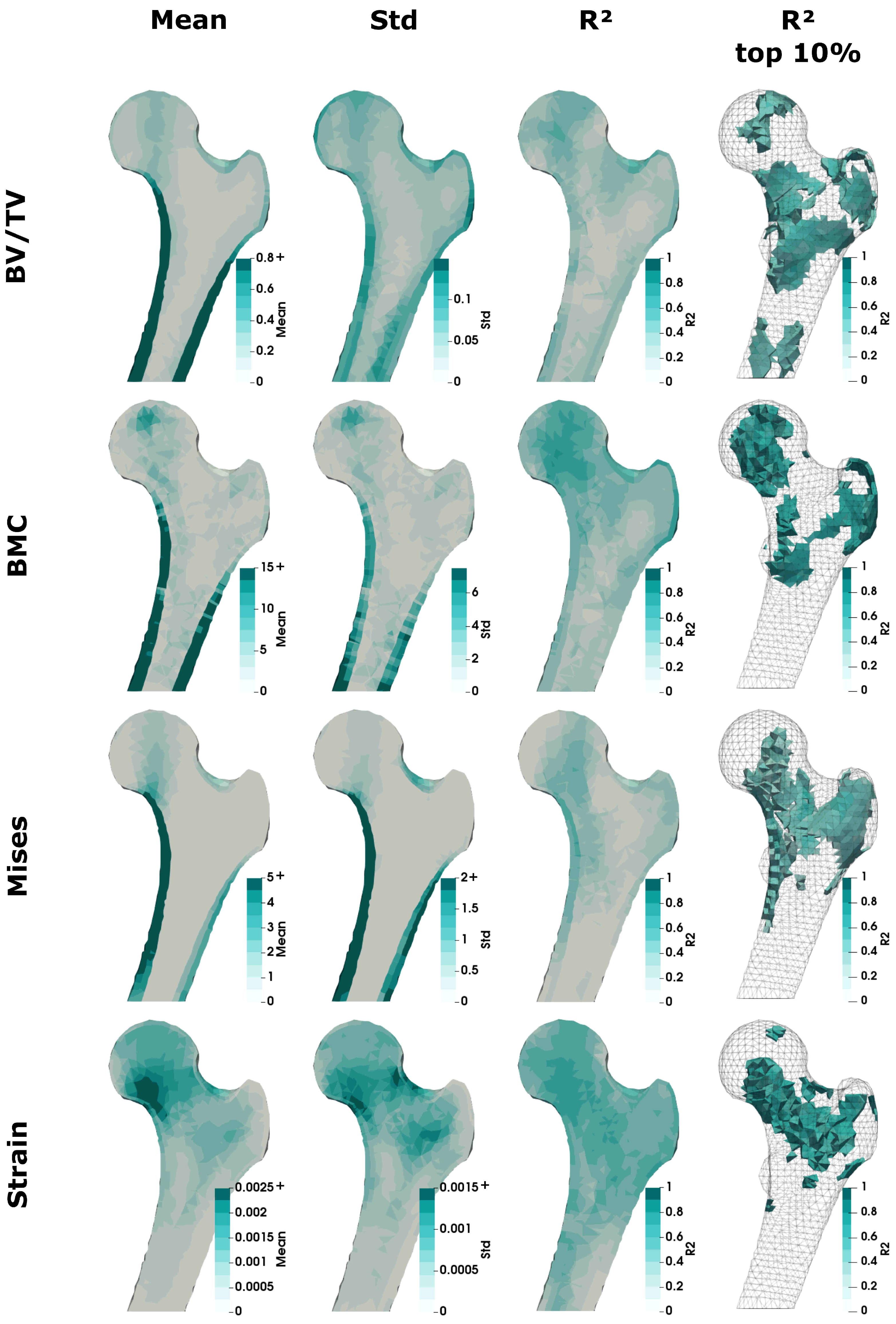
2.5. Regional Statistics
2.6. Computational Details
3. Results
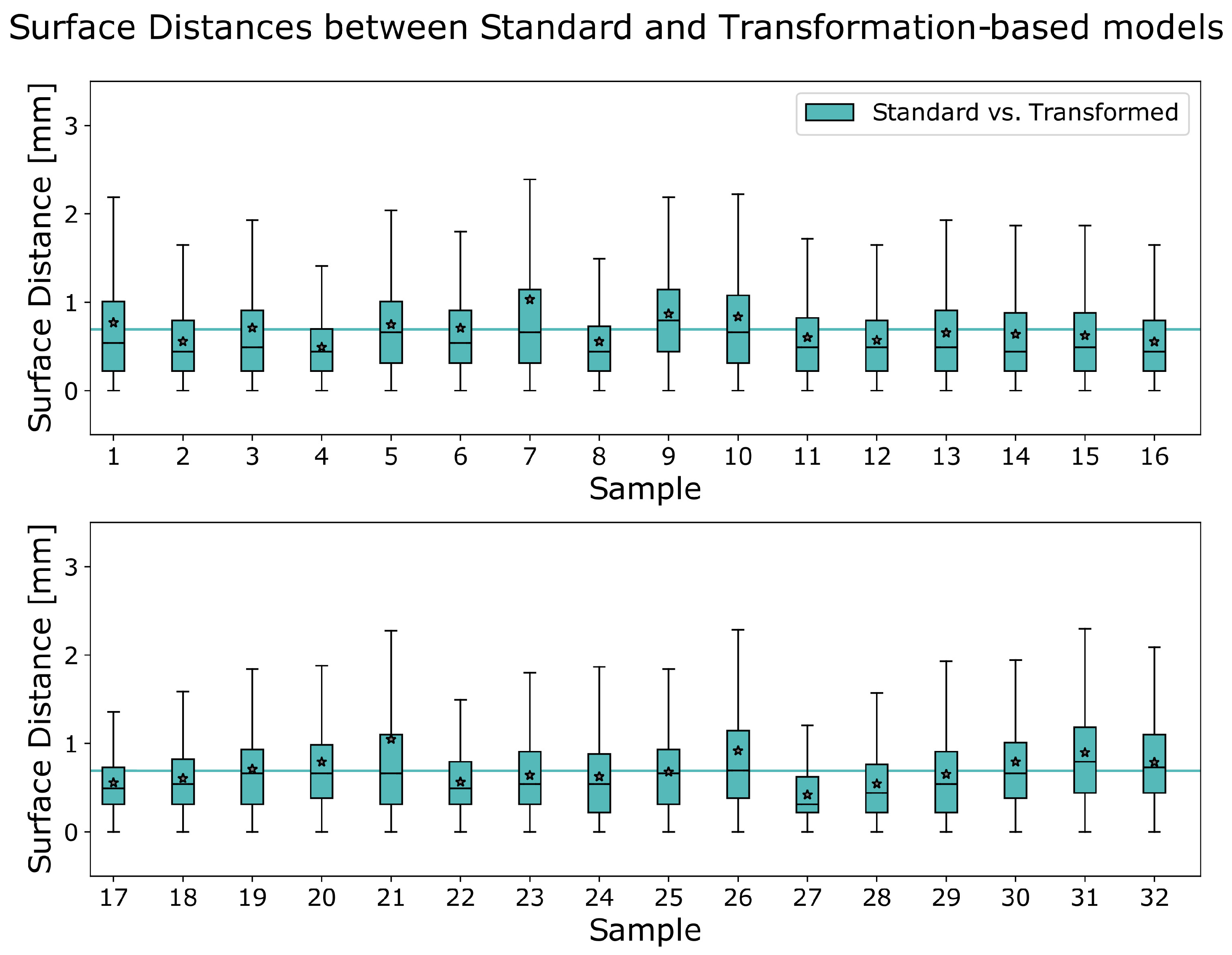
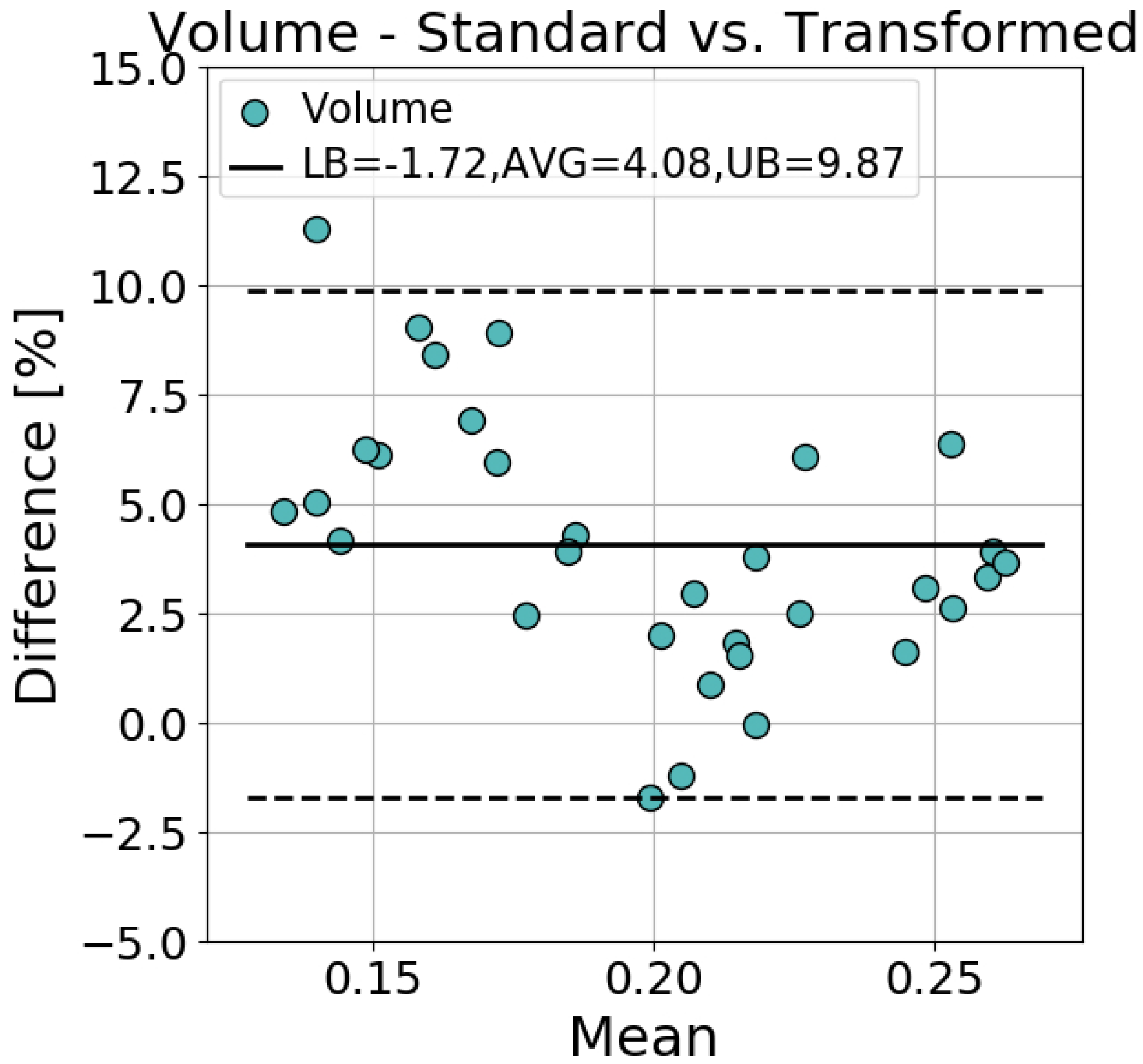
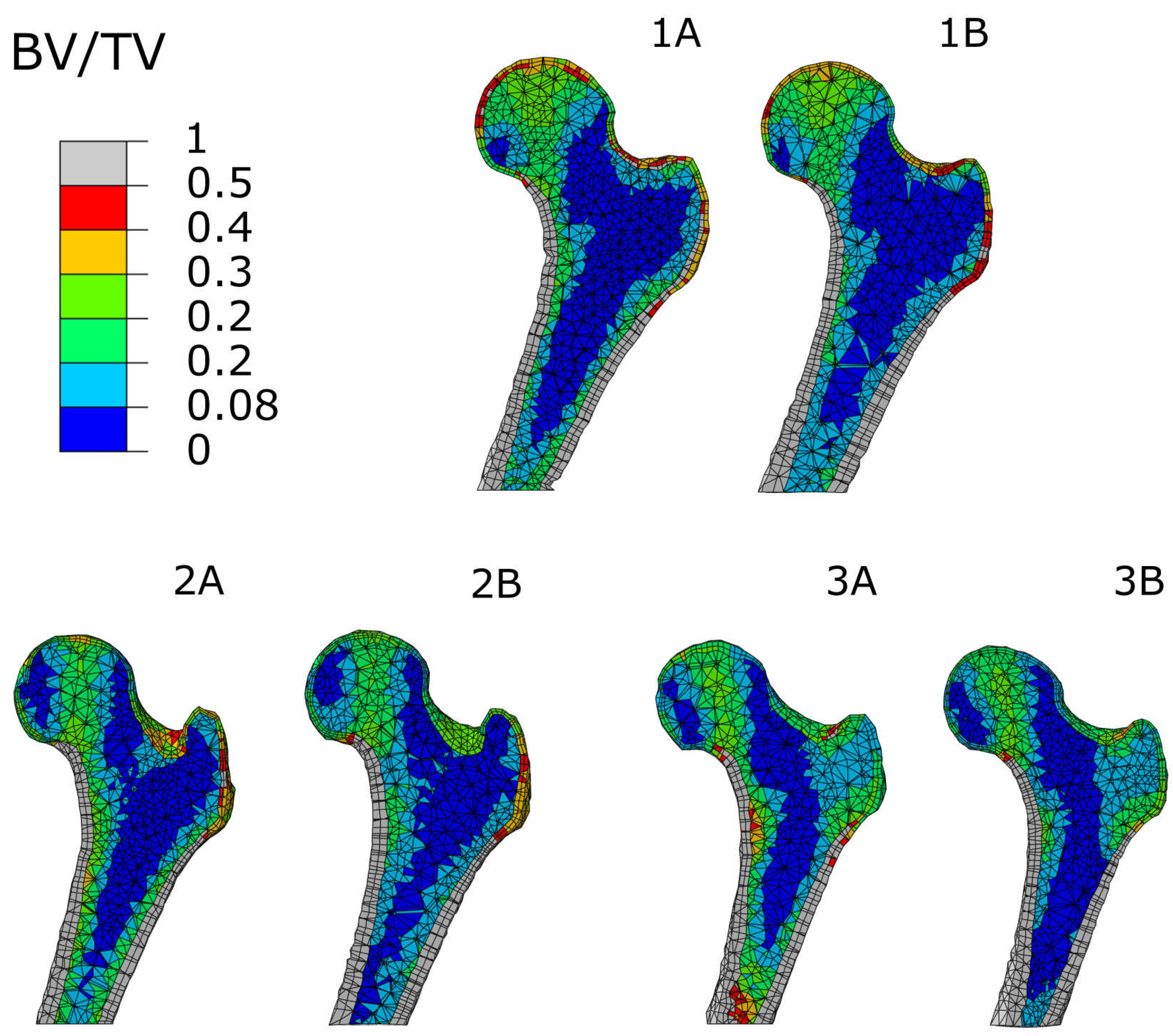
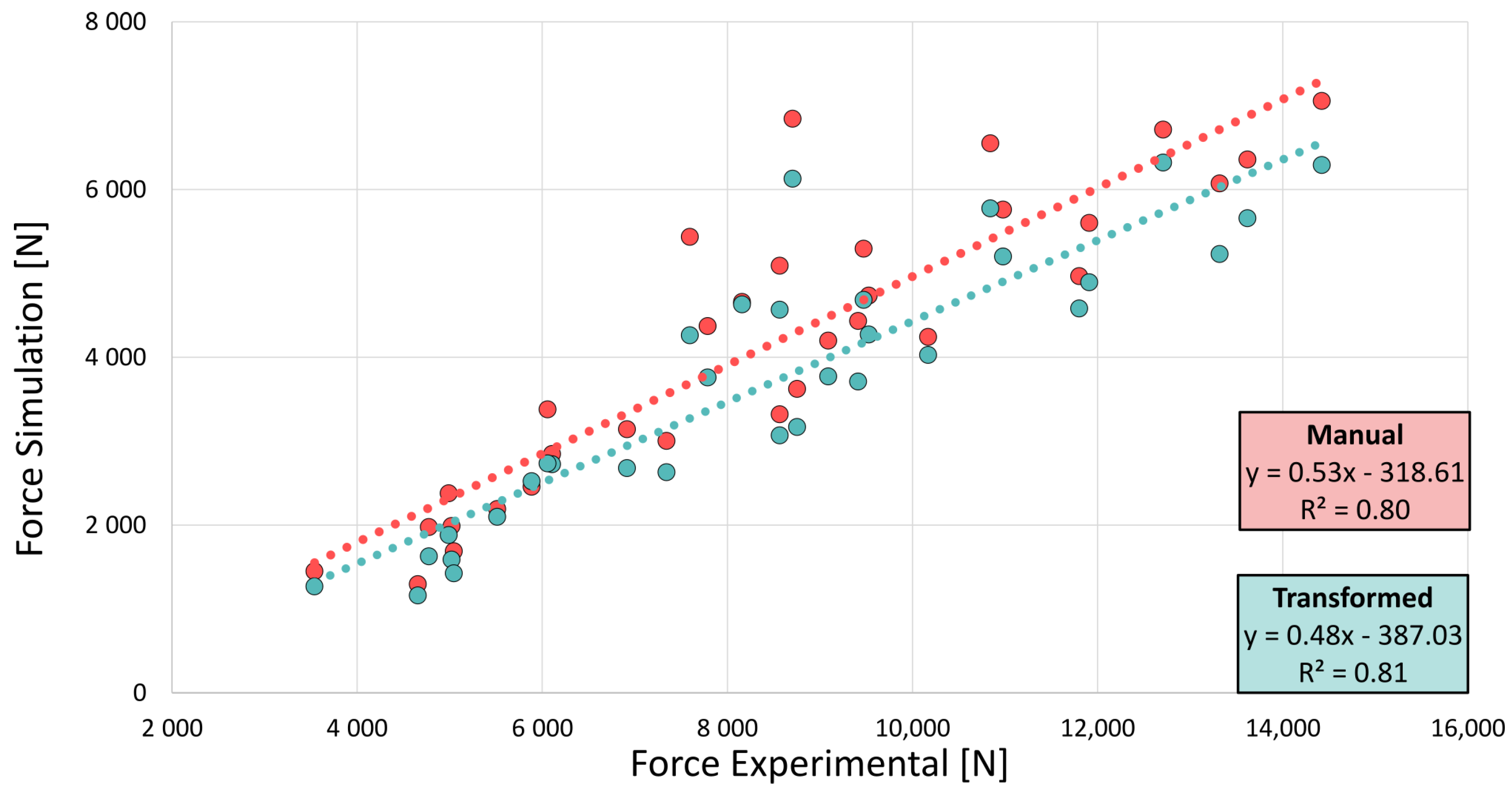
3.1. Accuracy of Transformed Meshes
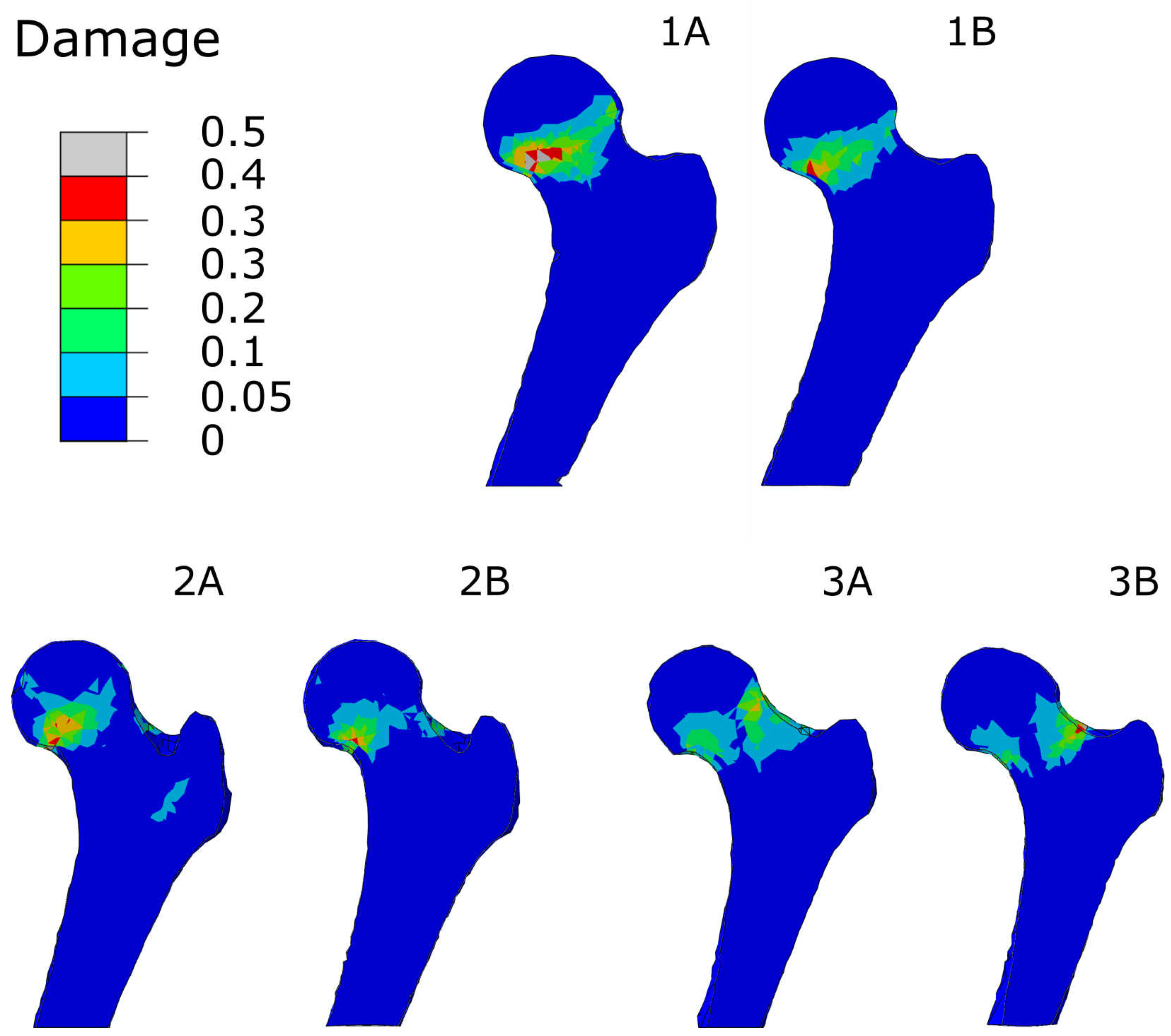
3.2. FE-Predicted Bone Strength
3.3. Regional Statistics
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Torres-Del-Pliego, E.; Vilaplana, L.; Güerri-Fernández, R.; Diez-Pérez, A. Measuring bone quality. Curr. Rheumatol. Rep. 2013, 15, 373. [Google Scholar] [CrossRef] [PubMed]
- Dall’Ara, E.; Pahr, D.; Varga, P.; Kainberger, F.; Zysset, P. QCT-based finite element models predict human vertebral strength in vitro significantly better than simulated DEXA. Osteoporos. Int. 2012, 23, 563–572. [Google Scholar] [CrossRef] [PubMed]
- Vincent, L.; Yohan, P.; Beatrice, C.; Pascal, S. Automatic 3D Finite Element Mesh Generation: Data Fitting from an Atlas. Available online: http://membres-timc.imag.fr/Yohan.Payan/papers/BBE01_Luboz.pdf (accessed on 30 July 2021).
- Sigal, I.A.; Hardisty, M.R.; Whyne, C.M. Mesh-morphing algorithms for specimen-specific finite element modeling. J. Biomech. 2008, 41, 1381–1389. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Ford, J.C.; Greenwald, R.M.; Beckwith, J.G.; Paulsen, K.D.; Flashman, L.A.; McAllister, T.W. Automated subject-specific, hexahedral mesh generation via image registration. Finite Elem. Anal. Des. 2011, 47, 1178–1185. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Dai, Y.; Niebur, G.L. A semi-automated method for hexahedral mesh construction of human vertebrae from CT scans. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 599–606. [Google Scholar] [CrossRef] [PubMed]
- Bucki, M.; Lobos, C.; Payan, Y. A fast and robust patient specific Finite Element mesh registration technique: Application to 60 clinical cases. Med. Image Anal. 2010, 14, 303–317. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Grassi, L.; Hraiech, N.; Schileo, E.; Ansaloni, M.; Rochette, M.; Viceconti, M. Evaluation of the generality and accuracy of a new mesh morphing procedure for the human femur. Med. Eng. Phys. 2011, 33, 112–120. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Qasim, M.; Farinella, G.; Zhang, J.; Li, X.; Yang, L.; Eastell, R.; Viceconti, M. Patient-specific finite element estimated femur strength as a predictor of the risk of hip fracture: The effect of methodological determinants. Osteoporos. Int. 2016, 27, 2815–2822. [Google Scholar] [CrossRef] [PubMed]
- Slagmolen, P.; Elen, A.; Seghers, D.; Loeckx, D.; Maes, F.; Haustermans, K. Atlas Based Liver Segmentation Using Nonrigid Registration with a B-Spline Transformation Model. In 3D Segmentation in The Clinic: A Grand Challenge; Heimann, T., Styner, M., van Ginneken, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 197–206. [Google Scholar]
- Castellano-Smith, A.D.; Hartkens, T.; Schnabel, J.A.; Hose, R.; Liu, H.; Hall, W.; Truwit, C.; Hawkes, D.J.; Hill, D.L. A Registration Based Mesh Construction Technique for Finite Element Models of Brains. In Proceedings of the Medical Imaging 2002: Image Processing, San Diego, CA, USA, 9 May 2002; pp. 538–549. [Google Scholar]
- Bijar, A.; Rohan, P.Y.; Perrier, P.; Payan, Y. Atlas-Based Automatic Generation of Subject-Specific Finite Element Tongue Meshes. Ann. Biomed. Eng. 2016, 44, 16–34. [Google Scholar] [CrossRef]
- Fougeron, N.; Rohan, P.Y.; Macron, A.; Travert, C.; Pillet, H.; Skalli, W. Subject specific finite element mesh generation of the pelvis from biplanar x-ray images: Application to 120 clinical cases. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 408–412. [Google Scholar] [CrossRef]
- Steiner, L.; Synek, A.; Pahr, D.H. Femoral strength can be predicted from 2D projections using a 3D statistical deformation and texture model with finite element analysis. Med. Eng. Phys. 2021. [Google Scholar] [CrossRef] [PubMed]
- Crabtree, N.J.; Kroger, H.; Martin, A.; Pols, H.A.; Lorenc, R.; Nijs, J.; Stepan, J.J.; Falch, J.A.; Miazgowski, T.; Grazio, S.; et al. Improving risk assessment: Hip geometry, bone mineral distribution and bone strength in hip fracture cases and controls. The EPOS study. Osteoporos. Int. 2002, 13, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Wachter, N.J.; Krischak, G.D.; Mentzel, M.; Sarkar, M.R.; Ebinger, T.; Kinzl, L.; Claes, L.; Augat, P. Correlation of bone mineral density with strength and microstructural parameters of cortical bone in vitro. Bone 2002, 31, 90–95. [Google Scholar] [CrossRef]
- Augat, P.; Schorlemmer, S. The role of cortical bone and its microstructure in bone strength. Age Ageing 2006, 35, ii27–ii31. [Google Scholar] [CrossRef] [PubMed]
- Davison, K.S.; Siminoski, K.; Adachi, J.D.; Hanley, D.A.; Goltzman, D.; Hodsman, A.B.; Josse, R.; Kaiser, S.; Olszynski, W.P.; Papaioannou, A.; et al. Bone Strength: The Whole Is Greater Than the Sum of Its Parts. Semin. Arthritis Rheum. 2006, 36, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Bouxsein, M.L.; Seeman, E. Quantifying the material and structural determinants of bone strength. Best Pract. Res. Clin. Rheumatol. 2009, 23, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.J.; Ruff, C.B.; Warden, K.E.; Scott, W.W.; Rao, G.U. Predicting femoral neck strength from bone mineral data: A structural approach. Investig. Radiol. 1990, 25, 6–18. [Google Scholar] [CrossRef]
- Beck, T. Measuring the structural strength of bones with dual-energy X-ray absorptiometry: Principles, technical limitations, and future possibilities. Osteoporos. Int. 2003, 14, 81–88. [Google Scholar] [CrossRef]
- Ammann, P.; Rizzoli, R. Bone strength and its determinants. Osteoporos. Int. 2003, 14, 13–18. [Google Scholar] [CrossRef]
- Humadi, A.; Alhadithi, R.; Alkudiari, S. Validity of the DEXA diagnosis of involutional osteoporosis in patients with femoral neck fractures. Indian J. Orthop. 2010, 44. [Google Scholar] [CrossRef]
- Sapthagirivasan, V.; Anburajan, M.; Janarthanam, S. Extraction of 3D femur neck trabecular bone architecture from clinical CT images in osteoporotic evaluation: A novel framework. J. Med. Syst. 2015, 39. [Google Scholar] [CrossRef] [PubMed]
- Keyak, J.H.; Rossi, S.A. Prediction of femoral fracture load using finite element models: An examination of stress- and strain-based failure theories. J. Biomech. 2000, 33, 209–214. [Google Scholar] [CrossRef]
- Schileo, E.; Taddei, F.; Cristofolini, L.; Viceconti, M. Subject-specific finite element models implementing a maximum principal strain criterion are able to estimate failure risk and fracture location on human femurs tested in vitro. J. Biomech. 2008, 41, 356–367. [Google Scholar] [CrossRef] [PubMed]
- Iori, G.; Schneider, J.; Reisinger, A.; Heyer, F.; Peralta, L.; Wyers, C.; Glüer, C.C.; van den Bergh, J.P.; Pahr, D.; Raum, K. Cortical thinning and accumulation of large cortical pores in the tibia reflect local structural deterioration of the femoral neck. Bone 2020, 137, 115446. [Google Scholar] [CrossRef] [PubMed]
- Dall’Ara, E.; Luisier, B.; Schmidt, R.; Kainberger, F.; Zysset, P.; Pahr, D. A nonlinear QCT-based finite element model validation study for the human femur tested in two configurations in vitro. Bone 2013, 52, 27–38. [Google Scholar] [CrossRef] [PubMed]
- Zysset, P.; Pahr, D.; Engelke, K.; Genant, H.K.; McClung, M.R.; Kendler, D.L.; Recknor, C.; Kinzl, M.; Schwiedrzik, J.; Museyko, O.; et al. Comparison of proximal femur and vertebral body strength improvements in the FREEDOM trial using an alternative finite element methodology. Bone 2015, 81, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Dall’Ara, E.; Luisier, B.; Schmidt, R.; Pretterklieber, M.; Kainberger, F.; Zysset, P.; Pahr, D. DXA predictions of human femoral mechanical properties depend on the load configuration. Med. Eng. Phys. 2013, 35, 1564–1572. [Google Scholar] [CrossRef] [PubMed]
- Luisier, B.; Ara, E.D.; Pahr, D.H. Orthotropic HR-pQCT-based FE models improve strength predictions for stance but not for side-way fall loading compared to isotropic QCT-based FE models of human femurs. J. Mech. Behav. Biomed. Mater. 2014, 32, 287–299. [Google Scholar] [CrossRef] [PubMed]
- Pahr, D.H.; Zysset, P.K. A comparison of enhanced continuum FE with micro FE models of human vertebral bodies. J. Biomech. 2009, 42, 455–462. [Google Scholar] [CrossRef] [PubMed]
- Gross, T.; Kivell, T.L.; Skinner, M.M.; Nguyen, N.H.; Pahr, D.H. A CT-image-based framework for the holistic analysis of cortical and trabecular bone morphology. Palaeontol. Electron. 2014, 17, 1–13. [Google Scholar] [CrossRef]
- Schwiedrzik, J.J.; Zysset, P.K. An anisotropic elastic-viscoplastic damage model for bone tissue. Biomech. Model. Mechanobiol. 2013, 12, 201–213. [Google Scholar] [CrossRef] [PubMed]
- Lowekamp, B.C.; Chen, D.T.; Ibáñez, L.; Blezek, D.; Johnson, H.J. The Design of SimpleITK. Front. Neuroinform. 2013. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Schulte, F.A.; Zwahlen, A.; Lambers, F.M.; Kuhn, G.; Ruffoni, D.; Betts, D.; Webster, D.J.; Müller, R. Strain-adaptive in silico modeling of bone adaptation - A computer simulation validated by in vivo micro-computed tomography data. Bone 2013, 52, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Zysset, P.K.; Dall’ara, E.; Varga, P.; Pahr, D.H. Finite element analysis for prediction of bone strength. BoneKey Rep. 2013, 2, 386. [Google Scholar] [CrossRef] [PubMed]
- Maquer, G.; Musy, S.N.; Wandel, J.; Gross, T.; Zysset, P.K. Bone volume fraction and fabric anisotropy are better determinants of trabecular bone stiffness than other morphological variables. J. Bone Miner. Res. 2015, 30, 1000–1008. [Google Scholar] [CrossRef] [PubMed]
- Pauly, H.M.; Larson, B.E.; Coatney, G.A.; Button, K.D.; DeCamp, C.E.; Fajardo, R.S.; Haut, R.C.; Haut Donahue, T.L. Assessment of cortical and trabecular bone changes in two models of post-traumatic osteoarthritis. J. Orthop. Res. 2015, 33, 1835–1845. [Google Scholar] [CrossRef] [PubMed]
- Musy, S.N.; Maquer, G.; Panyasantisuk, J.; Wandel, J.; Zysset, P.K. Not only stiffness, but also yield strength of the trabecular structure determined by non-linear μFE is best predicted by bone volume fraction and fabric tensor. J. Mech. Behav. Biomed. Mater. 2017, 65, 808–813. [Google Scholar] [CrossRef] [PubMed]
- Schileo, E.; Taddei, F.; Malandrino, A.; Cristofolini, L.; Viceconti, M. Subject-specific finite element models can accurately predict strain levels in long bones. J. Biomech. 2007, 40, 2982–2989. [Google Scholar] [CrossRef] [PubMed]
- Dall’Ara, E.; Eastell, R.; Viceconti, M.; Pahr, D.; Yang, L. Experimental validation of DXA-based finite element models for prediction of femoral strength. J. Mech. Behav. Biomed. Mater. 2016, 63, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, M.A.; Langenderfer, J.E.; Rullkoetter, P.J.; Laz, P.J. Development of subject-specific and statistical shape models of the knee using an efficient segmentation and mesh-morphing approach. Comput. Methods Programs Biomed. 2010, 97, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Poole, K.E.; Skingle, L.; Gee, A.H.; Turmezei, T.D.; Johannesdottir, F.; Blesic, K.; Rose, C.; Vindlacheruvu, M.; Donell, S.; Vaculik, J.; et al. Focal osteoporosis defects play a key role in hip fracture. Bone 2017, 94, 124–134. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.G.; Lowet, G.; Boonen, S.; Nicholson, P.H.; Brys, P.; Nijs, J.; Dequeker, J. Assessment of the strength of proximal femur in vitro: Relationship to femoral bone mineral density and femoral geometry. Bone 1997, 20, 213–218. [Google Scholar] [CrossRef]
| Elasticity | Yield/Strength | ||||||
|---|---|---|---|---|---|---|---|
| [GPa] | [GPa] | k [-] | [MPa] | [-] | [MPa] | ||
| Tension | 6.614 | 0.246 | 2.654 | 1.333 | 54.8 | −0.246 | 40.55 |
| Compression | 72.9 | 0.333 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steiner, L.; Synek, A.; Pahr, D.H. Femoral Bone Strength Prediction Using Isotopological B-Spline-Transformed Meshes. Biomechanics 2022, 2, 125-137. https://doi.org/10.3390/biomechanics2010012
Steiner L, Synek A, Pahr DH. Femoral Bone Strength Prediction Using Isotopological B-Spline-Transformed Meshes. Biomechanics. 2022; 2(1):125-137. https://doi.org/10.3390/biomechanics2010012
Chicago/Turabian StyleSteiner, Lukas, Alexander Synek, and Dieter H. Pahr. 2022. "Femoral Bone Strength Prediction Using Isotopological B-Spline-Transformed Meshes" Biomechanics 2, no. 1: 125-137. https://doi.org/10.3390/biomechanics2010012
APA StyleSteiner, L., Synek, A., & Pahr, D. H. (2022). Femoral Bone Strength Prediction Using Isotopological B-Spline-Transformed Meshes. Biomechanics, 2(1), 125-137. https://doi.org/10.3390/biomechanics2010012






