1. Introduction
Serious trauma, tumors, osteoporosis or inflammatory processes can damage one or more vertebral bodies to such an extent that they are no longer stable. With such massive damage, instabilities and the narrowing of the spinal canal often occur. To stabilize the spine, to prevent irreversible neurological lesions and to reduce the pain of the patient, the affected vertebral bodies are removed and a vertebral body replacement implant is inserted. As anterior implant placements are considered less traumatic and cause less complications than the posterior implant placements, anterior cervical intervertebral body cages combined with plates are commonly used to address these disorders [
1].
In various experimental studies, the biomechanical behavior of spinal posterior and anterior pedicle screws has been analyzed. According to Naoum et al. [
2], the applications of FE modeling in the spine have contributed to the understanding of bone biomechanics, both in healthy and abnormal conditions, such as scoliosis, fractures, degenerative disc disease and osteoporosis. Rosa et al. [
3] aimed to verify the pullout resistance of lumbar pedicle screws obtained by the process of additive manufacturing and to compare them with the screws obtained with traditional techniques. They demonstrated that the pedicle screw produced by EBM exhibited a lower resistance to pull-out tests with respect to other commercial screws, even if it had a rough and microporous surface.
The experimental study by Kotekir et al. [
4] included both radiological and anatomical investigations to explore the feasibility of anterior transpedicular screw (ATPS) fixation in the cervical spine. Furthermore, the morphological measurements for technical requirements were obtained and the accuracy of the ATPS was evaluated using fluoroscopy. The morphological measurements of this study demonstrated that ATPS fixation was feasible in selected cases, especially at the C6–C7 level, if the fluoroscopy-assisted pedicle axis view was used. To assess the relationship of screw pullout and screw insertional torque across a wide range of bone mineral densities (BMDs), Reitman et al. [
5] analyzed the correlation between screw pullout strength and BMD. It could be shown that a high correlation between screw pullout strength and bone mineral density was observed. The objectives of Koller et al. [
6] were to assess the ex vivo accuracy of placing an ATPS into the cervical vertebra as well as the biomechanical performance of ATPSs in comparison with traditional vertebral body screws in terms of pullout strength. Another possibility to analyze the interactions between human spinal structures and medical devices is finite element (FE) modeling. Compared with experiments, FE models provide the opportunity to document related mechanical responses during simulations [
7]. A variety of FE studies have investigated load situations of healthy spines and the effect of spinal stabilization devices on lumbar spine segments. Mas et al. [
8] designed an FE model of the lumbar spine to compare the differences in the biomechanical behavior between a healthy spine and a spine with two different fixation systems inserted at the L4–L5 level. The results of this study reveal that dynamic systems, used as single systems without vertebral fusion, could be a good alternative for patients affected by Pfirrmann grade II and grade III degenerative disc disease. The study by Schmidt et al. [
9] focused on the determination of the stiffness values of posterior stabilization devices capable of achieving a flexible, semi-flexible, or rigid connection between vertebrae L4 and L5 using an FE model. They found that even small stiffness values were enough to cause a stiffening of the functional spine unit. While the study by Goel et al. [
10] determined the effects of a specific disc implant (Charité artificial disc) on the implanted and adjacent segments, the focus of Schmidt et al. [
9] was to determine the stiffness values of posterior stabilization devices capable of achieving a flexible, semi-flexible, or rigid connection between vertebrae L4 and L5 using an FE model.
Sun et al. [
11] and Galbusera et al. [
12] examined via FE simulation the possible subsidence of the cage. The highest risk of subsidence was obtained with a standalone cage and it was shown that a subsidence was less likely to occur in the cage with lower stiffness.
Sun et al. [
11] investigated the biomechanical behavior of the cervical spine after implanting different interbody fusion cages. FE models of C4–C7 segments were built to determine the segmental principal ranges of motion and the load shared by the interbody cage. The investigations of Becker et al. [
7] and Liu et al. [
13] specialized in the analysis of screw–bone interactions. The bone was modeled in a simplified way as a rectangle, with the corresponding material characteristics of cortical and spongious bone [
7] and as an alternative test medium consisting of two different types of polyurethane foam [
13]. It was shown that the interaction between the screw and the surrounding bony area depended on the bone material characteristics and the material of the screw.
The focus of the following studies was the analysis of the mechanical properties of the screws–vertebrae structure and the effects of traditional and cortical bone trajectory pedicle systems using FE modeling. Abbeele et al. [
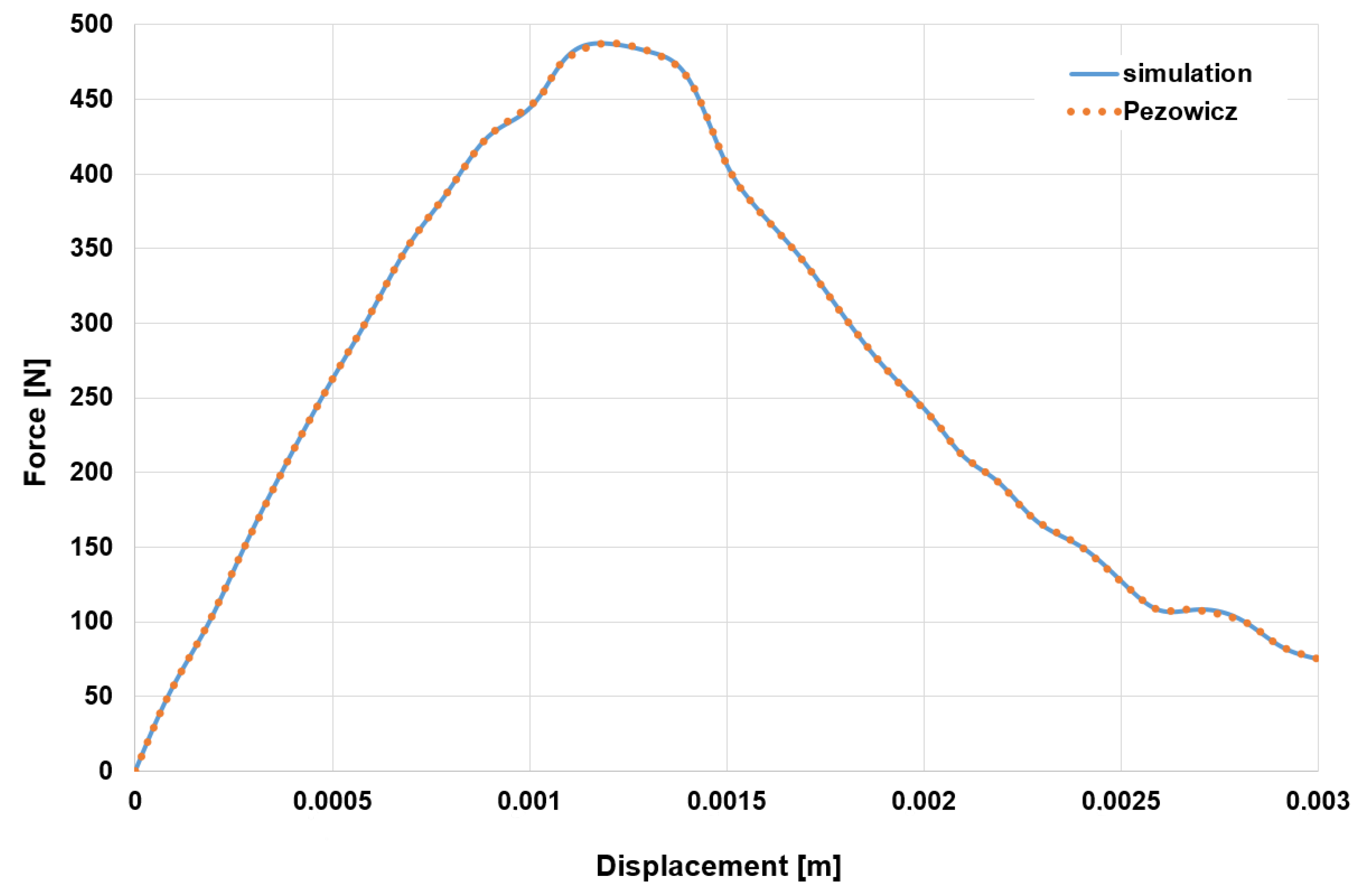
14] predicted the intraoperative pullout strength through a patient-specific FE model of a standard cylindrical pedicle screw inserted in the lumbar vertebra. With the FE model, the linear part of the experimental force–displacement curve was reproduced in a good manner. Moreover, a highly positive correlation was found between numerical and experimental pullout stiffness values. The studies by Qi et al. [
15], Matsukawa et al. [
16] and Senale et al. [
17] specified that an increase in the screw diameter could improve the distribution of pullout stress and could have a greater impact on maximum screw displacement. Xu et al. [
18] created a lumbar spine FE model instrumented with pedicle screws and rods to identify the limitations and advantages of the three types of screw–bone connection models. In this study, only static loading conditions were tested. Su et al. [
19] investigated the effects of the traditional pedicle screw and cortical bone trajectory screw implantation on the lumbar spine using FE methods. The results show that there was no significant difference in the structural stability of the lumbar spine model between the cortical bone trajectory system and the traditional pedicle screw system. However, the endplate loading could be reduced by the trajectory of the cortical bone.
Several FE studies have assessed the characteristics of screw failure and discussed the typical internal stress distribution. The research of Somtual et al. [
20] analyzed the failure of pedicle screw fixation implemented in a cervical spine vertebra under the screw pullout process. Nine pedicle screw FE models were created and the results were compared using the stress transfer parameter of each screw to show how the screws’ parameters affected the pullout strength. With a larger outer diameter (OD) and core diameter (CD) of the screw, the maximum stress transfer parameters was achieved. Furthermore, it was found that large pitch decreased the stress concentration of each screw thread and the small proximal root radius, and distal root radius increased the slope of the blade to resist the pullout load. Wu et al. [
1] used an FE model of the lower cervical spine to compare the biomechanical properties of a novel anterior transpedicular screw artificial vertebral body system (AVBS) with a conventional anterior screw plate system (ASPS) that fixes the lower cervical spine. The characterization of the failure of a posterior bone screw during the screw pullout process using FE analysis was focused on by Ritddech et al. [
21]. The results show that the bone screw should have a large outer diameter, core diameter and proximal root radius to increase the pullout strength.
Although FE models are able to deal with stresses, deformations and complex material behavior, they require a long computational time [
22]. The study of Bonnheim et al. [
23] included a
CT-based FE analysis of a vertebral body implanted with prosthetic disc implants of various sizes and stiffness. The model was loaded with compression- and flexion-induced anterior impingement. It has been reported that a typical analysis utilizes 1100 processors, 3000 GB of memory, and requires over 200 CPU hours. Additionally, Matsukawa et al. [
16] reported a computer solution time per simulation of 12–36 h to analyze the impact of screw diameter and length on pedicle screw fixation strength in osteoporotic vertebrae via a lumbar FE screw–vertebra model. Moreover, the above-mentioned FE models are very specifically tailored to an explicit implant and screw design. Out of the published results, no generally valid statements can be made for other implant and screw types. It is certain that the screw design influences the pullout resistance [
15]. In particular, the screw length and the screw diameter impact the pullout strength [
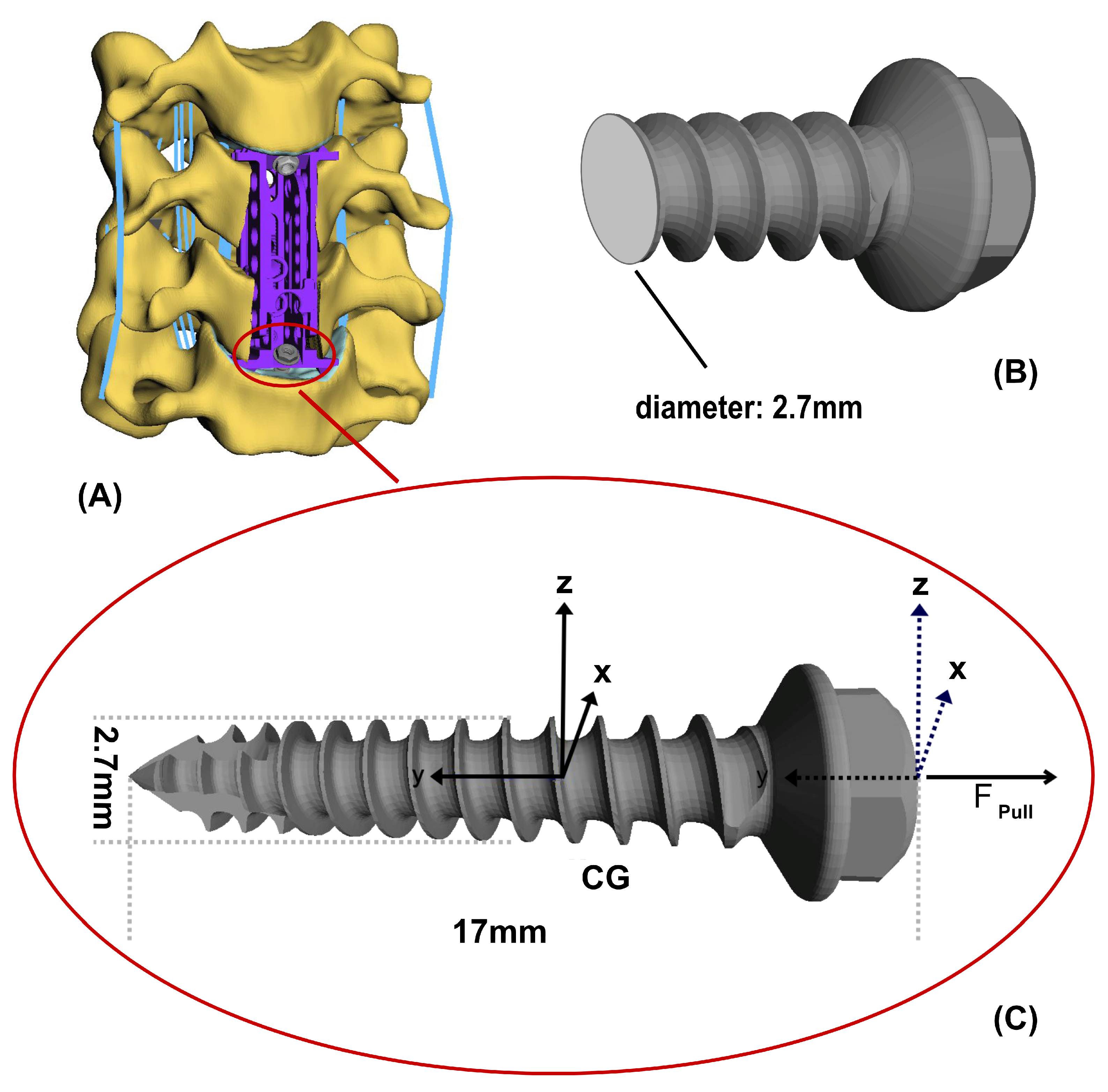
16]. The screw design of our present study differs considerably from the screw designs available in the literature. While screw lengths of 30–50.74 mm and a screw diameter of 3.5–5.5 mm [
4,
7,
13,
15,
16] were examined in the literature, the examined screw in this study had a screw length of 17 mm and a screw diameter of 1.7 mm.
In the current literature, there is no existing way to directly measure biomechanical properties such as stiffness and the damping of the screw inserted in a human spine in vivo. In this context, damping is the decrease in amplitude of an oscillating system or circumstance. The damping can be so strong that no more vibrations occur. Stiffness, on the other hand, is defined as the ratio between the load F on the material and the associated deformation.
In the most cases, these parameters are inferred using pullout experiments on cadaver or animal vertebrae [
14,
24,
25]. A few approaches that apply optimization methods have been proposed in the literature to identify the stiffness and damping values for the various spinal flexible structures [
26,
27]. Rohlmann et al. [
28] determined an optimal stiffness of the solid longitudinal rods in the pedicle-screw-based implant applying optimization criteria defined upon the ranges of motion as well as loads in the facet joints, bulgings of the intervertebral disc and the intradiscal pressure in the FE model of the lumbar spine. To our knowledge, no existing study has dealt with the calculation of the unidentified biomechanical parameters of the spinal screw using MBS models.
Therefore, we propose a sensitivity method for MBS models with which a priori unknown parameters can be approximated without the need of longer simulation times. In this study, a simplified screw–vertebra model is used in order to simultaneously exchange the model parameters and calculate the effects of said parameters. The main focus is on determining stiffness and damping characteristics for an analysis of the interaction between the implant anchor screw and the vertebral body.
3. Results
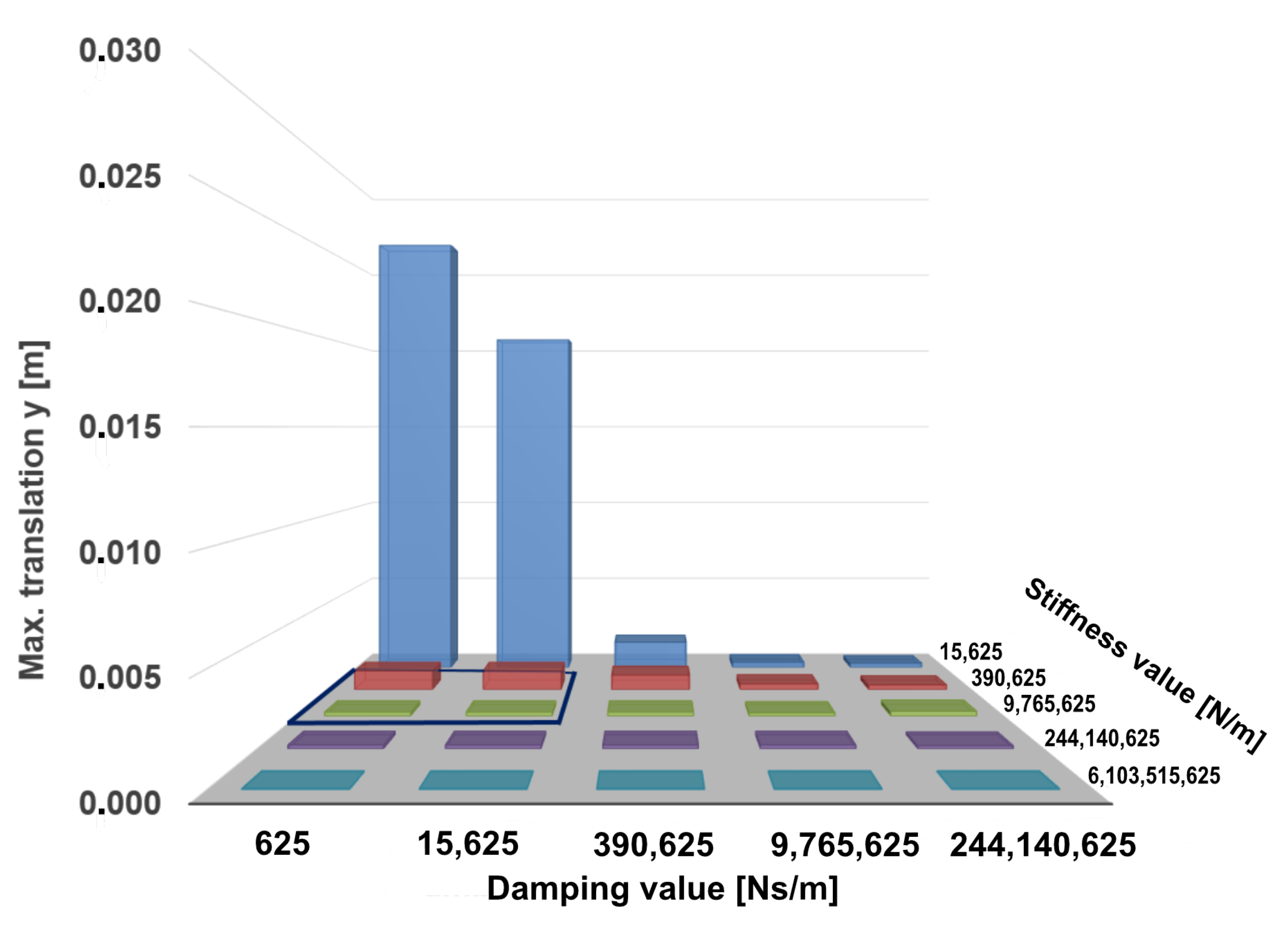
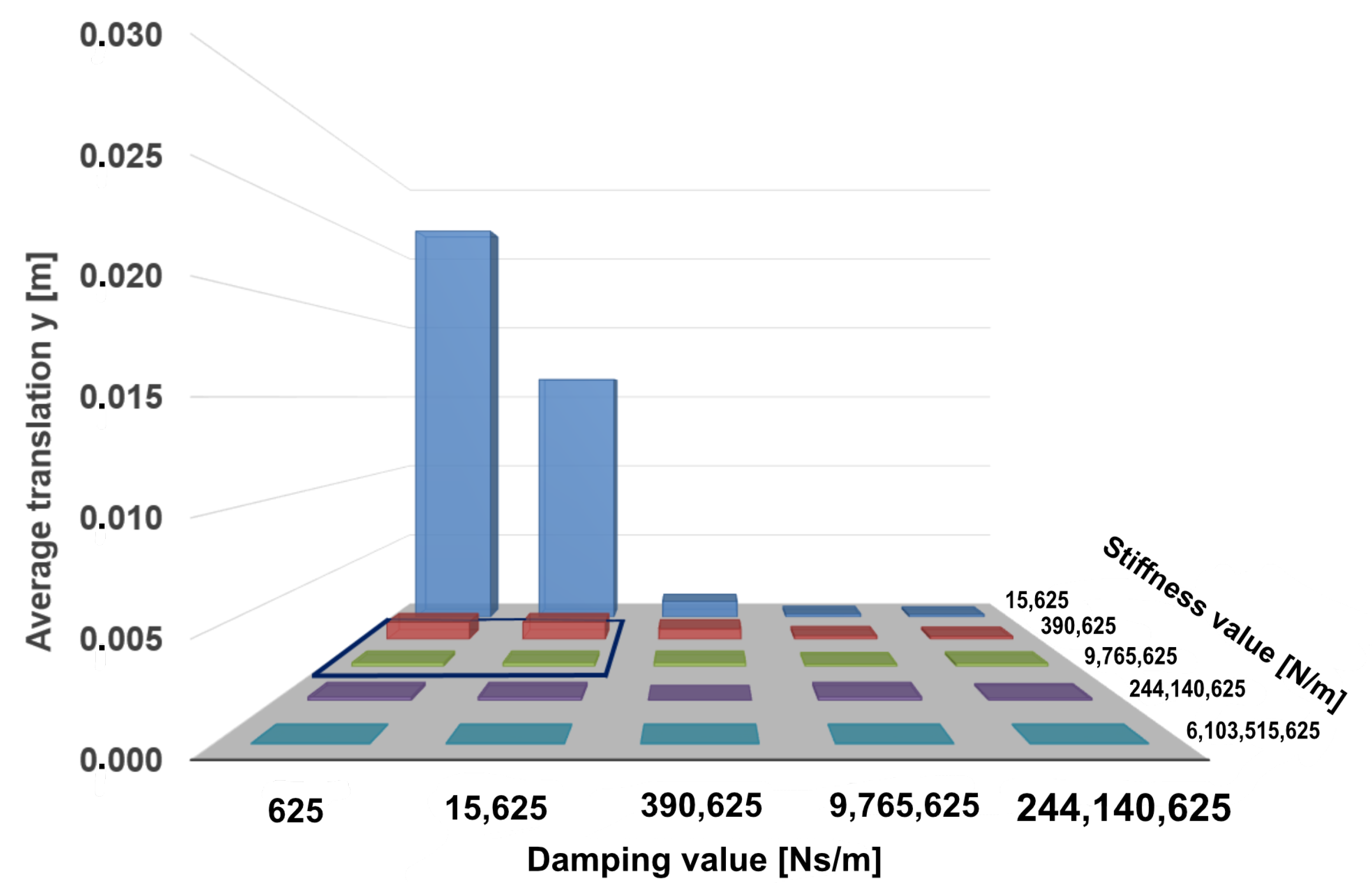
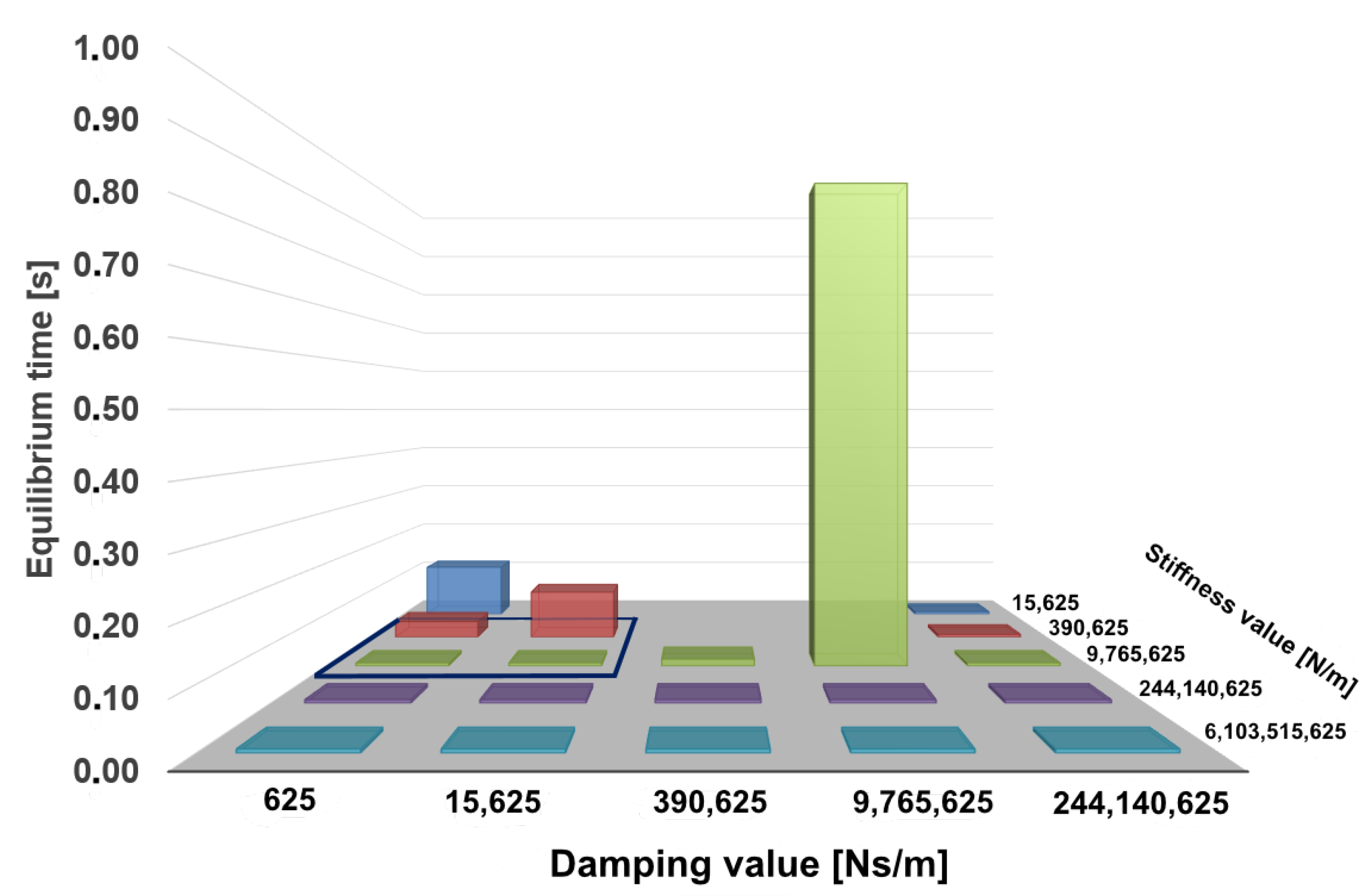
The bar charts shown in
Figure 5 and
Figure 6 represent the maximum and average screw translation calculated in the simulation for the pullout force of 411 N using defined pairs of stiffness and damping values. It can be seen from the diagram in
Figure 5 that high screw displacements are achieved for the combined parameter values
N/m to
N/m and
Ns/m to
Ns/m with a displacement between
m and
m. The highest screw displacement of
m is reached with the parameter values
N/m and
Ns/m. Both diagrams in
Figure 5 and
Figure 6 show that the values of the maximum displacement do not deviate much from the average translations. The system outcome indicates the general stability of the presented model.
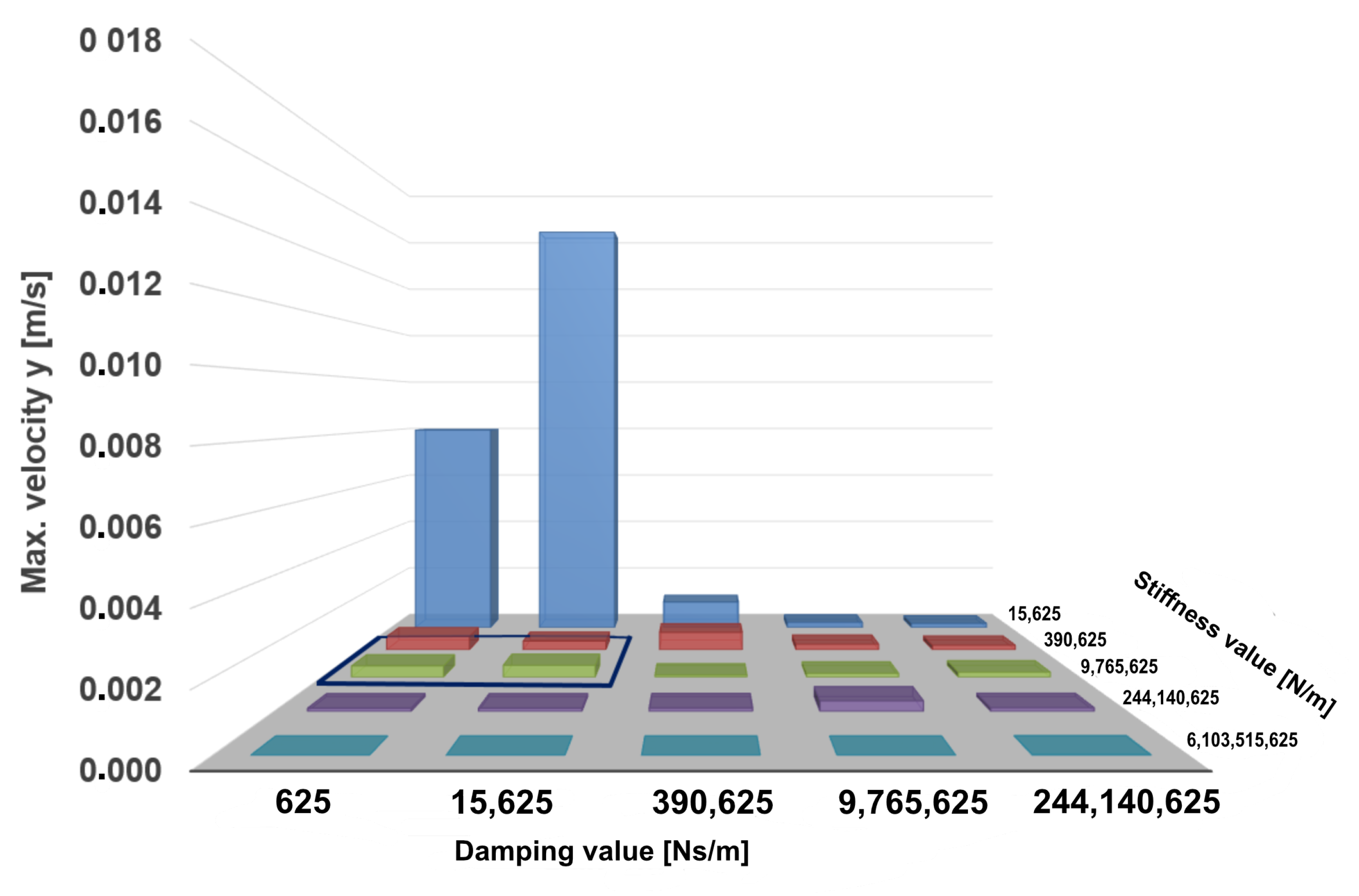
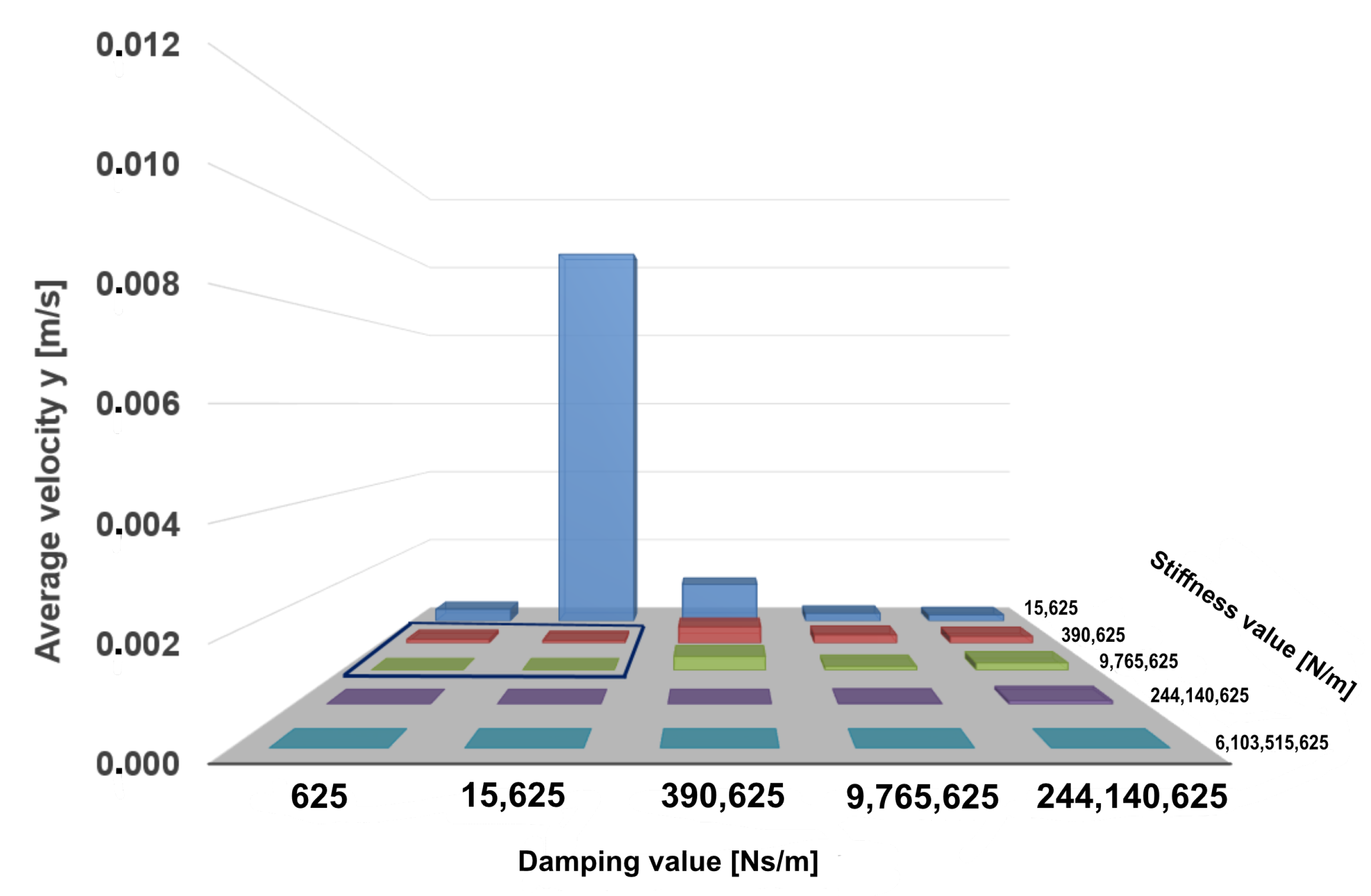
The maximum and the average screw velocities are shown in
Figure 7 and
Figure 8. From the presented results it can be seen that the highest velocity values are reached by the screw with a relatively small stiffness term of
N/m and damping values
. The maximum screw velocity of
m/s is achieved with a parameter combination of
N/m and
Ns/m.
The deviations of the maximum screw velocity from its average values are comparatively greater than those shown in the case of screw displacement. When the stiffness term increases from Ns/m up to N/m, and for damping terms up to Ns/m, the maximum velocity deviates further from its average values than in any other parameter sets.
Another parameter that was analyzed within the scope of this study was the time needed for the system to reach a static equilibrium. For the determination of the equilibrium state the velocity of the screw was compared in each time step until the simulation’s end. We considered the rest state to be reached from the point the velocity of the screw was continuously smaller then the pre-defined constraint
. As shown in
Figure 9, no equilibrium state could be reached when damping values dominated stiffness coefficients. The only exceptions were the simulation runs with the maximum damping term of
Ns/m, where the system could reach the rest state in the very short time of
s. The same model behavior was observed for large stiffness values of
N/m and
N/m.
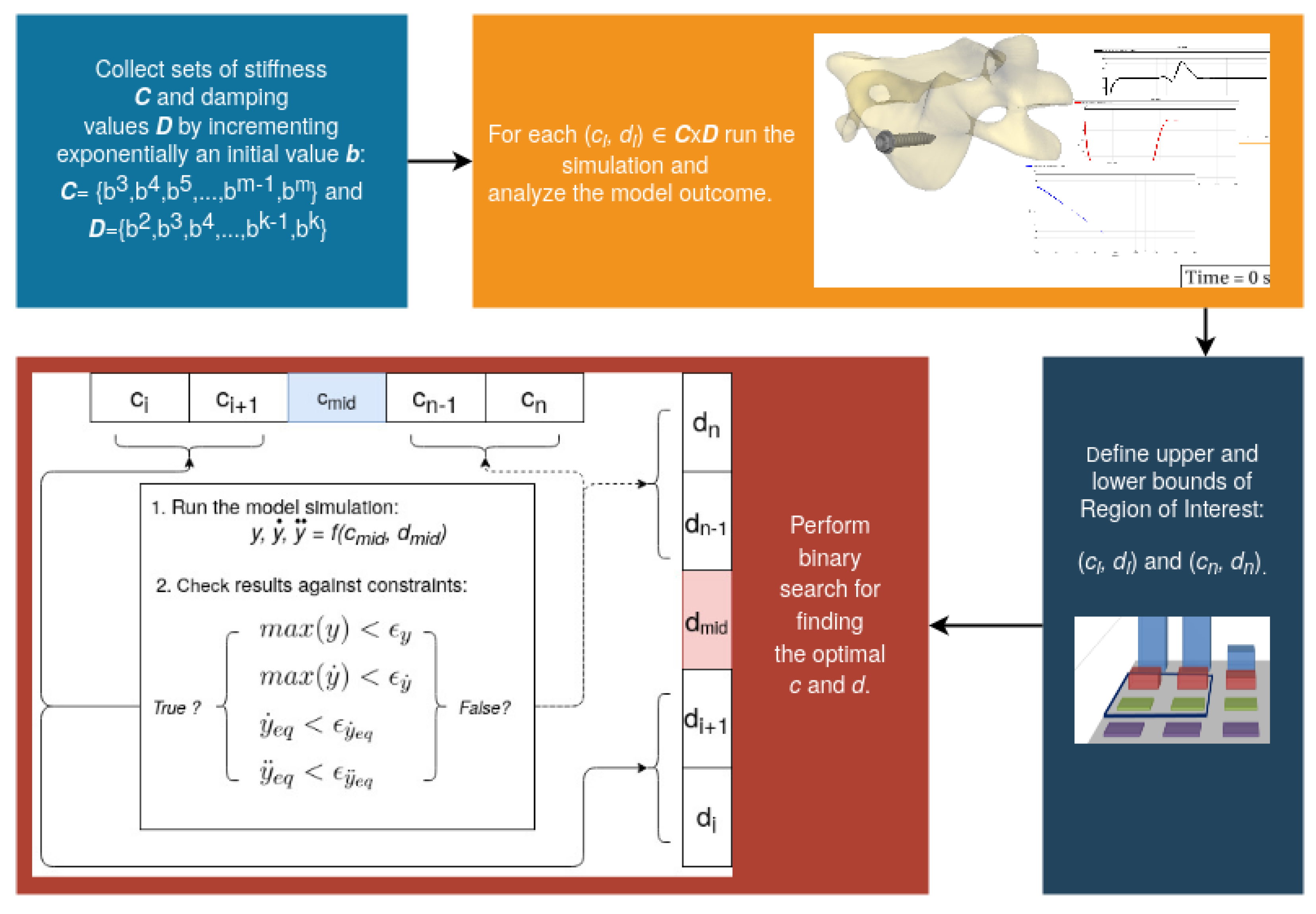
The obtained results show that high stiffness and damping values guarantee reaching the screw equilibrium state. However, the goal of this study is to find the smallest values of the input model parameters that bring the screw into a resting state and do not violate the translational constraint . Therefore, the Region of Interest (RoI) for the fine-grained parameter search was chosen to be N/m, …, 9.77 N/m} and {0 Ns/m, …, 1.56 Ns/m}.
With the initial set of parameters, the search for the general influence of the stiffness and damping parameter was analyzed and the RoI was defined. We determined the RoI analytically by comparing the model translation, its velocity and the time it took to reach equilibrium. Since our goal was to find the minimum damping and stiffness coefficients that fit the requirements from Equation (
2), the selected RoI was defined by its boundaries:
N/m,
N/m and
Ns/m and
Ns/m. The RoI is highlighted in
Figure 5,
Figure 6 and
Figure 7 , and in
Figure 8 and
Figure 9 with a blue border.
After the RoI was determined, the optimal parameters for c and d could be found using a binary search method in order to reduce long computing times in cases when the parameters values would be determined linearly within the selected RoI. In the current implementation of the binary search we monitored the simulation outcome in each loop iteration in order to find the aforementioned smallest c and d, which had a significant impact on the screw translation and velocity. When at least one set of parameters was found and no changes were indicated in the model response for two consecutive parameter pairs, the search was stopped.
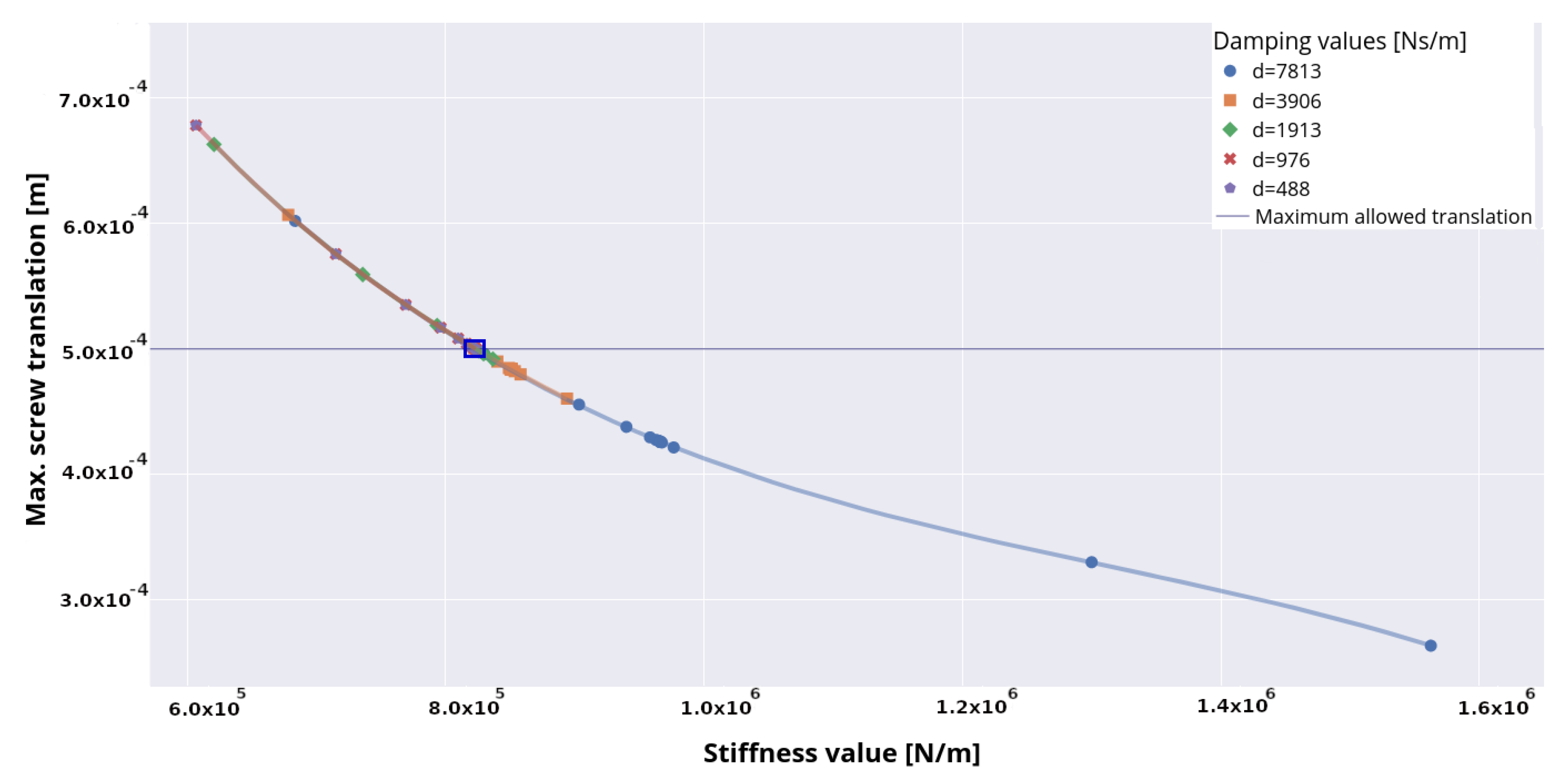
The results of the parameter determination using a binary search method are presented in
Figure 10, where the distribution of stiffness and damping values with regard to screw translation is pictured. It can be observed that for the damping values
d < 7813 Ns/m the majority of identified stiffness coefficients are distributed between 6
N/m and 9
N/m. Within this parameter interval the maximum screw displacement of 6.78
m was reached. Through the combination of damping value
d = 7813 Ns/m with the stiffness coefficient
N/m very small screw displacements of up to 2.6 × 10
m could be achieved.
Another observation is that the screw displacement data perfectly fit a curve defined by the third-order polynomial equation:
where
(m) is a screw displacement,
x (N/m) is the stiffness value and the following regression coefficients are
(m),
(m
2/N),
(m
3/N
2) and
(m
4/N
3). The suitable fit of the regression curve shows a strong relationship between the stiffness term and screw translation. Using the determined parameters of the regression curve and a given stiffness value
x, the screw displacement
can be estimated along the selected RoI.
In order to determine the final set of parameters, we consider the screw displacement values that are on or below the purple line, which represents the translation constraint . It is evident that a stiffness value of c = 823,224 N/m and a damping value of d = 488 Ns/m are found to be an optimal parameter pair, for which the sufficient maximum screw translation of m is reached.
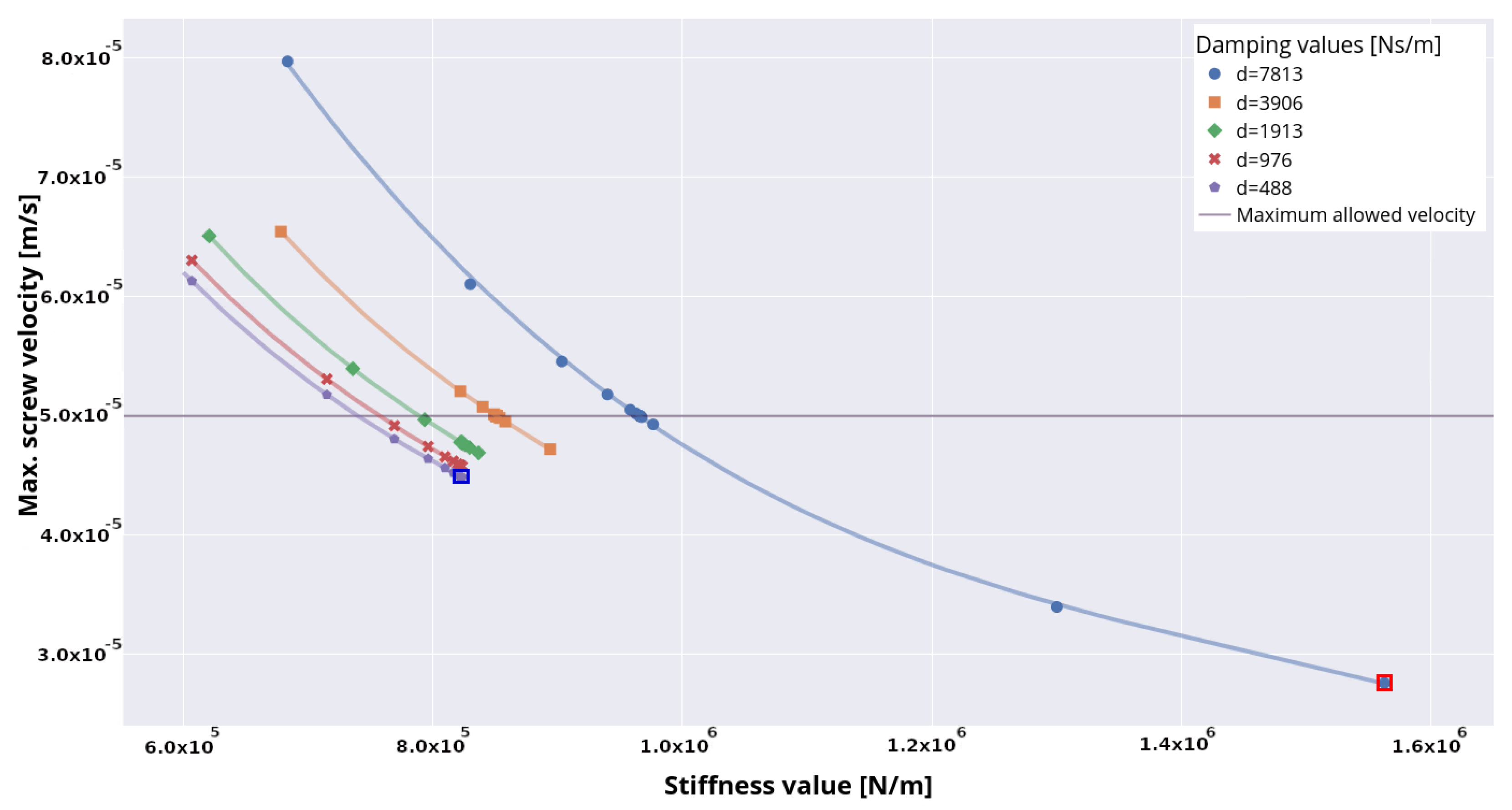
We now look at simulation outcomes in terms of the maximum screw velocities as shown in
Figure 11. The maximum allowed velocity constraint from
Table 2 is represented in the plot by a purple line. It can be seen that for the damping values
7813 Ns/m the corresponding stiffness coefficients that are sufficient to hold the pre-defined constraints are distributed in the interval of
c > 7.5 × 10
N/m and
c < 1.6 × 10
N/m. Although the lowest screw velocity, which is marked red in the figure, is achieved at damping
d = 7813 Ns/m and stiffness
c = 1,562,499 N/m, the pair of minimum parameters is decided to be
c = 823,224 N/m and
d = 488 Ns/m, which supports the above statement concerning the optimal parameter set found with regard to maximum screw translation. The maximal velocity for optimal
c and
d is highlighted in dark blue.
The results from
Figure 11 show that velocity data points fit the separate regression curve for each damping term by applying the same polynomial from Equation (
3) with different
coefficients. In order to estimate the screw velocity, the stiffness term itself is not enough; the damping term also has to be considered.
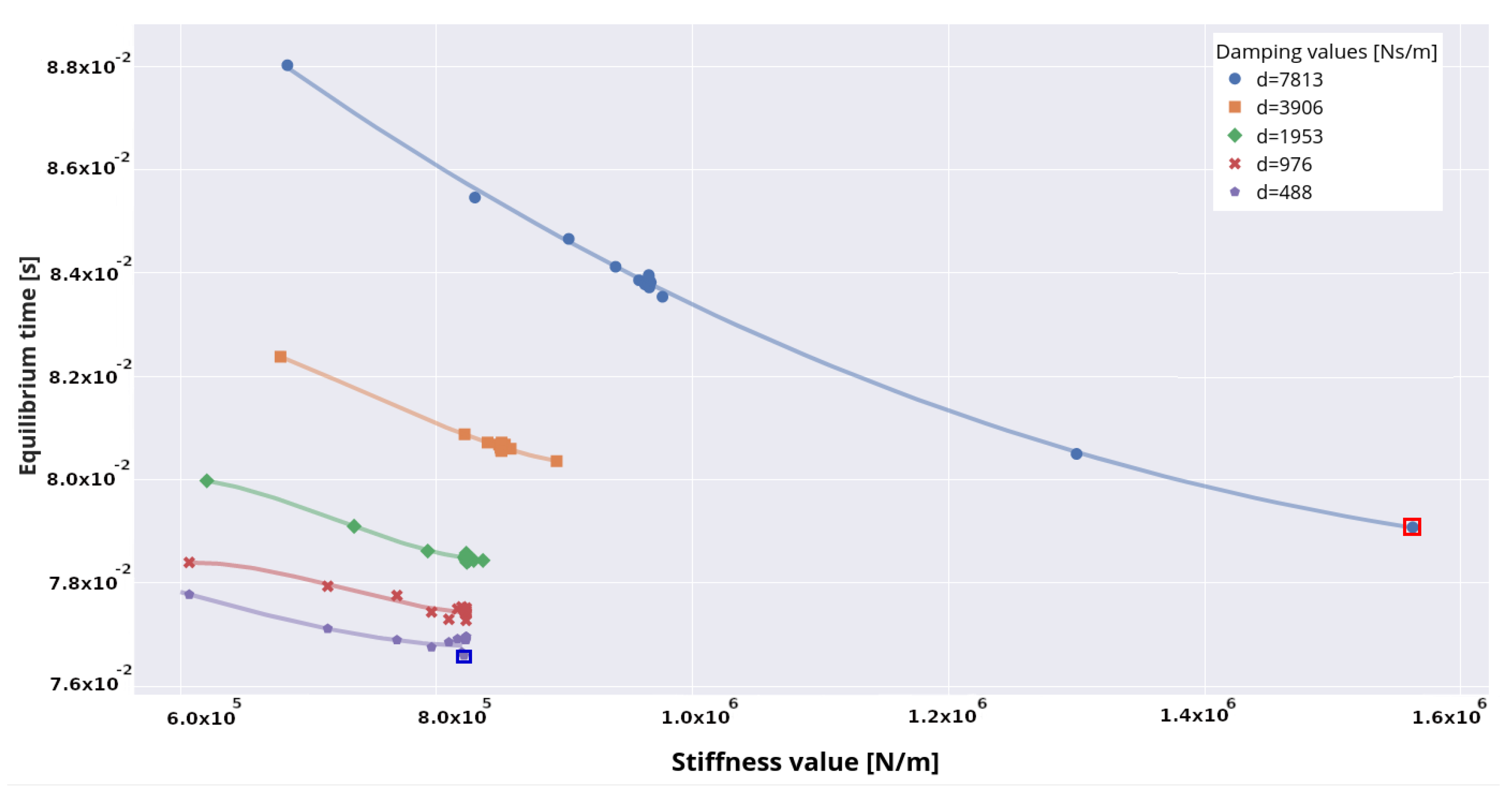
The time at which the screw reaches the static equilibrium state is plotted in
Figure 12. The shortest time of 0.07674 s to reach the equilibrium state is guaranteed by
c = 823,224 N/m and
Ns/m and is highlighted by the blue frame. By applying the highest parameter values of
d = 7813 Ns/m and
c = 1,562,499 N/m to the model, the screw enters the rest state in 0.07908 s time, which is marked red in the plot.
The average CPU time per simulation was 5 s.
4. Discussion
A basic requirement for a valid model is the adequate definition of model input parameters. Because model parameters are generally vague, their predictive power is frequently questioned [
35]. A comprehensive sensitivity analysis is essential in order to stand firmly against these sensible critical arguments. Therefore, the aim of this study was the development of a sensitivity analysis method to identify valid input parameters for a highly simplified rigid body model composed of an implant screw and vertebral body C4. For this purpose, a two-step sensitivity analysis was developed and applied to solve the parameter optimization problem: in the first step, the initial set of the stiffness and damping coefficients was created and a model simulation for each pair of the parameter values was performed. Based on the obtained simulation results, the region of interest for further parameter search was determined. In the final step, the binary search with constraint checking was utilized in order to define the minimal input parameter values. The resulting optimal model parameters were found to be
c = 823,224 N/m for the stiffness value and
Ns/m for the damping value. Parameters smaller than those presented here were not analyzed, as they did not indicate any significant change in neither screw velocity nor screw translation.
In the case of a specific simulation scenario in which the input parameters are unavailable in the literature, and no possibility to conduct an experiment is given, the proposed method can be applied. Additionally, the obtained results can be used in more complex MBS and FE studies as valid model parameters for models of the different spinal regions featuring different degrees of abstraction.
There are some limitations to this study, which can be divided into two categories: model-related limitations and sensitivity-analysis-related limitations. The model-related limitation of the current model configuration is that only the elasticity in the longitudinal direction of the screw has been taken into account. However, in real scenarios, forces along the transverse and sagittal axes could also influence the screw. Furthermore, only the transnational movement was examined. However, if one wants to capture the entire mechanical behavior between bone and screw, torques must also be taken into account, as they can act on the screw when present during load. Therefore, the elasticity of the “implant screw–bone” combination will be taken into account in future work and analyzed in all spatial directions for both transnational and rotational movements.
Another model-related limitation is that the specific mass properties of a certain screw are included as model parameters that can influence the biomechanical behavior of the system. The analysis of the effects of mass properties such as mass, center of mass and inertia tensors on the model mechanics would provide further insight about the dependencies of the model parameters. The effects of variations in mass properties will be investigated in a future study.
The major sensitivity analysis limitation of the proposed approach is related to the search method used in order to find the optimal input parameters. Although the binary search operation has been shown to be an effective method for finding the optimal parameters, it depends on the quality of the previously selected RoI. Consequently, it is important to define an adequate RoI, which possesses the desired behavior of the screw regarding its translation and velocity. In the proposed approach, the boundaries of the RoI were selected manually by considering the results of the sensitivity analysis. However, this step can be automated by comparing simulation outcomes and defining the conditions that describe the RoI, which shall be considered in a future work. Another limitation of the binary search is that the function it is applied to needs to be monotonic. In our case, the monotonicity of the simulation function is given by the nature of the screw force in Equation (
2).
Furthermore, we plan to expand the method by introducing parameters so that the patient-specific bone density is taken into account.
Despite the listed limitations, this study confirms the possibility of using multibody simulation as an adequate method for determining and analyzing biomechanical parameters. It shows that a real scenario, in this case a screw pullout test, could be reproduced by means of an MBS model and that the simulation results concur with the experimental results. Furthermore, we used our proposed method to demonstrate how sensitivity analysis can be used to define optimal model parameters.
In conclusion, this analysis should be seen as a part of our longstanding research focus. An MBS model of the spine is continuously being developed for the interactive advance planning of operative interventions. Our idea is to develop a tool based on a patient-specific MBS model to make preoperative patient-specific statements about the load situation. Furthermore, in contrast to FE simulations, the short computing times of the MBS models open up the possibility of simulating dynamic processes, and thus analyzing the stress of the spinal structures during a patient’s daily activities.
In the systematic literature review of Alizadeh et al. [
36], concerning the biomechanical musculoskeletal models of the cervical spine, it is described that the dynamic MBS seems more suitable to investigate the risk of injuries to the cervical spine in connection with occupational environments or effects, because of the lack of dynamic loading in the FE models. Despite existing knowledge on the load situation of spinal structures, which is provided by sophisticated FE model structures, the basic load transfer behavior during dynamic movements remains initially unknown. Therefore, a holistic approach is warranted to close this knowledge gap in the future. The aim is to create MBS models of the entire human body with a finely structured spinal model, with which stresses within spinal structures can be analyzed during movements in daily life. With this approach new insights into the influences of an inserted implant on the human body during dynamic scenarios can be obtained. The parameter search method proposed in this study can be used to define the unknown biomechanical parameters describing the characteristics of spinal structures, as well as implants, especially in cases when conducting in vivo experiments is impossible.