Abstract
An important property of arylboronic acids, particularly when considering their use in medicinal chemistry, is their pKa in aqueous solution. The results of computational determination of absolute pKas of arylboronic acids can be very disappointing in comparison to available experimental results, particularly in the case of large substituents. In this paper, the main origin of this problem is identified. It is shown that in order to obtain accurate pKa values for arylboronic acids from computational quantum chemistry, it is necessary to consider the effect of different possible conformations of the hydroxyl groups in the acid and its conjugate base together with the low-energy conformations of their substituents. An improved practical procedure for the computational determination of the pKas of arylboronic acids is proposed and applied to a set of recently synthesized arylboronic acids, yielding consistent results.
1. Introduction
Arylboronic acids are the molecules of the general formula “”, where “” is an aryl or a heteroaryl group [1]. They are best known for their role in Suzuki coupling reactions, ref. [2] constituting one of the most versatile ways to form carbon-carbon bonds. Besides that, they form an important class of molecules, employed in a large array of applications from medicinal chemistry to analytical chemistry and material science [3].
Regarding their applications to medicinal chemistry, it is of paramount importance to have knowledge of their acidity. The practical use of arylboronic acids as drugs is dependent on their solubility in water, which is in turn dependent on their pKa. In general, arylboronic acids have a lower pKa than alkylboronic acids, usually within the 4–10 range. This is somewhat expected since in arylboronic acids, boron is bonded to a sp2 carbon, while in alkylboronic acids, it is bonded to a sp3 carbon. Furthermore, the pKa of arylboronic acids can be modulated depending on the substituents present in the ring, which may allow the appropriate pKa to be tuned to the desired application. These characteristics make arylboronic acids among the most widely used organoborons in different areas. To cite an example of the importance of understanding the pKa of these organoborons, it can be mentioned that the pH range for the analysis of biomolecules by boronate affinity chromatography (BAC) is influenced by the pKa of the boronic acid used as a ligand in the stationary phase. The pH at which the analysis is performed plays a crucial role in the BAC technique, since biomolecules are very sensitive to pH, and this can limit the number of species that could be investigated in BAC [4]. In a recent review on the acidity of arylboronic acids, Sporzynski et al. claimed that computational methods were unsuited for the prediction of pKa of these molecules due to the significant differences in the results calculated from the ones measured [5]. In our own preliminary calculations, following general procedures for pKa determination existing in the literature [6], depending on specific details of the solvent model employed, some pKas were off by five or more units, usually above the experimental pKa. The physical origin of this problem was indirectly hinted at by some authors, being partly associated with the difficulty of quantitatively modeling the interaction of the hydroxyl moieties in the acid and conjugate base with the solvent [7,8]. Specifically, boronic acids may have multiple low-energy conformations [9]; all these conformations should be accounted for and somewhat included in a computational determination of their pKa. However, to our knowledge, no general procedure is yet available to generate accurate absolute pKa values for large arylboronic acids, having multiple low-energy conformations.
In this paper, a practical procedure for the computational calculation of accurate values for the pKa of arylboronic acids is presented. The procedure is validated by the correct reproduction of the experimentally known pKa of the simplest of the arylboronic acids. Then, it is applied to a set of recently synthesized arylboronic acids, yielding consistent results. A more in-depth discussion of the electronic factors influencing the pKa of the arylboronic acids will be presented in a separate publication.
2. Materials and Methods
From a conceptual point of view, arylboronic acids are best understood as Lewis acids rather than Brönsted acids, since their general acid–base reaction in aqueous media can be written as follows:
Instead of directly donating a proton to the solvent, the arylboronic acid incorporates a hydroxyl group from the water media in a typical Lewis acid–base reaction. As a byproduct of this process, a proton is released to the solvent, as occurs for the typical Brönsted acids, allowing a similar quantitative definition of pKa [5,10]. The thermodynamic equilibrium constant that characterizes its acidic behavior can be expressed in terms of the activities of the reaction constituents as follows:
The relationship between activities and concentrations is modulated by the activity coefficients .
For dilute solutions where the reaction constituents interact only with the solvent, the activities can be approximated by the corresponding concentrations:
is the acidity constant in water as a solvent. Thus, the free energy associated with the acid–base reaction in standard conditions is given by the following:
Therefore, the can be expressed as follows:
The final expression is obtained by replacing and :
Finally, the must be expressed in terms of free energies of the species involved in the acid–base reaction. All the quantities in the expression below are amenable to computational determination or known from experimental data [6]:
For the terms associated with the arylboronic acid and its conjugate base, one has the following:
The first two terms on the right are determined from Density Functional Theory calculations performed with the M06-2X functional [11] using the quantum chemical program ORCA 4.0 [12]. One of the best features of the Minnesota density functional set is that they are adjusted against a very large database of molecular properties, the M06-2X variation being particularly suited for representative elements. Calculations determining the possible geometry minima, including free energy corrections for all relevant conformations, were performed within the 6-31+G(d,p) basis set. The term corresponds to the lowest energy conformer corrected at the M06-2X/6-311++G(3df,3p) level. All the DFT calculations were performed using the Lebedev angular grids with 96 radial shells and 770 angular points. The geometries were optimized under very tight optimization criteria. The term is associated with the thermic contribution to the free energy from all possible locally stable conformations of the arylboronic acid and its conjugate base. The partition function of each boronic acid and corresponding anion was determined as a Boltzmann-weighted average of the partition functions of individual conformers, in the spirit of the Multi-Structure Local Harmonic (MS-LH) approximation of Zheng and Truhlar [13]. This general procedure is also able to generate improved values for other sensitive properties such as reaction rates [14,15,16]. The solvent effects were modeled by the Solvent Model Density (SMD) approach with Polarizable Continuum Model (PCM) electrostatics [17]. Finally, the term points to the change in standard state from 1 atm to 1 mol/L at 298 K.
The free energy in aqueous media for was obtained from the following:
The terms in Equation (10) have the same meaning as in Equation (9), with the addition of the experimental value of solvation of water in aqueous media, [18].
For the proton, the free energy in solution was determined from experimental values as follows [19]:
From the experimental values of and one obtains ; combined with [20], and , the free energy of a proton in water solution is finally obtained as .
The methodology outlined above is applied here to a set of eleven arylboronic acids. The phenylboronic acid (PhB(OH)2, 1), whose pKa is experimentally known, served as a reference for the development of the approach attempted herein. The other ten arylboronic acids (4a–j) were recently synthesized and, to our knowledge, have not had their pKa experimentally measured (Scheme 1, Table 1).
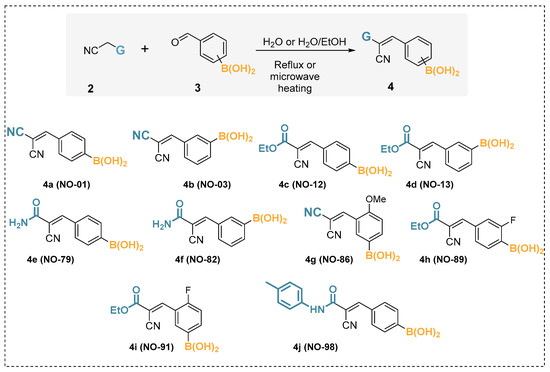
Scheme 1.
Synthesis of the boronic acids by Knoevenagel condensation plus the structural formulas and identification of the molecules considered herein.

Table 1.
Relative energies of non-equivalent conformations of phenylboronic acid and its conjugated base. The potential energy (kcal.mol−1) is calculated relative to the global minimum. Rotational–vibrational partition functions at 298 K for each structure are calculated relative to the global minimum, including the rotational symmetry number (). The weight accounts for mirror images. All the values were calculated at the M06-2X/6-31+G(d,p). Geometries for the global minima of all species, Tables S1–S22 (Supplementary Materials).
The boronic acids (4a–j) were synthesized by Knoevenagel condensation between arylboronic acids containing the formyl group and active methylenes such as malononitrile and cyanoacetic acid derivatives (Scheme 1). In this obtained series of boronic acids, the aromatic ring of arylboronic acid is linked to an electron-poor vinyl system CH=C(CN)G, where G can be a nitrile or an ethoxycarboxyl, or even an amidic carboxyl. The compounds synthesized by the Knoevenagel reaction were considered as cyano derivatives of borated cinnamic acids, and these compounds were referred to as α-cyanocinnamylboronic acid derivatives. These organoborons were chosen because they are considered relevant from the medicinal chemistry point of view due to the potent anti-inflammatory activity associated with the selective inhibition of the purinergic receptor P2X7, a biological target of great interest for the development of new anti-inflammatory therapies [21,22]. The boronic acids studied in the present work (4a–j) were reported in previously published articles, which involved anti-inflammatory activity. In those works, laboratory codes were given to the molecules (NO series). Thus, so that the reader can maintain comparison with previous works, the NO codes are given in parentheses.
3. Results
As explained in the Section 2, for each of the arylboronic acids, a comprehensive scan was performed to identify all the low-energy conformations. The searches were conducted by selecting the relevant dihedral coordinates and sampling the conformational space, encompassing all the possible combinations of angles. Geometries were optimized without constraints. Hessian calculations were performed only for non-equivalent geometries. Regarding the unsubstituted phenylboronic acid, the rotation of its two O–H bonds leads to four conformations, two of which are mirror images and therefore have the same energy and vibrational frequencies. The two torsion coordinates are measured by the dihedral angle calculated using the atoms C–B–O–H. The configuration is labeled anti/syn according to whether the dihedral angle is 180° or 0°, respectively. In Figure 1, the most common minimum conformations of the hydroxyl moieties are shown for the phenylboronic acid.
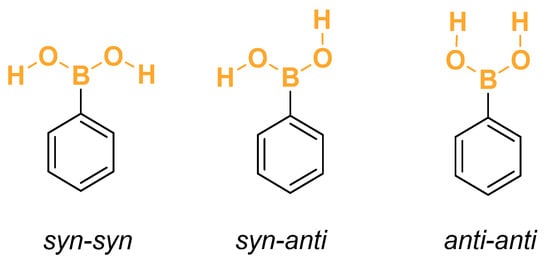
Figure 1.
Conformers of phenylboronic acid.
The designations syn and anti are employed when there is a clearly defined, unique reference plane. For the phenylboronic acid conjugated base, there is no such unique plane. Therefore, the conformations labeled syn and anti are replaced by the designations syn, gauche+, and gauche−. These are associated with dihedral angles of +60° and 60°, respectively. In principle, 27 combinations of anti, gauche+, and gauche− would be expected. However, the actual number is twelve pairs of mirror-image structures and 3 Cs structures, as shown in Figure 2. Both conformations within each pair of mirror images have the same energy and vibrational frequencies. Therefore, the rotational–vibrational partition function can be calculated only for one member of each pair and multiplied by two. The complete list containing the relative energies, Boltzmann-weighted rotational–vibrational partition functions, rotational symmetry numbers, and weight of each structure can be found in Table 1. As discussed above, the weight factor is equal to two if the configuration has a mirror image or one if it has a plane of symmetry. All the conformations of and are within 1 kcal.mol−1 from the global minimum (the only exception is the anti-anti-anti configuration of ).
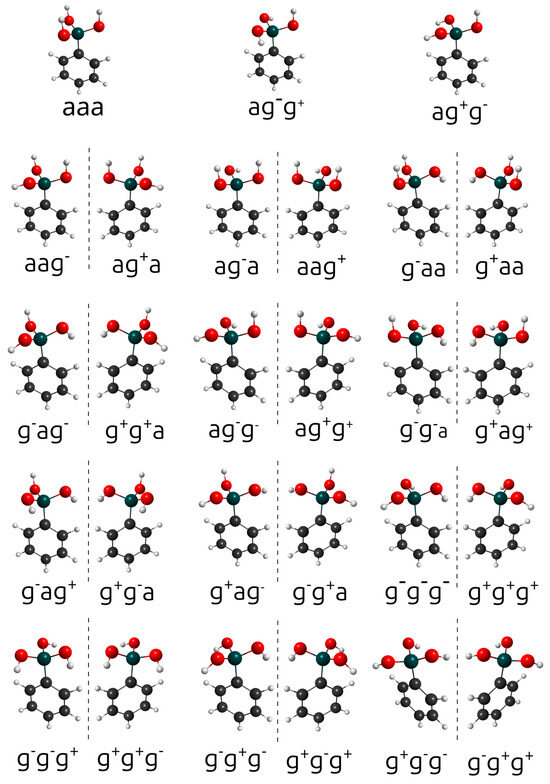
Figure 2.
Twenty-seven conformations of the phenylboronic conjugated base. The mirror images are separated by dashed vertical lines. The labels a, g+, and g− represent anti, gauche+, and gauche−, respectively.
For the other arylboronic acids considered here, it was also necessary to consider alternative conformations. The variation in the pKa brought forth by considering the effect of alternative conformations could be up to five units of pKa. Table 2 summarizes the number of structures calculated for the α-cyanocinnamylboronic acids shown in Scheme 1, together with their respective conjugated bases. The number of distinguishable structures may be computed as 2 (mirror-image pairs) + (calculated structures mirror-image pairs). Incorporation of all the conformations is crucial for the reliable calculation of the thermochemistry of substituted arylboronic acids. The effect of the multiple conformations can be approximately evaluated by the ratio between the rotational–vibrational partition functions calculated using multi-structure (MS) and single-structure (SS) evaluated at the global minimum, i.e., . For the , and the ratio is just 1.9 at 298.15 K, while for its conjugated base, the ratio is 27.7 at the same temperature. This changes the Gibbs free energy by 1.98 kcal.mol−1, resulting in an increase in the pKa calculated by Equation (7). The ratio is much more pronounced for the conjugated bases than for the acids. However, this ratio does not correlate with the number of conformations. For instance, there are 31 and 132 conformations calculated for 4g (NO-86) in acid and base forms, respectively. Yet, the ratios are only ~15 and ~25. On the other hand, the conjugated base of 4f (NO-82) has 54 conformations with a ratio of 133, and 4c’s (NO-12) base, with 49 conformers, shows a ratio of 143. The difference arises from the relative energies of the conformers: many lie several kcal.mol−1 above the global minimum and contribute negligibly to the total rotational–vibrational partition function. As an example, the acid form of 4g (NO-86) has 31 conformations, but only 12 conformers are within 1 kcal.mol−1 of the global minimum. The remaining nineteen conformations lie around 3–5 kcal.mol−1. Conversely, the acid form of 4c (NO-12) has 12 conformations all within 1 kcal.mol−1. Thus, it is not the total number of conformations, but rather the number of low-energy conformers near the global minimum that significantly impacts the rotational–vibrational partition function.

Table 2.
The calculated structures include all conformations for which harmonic vibrational frequencies were computed. The number of mirror-image pairs accounts for the number of conformations, of which the rotational–vibrational partition function must be multiplied by two. is the ratio of the rotational–vibrational partition function calculated including all conformations to the one calculated using only the lowest energy conformation.
The calculated pKa of the synthesized α-cyanocinnamylboronic acids are shown in Table 3, considering both the multi-structure and single-structure approximations. In the latter, the energy and thermochemistry are evaluated only at the global minimum. The experimental pKa for phenylboronic acid (1) is estimated to lie in the range 8.64–8.90 [5], which deviates by 0.3–0.56 from our calculated value of 9.20. Comparing the pairs with equal ligands, attachment to the para position results in a lower value of pKa compared to the same ligand attached to the meta position. The difference is larger for the pair (NO-12: 4c, NO-13: 4d). While 4d (NO-13) is slightly basic (pKa 8.82), 4c (NO-12) is considerably acidic (pKa 4.20). This is the only acid pKa among the compounds studied (neglecting the nearly neutral (NO-89) 4h with pKa 6.50). For instance, 4g (NO-86), which features the same substituent as 4b (NO-03) at the meta position, exhibits a higher pKa. This increase can be attributed to the presence of the methoxy group (OMe) at the para position, which exerts an electron-donating effect that counteracts the electron-withdrawing effect of the α-cyanocinnamyl group.

Table 3.
Calculated pKas of phenylboronic acids in water. MS stands for multi-structure and SS for single-structure. The difference between the values reflects the importance of considering the available conformations in the rotational–vibrational partition function. Dual-Level corrects the global minimum energy at the M06-2X/6-311++G(3df,3p) level of theory, while in Single-Level, the energy of the global minimum is calculated at the same level of the partition function, namely M06-2X/6-31+G(d,p). The experimental pKa of PhB(OH)2 is in the range 8.648.90 [5]. Geometries for the global minima of all species, Tables S1–S22 (Supplementary Materials).
Comparison between 4c (NO-12) and 4h (NO-89) suggests that the presence of a fluoro group at the ortho position in NO-89 (4h; pKa 6.50) increases the pKa by approximately two units relative to NO-12 (4c; pKa 4.20). This result suggests that at the ortho position, the “pi” electron pair of the fluorine atom exerts a net electron-donating effect to the aromatic system (relative to NO-12; 4c), thereby destabilizing the conjugate base and raising the pKa. In contrast, the presence of a fluoro group at the para position in NO-91 (4i; pKa 8.27) produces a negligible change in the pKa relative to the 4d (NO-13) molecule (pKa 8.35). These results are in line with the experimentally observed effect of the fluorine atom on the pKa of phenylboronic acid [5]. These effects will be further explored below.
Considering the multi-structure/Dual-Level (MS/DL) pKa as the reference, in Figure 3, we evaluate the deviation in the final pKa in each level of approximation. In general, Single-Level (SL) approximation underestimates most pKa values, except for 4c (NO-12) and 4g (NO-86). This difference may arise from the chosen level of theory. In this work, low-level calculations were performed at M06-2X/6-31+G(d,p). A slightly larger basis set could reduce these differences. In contrast to the SL results, the Dual-Level (DL) with evaluation with single-structure (SS) rotational–vibrational partition function overestimates the pKa values, as illustrated in Figure 2 by the SS/DL bars. The difference between MS and SS is determined by the difference between the logarithms of as shown in Equation (13).
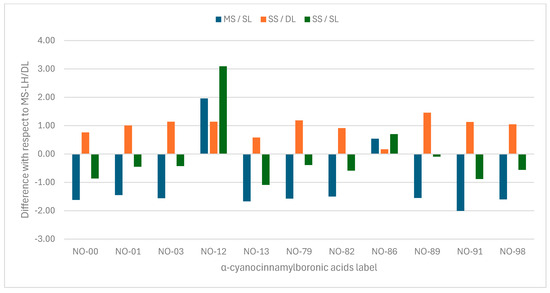
Figure 3.
Error bars of pKa with respect to the multi-structure/Dual-Level results presented in Table 3.
In some cases, a compensatory effect may occur if is similarly large for both the acid and base forms. As seen in Table 2, the largest difference is observed for NO-89, corresponding to the tallest orange bar in Figure 3. On the other hand, the smallest difference occurs for NO-86, represented by the shortest orange bar. Since the conjugate base has more conformations than the acid, the MS correction is expected to be more significant for the former. The presence of a substituent in the meta position reduces the ratio in comparison to the same substituent in para, as discussed above. This reduction is more pronounced for the base than for the acid, resulting in a net decrease in the difference between the pK values calculated under the MS and SS approximations.
According to Equation (7), the pKa is proportional to the ionization free energy of the acid, which in turn depends on the change in enthalpy and entropy between ionized and unionized compounds. Although linear free-energy relationships can be established for several compounds, the same is not true for enthalpy and entropy changes [22]. The enthalpic, entropic, and free energy contributions to the pKa may be evaluated by computing the difference and , using as reference the ionization of phenylboronic acid. In Table 4, we show the difference in enthalpy, entropy, and Gibbs free energy of the acid–base reaction of compounds 4a–j with respect to PhB(OH)2. The MS-DL ΔpKa values are also shown in the second column. Note that ΔpKa for all the compounds, given that the reactions are less endothermic than PhB(OH)2, resulting in the net decrease in the Gibbs free energy, and hence of the pKa. The more pronounced effect is found for the 4c (NO-12), with the reaction enthalpy of 7 kcal.mol−1 below that of the phenylboronic acid. Considering the relatively small decrease in reaction entropy, the resulting net decrease in the Gibbs free energy is 6.8 kcal.mol−1, leading to the reduction of the pKa by 5 units.

Table 4.
Calculated changes in pKa, reaction enthalpy, entropy, and Gibbs free energy relative to PhB(OH)2. All the values refer to the MS-DL.
As discussed above, the presence of fluorine at the para position in NO-91 (4i) results in a very small pKa decrease (≈−0.09) relative to NO-13 (4b). Table 4 shows this corresponds to a minor enthalpy increase (+0.2 kcal.mol−1) outweighed by a large entropy gain (>1 cal.K−1.mol−1), yielding a negligible net change in free energy. In contrast, the presence of fluorine in ortho increases the pKa of NO-89 (4h) by 2.3 units compared to NO-12 (4c). The data in Table 4 indicate this stems primarily from a substantial enthalpy difference. This is attributed to the interaction of FHO in the minimum energy conformation of NO-89 (4h), resulting in the stabilization of the unionized form. Thus, the ionization of NO-89 is more endothermic than that of NO-12. Given the dominant enthalpic contribution to the free energy change, NO-89 exhibits weaker acidity than NO-12.
There is a correlation between the variation in pKa and that in reaction enthalpy, as shown in Figure 4. It could be argued that this would be the main contributor to the variation in reaction enthalpy, i.e., energetic or thermal correction. The latter arises from the temperature variation in the total partition function, while the former is the change in electronic energy, nuclear repulsion, and vibrational zero-point energy. Although thermal correction is important for the consistent final calculation of pKa values, the main contributor to is the reaction energy ΔE (the difference in the total energy of the products and reactants). No correlation is found against the variation in entropy.
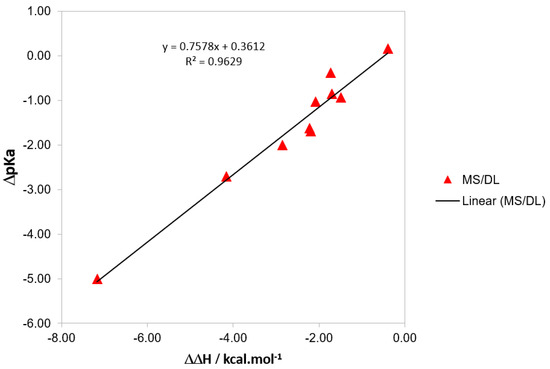
Figure 4.
Variation of pKa plotted against the variation in reaction enthalpy relative to PhB(OH)2.
4. Discussion
In light of the obtained results and previous discussions on the literature [5], some principles on the relationship between the pKa of arylboronic acids and their substituents can be gleaned. In the following discussion, it is essential to discriminate between electronic and non-electronic effects.
First of all, it should be clear from the general acid–base reaction of arylboronic acids (1) that the new bond that is formed upon the addition of a hydroxyl anion to the boron atom is somewhat isolated from the aromatic ring, since there is no “resonance” between the boron atom and the aromatic electron sextet. This means that the electronic effects of substituents on the pKa should be less intense, which is in line with the comparative data between substituted benzoic acids and arylboronic acids laid out in reference [5]. Nevertheless, some electronic effects are recognizable in the final pKa values. The “cyano-cinammyl” substituents are definitely strongly electron-withdrawing, contributing to reducing the pKa in relation to the phenylboronic acid. Nonetheless, a more detailed account of the electronic effects is dependent on a proper bonding model for arylboronic acids. A more specific work concerning this point is in preparation.
According to Laidler [23], the effects of substituents on thermochemical quantities—and consequently on pKa—can be classified as polar, steric, or solvent effects. Linear free-energy relationships may still hold, provided certain conditions are met. Polar effects, arising from inductive and resonance interactions of substituents, tend to influence enthalpy more significantly than entropy. Steric effects, on the other hand, have a larger impact on entropy. Because entropy changes are inherently more difficult to predict than enthalpic ones, steric effects can reduce the linearity of free-energy relationships. However, in certain cases, there may be enthalpy–entropy compensation, restoring the linearity in ΔG. Solvent effects can impact both enthalpy and entropy in a compensatory fashion as well, often preserving the predictability of free energy through linear structure–property relationships. Under this perspective, the correlation observed in Figure 3 suggests that polar effects are mainly responsible for the computed pKa values. However, steric effects cannot be neglected given the large chain of the substituent’s groups. In contrast to small substituents that have very small effects on [24], the results presented in Table 4 show that, in the present study, the substituent groups do have some impact on the entropy change. The decrease in entropy relative to PhB(OH)2, i.e., ΔΔS, is more pronounced for groups attached to the meta position (NO-03: 4b, NO-13: 4d, NO-82: 4f) in comparison to the same group at the para (NO-01: 4a, NO-12: 4c, NO-79: 4e). An exception to this is found for the pair 4h (NO-89; para) vs. 4i (NO-91; meta), where the ΔΔS of the former is lower than that of the latter. This can be attributed to the presence of the fluorine atom at the ortho position in 4h (NO-89).
The important underlying point is that all these thermodynamic considerations can only be performed with confidence because all the low-energy conformations were considered in the calculations. Due to the results presented, particularly in Table 3, it can be concluded that a proper calculation of the pKa of arylboronic acids should recognize the actual experimental situation, which deals necessarily with the presence of multiple conformations simultaneously, particularly at a room temperature of 298 K.
5. Conclusions
In summary, in this paper, the pKas of ten α-cyanocinnamylboronic acids were computationally determined. The procedure adopted employed multi-structure/Dual-Level calculation, with conformational analysis and harmonic vibrational frequencies calculated using M06-2X density functional with a relatively small basis set, 6-31+G(d,p), followed by single-point energy correction using a larger basis (6-311++G(3df,3p)). The rotational–vibrational partition functions used in the calculation of thermodynamic functions were evaluated considering all the non-equivalent conformations. It is important to point out that the inclusion of all the low-energy conformations brings the computational calculations much closer to the real experimental situation. This procedure decreases the pKa relative to the single-structure approach, where only the energy and partition function of the minimum-energy conformation are used.
All α-cyanocinnamyl-substituted arylboronic acids have a lower pKa than the unsubstituted phenylboronic acid. The decrease was most pronounced in two compounds, NO-12 (4c; pKa 4.20) and NO-89 (4h; pKa 6.50). Both have the same substituent attached to the para position, but (NO-89) 4h also features a fluorine atom in the ortho position. The observed decrease in pKa relative to phenylboronic acid was found to correlate approximately with the variation in reaction enthalpy. This suggests that polar effects may dominate over steric and solvent contributions. A more comprehensive study addressing this, and related issues, is currently in preparation.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/compounds5030028/s1. Geometries for the global minima of all species, Tables S1–S22.
Author Contributions
Conceptualization, D.d.L.M. and N.d.J.H.; methodology, investigation, and formal analysis, J.G.S.M. and A.G.H.B.; writing—original draft preparation and review and editing, A.G.H.B., J.G.S.M. and D.d.L.M.; project administration, D.d.L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FAPERJ (Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro), grant number E-26/211.025/2019 (Emergent Group of Research from Rio de Janeiro) and grant number E-26/210.242/2019 (APQ-1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank Robson Xavier Faria for co-supervising the doctoral thesis of Noemi de Jesus Hiller, co-author of this work.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BAC | Boronate Affinity Chromatography |
| DL | Dual-Level |
| LH | Local Harmonic |
| MS | Multi-Structure |
| PCM | Polarizable Continuum Model |
| SL | Single-Level |
| SMD | Solvent Model Density |
| SS | Single-Structure |
References
- Hall, D.G. (Ed.) Boronic Acids: Preparation and Applications in Organic Synthesis, Medicine and Materials, 2nd ed.; Wiley-VCH: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Beletskaya, I.P.; Alonso, F.; Tyurin, V. The Suzuki-Miyaura reaction after the Nobel prize. Coord. Chem. Rev. 2019, 385, 137–173. [Google Scholar] [CrossRef]
- Hiller, N.J.; Silva, N.A.A.; Tavares, T.A.; Faria, R.X.; Eberlin, M.N.; Martins, D.L. Arylboronic Acids and their Myriad of Applications Beyond Organic Synthesis. Eur. J. Org. Chem. 2020, 31, 4841–4877. [Google Scholar] [CrossRef]
- Li, D.J.; Chen, Y.; Liu, Z. Boronate affinity materials for separation and molecular recognition: Structure, properties and applications. Chem. Soc. Rev. 2015, 44, 8097–8123. [Google Scholar] [CrossRef] [PubMed]
- Sporzynski, A.; Adamczyk-Wozniak, A.; Zarzeczanska, D.; Gozdalik, J.T.; Ramotowska, P.; Abramczyk, W. Acidity Constants of Boronic Acids as Simply as Possible: Experimental, Correlations, and Prediction. Molecules 2024, 29, 2713. [Google Scholar] [CrossRef] [PubMed]
- Silva, C.O.; Nascimento, M.A.C. Computational Chemistry of Acids. Adv. Chem. Phys. 2002, 123, 423–468. [Google Scholar] [CrossRef]
- Tossell, J.A. Boric acid, “carbonic acid”, and N-containing oxyacids in aqueous solution: Ab initio studies of structure, pKa, NMR shifts, and isotopic fractionations. Geochim. Cosmochim. Acta 2005, 69, 5647–5658. [Google Scholar] [CrossRef]
- Lopalco, A.; Stella, V.J.; Thompson, W.H. Origins, and formulation implications, of the pKa difference between boronic acids and their esters: A density functional study. Eur. J. Pharm. Sci. 2018, 124, 10–16. [Google Scholar] [CrossRef]
- Georgiou, I.; Kervyn, S.; Rossignon, A.; De Leo, F.; Wouters, J.; Bruylants, G.; Bonifazi, D. Versatile Self-Adapting Boronic Acids for H-Bond Recognition: From Discrete to Polymeric Supermolecules. J. Am. Chem. Soc. 2017, 139, 2710–2727. [Google Scholar] [CrossRef]
- Cox, P.A.; Reid, M.; Leach, A.G.; Campbell, A.D.; King, E.J.; Lloyd-Jones, G.C. Base-Catalyzed Aryl-B(OH)2 Protodeboronation Revisited: From Concerted Proton Transfer to Liberation of a Transient Aryl Anion. J. Am. Chem. Soc. 2017, 139, 13156–13165. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Zheng, J.J.; Truhlar, D.G. Quantum Thermochemistry: Multistructural Method with Torsional Anharmonicity Based on a Coupled Torsional Potential. J. Chem. Theor. Comput. 2013, 9, 1356–1367. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.J.; Truhlar, D.G. Including Torsional Anharmonicity in Canonical and Microcanonical Reaction Path Calculations. J. Chem. Theor. Comput. 2013, 9, 2875–2881. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, J.G.S.; Barbosa, A.G.H.; Henriques, A.M.; Neves, P.H.G.; Furtado, R.S.; Menezes, R.M.; dos Santos, A.R.; Fleming, F.P. Assessing the Molecular Basis of the Fuel Octane Scale: A Detailed Investigation on the Rate Controlling Steps of the Autoignition of Heptane and Isoctane. J. Phys. Chem. A 2018, 122, 610–630. [Google Scholar] [CrossRef]
- Monteiro, J.G.S.; Neves, D.C.G.; Ventura, A.C.P.G.; Lindgren, E.B.; Oliveira, G.N.; Fleming, F.P.; dos Santos, A.R.; Barbosa, A.G.H. Temperature and pressure dependent rate constants of the reactions of ∙OH with cyclopentene from variational TST and SS-RRK methods. J. Chem. Phys. 2022, 157, 214303. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Bryantsev, V.S.; Diallo, M.S.; Goddard, W.A., III. Calculation of solvation free energies of charged solutes using mixed cluster/continuum models. J. Phys. Chem. B 2008, 112, 9709–9719. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST), NIST Chemistry WebBook, NIST Standard Reference Database Number 69. 2017. Available online: https://janaf.nist.gov/ (accessed on 16 June 2025).
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Aqueous solvation free energies of ions and ion-water clusters based on an accurate value for the absolute aqueous solvation free energy of the proton. J. Phys. Chem. B 2006, 110, 16066–16081. [Google Scholar] [CrossRef]
- Faria, R.X.; Hiller, N.J.; Salles, J.P.; Resende, J.A.L.C.; Diogo, R.T.; von Hanke, N.L.; Bello, M.L.; Rodrigues, C.R.; Castro, H.C.; Martins, D.L. Arylboronic acids inhibit P2X7 receptor function and the acute inflammatory response. J. Bioenerg. Biomembr. 2019, 51, 277–290. [Google Scholar] [CrossRef]
- Hiller, N.J.; Salles, J.P.; Hoelz, L.V.B.; Zorzanelli, B.C.; Fernandes, T.V.A.; Boechat, N.; Martins, D.L.; Faria, R.X. α-Cyanocinnamylboronic acid derivatives are safe, selective anti-inflammatory molecules that inhibit P2X7 receptor function and signaling. Biomed. Pharmacother. 2025, 185, 117945. [Google Scholar] [CrossRef]
- Laidler, K.J. Thermodynamics of Ionization Processes in Aqueous Solution: Part 1.-General Theory of Substituent Effects. Trans. Faraday Soc. 1959, 55, 1725–1730. [Google Scholar] [CrossRef]
- Zawidzki, T.W.; Papée, H.M.; Laidler, K.J. Thermodynamics of ionization processes in aqueous solution: Part 5.—Substituted benzoic acids. Trans. Faraday Soc. 1959, 55, 1743–1745. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).