Abstract
In the manufacturing sector, transport phenomena near the stagnation region are frequent, particularly in the polymer and extrusion processes, which require continuous improvement to raise the process’s quality standards. The aim of this study is to explore the improvement of heat and mass transmission using unsteady magnetohydrodynamic (MHD) hybrid nanofluid (HNF) flow over a stretching/shrinking cylinder with variable viscosity and Stefan blowing. The governed equations of heat and mass transfer processes are converted into ordinary differential equations (ODEs) using the appropriate transformations, and the resulting equations are then solved using the MATLAB package bvp4c. With an upsurge in the volume fraction of nanoparticles, the skin friction increases, but the reverse trend is detected with negative values for the unsteadiness constraint. The use of 2D graphs to show how important parameters affect the velocity, temperature, and concentration is thoroughly discussed. There is a discussion of the quantitative findings from the wall shear factor and the heat and mass transfer rates calculated for the stretching/shrinking cases.
1. Introduction
Scientists, researchers, and engineers are attentive to the boundary layer flow, heat transfer, and mass transfer of Newtonian fluids over a stretching/shrinking cylinder due to their many applications, including hardening, mining of metals, swelling processes, pipe manufacturing, wire diminishing, etc. Crane [1] highlighted the boundary layer flow on the stretching plate. Anuar et al. [2] explored heat transfer past an unstable stretchy sheet. Kumbhakar and Nandi [3] explored an HNF unsteady MHD radiative flow over a stretchy sheet with slip. Khashi et al. [4] examined the axisymmetric flow and heat transmission of an HNF flow past a shrinking/shrinking disc. Sreedevi et al. [5] conducted an investigation into the unsteady MHD heat and mass transfer of HNF flow through a stretching sheet and found that the temperature profile intensified as the tiny (nano) particle volume fraction rose. Raju et al. [6] conducted research on the nonlinear motions of axisymmetric ternary hybrid nanofluids in thermally radiated Darcy Walls with various shapes. Zainal et al. [7] investigated the unsteady MHD flow towards a horizontal cylinder with two different nanoparticles and found that the unsteadiness parameter improves the thermal performance. Zainal et al. [8] scrutinized the stability of an unstable HNF flow passing a permeable stretching/shrinking cylinder. Raju et al. [9] examined the role of body acceleration and gold nanoparticles in an uneven/composite inclined stenosis artery’s blood flow. Raju et al. [10] studied the stagnant power-law fluid flow over a stretching spinning disc containing homogeneous–heterogeneous chemical reactions. Hussain et al. [11] conducted a heat transport investigation of HNF under the thermal radiation regime.
Applications of magnetohydrodynamics (MHD) include energy conversion, low-emission power generation systems, high-efficiency MHD accelerations and thrusters, etc. [12,13,14]. Ashwinkumar et al. [15] scrutinized HNF flow over a convectively heated cylinder with MHD with different geometries. The effect of a stagnant flow of HNF with MHD was scrutinized by Mabood et al. [16]. Liu et al. [17] discovered the slip flow of an unsteady nanofluid flow past a stretching plate. An investigation into an unstable MHD nanofluid stretching cylinder with a heat cause and sink was conducted by Song et al. [18]. Waini et al. [19] studied unsteady HNF flow over a permeable shrinking/stretching surface and found that skin friction decreases but heat transmission rises with an increasing volume fraction of copper. Bilal et al. [20] inspected unsteady HNF flow through a horizontal channel. An unsteady stagnant flow of nanofluid stretching/shrinking over an outward surface with partial slip was investigated by Rajput et al. [21]. Related work was carried out by Wang [22] and Waini et al. [23]. The study of the stagnation-point flow of a viscous or non-Newtonian fluid is important in several engineering and industrial applications. Knowledge of the stagnation flow assists in the design of thrust bearings and radial diffusers, drag reduction, and transpiration cooling, as well as thermal oil recovery.
The assumption made in each of the aforementioned studies was that the fluid viscosity would remain constant. However, it is well known that temperature changes can significantly alter the fluid’s physical characteristics. The viscosity change with temperature variation must be taken into account, to correctly predict the flow performance. Numerous recent studies have looked into how heat transfer past a moving sheet is impacted by fluid viscosity and thermal conductivity variations. The effect of variable viscosity on the natural convection of HNF flow because of a stretching surface was deliberated by Tulu et al. [24]. The temperature-dependent viscosity variation in Maxwell nanofluid was predicted by Mabood et al. [25].
The species (concentration) field and the Stefan blowing effect are related. On an impermeable surface, the Stefan blowing effect appears. By stretching a cylinder to examine the HNF flow under Stefan blowing, Rana et al. [26] discovered that the increasing nanoparticle size and Stefan blowing have extreme effects on skin friction. Nanofluid flow towards a non-liner stretchy sheet with slip on unsteady MHD was studied by Jagan et al. [27]. Hassen [28] looked at the effects of Stefan suction and blowing on an HNF based on ethylene glycol and water that exhibits partial slip and nanoparticle shape effects. Kiran et al. [29] examined the thermal transport analysis of non-uniformly heated annular geometry unsteady buoyant convective flow. In recent years, the nanofluids are used as an emerging working medium for fluid flow and heat transfer under various conditions [30,31,32].
Velocity slip is a phenomenon that occurs when fluids do not adhere to the surface of the body. One of the frequently occurring boundary conditions at which the surface velocity linearly falls on the fluid shear stress is Navier’s partial slip. There are numerous fields where the slip state at the boundary surface is used, including lubrication, medicine, polishing artificial heart valves, etc. The HNF flow and heat transfer past a stretchy surface were researched by Kumar [33]. MHD nanofluid flow with the effect of partial slip was scrutinized by Iskander et al. [34]. Nadeem et al. [35] considered the slip effect in a cylinder of micropolar HNF.
The current research focuses on an HNF flow along a stretching/shrinking cylinder with an unsteady stagnation point that is subject to Stefan blowing and variable viscosity. In addition, the impact of the partial slip on the surface and magnetic field are taken into account. With the aid of the MATLAB bvp4c package, the resulting nonlinear dimensionless ODEs were solved, and the explanations were determined in terms of the velocity, friction drag, concentration, temperature, heat and mass transmission of the HNF, all of which were identified while they were constrained by the associated flow conditions.
2. Mathematical Formulation
Consider an incompressible, unsteady stagnation-point HNF flow past a stretching/shrinking cylinder with radius a = 1. Here, the magnetic field is applied vertically to the fluid flow path. The cylinder free stream velocity and surface are denoted by and . When c2 = 0, the cylinder is static; when c2 > 0, the cylinder is stretched; when c2 < 0, the cylinder is shrunk; c1, c2, and c3 are factors, and the characteristic length is L. The surface temperature, upstream temperature, surface concentration, and free stream concentration are symbolized as , , , and . Stefan blowing, stagnation point, variable viscosity, unsteady MHD, and partial slip effects are included as shown in Figure 1. When we start the stretch/shrink cylinder, the fluid starts flowing in x- direction but, in our model, we consider only the positive x- direction. The Stefan blowing effect applied is vertical to the fluid flow direction. Since water is used as the base fluid in our model, the Schmidt number is fixed.
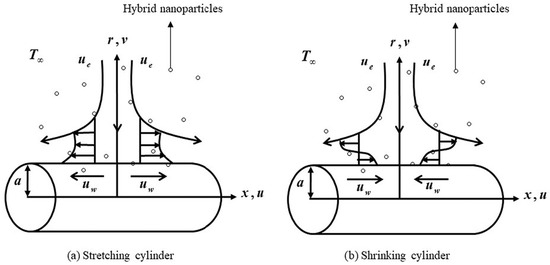
Figure 1.
Physical model for the stretching/shrinking cylinder.
From this model, the governing equations (referring to Zainal [7] and Waini et al. [19]) are described as
Continuity Equation
Momentum Equation
Temperature Equation
Concentration Equation
The physical realistic boundary conditions are
where the velocity mechanisms are u and v in the directions x and r. T represents the temperature of HNF. Moreover, lists of the thermophysical features of the base fluid and nanoparticles and the physical attributes of the HNF are described by Waini et al. [19,23]. The temperature-dependent variable viscosity is taken as . B > 0 denotes an accelerating flow, while B < 0 denotes a reversing flow. In this study, we examine the fluid flow features and locate the point of separation for a decelerating stretching/shrinking cylinder (B < 0). Here, the nanoparticle volume fraction of Al2O3 and Cu are designated by and . The nanoparticle volume fraction HNF is defined in Equation (6):
The suitable transformations are
when Equation (7) is substituted into (1), (1) is satisfied exactly. The following equations result from substituting (7) into Equations (2)–(5).
with the boundary conditions:
where Stefan blowing parameter, magnetic parameter, variable viscosity parameter, unsteady parameter, Prandtl number, curvature parameter, Schmidt number, , , , , , and .
Meanwhile, the coefficient of skin friction (Cf), Nusselt number (Nu), and Sherwood number (Sh) (refer to Waini et al. [23]) are expressed as follows.
Through the adoption of the similarity transformations Equations (7) and (13) by Equation (12), the following Equation is obtained.
3. Numerical Methods
The simplified form of the mathematical model boundary value problem solver MATLAB (version 7.50) bvp4c package is utilized to solve Equations (8)–(11) mathematically, as designated by Waini et al. [23], and the following equations are obtained.
Equation (8) is transformed into
Equation (9) becomes
Equation (10) written as
with the boundary conditions
The bvp4c MATLAB package is then utilized to solve Equations (15)–(18), yielding the required results.
4. Results and Discussion
Different combinations of significant parameters are discussed in this study. Alumina Al2O3 () and copper Cu () from 0 to 0.02 (2%), respectively, are used in the nanoparticle volume fraction. In Table 1, the current fallouts of are compared with those of Wang [22] and Waini et al. [23]. In Table 2, the mathematical values of Cf, Nu, and Sh are obtainable for different values of Sb, M, , A, and ε, and it is numerically found that the skin friction, heat transfer, and mass diffusion increase with a rise in the variable viscosity parameter.

Table 1.
Comparison with Sb = λ = M = Bi= Rd = K = Ec = Sc = 0 when Pr = 6.2 as .

Table 2.
Numerical values of Cf, Nu, and Sh when = 0.02.
From Figure 2a, increasing the Stefan blowing parameter velocity profile increases for the stretching case but decreases for the shrinking case. We can infer that, physically, mass diffusion causes a slowing of HNF as it approaches the surface due to an increase in Stefan blowing from the surface to the free stream when the cylinder is shrinking, but the opposite trend is obtained in the stretching case. Figure 2b,c show how the rising Stefan blowing parameter profile for the temperature and concentration are enhanced for both the stretching and the shrinking case. The presence of nanoparticles in the base fluid energizes species diffusion physically, which raises the temperature and concentration profiles.
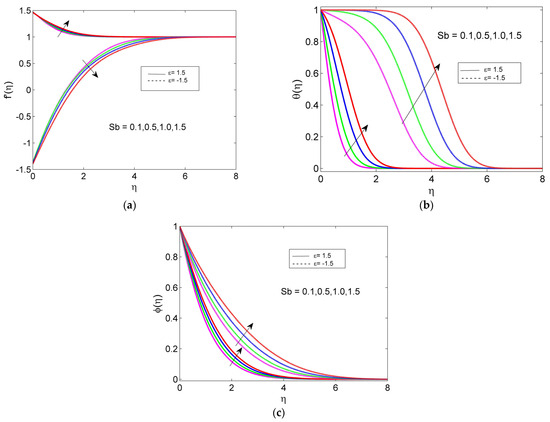
Figure 2.
Effects of Sb on (a) velocity profile , (b) temperature profile , and (c) concentration profile .
From Figure 3a,b, it can be seen that, with an increasing stretching/shrinking parameter, the velocity rises, but the temperature profile decreases. This is because the stretching/shrinking state improves the HNF velocity, which, in turn, increases the thermal boundary layer thickness and results in high temperature gradients on the surface; the temperature drops as the stretching/shrinking parameter upsurges. The velocity profile declines as the velocity slip parameter increases in the stretching case but, in the shrinking case, the velocity profile is boosted (see Figure 4a). In fact, the velocity is partially transported to the fluid with an upsurge in the slip parameter when the cylinder is stretching, whereas the opposite trend is seen in the shrinking case. The velocity decreases as the magnetic field rises for the stretching case, but it increases for the shrinking case (see Figure 4b). The retarding force increases along with the values of M, which causes the velocity to decrease.
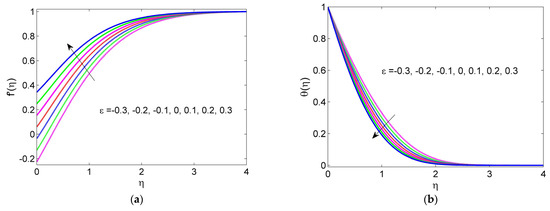
Figure 3.
Effects of ε on (a) velocity profile , (b) temperature profile .
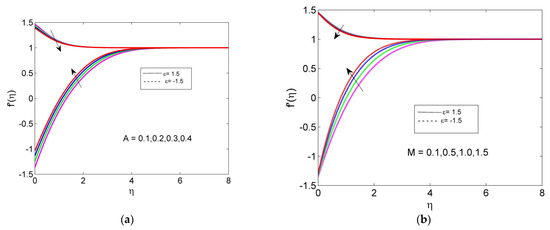
Figure 4.
Velocity profiles for (a) different A and (b) different M values.
Both the temperature and concentration profile reduce for negative values of the unsteadiness parameter for both the stretching and the shrinking case, as depicted in Figure 5a,b. When the unsteadiness parameter increases, the stretching/shrinking cylinder loses heat physically. As a result, the temperature of the HNF drops.
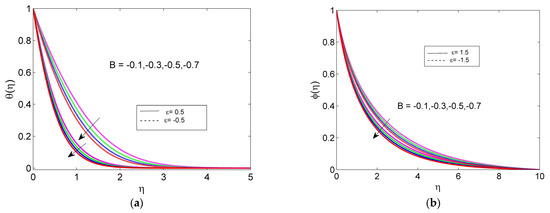
Figure 5.
Impacts of B on (a) temperature profile , and (b) concentration profile .
Figure 6a shows that, with negative values for the unsteadiness parameter in contradiction to the stretching/shrinking state, the skin friction coefficient decreases. According to the graph, parameter B is dependent on the buoyancy force, and the flow is in an upward direction because of a stronger buoyancy influence that causes the velocity field for the flow of fluid to decrease. Figure 6b demonstrates that Cf rises as a volume fraction of and from 0 to 2% against the stretching/shrinking case. The volume fraction of nanoparticles served to significantly improve the skin-friction coefficient for both the stretching and contracting states.
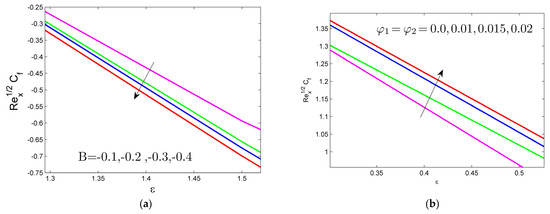
Figure 6.
Skin friction for different (a) B values (b) , and values.
5. Conclusions
In this numerical study, the unsteady MHD transport phenomenon of HNF flow near a stagnation point over a stretching/shrinking cylinder is explored. Using suitable similarity, the governing PDEs are transformed into ODEs and solved via bvp4c code. The study’s main conclusions are listed below:
- As the Stefan blowing parameter increases, the profiles of the temperature and concentration rise;
- With a rise in the variable viscosity parameter, the velocity profile decreases, but this is more significant for skin friction;
- The velocity, temperature, and concentration profiles decrease while there are negative values for the unsteadiness parameter;
- The addition of the nanoparticle volume fraction leads to a better thermal conductivity performance, resulting in an increase in thermal performance;
- The skin friction decreases with negative values for the unsteadiness parameter.
Author Contributions
Conceptualization, J.K. and S.S.; methodology, J.K. and M.K.N.; software, J.K. and M.K.N.; validation, J.K.; formal analysis, J.K., S.S. and M.K.N.; investigation, J.K. and M.K.N.; resources, J.K.; writing—original draft preparation, J.K. and M.K.N.; writing—review and editing, J.K. and S.S.; visualization, J.K.; supervision, J.K. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations/Nomenclature
In this manuscript, the following abbreviations are used.
| MHD | magnetohydrodynamics |
| HNF | hybrid nanofluid |
| u, v | velocity components along the x- and y-axis (M·s−1) |
| L | characteristic length (m) |
| T | fluid temperature (K) |
| ue | free stream velocity (m·s−1) |
| uw | surface velocity (m·s−1) |
| C∞ | ambient concentration (mol/m3) |
| T∞ | ambient temperature (K) |
| D | mass diffusivity (m2·s−1) |
| Cp | specific heat (kg−1·J) |
| Cs | concentration susceptibility |
| k | thermal conductivity (W·m−1·K−1) |
| Tw | surface temperature (K) |
| Cw | surface concentration (mol/m3) |
| Sc | Schmidt number |
| Pr | Prandtl number |
| Sb | Stefan blowing parameter |
| Sh | local Sherwood number |
| A | velocity slip parameter |
| B | unsteadyness parameter |
| M | magnetic parameter |
| Rex | local Reynolds number |
| Greek symbols | |
| v | kinematic viscosity (m2·s−1) |
| σ | electrical conductivity (S·m−1) |
| μ | dynamic viscosity (m2·s−1) |
| ρ | density of the fluid (kg·m−3) |
| λ | curvature parameter |
| Subscripts | |
| ∞ | ambient |
| f | base fluid |
| nf | nanofluid |
| hnf | hybrid nanofluid |
References
- Crane, L.R. Boundary Layer Flow due to a Stretching Cylinder. Z. Angew. Math. Phys. ZAMP 1975, 26, 619–622. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. Numerical Computation of Dusty Hybrid Nanofluid Flow and Heat Transfer over a Deformable Sheet with Slip Effect. Mathematics 2021, 9, 643. [Google Scholar] [CrossRef]
- Kumbhakar, B.; Nandi, S. Unsteady MHD radiative-dissipative flow of Cu-Al2O3/H2O hybrid nanofluid past a stretching sheet with slip and convective conditions: A regression analysis. Math. Comput. Simul. 2022, 194, 563–587. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Unsteady Axisymmetric Flow and Heat Transfer of a Hybrid Nanofluid over a Permeable Stretching/Shrinking Disc. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 2005–2021. [Google Scholar] [CrossRef]
- Sreedevi, P.; Sudarsana Reddy, P.; Chamkha, A. Heat and Mass Transfer Analysis of Unsteady Hybrid Nanofluid Flow over a Stretching Sheet with Thermal Radiation. SN Appl. Sci. 2020, 2, 1222. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Ahammad, N.A.; Sajjan, K.; Shah, N.A.; Yook, S.J.; Kumar, M.D. Nonlinear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable Darcy Walls with different shapes and densities: Simple linear regression. Int. Commun. Heat Mass Transf. 2022, 135, 106110. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady MHD Hybrid Nanofluid Flow towards a Horizontal Cylinder. Int. Commun. Heat Mass Transf. 2022, 134, 106020. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady Three-Dimensional MHD Non-Axisymmetric Homann Stagnation Point Flow of a Hybrid Nanofluid with Stability Analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Basha, H.T.; Noor, N.F.M.; Shah, N.A.; Yook, S.J. Significance of body acceleration and gold nanoparticles through blood flow in an uneven/composite inclined stenosis artery. A finite difference computation. Math. Comput. Simul. 2024, 215, 399–419. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Saleem, S. Homogeneous-Hetrogeneous Reactions on Stagnation-Point Flow of a Casson Fluid with Induced Magnetic Field. 2015. Available online: https://www.researchgate.net/profile/Dr-Salman-Saleem/publication/286452438_Effects_of_induced_magnetic_field_and_homogeneous-heterogeneous_reactions_on_stagnation_flow_of_a_Casson_fluid/links/567454a608ae0ad265ba7793/Effects-of-induced-magnetic-field-and-homogeneous-heterogeneous-reactions-on-stagnation-flow-of-a-Casson-fluid.pdf (accessed on 1 October 2023).
- Hussain, A.; Hassan, A.; Al Mdallal, Q.; Ahmad, H.; Rehman, A.; Altanji, M.; Arshad, M. Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Stud. Therm. Eng. 2021, 27, 101244. [Google Scholar] [CrossRef]
- Reddy, V.S.; Kandasamy, J.; Sivanandam, S. Stefan Blowing Impacts on Hybrid Nanofluid Flow over a Moving Thin Needle with Thermal Radiation and MHD. Computation 2023, 11, 128. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Chandrapushpam, T.; Bhuvaneswari, M.; Karthikeyan, S.; Alzahrani, A.K. Effect of chemical reaction on double diffusive MHD squeezing copper water nanofluid flow between parallel plates. J. Mol. Liq. 2022, 368 Pt B, 120768. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Bhuvaneswari, M.; Alzahrani, A.K. Numerical study on influence of magnetic field and discrete heating on free convection in a porous container. Sci. Iran. B Mech. Eng. 2022, 29, 3063–3071. [Google Scholar]
- Ashwinkumar, G.P.; Samrat, S.P.; Sandeep, N. Convective Heat Transfer in MHD Hybrid Nanofluid Flow over Two Different Geometries. Int. Commun. Heat Mass Transf. 2021, 127, 105563. [Google Scholar] [CrossRef]
- Mahmood, Z.; Iqbal, Z.; Alyami, M.A.; Alqahtani, B.A.; Yassen, M.F.; Khan, U. Influence of Suction and Heat Source on MHD Stagnation Point Flow of Ternary Hybrid Nanofluid over Convectively Heated Stretching/Shrinking Cylinder. Adv. Mech. Eng. 2022, 14, 168781322211262. [Google Scholar] [CrossRef]
- Liu, J.; Abidi, A.; Khan, M.I.; Rasheed, S.; Allehiany, F.M.; Mahmoud, E.E.; Galal, A. Thermal Analysis of a Radiative Slip Flow of an Unsteady Casson Nanofluid toward a Stretching Surface Subject to the Convective Condition. J. Mater. Res. Technol. 2021, 15, 468–476. [Google Scholar] [CrossRef]
- Song, Y.-Q.; Hamid, A.; Sun, T.-C.; Khan, M.I.; Qayyum, S.; Kumar, R.; Prasannakumara, B.C.; Khan, S.U.; Chinram, R. Unsteady Mixed Convection Flow of Magneto-Williamson Nanofluid due to Stretched Cylinder with Significant Non-Uniform Heat Source/Sink Features. Alex. Eng. J. 2022, 61, 195–206. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady Flow and Heat Transfer Past a Stretching/Shrinking Sheet in a Hybrid Nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Bilal, M.; Arshad, H.; Ramzan, M.; Shah, Z.; Kumam, P. Unsteady Hybrid-Nanofluid Flow Comprising Ferrousoxide and CNTs through Porous Horizontal Channel with Dilating/Squeezing Walls. Sci. Rep. 2021, 11, 12637. [Google Scholar] [CrossRef]
- Rajput, S.; Bhattacharyya, K.; Verma, A.K.; Mandal, M.S.; Chamkha, A.J.; Yadav, D. Unsteady Stagnation-Point Flow of CNTs Suspended Nanofluid on a Shrinking/Expanding Sheet with Partial Slip: Multiple Solutions and Stability Analysis. Waves Random Complex Media 2022, 14, 1–22. [Google Scholar] [CrossRef]
- Wang, C.H. Slip Flow due to a Stretching Cylinder. Int. J. Nonlinear Mech. 2011, 46, 1191–1194. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid Nanofluid Flow on a Shrinking Cylinder with Prescribed Surface Heat flux. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1987–2004. [Google Scholar] [CrossRef]
- Tulu, A.; Ibrahim, W. Effects of Second-Order Slip Flow and Variable Viscosity on Natural Convection Flow of CNTs − Fe3O 4/Water Hybrid Nanofluids due to Stretching Surface. Math. Probl. Eng. 2021, 2021, 8407194. [Google Scholar] [CrossRef]
- Mabood, F.; Rauf, A.; Prasannakumara, B.C.; Izadi, M.; Shehzad, S.A. Impacts of Stefan Blowing and Mass Convention on Flow of Maxwell Nanofluid of Variable Thermal Conductivity about a Rotating Disk. Chin. J. Phys. 2021, 71, 260–272. [Google Scholar] [CrossRef]
- Rana, P.; Makkar, V.; Gupta, G. Finite element study of bio-convective Stefan blowing Ag-MgO/water hybrid nanofluid induced by stretching cylinder utilizing non-Fourier and non-Fick’s laws. Nanomaterials 2021, 11, 1735. [Google Scholar] [CrossRef] [PubMed]
- Jagan, K.; Sivasankaran, S. Soret & Dufour and Triple Stratification Effect on MHD Flow with Velocity Slip towards a Stretching Cylinder. Math. Comput. Appl. 2022, 27, 25. [Google Scholar]
- Hassan, A.; Alsubaie, N.; Alharbi, F.; Alhushaybari, A.; Galal, A. Scrutinization of Stefan Suction/Blowing on Thermal Slip Flow of Ethylene Glycol/Water Based Hybrid Ferro-Fluid with Nano-Particles Shape Effect and Partial Slip. J. Magn. Magn. Mater. 2023, 565, 170276. [Google Scholar] [CrossRef]
- Kiran, S.; Sankar, M.B.; Swamy, K.; Makinde, O.D. Unsteady buoyant convective flow and thermal transport analysis in a nonuniformly heated annular geometry. Comput. Therm. Sci. Int. J. 2022, 14, 1–17. [Google Scholar] [CrossRef]
- Jagan, K.; Sivasankaran, S.; Bhuvaneswari, M.; Rajan, S. Effect of thermal radiation on magneto-convection of a micropolar nanoliquid towards a non-linear stretching surface with convective boundary. Int. J. Eng. Technol. 2018, 7, 417–421. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Bhuvaneswari, M. Numerical study on influence of water based hybrid nanofluid and porous media on heat transfer and pressure loss. Case Stud. Therm. Eng. 2022, 34, 102022. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Mallawi, F.O.M. Numerical study on convective flow boiling of nanoliquid inside a pipe filling with aluminum metal foam by two-phase model. Case Stud. Therm. Eng. 2021, 26, 101095. [Google Scholar] [CrossRef]
- Kumar, T.S. Hybrid Nanofluid Slip Flow and Heat Transfer over a Stretching Surface. Partial. Differ. Equ. Appl. Math. 2021, 4, 100070. [Google Scholar] [CrossRef]
- Tlili, I.; Ramzan, M.; Nisa, H.U.; Shutaywi, M.; Sheikholeslami, M.; Kumam, P. Onset of Gyrotactic Microorganisms in MHD Micropolar Nanofluid Flow with Partial Slip and Double Stratification. J. King Saud Univ. Sci. 2020, 32, 2741–2751. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N. On Both MHD and Slip Effect in Micropolar Hybrid Nanofluid Past a Circular Cylinder under Stagnation Point Region. Can. J. Phys. 2019, 97, 392–399. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).