Abstract
This paper presents equations for the electron density of the two-dimensional electron gas (2DEG) in AlGaN/GaN heterostructures in three realistic scenarios: (1) AlGaN/GaN heterostructure with surface exposed to ambient with mobile ions, (2) metal gate deposited on the AlGaN surface, and (3) a thick dielectric passivation layer on the AlGaN surface. To derive the equations, we analyzed these scenarios by applying Gauss’s law. In contrast to the idealistic models, our analysis shows that the 2DEG charge density is proportional to the difference between spontaneous polarization of AlGaN and GaN, whereas surprisingly, it is independent of the piezoelectric polarization.
1. Introduction
Aluminium Gallium Nitride/Gallium Nitride (AlGaN/GaN) heterostructures are widely used in devices for high power and radio frequency applications because they enable higher current and faster switching speed [1,2,3,4,5]. Both capabilities are the results of high electron mobility and high electron density of the two-dimensional electron gas (2DEG), which is formed at the AlGaN/GaN heterojunction even in the absence of intentional doping [6]. The formation of 2DEG is considered to be due to the spontaneous and piezoelectric polarizations in the AlGaN/GaN heterostructure [7,8], however, the existing equations for the electron density in the 2DEG, N2DEG, are inconsistent and confusing [6,9]. For example, the prevalent equations for N2DEG do not include its dependence on the polarization charges [10,11]. This confusing result corresponds to the implicit assumption that the polarization charges at the AlGaN/GaN heterojunction and AlGaN surface balance each other [10,11]. It should be noted that there have been follow-up works to revise the original equations. In our approach presented herein, we analyze the charge balance for the following three realistic scenarios:
- (1)
- AlGaN surface is unpassivated and accessible by free ions from the ambient;
- (2)
- Metal gate is deposited on the AlGaN surface;
- (3)
- The AlGaN surface is passivated by a thick dielectric layer.
The results of this analysis are realistic equations for N2DEG.
2. Equations for 2DEG in AlGan/GaN Heterostructures
2.1. Unpassivated AlGaN Surface Accessible to Free Ions from Air
GaN is a polar crystal because the formation of the interatomic bonds creates asymmetric electron clouds of Ga and N atoms [11], which is illustrated by the dipole symbols in Figure 1. This effect leads to the spontaneous polarization in GaN, which is quantified by the effective spontaneous polarization charge per unit area, Np-GaN. In AlGaN, the polarization effect is analogous, with the difference that the spontaneous polarization charge per unit area (Np-AlGaN) is larger [9,12,13]. The fact that Np-AlGaN > Np-GaN is illustrated in Figure 1 by showing five columns of dipoles in AlGaN and three columns of dipoles in GaN. The arrows in Figure 1 show electric field lines.
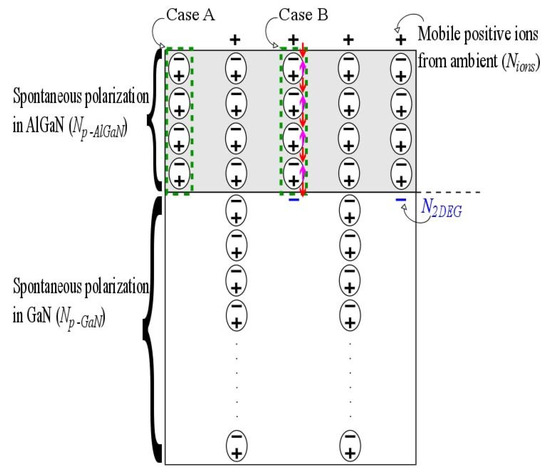
Figure 1.
Impact of spontaneous polarization (modelled using dipoles) on the electron density at the AlGaN/GaN heterojunction (N2DEG) and on the density of mobile ions at the surface (Nions). Cases A and B show dashed rectangles enclosing zero net charge. Case A corresponds to the ideal case of AlGaN surface in vacuum without mobile ions that could be attracted to the surface, whereas Case B shows electric fields attracting mobile positive ions to the AlGaN surface and electrons to the 2DEG at the heterojunction.
The statement by Ibbetson et al. that “polarization charge in AlGaN is balanced” [10] implies that there is no field outside the AlGaN layer and that there is no impact on N2DEG from the spontaneous polarization charge. This result can be obtained by applying Gauss’s theorem in a way that is illustrated by the dashed rectangle labeled as Case A in Figure 1. However, this case excludes the possibility that the positive polarization charge at the heterojunction can attract mobile electrons to the 2DEG and that, likewise, the negative polarization charge at the AlGaN surface can attract positive mobile ions from the ambient. The dashed rectangle in case B shows the application of Gauss’s law that includes electrons next to the heterojunction and positive ions at the AlGaN surface. The total charge inside the Gauss’s rectangle is equal to zero in both cases, which means that the following Gauss’s equation applies to each of them:
In (1), Es is the electric field at the AlGaN surface, Eh is the electric field at the AlGaN/GaN heterojunction, and is the permittivity of AlGaN. Case A, which excludes both the electrons next to the heterojunction and the positive ions at the surface, corresponds to Es = 0 and Eh = 0. In case B, the heterojunction and the surface fields are equal to each other, Es = Eh, but they are not equal to zero. The field Es attracts mobile positive ions from the ambient, whereas the field Eh attracts mobile electrons to the 2DEG. This means that the density of 2DEG electrons balances the difference between the spontaneous polarizations of AlGaN and GaN:
It should be noted that the potential impact of the piezoelectric polarization charge, Npz, is not included by the analysis based on Figure 1. However, the AlGaN bonds near the heterojunction are strained, which distorts the electron-cloud asymmetry of the nonstrained AlGaN bonds and changes the spontaneous polarization charge, Np-AlGaN, by the value of Npz. Therefore, the piezoelectric polarization charge can be modelled by additional dipoles next to the heterojunction, as illustrated in Figure 2. Case A shows that a mobile electron cannot be attracted to the heterojunction, and likewise, a mobile positive charge cannot be attracted to AlGaN surface due to the piezoelectric dipole. The charge enclosed by the dashed rectangle in this case is zero, which means Es = Eh. If we assume that Es = Eh is not equal to zero, we violate Kirchhoff’s voltage law because Esd1 > Ehd2. This is not possible as the potential difference between the AlGaN surface and AlGaN/GaN heterojunction has to be equal to zero because there is no electric field above the AlGaN surface and no electric field below the AlGaN/GaN heterojunction. Case B shows a dashed rectangle around a piezoelectric dipole with no mobile charges attracted towards it. This case satisfies both the Gauss’s law and Kirchhoff’s voltage law and shows that piezoelectric polarization near the heterojunction does not impact N2DEG. Thus, as presented in (2), spontaneous polarization is the only reason for N2DEG at the AlGaN/GaN heterojunction when the surface is exposed to ambient ions.
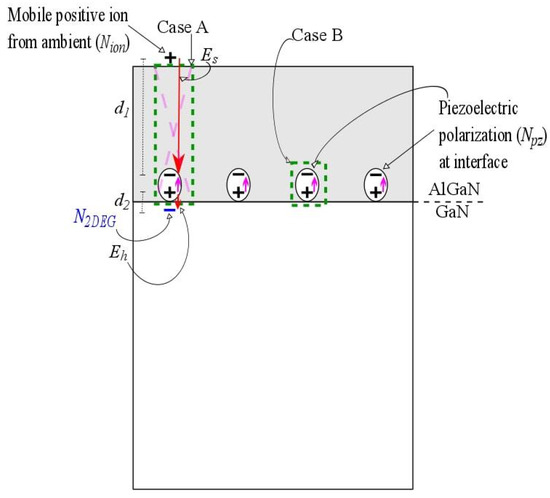
Figure 2.
Illustration of the lack of impact of piezoelectric polarization (modelled using dipoles at AlGaN/GaN heterojunction) on the electron density in 2DEG. Cases A and B show dashed rectangles with zero enclosed charge. The possibility of Case A is crossed out as it violates Kirchhoff’s voltage law. Case B shows no mobile charges attracted from surroundings due to piezoelectric polarization.
2.2. Metal Gate Deposited on AlGaN Surface
The electron density at the AlGaN/GaN heterojunction with a metal gate deposited on the AlGaN surface, N2DEG−M can also be stated in terms of spontaneous polarization in AlGaN and GaN, with the difference that this parameter also depends on the metal–semiconductor work function difference,, between the metal and the GaN acting as the semiconductor. This structure is analogous to metal–oxide–semiconductor (MOS) structures, the only difference being that the dielectric role of the oxide between the metal and the semiconductor is played by the AlGaN layer. Adopting the dependence of electron density on the work–function difference from MOS theory [14,15], we obtain the following equation for N2DEG−M:
In (3), CAlGaN is the AlGaN capacitance per unit area.
2.3. Thick Passivating Dielectric on AlGaN Surface
In the case of thick passivating dielectric, there are ions at the AlGaN surface, but they are fixed. This means that the electron density in the passivated case, N2DEG-P, can be given in terms of the charge density at the passivation interface, Npass, and the spontaneous polarizations in AlGaN and GaN layers by the following equation:
3. Comparison with Other Models
For the first scenario elucidated in Section 2.1, our model using Gauss’s law indicates that 2DEG electron density is proportional to the difference between spontaneous polarization of AlGaN and GaN, whereas it is independent of the piezoelectric polarization. The simplified model by Ibbetson et al. [10] does not consider these factors. The other well-known model is developed by Ambacher et al. [12]. Their model states the dependence of 2DEG on both polarization and piezoelectric charges. Later on, several groups came up with more accurate models [9,16,17,18].
For the second scenario, as explained in Section 2.2, our model using MOS theory shows that 2DEG electron density is dependent on the difference between spontaneous polarization of AlGaN and GaN, as well as the work–function difference due to the metal-semiconductor junction. We have not seen other published model for the same scenario e.g. Morkoc [11] that employ the same approach.
For the third scenario, as documented in Section 2.3, our model indicates that 2DEG electron density is dependent on the difference between spontaneous polarization of AlGaN and GaN, as well as the charge density due to fixed ions at the insulator/AlGaN interface. There are several groups that have investigated this scenario, for example Shealy et al. [19] and Maeda et al. [20]. Both groups conducted experiments with variety of passivation dielectrics before deriving their equations. Despite differing complexities, all models agree that charge density of the passivation interface majorly influences the electron density of 2DEG.
4. Conclusions
We show that N2DEG depends on the difference between spontaneous polarizations of AlGaN and GaN, but surprisingly, it is independent of the piezoelectric polarization in all realistic scenarios: AlGaN surface exposed to free air with mobile ions, metal gate deposited on the AlGaN surface, and the AlGaN surface passivated by a thick dielectric layer. When a metal gate is deposited on the AlGaN surface, the work–function difference impacts N2DEG in analogous way to the well-established dependence of the semiconductor-charge density on the work–function difference in MOS capacitors. Finally, the fixed charge at the interface between AlGaN and a thick passivating layer, which is usually positive, attracts equivalent density of electrons to the 2DEG. The resulting equations from this new analysis provide the ability to distinguish between these differences and realistic scenarios, which is a specific addition to the existing body of literature.
Author Contributions
Conceptualization, S.D.; methodology, S.U.R. and S.D.; validation, S.U.R., S.D., F.M.-Y. and H.A.M.; formal analysis, S.U.R., S.D. and F.M.-Y.; investigation, S.U.R., S.D., F.M.-Y. and H.A.M.; writing—original draft preparation, S.U.R. and S.D.; writing—review and editing, S.U.R., S.D., F.M.-Y. and H.A.M.; visualization, S.U.R. and S.D.; supervision, S.D. and F.M.-Y.; project administration, S.D. and F.M.-Y.; funding acquisition, S.D. and F.M.-Y.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Innovative Manufacturing Cooperative Research Centre (IMCRC), and BlueGlass as the industry partner, grant number 220132.
Data Availability Statement
Data is contained within the article.
Acknowledgments
This work was performed in part at the Queensland node of the Australian National Fabrication Facility, a company established under the National Collaborative Research Infrastructure Strategy to provide nano- and micro-fabrication facilities for Australia’s researchers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yu, E.T.; Sullivan, G.J.; Asbeck, P.M.; Wang, C.D.; Qiao, D.; Lau, S.S. Measurement of piezoelectrically induced charge in GaN/AlGaN heterostructure field-effect transistors. Appl. Phys. Lett. 1997, 71, 2794–2796. [Google Scholar] [CrossRef] [Green Version]
- Mishra, U.K.; Shen, L.; Kazior, T.E.; Wu, Y.-F. GaN-based RF power devices and amplifiers. Proc. IEEE 2008, 96, 287–305. [Google Scholar] [CrossRef]
- Lee, B.H.; Kim, R.H.; Lim, B.O.; Choi, G.W.; Kim, H.J.; Hong, I.P.; Lee, J.H. High RF performance improvement using surface passivation technique of AlGaN/GaN HEMTs at K-band application. Electron. Lett. 2013, 49, 1013–1015. [Google Scholar] [CrossRef]
- Hanawa, H.; Satoh, Y.; Horio, K. Effects of buffer leakage current on breakdown characteristics in AlGaN/GaN HEMTs with a high-k passivation layer. Microelectron. Eng. 2015, 147, 96–99. [Google Scholar] [CrossRef]
- Yu, C.-H.; Luo, Q.-Z.; Luo, X.-D.; Liu, P.-S. Donor-like surface traps on two-dimensional electron gas and current collapse of AlGaN/GaN HEMTs. Sci. World J. 2013, 2013, 931980. [Google Scholar] [CrossRef] [Green Version]
- Jang, H.W.; Jeon, C.M.; Kim, K.H.; Kim, J.K.; Bae, S.-B.; Lee, J.-H.; Choi, J.W.; Lee, J.-L. Mechanism of two-dimensional electron gas formation in AlxGa1-xN/GaN heterostructures. Appl. Phys. Lett. 2002, 81, 1249–1251. [Google Scholar] [CrossRef] [Green Version]
- Miller, E.J.; Yu, E.T.; Poblenz, C.; Elsass, C.; Speck, J.S. Direct measurement of the polarization charge in AlGaN/GaN heterostructures using capacitance–voltage carrier profiling. Appl. Phys. Lett. 2002, 80, 3551–3553. [Google Scholar] [CrossRef]
- Ramanan, N.; Lee, B.; Kirkpatrick, C.; Suri, R.; Misra, V. Properties of atomic layer deposited dielectrics for AlGaN/GaN device passivation. Semicond. Sci. Technol. 2013, 28, 074004. [Google Scholar] [CrossRef]
- Xiao-Guang, H.; De-Gang, Z.; De-Sheng, J. Formation of two-dimensional electron gas at AlGaN/GaN heterostructure and the derivation of its sheet density expression. Chin. Phys. B 2015, 24, 067301. [Google Scholar]
- Ibbetson, J.P.; Fini, P.T.; Ness, K.D.; DenBaars, S.P.; Speck, J.S.; Mishra, U.K. Polarization effects, surface states, and the source of electrons in AlGaN/GaN heterostructure field effect transistors. Appl. Phys. Lett. 2000, 77, 250–252. [Google Scholar] [CrossRef]
- Morkoc, H. Nitride Semiconductor Devices: Fundamentals and Applications; John Wiley & Sons: Weinheim, Germany, 2013; pp. 31–51. [Google Scholar]
- Ambacher, O.; Foutz, B.; Smart, J.; Shealy, J.R.; Weimann, N.G.; Chu, K.; Murphy, M.; Sierakowski, A.J.; Schaff, W.J.; Eastman, L.F.; et al. Two dimensional electron gases induced by spontaneous and piezoelectric polarization in undoped and doped AlGaN/GaN heterostructures. J. Appl. Phys. 2000, 87, 334–344. [Google Scholar] [CrossRef]
- Ambacher, O.; Smart, J.; Shealy, J.R.; Weimann, N.G.; Chu, K.; Murphy, M.; Schaff, W.J.; Eastman, L.F.; Dimitrov, R.; Wittmer, L.; et al. Two-dimensional electron gases induced by spontaneous and piezoelectric polarization charges in N-and Ga-face AlGaN/GaN heterostructures. J. Appl. Phys. 1999, 85, 3222–3233. [Google Scholar] [CrossRef] [Green Version]
- Dimitrijev, S. Principles of Semiconductor Devices, 2nd ed.; Oxford University Press: New York, NY, USA, 2012; pp. 252–290. [Google Scholar]
- Bhattacharya, D.K.; Sharma, R. Solid State Electronic Devices, 2nd ed.; Oxford University Press: New Delhi, India, 2013; pp. 318–362. [Google Scholar]
- Koley, G.; Spencer, M. On the origin of the two-dimensional electron gas at the Al Ga N/Ga N heterostructure interface. Appl. Phys. Lett. 2005, 86, 042107. [Google Scholar] [CrossRef]
- Higashiwaki, M.; Chowdhury, S.; Miao, M.-S.; Swenson, B.L.; van de Walle, C.G.; Mishra, U.K. Distribution of donor states on etched surface of AlGaN/GaN heterostructures. J. Appl. Phys. 2010, 108, 063719. [Google Scholar] [CrossRef] [Green Version]
- Gordon, L.; Miao, M.-S.; Chowdhury, S.; Higashiwaki, M.; Mishra, U.K.; van de Walle, C.G. Distributed surface donor states and the two-dimensional electron gas at AlGaN/GaN heterojunctions. J. Phys. D 2010, 43, 505501. [Google Scholar] [CrossRef]
- Shealy, J.; Prunty, T.; Chumbes, E.; Ridley, B. Growth and passivation of AlGaN/GaN heterostructures. J. Cryst. Growth 2003, 250, 7–13. [Google Scholar] [CrossRef]
- Maeda, N. Systematic study of insulator deposition effect (Si3N4, SiO2, AlN, and Al2O3) on electrical properties in AlGaN/GaN heterostructures. Jpn. J. Appl. Phys. 2007, 46, 547. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).