Luminescence Properties of Defects in GaN: Solved and Unsolved Problems
Abstract
1. Introduction
- The YL band (2.2 eV) in undoped GaN is now conclusively attributed to the CN acceptor (Section 3.1.2). Remaining issue: Reliable experimental data are lacking for the charge transition levels and PL signatures of VGa and VGaON complexes (Section 3.1.5 and Section 3.6).
- The UVL band (3.28 eV) in undoped GaN originates from the MgGa acceptor, and not from CN, SiGa, VGa-related, or structural defects (Section 3.5). Remaining issue: The theoretically predicted dual nature of the MgGa acceptor has not been confirmed experimentally (Section 4.3.2).
- The GL2 and RL2 bands are associated with isolated nitrogen vacancies (VN) and the AVN complexes, where A denotes a cation-site acceptor (Section 3.2.2 and Section 3.3.2). Remaining questions: What is A in the RL2 from undoped GaN? Is there PL from the AVN complexes with A = ZnGa, CdGa, or HgGa? Can GL2 and RL2 be linked to different charge transition levels of these multi-charged defects?
- The fundamental properties of the isolated BeGa acceptor have been well established (Section 4.2.2). Remaining uncertainties: The identities of the shallow acceptor and deep donor responsible for the UVLBe (3.38 eV) and BLBe (2.6 eV) bands, respectively, should be verified (Section 4.2.3 and Section 4.2.5).
- The origin of the aquamarine band in undoped GaN has been clarified (Section 4.6.2).
- Novel mechanisms of PL quenching emerged (Section 2.2.2 and Section 4.4.2).
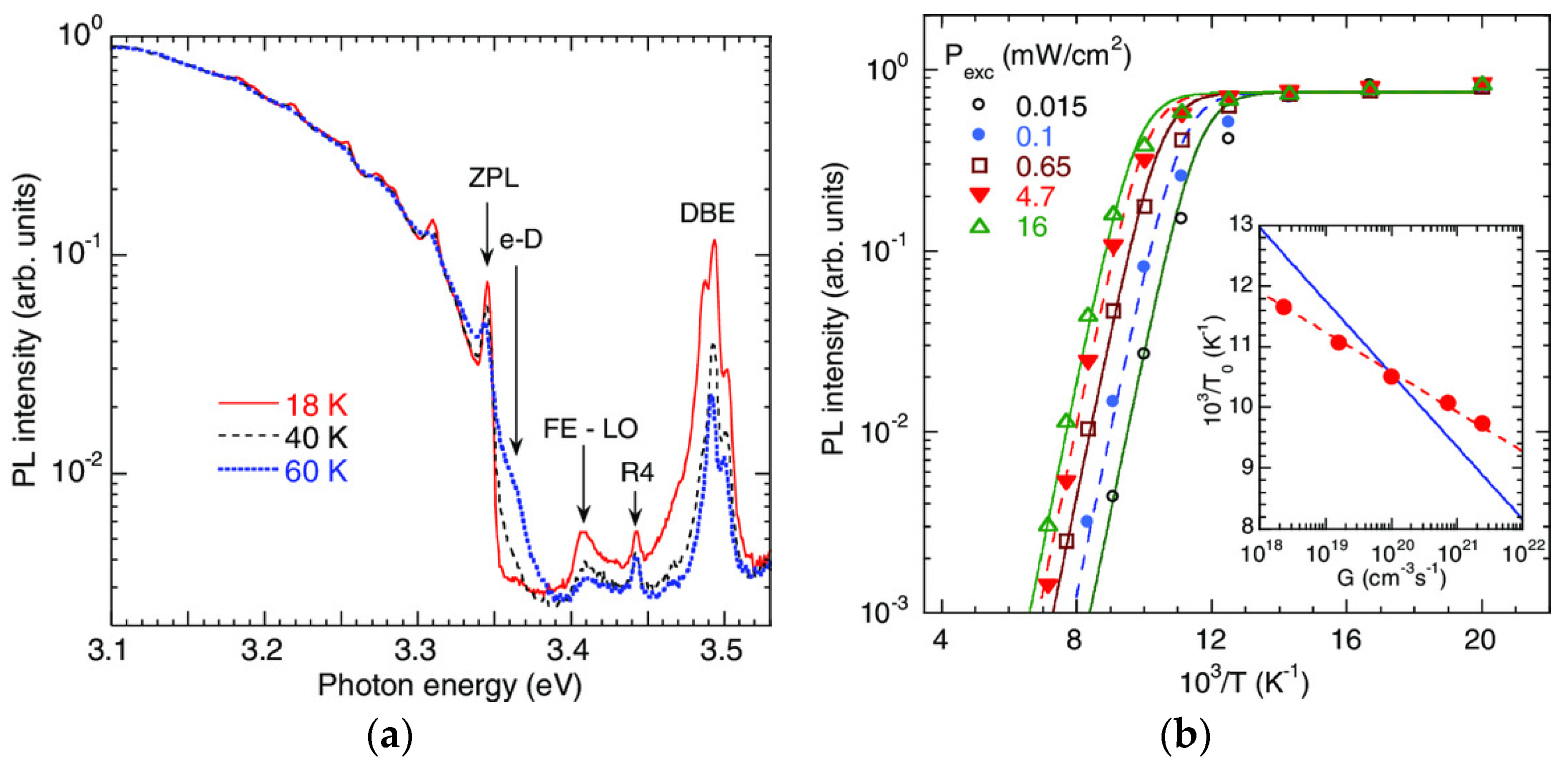
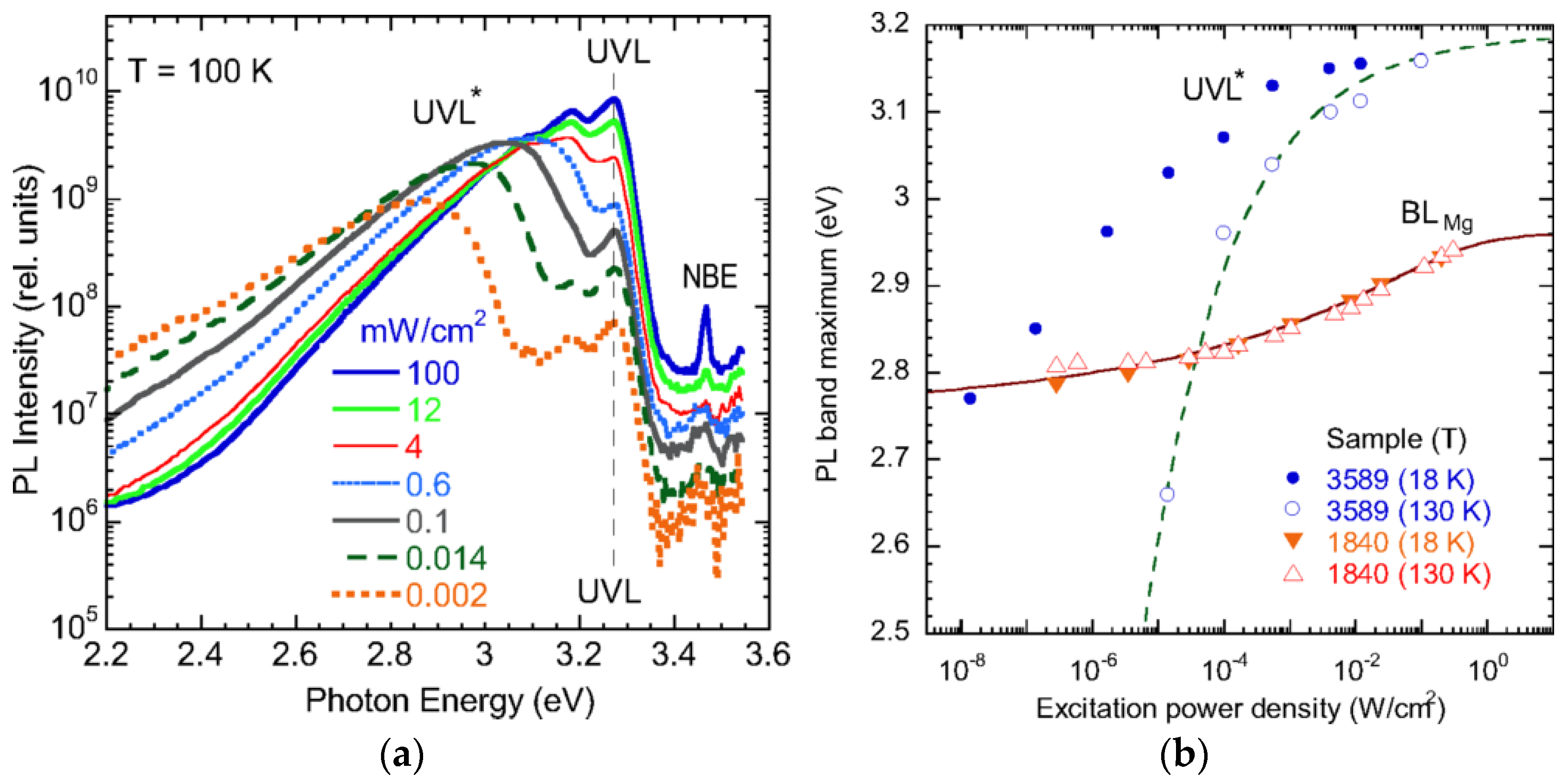
- Significant redshifts of PL bands with decreasing excitation intensity have been explained (Section 4.3.4 and Section 4.4.5).
- The predicted dual nature of acceptors (excluding BeGa) remains unverified experimentally (Section 4.3.2 and Section 4.4.1).
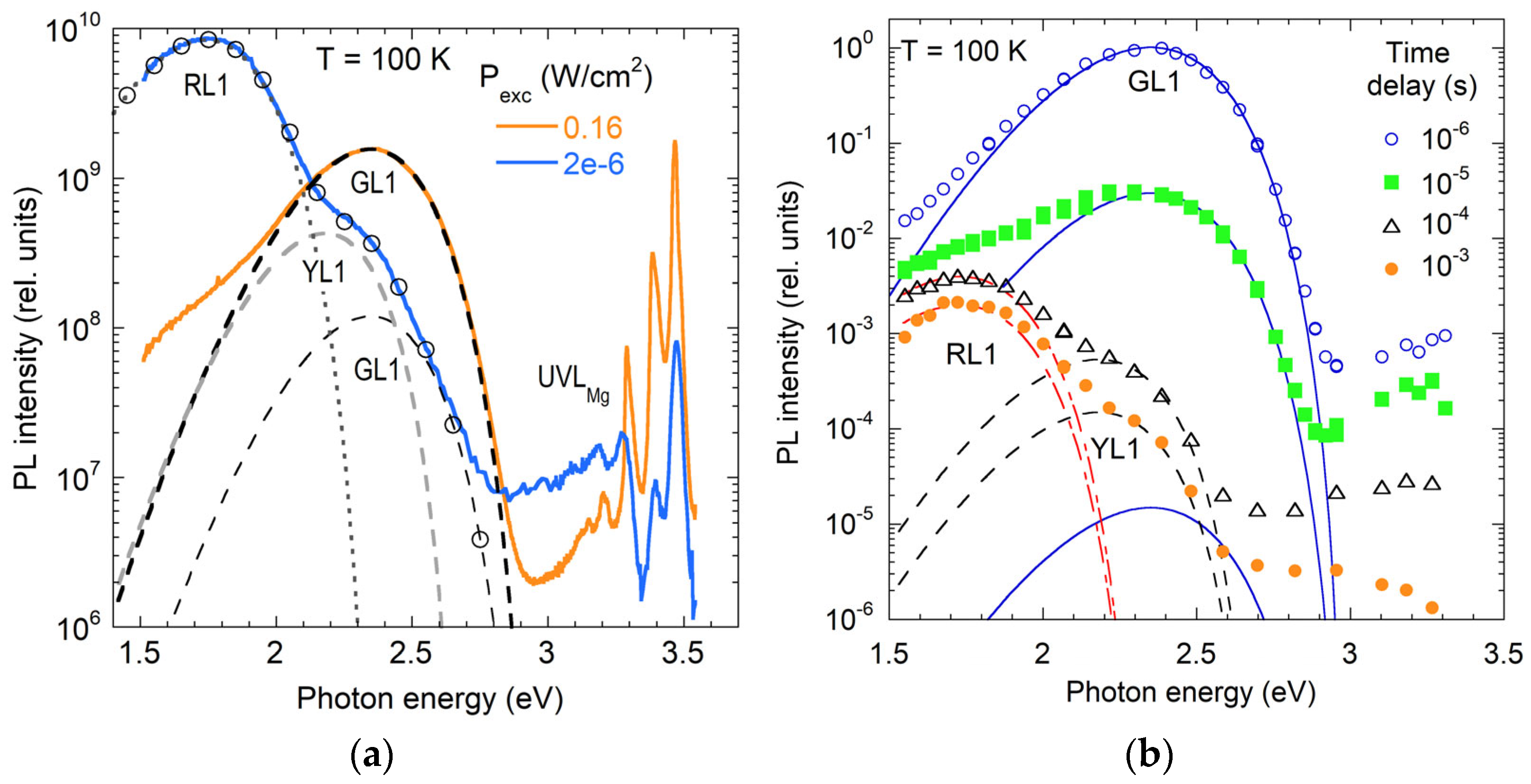
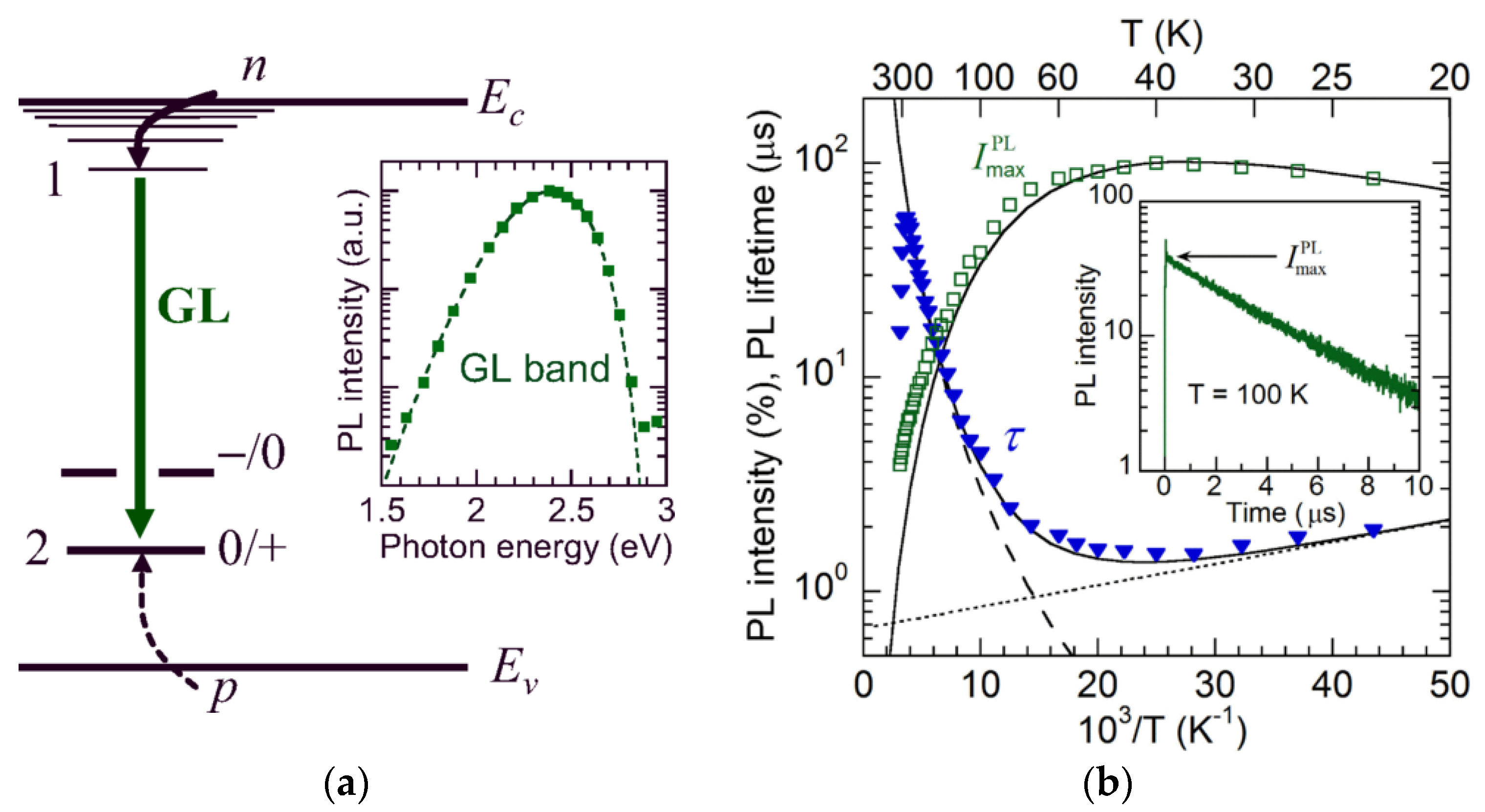
- The origins of the GL1 and RL1 bands are still unknown (Section 3.2.1 and Section 3.3.1).
- The influence of mobile defects at growth temperatures on the formation of complexes is not yet fully understood.
- The effect of the surface and structural defects on PL from point defects remains insufficiently explored.
- Significant discrepancies persist between predictions of first-principles calculations and experimental observations (Section 5.6).
2. Luminescence Methods
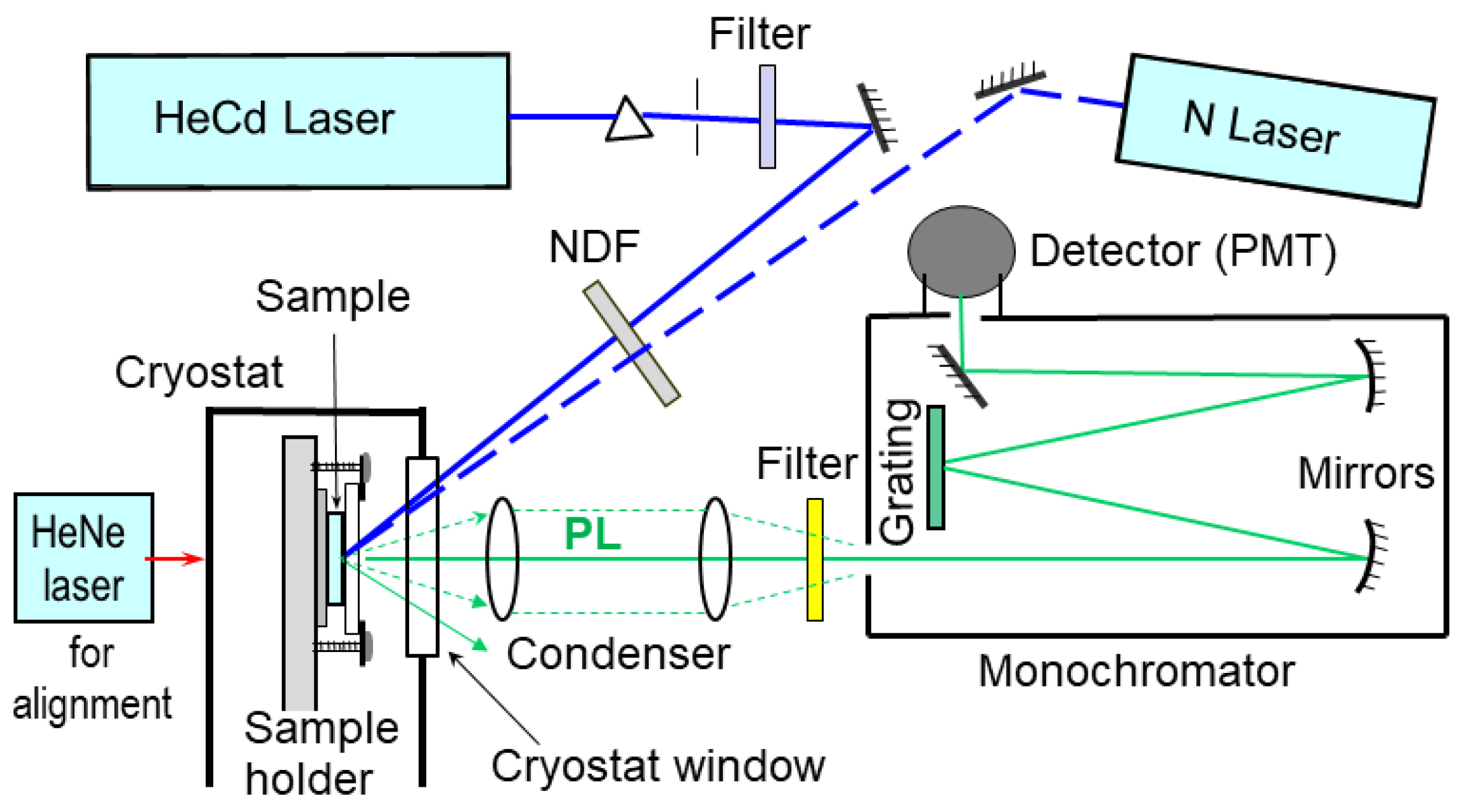
2.1. Photoluminescence Setup
2.2. Phenomenological Models for Defect-Related PL in GaN
2.2.1. TRPL and Electron-Capture Coefficient
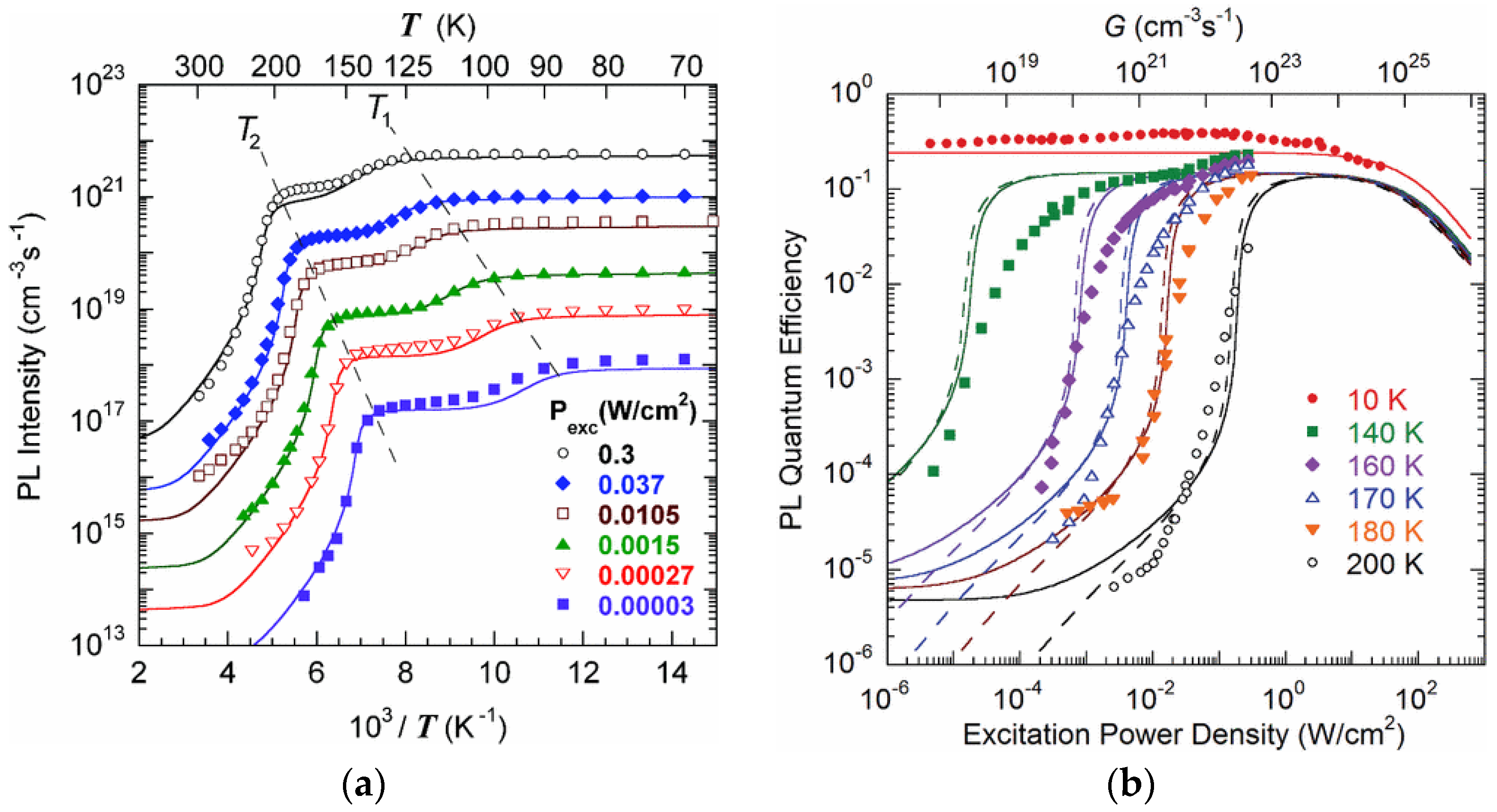
2.2.2. Temperature Dependence of PL and Hole-Capture Coefficient
2.2.3. Excitation Intensity Dependence
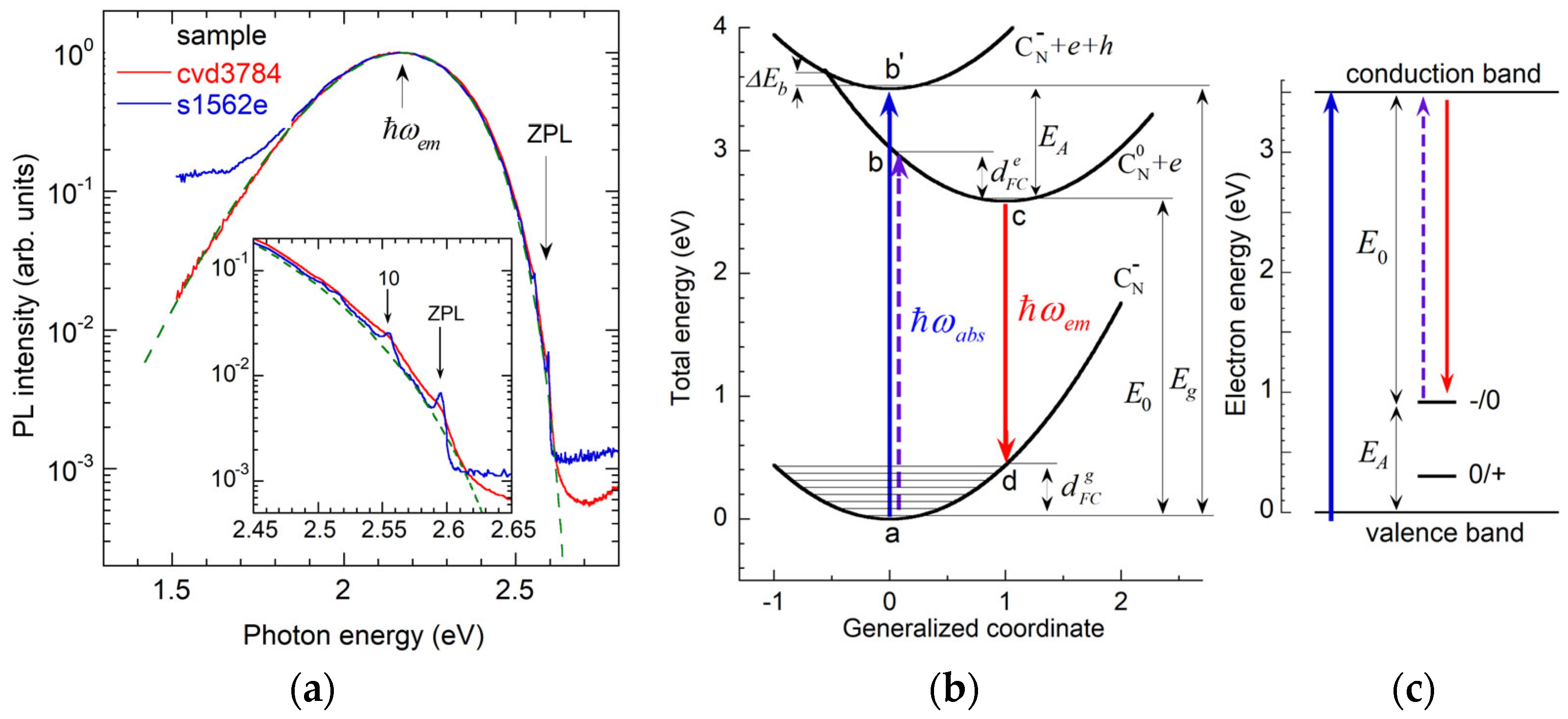
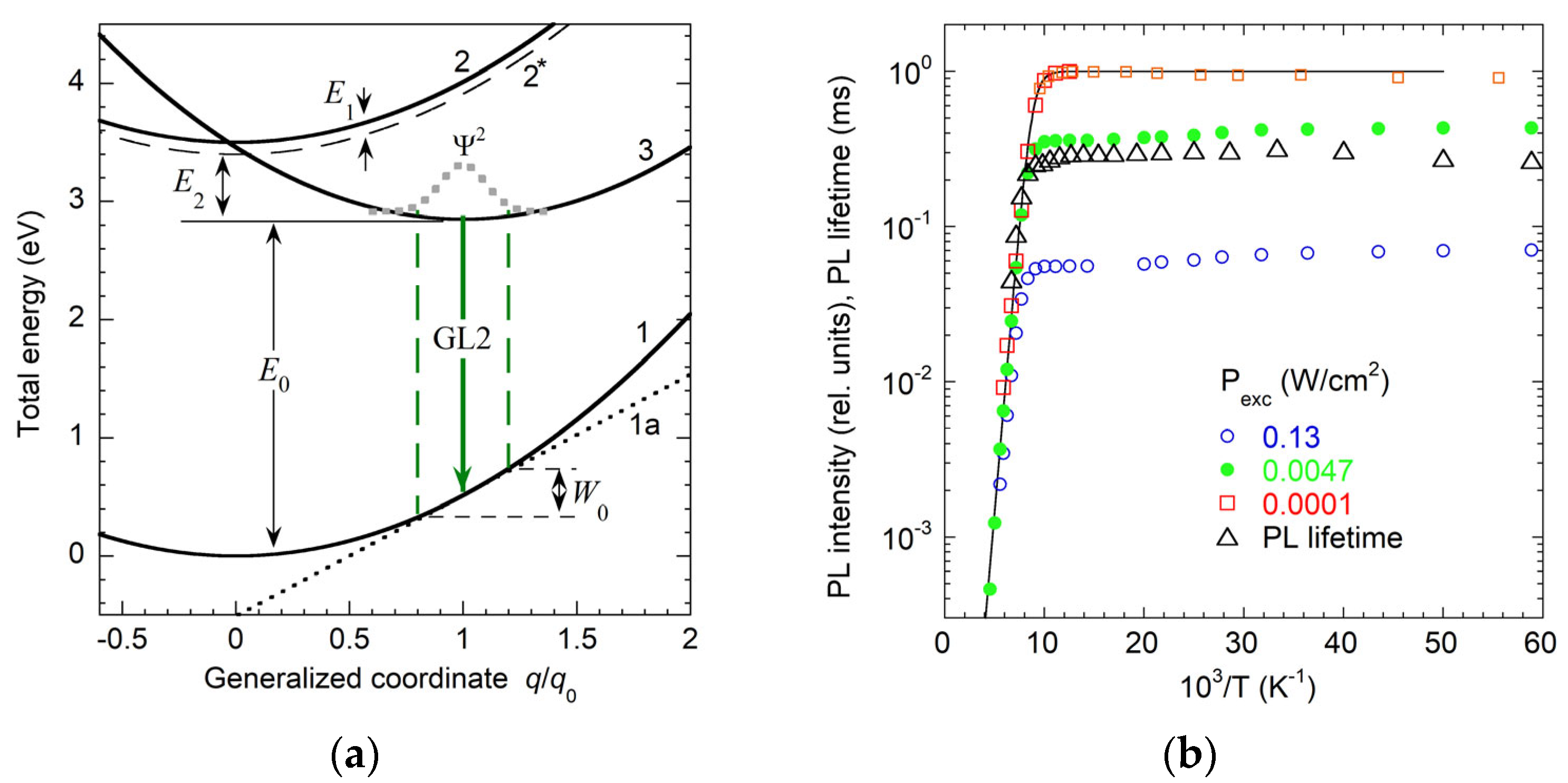
2.3. Configuration Coordinate Model for Defect-Related PL
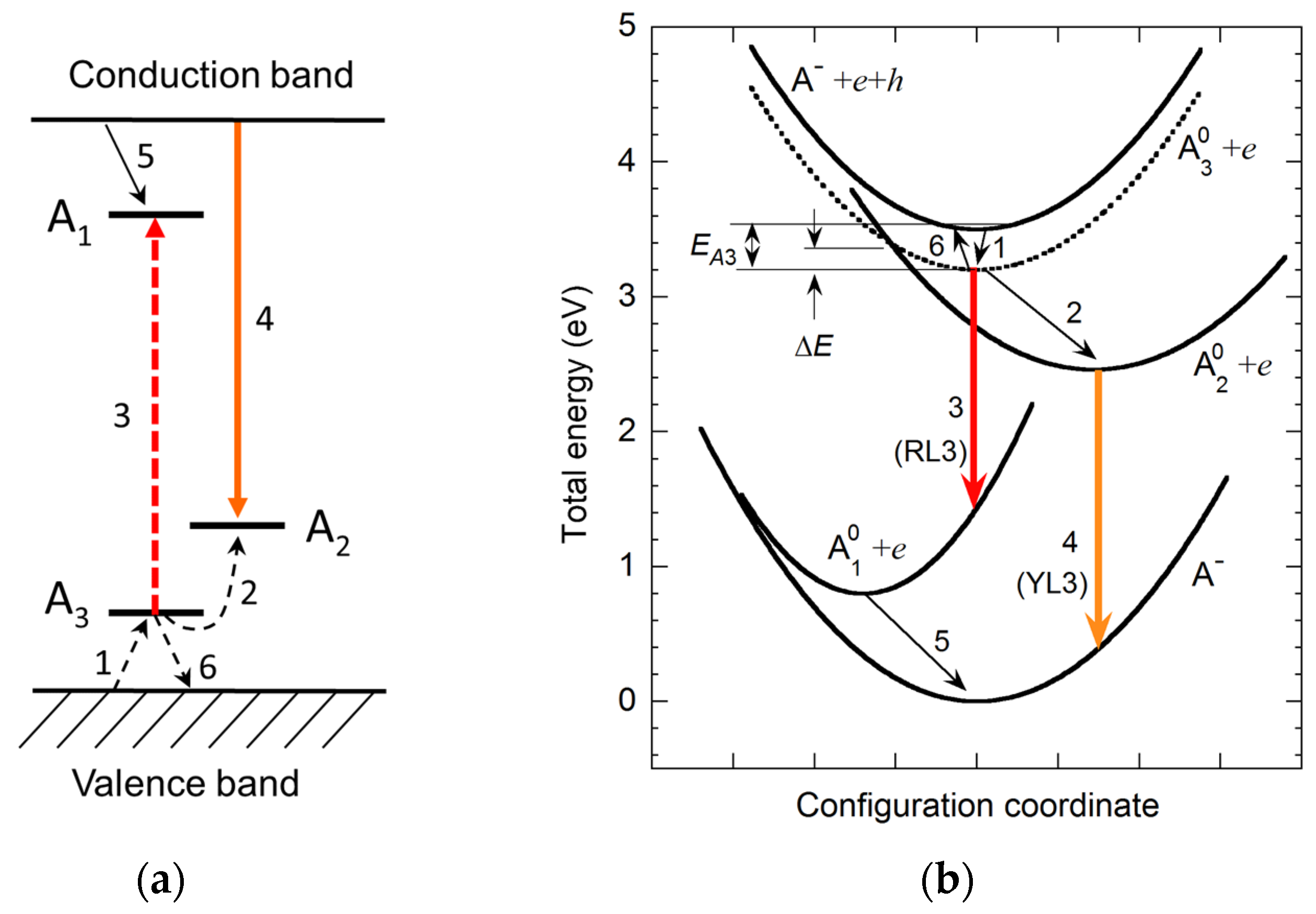
2.4. Electron Transition Mechanisms
3. Luminescence Associated with Defects in Undoped GaN
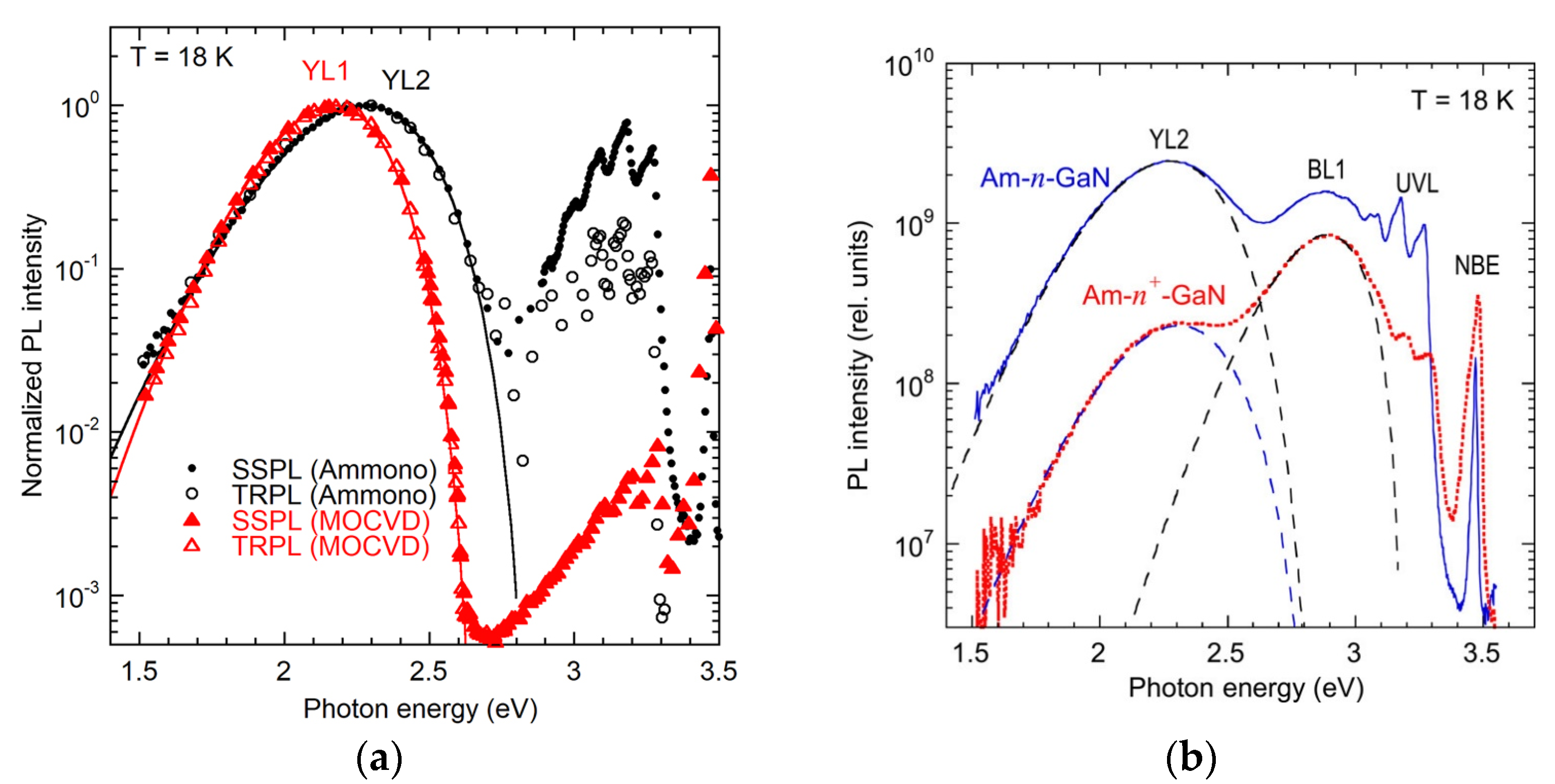
3.1. Yellow Luminescence in Undoped GaN (YL1, YL2, YL3)
3.1.1. Historical Overview
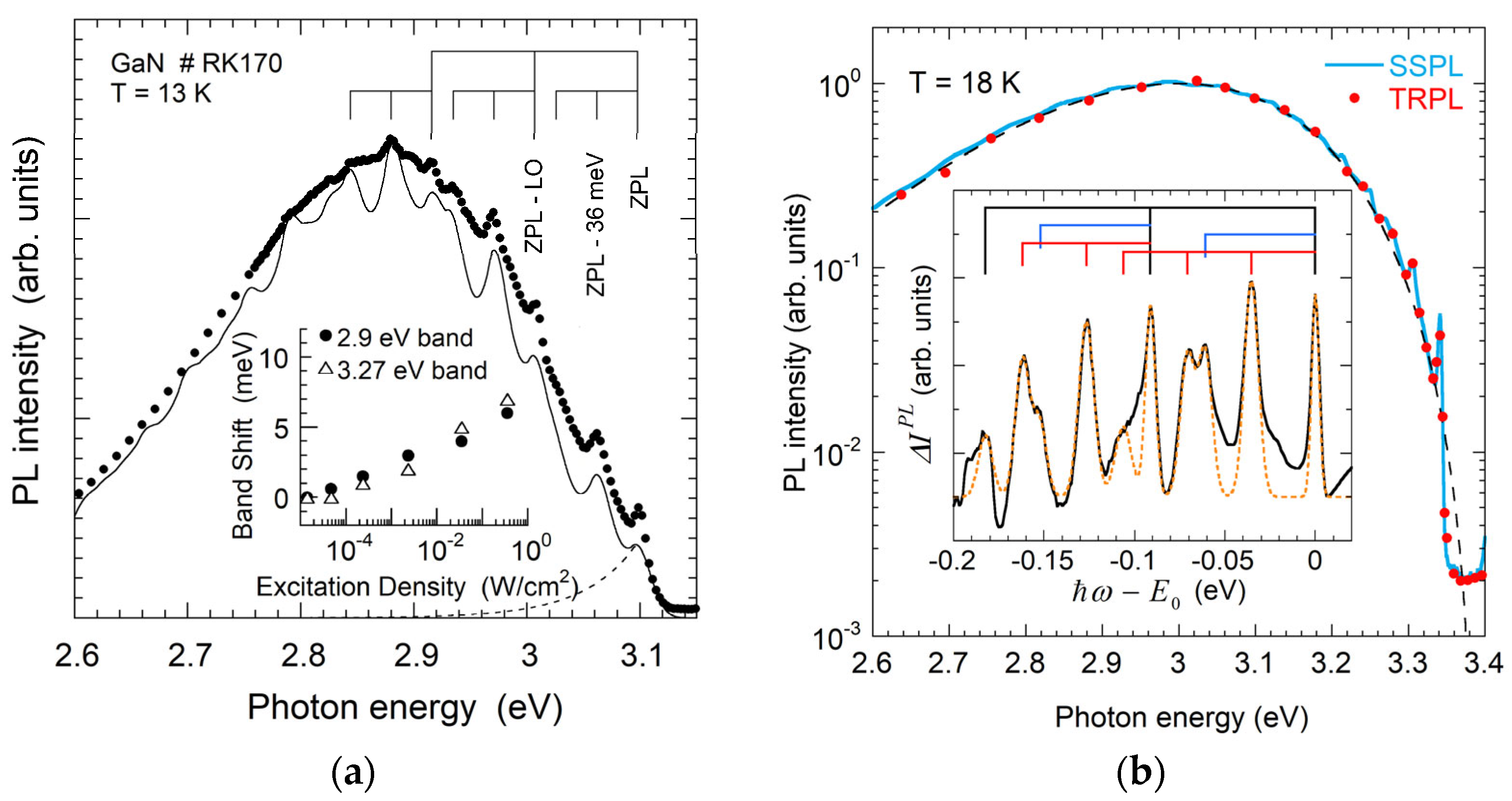
3.1.2. CN-Related YL1 Band
3.1.3. YL2 Band in Ammonothermal GaN
3.1.4. YL3 Band in HVPE GaN
3.1.5. Exclusion of VGa and VGaON as Sources of the YL Band
3.2. Red Luminescence Bands in Undoped GaN (RL1, RL2, RL3, RL4)
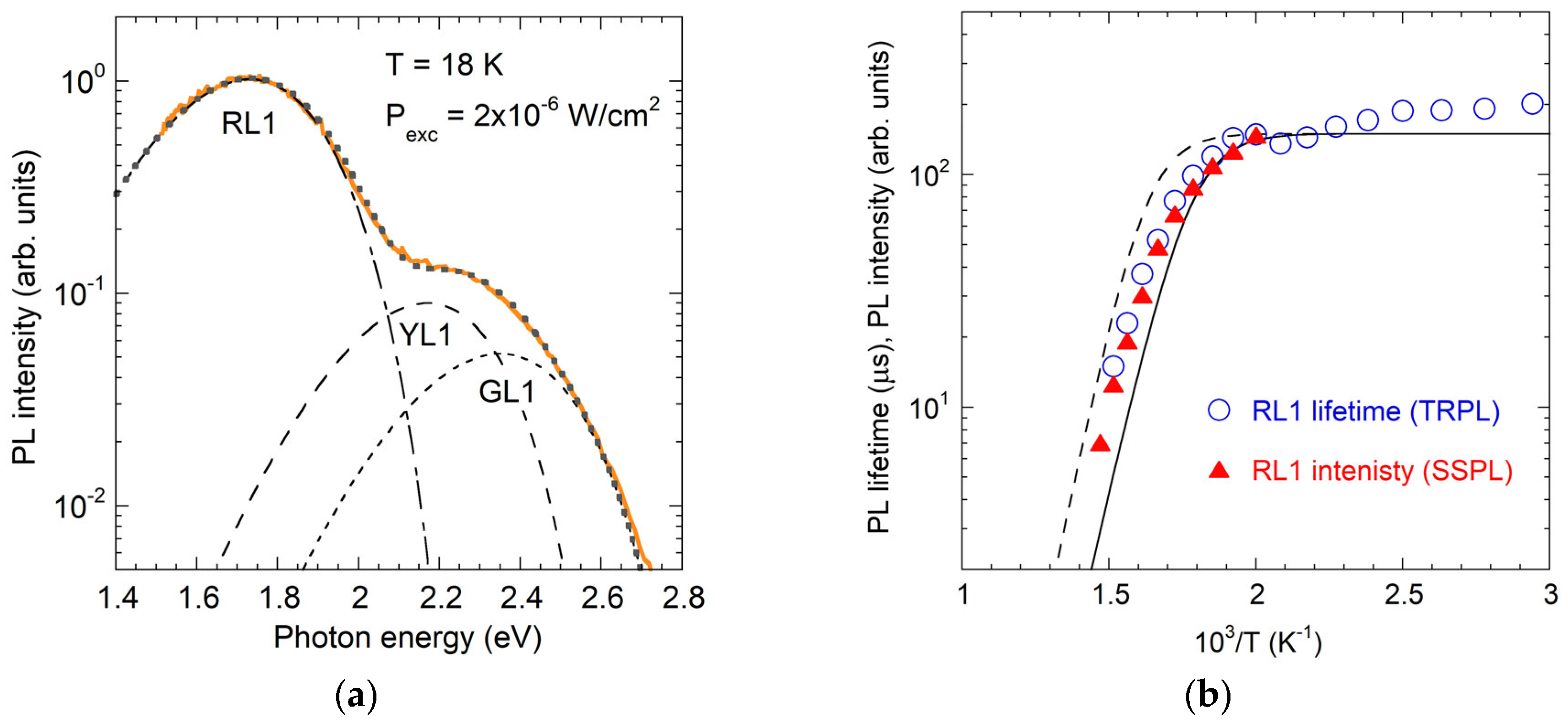
3.2.1. RL1 Band in HVPE GaN
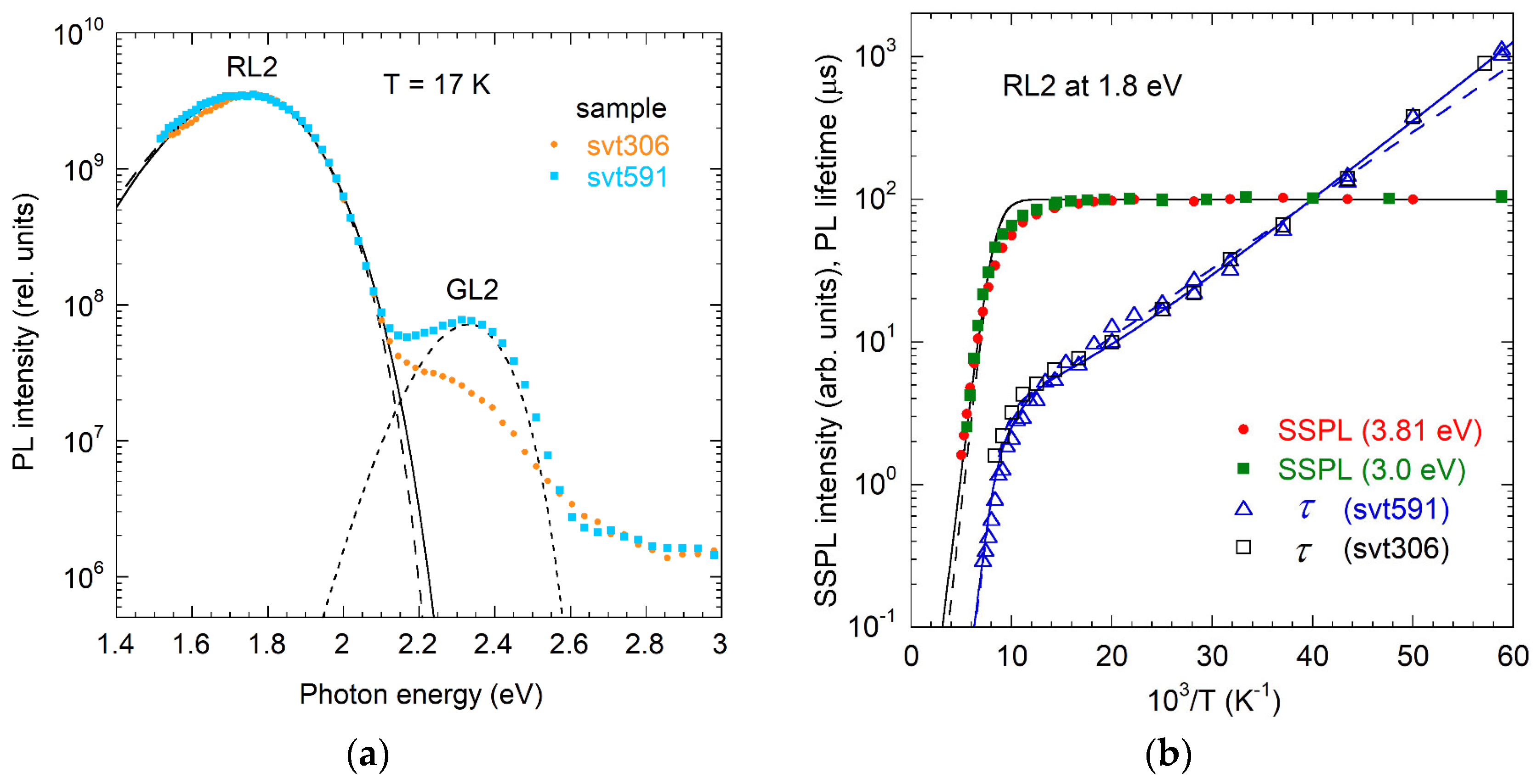
3.2.2. VN-Related RL2 Band
3.2.3. RL3 Band in HVPE GaN
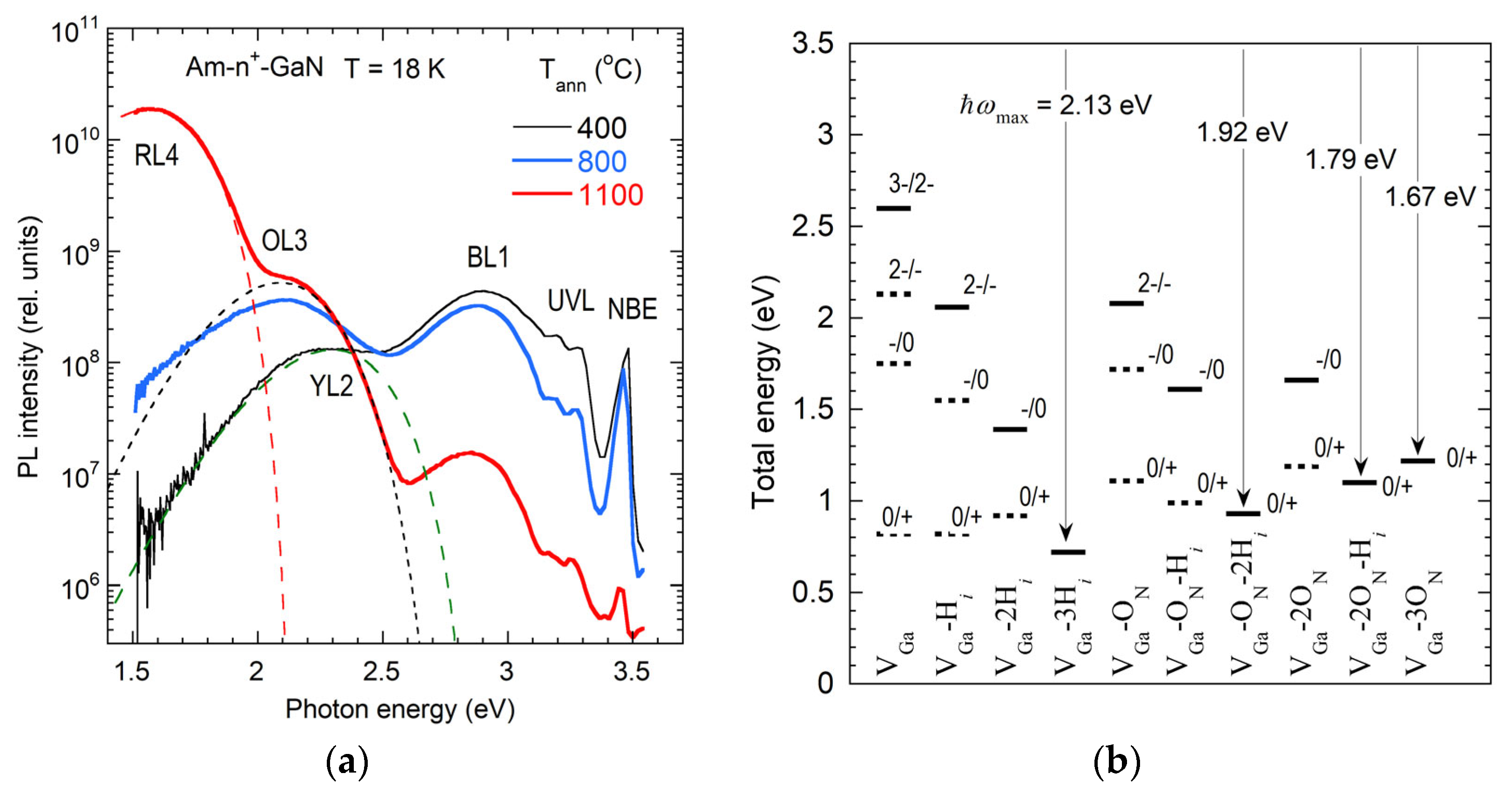
3.2.4. RL4 Band in Ammonothermal GaN
3.3. Green Luminescence Bands (GL1, GL2, GLCa)
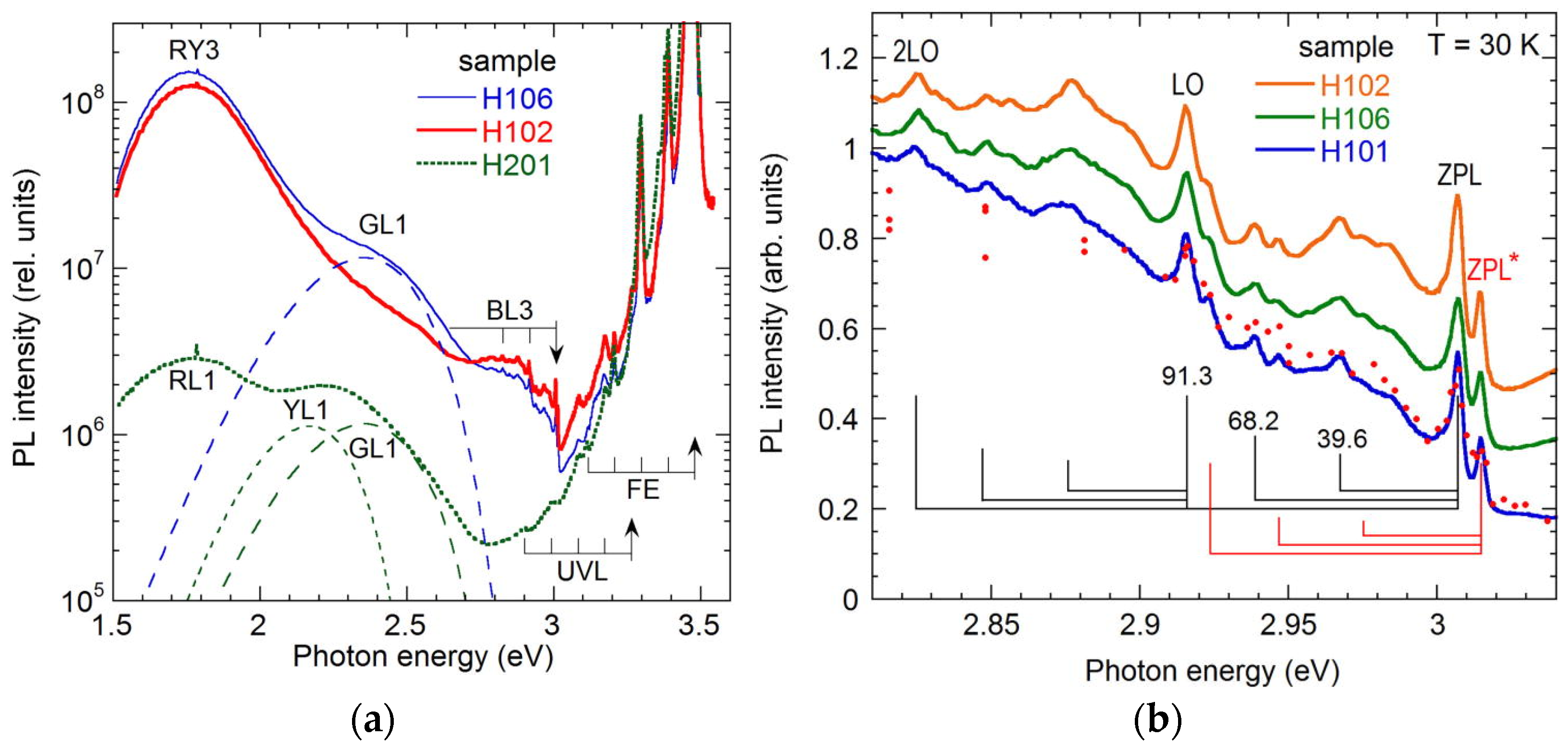
3.3.1. Unidentified GL1 Band in HVPE GaN
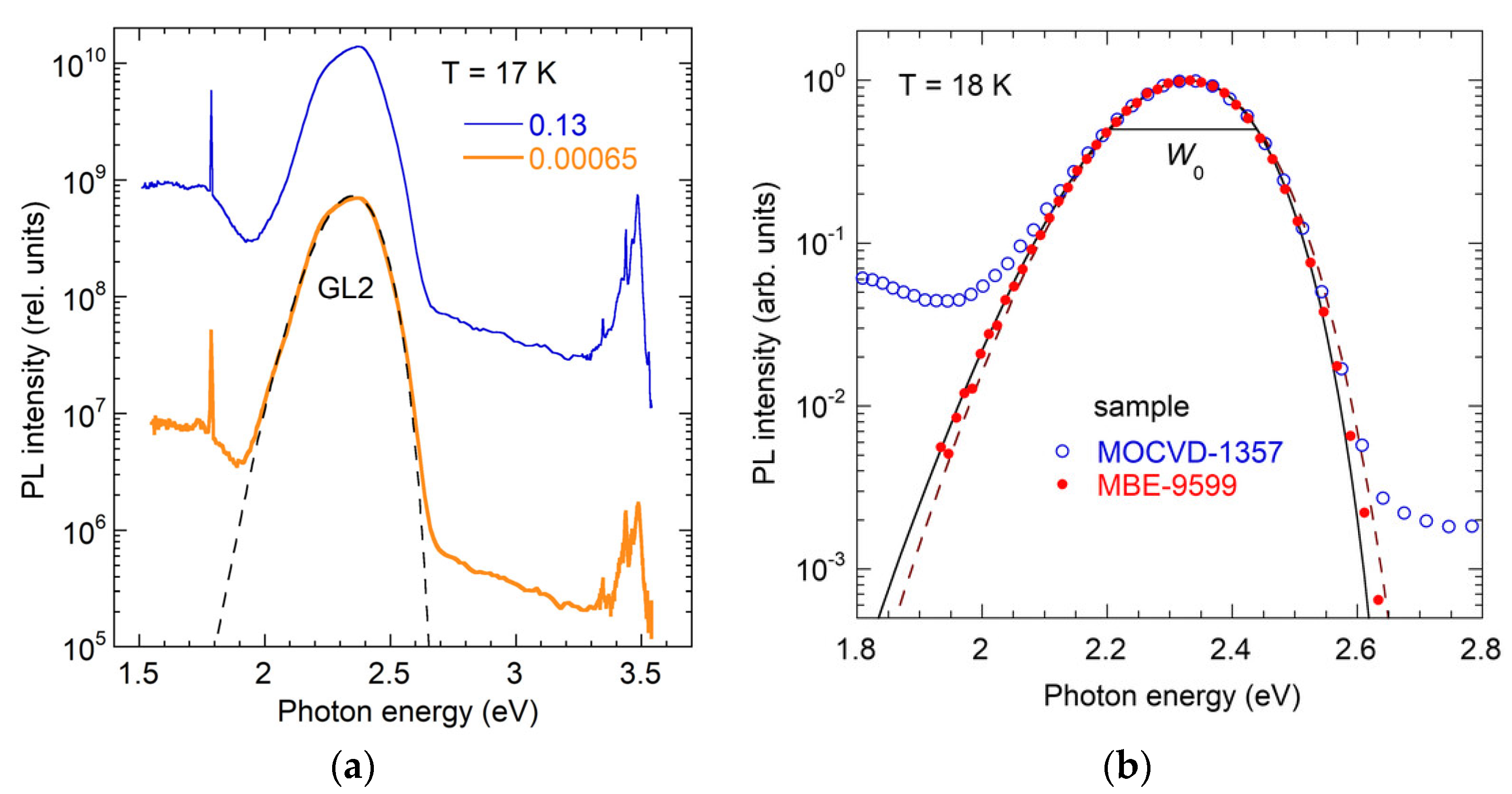
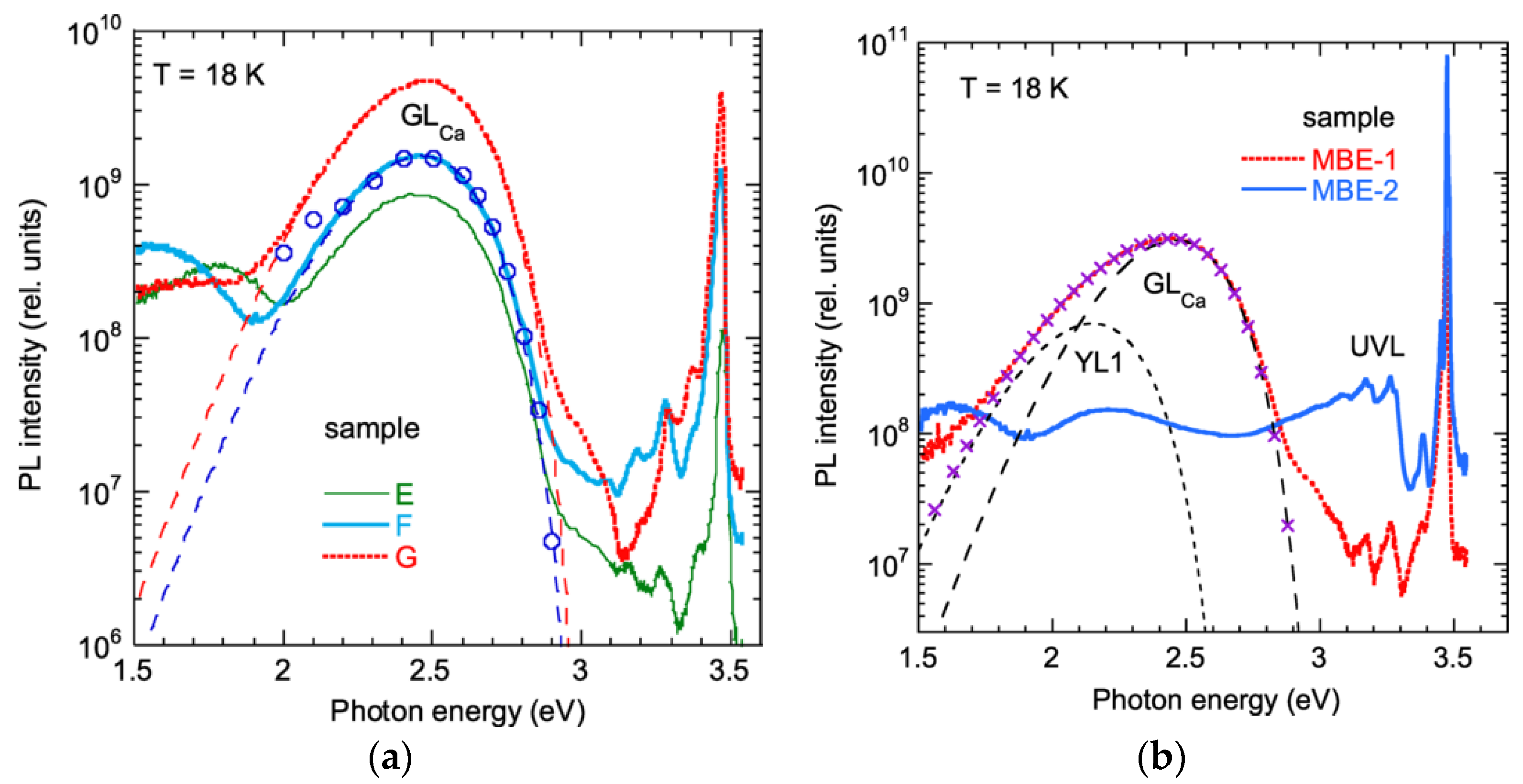
3.3.2. VN-Related GL2 Band
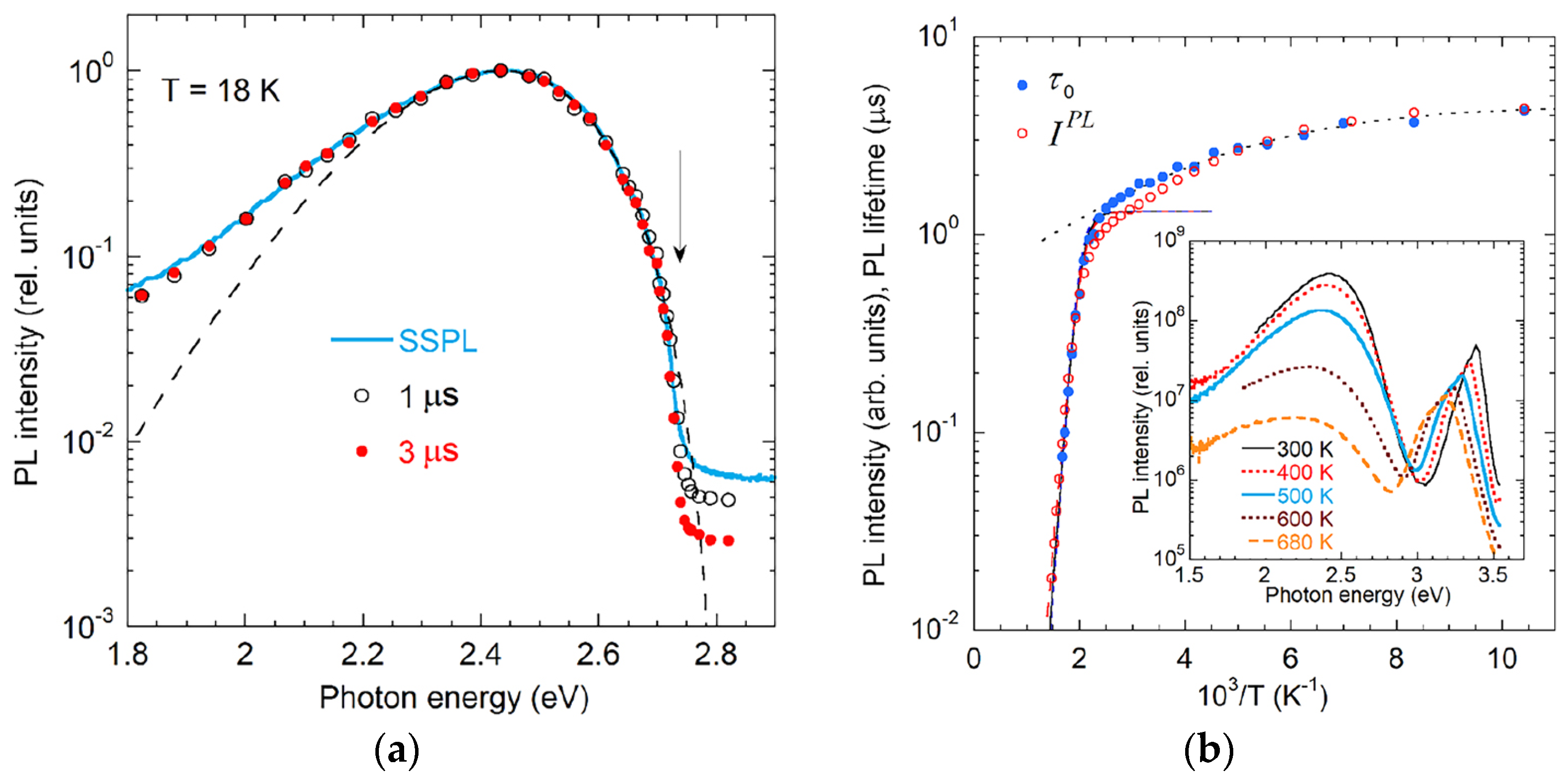
3.3.3. Aquamarine Band in MBE GaN
3.4. Blue Luminescence Bands in Undoped GaN (BL1, BL2, BL3)
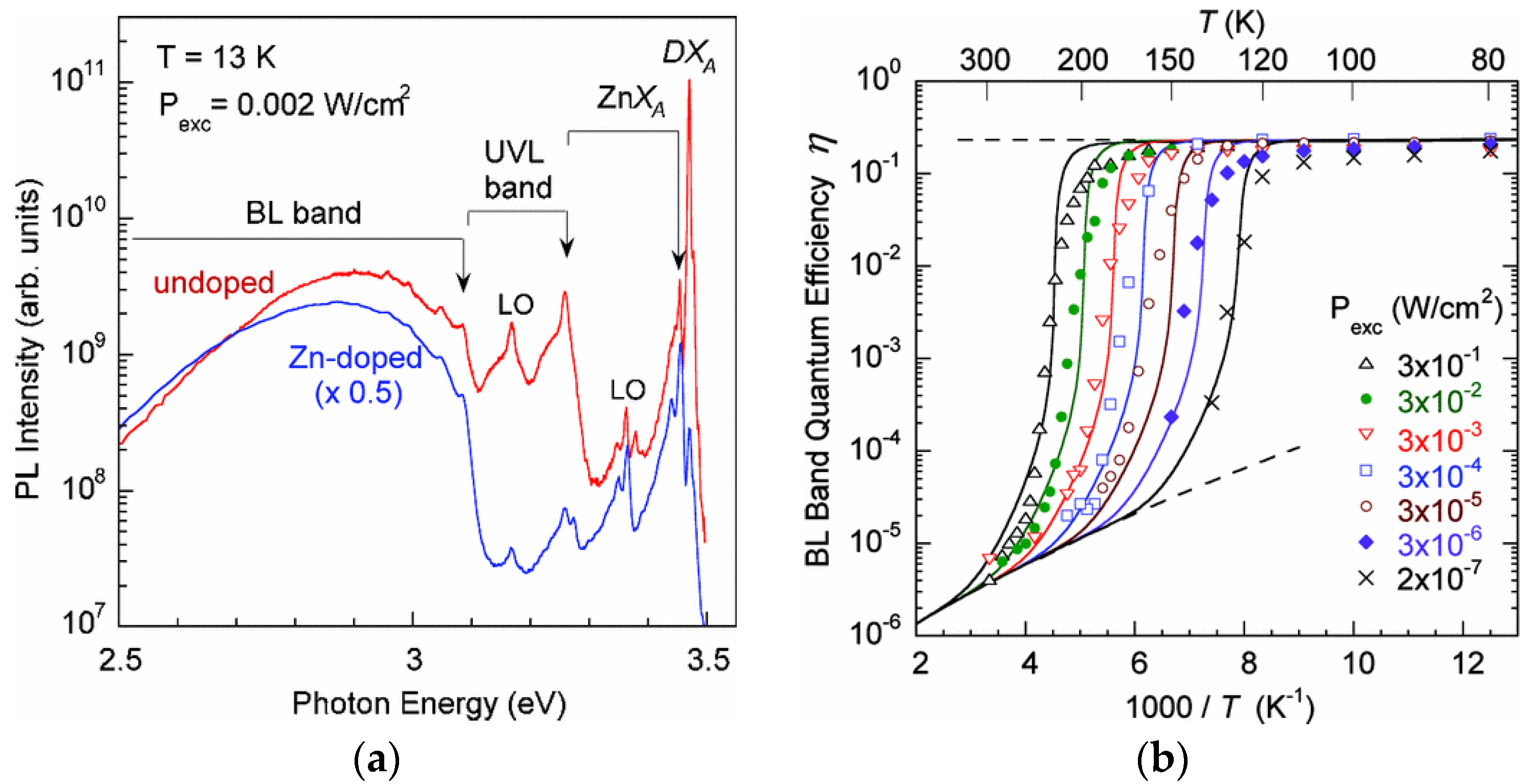
3.4.1. ZnGa-Related BL1 Band
3.4.2. CNHi-Related BL2 Band
3.4.3. RY3-Related BL3 Band
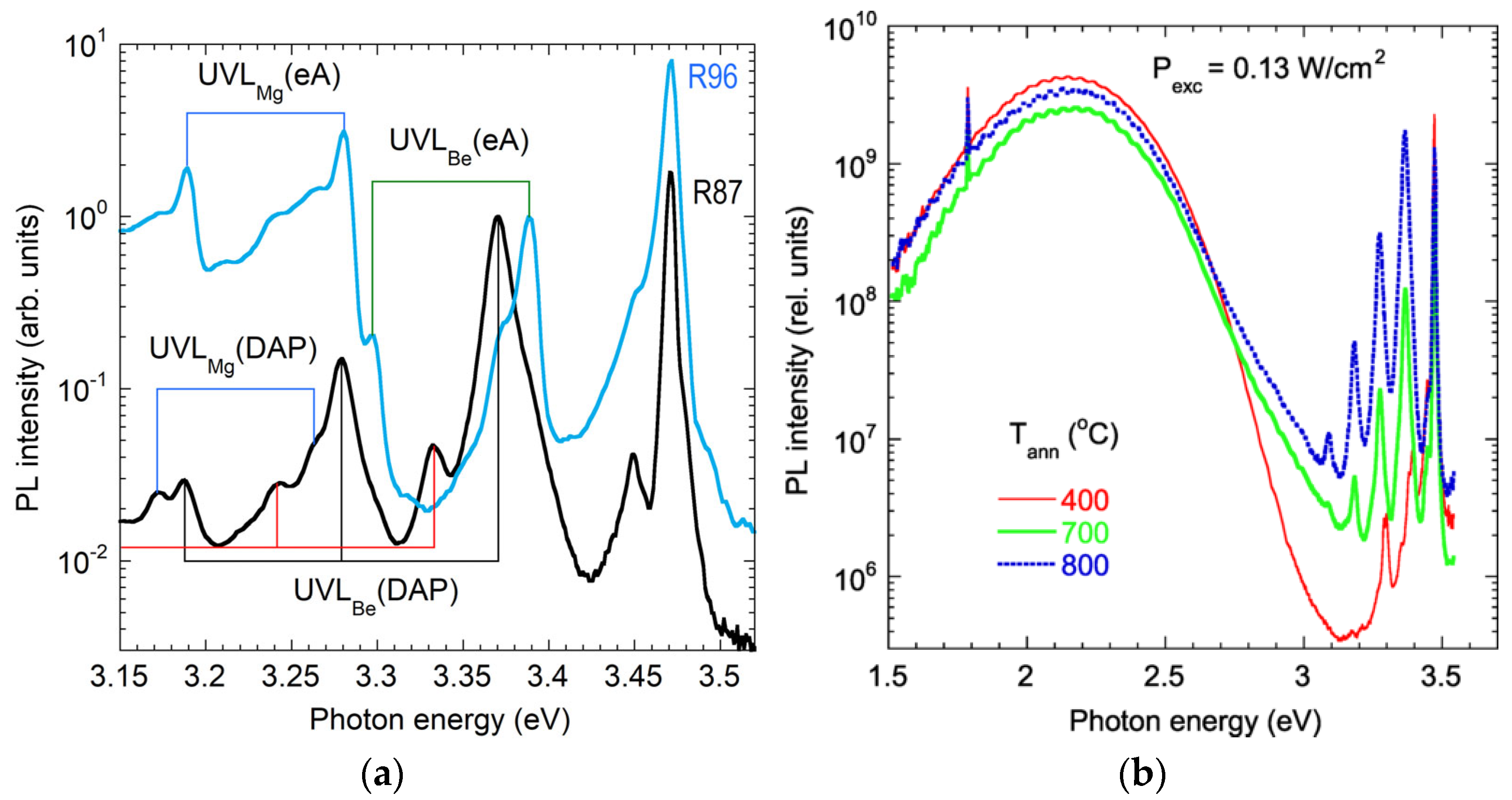
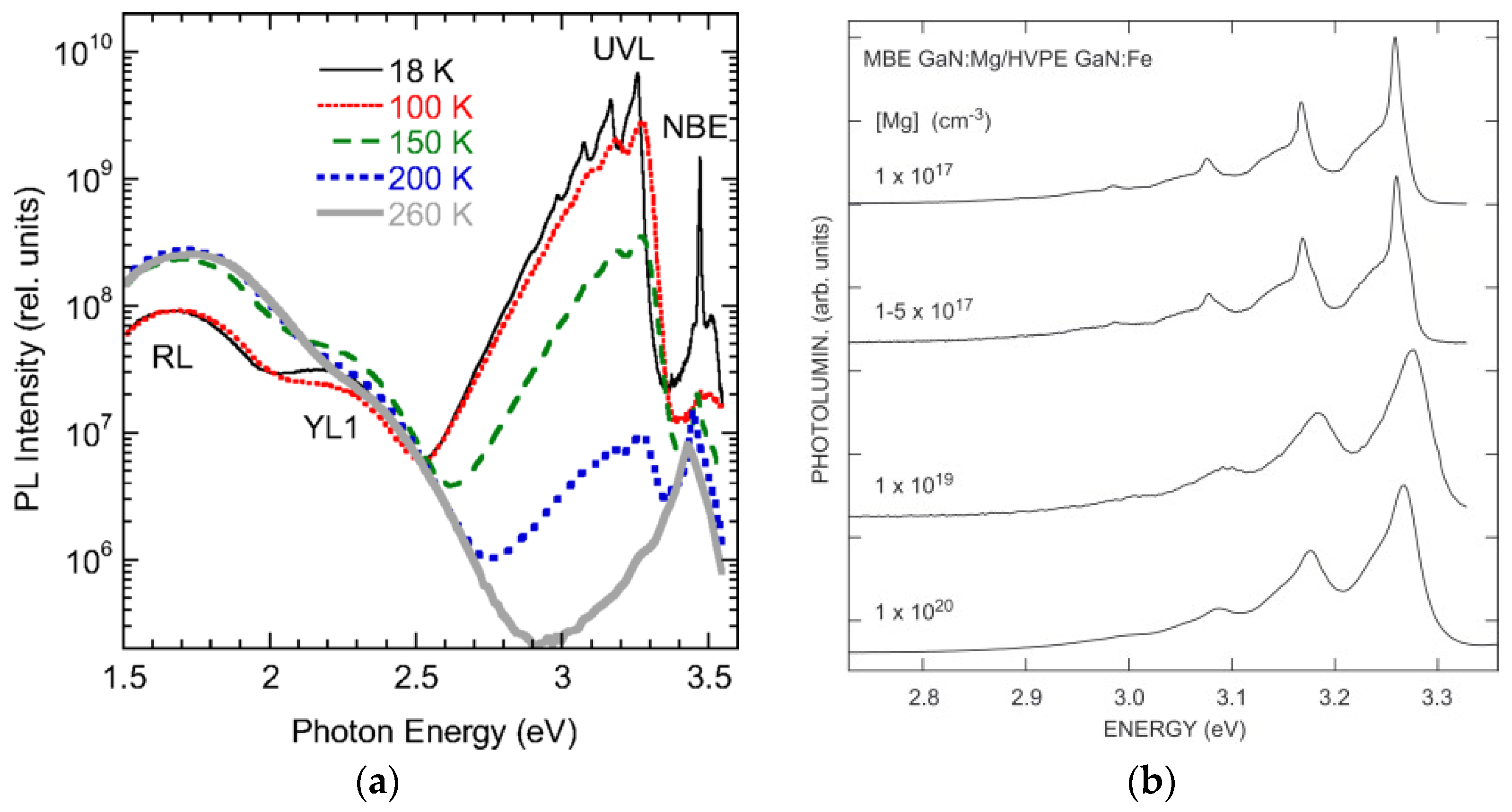
3.5. Ultraviolet Luminescence Band (UVL)
3.6. Role of VGa in GaN Luminescence
4. Luminescence from Intentionally Introduced Defects
4.1. Carbon-Related Defects (YL1, BLC, BL2, RLC)
4.1.1. PL from the −/0 and 0/+ States of CN (YL1 and BLC)
4.1.2. PL from the CN and CNHi (YL1 and BL2)
4.1.3. RLC Band in C-Doped GaN
4.1.4. Other Carbon-Related Complexes
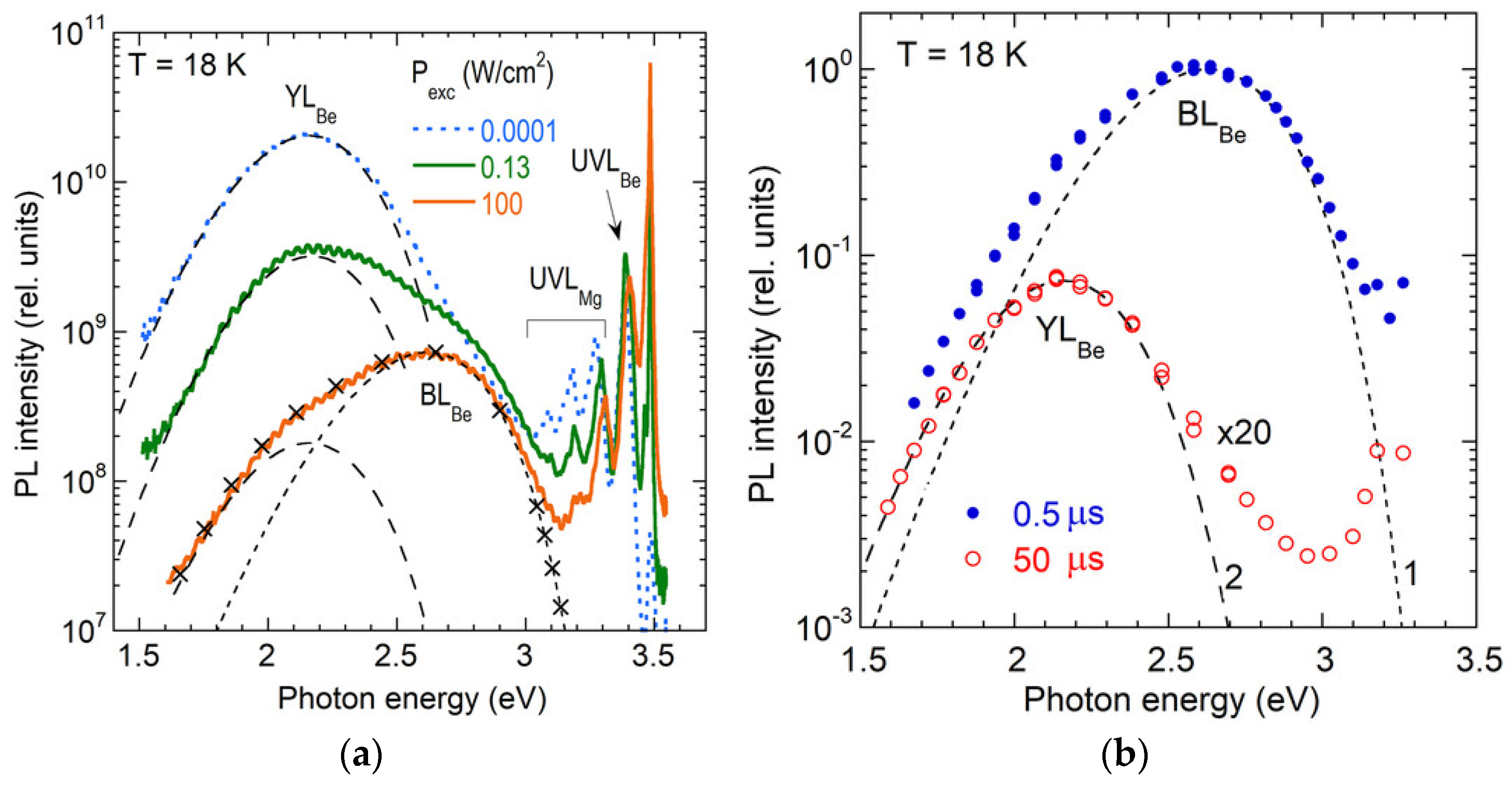
4.2. Beryllium-Related Defects (YLBe, UVLBe3, UVLBe, RLBe, BLBe, GLBe)
4.2.1. Historical Overview
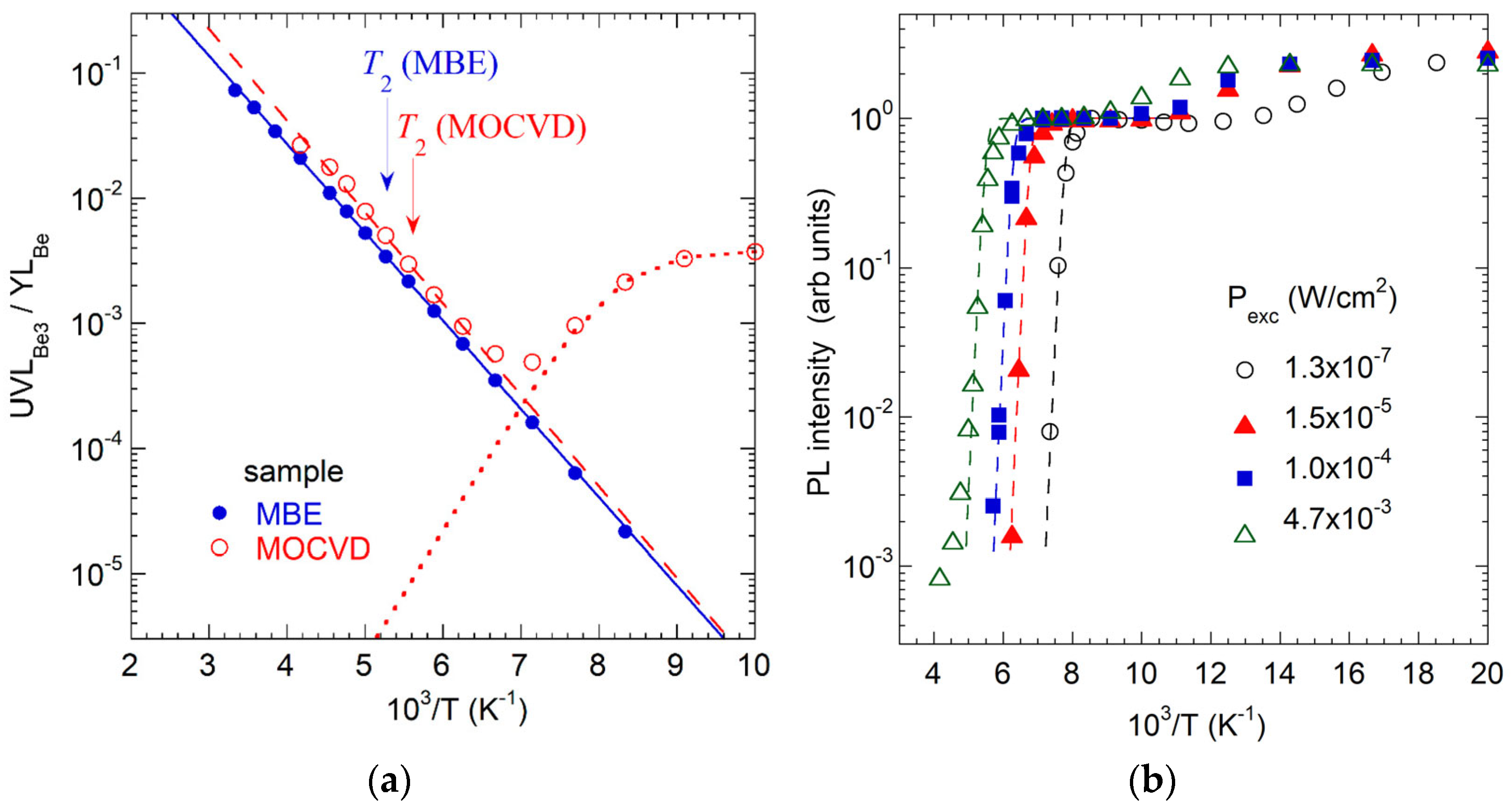
4.2.2. Three States of Isolated BeGa (YLBe1, YLBe2, UVLBe3)
4.2.3. Shallowest Acceptor in GaN (UVLBe)
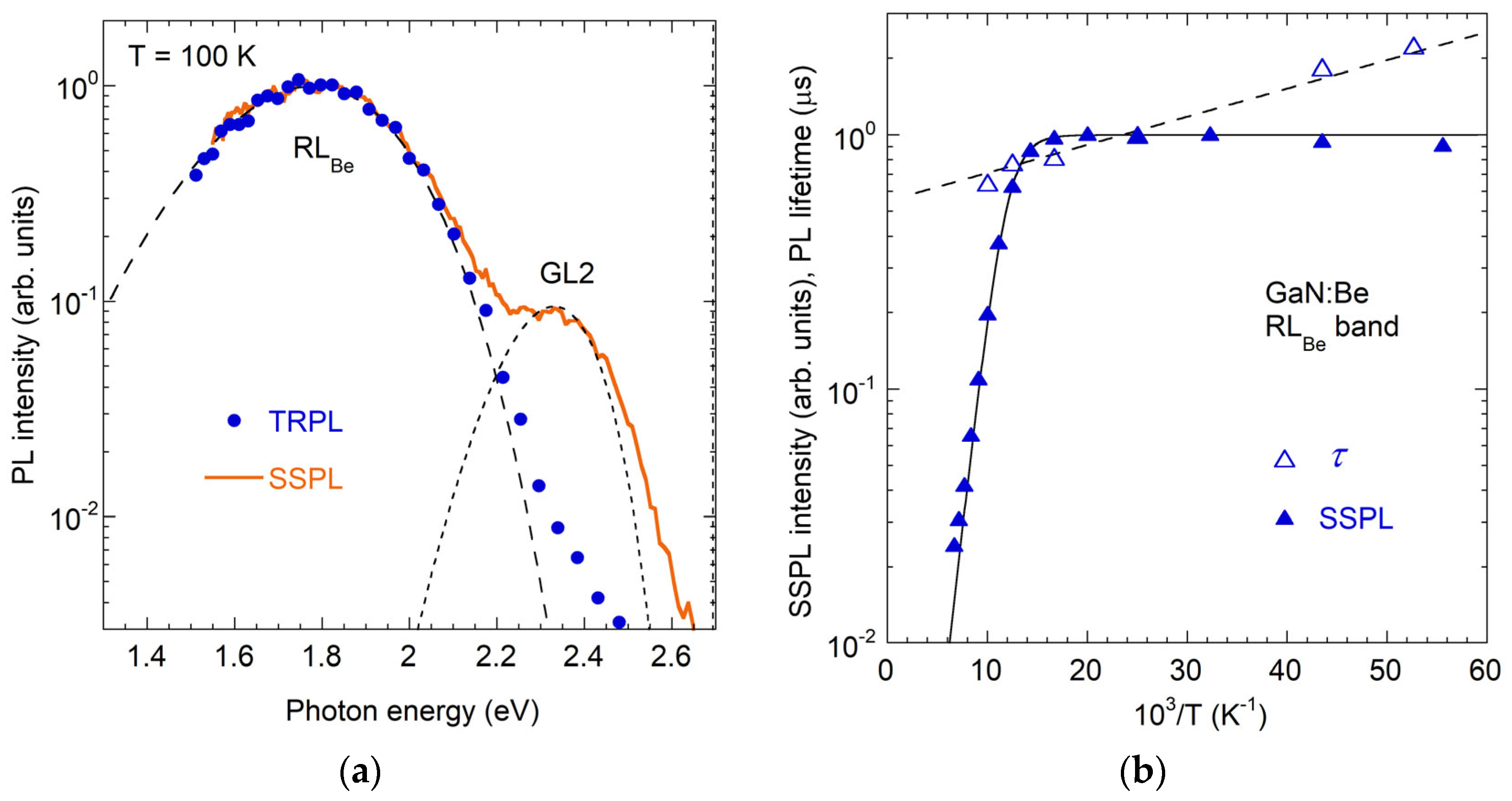
4.2.4. BeGaVN-Related RLBe Band
4.2.5. Deep Donor PL (BLBe)
4.2.6. Other Be-Related Defects
4.3. Magnesium-Related Defects (UVLMg, BLMg, RLMg)
4.3.1. Historical Overview
4.3.2. Shallow or Dual-Nature Acceptor?
4.3.3. BLMg Band in Heavily Doped GaN:Mg
4.3.4. Giant Shifts in PL Bands in GaN:Mg
4.3.5. MgGaVN-Related RLMg Band
4.4. Zinc (BLZn)
4.4.1. BLZn Band in Zn-Doped GaN
4.4.2. Tunable and Abrupt Quenching
4.4.3. Two-Step Quenching
4.4.4. Superlinear Excitation Intensity Dependence
4.4.5. Other PL Bands in Zn-Doped GaN
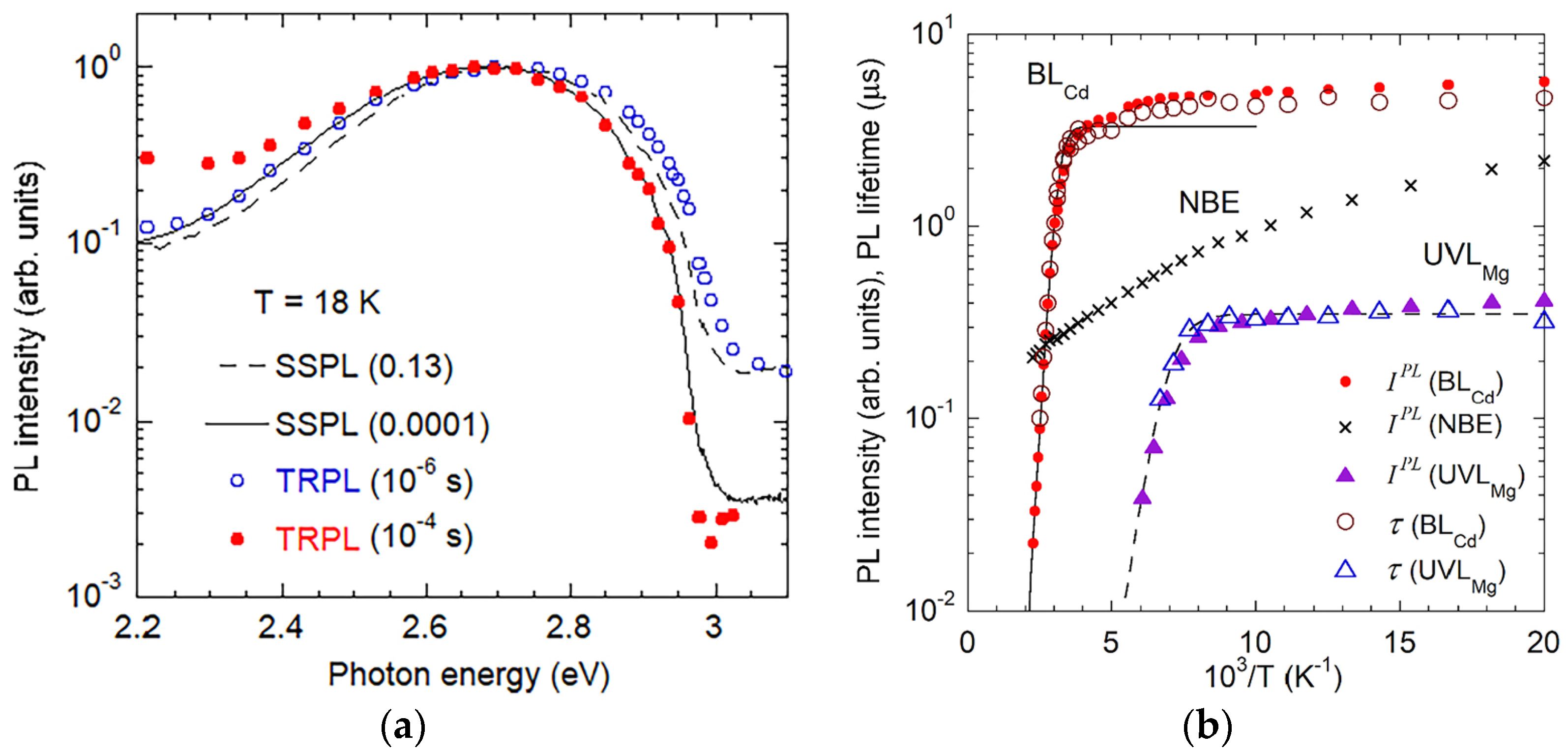
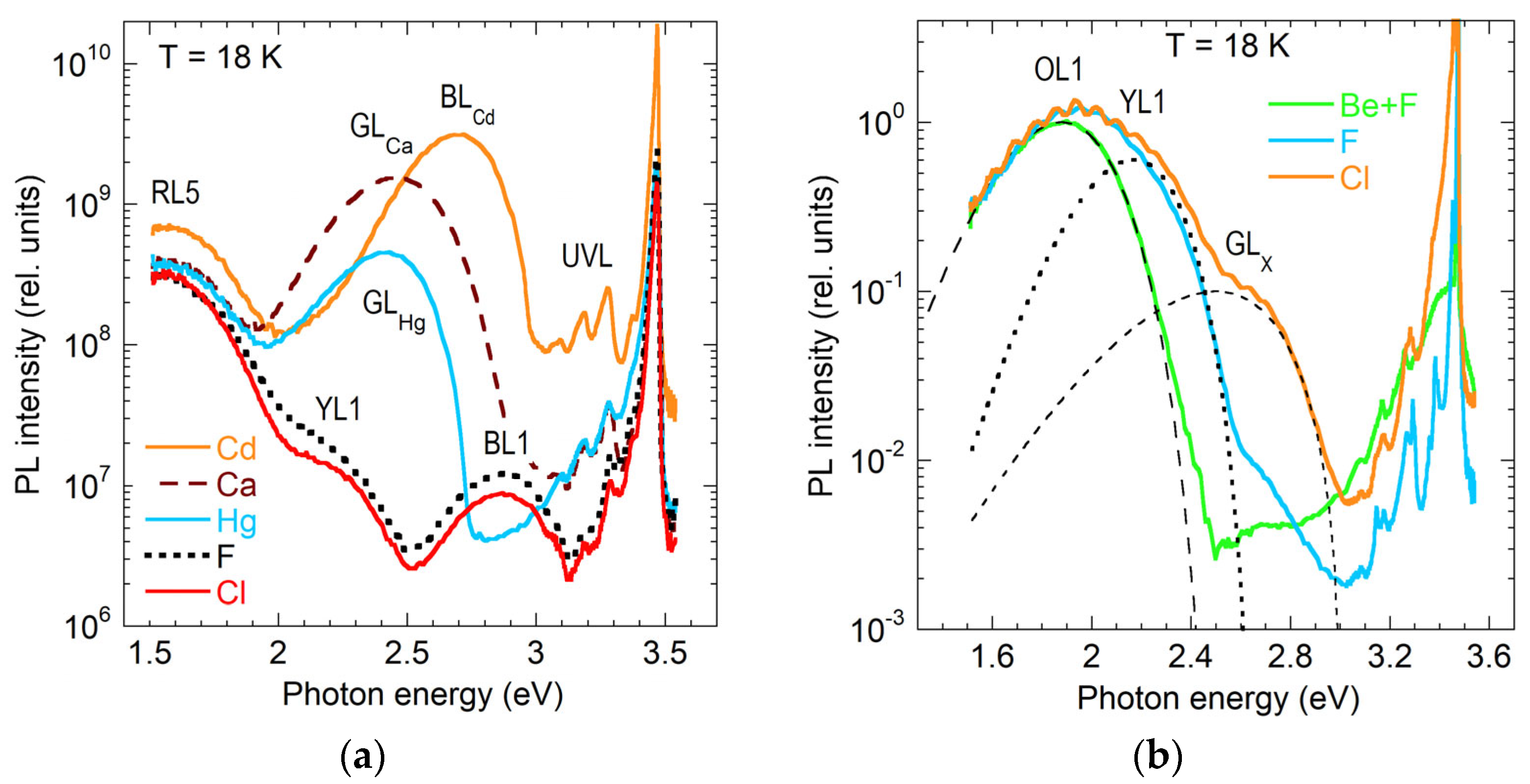
4.5. Cadmium (BLCd)
4.6. Calcium (GLCa, RLCa)
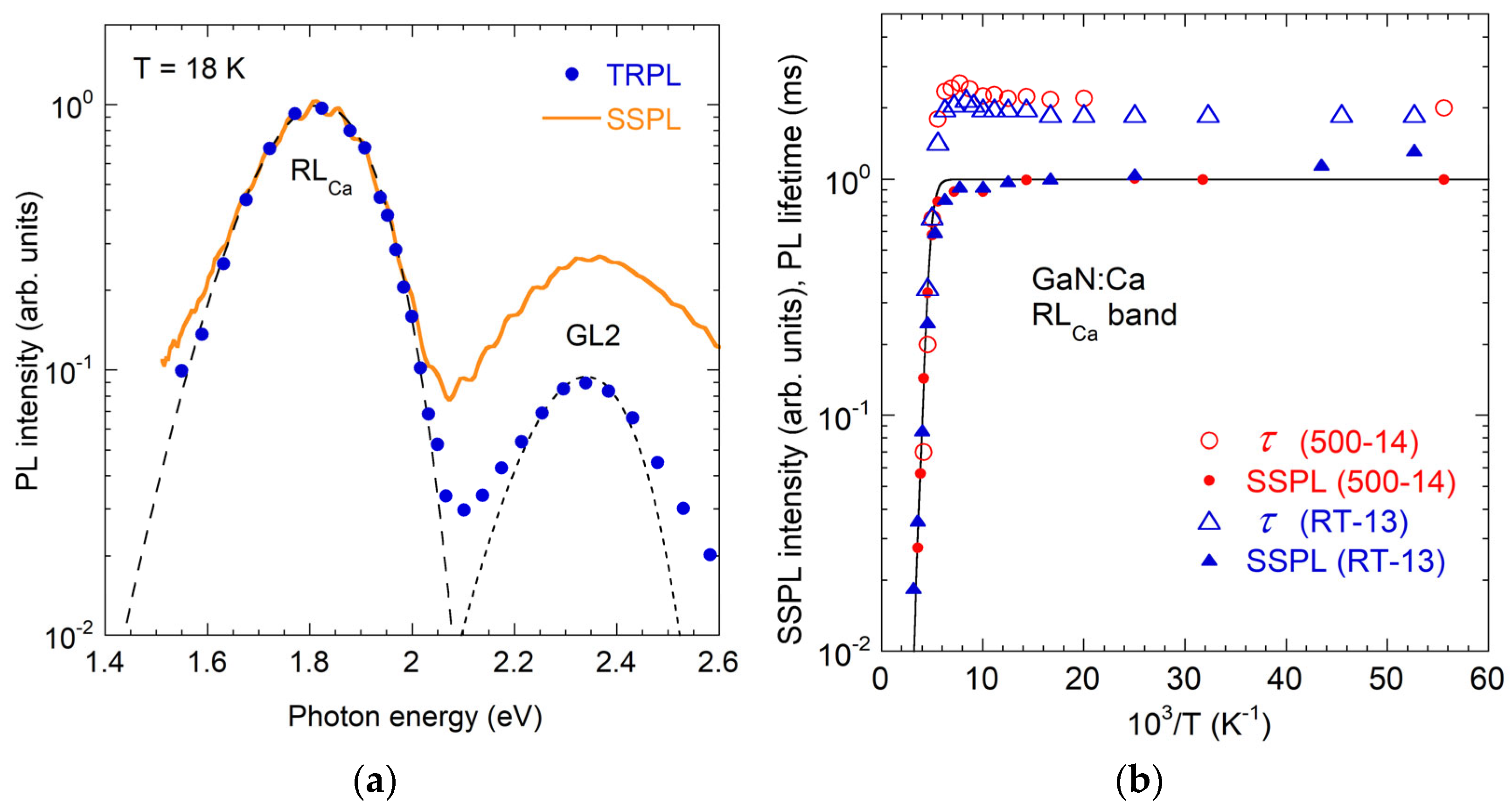
4.6.1. CaGa-Related GLCa Band
4.6.2. GLCa Band in Undoped GaN
4.6.3. CaGaVN-Related RLCa Band
4.7. Mercury (GLHg)
4.8. PL from Other Defects
4.8.1. Isoelectronic Impurities
4.8.2. PL from Implantation Damage
5. Advances in Defect-Related Photoluminescence in GaN Since 2005
5.1. PL Bands in Undoped GaN
5.2. Mechanisms of PL Quenching
5.3. Radiative and Nonradiative Recombination
5.3.1. Internal Quantum Efficiency
5.3.2. Nonradiative Recombination
5.3.3. Surface Effects on PL
5.4. Electronic Structure
5.4.1. Multi-Charged Defects
5.4.2. Dual-Nature Defects
5.4.3. Excited States
5.5. Identification of Defects
5.5.1. Conventional Approaches
5.5.2. Identification from Radioactive Isotopes
5.5.3. Confidence Levels
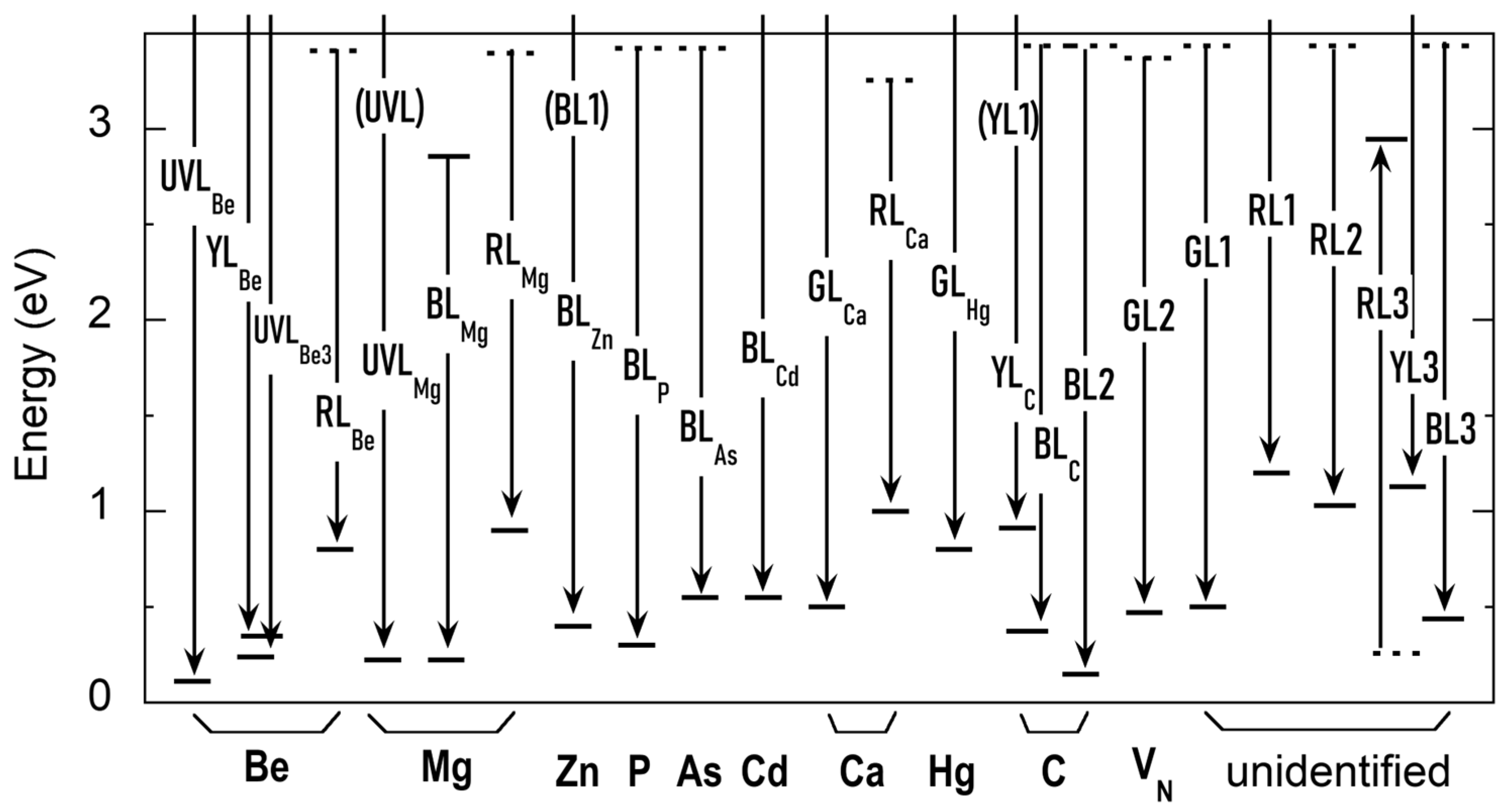
- High Confidence (90–99%): YL1 and BLC (CN), UVL or UVLMg (MgGa), BL1 or BLZn (ZnGa), YLBe and UVLBe3 (BeGa), BL2 (CNHi), BLCa or AL (CaGa), BLCd (CdGa), GLHg (HgGa).
- Moderate Confidence (50–80%): GL2 (+/2+ level of VN), RLMg (+/0 level of MgGaVN), RLCa (+/0 level of CaGaVN), RLBe (+/0 level of BeGaVN), BLMg (Deep DAP), BLAs (AsN), BLP (PN), UVLBe (BeGaONBeGa). The VGa, VGaON, VGaHi, BeGaON, CNON, and CNSiGa defects do not contribute to PL, at least at ħω > 1.5 eV.
- Low Confidence (20–40%): YL2, OL3, and RL4 (VGaxONyH donors with x, y = 1,2), RLC (tri-carbon complex), BLBe (0/+ level of BeGa).
- Speculative (<10%): RL3, YL3, and BL3 (FeGa or FeGa-containing complex), RL1 and GL1 (Cl), RL2 (AVN, with A being an acceptor other than Be, Mg, or Ca), GLBe (Be-containing complex), RL5 (unknown defect from implantation damage), OL1 (F or implantation damage-related defects).
5.6. Advances in First-Principles Calculations
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AL | Aquamarine luminescence |
| AT | Ammonothermal |
| BL | Blue luminescence |
| CL | Cathodoluminescence |
| DAP | Donor-acceptor pair |
| DFT | Density functional theory |
| DLOS | Deep level optical spectroscopy |
| DLTS | Deep level transient spectroscopy |
| EQE | External quantum efficiency |
| EPR | Electron paramagnetic resonance |
| FTIR | Fourier transform infrared |
| FWHM | Full width at half maximum |
| GL | Green luminescence |
| HSE | Heyd-Scuseria-Ernzerhof |
| HNPS | High nitrogen pressure solution |
| HVPE | Hydride vapor phase epitaxy |
| IQE | Internal quantum efficiency |
| LED | Light-emitting diode |
| LEEBI | Low energy electron beam irradiation |
| LO | Longitudinal optical |
| MBE | Molecular beam epitaxy |
| MOCVD | Metalorganic chemical vapor deposition |
| NBE | Near-band-edge |
| NDF | Neutral density filter |
| ODMR | Optically detected magnetic resonance |
| OL | Orange luminescence |
| PAS | Positron annihilation spectroscopy |
| PL | Photoluminescence |
| PLE | Photoluminescence excitation |
| PMT | Photomultiplier tube |
| RL | Red luminescence |
| SD-SA | Shallow donor-shallow acceptor |
| SI | Semi-insulating |
| SIMS | Secondary ion mass spectrometry |
| SSPL | Steady-state photoluminescence |
| TAAM | Trap-assisted Auger-Meitner |
| TAQ | Tunable and abrupt quenching |
| TRPL | Time-resolved photoluminescence |
| UV | Ultraviolet |
| UVL | Ultraviolet luminescence |
| VBM | Valence band maximum |
| YL | Yellow luminescence |
| ZPL | Zero-phonon line |
References
- Nakamura, S.; Fosol, G. The Blue Laser Diode; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Morkoç, H. Handbook of Nitride Semiconductors and Devices; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Mishra, U.K.; Shen, L.; Kazior, T.E.; Wu, Y. GaN-Based RF Power Devices and Amplifiers. Proc. IEEE 2008, 96, 287–305. [Google Scholar] [CrossRef]
- Nakamura, S.; Krames, M.R. History of Gallium–Nitride-Based Light-Emitting Diodes for Illumination. Proc. IEEE 2013, 101, 2211–2220. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Point defects in GaN. In Semiconductors and Semimetals: Defects in Semiconductors; Jagadish, C., Privitera, V., Romano, L., Eds.; Academic Press: Burlington, UK, 2015; Volume 91, pp. 315–367. [Google Scholar]
- Monemar, B.; Paskov, P.P.; Bergman, J.P.; Toropov, A.A.; Shubina, T.V. Recent developments in the III-nitride materials. Phys. Status Sol. B 2007, 244, 1759–1768. [Google Scholar] [CrossRef]
- Kornitzer, K.; Ebner, T.; Thonke, K.; Sauer, R.; Kirchner, C.; Schwegler, V.; Kamp, M.; Leszczynski, M.; Grzegory, I.; Porowski, S. Photoluminescence and reflectance spectroscopy of excitonic transitions in high-quality homoepitaxial GaN films. Phys. Rev. B 1999, 60, 1471–1473. [Google Scholar] [CrossRef]
- Monemar, B.; Paskov, P.P.; Bergman, J.P.; Toropov, A.A.; Shubina, T.V.; Malinauskas, T.; Usui, A. Recombination of free and bound excitons in GaN. Phys. Stat. Sol. B 2008, 245, 1723–1740. [Google Scholar] [CrossRef]
- Freitas, J.A., Jr.; Culbertson, J.C.; Glaser, E.R. Characterization of Defects in GaN: Optical and Magnetic Resonance Techniques. Crystals 2022, 12, 1294. [Google Scholar] [CrossRef]
- Callsen, G.; Kure, T.; Wagner, M.R.; Butte, R.; Grandjean, N. Excited states of neutral donor bound excitons in GaN. J. Appl. Phys. 2018, 123, 215702. [Google Scholar] [CrossRef]
- Freitas, J.A., Jr.; Moore, W.J.; Shanabrook, B.V.; Braga, G.C.B.; Koleske, D.D.; Lee, S.K.; Park, S.S.; Han, J.Y. Shallow donors in GaN. Phys. Stat. Sol. B 2003, 240, 330–336. [Google Scholar] [CrossRef]
- Wysmolek, A.; Stepniewski, R.; Potemski, M. Magneto-spectroscopy of donor-bound excitons in GaN. Phys. B 2007, 401–402, 441–446. [Google Scholar] [CrossRef]
- Ishitani, Y.; Takeuchi, K.; Oizumi, N.; Sakamoto, H.; Ma, B.; Morita, K.; Miyake, H.; Hiramatsu, K. Excitation and deexcitation dynamics of excitons in a GaN film based on the analysis of radiation from high-order states. J. Phys. D Appl. Phys. 2016, 49, 245102. [Google Scholar] [CrossRef]
- Chichibu, S.F.; Uedono, A.; Kojima, K.; Ikeda, H.; Fujito, K.; Takashima, S.; Edo, M.; Ueno, K.; Ishibashi, S. The origins and properties of intrinsic nonradiative recombination centers in wide bandgap GaN and AlGaN. J. Appl. Phys. 2018, 123, 161413. [Google Scholar] [CrossRef]
- Rodina, A.V.; Dietrich, M.; Göldner, A.; Eckey, L.; Hoffmann, A.; Efros, A.L.; Rosen, M.; Meyer, B.K. Free excitons in wurtzite GaN. Phys. Rev. B 2001, 64, 115204. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Morkoç, H. Luminescence properties of defects in GaN. J. Appl. Phys. 2005, 97, 061301. [Google Scholar] [CrossRef]
- Van de Walle, C.G.; Neugebauer, J. First-principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 2004, 95, 3851–3879. [Google Scholar] [CrossRef]
- Boguslawski, P.; Bernholc, J. Doping properties of C, Si, and Ge impurities in GaN and AlN. Phys. Rev. B 1997, 56, 9496–9505. [Google Scholar] [CrossRef]
- Ramos, L.E.; Furthmüller, J.; Leite, J.R.; Scolfaro, L.M.; Bechstedt, F. Carbon-Based Defects in GaN: Doping Behavior. Phys. Stat. Sol. B 2002, 234, 864–867. [Google Scholar] [CrossRef]
- Eberlein, T.A.G.; Jones, R.; Öberg, S.; Briddon, P.R. Shallow acceptors in GaN. Appl. Phys. Lett. 2007, 91, 132105. [Google Scholar] [CrossRef]
- Wright, A.F. Substitutional and interstitial carbon in wurtzite GaN. J. Appl. Phys. 2002, 92, 2575–2585. [Google Scholar] [CrossRef]
- Neugebauer, J.; Van de Walle, C.G. Gallium vacancies and the yellow luminescence in GaN. Appl. Phys. Lett. 1996, 69, 503–505. [Google Scholar] [CrossRef]
- Fischer, S.; Wetzel, C.; Haller, E.E.; Meyer, B.K. On p-type doping in GaN-acceptor binding energies. Appl. Phys. Lett. 1995, 67, 1298–1300. [Google Scholar] [CrossRef]
- Lyons, J.L.; Janotti, A.; Van de Walle, C.G. Carbon impurities and the yellow luminescence in GaN. Appl. Phys. Lett. 2010, 97, 152108. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Vorobiov, M.; Demchenko, D.O.; Özgür, Ü.; Morkoç, H.; Lesnik, A.; Hoffmann, M.P.; Hörich, F.; Dadgar, A.; Strittmatter, A. Two charge states of the CN acceptor in GaN: Evidence from photoluminescence. Phys. Rev. B 2018, 98, 125207. [Google Scholar] [CrossRef]
- Narita, T.; Tomita, K.; Tokuda, Y.; Kogiso, T.; Horita, M.; Kachi, T. The origin of carbon-related carrier compensation in p-type GaN layers grown by MOVPE. J. Appl. Phys. 2018, 124, 215701. [Google Scholar] [CrossRef]
- Zimmermann, F.; Beyer, J.; Röder, C.; Beyer, F.C.; Richter, E.; Irmscher, K.; Heitmann, J. Current Status of Carbon-Related Luminescence in GaN. Phys. Stat. Sol. A 2021, 218, 2100235. [Google Scholar] [CrossRef]
- Saarinen, K.; Laine, T.; Kuisma, S.; Nissilä, J.; Hautojärvi, P.; Dobrzynski, L.; Baranowski, J.M.; Pakula, K.; Stepniewski, R.; Wojdak, M.; et al. Observation of Native Ga Vacancies in GaN by Positron Annihilation. Phys. Rev. Lett. 1997, 79, 3030–3033. [Google Scholar] [CrossRef]
- Lyons, J.L.; Alkauskas, A.; Janotti, A.; Van de Walle, C.G. First-principles theory of acceptors in nitride semiconductors. Phys. Stat. Sol. B 2015, 252, 900–908. [Google Scholar] [CrossRef]
- Diallo, I.C.; Demchenko, D.O. Native Point Defects in GaN: A Hybrid-Functional Study. Phys. Rev. Appl. 2016, 6, 064002. [Google Scholar] [CrossRef]
- Edwards, A.H.; Schultz, P.A.; Dobzynski, R.M. Electronic structure of intrinsic defects in c-gallium nitride: Density functional theory study without the jellium approximation. Phys. Rev. B 2022, 105, 235110. [Google Scholar] [CrossRef]
- Miceli, G.; Pasquerello, A. Energetics of native point defects in GaN: A density-functional study. Microelectron. Eng. 2015, 147, 51–54. [Google Scholar] [CrossRef]
- Zimmermann, F.; Beyer, J.; Beyer, F.C.; Gärtner, G.; Gamov, I.; Irmscher, K.; Richter, E.; Weyers, M.; Heitmann, J. A carbon-doping related luminescence band in GaN revealed by below bandgap excitation. J. Appl. Phys. 2021, 130, 055703. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Photoluminescence from defects in GaN. In Gallium Nitride Materials and Devices XVIII; Fujioka, H., Morkoç, H., Schwarz, U., Eds.; Proceedings SPIE: San Francisco, CA, USA, 2023; Volume 12421, p. 1242109. [Google Scholar]
- Reshchikov, M.A. Photoluminescence from Vacancy-Containing Defects in GaN. Phys. Stat. Sol. A 2023, 220, 2200402. [Google Scholar] [CrossRef]
- Vorobiov, M.; Andrieiev, O.; Demchenko, D.O.; Reshchikov, M.A. Nitrogen vacancy-acceptor complexes in GaN. J. Appl. Phys. 2024, 135, 155701. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Red luminescence band in undoped GaN. J. Lumin. 2025, 286, 121370. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Sayeed, R.M.; Özgür, Ü.; Demchenko, D.O.; McNamara, J.D.; Prozheeva, V.; Tuomisto, F.; Helava, H.; Usikov, A.; Makarov, Y. Unusual properties of the RY3 center in GaN. Phys. Rev. B 2019, 100, 045204. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Demchenko, D.O.; Ye, D.; Andrieiev, O.; Vorobiov, M.; Grabianska, K.; Zajac, M.; Nita, P.; Iwinska, M.; Bockowski, M.; et al. The effect of annealing on photoluminescence from defects in ammonothermal GaN. J. Appl. Phys. 2022, 131, 035704. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; McNamara, J.D.; Zhang, F.; Monavarian, M.; Usikov, A.; Helava, H.; Makarov, Y.; Morkoç, H. Zero-phonon line and fine structure of the yellow luminescence band in GaN. Phys. Rev. B 2016, 94, 035201. [Google Scholar] [CrossRef]
- Reshchikov, M.A. On the Origin of the Yellow Luminescence Band in GaN. Phys. Stat. Sol. B 2023, 260, 2200488. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Vorobiov, M.; Grabianska, K.; Zajac, M.; Iwinska, M.; Bockowski, M. Defect-related photoluminescence from ammono GaN. J. Appl. Phys. 2021, 129, 095703. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Usikov, A.; Helava, H.; Makarov, Y. Fine structure of the red luminescence band in GaN. Appl. Phys. Lett. 2014, 104, 032103. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; McNamara, J.D.; Helava, H.; Usikov, A.; Makarov, Y. Two yellow luminescence bands in GaN. Sci. Rep. 2018, 8, 8091. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Vorobiov, M.; Andrieiev, O.; Demchenko, D.O.; McEwen, B.; Shahedipour-Sandvik, F. Dual Nature of the BeGa Acceptor in GaN: Evidence from Photoluminescence. Phys. Rev. B 2023, 108, 075202. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Bockowski, M. The Origin of the Yellow Luminescence Band in Bulk Be-doped GaN. Solids 2024, 5, 29–44. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Demchenko, D.O.; McNamara, J.D.; Fernández-Garrido, S.; Calarco, R. Green luminescence in Mg-doped GaN. Phys. Rev. B 2014, 90, 035207. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Andrieiev, O.; Vorobiov, M.; Demchenko, D.O.; McEwen, B.; Shahedipour-Sandvik, F. Photoluminescence from CdGa and HgGa acceptors in GaN. J. Appl. Phys. 2024, 135, 155706. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Demchenko, D.O.; Vorobiov, M.; Andrieiev, O.; McEwen, B.; Shahedipour-Sandvik, F.; Sierakowski, K.; Jaroszynski, P.; Bockowski, M. Photoluminescence related to Ca in GaN. Phys. Rev. B 2022, 106, 035206. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Shahedipour, F.; Korotkov, R.Y.; Ulmer, M.P.; Wessels, B.W. Photoluminescence band near 2.9 eV in undoped GaN epitaxial layers. J. Appl. Phys. 2000, 87, 3351–3354. [Google Scholar] [CrossRef]
- Demchenko, D.O.; Reshchikov, M.A. Blue luminescence and Zn acceptor in GaN. Phys. Rev. B 2013, 88, 115204. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Kvasov, A.A.; Bishop, M.F.; McMullen, T.; Usikov, A.; Soukhoveev, V.; Dmitriev, V.A. Tunable and abrupt thermal quenching of photoluminescence in high-resistivity Zn-doped GaN. Phys. Rev. B 2011, 84, 075212. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Foussekis, M.A.; McNamara, J.D.; Behrends, A.; Bakin, A.; Waag, A. Determination of the absolute internal quantum efficiency of photoluminescence in GaN co-doped with Zn and Si. J. Appl. Phys. 2012, 111, 073106. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Giant shifts of photoluminescence bands in GaN. J. Appl. Phys. 2020, 127, 055701. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Andrieiev, O.; Vorobiov, M.; McEwen, B.; Shahedipour-Sandvik, F.; Ye, D.; Demchenko, D.O. Stability of the CNHi complex and the blue luminescence band in GaN. Phys. Stat. Sol. B 2021, 258, 2100392. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Fine structure of another blue luminescence band in undoped GaN. Appl. Phys. Lett. 2019, 115, 262102. [Google Scholar] [CrossRef]
- Chen, L.; Skromme, B.J. Spectroscopic Characterization of Ion Implanted GaN. MRS Online Proc. Libr. (OPL) 2003, 743, L11.35. [Google Scholar] [CrossRef]
- Ogino, T.; Aoki, M. Photoluminescence in P-doped GaN. Jpn. J. Appl. Phys. 1979, 18, 1049–1052. [Google Scholar] [CrossRef]
- Lagerstedt, O.; Monemar, B. Luminescence in epitaxial GaN:Cd. J. Appl. Phys. 1974, 45, 2266–2271. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Fine Structure of the Carbon-Related Blue Luminescence Band in GaN. Solids 2022, 3, 231–236. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; McEwen, B.; Shahedipour-Sandvik, F. Photoluminescence from Defects in Be-Doped GaN. Phys. Stat. Sol. B 2025, 202400656, Early View. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Ghimire, P.; Demchenko, D.O. Magnesium acceptor in gallium nitride: I. Photoluminescence from Mg-doped GaN. Phys. Rev. B 2018, 97, 20520. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Yi, G.-C.; Wessels, B.W. Behavior of 2.8-and 3.2-eV photoluminescence bands in Mg-doped GaN at different temperatures and excitation densities. Phys. Rev. B 1999, 59, 13176–13183. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Demchenko, D.O.; McEwen, B.; Shahedipour-Sandvik, F. Identity of the shallowest acceptor in GaN. Phys. Rev. B 2025, 111, 045202. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; McNamara, J.D.; Toporkov, M.; Avrutin, V.; Morkoç, H.; Usikov, A.; Helava, H.; Makarov, Y. Determination of the electron-capture coefficients and the concentration of free electrons in GaN from photoluminescence. Sci. Rep. 2016, 6, 37511. [Google Scholar] [CrossRef] [PubMed]
- Reshchikov, M.A. Measurement and analysis of photoluminescence in GaN. J. Appl. Phys. 2021, 129, 121101. [Google Scholar] [CrossRef]
- Kojima, K.; Ohtomo, T.; Ikemura, K.-I.; Yamazaki, Y.; Saito, M.; Ikeda, H.; Fujito, K.; Chichibu, S.F. Determination of absolute value of quantum efficiency of radiation in high quality GaN single crystals using an integrating sphere. J. Appl. Phys. 2016, 120, 015704. [Google Scholar] [CrossRef]
- Kojima, K.; Ikeda, H.; Fujito, K.; Chichibu, S.F. Demonstration of omnidirectional photoluminescence (ODPL) spectroscopy for precise determination of internal quantum efficiency of radiation in GaN single crystals. Appl. Phys. Lett. 2017, 111, 032111. [Google Scholar] [CrossRef]
- Kojima, K.; Ikemura, K.; Chichibu, S.F. Quantification of the quantum efficiency of radiation of a freestanding GaN crystal placed outside an integrating sphere. Appl. Phys. Express 2019, 12, 062010. [Google Scholar] [CrossRef]
- Kojima, K.; Ikemura, K.; Chichibu, S.F. Temperature dependence of quantum efficiency of radiation for the near-band-edge emission of GaN crystals quantified by omnidirectional photoluminescence spectroscopy. Appl. Phys. Express 2020, 13, 105504. [Google Scholar] [CrossRef]
- Kojima, K.; Chichibu, S.F. Correlation between the internal quantum efficiency and photoluminescence lifetime of the near-band-edge emission in a ZnO single crystal grown by the hydrothermal method. Appl. Phys. Express 2020, 13, 121005. [Google Scholar] [CrossRef]
- Shockley, W.; Read, J.W.T. Statistics of the recombinations of holes and electrons. Phys. Rev. 1952, 87, 835–842. [Google Scholar] [CrossRef]
- Hall, R.N. Germanium rectifier characteristics. Phys. Rev. 1951, 83, 228. [Google Scholar]
- Reshchikov, M.A. Temperature dependence of defect-related photoluminescence in III-V and II-VI semiconductors. J. Appl. Phys. 2014, 115, 012010. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Mechanisms of Thermal Quenching of Defect-Related Luminescence in Semiconductors. Phys. Stat. Sol. A 2020, 218, 2000101. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Korotkov, R.Y. Analysis of the temperature and excitation intensity dependencies of photoluminescence in undoped GaN films. Phys. Rev. B 2001, 64, 115205. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Time-resolved photoluminescence from defects in GaN. J. Appl. Phys. 2014, 115, 103503. [Google Scholar] [CrossRef]
- Korotkov, R.Y.; Reshchikov, M.A.; Wessels, B.W. Acceptors in undoped GaN studied by transient photoluminescence. Phys. B 2003, 325, 1–7. [Google Scholar] [CrossRef]
- Klasens, H.A. The temperature-dependence of the fluorescence of photoconductors. J. Phys. Chem. Solids 1959, 9, 185–197. [Google Scholar] [CrossRef]
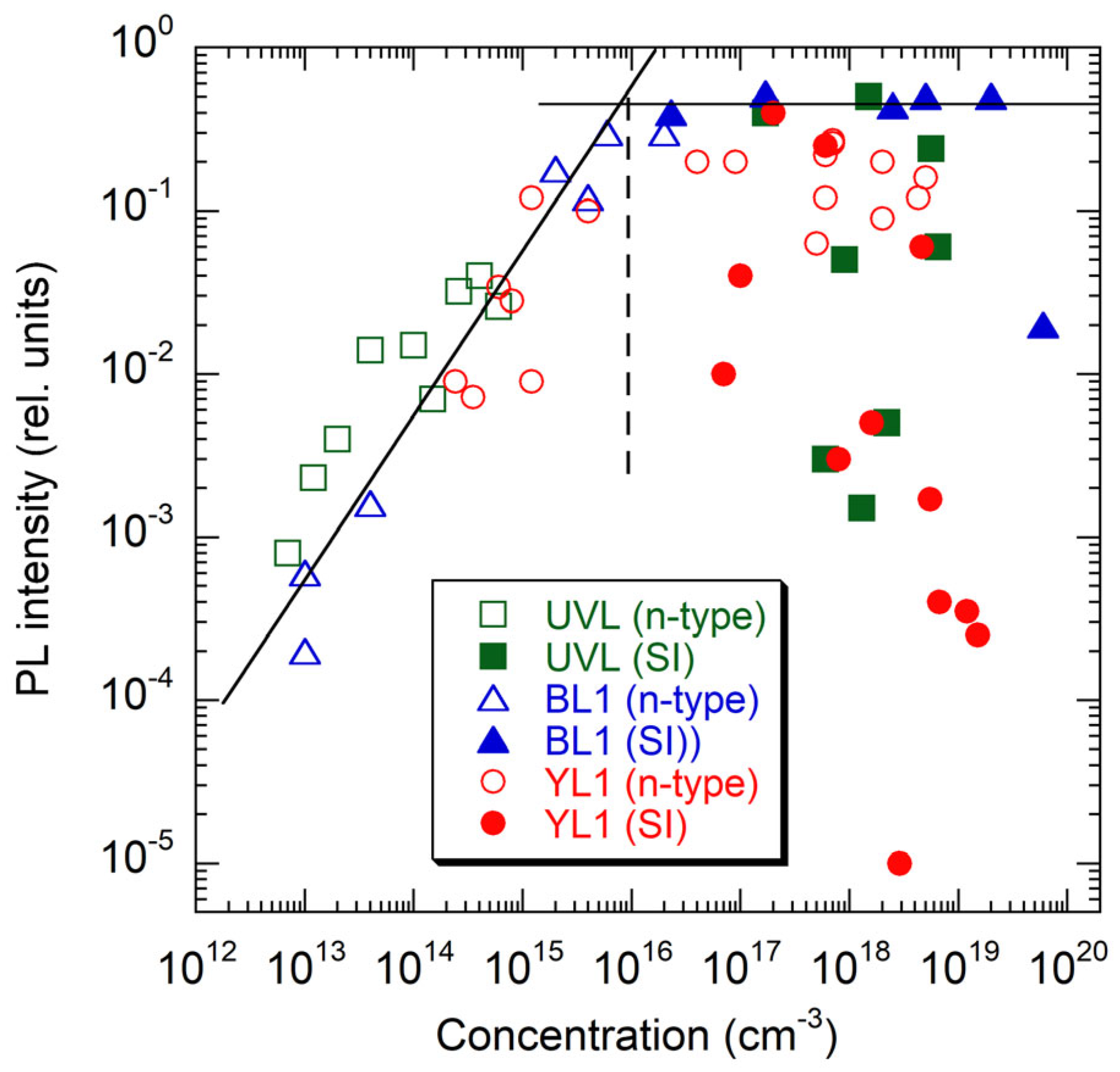
- Reshchikov, M.A. Determination of acceptor concentration in GaN from photoluminescence. Appl. Phys. Lett. 2006, 88, 202104. [Google Scholar]
- Reshchikov, M.A. Internal Quantum Efficiency of Photoluminescence in Wide-Bandgap Semiconductors. In Photoluminescence: Applications, Types and Efficacy; Case, M.A., Stout, B.C., Eds.; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2012; pp. 53–120. ISBN 978-1-61942-426-5. [Google Scholar]
- Muth, J.F.; Lee, J.H.; Shmagin, I.K.; Kolbas, R.M.; Casey, H.C., Jr.; Keller, B.P.; Mishra, U.K.; DenBaars, S.P. Absorption coefficient, energy gap, exciton binding energy, and recombination lifetime of GaN obtained from transmission measurement. Appl. Phys. Lett. 1997, 71, 2572–2574. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Usikov, A.; Helava, H.; Makarov, Y.; Prozheeva, V.; Makkonen, I.; Tuomisto, F.; Leach, J.H.; Udwary, K. Evaluation of the concentration of point defects in GaN. Sci. Rep. 2017, 7, 9297. [Google Scholar] [CrossRef] [PubMed]
- Williams, F. Donor-acceptor pairs in semiconductors. Phys. Stat. Sol. 1968, 25, 493–512. [Google Scholar] [CrossRef]
- Thomas, D.G.; Hopfield, J.J.; Augustyniak, W.M. Kinetics of radiative recombination at randomly distributed donors and acceptors. Phys. Rev. 1965, 140, A202–A220. [Google Scholar] [CrossRef]
- Ogino, T.; Aoki, M. Mechanism of Yellow Luminescence in GaN. Jpn. J. Appl. Phys. 1980, 19, 2395–2405. [Google Scholar] [CrossRef]
- Pankove, J.I.; Hutchby, J.A. Photoluminescence of ion-implanted GaN. J. Appl. Phys. 1976, 47, 5387–5390. [Google Scholar] [CrossRef]
- Kucheyev, S.O.; Toth, M.; Phillips, M.R.; Williams, J.S.; Jagadish, C.; Li, G. Chemical origin of the yellow luminescence in GaN. J. Appl. Phys. 2002, 91, 5867–5874. [Google Scholar] [CrossRef]
- Armitage, R.; Hong, W.; Yang, Q.; Feick, H.; Gebauer, J.; Weber, E.R.; Hautakangas, S.; Saarinen, K. Contributions from gallium vacancies and carbon-related defects to the “yellow luminescence” in GaN. Appl. Phys. Lett. 2003, 82, 3457–3459. [Google Scholar] [CrossRef]
- You, W.; Zhang, X.D.; Zhang, L.M.; Yang, Z.; Bian, H.; Ge, Q.; Guo, W.X.; Wang, W.X.; Liu, Z.M. Effects of different ions implantation on yellow luminescence from GaN. Phys. B 2008, 403, 2666–2670. [Google Scholar] [CrossRef]
- Xu, F.J.; Shen, B.; Lu, L.; Miao, Z.L.; Song, J.; Yang, Z.J.; Zhang, G.Y.; Hao, X.P.; Wang, B.Y.; Shen, X.Q.; et al. Different origins of the yellow luminescence in as-grown high-resistance GaN and unintentional-doped GaN films. J. Appl. Phys. 2010, 107, 023528. [Google Scholar] [CrossRef]
- Reurings, F.; Tuomisto, F. Interplay of Ga vacancies, C Impurities and Yellow Luminescence in GaN. In Gallium Nitride Materials and Devices II; Morkoç, H., Litton, C.W., Eds.; Proceedings SPIE: San Francisco, CA, USA, 2007; Volume 6473, p. 64730M. [Google Scholar]
- Reshchikov, M.A.; Morkoç, H.; Park, S.S.; Lee, K.Y. Photoluminescence study of deep-level defects in undoped GaN. Mat. Res. Soc. Symp. Proc. 2002, 693, 596–601. [Google Scholar] [CrossRef]
- Alkauskas, A.; McCluskey, M.; Van de Walle, C.G. Tutorial: Defects in semiconductors–Combining experiment and theory. J. Appl. Phys. 2016, 119, 181101. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Albarakati, N.M.; Monavarian, M.; Avrutin, V.; Morkoç, H. Thermal quenching of the yellow luminescence in GaN. J. Appl. Phys. 2018, 123, 161520. [Google Scholar] [CrossRef]
- Matsubara, M.; Bellotti, E. A first-principles study of carbon-related energy levels in GaN. I. Complexes formed by substitutional/imterstitial carbons and gallium/nitrogen vacancies. J. Appl. Phys. 2017, 121, 195701. [Google Scholar] [CrossRef]
- Deak, P.; Lorke, M.; Aradi, B.; Frauenheim, T. Carbon in GaN: Calculations with an optimized hybrid functional. Phys. Rev. B 2019, 99, 085206. [Google Scholar] [CrossRef]
- Christenson, S.G.; Xie, W.; Sun, Y.Y.; Zhang, S.B. Carbon as a source for yellow luminescence in GaN: Isolated CN defect or its complexes. J. Appl. Phys. 2015, 118, 135708. [Google Scholar] [CrossRef]
- Dreyer, C.E.; Alkauskas, A.; Lyons, J.L.; Van de Walle, C.G. Radiative capture rates at deep defects from electronic structure calculations. Phys. Rev. B 2020, 102, 085305. [Google Scholar] [CrossRef]
- Alkauskas, A.; Yan, Q.; Van de Walle, C.G. First-principles theory of nonradiative carrier capture via multiphonon emission. Phys. Rev. B 2014, 90, 075202. [Google Scholar] [CrossRef]
- Wickramaratne, D.; Dreyer, C.E.; Monserrat, B.; Shen, J.-X.; Lyons, J.L.; Alkauskas, A.; Van de Walle, C.G. Defect identification based on first-principles calculations for deep level transient spectroscopy. Appl. Phys. Lett. 2018, 113, 192106. [Google Scholar] [CrossRef]
- Alkauskas, A.; Lyons, J.L.; Steiauf, D.; Van de Walle, C.G. First-Principles Calculations of Luminescence Spectrum Line Shapes for Defects in Semiconductors: The Example of GaN and ZnO. Phys. Rev. Lett. 2012, 109, 267401. [Google Scholar] [CrossRef]
- Matsubara, M.; Bellotti, E. A first-principles study of carbon-related energy levels in GaN. II. Complexes formed by carbon and hydrogen, silicon or oxygen. J. Appl. Phys. 2017, 121, 195702. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Demchenko, D.O. Roadmap for Point Defects in GaN. In Semiconductors and Semimetals; Mi, Z., Tan, H.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; Volume 111, pp. 133–152. [Google Scholar]
- Demchenko, D.O.; Diallo, I.C.; Reshchikov, M.A. Yellow luminescence of gallium nitride generated by carbon defect complexes. Phys. Rev. Lett. 2013, 110, 087404. [Google Scholar] [CrossRef]
- Zhang, H.-S.; Shi, L.; Yang, X.-B.; Zhao, Y.-J.; Xu, K.; Wang, L.-W. First-Principles Calculations of Quantum Efficiency for Point Defects in Semiconductors: The Example of Yellow Luminance by GaN: CN+ ON and GaN: CN. Adv. Opt. Mater. 2017, 5, 1700404. [Google Scholar] [CrossRef]
- Lyons, J.L.; Janotti, A.; Van de Walle, C.G. Effects of carbon on the electrical and optical properties of InN, GaN, and AlN. Phys. Rev. B 2014, 89, 035204. [Google Scholar] [CrossRef]
- Tuomisto, F.; Mäki, J.-M.; Zając, M. Vacancy defects in bulk ammonothermal GaN crystals. J. Cryst. Growth 2010, 312, 2620–2623. [Google Scholar] [CrossRef]
- Uedono, A.; Tsukada, Y.; Mikawa, Y.; Mochizuki, T.; Fujisawa, H.; Ikeda, H.; Kurihara, K.; Fujito, K.; Terada, S.; Ishibashi, S.; et al. Vacancies and electron trapping centers in acidic ammonothermal GaN probed by a monoenergetic positron beam. J. Cryst. Growth 2016, 448, 117–121. [Google Scholar] [CrossRef]
- Suihkonen, S.; Pimputkar, S.; Speck, J.S.; Nakamura, S. Infrared absorption of hydrogen-related defects in ammonothermal GaN. Appl. Phys. Lett. 2016, 108, 202105. [Google Scholar] [CrossRef]
- Zajac, M.; Kucharski, R.; Grabianska, K.; Gwardys-Bak, A.; Puchalski, A.; Wasik, D.; Litwin-Staszewska, E.; Piotrzkowski, R.; Domagala, J.Z.; Bockowski, M. Basic ammonothermal growth of Gallium Nitride—State of the art, challenges, perspectives. Prog. Cryst. Growth Charact. Mater. 2018, 64, 63–74. [Google Scholar] [CrossRef]
- Malguth, E.; Hoffmann, A.; Gehloff, W.; Gelhausen, O.; Phillips, M.R.; Xu, X. Structural and electronic properties of Fe3+ and Fe2+ centers in GaN from optical and EPR experiments. Phys. Rev. B 2006, 74, 165202. [Google Scholar] [CrossRef]
- Tanaka, D.; Iso, K.; Suda, J. Comparative study of electrical properties of semi-insulating GaN substrates grown by hydride vapor phase epitaxy and doped with Fe, C, or Mn. J. Appl. Phys. 2023, 133, 055701. [Google Scholar] [CrossRef]
- Richter, E.; Gridneva, E.; Weyers, M.; Tränkle, G. Fe-doping in hydride vapor-phase epitaxy for semi-insulating gallium nitride. J. Cryst. Growth 2016, 456, 97–100. [Google Scholar] [CrossRef]
- Laaksonen, K.; Ganchenkova, M.G.; Nieminen, R.M. Vacancies in wurtzite GaN and AlN. J. Phys. Condens. Matter 2009, 21, 015803. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, D.; Jiang, X.; Zhao, J. Point defects in group III nitrides: A comparative first-principles study. J. Appl. Phys. 2019, 125, 215705. [Google Scholar] [CrossRef]
- Wang, Q.-J.; Zhang, H.-S.; Shi, L.; Gong, J. Origin of Ga vacancy-related YL center in n-type GaN: A first-principles study. J. Lumin. 2023, 255, 119561. [Google Scholar] [CrossRef]
- Alkauskas, A.; Dreyer, C.E.; Lyons, J.L.; Van de Walle, C.G. Role of excited states in Schockley-Read-Hall recombination in wide-band-gap semiconductors. Phys. Rev. B 2016, 93, 201304. [Google Scholar] [CrossRef]
- Dreyer, C.E.; Alkauskas, A.; Lyons, J.L.; Speck, J.S.; Van de Walle, C.G. Gallium vacancy complexes as a cause of Schockley-Read-Hall recombination in III-nitride light emitters. Appl. Phys. Lett. 2016, 108, 141101. [Google Scholar] [CrossRef]
- Suihkonen, S.; Nykänen, H.; Tanikawa, T.; Yamaguchi, M.; Honda, Y.; Amano, H. Effects of low energy e-beam irradiation on cathodoluminescence from GaN. Phys. Stat. Sol. A 2013, 210, 383–385. [Google Scholar] [CrossRef]
- Huber, M.; Silvestri, M.; Knuuttila, L.; Pozzovivo, G.; Andreev, A.; Kadashchuk, A.; Bonanni, A.; Lundskog, A. Impact of residual carbon impurities and gallium vacancies on trapping effects in AlGaN/GaN metal insulator semiconductor high electron mobility transistors. Appl. Phys. Lett. 2015, 107, 032106. [Google Scholar] [CrossRef]
- Glaser, E.R.; Freitas, J.A., Jr.; Braga, G.C.; Carlos, W.E.; Twigg, M.E.; Wickenden, A.E.; Koleske, D.D.; Henry, R.L.; Leszczynski, M.; Grzegory, I.; et al. Magnetic resonance studies of defects in GaN with reduced dislocation densities. Phys. B 2001, 310, 51–57. [Google Scholar] [CrossRef]
- McNamara, J.D.; Foussekis, M.A.; Baski, A.A.; Li, X.; Avrutin, V.; Morkoç, H.; Leach, J.H.; Paskova, T.; Udwary, K.; Preble, E.; et al. Electrical and optical properties of bulk GaN substrates studied by Kelvin probe and photoluminescence. Phys. Stat. Sol. C 2013, 10, 536–539. [Google Scholar]
- Reshchikov, M.A.; Zhang, M.H.; Cui, J.; Visconti, P.; Yun, F.; Morkoç, H. Photoluminescence study of defects in GaN grown by molecular beam epitaxy. Mat. Res. Soc. Symp. Proc. 2001, 639, 67. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Molnar, R.; Morkoç, H. Photoluminescence and excitation spectra of deep defects in GaN. Mat. Res. Soc. Symp. Proc. 2001, 680, E5.6. [Google Scholar] [CrossRef]
- Goldys, E.M.; Godlewski, M.; Paskova, T.; Pozina, G.; Monemar, B. Characterization of Red Emission in Nominally Undoped Hydride Vapor Phase Epitaxy. MRS Internet J. Nitride Semicond. Res. 2001, 6, 1. [Google Scholar] [CrossRef]
- Uehara, D.; Kikuchi, M.; Ma, B.; Miyake, H.; Ishitani, Y. Charge transfer processes related to deep levels in free standing n-GaN layer analyzed by above and sub-bandgap energy excitation. Appl. Phys. Express 2020, 13, 061003. [Google Scholar] [CrossRef]
- Wang, L.; Zeimer, U.; Richter, E.; Herms, M.; Weyers, M. Characterisation of free standing GaN grown by HVPE on a LiAlO2 substrate. Phys. Stat. Sol. A 2006, 203, 1663–1666. [Google Scholar]
- Wang, L.; Richter, E.; Weyers, M. Red luminescence from freestanding GaN grown on LiAlO2 substrate by hydride vapor phase epitaxy. Phys. Stat. Sol. A 2007, 204, 846–849. [Google Scholar] [CrossRef]
- Dingle, R. Luminescent transitions associated with divalent copper impurities and the green emission from semiconducting zinc oxide. Phys. Rev. Lett. 1969, 23, 579–581. [Google Scholar] [CrossRef]
- Dahan, P.; Fleurov, V.; Thurian, P.; Heitz, R.; Hoffmann, A.; Broser, I. Properties of the intermediately bound α-, β-, and γ-excitons in ZnO:Cu. J. Phys. Condens. Matter. 1998, 10, 2007–2019. [Google Scholar] [CrossRef]
- Garces, N.Y.; Wang, L.; Bai, L.; Giles, N.C.; Halliburton, L.E. Role of copper in the green luminescence from ZnO crystals. Appl. Phys. Lett. 2002, 81, 622–624. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Avrutin, V.; Izyumskaya, N.; Shimada, R.; Morkoç, H.; Novak, S.W. About the Cu-related green luminescence band in ZnO. J. Vac. Sci. Tech. B 2009, 27, 1749–1754. [Google Scholar] [CrossRef]
- Kuhnert, R.; Helbig, R. Vibronic structure of the green photoluminescence due to copper impurities in ZnO. J. Lumin. 1981, 26, 203–206. [Google Scholar] [CrossRef]
- Malguth, E.; Hoffmann, A.; Phillips, M.R. Fe in III-V and II-VI semiconductors. Phys. Stat. Sol. B 2008, 245, 455–480. [Google Scholar] [CrossRef]
- Wegscheider, M.; Simbrunner, C.; Przybylinska, H.; Kiecana, M.; Sawicki, M.; Navarro-Quezada, A.; Sitter, H.; Jantsch, W.; Dietl, T.; Bonanni, A. Photoluminescence and Hall studies of GaN:Fe and (Ga,Fe)N:Mg layers. Phys. Stat. Sol. A 2007, 204, 86–91. [Google Scholar] [CrossRef]
- Freitas, J.A., Jr.; Culbertson, J.C.; Glaser, E.R.; Richter, E.; Weyers, M.; Oliveira, A.C.; Garg, V.K. Efficient iron doping of HVPE GaN. J. Cryst. Growth 2018, 500, 111–116. [Google Scholar] [CrossRef]
- Jiang, W.; Nolan, M.; Ehrentraut, D.; D’Evelyn, M.P. Electrical and optical properties of gallium vacancy complexes in ammonothermal GaN. Appl. Phys. Express 2017, 10, 075506. [Google Scholar] [CrossRef]
- Suihkonen, S.; Pimputkar, S.; Sintonen, S.; Tuomisto, F. Defects in single crystalline ammonothermal gallium nitride. Adv. Electron. Mater. 2017, 3, 1600496. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Morkoç, H.; Park, S.S.; Lee, K.Y. Two charge states of dominant acceptor in unintentionally doped GaN: Evidence from photoluminescence study. Appl. Phys. Lett. 2002, 81, 4970–4972. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Morkoç, H.; Park, S.S.; Lee, K.Y. Unusual properties of the dominant acceptor in freestanding GaN. Phys. B 2003, 340–342, 448–451. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Demchenko, D.O.; Usikov, A.; Helava, H.; Makarov, Y. Carbon defects as sources of the yellow and green luminescence bands in undoped GaN. Phys. Rev. B 2014, 90, 235203. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Usikov, A.; Helava, H.; Makarov, Y. Defect-related luminescence in undoped GaN grown by HVPE. J. Electron. Mater. 2015, 44, 1281–1286. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; McNamara, J.D.; Usikov, A.; Helava, H.; Makarov, Y. Optically-generated giant traps in high-purity GaN. Phys. Rev. B 2016, 93, 081202. [Google Scholar] [CrossRef]
- Lax, M. Cascade Capture of Electrons in Solids. Phys. Rev. 1960, 119, 1502–1523. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Vorobiov, M.; Andrieiev, A.; Ding, K.; Avrutin, V.; Usikov, A.; Helava, H.; Makarov, Y. Determination of the concentration of impurities in GaN from photoluminescence and secondary-ion mass spectrometry. Sci. Rep. 2020, 10, 2223. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, M.; Tanaka, A.; Ando, Y.; Watanabe, H.; Deki, M.; Kushimoto, M.; Nitta, S.; Honda, Y.; Shima, K.; Kojima, K.; et al. Suppression of Green Luminescence of Mg-Ion-Implanted GaN by Subsequent Implantation of Fluorine Ions at High Temperature. Phys. Stat. Sol. B 2020, 257, 1900554. [Google Scholar] [CrossRef]
- Meyers, V.; Rocco, E.; Hogan, K.; McEwen, B.; Shevelev, M.; Sklyar, V.; Jones, K.; Derenge, M.; Shahedipour-Sandvik, F. P-type conductivity and suppression of green luminescence in Mg/N co-implanted GaN by gyrotron microwave annealing. J. Appl. Phys. 2021, 130, 085704. [Google Scholar] [CrossRef]
- Kojima, K.; Takashima, S.; Edo, M.; Ueno, K.; Shimizu, M.; Takahashi, T.; Ishibashi, S.; Uedono, A.; Chichibu, S.F. Nitrogen vacancies as a common element of the green luminescence and nonradiative recombination centers in Mg-implanted GaN layers formed on a GaN substrate. Appl. Phys. Express 2017, 10, 061002. [Google Scholar] [CrossRef]
- Vorobiov, M.; Andrieiev, O.; Demchenko, D.O.; Reshchikov, M.A. Point Defects in Beryllium Doped GaN. Phys. Rev. B 2021, 104, 245203. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Andrieiev, O.; Vorobiov, M.; Ye, D.; Demchenko, D.O.; Sierakowski, K.; Bockowski, M.; McEwen, B.; Meyers, V.; Shahedipour-Sandvik, F. Thermal annealing of GaN implanted with Be. J. Appl. Phys. 2022, 131, 125704. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Morkoç, H. Unusual Properties of the Red and Green Luminescence Bands in Ga-rich GaN. MRS Online Proc. Libr. (OPL) 2005, 831, E3.7. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; He, L.; Molnar, R.J.; Park, S.S.; Lee, K.Y.; Morkoç, H. Aquamarine luminescence band in undoped GaN. MRS Online Proc. Libr. 2005, 831, 537–542. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Yun, F.; Huang, D.; He, L.; Morkoç, H.; Park, S.S.; Lee, K.Y. Photoluminescence of GaN grown by molecular beam epitaxy on freestanding GaN template. MRS Online Proc. Libr. 2002, 722, 14. [Google Scholar] [CrossRef]
- Young, E.C.; Grandjean, N.; Mates, T.E.; Speck, J.S. Calcium impurity as a source of non-radiative recombination in (In,Ga)N layers grown by molecular beam epitaxy. Appl. Phys. Lett. 2016, 109, 212103. [Google Scholar] [CrossRef]
- Chèze, C.; Feix, F.; Lahnemann, J.; Flissikowski, T.; Krysko, M.; Wolny, P.; Turski, H.; Skierbiszewski, C.; Brandt, O. Luminescent N-polar (In,Ga)N/GaN quantum wells achieved by plasma-assisted molecular beam epitaxy at temperatures exceeding 700 °C. Appl. Phys. Lett. 2018, 112, 022102. [Google Scholar] [CrossRef]
- Auzelle, T.; Sinito, C.; Lähnemann, J.; Gao, G.; Flissikowski, T.; Trampert, A.; Brandt, O.; Fernández-Garrido, S. Interface Recombination in Ga- and N-Polar GaN/(Al,Ga)N Quantum Wells Grown by Molecular Beam Epitaxy. Phys. Rev. Appl. 2022, 17, 044030. [Google Scholar] [CrossRef]
- Zacks, E.; Halperin, A. Dependence of the Peak Energy of the Pair-Photoluminescence Band on Excitation Intensity. Phys. Rev. B 1972, 6, 3072–3075. [Google Scholar] [CrossRef]
- Xu, S.J.; Li, G.; Chua, S.J.; Wang, X.C.; Wang, W. Observation of optically-active metastable defects in undoped GaN epilayers. Appl. Phys. Lett. 1998, 72, 2451–2453. [Google Scholar] [CrossRef]
- Brown, S.A.; Reeves, R.J.; Haase, C.S.; Cheung, R.; Kirchner, C.; Kamp, M. Reactive-ion-etched gallium nitride: Metastable defects and yellow luminescence. Appl. Phys. Lett. 1999, 75, 3285–3287. [Google Scholar] [CrossRef]
- Kim, B.; Kuskovsky, I.; Herman, I.P.; Li, D.; Neumark, G.F. Reversible ultraviolet-induced photoluminescence degradation and enhancement in GaN films. J. Appl. Phys. 1999, 86, 2034–2037. [Google Scholar] [CrossRef]
- Dhar, S.; Ghosh, S. Optical metastability in undoped GaN grown on Ga-rich GaN buffer layers. Appl. Phys. Lett. 2002, 80, 4519–4521. [Google Scholar] [CrossRef]
- Ryan, B.J.; Henry, M.O.; McGlynn, E.; Fryar, J. Investigation of optical metastability in GaN using photoluminescence spectroscopy. Phys. B Condens. Matt. 2003, 340–342, 452–456. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Moon, Y.T.; Morkoç, H. Origin of unstable photoluminescence in GaN: Metastable defects or surface states? Phys. Stat. Sol. C 2005, 2, 2716–2719. [Google Scholar] [CrossRef]
- Monemar, B.; Paskov, P.P.; Pozina, G.; Hemmingsson, C.; Bergman, J.P.; Khromov, S.; Izyumskaya, V.N.; Avrutin, V.; Li, X.; Morkoç, H.; et al. Properties of the main Mg-related acceptors in GaN from optical and structural studies. J. Appl. Phys. 2014, 115, 053507. [Google Scholar] [CrossRef]
- Glaser, E.R.; Freitas, J.A., Jr.; Shanabrook, B.V.; Koleske, D.D.; Lee, S.K.; Park, S.S.; Han, J.Y. Optically detected magnetic resonance of (effective-mass) shallow acceptors in Si-doped GaN homoepitaxial layers. Phys. Rev. B 2003, 68, 195201. [Google Scholar] [CrossRef]
- Murthy, M.; Freitas, J.A., Jr.; Kim, J.; Glaser, E.R.; Storm, D. Residual impurities in GaN substrates and epitaxial layers grown by various techniques. J. Cryst. Growth 2007, 305, 393–398. [Google Scholar] [CrossRef]
- Kamiura, Y.; Ogasawara, M.; Fukutani, K.; Ishiyama, T.; Yamashita, Y.; Mitani, T.; Mukai, T. Enhancement of blue emission from GaN films and diodes by water vapor remote plasma treatment. Phys. B 2007, 401–402, 331–334. [Google Scholar] [CrossRef]
- Glaser, E.R.; Murthy, M.; Freitas, J.A., Jr.; Storm, D.F.; Zhou, L.; Smith, D.J. Optical and magnetic resonance studies of Mg-doped GaN homoepitaxial layers grown by molecular beam epitaxy. Phys. B 2007, 401–402, 327–330. [Google Scholar] [CrossRef][Green Version]
- Lyons, J.L.; Janotti, A.; Van de Walle, C.G. Effects of hole localization on limiting p-type conductivity in oxide and nitride semiconductors. J. Appl. Phys. 2014, 115, 012014. [Google Scholar] [CrossRef]
- Saarinen, K.; Suski, T.; Grzegory, I.; Look, D.C. Thermal stability of isolated and complexed Ga vacancies in GaN bulk crystals. Phys. Rev. B 2001, 64, 233201. [Google Scholar] [CrossRef]
- Tuomisto, F.; Mäki, J.-M.; Rauch, C.; Makkonen, I. On the formation of vacancy defects in III-nitride semiconductors. J. Cryst. Growth 2012, 350, 93–97. [Google Scholar] [CrossRef]
- Oila, J.; Kivioja, J.; Ranki, V.; Saarinen, K.; Look, D.C.; Molnar, R.J.; Park, S.S.; Lee, S.K.; Han, J.Y. Ga vacancies as dominant intrinsic acceptors in GaN grown by hydride vapor phase epitaxy. App. Phys. Lett. 2003, 82, 3433–3435. [Google Scholar] [CrossRef]
- Tuomisto, F.; Hautakangas, S.; Makkonen, I.; Ranki, V.; Puska, M.J.; Saarinen, K.; Bockowski, M.; Suski, T.; Paskova, T.; Monemar, B.; et al. Dissociation of VGa-ON complexes in HVPE GaN by high pressure and high temperature annealing. Phys. Stat. Sol. B 2006, 243, 1436–1440. [Google Scholar] [CrossRef]
- Tuomisto, F.; Saarinen, K.; Paskova, T.; Monemar, B.; Bockowski, M.; Suski, T. Thermal stability of in-grown vacancy defects in GaN grown by hydride vapor phase epitaxy. J. Appl. Phys. 2006, 99, 066105. [Google Scholar] [CrossRef]
- Prozheev, I.; Iwinska, M.; Sochacki, T.; Bockowski, M.; Bes, R.; Tuomisto, F. Origins of Electrical Compensation in Si-doped HVPE GaN. Phys. Stat. Sol. B 2023, 260, 2200568. [Google Scholar] [CrossRef]
- Hautakangas, S.; Makkonen, I.; Ranki, V.; Puska, M.J.; Saarinen, K.; Xu, X.; Look, D.C. Direct evidence of impurity decoration of Ga vacancies in GaN from positron annihilation spectroscopy. Phys. Rev. B 2006, 73, 193301. [Google Scholar] [CrossRef]
- Nykänen, H.; Suihkonen, S.; Kilanski, L.; Sopanen, M.; Tuomisto, F. Low energy beam induced vacancy activation in GaN. Appl. Phys. Lett. 2012, 100, 122105. [Google Scholar] [CrossRef]
- Chichibu, S.F.; Shima, K.; Uedono, A.; Ishibashi, S.; Iguchi, H.; Narita, T.; Kataoka, K.; Tanaka, R.; Takashima, S.; Ueno, K.; et al. Impacts of vacancy complexes on the room-temperature photoluminescence lifetimes of state-of-the-art GaN substrates, epitaxial layers, and Mg-implanted layers. J. Appl. Phys. 2024, 135, 185701. [Google Scholar] [CrossRef]
- Uedono, A.; Takino, J.; Sumi, T.; Okayama, Y.; Imanishi, M.; Ishibashi, S.; Mori, Y. Vacancy-type defects in bulk GaN grown by oxide vapor phase epitaxy probed using positron annihilation. J. Cryst. Growth 2021, 570, 126219. [Google Scholar] [CrossRef]
- Li, H.; Huang, M.; Chen, S. First-principles exploration of defect-pairs in GaN. J. Semicond. 2020, 41, 032104. [Google Scholar] [CrossRef]
- Jiang, H.; Wan, P.; Yang, J.; Xu, X.; Li, W.; Li, X. Analysis of radiation defects in gallium nitride using deep level transient spectra and first principles methods. Nuclar Instr. Meth. Phys. Res. B 2023, 545, 105120. [Google Scholar] [CrossRef]
- Linde, M.; Uftring, S.J.; Watkins, G.D.; Härle, V.; Scholz, F. Optical detection of magnetic resonance in electron-irradiated GaN. Phys. Rev. B 1997, 55, 10177–10180. [Google Scholar] [CrossRef]
- Kogiso, T.; Narita, T.; Yoshida, H.; Tokuda, Y.; Tomita, K.; Kachi, T. Characterization of hole traps in MOVPE-grown p-GaN layers using low-frequency capacitance deep-level transient spectroscopy. Jap. J. Appl. Phys. 2019, 58, SCCB36. [Google Scholar] [CrossRef]
- Zhao, F.; Guan, H.; Turiansky, M.E.; Van de Walle, C.G. Carbon in GaN as a nonradiative recombination center. Appl. Phys. Lett. 2025, 126, 201106. [Google Scholar] [CrossRef]
- Neugebauer, J.; Van de Walle, C.G. Hydrogen in GaN: Novel Aspects of a Common Impurity. Phys. Rev. Lett. 1995, 75, 4452–4455. [Google Scholar] [CrossRef] [PubMed]
- Limpijumnong, S.; Van de Walle, C.G. Stability, diffusivity, and vibrational properties of monoatomic and molecular hydrogen in wurtzite GaN. Phys. Rev. B 2003, 68, 235203. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Andrieiev, O.; Vorobiov, M.; Ye, D.; Demchenko, D.O.; McEwen, B.; Shahedipour-Sandvik, F. Passivation of defects in GaN by hydrogen and their activation by annealing. Nanotechnology 2025, 36, 105704. [Google Scholar] [CrossRef]
- Demchenko, D.O.; Diallo, I.C.; Reshchikov, M.A. Hydrogen-carbon complexes and the blue luminescence band in GaN. J. Appl. Phys. 2016, 119, 035702. [Google Scholar] [CrossRef]
- Wu, S.; Yang, X.; Zhang, Q.; Shang, Q.; Huang, H.; Shen, J.; He, X.; Xu, F.; Wang, X.; Ge, W.; et al. Direct evidence of hydrogen interaction with carbon: C-H complex in semi-insulating GaN. Appl. Phys. Lett. 2020, 116, 262101. [Google Scholar] [CrossRef]
- Richter, E.; Beyer, F.C.; Zimmermann, F.; Gärtner, G.; Irmscher, K.; Gamov, I.; Heitmann, J.; Weyers, M.; Tränkle, G. Growth and Properties of Intentionally Carbon-Doped GaN Layers. Cryst. Res. Technol. 2020, 55, 1900129. [Google Scholar] [CrossRef]
- Gamov, I.; Richter, E.; Weyers, M.; Gärtner, G.; Irmscher, K. Carbon doping of GaN: Proof of the formation of electrically active tri-carbon defects. J. Appl. Phys. 2020, 127, 205701. [Google Scholar] [CrossRef]
- Reuter, E.E.; Zhang, R.; Kuech, T.F.; Bishop, S.G. Photoluminescence excitation spectroscopy of carbon-doped gallium nitride. MRS Internet J. Nitride Semicond. Res. 1999, 4S1, G3.67. [Google Scholar] [CrossRef]
- Stoneham, A.M. Theory of Defects in Solids; Oxford University Press: New York, NY, USA, 1975; 955p. [Google Scholar]
- Baldacchini, G. Radiative and nonradiative processes in color centers. In Advances in Nonradiative Processes in Solids; Di Bartolo, B., Ed.; Plenum Press: New York, NY, USA, 1991; pp. 219–259. [Google Scholar]
- Asami, K.; Naka, T.; Ishiguro, M. Luminescence quenching in F centers under pressure. Phys. Rev. B 1986, 34, 5658–5664. [Google Scholar] [CrossRef] [PubMed]
- Swank, R.K.; Brown, F.C. Lifetime of the Excited F Center. Phys. Rev. 1963, 130, 34–41. [Google Scholar] [CrossRef]
- Timusk, T.; Martienssen, W. Recombination Luminescence in Alkali Halides. Phys. Rev. 1962, 128, 1656–1663. [Google Scholar] [CrossRef]
- Sánchez, F.J.; Calle, F.; Sánchez-Garcia, M.A.; Calleja, E.; Munoz, E.; Molloy, C.H.; Somerford, D.J.; Serrano, J.J.; Blanco, J.M. Experimental evidence for a Be shallow acceptor in GaN grown on Si(111) by molecular beam epitaxy. Semicond. Sci. Technol. 1998, 13, 1130–1133. [Google Scholar] [CrossRef]
- Jaworek, M.; Wysmolek, A.; Kaminska, M.; Twardowski, A.; Bockowski, M.; Grzegory, I. Photoluminescence study of bulk GaN doped with beryllium. Acta Phys. Pol. 2005, 108, 705–710. [Google Scholar] [CrossRef]
- Kawaharazuka, A.; Tanimoto, T.; Nagai, K.; Tanaka, Y.; Horikoshi, Y. Be and Mg co-doping in GaN. J. Cryst. Growth 2007, 301–302, 414. [Google Scholar] [CrossRef]
- Teisseyre, H.; Gorczyca, I.; Christensen, N.E.; Svane, A.; Naranjo, F.B.; Calleja, E. Pressure behavior of beryllium-acceptor level in gallium nitride. J. Appl. Phys. 2005, 97, 043704. [Google Scholar] [CrossRef]
- Al Tahtamouni, T.M.; Sedhain, A.; Lin, J.Y.; Jiang, H.X. Beryllium Doped p-type GaN Grown by Metal-Organic Chemical Vapor Deposition. Jordan. J. Phys. 2010, 3, 77–81. [Google Scholar]
- Van de Walle, C.G.; Limpijumnong, S. First-Principles studies of beryllium doping of GaN. Phys. Rev. B 2001, 63, 245205. [Google Scholar] [CrossRef]
- Wang, H.; Chen, A.-B. Calculations of acceptor ionization energies in GaN. Phys. Rev. B 2001, 63, 125212. [Google Scholar] [CrossRef]
- Lany, S.; Zunger, A. Dual nature of acceptors in GaN and ZnO: The curious case of the shallow MgGa deep state. Appl. Phys. Lett. 2010, 96, 142114. [Google Scholar] [CrossRef]
- Lyons, J.L.; Janotti, A.; Van de Walle, C.G. Impact of group-II acceptors on the electrical and optical properties of GaN. Jap. J. Appl. Phys. 2013, 52, 08JJ04. [Google Scholar] [CrossRef]
- Cai, X.; Yang, J.; Zhang, P.; Wei, S.-H. Origin of Deep Be Acceptor Levels in Nitride Semiconductors: The Roles of Chemical and Strain Effects. Phys. Rev. Appl. 2019, 11, 034019. [Google Scholar] [CrossRef]
- Jin, S.; Li, X.; Yang, W.; Zhao, Y.; Bian, L.; Lu, S. Electrical and optical properties of Beryllium Deep Acceptors in GaN. J. Electron. Mater. 2020, 49, 7472–7478. [Google Scholar] [CrossRef]
- Demchenko, D.O.; Vorobiov, M.; Andrieiev, O.; Myers, T.H.; Reshchikov, M.A. Shallow and deep states of beryllium acceptor in GaN: Why photoluminescence experiments do not reveal small polarons for defects in semiconductors. Phys. Rev. Lett. 2021, 126, 027401. [Google Scholar] [CrossRef]
- Teisseyre, H.; Lyons, J.L.; Kaminska, A.; Jankowski, D.; Jarosz, D.; Bockowski, M.; Suchocki, A.; Van de Walle, C.G. Identification of yellow luminescence centers in Be-doped GaN through pressure-dependent studies. J. Phys. D: Appl. Phys. 2017, 50, 22LT03. [Google Scholar] [CrossRef]
- Naranjo, F.B.; Sánchez-García, M.A.; Pau, J.L.; Jiménez, A.; Calleja, E.; Muñoz, E.; Oila, J.; Saarinen, K.; Hautojärvi, P. Study of the Effects of Mg and Be Co-doping in GaN Layers. Phys. Stat. Sol. A 2000, 180, 97–102. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Vorobiov, M.; Andrieiev, O.; McEwen, B.; Rocco, E.; Meyers, V.; Demchenko, D.O.; Shahedipour-Sandvik, F. Photoluminescence from Be-Doped GaN Grown by Metal-Organic Chemical Vapor Deposition. Phys. Stat. Sol. B 2023, 260, 2200487. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Andrieiev, O.; Vorobiov, M.; Demchenko, D.O.; McEwen, B.; Shahedipour-Sandvik, F. Photoluminescence from GaN implanted with Be and F. Phys. Stat. Sol. B 2023, 260, 2300131. [Google Scholar] [CrossRef]
- Zajac, M.; Reshchikov, M.A.; McEwen, B.; Shahendipour-Sandvik, F. P-type conductivity in GaN:Be epitaxial layers. J. Appl. Phys. 2025, 138, 095705. [Google Scholar] [CrossRef]
- Glaser, E.R.; Carlos, W.; Braga, G.; Freitas, J.; Moore, W.; Shanabrook, B.; Wickenden, A.; Koleske, D.; Henry, R.; Bayerl, M.; et al. Characterization of nitrides by electron paramagnetic resonance (EPR) and optically detected magnetic resonance (ODMR). Mater. Sci. Eng. B 2002, 93, 39–48. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Sierakowski, K.; Jakiela, R.; Fijalkowski, M.; Sochacki, T.; Demchenko, D.O.; Bockowski, M. Photoluminescence from a- and m-plane GaN:Be,O. In Proceedings of the International Conference on Nitride Semiconductors (ICNS-15), Malmö, Sweden, 6–11 July 2025. [Google Scholar]
- Takeya, M.; Ikeda, M. Novel Methods of p-type Activation in Mg-doped GaN. Jpn. J. Appl. Phys. 2001, 40, 6260–6262. [Google Scholar] [CrossRef]
- Demchenko, D.O.; Reshchikov, M.A. Passivation of the beryllium acceptor in GaN and a possible route for p-type doping. Appl. Phys. Lett. 2021, 118, 142103. [Google Scholar] [CrossRef]
- Maruska, H.P.; Stevenson, D.A.; Pankove, J.I. Violet luminescence of Mg-doped GaN. Appl. Phys. Lett. 1973, 22, 303–305. [Google Scholar] [CrossRef]
- Amano, H.; Kito, M.; Hiramatsu, K.; Akasaki, I. P-Type Conduction in Mg-Doped GaN Treated with Low-Energy Electron Beam Irradiation (LEEBI). Jap. J. Appl. Phys. 1989, 28, L2112–L2114. [Google Scholar] [CrossRef]
- Nakamura, S.; Mukai, T.; Senoh, M. Candela-class high-brightness InGaN/AIGaN double-heterostructure blue-light-emitting diodes. Appl. Phys. Lett. 1994, 64, 1687–1689. [Google Scholar] [CrossRef]
- Akasaki, I.; Amano, H.; Kito, M.; Hiramatsu, K. Photoluminescence of Mg-doped p-type GaN and electroluminescence of GaN p-n junction LED. J. Lumin. 1991, 48–49, 666–670. [Google Scholar] [CrossRef]
- Amano, H.; Kito, M.; Hiramatsu, K.; Akasaki, I. Growth and Luminescence Properties of Mg- Doped GaN Prepared by MOVPE. J. Electrochem. Soc. 1990, 137, 1639–1641. [Google Scholar] [CrossRef]
- Nakamura, S.; Mukai, T.; Senoh, M.; Iwasa, N. Thermal annealing effects on p-type Mg-doped GaN films. Jpn. J. Appl. Phys. 1992, 31 Pt 2, L139–L142. [Google Scholar] [CrossRef]
- Nakamura, S.; Iwasa, N.; Senoh, M.; Mukai, T. Hole compensation mechanism of p-type GaN films. Jpn. J. Appl. Phys. 1992, 31 Pt 2, 1258–1266. [Google Scholar] [CrossRef]
- Kaufmann, U.; Kunzer, M.; Maier, M.; Obloh, H.; Ramakrishnan, A.; Santic, B. Nature of the 2.8 eV photoluminescence band in Mg doped GaN. Appl. Phys. Lett. 1998, 72, 1326–1328. [Google Scholar] [CrossRef]
- Eckey, L.; Von Gfug, U.; Holst, J.; Hoffmann, A.; Kaschner, A.; Siegle, H.; Thomsen, C.; Schineller, B.; Heime, K.; Heuken, M.; et al. Photoluminescence and Raman study of compensation effects in Mg-doped GaN epilayers. J. Appl. Phys. 1998, 84, 5828–5830. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Li, W.; Cabalu, J.; Moustakas, T.D.; Smith, D.J.; Hervig, R.L. Efficient p-type doping of GaN films by plasma-assisted molecular beam epitaxy. Appl. Phys. Lett. 2004, 85, 4956–4958. [Google Scholar] [CrossRef]
- Fischer, A.M.; Wang, S.; Ponce, F.A.; Gunning, B.P.; Fabien, C.A.; Doolittle, W.A. Origin of high hole concentrations in Mg-doped GaN films. Phys. Stat. Sol. B 2017, 254, 1600668. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Abtew, A.; Zhang, P.; Zhang, S.B. Anisotropic polaron localization and spontaneous symmetry breaking: Comparison of cation-site acceptors in GaN and ZnO. Phys. Rev. B. 2014, 90, 165301. [Google Scholar] [CrossRef]
- Demchenko, D.O.; Diallo, I.; Reshchikov, M.A. Magnesium acceptor in gallium nitride: II. Koopmans tuned HSE hybrid functional calculations of dual nature and optical properties. Phys. Rev. B 2018, 97, 205205. [Google Scholar] [CrossRef]
- Lyons, J.L.; Janotti, A.; Van de Walle, C.G. Shallow versus Deep Nature of Mg Acceptors in Nitride Semiconductors. Phys. Rev. Lett. 2012, 108, 156403. [Google Scholar] [CrossRef] [PubMed]
- Miceli, G.; Pasquarello, A. Self-compensation due to point defects in Mg-doped GaN. Phys. Rev. B 2016, 93, 165207. [Google Scholar] [CrossRef]
- Demchenko, D.O.; Vorobiov, M.; Andrieiev, O.; Reshchikov, M.A.; McEwen, B.; Shahedipour-Sandvik, F. Koopmans-tuned Heyd-Scuseria-Ernzerhof hybrid functional calculations of acceptors in GaN. Phys. Rev. B 2024, 110, 035203. [Google Scholar] [CrossRef]
- Monemar, B.; Paskov, P.P.; Pozina, G.; Hemmingsson, C.; Bergman, J.P.; Kawashima, T.; Amano, H.; Akasaki, I.; Paskova, T.; Figge, S.; et al. Evidence for Two Mg Related Acceptors in GaN. Phys. Rev. Lett. 2009, 102, 235501. [Google Scholar] [CrossRef]
- Pozina, G.; Hemmingsson, C.; Paskov, P.P.; Bergman, J.P.; Monemar, B.; Kawashima, T.; Amano, H.; Akasaki, I.; Usui, A. Effect of annealing on metastable shallow acceptors in Mg-doped GaN layers grown on GaN substrates. Appl. Phys. Lett. 2008, 92, 151904. [Google Scholar] [CrossRef]
- Gelhausen, O.; Phillips, M.R.; Goldys, E.M.; Paskova, T.; Monemar, B.; Strassburg, M.; Hoffmann, A. Dissociation of H-related defect complexes in Mg-doped GaN. Phys. Rev. B 2004, 69, 125210. [Google Scholar] [CrossRef]
- Pozina, G.; Paskov, P.P.; Bergman, J.P.; Hemmingsson, C.; Hultman, L.; Monemar, B.; Amano, H.; Akasaki, I.; Usui, A. Metastable behavior of the UV luminescence in Mg-doped GaN layers grown on quasibulk GaN templates. Appl. Phys. Lett. 2007, 91, 221901. [Google Scholar] [CrossRef]
- Callsen, G.; Wagner, M.R.; Kure, T.; Reparaz, J.S.; Bügler, M.; Brunnmeier, J.; Nenstiel, C.; Hoffmann, A.; Hoffmann, M.; Tweedie, J.; et al. Optical signature of Mg-doped GaN: Transfer processes. Phys. Rev. B 2012, 86, 075207. [Google Scholar] [CrossRef]
- Liu, H.; Su, P.-Y.; Wu, Z.; Liu, R.; Ponce, F.A. Influence of substrate misorientation on the optical properties of Mg-doped GaN. J. Appl. Phys. 2020, 127, 195701. [Google Scholar] [CrossRef]
- Levanyuk, A.P.; Osipov, V.V. Edge luminescence of direct-gap semiconductors. Sov. Phys. Usp. 1981, 24, 187–215. [Google Scholar] [CrossRef]
- Takahashi, M.; Tanaka, A.; Ando, Y.; Watanabe, H.; Deki, M.; Kushimoto, M.; Nitta, S.; Honda, Y.; Shima, K.; Kojima, K.; et al. Impact of high-temperature implantation of Mg ions into GaN. Jap. J. Appl. Phys. 2020, 59, 056502. [Google Scholar] [CrossRef]
- Kumar, A.; Yi, W.; Uzuhashi, J.; Ohkubo, T.; Chen, J.; Sekiguchi, T.; Tanaka, R.; Takashima, S.; Edo, M.; Hono, K. Influence of implanted Mg concentration on defects and Mg distribution in GaN. J. Appl. Phys. 2020, 128, 065701. [Google Scholar] [CrossRef]
- Itoh, Y.; Watanabe, H.; Ando, Y.; Kano, E.; Deki, M.; Nitta, S.; Honda, Y.; Tanaka, A.; Ikarashi, N.; Amano, H. Effect of beam current on defect formation by high-temperature implantation of Mg ions into GaN. Appl. Phys. Express 2022, 15, 021003. [Google Scholar] [CrossRef]
- Sukarai, H.; Omori, M.; Yamada, S.; Furukawa, Y.; Suzuki, H.; Narita, T.; Kataoka, K.; Horita, M.; Bockowski, M.; Suda, J.; et al. Highly effective activation of Mg-implanted p-type GaN by ultra-high-pressure annealing. Appl. Phys. Lett. 2019, 115, 142104. [Google Scholar] [CrossRef]
- Tsuge, H.; Ikeda, K.; Kato, S.; Nishimura, T.; Nakamura, T.; Kuriyama, K.; Mishima, T. Impact of Mg-ion implantation with various fluence ranges on optical properties of n-type GaN. Nucl. Instr. Meth. Phys. Res. B 2017, 409, 50–52. [Google Scholar] [CrossRef]
- Uedono, A.; Iguchi, H.; Narita, T.; Kataoka, K.; Egger, W.; Koschine, T.; Hugenschmidt, C.; Dickmann, M.; Shima, K.; Kojima, K.; et al. Annealing Behavior of Vacancy-Type Defects in Mg- and H-Implanted GaN Studied Using Monoenergetic Positron Beams. Phys. Stat. Sol. B 2019, 256, 1900104. [Google Scholar] [CrossRef]
- Monemar, B.; Paskov, P.P.; Bergman, J.P.; Paskova, T.; Figge, S.; Dennemarck, J.; Hommel, D. The dominant shallow 0.225 eV acceptor in GaN. Phys. Stat. Sol. B 2006, 243, 1604–1608. [Google Scholar] [CrossRef]
- Kamiura, Y.; Kaneshiro, M.; Tamura, J.; Ishiyama, T.; Yamashita, Y.; Mitani, T.; Mukai, T. Enhancement of blue emission from Mg-doped GaN using remote plasma containing atomic hydrogen. Jap. J. Appl. Phys. 2005, 44, L926–L928. [Google Scholar] [CrossRef]
- Alves, H.; Leiter, F.; Pfisterer, D.; Hofmann, D.M.; Meyer, B.K.; Einfeld, S.; Heinke, H.; Hommel, D. Mg in GaN: The structure of the acceptor and the electrical activity. Phys. Stat. Sol. C 2003, 1770–1782. [Google Scholar] [CrossRef]
- Shahedipour, F.; Wessels, B.W. Investigation of the formation of the 2.8 eV luminescence band in p-type GaN:Mg. Appl. Phys. Lett. 2000, 76, 3011–3013. [Google Scholar] [CrossRef]
- Nayak, S.; Gupta, M.; Waghmare, U.V.; Shivaprasad, S.M. Origin of Blue Luminescence in Mg-Doped GaN. Phys. Rev. Appl. 2019, 11, 014027. [Google Scholar] [CrossRef]
- Yan, Q.; Janotti, A.; Scheffler, M.; Van de Walle, C.G. Role of nitrogen vacancies in the luminescence of Mg-doped GaN. Appl. Phys. Lett. 2012, 100, 142110. [Google Scholar] [CrossRef]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer: Berlin/Heidelberg, Germany, 1984; pp. 53–73, 253–313. [Google Scholar]
- Zeng, S.; Aliev, G.N.; Wolverson, D.; Davies, J.J.; Bingham, S.J.; Abdulmalik, D.A.; Coleman, P.G.; Wang, T.; Parbrook, P.J. The role of vacancies in the red luminescence from Mg-doped GaN. Phys. Stat. Sol. C 2006, 3, 1919–1922. [Google Scholar] [CrossRef]
- Shima, K.; Tanaka, R.; Takashima, S.; Ueno, K.; Edo, M.; Kojima, K.; Uedono, A.; Ishibashi, S.; Chichibu, S.F. Improved minority carrier lifetime in p-type GaN segments prepared by vacancy-guided redistribution of Mg. Appl. Phys. Lett. 2021, 119, 182106. [Google Scholar] [CrossRef]
- Bayerl, M.W.; Brandt, M.S.; Glaser, E.R.; Wickenden, A.E.; Koleske, D.D.; Henry, R.L.; Stutzmann, M. The Origin of Red Luminescence from Mg-doped GaN. Phys. Stat. Sol. B 1999, 216, 547–550. [Google Scholar] [CrossRef]
- Bayerl, M.W.; Brandt, M.S.; Ambacher, O.; Stutzmann, M.; Glaser, E.R.; Henry, R.L.; Wickenden, A.E.; Koleske, D.D.; Suski, T.; Grzegory, I.; et al. Optically detected magnetic resonance of red and near-infrared luminescence in Mg-doped GaN. Phys. Rev. B 2001, 63, 125203. [Google Scholar] [CrossRef]
- Zajac, M.; Konczewicz, L.; Litwin-Staszewska, E.; Iwinska, M.; Kucharski, R.; Juillaguet, S.; Contreras, S. P-type conductivity in GaN:Zn monocrystals grown by ammonothermal method. J. Appl. Phys. 2021, 129, 135702. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Two-step thermal quenching of photoluminescence in Zn-doped GaN. Phys. Rev. B 2012, 85, 245203. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Olsen, A.J.; Bishop, M.F.; McMullen, T. Superlinear increase of photoluminescence with excitation intensity in Zn-doped GaN. Phys. Rev. B. 2013, 88, 075204. [Google Scholar] [CrossRef]
- Monemar, B.; Lagerstedt, O.; Gislason, H.P. Properties of Zn-doped VPE-grown GaN. I. Luminescence data in relation to doping conditions. J. Appl. Phys. 1980, 51, 625–639. [Google Scholar] [CrossRef]
- Pankove, J.I. Luminescence in GaN. J. Lumin. 1973, 7, 114–126. [Google Scholar] [CrossRef]
- Shi, L.; Xu, K.; Wang, L.-W. Comparative study of ab initio nonradiative recombination rate calculations under different formalisms. Phys. Rev. B 2015, 91, 205315. [Google Scholar] [CrossRef]
- Bergman, P.; Ying, G.; Monemar, B.; Holtz, P.O. Time-resolved spectroscopy of Zn- and Cd-doped GaN. J. Appl. Phys. 1987, 61, 4589–4592. [Google Scholar] [CrossRef]
- Henry, M.O.; Deicher, M.; Magerle, R.; McGlynn, E.; Stötzler, A. Photoluminescence analysis of semiconductors using radioactive isotopes. Hyperfine Interact. 2000, 129, 443–460. [Google Scholar] [CrossRef]
- Stötzler, A.; Weissenborn, R.; Deicher, M.; The ISOLDE Collaboration. Identification of Ag and Cd in photoluminescence in 111Ag-doped GaN. Phys. B 1999, 273–274, 144–147. [Google Scholar] [CrossRef]
- Monteiro, T.; Boemare, C.; Soares, M.J.; Alves, E.; Liu, C. Green and red emission in Ca implanted GaN samples. Phys. B 2001, 308–310, 42–46. [Google Scholar] [CrossRef]
- Shen, J.-X.; Wickramaratne, D.; Dreyer, C.E.; Alkauskas, A.; Young, E.; Speck, J.S.; Van de Walle, C.G. Calcium as a nonradiative recombination center in InGaN. Appl. Phys. Express 2017, 10, 021001. [Google Scholar] [CrossRef]
- Lyons, J.L.; Wickramaratne, D.; Van de Walle, C.G. A first-principles understanding of point defects and impurities in GaN. J. Appl. Phys. 2021, 129, 111101. [Google Scholar] [CrossRef]
- Eider, E.; Grimmeiss, H.G. Optical Investigations of Zn, Hg and Li Doped GaN. Appl. Phys. 1974, 5, 275–279. [Google Scholar]
- Van de Walle, C.G.; Neugebauer, J. Arsenic impurities in GaN. Appl. Phys. Lett. 2000, 76, 1009–1011. [Google Scholar] [CrossRef]
- Mattila, T.; Zunger, A. Deep electronic gap levels induced by isovalent P and As impurities in GaN. Phys. Rev. B 1998, 58, 1367–1373. [Google Scholar] [CrossRef]
- Gil, B.; Morel, A.; Taliercio, T.; Lefebre, P.; Foxon, C.T.; Winser, A.J.; Novikov, S.V. Carrier relaxation dynamics for As defects in GaN. Appl. Phys. Lett. 2001, 79, 69–71. [Google Scholar] [CrossRef]
- Li, X.; Kim, S.; Reuter, E.E.; Bishop, S.G.; Coleman, J.J. The incorporation of arsenic in GaN by metalorganic chemical vapor deposition. Appl. Phys. Lett. 1998, 72, 1990–1992. [Google Scholar] [CrossRef]
- Jin, S.R.; Ramsteiner, M.; Grahn, H.T.; Ploog, K.H.; Zhu, Z.Q.; Shen, D.X.; Li, A.Z.; Metev, P.; Guido, L.J. Suppression of yellow luminescence in As-doped GaN epilayers grown by metalorganic chemical vapor deposition. J. Cryst. Growth 2000, 212, 56–60. [Google Scholar] [CrossRef]
- Guido, L.J.; Mitev, P.; Gherasimova, M.; Gaffey, B. Electronic properties of arsenic-doped gallium nitride. Appl. Phys. Lett. 1998, 72, 2005–2007. [Google Scholar] [CrossRef]
- Sierakowski, K.; Jakiela, R.; Jaroszynski, P.; Fijalkowski, M.; Sochacki, T.; Iwinska, M.; Turek, M.; Uedono, A.; Reshchikov, M.A.; Bockowski, M. Analysis of Zn diffusion in various crystallographic directions of GaN grown by HVPE. Mater. Sci. Semicond. Process. 2023, 167, 107808. [Google Scholar] [CrossRef]
- Skromme, B.J.; Martinez, G.L.; Suvkhanov, A.; Krasnobaev, L.; Poker, D.B. Optical characterization of acceptor implantation in GaN. In High-Speed Compound Semiconductor Devices for Wireless Applications and State-of-the-Art Program on Compound Semiconductors (XXXIII); Baca, A.G., Kopf, R.F., Eds.; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2000; Volume 2000-18, pp. 120–131. ISBN 1-56677-285-0. [Google Scholar]
- Zhao, F.; Turiansky, M.E.; Alkauskas, A.; Van de Walle, C.G. Trap-Assisted Auger-Meitner Recombination from First Principles. Phys. Rev. Lett. 2023, 131, 056402. [Google Scholar] [CrossRef] [PubMed]
- Espenlaub, A.C.; Myers, D.J.; Young, E.C.; Marcinkevičius, S.; Weisbuch, C.; Speck, J.S. Evidence of trap-assisted Auger recombination in low radiative efficiency MBE-grown III-nitride LEDs. J. Appl. Phys. 2019, 126, 184502. [Google Scholar] [CrossRef]
- Lähnemann, J.; Kaganer, V.M.; Sabelfeld, K.K.; Kireeva, A.E.; Jahn, U.; Chèze, C.; Calarco, R.; Brandt, O. Carrier Diffusion in GaN: A Cathodoluminescence Study. III. Nature of Nonradiative Recombination at Threading Dislocations. Phys. Rev. Appl. 2022, 17, 024019. [Google Scholar] [CrossRef]
- Xu, Z.; Daeumer, M.; Cho, M.; Yoo, J.-H.; Detchprohm, T.; Bakhtiary-Noodeh, M.; Shao, Q.; Laurence, T.A.; Key, D.; Letts, E.; et al. Breakdown characteristics analysis of kV-class vertical GaN PIN rectifiers by wafer-level sub-bandgap photoluminescence mapping. J. Appl. Phys. 2024, 135, 205704. [Google Scholar] [CrossRef]
- Pauc, N.; Phillips, M.R.; Aimez, V.; Drouin, D. Carrier recombination near threading dislocations in GaN epilayers by low voltage cathodoluminescence. Appl. Phys. Lett. 2006, 89, 161905. [Google Scholar] [CrossRef]
- Shiozaki, N.; Hashizume, T. Improvements of electronic and optical characteristics of n-GaN-based structures by photoelectrochemical oxidation in glycol solution. J. Appl. Phys. 2009, 105, 064912. [Google Scholar] [CrossRef]
- Martinez, G.L.; Curiel, M.R.; Skromme, B.J.; Molnar, R.J. Surface recombination and sulfide passivation of GaN. J. Electron. Mat. 2000, 29, 325–331. [Google Scholar] [CrossRef]
- Liu, W.; Sun, X.; Zhang, S.; Chen, J.; Wang, H.; Wang, X.; Zhao, D.; Yang, H. Photoluminescence degradation in GaN induced by light enhanced surface oxidation. J. Appl. Phys. 2007, 102, 076112. [Google Scholar] [CrossRef]
- Pfüller, C.; Brandt, O.; Grosse, F.; Flissikowski, T.; Cheze, C.; Consonni, V.; Geelhaar, L.; Grahn, H.T.; Riechert, H. Unpinning the Fermi level of GaN nanowires by ultraviolet radiation. Phys. Rev. B 2010, 82, 045320. [Google Scholar] [CrossRef]
- Reshchikov, M.A. Strong suppression of the yellow luminescence in GaN in air ambient. Appl. Phys. Lett. 2006, 89, 232106. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Foussekis, M.; Baski, A.A. Surface photovoltage in undoped n-type GaN. J. Appl. Phys. 2010, 107, 113535. [Google Scholar] [CrossRef]
- Reshchikov, M.A.; Sabuktagin, S.; Johnstone, D.K.; Morkoç, H. Transient photovoltage in GaN as measured by atomic force microscope tip. J. Appl. Phys. 2004, 96, 2556–2560. [Google Scholar] [CrossRef]
- Barbet, S.; Aubry, R.; di Forte-Poisson, M.A.; Jacquet, J.-C.; Deresmes, D.; Melin, T.; Theron, D. Surface potential of n- and p-type GaN measured by Kelvin force microscopy. Appl. Phys. Lett. 2008, 93, 212107. [Google Scholar] [CrossRef]
- Wolkenstein, T.; Peka, G.P.; Malakhov, V.V. The influence of adsorption on the luminescence of semiconductors. Part II. Exciton luminescence. J. Lumin. 1972, 5, 261–268. [Google Scholar] [CrossRef]
- Kumakura, K.; Makimoto, T.; Kobayashi, N.; Hashizume, T.; Fukui, T.; Hasegawa, H. Minority carrier diffusion length in GaN: Dislocation density and doping concentration dependence. Appl. Phys. Lett. 2005, 86, 052105. [Google Scholar] [CrossRef]
- Matys, M.; Adamowicz, B.; Kachi, T.; Hashizume, T. Effect of carrier drift-diffusion transport process on thermal quenching of photoluminescence in GaN. J. Phys. D: Appl. Phys. 2021, 54, 055106. [Google Scholar] [CrossRef]
- Foussekis, M.A.; Baski, A.A.; Reshchikov, M.A. Electrical and optical properties of GaN studied by surface photovoltage and photoluminescence. Phys. Stat. Sol. C 2011, 8, 2148–2150. [Google Scholar] [CrossRef]
- Foussekis, M.; McNamara, J.D.; Baski, A.A.; Reshchikov, M.A. Temperature-dependent Kelvin probe measurements of band bending in p-type GaN. Appl. Phys. Lett. 2012, 101, 082104. [Google Scholar] [CrossRef]
- Long, J.P.; Bermudez, V.M. Band bending and photoemission-induced surface photovoltages on clean n- and p-GaN (0001) surfaces. Phys. Rev. B 2002, 66, 121308. [Google Scholar] [CrossRef]
- Curie, D.; Garlick, G.F.J. Luminescence in Crystals; Methuen and Co., Ltd.: London, UK, 1963; 332p. [Google Scholar]
- Riehl, N. Intrinsic defects and luminescence in II-VI compounds. J. Lumin. 1981, 24/25, 335–342. [Google Scholar] [CrossRef]
- Zvanut, M.E.; Paudel, S.; Glaser, E.R.; Iwinska, M.; Sochacki, T.; Bockowski, M. Incorporation of Carbon in Free-Standing HVPE-Grown GaN Substrates. J. Electron. Mater. 2019, 48, 2226–2232. [Google Scholar] [CrossRef]
- Zvanut, M.E.; Paudel, S.; Sunay, U.R.; Willoughby, W.R.; Iwinska, M.; Sochacki, T.; Bockowski, M. Charge transfer process for carbon-related center in semi-insulating carbon-doped GaN. J. Appl. Phys. 2018, 124, 075701. [Google Scholar] [CrossRef]
- Paudel, S.; Zvanut, M.E.; Iwinska, M.; Sochacki, T.; Bockowski, M. A Deep Carbon-Related Acceptor Identified through Photoinduced Electron Paramagnetic Resonance. Phys. Stat. Sol. B 2020, 257, 1900593. [Google Scholar] [CrossRef]
- Hofmann, D.M.; Kovalev, D.; Steude, G.; Meyer, B.K.; Hoffmann, A.; Eckey, L.; Heitz, R.; Detchprom, T.; Amano, H.; Akasaki, I. Properties of the yellow luminescence in undoped GaN epitaxial layers. Phys. Rev. B 1995, 52, 16702–16706. [Google Scholar] [CrossRef] [PubMed]
- Honda, U.; Yamada, Y.; Tokuda, Y.; Shiojima, K. Deep levels in n-GaN doped with carbon studied by deep level and minority carrier transient spectroscopies. Jap. J. Appl. Phys. 2012, 51, 04DF04. [Google Scholar] [CrossRef]
- Look, D.C. Defect-Related Donors, Acceptors, and Traps in GaN. Phys. Stat. Sol. B 2001, 228, 293–302. [Google Scholar] [CrossRef]
- Horita, M.; Narita, T.; Kachi, T.; Suda, J. Nitrogen displacement-related electron traps in n-type GaN grown on a GaN freestanding substrate. Appl. Phys. Lett. 2021, 118, 012106. [Google Scholar] [CrossRef]
- Endo, M.; Horita, M.; Suda, J. Hole traps related to nitrogen displacement in p-type GaN grown by metalorganic vapor phase epitaxy on freestanding GaN. Appl. Phys. Lett. 2022, 120, 142104. [Google Scholar] [CrossRef]
- Zajac, M.; Kaminski, P.; Kozlowski, R.; Litwin-Staszewska, E.; Piotrzkowski, R.; Grabianska, K.; Kucharski, R.; Jakiela, R. Formation of Grown-In Nitrogen Vacancies and Interstitials in Highly Mg-Doped Ammonothermal GaN. Materials 2024, 17, 1160. [Google Scholar] [CrossRef]
- Narita, T.; Horita, M.; Tomita, K.; Kachi, T.; Suda, J. Why do electron traps at EC-0.6 eV have inverse correlation with carbon concentrations in n-type GaN layer? Jap. J. Appl. Phys. 2020, 59, 105505. [Google Scholar] [CrossRef]
- Albrecht, F.; Reislöhner, U.; Hülsen, C.; Witthuhn, W.; Grillenberger, J.; Dietrich, M.; the ISOLDE collaboration. Observation of a Be-correlated donor state in GaN. Appl. Phys, Lett. 2004, 84, 3876–3878. [Google Scholar] [CrossRef]
- Polyakov, A.Y.; Lee, I.-H. Deep traps in GaN-based structures as affecting the performance of GaN devices. Mater. Sci. Eng. R Rep. 2015, 94, 1–56. [Google Scholar] [CrossRef]
- Bisi, D.; Meneghini, M.; De Santi, C.; Chini, A.; Dammann, M.; Brückner, P.; Mikulla, M.; Meneghesso, G.; Zanoni, E. Deep-Level Characterization in GaN HEMTs-Part I: Advantages and Limitations of Drain Current Transient Measurements. IEEE Trans. Electron. Devices 2013, 60, 3166–3175. [Google Scholar] [CrossRef]
- Stötzler, A.; Weissenborn, R.; Deicher, M.; The ISOLDE Collaboration. Identification of As, Ge and Se Photoluminescence in GaN Using Radioactive Isotopes. MRS Internet J. Nitride Semicond. Res. 2000, 5, 990–996. [Google Scholar] [CrossRef]
- Stötzler, A.; Deicher, M.; The ISOLDE Collaboration. Photoluminescence in platinum doped GaN. Phys. B 2003, 340–342, 377–380. [Google Scholar] [CrossRef]
- Neugebauer, J.; Van de Walle, C.G. Chemical trends for acceptor impurities in GaN. J. Appl. Phys. 1999, 85, 3003–3005. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van de Walle, C.G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014, 86, 253–305. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Nichols, L.R.; Li, G.; Yu, Y.; Jiang, J.; O’Hara, A.; Barmparis, G.D.; Pantelides, S.; Zhang, X.-G. Multiphonon carrier capture by defects in semiconductors. Phys. Rev. B 2025, 111, 045201. [Google Scholar] [CrossRef]
- Deák, P.; Aradi, B.; Frauenheim, T.; Janzén, E.; Gali, A. Accurate defect levels obtained from the HSE06 range-separated hybrid functional. Phys. Rev. B 2010, 81, 153203. [Google Scholar] [CrossRef]
- Freysoldt, C.; Neugebauer, J.; Van de Walle, C.G. Fully Ab Initio Finite-Size Corrections for Charged-Defect Supercell Calculations. Phys. Rev. Lett. 2009, 102, 016402. [Google Scholar] [CrossRef] [PubMed]
- Freysoldt, C.; Neugebauer, J.; Van de Walle, C.G. Electrostatic interactions between charged defects in supercells. Phys. Stat. Sol. B 2010, 248, 1067–1076. [Google Scholar] [CrossRef]
- Meneghini, M.; De Santi, C.; Abid, I.; Buffolo, M.; Cioni, M.; Abdul Khadar, R.; Nela, L.; Zagni, N.; Chini, A.; Medjdoub, F.; et al. GaN-based power devices: Physics, reliability, and perspectives. J. Appl. Phys. 2021, 130, 181101. [Google Scholar] [CrossRef]



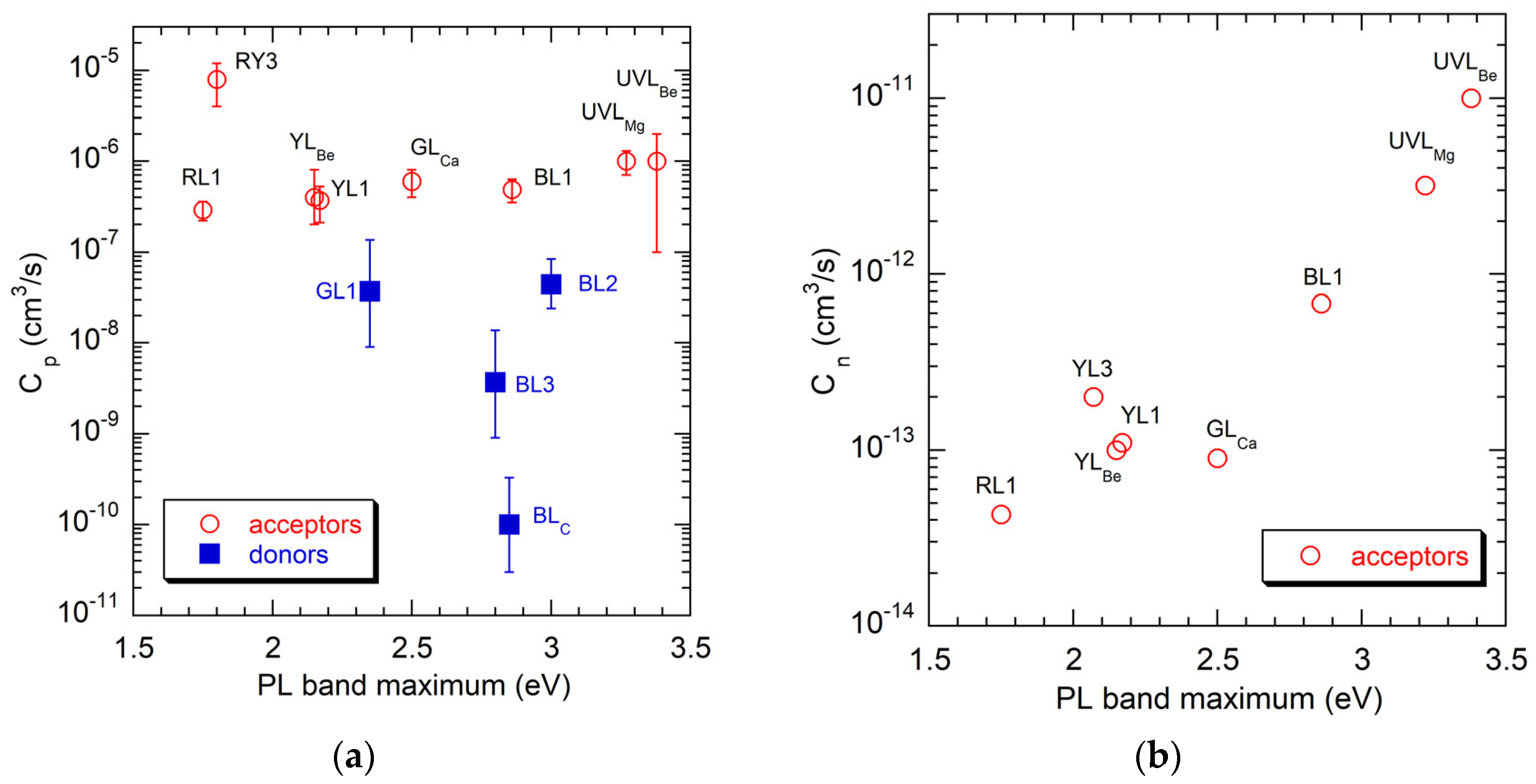



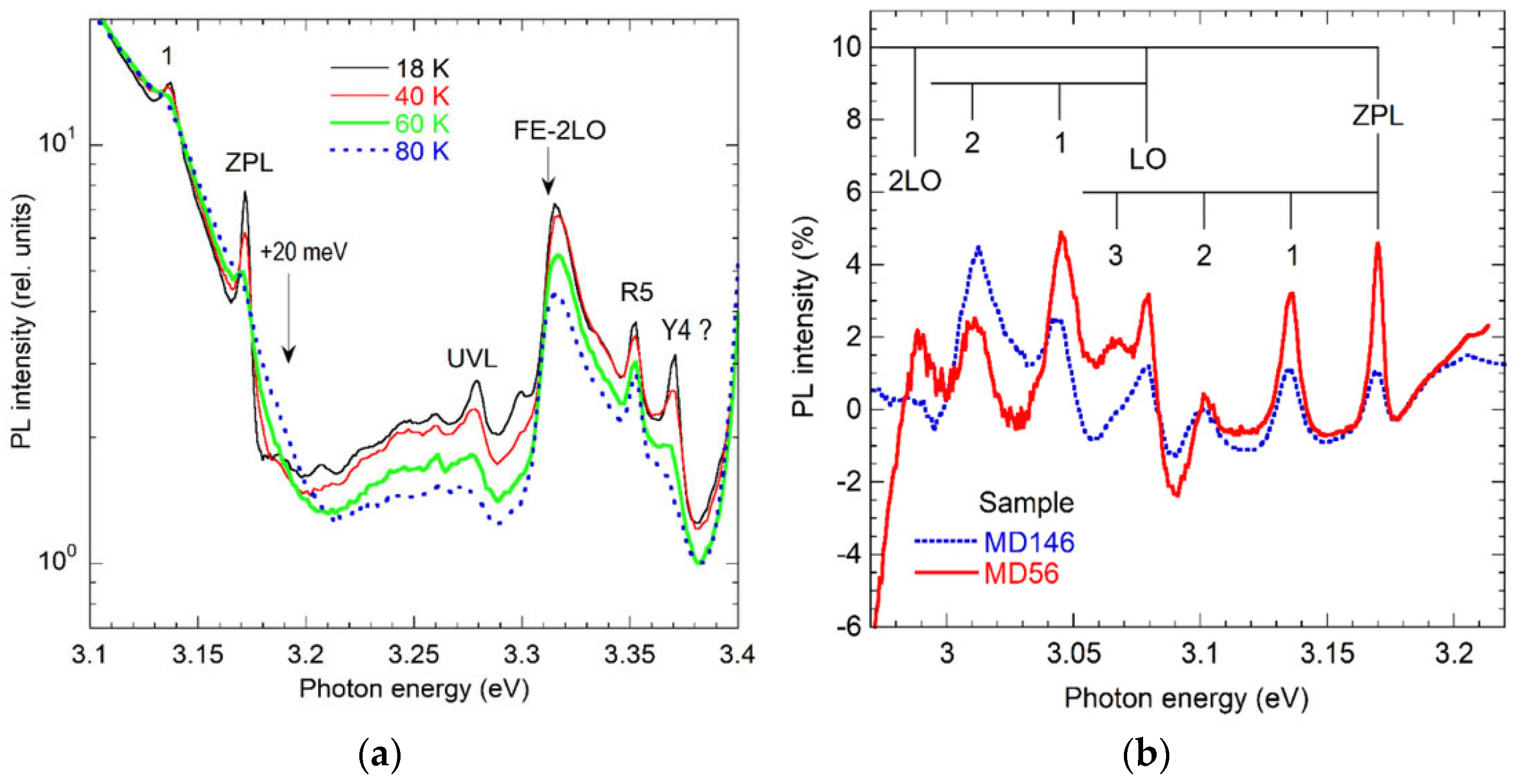
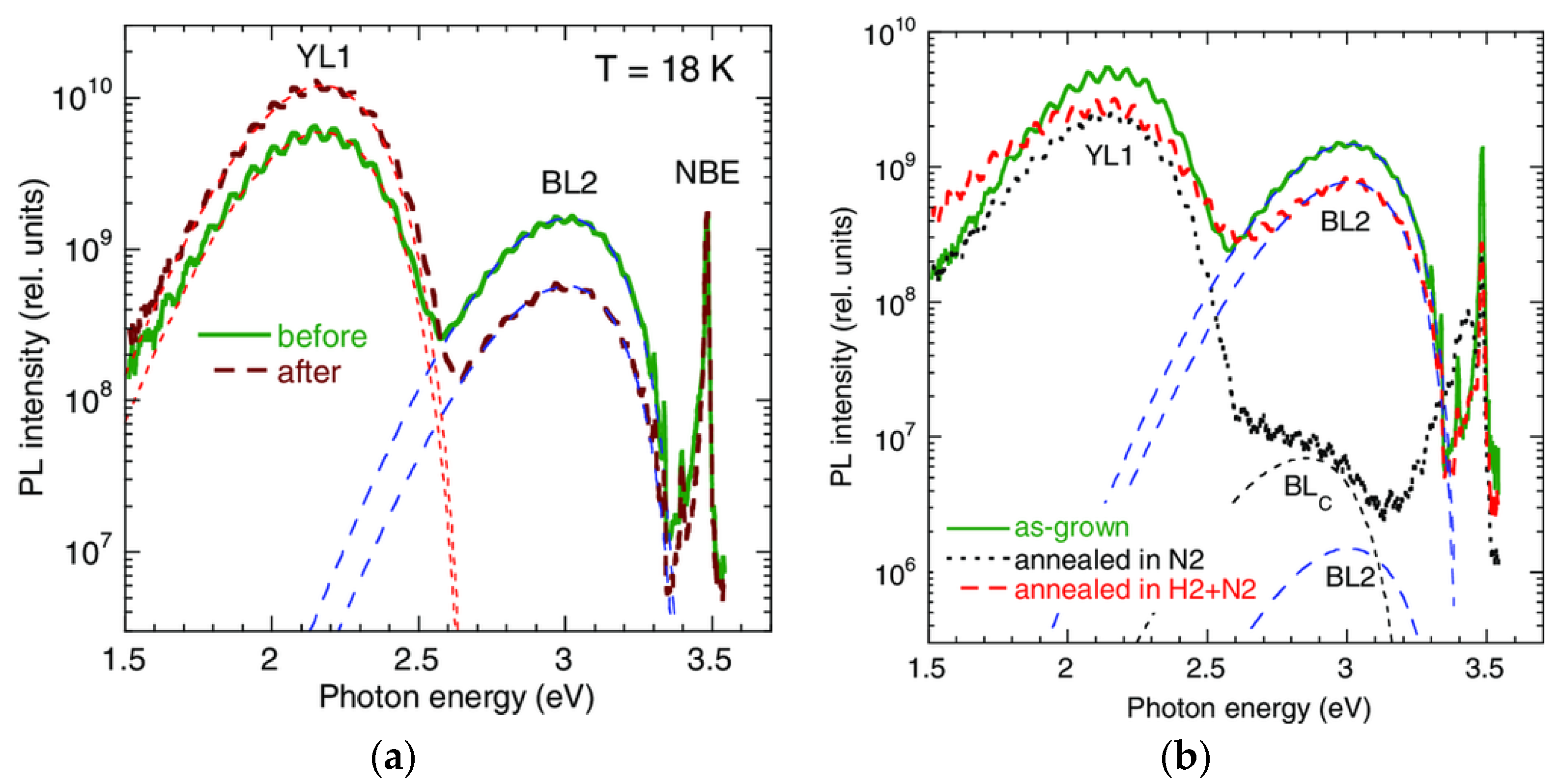
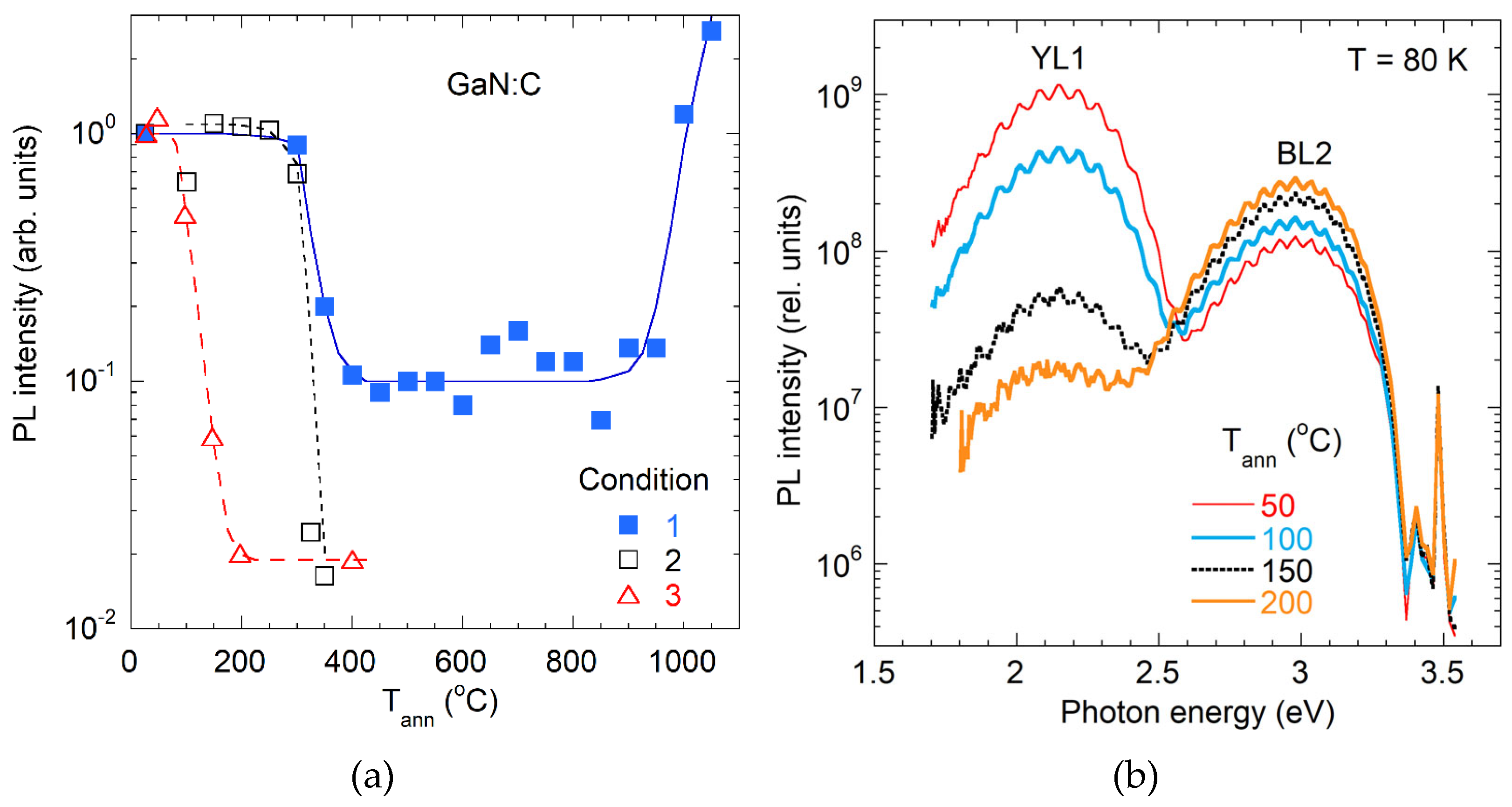
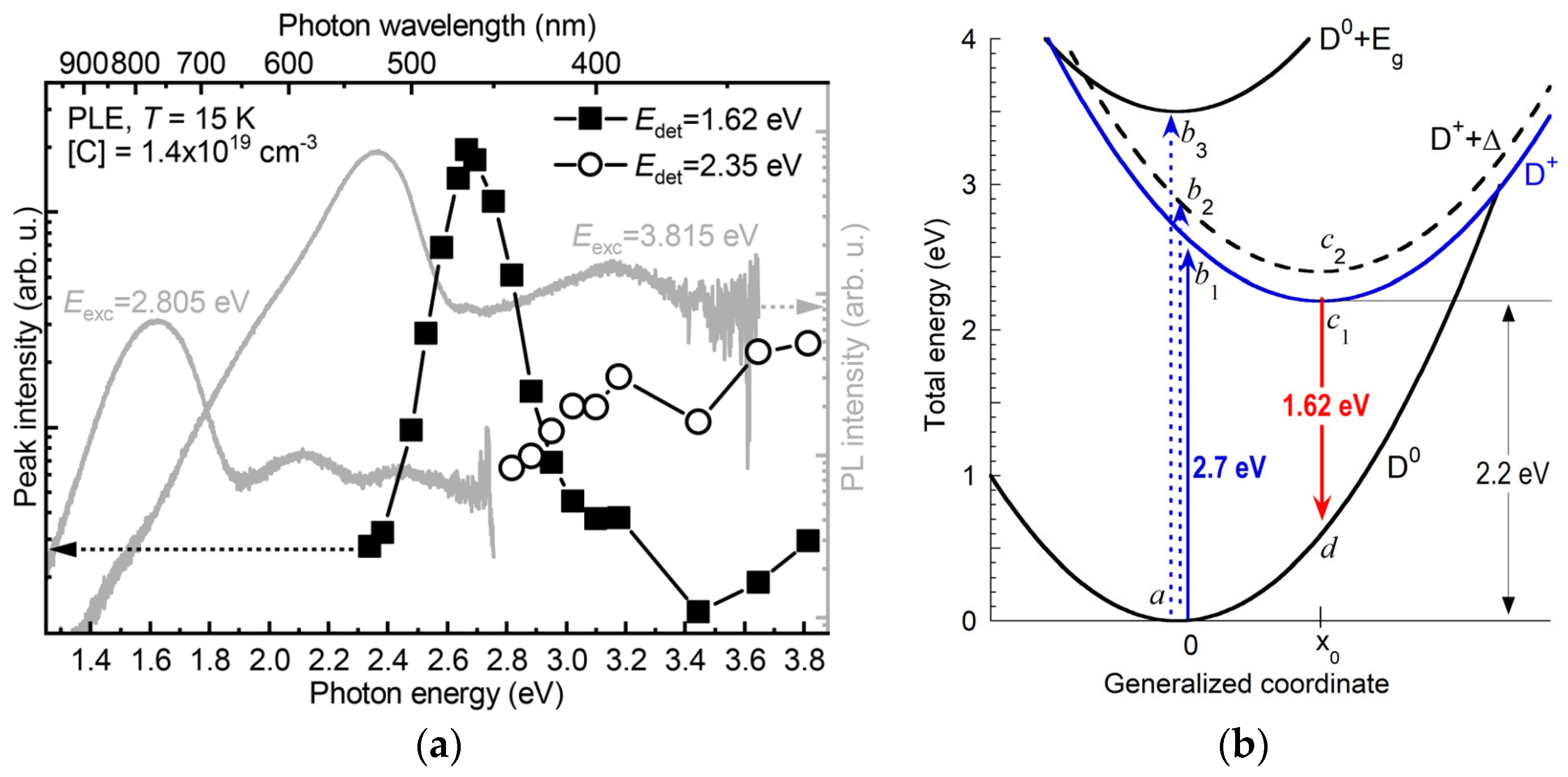






| Dopant | PL Band | ħωmax (eV) | ZPL (eV) | EA (eV) | FWHM (eV) | Cp (cm3s−1) | Cn (cm3s−1) | τ (μs) a) | Attribution | Comments | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | RLC | 1.62 | CN-CGa-CN ? | [C] > 1018 cm−3 | [33] | ||||||
| − | RL1 | 1.75 | ~1.1 | 0.42 | 3 × 10−7 | 4.3 × 10−14 | Cl? (−/0)? | HVPE GaN | [34] | ||
| − | RL2 | 1.74 | ~1 | 0.35 | 1000 | AVN? (0/+)? | SI, Ga-rich GaN | [16,35,36,37] | |||
| Mg | RLMg | 1.67 | ~0.9 | 0.41 | 1.3 | MgGaVN (0/+) | [36] | ||||
| Be | RLBe | 1.77 | ~0.8 | 0.44 | 3 | BeGaVN (0/+) | [36] | ||||
| Ca | RLCa | 1.82 | ~1.0 | 0.43 | 1900 | CaGaVN (0/+) | [36] | ||||
| − | RL3 | 1.77 | ~2.8 | 0.38 | ~10−5 | 0.010 | RY3 (−/0) | HVPE GaN | [38] | ||
| − | RL4 | 1.6–1.7 | ~1.2 | ~0.44 | VGa3ON ? (0/+)? | AT GaN | [39] | ||||
| F,Cl,Cd,Ca,Hg | RL5 | ~1.6 | ? | Implantation damage | |||||||
| F | OL1 | 1.88 | ~0.47 | VGaFN? | |||||||
| - | OL3 | 2.09 | ~0.47 | VGaON2Hi? (0/+)? | AT GaN | [39] | |||||
| − C | YL1, YLC | 2.19 | 2.59 | 0.916 | 0.43 | 3.7 × 10−7 | 1.1 × 10−13 | CN (−/0) | Omnipresent, MOCVD | [25,40,41] | |
| − | YL2 | 2.3 | ~0.6 | ~0.49 | VGa3Hi ? (0/+)? | AT GaN | [39,41,42] | ||||
| − | YL3 | 2.07 | 2.38 | 1.130 | 0.40 | ~10−7 | 2 × 10−13 | RY3 (−/0) | HVPE GaN | [38,41,43,44] | |
| Be | YLBe | 2.15 | 0.34 | 0.57 | ~1 × 10−6 | 1 × 10−13 | BeGa (−/0) | YLBe1, YLBe2 | [45,46] | ||
| − | GL1 | 2.35 | ~0.5 | 0.48 | 1 | ? (0/+) | HVPE GaN | [34] | |||
| − | GL2 | 2.33 | ~0.5 | 0.24 | 300 | VN (+/2+) | SI, Ga-rich GaN | [34,47] | |||
| Hg | GLHg | 2.44 | 0.8 | 0.39 | (1–5) × 10−7 | 3 × 10−13 | HgGa (−/0) | [48] | |||
| − Ca | GLCa | 2.49 | 0.50 | 0.43 | 6 × 10−7 | 1 × 10−13 | CaGa (−/0) | undoped MBE | [49] | ||
| − Zn | BL1, BLZn | 2.86 | 3.10 | 0.400 | 0.36 | 5 × 10−7 | 6.8 × 10−13 | ZnGa (−/0) | Dual nature? | [34,50,51,52,53,54] | |
| − C | BL2 | 3.00 | 3.33 | 0.15 | 0.42 | 4.5 × 10−8 | 0.3 | CNHi (0/+) | Bleaching | [55] | |
| − | BL3 | 2.8 | 3.01 | ~0.46 | 0.45 | ~10−9 | 0.001 | RY3 (0/+) | HVPE GaN | [56] | |
| P | BLP | 2.89 | 3.20 | 0.29 | 0.37 | PN (0/+) | [57,58] | ||||
| As | BLAs | 2.6 | 2.95 | 0.54 | ~0.4 | 0.09 | AsN (0/+) | [57] | |||
| Cd | BLCd | 2.70 | 2.95 | 0.55 | 0.35 | 3 × 10−7 | 2.6 × 10−13 | CdGa (−/0) | [48,59] | ||
| C | BLC | 2.85 | 3.15 | 0.33 | ~0.43 | 10−10 ? | 0.001 | CN (0/+) | [25,60] | ||
| Be | BLBe | 2.6 | 0.15 | 0.57 | ~10−8 | 0.8 | BeGa (0/+) ? | [61] | |||
| Mg | BLMg | ~2.8 | 0.22 | ~0.3 | DD→MgGa | Large shifts | [62,63] | ||||
| − Mg | UVL, UVLMg | 3.28 | 3.28 | 0.223 | 0.01 | 1 × 10−6 | 3.2 × 10−12 | MgGa (−/0) | Dual nature? | [40,62,63] | |
| Be | UVLBe | 3.38 | 3.38 | 0.113 | 0.01 | ~1 × 10−6 | 1 × 10−11 | BeGaONBeGa (−/0) | Dual nature? | [64] |
| PL Band | ħωmax (eV) | E0* (eV) | Se | dFCg (eV) | W0 (eV) | ħΩe (eV) |
|---|---|---|---|---|---|---|
| RL1 | 1.73 | 2.3 | 9.5 | 0.57 | 0.42 | |
| RL2 | 1.74 | 2.3 | 12.5 | 0.56 | 0.35 | 0.033 |
| RLMg | 1.67 | 2.6 | 27 | 0.93 | 0.41 | |
| RLBe | 1.78 | 2.65 | 20 | 0.87 | 0.44 | 0.042 |
| RLCa | 1.82 | 2.23 | 15 | 0.41 | 0.25 | 0.027 |
| RL4 | 1.6–1.7 | 2.26 | 9 | 0.56–0.66 | 0.44 | |
| OL1 | 1.88 | 2.6 | 12 | 0.72 | 0.47 | |
| OL3 | 2.09 | 2.8 | 13 | 0.71 | 0.47 | |
| YL1 | 2.17 | 2.67 | 7.8 | 0.50 | 0.43 | 0.056 |
| YL2 | 2.30 | 2.86 | 7.3 | 0.56 | 0.49 | |
| YL3 | 2.07 | 2.45 | 5.0 | 0.38 | 0.40 | 0.06 |
| YLBe | 2.15 | 3.2 | 24 | 1.05 | 0.52 | 0.038 |
| GL1 | 2.35 | 2.97 | 10.3 | 0.62 | 0.48 | 0.041 |
| GL2 | 2.33 | 2.70 | 13.5 | 0.24 | 0.24 | 0.023 |
| GLHg | 2.44 | 2.7 | 5 | 0.26 | 0.39 | 0.053 |
| GLCa | 2.49 | 3.02 | 8.5 | 0.53 | 0.43 | 0.041 |
| BL1 | 2.86 | 3.10 | 3.2 | 0.36 | 0.36 | 0.043 |
| BL2 | 3.00 | 3.38 | 4.6 | 0.38 | 0.42 | |
| BL3 | 2.81 | 3.08 | 2.0 | 0.27 | 0.45 | |
| BLCd | 2.70 | 3.0 | 4.0 | 0.3 | 0.35 | 0.053 |
| BLC | 2.85 | 3.20 | 3.7 | 0.35 | 0.43 | |
| BLP | 2.88 | 0.37 | 0.050 | |||
| BLBe | 2.6 | 3.4 | 12 | 0.8 | 0.57 | |
| BLMg | 2.8 | 3.1 | 5.0 | 0.4 | 0.31 |
| PL Band | Attribution | E0 (eV) | ħωmax (eV) | ħΩLO (meV) | ħΩ1 (meV) | ħΩ2 (meV) | ħΩ3 (meV) | Reference |
|---|---|---|---|---|---|---|---|---|
| YL1 | CN (−/0) | 2.57 | 2.17 | 91.5 | − | 39.5 | − | [40] |
| YL3 | Fe? (−/0) | 2.38 | 2.07 | 91 | 19 | 36 | − | [43,44] |
| BL1 | ZnGa (−/0) | 3.10 | 2.86 | 91 | − | 36 | − | [50] |
| BL2 | CNHi (0/+) | 3.33 | 3.0 | 91.2 | − | 35.4 | 61 | [55] |
| BL3 | Fe? (0/+) | 3.01 | 2.81 | 91.3 | − | 39.6 | 68.2 | [56] |
| BLC | CN (0/+) | 3.15 | 2.85 | 91.2 | − | 34.3 | − | [60] |
| BLCd | CdGa (−/0) | 2.95 | 2.70 | 91 | − | 39 | 74 | [48,59] |
| BLAs | AsN (0/+) | 2.95 | 2.60 | 91 | − | 38 | 75 | [57] |
| BLP | PN (0/+) | 3.20 | 2.89 | 91 | − | 37–39 | 73–77 | [57] |
| UVLMg | MgGa (−/0) | 3.28 | 3.28 | 91.5 | − | − | − | [62] |
| UVLBe3 | BeGa (−/0) | 3.26 | 3.26 | 91.5 | − | − | − | [45,46] |
| UVLBe | BeGaONBeGa (−/0) | 3.38 | 3.38 | 91.5 | − | 37.5 | − | [64] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reshchikov, M.A. Luminescence Properties of Defects in GaN: Solved and Unsolved Problems. Solids 2025, 6, 52. https://doi.org/10.3390/solids6030052
Reshchikov MA. Luminescence Properties of Defects in GaN: Solved and Unsolved Problems. Solids. 2025; 6(3):52. https://doi.org/10.3390/solids6030052
Chicago/Turabian StyleReshchikov, Michael A. 2025. "Luminescence Properties of Defects in GaN: Solved and Unsolved Problems" Solids 6, no. 3: 52. https://doi.org/10.3390/solids6030052
APA StyleReshchikov, M. A. (2025). Luminescence Properties of Defects in GaN: Solved and Unsolved Problems. Solids, 6(3), 52. https://doi.org/10.3390/solids6030052







