Correlation Between C–H∙∙∙Br and N–H∙∙∙Br Hydrogen Bond Formation in Perovskite CH3NH3PbBr3: A Study Based on Statistical Analysis
Abstract
1. Introduction

2. Materials and Methods
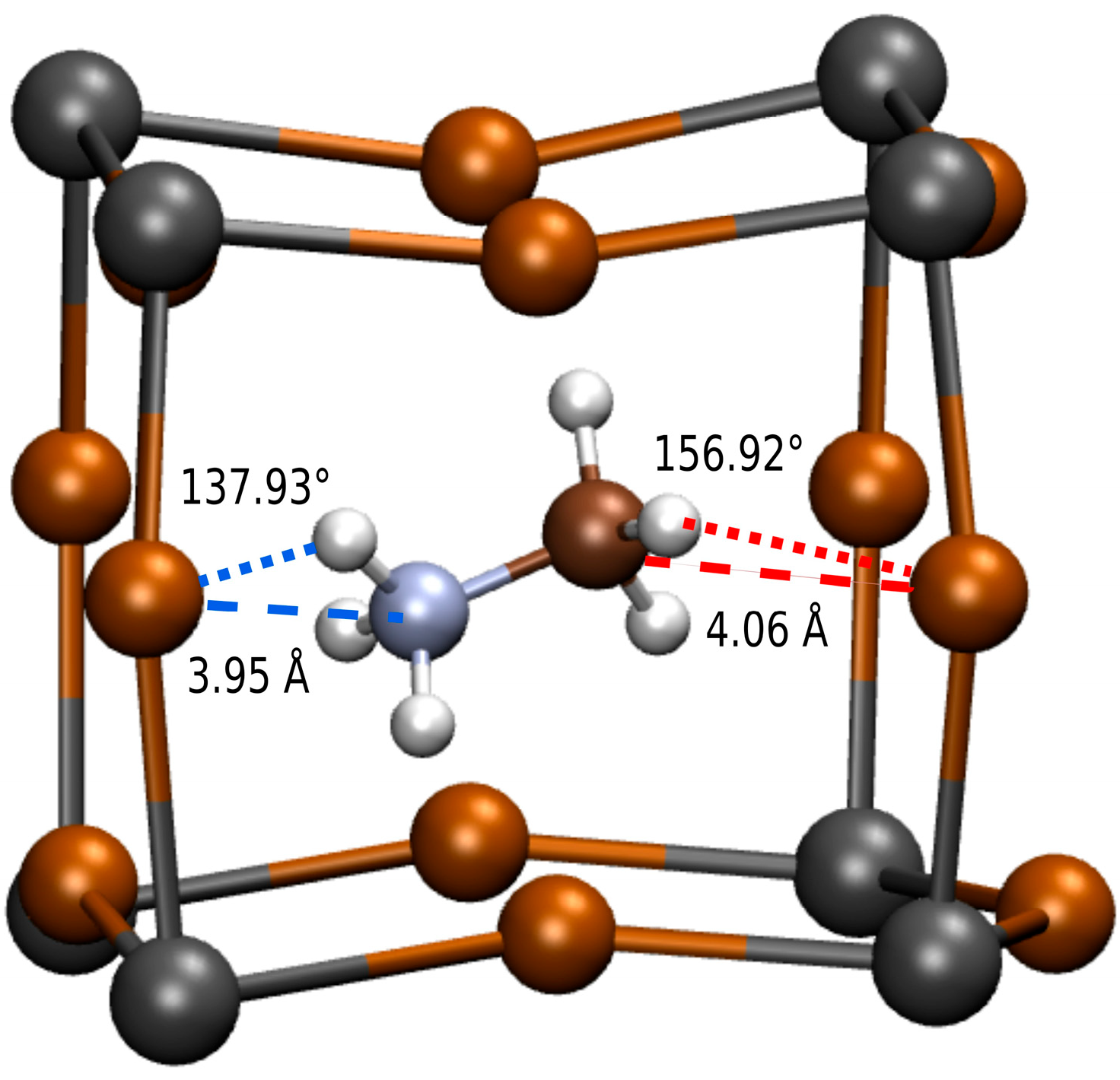
2.1. Molecular Dynamics Simulations and Hydrogen Bond Characterization
2.2. Correlation Analysis
2.3. Data Averaging and Correlation Stability Evaluation
3. Results
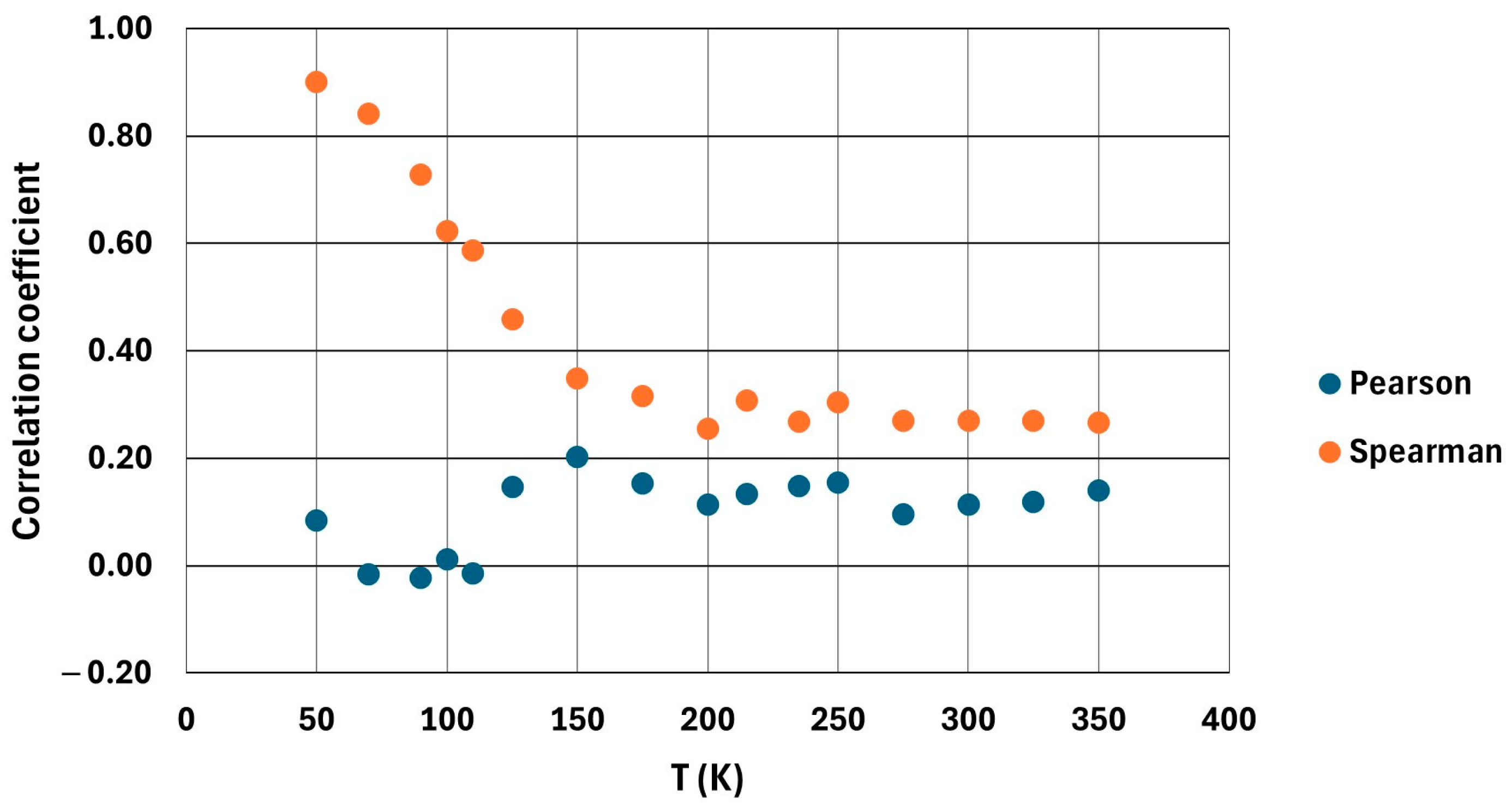
3.1. Correlation Analysis with the Complete Dataset
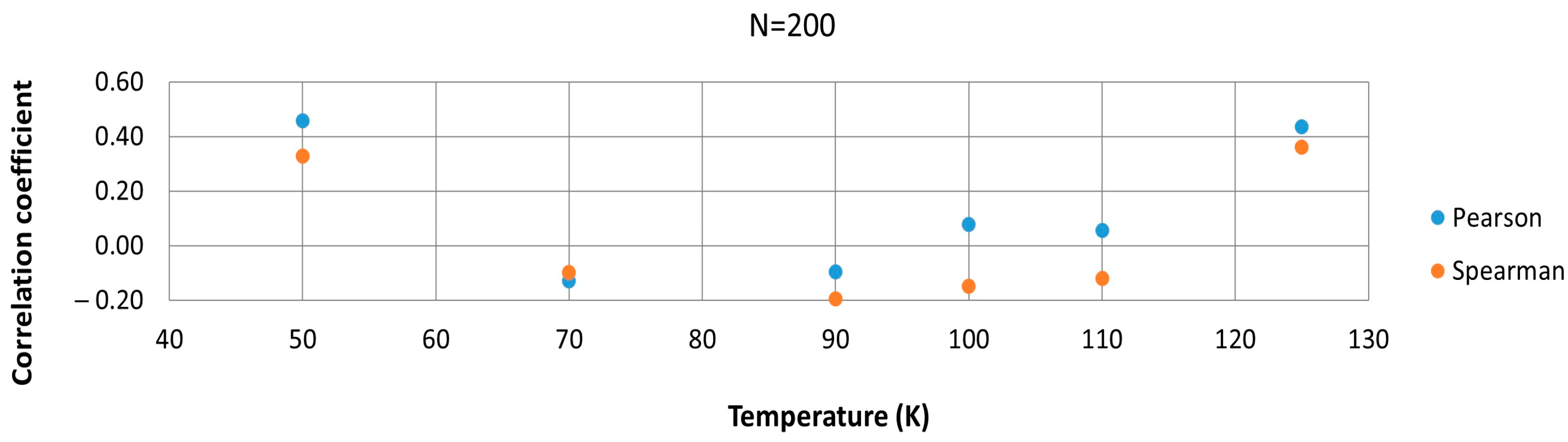
3.2. Correlation Analysis with Fragmented Dataset
3.3. Correlation Analysis with Block-Averaged Dataset
4. Discussion
5. Conclusions
- No definitive correlation was found between N–H···Br and C–H···Br formations over the temperature range studied. The analysis shows that the occurrences of N-type and C-type HBs are uncorrelated, indicating that these two types of interactions form and fluctuate independently throughout the simulations.
- The initially high Spearman correlation observed at 50 K is neither reliable nor representative of a true coupling between the two types of HB. While a Spearman ρ ≈ 0.9 at 50 K suggested a possible monotonic relationship, this turned out to be an artifact of limited sampling and specific conditions. When examining the 50 K data more rigorously, dividing them into shorter segments, and averaging/blocking the data points, the correlation coefficients varied considerably and often approached zero. This instability implies that the apparent 50 K correlation cannot be considered statistically robust or significant.
- A clear change in Spearman coefficient behavior is observed around 125 K, which coincides with the system’s phase transition region. This point marks the transition from a possible monotonic correlation at low temperatures to a weak or negligible correlation at higher temperatures, suggesting that the structural reorganization associated with the phase change affects the dynamics of HB.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HBs | Hydrogen bonds |
| IUPAC | International Union of Pure and Applied Chemistry |
| LT | Lifetime |
| MD | Molecular dynamics |
| PSC | Perovskite solar cells |
References
- Tao, S.; Schmidt, I.; Brocks, G.; Jiang, J.; Tranca, I.; Meerholz, K.; Olthof, S. Absolute Energy Level Positions in Tin- and Lead-Based Halide Perovskites. Nat. Commun. 2019, 10, 2560. [Google Scholar] [CrossRef] [PubMed]
- Jellicoe, T.C.; Richter, J.M.; Glass, H.F.J.; Tabachnyk, M.; Brady, R.; Dutton, S.E.; Rao, A.; Friend, R.H.; Credgington, D.; Greenham, N.C.; et al. Synthesis and Optical Properties of Lead-Free Cesium Tin Halide Perovskite Nanocrystals. J. Am. Chem. Soc. 2016, 138, 2941–2944. [Google Scholar] [CrossRef]
- Savill, K.J.; Ulatowski, A.M.; Herz, L.M. Optoelectronic Properties of Tin–Lead Halide Perovskites. ACS Energy Lett. 2021, 6, 2413–2426. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, C.; Chen, H.; Lv, M.; Liu, T.; Chen, H.; Xue, D.-J.; Hu, J.-S.; Han, L.; Yang, S.; et al. Oriented Attachment of Tin Halide Perovskites for Photovoltaic Applications. ACS Energy Lett. 2023, 8, 1590–1596. [Google Scholar] [CrossRef]
- Kaiser, W.; Ricciarelli, D.; Mosconi, E.; Alothman, A.A.; Ambrosio, F.; De Angelis, F. Stability of Tin- versus Lead-Halide Perovskites: Ab Initio Molecular Dynamics Simulations of Perovskite/Water Interfaces. J. Phys. Chem. Lett. 2022, 13, 2321–2329. [Google Scholar] [CrossRef]
- Seo, J.; Noh, J.H.; Seok, S. Il Rational Strategies for Efficient Perovskite Solar Cells. Acc. Chem. Res. 2016, 49, 562–572. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Khadka, D.B.; Shirai, Y.; Yanagida, M.; Ryan, J.W.; Song, Z.; Barker, B.G.; Dhakal, T.P.; Miyano, K. Advancing Efficiency and Stability of Lead, Tin, and Lead/Tin Perovskite Solar Cells: Strategies and Perspectives. Solar RRL 2023, 7, 2300535. [Google Scholar] [CrossRef]
- NREL Chart on Record Cell Efficiencies. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 23 April 2025).
- Zhu, M.; Cao, G.; Zhou, Z. Recent Progress toward Highly Efficient Tin-Based Perovskite (ASnX3) Solar Cells. Nano Select 2021, 2, 1023–1054. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, J.-W.; Jung, H.S.; Shin, H.; Park, N.-G. High-Efficiency Perovskite Solar Cells. Chem. Rev. 2020, 120, 7867–7918. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Hao, Y.; Zhu, M.; Cao, G.; Zhou, Z. Hydrogen Bonds in Perovskite for Efficient and Stable Photovoltaic †. Chin. J. Chem. 2024, 42, 1284–1306. [Google Scholar] [CrossRef]
- Gu, S.; Lin, R.; Han, Q.; Gao, Y.; Tan, H.; Zhu, J. Tin and Mixed Lead–Tin Halide Perovskite Solar Cells: Progress and Their Application in Tandem Solar Cells. Adv. Mater. 2020, 32, 1907392. [Google Scholar] [CrossRef]
- Ramadan, A.J.; Oliver, R.D.J.; Johnston, M.B.; Snaith, H.J. Methylammonium-Free Wide-Bandgap Metal Halide Perovskites for Tandem Photovoltaics. Nat. Rev. Mater. 2023, 8, 822–838. [Google Scholar] [CrossRef]
- Aktas, E.; Rajamanickam, N.; Pascual, J.; Hu, S.; Aldamasy, M.H.; Di Girolamo, D.; Li, W.; Nasti, G.; Martínez-Ferrero, E.; Wakamiya, A.; et al. Challenges and Strategies toward Long-Term Stability of Lead-Free Tin-Based Perovskite Solar Cells. Commun. Mater. 2022, 3, 104. [Google Scholar] [CrossRef]
- McGovern, L.; Futscher, M.H.; Muscarella, L.A.; Ehrler, B. Understanding the Stability of MAPbBr3 versus MAPbI3: Suppression of Methylammonium Migration and Reduction of Halide Migration. J. Phys. Chem. Lett. 2020, 11, 7127–7132. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Y.; Chen, H.; Xu, J.; Liu, A.; Bati, A.S.R.; Zhu, H.; Grater, L.; Hadke, S.S.; Huang, C.; et al. Bimolecularly Passivated Interface Enables Efficient and Stable Inverted Perovskite Solar Cells. Science 2023, 382, 810–815. [Google Scholar] [CrossRef]
- Li, T.; Xu, J.; Lin, R.; Teale, S.; Li, H.; Liu, Z.; Duan, C.; Zhao, Q.; Xiao, K.; Wu, P.; et al. Inorganic Wide-Bandgap Perovskite Subcells with Dipole Bridge for All-Perovskite Tandems. Nat. Energy 2023, 8, 610–620. [Google Scholar] [CrossRef]
- Zhao, Y.; Heumueller, T.; Zhang, J.; Luo, J.; Kasian, O.; Langner, S.; Kupfer, C.; Liu, B.; Zhong, Y.; Elia, J.; et al. A Bilayer Conducting Polymer Structure for Planar Perovskite Solar Cells with over 1,400 Hours Operational Stability at Elevated Temperatures. Nat. Energy 2021, 7, 144–152. [Google Scholar] [CrossRef]
- Li, G.; Su, Z.; Canil, L.; Hughes, D.; Aldamasy, M.H.; Dagar, J.; Trofimov, S.; Wang, L.; Zuo, W.; Jerónimo-Rendon, J.J.; et al. Highly Efficient P-i-n Perovskite Solar Cells That Endure Temperature Variations. Science 2023, 379, 399–403. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Bi, E.; Jiang, F.; Park, S.M.; Li, Y.; Chen, L.; Wang, Z.; Zeng, L.; Chen, H.; et al. Rational Design of Lewis Base Molecules for Stable and Efficient Inverted Perovskite Solar Cells. Science 2023, 379, 690–694. [Google Scholar] [CrossRef]
- Bai, S.; Da, P.; Li, C.; Wang, Z.; Yuan, Z.; Fu, F.; Kawecki, M.; Liu, X.; Sakai, N.; Wang, J.T.-W.; et al. Planar Perovskite Solar Cells with Long-Term Stability Using Ionic Liquid Additives. Nature 2019, 571, 245–250. [Google Scholar] [CrossRef] [PubMed]
- Doherty, T.A.S.; Nagane, S.; Kubicki, D.J.; Jung, Y.-K.; Johnstone, D.N.; Iqbal, A.N.; Guo, D.; Frohna, K.; Danaie, M.; Tennyson, E.M.; et al. Stabilized Tilted-Octahedra Halide Perovskites Inhibit Local Formation of Performance-Limiting Phases. Science 2021, 374, 1598–1605. [Google Scholar] [CrossRef] [PubMed]
- Tavakoli, M.M.; Bi, D.; Pan, L.; Hagfeldt, A.; Zakeeruddin, S.M.; Grätzel, M. Adamantanes Enhance the Photovoltaic Performance and Operational Stability of Perovskite Solar Cells by Effective Mitigation of Interfacial Defect States. Adv. Energy Mater. 2018, 8, 1800275. [Google Scholar] [CrossRef]
- Saleh, G.; Biffi, G.; Di Stasio, F.; Martín-García, B.; Abdelhady, A.L.; Manna, L.; Krahne, R.; Artyukhin, S. Methylammonium Governs Structural and Optical Properties of Hybrid Lead Halide Perovskites through Dynamic Hydrogen Bonding. Chem. Mater. 2021, 33, 8524–8533. [Google Scholar] [CrossRef]
- Ibaceta-Jaña, J.; Chugh, M.; Novikov, A.S.; Mirhosseini, H.; Kühne, T.D.; Szyszka, B.; Wagner, M.R.; Muydinov, R. Do Lead Halide Hybrid Perovskites Have Hydrogen Bonds? J. Phys. Chem. C. 2022, 126, 16215–16226. [Google Scholar] [CrossRef]
- Maity, S.; Verma, S.; Ramaniah, L.M.; Srinivasan, V. Deciphering the Nature of Temperature-Induced Phases of MAPbBr3 by Ab Initio Molecular Dynamics. Chem. Mater. 2022, 34, 10459–10469. [Google Scholar] [CrossRef]
- Svane, K.L.; Forse, A.C.; Grey, C.P.; Kieslich, G.; Cheetham, A.K.; Walsh, A.; Butler, K.T. How Strong Is the Hydrogen Bond in Hybrid Perovskites? J. Phys. Chem. Lett. 2017, 8, 6154–6159. [Google Scholar] [CrossRef]
- Garrote-Márquez, A.; Lodeiro, L.; Suresh, R.; Cruz Hernández, N.; Grau-Crespo, R.; Menéndez-Proupin, E. Hydrogen Bonds in Lead Halide Perovskites: Insights from Ab Initio Molecular Dynamics. J. Phys. Chem. C 2023, 127, 15901–15910. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Defining the Hydrogen Bond: An Account (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 1619–1636. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the Hydrogen Bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Significance of Hydrogen Bonding and Other Noncovalent Interactions in Determining Octahedral Tilting in the CH3NH3PbI3 Hybrid Organic-Inorganic Halide Perovskite Solar Cell Semiconductor. Sci. Rep. 2019, 9, 50. [Google Scholar] [CrossRef] [PubMed]
- Garrote-Márquez, A.; Lodeiro, L.; Hernández, N.C.; Liang, X.; Walsh, A.; Menéndez-Proupin, E. Picosecond Lifetimes of Hydrogen Bonds in the Halide Perovskite CH3NH3PbBr3. J. Phys. Chem. C 2024, 128, 20947–20956. [Google Scholar] [CrossRef]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A Free Analyzer for Trajectories from Molecular Simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lange, O.F.; Grubmüller, H. Full Correlation Analysis of Conformational Protein Dynamics. Proteins 2008, 70, 1294–1312. [Google Scholar] [CrossRef] [PubMed]
- Diez, G.; Nagel, D.; Stock, G. Correlation-Based Feature Selection to Identify Functional Dynamics in Proteins. J. Chem. Theory Comput. 2022, 18, 5079–5088. [Google Scholar] [CrossRef]
- Nagel, D.; Diez, G.; Stock, G. Accurate Estimation of the Normalized Mutual Information of Multidimensional Data. J. Chem. Phys. 2024, 161, 054108. [Google Scholar] [CrossRef] [PubMed]
- McClendon, C.L.; Friedland, G.; Mobley, D.L.; Amirkhani, H.; Jacobson, M.P. Quantifying Correlations Between Allosteric Sites in Thermodynamic Ensembles. J. Chem. Theory Comput. 2009, 5, 2486–2502. [Google Scholar] [CrossRef]
- Weaver, K.F.; Morales, V.; Dunn, S.L.; Godde, K.; Weaver, P.F. Pearson’s and Spearman’s Correlation. In An Introduction to Statistical Analysis in Research; Weaver, K.F., Morales, V., Dunn, S.L., Godde, K., Weaver, P.F., Eds.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Xiao, C.; Ye, J.; Esteves, R.M.; Rong, C. Using Spearman’s Correlation Coefficients for Exploratory Data Analysis on Big Dataset. Concurr. Comput. 2016, 28, 3866–3878. [Google Scholar] [CrossRef]
- Nosé, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Klarbring, J.; Baldwin, W.J.; Li, Z.; Csányi, G.; Walsh, A. Structural Dynamics Descriptors for Metal Halide Perovskites. J. Phys. Chem. C 2023, 127, 19141–19151. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Liu, Y.; Wang, S.; Wang, L. Effective Prediction of Short Hydrogen Bonds in Proteins via Machine Learning Method. Sci. Rep. 2022, 12, 469. [Google Scholar] [CrossRef] [PubMed]

| PEARSON | ||||||
| Temperature/Frames | 10,000 | 20,000 | 30,000 | 40,000 | 50,000 | 60,000 |
| 50 | −0.24 | 0.13 | 0.10 | 0.08 | 0.12 | 0.08 |
| 70 | −0.05 | −0.02 | −0.05 | −0.04 | −0.05 | −0.02 |
| 90 | −0.02 | −0.02 | 0.01 | −0.03 | −0.02 | −0.02 |
| 100 | 0.10 | 0.06 | 0.05 | 0.02 | 0.02 | 0.01 |
| 110 | 0.08 | 0.04 | −0.03 | 0.01 | 0.00 | −0.01 |
| 125 | 0.12 | 0.14 | 0.16 | 0.15 | 0.14 | 0.15 |
| Temperature/Frames | 5000 | 10,000 | 15,000 | 20,000 | ||
| 150 | 0.07 | 0.10 | 0.22 | 0.20 | ||
| 175 | 0.19 | 0.20 | 0.13 | 0.15 | ||
| 200 | 0.15 | 0.11 | 0.10 | 0.11 | ||
| 215 | 0.01 | 0.12 | 0.12 | 0.13 | ||
| 235 | 0.19 | 0.15 | 0.14 | 0.15 | ||
| 250 | 0.12 | 0.20 | 0.18 | 0.15 | ||
| 275 | 0.10 | 0.12 | 0.09 | 0.10 | ||
| 300 | 0.08 | 0.09 | 0.10 | 0.11 | ||
| 325 | 0.10 | 0.14 | 0.11 | 0.12 | ||
| 350 | 0.13 | 0.16 | 0.13 | 0.14 | ||
| SPEARMAN | ||||||
| Temperature/Frames | 10,000 | 20,000 | 30,000 | 40,000 | 50,000 | 60,000 |
| 50 | 0.88 | 0.86 | 0.89 | 0.89 | 0.89 | 0.90 |
| 70 | 0.84 | 0.83 | 0.80 | 0.80 | 0.82 | 0.84 |
| 90 | 0.79 | 0.75 | 0.73 | 0.73 | 0.73 | 0.73 |
| 100 | 0.57 | 0.61 | 0.64 | 0.62 | 0.64 | 0.62 |
| 110 | 0.77 | 0.75 | 0.68 | 0.62 | 0.61 | 0.59 |
| 125 | 0.46 | 0.48 | 0.52 | 0.53 | 0.48 | 0.46 |
| Temperature/Frames | 5000 | 10,000 | 15,000 | 20,000 | ||
| 150 | 0.37 | 0.38 | 0.36 | 0.35 | ||
| 175 | 0.40 | 0.30 | 0.31 | 0.32 | ||
| 200 | 0.30 | 0.26 | 0.23 | 0.25 | ||
| 215 | 0.31 | 0.32 | 0.34 | 0.31 | ||
| 235 | 0.23 | 0.26 | 0.20 | 0.27 | ||
| 250 | 0.29 | 0.30 | 0.31 | 0.30 | ||
| 275 | 0.33 | 0.28 | 0.30 | 0.27 | ||
| 300 | 0.34 | 0.30 | 0.28 | 0.27 | ||
| 325 | 0.27 | 0.22 | 0.24 | 0.27 | ||
| 350 | 0.24 | 0.21 | 0.27 | 0.27 | ||
| Pearson | 60,000 | 2000 | 400 | 200 | 60 | 40 | 20 | 6 |
| 50 K | 0.08 | 0.15 | 0.36 | 0.46 | 0.54 | 0.65 | 0.68 | 0.57 |
| 70 K | −0.02 | −0.04 | −0.04 | −0.13 | −0.20 | −0.38 | −0.51 | −0.56 |
| 90 K | −0.02 | −0.03 | −0.01 | −0.10 | −0.14 | −0.39 | −0.56 | −0.61 |
| 100 K | 0.01 | 0.02 | 0.05 | 0.08 | 0.28 | 0.29 | 0.18 | 0.24 |
| 110 K | −0.01 | −0.01 | 0.08 | 0.05 | 0.31 | 0.22 | 0.22 | −0.11 |
| 125 K | 0.15 | 0.21 | 0.40 | 0.44 | 0.46 | 0.53 | 0.48 | 0.65 |
| Spearman | 60,000 | 2000 | 400 | 200 | 60 | 40 | 20 | 6 |
| 50 K | 0.90 | 0.76 | 0.49 | 0.33 | 0.29 | 0.16 | 0.13 | 0.54 |
| 70 K | 0.84 | 0.57 | 0.10 | −0.10 | −0.21 | −0.33 | −0.46 | −0.43 |
| 90 K | 0.73 | 0.38 | −0.06 | −0.19 | −0.20 | −0.44 | −0.42 | −0.60 |
| 100 K | 0.62 | 0.26 | −0.06 | −0.15 | −0.09 | 0.04 | 0.02 | 0.03 |
| 110 K | 0.59 | 0.24 | −0.03 | −0.12 | 0.19 | 0.06 | 0.11 | −0.03 |
| 125 K | 0.46 | 0.27 | 0.28 | 0.36 | 0.41 | 0.54 | 0.47 | 0.77 |
| T (K) | Frames | Pearson | Spearman | τ (ps) HBs_C | τ (ps) HBs_N |
|---|---|---|---|---|---|
| 50 | 60,000 | 0.08 | 0.90 | - | - |
| 70 | 60,000 | −0.02 | 0.84 | 7.6408 | 6.6992 |
| 90 | 60,000 | −0.02 | 0.73 | 3.4374 | 2.7417 |
| 100 | 60,000 | 0.01 | 0.62 | 2.5533 | 2.0081 |
| 110 | 60,000 | −0.01 | 0.59 | 1.5975 | 1.4053 |
| 125 | 60,000 | 0.15 | 0.46 | 0.7176 | 0.9616 |
| 150 | 20,000 | 0.20 | 0.35 | 0.5085 | 0.6800 |
| 175 | 20,000 | 0.15 | 0.32 | 0.3878 | 0.5150 |
| 200 | 20,000 | 0.11 | 0.25 | 0.3409 | 0.4166 |
| 215 | 20,000 | 0.13 | 0.31 | 0.3044 | 0.3830 |
| 235 | 20,000 | 0.15 | 0.27 | 0.2464 | 0.3383 |
| 250 | 20,000 | 0.15 | 0.30 | 0.2349 | 0.3188 |
| 275 | 20,000 | 0.10 | 0.27 | 0.2082 | 0.2787 |
| 300 | 20,000 | 0.11 | 0.27 | 0.1933 | 0.2532 |
| 325 | 20,000 | 0.12 | 0.27 | 0.1774 | 0.2267 |
| 350 | 20,000 | 0.14 | 0.27 | 0.1635 | 0.2035 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garrote-Márquez, A.; Cruz Hernández, N.; Menéndez-Proupin, E. Correlation Between C–H∙∙∙Br and N–H∙∙∙Br Hydrogen Bond Formation in Perovskite CH3NH3PbBr3: A Study Based on Statistical Analysis. Solids 2025, 6, 29. https://doi.org/10.3390/solids6020029
Garrote-Márquez A, Cruz Hernández N, Menéndez-Proupin E. Correlation Between C–H∙∙∙Br and N–H∙∙∙Br Hydrogen Bond Formation in Perovskite CH3NH3PbBr3: A Study Based on Statistical Analysis. Solids. 2025; 6(2):29. https://doi.org/10.3390/solids6020029
Chicago/Turabian StyleGarrote-Márquez, Alejandro, Norge Cruz Hernández, and Eduardo Menéndez-Proupin. 2025. "Correlation Between C–H∙∙∙Br and N–H∙∙∙Br Hydrogen Bond Formation in Perovskite CH3NH3PbBr3: A Study Based on Statistical Analysis" Solids 6, no. 2: 29. https://doi.org/10.3390/solids6020029
APA StyleGarrote-Márquez, A., Cruz Hernández, N., & Menéndez-Proupin, E. (2025). Correlation Between C–H∙∙∙Br and N–H∙∙∙Br Hydrogen Bond Formation in Perovskite CH3NH3PbBr3: A Study Based on Statistical Analysis. Solids, 6(2), 29. https://doi.org/10.3390/solids6020029







