Octahedral Dominance and Band Gap Tuning via Pb2+-Driven Structural Evolution in α-β-γ CsZnI3
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
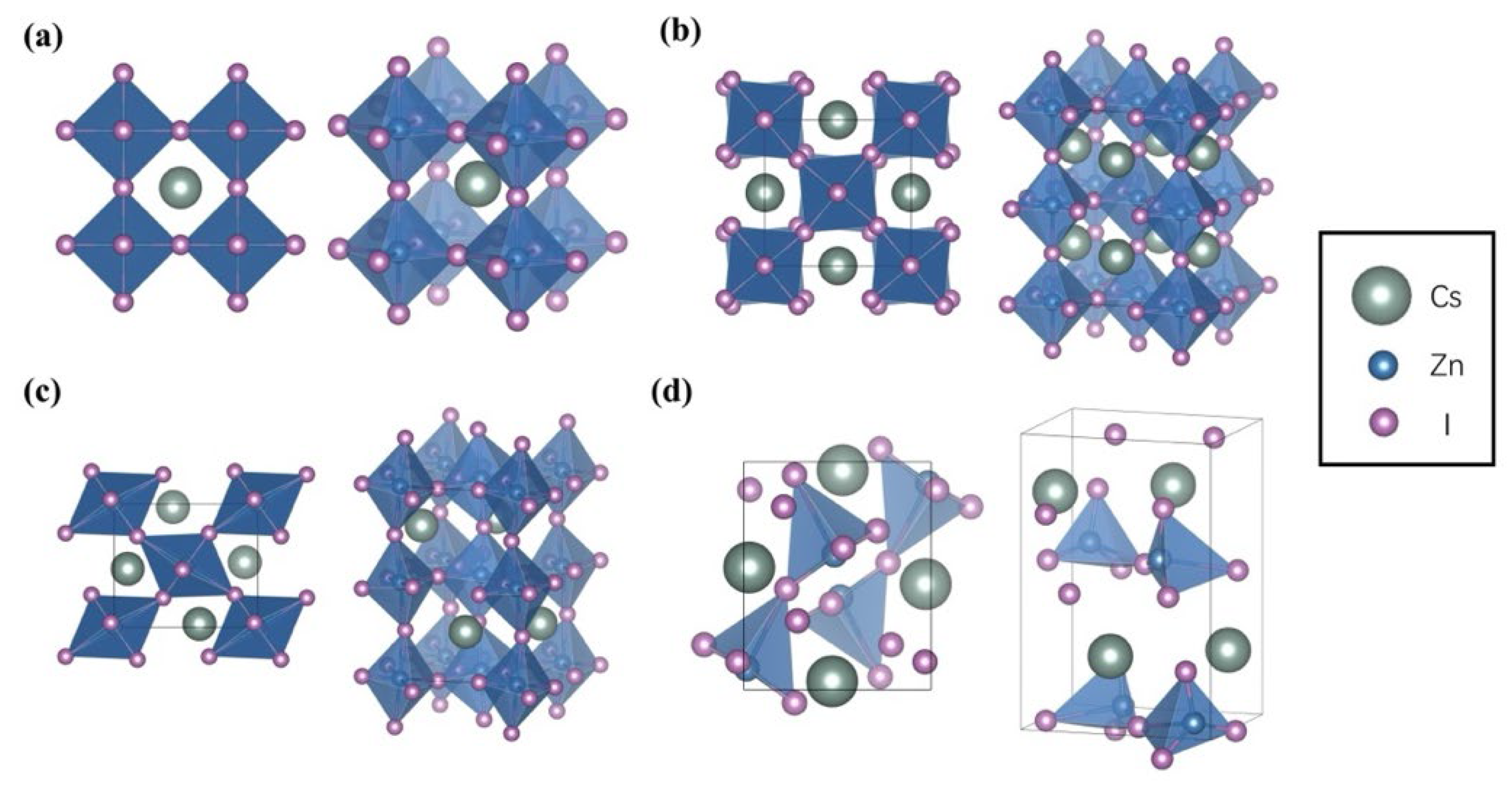
3.1. Structural Properties
3.2. Electronic Properties
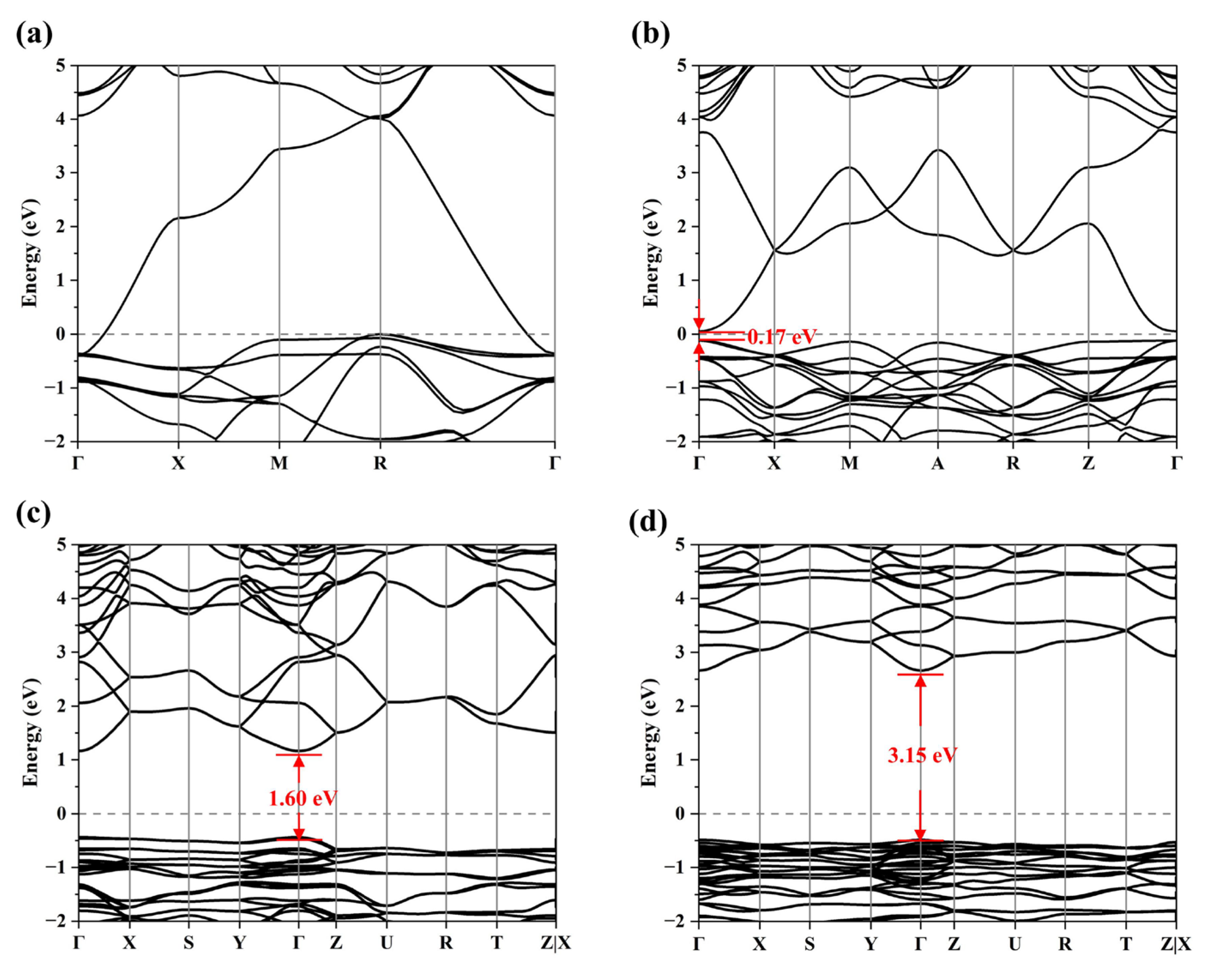
3.2.1. Band Structure
3.2.2. Density of States
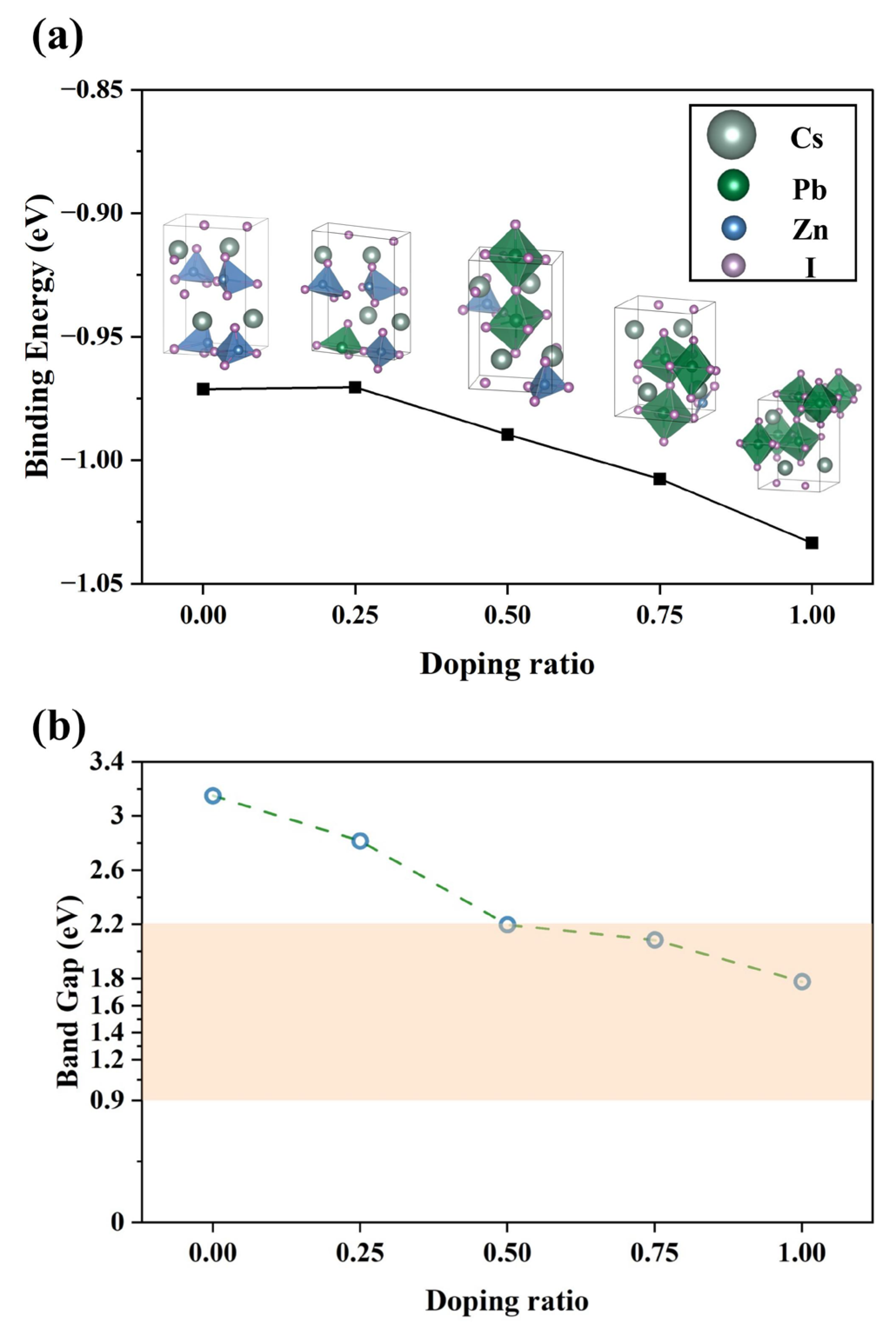
3.3. Doping Analysis and Structural Evolution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Green, M.A.; Dunlop, E.D.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Siefer, G.; Hao, X.; Jiang, J.Y. Solar Cell Efficiency Tables (Version 66). Prog. Photovolt. 2025. [Google Scholar] [CrossRef]
- Juarez-Perez, E.J.; Hawash, Z.; Raga, S.R.; Ono, L.K.; Qi, Y. Thermal Degradation of CH3NH3PbI3 Perovskite into NH3 and CH3I Gases Observed by Coupled Thermogravimetry–Mass Spectrometry Analysis. Energy Environ. Sci. 2016, 9, 3406–3410. [Google Scholar] [CrossRef]
- Sutton, R.J.; Eperon, G.E.; Miranda, L.; Parrott, E.S.; Kamino, B.A.; Patel, J.B.; Hörantner, M.T.; Johnston, M.B.; Haghighirad, A.A.; Moore, D.T.; et al. Bandgap-Tunable Cesium Lead Halide Perovskites with High Thermal Stability for Efficient Solar Cells. Adv. Energy Mater. 2016, 6, 1502458. [Google Scholar] [CrossRef]
- Wang, S.; Wang, L.; Wang, D.; Li, Y. Recent Advances of Single-Atom Catalysts in CO2 Conversion. Energy Environ. Sci. 2023, 16, 2759–2803. [Google Scholar] [CrossRef]
- Liu, D.; Shao, Z.; Li, C.; Pang, S.; Yan, Y.; Cui, G. Structural Properties and Stability of Inorganic CsPbI3 Perovskites. Small Struct. 2021, 2, 2000089. [Google Scholar] [CrossRef]
- Noel, N.K.; Stranks, S.D.; Abate, A.; Wehrenfennig, C.; Guarnera, S.; Haghighirad, A.-A.; Sadhanala, A.; Eperon, G.E.; Pathak, S.K.; Johnston, M.B.; et al. Lead-Free Organic–Inorganic Tin Halide Perovskites for Photovoltaic Applications. Energy Environ. Sci. 2014, 7, 3061–3068. [Google Scholar] [CrossRef]
- Ravidas, B.K.; Roy, M.K.; Samajdar, D.P. Investigation of Photovoltaic Performance of Lead-Free CsSnI3-Based Perovskite Solar Cell with Different Hole Transport Layers: First Principle Calculations and SCAPS-1D Analysis. Sol. Energy 2023, 249, 163–173. [Google Scholar] [CrossRef]
- Mehrabian, M.; Akhavan, O.; Rabiee, N.; Afshar, E.N.; Zare, E.N. Lead-Free MAGeI3 as a Suitable Alternative for MAPbI3 in Nanostructured Perovskite Solar Cells: A Simulation Study. Environ. Sci. Pollut. Res. 2023, 30, 57032–57040. [Google Scholar] [CrossRef]
- Hamideddine, I.; Tahiri, N.; Bounagui, O.E.; Ez-Zahraouy, H. Ab Initio Study of Structural and Optical Properties of the Halide Perovskite KBX3 Compound. J. Korean Ceram. Soc. 2022, 59, 350–358. [Google Scholar] [CrossRef]
- Alam, M.S.; Saiduzzaman, M.; Biswas, A.; Ahmed, T.; Sultana, A.; Hossain, K.M. Tuning Band Gap and Enhancing Optical Functions of AGeF3 (A = K, Rb) under Pressure for Improved Optoelectronic Applications. Sci. Rep. 2022, 12, 8663. [Google Scholar] [CrossRef]
- Zhu, S.; Ye, J.; Zhao, Y.; Qiu, Y. Structural, Electronic, Stability, and Optical Properties of CsPb1– x SnxIBr2 Perovskites: A First-Principles Investigation. J. Phys. Chem. C 2019, 123, 20476–20487. [Google Scholar] [CrossRef]
- Huang, X.; Hu, J.; Bi, C.; Yuan, J.; Lu, Y.; Sui, M.; Tian, J. B-Site Doping of CsPbI3 Quantum Dot to Stabilize the Cubic Structure for High-Efficiency Solar Cells. Chem. Eng. J. 2021, 421, 127822. [Google Scholar] [CrossRef]
- Agouri, M.; Ouhenou, H.; Waqdim, A.; Zaghrane, A.; Darkaoui, E.; Abbassi, A.; Manaut, B.; Taj, S.; Driouich, M. Computational Study of Stability, Photovoltaic, and Thermoelectric Properties of New Inorganic Lead-Free Halide Perovskites. EPL 2024, 146, 16005. [Google Scholar] [CrossRef]
- Eremin, R.A.; Humonen, I.S.; Kazakov, A.A.; Lazarev, V.D.; Pushkarev, A.P.; Budennyy, S.A. Graph Neural Networks for Predicting Structural Stability of Cd- and Zn-Doped γ-CsPbI3. Comput. Mater. Sci. 2024, 232, 112672. [Google Scholar] [CrossRef]
- Li, D.; Xie, P.; Zhang, Y.; Meng, Y.; Chen, Y.; Zheng, Y.; Wang, W.; Yin, D.; Li, B.; Wu, Z.; et al. Phase Engineering for Stability of CsPbI3 Nanowire Optoelectronics. Adv. Funct. Mater. 2024, 34, 2314309. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Xu, L.; Liu, S.; Lan, S.; Li, X.; Song, J. A Zinc Non-Halide Dopant Strategy Enables Efficient Perovskite CsPbI3 Quantum Dot-Based Light-Emitting Diodes. Mater. Chem. Front. 2020, 4, 1444–1453. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, Y.; Kershaw, S.V.; Li, T.; Wang, C.; Zhang, X.; Wang, W.; Li, D.; Wang, Y.; Lu, M.; et al. Zn-Alloyed CsPbI3 Nanocrystals for Highly Efficient Perovskite Light-Emitting Devices. Nano Lett. 2019, 19, 1552–1559. [Google Scholar] [CrossRef]
- Bi, C.; Sun, X.; Huang, X.; Wang, S.; Yuan, J.; Wang, J.X.; Pullerits, T.; Tian, J. Stable CsPb1– xZnxI3 Colloidal Quantum Dots with Ultralow Density of Trap States for High-Performance Solar Cells. Chem. Mater. 2020, 32, 6105–6113. [Google Scholar] [CrossRef]
- Badrooj, M.; Jamali-Sheini, F.; Torabi, N. Zn-Doped Pb/Sn Hybrid Perovskite Solar Cells: Towards High Photovoltaic Performance. Sol. Energy 2022, 236, 63–74. [Google Scholar] [CrossRef]
- Aqili, A.; Al-Reyahi, A.Y.; Al Azar, S.M.; Saad Essaoud, S.; Elamin Ketfi, M.; Maghrabi, M.; Al Aqtash, N.; Mufleh, A. Investigating the Physical Characteristics of Inorganic Cubic Perovskite CsZnX3 (X = F, Cl, Br, and I): An Extensive Ab Initio Study towards Potential Applications in Photovoltaic Perovskite Devices. Comput. Theor. Chem. 2024, 1238, 114721. [Google Scholar] [CrossRef]
- Sutherland, B.R. Solar Materials Find Their Band Gap. Joule 2020, 4, 984–985. [Google Scholar] [CrossRef]
- Song, Z.; Chen, C.; Li, C.; Awni, R.A.; Zhao, D.; Yan, Y. Wide-Bandgap, Low-Bandgap, and Tandem Perovskite Solar Cells. Semicond. Sci. Technol. 2019, 34, 093001. [Google Scholar] [CrossRef]
- Yu, M.L.; Los, A.; Xiong, G. Thin Film Absorbers for Tandem Solar Cells: An Industrial Perspective. J. Phys. Energy 2023, 5, 042002. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Wang, J.; Chen, H.; Wei, S.; Yin, W. Materials Design of Solar Cell Absorbers Beyond Perovskites and Conventional Semiconductors via Combining Tetrahedral and Octahedral Coordination. Adv. Mater. 2019, 31, 1806593. [Google Scholar] [CrossRef]
- Lin, Z.; Lei, J.; Wang, P.; Zhang, X.; Xu, L.; Chen, M.; Kang, Y.; Wei, G. Density Functional Study of Structural, Electronic and Optical Properties of Bromine-Doped CsPbI3 with the Tetragonal Symmetry. J. Alloys Compd. 2022, 892, 162165. [Google Scholar] [CrossRef]
- Ke, F.; Wang, C.; Jia, C.; Wolf, N.R.; Yan, J.; Niu, S.; Devereaux, T.P.; Karunadasa, H.I.; Mao, W.L.; Lin, Y. Preserving a Robust CsPbI3 Perovskite Phase via Pressure-Directed Octahedral Tilt. Nat. Commun. 2021, 12, 461. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, B.; Li, A.; Kuang, Z.; Qu, Y.; Xu, H.; Tang, T.; Shi, T.; Xie, W. Octahedral Dominance and Band Gap Tuning via Pb2+-Driven Structural Evolution in α-β-γ CsZnI3. Solids 2025, 6, 30. https://doi.org/10.3390/solids6020030
Liang B, Li A, Kuang Z, Qu Y, Xu H, Tang T, Shi T, Xie W. Octahedral Dominance and Band Gap Tuning via Pb2+-Driven Structural Evolution in α-β-γ CsZnI3. Solids. 2025; 6(2):30. https://doi.org/10.3390/solids6020030
Chicago/Turabian StyleLiang, Baoyun, Ang Li, Ziming Kuang, Yating Qu, Hao Xu, Tianyi Tang, Tingting Shi, and Weiguang Xie. 2025. "Octahedral Dominance and Band Gap Tuning via Pb2+-Driven Structural Evolution in α-β-γ CsZnI3" Solids 6, no. 2: 30. https://doi.org/10.3390/solids6020030
APA StyleLiang, B., Li, A., Kuang, Z., Qu, Y., Xu, H., Tang, T., Shi, T., & Xie, W. (2025). Octahedral Dominance and Band Gap Tuning via Pb2+-Driven Structural Evolution in α-β-γ CsZnI3. Solids, 6(2), 30. https://doi.org/10.3390/solids6020030







