Rotational Mobility of TEMPO Spin Probe in Polypropylene: EPR Spectra Simulation and Calculation via Approximated Formulas
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. EPR Spectroscopy
2.4. EPR Spectra Simulation
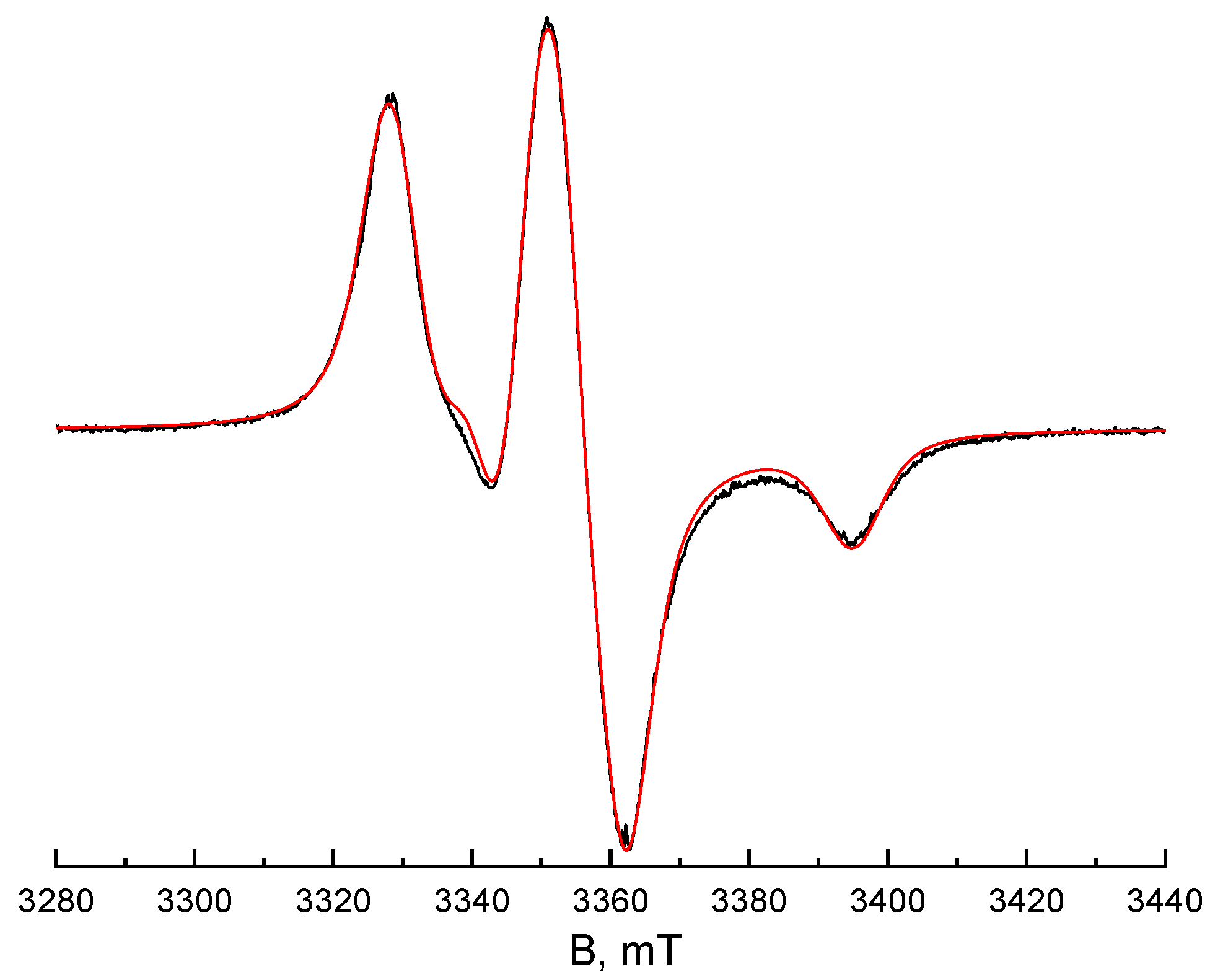
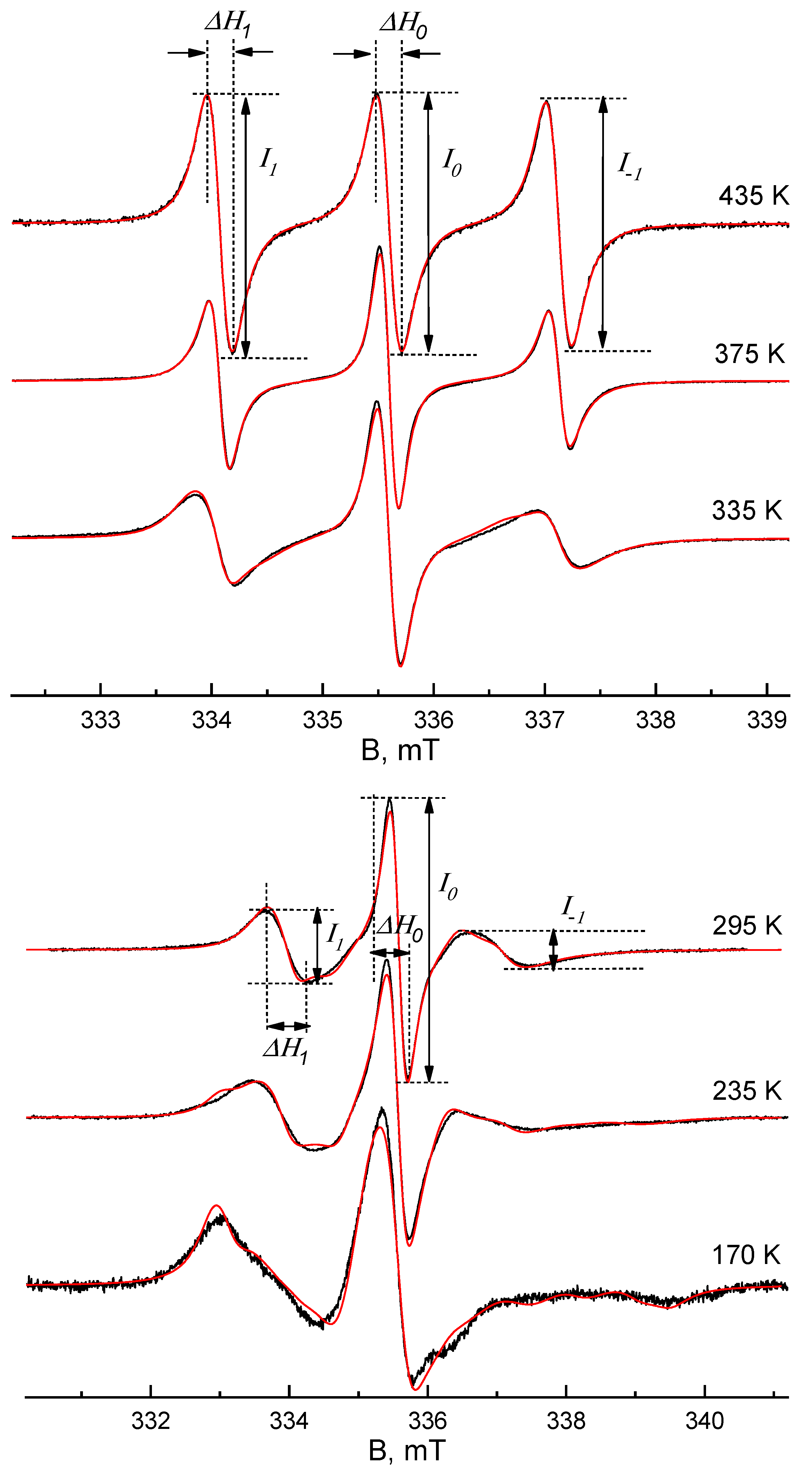
3. Results
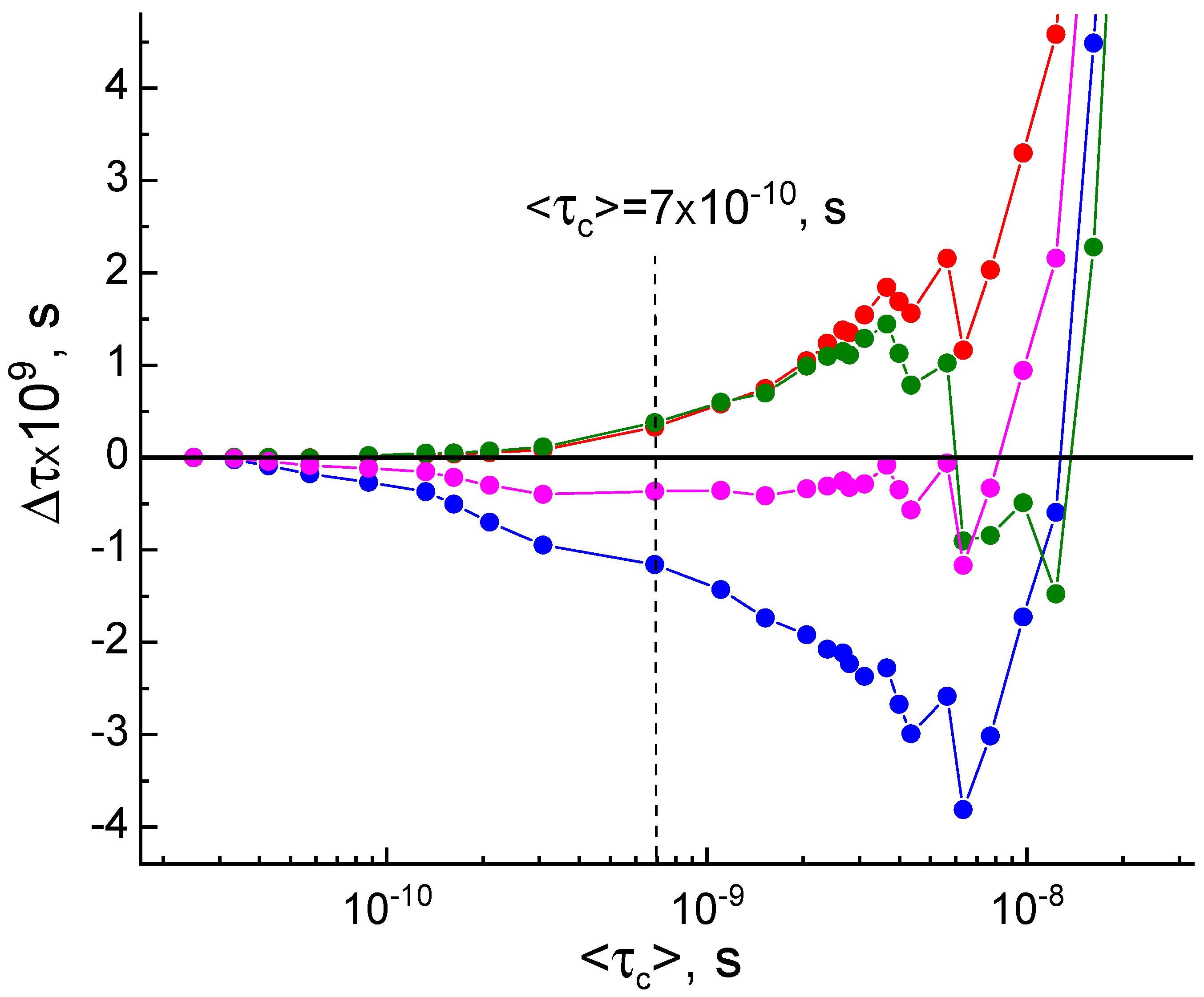
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rånby, B.; Rabek, J.F. ESR Spectroscopy in Polymer Research; Springer: Berlin/Heidelberg, Germany, 1977; Volume 1, ISBN 9783642666025. [Google Scholar]
- Naveed, K.-R.; Wang, L.; Yu, H.; Ullah, R.S.; Haroon, M.; Fahad, S.; Li, J.; Elshaarani, T.; Khan, R.U.; Nazir, A. Recent Progress in the Electron Paramagnetic Resonance Study of Polymers. Polym. Chem. 2018, 9, 3306–3335. [Google Scholar] [CrossRef]
- Veksli, Z. ESR Spectroscopy for the Study of Polymer Heterogeneity. Prog. Polym. Sci. 2000, 25, 949–986. [Google Scholar] [CrossRef]
- Schlick, S. (Ed.) Advanced ESR Methods in Polymer Research; John Wiley & Sons, Inc.: Hobokken, NJ, USA, 2006; ISBN 0471731897. [Google Scholar]
- Švajdlenková, H.; Račko, D.; Bartoš, J. Spin Probe Reorientation and Its Connections with Free Volume and Relaxation Dynamics: Diglycidyl-Ether of Bis-Phenol A. J. Non. Cryst. Solids 2008, 354, 1855–1861. [Google Scholar] [CrossRef]
- Kivelson, D. Theory of ESR Linewidths of Free Radicals. J. Chem. Phys. 1960, 33, 1094–1106. [Google Scholar] [CrossRef]
- Schreier, S.; Polnaszek, C.F.; Smith, I.C.P. Spin Labels in Membranes Problems in Practice. Biochim. Biophys. Acta—Rev. Biomembr. 1978, 515, 395–436. [Google Scholar] [CrossRef]
- Santangelo, M.G.; Levantino, M.; Cupane, A.; Jeschke, G. Solvation of a Probe Molecule by Fluid Supercooled Water in a Hydrogel at 200 K. J. Phys. Chem. B 2008, 112, 15546–15553. [Google Scholar] [CrossRef] [PubMed]
- Stoll, S.; Schweiger, A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Budil, D.E.; Lee, S.; Saxena, S.; Freed, J.H. Nonlinear-Least-Squares Analysis of Slow-Motion EPR Spectra in One and Two Dimensions Using a Modified Levenberg–Marquardt Algorithm. J. Magn. Reson. Ser. A 1996, 120, 155–189. [Google Scholar] [CrossRef]
- Faetti, M.; Giordano, M.; Leporini, D.; Pardi, L. Scaling Analysis and Distribution of the Rotational Correlation Times of a Tracer in Rubbery and Glassy Poly(Vinyl Acetate): An Electron Spin Resonance Investigation. Macromolecules 1999, 32, 1876–1882. [Google Scholar] [CrossRef]
- Bercu, V.; Martinelli, M.; Massa, C.A.; Pardi, L.A.; Leporini, D. Signatures of the Fast Dynamics in Glassy Polystyrene: First Evidence by High-Field Electron Paramagnetic Resonance of Molecular Guests. J. Chem. Phys. 2005, 123, 174906. [Google Scholar] [CrossRef]
- Chernova, D.A.; Vorobiev, A.K. Molecular Mobility of Nitroxide Spin Probes in Glassy Polymers: Models of the Complex Motion of Spin Probes. J. Appl. Polym. Sci. 2011, 121, 102–110. [Google Scholar] [CrossRef]
- Dubinskii, A.A.; Maresch, G.G.; Spiess, H.-W. Two-Dimensional Electron Paramagnetic Resonance Spectroscopy of Nitroxides: Elucidation of Restricted Molecular Motions in Glassy Solids. J. Chem. Phys. 1994, 100, 2437–2448. [Google Scholar] [CrossRef]
- Saalmueller, J.W.; Long, H.W.; Volkmer, T.; Wiesner, U.; Maresch, G.G.; Spiess, H.W. Characterization of the Motion of Spin Probes and Spin Labels in Amorphous Polymers with Two-Dimensional Field-Step ELDOR. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1093–1104. [Google Scholar] [CrossRef]
- Karpova, S.G.; Chumakova, N.A.; Lobanov, A.V.; Olkhov, A.A.; Vetcher, A.A.; Iordanskii, A.L. Evaluation and Characterization of Ultrathin Poly(3-Hydroxybutyrate) Fibers Loaded with Tetraphenylporphyrin and Its Complexes with Fe(III) and Sn(IV). Polymers 2022, 14, 610. [Google Scholar] [CrossRef] [PubMed]
- Yankova, T.S.; Chumakova, N.A.; Nedorezova, P.M.; Palaznik, O.M.; Kokorin, A.I. Behavior of Spin Probe TEMPO in Composites Based on Polypropylene with Different Content of Single-Wall Carbon Nanotubes. Polym. Sci. Ser. A 2024, 66, 121–128. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Kokorin, A. (Ed.) Nitroxides—Theory, Experiment and Applications; InTech: Vienna, Austria, 2012; ISBN 978-953-51-0722-4. [Google Scholar]
- Vorobiev, A.K.; Bogdanov, A.V.; Yankova, T.S.; Chumakova, N.A. Spin Probe Determination of Molecular Orientation Distribution and Rotational Mobility in Liquid Crystals: Model-Free Approach. J. Phys. Chem. B 2019, 123, 5875–5891. [Google Scholar] [CrossRef]
- Chernova, D.A.; Vorobiev, A.K. Molecular Mobility of Nitroxide Spin Probes in Glassy Polymers. Quasi-libration Model. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 107–120. [Google Scholar] [CrossRef]
- Vorobiev, A.K.; Gurman, V.S.; Klimenko, T.A. Rotational Mobility of Guest Molecules Studied by Method of Oriented Spin Probe. Phys. Chem. Chem. Phys. 2000, 2, 379–385. [Google Scholar] [CrossRef]
- Švajdlenková, H.; Šauša, O.; Adichtchev, S.V.; Surovtsev, N.V.; Novikov, V.N.; Bartoš, J. On the Mutual Relationships between Molecular Probe Mobility and Free Volume and Polymer Dynamics in Organic Glass Formers: Cis-1,4-Poly(Isoprene). Polymers 2021, 13, 294. [Google Scholar] [CrossRef]
- Vasserman, A.M.; Barashkova, I.I.; Yasina, L.L.; Pupov, V.S. Rotary and Progressive Diffusion of the Nitroxyl Radical in Amorphous Polymers. Polym. Sci. U.S.S.R. 1977, 19, 2389–2398. [Google Scholar] [CrossRef]

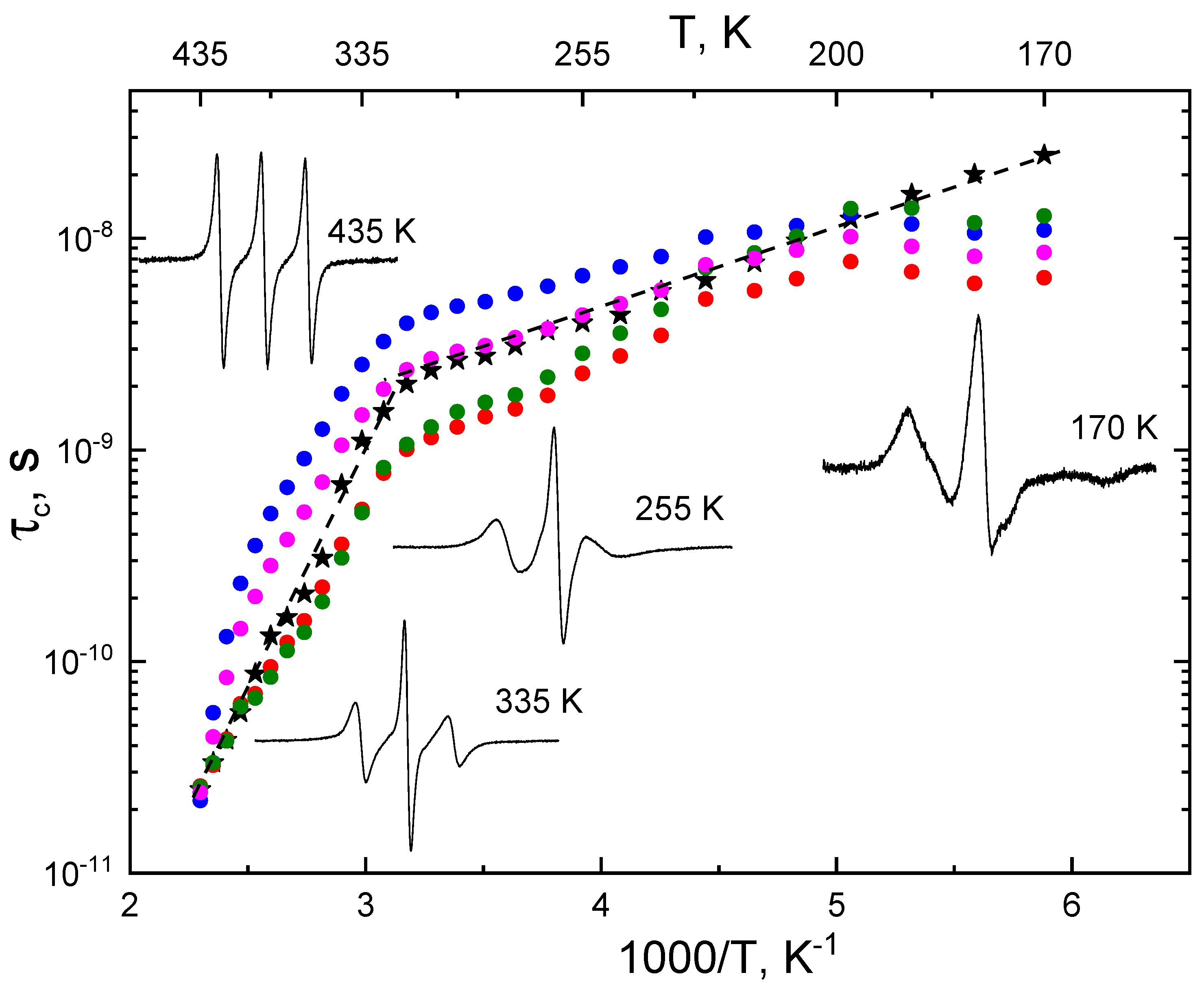
| T,K | τx (s) | τy (s) | τz (s) | <τc> (s) | <σ> | Libr | τc*(1) (s) | τc*(2) (s) | τc*(3) (s) | τc*(4) (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| 435 | 2.5 × 10−11 | 2.5 × 10−11 | 0.70 # | − | 2.58 × 10−11 | 2.20 × 10−11 | 2.55 × 10−11 | 2.41 × 10−11 | ||
| 425 | 3.3 × 10−11 | 3.3 × 10−11 | 0.70 # | − | 3.24 × 10−11 | 5.72 × 10−11 | 3.32 × 10−11 | 4.40 × 10−11 | ||
| 415 | 4.25 × 10−9 | 1.53 × 10−11 | 2.09 × 10−10 | 4.26 × 10−11 | 0.70 # | − | 4.29 × 10−11 | 1.31 × 10−10 | 4.21 × 10−11 | 8.41 × 10−11 |
| 405 | 7.15 × 10−8 | 2.02 × 10−11 | 3.58 × 10−10 | 5.74 × 10−11 | 0.70 # | − | 6.31 × 10−11 | 2.34 × 10−10 | 6.10 × 10−11 | 1.43 × 10−10 |
| 395 | 1.67 × 10−7 | 3.09 × 10−11 | 5.31 × 10−10 | 8.76 × 10−11 | 0.70 # | − | 7.05 × 10−11 | 3.54 × 10−10 | 6.72 × 10−11 | 2.03 × 10−10 |
| 385 | 1.7 × 10−7 # | 4.68 × 10−11 | 7.72 × 10−10 | 1.32 × 10−10 | 0.70 # | − | 9.43 × 10−11 | 5.00 × 10−10 | 8.45 × 10−11 | 2.84 × 10−10 |
| 375 | 1.7 × 10−7 # | 5.65 × 10−11 | 1.24 × 10−9 | 1.62 × 10−10 | 0.70 # | − | 1.23 × 10−10 | 6.66 × 10−10 | 1.13 × 10−10 | 3.77 × 10−10 |
| 365 | 1.7 × 10−7 # | 7.31 × 10−11 | 1.59 × 10−9 | 2.10 × 10−10 | 0.70 # | − | 1.56 × 10−10 | 9.10 × 10−10 | 1.37 × 10−10 | 5.08 × 10−10 |
| 355 | 1.7 × 10−7 # | 1.08 × 10−10 | 2.03 × 10−9 | 3.08 × 10−10 | 0.70 # | − | 2.24 × 10−10 | 1.25 × 10−9 | 1.92 × 10−10 | 7.05 × 10−10 |
| 345 | 1.7 × 10−7 # | 2.43 × 10−10 | 4.31 × 10−9 | 6.88 × 10−10 | 0.70 # | 27° | 3.58 × 10−10 | 1.84 × 10−9 | 3.09 × 10−10 | 1.05 × 10−9 |
| 335 | 1.7 × 10−7 # | 3.92 × 10−10 | 6.41 × 10−9 | 1.11 × 10−9 | 0.70 # | 28° | 5.23 × 10−10 | 2.53 × 10−10 | 5.05 × 10−10 | 1.46 × 10−10 |
| 325 | 1.7 × 10−7 # | 5.46 × 10−10 | 7.47 × 10−9 | 1.52 × 10−9 | 0.70 # | 25° | 7.76 × 10−10 | 3.26 × 10−10 | 8.25 × 10−10 | 1.94 × 10−10 |
| 315 | 1.7 × 10−7 # | 5.44 × 10−10 | 9.06 × 10−9 | 2.05 × 10−9 | 0.70 # | 25° | 1.01 × 10−9 | 3.97 × 10−9 | 1.06 × 10−9 | 2.39 × 10−9 |
| 305 | 1.7 × 10−7 # | 8.68 × 10−10 | 9.86 × 10−9 | 2.38 × 10−9 | 0.70 # | 21° | 1.14 × 10−9 | 4.45 × 10−9 | 1.28 × 10−9 | 2.69 × 10−9 |
| 295 | 1.7 × 10−7 # | 9.80 × 10−10 | 9.98 × 10−9 | 2.66 × 10−9 | 0.70 # | 19° | 1.29 × 10−9 | 4.78 × 10−9 | 1.52 × 10−9 | 2.92 × 10−9 |
| 285 | 1.7 × 10−7 # | 1.03 × 10−9 | 1.03 × 10−8 | 2.79 × 10−9 | 0.70 # | 20° | 1.44 × 10−9 | 5.02 × 10−9 | 1.68 × 10−9 | 3.11 × 10−9 |
| 275 | 1.7 × 10−7 # | 1.16 × 10−9 | 1.05 × 10−8 | 3.11 × 10−9 | 0.70 # | 17° | 1.56 × 10−9 | 5.47 × 10−9 | 1.82 × 10−9 | 3.39 × 10−9 |
| 265 | 1.7 × 10−7 # | 1.39 × 10−9 | 1.05 × 10−8 | 3.65 × 10−9 | 0.70 # | 15° | 1.81 × 10−9 | 5.92 × 10−9 | 2.21 × 10−9 | 3.73 × 10−9 |
| 255 | 1.7 × 10−7 # | 1.54 × 10−9 | 1.02 × 10−8 | 3.99 × 10−9 | 0.70 # | 10° | 2.30 × 10−9 | 6.66 × 10−9 | 2.86 × 10−9 | 4.34 × 10−9 |
| 245 | 1.7 × 10−7 # | 1.69 × 10−9 | 1.09 × 10−8 | 4.35 × 10−9 | 0.70 # | <1° | 2.78 × 10−9 | 7.34 × 10−9 | 3.56 × 10−9 | 4.91 × 10−9 |
| 235 | 1.7 × 10−7 # | 2.44 × 10−9 | 8.55 × 10−9 | 5.63 × 10−9 | 0.89 | − | 3.48 × 10−9 | 8.22 × 10−9 | 4.61 × 10−9 | 5.70 × 10−9 |
| 225 | 1.7 × 10−7 # | 2.91 × 10−9 | 8.05 × 10−9 | 6.33 × 10−9 | 0.86 | − | 5.17 × 10−9 | 1.01 × 10−8 | 7.24 × 10−9 | 7.50 × 10−9 |
| 215 | 1.7 × 10−7 # | 3.59 × 10−9 | 9.47 × 10−9 | 7.69 × 10−9 | 0.88 | − | 5.66 × 10−9 | 1.07 × 10−8 | 8.54 × 10−8 | 8.02 × 10−9 |
| 207 | 1.7 × 10−7 # | 4.79 × 10−9 | 1.08 × 10−8 | 9.75 × 10−9 | 0.91 | − | 6.45 × 10−9 | 1.14 × 10−8 | 1.02 × 10−8 | 8.80 × 10−9 |
| 198 | 1.7 × 10−7 # | 6.24 × 10−9 | 1.30 × 10−8 | 1.23 × 10−8 | 0.94 | − | 7.76 × 10−9 | 1.29 × 10−8 | 1.38 × 10−8 | 1.02 × 10−8 |
| 188 | 1.7 × 10−7 # | 8.77 × 10−9 | 1.53 × 10−8 | 1.62 × 10−8 | 0.93 | − | 6.94 × 10−9 | 1.16 × 10−8 | 1.39 × 10−8 | 9.17 × 10−9 |
| 179 | 1.7 × 10−7 # | 1.20 × 10−8 | 1.67 × 10−8 | 2.01 × 10−8 | 0.92 | − | 6.13 × 10−9 | 1.06 × 10−8 | 1.19 × 10−8 | 8.23 × 10−9 |
| 170 | 1.7 × 10−7 # | 1.71 × 10−8 | 1.77 × 10−8 | 2.48 × 10−8 | 0.90 | − | 6.52 × 10−9 | 1.09 × 10−8 | 1.28 × 10−8 | 8.59 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chumakova, N.A.; Yankova, T.S.; Kokorin, A.I. Rotational Mobility of TEMPO Spin Probe in Polypropylene: EPR Spectra Simulation and Calculation via Approximated Formulas. Solids 2024, 5, 499-509. https://doi.org/10.3390/solids5040033
Chumakova NA, Yankova TS, Kokorin AI. Rotational Mobility of TEMPO Spin Probe in Polypropylene: EPR Spectra Simulation and Calculation via Approximated Formulas. Solids. 2024; 5(4):499-509. https://doi.org/10.3390/solids5040033
Chicago/Turabian StyleChumakova, Natalia A., Tatiana S. Yankova, and Alexander I. Kokorin. 2024. "Rotational Mobility of TEMPO Spin Probe in Polypropylene: EPR Spectra Simulation and Calculation via Approximated Formulas" Solids 5, no. 4: 499-509. https://doi.org/10.3390/solids5040033
APA StyleChumakova, N. A., Yankova, T. S., & Kokorin, A. I. (2024). Rotational Mobility of TEMPO Spin Probe in Polypropylene: EPR Spectra Simulation and Calculation via Approximated Formulas. Solids, 5(4), 499-509. https://doi.org/10.3390/solids5040033









