Abstract
Compacted graphite iron (CGI) is an engineering material with the potential to fill the application gap between flake- and spheroidal-graphite irons thanks to its unique microstructure and competitive price. Despite its wide use and considerable past research, its complex microstructure often leads researchers to focus on models based on representative volume elements with multiple particles, frequently overlooking the impact of individual particle shapes and interactions between the neighbouring particles on crack initiation and propagation. This study focuses on the effects of graphite morphology and spacing between inclusions on the mechanical and fracture behaviours of CGI at the microscale. In this work, 2D cohesive-zone-element-based models with different graphite morphologies and spacings were developed to investigate the mechanical behaviour as well as crack initiation and propagation. ImageJ and scanning electron microscopy were used to characterise and analyse the microstructure of CGI. In simulations, both graphite particles and metallic matrix were assumed isotropic and ductile. Cohesive zone elements (CZEs) were employed in the whole domain studied. It was found that graphite morphology had a negligible effect on interface debonding but nodular inclusions can notably enhance the stiffness of the material and effectively impede the propagation of cracks within the matrix. Besides, a small distance between graphite particles accelerates the crack growth. These results can be used to design and manufacture better metal-matrix composites.
Keywords:
CGI; CZE; crack growth; microstructure; graphite morphology; graphite spacing; numerical modelling 1. Introduction
Cast iron has been one of the most broadly used materials in automotive engines since 1948, as it has good thermal and mechanical properties, and competitive price [1]. Compacted graphite iron (CGI) exhibits complex microstructures, mainly composed of graphite, ferrite, and pearlite constituents [2]. Graphite particles of varying shapes and sizes are reported, which can be divided into three categories: nodular, vermicular, and flake, as shown in Figure 1 [3]. The flake graphite particles tend to be very long and thin, whereas vermicular ones have an intermediate shape between flake and nodular [3]. As a result of such a complex microstructure, its fracture mechanisms at the microscale were not fully studied. It is also well known that the size and shape of graphite particles in CGI significantly determine its various properties [4]. Researchers in [5,6] compared the tensile behaviour and hardness of cast irons, and concluded that the size, distribution, and shape of the incorporated graphite particles significantly affected their mechanical properties. The mechanical and physical properties of CGI are determined by its complex microstructure. Besides, the alloying elements, temperature, holding time, and thickness of the casting affect CGI’s microstructures and, thus, influence its mechanical properties. Although it is hard to control the nucleation and growth mechanisms as well as the degeneration of graphite particles, interrupting the solidification process with proper tracing elements (Ce2S3, La2S3, and Ti2S3) could partially control the shape and size of graphite inclusions [7]. In the work of Muhond et al. [8], some trace elements (S, B, Se) were observed to stabilise the flake or nodular growth morphology of graphite, while F, O, N, P failed to do so.

Figure 1.
Microstructure of CGI.
In general, there are two main approaches used for modelling the mechanical behaviour of CGI: representative volume element (RVE) and unit cell [9,10,11,12]. To the best of the author’s knowledge, these two approaches are widely used in the field of computational mechanics to simulate the fracture behaviours of heterogeneous materials. RVE-based models usually contain at least 10 inclusions or even incorporate the real microstructures (e.g., obtained with computed tomography), which are selected from a larger structure or materials [9,13]. The goal of RVE modelling is to capture the mechanical response or fracture response by considering the interactions between graphite inclusions. RVE modelling is also usually combined with multi-scale modelling to analyse the behaviour of metal-matrix composites [14,15]. On the other hand, the unit-cell approach only focuses on a single repeating element. The single inclusion, which represents the basic building block of the material’s microstructure, is analysed in isolation to gain insights into the overall macroscopic behaviour of the materials [16,17]. Still, the unit-cell approach provides a useful tool to interpret the mechanical response of materials with complex microstructures. The influence of interaction between neighbouring particles and their morphology was often overlooked when elucidating the failure of microstructures. The interaction of graphite inclusions can lead to stress concentration in the matrix area between them, in turn, accelerating the coalescence and propagation of microcracks [18]. There were several attempts to research the mechanism of fracture in metals, focusing on white and grey cast irons [19], silicon carbide [1,20,21], and TiC–Fe [15], but not enough information is available about CGI. Hence, in this study, the effects of distance between the graphite particles, graphite morphology, and boundary conditions were studied to investigate the microcrack growth and interface debonding in CGI.
In the last decades, four main methods were used to simulate the fracture behaviours of materials [9,10,15,22,23,24]: (i) the cohesive-zone model (CZM); (ii) the extended finite-element method (XFEM); (iii) the Johnson–Cook (JC) damage model; and (IV) phase-field modelling. XFEM is a mesh-free method that can be used to simulate crack initiation and propagation in static, quasi-static, and dynamic problems. Besides, XFEM is usually used to predict the stress–strain behaviour without a predefined crack [9,10]. With its need for additional degrees of freedom, XFEM may require more computational resources, while the JC method is more accurate in large-deformation problems [25]. The JC constitutive model that can naturally account for large strains and high strain rates was used to describe the grinding process of CGI, where these factors play an important role [15]. So, inserting cohesive-zone elements globally may get more precise results for a single-inclusion unit-cell problem without any predefined crack. Comparing these three approaches, CZM can be more accurate at predicting the fracture behaviour of non-cracked structures and fractures with nonlinear plasticity, which is why it is frequently used to analyse delamination or adhesive failure in composite structures [23,26]. Eiken [27] used a volumetric multi-phase-field approach to explore the dynamic chemical gradients and their potential impact on carbon diffusion in cast-iron cells. The influence of the distribution and size of the graphite particle on the machinability of nodular cast iron was experimentally examined and quantitatively analysed by Yang et al. [28]. Their findings revealed that the sizes and character of distribution of graphite particles affected the stress and strain fields in the cutting region of the materials. However, this study was limited to 2D cohesive-zone-element-based models due to the complex microstructure morphology of CGI. A 3D CZE model could be considered by using in situ synchrotron X-ray tomography in the future [29].
The complex microstructure of CGI is the main reason that hinders researchers from an in-depth exploration of its fracture behaviour. Although there are a variety of micromechanical models investigating compacted graphite iron, few of them focused on the fracture behaviour of CGI under tensile loading, and the authors are unaware of any studies into the effect of single inclusion on it. Cracks affect the mechanical properties, service life, and durability of CGI. Hence, their prediction is vital for the enhancement of the service life and sustainability of structures [30]. To mitigate the influence of other particles on adjacent inclusions, this model, combining CZEs and periodic boundary conditions (PBCs), provides a strategy to investigate the effect of graphite morphology and spacing without any predefined cracks. Cohesive zone elements were employed in the entire studied domain, assigned with three different properties, corresponding to the respective material domains they represented. This approach proved more efficient than previous studies as it does not use any mesh refinement during crack advancement.
2. Methodology
2.1. Model Geometry
The geometrical configuration of representative one- and two-inclusion models are presented in Figure 2 (grey and green parts represent graphite and matrix, respectively). The bottom faces of all nodes were fully constrained, and a uniaxial stress state was created by applying incremental axial displacement to the top face of the model. To achieve crack propagation, cohesive elements were inserted into the graphite and matrix domain. Furthermore, the layer around the inclusion (in red in Figure 2) depicts the interface between the matrix and graphite, with the cohesive thickness being zero.
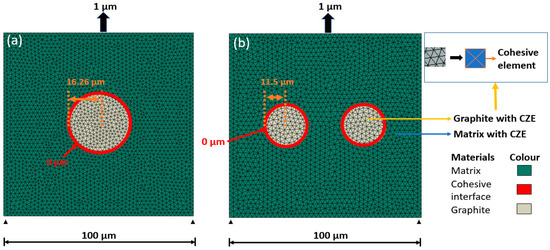
Figure 2.
Geometry and mesh used in numerical simulations: (a) Single inclusion; (b) two inclusions.
As mentioned, CGI’s microstructure has graphite inclusions with three main morphologies: nodular, flake, and vermicular. Hence, three single-inclusion models were developed in this study, corresponding to these basic inclusion geometries, presented by circular and ellipse domains, as shown in Figure 3. In all cases, the volume fraction was based on the results of microstructural characterisation and kept equal to 8.3% based on statistical results [31]. Therefore, the radius of nodular inclusion was assumed to be 16.26 μm, the semi-major and semi-minor axes of the vermicular inclusion were 26.44 μm and 10 μm, while those of the flake inclusion were 52.88 μm and 5 μm, respectively. The side length of the square domain in all three models was 100 μm. The area of the unit cell was calculated to fit the average volume fraction of graphite. The fractions of each microconstituent’s domain were calculated by counting the number of pixels corresponding to the respective colours. Further, eight cases of particle interactions were considered in this work (Figure 4).
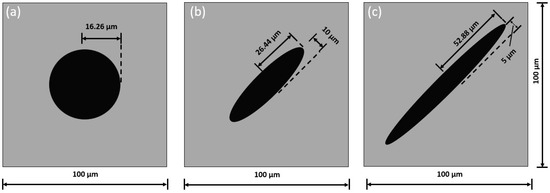
Figure 3.
Geometry of nodular (a), vermicular (b), and flake (c) inclusions.
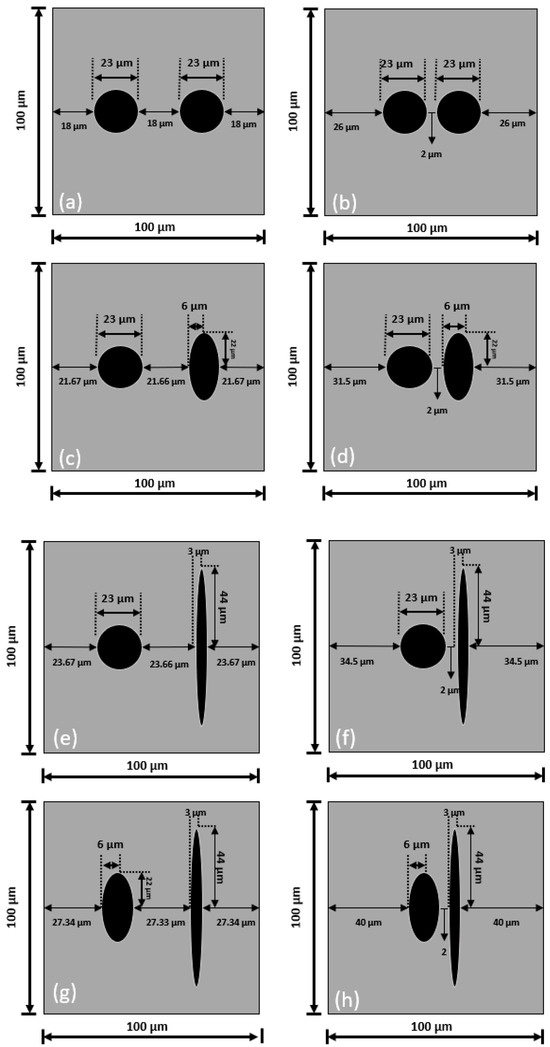
Figure 4.
Geometrical parameters of unit cells for analysis of particle interaction: (a,c,e,g) maximum distance; (b,d,f,h) minimum distance.
Figure 4 shows the geometrical configuration of these cases with the graphite volume fraction fixed at 8.3%. Hence, the diameter of nodular graphite was 23 μm, the semi-major and semi-minor axes of the vermicular graphite were 22 μm and 6 μm, respectively, and those of the flake graphite were 44 μm and 3 μm. Also, the maximum and minimum distances were selected based on the statistical data [31]. The minimum distance between inclusions was selected to be 2 μm (Figure 4b,d,f,h). The maximum distance between two particles should be as large as possible but it cannot result in particles being too close to the model boundary to avoid the errors introduced by interaction with it [31]. So, the distance from each inclusion to the boundaries was kept equal to the distance between the inclusions in that case (Figure 4a,c,e,g). More geometrical configurations are presented below in the paper.
The mathematical formulations of CZM described in Section 2.3 were implemented into a 2D nonlinear FE model using Abaqus/Explicit software 2021.HF6. To prevent the generation of sawtooth particle boundaries that can result in stress concentration, a 3-node linear plane-strain triangle (CPE3) element was utilised to model the unit cell. After conducting a mesh convergence study, 2 µm was selected as the element size. The dynamic explicit method was used in this model. The model details are summarised in Table 1.

Table 1.
Model details.
2.2. Boundary Conditions
The implementation of PBCs requires opposite pairs of surfaces (or edges) to undergo identical deformations, thereby reducing the impact of edge effects on the boundary of a representative volume element (RVE) [32]. By employing PBCs in simulations, the computational requirements are significantly reduced since a smaller number of particles or entities can effectively model an infinite system compared to those, explicitly representing the entire infinite system. This reduction in particle count improves the computational feasibility of the simulation. The realisation of PBCs in the studied domain is shown in Figure 5: PBCs were applied to nodes in red and blue, while the yellow nodes were corner nodes. The basic equations of PBCs are:
where is the displacement in the and axis.
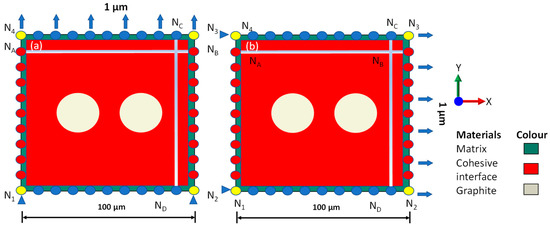
Figure 5.
Schematics of PBCs with CZM under vertical (a) and horizontal (b) loading regimes.
PBCs require the number of nodes in the referred set to be equal to the number of appended nodes. PBCs conflict with cohesive elements with 4 nodes in each cohesive element. Hence, at the outermost layer of the model, cohesive elements were not inserted (see Figure 5). The PBCs were also used in the single-particle model.
2.3. Constitutive Relations
A constitutive law assuming elastoplastic behaviour was employed for the metallic matrix and graphite particles, considering isotropy. Table 2 and Table 3 list the constitutive parameters for these two domains, respectively. Mechanical tests were used to derive the constitutive values for the metallic matrix, as described in [11]. The behaviour of a material can be significantly influenced by microstructural features. Dynamic analysis allows for the investigation of the interaction of these microstructural elements with the applied loading and their effect on the overall response. The crack growth and energy dissipation within the RVE can be studied by considering its mechanical response [33].

Table 2.
Constitutive parameters for graphite (room temperature) [11,34].

Table 3.
Constitutive parameters for matrix (room temperature) [11].
The modelling of material softening near the crack tip involved incorporating a traction–separation relationship into the cohesive elements (as illustrated in Figure 6). The cohesive element with zero thickness exhibited a linear-elastic response. Upon reaching the critical point defined by the parameters and , the initiation of a crack was assumed to occur at . Subsequently, the cohesive element’s reaction force decreased due to damage softening until reaching the failure point at .
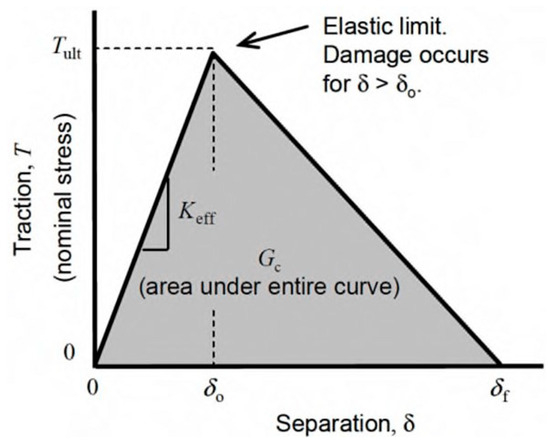
Figure 6.
Traction–separation relationship (Reprinted with permission from Ref. [35]. 2016, D. Zhang).
Constitutive parameters of the cohesive model used in numerical simulations are shown in Table 4. The material parameters include damage initiation stress , fracture energy , failure relative displacement , and density . The cohesive interface parameters were obtained from the in-house nano-indentation experiments, the data for the cohesive matrix from in situ experiments (for more details see [36,37]), and the cohesive data for graphite were based on [38]. In this study, the properties of graphite inclusions were considered the same irrespective of their morphology.

Table 4.
Constitutive parameters for cohesive element [36,38].
3. Results and Discussion
3.1. Effect of Graphite Morphology: Single-Particle Unit Cells
At the first stage of the analysis, single-particle models were used to analyse the initiation and propagation of cracks. Figure 7 illustrates the distribution of von Mises stress for three graphite inclusions with different morphologies, utilising a model that incorporated both PBCs and CZEs. The edge effect triggered stress concentrations in the matrix area as well as near left- and right-hand tips of inclusions. This resulted in the occurrence of graphite debonding, with cracking subsequently propagating to the matrix. It is worth noting that cracks propagated not only around the graphite particle but also to the side borders, characterised by strong interaction with stress raisers in virtual neighbouring cells as a result of the application of PBCs. As a result, the crack propagation in mode I (i.e., horizontal) changed to a mixed-mode regime.
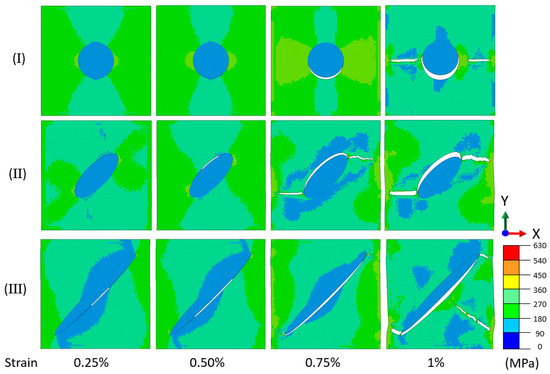
Figure 7.
Evolution of von Mises stress distribution and crack growth under vertical tensile loading for different graphite morphology: (I) nodular; (II) vermicular; (III) flake.
Crack evolution in each graphite inclusion was further assessed to evaluate the effect of graphite morphology on the characteristics of fracture propagation, as shown in Figure 8. The uncracked ligament of the CGI sample was calculated as follows:
where is the projection of the length of the ith crack in the direction perpendicular to the loading, is the total model’s length, and N is the total number of cracks in the cell.
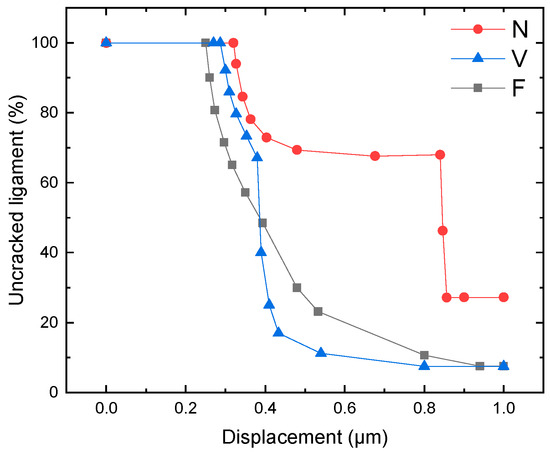
Figure 8.
Effect of graphite morphology on evolution of uncracked-ligament length with external displacement (N—nodular, V—vermicular, F—flake).
Figure 8 illustrates the effect of graphite-particle morphology on uncracked ligaments. Overall, all the uncracked ligaments steadily declined with the increase in applied displacement after the crack initiation. The first crack initiated at a displacement of around 0.28 µm in the flake graphite, while the nodular graphite began at 0.35 µm. Although the cell with the flake graphite appears to develop cracks first, the vermicular graphite generated cracks at a faster rate. In fact, at a displacement of about 0.4 µm, the vermicular particle produced more transverse cracks than the flake one. Eventually, both cases converged in terms of transverse cracking. On the other hand, the nodular particle not only exhibited interface debonding later but also had fewer transverse cracks compared to the other two studied morphologies. In the case of the nodular particle, it prevented microcrack initiation and propagation, leading to enhanced ductility and toughness while the strength level remained high. The crack initiated and propagated more easily in the matrix in the case of vermicular particles. Apparently, the nodular graphite can effectively delay the appearance of matrix cracks (see Figure 9). It should be highlighted that graphite morphology had little effect on interface debonding. All interface debonding appeared in a relatively low range of external load—at around 0.28% to 0.35% strain. Hence, increasing the nodularity of graphite particles can improve material strength and stiffness and reduce the probability of crack occurrence.
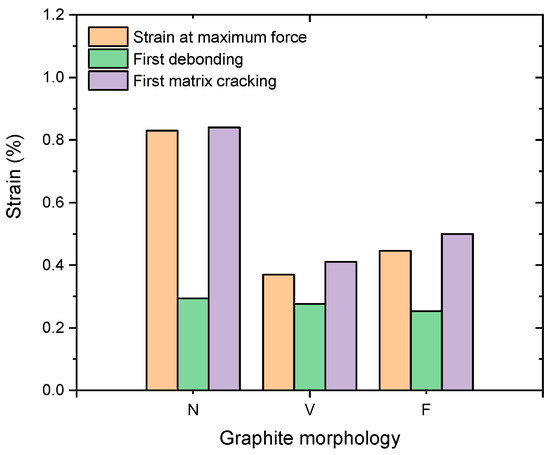
Figure 9.
Main stages of crack propagation in terms of applied displacement for different graphite morphology (N—nodular, V—vermicular, F—flake).
3.2. Effect of Periodic Boundary Conditions: Two-Particle Unit Cells
The effect of boundary conditions and CZM was investigated by considering different combinations of periodic boundary conditions and cohesive zone elements. The crack evaluation in each microstructural model is analysed in this section for three modelling cases of unit cells: I—without cohesive elements and PBCs; II—with CZM; III—CZM combined with PBCs. The crack growth and the distribution of von Mises stress in CGI for different boundary conditions are presented in Figure 10 (the deformation scale factor was set to five to increase the visibility of the crack path).
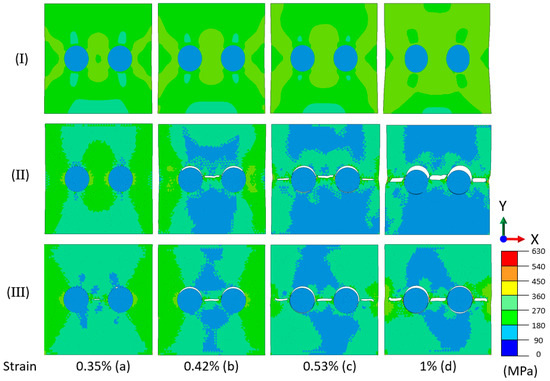
Figure 10.
Crack propagation and von Mises stress distribution for vertical tensile loading in CGI for various cases of formulation: (I) without CZM; (II) with CZM; (III) CZM-PBCs.
Besides, the macroscopic engineering stress–strain curves of these models are depicted in Figure 11. Stages a, b, c, and d in Figure 10 represent different strain levels, as marked in the strain–stress diagram of Figure 11. The crack initiated when the cohesive elements completely degraded under tension. At stage a, the crack first initiated in Case III and then propagated in the matrix. The propagation of cracks in the unit cell with periodic boundary conditions was easier in stage b when comparing Cases II and III. This can be elucidated by examining the engineering stress–strain curves, as the macroscopic stress in Case III exhibited an earlier drop compared to Case II (see Figure 11). This drop reflected the crack formation accompanied by the local unloaded zones due to the shielding effect. The stress concentration usually appeared near opposite sides of the graphite inclusions (on the line perpendicular to the loading direction), consistent with the single-inclusion unit-cell model. The incomplete connection between the interface cracks and matrix cracks is attributed to the relatively low level of the macroscopic strain—only 1%—in these models. Case III was found to represent the debonding and fracture processes in CGI in the most realistic way, so the results below were obtained with this formulation.
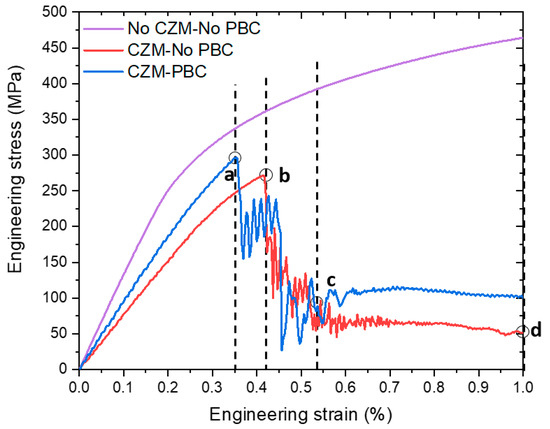
Figure 11.
Effect of boundary conditions and CZM on macroscopic engineering stress–strain curve of CGI.
3.3. Effect of Graphite Morphology and Spacing: Two-Particle Unit Cells
The crack evolution was further analysed to understand the effect of micro-morphology and interparticle distance. The geometry of graphite inclusions was generated based on statistical data [31] and the shape of particles and distances between them (and from the domain borders) are described in Figure 4. The von Mises stresses reached high levels—up to 650 MPa, with the stress concentration appearing at the left- and right-hand sides of the unit cell. It is noted that the combination of vermicular and flake particles at a minimal distance (see Figure 12I(V-F)) demonstrated the crack extending into the graphite without any interface debonding happening in the neighbouring graphite particle, unlike the other seven models, due to a mixture of mode I (opening mode) and mode II (shearing mode). Consequently, such cases of the orientation and mutual position of particles could significantly affect the structural integrity. Stress concentration primarily occurred in the middle section between the left and right sides of the model, as well as between the two particles, i.e., in the areas with the smallest matrix ligaments. The eight models studied herein all exhibited interface debonding before the cracks propagated into the matrix, which is consistent with experimental observations in [36].
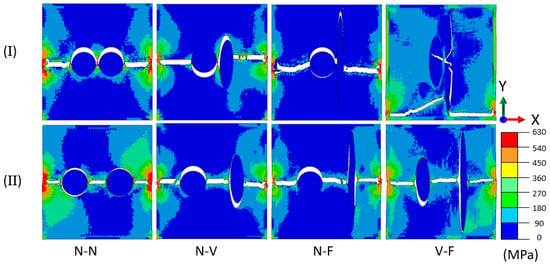
Figure 12.
Crack propagation and von Mises stress distribution for vertical tensile loading in CGI for various graphite distances and particle morphologies: (I) minimum spacing; (II) maximum spacing (N—nodular, V—vermicular, F—flake).
The main results for the crack evolution are summarised in Figure 13. When a cohesive element fulfils the initial cracking criterion, damage evolution starts, eventually followed by complete failure. In a 2D cohesive-element model, the four nodes are numbered in such a way that nodes 1 and 4 are located at the side of the crack, while nodes 2 and 3 are located at its other side. Therefore, the crack length can be represented by the distance between the midpoints of node 1, node 2 and node 2, node 3. By examining the value of the damage field variable, it can be determined whether the element failed. If it failed, the length of the crack can be increased by the respective amount, thus providing the overall crack length of the model. All the curves in Figure 13a present a similar trend, with a stable initial part, followed by a rapid decline and a final plateau. Interface debonding was first exhibited in the two nodular graphite particles model with the minimum distance between them (N-N min), while the combination of vermicular and flake particles with the maximum distance (V-F max) exhibited the latest onset of debonding. It can be observed that the distance between particles had a minor influence on crack initiation and propagation. The comparison of cases with minimal (I) and maximal (II) distances showed that the former case resulted in accelerated crack initiation and propagation (see Figure 13a). The cells with the vermicular inclusion interacting with the flake one exhibited the best crack resistance compared to all the other combinations of particles, when the major axes of both vermicular and flake graphite particles were parallel, and aligned along the loading direction. A sharp contrast in crack length was evident between the cases N-N min (0.12 mm) and V-F max (0.26 mm).
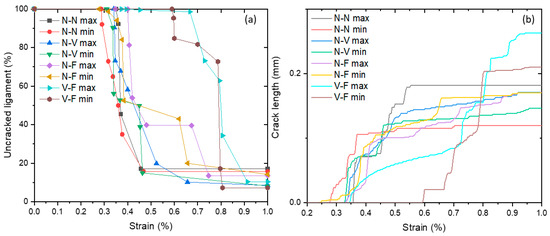
Figure 13.
Evolution of uncracked ligament (a) and crack length (b) for different morphologies of graphite inclusions in tow-particle models and distances between them.
3.4. Effect of Inter-Particle Distance on Interactions of Nodular and Flake Inclusions
The distance between the graphite inclusions influenced the crack initiation and propagation, as presented in previous sections. To further explore the impact of this distance on these processes, this section focuses on the analysis of nodular and flake graphite particles. These two types of graphite inclusions were selected because they represent two extreme graphite shapes. An examination of the fracture behaviours for these graphite particles at different distances can provide insights into their influence on the overall system.
The geometrical configurations of the models discussed in this section are illustrated in Figure 14. These models were used to further explore the effect of distance on crack growth. The distance between the two graphite particles was set at various distances: 37 μm; 23.66 μm; 12 μm; and 2 μm. Since PBCs were applied in all models, the choice of 37 μm (Figure 14a) created an infinite number of equidistant graphite particles, with flakes aligned with the loading direction). In the case of 23.66 μm, the distance between the particles was equal to the distance from the particles to the domain boundaries. The selection of 2 μm was based on statistical data, and the distance of 12 μm was selected as an intermediate value between 23.66 μm and 2 μm; the dimensions of the particles remained the same.
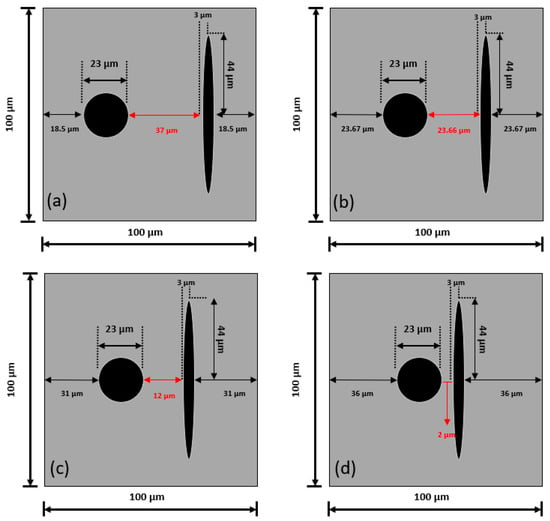
Figure 14.
Geometrical parameters of unit cells for N-F models with different distances between particles: (a) 37 μm; (b) 23.66 μm; (c) 12 μm; (d) 2 μm.
Apparently, the crack initiated quickest when the distance between the two particles was the smallest—2 μm (yellow lines in Figure 15), while it took the longest to initiate when the distance between the two graphite inclusions was the highest—37 μm (green lines). This observation demonstrates that for such morphology of the unit cell, the crack initiation process was influenced by the distance of the graphite inclusions, with closer positions leading to earlier crack initiation (see Figure 15a). Besides, the case with the distance of 2 μm exhibited the longest crack length compared to all other models. This suggests that the crack resistance of the material is enhanced in cases of larger spacings between the two neighbouring graphite inclusions.
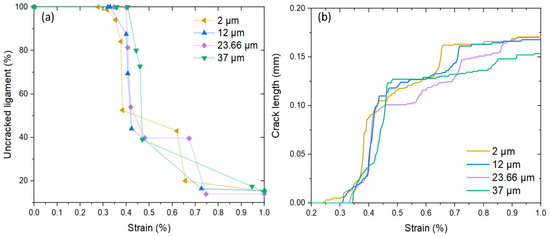
Figure 15.
Effect of inter-particle spacing on evolution of uncracked ligament (a) and crack length (b) for N-F combination.
3.5. Effect of Loading Direction: Two-Particle Unit Cells
In this part of the study, four different microstructure models with zero-thickness cohesive elements were developed to assess the influence of loading directions on crack initiation and propagation. The schematics of boundary conditions corresponding to the vertical and horizontal loading schemes are given in Figure 5. The influence of the loading direction on the deformation and damage behaviours of CGI is investigated in this section, accounting for the possibility of different loading directions in real-life applications, as demonstrated in Figure 16. In general, the initiation of cracks began predominantly at the interface of the graphite flake, where the local strain energy was higher due to edge effects. This phenomenon was especially prominent in the horizontal loading (see Figure 16a,c). However, the propagation of the cracks was much more complex for the vertical loading case (see Figure 16b). Multiple cracks initiated at the same time near the interface between the graphite particle and the matrix. After that, the cracks propagated into the graphite, subsequently merging with the interface debonding. At the end stage, the secondary crack initiated in the matrix and propagated towards the graphite particle. In the case of the maximum distance between the particles under the vertical loading (Figure 16d), the interface of the flake started debonding first, followed by the interface of the vermicular particle. After that, the crack initiated and propagated into the matrix. Besides, the flake inclusion could protect the vermicular inclusion from the interface debonding due to the shielding effect, as shown in Figure 16a,c. The formation of traction-free debonding of the flake particle (Figure 16a,c) caused the stress relief in the area in its vicinity along the direction of the loading force, hence producing a shielding effect.
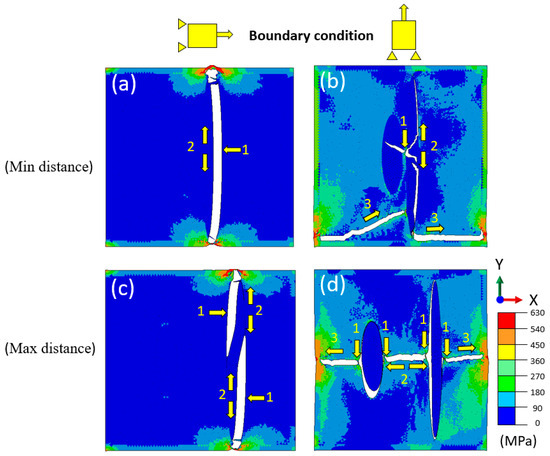
Figure 16.
Crack propagation and von Mises stress distribution in CGI under horizontal (a,c) and vertical (b,d) loading regimes for two-particle V-F model with different spacings (1—crack initiation point; 2—beginning of crack propagation; 3—end of crack propagation).
To clearly present the damage behaviour as well as the evolution of crack growth in CGI, the results of numerical analysis for the uncracked ligament and the crack length are presented in Figure 17. It is evident that the horizontal loading significantly accelerated the crack initiation and propagation (see Figure 17b); however, the crack length was reduced due to the shielding effect from the flake inclusion.
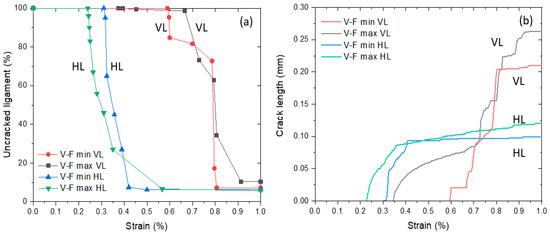
Figure 17.
Evolution of uncracked ligament (a) and crack length (b) for different loading directions for two-particle V-F model with different spacings (VL—vertical loading; HL—horizontal loading).
4. Conclusions
In this work, the effects of the morphology of graphite particles in compacted graphite iron, the distance between them, and their orientation with regard to the tensile-loading direction were investigated. The main conclusions are as follows:
- Although graphite morphology had a minimal effect on the debonding of CGI interfaces, the presence of nodular inclusions could notably enhance the macroscopic stiffness of the material and effectively impede the propagation of cracks within the metallic matrix.
- The introduction of the periodic boundary conditions enhanced the propagation of cracks in the unit cells, especially with the particle’s end situated close to the model boundaries.
- The minimal distance between the graphite particles could significantly accelerate the crack initiation and propagation when the loading is aligned with the main axis of graphite inclusions.
- The case of neighbouring vermicular and flake particles aligned along the loading direction exhibited the best crack resistance compared to all the other combinations of particles when both vermicular and flake graphite particles were orthogonal to this direction (for the same loading direction). The change in the loading direction for this case of particles to the orthogonal one could promote the crack initiation and accelerate the crack propagation rate, with the flake graphite preventing the interfacial debonding for another particle due to the shielding effect.
Author Contributions
Conceptualisation, X.L., K.P.B. and V.V.S.; methodology, X.L., K.P.B. and V.V.S.; software, X.L.; validation, X.L.; formal analysis, X.L., K.P.B. and V.V.S.; investigation, X.L.; resources, X.L.; data curation, X.L.; writing—original draft preparation, X.L.; writing—review and editing, K.P.B. and V.V.S.; supervision, K.P.B. and V.V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Scholarship Council (CSC) (Contract No. 202208060383).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to Evangelia Palkanoglou for the data on graphite in CGI.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gad, S.I.; Attia, M.A.; Hassan, M.A.; El-Shafei, A.G. Predictive computational model for damage behavior of metal-matrix composites emphasizing the effect of particle size and volume fraction. Materials 2021, 14, 2143. [Google Scholar] [CrossRef] [PubMed]
- Collini, L.; Nicoletto, G. Determination of the relationship between microstructure and constitutive behaviour of nodular cast iron with a unit cell model. J. Strain Anal. Eng. Des. 2005, 40, 107–116. [Google Scholar] [CrossRef]
- Lim, C.H.; Goo, B.C. Development of compacted vermicular graphite cast iron for railway brake discs. Met. Mater. Int. 2011, 17, 199–205. [Google Scholar] [CrossRef]
- Ghahremaninezhad, A.; Ravi-Chandar, K. Deformation and failure in nodular cast iron. Acta Mater. 2012, 60, 2359–2368. [Google Scholar] [CrossRef]
- Coronado, J.J.; Sinatora, A. Particle size effect on abrasion resistance of mottled cast iron with different retained austenite contents. Wear 2009, 267, 2077–2082. [Google Scholar] [CrossRef]
- König, M. Literature review of microstructure formation in compacted graphite Iron. Int. J. Cast Met. Res. 2010, 23, 185–192. [Google Scholar] [CrossRef]
- Shi, G.Q.; Yang, Z.; Li, J.P.; Tao, D.; Ma, Z.J. Investigation on the graphite nucleation and growth mechanism of the compacted graphite iron. J. Mater. Res. Technol. 2020, 9, 8186–8196. [Google Scholar] [CrossRef]
- Muhmond, H.M.; Fredriksson, H. Relationship between the trace elements and graphite growth morphologies in cast iron. Metall. Mater. Trans. A 2014, 45, 6187–6199. [Google Scholar] [CrossRef]
- Vajragupta, N.; Uthaisangsuk, V.; Schmaling, B.; Münstermann, S.; Hartmaier, A.; Bleck, W. A micromechanical damage simulation of dual phase steels using XFEM. Comput. Mater. Sci. 2012, 54, 271–279. [Google Scholar] [CrossRef]
- Hosseini-Toudeshky, H.; Jamalian, M. Simulation of micromechanical damage to obtain mechanical properties of bimodal Al using XFEM. Mech. Mater. 2015, 89, 229–240. [Google Scholar] [CrossRef]
- Palkanoglou, E.N.; Baxevanakis, K.P.; Silberschmidt, V. Thermal debonding of inclusions in compacted graphite iron: Effect of matrix phases. Eng. Fail. Anal. 2022, 139, 1–13. [Google Scholar]
- Cao, M.; Baxevanakis, K.P.; Silberschmidt, V.V. Effect of graphite morphology on the thermomechanical performance of compacted graphite iron. Metals 2023, 13, 473. [Google Scholar] [CrossRef]
- Collini, L.; Pirondi, A. Microstructure-based RVE modeling of the failure behavior and LCF resistance of ductile cast iron. Procedia Struct. Integr. 2019, 24, 324–336. [Google Scholar] [CrossRef]
- Mao, C.; Zhang, R.; Guo, R.; Zhao, X. Two-scale modeling of particle crack initiation and propagation in particle-reinforced composites by using microscale analysis based on Voronoi cell finite element model. Compos. Struct. 2023, 316, 116989. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Chen, H.; Song, B.; Zhao, Y.; Yu, T.; Zhao, J. Meso-scale numerical simulation and experimental verification of single grain grinding TiC–Fe composites. Ceram. Int. 2022, 48, 12299–12310. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Tiedje, N.S.; Hattel, J. Modeling of damage in ductile cast iron—The effect of including plasticity in the graphite nodules. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 012027. [Google Scholar] [CrossRef]
- Andriollo, T.; Thorborg, J.; Hattel, J. Modeling the elastic behavior of ductile cast iron including anisotropy in the graphite nodules. Int. J. Solids Struct. 2016, 100–101, 523–535. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, M. Prediction of fracture toughness of ceramic composites as function of microstructure: I. Numerical simulations. J. Mech. Phys. Solids 2013, 61, 472–488. [Google Scholar] [CrossRef]
- Sjögren, T.; Svensson, I.L. Studying elastic deformation behaviour of cast irons by acoustic emission. Int. J. Cast Met. Res. 2005, 18, 249–256. [Google Scholar] [CrossRef]
- Leyens, C.; Hausmann, J.; Kumpfert, J. Continuous fiber reinforced titanium matrix composites: Fabrication, properties and applications. Adv. Eng. Mater. 2003, 5, 399–410. [Google Scholar] [CrossRef]
- Papakaliatakis, G.; Karalekas, D. Damage growth by debonding in a single fibre metal matrix composite: Elastoplasticity and strain energy density criterion. Theor. Appl. Fract. Mech. 2010, 53, 152–157. [Google Scholar] [CrossRef]
- García, I.G.; Paggi, M.; Mantic, V. Fiber-size effects on the onset of fiber-matrix debonding under transverse tension: A comparison between cohesive zone and finite fracture mechanics models. Eng. Fract. Mech. 2014, 115, 96–110. [Google Scholar] [CrossRef]
- Xu, J.; El Mansori, M. Cutting modeling using cohesive zone concept of titanium/CFRP composite stacks. Int. J. Precis. Eng. Manuf. 2015, 16, 2091–2100. [Google Scholar] [CrossRef]
- Chuang, C.; Singh, D.; Kenesei, P.; Almer, J.; Hryn, J.; Huff, R. 3D quantitative analysis of graphite morphology in high strength cast iron by high-energy X-ray tomography. Scr. Mater. 2015, 106, 5–8. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G. Mixed-mode decohesion finite elements for the simulation of delamination in composite materials. NASA Tech. Pap. 2002, 211737, 42. [Google Scholar]
- Eiken, J. Calphad-based phase-field study of the interplay between spheroidal graphite growth and chemical segregation in ductile cast iron. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012055. [Google Scholar] [CrossRef]
- Yang, H.W.; Wang, X.M.; Liu, W.; Huang, W.; Wu, M.; Xue, M.L.; Li, L. Influence of distribution and size of graphite particle on the machinability of nodular cast iron. Eng. Fract. Mech. 2024, 297, 109882. [Google Scholar] [CrossRef]
- Xu, C.; Wigger, T.; Azeem, M.A.; Andriollo, T.; Fæster, S.; Clark, S.J.; Gong, Z.; Atwood, R.; Grivel, J.C.; Hattel, J.H.; et al. Unraveling compacted graphite evolution during solidification of cast iron using in-situ synchrotron X-ray tomography. Carbon N. Y. 2021, 184, 799–810. [Google Scholar] [CrossRef]
- Dessart, L.; Standaert, W.S. storytelling in the age of sustainability. B.H. Creep deformation and damage mechanism of compact graphite cast iron with different pearlite contents. Int. J. Disaster Risk Reduct. 2023, 23. [Google Scholar] [CrossRef]
- Palkanoglou, E.N.; Baxevanakis, K.P.; Silberschmidt, V.V. Thermal debonding in compacted graphite iron: Effect of interaction of graphite inclusions. Procedia Struct. Integr. 2021, 37, 209–216. [Google Scholar] [CrossRef]
- Okereke, M.; Keates, S. Finite Element Applications; Springer International Publishing AG: Cham, Germany; Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Beskou, N.D.; Muho, E. V Microstructural effects on dynamic response of rigid and flexible pavements to moving load under plane strain. Soil Dyn. Earthq. Eng. 2022, 163, 107544. [Google Scholar] [CrossRef]
- Greenstreet, W.L.; Yahr, G.T.; Valachovic, R.S. The behavior of graphite under biaxial tension. Carbon N. Y. 1969, 11, 43–57. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Q.; Dong, J. Simulation study on CFRP strengthened reinforced concrete beam under four-point bending. Comput. Concr. 2016, 17, 407–421. [Google Scholar] [CrossRef]
- Qiu, Y.; Pang, J.C.; Yang, E.N.; Li, S.X.; Zhang, Z.F. Transition of tensile strength and damaging mechanisms of compacted graphite iron with temperature. Mater. Sci. Eng. A 2016, 677, 290–301. [Google Scholar] [CrossRef]
- Palkanoglou, E.N.; Baxevanakis, K.P.; Silberschmidt, V. V Interfacial debonding in compacted graphite iron: Effect of thermal loading. Procedia Struct. Integr. 2020, 28, 1286–1294. [Google Scholar] [CrossRef]
- Zhang, Y.; Pang, J.; Shen, R.; Qiu, Y.; Li, S.; Zhang, Z. Investigation on tensile deformation behavior of compacted graphite iron based on cohesive damage model. Mater. Sci. Eng. A 2018, 713, 260–268. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).