Experimental Investigation of the Vibration-Induced Heating of Polyetheretherketone for High-Frequency Applications

Abstract

Dynamically loaded structures made of thermoplastic polymers have been extensively exploited in several demanding industries. Due to the viscoelastic and thermal properties of thermoplastic polymers, self-heating is generally inevitable, especially during dynamic deformations at high frequencies. Therefore, the thermoplastic polyether ether ketone (PEEK), with its high temperature resistance and high specific strength, is a particularly ideal candidate for dynamically loaded applications. Using scanning laser Doppler vibrometry and infrared thermography, an experimental study of the vibration characteristics and the vibration-induced heating of flat-sheet PEEK specimens was carried out. The specimens were base-excited by means of a piezoelectric actuator at high frequencies in the range between 1 and 16 kHz. As a result, a maximum temperature rise of approximately 6.4 K was detected for the highest investigated excitation. A high correlation between the spatial distribution of the velocity along the beam’s axial direction and the resulting temperature increase was measured. To summarize, the occurring self-heating of PEEK due to the dissipation of vibrational energy has to be critically considered for dynamically loaded structural applications, especially areas with high displacement amplitudes, such as antinodes, which yield the highest temperature increase.

1. Introduction

Polymer-based structures are being increasingly used in several applications where they are subject to dynamic loads. The viscoelastic material behavior and the thermal properties in structural polymers result in undesired self-heating. This self-heating is a threatening phenomenon which may significantly influence structural degradation and durability as a consequence [1]. The effect of self-heating becomes even more pronounced during dynamic deformations of thermoplastic polymers, such as polyether ether ketone (PEEK), at high frequencies (as demonstrated by Kucher et al. [2]) or in the high-stress tensile regime (as analyzed by Berer et al. [3]). Particularly, PEEK possesses, both in its neat-polymer and polymer-based composite configurations, excellent properties such as high thermostability [4], high specific strength, favorable tribological properties [5,6], chemical stability [7] and superior machinability [8,9,10]. These properties prove the polymer PEEK to be a suitable option for advanced, dynamically loaded applications at a high frequency range, such as dental instruments for root canal irrigation [11,12], polymer micro-cantilever arrays for sensing [13] or as material for ultrasonic pulse echo systems [14]. In addition to its high thermal resistance, the polymer PEEK has low material damping compared to other thermoplastics (compare reference [15]). Furthermore, manufacturing processes could also involve dynamic loading, as in ultrasonic welding processes investigated by Abdulfattah et al. [16] and Tutunjian et al. [17,18] or in high-speed dry milling researched by Song et al. [19].

Due to the material damping of PEEK and its low thermal conductivity, the resulting dissipated energy leads to heat generation of the material during cyclic loading [20,21,22,23,24]. In the literature, there are several studies which investigate the conditions of high-frequency mechanical loading and the resulting self-heating of PEEK [25,26,27,28,29,30,31,32,33,34]. However, these studies only consider the self-heating of PEEK at low frequencies. Self-heating effects at the ultrasonic frequency range are investigated for various polymers. For example, the self-heating of polyethylene terephthalate (PETP), polyethylene (PE) and polyamide (PA) was studied by Fayerman [35]. Similarly, Mignogna et al. analyzed the effect in polychlorotrifluoroethylene (PCTFE) [36]. The same effect was observed in carbon fiber-reinforced polyphenylensulfide (CF-PPS) by Backe [37]. Acrylonitrile butadiene styrene (ABS) [38] and polymethyl methacrylate (PMMA) also showed self-heating at an ultrasonic frequency range [39]. Nevertheless, there are currently no studies analyzing the self-heating of PEEK in a high frequency regime. For these measurements, a combination of scanning laser Doppler vibrometry (SLDV) and infrared thermography (IRT) is an efficient non-destructive testing (NDT) method for the defect analysis of these materials [40] and for the analysis of vibration-induced thermal effects in both neat and polymer-based composite materials (see, e.g., Katunin [41]).

Vibration-induced heating and defect analysis of polymeric materials using SLDV is widely studied (see, e.g., references [42,43,44,45]). In particular, Holland analyzed different thermographic signal reconstructions for vibrothermography [46] and used vibrothermography to identify the resonant modes by means of the full-field vibration coverage measurement in absorptive viscoelastic coatings [47]. Mihalec et al. [48] analyzed a base-excited PMMA beam’s heating due to the introduced vibrational energy using an electrodynamic shaker for excitation, a thermographic camera for temperature measurement and a high-speed camera for the determination of the beam’s displacement. Montanini and Freni [49] analyzed the correlation between the vibrational mode shapes and the resulting maximum temperature increase. The applied test configuration in their research consisted of an ultrasound generation unit with an ultrasonic sonotrode which excites a double-sided clamped metallic beam in the ultrasonic frequency range. They obtained a high correlation between the beam’s velocity amplitudes at resonance frequencies and the temperature increase. Katunin established the concept of a thermographic method for the non-destructive testing of polymeric composite structures using self-heating [41]. The specimens were excited by means of an electrodynamic shaker through a steel stinger. Using the same approach, the author adopted the non-destructive testing method by involving additional thermal tests to investigate the criticality of the self-heating in polymers and polymer matrix composites during fatigue testing [50]. Luo et al. [51] quantified the heat build-up of rubber materials when subjected to cyclic deformation using thermographic methods. Using the approach of vibrothermography, Segers et al. [52] investigated the in-plane local defect resonances of impacted carbon fiber-reinforced polymers. Wronkowicz et al. [23] introduced a vibrothermography setup for notched polymeric composite structures with single-side access. Mevissen and Meo [53] used an ultrasonic stimulated thermographic test system for the detection of cracks in turbine blades. The applied technique was based on ultrasound excitation with a piezoelectric actuator. Kucher et al. [2] used a piezoelectric-driven base excitation to determine the vibration behavior of polymeric specimens. They concluded that the resulting self-heating effect depended on the frequency and the velocity amplitude of the excitation.

In the current study, the vibration characteristics and the subsequent vibration-introduced heating were determined for flat-sheet specimens made of PEEK using the experimental procedures described by Kucher et al. [2]. The normal velocity—the normal direction was defined in the beam’s thickness direction—and the resulting surface temperature of the whole specimen were determined by means of the non-invasive testing methods SLDV and IRT, respectively. The test setup consists of a piezoelectrically driven base excitation of the polymeric specimens to enable the investigation of high frequencies. Using the described approach, the specimen’s vibration characteristics (resonance frequencies and loss factors) and the vibration-induced self-heating for different velocity amplitudes of the base excitation were experimentally analyzed. For the first time, the high-performance thermoplastic polymer PEEK was investigated at a high frequency range. Finally, the correlation between the vibrational mode shapes and the resulting temperature increase after a certain amount of time was established. For the applied excitation parameters, i.e., frequency and velocity amplitude, the maximum resulting temperature increase was quantified. Using the findings of the current study, the applicability of PEEK as a potential material for dynamically loaded applications at high frequencies was assessed and the resulting temperature increase was quantified.

2. Materials and Methods

2.1. Specimen Preparation

The investigations were carried out for commercially available extruded plates made of the polymer PEEK (SustaPEEK, Röchling Industrial, Lahnstein, Germany). From this plate, a flat-sheet specimen with the dimensions $l\times b\times d=$ 140.14 ± 0.02 mm $\times$ 4.83 ± 0.06 mm $\times$ 1.21 ± 0.001 mm and a mass of $m=$ 1.05 ± 0.01 g was prepared by means of a fully automatic high-volume cutting machine (Axitom, Struers, Willich, Germany). The material properties of the semi-finished product are summarized in

Table 1. Material properties of PEEK (SustaPEEK, data from data sheet [54]).

Property	Test Method	Unit	Value
Density	DIN EN ISO 1183-1	g cm−3	1.31
Yield stress	DIN EN ISO 527	MPa	110
Tensile modulus of elasticity	DIN EN ISO 527	MPa	4000
Melting temperature	ISO 11357-3	°C	343
Thermal conductivity	DIN 52612-1	W m−1 K−1	0.25
Thermal capacity	DIN 52612	kJ kg−1 K−1	1.34
Coefficient of linear thermal expansion	DIN 53752	K−1	50 × 10−6
Service temperature, long-term	-	°C	−60…250
Service temperature, short-term	-	°C	310
Heat deflection temperature	DIN EN ISO 75	°C	152

. Prior to testing and during the measurements, the specimen was stored under standard atmosphere at an ambient temperature of $\vartheta =$ 22.9 ± 0.7 °C and at a relative humidity of 31.0 ± 1.8%.

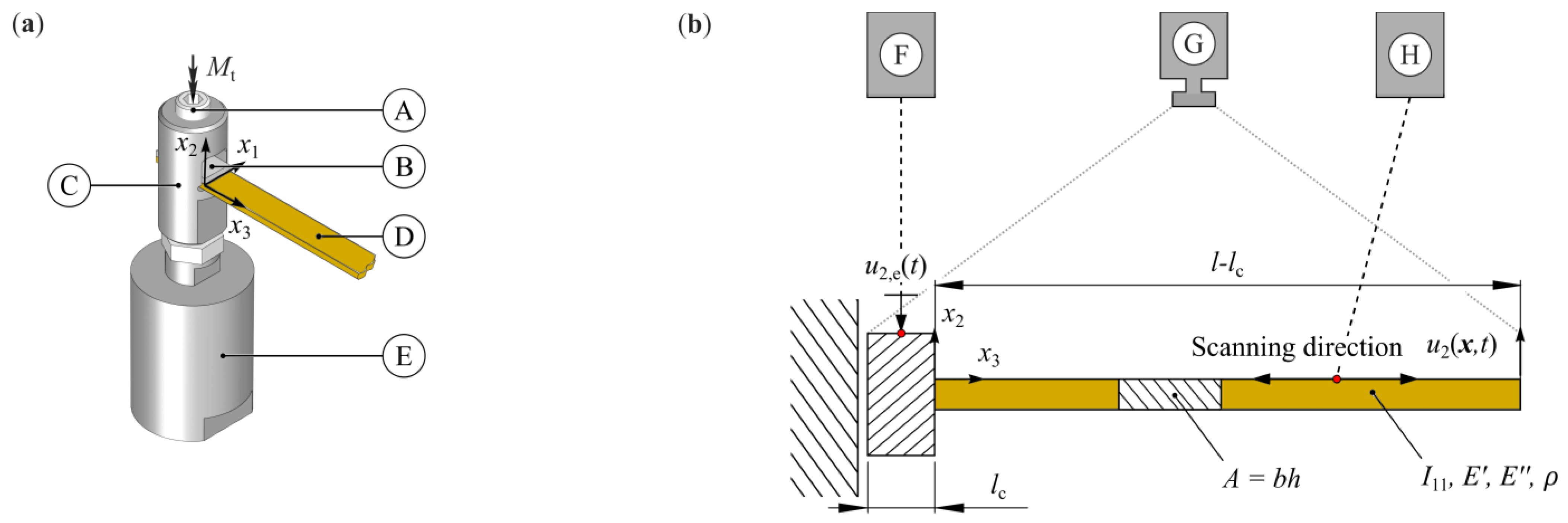
2.2. Experimental Setup and Procedure

The polymeric specimen was clamped with a length of $l_{\mathrm{c}}=$ 10.3 ± 0.3 mm using a clamping adapter, which was a modified one-end threaded circular post (Figure 1a, component C). The specimen was held in position by tightening a grub screw (Figure 1a, component A) with a defined tightening torque $M_t$, which compresses the clamping area of the specimen by means of an insertion plate (Figure 1a, component B). A nominal tightening torque of $M_t=$ 1.1 Nm was used for all investigations (compare Kucher et al. [2]). The adapter was excited by means of a piezoelectric actuator (PSt 1000/10/7 VS18, Piezosystem, Jena, Germany), which was driven by a signal generator (PSV-400 junction box, Polytec, Waldbronn, Germany) and amplified by a voltage amplifier (LE 150/100 EBW, Piezosystem, Jena, Germany). Therefore, a mono-frequent sinusoidal voltage signal

$$U_{\mathrm{e}}\left(t\right)={\widehat{U}}_{\mathrm{e}}\sin \left(2\pi f_{\mathrm{e}}t\right)+{\widehat{U}}_{\mathrm{e}}$$

(1)

as well as a linear voltage sweep signal

$$U_{\mathrm{e}}\left(t\right)={\widehat{U}}_{\mathrm{e}}\sin \left(2\pi \left[f_{\mathrm{e},1}t+\left(f_{\mathrm{e},2}-f_{\mathrm{e},1}\right)\frac{t^2}{t_{\mathrm{e}}}\right]\right)+{\widehat{U}}_{\mathrm{e}}$$

(2)

were used, where ${\widehat{U}}_{\mathrm{e}}$ is the actuator’s input voltage amplitude as well as the signal’s offset and $f_{\mathrm{e}}$ is the frequency of excitation in the case of a mono-frequent sinusoidal voltage signal according to Equation (1). Moreover, the voltage sweep signal was defined using Equation (2), where $f_{\mathrm{e},1}$ is the initial sweep frequency, $f_{\mathrm{e},2}$ is the final sweep frequency and $t_{\mathrm{e}}$ is the duration of the sweep. The actuator was mounted on a steel profile at an optical table. The measuring campaign was carried out with an actuator input voltage amplitude from ${\widehat{U}}_{\mathrm{e}}$ = 11 V to 54 V and an excitation frequency in the range between $f_{\mathrm{e}}$ = 1 and 16 kHz.

The beam’s velocities were measured using a scanning laser Doppler vibrometer (PSV-400 scanning head, Polytec, Waldbronn, Germany), which allowed the full-field measurement of the beam’s normal velocity $u_2\left(x_i,t\right)$ with i = 1, 2, 3 at different visible measurement positions (Figure 1b). This vibrometer operated at velocities up to 20 m/s with a maximum sampling frequency of 20 MHz. Simultaneously, the base excitation’s velocity $u_{2,\mathrm{e}}\left(t\right)$ was determined by means of an additional one-point laser Doppler vibrometer (OFV-505 sensor head, Polytec GmbH, Germany). To derive the mode shape in the current study, the response of the structure in the form of its measured velocity $u_2\left(x_i,t\right)$ was used. For a one-dimensional bending vibration, this yields the mode shape $\varphi \left(x_3\right)$. For the harmonic steady-state vibrations studied here, the velocity $u_i$ can be determined from the displacement $w_i$ of the beam:

$$u_i \left(x_i,t\right)=\frac{\partial w_i \left(x_i,t\right)}{\partial t}=\underset{{\widehat{u}}_i\left(x_i\right)}{\underbrace{2\pi f{\widehat{w}}_i \left(x_i\right)}}\cos \left(2\pi ft\right) \mathrm{with} i=1, 2, 3,$$

(3)

where $\partial (\cdot )/\partial t$is the partial derivative with respect to time $t$, $f$ is the frequency, ${\widehat{w}}_i$ is the amplitude of the displacement and ${\widehat{u}}_i$ is the amplitude of the velocity. Using Equation (3), the beam’s displacement amplitudes were calculated, since these values cannot be determined directly with the help of the SLDV used.

The surface temperature of the specimen as well as the surface temperature of the clamping adapter and the piezoelectric actuator were measured using an IR camera (Variocam, Jenoptik, Jena, Germany). Using this technique, the temperature signal’s thermal drift was determined with a sampling frequency of 3 Hz. The registration of the IR camera according to the camera of the SLDV system was carried out by means of a linear least squares regression using a linear function. This image registration was used as a process of transforming the different sets of data into one coordinate system.

For quantification of the self-heating, the resulting temperature increase in the specimen’s surface $\mathsf{\Delta }\vartheta \left(t\right)=\vartheta \left(x_i,t\right)-\vartheta \left(x_i,t=0\right)$ and the maximum temperature increase $\max \left\{\mathsf{\Delta }\vartheta \left(t\right)\right\}$ were analyzed to identify the temperature-related effects on the polymer’s cyclic deformations. The mean temperature rise slope (MTRS) was calculated to compare the results of the different measurements using the maximum temperature increase $\max \left\{\mathsf{\Delta }\vartheta \left(t\right)\right\}$ and the measuring time of $t$ = 32.8 s. The vibration-induced heating ratio (VHR) was determined from the ratio between MTRS and the approximated maximum velocity amplitude at a voltage amplitude of the piezoelectric actuator of ${\widehat{U}}_{\mathrm{e}}$ = 54 V, calculated by means of a power law approximation, as expressed by:

$${\widehat{u}}_2\left({\widehat{U}}_{\mathrm{e}}\right)=a{\widehat{U}}_{\mathrm{e}}^b+c$$

(4)

where a, $b$ and $c$ are constants. Using Equation (4), the approximated velocity was calculated with the following expression:

$${{\widehat{u}}_2|}_{{\widehat{U}}_{\mathrm{e}}=54 \mathrm{V}}=\frac{{{\widehat{u}}_2|}_{{\widehat{U}}_{\mathrm{e}}=11 \mathrm{V}}\left(a54V^b+c\right)}{\left(a11V^b+c\right)},$$

(5)

where ${{\widehat{u}}_2|}_{{\widehat{U}}_{\mathrm{e}}=11 \mathrm{V}}$ is the measured velocity amplitude at a voltage amplitude of ${\widehat{U}}_{\mathrm{e}}$ = 11 V. For an average temperature increase of $\mathsf{\Delta }\vartheta \ge$ 0.2 K, the steady-state temperature increase $\mathsf{\Delta }{\vartheta }_{\infty }$ was calculated using the following exponential approximation (compare, e.g., Muller et al. [55]):

$$\mathsf{\Delta }\vartheta \left(t\right)=\mathsf{\Delta }{\vartheta }_{\infty }\left(1-e^{-\frac{t}{\tau }}\right)$$

(6)

where $\tau$ is a characteristic time constant of the polymeric structure’s heating process. The values $\mathsf{\Delta }{\vartheta }_{\infty }$ and $\tau$ were determined using the nonlinear least squares fitting method by means of the numeric computing software (MATLAB version 9.12.0, Mathworks, Natick, MA, USA). Equation (6) includes all thermal and thermomechanical effects of the test setup used. In the case that the temperature distribution of the test specimen does not become stationary after the selected duration of observation, the maximum temperature increase $\mathsf{\Delta }{\vartheta }_{\infty }$ is estimated using Equation (6). This procedure is used to ensure the use of short measuring times and thus to prevent a change in the mechanical properties of the tested polymer as much as possible. For this purpose, further investigations ensure that the vibration behavior of the test specimens does not change significantly for the selected measurement time. In the case of $\mathsf{\Delta }\vartheta <$ 0.2 K, the temperature increase was not further considered.

The experimental procedure consisted of the following steps:

1.

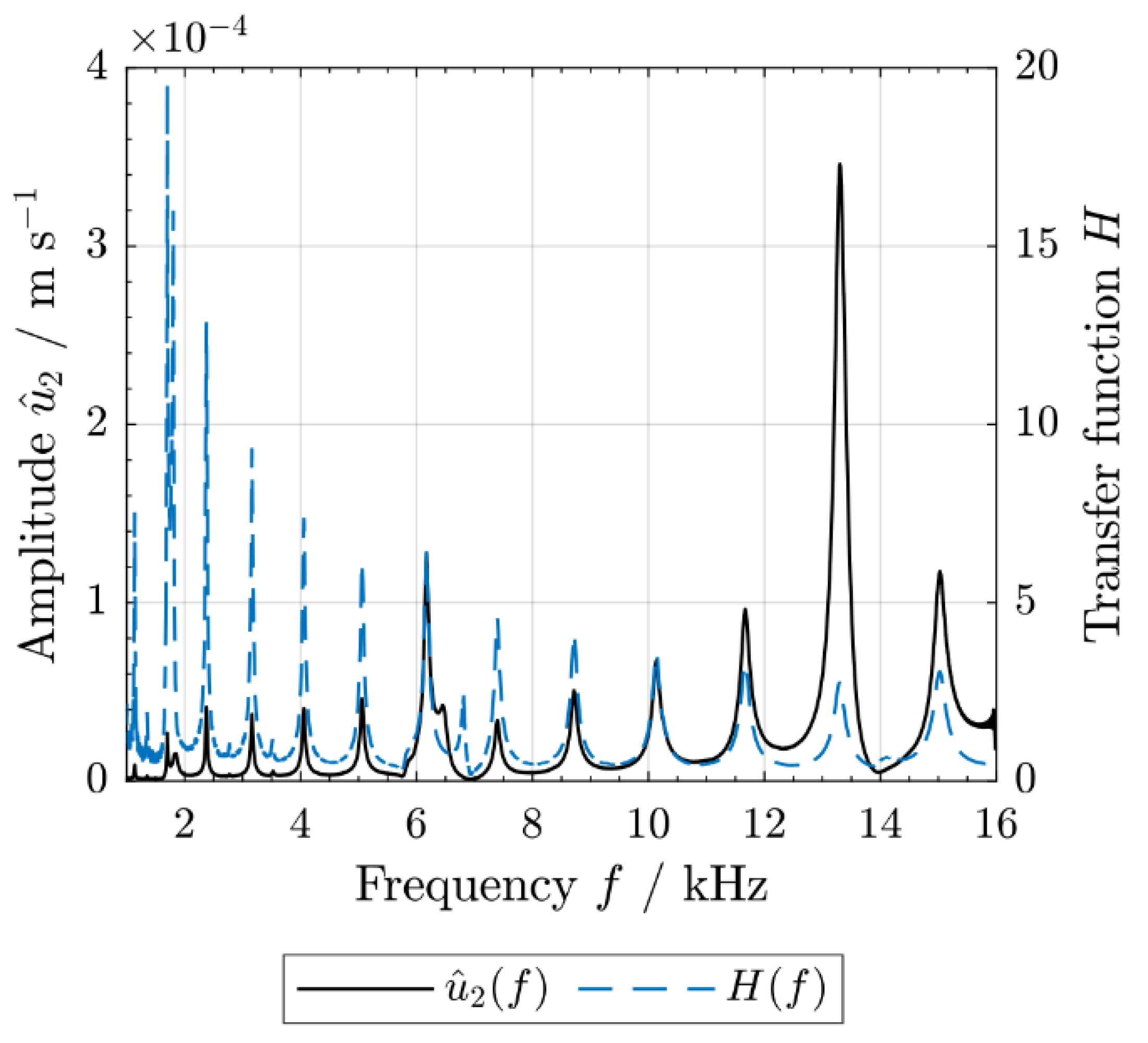
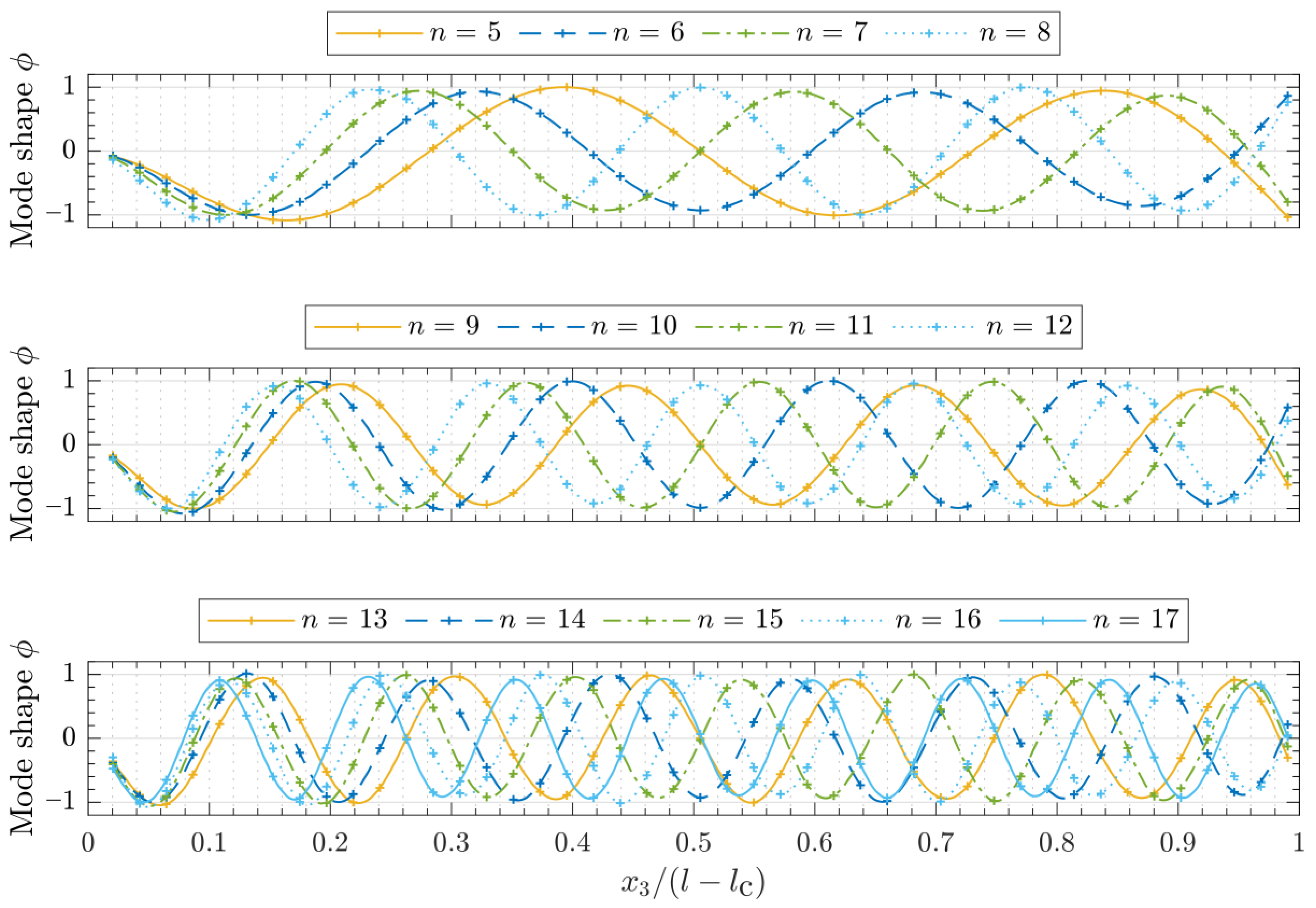
For the beam’s vibrational behavior (natural frequencies $f_n$, loss factors $\tan {\delta }_n$), a voltage sweep according to Equation (2) with a duration of the sweep of $t_{\mathrm{e}}$ = 12.8 s, a sampling frequency of 163.84 kHz, an initial sweep frequency of $f_{\mathrm{e},1}$ = 1 kHz, a final sweep frequency of $f_{\mathrm{e},2}$ = 16 kHz and a frequency resolution of 78.125 mHz was used as the actuator’s excitation signal $U_{\mathrm{e}}\left(t\right)$. Fast Fourier transform (FFT) and a rectangular window function without filtering of the time signals were applied to obtain the average frequency spectrum ${\widehat{u}}_2\left(x_i,f\right)$ and the transfer function $H\left(x_i,f\right)$, which represents the complex relationship between output signals $u_2\left(x_i,t\right)$ and input signals $u_{2,e}\left(t\right)$ as a function of frequency (Figure 2). Using this transfer function, the natural frequencies $f_n$ as well as the loss factors $\tan {\delta }_n=\mathsf{\Delta }{f}_n/f\_n$ were determined. The loss factors were calculated by means of the half-power bandwidth method, where $\mathsf{\Delta }{f}_n$, $f_n$ and $\varphi \left(x_3\right)$ are the 3 dB bandwidth, the associated resonance frequency (see, e.g., [56]) and the corresponding mode shapes (see Figure 3), respectively.

2.

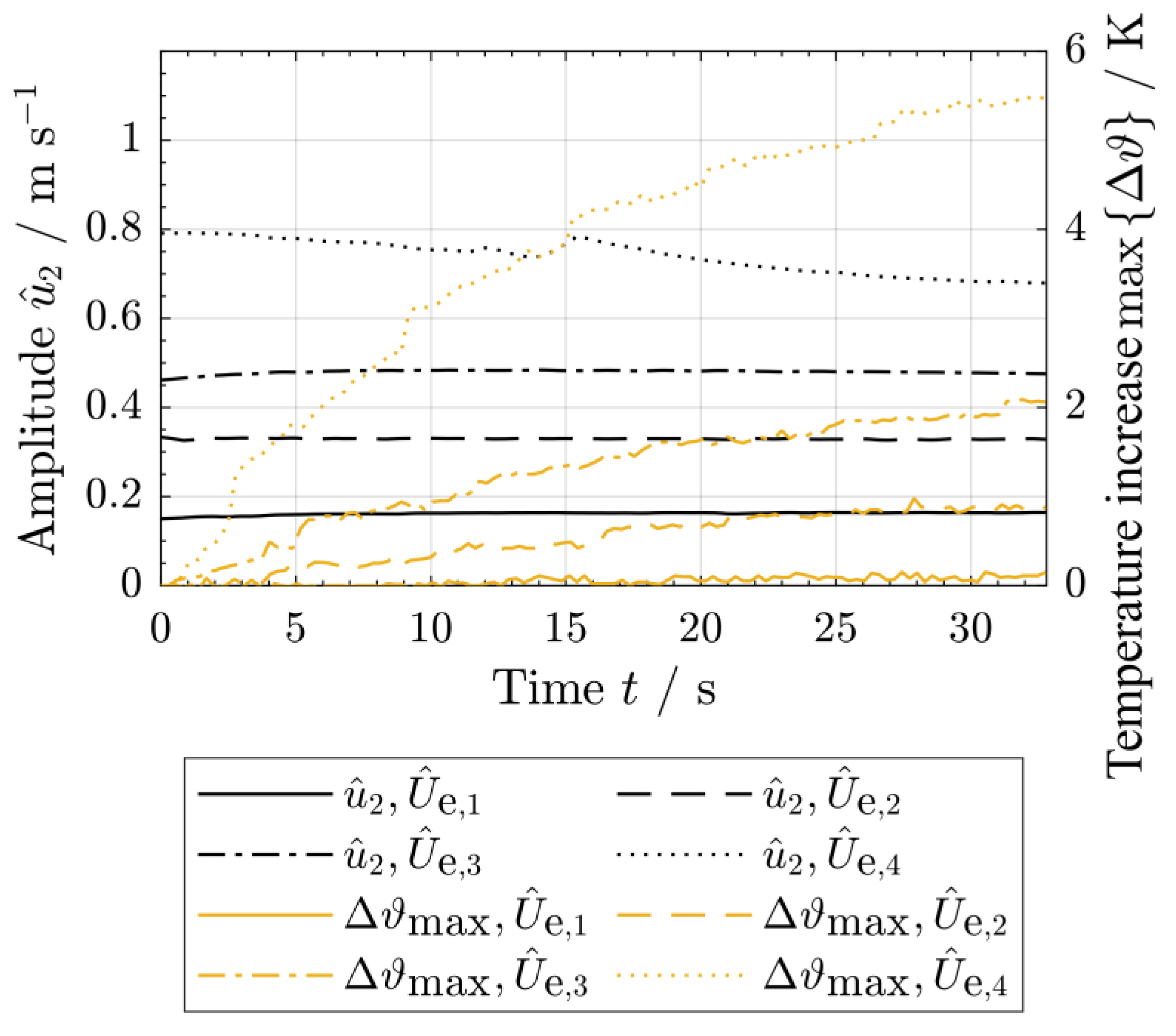
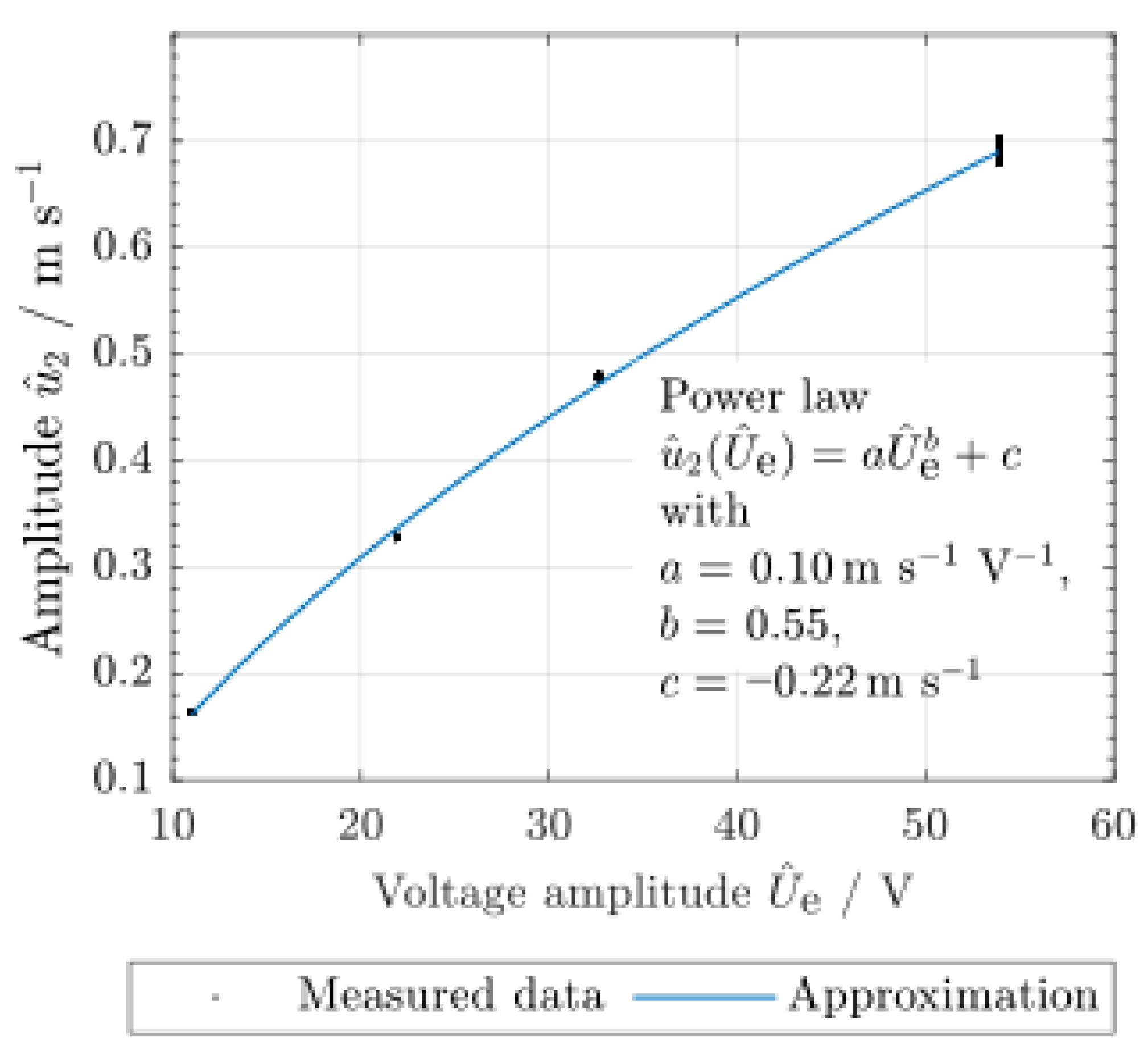
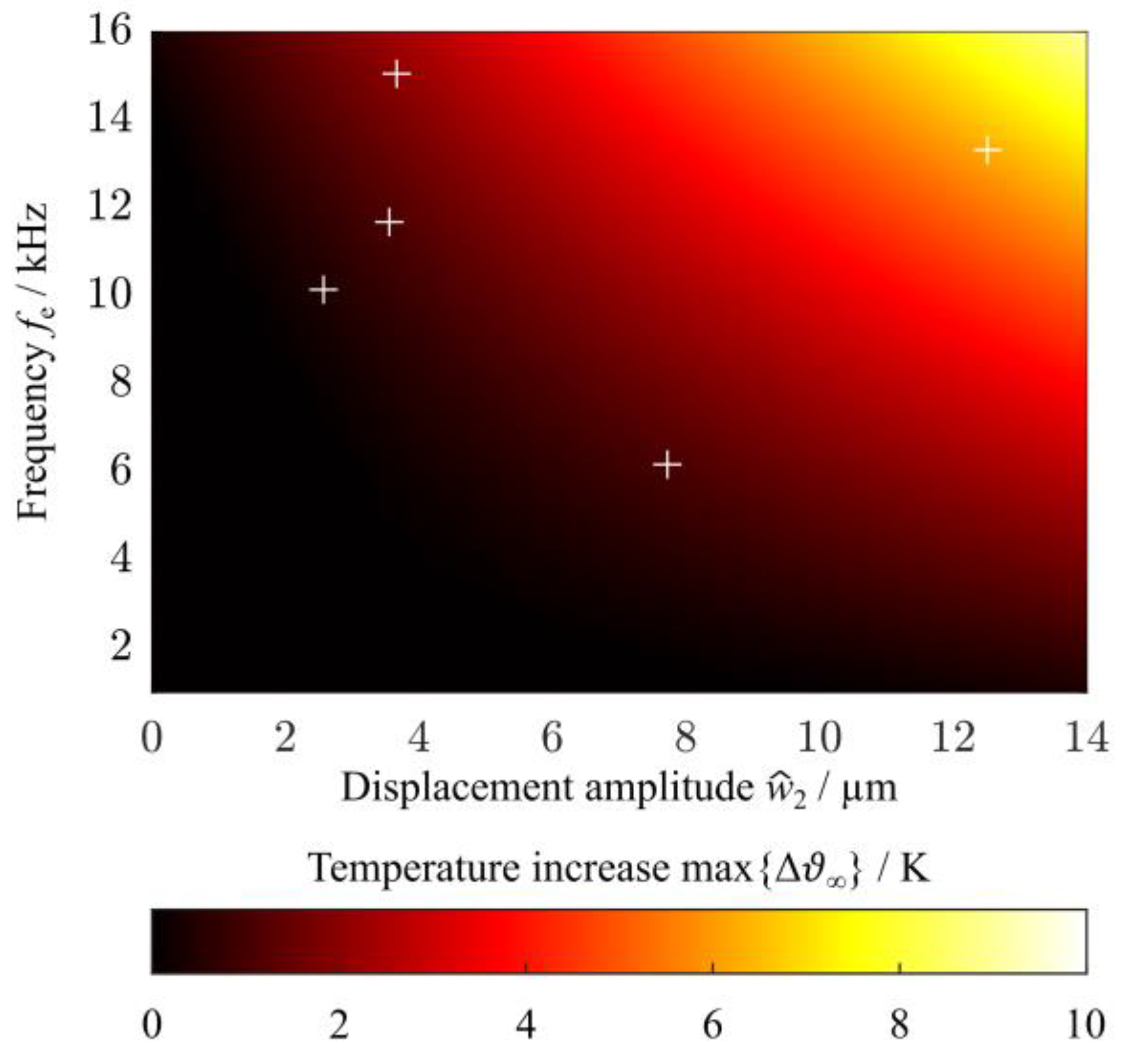
To quantify changes in mechanical and the related thermal phenomena, the resulting temperature increase $\max \left\{\mathsf{\Delta }\vartheta \left(t\right)\right\}$ of the whole specimen and the change in the velocity amplitude $\widehat{u}\left(x_i={\tilde{x}}_i\right)$ at the position $[{\tilde{x}}_i]$ = [2.5 mm, 0, 4.7 mm] (sampling frequency 128 kHz, frequency resolution 7.8 mHz) were measured for different input voltage amplitudes of ${\widehat{U}}_{\mathrm{e}}$ in the range between 11 V and 54 V (Figure 4). Therefore, the specimen was sinusoidally excited with a voltage signal $U_{\mathrm{e}}\left(t\right)$ as shown in Equation (1) and the natural frequencies were chosen for excitation so that the relationship $f_{\mathrm{e}}=f_n$ was fulfilled.

3.

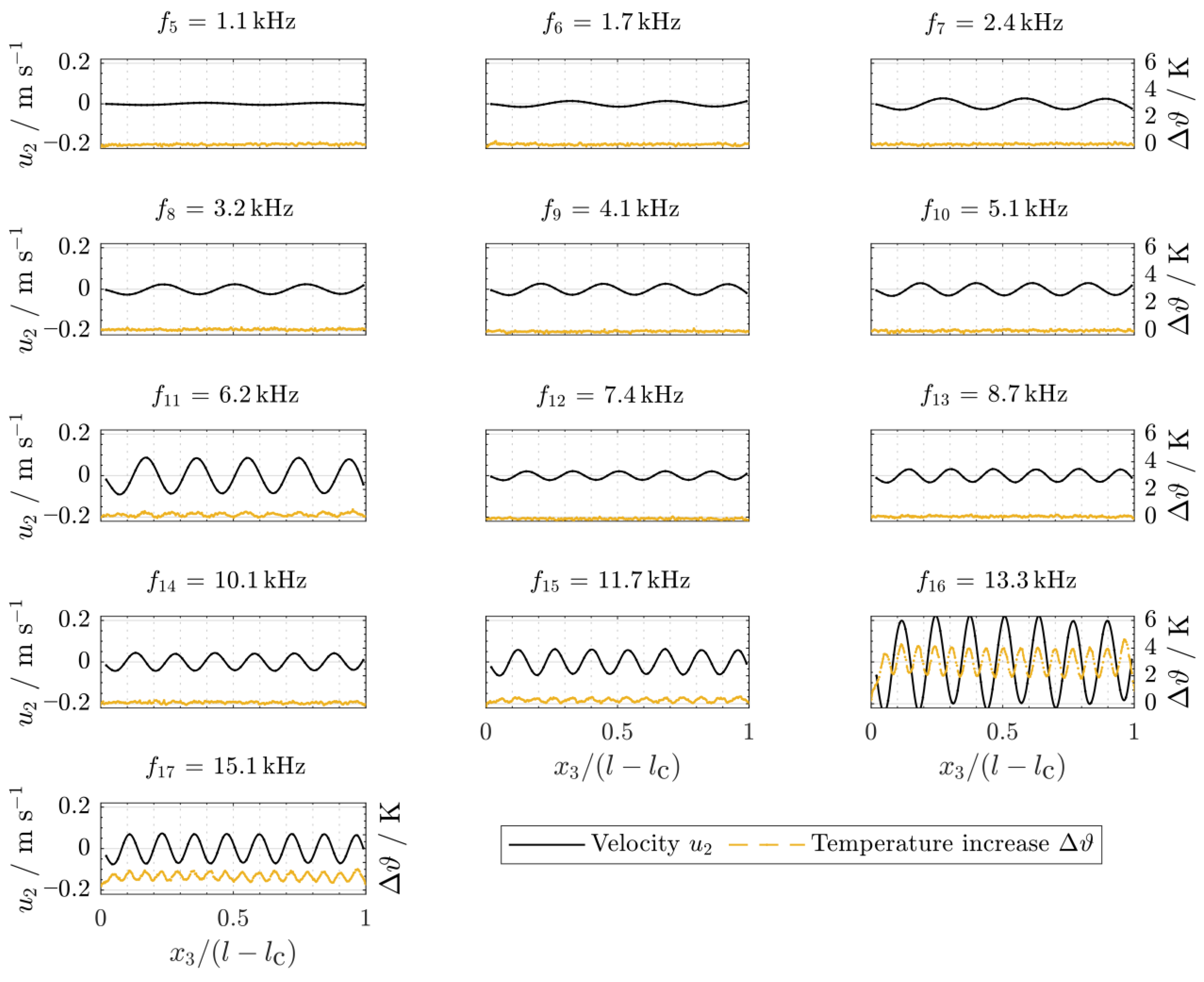
The mode shapes $\varphi \left(x_3\right)$ (see Figure 3) and the beam’s real physical velocity distribution $u_2\left(x_3\right)$ were determined by means of additional measurements with a mono-frequent sinusoidal voltage signal according to Equation (1) at the given natural frequencies $f_n$. Therefore, a sinusoidal excitation with an input voltage amplitude of ${\widehat{U}}_{\mathrm{e}}$ = 11 V was carried out with a sampling frequency of 128 kHz, a frequency resolution of 7.8 mHz and a measuring time of 512 ms.

4.

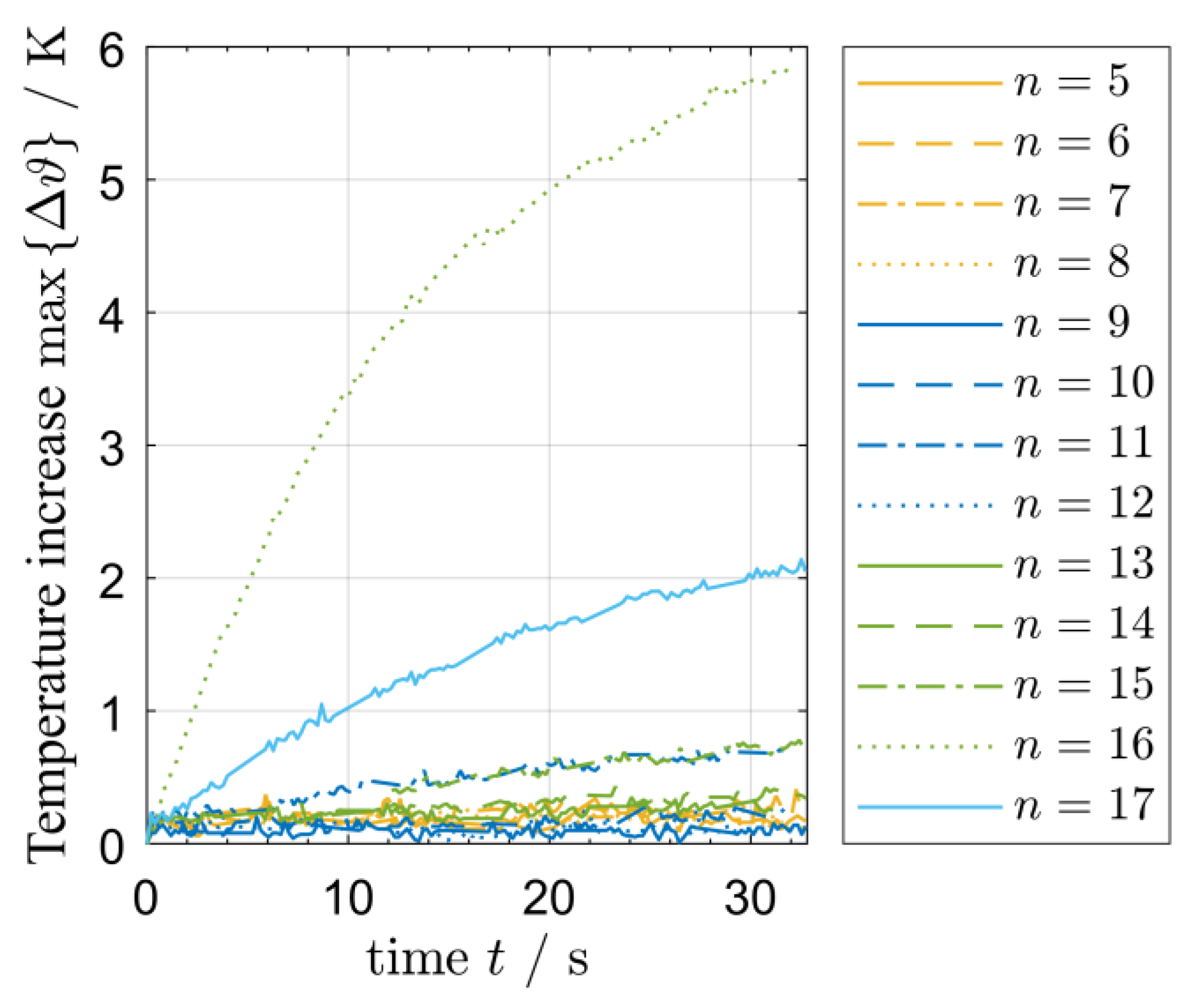
Additional measurements of the temperature increase $\mathsf{\Delta }\vartheta \left(t\right)$ for a duration of $t$= 32.8 s and the different natural frequencies $f_n$ were performed using an input voltage amplitude of ${\widehat{U}}_{\mathrm{e}}$ = 54 V. Due to the application of the highest investigated voltage amplitude ${\widehat{U}}_{\mathrm{e}}$, sufficient heating should be generated.

All vibrations and thermographic measurements were pre- and post-processed using the manufacturer’s original software (PSV 9.2, Polytec, Waldbronn, Germany; IRBIS 3, Jenoptik, Jena, Germany); the data were further analyzed by means of a numeric computing platform (MATLAB 9.12, MathWorks, Inc., Natick, MA, USA). To determine the correlation between the beam’s velocity and the temperature increase, the Pearson correlation coefficient (PCC) of the velocity distribution ${\widehat{u}}_2\left(x_3\right)$ and $\mathsf{\Delta }\vartheta \left(x_3\right)$ expressed by the value $c_{\mathrm{PCC},1}$ and the PCC of the velocity distribution’s magnitude $\left|{\widehat{u}}_2\left(x_3\right)\right|$ and $\mathsf{\Delta }\vartheta \left(x_3\right)$ defined by the quantity $c_{\mathrm{PCC},2}$ were calculated and compared for different excitation velocities.

Figure 2. Average frequency spectrum for a voltage amplitude of the piezoelectric actuator of ${\widehat{U}}_{\mathrm{e}}$ = 11 V.

Figure 2. Average frequency spectrum for a voltage amplitude of the piezoelectric actuator of ${\widehat{U}}_{\mathrm{e}}$ = 11 V.

Figure 3. Measured mode shapes as the response of the structure in the form obtained from its measured velocity $u_2\left(x_3,t\right)$ (crosses indicate measured velocities and their locations).

Figure 3. Measured mode shapes as the response of the structure in the form obtained from its measured velocity $u_2\left(x_3,t\right)$ (crosses indicate measured velocities and their locations).

Figure 4. Time series of the velocity amplitude $\widehat{u}\left(x_i={\tilde{x}}_i,t\right)$ at the position $[{\tilde{x}}_i]$= [2.5 mm, 0, 4.7 mm] and of the temperature increase $\max \left\{\mathsf{\Delta }\vartheta \left(t\right)\right\}$ for different voltage amplitudes of ${\widehat{U}}_{\mathrm{e}}$ = 11 V, 21.9 V, 32.6 V, 54 V and an excitation frequency of $f_e$ = 13.3 kHz.

Figure 4. Time series of the velocity amplitude $\widehat{u}\left(x_i={\tilde{x}}_i,t\right)$ at the position $[{\tilde{x}}_i]$= [2.5 mm, 0, 4.7 mm] and of the temperature increase $\max \left\{\mathsf{\Delta }\vartheta \left(t\right)\right\}$ for different voltage amplitudes of ${\widehat{U}}_{\mathrm{e}}$ = 11 V, 21.9 V, 32.6 V, 54 V and an excitation frequency of $f_e$ = 13.3 kHz.

3. Results and Discussion

3.1. Vibration Characteristic

The transverse base excitation of the beam’s clamping area resulted in flexural vibrations. The average vibration’s velocity amplitudes ${\widehat{u}}_2\left(f_n\right)$ varied depending on the actual natural frequency $f_n$ (see Figure 2). Due to the superposition of resonance effects of the test setup used and the bending beam, the velocities at the frequencies of 6.2 kHz and 13.3 kHz were further increased, which was verified by additional SLDV of the whole test setup. Considering the transfer function $H\left(x_i,f\right)$, it is evident that the amplitudes decrease with increasing frequencies $f_n$. An additional resonance frequency at approximately 7 kHz resulted due to resonance effects of the experimental setup. The resulting loss factors vary within the scope of the available measurement inaccuracies and showed a rather steady course (see

Table 2. Vibration behavior of base-excited beam (voltage amplitude of the piezoelectric actuator of ${\widehat{U}}_{\mathrm{e}}$ = 11 V).

$$\mathrm{Order} n$$	5	6	7	8	9	10	11	12	13	14	15	16	17
$$\mathrm{Frequency} {\mathrm{f}}_{\mathrm{n}} \mathrm{in} \mathrm{kHz}$$	1.1	1.7	2.4	3.2	4.1	5.1	6.2	7.4	8.7	10.1	11.7	13.3	15.0
$$\mathrm{Loss} \mathrm{factor} \tan \mathsf{\delta }$$	0.011	0.014	0.009	0.010	0.010	0.010	0.011	0.011	0.011	0.012	0.012	0.012	0.013

). With increasing order $n$, the number of nodes and antinodes of the natural modes increased (compare Figure 3). The nodes of the vibrational mode shape have to be considered as nodes in a coordinate system that moves with the velocity amplitude and the direction of the velocity of the specimen’s clamping. For an outside observer, these nodes move with the speed of the clamping and are not fixed in position (cf., [2]).

3.2. Influence of Excitation Amplitude on Temperature Increase

By increasing the input voltage amplitude ${\widehat{U}}_{\mathrm{e}}$, the velocity amplitudes grew and thus the maximum temperature increase expanded as well (Figure 4). Due to thermal phenomena, such as convection loss, a higher dissipation of thermal energy resulted for higher vibration velocities. Up to the investigated amplitude of ${\widehat{U}}_{\mathrm{e}}$ = 21.9 V, the surface temperature reached a stationary value within the applied measuring time. Due to the limits of random and systematic measurement inaccuracies, the measured velocity amplitudes could be considered as steady for input voltage amplitude values of up to ${\widehat{U}}_{\mathrm{e}}$ = 32.6 V and show only a small decrease in voltage amplitude values at ${\widehat{U}}_{\mathrm{e}}$ = 54 V (compare Figure 4). To ensure no change in the polymer’s mechanical properties during vibration measurement, the beam’s vibrational behavior was quantified at an input voltage amplitude of ${\widehat{U}}_{\mathrm{e}}$ = 11 V. As mentioned, the increase in the input voltage amplitude ${\widehat{U}}_{\mathrm{e}}$ results in the non-linear growth of the specimen’s steady-state velocities, especially at high input voltages (Figure 5). For the used test configuration and the investigated polymer PEEK, this relationship can be modeled in good agreement with a power law (goodness of fit $R^2>0.99$).

Several studies have focused on the modeling of the self-heating of thermoplastic polymers (compare, e.g., [57,58]). Using numerical modeling, the resulting temperature increase in dynamically loaded thermoplastic polymers can be determined. Therefore, the consideration of the balance laws, especially the balance of energy with respect to the reference configuration (compare, e.g., [59]), is as follows:

$${\rho }_0\dot{e}=P^I:\dot{F}-{\nabla }_0·h_0+{\rho }_{0}r,$$

(7)

where ${\rho }_0$ is the mass density in the reference configuration, $\dot{e}$ is the material time derivative of the internal energy per unit mass, $P^I$ is the first Piola–Kirchhoff stress tensor, $\dot{F}$ is the material time derivative of the deformation gradient, ${\nabla }_0·h_0$ is the divergence of the heat flux vector in the reference configuration and $r$ is the energy source per unit mass. To solve Equation (7), thermo-mechanical modeling including suitable constitutive equations and their model parameters is required. The term of ${\nabla }_0·h_0$ depends on the ambient conditions and is influenced by the fluid structure interactions between the vibrating beam and the surrounding media. The term ${\rho }_{0}r$ represents the energy source obtained from cyclic dissipation, which depends on frequency, stress amplitude, strain amplitude, geometrical and material properties [60,61] or the beam’s curvature [48]. The result in the current study can be used to validate future numerical models of the temperature increase in PEEK under dynamic loads.

3.3. Resulting Temperature Distribution and its Correlation with Vibrational Mode Shapes

For an input voltage amplitude of the piezoelectric actuator of ${\widehat{U}}_{\mathrm{e}}$ = 54 V and excitation frequency of $f_e$ = 13.3 kHz, the temperature increase obtained an alternating pattern along line L1 in Figure 6. With higher measuring times, the dimensions of the warmer areas grew. Similarly, the surrounding middle areas were heated up as well, as a result of thermal diffusion processes. At the same time, the surface temperature of the piezoelectric actuator and its power supply cable increased (see Figure 6, area A1). In the width direction, the specimen’s midpoint reaches the highest temperatures. Towards the edges, the temperatures drop (Figure 6).

The vibration-induced heating depends on the velocity amplitudes (compare Figure 4 and Figure 7). A maximum temperature increase of $\max \left\{\mathsf{\Delta }\vartheta \left(t\right)\right\}$ = 5.8 K was observed for the measured time period (see Figure 8). For some investigated excitation frequencies $f_e=f_n$, the generated heat did not result in a measurable temperature increase for the measured time (Figure 8). The resulting maximum velocity amplitudes ${\widehat{u}}_2$ and the maximum temperature increase $\max \left\{\mathsf{\Delta }\vartheta \right\}$ are summarized in

Table 3. Quantification of resulting vibration-induced heating for different orders $n$.

$$\mathit{n}$$	$$\begin{gathered} {\mathit{f}}_{\mathbf{n}} \\ \mathbf{in} \mathbf{kHz} \end{gathered}$$	$$\begin{gathered} {\widehat{\mathit{u}}}_{\mathbf{2}} \mathbf{at} \\ {\mathit{U}}_e\mathbf{=}\mathbf{11} {\mathbf{V} }^{\mathbf{a}} \\ \mathbf{in} \mathbf{m} {\mathbf{s}}^{-1} \end{gathered}$$	$$\begin{gathered} {\widehat{\mathit{u}}}_{\mathbf{2}} \mathbf{at} \\ {\mathit{U}}_e\mathbf{=}\mathbf{54} {\mathbf{V} }^{\mathbf{b}} \\ \mathbf{in} \mathbf{m} {\mathbf{s}}^{-\mathbf{1}} \end{gathered}$$	$$\begin{gathered} {\mathit{\tau } }^{\mathbf{c}} \\ \mathbf{in} \mathbf{s} \end{gathered}$$	$$\begin{gathered} {\mathbf{max}\left\{\Delta {\vartheta }_{\infty }\right\} }^{\mathbf{c}} \\ \mathbf{in} \mathbf{K} \end{gathered}$$	MTRS d in mK s−1	VHR e in mK m−1	$$\begin{gathered} c_{PCC,1} \\ \mathbf{in} {\mathbf{m}}^{\mathbf{2}} {\mathbf{s}}^{-\mathbf{2}} {\mathbf{K}}^{-\mathbf{2}} \end{gathered}$$	$$\begin{gathered} c_{PCC,2} \\ \mathbf{in} {\mathbf{m}}^{\mathbf{2}} {\mathbf{s}}^{-\mathbf{2}} {\mathbf{K}}^{-\mathbf{2}} \end{gathered}$$
5	1.1	0.006	0.018	-	<0.2	-	-	-	-
6	1.7	0.015	0.046	-	<0.2	-	-	-	-
7	2.4	0.029	0.088	-	<0.2	-	-	-	-
8	3.2	0.026	0.080	-	<0.2	-	-	-	-
9	4.1	0.028	0.089	-	<0.2	-	-	-	-
10	5.1	0.032	0.103	-	<0.2	-	-	-	-
11	6.2	0.091	0.300	10.6	0.7	21	70.2	0.2	0.6
12	7.4	0.022	0.076	-	<0.2	-	-	-	-
13	8.7	0.034	0.120	-	<0.2	-	-	-	-
14	10.1	0.044	0.164	7.9	0.4	11	65.7	0.1	0.5
15	11.7	0.066	0.261	21.4	0.9	29	110.6	0.2	0.7
16	13.3	0.241	1.047	13.2	6.4	194	185.3	−0.1	0.7
17	15.1	0.076	0.347	18.7	2.5	77	221.1	−0.1	0.8

^a measured by means of vibrometry; ^b approximated by Equation (5); ^c according to Equation (6); ^d mean temperature rise slope (MTRS) for a duration of $\Delta t$ = 32.8 s; ^e vibration-induced heating ratio (VHR).

. Considering the natural modes with $\mathsf{\Delta }\vartheta \ge$ 0.2 K, a correlation between temperature and velocities can be seen. Thereby, the correlation coefficients $c_{\mathrm{PCC},1}$ and $c_{\mathrm{PCC},2}$ can be seen. The correlation coefficient $c_{\mathrm{PCC},2}$ resulted in higher values due to the better correlation between the temperature distribution and the velocity’s magnitude (see Table 3). Furthermore, due to the influence of the beam’s clamping at $x_3/\left(l-l_{\mathrm{c}}\right)$ = 0 and of its free end at $x_3/\left(l-l_{\mathrm{c}}\right)$ = 1, the temperatures are reduced in these positions.

3.4. Implications for the Design of Dynamically Loaded PEEK Structures

The dynamic deformations of the PEEK beam at high frequencies result in the self-heating of the overall structure, obtaining the highest temperature increase at the mode shape’s antinodes. The resulting temperature rise depends, among other parameters, on the dimensions of the structure under investigation (cf., Muller et al. [56]). For a specimen investigated and the determined parameters (see Table 3), Equation (6) can be used to estimate the temperature development over time. Here, the maximum occurring temperatures are considered in particular. For the practical relevant design process of thermoplastic polymer structures, the resulting maximum temperature increase for a given displacement amplitude ${\widehat{w}}_2$ according to Equation (3) and a certain excitation frequency $f_{\mathrm{e}}$ can be estimated (see Figure 9). Therefore, the two-dimensional polynomial approximation, as expressed by,

$$\max \left\{\mathsf{\Delta }\vartheta \left({\widehat{w}}_2,f\right)\right\}=p_{00}+p_{10}{\widehat{w}}_2+p_{01}f+p_{20}{\widehat{w}}_2{}^2 +p_{11}{\widehat{w}}_{2}f+p_{02}{f}^2$$

(8)

was used. Therefore, a linear least squares regression was used, which resulted in the following coefficients:

$$\begin{gathered} p_{00}=0.196 \mathrm{K}, \\ {p}_{10}=-0.103 \mathrm{K} \mathrm{s} {\mathrm{m}}^{-1}, \\ {p}_{20}=0.006 \mathrm{K} {\mathrm{s}}^2 {\mathrm{m}}^{-2}, \\ {p}_{11}=0.040 \mathrm{K} {\mathrm{s}}^2 {\mathrm{m}}^{-1}, \\ {p}_{02}=0.011 \mathrm{K} {\mathrm{s}}^2. \end{gathered}$$

For the calculation of the parameter $p_{kl}$, the numerical computing software was used, as described in Section 2.2. Therefore, there is a linear regression of a polynomial surface of degree 2 in both coordinate directions. Using Equation (8), the temperature increase for different PEEK structures within the investigated parameter range is predictable. The quantification of the resulting self-heating according to the applied excitation frequency and the displacement amplitude could provide valuable implications for the design of dynamically loaded PEEK structures. Possible applications are the assessment of high-frequency mechanical loadings and the identification of critical operation scenarios of endodontic instruments made of PEEK [11,12]. Furthermore, the knowledge obtained can be used to validate simulations for ultrasonic welding of neat and fiber-reinforced thermoplastic [17,18].

In the current study, a maximum temperature increase of approximately 6.4 K was detected. For this temperature increase, only minimal changes in the beam’s velocities and an acceptable heating of the piezoelectric actuator were measurable. The measured temperatures were considerably below the permitted service temperature and can therefore be regarded as uncritical.

3.5. Limitations of the Experimental Approach

In the current study, the heat generation of the thermoplastic polymer PEEK was experimentally analyzed. Therefore, SLDV and IRT were performed for a base-excited flat-sheet polymeric specimen, as introduced by Kucher et al. [2]. The resulting beam’s displacement amplitudes are very small so that linear material modeling can be applied, which is suitable for many practically relevant, vibration-related applications. By using a piezoelectric actuator, the demonstrated measurement approach allows the investigation of the vibration characteristic and the material’s heating in higher frequency ranges compared to the experiments carried out by Katunin [41]. In comparison to the investigations of Montanini and Freni [49], the presented method also enables the non-destructive testing of polymers and composite materials. It should be noted that the setup determines the thermal drift of the specimen’s surface temperature. The analysis of the harmonics of the thermal signal was not possible with the IR camera used.

The heat generation occurs due to the superposition of both hysteresis and thermoelastic effects. Especially in polymers, the hysteresis effect results in a measurable temperature increase [62]. Mihalec et al. [48] described a theoretical modeling approach, which was related to the curvature of the beam’s displacement, the excitation frequency, its geometry, material properties and damping properties. The beam’s velocity is related to its displacement and the frequency of the specimen’s base excitation. Thus, the resulting self-heating depends on the strain energy density, which includes vibrational amplitude, operating frequency and mode shape. Due to a hysteretic deformation behavior, the resulting temperatures are related to the loss factor, which is a measure of the fraction of dissipated energy.

As mentioned by Ratner and Korobov [63], the heat released due to self-heating per unit time depends on the applied excitation frequency, the stress amplitude and the structure’s material properties. Based on hysteresis loop area, Katunin [64] showed that the dissipated energy of a plate is related again to the frequency, strain amplitude, the plate displacement and its bending stiffness. For an excitation at the PEEK beam’s bending resonance frequencies, the amount of dissipated energy and the associated temperature increase reached their highest values at the vibrational antinodes. This results in a close correlation between the velocity amplitudes and the resulting temperature increase. Similar findings were concluded by Dimarogonas et al. [65] for a rectangular plate of mild steel. However, further analytical and numerical investigations are required to understand the vibration-induced heating phenomena. Therefore, the obtained experimental data can be a good opportunity to validate these models.

Based on the experimental investigations, valuable information can be derived for the design of dynamically loaded polymer structures. Furthermore, with the help of the presented approach, a transfer to other polymer systems, other load conditions and other polymer-based materials is possible. In summary, the displacement amplitudes and frequencies of the specimen should not exceed critical values if excessive heating is to be avoided. One important requirement is that the specimen’s velocities remain unchanged during the individual measurements. Furthermore, an excessive heating of the specimen’s clamping area due to the heat introduced by the actuator needs to be avoided. In this way, the undesired degradation of the material properties and systematic errors can be minimized.

The current study confirms the applicability of PEEK as a material for dynamically loaded applications at high frequencies. However, additional experimental tests investigating the self-heating effect in PEEK under high-frequency mechanical loading are needed to study the effect of excitation frequency, load amplitude and load cycles [25,26,27,28,29,30,31,32,33,34]. This especially includes the fatigue behavior of PEEK under high frequencies. Nevertheless, for these applications, the displacement amplitudes and excitation frequencies must be strictly taken into consideration, so that the vibration-induced heating does not exceed a critical value and so that no material fatigue occurs for the applied loads. For this thermally dominated fatigue regime, further experiments, such as those carried out by Berer et al. [3] and Shrestha et al. [28], are required to analyze the effects of load amplitude, load ratio and frequency in combination with vibration-induced heating of polymers.

4. Conclusions

The combination of scanning laser Doppler vibrometry and infrared thermography of a polymeric base-excited cantilever beam using a piezoelectric actuator represents a powerful measuring approach for the determination of the beam’s vibrational characteristics and the resulting vibration-induced heating. This approach has the considerable advantage of analyzing small velocities of polymers at high frequencies up to the ultrasonic frequency range. For a resonant base excitation with sufficiently high excitation velocities, a correlation between the beam’s velocity and its resulting temperature increase with a maximum value of 6.4 K was observed. The resulting specimen’s temperatures depend on the displacement and the beam’s excitation frequency. Due to the moderate temperature increase, the thermoplastic polymer polyether ether ketone seems to be a suitable polymeric material for dynamically loaded structural applications. Therefore, additional experiments are needed to investigate the high-frequency mechanical loading and the resulting self-heating of PEEK. For these applications, regions with high vibrational amplitudes, especially at high frequencies, should be carefully considered. The presented experimental approach can be adapted to other polymeric materials and other load conditions.