Topology Optimization with Matlab: Geometrically Non-Linear Optimum Solid Structures at Random Force Strengths

Abstract

This paper aims to investigate multiple large-strain topology-optimized structures, by interpreting their overlay as a probability density function. Such a strategy is suited to finding an optimum design of silicon electrodes subject to a random contact. Using this method, and prescribing a zero net-force constraint on the global system, the optimum structure is identified with a Schwarz P minimum-surface structure. Then, the optimum structure is subject to chemo-mechanically coupled cycling, in terms of an irreversible thermodynamic process, which shows the interplay between the mechanical and chemical fields. The Matlab-based optimization code is attached.

1. Introduction

More than 60 years ago, Lucien Schmit [1] studied how to combine optimization techniques with the finite element method (FEM), and later, Bensøe and Kikuchi reported their seminal paper [2]. Since then, topology optimization techniques have been typically used in lightweight design [3,4,5,6,7], where only a percentage of a given volume is occupied by material, while meeting similar overall system stiffness requirements as the entire body. Technological advances in additive manufacturing in particular, make it possible to create structures that exceed conventional design [8]. However, optimum designs result predominantly from prescribed static boundary condition problems [9,10], even if the superordinate system is based on dynamic motion, e.g., a bicycle chain [11]. In such a system, a tensile force acts on the individual link of the chain. The optimum shape of a plate shows the positions for the bolted connections, see Figure 1. The resulting structure might be subject to a low volume constraint, so recent optimization algorithms also account for, e.g., buckling [12], fracture [13], or multi-material demands [14]. In addition, the optimum structure might be part of a periodic structure (the chain) [15], and other manufacturing constraints could be implemented by a projection-based approach [16].

However, while it is similar, it is also different from the silicon (Si) electrode particles in batteries, which are exposed to large deformations. According to [17], up to now, only a few structural designs, such as porous, core-shell, yolk-shell, and solid nanostructures, have been proposed for silicon anodes, some of them inspired by nature. However, recently, the topology optimization of electrodes has gained more and more attention [18,19]. For the anode design and the improvement of its electrochemical performance, it is crucial to identify the repeated volume expansions (up to about 300% [20]) and contractions during lithiation and de-lithiation, as the key failure mechanism of Si. Particle swelling leads to structural pulverization, electrical disconnection between the active materials and the current collector, continuous exfoliation, and consumption of the active Si and electrolyte of active Si particles [17,21,22]. All these failures can be assigned to the topology of the anode: (i) the increased consumption of the electrolyte (side reactions) could be related to a high surface area, (ii) a materials-dependent fracture occurrence above a specific particle size, and (iii) electrical conductivity issues due to point-to-point contact. As a result of the swelling, interactions with adjacent particles occur randomly, as shown in Figure 2. Most recently, contact has been added to the optimization, e.g., by [23,24,25,26]. Moreover, it was found that the contact stress is in the range of diffusion-induced stress under the free-expansion state [27].

A topology optimization problem is generally solved when finding the optimum material distribution subject to specific demands such as maximum stiffness, maximum conductivity, or others. The common algorithms rely on the finite element method, filtering methods, and the formulation of an optimality criterion [28]. Although numerous techniques exist in the scientific literature, e.g., evolutionary topology optimization (ETO [29]), smooth-edged material distribution for optimizing topology (SEMDOT [30]), floating projection topology optimization (FPTO [31]), etc., there are two popular methods: the Solid Isotropic Material with Penalization (SIMP) method and the Bidirectional Evolutionary Structural Optimization (BESO) method. The SIMP method is the most widely utilized approach, although the BESO method shows a fast convergence rate, with fewer iterations than the SIMP method [32]. In the literature, mainly the optimization problems of a linear-elastic material model are solved [32,33] and some studies address non-linear problems, e.g., [34,35,36]. Recently, a two-dimensional BESO algorithm for non-linear problems has been reported [32], which claims one can hardly find convenient and compact published code.

In this paper, the aim is to elaborate on the BESO approach, in terms of (i) extending the code to 3D, (ii) making it comparable with the Matlab code reported in the SIMP approach [37], (iii) validating the comparability between both approaches for small deformations, (iv) using the BESO approach for random large force interactions as typical in silicon, and (v) defining an optimum structure at large strains by overlapping the single results. Since we are interested in large deformations, we need to recap in Section 2.1, briefly, some continuum mechanics-based essential equations of non-linear elasticity, cf. [38,39]. Then we proceed in Section 2.2 by solving the non-linear equations using FEM. Density-based methods such as BESO and SIMP, and filtering techniques are briefly sketched in Section 2.3. In Section 2.4, we state the optimization problem at large strains. How the resulting structure must be modified to be used in a chemo-mechanically coupled investigation is sketched in Section 2.5. Finally, we show and discuss the optimum results in Section 3. The 3D non-linear optimization code is provided in Appendix A.

2. Materials and Methods

In the following, we elaborate on the governing equations and the method for solving a non-linear optimization problem. In general, the structure of a software presupposes a certain convention and symbolic expressions, which are declared in the following.

2.1. Continuum Mechanics

Any problem in elasticity is usually based on a strain–displacement relation, a constitutive equation (stress–strain relation), a traction-stress relation, and the formulation of linear and angular balance laws. Since all equations rely on the formulation of the displacement of a material point, we embed it in the environment of continuous media first.

2.1.1. Displacement of Continuous Media

Let $\mathit{X}$ refer to a point of a continuum in its reference (“material”) configuration ${\mathcal{B}}_0\subset {\mathbb{R}}^3$, and a motion moves the point to its actual (“spatial”) position $\mathit{x}(\mathit{X},t)$ at time t, in the current configuration ${\mathcal{B}}_t\subset {\mathbb{R}}^3$. Then, the corresponding displacement vector $\mathit{u}$, has the shortest distance between $\mathit{x}$ and $\mathit{X}$, and is defined by their difference as

$$\mathit{u}=\mathit{x}-\mathit{X}\to \left\{\begin{array}{cc}\mathrm{d}\mathit{u}=\mathrm{d}\mathit{x}-\mathrm{d}\mathit{X}\hfill & \left(\mathrm{infinitesimal}\right)\hfill \\ \mathrm{d}\mathit{u}=\mathit{u}(\mathit{X}+\mathrm{d}\mathit{X})-\mathit{u}\left(\mathit{X}\right)\hfill & (\mathrm{finite}\mathrm{difference})\hfill \\ \mathit{u}(\mathit{X}+\mathrm{d}\mathit{X})=\mathit{u}\left(\mathit{X}\right)+(\nabla \mathit{u})\mathrm{d}\mathit{X}+\dots \hfill & (\mathrm{Taylor}\mathrm{Series})\hfill \end{array}\right.$$

(1)

From Equation (1), there follows an expression for the differential line element

$$\mathrm{d}\mathit{x}=[\mathbf{1}+\nabla \mathit{u}]\mathrm{d}\mathit{X}=\mathit{F}\mathrm{d}\mathit{X}$$

(2)

directly, where $\mathbf{1}\in {\mathbb{R}}^{3\times 3}$ is the identity matrix and $\mathit{F}$ the deformation gradient. As usual, variables are denoted with capital letters when referring to the reference configuration. Moreover, the displacement has, in both configurations, the same values but different arguments, $\mathit{U}(\mathit{X},t)=\mathit{u}(\mathit{x},t)$.

2.1.2. Green–Lagrangian Strain Tensor

Both of the differential line elements in Equation (2), $\mathrm{d}\mathit{x}$ and $\mathrm{d}\mathit{X}$, are associated with a differential arc length, and their squares are coordinate-independent quantities. Thus, the difference between the squares of the differential line elements

$$\mathrm{d}\mathit{x}·\mathrm{d}\mathit{x}-\mathrm{d}\mathit{X}·\mathrm{d}\mathit{X}=:\mathrm{d}\mathit{X}·\left[2\mathit{E}\mathrm{d}\mathit{X}\right]$$

(3)

is considered as a measure of deformation, and defined as the Green–Lagrangian strain tensor. Together with Equation (2), there follows an expression for the Green–Lagrangian strain tensor

$$\mathit{E}=\frac{1}{2}[\nabla \mathit{u}+{(\nabla \mathit{u})}^T]+\frac{1}{2}[\nabla \mathit{u}{(\nabla \mathit{u})}^T]=\mathit{\epsilon }+{\mathit{\epsilon }}_N,$$

(4)

which is based on the gradient of the displacement. As long as $\parallel \nabla \mathit{u}\parallel \ll 1$ is satisfied, we are in the regime of infinitesimal strain theory, and then the strain tensor composes additively, $\mathit{E}\approx \mathit{\epsilon }=\frac{1}{2}({\mathit{F}}^T+\mathit{F})-\mathbf{1}$. Otherwise, the strain tensor composes multiplicatively, $\mathit{E}=\frac{1}{2}({\mathit{F}}^T\mathit{F}-\mathbf{1})$, and measures how much the right Cauchy–Green tensor $\mathit{C}={\mathit{F}}^T\mathit{F}$ differs from $\mathbf{1}$.

2.1.3. Hooke’s Law

In a small strain regime, Hooke’s law for continuous media relates the Cauchy (“true”) stresses $\mathit{\sigma }\in {\mathbb{R}}^{3\times 3}$ and the strains $\mathit{\epsilon }\in {\mathbb{R}}^{3\times 3}$ by using a fourth-order elasticity tensor $\mathcal{C}\in {\mathbb{R}}^{3\times 3\times 3\times 3}$, $\mathit{\sigma }=\mathcal{C}\mathit{\epsilon }$. Due to the inherent and material symmetries, and the assumption of isotropic media, the elasticity tensor can be reduced to only two independent Lamé parameters $(\lambda ,\mu )$, and then the Cauchy stresses reads

$$\mathit{\sigma }=2\mu \mathit{\epsilon }+\lambda \mathrm{tr}\left(\mathit{\epsilon }\right)\mathbf{1}\mathrm{with}\lambda =\frac{E\nu }{(1+\nu )(1-2\nu )}\mathrm{and}\mu =\frac{E}{2(1+\nu )}$$

(5)

Alternatively, the Lamé parameters can be expressed by using the Young’s modulus, E, and Poisson number, $\nu$.

2.1.4. Voigt Notation

Due to the symmetry of the Cauchy stress tensor, $\mathit{\sigma }={\mathit{\sigma }}^T$, it can be condensed to an array with six entries. Then, using a superscript V, to indicate Voigt notation, Hooke’s law is rewritten as

$$\mathit{\sigma }=\mathcal{C}\mathit{\epsilon }\to {\mathit{\sigma }}^V={\mathcal{C}}^V{\mathit{\epsilon }}^V\mathrm{where}\left\{\begin{array}{c}{\mathit{\sigma }}^V={\left[{\sigma }_{11}{\sigma }_{22}{\sigma }_{33}{\sigma }_{23}{\sigma }_{13}{\sigma }_{12}\right]}^T\hfill \\ {\mathit{\epsilon }}^V={\left[{\epsilon }_{11}{\epsilon }_{22}{\epsilon }_{33}2{\epsilon }_{23}2{\epsilon }_{13}2{\epsilon }_{12}\right]}^T\hfill \end{array}\right.$$

(6)

Alternative arrangements of the off-diagonal stress-tensor entries are possible, e.g., as used by the authors in [37], or given by the Nye notation which is often adapted due to convention in other software coding. However, the elasticity tensor in Voigt notation is dependent on the elasticity constants $(E,\nu )$ and partitioned into four $3\times 3$ blocks as

$${\mathcal{C}}^V(E,\nu )=\frac{E}{(1+\nu )(1-2\nu )}\left[\begin{array}{cc}\mathit{A}& \mathbf{0}\\ \mathbf{0}& \frac{(1-2\nu )}{2}\mathbf{1}\end{array}\right]\mathrm{with}\mathit{A}=\left[\begin{array}{ccc}1-\nu & \nu & \nu \\ \nu & 1-\nu & \nu \\ \nu & \nu & 1-\nu \end{array}\right]$$

(7)

where $\mathbf{0}=0\mathbf{1}$ is a zero matrix.

2.1.5. Cauchy Traction Vector

Now, the stresses (6) are related to infinitesimal acting forces $\mathrm{d}\mathit{f}$ per infinitesimal area of a region $\mathrm{d}a$, with outward normal $\mathit{n}$ to the surface,

$$\mathit{\sigma }\mathit{n}=\frac{\mathrm{d}\mathit{f}}{\mathrm{d}a}=:\mathit{t}$$

(8)

both in the spatial configuration, and defined as the Cauchy traction vector $\mathit{t}$.

2.1.6. Nanson’s Formula

The force-to-area ratio in Equation (8) refers to quantities in the current configuration. Nanson’s formula links the area in the current configuration $\mathrm{d}a$, with its outward normal $\mathit{n}$, to the same area in the reference configuration $\mathrm{d}A$, with outward normal $\mathit{N}$, by

$$\mathit{n}\mathrm{d}a=J{\mathit{F}}^{-T}\mathit{N}\mathrm{d}A\mathrm{with}J=det\left(\mathit{F}\right)=\frac{\mathrm{d}v}{\mathrm{d}V}$$

(9)

The determinant of the deformation gradient J, is the ratio of the volume elements $\mathrm{d}v$ and $\mathrm{d}V$, from the actual and reference configurations.

2.1.7. Static Equilibrium

With Equation (9) at hand, the transformations of the area and volume elements from the actual to the reference configuration are given. Let $\partial {\mathcal{B}}_t$ denote a surface within or on the boundary of ${\mathcal{B}}_t$. Then, the total force acting on this surface is given by

$$\mathit{f}\stackrel{\left(8\right)}{=}{\int }_{\partial {\mathcal{B}}_t}\mathit{t}\mathrm{d}a\stackrel{\left(8\right)}{=}{\int }_{\partial {\mathcal{B}}_t}\mathit{\sigma }\mathit{n}\mathrm{d}a\stackrel{\left(9\right)}{=}{\int }_{\partial {\mathcal{B}}_0}J\mathit{\sigma }{\mathit{F}}^{-T}\mathit{N}\mathrm{d}A\stackrel{\left(D\right)}{=}{\int }_{{\mathcal{B}}_0}\nabla ·\mathit{P}\mathrm{d}V$$

(10)

where the Cauchy traction vector (8), the Nanson formula (9), the divergence theorem (D), and the definition for the 1st Piola–Kirchhoff stress tensor

$$\mathit{P}=J\mathit{\sigma }{\mathit{F}}^{-T}$$

(11)

have been used. $\mathit{P}$ relates the forces $\mathit{f}$, in the spatial configuration, with areas in the material configuration. The forces $\mathit{f}$, can be assigned with a spatial body force density $\mathit{b}$,

$$\mathit{f}={\int }_{{\mathcal{B}}_t}\mathit{b}\mathrm{d}v={\int }_{{\mathcal{B}}_0}J\mathit{b}\mathrm{d}V\mathrm{where}\mathit{b}=\frac{\mathrm{d}\mathit{f}}{\mathrm{d}v}\mathrm{and}\tilde{\mathit{B}}=J\mathit{b}$$

(12)

With Equations (10)–(12), the static equilibrium equation reads in differential form

$$\nabla ·\mathit{P}-\tilde{\mathit{B}}=\mathbf{0}(\mathrm{quasi}-\mathrm{static}\mathrm{balance}\mathrm{of}\mathrm{linear}\mathrm{momentum})$$

(13)

with boundary conditions

$$\begin{array}{cccc}\hfill \mathit{P}\mathit{N}& =\overline{\mathit{T}}\hfill & \hfill & \mathrm{on}\partial {\mathcal{B}}_T(\mathrm{Neumann}\mathrm{boundary}\mathrm{condition})\hfill \end{array}$$

(14)

$$\begin{array}{cccc}\hfill \mathit{u}& =\overline{\mathit{u}}\hfill & \hfill & \mathrm{on}\partial {\mathcal{B}}_u(\mathrm{Dirichlet}\mathrm{boundary}\mathrm{condition})\hfill \end{array}$$

(15)

where $\partial {\mathcal{B}}_0=\partial {\mathcal{B}}_u\cup \partial {\mathcal{B}}_T$ with $\partial {\mathcal{B}}_u\cap \partial {\mathcal{B}}_T=\varnothing$, and the quantities with a bar are prescribed.

Moreover, the 2nd Piola–Kirchhoff stress tensor

$$\mathit{S}={\mathit{F}}^{-1}\mathit{P}$$

(16)

relates forces in the reference configuration to areas in the reference configuration.

2.1.8. Hyperelastic Material Model

For a hyperelastic material, the stress tensor (5) is derived from a strain energy density function $\Psi$,

$$\mathit{\sigma }=\frac{\partial {\Psi }_{\mathit{\epsilon }}}{\partial \mathit{\epsilon }}\mathrm{where}{\Psi }_{\mathit{\epsilon }}=\frac{1}{2}\lambda {\left(\mathrm{tr}\left(\mathit{\epsilon }\right)\right)}^2+\mu \mathrm{tr}\left({\mathit{\epsilon }}^2\right)$$

(17)

However, it is known that $\mathit{\sigma }$ is variant to pure rotations, while $\mathit{\epsilon }$ is not. Therefore, it is not suited as a constitutive model for large deformations. In the case of finite deformations, instead of $\mathit{\sigma }$, often the 2nd Piola–Kirchhoff stress tensor $\mathit{S}$ is used,

$$\mathit{S}=\frac{\partial {\Psi }_{\mathit{E}}}{\partial \mathit{E}}=2\frac{\partial {\Psi }_{\mathit{E}}}{\partial \mathit{C}}\mathrm{where}{\Psi }_{\mathit{E}}=\frac{1}{2}\lambda {\left(\mathrm{tr}\left(\mathit{E}\right)\right)}^2+\mu \mathrm{tr}\left({\mathit{E}}^2\right)={\Psi }_{\mathit{\epsilon }}+{\Psi }_{\Delta }$$

(18)

In Equation (18), the most straightforward hyperelastic strain energy density is formulated, i.e., the Saint Venant–Kirchhoff model, which is an extension of Equation (17). This gives $\mathit{S}=2\mu \mathit{E}+\lambda \mathrm{tr}\left(\mathit{E}\right)\mathbf{1}$, which is similar to Equation (5). The limitations of the Saint Venant–Kirchhoff material model in large strain regimes are discussed in [40]. Alternatively, many other strain energy density formulations, such as the Ogden model [41,42], neo-Hookean model, Money–Rivlin model, Simo–Pister model [43], etc., could be adapted to match with a specific material behavior of interest.

2.1.9. Non-Linear Hookes Law

In the case of non-linear strain, the 2nd Piola–Kirchhoff stress tensor in Voigt notation

$${\mathit{S}}^V=\mathcal{C}{\mathit{E}}^V\to {\mathit{\sigma }}^V=\mathcal{C}{\mathit{\epsilon }}^V\mathrm{at}\mathrm{small}\mathrm{strains}$$

(19)

has a similar form to Equation (6), and for infinitesimal deformations, the difference between the Cauchy and Piola–Kirchhoff stress tensors is marginal. The strain in Equation (19) has the components

$$E_{ij}=\frac{1}{2}[{\partial }_i{u}_j+{\partial }_j{u}_i+{\partial }_i{u}_1{\partial }_j{u}_1+{\partial }_i{u}_2{\partial }_j{u}_2+{\partial }_i{u}_3{\partial }_j{u}_3]\equiv E_{ji}$$

(20)

with indices as they are arranged for ${\mathit{\epsilon }}^V$ in Equation (6).

2.2. Finite Element Analysis

Having formulated $\mathit{S}$ in (18), the transformation of $\mathit{S}$ to $\mathit{P}$ in (16), and the equilibrium Equation (13) on the reference domain ${\mathcal{B}}_0$, it is now discretized into $n_{\mathrm{el}}$ elements within the finite element analysis. In the following, the weak form of the problem (13) is formulated, ansatz functions are declared, and the Newton–Raphson method is used to solve the non-linear problem.

2.2.1. Weak Form of Problem

As usual, the multiplication of Equation (13) with a smooth test function vector $\mathit{\lambda }$, and integration over the domain ${\mathcal{B}}_0$, gives

$${\int }_{{\mathcal{B}}_0}\mathit{\lambda }·\tilde{\mathit{B}}\mathrm{d}V\stackrel{\left(13\right)}{=}-{\int }_{{\mathcal{B}}_0}\mathit{\lambda }·(\nabla ·\mathit{P})\mathrm{d}V\stackrel{\left(PI\right)}{=}{\int }_{{\mathcal{B}}_0}(\nabla \mathit{\lambda }):\mathit{P}\mathrm{d}V\stackrel{\left(16\right)}{=}{\int }_{{\mathcal{B}}_0}({\mathit{F}}^T\nabla \mathit{\lambda }):\mathit{S}\mathrm{d}V$$

(21)

where $\left(PI\right)$ denotes partial integration, the Frobenius inner product reads $\mathit{A}:\mathit{B}=\mathrm{tr}\left({\mathit{A}}^T\mathit{B}\right)$, the trace of a product $\mathrm{tr}\left({\mathit{A}}^T\mathit{B}\right)=\mathrm{tr}\left(\mathit{B}{\mathit{A}}^T\right)$, and the test function vector $\mathit{\lambda }$ is chosen so that it vanishes at the boundary $\partial {\mathcal{B}}_u$. The integral expression in Equation (21) is called the weak form of the problem.

2.2.2. Element ID, Connectivity, and Edof

As in the simplest case, the reference geometry is assumed to be a cuboid to solve Equation (21). This reference cuboid is subdivided into ($n_1$,$n_2$,$n_3$) equidistant elements, such that the total number of elements is $n_{\mathrm{el}}=n_1{n}_2{n}_3$. The elements are numbered successively along the $X_1$, then the $X_2$, and lastly the $X_3$ direction, see Figure 3a.

Each node, which is a corner stone of an element, has three degrees of freedom (dof). Therefore, one element has in total $8·3=24$ dofs and the total number of dofs is $n_{\mathrm{dof}}=3(n_1+1)(n_2+1)(n_3+1)$. According to [37], the global node identification is ordered column-wise, with the rule: up-to-bottom, left-to-right, and back-to-front, see Figure 3b. The local node identification of the eight nodes within a single element does not necessarily follow the same convention, and is ordered in counter-clockwise direction instead, see Figure 3c. The global connectivity of each single local element, i.e., the mapping of the blue circled numbers to the red circled numbers, is stored for each element (index “el”) within an array

$${\mathrm{edof}}_{\mathrm{el}}={[{\mathrm{node}}_{1x}{\mathrm{node}}_{1y}{\mathrm{node}}_{1z}{\mathrm{node}}_{2x}\dots {\mathrm{node}}_{8z}]}^T\in {\mathbb{N}}^{24}$$

(22)

e.g., ${\mathrm{edof}}_1={[4,5,6,10,11,12,7,8,9,1,2,3,28,29,30,34,35,36,31,32,33,25,26,27]}^T$. With this at hand, the nodal values of the local displacement vector

$$\begin{array}{cc}\hfill {\mathit{u}}_{\mathrm{el}}& =\underset{\overline{}}{\mathit{u}}\left({\mathrm{edof}}_{\mathrm{el}}\right)\in {\mathbb{R}}^{24}\mathrm{and}{\mathit{\lambda }}_{\mathrm{el}}=\underset{\overline{}}{\mathit{\lambda }}\left({\mathrm{edof}}_{\mathrm{el}}\right)\in {\mathbb{R}}^{24}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \mathrm{e}.\mathrm{g}.,{\mathit{u}}_{\mathrm{el}=1}& =\underset{\overline{}}{\mathit{u}}\left({\mathrm{edof}}_{\mathrm{el}=1}\right)={[u_4{u}_5{u}_6{u}_{10}\dots u_{26}{u}_{27}]}^T\hfill \end{array}$$

(24)

can be extracted for each element from the global displacement vector $\underset{\overline{}}{\mathit{u}}=[{\underset{\overline{}}{u}}_1{\underset{\overline{}}{u}}_2\dots {\underset{\overline{}}{u}}_{n_{\mathrm{dof}}}]$. The underbar in the expression $\underset{\overline{}}{•}$, indicates that a quantity • refers to the ordered nodal values.

2.2.3. Parametric Domain

Now, the solution field inbetween the nodal values must be interpolated. Let a local coordinate vector $\mathit{\xi }={({\xi }_1,{\xi }_2,{\xi }_3)}^T$ and the parametric domain ${\mathcal{B}}_{\xi }=\{\mathit{\xi }\in {\mathbb{R}}^3|{\xi }_1,{\xi }_2,{\xi }_3\in [-1,1]\}$ be given. As we already performed the mapping from the current to the reference domain, ${\mathcal{B}}_t\to {\mathcal{B}}_0$ in Equation (10), by using the integration by substitution

$${\int }_{{\mathcal{B}}_t}•\mathrm{d}v={\int }_{{\mathcal{B}}_0}•J\mathrm{d}V$$

(25)

We must map each element to the reference domain ${\mathcal{B}}_{\xi }$, to perform Gaussian quadrature. In the following case, it is an affine transformation between the reference and the parametric domain,

$${\int }_{{\mathcal{B}}_0}•\mathrm{d}V=\sum _{\mathrm{el}=1}^{n_{\mathrm{el}}}{\int }_{{\mathcal{B}}_{\xi }}{•}_{\mathrm{el}}{J}_{\xi }\mathrm{d}\Omega \mathrm{and}{J}_{\mathit{\xi }}=det\left(\frac{\partial \mathit{X}}{\partial \mathit{\xi }}\right)={\left[\frac{h}{2}\right]}^3\equiv \frac{\mathrm{d}V}{\mathrm{d}\Omega }$$

(26)

where h is the equidistant nodal spacing in the physical domain (see Figure 3a) and 2 is the length of the parametric domain in each direction. Without loss of generality, we set $h=2$ in the following.

2.2.4. Ansatz Functions

The ansatz functions for both the displacement and the test function on each element are written in terms of the local coordinate vector $\mathit{\xi }$, as

$${\mathit{u}}_{\mathrm{el}}\left(\mathit{\xi }\right)=\sum _i{N}_i\left(\mathit{\xi }\right){\mathit{u}}_{\mathrm{el}}i\mathrm{and}{\mathit{\lambda }}_{\mathrm{el}}\left(\mathit{\xi }\right)=\sum _j{N}_j\left(\mathit{\xi }\right){\mathit{\lambda }}_{\mathrm{el}}j$$

(27)

where it is necessary to note that the entire dependency of ${\mathit{u}}_{\mathrm{el}}$ and ${\mathit{\lambda }}_{\mathrm{el}}$ on $\mathit{\xi }$, is carried by the interpolation functions $N_i$ only. For computational reasons, often low polynomial degree functions are used, e.g., linear Lagrangian interpolation functions, which read

$$N_i\left(\mathit{\xi }\right)=\frac{1}{2}(1+s_1^i{\xi }_1)\frac{1}{2}(1+s_2^i{\xi }_2)\frac{1}{2}(1+s_3^i{\xi }_3)\mathrm{where}\left\{\begin{array}{c}{s}_1^i={(-1)}^i\hfill \\ s_2^i=\mathrm{sign}(sin\left(\frac{\pi }{4}(1-2i)\right)\hfill \\ s_3^i=\mathrm{sign}(i-4.5)\hfill \end{array}\right.$$

(28)

and $i\in \{1,\dots ,8\}$. In accordance to the node identification of Section 2.2.2, the sequence of $s_1^i$ is $\{-1,1,-1,1,-1,1,-1,1\}$, the sequence of $s_2^i$ is $\{-1,-1,1,1,-1,-1,1,1\}$, and the sequence of $s_3^i$ is $\{-1,-1,-1,-1,1,1,1,1\}$. In the case of derivatives, one should note that ${\nabla }_{\mathit{X}}{N}_i\left(\mathit{X}\right)={\nabla }_{\mathit{\xi }}{N}_i\left(\mathit{\xi }\right){\mathit{J}}_{\mathit{\xi }}={\nabla }_{\mathit{\xi }}{N}_i\left(\mathit{\xi }\right)\frac{2}{h}$.

2.2.5. Strain–Displacement Matrix

With the ansatz functions at hand, and by using Equation (26), the weak problem (21) reads on each element

$${\int }_{{\mathcal{B}}_{\xi }}\left({\nabla }_{\xi }{N}_i{\mathit{F}}_{\mathrm{el}}^T\right):{\mathit{S}}_{\mathrm{el}}\mathrm{d}\Omega ={\int }_{{\mathcal{B}}_{\xi }}{\mathit{B}}_{\mathrm{el}}^T{\mathit{S}}_{\mathrm{el}}^V\mathrm{d}\Omega \mathrm{and}{\mathit{S}}_{\mathrm{el}}^V=\mathcal{C}{\mathit{E}}_{\mathrm{el}}^V\left({\mathit{u}}_{\mathrm{el}}\right)$$

(29)

A quantity called the “non-linear nodal strain–displacement matrix”

$${\mathit{B}}_i=\left[\begin{array}{ccc}{F}_{11}{\partial }_1{N}_i& F_{21}{\partial }_1{N}_i& F_{31}{\partial }_1{N}_i\\ F_{12}{\partial }_2{N}_i& F_{22}{\partial }_2{N}_i& F_{32}{\partial }_2{N}_i\\ F_{13}{\partial }_3{N}_i& F_{23}{\partial }_3{N}_i& F_{33}{\partial }_3{N}_i\\ F_{13}{\partial }_2{N}_i+F_{12}{\partial }_3{N}_i& F_{22}{\partial }_3{N}_i+F_{23}{\partial }_2{N}_i& F_{32}{\partial }_3{N}_i+F_{33}{\partial }_2{N}_i\\ F_{11}{\partial }_3{N}_i+F_{13}{\partial }_1{N}_i& F_{21}{\partial }_3{N}_i+F_{23}{\partial }_1{N}_i& F_{33}{\partial }_1{N}_i+F_{31}{\partial }_3{N}_i\\ F_{11}{\partial }_2{N}_i+F_{12}{\partial }_1{N}_i& F_{22}{\partial }_1{N}_i+F_{21}{\partial }_2{N}_i& F_{31}{\partial }_2{N}_i+F_{32}{\partial }_1{N}_i\end{array}\right]$$

(30)

is introduced, where $F_{ij}$ are the entries of the deformation gradient ${\mathit{F}}_{\mathrm{el}}$, and ${\partial }_j\equiv {\partial }_{{\xi }_j}$ is the derivative in the $j\mathrm{th}$ direction. The elemental strain–displacement matrix is composed by the nodal matrices as

$${\mathit{B}}_{\mathrm{el}}=[{\mathit{B}}_{i=1},\dots ,{\mathit{B}}_{i=8}]\in {\mathbb{R}}^{6\times 24}$$

(31)

Alternatively, one can show that the elemental variation in the strain $\delta {\mathit{E}}_{\mathrm{el}}={\mathit{B}}_{\mathrm{el}}\delta {\mathit{u}}_{\mathrm{el}}$ relates the non-linear ${\mathit{B}}_{\mathrm{el}}$-matrix to the variation in the elemental displacements.

2.2.6. Residual of Equilibrium Equation

Now, we can elaborate on the weak form (21) on element basis,

$$\sum _{\mathrm{el}=1}^{n_{\mathrm{el}}}\sum _{j=1}^8{\mathit{\lambda }}_{\mathrm{el}j}^T\left({\int }_{{\mathcal{B}}_{\xi }}{\mathit{B}}_{\mathrm{el}}^T{\mathit{S}}_{\mathrm{el}}^V\mathrm{d}\Omega -{\int }_{{\mathcal{B}}_{\xi }}{N}_j{\tilde{\mathit{B}}}_{\mathrm{el}}\mathrm{d}\Omega \right)=\sum _{\mathrm{el}=1}^{n_{\mathrm{el}}}\sum _{j=1}^8{\mathit{\lambda }}_{\mathrm{el}j}^T{\mathit{R}}_{\mathrm{el}}=0$$

(32)

where the term in parentheses is identified as elemental residuum ${\mathit{R}}_{\mathrm{el}}$, which in turn is given by the difference between internal and external forces on that element,

$${\mathit{R}}_{\mathrm{el}}\left(\mathit{u}\right)={\mathit{f}}_{\mathrm{int}}-{\mathit{f}}_{\mathrm{ext}}\in {\mathbb{R}}^{24}$$

(33)

and both, the internal and external elemental forces read

$${\mathit{f}}_{\mathrm{el}}^{\mathrm{int}}={\int }_{{\mathcal{B}}_{\xi }}{\mathit{B}}_{\mathrm{el}}^T{\mathit{S}}_{\mathrm{el}}^V\mathrm{d}\Omega \mathrm{and}{\mathit{f}}_{\mathrm{el}}^{\mathrm{ext}}={\int }_{{\mathcal{B}}_{\xi }}{N}_j{\tilde{\mathit{B}}}_{\mathrm{el}}\mathrm{d}\Omega$$

(34)

Since the nodal values ${\lambda }_i$, of the test function are arbitrary, we can find a residual expression

$$[{\lambda }_1{\lambda }_2\dots {\lambda }_{n_{\mathrm{dof}}}]\left[\begin{array}{c}{\displaystyle \sum _{\mathrm{el}=1}^{n_{\mathrm{el}}}}{\displaystyle \sum _{j=1}^8}\frac{\partial {\mathit{\lambda }}_{\mathrm{el}j}^T}{\partial {\lambda }_1}{\mathit{R}}_{\mathrm{el}}\\ ⋮\\ {\displaystyle \sum _{\mathrm{el}=1}^{n_{\mathrm{el}}}}{\displaystyle \sum _{j=1}^8}\frac{\partial {\mathit{\lambda }}_{\mathrm{el}j}^T}{\partial {\lambda }_{n_{\mathrm{dof}}}}{\mathit{R}}_{\mathrm{el}}\end{array}\right]={\underset{\overline{}}{\mathit{\lambda }}}^T\mathit{R}\left(\mathit{u}\right)=0$$

(35)

Practically, the assembly of the global residual vector $\mathit{R}$, is given by adding the local values on the corresponding global position as

$$\mathit{R}\left({\mathrm{edof}}_{\mathrm{el}}\right)=\mathit{R}\left({\mathrm{edof}}_{\mathrm{el}}\right)+{\mathit{R}}_{\mathrm{el}}\forall \mathrm{el}\in \{1,\dots ,n_{\mathrm{el}}\}$$

(36)

2.2.7. Tangential Stiffness Matrix

The tangential stiffness matrix follows from a variation in the residuum,

$$\begin{array}{cc}\hfill \delta {\mathit{R}}_{\mathrm{el}}\left(\mathit{u}\right)& ={\int }_{{\mathcal{B}}_{\xi }}{\mathit{B}}_{\mathrm{el}}^T\left(\delta {\mathit{S}}_{\mathrm{el}}^V\right)+\left(\delta {\mathit{B}}_{\mathrm{el}}^T\right){\mathit{S}}_{\mathrm{el}}^V\mathrm{d}\Omega ={\mathit{K}}_{\mathrm{el}}\delta {\mathit{u}}_{\mathrm{el}}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {\mathit{K}}_{\mathrm{el}}& ={\int }_{{\mathcal{B}}_{\xi }}{\mathit{B}}_{\mathrm{el}}^T\mathcal{C}{\mathit{B}}_{\mathrm{el}}+{\mathit{G}}_{\mathrm{el}}^T{\mathit{M}}_{\mathrm{el}}{\mathit{G}}_{\mathrm{el}}\mathrm{d}\Omega \in {\mathbb{R}}^{24\times 24}\hfill \end{array}$$

(38)

where ${\mathit{G}}_{\mathrm{el}}$ stores the linear derivatives of the ansatz functions,

$${\mathit{G}}_{\mathrm{el}}=[{\mathit{G}}_{k=1},\dots ,{\mathit{G}}_{k=8}]\in {\mathbb{R}}^{9\times 24}\mathrm{with}{\mathit{G}}_k=\left[\begin{array}{c}{\partial }_1{N}_k\mathbf{1}\\ {\partial }_2{N}_k\mathbf{1}\\ {\partial }_3{N}_k\mathbf{1}\end{array}\right]\in {\mathbb{R}}^{9\times 3}$$

(39)

and the components of the 1st Piola–Kirchhoff stress tensor $S_{ij}$ are stored in

$${\mathit{M}}_{\mathrm{el}}=\left[\begin{array}{c}{S}_{11}\mathbf{1}{S}_{12}\mathbf{1}{S}_{13}\mathbf{1}\\ S_{21}\mathbf{1}{S}_{22}\mathbf{1}{S}_{23}\mathbf{1}\\ S_{31}\mathbf{1}{S}_{32}\mathbf{1}{S}_{33}\mathbf{1}\end{array}\right]\in {\mathbb{R}}^{9\times 9}$$

(40)

Again, similar to Equation (33), the assembly of the global tangential stiffness matrix reads

$$\mathit{K}({\mathrm{edof}}_{\mathrm{el}},{\mathrm{edof}}_{\mathrm{el}})=\mathit{K}({\mathrm{edof}}_{\mathrm{el}},{\mathrm{edof}}_{\mathrm{el}})+{\mathit{K}}_{\mathrm{el}}\forall \mathrm{el}\in \{1,\dots ,n_{\mathrm{el}}\}$$

(41)

2.2.8. Gaussian Quadrature

Equation (38) has polynomial degree $d=3$, so exact integration of some function f, dependent on a polynomial expression of $\mathit{\xi }$,

$${\int }_{{\mathcal{B}}_{\xi }}f\left(\mathit{\xi }\right)\mathrm{d}\Omega =\sum _{\mathrm{gp}=1}^{n_{\mathrm{gp}}}f\left({\mathit{\xi }}_{\mathrm{gp}}\right)w_{\mathrm{gp}}$$

(42)

by summation, is given if the number of Gauss points is $n_{\mathrm{gp}}=\frac{d+1}{2}=2$, at positions ${\xi }_{\mathrm{gp}}=\pm \frac{1}{\sqrt{3}}$ and weights $w_{\mathrm{gp}}=1$.

2.2.9. Newton–Raphson Method

The nodal displacement is found iteratively by using the Newton–Raphson method,

$${\underset{\overline{}}{\mathit{u}}}^{it+1}={\underset{\overline{}}{\mathit{u}}}^{it}-{\left[\mathit{K}\left({\underset{\overline{}}{\mathit{u}}}^{it}\right)\right]}^{-1}\mathit{R}\left({\underset{\overline{}}{\mathit{u}}}^{it}\right)={\underset{\overline{}}{\mathit{u}}}^{\mathrm{it}}+\Delta {\underset{\overline{}}{\mathit{u}}}^{\mathrm{it}}$$

(43)

where $it$ is the iteration number. To calculate the displacement update $\Delta {\underset{\overline{}}{\mathit{u}}}^{\mathrm{it}}$, we use a direct solver until $\frac{\parallel \Delta {\underset{\overline{}}{\mathit{u}}}^{\mathrm{it}}\parallel }{\parallel {\underset{\overline{}}{\mathit{u}}}^{\mathrm{it}}\parallel }<0.001$ as the termination condition.

2.2.10. Compliance

The compliance of the system is defined in accordance with the strain energy as

$$c=\frac{1}{2}{\underset{\overline{}}{\mathit{u}}}^T\mathit{K}\underset{\overline{}}{\mathit{u}}\in \mathbb{R}$$

(44)

with tangential stiffness $\mathit{K}$, from Equation (41). Sometimes compliance is defined without the factor $\frac{1}{2}$ [37]. In terms of an optimization problem, it relates a maximum stiffness demand by means of a minimum compliance.

2.3. Density Based Methods and Filtering Techniques

Although the term density, suggests that the method relies on a quantity extended in space, the density variable $x_i\forall i\in \{1,\dots ,n_{\mathrm{el}}\}$, is considered only at the element’s center of mass. It is conceived as an effective quantity during the FEM calculation. The SIMP and BESO methods are based on the formulation that the density interpolates Young’s modulus, see Equation (7). We first review the core idea of the SIMP method, then explain the filtering methods used in the optimization procedure, and show parallels with the BESO method.

2.3.1. SIMP Method

There are many different approaches to keep the binary system, consisting of material and void, from becoming singular in the stiffness tensor, by ascribing either a minimum density $x_{\min }$,

$$E_i\left(x_i\right)=x_i^p{E}_0{x}_i\in [x_{\min },1]\forall i\in \{1,\dots ,n_{\mathrm{el}}\}$$

(45)

or a minimum Young’s modulus $E_{\min }>0$, to the voids. Within the (modified) SIMP approach the Young’s modulus is given by a convex combination between the solid material ($E_0$) and the void material ($E_{\min }0$)

$$E_i\left(\tilde{x}\right)=E_{\min }(1-{\tilde{x}}_i^p)+{\tilde{x}}^p{E}_0{x}_i\in [0,1]\forall i\in \{1,\dots ,n_{\mathrm{el}}\}$$

(46)

which is a function of a (normalized) density $\tilde{x}$, with penalization power $p>1$. Here, it is important to distinguish between the (relative) element density x and the filtered (physical) density $\tilde{x}$, as described in the following.

2.3.2. Density Filter

According to [44], a basic linear filter density function is defined as

$${\tilde{x}}_i=\sum _j{w}_{ij}{x}_j\mathrm{e}.\mathrm{g}.,\mathrm{with}\mathrm{conical}\mathrm{weights}{w}_{ij}=\left\{\begin{array}{cc}\frac{r_{\min }-\mathrm{dist}(i,j)}{{\sum }_j{r}_{\min }-\mathrm{dist}(i,j)}\hfill & ,j\in {\mathcal{N}}_i\hfill \\ 0\hfill & j\notin {\mathcal{N}}_i\hfill \end{array}\right.$$

(47)

where the weights should fulfill the partition of unity, ${\sum }_j{w}_{ij}=1\forall i$, and $r_{\min }$ is an (user) input radius defining the neighborhood ${\mathcal{N}}_i=(j:\mathrm{dist}(i,j)\le r_{\min })$. In general, the weights influence the resulting structure, and since there is no overall optimum result, they are somehow arbitrary [45]. Other filter types could be defined by Gaussian weights [44], Heaviside filter, dilate and erode filter [46], or filter based on the geometric mean [45]. Nevertheless, what is known for sure, without filtering, the optimum result tends to become a scattered structure, often referred to as a checkerboard, with thin structural parts and/or many tiny holes [45].

2.3.3. Sensitivity Filter

A similar procedure to Equation (47) is applied to the sensitivities, which are the derivatives of the objective function, and reads

$$\widetilde{\frac{\partial c}{\partial x_i}}=\frac{1}{x_i}\sum _{j\in {\mathcal{N}}_i}\frac{\partial c}{\partial x_j}{w}_{ij}{x}_j\forall i\in \{1,\dots ,n_{\mathrm{el}}\}$$

(48)

which is strictly speaking not a density filter because no filtering is conducted regarding the density itself. The sensitivities are used together with the design domain, $\underset{\tilde{}}{\mathit{v}}={[v_1,\dots ,v_n]}^T$ and a prescribed volume limit $\overline{v}$, to solve the Karush–Kuhn–Tucker (KKT) condition, which leads to an optimality condition $B_i=1$, where

$$B_i=-\frac{\partial c\left(\tilde{\mathit{x}}\right)}{\partial x_i}{\left(l_i\frac{\partial v\left(\tilde{\mathit{x}}\right)}{\partial x_i}\right)}^{-1}$$

(49)

should be fulfilled. The value of the Lagrange multiplier $l_i$, satisfying the condition $\mathit{v}\left(\tilde{\mathit{x}}\left(x^{new}\left(l_i\right)\right)\right)$, is the only unknown, and is found by the bisection method. With this, the update reads

$$x_i^{\mathrm{new}}=\left\{\begin{array}{cc}max(0,x_i-m)\hfill & x_i{B}_i^{\eta }\le max(0,x_i-m)\hfill \\ min(1,x_i+m)\hfill & x_i{B}_i^{\eta }\ge min(1,x_i-m)\hfill \\ x_i{B}_i^{\eta }\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(50)

where m is a positive move-limit, and $\eta$ is a numerical damping coefficient.

2.3.4. BESO Method

The BESO method relies also on the penalty method of the Young’s modulus, but here, the sensitivity of the objective function is assigned with the total strain energy, ${\alpha }_i$, of the removed element,

$$\frac{\partial c}{\partial x_i}\approx \frac{\Delta c}{1}=-{\alpha }_i\mathrm{and}{\alpha }_i=\frac{1}{2}{\mathit{u}}_i^T{\mathit{f}}_i^{\mathrm{int}}$$

(51)

Then, the element sensitivity is given by the linear density filter (47), and reads

$${\tilde{\alpha }}_i=\frac{\sum w_{ij}{\alpha }_j}{\sum w_{ij}}$$

(52)

To improve the convergence, [32], the sensitivity at the current iteration step (it) is averaged with that from the previous step,

$${\tilde{\alpha }}_j^{\left(\mathrm{it}\right)}\leftarrow \frac{{\tilde{\alpha }}_j^{\left(\mathrm{it}\right)}+{\tilde{\alpha }}_j^{(\mathrm{it}-1)}}{2},\mathrm{it}>1$$

(53)

Introducing the two threshold constants, ${\alpha }_{\mathrm{del}}^{\mathrm{th}}$ for material removal and ${\alpha }_{\mathrm{add}}^{\mathrm{th}}$ for material addition, the update reads

$$x_i^{(\mathrm{it}+1)}=\left\{\begin{array}{cc}{x}_{\min }\hfill & {\alpha }_i\le {\alpha }_{\mathrm{del}}^{\mathrm{th}}\hfill \\ 1\hfill & {\alpha }_i>{\alpha }_{\mathrm{add}}^{\mathrm{th}}\hfill \\ x_i^{\left(\mathrm{it}\right)}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(54)

The threshold constants are found by the bisection method. Moreover, the target volume

$$v^{\left(\mathrm{it}\right)}=max\{\overline{v},(1-c_{\mathrm{er}}{v}^{(\mathrm{it}-1)})\}$$

(55)

where $c_{\mathrm{er}}$ is the evolutionary ratio determining the percentage of material to be removed. The evolutionary ratio is a number initialized in the previous iteration, and is zero when the target volume is reached. Then, only the topology alters.

2.4. Problem Formulation

Finally, the optimization problem to be solved reads

$$\begin{array}{cc}\hfill \mathrm{find}& \underset{\tilde{}}{\mathit{x}}={[x_1,x_2,...,x_{n_{\mathrm{el}}}]}^T \left(\mathrm{density}\right)\hfill \\ \hfill \mathrm{minimize}& c=\frac{1}{2}{\underset{\overline{}}{\mathit{u}}}^T\mathit{K}\underset{\overline{}}{\mathit{u}} \left(\mathrm{compliance}\right)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& v={\underset{\tilde{}}{\mathit{x}}}^T\underset{\tilde{}}{\mathit{v}}=\overline{v}\hspace{1em} \left(\mathrm{volume}\right)\hfill \\ \hfill & \mathit{R}\left(\underset{\overline{}}{\mathit{u}}\right)={\underset{\overline{}}{\mathit{f}}}_{\mathrm{int}}-{\underset{\overline{}}{\mathit{f}}}_{\mathrm{ext}}=\underset{\overline{}}{\mathbf{0}} \left(\mathrm{residuum}\right)\hfill \\ \hfill & {\displaystyle \mathit{K}\left(\underset{\overline{}}{\mathit{u}}\right)={\delta }_{\underset{\overline{}}{\mathit{u}}}\mathit{R}\left(\underset{\overline{}}{\mathit{u}}\right)(\mathrm{tangential}\mathrm{stiffness})}\hfill \\ \hfill & x_i\in \{x_{\min },1\}\hspace{1em}(\mathrm{density}\mathrm{range})\hfill \end{array}$$

where in the non-linear case, the displacement $\underset{\overline{}}{\mathit{u}}$ is found iteratively, by using the Newton–Raphson method. The tilde in the expression $\underset{\tilde{}}{•}$, indicates that a quantity • refers to the ordered elemental values. The optimum structure is found if a termination criterion is fulfilled, e.g., if a certain number of iterations is reached (failure) or the density/compliance difference is marginal between two iteration steps (success), as explained in the following.

2.4.1. Termination Criterion: Density Change

The first termination criterion is density-based, and states that an optimum structure is found if the change between the densities

$$\parallel {\underset{\tilde{}}{\mathit{x}}}^{\mathrm{new}}-\underset{\tilde{}}{\mathit{x}}{\parallel }_{\infty }\le ϵ$$

(56)

according to the $L_{\infty }$-norm is sufficiently small, $ϵ\approx 0.001$. With this at hand, the updated structure would not change in the next iteration step regarding the previous one.

2.4.2. Termination Criterion: Compliance Change

Another termination criterion is based on the change in compliance, defined as a moving average

$$\frac{|{\sum }_{i=(\mathrm{it}-9)}^{(\mathrm{it}-4)}{c}_i-{\sum }_{j=(\mathrm{it}-4)}^{\left(\mathrm{it}\right)}{c}_j|}{{\sum }_{j=(\mathrm{it}-4)}^{\left(\mathrm{it}\right)}{c}_j}\le ϵ\mathrm{it}>9$$

(57)

Here, the size of the moving window is somehow arbitrary, and found empirically.

2.5. Chemo-Mechanically Coupled Model

If the optimum structure is found, we need a chemo-mechanically coupled material model to test the particles’ performance. In [47], we formulated a multi-field model for charging and discharging of lithium-ion battery electrodes. Briefly sketched, the model is based on a multiplicative split of the deformation gradient

$$\mathit{F}={\mathit{F}}_e{\mathit{F}}_i\mathrm{where}{\mathit{F}}_i=J_i^{-2/3}\mathbf{1}$$

(58)

into an elastic (index e) and purely volumetric inelastic (index i) deformation. The inelastic part should depend on the lithium (Li) concentration $c_{\mathrm{Li}}$, and reads

$$J_i\approx 1+\overline{\Omega }(c_{\mathrm{Li}}-c_0)$$

(59)

where $\overline{\Omega }$ is a normalized partial molar volume and $c_0$ a reference concentration. With this at hand, the total free energy density of Equation (18) is now, besides the right Cauchy-Green tensor $\mathit{C}$, dependent on another field variable $c_{\mathrm{Li}}$,

$$\Psi ={\Psi }^{\mathrm{ela}}\left(\mathit{C}\right)+{\Psi }^{\mathrm{con}}\left(c_{\mathrm{Li}}\right)+{\Psi }^{\mathrm{int}}(\nabla c_{\mathrm{Li}})$$

(60)

where ${\Psi }^{\mathrm{ela}}\left(\mathit{C}\right)$ is the elastic strain energy, e.g., ${\Psi }^{\mathrm{ela}}\left(\mathit{C}\right)={\Psi }_{\mathit{E}}$ from (18) but now with concentration dependent elastic moduli, ${\Psi }^{\mathrm{con}}\left(c_{\mathrm{Li}}\right)$ is a double-well potential and ${\Psi }^{\mathrm{int}}(\nabla c_{\mathrm{Li}})$ accounts for interfacial reactions. Moreover, besides the quasi-static balance of linear momentum, the Cahn–Hilliard equation

$${\dot{c}}_{\mathrm{Li}}=\nabla ·(\mathcal{M}\nabla {\delta }_{c_{\mathrm{Li}}}\Psi )$$

(61)

is an extension of Fickean diffusion, i.e., accounts for the irreversible temporal evolution of the additional concentration field and follows from mass conservation; $\mathcal{M}$, is called a mobility tensor. The Cahn–Hilliard equation is a fourth-order partial differential equation and needs, in the sense of finite element analysis at least, continuous differentiable ansatz functions. Therefore, the obtained optimum structure should be re-meshed by using quadratic B-Splines, and we follow the technique as proposed in [48]. Re-meshing is needed to evaluate the optimum structure in a post-process only, and thus does not affect the mesh during optimization.

3. Results

Here, we first compare the results obtained from linear and non-linear optimization. Then, we elaborate on the force limit, where the results are comparable (within a 3% deviation). With this, we show the simulation results obtained from a single force load. In the next step, we generate structures that result from random force strengths, subject to different constraints on the net force. Finally, all structures’ (normalized) overlays give the most probable shape of a resistant structure to a random contact. This structure is subject to a periodic mechanical motion, and the induced chemo-mechanically coupled change in lithium concentration is studied.

3.1. Reference Parameter Definition

The optimization code listed in Appendix A, relies, according to [32], on the user input ($n_x,n_y,n_z,\overline{v},c_{\mathrm{er}},r_{\min }$) and some constants anchored inside the program (see

Table 1. Variables (top row), their designation inside the Matlab code (middle row), and their reference values (bottom row).

E	$\mathit{\nu }$	${\mathit{x}}_{\mathbf{min}}$	p	$\overline{\mathit{v}}$	${\mathit{r}}_{\mathbf{min}}$	${\mathit{c}}_{\mathbf{er}}$	${\mathit{F}}_0$	$\mathit{ϵ}$
E	nu	xmin	penal	volfrac	rmin	er	F0	tolx
1	0.3	$3\times {10}^{-5}$	1	0.5	1.5	0.02	${10}^{-9}$	${10}^{-4}$

). If there is no user input, the parameters from the calibration calculation from Section 3.2, are passed automatically. Moreover, the common linear density filter (47) is used in all numerical examples, but can be exchanged by the user if necessary.

3.2. Calibration

For the calibration of the optimization algorithm, we first check that the results obtained from the small strain BESO method are comparable with the small strain SIMP method, in terms of a binarized density at threshold $x_i=0.5\forall i\in \{1,\dots ,n_{\mathrm{el}}\}$. To this end, we choose the well-known cantilever beam, and set the number of elements to $(50,16,4)$, see Figure 4a. Next, we declare a desired volume of 50% and the normalized force strength to be ${10}^{-9}$. The convergence plot is shown in Figure 4b and is very similar to the 2D case reported in [32]. The resulting structure from the BESO method is used as input structure for the SIMP optimization calculation, with similar parameters, i.e., we adapted $E_0=1,p=3,r_{\min }=1.5,\overline{v}=0.5$, and adjusted $E_{\min }=3.1\times {10}^{-2}$ (see Equations (45) and (46)) and $\mathrm{tolx}=0.015$. Since there is almost no difference (two elements change) between the SIMP and the BESO solution at small force strengths, we declare this structure as a reference solution. Then, we increase the force strength and define a deviation D, by element-wise density comparison. Finally, we count only those elements (dark cubes) that do not match the reference solution (see Figure 4c), i.e., the higher D, the more the structure deviates from the reference solution. 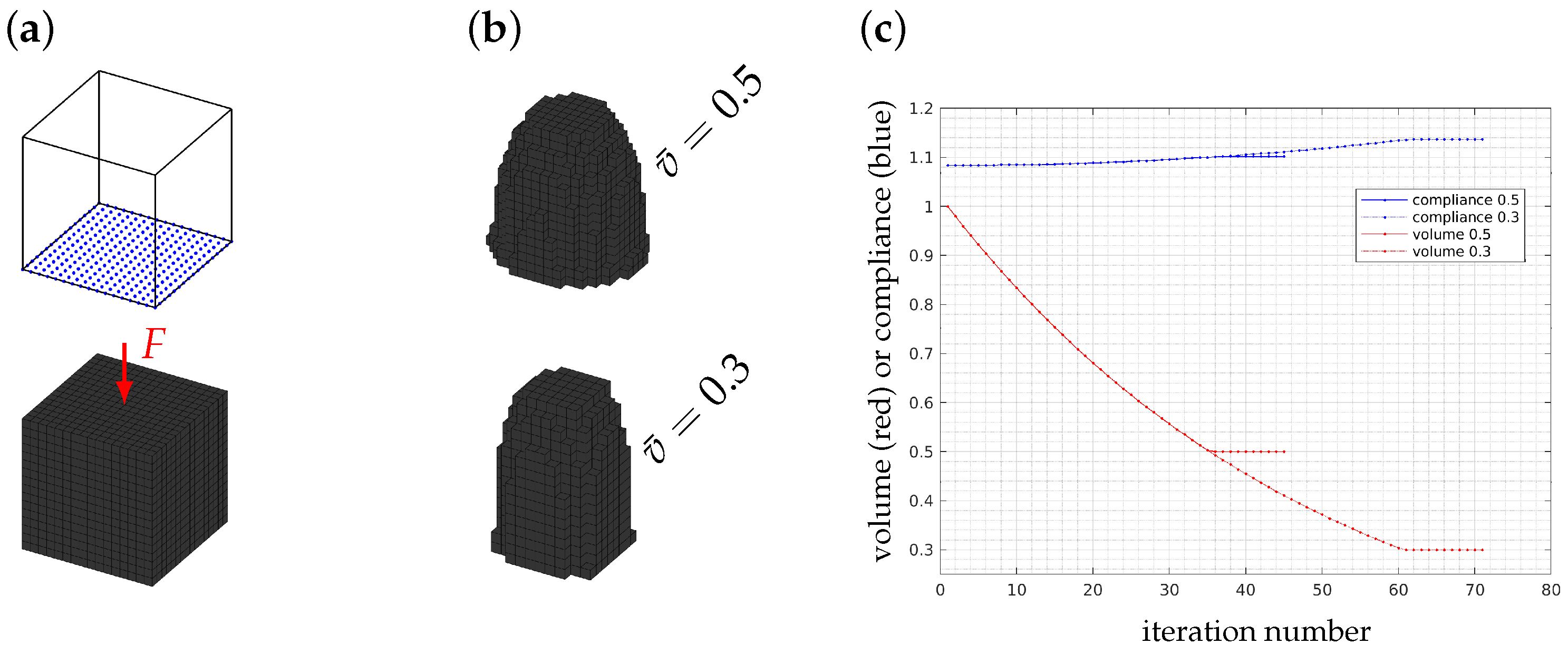As expected, the higher the force strength, the higher the deviation.

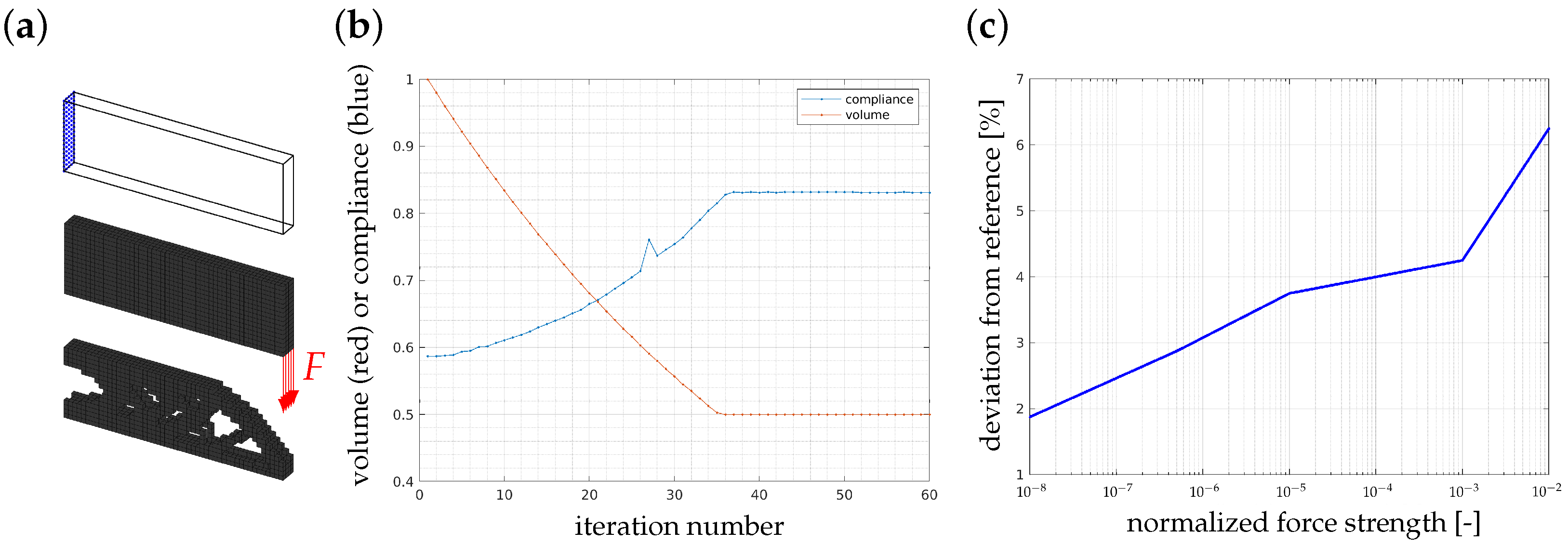
3.3. Central Single Force

Now, the reference geometry is given by a $(16,16,16)$ cube, which is subject to a fixture by Dirichlet boundary conditions on the bottom (see blue dots in Figure 5a), a single force acting on top of the surface, and a prescribed volume, of 30% and 50%, respectively. The optimization converges very fast (see Figure 5c) and leads to a conical structure (see Figure 5b), which is almost independent of the force strength applied. Conical structures have already been investigated experimentally in the context of Li-ion battery anodes, by [49], and numerically by [50]. Nevertheless, this kind of structure is resistant to one-sided loadings only, and therefore, we proceed with all-round random contact in the following.

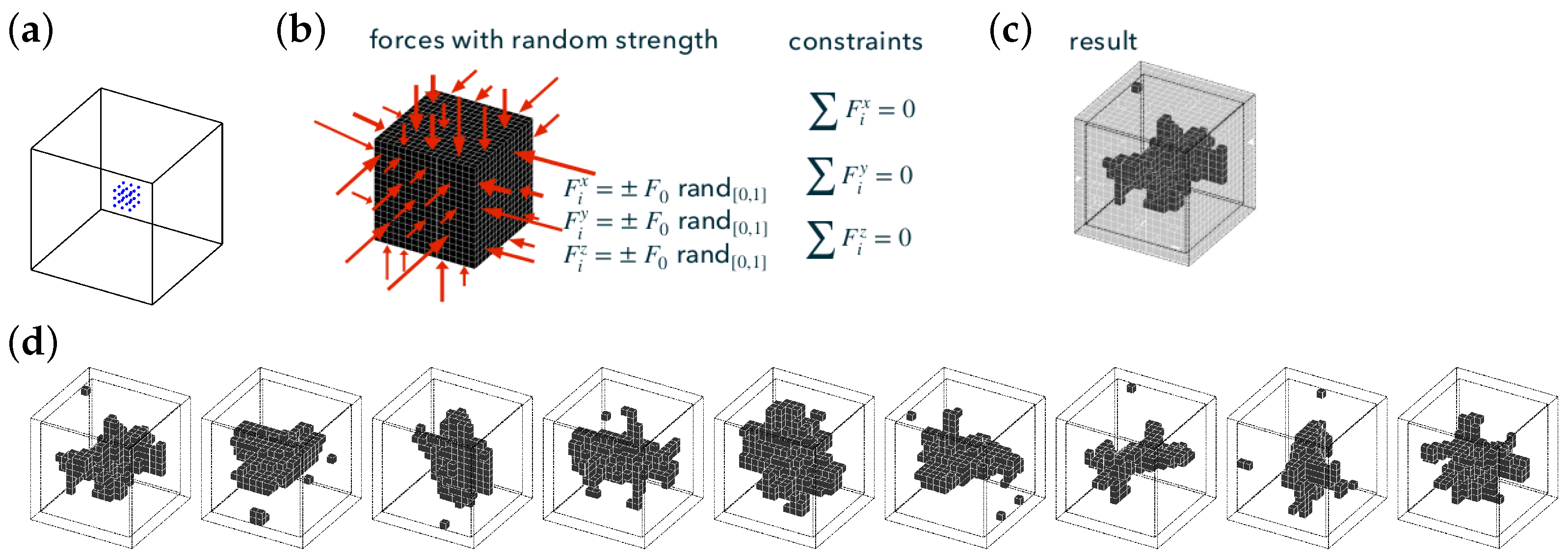
3.4. Forces with Random Strength and Zero Net Strength

Now, we consider again the $(16,16,16)$ cube, which is fixed at the center of mass (see blue dots in Figure 6a). We apply forces with random strength, but overall, they are constrained to zero net force (see Figure 6b). Doing so makes the resulting structures look arbitrary (see Figure 6c). The observed island phenomenon is likely due to the applied boundary conditions in the center of the geometry. Due to the randomness of the force strength, the optimum structures are not comparable if repeating the simulation. Especially in Figure 6d, we have omitted the structure’s walls, which were mostly filled with material. Therefore, we must consider a statistical interpretation of the internal structure, as explained in the following subsection.

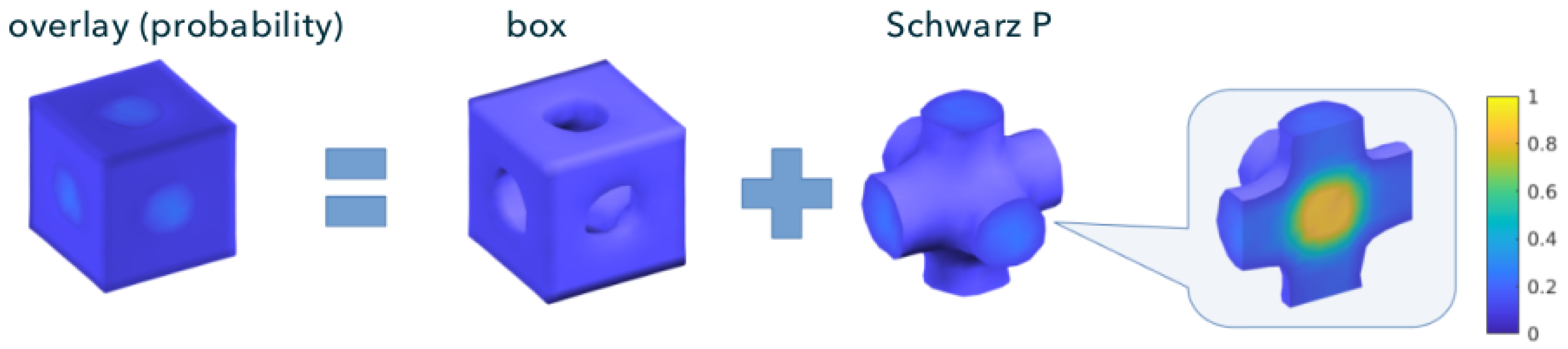
3.5. Probability Density

Since the underlying domain is always kept the same, we can define a probability

$$P_i=\frac{{\displaystyle \sum _{s=1}^{n_{\mathrm{sim}}}}{\left(x_i\right)}_s}{n_{\mathrm{sim}}}\forall i\in \{1,\dots ,n_{\mathrm{el}}\}$$

(62)

for each element, which indicates how often the optimized result in the specific domain is provided with material. The cube’s core has the highest probability that it must be filled with solid material, which decreases towards the cube’s corners. Instead of the prescribed volume $\overline{v}$, we can now consult the probability quantile as the superior optimization constraint, which we had to declare for the post-processing. Regarding the color distribution in Figure 7, the most likely structure is a ball (yellow region), very unlikely a fully filled cube (dark blue), and a Schwarz P minimum surface delimits the transition area to an intermediate structure. The Schwarz P surface itself can be described analytically by the function

$$cos\left(X_1\right)+cos\left(X_2\right)+cos\left(X_3\right)=0$$

(63)

In the following, we will mesh it as a solid and expose it to chemo-mechanical cycling.

3.6. Periodic Loading of Schwarz P Structure

The topology-optimized structure is now subjected to sinusoidal cyclic loading, and an initial value problem is solved using the chemo-mechanically coupled model. In Figure 8, the concentration distribution is shown, where the concentration is pushed outward in a compressive motion and vice versa. Since the constitutive law follows the thermodynamics of irreversible processes, it can be seen that after the first mechanical cycle, the concentration distribution does not return to the uniformly distributed original state, but an induced pattern persists.

3.7. Forces with Random Strength and Non-Zero Net Strength

Previously we assumed the constraint of a vanishing total force. Now, a net force on the object is prescribed, and then, the optimum topology changes to an eighth of a bee-shaped structure, with spikes in the diagonal corners, see Figure 9.

4. Discussion

The core question of this paper, was related to the optimal geometry of a silicon anode exposed to a random contact. It is known that silicon anodes swell to multiples of their original volume. Thus, depending on the charging behavior, the interaction between the particles is somewhat random, regarding the force strength and the local position of the occurrence. We have developed and provided a compact Matlab code to address the question of an optimal geometry that is as resistant as possible to this type of force action. The code is based on the two papers by [32,37]. The published code of the first reference is known for its particular simplicity of implementation of boundary conditions, and the second reference for its fast convergence rate, whereas the latter code had been published only in 2D. In addition, all studies we have performed using the new code, provide symmetric structures under symmetric loading, which is infrequent in the literature. Then, we subjected a cube to random loading but obtained structures challenging to interpret. However, we considered the normalized overlap as the probability density when overlapping the structures resulting from many simulations. As a result, we obtained the symmetric Schwarz P structure at a specific threshold, which has a minimum surface property. Such results sound promising in the context of electrodes, where structures with minimum surface area are desired. Furthermore, this method also yields what one would intuitively expect, e.g., a structure concentrated along the diagonal in the case of diagonal loading. Finally, the material model is chosen, so that it can be extended in the future by a crack density field, for a crack propagation study.

5. Conclusions

Here, we elaborated on large, geometrically non-linear deformations of battery anodes, intending to find an optimum (maximum stiff) electrode design when subject to random contact, in terms of random forces. The optimization technique relies on the BESO method, where the solution procedure includes non-linear finite element analysis, specific sensitivity filtering, and an improved weighting of the historical information, to ensure fast convergence. The existing 2D Matlab code reported in [32] was extended here to 3D, attached in the appendix, and applied to several design problems. Even at moderate volume fractions, the resulting topologies are hard to compare with each other. Thus, in such cases, the optimum structures are found by performing multiple simulations and interpreting their (normalized) overlap as a probability density.